1. Introduction
African savannas provide many ecosystem services to human societies [
1]. Their high primary production support livestock herding and smallholder farming [
2], while large mammal populations contribute to large-scale nutrient flows and tourism [
3,
4,
5]. The dynamic nature of such systems has been widely acknowledged, with water availability being the primary driver of vegetation [
1,
6] (and thus of wildlife, [
7]), but also of tourism [
8], pastoralism, and rain-fed agriculture. On the other hand, human activities locally retroact on wildlife and vegetation [
9,
10]. These feedbacks between social-ecological components thus call for integrated ecosystem management. However, a sound management strategy requires efficient forecasting methods for assessing the possible consequences of changes in environmental conditions. Here, we introduce an innovative modeling framework for assessing the effect of water availability and herbivores diversity on vegetation and socio-economic dynamics of an East African savanna.
Dynamic models are key for predicting the consequences of changes in drivers, such as changes in rainfall regime [
11] or the increase in herbivore populations [
12,
13]. So far, many savanna models consider a few variables (e.g., [
14]) and may thus overlook some possible outcomes of such changes on complex interaction networks. In addition, most models are quantitative and thus require precise quantitative data that are often unavailable or highly costly to obtain [
15,
16,
17]. This feature makes difficult for most dynamic models to take qualitative expert knowledge [
18] or historical anecdotes [
19] into account. Yet, a deep and abundant qualitative knowledge about social-ecological systems can be obtained from local people such as pastoral communities, land managers, and farmers [
20].
In contrast, qualitative modeling such as state-and-transition models [
21], loop analysis [
22], qualitative reasoning [
23], Boolean Networks [
24,
25], or timed automata [
26] enable using expert-knowledge and require few or no quantitative information for model conception. They have proven useful for assessing the effect of press perturbations on whole interaction networks [
27], providing recommendations for rangeland management [
28], modeling cerrado dynamics [
29,
30], or modeling the dynamics of fish communities in response to fisheries management [
26]. Qualitative modeling enables building models when numerical data are not available [
22,
31,
32] while assuring more general predictions (sensu [
33]) due to comparable quantitative models. Indeed, where a quantitative model would require precise parameter values to make predictions, a qualitative model with comparable variables, internal relations, and objectives will require less information for providing the same qualitative predictions [
23]. This in turn makes its qualitative predictions more (or totally) independent of parameter values, and thus keeps them valid when parameters change over time or between locations [
34]. Its lower reliance on quantitative data also facilitates the integration of multiple and heterogeneous components and relations from various knowledge sources [
35,
36,
37]. Moreover, quantitative predictions are not always required. For instance, if one simply wants to determine whether it is possible that a given ecosystem reaches a particular state (e.g., a more biodiverse or socially desirable state) [
38], then qualitative predictions can be sufficient, which does not preclude including quantitative aspects in further analyses. A qualitative perspective is also a convenient way to study long-term dynamics by averaging short-term quantitative variations [
25]. It also generally facilitates the representation of system structure and dynamics, as exemplified by state-and-transition models which represent reversible and irreversible vegetation changes as intuitive box-and-arrow diagrams [
28], or rule-based models generating complex dynamics from simple “if-then” rules [
30]. This facilitating role is especially useful for decision-makers which may seek robust and easily interpretable results for designing management actions.
However, most qualitative modeling frameworks are constrained by several assumptions or methodological limitations [
39]. Limitations, for instance, include (depending on the chosen method) determinism, assumptions about parameters values, and the form of interactions, the inability to make predictions of unobserved system states, or the tendency to produce ambiguous (undeterminate) predictions [
39]. These limitations thus call for an innovative modeling framework.
Discrete-event models [
40] have shown their ability to provide understanding and recommendations for ecosystem management [
26,
41]. These models represent system components as discrete (and often Boolean) variables while dynamics (called transitions) are defined by logical functions or “if-then” rules. Their initial and most successful applications can be found in systems biology, where they are used to model cell differentiation [
42] or response to cancer treatments [
43]. In ecology, they have been used to model the assembly of plant-pollinator networks [
44], their response to extinctions [
45], and their invasibility [
46], but also spatialized predator-prey dynamics [
47] and ecosystem services assessment [
48,
49]. Importantly, they are able to qualitatively grasp key features of ecosystem behavior, such as the bistable behavior of budworm-forest dynamics [
24] or bush encroachment in some Ethiopian savannas [
50], without requiring precise parameterization. In addition, like most qualitative models, they provide a graphical and intuitive representation of social-ecological dynamics (e.g., [
24]), thus improving communication of complex phenomena towards the non-scientific public such as stakeholders and students [
51]. Finally, their co-evolution with computer science contributed to the development of efficient analysis techniques such as model-checking [
52], which could be highly relevant for social-ecological applications [
50].
In this study, we introduce the Ecological Discrete-Event Network (EDEN) modeling framework [
53] for modeling the social-ecological dynamics of an East-African savanna. The EDEN framework relies on a qualitative discrete-event formalism deriving savanna dynamics from “if-then” rules that represent social-ecological events (e.g., species extinctions, rainfall occurrences, or livestock herds migrations). System dynamics are represented intuitively as a state-transition graph, which shares the same structure as the aforementioned state-and-transition models used for rangeland management [
28]. In contrast with existing rule-based models of vegetation dynamics [
54], an EDEN model computes all possible trajectories and can thus account for rare events and their far-reaching effects [
55].
Based on field surveys in northern Tanzania, on expert knowledge (from Istituto Oikos, Nelson Mandela African Institution of Science and Technology) and on scientific literature (e.g., [
56,
57,
58]), we built a qualitative model to study changes in vegetation and socio-economic dynamics in response to persistent changes in environmental conditions, namely surface water availability and herbivore diversity. More specifically, we aimed to answer three research questions, namely: (Q1) Did these changes in environmental conditions induce irreversible ecosystem transitions?; did they modify the set of existing (Q2) vegetation types and transitions and (Q3) socio-economic profiles and transitions, and why (i.e., which rules drove these vegetation and socio-economic changes)? Although vegetation dynamics are influenced by spatial structure [
59], the model presented here is spatially implicit, assuming that it still enables to test the following hypotheses.
We tested the following hypotheses: (Hypothesis 1) Permanently changing environmental conditions will induce an irreversible change (i.e., impossibility to reach back the initial savanna state); (Hypothesis 2) as water availability is known to modulate woody plant recruitment [
60], low (resp. high) water availability is expected to induce (resp. prevent) drought-related tree mortality (i.e., woodland-savanna, savanna-grassland, and woodland/savanna-bare soil). In addition, water scarcity is also expected to affect herbivores [
61], including livestock and thus pastoralism. Finally, (Hypothesis 3) reducing herbivores diversity (either directly or through water deprivation) is expected to modify vegetation transitions, but also tourism, which would be deprived of attraction (i.e., socio-economic transitions). After presenting the study site and data collection, we introduce the EDEN framework (i.e., the formalism and analysis tools) and the savanna model in more details. Results show that water availability directly and indirectly influences vegetation and socio-economic transitions, with herbivores often mediating this influence. Then we discuss the realism of such predictions and their policy implications.
4. Discussion
In this paper, we applied the Ecological Discrete-Event Network (EDEN) modeling framework to an east-African savanna ecosystem. We aimed to understand and explain how vegetation and socio-economic transitions are affected by changes in water availability and herbivores diversity. Model conception was based on (i) direct field observations from two northern-Tanzanian savannas, (ii) expert knowledge, and (iii) literature about savannas across Africa [
5,
75,
76,
77,
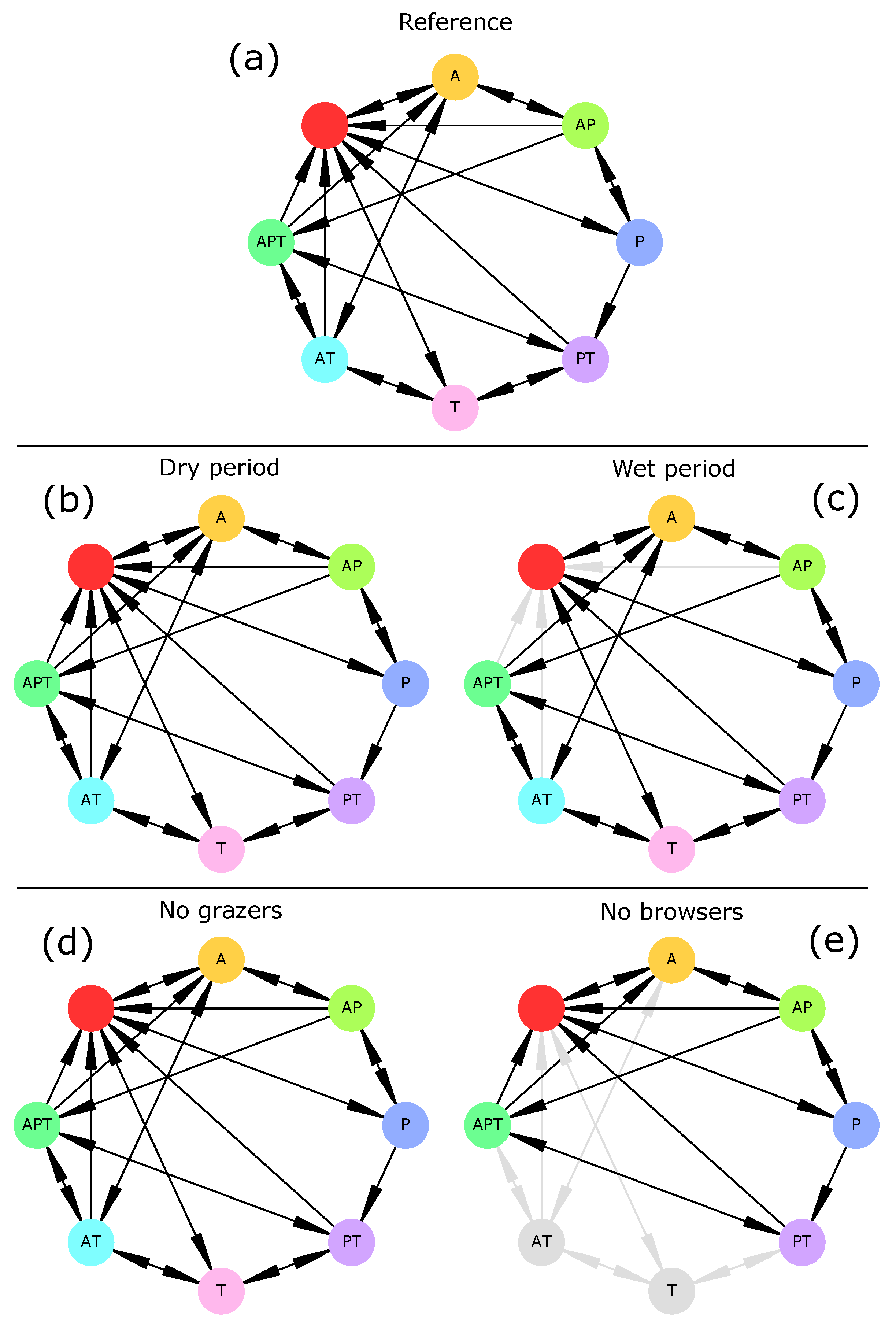
78]. For each of the five scenarios, the model computed State-Transition Graphs (STGs) representing all possible ecosystem trajectories given its predefined “if-then” rules. These STGs were then summarized to focus on vegetation and socio-economic aspects of the dynamics.
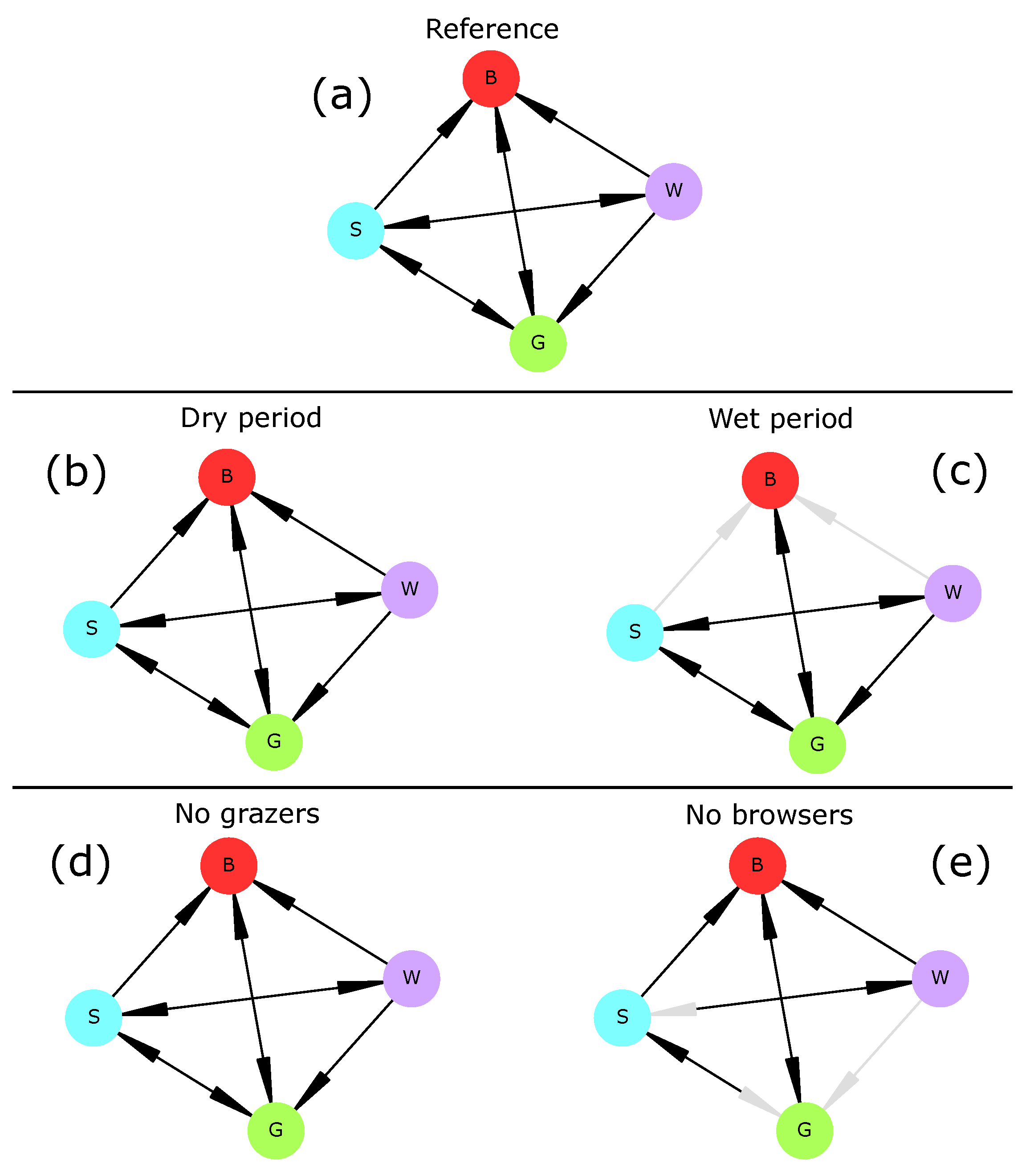
The reversibility of the STGs in all scenarios except the “dry period” suggests that the ecosystem is able to recover its initial state under most permanent changes. Only the “dry period” scenario displayed irreversible dynamics as the initial vegetation type (i.e., tree-grass coexistence) and socio-economic profile (a mix of agriculture, pastoralism, and tourism) could not be maintained. This invalidates hypothesis H1 which stated that any permanent change of the reference scenario would induce an irreversible ecosystem change.
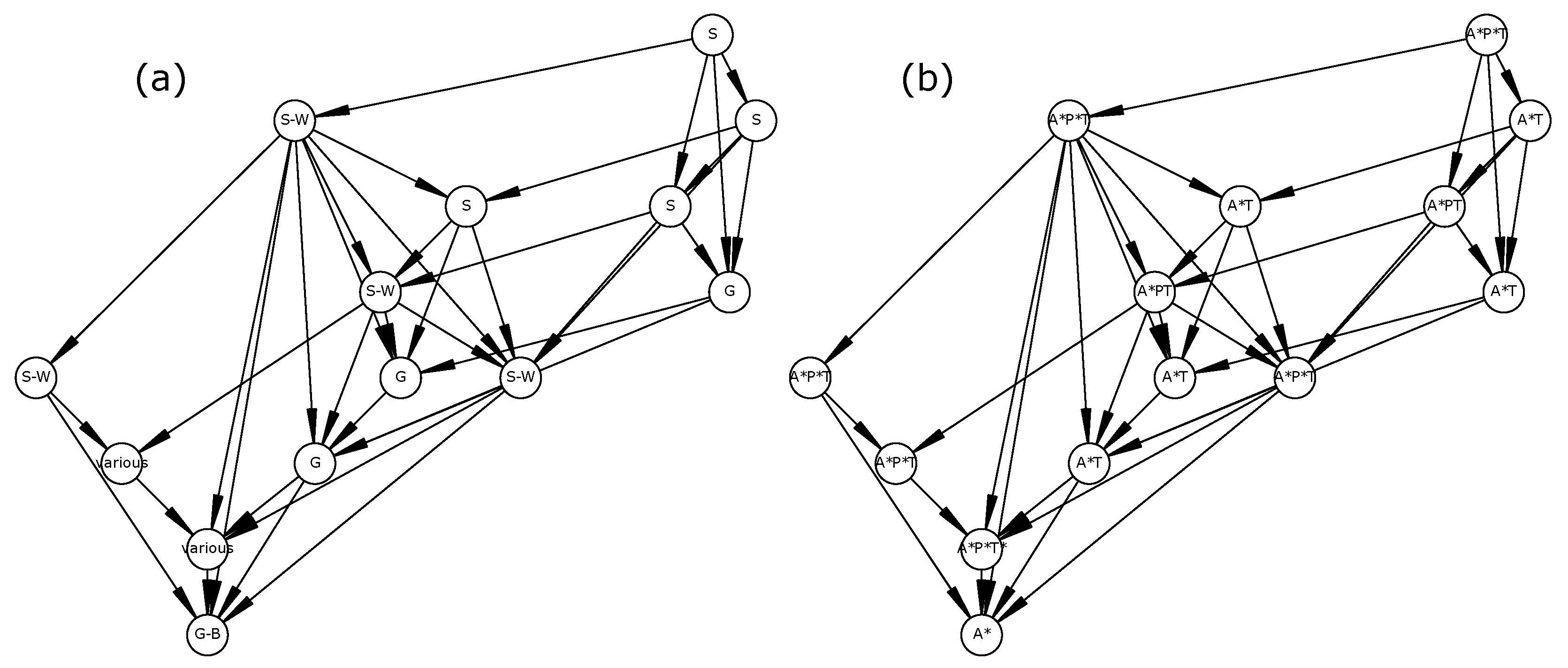
This result points to a need to clearly define reversibility and should be cautiously interpreted for at least two reasons. First, a reversible STG is defined by the existence of
at least one path from any reachable state towards the initial state, which does not preclude the existence of
potentially infinite trajectories (i.e., SCCs) inside it. For instance, in
Figure 1a, the ecosystem may remain inside the SCC (an infinite trajectory) without never reaching the attractor. Therefore, STG reversibility should not be equated with resilience [
79], but rather to a potential resilience. Second, our model is possibilistic and may thus include highly unlikely transitions. Therefore, using such models for management recommendations may require assessing the sensitivity of STG reversibility to rare events.
4.1. Vegetation Dynamics
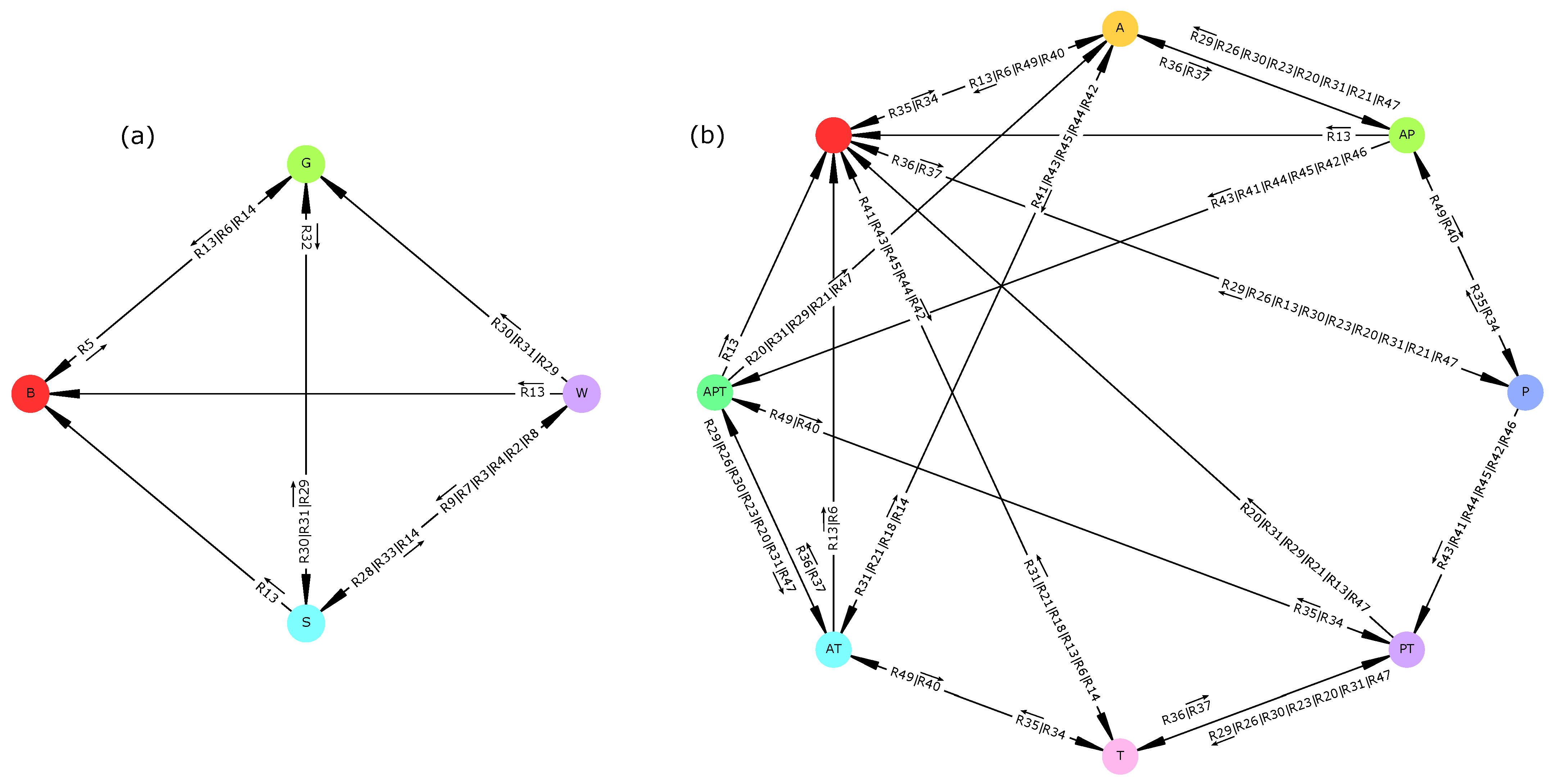
Vegetation transitions are a major issue for rangeland ecology as current increase in woody cover (i.e., generally composed of unpalatable plant species) threatens socio-economic activities such as pastoralism and especially cattle production [
80]. Based on two plant types (grasses and trees), we defined four vegetation types, namely bare soil, grassland, savanna, and woodland.
In the reference scenario, all transitions establishing one plant type at a time were realized and all vegetation types were able to shift to bare soil. Predicted transitions were realistic as most have already been reported or hypothesized [
60,
81].
When subjected to a persistent lack of surface water (“dry period” scenario), the savanna vegetation (i.e., the initial vegetation type) underwent an irreversible shift towards a seasonal grassland in which woody plants could not establish (
Figure A4). This transition was mediated by groundwater reserves, which requires the infiltration of surface water for being recharged (rule R11). The drying up of groundwater then affects woody plants which are assumed to rely on this resource (R32). Such drought-induced transitions have long been suggested [
60,
82]. Conversely, when water was non-limiting (“wet period” scenario), drought-induced transitions were not possible anymore, and thus transitions from savanna or woodland to bare soil were impossible. These two results do not invalidate hypothesis H2 and confirm the role of water availability in vegetation dynamics.
When herbivory was removed from the ecosystem (“no grazers” and “no browsers” scenarios), drought preserved most vegetation transitions. This was especially true for grazers whose extinction had no effect on vegetation transitions (
Figure 2). This was not in agreement with current knowledge as grazing is known to favor trees over grasses [
83]. Indeed, the only rule relating grazing mammals (here, livestock) and grasses was R14, i.e., overgrazing. This rule could be rewritten to better represent the effect of livestock (and grazing mammals in general) on the increase in woody cover. On the other hand, browsers were necessary to three transitions (Woodland→Grassland, Woodland→Savanna, and Savanna→Grassland) as those disappeared when browsers were removed from the system. Therefore, hypothesis H3 is invalidated and should be reassessed after model adjustments.
These results highlight the role of surface water (indirectly, through the watering of herbivores) and groundwater (directly, through its use by woody plants) as drivers of vegetation change [
60,
82,
84,
85,
86]. Browsers contributed to a reduction in woody cover, which confirms current knowledge [
87,
88]. These general results support management recommendations about the preservation of wild herbivores for managing vegetation [
81].
Fire and soil nutrients, which are not considered here, are well-known drivers of vegetation dynamics [
82] and could easily be included in later model versions. The vegetation part of the model can be improved by adding more components to it (e.g., shrubs, bushes, or different life stages for trees) or accounting for other plant-water-herbivore interactions. Such an improvement could involve experts from this domain and/or new field surveys. Besides, vegetation summary graphs (
Figure 2) share many similarities with State-and-Transition Models [
21] which have been extensively used to represent rangeland or savanna dynamics [
28,
81].
4.2. Socio-Economic Dynamics
Socio-economic transitions describe the loss and development of new economic activities. Here, we focused on three activities, namely agriculture, pastoralism, and tourism, which substantially contribute to east-African economies. However, agriculture and pastoralism are affected by changes in rainfall frequency and intensity [
89,
90]. In our model, on one hand, water scarcity (“dry period scenario”) and subsequent lack of forage constrained livestock production and pushed the system into a regime of purely rainfed agriculture (
Figure A4). For the same reasons, wildlife populations declined, thus making tourism disappear. This latter prediction corroborates other findings [
91]. On the other hand, increasing water availability (“wet period” scenario) did not prevent any socio-economic profile (
Figure 4). Rather, drought-induced transitions (here, general disruption of all socio-economic activities) disappeared. These results thus do not invalidate hypothesis H2.
The extinction of grazers and browsers had contrasting effects. The absence of grazers neither modified the set of reachable socio-economic profiles nor transitions compared to the reference scenario. On the contrary, the absence of browsers made tourism necessarily associated to pastoralism. We insist on the fact that this does not mean that they depended on each other. This is due to the fact that (1) cattle necessarily enter the system simultaneously to wild grazers when forage and water are available in the rainy season and (2) that cattle either leave the system simultaneously (through the lack of forage (C6), water scarcity (C9, C10), or diseases (R48)), or after (through cattle predation by carnivores (R19)) wild grazers. As in this scenario carnivores only rely on cattle and wild grazers (browsers are absent), once these preys have gone extinct, carnivores quickly go extinct, which deprives tourism of attraction. Herbivores diversity (species richness, abundance, and phylogenetic diversity) has been showed to be positively related to the number of tourists [
92]. Although this relationship is likely to be driven by the interest for biodiversity
per se, our results also suggest that herbivores diversity may play a role in maintaining tourism by sustaining predator populations. As for vegetation transitions, hypothesis H3 is partly invalidated as grazers did not affect socio-economic transitions, while browsers absence affected the dynamics.
Our results point to a link between herbivores diversity and socio-economic changes. Although this relationship may be explored in more detail (through another model), our model already suggest mechanisms relating these two aspects of the social-ecological system. This highlights the need, at least in some specific systems, to consider ecological and anthropogenic aspect integratively for designing management interventions.
4.3. From Predictions to Policy Implications
Although our model makes predictions, it is unable to provide management recommendations at this stage. What would be required for doing so? The first requirement is to find a clear agreement between predicted and observed dynamics for at least one specific location. Here, the agreement between predictions and data is partial (albeit groundwater availability and browsers indeed play a role in vegetation dynamics) and is not sufficient for providing recommendations. Second, even though predictions would be confirmed, management recommendations must benefit stakeholders (e.g., farmers, pastoralists, tourists, or wildlife managers) and thus, must be discussed before being proposed. This is not the case here as the aim of this study is mostly methodological and only involve stakeholders during model conception. Such discussions could however be pursued in the future. This is not an exhaustive list of the requirements for providing management recommendations from model predictions.
Nonetheless, this study provides some tools that may draw the attention of managers to EDEN models. For instance, the summary graphs presented share many similarities with State-and-Transition Models used for rangeland management and national parks [
28,
93]. The EDEN framework complements these empirical (i.e., non-formal) models by providing a mechanistic basis to ecosystem transitions and many tools to analyze them.
4.4. How to Cope with Model Structure Uncertainty
Generally, the presence or absence of specific variables and relations (i.e., model structure) is not certain and several model structures could correspond to available knowledge or observations. Such uncertainty could result from spatial heterogeneity [
94] or temporal changes of interaction networks. Alternative model structures often lead to contrasting dynamics [
95,
96] and choosing the right one(s) is challenging. In this study, we considered a single model structure to which we applied four press perturbations manipulating the value of specific variables. However, rules are not equally well supported (
Table A2). Instead of testing all possible alternative model structures (which would generate many ecologically meaningless models), we could use uncertain rules to generate alternative model structures. For instance, we assumed that cattle was able to exclude wild grazers (R22), while the reverse was assumed impossible. One way to assess the role of such uncertain rules (
r) would be to exclude them in all possible combinations (
) and verify a list of specific dynamical properties (e.g., vegetation transitions) for each of the
corresponding STGs. The same method could be applied to rules definitions. For instance, rule R47 assumes that wild (
Bw) and domestic (
Go) browsers should co-occur to enable epidemics to emerge. However, in areas where browsers are now extinct, livestock are still subject to diseases [
97]. Therefore, we could split this rule as
R47a: Bw+, Rf+, Sw+ >> Bw-, Go-, and
R47b: Go+, Rf+, Sw+ >> Bw-, Go-. These two rules can also be considered more parsimonious as goats and browsers can be subject to diseases independently of one another. Note that rules R47a and R47b are both general cases of R47 (their conditions include that of R47). Besides, automatically assessing dynamical properties of hundreds or thousands alternative models requires powerful and rigorous analysis tools. For that purpose, the visual analysis of summary graphs would be unworkable and should be replaced by model-checking techniques [
50].
4.5. The Scope and Verification of EDEN Models
This study showed how the EDEN modeling framework can make use of qualitative information, which is often the most abundant (and sometimes the only) knowledge source. Despite its qualitative nature, it can be used to derive predictions and explanations about specific social-ecological issues.
Here, questions were related to (1) the reachability of specific states from the initial state (e.g., “is woodland reachable from initial state under dry conditions?”) and (2) the existence of some transitions under various environmental conditions (e.g., “is the woodland-grassland transition possible under wet conditions?”). Such questions, or propositions, can be verified or refuted (e.g., “this state is not reachable” or “this transitions is impossible”). In addition, results can be “causally” explained, as studying model rules enables to identify which rule sequences (ecological events) are disrupted or forced by changes in environmental conditions. This form of event-based explanations may thus be promising for providing a coarse-grained mechanistic understanding of ecosystem trajectories. However, this by-hand explanation (by the visual examination of rules) is prone to errors and may require automated tools to be made more rigorous. Beside the comparison of model trajectories with observations, validation/refutation can be extended to the driving events behind them (approximated by model rules), i.e., assessing whether predicted trajectories are consistent with observed states and events. Model verification can also be improved by the use of model-checking techniques [
52] which enable the automatic exploration of large ecological State-Transition Graphs [
50]. Experts and managers may play a key role in this validation/refutation process and help designing and improving models, especially through State-and-Transition Models [
21]. In return, researchers can provide modeling tools to derive predictions from this abundant expert knowledge. Ultimately, this interaction between ecosystem management and modeling may be used to improve management interventions.
5. Conclusions
In this study, we proposed the EDEN modeling framework as a tool for computing trajectories of an ecosystem from a qualitative knowledge base in the form of “if-then” rules. This qualitative and possibilistic model aims to predict and explain ecosystem trajectories by the interplay between multiple socio-economic and ecological events.
Here, we chose to apply this framework for modeling the socio-economic and ecological aspects of an east African savanna. We focused on vegetation and socio-economic transitions and showed that a reduction in surface water may lead to a disruption of socio-economic activities and biodiversity which is mediated by groundwater reserves and herbivores. Removing grazers or browsers herbivores had contrasting effects and highlighted the potential role of drought in controlling woody cover by itself.
The EDEN framework is qualitative, which means that it cannot provide precise (i.e., quantitative) predictions. In addition, the model is non-deterministic and non-probabilistic, which implies that its predictions cannot be assigned a probability. However, these two “limitations” have an interesting counterpart: The model does not require quantitative data about parameters describing observed phenomena, and its predictions are robust to changes in parameters or to uncertain measurements. Therefore, they are more general, more parsimonious, albeit less precise and certain. Although rules may be more descriptive than explanatory (e.g., rules driving seasonality), they correspond to observed phenomena, can be easily explained and thus enable the use of expert-knowledge.
This study is a first step and the EDEN framework is still evolving. It has the potential to bridge, on one hand, expert knowledge, e.g., derived from rangeland managers who design State-and-Transition Models, and, on the other hand, modeling through an intuitive event-based approach. Such models could find applications in agroecology to assess the long-term impacts of management actions on biodiversity and livelihoods.