Exploring the Sensitivity of Recurrent Neural Network Models for Forecasting Land Cover Change
Abstract
1. Introduction
2. Theoretical Background and Geospatial Applications of RNNs
3. Materials and Methods
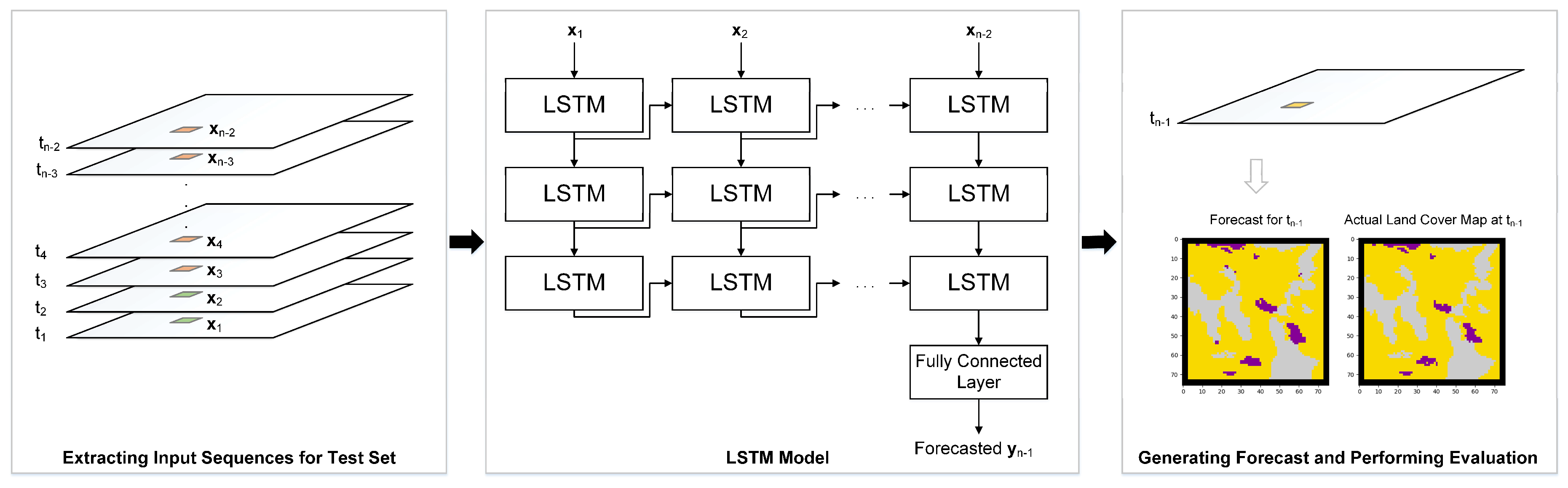
3.1. RNN Model Development
3.1.1. Modeling Scenarios
3.2. Sensitivity Analysis
4. Geospatial Datasets and Pre-Processing
4.1. Hypothetical Data
4.2. Real-World Data
4.3. Creating the Training and Test Sets
5. Results
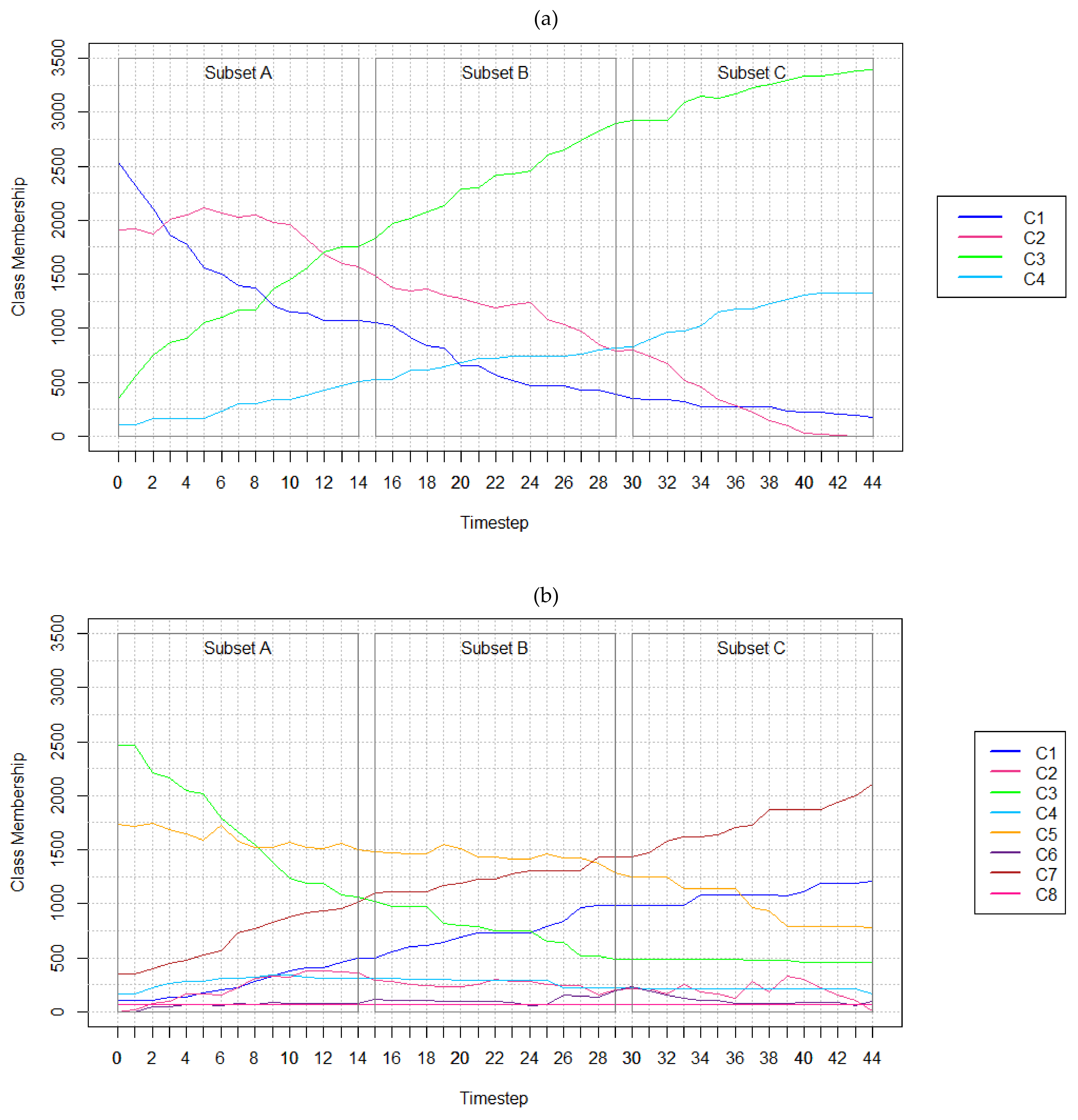
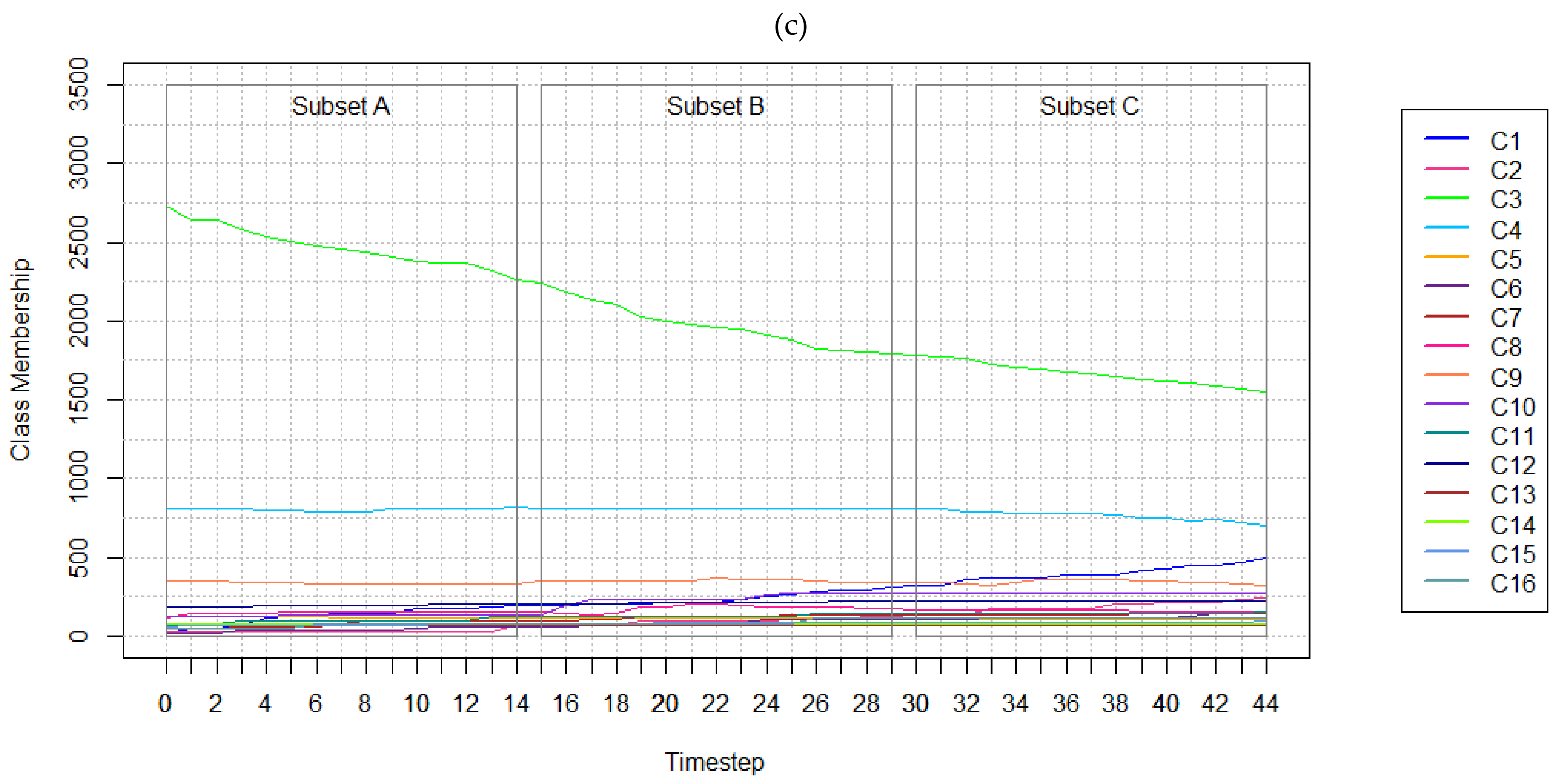
5.1. Results of Experiments with Hypothetical Data
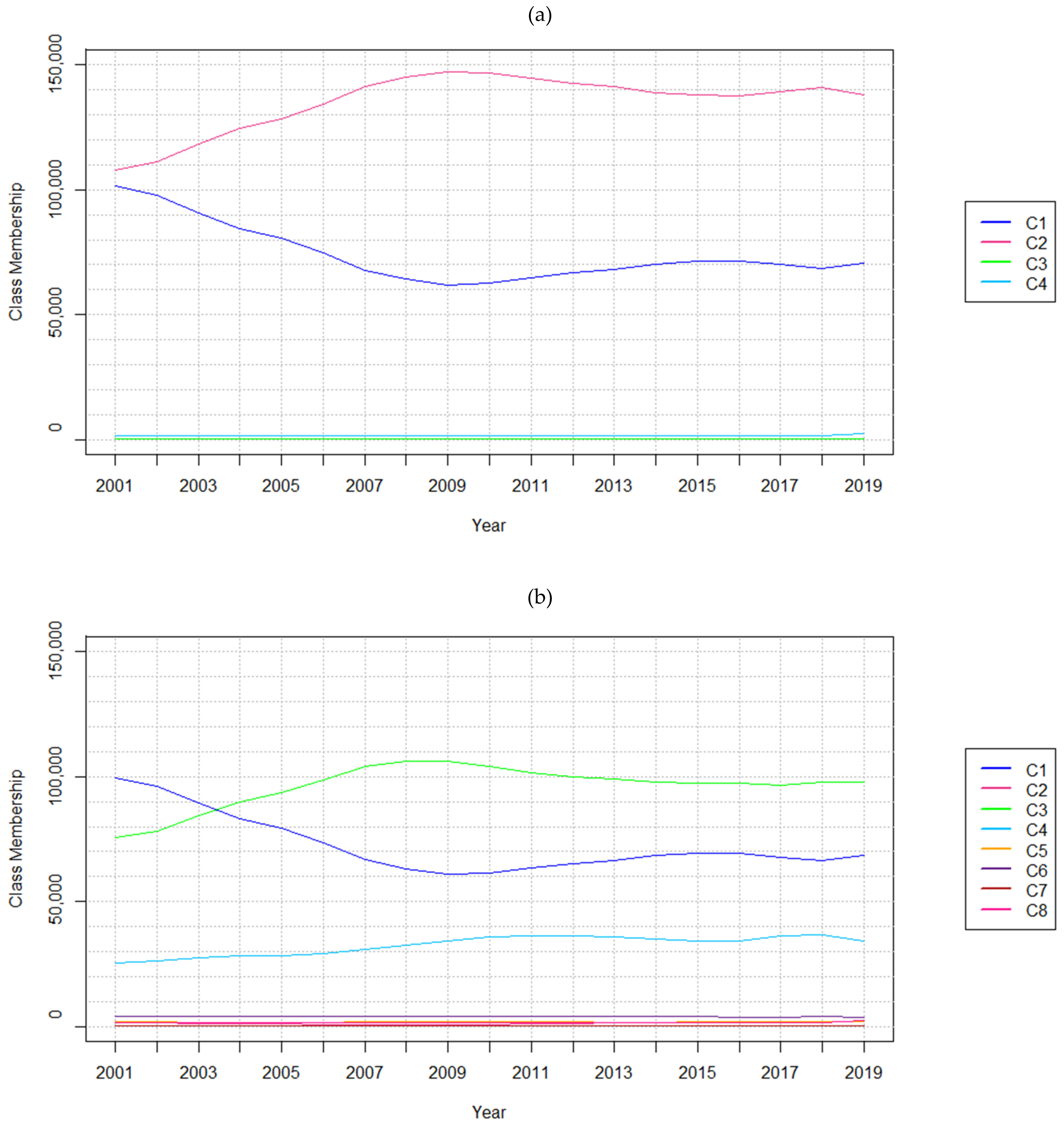
5.2. Results of Experiments with Real-world Data
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Meyer, W.B.; Turner, B. Land-use/land-cover change: Challenges for geographers. Geojournal 1996, 39, 237–240. [Google Scholar] [CrossRef]
- Friedl, M.A.; McIver, D.K.; Baccini, A.; Gao, F.; Schaaf, C.; Hodges, J.C.F.; Zhang, X.Y.; Muchoney, D.; Strahler, A.H.; Woodcock, C.E.; et al. Global land cover mapping from MODIS: Algorithms and early results. Remote Sens. Environ. 2002, 83, 287–302. [Google Scholar] [CrossRef]
- Findell, K.L.; Berg, A.; Gentine, P.; Krasting, J.P.; Lintner, B.R.; Malyshev, S.; Shevliakova, E. The impact of anthropogenic land use and land cover change on regional climate extremes. Nat. Commun. 2017, 8, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Turner, B.L., II; Lambin, E.F.; Reenberg, A. The emergence of land change science for global environmental change and sustainability. Proc. Natl. Acad. Sci. USA 2007, 104, 20666–20671. [Google Scholar] [CrossRef]
- Mayfield, H.; Smith, C.; Gallagher, M.; Hockings, M. Use of freely available datasets and machine learning methods in predicting deforestation. Environ. Model. Softw. 2017, 87, 17–28. [Google Scholar] [CrossRef]
- Novo-Fernández, A.; Franks, S.; Wehenkel, C.; López-Serrano, P.M.; Molinier, M.; López-Sánchez, C.A. Landsat time series analysis for temperate forest cover change detection in the Sierra Madre Occidental, Durango, Mexico. Int. J. Appl. Earth Obs. Geoinf. 2018, 73, 230–244. [Google Scholar] [CrossRef]
- Zadbagher, E.; Becek, K.; Berberoglu, S. Modeling land use/land cover change using remote sensing and geographic information systems: Case study of the Seyhan Basin, Turkey. Environ. Monit. Assess. 2018, 190, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Rahman, M.T.U.; Tabassum, F.; Rasheduzzaman; Saba, H.; Sarkar, L.; Ferdous, J.; Uddin, S.Z.; Islam, A.Z.M.Z. Temporal dynamics of land use/land cover change and its prediction using CA-ANN model for southwestern coastal Bangladesh. Environ. Monit. Assess. 2017, 189, 1–18. [Google Scholar] [CrossRef]
- Zhu, X.X.; Tuia, D.; Mou, L.; Xia, G.-S.; Zhang, L.; Xu, F.; Fraundorfer, F. Deep Learning in Remote Sensing: A Comprehensive Review and List of Resources. IEEE Geosci. Remote. Sens. Mag. 2017, 5, 8–36. [Google Scholar] [CrossRef]
- Torrens, P.M.; Benenson, I. Geographic Automata Systems. Int. J. Geogr. Inf. Sci. 2005, 19, 385–412. [Google Scholar] [CrossRef]
- Schreinemachers, P.; Berger, T. Land use decisions in developing countries and their representation in multi-agent systems. J. Land Use Sci. 2006, 1, 29–44. [Google Scholar] [CrossRef]
- Evans, T.P.; Kelley, H. Multi-scale analysis of a household level agent-based model of landcover change. J. Environ. Manag. 2004, 72, 57–72. [Google Scholar] [CrossRef]
- Batty, M.; Xie, Y. From Cells to Cities. Environ. Plan. B Plan. Des. 1994, 21, S31–S48. [Google Scholar] [CrossRef]
- White, R.; Engelen, G. High-resolution integrated modelling of the spatial dynamics of urban and regional systems. Comput. Environ. Urban. Syst. 2000, 24, 383–400. [Google Scholar] [CrossRef]
- Gharbia, S.S.; Alfatah, S.A.; Gill, L.; Johnston, P.; Pilla, F. Land use scenarios and projections simulation using an integrated GIS cellular automata algorithms. Model. Earth Syst. Environ. 2016, 2, 1–20. [Google Scholar] [CrossRef]
- Stevens, D.; Dragićević, S. A GIS-Based Irregular Cellular Automata Model of Land-Use Change. Environ. Plan. B Plan. Des. 2007, 34, 708–724. [Google Scholar] [CrossRef]
- Yang, Q.; Li, X.; Shi, X. Cellular automata for simulating land use changes based on support vector machines. Comput. Geosci. 2008, 34, 592–602. [Google Scholar] [CrossRef]
- Rienow, A.; Goetzke, R. Supporting SLEUTH—Enhancing a cellular automaton with support vector machines for urban growth modeling. Comput. Environ. Urban. Syst. 2015, 49, 66–81. [Google Scholar] [CrossRef]
- Kamusoko, C.; Gamba, J. Simulating Urban Growth Using a Random Forest-Cellular Automata (RF-CA) Model. ISPRS Int. J. Geo Inf. 2015, 4, 447–470. [Google Scholar] [CrossRef]
- Azari, M.; Tayyebi, A.; Helbich, M.; Reveshty, M.A. Integrating cellular automata, artificial neural network, and fuzzy set theory to simulate threatened orchards: Application to Maragheh, Iran. GISci. Remote Sens. 2016, 53, 183–205. [Google Scholar] [CrossRef]
- Samat, N.; Mahamud, M.A.; Tan, M.L.; Tilaki, M.J.M.; Tew, Y.L. Modelling Land Cover Changes in Peri-Urban Areas: A Case Study of George Town Conurbation, Malaysia. Land 2020, 9, 373. [Google Scholar] [CrossRef]
- Liu, D.; Zheng, X.; Wang, H. Land-use Simulation and Decision-Support system (LandSDS): Seamlessly integrating system dynamics, agent-based model, and cellular automata. Ecol. Model. 2020, 417, 108924. [Google Scholar] [CrossRef]
- Noszczyk, T. A review of approaches to land use changes modeling. Hum. Ecol. Risk Assess. Int. J. 2019, 25, 1377–1405. [Google Scholar] [CrossRef]
- Otukei, J.; Blaschke, T. Land cover change assessment using decision trees, support vector machines and maximum likelihood classification algorithms. Int. J. Appl. Earth Obs. Geoinf. 2010, 12, S27–S31. [Google Scholar] [CrossRef]
- Ienco, D.; Gaetano, R.; Dupaquier, C.; Maurel, P. Land Cover Classification via Multitemporal Spatial Data by Deep Recurrent Neural Networks. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1685–1689. [Google Scholar] [CrossRef]
- Mertens, B.; Lambin, E.F. Land-Cover-Change Trajectories in Southern Cameroon. Ann. Assoc. Am. Geogr. 2000, 90, 467–494. [Google Scholar] [CrossRef]
- Li, S.; Dragicevic, S.; Anton, F.; Sester, M.; Winter, S.; Çöltekin, A.; Pettit, C.; Jiang, B.; Haworth, J.; Stein, A.; et al. Geospatial big data handling theory and methods: A review and research challenges. ISPRS J. Photogramm. Remote Sens. 2016, 115, 119–133. [Google Scholar] [CrossRef]
- Maithani, S. Neural networks-based simulation of land cover scenarios in Doon valley, India. Geo. Int. 2014, 30, 1–23. [Google Scholar] [CrossRef]
- Boulila, W.; Farah, I.; Ettabaa, K.S.; Solaiman, B.; Ben Ghézala, H. A data mining based approach to predict spatiotemporal changes in satellite images. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 386–395. [Google Scholar] [CrossRef]
- Patil, S.D.; Gu, Y.; Dias, F.S.A.; Stieglitz, M.; Turk, G. Predicting the spectral information of future land cover using machine learning. Int. J. Remote Sens. 2017, 38, 5592–5607. [Google Scholar] [CrossRef]
- Marondedze, A.K.; Schütt, B. Dynamics of Land Use and Land Cover Changes in Harare, Zimbabwe: A Case Study on the Linkage between Drivers and the Axis of Urban Expansion. Land 2019, 8, 155. [Google Scholar] [CrossRef]
- Kong, Y.-L.; Huang, Q.; Wang, C.; Chen, J.; Chen, J.; He, D. Long Short-Term Memory Neural Networks for Online Disturbance Detection in Satellite Image Time Series. Remote Sens. 2018, 10, 452. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- RuBwurm, M.; Korner, M. Temporal Vegetation Modelling Using Long Short-Term Memory Networks for Crop Identification from Medium-Resolution Multi-spectral Satellite Images. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Honolulu, HI, USA, 21–26 July 2017; pp. 1496–1504. [Google Scholar]
- Lyu, H.; Lu, H.; Mou, L. Learning a Transferable Change Rule from a Recurrent Neural Network for Land Cover Change Detection. Remote Sens. 2016, 8, 506. [Google Scholar] [CrossRef]
- Van Vliet, J.; Bregt, A.K.; Brown, D.G.; Van Delden, H.; Heckbert, S.; Verburg, P.H. A review of current calibration and validation practices in land-change modeling. Environ. Model. Softw. 2016, 82, 174–182. [Google Scholar] [CrossRef]
- Ligmann-Zielinska, A.; Sun, L. Applying time-dependent variance-based global sensitivity analysis to represent the dynamics of an agent-based model of land use change. Int. J. Geogr. Inf. Sci. 2010, 24, 1829–1850. [Google Scholar] [CrossRef]
- Kocabas, V.; Dragicevic, S. Assessing cellular automata model behaviour using a sensitivity analysis approach. Comput. Environ. Urban. Syst. 2006, 30, 921–953. [Google Scholar] [CrossRef]
- Li, X.; Ling, F.; Foody, G.M.; Ge, Y.; Zhang, Y.; Wang, L.; Shi, L.; Li, X.; Du, Y. Spatial–Temporal Super-Resolution Land Cover Mapping with a Local Spatial–Temporal Dependence Model. IEEE Trans. Geosci. Remote Sens. 2019, 57, 4951–4966. [Google Scholar] [CrossRef]
- Boulila, W.; Ayadi, Z.; Farah, I.R. Sensitivity analysis approach to model epistemic and aleatory imperfection: Application to Land Cover Change prediction model. J. Comput. Sci. 2017, 23, 58–70. [Google Scholar] [CrossRef]
- Shafizadeh-Moghadam, H.; Asghari, A.; Taleai, M.; Helbich, M.; Tayyebi, A. Sensitivity analysis and accuracy assessment of the land transformation model using cellular automata. GISci. Remote Sens. 2017, 54, 639–656. [Google Scholar] [CrossRef]
- Huang, Z.; Laffan, S.W. Sensitivity analysis of a decision tree classification to input data errors using a general Monte Carlo error sensitivity model. Int. J. Geogr. Inf. Sci. 2009, 23, 1433–1452. [Google Scholar] [CrossRef]
- Samardžić-Petrović, M.; Kovačević, M.; Bajat, B.; Dragićević, S. Machine Learning Techniques for Modelling Short Term Land-Use Change. ISPRS Int. J. Geo Inf. 2017, 6, 387. [Google Scholar] [CrossRef]
- Zhang, Y.; Wallace, B. A Sensitivity Analysis of (and Practitioners’ Guide to) Convolutional Neural Networks for Sentence Classification. arXiv 2015, arXiv:1510.03820. [Google Scholar]
- Rodner, E.; Simon, M.; Fisher, R.; Denzler, J.; Wilson, R.C.; Hancock, E.R.; Smith, W.A.P.; Pears, N.E.; Bors, A.G. Fine-grained Recognition in the Noisy Wild: Sensitivity Analysis of Convolutional Neural Networks Approaches. In Proceedings of the British Machine Vision Conference 2016, York, UK, 19–22 September 2016. [Google Scholar] [CrossRef]
- Khoshroo, A.; Emrouznejad, A.; Ghaffarizadeh, A.; Kasraei, M.; Omid, M. Sensitivity analysis of energy inputs in crop production using artificial neural networks. J. Clean. Prod. 2018, 197, 992–998. [Google Scholar] [CrossRef]
- Lambin, E.F. Modelling and monitoring land-cover change processes in tropical regions. Prog. Phys. Geogr. Earth Environ. 1997, 21, 375–393. [Google Scholar] [CrossRef]
- Van Duynhoven, A.; Dragićević, S. Analyzing the Effects of Temporal Resolution and Classification Confidence for Modeling Land Cover Change with Long Short-Term Memory Networks. Remote Sens. 2019, 11, 2784. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2006; ISBN 0387310738. [Google Scholar]
- Le Cun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Pascanu, R.; Mikolov, T.; Bengio, Y. On the difficulty of training recurrent neural networks. In Proceedings of the 30th International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2013; pp. 2347–2355. [Google Scholar]
- Hochreiter, S. The Vanishing Gradient Problem During Learning Recurrent Neural Nets and Problem Solutions. Int. J. Uncertain. Fuzziness Knowl. Based Syst. 1998, 6, 107–116. [Google Scholar] [CrossRef]
- Gers, F.A.; Schmidhuber, J.; Cummins, F. Learning to Forget: Continual Prediction with LSTM. Neural Comput. 2000, 12, 2451–2471. [Google Scholar] [CrossRef]
- Donahue, J.; Hendricks, L.A.; Guadarrama, S.; Rohrbach, M.; Venugopalan, S.; Darrell, T.; Saenko, K. Long-term recurrent convolutional networks for visual recognition and description. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 2625–2634. [Google Scholar]
- Sauter, T.; Weitzenkamp, B.; Schneider, C. Spatio-temporal prediction of snow cover in the Black Forest mountain range using remote sensing and a recurrent neural network. Int. J. Clim. 2010, 30, 2330–2341. [Google Scholar] [CrossRef]
- Chi, J.; Kim, H.-C. Prediction of Arctic Sea Ice Concentration Using a Fully Data Driven Deep Neural Network. Remote Sens. 2017, 9, 1305. [Google Scholar] [CrossRef]
- Greff, K.; Srivastava, R.K.; Koutnik, J.; Steunebrink, B.R.; Schmidhuber, J. LSTM: A Search Space Odyssey. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 2222–2232. [Google Scholar] [CrossRef] [PubMed]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Gated Feedback Recurrent Neural Networks. In Proceedings of the ICML’15 Proceedings of the 32nd International Conference on International Conference on Machine Learning, Lille, France, 7–9 July 2015; pp. 2067–2075. [Google Scholar]
- Britz, D.; Goldie, A.; Luong, M.-T.; Le, Q. Massive Exploration of Neural Machine Translation Architectures. In Proceedings of the 2017 Conference on Empirical Methods in Natural Language Processing, Copenhagen, Denmark, 9–11 September 2017; pp. 1442–1451. [Google Scholar]
- Pascanu, R.; Gulcehre, C.; Cho, K.; Bengio, Y. How to Construct Deep Recurrent Neural Networks. In Proceedings of the 2nd International Conference on Learning Representations (ICLR), Banff, AB, Canada, 14–16 April 2014. [Google Scholar]
- Hermans, M.; Schrauwen, B. Training and Analysing Deep Recurrent Neural Networks. Adv. Neural Inf. Process. Syst. 2013, 26, 190–198. [Google Scholar]
- Potdar, K. A Comparative Study of Categorical Variable Encoding Techniques for Neural Network Classifiers. Int. J. Comput. Appl. 2017, 175, 7–9. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. In Proceedings of the International Conference Learn, Represent. (ICLR), San Diego, CA, USA, 5–8 May 2015. [Google Scholar]
- van Rossum, G. Python 3.6 Language Reference; Samurai Media Limited: London, UK, 2016. [Google Scholar]
- Keras: The Python Deep Learning API. Available online: https://keras.io/ (accessed on 27 August 2020).
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Distributed Systems. arXiv 2015, arXiv:1603.04467. Available online: https://www.Tensorflow.org (accessed on 20 December 2019).
- Pham, V.; Bluche, T.; Kermorvant, C.; Louradour, J. Dropout Improves Recurrent Neural Networks for Handwriting Recognition. In Proceedings of the 2014 14th International Conference on Frontiers in Handwriting Recognition, Hersonissos, Greece, 1–4 September 2014; pp. 285–290. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning Book; MIT Press: Cambridge, MA, USA, 2016; ISBN 9780262035613. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Salakhutdinov, R.R.; Sutskever, I.; Hinton, G.; Krizhevsky, A.; Sala-khutdinov, R.R. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Ligmann-Zielinska, A.; Siebers, P.-O.; Magliocca, N.; Parker, D.C.; Grimm, V.; Du, J.; Cenek, M.; Radchuk, V.; Arbab, N.N.; Li, S.; et al. ‘One Size Does Not Fit All’: A Roadmap of Purpose-Driven Mixed-Method Pathways for Sensitivity Analysis of Agent-Based Models. J. Artif. Soc. Soc. Simul. 2020, 23. [Google Scholar] [CrossRef]
- Lipton, Z.C.; Berkowitz, J.; Elkan, C. A Critical Review of Recurrent Neural Networks for Sequence Learning. arXiv 2015, arXiv:1506.00019. [Google Scholar] [CrossRef]
- Raimbault, J.; Cottineau, C.; Le Texier, M.; Le Nechet, F.; Reuillon, R. Space Matters: Extending Sensitivity Analysis to Initial Spatial Conditions in Geosimulation Models. J. Artif. Soc. Soc. Simul. 2019, 22, 1–23. [Google Scholar] [CrossRef]
- Brown, D.G.; Page, S.; Riolo, R.; Zellner, M.; Rand, W. Path dependence and the validation of agent-based spatial models of land use. Int. J. Geogr. Inf. Sci. 2005, 19, 153–174. [Google Scholar] [CrossRef]
- Hagen, A. Multi-method assessment of map similarity. In Proceedings of the 5th AGILE Conference on Geographic Information Science, Palma, Spain, 25–27 April 2002; pp. 1–8. [Google Scholar]
- Bone, C.; Johnson, B.; Sproles, E.; Bolte, J.; Nielsen-Pincus, M. A Temporal Variant-Invariant Validation Approach for Agent-based Models of Landscape Dynamics. Trans. GIS 2013, 18, 161–182. [Google Scholar] [CrossRef]
- Rußwurm, M.; Körner, M. Multi-Temporal Land Cover Classification with Sequential Recurrent Encoders. ISPRS Int. J. Geo Inf. 2018, 7, 129. [Google Scholar] [CrossRef]
- Van Vliet, J.; Bregt, A.K.; Hagen-Zanker, A. Revisiting Kappa to account for change in the accuracy assessment of land-use change models. Ecol. Model. 2011, 222, 1367–1375. [Google Scholar] [CrossRef]
- Sakieh, Y.; Salmanmahiny, A. Performance assessment of geospatial simulation models of land-use change—A landscape metric-based approach. Environ. Monit. Assess. 2016, 188, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Pontius, R.G.; Boersma, W.; Castella, J.-C.; Clarke, K.; De Nijs, T.; Dietzel, C.; Duan, Z.; Fotsing, E.; Goldstein, N.; Kok, K.; et al. Comparing the input, output, and validation maps for several models of land change. Ann. Reg. Sci. 2008, 42, 11–37. [Google Scholar] [CrossRef]
- Bone, C.; Dragićević, S. Defining Transition Rules with Reinforcement Learning for Modeling Land Cover Change. Simulation 2009, 85, 291–305. [Google Scholar] [CrossRef]
- Burlacu, I.; O’Donoghue, C.; Sologon, D.M. Hypothetical Models. In Water Science and Technology; Emerald Group Publishing Limited: Bingley, UK, 2014; Volume 45, pp. 23–46. ISBN 0273-1223. [Google Scholar]
- Hermes, K.; Poulsen, M. A review of current methods to generate synthetic spatial microdata using reweighting and future directions. Comput. Environ. Urban. Syst. 2012, 36, 281–290. [Google Scholar] [CrossRef]
- Homer, C.; Huang, C.; Yang, L.; Wylie, B.; Coan, M. Development of a 2001 National Land-Cover Database for the United States. Photogramm. Eng. Remote Sens. 2004, 70, 829–840. [Google Scholar] [CrossRef]
- Sulla-Menashe, D.; Friedl, M.A. User Guide to Collection 6 MODIS Land Cover (MCD12Q1 and MCD12C1) Product; USGS: Reston, VA, USA, 2018; pp. 1–18. [Google Scholar] [CrossRef]
- Esri. ArcGIS Pro: 2.0; Esri: Redlands, CA, USA, 2017. [Google Scholar]
- Fotheringham, A.S.; Rogerson, P.A. GIS and spatial analytical problems. Int. J. Geogr. Inf. Syst. 1993, 7, 3–19. [Google Scholar] [CrossRef]
- Sulla-Menashe, D.; Friedl, M. The Terra and Aqua Combined Moderate Resolution Imaging Spectroradiometer (MODIS) Land Cover Type (MCD12Q1) Version 6 Data Product. Available online: https://lpdaac.usgs.gov/dataset_discovery/modis/modis_products_table/mcd12q1_v006 (accessed on 30 January 2019).
- Ministry of Municipal Affairs and Housing Regional Districts—Legally Defined Administrative Areas of BC. Available online: https://catalogue.data.gov.bc.ca/dataset/d1aff64e-dbfe-45a6-af97-582b7f6418b9 (accessed on 3 October 2020).
- Venture Kamloops Kamloops Population Data. Available online: https://www.venturekamloops.com/why-kamloops/community-profile/demographics (accessed on 8 October 2020).
- Krawczyk, B. Learning from imbalanced data: Open challenges and future directions. Prog. Artif. Intell. 2016, 5, 221–232. [Google Scholar] [CrossRef]
- Li, X.; Yeh, A.G.-O. Neural-network-based cellular automata for simulating multiple land use changes using GIS. Int. J. Geogr. Inf. Sci. 2002, 16, 323–343. [Google Scholar] [CrossRef]
- Sun, Z.; Di, L.; Fang, H. Using long short-term memory recurrent neural network in land cover classification on Landsat and Cropland data layer time series. Int. J. Remote Sens. 2018, 40, 593–614. [Google Scholar] [CrossRef]
- Jiang, Z. A Survey on Spatial Prediction Methods. IEEE Trans. Knowl. Data Eng. 2019, 31, 1645–1664. [Google Scholar] [CrossRef]
- Saltelli, A.; Aleksankina, K.; Becker, W.; Fennell, P.; Ferretti, F.; Holst, N.; Li, S.; Wu, Q. Why so many published sensitivity analyses are false: A systematic review of sensitivity analysis practices. Environ. Model. Softw. 2019, 114, 29–39. [Google Scholar] [CrossRef]
- McDermott, P.L.; Wikle, C.K. Bayesian Recurrent Neural Network Models for Forecasting and Quantifying Uncertainty in Spatial-Temporal Data. Entropy 2019, 21, 184. [Google Scholar] [CrossRef] [PubMed]
- Reichstein, M.; Camps-Valls, G.; Stevens, B.; Jung, M.; Denzler, J.; Carvalhais, N. Prabhat Deep learning and process understanding for data-driven Earth system science. Nat. Cell Biol. 2019, 566, 195–204. [Google Scholar] [CrossRef]
- USGS EROS Center National Land Cover Database (NLCD). Available online: https://www.usgs.gov/centers/eros/science/national-land-cover-database?qt-science_center_objects=0# (accessed on 10 October 2020).



| Metric | Equation |
|---|---|
| Intermediate Expressions | Equation |
| where , , , , | |
| 4 Class Dataset | 8 Class Dataset | 16 Class Dataset |
|---|---|---|
| C1—Cropland | C1—Cropland | C1—Cropland |
| C2—Forest Land | C2—Pasture | C2—Pasture |
| C3—High Intensity Development | C3—Forest Land | C3—Deciduous Forest |
| C4—Low Intensity Development | C4—Barren Land | C4—Evergreen Forest |
| C5—Grasslands | C5—Mixed Forest | |
| C6—High Intensity Development | C6—High Intensity Development | |
| C7—Low Intensity Development | C7—Low Intensity Development | |
| C8—Water | C8—Shrubland | |
| C9—Grasslands | ||
| C10—Road Surfaces | ||
| C11—Barren Land | ||
| C12—Lakes | ||
| C13—Streams | ||
| C14—Wetland | ||
| C15—Beaches | ||
| C16—Bare Exposed Rock |
| (a) | Timestep | 0 | 11 | 22 | 33 | 44 |
|---|---|---|---|---|---|---|
| C1—Cropland | 2537 | 1137 | 566 | 325 | 179 | |
| C2—Forest Land | 1906 | 1820 | 1192 | 517 | 0 | |
| C3—High Intensity Development | 352 | 1561 | 2422 | 3086 | 3393 | |
| C4—Low Intensity Development | 105 | 382 | 720 | 972 | 1328 | |
| (b) | Timestep | 0 | 11 | 22 | 33 | 44 |
| C1—Cropland | 105 | 412 | 730 | 988 | 1209 | |
| C2—Pasture | 0 | 386 | 301 | 252 | 14 | |
| C3—Forest Land | 2469 | 1191 | 747 | 485 | 456 | |
| C4—Barren Land | 166 | 320 | 295 | 214 | 170 | |
| C5—Grasslands | 1738 | 1523 | 1433 | 1142 | 777 | |
| C6—High Intensity Development | 0 | 82 | 95 | 130 | 103 | |
| C7—Low Intensity Development | 352 | 916 | 1229 | 1619 | 2101 | |
| C8—Water | 70 | 70 | 70 | 70 | 70 | |
| (c) | Timestep | 0 | 11 | 22 | 33 | 44 |
| C1—Cropland | 19 | 176 | 219 | 368 | 502 | |
| C2—Pasture | 28 | 35 | 103 | 173 | 245 | |
| C3—Deciduous Forest | 2725 | 2365 | 1961 | 1726 | 1550 | |
| C4—Evergreen Forest | 812 | 809 | 814 | 787 | 706 | |
| C5—Mixed Forest | 128 | 118 | 114 | 112 | 104 | |
| C6—High Intensity Development | 20 | 61 | 83 | 118 | 153 | |
| C7—Low Intensity Development | 49 | 99 | 131 | 135 | 151 | |
| C8—Shrubland | 115 | 160 | 207 | 165 | 161 | |
| C9—Grasslands | 348 | 328 | 367 | 320 | 320 | |
| C10—Road Surfaces | 131 | 134 | 235 | 271 | 271 | |
| C11—Barren Land | 68 | 101 | 128 | 148 | 153 | |
| C12—Lakes | 186 | 204 | 216 | 223 | 227 | |
| C13—Streams | 75 | 67 | 68 | 67 | 67 | |
| C14—Wetland | 83 | 82 | 84 | 83 | 80 | |
| C15—Beaches | 64 | 80 | 86 | 88 | 95 | |
| C16—Bare Exposed Rock | 49 | 81 | 84 | 116 | 115 |
| 4 Class Dataset | 8 Class Dataset | 15 Class Dataset |
|---|---|---|
| C1—Forests | C1—Evergreen Forests | C1—Evergreen Needleleaf Forests |
| C2—Deciduous Forests and Mixed Forests | C2—Deciduous Needleleaf Forests | |
| C3—Deciduous Broadleaf Forests | ||
| C4—Mixed Forests | ||
| C2—Non-Forest | C3—Shrublands and Savannas | C5—Closed Shrublands |
| C6—Open Shrublands | ||
| C7—Savannas | ||
| C8—Woody Savannas | ||
| C4—Grasslands and Permanent Wetlands | C9—Grasslands | |
| C10—Permanent Wetlands | ||
| C5—Permanent Snow and Ice | C11—Permanent Snow and Ice | |
| C6—Barren | C12—Barren | |
| C3—Anthropogenic Areas | C7—Anthropogenic Areas | C13—Urban and Built-up Lands |
| C14—Croplands, Cropland/Natural Vegetation Mosaics | ||
| C4—Water Bodies | C8—Water Bodies | C15—Water Bodies |
| (a) | Timestep | 2001 | 2004 | 2007 | 2010 | 2013 | 2016 | 2019 |
|---|---|---|---|---|---|---|---|---|
| C1—Forests | 101,419 | 84,521 | 67,773 | 62,591 | 68,073 | 71,632 | 70,457 | |
| C2—Non-Forest | 107,704 | 124,502 | 141,231 | 146,452 | 141,034 | 137,527 | 137,954 | |
| C3—Anthropogenic Areas | 604 | 637 | 658 | 641 | 593 | 559 | 496 | |
| C4—Water Bodies | 1787 | 1854 | 1852 | 1830 | 1814 | 1796 | 2607 | |
| (b) | Timestep | 2001 | 2004 | 2007 | 2010 | 2013 | 2016 | 2019 |
| C1—Evergreen Forests | 99,551 | 83,240 | 66,792 | 61,536 | 66,516 | 69,462 | 68,445 | |
| C2—Deciduous Forests and Mixed Forests | 1868 | 1281 | 981 | 1055 | 1557 | 2170 | 2012 | |
| C3—Shrublands and Savannas | 75,703 | 89,976 | 104,072 | 104,174 | 98,973 | 97,328 | 97,598 | |
| C4—Grasslands and Permanent Wetlands | 25,569 | 28,301 | 30,869 | 35,926 | 35,902 | 34,120 | 34,332 | |
| C5—Permanent Snow and Ice | 2098 | 1824 | 1963 | 1965 | 1881 | 2150 | 2307 | |
| C6—Barren | 4334 | 4401 | 4327 | 4387 | 4278 | 3929 | 3717 | |
| C7—Anthropogenic Areas | 604 | 637 | 658 | 641 | 593 | 559 | 496 | |
| C8—Water Bodies | 1787 | 1854 | 1852 | 1830 | 1814 | 1796 | 2607 | |
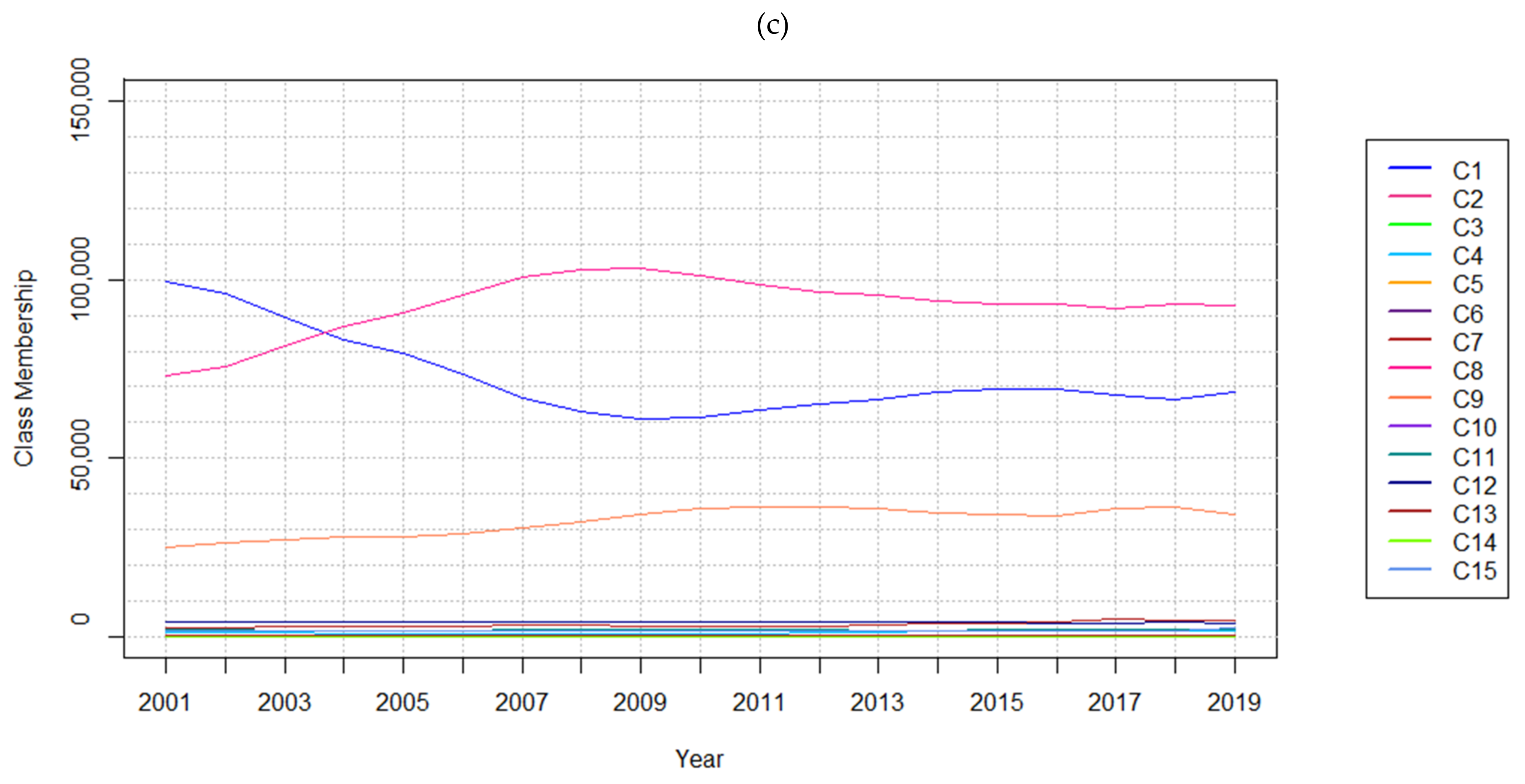
| (c) | Timestep | 2001 | 2004 | 2007 | 2010 | 2013 | 2016 | 2019 |
| C1—Evergreen Needleleaf Forests | 99,551 | 83,240 | 66,792 | 61,536 | 66,516 | 69,462 | 68,445 | |
| C2—Deciduous Needleleaf Forests | 1 | 6 | 7 | 7 | 13 | 16 | 15 | |
| C3—Deciduous Broadleaf Forests | 494 | 269 | 153 | 168 | 257 | 343 | 197 | |
| C4—Mixed Forests | 1373 | 1006 | 821 | 880 | 1287 | 1811 | 1800 | |
| C5—Closed Shrublands | 18 | 27 | 30 | 26 | 18 | 11 | 6 | |
| C6—Open Shrublands | 5 | 8 | 11 | 14 | 15 | 17 | 11 | |
| C7—Savannas | 2565 | 2938 | 3207 | 2949 | 3418 | 4230 | 4687 | |
| C8—Woody Savannas | 73,115 | 87,003 | 100,824 | 101,185 | 95,522 | 93,070 | 92,894 | |
| C9—Grasslands | 25,292 | 28,030 | 30,637 | 35,773 | 35,756 | 33,886 | 34,165 | |
| C10—Permanent Wetlands | 277 | 271 | 232 | 153 | 146 | 234 | 167 | |
| C11—Permanent Snow and Ice | 2098 | 1824 | 1963 | 1965 | 1881 | 2150 | 2307 | |
| C12—Barren | 4334 | 4401 | 4327 | 4387 | 4278 | 3929 | 3717 | |
| C13—Urban and Built-up Lands | 409 | 410 | 411 | 412 | 412 | 412 | 412 | |
| C14 - Croplands, Cropland/Natural Vegetation Mosaics | 195 | 227 | 247 | 229 | 181 | 147 | 84 | |
| C15—Water Bodies | 1787 | 1854 | 1852 | 1830 | 1814 | 1796 | 2607 |
| Model Training | Model Testing | |||
|---|---|---|---|---|
| Temporal Resolution (Years) | Years in Input Sequence | Target Year | Years in Input Sequence | Target Year |
| 1 | 2001, 2002, 2003, 2004, 2005, 2006, 2007, 2008, 2009, 2010, 2011, 2012, 2013, 2014, 2015, 2016, 2017 | 2018 | 2002, 2003, 2004, 2005, 2006, 2007, 2008, 2009, 2010, 2011, 2012, 2013, 2014, 2015, 2016, 2017, 2018 | 2019 |
| 2 | 2001, 2003, 2005, 2007, 2009, 2011, 2013, 2015 | 2017 | 2003, 2005, 2007, 2009, 2011, 2013, 2015, 2017 | |
| 3 | 2001, 2004, 2007, 2010, 2013 | 2016 | 2004, 2007, 2010, 2013, 2016 | |
| 6 | 2001, 2007 | 2013 | 2007, 2013 | |
| 9 | 2001 | 2010 | 2010 | |
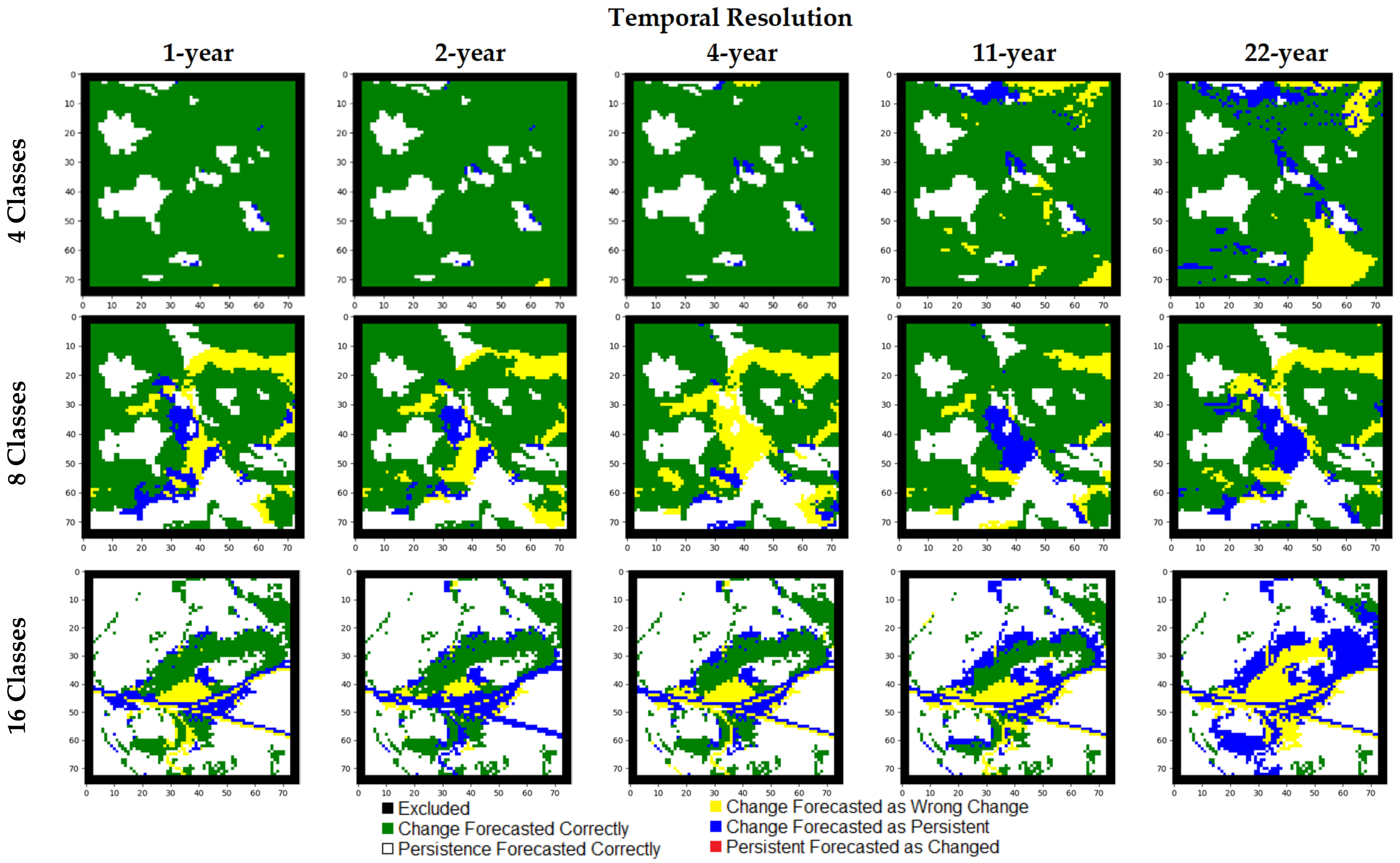
| Performance Metric | Temporal Resolution | 4 Classes | 8 Classes | 16 Classes |
|---|---|---|---|---|
| Changed Cell Forecasting Accuracy | 1 | 99.50% | 76.20% | 71.50% |
| 2 | 99.10% | 76.30% | 68.60% | |
| 4 | 98.60% | 67.60% | 66.10% | |
| 11 | 90.10% | 79.20% | 57.30% | |
| 22 | 78.50% | 64.90% | 16.40% | |
| Kappa | 1 | 0.991 | 0.775 | 0.837 |
| 2 | 0.982 | 0.777 | 0.826 | |
| 4 | 0.973 | 0.701 | 0.817 | |
| 11 | 0.812 | 0.797 | 0.783 | |
| 22 | 0.58 | 0.538 | 0.605 | |
| KHistogram | 1 | 0.992 | 0.813 | 0.846 |
| 2 | 0.983 | 0.793 | 0.837 | |
| 4 | 0.979 | 0.729 | 0.839 | |
| 11 | 0.918 | 0.825 | 0.829 | |
| 22 | 0.721 | 0.583 | 0.624 | |
| KLocation | 1 | 0.999 | 0.953 | 0.989 |
| 2 | 0.999 | 0.98 | 0.987 | |
| 4 | 0.994 | 0.961 | 0.975 | |
| 11 | 0.885 | 0.966 | 0.945 | |
| 22 | 0.804 | 0.923 | 0.97 | |
| KSimulation | 1 | 0.989 | 0.744 | 0.731 |
| 2 | 0.979 | 0.746 | 0.713 | |
| 4 | 0.968 | 0.661 | 0.694 | |
| 11 | 0.778 | 0.768 | 0.627 | |
| 22 | 0.526 | 0.477 | 0.307 | |
| KTransition | 1 | 0.989 | 0.773 | 0.733 |
| 2 | 0.979 | 0.764 | 0.721 | |
| 4 | 0.976 | 0.693 | 0.718 | |
| 11 | 0.88 | 0.8 | 0.682 | |
| 22 | 0.628 | 0.528 | 0.326 | |
| KTranslocation | 1 | 1 | 0.963 | 0.998 |
| 2 | 1 | 0.977 | 0.989 | |
| 4 | 0.992 | 0.954 | 0.966 | |
| 11 | 0.884 | 0.96 | 0.919 | |
| 22 | 0.837 | 0.903 | 0.942 |
| Performance Metric | Temporal Resolution | 4 Classes | 8 Classes | 16 Classes |
|---|---|---|---|---|
| Changed Cell Forecasting Accuracy | 1 | 89.37% | 77.26% | 83.13% |
| 2 | 94.91% | 75.61% | 78.51% | |
| 7 | 45.85% | 35.50% | 57.73% | |
| Kappa | 1 | 0.927 | 0.859 | 0.973 |
| 2 | 0.964 | 0.85 | 0.966 | |
| 7 | 0.3 | 0.567 | 0.933 | |
| KHistogram | 1 | 0.938 | 0.887 | 0.977 |
| 2 | 0.964 | 0.91 | 0.969 | |
| 7 | 0.387 | 0.752 | 0.944 | |
| KLocation | 1 | 0.988 | 0.969 | 0.997 |
| 2 | 1 | 0.934 | 0.997 | |
| 7 | 0.776 | 0.754 | 0.988 | |
| KSimulation | 1 | 0.91 | 0.813 | 0.898 |
| 2 | 0.956 | 0.801 | 0.868 | |
| 7 | 0.222 | 0.423 | 0.712 | |
| KTransition | 1 | 0.921 | 0.838 | 0.898 |
| 2 | 0.956 | 0.844 | 0.868 | |
| 7 | 0.318 | 0.544 | 0.712 | |
| KTranslocation | 1 | 0.989 | 0.971 | 1 |
| 2 | 1 | 0.948 | 1 | |
| 7 | 0.697 | 0.776 | 1 |
| Performance Metric | Temporal Resolution | 4 Classes | 8 Classes | 16 Classes |
|---|---|---|---|---|
| Changed Cell Forecasting Accuracy | 1 | 89.83% | 72.93% | 95.31% |
| 2 | 84.71% | 67.01% | 82.18% | |
| 7 | 61.74% | 37.23% | 54.97% | |
| Kappa | 1 | 0.944 | 0.862 | 0.994 |
| 2 | 0.917 | 0.864 | 0.976 | |
| 7 | 0.803 | 0.713 | 0.939 | |
| KHistogram | 1 | 0.944 | 0.878 | 0.994 |
| 2 | 0.917 | 0.921 | 0.976 | |
| 7 | 0.815 | 0.845 | 0.939 | |
| KLocation | 1 | 1 | 0.982 | 1 |
| 2 | 1 | 0.938 | 1 | |
| 7 | 0.985 | 0.844 | 1 | |
| KSimulation | 1 | 0.9 | 0.697 | 0.973 |
| 2 | 0.85 | 0.703 | 0.891 | |
| 7 | 0.629 | 0.365 | 0.693 | |
| KTransition | 1 | 0.9 | 0.699 | 0.973 |
| 2 | 0.85 | 0.724 | 0.893 | |
| 7 | 0.652 | 0.416 | 0.693 | |
| KTranslocation | 1 | 1 | 0.998 | 1 |
| 2 | 1 | 0.972 | 0.999 | |
| 7 | 0.964 | 0.877 | 1 |
| Performance Metric | Temporal Resolution | 4 Classes | 8 Classes | 16 Classes |
|---|---|---|---|---|
| Changed Cell Forecasting Accuracy | 1 | 98.25% | 87.17% | 86.34% |
| 2 | 95.88% | 72.56% | 73.79% | |
| 7 | 82.30% | 71.92% | 38.33% | |
| Kappa | 1 | 0.992 | 0.928 | 0.985 |
| 2 | 0.982 | 0.888 | 0.971 | |
| 7 | 0.924 | 0.887 | 0.932 | |
| KHistogram | 1 | 0.992 | 0.948 | 0.986 |
| 2 | 0.983 | 0.949 | 0.975 | |
| 7 | 0.926 | 0.909 | 0.942 | |
| KLocation | 1 | 1 | 0.979 | 0.999 |
| 2 | 0.999 | 0.936 | 0.996 | |
| 7 | 0.999 | 0.975 | 0.99 | |
| KSimulation | 1 | 0.97 | 0.76 | 0.919 |
| 2 | 0.93 | 0.627 | 0.835 | |
| 7 | 0.688 | 0.574 | 0.533 | |
| KTransition | 1 | 0.97 | 0.772 | 0.919 |
| 2 | 0.93 | 0.727 | 0.845 | |
| 7 | 0.688 | 0.574 | 0.545 | |
| KTranslocation | 1 | 1 | 0.985 | 1 |
| 2 | 1 | 0.862 | 0.989 | |
| 7 | 1 | 1 | 0.979 |
| Performance Metric | Temporal Resolution | 4 Classes | 8 Classes | 16 Classes |
|---|---|---|---|---|
| Changed Cell Forecasting Accuracy | 1 | 89.17% | 85.50% | 83.93% |
| 2 | 82.45% | 77.55% | 75.62% | |
| 3 | 78.39% | 72.17% | 70.00% | |
| 6 | 71.54% | 64.10% | 61.50% | |
| 9 | 79.52% | 66.04% | 62.89% | |
| Kappa | 1 | 0.908 | 0.888 | 0.879 |
| 2 | 0.860 | 0.835 | 0.822 | |
| 3 | 0.829 | 0.803 | 0.788 | |
| 6 | 0.773 | 0.748 | 0.733 | |
| 9 | 0.049 | 0.327 | 0.319 | |
| KHistogram | 1 | 0.971 | 0.977 | 0.976 |
| 2 | 0.988 | 0.982 | 0.981 | |
| 3 | 0.987 | 0.990 | 0.987 | |
| 6 | 0.967 | 0.974 | 0.954 | |
| 9 | 0.052 | 0.443 | 0.425 | |
| KLocation | 1 | 0.935 | 0.909 | 0.901 |
| 2 | 0.871 | 0.851 | 0.838 | |
| 3 | 0.839 | 0.812 | 0.798 | |
| 6 | 0.799 | 0.768 | 0.768 | |
| 9 | 0.938 | 0.737 | 0.751 | |
| KSimulation | 1 | 0.865 | 0.830 | 0.818 |
| 2 | 0.791 | 0.746 | 0.730 | |
| 3 | 0.743 | 0.693 | 0.675 | |
| 6 | 0.652 | 0.601 | 0.582 | |
| 9 | 0.003 | 0.111 | 0.103 | |
| KTransition | 1 | 0.957 | 0.956 | 0.955 |
| 2 | 0.933 | 0.940 | 0.937 | |
| 3 | 0.918 | 0.929 | 0.925 | |
| 6 | 0.888 | 0.895 | 0.874 | |
| 9 | 0.005 | 0.242 | 0.224 | |
| KTranslocation | 1 | 0.904 | 0.868 | 0.856 |
| 2 | 0.848 | 0.794 | 0.779 | |
| 3 | 0.809 | 0.746 | 0.730 | |
| 6 | 0.735 | 0.671 | 0.666 | |
| 9 | 0.597 | 0.461 | 0.459 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
van Duynhoven, A.; Dragićević, S. Exploring the Sensitivity of Recurrent Neural Network Models for Forecasting Land Cover Change. Land 2021, 10, 282. https://doi.org/10.3390/land10030282
van Duynhoven A, Dragićević S. Exploring the Sensitivity of Recurrent Neural Network Models for Forecasting Land Cover Change. Land. 2021; 10(3):282. https://doi.org/10.3390/land10030282
Chicago/Turabian Stylevan Duynhoven, Alysha, and Suzana Dragićević. 2021. "Exploring the Sensitivity of Recurrent Neural Network Models for Forecasting Land Cover Change" Land 10, no. 3: 282. https://doi.org/10.3390/land10030282
APA Stylevan Duynhoven, A., & Dragićević, S. (2021). Exploring the Sensitivity of Recurrent Neural Network Models for Forecasting Land Cover Change. Land, 10(3), 282. https://doi.org/10.3390/land10030282







