Comparison of SWAT and GWLF Model Simulation Performance in Humid South and Semi-Arid North of China
Abstract
:1. Introduction
2. Materials and Methods
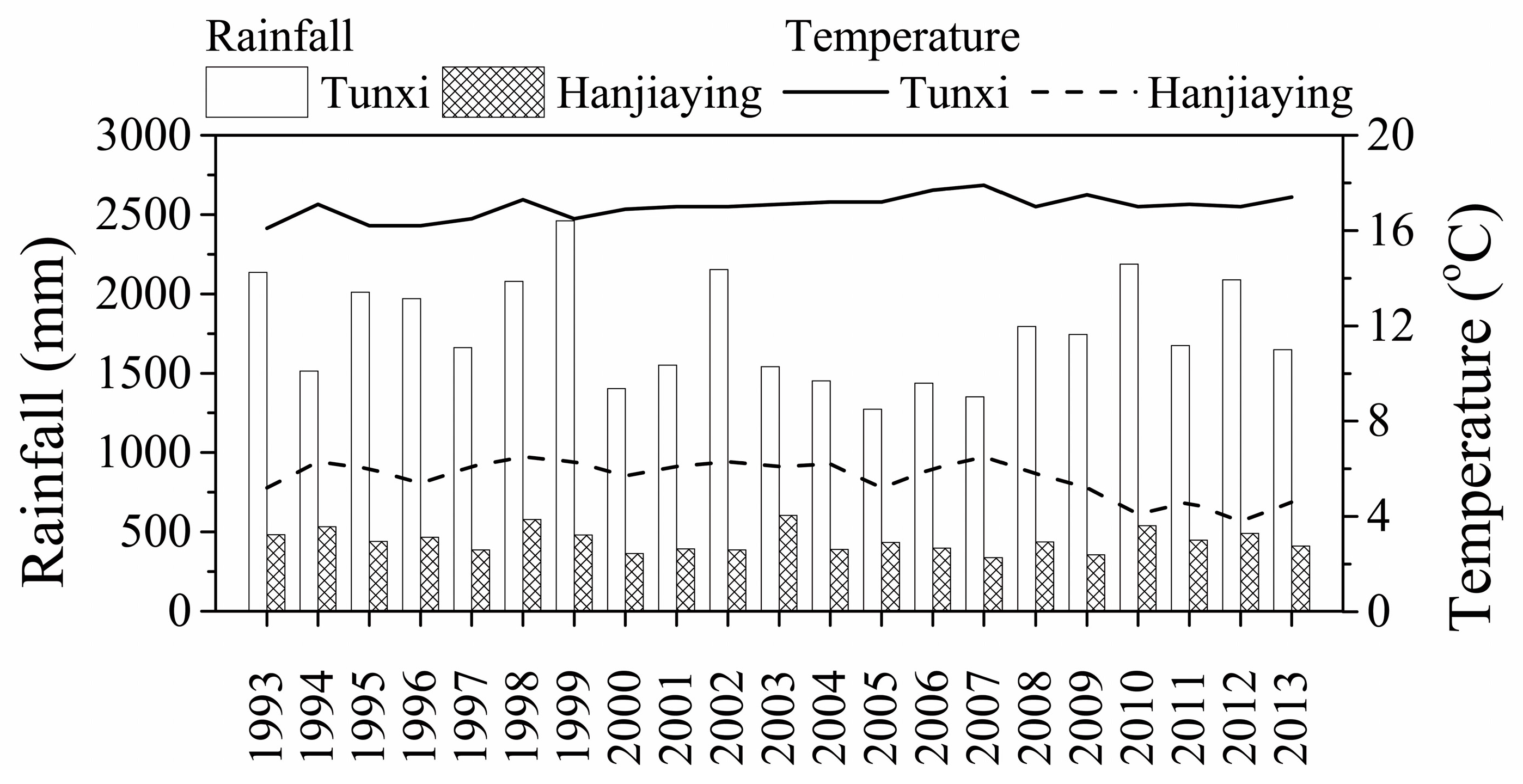
2.1. Study Sites
2.2. Watershed Models
2.3. Model Inputs
2.4. Model Calibration, Validation, and Evaluation
3. Results and Discussion
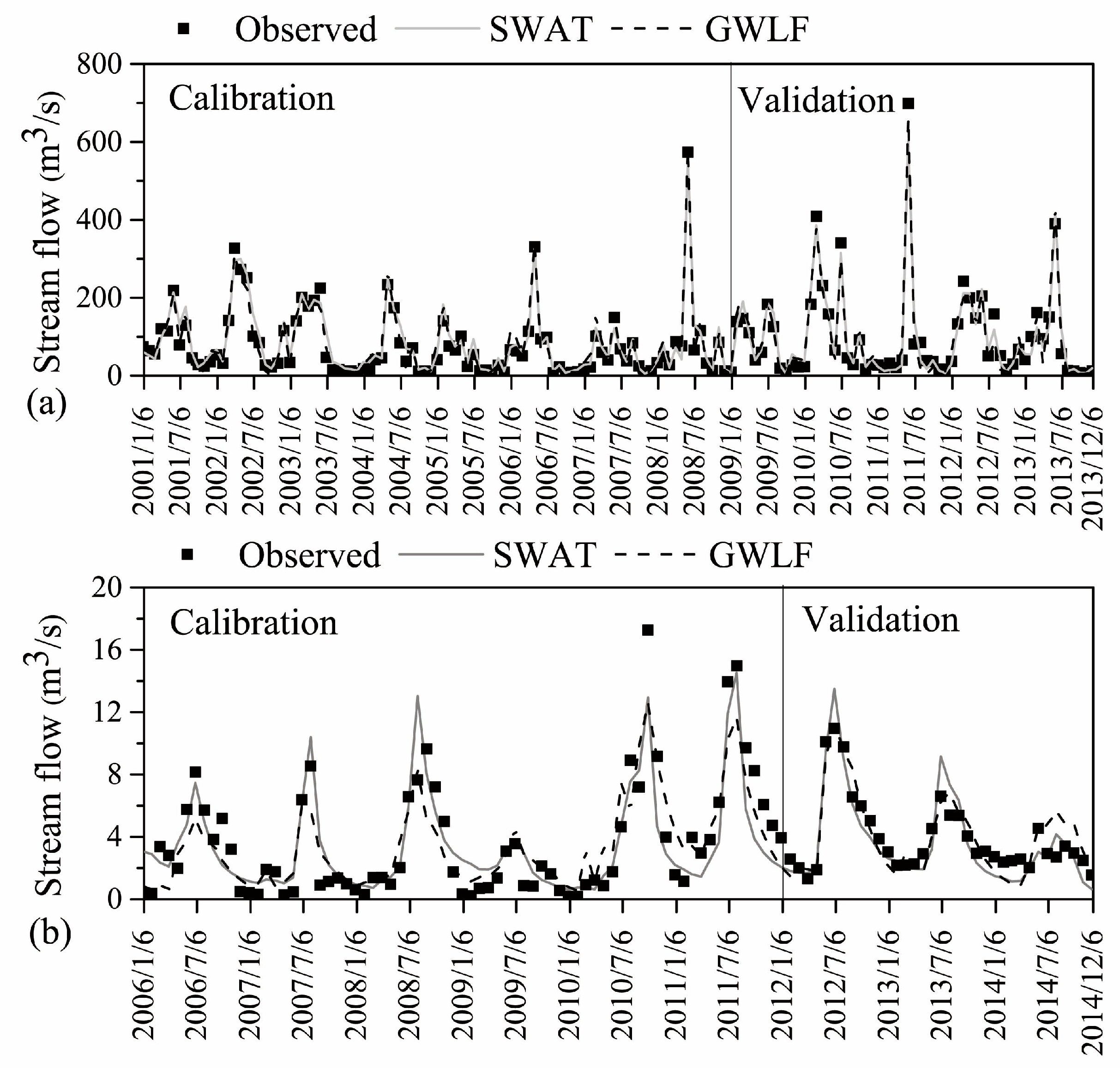
3.1. Flow
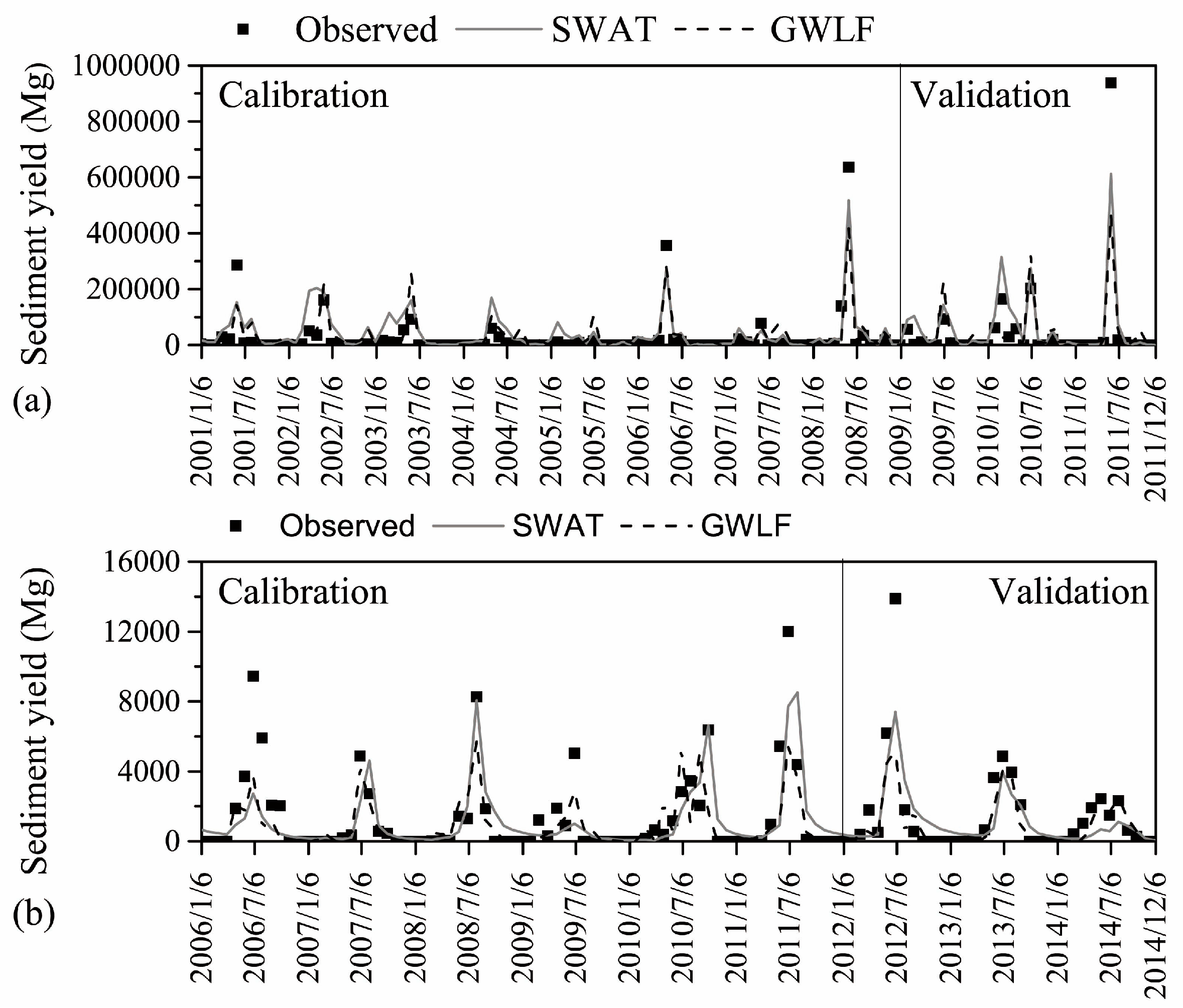
3.2. Sediment
3.3. Total Nitrogen
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Qu, J.; Fan, M. The Current State of Water Quality and Technology Development for Water Pollution Control in China. Crit. Rev. Environ. Sci. Technol. 2010, 40, 519–560. [Google Scholar] [CrossRef]
- Ongley, E.D.; Zhang, X.; Yu, T. Current status of agricultural and rural non-point source Pollution assessment in China. Environ. Pollut. 2010, 158, 1159–1168. [Google Scholar] [CrossRef] [PubMed]
- Sha, J.; Liu, M.; Wang, D.; Swaney, D.P.; Wang, Y. Application of the ReNuMa model in the Sha He river watershed: Tools for watershed environmental management. J. Environ. Manag. 2013, 124, 40–50. [Google Scholar] [CrossRef] [PubMed]
- Shoemaker, L.; Dai, T.; Koenig, J.; Hantush, M. TMDL Model Evaluation and Research Needs; National Risk Management Research Laboratory, US Environmental Protection Agency: Washington, DC, USA, 2005.
- Wellen, C.; Kamran-Disfani, A.-R.; Arhonditsis, G.B. Evaluation of the Current State of Distributed Watershed Nutrient Water Quality Modeling. Environ. Sci. Technol. 2015, 49, 3278–3290. [Google Scholar] [CrossRef] [PubMed]
- Borah, D.K.; Bera, M. Watershed-scale hydrologic and nonpoint-source pollution models: Review of mathematical bases. Trans. ASAE 2003, 46, 1553–1566. [Google Scholar] [CrossRef]
- Butts, M.B.; Payne, J.T.; Kristensen, M.; Madsen, H. An evaluation of the impact of model structure on hydrological modelling uncertainty for streamflow simulation. J. Hydrol. 2004, 298, 242–266. [Google Scholar] [CrossRef]
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large area hydrologic modeling and assessment—Part 1: Model development. JAWRA 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Arnold, J.G.; Moriasi, D.N.; Gassman, P.W.; Abbaspour, K.C.; White, M.J.; Srinivasan, R.; Santhi, C.; Harmel, R.D.; van Griensven, A.; Van Liew, M.W.; et al. Swat: Model Use, Calibration, And Validation. Trans. ASABE 2012, 55, 1491–1508. [Google Scholar] [CrossRef]
- Gassman, P.W.; Reyes, M.R.; Green, C.H.; Arnold, J.G. The soil and water assessment tool: Historical development, applications, and future research directions. Trans. ASABE 2007, 50, 1211–1250. [Google Scholar] [CrossRef]
- Yang, Q.; Zhang, X. Improving SWAT for simulating water and carbon fluxes of forest ecosystems. Sci. Total Environ. 2016, 569, 1478–1488. [Google Scholar] [CrossRef] [PubMed]
- Begou, J.C.; Jomaa, S.; Benabdallah, S.; Bazie, P.; Afouda, A.; Rode, M. Multi-Site Validation of the SWAT Model on the Bani Catchment: Model Performance and Predictive Uncertainty. Water 2016, 8, 178. [Google Scholar] [CrossRef]
- Sun, H.; Cornish, P.S. Estimating shallow groundwater recharge in the headwaters of the Liverpool Plains using SWAT. Hydrol. Process. 2005, 19, 795–807. [Google Scholar] [CrossRef]
- Yang, J.; Reichert, P.; Abbaspour, K.C.; Xia, J.; Yang, H. Comparing uncertainty analysis techniques for a SWAT application to the Chaohe Basin in China. J. Hydrol. 2008, 358, 1–23. [Google Scholar] [CrossRef]
- Li, Z.; Shao, Q.; Xu, Z.; Cai, X. Analysis of parameter uncertainty in semi-distributed hydrological models using bootstrap method: A case study of SWAT model applied to Yingluoxia watershed in northwest China. J. Hydrol. 2010, 385, 76–83. [Google Scholar] [CrossRef]
- Shen, Z.Y.; Chen, L.; Chen, T. Analysis of parameter uncertainty in hydrological and sediment modeling using GLUE method: A case study of SWAT model applied to Three Gorges Reservoir Region, China. Hydrol. Earth Syst. Sci. 2012, 16, 121–132. [Google Scholar] [CrossRef]
- Easton, Z.M.; Fuka, D.R.; Walter, M.T.; Cowan, D.M.; Schneiderman, E.M.; Steenhuis, T.S. Re-conceptualizing the soil and water assessment tool (SWAT) model to predict runoff from variable source areas. J. Hydrol. 2008, 348, 279–291. [Google Scholar] [CrossRef]
- Spruill, C.A.; Workman, S.R.; Taraba, J.L. Simulation of daily and monthly stream discharge from small watersheds using the SWAT model. Trans. ASAE 2000, 43, 1431–1439. [Google Scholar] [CrossRef]
- Stewart, G.R.; Munster, C.L.; Vietor, D.M.; Arnold, J.G.; McFarland, A.M.S.; White, R.; Provin, T. Simulating water quality improvements in the Upper North Bosque River watershed due to phosphorus export through turfgrass sod. Trans. ASABE 2006, 49, 357–366. [Google Scholar] [CrossRef]
- Dlamini, N.S.; Kamal, M.R.; Soom, M.A.B.M.; bin Mohd, M.S.F.; Abdullah, A.F.B.; Hin, L.S. Modeling Potential Impacts of Climate Change on Streamflow Using Projections of the 5th Assessment Report for the Bernam River Basin, Malaysia. Water 2017, 9, 226. [Google Scholar] [CrossRef]
- Franczyk, J.; Chang, H. The effects of climate change and urbanization on the runoff of the Rock Creek basin in the Portland metropolitan area, Oregon, USA. Hydrol. Process. 2009, 23, 805–815. [Google Scholar] [CrossRef]
- Schneiderman, E.M.; Pierson, D.C.; Lounsbury, D.G.; Zion, M.S. Modeling the hydrochemistry of the Cannonsville watershed with Generalized Watershed Loading Functions (GWLF). JAWRA 2002, 38, 1323–1347. [Google Scholar] [CrossRef]
- Jennings, E.; Allott, N.; Pierson, D.C.; Schneiderman, E.M.; Lenihan, D.; Samuelsson, P.; Taylor, D. Impacts of climate change on phosphorus loading from a grassland catchment: Implications for future management. Water Res. 2009, 43, 4316–4326. [Google Scholar] [CrossRef] [PubMed]
- Lin, C.-H.; Huang, T.-H.; Shaw, D. Applying Water Quality Modeling to Regulating Land Development in a Watershed. Water Resour. Manag. 2010, 24, 629–640. [Google Scholar] [CrossRef]
- DPPC. Guidelines for the Programming of Water Bodies Meeting Standards; Department of Pollution Prevention and Control, Ministry of Environmental Protection of the People’s Republic of China: Beijing, China, 2016.
- Borah, D.K.; Yagow, G.; Saleh, A.; Barnes, P.L.; Rosenthal, W.; Krug, E.C.; Hauck, L.M. Sediment and nutrient modeling for TMDL development and implementation. Trans. ASABE 2006, 49, 967–986. [Google Scholar] [CrossRef]
- Li, Z.; Xu, Z.; Li, Z. Performance of WASMOD and SWAT on hydrological simulation in Yingluoxia watershed in northwest of China. Hydrol. Process. 2011, 25, 2001–2008. [Google Scholar] [CrossRef]
- Parajuli, P.B.; Nelson, N.O.; Frees, L.D.; Mankin, K.R. Comparison of AnnAGNPS and SWAT model simulation results in USDA-CEAP agricultural watersheds in south-central Kansas. Hydrol. Process. 2009, 23, 748–763. [Google Scholar] [CrossRef]
- Wilcox, B.P.; Rawls, W.J.; Brakensiek, D.L.; Wight, J.R. Predicting runoff from Rangeland Catchments: A comparison of two models. Water Resour. Res. 1990, 26, 2401–2410. [Google Scholar] [CrossRef]
- Niraula, R.; Kalin, L.; Srivastava, P.; Anderson, C.J. Identifying critical source areas of nonpoint source pollution with SWAT and GWLF. Ecol. Model. 2013, 268, 123–133. [Google Scholar] [CrossRef]
- Neitsch, S.L.; Williams, J.; Arnold, J.; Kiniry, J. Soil and Water Assessment Tool Theoretical Documentation Version 2009; Texas Water Resources Institute: College Station, TX, USA, 2011. [Google Scholar]
- Haith, D.A.; Shoemaker, L.L. Generalized Watershed Loading Functions for Stream Flow Nutrients. JAWRA 1987, 23, 471–478. [Google Scholar] [CrossRef]
- Evans, B.M.; Lehning, D.W.; Corradini, K.J.; Petersen, G.W.; Nizeyimana, E.; Hamlett, J.M.; Robillard, P.D. A Comprehensive GIS-Based Modeling Approach for Predicting Nutrient Loads in Watersheds. J. Spat. Hydrol. 2002, 2, 1–18. [Google Scholar]
- Mockus, V. National Engineering Handbook Section 4, Hydrology; NTIS: Alexandria, VA, USA, 1972. [Google Scholar]
- Priestley, C.; Taylor, R. On the assessment of surface heat flux and evaporation using large-scale parameters. Mon. Weather Rev. 1972, 100, 81–92. [Google Scholar] [CrossRef]
- Hargreaves, G.H.; Samani, Z.A. Reference crop evapotranspiration from temperature. Appl. Eng. Agric. 1985, 1, 96–99. [Google Scholar] [CrossRef]
- Hamon, W.R. Estimating Potential Evapotranspiration. Proc. Am. Soc. Civ. Eng. 1961, 87, 107–120. [Google Scholar]
- Green, W.H.; Ampt, G. Studies on Soil Phyics. J. Agric. Sci. 1911, 4, 1–24. [Google Scholar] [CrossRef]
- Ogrosky, H.O.; Mockus, V. Hydrology of Agricultural Lands. In Handbook of Applied Hydrology; Chow, V.T., Ed.; McGraw-Hill: New York, NY, USA, 1964. [Google Scholar]
- Sloan, P.G.; Moore, I.D. Modeling subsurface stormflow on steeply sloping forested watersheds. Water Resour. Res. 1984, 20, 1815–1822. [Google Scholar] [CrossRef]
- Haan, C. A water yield model for small watersheds. Water Resour. Res. 1972, 8, 58–69. [Google Scholar] [CrossRef]
- Williams, J.R. Sediment Routing for Agricultural Watersheds. JAWRA 1975, 11, 965–974. [Google Scholar] [CrossRef]
- Williams, J.R. Sediment-yield prediction with universal equation using runoff energy factor. Present Prospect. Technol. Predict. Sedim. Yield Sources 1975, 40, 244–252. [Google Scholar]
- Wischmeier, W.H.; Smith, D.D. Predicting rainfall erosion losses-a guide to conservation planning. In Predicting Rainfall Erosion Losses—A Guide to Conservation Planning; Department of Agriculture: Washington, DC, USA, 1978. [Google Scholar]
- Brown, L.C.; Barnwell, T.O. The Enhanced Stream Water Quality Models QUAL2E and QUAL2E-UNCAS: Documentation and User Manual; US Environmental Protection Agency, Office of Research and Development, Environmental Research Laboratory: Washington, DC, USA, 1987.
- Zhai, X.; Zhang, Y.; Wang, X.; Xia, J.; Liang, T. Non-point source pollution modelling using Soil and Water Assessment Tool and its parameter sensitivity analysis in Xin’anjiang catchment, China. Hydrol. Process. 2014, 28, 1627–1640. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; Yang, J.; Maximov, I.; Siber, R.; Bogner, K.; Mieleitner, J.; Zobrist, J.; Srinivasan, R. Modelling hydrology and water quality in the pre-ailpine/alpine Thur watershed using SWAT. J. Hydrol. 2007, 333, 413–430. [Google Scholar] [CrossRef]
- Smedema, L.K.; Rycroft, D.W. Land Drainage: Planning and Design of Agricultural Systems; Batsford Academic and Educational Ltd.: London, UK, 1983. [Google Scholar]
- Haith, D.; Mandel, R.; Wu, R. GWLF: Generalized Watershed Loading Functions User’s Manual, Version 2.0; Cornell University: Ithaca, NY, USA, 1992. [Google Scholar]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Legates, D.R.; McCabe, G.J. Evaluating the use of “goodness-of-fit” measures in hydrologic and hydroclimatic model validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Gupta, H.V.; Sorooshian, S.; Yapo, P.O. Status of Automatic Calibration for Hydrologic Models: Comparison with Multilevel Expert Calibration. J. Hydrol. Eng. 1999, 4, 135–143. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Shen, Z.Y.; Gong, Y.W.; Li, Y.H.; Hong, Q.; Xu, L.; Liu, R.M. A comparison of WEPP and SWAT for modeling soil erosion of the Zhangjiachong Watershed in the Three Gorges Reservoir Area. Agric. Water Manag. 2009, 96, 1435–1442. [Google Scholar] [CrossRef]
- Suliman, A.H.A.; Jajarmizadeh, M.; Harun, S.; Mat Darus, I.Z. Comparison of Semi-Distributed, GIS-Based Hydrological Models for the Prediction of Streamflow in a Large Catchment. Water Resour. Manag. 2015, 29, 3095–3110. [Google Scholar] [CrossRef]
- Chahinian, N.; Moussa, R.; Andrieux, P.; Voltz, M. Comparison of infiltration models to simulate flood events at the field scale. J. Hydrol. 2005, 306, 191–214. [Google Scholar] [CrossRef]
- Lv, Y.Z.; Li, B.G. Pedology, 1st ed.; China Agriculture Press: Beijing, China, 2006; pp. 252–253. [Google Scholar]
- Jha, M.K.; Gassman, P.W.; Arnold, J.G. Water quality modeling for the Raccoon River watershed using SWAT. Trans. ASABE 2007, 50, 479–493. [Google Scholar] [CrossRef]


| Description | SWAT | GWLF |
|---|---|---|
| Model capabilities | Hydrology, sediment, nutrients, pesticides, bacteria, and other water quality factors; channel and reservoir routing, crop growth, transport in soil, management practices, and impoundment structures | Hydrology, sediment, and nutrients |
| Temporal resolution | Daily | Monthly |
| Spatial representation | Hydrologic response units | Landuse category |
| Interception | Water balance | - |
| Potential evapotranspiration (PET) | Penman–Monteith method; Priestley-Taylor method [35]; Hargreaves method [36] | Hamon method [37] |
| Runoff | SCS-CN [34]; Green and Ampt [38] | SCS-CN [39] |
| Infiltration/percolation | Water balance | Water balance |
| Lateral flow | Kinematic storage model [40] | - |
| Base flow | Empirical relations | Linear reservoir model [41] |
| River flow routing | Manning’s equation; variable storage routing method or Muskingum river routing method | - |
| Sediment yield | Modified Universal Soil Loss Equation (MUSLE) [42,43] | Universal Soil Loss Equation [44] |
| Sediment channel routing | Simplified Bagnold model or physics based approach | - |
| Nitrogen forms in output | Organic nitrogen, nitrate, nitrite, ammonium, and total nitrogen | Dissolved nitrogen, solid-phase nitrogen, and total nitrogen |
| Atmospheric nitrogen deposition | Wet and dry deposition | Nitrogen deposition |
| Nitrogen cycle and transmission in land phase | Mass balance and empirical relation | - |
| Nitrogen cycle and transmission in routing phase | QUAL2E model [45] | - |
| Nitrogen load | Empirical relations | User defined concentration |
| Type of Data | SWAT | GWLF | Tunxi | Hanjiaying |
|---|---|---|---|---|
| DEM | Digital elevation map | Digital elevation map | 30 m | 30 m |
| Landuse | Grid | Proportion | 1:100,000 | 1:100,000 |
| Soil | Grid and properties | - | 1:1,000,000 | 1:1,000,000 |
| Meteorological data | Daily air temperature (maximum, minimum, average), | Daily average temperature and precipitation | 28 stations | 30 stations |
| daily precipitation, daily wind, | ||||
| daily solar radiation, | (2000–2013) | (2006–2014) | ||
| daily relative humidity | ||||
| Flow discharge | monthly | Monthly | 1 station | 1 station |
| (2000–2013) | (2006–2014) | |||
| Sediment yield | monthly | Monthly | 1 station | 1 station |
| (2000–2011) | (2006–2014) | |||
| Nutrient load | monthly | Monthly | 1 station | 1 station |
| (2002–2013) | (2006–2014) |
| Model | Parameter Name | Description | Default Range | Calibrated Value | |
|---|---|---|---|---|---|
| Tunxi Watershed | Hanjiaying Watershed | ||||
| SWAT | CN2 | Initial SCS Runoff curve number for moisture condition II | 40–100 | Varies (45–95) 1 | Varies (43–77) 1 |
| GWQMN | Threshold depth of water in shallow aquifer required for the return flow to occur | 0–500 | 364.2203 | 201.3421 | |
| ALPHA_BF | Base flow alpha factor | 0–1 | 0.7759 | 0.381446 | |
| RCHRG_DP | Deep aquifer percolation factor | 0–0.5 | 0.0493 | 0.042637 | |
| ESCO | Soil evaporation compensation factor | 0–1 | 0.6737 | 0.59 | |
| CH_N2 | Manning’s “n” value for the main channel | 0.01–0.3 | 0.0148 | 0.22892 | |
| CH_K2 | Main channel conductivity | 0.01–500 | 102.495 | 407.831421 | |
| SLSOIL | Slope length for lateral subsurface flow | 10–120 | Varies (21–99) 2 | Varies (145–258) 2 | |
| SNOCOVMX | Minimum snow water content that corresponds to 100% snow cover | 0–500 | - | 12.482321 | |
| SMTMP | Snowmelt base temperature | −20–20 | - | −1.019328 | |
| SOL_K | Saturated hydraulic conductivity | 0–2000 | - | Varies (7–66) 1 | |
| GWLF | CN2 | Initial SCS Runoff curve number for moisture condition II | 0–100 | Varies (45–100) 1 | Varies (23–98) 1 |
| Recession coefficient | Groundwater discharge coefficient | 0.1 | 0.25 | 0.0017 | |
| Seepage coefficient | Groundwater seepage constant | 0 | 0.044 | 0.0096 | |
| Unsaturated available water | Available soil water capacity | - | 8.75 | 17.54 | |
| Model | Parameter Name | Description | Default Range | Calibrated Value | |
|---|---|---|---|---|---|
| Tunxi Watershed | Hanjiaying Watershed | ||||
| SWAT | USLE_K | USLE equation soil erodibility (K) factor | 0–0.65 | Varied (0.12–0.60) 3 | Varied (0.09–0.54) 3 |
| USLE_P | USLE equation support parameter | 0–1 | Varied (0.22–0.49) 2 | Varied (0.28–0.40) 2 | |
| PRF_BSN | Peak rate adjustment factor for sediment routing in the main channel | 0–2 | 0.0483 | 0.795668 | |
| SPEXP | Exponent parameter for calculating sediment re-entrained in channel | 1–1.5 | 1.3454 | 1.171564 | |
| SPCON | Linear parameter for calculating sediment re-entrained in channel | 0.0001–0.01 | 0.0052 | 0.00255 | |
| CH_COV1 | Channel erodibility factor | −0.05–0.6 | 0.26 | 0.193029 | |
| CH_COV2 | Channel cover factor | −0.001–1 | 0.4776 | 0.26354 | |
| CMN | Rate factor for humus mineralization of active organic nitrogen | 0.0001–0.003 | 0.0014 | 0.0004 | |
| CDN | Denitrification exponential rate coefficient | 0–3 | 1.0039 | 0.004 | |
| SDNCO | Denitrification threshold water content | 0–1 | 0.3846 | 0.1541 | |
| NPERCO | Nitrite percolation coefficient | 0–1 | 0.3646 | 0.3441 | |
| SHALLST_N | Concentration of nitrate in groundwater contribution to streamflow from subbasin | 0–1000 | 0.735 | 25.5726 | |
| ERORGN | Organic N enrichment ratio | 0–5 | 0.0025 | 0.1253 | |
| GWLF | Sediment delivery ratio | Used to calculate sediment supply | - | 0.039 | 0.1078 |
| Erosivity coefficient | Used to calculate rainfall erosivity | - | 0.08 (November–February) | 0.1 (November–February) | |
| 0.45 (March–October) | 0.27 (March–October) | ||||
| USLE parameter | Integrated parameter | - | Varied (0–0.14) 1 | Varied (0–0.1) 1 | |
| Urban N accumulation rate | - | - | 0.045 | 0.1 | |
| Nitrogen runoff coefficient | Rural runoff N concentration | - | Varied (0.4–2) 1 | Varied (0.5–4.5) 1 | |
| N (mg/L) in groundwater | N concentration in groundwater | - | 0.6 | 7 | |
| N (mg/kg) in sediment | N concentration in sediment | - | 1000 | 2147 | |
| Statistics | Excellent | Very Good | Good | Fair | Unsatisfactory |
|---|---|---|---|---|---|
| (0.90, 1] | (0.75, 0.9] | (0.65, 0.75] | (0.50, 0.65] | (0, 0.5] | |
| (0.90, 1] | (0.75, 0.9] | (0.65, 0.75] | (0.50, 0.65] | (−∞, 0.5] | |
| [0.00, 0.25) | [0.25, 0.50) | [0.50, 0.60) | [0.60, 0.70) | [0.70, +∞) | |
| [0, 5) | [5, 10) | [10, 15) | [15, 25) | [25, +∞) | |
| [0, 5) | [5, 15) | [15, 30) | [30, 55) | [55, +∞) | |
| [0,10) | [10, 25) | [25, 40) | [40, 70) | [70, +∞) |
| Statistics | Tunxi Watershed | Hanjiaying Watershed | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Flow | Sediment | TN | Flow | Sediment | TN | |||||||
| SWAT | GWLF | SWAT | GWLF | SWAT | GWLF | SWAT | GWLF | SWAT | GWLF | SWAT | GWLF | |
| Calibration Period | ||||||||||||
| Mean Observed | 78.8 | 24394.8 | 248689.4 | 3.6 | 1340.3 | 80542.8 | ||||||
| Mean Simulated | 86.4 | 82.0 | 43,403.3 | 29,324.6 | 137,255.9 | 24,1884.4 | 3.4 | 3.4 | 1140.1 | 929.8 | 65,820.1 | 85,912.1 |
| R2 | 0.95 | 0.96 | 0.75 | 0.75 | 0.89 | 0.88 | 0.78 | 0.80 | 0.57 | 0.59 | 0.81 | 0.79 |
| NSE | 0.94 | 0.95 | 0.68 | 0.74 | 0.65 | 0.87 | 0.78 | 0.77 | 0.57 | 0.54 | 0.77 | 0.77 |
| RSR | 0.24 | 0.21 | 0.56 | 0.51 | 0.58 | 0.35 | 0.47 | 0.48 | 0.65 | 0.67 | 0.48 | 0.47 |
| PBIAS | −9.69 | −4.03 | −77.92 | −20.21 | 39.85 | −9.32 | 5.31 | 4.97 | 14.93 | 30.63 | 18.28 | −6.67 |
| Validation Period | ||||||||||||
| Mean Observed | 100.5 | 46960.5 | 319899.5 | 3.9 | 1417.1 | 84859.2 | ||||||
| Mean Simulated | 99.3 | 97.5 | 63,640.2 | 38,824.1 | 179,762.7 | 283,900.1 | 3.6 | 3.9 | 1107.2 | 953.8 | 76,385.6 | 76,626.8 |
| R2 | 0.96 | 0.96 | 0.84 | 0.74 | 0.85 | 0.88 | 0.87 | 0.82 | 0.79 | 0.76 | 0.70 | 0.35 |
| NSE | 0.96 | 0.96 | 0.80 | 0.67 | 0.60 | 0.86 | 0.77 | 0.78 | 0.68 | 0.61 | 0.72 | 0.57 |
| RSR | 0.21 | 0.21 | 0.44 | 0.56 | 0.63 | 0.36 | 0.47 | 0.46 | 0.56 | 0.61 | 0.52 | 0.65 |
| PBIAS | 1.17 | 2.97 | −35.51 | 17.32 | 43.81 | 11.25 | 8.98 | −0.50 | 21.86 | 32.69 | 9.99 | 9.70 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qi, Z.; Kang, G.; Chu, C.; Qiu, Y.; Xu, Z.; Wang, Y. Comparison of SWAT and GWLF Model Simulation Performance in Humid South and Semi-Arid North of China. Water 2017, 9, 567. https://doi.org/10.3390/w9080567
Qi Z, Kang G, Chu C, Qiu Y, Xu Z, Wang Y. Comparison of SWAT and GWLF Model Simulation Performance in Humid South and Semi-Arid North of China. Water. 2017; 9(8):567. https://doi.org/10.3390/w9080567
Chicago/Turabian StyleQi, Zuoda, Gelin Kang, Chunli Chu, Yu Qiu, Ze Xu, and Yuqiu Wang. 2017. "Comparison of SWAT and GWLF Model Simulation Performance in Humid South and Semi-Arid North of China" Water 9, no. 8: 567. https://doi.org/10.3390/w9080567
APA StyleQi, Z., Kang, G., Chu, C., Qiu, Y., Xu, Z., & Wang, Y. (2017). Comparison of SWAT and GWLF Model Simulation Performance in Humid South and Semi-Arid North of China. Water, 9(8), 567. https://doi.org/10.3390/w9080567




