Modeling the Fate and Transport of Malathion in the Pagsanjan-Lumban Basin, Philippines
Abstract
:1. Introduction
2. Materials and Methods
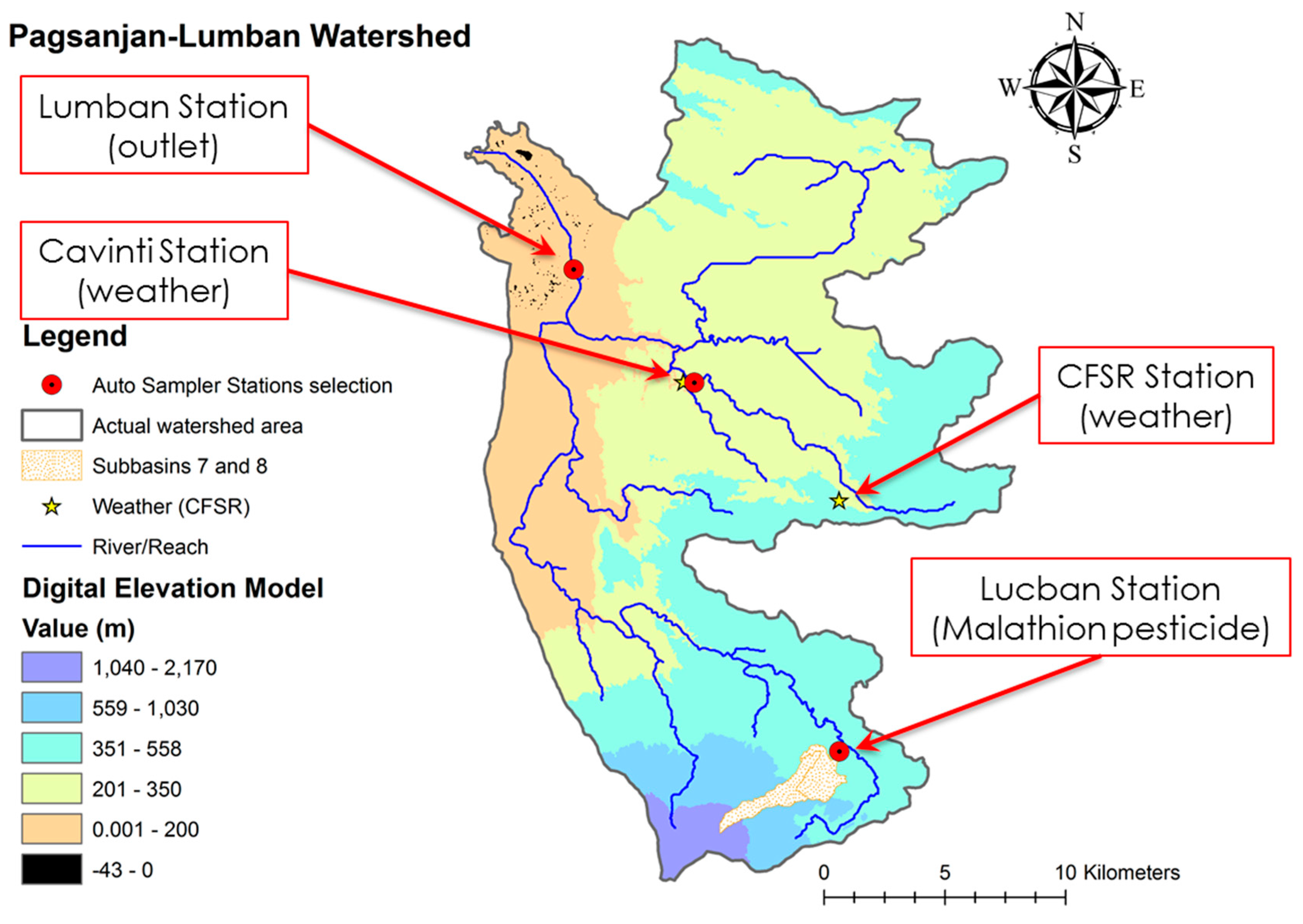
2.1. Study Area
2.2. Monitoring Data
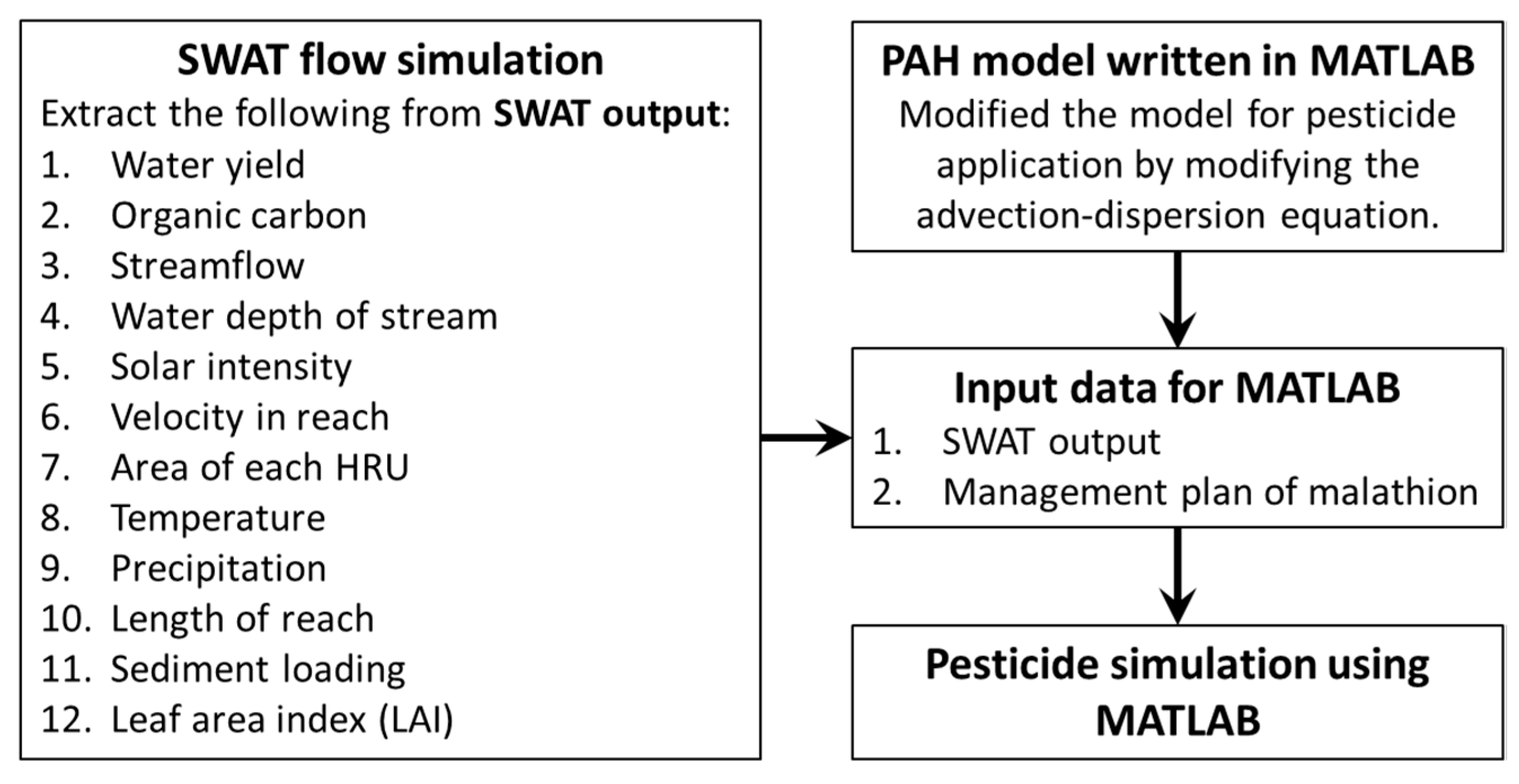
2.3. Hydrology Model
2.4. Pesticide Modeling
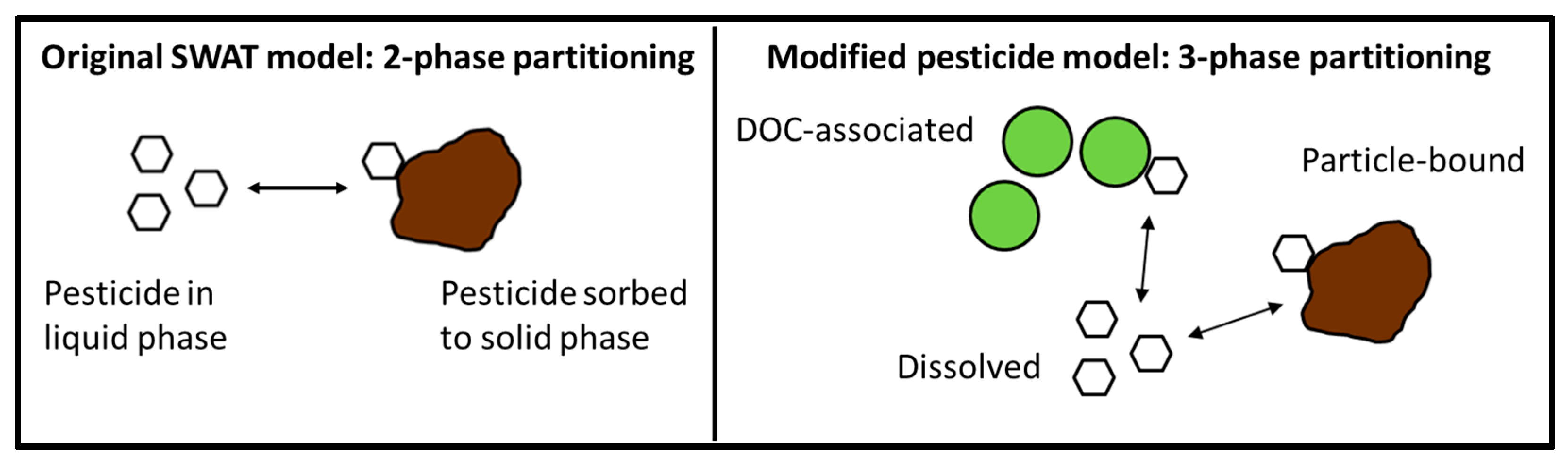
2.4.1. Original SWAT Pesticide Model
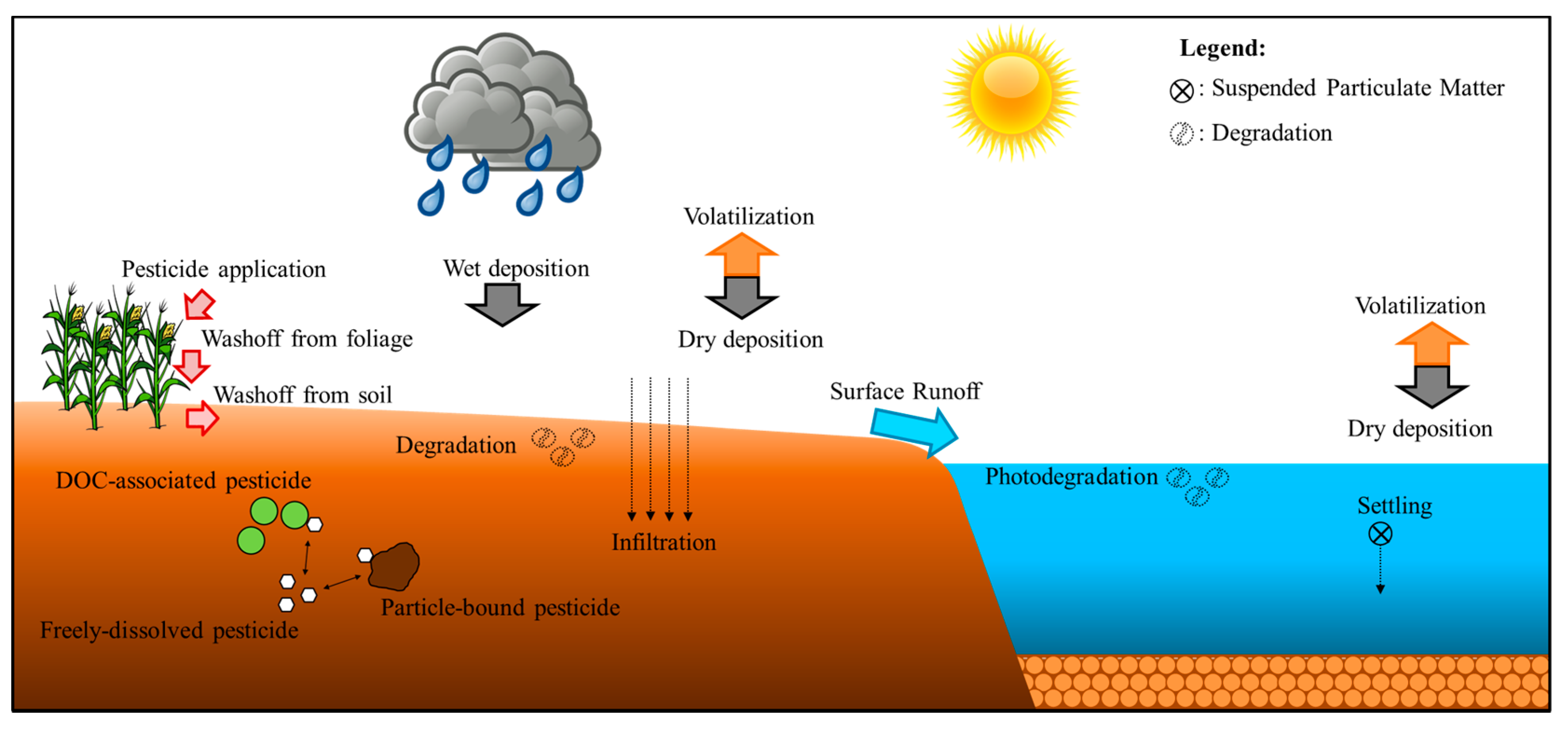
2.4.2. Modified Pesticide Model
Accumulation of Pesticide
Pesticides on Soil
Pesticides in Water
2.5. Sensitivity Analyses
2.6. Evaluation Criteria
3. Results and Discussion
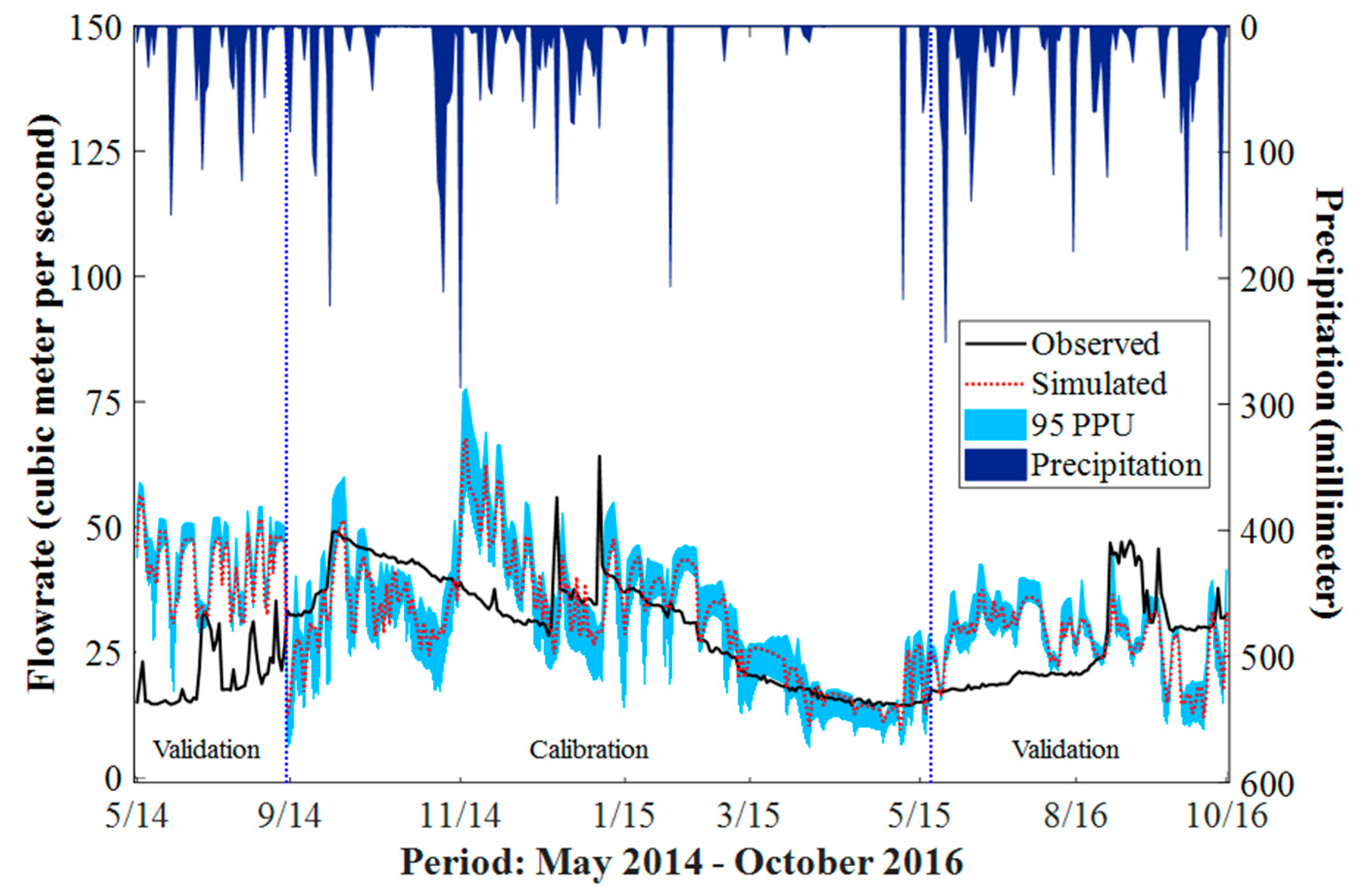
3.1. Flowrate Calibration
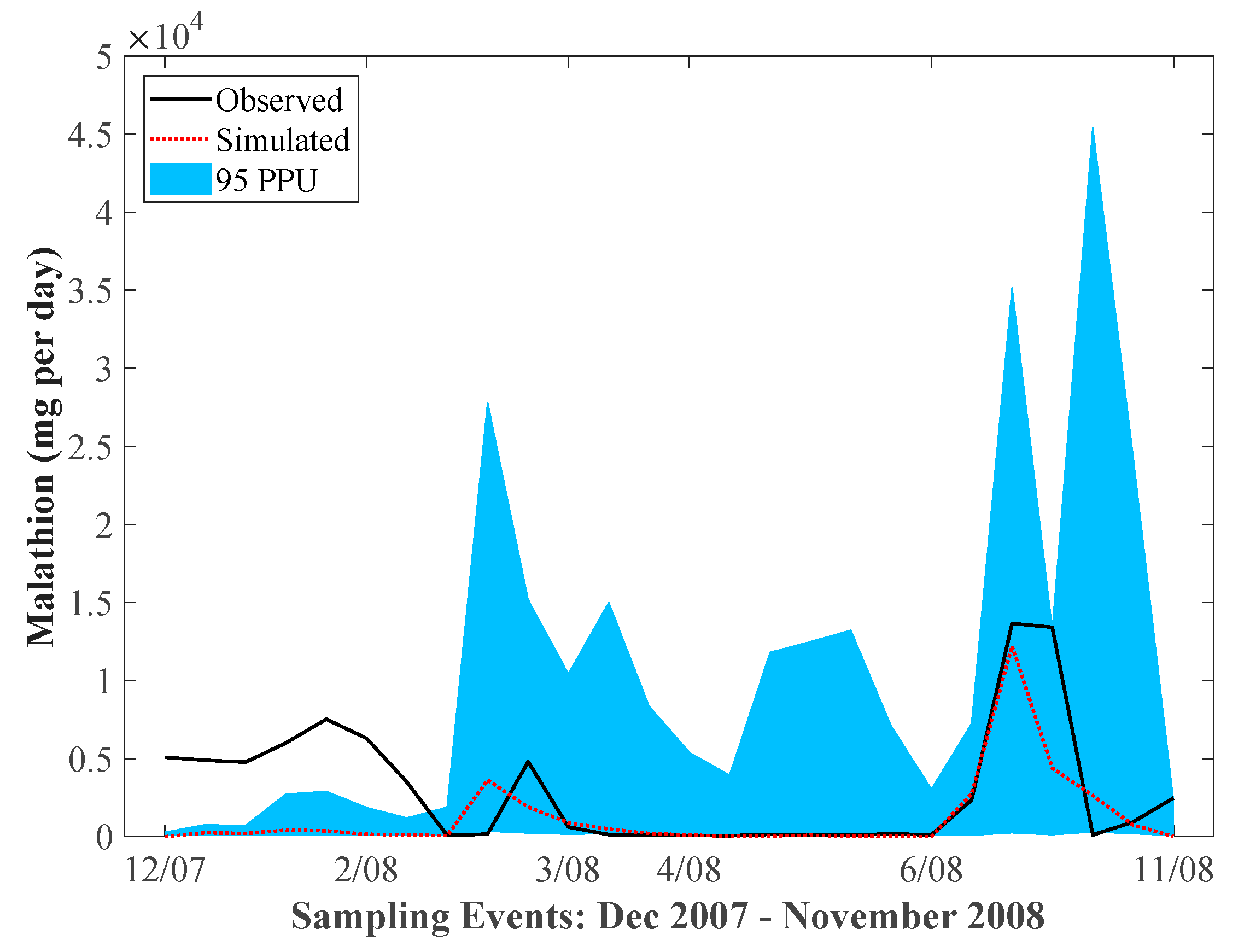
3.2. Pesticide Calibration with SWAT Pesticide Model
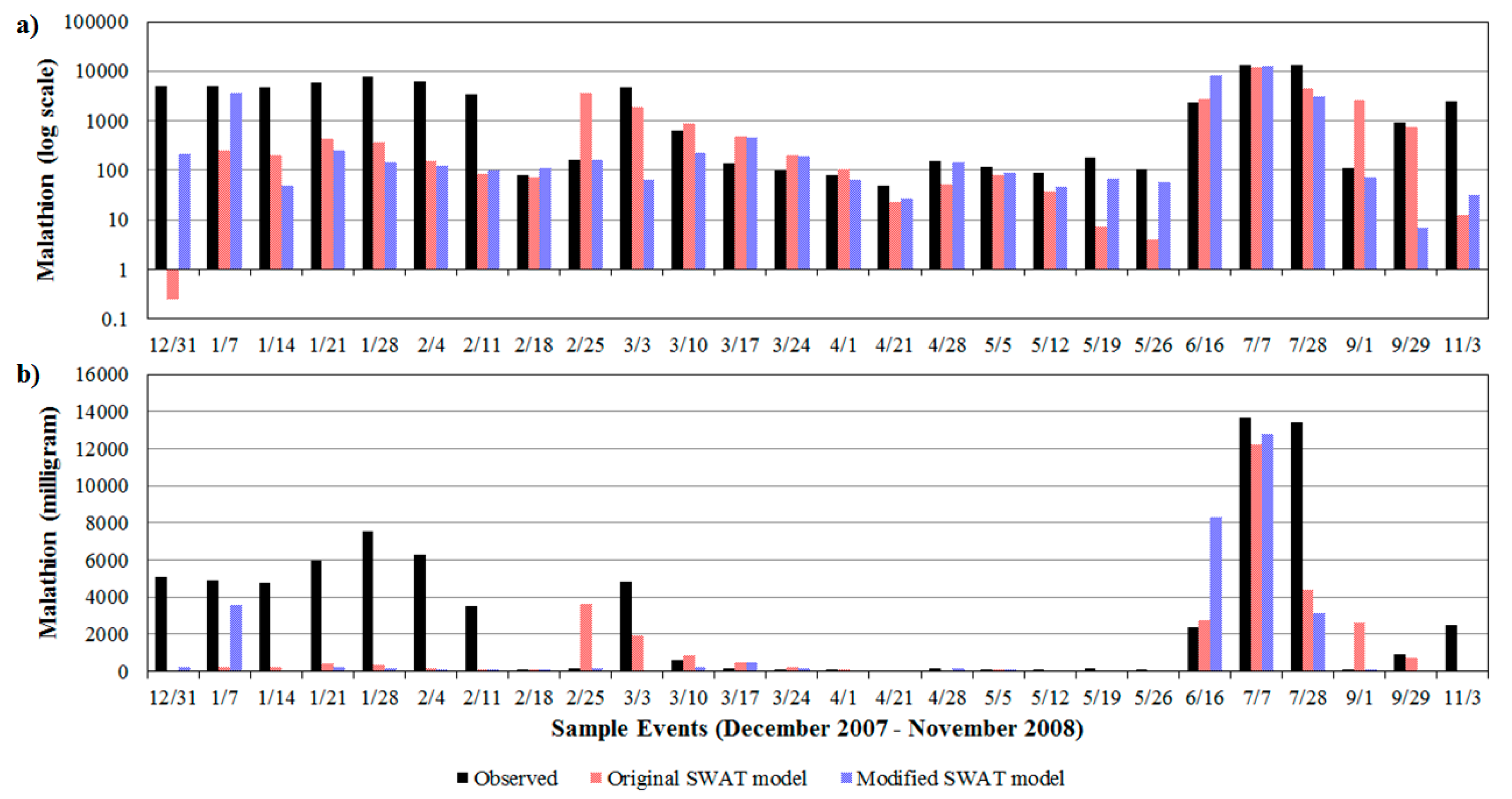
3.3. Pesticides Calibration with Modified Pesticide Model
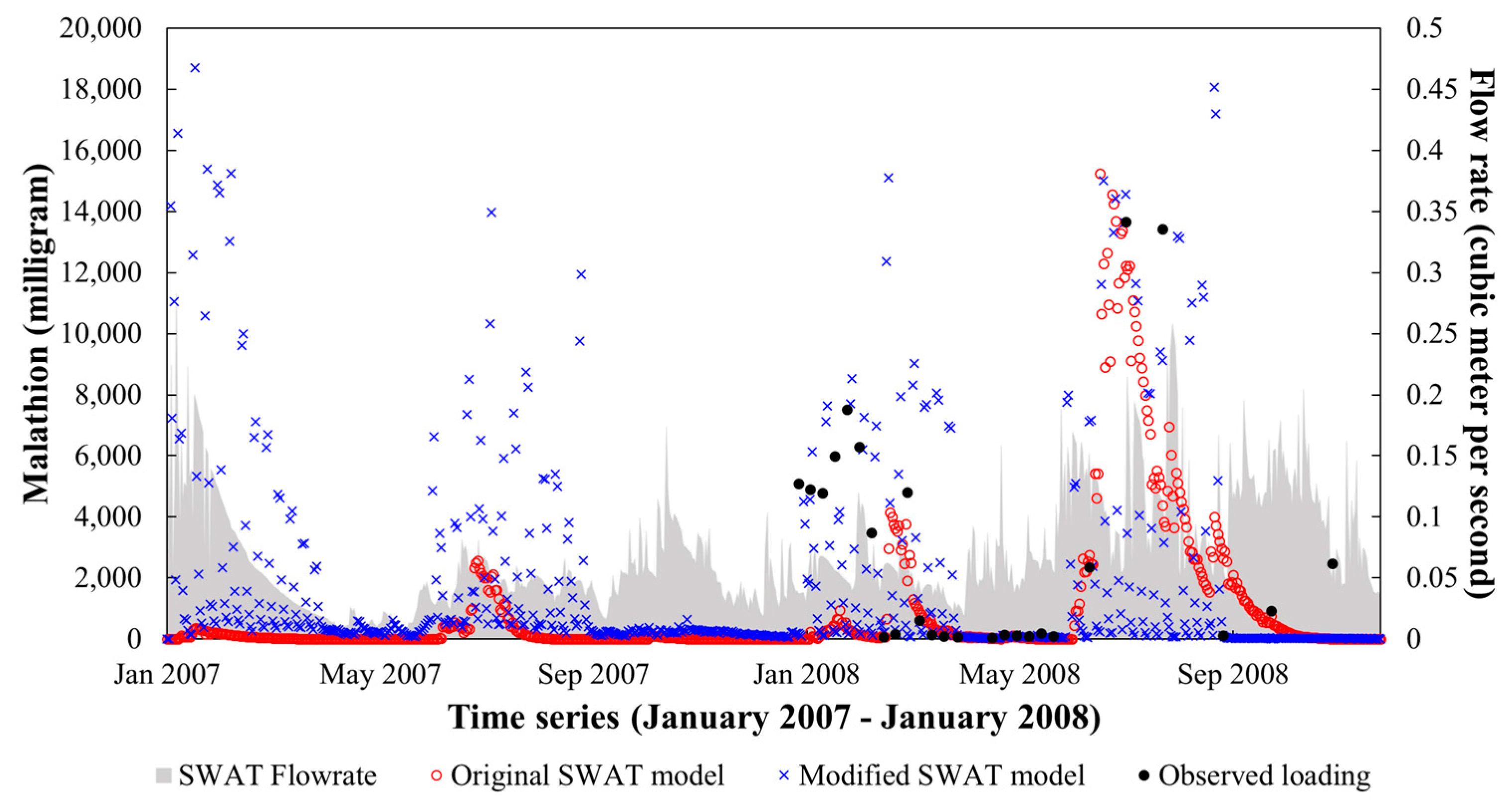
3.4. Comparison of Observed and Simulated Malathion Loading
4. Conclusions
- The sensitivity analysis of the hydrology model revealed that the flowrate of the PL basin is greatly influenced by the perviousness of the soil and the characteristics of the tributary channel that stores and retains the water in the basin.
- The modified pesticide model gave a slightly better performance compared to the original SWAT model, considering the statistical analyses performed (R2, NSE, PBIAS, and RMSE).
- Application efficiency was the most sensitive parameters for the original SWAT model, suggesting a possible need to improve the pesticide application and management practices of farmers in the basin, while settling velocity was the most sensitive for the modified models. Parameters associated with particulate-phase malathion, especially the degradation of particle-bound malathion, were also significant to both models.
- The temporal patterns of the target subbasin simulated by the models showed that the modified model has more consistent peaks during the duration of pesticide application compared to SWAT.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- The World Bank. Agriculture, Value Added (% of GDP). In World Development Indicators, 17 November 2016 ed.; The World Bank Group: Washington, DC, USA, 2016. [Google Scholar]
- Bassil, K.L.; Vakil, C.; Sanborn, M.; Cole, D.C.; Kaur, J.S.; Kerr, K.J. Cancer health effects of pesticides: Systematic review. Can. Fam. Phys. 2007, 53, 1704–1711. [Google Scholar]
- Colborn, T.; vom Saal, F.S.; Soto, A.M. Developmental effects of endocrine-disrupting chemicals in wildlife and humans. Environ. Health Perspect. 1993, 101, 378–384. [Google Scholar] [CrossRef] [PubMed]
- Bolognesi, C. Genotoxicity of pesticides: A review of human biomonitoring studies. Mutat. Res. 2003, 543, 251–272. [Google Scholar] [CrossRef]
- Jacobsen, C.S.; Hjelmsø, M.H. Agricultural soils, pesticides and microbial diversity. Curr. Opin. Biotechnol. 2014, 27, 15–20. [Google Scholar] [CrossRef] [PubMed]
- Geiger, F.; Bengtsson, J.; Berendse, F.; Weisser, W.W.; Emmerson, M.; Morales, M.B.; Ceryngier, P.; Liira, J.; Tscharntke, T.; Winqvist, C.; et al. Persistent negative effects of pesticides on biodiversity and biological control potential on european farmland. Basic Appl. Ecol. 2010, 11, 97–105. [Google Scholar] [CrossRef]
- Schäfer, R.B.; Caquet, T.; Siimes, K.; Mueller, R.; Lagadic, L.; Liess, M. Effects of pesticides on community structure and ecosystem functions in agricultural streams of three biogeographical regions in Europe. Sci. Total Environ. 2007, 382, 272–285. [Google Scholar] [CrossRef] [PubMed]
- Wauchope, R. The pesticide content of surface water draining from agricultural fields—A review. J. Environ. Qual. 1978, 7, 459–472. [Google Scholar] [CrossRef]
- Ritter, W. Pesticide contamination of ground water in the United States—A review. J. Environ. Sci. Health Part B 1990, 25, 1–29. [Google Scholar] [CrossRef]
- Balinova, A.; Mondesky, M. Pesticide contamination of ground and surface water in Bulgarian Danube plain. J. Environ. Sci. Health Part B 1999, 34, 33–46. [Google Scholar] [CrossRef] [PubMed]
- Kumari, B.; Madan, V.; Kathpal, T. Status of insecticide contamination of soil and water in Haryana, India. Environ. Monit. Assess. 2008, 136, 239–244. [Google Scholar] [CrossRef] [PubMed]
- Snelder, D.J.; Masipiqueña, M.D.; de Snoo, G.R. Risk assessment of pesticide usage by smallholder farmers in the Cagayan Valley (Philippines). Crop Prot. 2008, 27, 747–762. [Google Scholar] [CrossRef]
- Lapong, E.R.; Ella, V.B.; Villano, M.G.; Bato, P.M. Effects of climatic factors and land use on runoff, sediment load, and pesticide loading in upland microcatchments in Bukidnon, Philippines. Philipp. J. Agric. Biosys. Eng. 2008, 6, 49–56. [Google Scholar]
- Senoro, D.B.; Maravillas, S.L.; Ghafari, N.; Rivera, C.C.; Quiambao, E.C.; Lorenzo, M.C.M. Modeling of the residue transport of lambda cyhalothrin, cypermethrin, malathion and endosulfan in three different environmental compartments in the Philippines. Sustain. Environ. Res. 2016, 26, 168–176. [Google Scholar] [CrossRef]
- Santos-Borja, A.; Nepomuceno, D. Laguna de bay: Experience and lessons learned brief. World Lake Database. 2006, 15, 225–258. Available online: http://wldb.ilec.or.jp/data/gef_reports/15_Laguna_de_Bay_27February2006.pdf (accessed on 20 June 2017).
- Varca, L.M. Pesticide residues in surface waters of Pagsanjan-Lumban catchment of Laguna de Bay, Philippines. Agric. Water Manag. 2012, 106, 35–41. [Google Scholar] [CrossRef]
- Bajet, C.M.; Kumar, A.; Calingacion, M.N.; Narvacan, T.C. Toxicological assessment of pesticides used in the Pagsanjan-Lumban catchment to selected non-target aquatic organisms in Laguna Lake, Philippines. Agric. Water Manag. 2012, 106, 42–49. [Google Scholar] [CrossRef]
- Sanchez, P.B.; Oliver, D.P.; Castillo, H.C.; Kookana, R.S. Nutrient and sediment concentrations in the Pagsanjan-Lumban catchment of Laguna de Bay, Philippines. Agric. Water Manag. 2012, 106, 17–26. [Google Scholar] [CrossRef]
- Hallare, A.V.; Kosmehl, T.; Schulze, T.; Hollert, H.; Köhler, H.R.; Triebskorn, R. Assessing contamination levels of Laguna Lake sediments (Philippines) using a contact assay with zebrafish (Danio rerio) embryos. Sci. Total Environ. 2005, 347, 254–271. [Google Scholar] [CrossRef] [PubMed]
- Marín-Benito, J.M.; Pot, V.; Alletto, L.; Mamy, L.; Bedos, C.; Barriuso, E.; Benoit, P. Comparison of three pesticide fate models with respect to the leaching of two herbicides under field conditions in an irrigated maize cropping system. Sci. Total Environ. 2014, 499, 533–545. [Google Scholar] [CrossRef] [PubMed]
- Brisson, N.; Gary, C.; Justes, E.; Roche, R.; Mary, B.; Ripoche, D.; Zimmer, D.; Sierra, J.; Bertuzzi, P.; Burger, P.; et al. An overview of the crop model stics. Eur. J. Agron. 2003, 18, 309–332. [Google Scholar] [CrossRef]
- Boithias, L.; Sauvage, S.; Srinivasan, R.; Leccia, O.; Sánchez-Pérez, J.-M. Application date as a controlling factor of pesticide transfers to surface water during runoff events. CATENA 2014, 119, 97–103. [Google Scholar] [CrossRef]
- Boithias, L.; Sauvage, S.; Taghavi, L.; Merlina, G.; Probst, J.-L.; Sánchez Pérez, J.M. Occurrence of metolachlor and trifluralin losses in the save river agricultural catchment during floods. J. Hazard. Mater. 2011, 196, 210–219. [Google Scholar] [CrossRef] [PubMed]
- Fohrer, N.; Dietrich, A.; Kolychalow, O.; Ulrich, U. Assessment of the environmental fate of the herbicides flufenacet and metazachlor with the SWAT model. J. Environ. Qual. 2014, 43, 75–85. [Google Scholar] [CrossRef] [PubMed]
- Holvoet, K.; Gevaert, V.; van Griensven, A.; Seuntjens, P.; Vanrolleghem, P.A. Modelling the effectiveness of agricultural measures to reduce the amount of pesticides entering surface waters. Water Resour. Manag. 2007, 21, 2027–2035. [Google Scholar] [CrossRef]
- Zettam, A.; Taleb, A.; Sauvage, S.; Boithias, L.; Belaidi, N.; Sánchez-Pérez, J. Modelling hydrology and sediment transport in a semi-arid and anthropized catchment using the SWAT model: The case of the Tafna river (northwest Algeria). Water 2017, 9, 216. [Google Scholar] [CrossRef]
- Wu, Y.; Shi, X.; Li, C.; Zhao, S.; Pen, F.; Green, T. Simulation of hydrology and nutrient transport in the Hetao Irrigation District, Inner Mongolia, China. Water 2017, 9, 169. [Google Scholar] [CrossRef]
- Kintanar, R.L. Climate of the Philippines; PAGASA: Quezon City, Philippines, 1984. [Google Scholar]
- Cruz, R.V.O.; Pillas, M.; Castillo, H.C.; Hernandez, E.C. Pagsanjan-Lumban catchment, Philippines: Summary of biophysical characteristics of the catchment, background to site selection and instrumentation. Agric. Water Manag. 2012, 106, 3–7. [Google Scholar] [CrossRef]
- Dile, Y.T.; Srinivasan, R. Evaluation of CFSR climate data for hydrologic prediction in data-scarce watersheds: An application in the Blue Nile River Basin. J. Am. Water Resour. Assoc. 2014, 50, 1226–1241. [Google Scholar] [CrossRef]
- Fuka, D.R.; Walter, M.T.; MacAlister, C.; Degaetano, A.T.; Steenhuis, T.S.; Easton, Z.M. Using the climate forecast system reanalysis as weather input data for watershed models. Hydrol. Proc. 2014, 28, 5613–5623. [Google Scholar] [CrossRef]
- Holvoet, K.; van Griensven, A.; Seuntjens, P.; Vanrolleghem, P.A. Sensitivity analysis for hydrology and pesticide supply towards the river in SWAT. Phys. Chem. Earth Parts A/B/C 2005, 30, 518–526. [Google Scholar] [CrossRef]
- Ligaray, M.; Kim, H.; Sthiannopkao, S.; Lee, S.; Cho, K.; Kim, J. Assessment on hydrologic response by climate change in the Chao Phraya River Basin, Thailand. Water 2015, 7, 6892–6909. [Google Scholar] [CrossRef]
- Luo, Y.; Zhang, M. Management-oriented sensitivity analysis for pesticide transport in watershed-scale water quality modeling using SWAT. Environ. Pollut. 2009, 157, 3370–3378. [Google Scholar] [CrossRef] [PubMed]
- Fabro, L.; Varca, L.M. Pesticide usage by farmers in Pagsanjan-Lumban catchment of Laguna de Bay, Philippines. Agric. Water Manag. 2012, 106, 27–34. [Google Scholar] [CrossRef]
- Ligaray, M.; Baek, S.S.; Kwon, H.-O.; Choi, S.-D.; Cho, K.H. Watershed-scale modeling on the fate and transport of polycyclic aromatic hydrocarbons (PAHs). J. Hazard. Mater. 2016, 320, 442–457. [Google Scholar] [CrossRef] [PubMed]
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Williams, J.R. Soil and Water Assessment Tool Theoretical Documentation Version 2009; Texas Water Resources Institute: College Station, TX, USA, 2011. [Google Scholar]
- Bergknut, M.; Meijer, S.; Halsall, C.; Ågren, A.; Laudon, H.; Köhler, S.; Jones, K.C.; Tysklind, M.; Wiberg, K. Modelling the fate of hydrophobic organic contaminants in a boreal forest catchment: A cross disciplinary approach to assessing diffuse pollution to surface waters. Environ. Pollut. 2010, 158, 2964–2969. [Google Scholar] [CrossRef] [PubMed]
- Van Griensven, A.; Meixner, T.; Grunwald, S.; Bishop, T.; Diluzio, M.; Srinivasan, R. A global sensitivity analysis tool for the parameters of multi-variable catchment models. J. Hydrol. 2006, 324, 10–23. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Gitau, M.W.; Pai, N.; Daggupati, P. Hydrologic and water quality models: Performance measures and evaluation criteria. Trans. ASABE 2015, 58, 1763–1785. [Google Scholar]
- Roy, K.; Das, R.N.; Ambure, P.; Aher, R.B. Be aware of error measures. Further studies on validation of predictive qsar models. Chem. Intell. Lab. Syst. 2016, 152, 18–33. [Google Scholar] [CrossRef]
- Moriasi, D.; Arnold, J.; Van Liew, M.; Bingner, R.; Harmel, R.; Veith, T. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Abbaspour, K.C. SWAT Calibration and Uncertainty Programs—A User Manual; Eawag—Swiss Federal Institute of Aquatic Science and Technology: Dübendorf, Switzerland, 2007; Volume 103. [Google Scholar]
- Bouraoui, F.; Benabdallah, S.; Jrad, A.; Bidoglio, G. Application of the swat model on the Medjerda river basin (Tunisia). Phys. Chem. Earth Parts A/B/C 2005, 30, 497–507. [Google Scholar] [CrossRef]
- Li, Z.; Xu, Z.; Shao, Q.; Yang, J. Parameter estimation and uncertainty analysis of SWAT model in upper reaches of the Heihe river basin. Hydrol. Proc. 2009, 23, 2744–2753. [Google Scholar] [CrossRef]
- Neitsch, S.; Arnold, J.G.; Kiniry, J.R.; Srinivasan, R.; Williams, J.R. Soil and Water Assessment Tool Input/Output File Documentation Version 2009; Texas Water Resources Institute: Forney, TX, USA, 2010; Volume 365. [Google Scholar]
- Me, W.; Abell, J.M.; Hamilton, D.P. Effects of hydrologic conditions on SWAT model performance and parameter sensitivity for a small, mixed land use catchment in New Zealand. Hydrol. Earth Syst. Sci. 2015, 19, 4127–4147. [Google Scholar] [CrossRef]
- Schuol, J.; Abbaspour, K.C.; Srinivasan, R.; Yang, H. Estimation of freshwater availability in the West African sub-continent using the SWAT hydrologic model. J. Hydrol. 2008, 352, 30–49. [Google Scholar] [CrossRef]
- Newhart, K. Environmental Fate of Malathion; California Environmental Protection Agency: Sacramento, CA, USA, 2006. [Google Scholar]
| Process | Period |
|---|---|
| Spinup Time (2 years) | January 2005–December 2006 |
| Pesticide Calibration | December 2007–November 2008 |
| Flow Calibration | September 2014–May 2015 |
| Flow Validation | May 2014–July 2014 and June 2016–September 2016 |
| Parameter | Description | Module | Method | MIN | MAX |
|---|---|---|---|---|---|
| CN2 | Initial SCS runoff curve number for moisture condition II | MGT | Relative | −0.1 | 0.1 |
| BIOMIX | Biological mixing coefficiency | MGT | Replace | 0 | 1 |
| ALPHA_BF | Baseflow alpha factor (days) | GW | Replace | 0.01 | 1 |
| GW_DELAY | Groundwater delay time (days) | GW | Replace | 0 | 500 |
| GWQMN | Threshold depth of water in the shallow aquifer required for return flow to occur (mm H2O) | GW | Replace | 0 | 50 |
| REVAPMN | Threshold depth of water in the shallow aquifer for revap or percolation to the deep aquifer to occur (mm H2O) | GW | Replace | 0 | 750 |
| RCHRG_DP | Deep aquifer percolation fraction | GW | Replace | 0.01 | 0.99 |
| GW_REVAP | Groundwater “revap” coefficient | GW | Replace | 0.02 | 0.2 |
| ESCO | Soil evaporation compensation factor | HRU | Replace | 0.7 | 1 |
| EPCO | Plant uptake compensation factor | HRU | Replace | 0.7 | 1 |
| SLSUBBSN | Average slope length (m) | HRU | Replace | 10 | 150 |
| LAT_TTIME | Lateral flow travel time (days) | HRU | Replace | 0 | 180 |
| OV_N | Manning’s “n” value for overland flow | HRU | Replace | 0.01 | 0.5 |
| CANMX | Maximum canopy storage (mm H2O) | HRU | Replace | 0 | 100 |
| CH_K2 | Effective hydraulic conductivity in main channel alluvium (mm/h) | RTE | Replace | 0.025 | 76 |
| CH_N2 | Manning’s “n” value for the main channel | RTE | Replace | 0.025 | 0.15 |
| SOL_BD | Moist bulk density (Mg/m3 or g/cm3) | SOL | Relative | −0.1 | 0.1 |
| SOL_CBN | Organic carbon content (% soil content) | SOL | Relative | −0.1 | 0.1 |
| SOL_K | Saturated hydraulic conductivity (mm/h) | SOL | Relative | −0.1 | 0.1 |
| SOL_AWC | Available water capacity of the soil layer (mm H2O/mm soil) | SOL | Relative | −0.1 | 0.1 |
| CH_K1 | Effective hydraulic conductivity in tributary channel alluvium (mm/h) | SUB | Replace | 0.025 | 76 |
| CH_N1 | Manning’s “n” value for the tributary channel | SUB | Replace | 0.025 | 0.15 |
| SURLAG | Surface runoff lag coefficient (h) | BSN | Replace | 0.05 | 10 |
| Parameter | Description | Module | Method | MIN | MAX |
|---|---|---|---|---|---|
| SKOC | Soil adsorption coefficient normalized for soil organic carbon (L·kg−1) | PEST | Replace | 1 | 5000 |
| HLIFE_S | Degradation half-life of the chemical on the soil (day−1) | PEST | Replace | 0 | 100 |
| HLIFE_F | Degradation half-life of the chemical on the foliage (day−1) | PEST | Replace | 0 | 100 |
| WSOL | Solubility of the chemical in water | PEST | Replace | 0 | 1000 |
| WOF | Wash off fraction | PEST | Replace | 0 | 1 |
| AP_EF | Application efficiency | PEST | Replace | 0 | 1 |
| PST_DEP | Depth of pesticide incorporation in the soil (mm) | MGT | Replace | 0 | 500 |
| PERCOP | Pesticide percolation coefficient | BSN | Replace | 0 | 1 |
| CHPST_KOC | Pesticide partition coefficient between water and sediment in reach (m3·g−1) | SWQ | Replace | 0 | 0.1 |
| CHPST_REA | Pesticide reaction coefficient in reach (day−1) | SWQ | Replace | 0 | 0.1 |
| CHPST_VOL | Pesticide volatilization coefficient in reach (m·day−1) | SWQ | Replace | 0 | 10 |
| CHPST_STL | Settling velocity for pesticide sorbed to sediment (m·day−1) | SWQ | Replace | 0 | 10 |
| SEDPST_REA | Pesticide reaction coefficient in reach bed sediment (day−1) | SWQ | Replace | 0 | 0.1 |
| CHPST_RSP | Resuspension velocity for pesticide sorbed to sediment (m·day−1) | SWQ | Replace | 0 | 1 |
| SEDPST_ACT | Depth of active sediment layer for pesticide (m) | SWQ | Replace | 0 | 1 |
| CHPST_MIX | Mixing velocity (diffusion/dispersion) for pesticide in reach (m·day−1) | SWQ | Replace | 0 | 0.1 |
| SEDPST_BRY | Pesticide burial velocity in reach bed sediment (m·day−1) | SWQ | Replace | 0 | 0.1 |
| PSTENR | Enrichment ratio for pesticide in the soil | CHM | Replace | 0 | 5 |
| Parameter | Description | Unit |
|---|---|---|
| foc | Organic carbon fraction in soil | - |
| ρsoil | Soil density | kg·m−3 |
| poro | Porosity | |
| fDOC | Fraction of the dissolve organic carbon | - |
| x1 | Enrichment ratio coefficient 1 | - |
| x2 | Enrichment ratio coefficient 2 | - |
| vs | Settling velocity of suspended particles in the channel | m·s−1 |
| En | Diffusion coefficient | - |
| Cp,1 | Wash off coefficient for particle-bound pesticide | - |
| Cfd,1 | Wash off coefficient for dissolved pesticide | - |
| Cp,2 | Wash off exponent for particle-bound pesticide | - |
| Cfd,2 | Wash off exponent for dissolved pesticide | - |
| α | Decay coefficient in water due to solar intensity | - |
| CDOC,1 | Wash off coefficient for DOC-associated pesticide | - |
| CDOC,2 | Wash off exponent for DOC-associated pesticide | - |
| µk,p | Degradation rate constant for the particle-bound pesticide on the soil surface | s−1 |
| θk,p | Temperature adjustment factor for particle-bound pesticide | - |
| µk,fd | Degradation rate constant for the dissolved pesticide on the soil surface | s−1 |
| θk,fd | Temperature adjustment factor for dissolved pesticide | - |
| µk,DOC | Degradation rate constant for the DOC-associated pesticide on the soil surface | s−1 |
| θk,DOC | Temperature adjustment factor for DOC-associated pesticide | - |
| Rank | Parameter | Fitted Value |
|---|---|---|
| 1 | SURLAG | 0.051 |
| 2 | CH_N1 | 0.12 |
| 3 | CN2 | −0.096 |
| 4 | ALPHA_BF | 0.46 |
| 5 | CH_K1 | 48.4 |
| 6 | RCHRG_DP | 0.97 |
| 7 | CH_K2 | 42.2 |
| 8 | SLSUBBSN | 75.8 |
| 9 | OV_N | 0.33 |
| Rank | Parameters | Fitted Value |
|---|---|---|
| 1 | AP_EF | 0.13 |
| 2 | CHPST_KOC | 0.0012 |
| 3 | HLIFE_S | 6.26 |
| 4 | CHPST_REA | 0.037 |
| 5 | SKOC | 3594.52 |
| Rank | Parameters | Fitted Value |
|---|---|---|
| 1 | vs | 0.0001 |
| 2 | µk,fd | 4.25 × 10−5 |
| 3 | Cfd,1 | 1.14 |
| 4 | Cfd,2 | 0.549 |
| 5 | poro | 0.50 |
| 6 | foc | 0.20 |
| 7 | En | 0.1006 |
| 8 | θk,p | 1.16 × 10−5 |
| 9 | ρsoil | 1.06 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ligaray, M.; Kim, M.; Baek, S.; Ra, J.-S.; Chun, J.A.; Park, Y.; Boithias, L.; Ribolzi, O.; Chon, K.; Cho, K.H. Modeling the Fate and Transport of Malathion in the Pagsanjan-Lumban Basin, Philippines. Water 2017, 9, 451. https://doi.org/10.3390/w9070451
Ligaray M, Kim M, Baek S, Ra J-S, Chun JA, Park Y, Boithias L, Ribolzi O, Chon K, Cho KH. Modeling the Fate and Transport of Malathion in the Pagsanjan-Lumban Basin, Philippines. Water. 2017; 9(7):451. https://doi.org/10.3390/w9070451
Chicago/Turabian StyleLigaray, Mayzonee, Minjeong Kim, Sangsoo Baek, Jin-Sung Ra, Jong Ahn Chun, Yongeun Park, Laurie Boithias, Olivier Ribolzi, Kangmin Chon, and Kyung Hwa Cho. 2017. "Modeling the Fate and Transport of Malathion in the Pagsanjan-Lumban Basin, Philippines" Water 9, no. 7: 451. https://doi.org/10.3390/w9070451
APA StyleLigaray, M., Kim, M., Baek, S., Ra, J.-S., Chun, J. A., Park, Y., Boithias, L., Ribolzi, O., Chon, K., & Cho, K. H. (2017). Modeling the Fate and Transport of Malathion in the Pagsanjan-Lumban Basin, Philippines. Water, 9(7), 451. https://doi.org/10.3390/w9070451








