Next Article in Journal
Optimal Hedging Rules for Water Supply Reservoir Operations under Forecast Uncertainty and Conditional Value-at-Risk Criterion
Previous Article in Journal
Comparison of SWAT and GWLF Model Simulation Performance in Humid South and Semi-Arid North of China
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Water
Volume 9
Issue 8
10.3390/w9080566
water-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Simulating the Effects of Lake Wind Waves on Water and Solute Exchange across the Lakeshore Using Hydrus-2D

by
Yong Li
1,2,*,
Jirka Šimůnek
3,
Shuang Wang
2,
Weiwei Zhang
2 and
Jiahui Yuan
2
1
Ministry of Education Key Laboratory of Integrated Regulation and Resource Development on Shallow Lakes, Hohai University, Nanjing 210098, China
2
College of Environment, Hohai University, Nanjing 210098, China
3
Department of Environmental Sciences, University of California, Riverside, CA 92521, USA
*
Author to whom correspondence should be addressed.
Water 2017, 9(8), 566; https://doi.org/10.3390/w9080566
Submission received: 28 March 2017 / Revised: 23 July 2017 / Accepted: 26 July 2017 / Published: 30 July 2017
Browse Figures
Versions Notes

Abstract

:
Wind waves, which frequently occur on large surface water bodies such as lakes, may temporarily alter flow patterns in a subsurface zone and the corresponding water and nutrient interactions between surface waters and shallow groundwaters. To better understand these processes, soil flume experiments were carried out to investigate wind wave-driven water and chloride interactions across the lake–groundwater interface, and the Hydrus-2D model was used to analyze and evaluate the observed experimental results. Two interaction cases between the lake and groundwater systems were considered: groundwater discharging into a lake (the GDL case), and lake water recharging groundwater (the LRG case). For comparison, no-wave conditions for both the GDL and LRG cases were also analyzed. The results revealed that, similarly to no-wave conditions, water and chloride exchange fluxes between the lake and groundwater systems under wave conditions occurred mainly within narrow bands near the intersection of the water level in the lake and the interface in both the GDL and LRG cases, and then exponentially decreased along the interface. Most water and chloride that infiltrated into the subsurface zone through the upper part of the interface during a wave crest returned to the lake through the lower part during a wave trough in both the GDL and LRG cases, creating local recirculation zones in the subsurface near the interface. Such recirculation produced a more frequent exchange of water and solute across the interface compared with those under no-wave conditions. During a one-day period after wind waves started, the total exchange fluxes of water and chloride to the lake decreased by 36.2% and 71.9%, respectively, compared to the no-wave conditions in the GDL case. In the LRG case, the total exchange water fluxes to the subsurface increased by 89.7%, while the total exchange chloride fluxes increased only slightly (4.5%) compared to the no-wave conditions due to the difference in chloride concentrations between the upper and lower parts of the interface. The sensitivity analysis revealed that the hydraulic conductivity of the lakeshore zone and the characteristics of the waves were important factors influencing water and chloride exchange between the lake and groundwater systems. The simulated results helped us to better understand water and solute interactions in the lake–groundwater system during windy periods.

1. Introduction

The exchange of water and nutrients between groundwater and surface water bodies, such as lakes, occurs everywhere where aquifers are hydraulically connected to surface water bodies [1]. Interactions between lake and groundwater systems have become major concerns during recent decades [2,3,4,5], since they may exert an important control on lake ecology [6,7] and on the nearshore water quality [8] in multiple ways. An understanding of the distribution and rate of seepage to and from lakes is therefore needed for environmental management and the restoration of lake ecosystems [8,9,10].
Studies evaluating water and solute exchange between surface waters and groundwater have been frequently reported for coastal regions, especially with respect to tide (or wave)-driven water level fluctuations [5,11,12]. For example, Harvey et al. [13] used a one-dimensional numerical model to explore the effects of tidal amplitudes and mean water levels on the groundwater flow of a Virginia salt marsh (USA). They found that an increase in the elevation of the mean water level relative to the top of the marsh platform caused a significant decrease in the total volume of groundwater exchange over a tidal cycle. A two-dimensional numerical model developed by Wilson and Gardner [14] showed that, for the same tidal amplitude, the groundwater exchange in a simulated marsh was higher when the marsh was inundated by the tide than when it was not. Waves create steep hydraulic gradients near the interface between the surface and groundwater and local water circulations in the subsurface zone, which largely accelerates water exchange [15,16,17,18]. Xin et al. [19] reported that wave-induced circulations increased both water flows in the nearshore zone and the exchange between the subterranean estuary and ocean, contributing 61% of the total submarine groundwater discharge for simulated conditions.
Furthermore, tide (or wave)-driven groundwater table fluctuations in coastal regions were also shown to impact solute exchange across the sediment–surface water interface [19,20,21,22]. Chen and Pinder [1] reported that tidal fluctuations decrease the average concentrations of groundwater contaminants discharging into coastal waters. Wilson and Morris [23] reported that tidal fluctuations are the most important driver for groundwater exchange in coastal areas. Small increases in the mean water level associated with sea level rise could significantly increase nutrient export into marshes with elevations that are equilibrated with mean water levels; on the other hand, the rising sea level could decrease the export of nutrients into estuaries adjacent to these marshes. Anwar et al. [24] demonstrated, using a numerical investigation, that tides and waves modify the subsurface discharge pathways of land-derived nutrients by changing the nearshore groundwater flow dynamics.
As discussed above, many studies focused on the sea–groundwater interactions in subsurface beach zones, which are substantially influenced by waves and tides, and are subject to density-dependent flow patterns [22,25,26,27]. Additionally, the effects of fluctuating water levels due to waves are much more significant than the effects of variations in water densities as reported by Rimmer et al. [28]. They produce a change in the local direction and velocity of subsurface flow by temporarily uplifting the groundwater table near the interface during windy days, depending on the duration and characteristics of the waves. A hypothesis was proposed that, similar to the effects of tidal waves in coastal areas, in lakes subjected to wind waves, fluctuating water levels alter subsurface flow patterns and corresponding water and solute exchange between the lakes and the surrounding groundwater. Wind waves particularly occur on large and shallow lakes in plain regions during windy seasons, where the groundwater table surrounding these lakes is generally shallow and approaches the mean water level in the lake [29]. Once wind waves occur, the original subsurface flow direction and velocity near the shoreline may be changed, and consequently the nutrient exchange [18] and nearshore water quality [16,18,24,30,31] are affected.
To verify the hypothesis mentioned above, this study therefore is to evaluate the subsurface flow patterns and solute exchange between a lake and groundwater due to wind waves. We first evaluate subsurface flow patterns and chloride distributions in a subsurface zone at no-wave conditions for the cases of groundwater discharging into a lake (the GDL case) and lake water recharging groundwater (the LRG case). Then, we compare the results of the water and solute exchange flux and distribution for these two no-wave conditions with the results for conditions with wind waves. The effects of wind waves in a lake on the water and solute exchanges with groundwater are discussed. Finally, a sensitivity analysis evaluating the effects of the hydraulic conductivity of the lakeshore zone and wave characteristics on water and chloride exchange is carried out. Hydrus-2D modeling is used to better understand water and solute exchange between the lake and groundwater systems driven by wind waves. The simulated results are compared with experimental data obtained during experiments conducted in a large soil flume.

2. Materials and Methods

2.1. Soil Flume Experiments

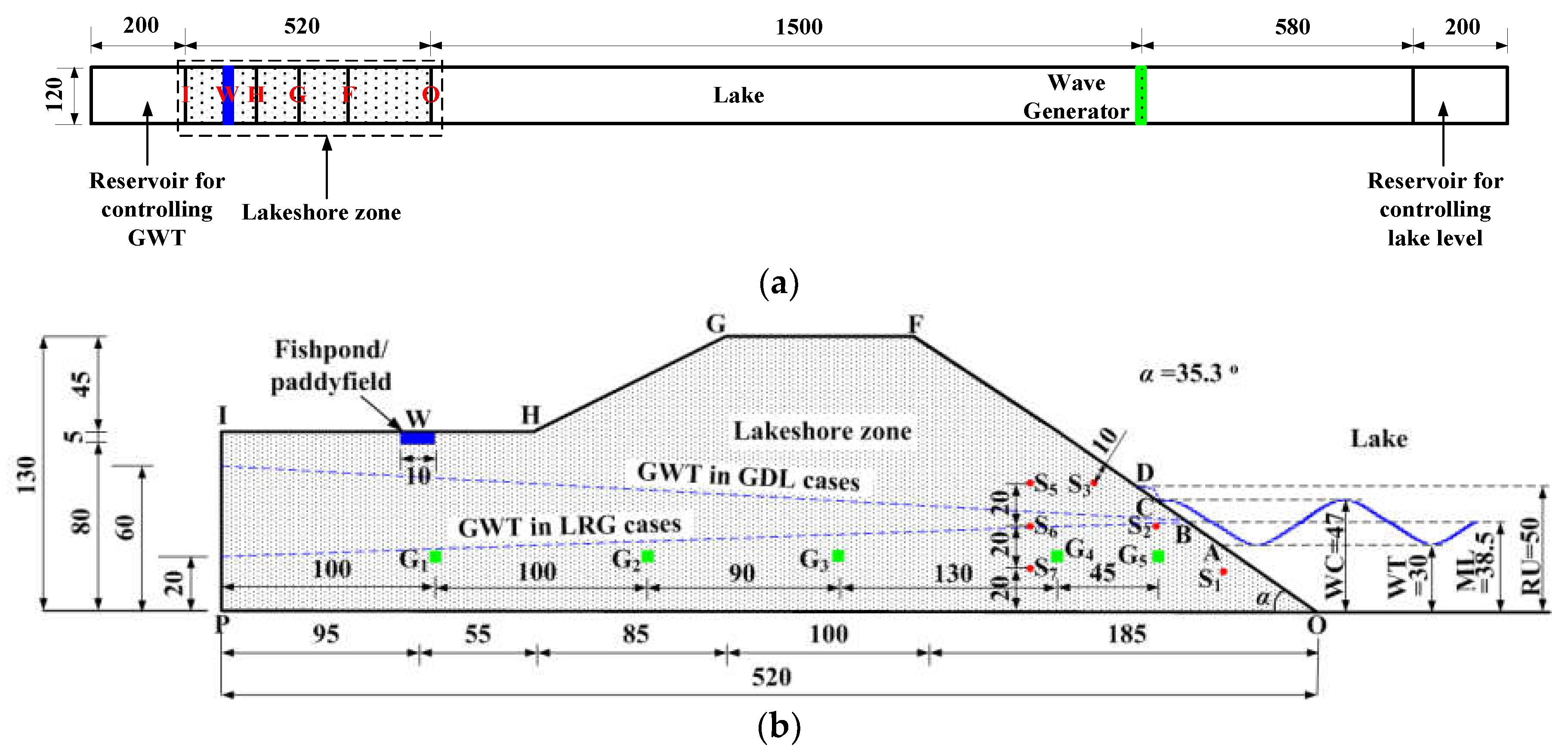
2.1.1. Experimental Set Up and Design

A large flume in a laboratory, partially filled with a loamy sand soil to represent a lakeshore zone (Figure 1), was used to observe flow patterns and solute transport in a subsurface zone subjected to wind waves in a lake. The loamy sand soil (with 87.4% sand, 10.2% silt, 0.18% organic matter, and 1.43 g cm−3 bulk density) was filled into the flume and compacted layer by layer. The lakeshore slope (α) was set at about 35°. A hydraulically driven piston-type wave maker was installed 15 m away from point O (Figure 1a). Two types of interactions between a lake and surrounding groundwater were considered in this study: (1) the GDL case, and (2) LRG cases, each at either no-wave or wave conditions. A hypothetical pollution source was set up outside of the lakeshore to represent a fishpond/paddyfield, which usually locates around lakes in plain regions, from which pollutants at relatively high concentrations leached into the shallow groundwater.
First, steady-state flow conditions in the subsurface zone were established by maintaining a constant groundwater table (60 cm for GDL and 20 cm for LRG) and a constant lake water level (38.5 cm) (Table 1, Figure 1b). Next, for the GDL case with wind waves, the groundwater table (at the IP boundary in Figure 1b) was still kept constant at 60 cm, but the lake water level (on the OF boundary in Figure 1b) was varied following a sinusoidal function with a mean level of 38.5 cm, an amplitude of 8.5 cm, and a time period of 3 s. An observed mean run-up height (RU) of lake water driven by wind waves was about 3.0 cm, i.e., the maximum height of the lake water level on the lakeshore slope reached about 50 cm. For the LRG case with wind waves, the groundwater table at the IP boundary was maintained at a constant depth of 20 cm as during steady-state conditions, while the lake water level followed the same sine function as for the GDL cases. Each of the two experiments for both the GDL and LRG cases with wind waves lasted one day (24 h). In all of the experiments, a hypothetical pollution source representing a fishpond/paddyfield was set up on the land surface 95 cm away from the IP boundary (Figure 1b) with a constant flux of 10 cm day−1 controlled by a micro pump.
The GDL experiment at steady-state condition was conducted first, and continued for one month. The chloride concentrations in the upstream reservoir (the IP boundary, Figure 1b) and in the lake were about 0.5–1.6 mg L−1 (tap water). Next, the chloride concentrations in the lake were set at 80 mg L−1, and the experiment with wind waves was conducted for one day. After the GDL experiments were concluded, the soil flume was slowly flushed for one month until the chloride concentrations at all observation points stabilized. The LRG steady-state experiment was carried out next, and it also continued for one month after the chloride concentration in the lake water was again initially set at 80 mg L−1. Finally, the LRG experiment with wind waves was carried out during one day, and the chloride concentration in lake water was still set at 80 mg L−1. In all of the experiments, the chloride concentration in the fishpond/paddyfield at point W (Figure 1) was constant and equal to 160 mg L−1 (Table 1).

2.1.2. Measurements and Analyses

In the 30-day preliminary experiments, water fluxes across the IP boundary, pressure heads, and chloride concentrations in the subsurface zone (Figure 1b) were measured once every three days. After wind waves started, the inflow/outflow fluxes across the IP boundary and from a fishpond/paddyfield (Figure 1b) were recorded once every three hours using flow meters. Pressure heads in the subsurface zone were observed once every three hours using automatic pressure transducers (PT, Model no. 1151AP, Fisher, a detection limit of 0.1 cm), which were installed beneath the groundwater table at 100, 200, 290, 420, and 465 cm away from the IP boundary. Three micro pressure transducers (5 kPa, 13.5 mm in diameter and 9.5 mm in height, a detection limit of 0.01 kPa) were set at point C (Figure 1b) to measure the pressure heads at wave crest stages. The height of lake levels on the lakeshore slope was observed using an automatic electronic gauge (WG, Model no. LV5900, Omega Engineering, a detection limit of 0.1 cm). In addition, soil solutions were collected once every three hours after wind waves started, using porous ceramic suction cups at observation points S1–S3 and S5–S7 (Figure 1b). The chloride concentration was analyzed using a continuous flow auto-analyzer (FIA-6000, Skalar, Breda, The Netherlands).

2.2. Hydrus-2D Model Simulations

2.2.1. Model Description

To improve our understanding of subsurface flow patterns and solute exchange between a lake and groundwater driven by wind waves, the Hydrus-2D software [32,33] was used to reproduce the results of the soil flume experiments. The two-dimensional, isothermal, Darcian water flow and solute transport in a variably-saturated, rigid porous medium, assuming that the air phase plays an insignificant role in the liquid flow process, can be described using the Richards and convection-dispersion equations, respectively. Both governing equations are numerically solved in Hydrus-2D using the method of finite elements. An appropriate spatial discretization is crucial to avoid numerical oscillations and to achieve acceptable mass balance errors [32]. In all simulations, the total number of triangular finite elements (FE) was 18,167. At the slope surface and near the fishpond/paddyfield (areas with large pressure head gradients), the size of the FE was approximately 1 cm, while in other parts of the transport domain it was approximately 1–6 cm. Time steps were automatically controlled by the Hydrus-2D model within the initially specified range of 0.001 and 0.1 s. As suggested in the manual of the Hydrus-2D model for minimizing or eliminating numerical oscillations, the Peclet (Pe) and Courant (Cr) numbers were controlled by a stability condition “Pe × Cr ≤ 2” [34].

2.2.2. Input Parameters

Soil hydraulic and solute transport parameters are required to characterize the water flow and chloride transport in soils using the Hydrus-2D model. The van Genuchten soil hydraulic parameters [35], which include the residual water content θr (0.055 cm−3 cm−3), the saturated water content θS (0.40 cm−3 cm−3), shape parameters α (0.121 cm−1) and n (2.16), and the saturated hydraulic conductivity Ks (338.9 cm day−1), were directly adopted from our previous study using the same experimental set up [36]. The pore connectivity parameter (l) was assumed to be equal to an average value of 0.5 [35]. The solute transport parameters were considered using the following values: the molecular diffusion coefficient in free water (Dw) for Cl− was 1.64 cm2 day−1, and the longitudinal dispersivity (αL) and transverse dispersivity (αT) were 7.0 cm and 0.5 cm, respectively [36].

2.2.3. Initial and Boundary Conditions

The steady-state water flow and chloride transport for the GDL and LRG cases were established first during a 30-day period. The final results were then used as initial conditions in simulations during a one-day period under no-wave and wave conditions (Table 1).
For the GDL and LRG cases, the groundwater tables at the IP boundary were assumed to be 60 and 20 cm above the bottom of the soil flume, respectively (Figure 1b and Table 1). The mean lake level (ML) was set as 38.5 cm at steady-state conditions in both the GDL and LRG cases and for both no-wave and wave conditions. The boundary (line OF) exposed to lake water was assigned a linearly increasing pressure head. A dynamic seepage boundary condition was prescribed at the upper part of the OF line (above the wave trough, Figure 1b) with an option to allow the development of a seepage zone [14,37]. When wind waves started, the lake level at the OF boundary followed a sine function, with a wave period of 3 s and an amplitude of 8.5 cm. The wave run up section of the OF boundary (above the wave crest) was simply assigned a linearly increasing pressure head based on the measured pressure heads at point C (Figure 1b). In all simulations, a constant flux boundary condition (10 cm day−1) was assigned to the boundary representing a fishpond/paddyfield at point W (Figure 1). Evaporation was neglected in this study due to relatively its low effect on the water and solute exchanges.
At steady-state conditions, the constant relative chloride concentrations were set at C/C0 = 0.0 on the IP boundary in the GDL case and at C/C0 = 0.5 (about 80.0 mg L−1, Table 1) on the OF boundary in the LRG case, respectively. When wind waves started, the OF boundary in both the GDL and LRG cases was set to be equal to a constant relative chloride concentration of C/C0 = 0.5 (about 80.0 mg L−1); the IP boundary condition remained the same as at steady-state conditions. The chloride concentrations in the fishpond/paddyfield in both the GDL and LRG cases were set at C/C0 = 1.0 (about 160.0 mg L−1) in all simulations.

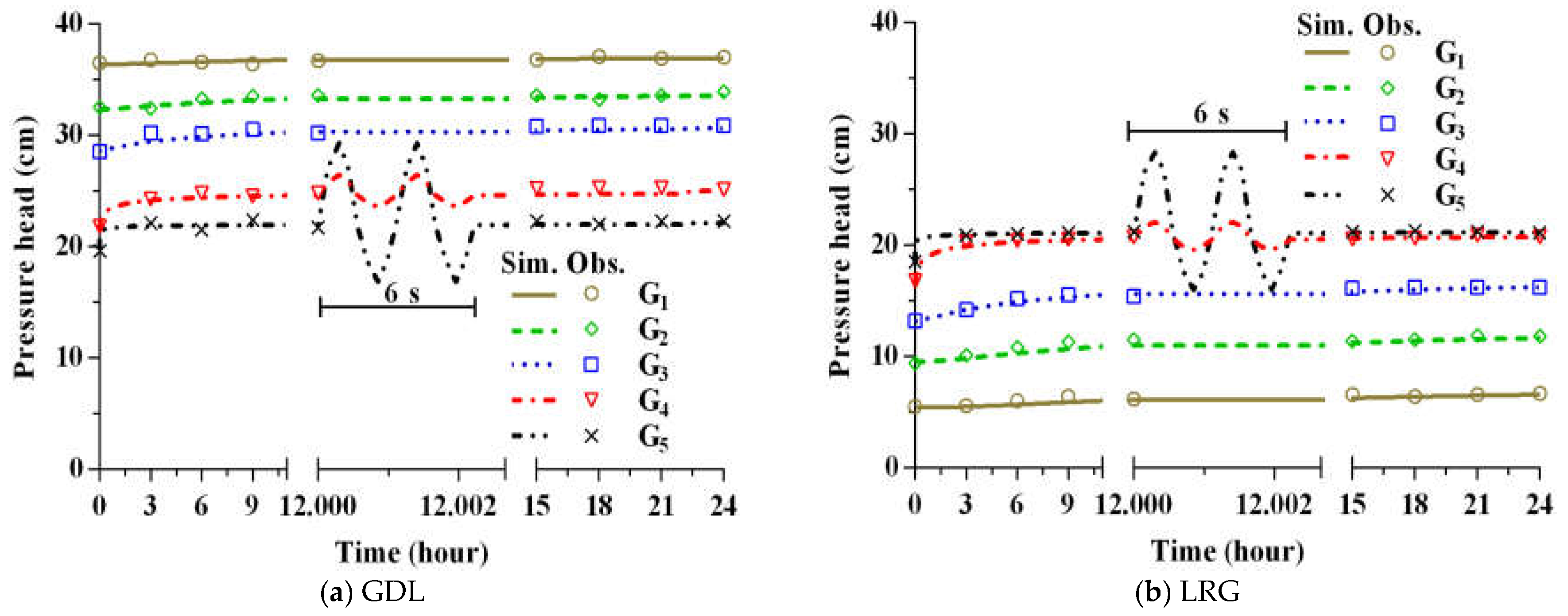
2.3. Model Evaluation

The simulated values of the pressure heads, total water fluxes, and chloride concentrations in the soil were compared with the corresponding values recorded during the soil flume experiments. The correspondence between the simulated and observed data was evaluated using the coefficient of determination (R2) and the root mean square error (RMSE). The coefficient of determination was calculated as:
R 2 = 1 − S S e r r S S t o t
where SSerr is the sum of squared differences between modeled and observed values, and SStot is the sum of squared differences between observed values and the mean of observed values.
The RMSE was calculated as:
R M S E = 1 n ∑ 1 n ( S i − M i ) 2
where Si and Mi are simulated and measured values, respectively, and n is the number of compared values.

3. Results

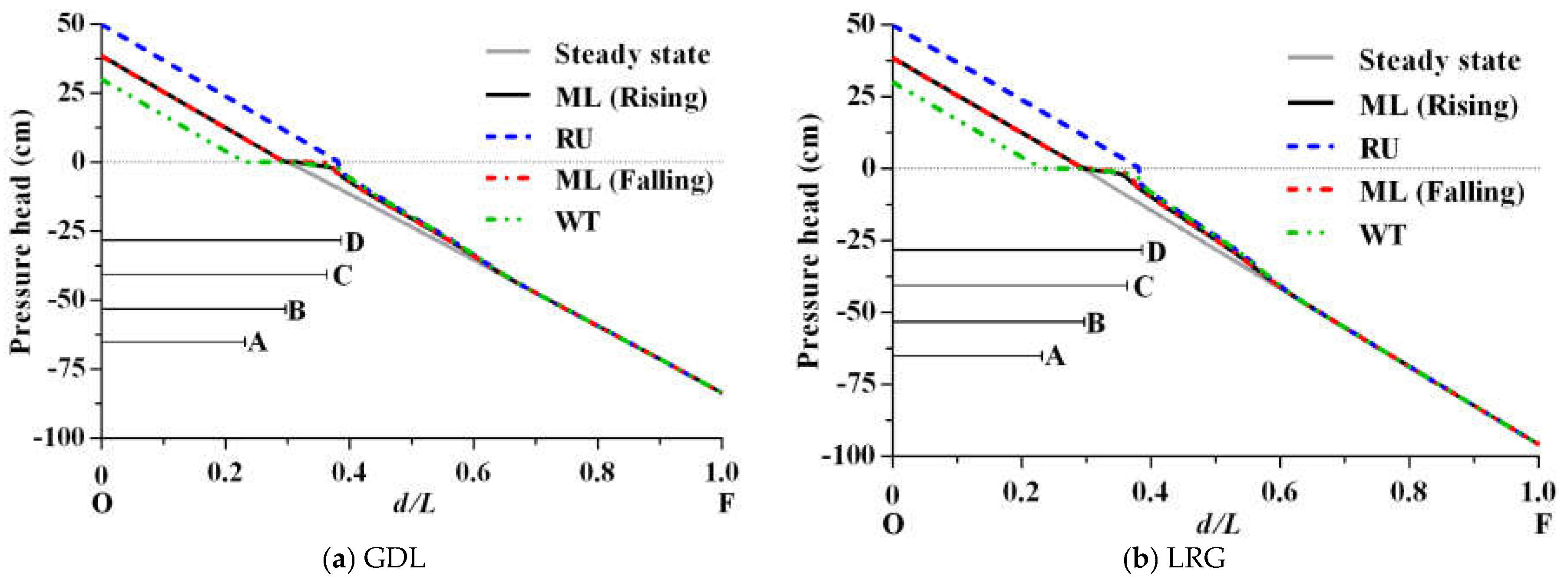
3.1. Groundwater Table

The simulated pressure heads in the subsurface zone at both steady-state conditions and conditions with wind waves (Figure 2) show good agreement with the observed data at G1–G5, with RMSE = 0.62 cm (n = 55, R2 = 0.96, note that the range of pressure head values during the simulation was about 130 cm) in the GDL cases and with RMSE = 0.45 cm (n = 55, R2 = 0.97) in the LRG cases. It is clear that the pressure heads in the subsurface zone near the interface (OF line, Figure 1b) quickly varied when wind waves occurred. The pressure heads at G1–G5 in both the GDL and LRG cases with wind waves clearly increased from their initial values, which were the average pressure heads at their respective steady-state conditions. In the GDL case, the average pressure head at G1 increased slightly (0.6 cm) during a one-day period after the wind waves started compared to steady-state conditions, but increased much more at G2, G3, G4, and G5 by 1.4, 2.2, 3.5, and 2.4 cm, respectively (Figure 2a). In the LRG case with waves, the average pressure heads at G1, G2, G3, G4, and G5 increased 1.2, 2.1, 3.1, 4.2, and 2.7 cm, respectively, compared to steady-state conditions (Figure 2b).
Furthermore, in the GDL case, wind waves produced quick fluctuations of the pressure heads at both G4 and G5 with amplitudes of 1.1–1.9 cm and 5.1–7.4 cm, respectively, but only had a small effect on G3 (0.05 cm) and G2 (0.004 cm), and almost no effect on G1 (Figure 2a). In the LRG case, while the pressure heads at G4 and G5 fluctuated with amplitudes of about 0.9-1.6 cm and 5.0–7.3 cm, respectively, they displayed little fluctuations in G1, G2, and G3 (Figure 2b). The variations of hydraulic heads in the subsurface zone due to wind waves are smaller than the variations of the lake water level (8.5 cm). As the distance of the observation points from the shoreline increased, the effect of wind waves on the pressure heads decreased.
The wind waves also greatly influenced the pressure head distributions along the OF line (Figure 1b). At no-wave conditions, the pressure heads linearly increased along the OF line, ranging from −83.6 to 38.5 cm in the GDL case (Figure 3a) and from −95.8 to 38.5 cm in the LRG case (Figure 3b). Once wind waves occurred, the pressure heads below a point of about d/L = 0.6 (The ratio d/L represents a relative distance of a point on the OF line from point O or a relative height above point O, and L represents the length or height of the OF line) were different from their respective steady-state conditions in both the GDL and LRG cases. Furthermore, the pressure heads below point D differed depending on the stage of a wave cycle. At the mean lake level (ML) stage for both rising and falling water levels, the pressure heads between points B and C were approximately zero, similar to the pressure heads between points A and C at the wave trough (WT) stage. The pressure heads in the LRG case at each stage of a wave cycle were similarly distributed as they were in the GDL case.

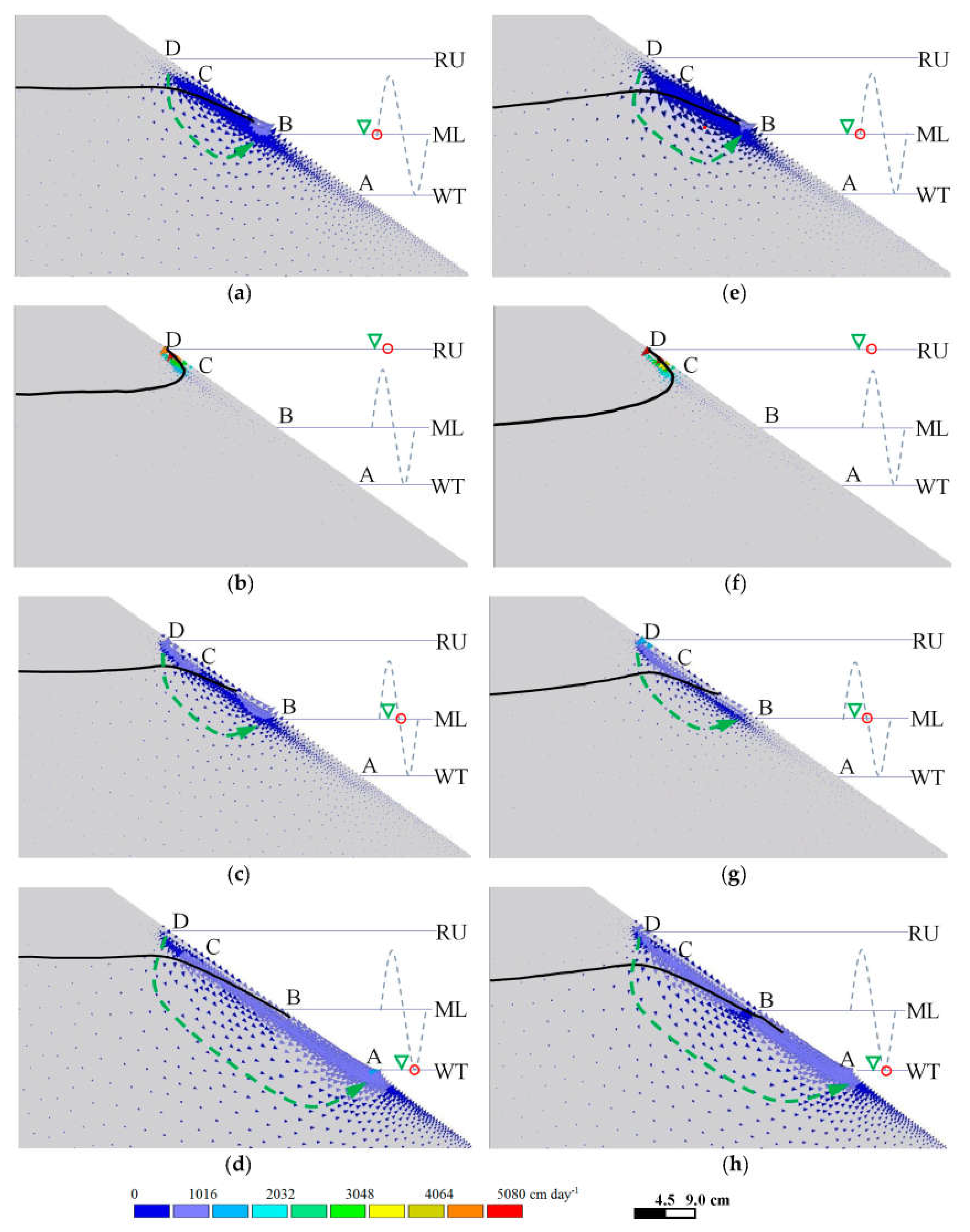
3.2. Subsurface Flow Patterns

The subsurface flow patterns near the OF line (Figure 1b), including flow directions and flux distributions, changed after wind waves started and depended on wave stages (Figure 4). At no-wave conditions in the GDL case, the subsurface discharge (to the lake) peaked at a maximum value of 113 cm day−1 at point B (Figure 5a), while in the LRG case, the maximum infiltration flux of −53 cm day−1 also occurred at point B (Figure 5b). Below point B, fluxes declined rapidly along the OF line and reached zero at point O. After wind waves started, the discharge velocities of the subsurface flow near the OF line at the ML stage (rising) of a wave cycle in the GDL (Figure 4a) and LRG (Figure 4e) cases peaked at point B (Figure 5), with maximum discharge velocities of 210 and 164 cm day−1, respectively. The subsurface flow above point B was directed downwards along the interface and vertically upward (into the lake) below point B. At the RU stage of both the GDL and LRG cases (Figure 4b,f), the subsurface flow had much higher fluxes than at the ML stage (Figure 4a,e). The water exchange flux at the RU stage occurred mainly within a narrow band near point D, with the maximum fluxes at point D of 1800 cm day−1 in the GDL case and 5080 cm day−1 in the LRG case (Figure 5).
When the lake level declined between the RU and ML (falling) stages in both the GDL and LRG cases, the groundwater table near the OF line also dropped rapidly (Figure 4c,g). The maximum fluxes of 240 cm day−1 in the GDL case (Figure 4c and Figure 5a) and 199 cm day−1 in the LRG case (Figure 4g and Figure 5b) occurred at point B. During this stage in both the GDL and LRG cases, the subsurface flow discharge into the lake was mainly concentrated near point B (Figure 4c,g). Above point B, most subsurface flow was directed downwards along the interface. Finally, at the wave trough stage (WT), the subsurface flow near the interface was directed downwards to point A, where water was discharged into the lake with the maximum fluxes of 178 cm day−1 in the GDL case (Figure 4d and Figure 5a) and 170 cm day−1 in the LRG case (Figure 4h and Figure 5b). Overall, during an entire wave cycle in both the GDL and LRG cases, lake water infiltrated into the subsurface zone with relatively high fluxes during the wave crest, while subsurface flow discharged into the lake during other stages. Wind waves thus produced the formation of water circulations in the subsurface zone near the interface (Figure 4).
Additionally, lake waves produce rapid changes in the extent of the seepage face along the interface. At the rising ML stage of a wave cycle in the GDL case, a short seepage face (3.1 cm long along the interface, 1.8 cm in height) developed above point B (Figure 4a), and no seepage face was observed at this stage in the LRG case (Figure 4e). No seepage face occurred at the RU stage in both the GDL and LRG cases (Figure 4b,f). While the flow patterns near the interface at the falling ML stage were similar to those at the rising ML stage, the seepage faces above point B were longer, 5.0 cm (2.9 cm in height) in the GDL case and 4.1 cm (2.4 cm in height) in the LRG case (Figure 4c,g). Finally, the longest seepage faces above point A developed at the WT stage in both the GDL and LRG cases, with lengths of 14.4 cm (8.3 cm in height) and 11.5 cm (6.7 cm in height), respectively. The location and length of the seepage face along the interface responded to the fluctuations of the lake water level driven by waves. Seepage face lengths due to wind waves increased when the lake level was rapidly falling, but decreased when it was rapidly rising in both the GDL and LRG cases (Figure 4 and Figure 5).

3.3. Water Exchange

The simulated cumulative water fluxes (412.8–820.8 cm2 day−1) agreed well with the observed data during a one-day period, including inflow and outflow fluxes across the IP boundary (Figure 1b), with RMSE = 18.3 cm2 day−1 (n = 8, and R2 = 0.95) in the GDL case and RMSE = 15.7 cm2 day−1 (n = 8, and R2 = 0.96) in the LRG case. Changes in the pressure head and flow patterns in the subsurface zone due to wind waves caused changes in the exchange water fluxes across the interface (Figure 5). The exchange water fluxes varied in phase with wind waves. The distributions of water fluxes on the interface were significantly different for no-wave conditions and for conditions with wind waves at different stages of a wave cycle.
For no-wave conditions in the GDL case, discharging water fluxes (into the lake) peaked at point B (Figure 5a), and 50% of the flux occurred within a narrow band (6.2 cm in length on the interface) below point B. For conditions with wind waves, discharging water fluxes at the ML stages (both rising and falling) still peaked at point B. However, both fluxes were relatively higher, and 50% of their volume was concentrated within narrow bands (7.1 cm for the rising stage and 8.0 cm for the falling stages) below point B. At the RU stage, the infiltration fluxes peaked at point D. At the WT stage, the discharging fluxes were mainly distributed near point A where they peaked. The exchange water fluxes at each stage of a wave cycle in the LRG case (Figure 5b) had similar distributions to those in the GDL case (Figure 5a), except for different values of flux peaks and reverse directions at no-wave conditions. After wind waves started, lake water infiltrated into the subsurface zone through the upper part of the interface near the run-up height (at point D), and exfiltrated through its lower part (at point A) in both the GDL (Figure 4a–d) and LRG (Figure 4e–h) cases.
Cumulative exchange water fluxes (CEWFs) during a one-day period with wind waves were different than those at no-wave conditions (Table 2). At no-wave conditions in the GDL case, the CEWF was about −826 cm2 day−1 (negative values represent groundwater discharging into lake), and the part of the lakeshore above the mean lake level accounted for about 9.5% of the total flux. On the other hand, at no-wave conditions in the LRG case, the CEWF was about 412 cm2 day−1 (positive values represent groundwater receiving lake water), and the part of the lakeshore above the mean lake level accounted for about 8.8% of the total flux. The simulated results also showed that inflow and outflow between the lake and groundwater coexisted when wind waves were present in both the GDL and LRG cases. However, although the CEWF (−527 cm2 day−1) during a one-day period with wind waves in the GDL case was lower than for the no-wave conditions, the overall flow was still directed into the lake. In the LRG case with wind waves, the CEWF (832 cm2 day−1) was higher than that for the no-wave conditions, but was still directed into the subsurface zone.

3.4. Solute Concentrations

The simulated chloride concentrations (0.0–80.0 mg L−1) agreed well with the observed data at S1–S3 and S5–S7, with an average RMSE value of 0.13 mg L−1 (n = 59, and R2 = 0.95) in both the GDL and LRG cases. At no-wave conditions in both the GDL and LRG cases, the chloride concentrations at all observation points remained constant (not shown) and the same as the initial concentration values for conditions with wind waves (Figure 6). In the GDL case with one-day wind waves, the chloride concentrations increased at S1 and S2, and remained almost constant at other observation points (Figure 6a). The chloride concentrations at S2 quickly increased and stabilized at C/C0 = 0.5 (the chloride concentration in lake water) after wind waves started, while those at S1 increased more gradually. Th chloride concentrations at S3, S5, S6, and S7 were dominated by the transport of chloride from the upstream pollutions source at point W (Figure 1). However, in the LRG case, the presence of wind waves did not lead to any changes in chloride concentrations at the six observation points (Figure 6b) that were dominated by chloride concentration in the lake water.
The chloride concentrations in the subsurface zone at no-wave and wave conditions are shown in Figure 7. These concentration distributions can more clearly explain the changes of chloride concentrations at the observation points. In the GDL case at no-wave condition, water and solute flow into the lake and the subsurface concentration profiles are not affected by concentrations in the lake (Figure 7a). After wind waves started, lake water and its solutes gradually infiltrated (mainly during the wave crest stage) into the subsurface zone through the interface between points A and D, and the area affected by lake water gradually extended into the subsurface zone (Figure 7a). This affected area gradually increased with time until an equilibrium distribution on the vertical profile was reached. On the other hand, in the LRG case with wind waves, no apparent changes of the chloride distribution were observed compared to no-wave conditions (Figure 7b). Chloride distribution in the subsurface zone in the LRG case was always determined by chloride concentrations in lake water.
Furthermore, while in the GDL case chloride distributions on the interface were greatly influenced by the occurrence of wind waves, there were almost no changes in chloride distributions at the interface in the LRG cases with and without waves (Figure 8). In the GDL case with wind waves, chloride concentrations between points A and D were about equal to the chloride concentration in lake water (C/C0 = 0.5), and declined rapidly above point D and below point A (Figure 8a). Chloride concentrations below point A, and even near point O, changed compared to no-wave conditions, apparently as a result of water circulation due to wind waves. Chloride concentrations above a point of d/L = 0.45 were not influenced by wind waves. In the LRG cases, chloride concentrations below a point of d/L = 0.5 were equal to the chloride concentration in the lake water (C/C0 = 0.5), and declined rapidly to zero above this point (Figure 8b). In both the GDL and LRG cases, chloride concentrations above a point of about d/L = 0.75 approached zero at both no-wave and wave conditions.

3.5. Solute Exchange

Overall, the chloride exchange fluxes across the interface (Table 2) corresponded with their respective water exchange fluxes. At no-wave conditions in the GDL case, the cumulative exchange chloride flux (CECF) across the whole interface during a one-day period was −128 mg cm−1 day−1 (negative values indicate fluxes into the lake). The solute flux through the upper part of the interface above the mean lake level (ML) accounted for about 20.7% of the total solute flux. After wind waves occurred, the CECF across the whole interface declined by about 72%. Wind waves resulted in a simultaneous increase in the CECFs across both the upper (above ML) and lower (below ML) parts of the interface, although in opposite directions.
At no-wave conditions in the LRG case (Table 2), the CECF across the upper part of the boundary was 26 mg cm−1 day−1 (into the subsurface) and accounted for about 11.3% of the total solute flux of 232 mg cm−1 day−1. After wind waves occurred, while the overall CECF remained about the same, it greatly increased across the upper part of the boundary to 736 cm−1 day−1, as well as across the lower part of the boundary (in the opposite direction) to −493 mg cm−1 day−1.

3.6. Sensitivity Analysis

The sensitivity analysis was carried out in this study to evaluate the effects of the aquifer hydraulic conductivity (Ks) and wind wave characteristics (a wave period, P, and a wave amplitude, A) both on the water and solute exchange between the lake and the subsurface, and on the flow patterns in the subsurface zone. A sensitivity analysis of the solute transport parameters has not been evaluated in this study.
Simulations were carried out using the Hydrus-2D model for the same conditions as for which the model was calibrated (i.e., a loamy sand soil, waves with a period P of 3 s and an amplitude A of 8.5 cm), except for Ks being either half or double the original value (338.9 cm day−1) in the original simulations (Table 2). When the Ks value of the aquifer decreased by 50%, the CEWFs across the interface during a one-day period declined by about 67.3% in the GDL case and 69.1% in the LRG case at their no-wave conditions, but declined by about 80.1% and 59.5% in the GDL and LRG cases with wind waves, respectively. Similarly, the CECFs declined by about 38.4% in the GDL case and 69.0% in the LRG case at their no-wave conditions, but changed from −36 to 55 mg cm−1 day−1 (in a reversed direction) and declined by about 45.0% in the GDL and LRG cases with wind waves, respectively. On the other hand, when the Ks value increased by 100%, the CEWFs during a one-day period increased by about 108.5% in the GDL case and 101.9% in the LRG case at their no-wave conditions, and increased by about 131.1% and 83.3% in the GDL and LRG cases with wind waves, respectively. Concurrently, the CECFs increased by about 7.2% in the GDL case and 101.9% in the LRG case at their no-wave conditions, but increased by about 205.3% and 131.4% in the GDL and LRG cases with wind waves, respectively. The Ks value of the aquifer thus greatly influences the water and solute exchange fluxes between the lake and groundwater.
The characteristics of wind waves, including the cycle period and wave amplitude, also influence lake–groundwater interactions. When the cycle period increased from 3 to 6 s, the CEWFs slightly decreased (by about 2.1%) in the GDL case and slightly increased (by 5.7%) in the LRG case (Table 2). However, the CECFs in the GDL case reversed their direction (from −36 to 39 mg cm−1 day−1) and in the LRG case, increased by about 12.3% (from 243 to 272 mg cm−1 day−1). Consequently, increasing a wave period (from 3 to 6 s) apparently increased the water and solute exchange fluxes in the LRG cases, but decreased the water exchange flux and reversed the solute exchange direction in the GDL case. On the other hand, the simulations showed that an increase in the wind amplitude from 8.5 to 17.0 cm (Table 2) produces a decrease in the CEWFs of about 45.2% in the GDL case and an increase of about 41.8% in the LRG case, compared to the original simulations. Similar to the effects of increasing a wave period, the CECFs reversed their direction (from 87 cm2 day−1 to −36 cm2 day−1) in the GDL case and increased by about 13.3% in the LRG case.

4. Discussion

The groundwater table and water flow in the subsurface zone were substantially influenced by wind waves in the lake. The groundwater table was locally uplifted near point D in the subsurface zone in both the GDL and LRG cases (Figure 2). It is interesting that the largest increases of pressure heads after wind waves started appeared at G4 but not at G5 in both the GDL and LRG cases due to high-frequency wind waves. Wave run-up further elevated the groundwater tables in the vicinity of the shoreline, similarly as observed in other studies [22,25,31]. Furthermore, wave run-up caused a relatively rapid infiltration of water near point D to the subsurface zone (Figure 4b,f), which resulted in a local uplift of the groundwater table at G4 and a relatively slow subsurface flow. The temporarily uplifted groundwater table at G5 (near the interface) caused by wave run-up then quickly declined due to downwards flow and seepage during other stages of the wave cycle (Figure 4a,c–e,g,h). An average increase of the groundwater table at G5 remained relatively lower than at G4. Additionally, in both the GDL and LRG cases, after wind waves occurred, zero pressure head regions were formed between points A and C at the WT stage and between points B and C at the ML stage, which markedly differed with those for no-wave conditions (Figure 3). Boufadel et al. [38] reported that water and solute can move in both directions at locations where the pressure head is zero.
Many studies, including modeling and field investigations of groundwater–lake systems, reported that seepage inflow to lakes is generally highest near the lakeshore and decreases with the distance from the shore, and the seepage of lake water to ground water does not occur near the shore of lakes that are bounded by water-table mounds [2,39,40,41]. In this study, when wind waves occurred, seepage of lake water to groundwater increased near the shore of the lakes in the LRG case, and decreased with the distance from the shore (Figure 5) even though water-table mounds existed (Figure 4). In general, similarly as in other studies [2,5,10,36,39,40,42], seepage fluxes at steady-state conditions were concentrated within a narrow band on the surface–groundwater interface, and the discharge then exponentially decreased with the distance offshore. Our simulation results additionally showed that, in the presence of wind waves, the exchange water fluxes were also concentrated within a narrow band near the intersection point of the lakeshore with the lake level (Figure 5), and that this band moved up and down along the interface with the lake water level. Gardner [43] and Gardner and Wilson [44] reported for a creek–groundwater system that groundwater flow occurred primarily in the creek bank, even when the marsh platform was inundated at high tide; at all stages of the tide the largest flow velocities developed just below the intersection of the tide at the creek bank, and most flow developed within 15 m of the creek.
Wind waves in the lake increased the recharging flux from the lake into the subsurface zone in the LRG case, but decreased the discharging flux from the subsurface zone into the lake in the GDL case. The temporary uplift of the groundwater table (mounding) due to waves was created by the asymmetry in the instantaneous recharging-discharging (Figure 5), with high-volume infiltration occurring during the wave crest, followed by lower volume exfiltration during the wave trough. This groundwater surface uplift was sufficient to temporarily reverse the direction of the water exchange flux, as also reported in other studies [18,22,45]. Compared to the no-wave conditions, waves modified the groundwater flow pattern and substantially increased the magnitude of the groundwater flow velocity near the interface, suggesting that waves would induce large infiltration and exfiltration across the interface. The waves created a steep hydraulic gradient in the subsurface zone near the lakeshore face, which substantially slowed the discharging flux into the lake in the GDL case and accelerated the recharging flux into the subsurface zone in the LRG case (Table 2). Similar to the CEWFs across the interface, wind waves resulted in both a more proportional chloride exchange across the upper part of the interface and a simultaneous increase in both the recharge and discharge of chloride across the upper and lower parts of the interface, respectively. These increases were mainly ascribed to local water circulations driven by wind waves (Figure 4). Rosenberry et al. [46] reported for the Great Salt Lake (USA) that there may be infiltration/exfiltration reversals due to waves, as well as reversals in the flow direction across the sediment–water interface. Similarly, Longuet-Higgins [47], Lenkopane et al. [48], Wilson and Gardner [14], and Gibbes et al. [49] reported that the mean onshore pressure gradient due to wave run up drives a groundwater circulation within the beach zone. Such circulations substantially enhanced the local water and solute exchanges between lake water and groundwater in both the GDL and LRG cases.
Wind waves could temporarily slow down groundwater discharge (in the GDL case) or accelerate infiltration from the lake (in the LRG case), and the resulting local water cycles could substantially promote the exchange of water and nutrients in the lake–groundwater system. For some non-conservative solutes, such as nitrogen species, waves correspondingly increased the residence time in the subsurface zone from a fishpond/paddyfield to the lake in the GDL case and consequently changed their concentrations on the interface. As Boufadel et al. [16] and Geng et al. [22] reported, wind waves also created additional pathways for the transport of solutes to the interface and shifted the solute exchange zone in comparison with no-wave conditions. Had the solute concentrations in the lake in the GDL case been lower than those in the subsurface zone, the solute concentrations near the interface would have decreased once wind waves occurred. This diluted solute in the subsurface zone near the interface would then be discharged into the lake by the local water circulation or when wind waves ceased. Several studies [1,50] have reported a decrease in solute concentrations in downstream reservoirs driven by tidally fluctuating water levels, while solute concentrations in groundwater were higher than those in the downstream reservoirs. As Lewandowski et al. [8] reported, the biogeochemical turnover of nitrogen is common at the reactive aquifer–lake interface, in particular when driven by local water circulations. Furthermore, local water cycles driven by wind waves activated water and solute exchange between two water bodies at the lakeshore bottom (Figure 4d,h and Figure 8), which were previously commonly considered to be stagnant zones [51,52].
The sensitivity analysis showed that, after wind waves started, the hydraulic conductivity of the lakeshore zone was a key factor influencing water and solute exchange between the lake and groundwater systems, while the amplitude and period of the waves were less important. Many studies have shown that Ks of the aquifer is a key factor influencing the subsurface flow patterns and the exchange of water and solutes between the surface and groundwater [22]. It is interesting that when Ks changed, in both the GDL and LRG cases, the CECFs during a one-day period did not proportionally change with the corresponding CEWFs. This could be related to the differences in chloride concentrations and in CECFs between the upper and lower parts of the interface as discussed earlier (Figure 7a and Figure 8a). Additional parameters (e.g., solute transport parameters) and scenarios (e.g., waves with different characteristics) should be considered when evaluating the effects of waves on the interaction between a lake and the surrounding shallow groundwater.

5. Conclusions

Wind waves frequently occur on large lakes during windy seasons, producing oscillations in the lake level and corresponding changes in the water and solute interactions between lakes and groundwater. Our results indicate that wind waves may substantially change the subsurface flow patterns (such as temporarily uplifting the groundwater table, increasing subsurface flow velocity, and changing the flow direction) near the lake–groundwater interface compared to steady-state conditions. Local water circulations were produced in the subsurface zone due to wind waves, resulting in most water and solutes that infiltrated from the lake into the groundwater during the wave crest being discharged back into the lake through the lower interface during the remainder of a wave cycle. Such water circulations driven by wind waves accelerate water and solute exchange between lake and groundwater systems, and activate a relatively stagnant zone at the lakeshore bottom. Overall, wind waves may decrease the cumulative water and solute exchange fluxes between the lake and the surrounding groundwater, redistribute solute concentrations on the interface in the GDL cases, and increase them in the LRG cases, as compared to their respective no-wave conditions.
The results of the sensitivity analysis carried out using the Hydrus-2D simulations show that the hydraulic conductivity of the subsurface zone plays a relatively more important role in water and solute exchange than the characteristics of the waves. The simulated results provide detailed information both about the water and solute source/sink interactions between groundwater and nearshore lake areas, and their redistributions along the lakeshore slope during windy seasons.

Acknowledgments

The work described in this publication was supported by the National Natural Science Foundation of China (Nos: 51579074 and 51079048), the Fundamental Research Funds for the Central Universities (No: 2009B16914), the Priority Academic Program Development of Jiangsu Higher Education Institutions (PAPD), and the China Scholarship Council. The authors would like to thank two anonymous reviewers for providing thoughtful comments that helped us to significantly improve the manuscript and the editors for their careful and responsible work.

Author Contributions

Yong Li conceived and designed the experiments; Shuang Wang, Weiwei Zhang, and Jiahui Yuan performed the experiments; Shuang Wang, Weiwei Zhang, and Jiahui Yuan analyzed the data; Yong Li and Jirka Šimůnek contributed reagents/materials/analysis tools; Yong Li and Jirka Šimůnek wrote the paper.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Chen, H.; Pinder, G.F. Investigation of Groundwater Contaminant Discharge into Tidally influenced Surface-water Bodies: Theoretical Analysis. Transp. Porous Media 2011, 89, 289–306. [Google Scholar] [CrossRef]
  2. Shaw, R.D.; Prepas, E.E. Groundwater-lake interactions: II. Nearshore seepage patterns and the contribution of ground water to lakes in central alberta. J. Hydrol. 1990, 119, 121–136. [Google Scholar] [CrossRef]
  3. Cheng, X.; Anderson, M.P. Numerical simulation of groundwater interaction with lakes allowing for fluctuating lake levels. GroundW. 1993, 31, 929–933. [Google Scholar] [CrossRef]
  4. Gosselin, D.C.; Khisty, M.J. Simulating the influence of two shallow, flow-through lakes on a groundwater system: Implications for groundwater mounds and hinge lines. Hydrogeol. J. 2001, 9, 476–486. [Google Scholar] [CrossRef]
  5. Shaw, G.D.; White, E.S.; Gammons, C.H. Characterizing groundwater—Lake interactions and its impact on lake water quality. J. Hydrol. 2013, 492, 69–78. [Google Scholar] [CrossRef]
  6. Kidmose, J.; Nilsson, B.; Engesgaard, P.; Frandsen, M.; Karan, S.; Landkildehus, F.; Søndergaard, M.; Jeppesen, E. Focused groundwater discharge of phosphorus to a eutrophic seepage lake (Lake Væng, Denmark): Implications for lake ecological state and restoration. Hydrogeol. J. 2013, 21, 1787–1802. [Google Scholar] [CrossRef]
  7. Shaw, R.D.; Shaw, J.F.H.; Fricker, H.; Prepas, E.E. An integrated approach to quantify groundwater transport of phosphorus to Narrow Lake, Alberta. Limnol. Oceanogr. 1990, 35, 870–886. [Google Scholar] [CrossRef]
  8. Lewandowski, J.; Meinikmann, K.; Nützmann, G.; Rosenberry, D.O. Groundwater—The disregarded component in lake water and nutrient budgets. Part 2: Effects of groundwater on nutrients. Hydrol. Process. 2015, 29, 2922–2955. [Google Scholar] [CrossRef]
  9. Gleeson, T.; Novakowski, K.; Cook, P.G.; Kyser, T.K. Constraining groundwater discharge in a large watershed: Integrated isotopic, hydraulic, and thermal data from the Canadian shield. Water Resour. Res. 2009, 45, W08402. [Google Scholar] [CrossRef]
  10. Kidmose, J.; Engesgaard, P.; Nilsson, B.; Laier, T.; Looms, M.C. Spatial Distribution of Seepage at a Flow-Through Lake: Lake Hampen, Western Denmark. Vadose Zone J. 2011, 10, 110–124. [Google Scholar] [CrossRef]
  11. Huang, P.; Liu, Z. The effect of wave-reduction engineering on sediment resuspension in a large, shallow, eutrophic lake (Lake Taihu). Ecol. Eng. 2009, 35, 1619–1623. [Google Scholar] [CrossRef]
  12. Smith, A.J.; Herne, D.E.; Turner, J.V. Wave effects on submarine groundwater seepage measurement. Adv. Water Resour. 2009, 32, 820–833. [Google Scholar] [CrossRef]
  13. Harvey, J.W.; Conklin, M.H.; Koelsch, R.S. Predicting changes in hydrologic retention in an evolving semi-arid alluvial stream. Adv. Water Resour. 2003, 26, 939–950. [Google Scholar] [CrossRef]
  14. Wilson, A.M.; Gardner, L.R. Tidally driven groundwater flow and solute exchange in a marsh: Numerical simulations. Water Resour. Res. 2006, 42, W01405. [Google Scholar] [CrossRef]
  15. Massel, S.R.; Przyborska, A.; Przyborski, M. Attenuation of wave-induced groundwater pressure in shallow water. Part 1. Oceanologia 2004, 46, 383–404. [Google Scholar]
  16. Boufadel, M.C.; Li, H.; Suidan, M.T.; Venosa, A.D. Tracer Studies in a Laboratory Beach Subjected to Waves. J. Environ. Eng. 2007, 133, 722–732. [Google Scholar] [CrossRef]
  17. Sous, D.; Lambert, A.; Vincent, R.; Michallet, H. Swash—Groundwater dynamics in a sandy beach laboratory experiment. Coast. Eng. 2013, 80, 122–136. [Google Scholar] [CrossRef]
  18. Turner, I.L.; Rau, G.C.; Austin, M.J.; Andersen, M.S. Groundwater fluxes and flow paths within coastal barriers: Observations from a large-scale laboratory experiment (BARDEX II). Coast. Eng. 2016, 113, 104–116. [Google Scholar] [CrossRef]
  19. Xin, P.; Robinson, C.; Li, L.; Barry, D.A.; Bakhtyar, R. Effects of wave forcing on a subterranean estuary. Water Resour. Res. 2010, 46, W12505. [Google Scholar] [CrossRef]
  20. Moore, W.S. The subterranean estuary: A reaction zone of ground water and sea water. Mar. Chem. 1999, 65, 111–125. [Google Scholar] [CrossRef]
  21. Taniguchi, M. Tidal effects on submarine groundwater discharge into the ocean. Geophys. Res. Lett. 2002, 29, 21–23. [Google Scholar] [CrossRef]
  22. Geng, X.; Boufadel, M.C.; Xia, Y.; Li, H.; Zhao, L.; Jackson, N.L.; Miller, R.S. Numerical study of wave effects on groundwater flow and solute transport in a laboratory beach. J. Contam. Hydrol. 2014, 165, 37–52. [Google Scholar] [CrossRef] [PubMed]
  23. Wilson, A.M.; Morris, J.T. The influence of tidal forcing on groundwater flow and nutrient exchange in a salt marsh-dominated estuary. Biogeochemistry 2012, 108, 27–38. [Google Scholar] [CrossRef]
  24. Anwar, N.; Robinson, C.; Barry, D.A. Influence of tides and waves on the fate of nutrients in a nearshore aquifer: Numerical simulations. Adv. Water Resour. 2014, 73, 203–213. [Google Scholar] [CrossRef]
  25. Li, L.; Barry, D.A. Wave-induced beach groundwater flow. Adv. Water Resour. 2000, 23, 325–337. [Google Scholar] [CrossRef]
  26. Belibassakis, K.A. Water-wave induced groundwater pressure and flow in variable bathymetry regions and sandy beaches by an enhanced coupled-mode model. Ocean Eng. 2012, 47, 104–118. [Google Scholar] [CrossRef]
  27. Rosenberry, D.O.; Lewandowski, J.; Meinikmann, K.; Nützmann, G. Groundwater—The disregarded component in lake water and nutrient budgets. Part 1: Effects of groundwater on hydrology. Hydrol. Process. 2015, 13, 2895–2921. [Google Scholar] [CrossRef]
  28. Rimmer, A.; Hurwitz, S.; Gvirtzman, H. Spatial and Temporal Characteristics of Saline Springs: Sea of Galilee, Israel. GroundWater 1999, 37, 663–673. [Google Scholar] [CrossRef] [PubMed]
  29. Huang, Y. Water Environment and Pollution control of Taihu Lake; China Science Press: Beijing, China, 2001. [Google Scholar]
  30. Carniello, L.; Alpaos, A.D.; Defina, A. Modeling wind waves and tidal flows in shallow micro-tidal basins. Estuar. Coast. Shelf Sci. 2011, 92, 263–276. [Google Scholar] [CrossRef]
  31. Cartwright, N.; Nielsen, P.; Li, L. Experimental observations of watertable waves in an unconfined aquifer with a sloping boundary. Adv. Water Resour. 2004, 27, 991–1004. [Google Scholar] [CrossRef]
  32. Šimůnek, J.; Van Genuchten, M.T.; Šejna, M. Development and applications of the HYDRUS and STANMOD software packages, and related codes. Vadose Zone J. 2008, 7, 587–600. [Google Scholar] [CrossRef]
  33. Šimůnek, J.; Van Genuchten, M.T.; Šejna, M. Recent developments and applications of the HYDRUS computer software packages. Vadose Zone J. 2016, 15, 10–2136. [Google Scholar] [CrossRef]
  34. Šimůnek, J.; Van Genuchten, M.T.; Šejna, M. The HYDRUS software package for simulating the two- and three-dimensional movement of water, heat, and multiple solutes in variably-saturated porous media. PC-Progress: Prague, Czech Republic, 2012; p. 258. [Google Scholar]
  35. Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
  36. Li, Y.; Šimůnek, J.; Zhang, Z.; Huang, M.; Ni, L.; Zhu, L.; Hua, J.; Chen, Y. Water flow and nitrate transport through a lakeshore with different revetment materials. J. Hydrol. 2015, 520, 123–133. [Google Scholar] [CrossRef]
  37. Šimůnek, J.; Van Genuchten, M.T.; Šejna, M. HYDRUS: Model use, calibration, and validation. Am. Soc. Agric. Biol. Eng. 2012, 55, 1261–1274. [Google Scholar]
  38. Boufadel, M.C.; Xia, Y.; Li, H. Modeling solute transport and transient seepage in a laboratory beach under tidal influence. Environ. Modell. Softw. 2011, 26, 899–912. [Google Scholar] [CrossRef]
  39. Winter, T.C. Numerical simulation of steady-state three dimensional groundwater flow near lakes. Water Resour. Res. 1978, 14, 245–254. [Google Scholar] [CrossRef]
  40. McBride, M.; Pfannkuch, H.O. Distribution of seepage within lake beds. J. Res. USA Geol. Surv. 1975, 3, 505–512. [Google Scholar]
  41. Lee, T.M. Hydrogeologic Controls on the Groundwater Interactions with an Acidic Lake in Karst Terrain, Lake Barco, Florida. Water Resour. Res. 1996, 32, 831–844. [Google Scholar] [CrossRef]
  42. Burnett, W.C.; Aggarwal, P.K.; Aureli, A.; Bokuniewicz, H.; Cable, J.E.; Charette, M.A.; Kontar, E.; Krupa, S.; Kulkarni, K.M.; Loveless, A.; et al. Quantifying submarine groundwater discharge in the coastal zone via multiple methods. Sci. Total Environ. 2006, 367, 498–543. [Google Scholar] [CrossRef] [PubMed]
  43. Gardner, L.R. A modeling study of the dynamics of pore water seepage from intertidal marsh sediments. Estuar. Coast. Shelf Sci. 2005, 62, 691–698. [Google Scholar] [CrossRef]
  44. Gardner, L.R.; Wilson, A.M. Comparison of four numerical models for simulating seepage from salt marsh sediments. Estuar. Coast. Shelf Sci. 2006, 69, 427–437. [Google Scholar] [CrossRef]
  45. Turner, I.L.; Coates, B.P.; Acwort, R.I. Tides, Waves and the Super-elevation of Groundwater at the Coast. J. Coast. Res. 1997, 13, 46–60. [Google Scholar]
  46. Rosenberry, D.O.; Sheibley, R.W.; Cox, S.E.; Simonds, F.W.; Naftz, D.L. Temporal variability of exchange between groundwater and surface water based on high-frequency direct measurements of seepage at the sediment-water interface. Water Resour. Res. 2013, 49, 2975–2986. [Google Scholar] [CrossRef]
  47. Longuet-Higgins, F. Wave set-up, percolation and underflow in the surf zone. Proc. R. Soc. London A 1983, 390, 283–291. [Google Scholar] [CrossRef]
  48. Lenkopane, M.; Werner, A.D.; Lockington, D.A.; Li, L. Influence of variable salinity conditions in a tidal creek on riparian groundwater flow and salinity dynamics. J. hydrol. 2009, 375, 536–545. [Google Scholar] [CrossRef]
  49. Gibbes, B.; Robinson, C.; Li, L.; Lockington, D.; Li, H. Tidally driven pore water exchange within offshore intertidal sandbanks: Part II numerical simulations. Estuar. Coast. Shelf Sci. 2008, 80, 472–482. [Google Scholar] [CrossRef]
  50. Yim, C.; Mohsen, M. Simulation of tidal effects on contaminant transport in porous media. GroundWater 1992, 30, 78–86. [Google Scholar] [CrossRef]
  51. Taniguchi, M.; Burnett, W.C.; Smith, C.F.; Paulsen, R.J.; O’rourke, D.; Krupa, S.L.; Christoff, J.L. Spatial and temporal distributions of submarine groundwater discharge rates obtained from various types of seepage meters at a site in the Northeastern Gulf of Mexico. Biogeochemistry 2003, 66, 35–53. [Google Scholar] [CrossRef]
  52. Hosono, T.; Ono, M.; Burnett, W.C.; Tokunaga, T.; Taniguchi, M.; Akimichi, T. Spatial Distribution of Submarine Groundwater Discharge and Associated Nutrients within a Local Coastal Area. Environ. Sci. Technol. 2012, 46, 5319–5326. [Google Scholar] [CrossRef] [PubMed]
Water 09 00566 g001 550
Figure 1. Schematic view of the experimental set up and positions of observation points. All units are in cm. (GWT, ground water table; WT, a wave trough height (point A), 30.0 cm; ML, a mean lake level height (point B), 38.5 cm; WC, a wave crest height (point C), 47 cm, and RU, a run-up height (point D), 50 cm, respectively; point W, a hypothetical pollution source representing a fishpond/paddyfield). (a) Plan view of the experimental set-up; (b) Side view of the lakeshore zone (observation points for solute concentrations (●: S1–S3 and S5–S7) and groundwater table (GWT, ■: G1–G5)). GDL, groundwater discharging into a lake; LRG, lake water recharging groundwater.
Figure 1. Schematic view of the experimental set up and positions of observation points. All units are in cm. (GWT, ground water table; WT, a wave trough height (point A), 30.0 cm; ML, a mean lake level height (point B), 38.5 cm; WC, a wave crest height (point C), 47 cm, and RU, a run-up height (point D), 50 cm, respectively; point W, a hypothetical pollution source representing a fishpond/paddyfield). (a) Plan view of the experimental set-up; (b) Side view of the lakeshore zone (observation points for solute concentrations (●: S1–S3 and S5–S7) and groundwater table (GWT, ■: G1–G5)). GDL, groundwater discharging into a lake; LRG, lake water recharging groundwater.
Water 09 00566 g001
Water 09 00566 g002 550
Figure 2. Simulated (lines) and observed (points) pressure heads during a one-day period after wind waves started in the GDL (a) and LRG (b) cases. All observation points were at the same height of 20 cm (Figure 1b). Except for time between 12.000 and 12.002 h, only values when the lake water level was at its mean position are shown.
Figure 2. Simulated (lines) and observed (points) pressure heads during a one-day period after wind waves started in the GDL (a) and LRG (b) cases. All observation points were at the same height of 20 cm (Figure 1b). Except for time between 12.000 and 12.002 h, only values when the lake water level was at its mean position are shown.
Water 09 00566 g002
Water 09 00566 g003 550
Figure 3. Pressure head distributions on the lakeshore (the OF line, Figure 1) during no-wave conditions and at different stages of a wave cycle for the GDL (a) and LRG (b) cases. See Figure 1 for locations of points A, B, C, D, F, and O. Horizontal solid lines represent relative distances of points A, B, C, and D from point O. The gray horizontal line represents a zero pressure head. The ratio d/L represents a relative distance of a point on the OF line from point O or a relative height above point O (L represents the length or height of the OF line).
Figure 3. Pressure head distributions on the lakeshore (the OF line, Figure 1) during no-wave conditions and at different stages of a wave cycle for the GDL (a) and LRG (b) cases. See Figure 1 for locations of points A, B, C, D, F, and O. Horizontal solid lines represent relative distances of points A, B, C, and D from point O. The gray horizontal line represents a zero pressure head. The ratio d/L represents a relative distance of a point on the OF line from point O or a relative height above point O (L represents the length or height of the OF line).
Water 09 00566 g003
Water 09 00566 g004 550
Figure 4. Local water flow patterns near the lake-groundwater interface at different stages of a wave cycle (indicated by a point on a sine wave) in the GDL (a,b,c,d, left) and LRG (e,f,g,h, right) cases. Black solid lines and green dashed arrow lines represent the groundwater table (zero pressure heads) and flow directions at a corresponding stage, respectively. ML, RU, and WT represent the mean lake level (38.5 cm), the run-up height (50 cm), and the wave trough (30 cm), respectively.
Figure 4. Local water flow patterns near the lake-groundwater interface at different stages of a wave cycle (indicated by a point on a sine wave) in the GDL (a,b,c,d, left) and LRG (e,f,g,h, right) cases. Black solid lines and green dashed arrow lines represent the groundwater table (zero pressure heads) and flow directions at a corresponding stage, respectively. ML, RU, and WT represent the mean lake level (38.5 cm), the run-up height (50 cm), and the wave trough (30 cm), respectively.
Water 09 00566 g004
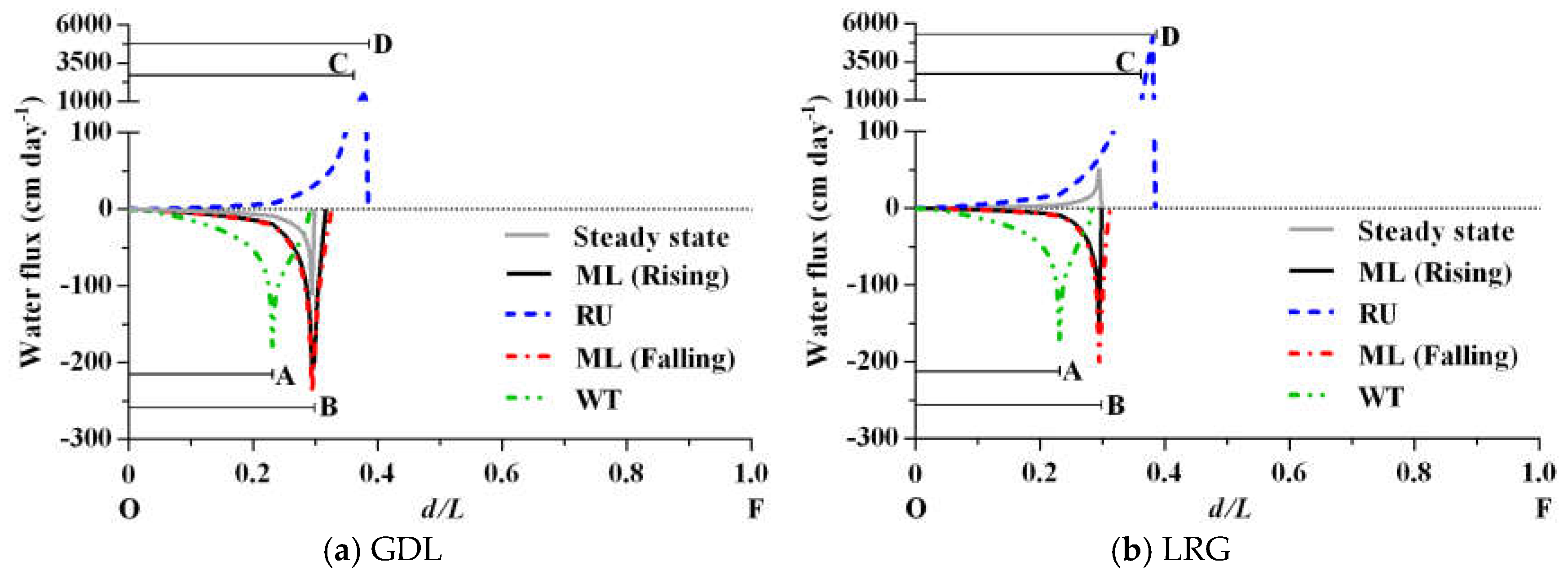
Water 09 00566 g005 550
Figure 5. Distributions of water fluxes along the lake–groundwater interface (OF) for no-wave conditions and at different stages of a wave cycle for the GDL (a) and LRG (b) cases. (ML, RU, and WT represent the mean lake level (38.5 cm), the run-up height (50 cm), and the wave trough (30 cm), respectively; positive fluxes are into the subsurface zone and negative fluxes into the lake). See Figure 1 for locations of points A, B, C, D, F, and O. Horizontal solid lines represent relative distances of points A, B, C, and D from point O. The gray horizontal line represents zero water flux. Notice the break in the vertical axis.
Figure 5. Distributions of water fluxes along the lake–groundwater interface (OF) for no-wave conditions and at different stages of a wave cycle for the GDL (a) and LRG (b) cases. (ML, RU, and WT represent the mean lake level (38.5 cm), the run-up height (50 cm), and the wave trough (30 cm), respectively; positive fluxes are into the subsurface zone and negative fluxes into the lake). See Figure 1 for locations of points A, B, C, D, F, and O. Horizontal solid lines represent relative distances of points A, B, C, and D from point O. The gray horizontal line represents zero water flux. Notice the break in the vertical axis.
Water 09 00566 g005
Water 09 00566 g006 550
Figure 6. Simulated and observed chloride concentrations near the lake–groundwater interface during a one-day period after wind waves started in the GDL (a) and LRG (b) cases. (lines: simulated by Hydrus-2D; symbols: observed during the soil flume experiments). C0: the input chloride concentration from the fishpond/paddyfield.
Figure 6. Simulated and observed chloride concentrations near the lake–groundwater interface during a one-day period after wind waves started in the GDL (a) and LRG (b) cases. (lines: simulated by Hydrus-2D; symbols: observed during the soil flume experiments). C0: the input chloride concentration from the fishpond/paddyfield.
Water 09 00566 g006
Water 09 00566 g007 550
Figure 7. Chloride concentration profiles in the subsurface zone at no-wave (top) and wave (bottom) conditions in the GDL (a) and LRG (b) cases. Distributions of chloride in both no-wave and wave conditions are the final results of one-day simulations starting from respective initial conditions (steady-state). Red points represent the locations of observation points for chloride concentration.
Figure 7. Chloride concentration profiles in the subsurface zone at no-wave (top) and wave (bottom) conditions in the GDL (a) and LRG (b) cases. Distributions of chloride in both no-wave and wave conditions are the final results of one-day simulations starting from respective initial conditions (steady-state). Red points represent the locations of observation points for chloride concentration.
Water 09 00566 g007
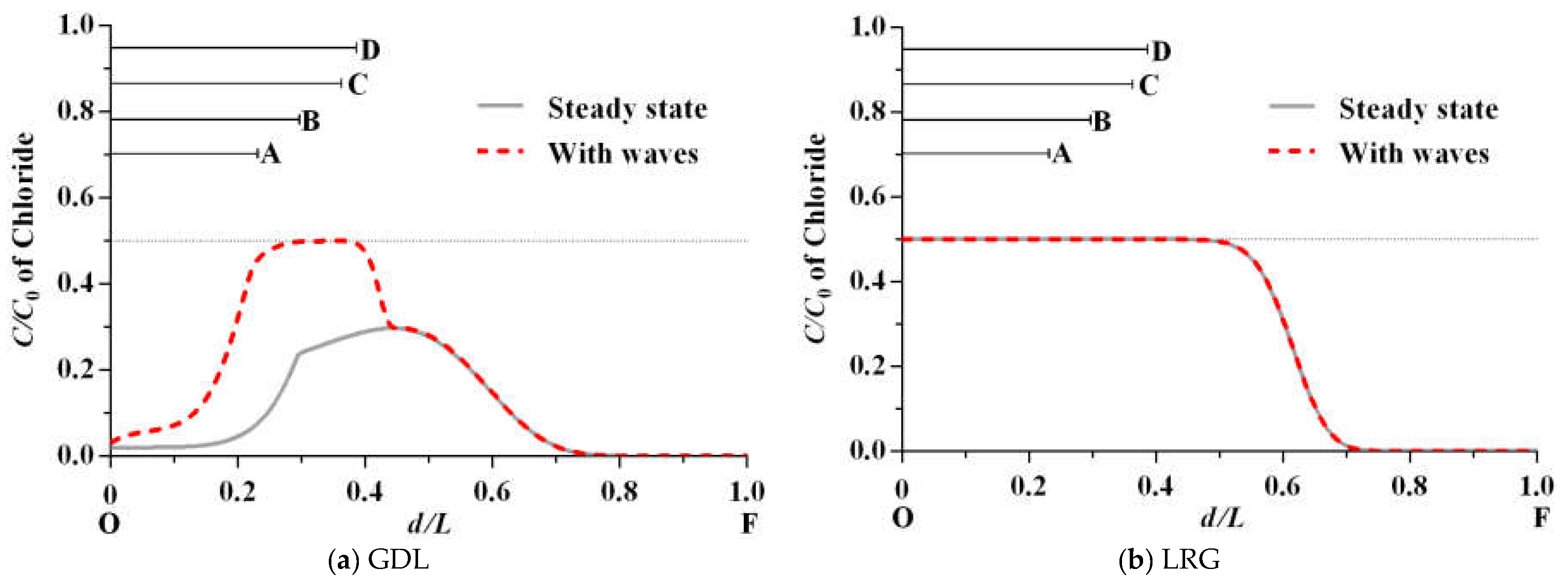
Water 09 00566 g008 550
Figure 8. Distributions of chloride concentrations along the lake–groundwater interface (OF) at no-wave conditions in the GDL (a) and LRG (b) cases and one day after wind waves started. See Figure 1 for the locations of points A, B, C, D, F, and O. Horizontal solid lines represent relative distances of points A, B, C, and D from point O. C0: the input chloride concentration from the fishpond/paddyfield. The gray horizontal dashed line at C/C0 = 0.5 represents the relative chloride concentration in lake water.
Figure 8. Distributions of chloride concentrations along the lake–groundwater interface (OF) at no-wave conditions in the GDL (a) and LRG (b) cases and one day after wind waves started. See Figure 1 for the locations of points A, B, C, D, F, and O. Horizontal solid lines represent relative distances of points A, B, C, and D from point O. C0: the input chloride concentration from the fishpond/paddyfield. The gray horizontal dashed line at C/C0 = 0.5 represents the relative chloride concentration in lake water.
Water 09 00566 g008
Table
Table 1. Water flow and solute transport conditions for experiments in the soil flume and in HYDRUS-2D simulations (GDL, groundwater discharge into a lake; LRG, a lake recharging groundwater, IP Boundary, a groundwater boundary in the lakeshore zone; OF Boundary, the lake–groundwater interface).
Table 1. Water flow and solute transport conditions for experiments in the soil flume and in HYDRUS-2D simulations (GDL, groundwater discharge into a lake; LRG, a lake recharging groundwater, IP Boundary, a groundwater boundary in the lakeshore zone; OF Boundary, the lake–groundwater interface).
CaseConditionIP BoundaryPollution SourceOF BoundaryRunning Time
GDLSteady-state60 cm, 0 mg L−110 cm day−1, 160 mg L−1Constant head of 38.5 cm, zero gradient **30 days
No-wave *Constant head of 38.5 cm, zero gradient **1 day
Wave *Variable head (waves), 80 mg L−11 day
LRGSteady-state20 cm, zero gradient **10 cm day−1, 160 mg L−1Constant head of 38.5 cm, 80 mg L−130 days
No-wave *Constant head of 38.5 cm, 80 mg L−11 day
Wave *Variable head (waves) , 80 mg L−11 day
* All experiments and simulations under no-wave and wave conditions use the final results of steady-state conditions (a preliminary run for 30 days) as initial conditions; ** The solute concentration was set as a zero gradient boundary condition.
Table
Table 2. Cumulative exchange water and chloride fluxes during a one-day period and sensitivity analysis due to the aquifer hydraulic conductivity (Ks), the wave cycle period (P), and amplitude (A).
Table 2. Cumulative exchange water and chloride fluxes during a one-day period and sensitivity analysis due to the aquifer hydraulic conductivity (Ks), the wave cycle period (P), and amplitude (A).
CaseBC at Line OF *Ks (cm day−1)P (s)A (cm)CEWF *** (cm2 day−1)CECF *** (mg cm−1 day−1)
AML **BML **TotalAML **BML **Total
GDLNo-wave338.938.5−79−747−826−26−101−128
Wave338.938.51063−1590−527427−463−36
No-wave677.838.5−165−1557−1722−29−108−137
Wave677.838.52043−3261−1218826−935−110
No-wave169.538.5−26−244−270−16−63−79
Wave169.538.5369−475−105176−12155
Wave338.968.51073−1589−516496−45639
Wave338.9317.01656−2032−376667−62542
LRGNo-wave338.938.53637641226206232
Wave338.938.51742−960832736−493243
No-wave677.838.57375941253416469
Wave677.838.53270−183614341512−951561
No-wave169.538.51111612886472
Wave169.538.5597−280317279−145133
Wave338.968.51783−959824769−496272
Wave338.9317.02489−1496993992−763229
* BC: boundary condition; line OF: lake–groundwater interface, see Figure 1b; ** AML: above the mean lake level (namely above 38.5 cm); BML: below the mean lake level; *** CEWF: a cumulative exchange water flux during a one-day period (negative into the lake); CECF: a cumulative exchange chloride flux during a one-day period.

Share and Cite

MDPI and ACS Style

Li, Y.; Šimůnek, J.; Wang, S.; Zhang, W.; Yuan, J. Simulating the Effects of Lake Wind Waves on Water and Solute Exchange across the Lakeshore Using Hydrus-2D. Water 2017, 9, 566. https://doi.org/10.3390/w9080566

AMA Style

Li Y, Šimůnek J, Wang S, Zhang W, Yuan J. Simulating the Effects of Lake Wind Waves on Water and Solute Exchange across the Lakeshore Using Hydrus-2D. Water. 2017; 9(8):566. https://doi.org/10.3390/w9080566

Chicago/Turabian Style

Li, Yong, Jirka Šimůnek, Shuang Wang, Weiwei Zhang, and Jiahui Yuan. 2017. "Simulating the Effects of Lake Wind Waves on Water and Solute Exchange across the Lakeshore Using Hydrus-2D" Water 9, no. 8: 566. https://doi.org/10.3390/w9080566

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop