Optimal Combinations of Non-Sequential Regressors for ARX-Based Typhoon Inundation Forecast Models Considering Multiple Objectives
Abstract
:1. Introduction
2. Materials and Methods
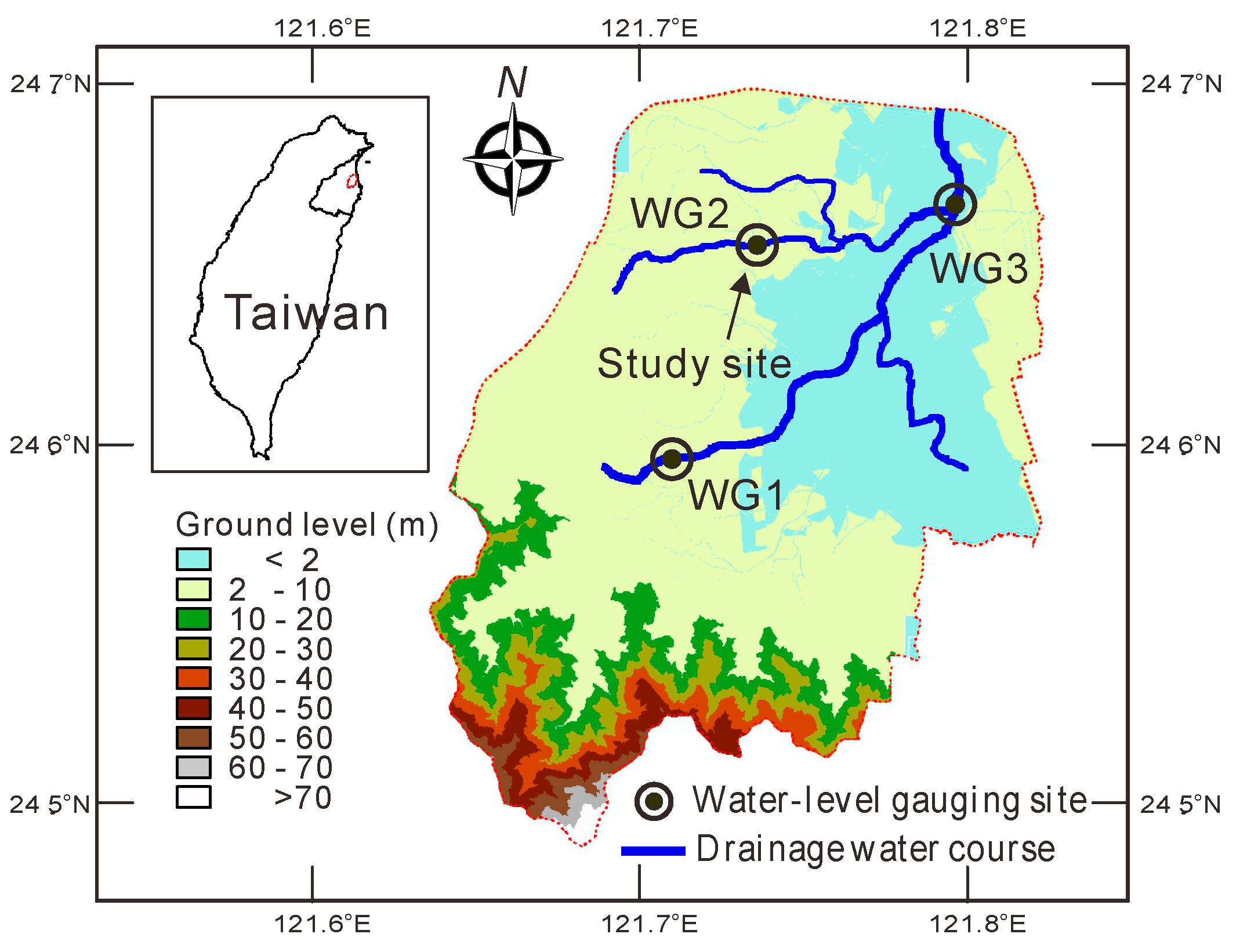
2.1. Study Area
2.2. Model Construction
2.2.1. Linear ARX
2.2.2. Nonlinear ARX
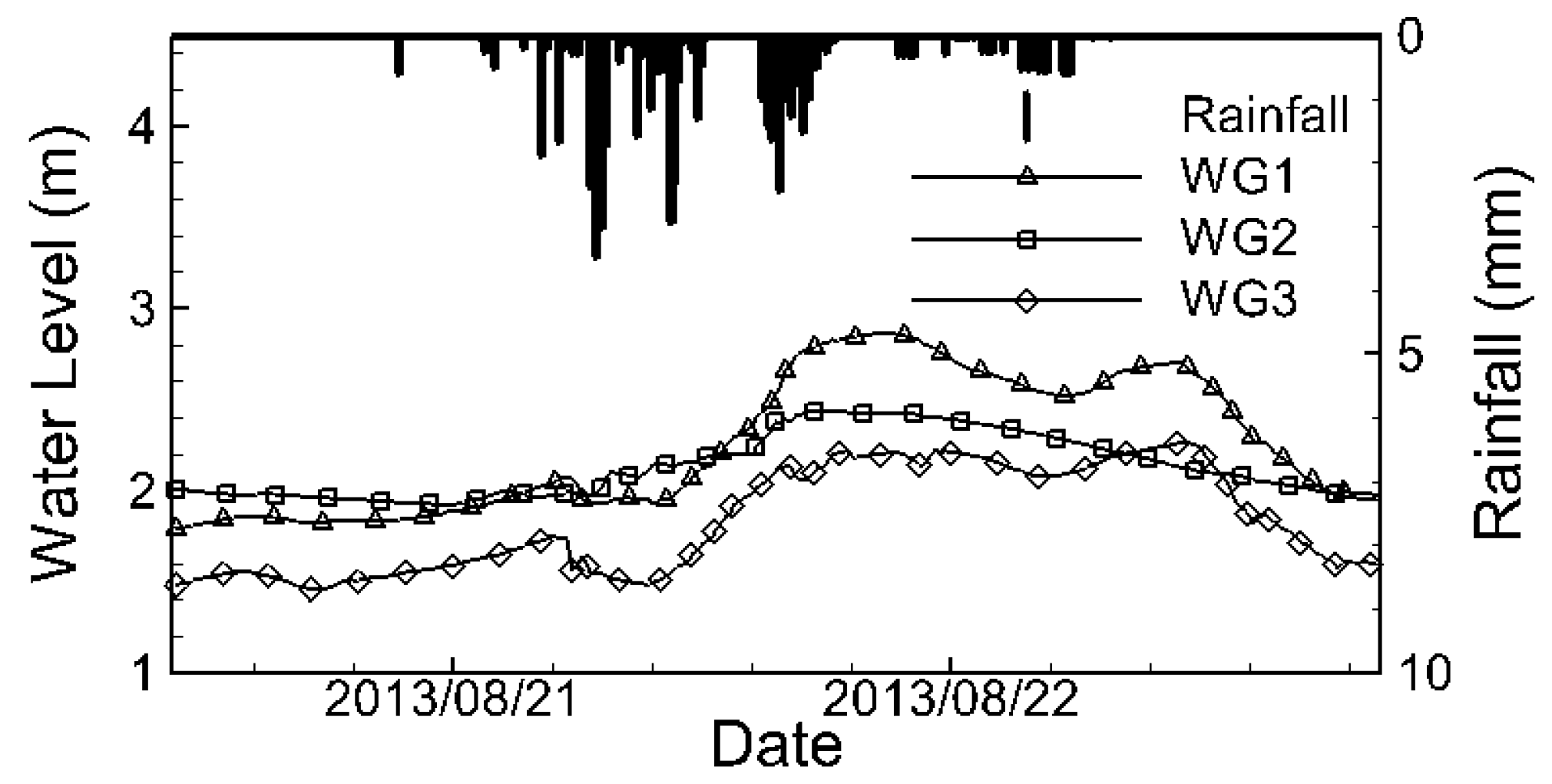
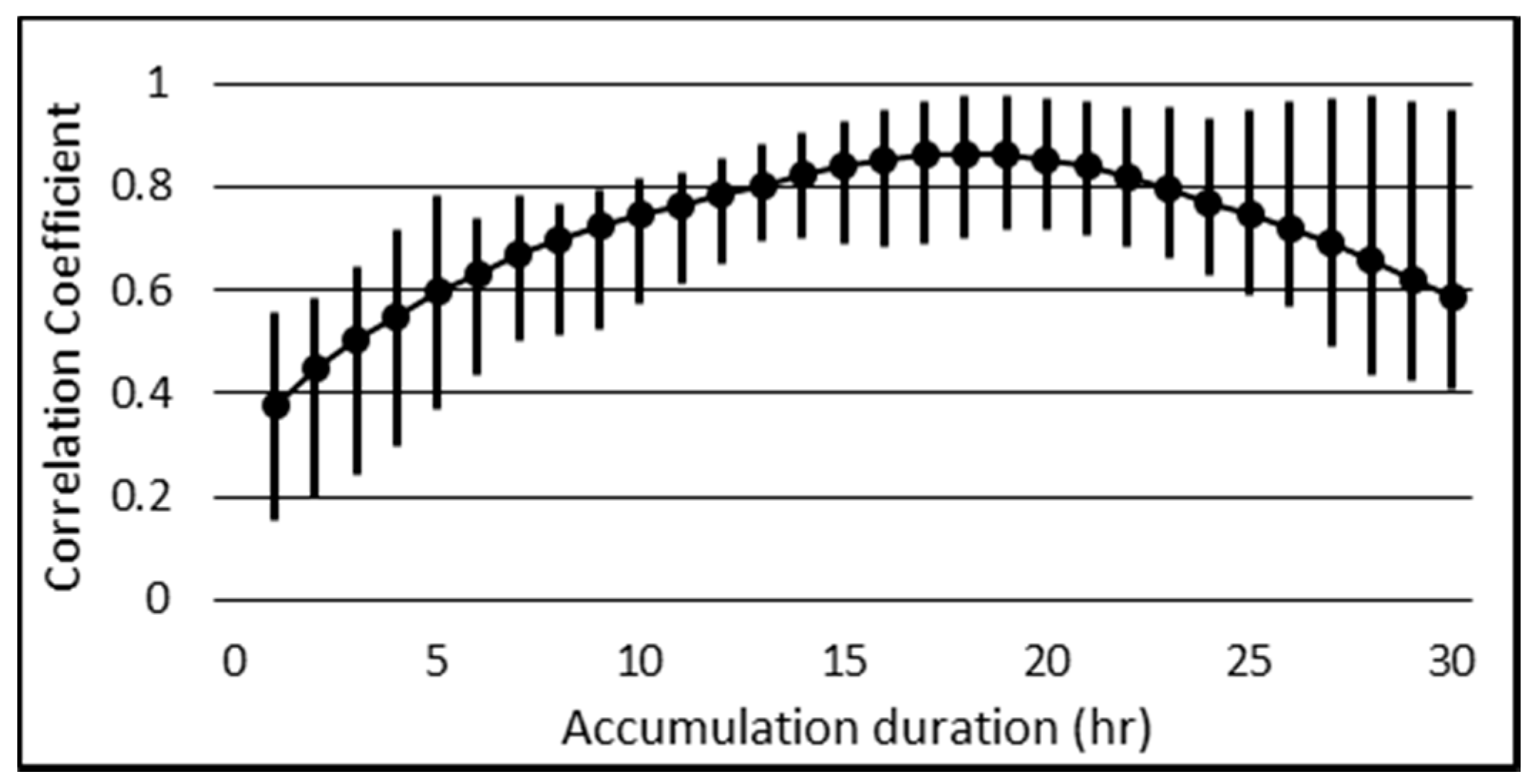
2.2.3. Rainfall Data Analysis
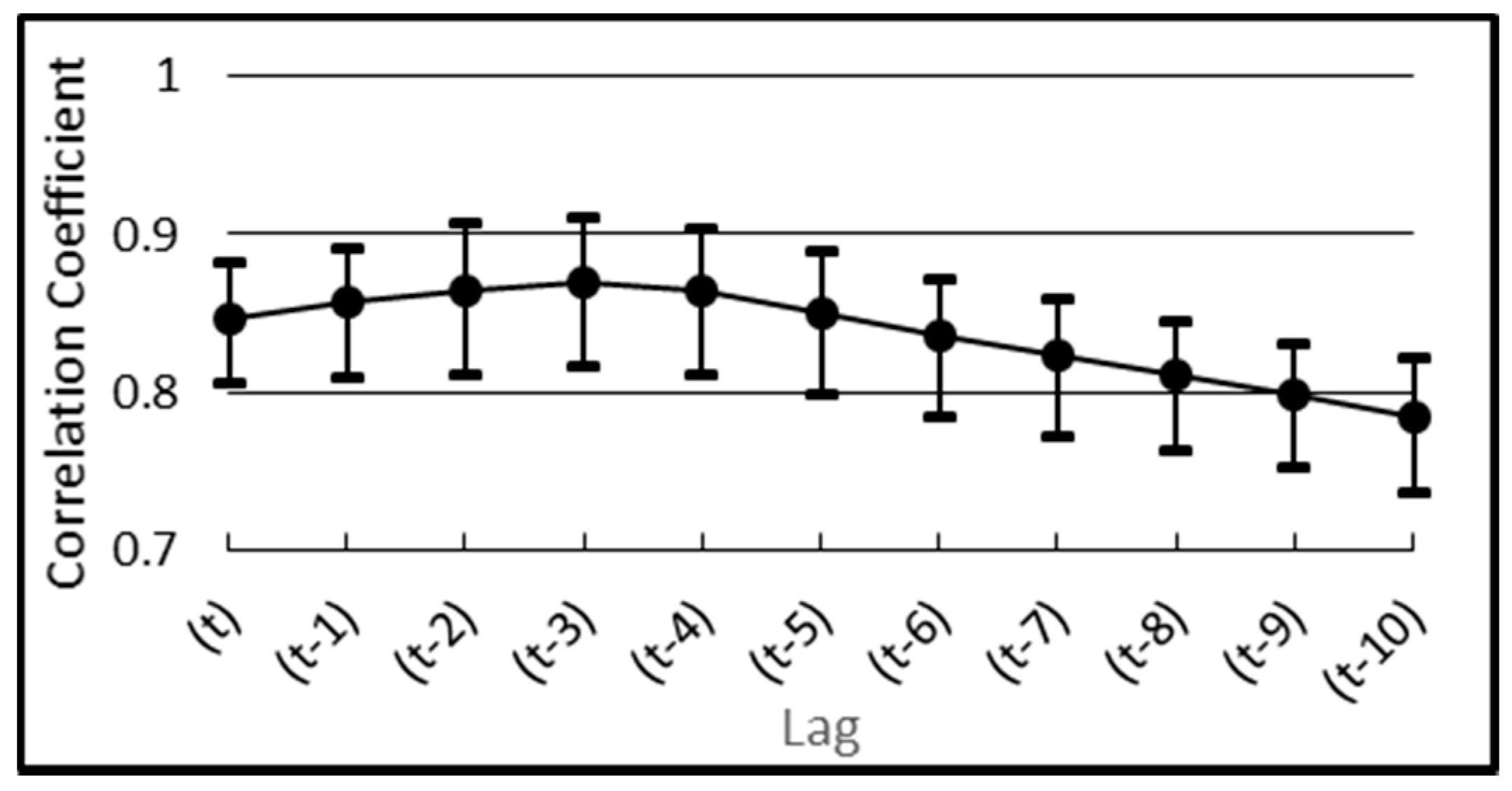
2.2.4. Regressors
2.2.5. Assessing Indexes
Coefficient of Efficiency (CE)
Relative Time Shift Error (RTS)
Threshold Statistic for a Level of
2.2.6. Data Processing
2.3. Model Optimization
2.3.1. Multi-Objective Genetic Algorithm
2.3.2. Objective Functions
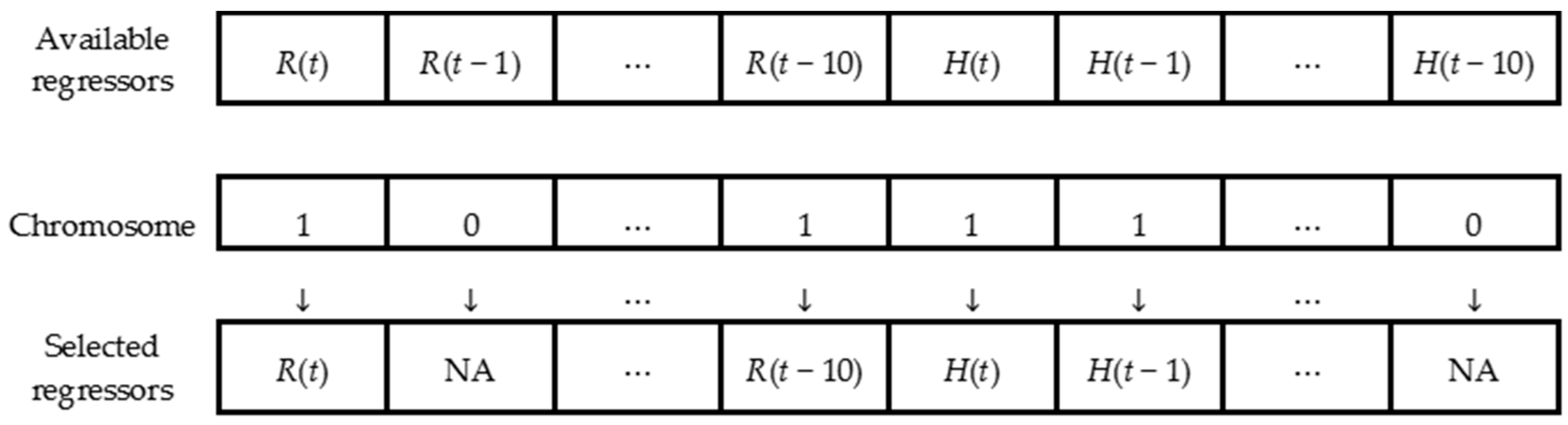
2.3.3. Codification of Regressor Combinations
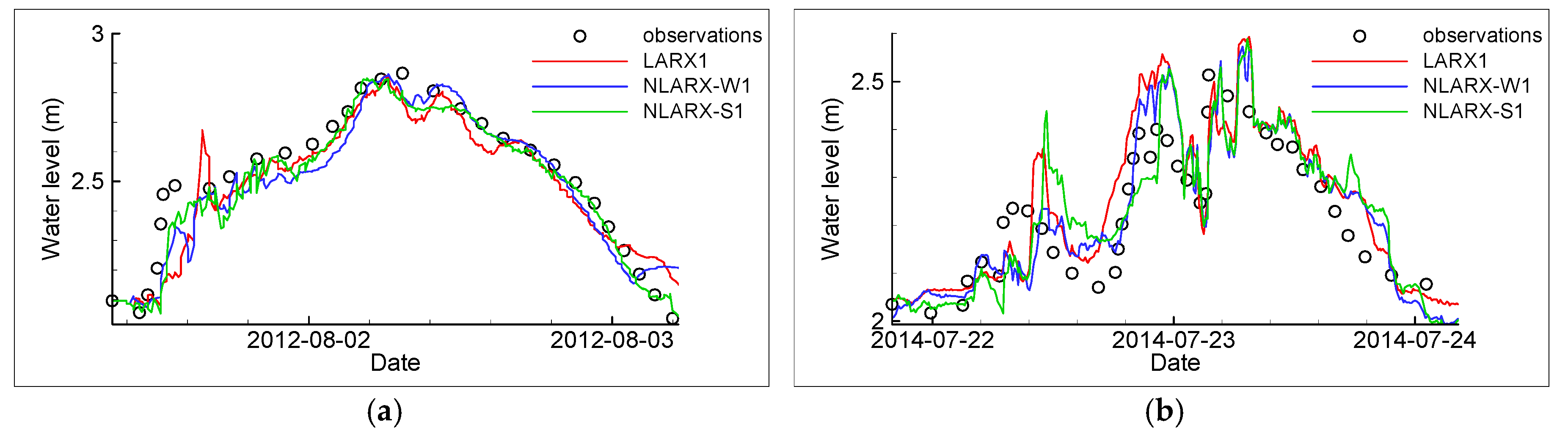
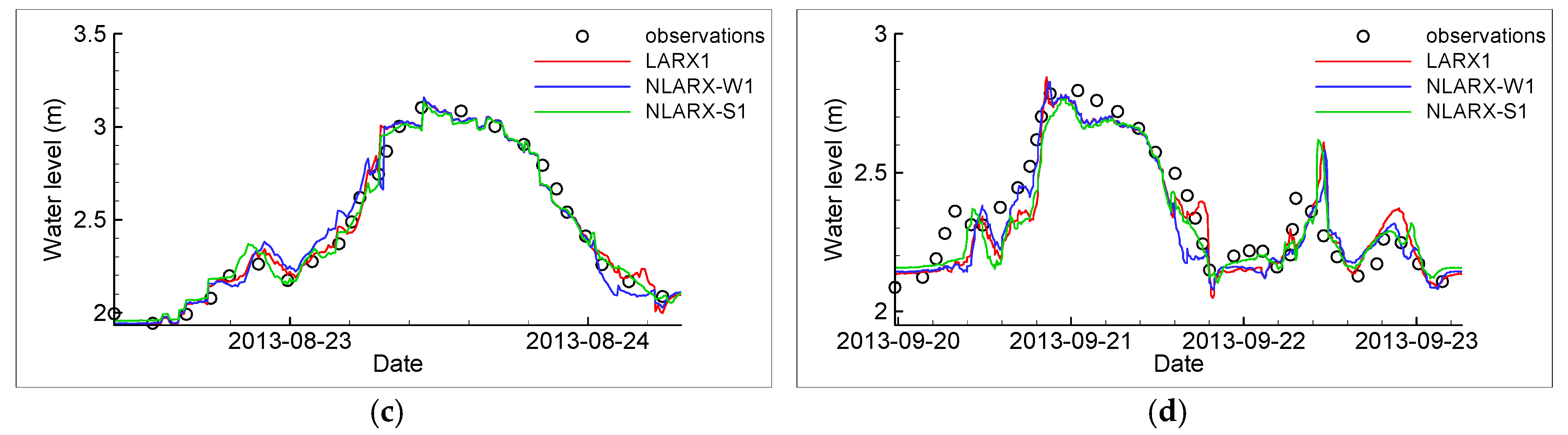
3. Results and Discussion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Karlsson, M.; Yakowitz, S. Rainfall-runoff forecasting methods, old and new. Stoch. Hydrol. Hydraul. 1987, 1, 303–318. [Google Scholar] [CrossRef]
- Liong, S.Y.; Lim, W.H.; Paudyal, G.N. River stage forecasting in Bangladesh: Neural network approach. J. Comput. Civ. Eng. 2000, 14, 1–8. [Google Scholar] [CrossRef]
- Campolo, M.; Soldati, A.; Andreussi, P. Artificial neural network approach to flood forecasting in the River Arno. Hydrol. Sci. J. 2003, 48, 381–398. [Google Scholar] [CrossRef]
- Keskin, M.E.; Taylan, D.; Terzi, O. Adaptive neural-based fuzzy inference system (ANFIS) approach for modeling hydrological time series. Hydrol. Sci. J. 2006, 51, 588–598. [Google Scholar] [CrossRef]
- Shu, C.; Ouarda, T.B.M.J. Regional flood frequency analysis at ungauged sites using the adaptive neuro-fuzzy inference system. J. Hydrol. 2008, 349, 31–43. [Google Scholar] [CrossRef]
- Kia, M.B.; Pirasteh, S.; Pradhan, B.; Mahmud, A.R.; Sulaiman, W.N.A.; Moradi, A. An artificial neural network model for flood simulation using GIS: Johor River Basin, Malaysia. Environ. Earth Sci. 2012, 67, 251–264. [Google Scholar] [CrossRef]
- Lin, G.F.; Lin, H.Y.; Chou, Y.C. Development of a real-time regional-inundation forecasting model for the inundation warning system. J. Hydroinf. 2013, 15, 1391–1407. [Google Scholar] [CrossRef]
- Tehrany, M.S.; Pradhan, B.; Jebur, M.N. Flood susceptibility mapping using a novel ensemble weights-of-evidence and support vector machine models in GIS. J. Hydrol. 2014, 512, 332–343. [Google Scholar] [CrossRef]
- Del Giudice, D.; Reichert, P.; Bareš, V.; Albert, C.; Rieckermann, J. Model bias and complexity–Understanding the effects of structural deficits and input errors on runoff predictions. Environ. Model. Softw. 2015, 64, 205–214. [Google Scholar] [CrossRef]
- Chang, F.J.; Tsai, M.J. A nonlinear spatio-temporal lumping of radar rainfall for modeling multi-step-ahead inflow forecasts by data-driven techniques. J. Hydrol. 2016, 535, 256–269. [Google Scholar] [CrossRef]
- Pan, T.Y.; Chang, L.Y.; Lai, J.S.; Chang, H.K.; Lee, C.S.; Tan, Y.C. Coupling typhoon rainfall forecasting with overland-flow modeling for early warning of inundation. Nat. Hazards 2014, 70, 1763–1793. [Google Scholar] [CrossRef]
- Gourley, J.J.; Maddox, R.A.; Howard, K.W.; Burgess, D.W. An exploratory multisensor technique for quantitative estimation of stratiform rainfall. J. Hydrometeorol. 2002, 3, 166–180. [Google Scholar] [CrossRef]
- Thirumalaiah, K.; Deo, M.C. Real-time flood forecasting using neural networks. Comput. Aided Civ. Infrastruct. Eng. 1998, 13, 101–111. [Google Scholar] [CrossRef]
- Bazartseren, B.; Hildebrandt, G.; Holz, K.P. Short-term water level prediction using neural networks and neuro-fuzzy approach. Neurocomputing 2003, 55, 439–450. [Google Scholar] [CrossRef]
- Yu, P.S.; Chen, S.T.; Chang, I.F. Support vector regression for real-time flood stage forecasting. J. Hydrol. 2006, 328, 704–716. [Google Scholar] [CrossRef]
- Yule, G.U. On a method of investigating periodicities in disturbed series, with special reference to Wolfer’s sunspot numbers. Philos. Trans. R. Soc. Lond. Ser. A Contain. Pap. Math. Phys. Charact. 1927, 226, 267–298. [Google Scholar] [CrossRef]
- Grossmann, A.; Morlet, J. Decomposition of Hardy functions into square integrable wavelets of constant shape. Siam J. Math. Anal. 1984, 15, 723–736. [Google Scholar] [CrossRef]
- Gayen, A.K. The frequency distribution of the product-moment correlation coefficient in random samples of any size drawn from non-normal universes. Biometrika 1951, 38, 219–247. [Google Scholar] [CrossRef] [PubMed]
- Ouyang, H.T. Multi-objective optimization of typhoon inundation forecast models with cross-site structures for a water-level gauging network by integrating ARMAX with a genetic algorithm. Nat. Hazards Earth Syst. Sci. 2016, 16, 1897–1909. [Google Scholar] [CrossRef]
- Furundzic, D. Application example of neural networks for time series analysis: Rainfall–runoff modeling. Signal Process. 1998, 64, 383–396. [Google Scholar] [CrossRef]
- Tokar, A.S.; Markus, M. Precipitation-runoff modeling using artificial neural networks and conceptual models. J. Hydrol. Eng. 2000, 5, 156–161. [Google Scholar] [CrossRef]
- Riad, S.; Mania, J.; Bouchaou, L.; Najjar, Y. Predicting catchment flow in a semi-arid region via an artificial neural network technique. Hydrol. Process. 2004, 18, 2387–2393. [Google Scholar] [CrossRef]
- Chua, L.H.; Wong, T.S.; Sriramula, L.K. Comparison between kinematic wave and artificial neural network models in event-based runoff simulation for an overland plane. J. Hydrol. 2008, 357, 337–348. [Google Scholar] [CrossRef]
- Mitra, S.; Hayashi, Y. Neuro-fuzzy rule generation: Survey in soft computing framework. IEEE Trans. Neural Netw. 2000, 11, 748–768. [Google Scholar] [CrossRef] [PubMed]
- Nayak, P.C.; Sudheer, K.P.; Jain, S.K. Rainfall-runoff modeling through hybrid intelligent system. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Talei, A.; Chua, L.H.C.; Wong, T.S. Evaluation of rainfall and discharge inputs used by Adaptive Network-based Fuzzy Inference Systems (ANFIS) in rainfall–runoff modeling. J. Hydrol. 2010, 391, 248–262. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Talei, A.; Chua, L.H. Influence of lag time on event-based rainfall–runoff modeling using the data driven approach. J. Hydrol. 2012, 438, 223–233. [Google Scholar] [CrossRef]
- Jain, A.; Ormsbee, L.E. Short-term water demand forecast modeling techniques—Conventional methods versus AI. J. Am. Water Works Assoc. 2012, 94, 64–72. [Google Scholar]
- Jain, A.; Varshney, A.K.; Joshi, U.C. Short-term water demand forecast modeling at IIT Kanpur using artificial neural networks. Water Resour. Manag. 2001, 15, 299–321. [Google Scholar] [CrossRef]
- Rajurkar, M.P.; Kothyari, U.C.; Chaube, U.C. Artificial neural networks for daily rainfall—Runoff modeling. Hydrol. Sci. J. 2002, 47, 865–877. [Google Scholar] [CrossRef]
- Holland, J.H. Genetic algorithms and the optimal allocation of trials. SIAM J. Comput. 1973, 2, 88–105. [Google Scholar] [CrossRef]
- Goldberg, D.E.; Holland, J.H. Genetic algorithms and machine learning. Mach. Learn. 1988, 3, 95–99. [Google Scholar] [CrossRef]
- Bagchi, T.P. Multi-Objective Scheduling by Genetic Algorithms; Springer Science & Business Media: New York, NY, USA, 1999; pp. 143–145. [Google Scholar]
| Typhoon | Year | Time of Official Typhoon Sea Warning Issued h/Day/Month (UTC) | Affecting Period (h) | Maximum Rainfall Intensity (mm/h) | Cumulative Rainfall (mm) |
|---|---|---|---|---|---|
| Songda | 2011 | 0230/27/May | 36 | 28.5 | 213 |
| Nanmadol | 2011 | 0530/27/August | 99 | 26.5 | 172 |
| Saola | 2012 | 2030/30/July | 90 | 37.5 | 537 |
| Soulik | 2013 | 0830/11/July | 63 | 30.0 | 133 |
| Trami | 2013 | 1130/20/August | 45 | 22.0 | 461 |
| Usagi | 2013 | 2330/20/September | 93 | 23.0 | 165 |
| Matmo | 2014 | 1730/21/July | 54 | 35.5 | 98 |
| Fung-wong | 2014 | 0830/19/September | 72 | 41.0 | 72 |
| Soudelor | 2015 | 1130/6/August | 69 | 87.5 | 421 |
| Dujuan | 2015 | 0830/27/September | 57 | 42.0 | 218 |
| Index | Model | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| L1 | L2 | L3 | W1 | W2 | W3 | S1 | S2 | S3 | |
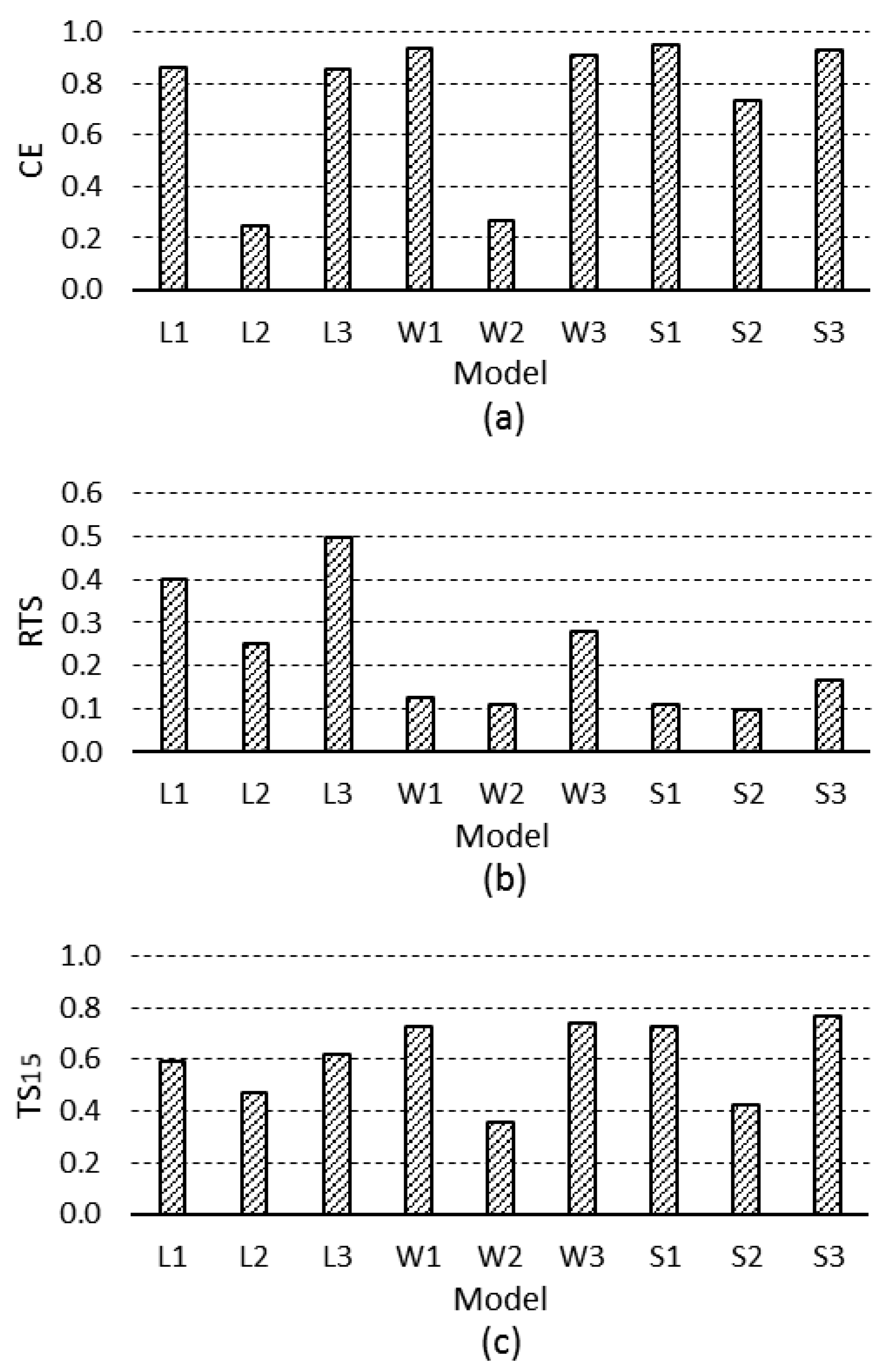
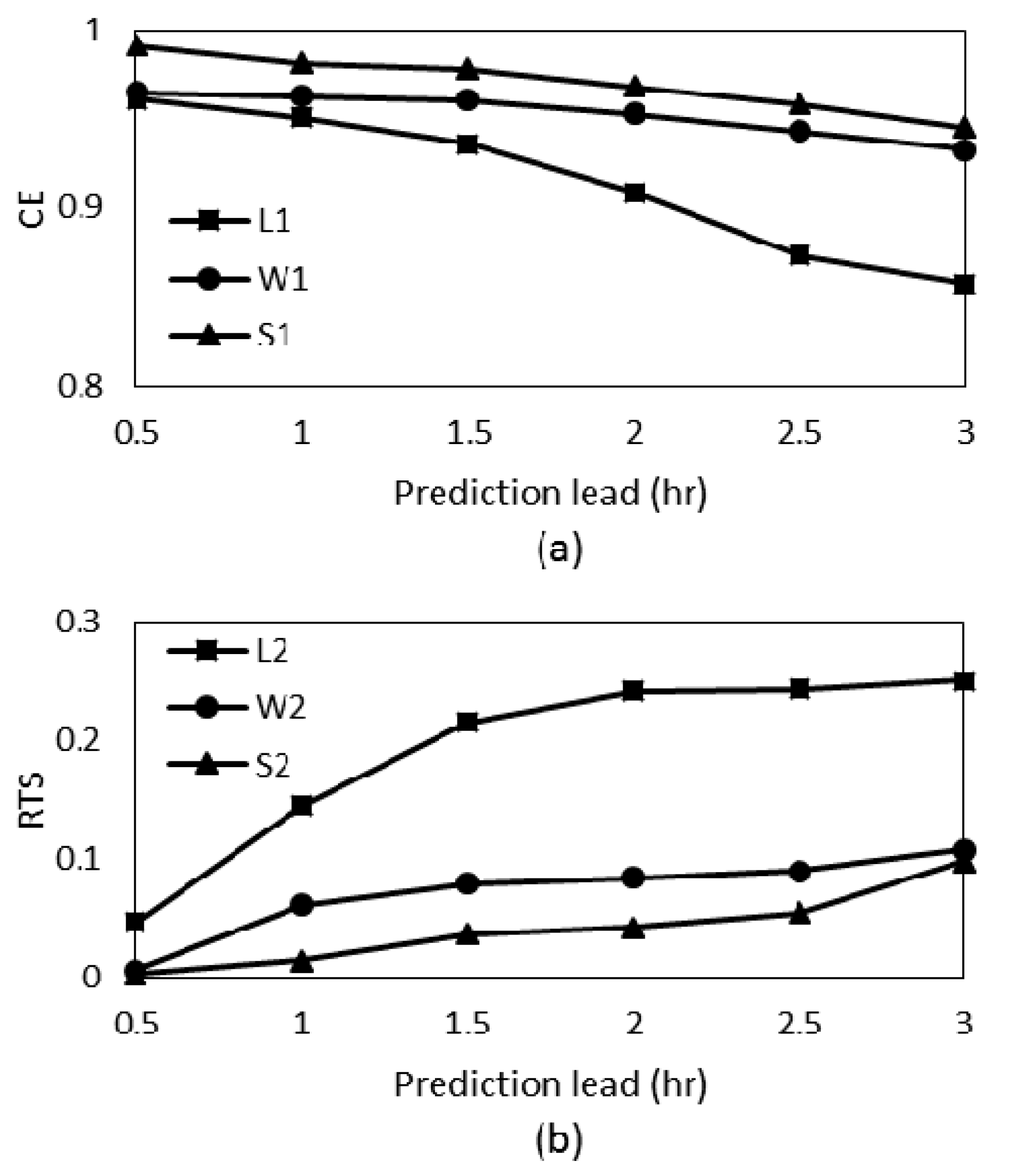
| CE | 0.859 | 0.245 | 0.852 | 0.933 | 0.269 | 0.911 | 0.946 | 0.734 | 0.929 |
| RTS | 0.403 | 0.251 | 0.500 | 0.125 | 0.108 | 0.278 | 0.111 | 0.098 | 0.167 |
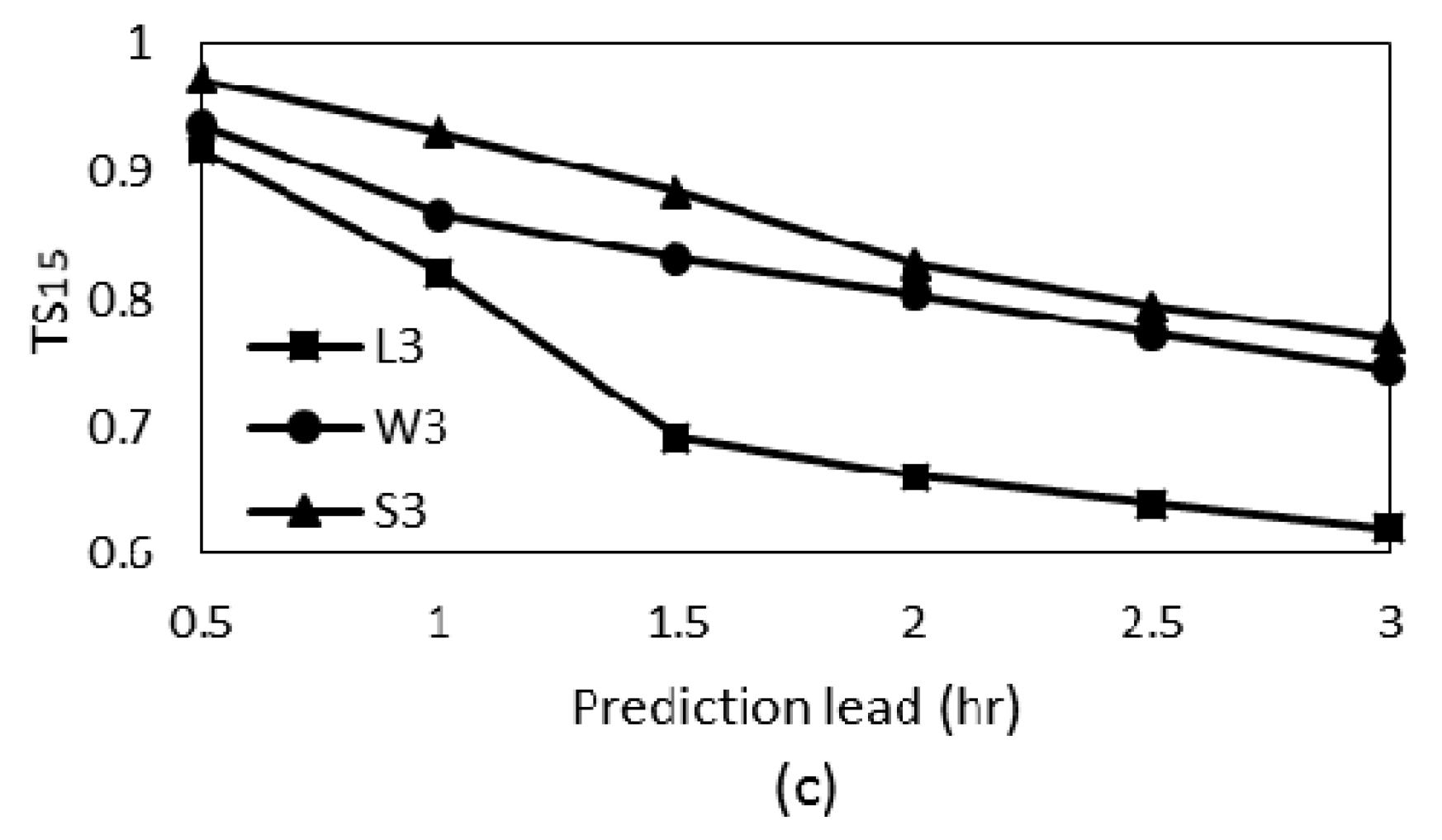
| TS15 | 0.590 | 0.472 | 0.618 | 0.728 | 0.356 | 0.743 | 0.725 | 0.426 | 0.768 |
| Available regressor | Chromosome (Selected regressor) | ||||||||
| R(t − 1) | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| R(t − 2) | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| R(t − 3) | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| R(t − 4) | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 |
| R(t − 5) | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| R(t − 6) | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| R(t − 7) | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| R(t − 8) | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 |
| R(t − 9) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| R(t − 10) | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| H(t − 1) | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| H(t − 2) | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 |
| H(t − 3) | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 |
| H(t − 4) | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| H(t − 5) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| H(t − 6) | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 |
| H(t − 7) | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| H(t − 8) | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 |
| H(t − 9) | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| H(t − 10) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Prediction lead: k = 18 (3 h) | |||||||||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ouyang, H.-T.; Shih, S.-S.; Wu, C.-S. Optimal Combinations of Non-Sequential Regressors for ARX-Based Typhoon Inundation Forecast Models Considering Multiple Objectives. Water 2017, 9, 519. https://doi.org/10.3390/w9070519
Ouyang H-T, Shih S-S, Wu C-S. Optimal Combinations of Non-Sequential Regressors for ARX-Based Typhoon Inundation Forecast Models Considering Multiple Objectives. Water. 2017; 9(7):519. https://doi.org/10.3390/w9070519
Chicago/Turabian StyleOuyang, Huei-Tau, Shang-Shu Shih, and Ching-Sen Wu. 2017. "Optimal Combinations of Non-Sequential Regressors for ARX-Based Typhoon Inundation Forecast Models Considering Multiple Objectives" Water 9, no. 7: 519. https://doi.org/10.3390/w9070519
APA StyleOuyang, H.-T., Shih, S.-S., & Wu, C.-S. (2017). Optimal Combinations of Non-Sequential Regressors for ARX-Based Typhoon Inundation Forecast Models Considering Multiple Objectives. Water, 9(7), 519. https://doi.org/10.3390/w9070519






