Evaluation of Groundwater Remediation Technologies Based on Fuzzy Multi-Criteria Decision Analysis Approaches

Abstract

Petroleum is an essential resource for the development of society and its production is huge. There is a great risk of leakage of oil during production, refining, and transportation. After entering the environment, the oil pollutants will be a great threat to the environment and may endanger human health. Therefore, it is very important to remediate oil pollution in the subsurface. However, it is necessary to choose the appropriate remediation technology. In this paper, 18 technologies are evaluated through constructing a parameter matrix with each technology and seven performance indicators, and a comprehensive analysis model is presented. In this model, four MCDA methods are used. They are SWA (Simple Weighted Addition Method), WP (Weighted Product Method), CGT (Cooperative Game Theory), and TOPSIS (Technique for Order Preference by Similarity to Ideal Solution). Mean ranking and Borda ranking methods are used to integrate the results of SWA, WP, CGT, and TOPSIS. Then two selection priorities of each method (mean ranking and Borda ranking) are obtained. The model is proposed to help decide the best choice of remediation technologies. It can effectively reduce contingency, subjectivity, one-sidedness of the traditional methods and provide scientific reference for effective decision-making.

1. Introduction

Petroleum is fundamental for human and social development. Since the Industrial Revolution, petroleum refinery products (PRPs) have been widely used as fuels and industrial raw materials. Approximately 2 to 3 billion tons of crude oil are produced every year across the world (2016). At the same time, over 100 million tons of oil and associated PRPs are entering the environment [1]. Along with extensive utilization of petroleum and related products, a large amount of leakage and spillage get into the soil and groundwater, causing significant pollution to the environment [2]. This may consequentially lead to pollution to surface water, air, and agricultural crops, affecting human and ecosystem health [3]. Such pollution is causing increasing concerns across the world. More recently, many tools and technologies have been developed for dealing with oil pollution in both soil and groundwater [4]. However, for many petroleum production managers, as well as decision makers, it is of great difficulty to identify and evaluate cost-effective tools and technologies for mitigating oil pollution and remediating contaminated soil and groundwater due to their diversities in many factors such as cost, occupational area, and efficiency [5]. Therefore, it is a necessity to advance effective tools for facilitating decision-making and technology identification/evaluation of mitigating and remediating technologies for oil pollution in soil and groundwater.

Generally, a number of processes and factors may affect the generation of oil pollution in soil and groundwater, such as waste from petroleum drilling, leakage of underground tanks and pipelines, and pollution discharge of many accidents [6]. For example, under the United States Environmental Protection Agency and its designated State Administration, approximately 2 million storage tanks are in operation in the USA. According to the technical management rules of underground storage tanks, the United States has monitored 210 thousand gas stations in operation and the results show that gas stations constructed before 1970s are most prone to leakage [7]. Approximately 510 thousand oil storage tanks have leaking problems and 130 thousand leaking points need to be cleaned in the USA. Sewage irrigation, oil leakage sludge, and garbage piling up would also cause oil to leak into the groundwater [1]. Thus, since 1984 (the implementation of a United States federal government underground storage tank program), the government has disabled 1.7 million underground storage tanks [8]. In 1993, Shell Oil Company made a survey of 1100 gas stations in the United Kingdom and found that 33% of the sites had contaminated soil and groundwater [9]. In Canada, underground storage tanks and pipelines at the gas station constructed before 1990 almost all appeared to leak, causing serious pollution of the groundwater [10,11]. In 2011, the Peru oil pipeline was leaking and approximately 1100 barrels of crude oil caused serious pollution to the original forest of the Amazon [12]. Groundwater is extremely vulnerable since the corresponding water circulation system is relatively closed. Once contaminated, the water may endanger the environment not only for a long time [3].

Particularly in China, groundwater pollution is serious in many gas stations, oil and gas fields, as well as oil and chemical plants [13]. Comparatively, China has over 100 thousand gas stations, including over 1000 in Beijing. There are approximately 6000 underground storage tanks in Shanghai [14]. According to the survey, in the 1980s the establishment of gas station underground storage tanks and pipelines have caused corrosion and leakage. According to groundwater pollution survey data (2015) in gas stations in Beijing and Tianjin, approximately 50% of gas station areas in Beijing exceeded the standard (i.e., Groundwater Petroleum Hydrocarbon Pollutants) and the detection rate of petroleum hydrocarbons in the groundwater of Tianjin gas station area was approximately 85% [15]. Due to the leakage of oil storage tanks and pipelines, a large area of the soil and groundwater in Zhongyuan Oilfield of Henan Province was polluted, and the content of petroleum hydrocarbons in contaminated soil varied from 1% to 10% [16]. Petroleum hydrocarbons have become common pollutants in the organic pollution of groundwater in China. Because of the good quality, wide distribution, and convenient access of groundwater, it represents an ideal source of water supply. In China, groundwater accounted for 20% of the total water supply, 70% of drinking water supply, 40% of irrigation water demand, and 38% of industrial water demand [17]. Therefore, groundwater plays an important role in China’s national production and life. The sustainable use of groundwater resources has become an increasingly concerning issue.

At present, the treatment of oil pollution in soil and groundwater mainly consists of physical, chemical, and biological methods, including: (a) physical treatment technologies that are mainly employing physical means to control contaminated groundwater through various physical methods, such as technologies of shielding, passive collection, and extraction treatment; (b) chemical treatment technologies that mainly comprise technologies of dosing, permeable treatment bed and soil modification technology; and (c) bioremediation to stimulate the growth of indigenous microorganisms through artificial measures including the injection of oxygen and nutrients, thereby enhancing the natural biodegradation process of pollutants. Usually, bioremediation technologies should be combined with a well system to accelerate the diffusion of oxygen and nutrients under the combined action of pumping wells, which can shorten the recovery time. Bioremediation technologies of groundwater oil pollution mainly include methods of biological injection, organic clay, and biological reactors. There are 18 commonly used remediation technologies included in this research [1,2,5,10,12,13,15]: passive collection, shielding, hydrodynamic and control, pump and treat, light non-aqueous phase liquid recovery, in situ air sparging, enhanced bioremediation, permeable reactive barrier, in situ chemical oxidation, organic clay, electrochemical dynamics, groundwater circulation well, monitoring natural attenuation, soil vapor extraction and in situ aeration, biological aeration in situ aeration, dual phase extraction single pump system, dual phase extraction double pump system, and surfactant enhanced remediation.

Obviously, there are many ways to remediate groundwater. However, different methods should be adopted under different pollution conditions and geographical features. At the same time, such technologies might be performed at different efficiencies and expenses. Therefore, identification and evaluation of groundwater remediation technologies is desired. In order to deal with identification of pollution mitigation and remediation technologies, many conditions and criteria need to be considered. About the selection of remediation technologies, we should take into account many features such as pollutant characteristics, hydrogeological conditions of the contaminated sites, and costs of the remediation technologies. Due to the complexities of actual ground water pollution sites, only through comprehensive analysis and evaluation can the most scientific repair technology or combination of technologies be determined. Such analysis and evaluation processes are normally subjective, and may lead to multiple results based on the varying opinions of relevant experts. There are no fixed patterns for the evaluation of remediation techniques. For example, Zhao (2012) presented a screening method based on Standard Guide for Remedy Selection Integrating Risk-based Corrective Action and Non-Risk Consideration of America [18]. Firstly, through eliminating of unsuitable repair technologies, he selected and evaluated alternative repair techniques. He also gave an evaluation matrix for remediation technologies and indicators (e.g., technical acceptability, site availability, effectiveness, time and costs) [19]. Li (2016) used PROMETHEE (Preference Ranking Organization Methods for Enrichment Evaluations) to identify desired remediation technologies based on indicators such as pollutants migration, degradation, human health risk, and characteristics of technologies [20]. Bai (2015) established the method and index system of soil remediation, and carried on the gradation of remediation technologies [21]. Li (2016) used the PROMETHEE method to select remediation technologies for the ruins of a chemical plant [20]. Also, a few studies focused on the selection of indicators but covered few technologies.

Previous studies have the following limitations: (a) the integrated approach to remediation of groundwater pollution is usually analyzed unilaterally, but the technology selection is a multi-attribute problem that includes a number of discrete variables and fuzzy factors. Thus, the quantitative and qualitative description of the problem needs further consideration. (b) A single method is accompanied by strong randomness, and the result can lead to serious uncertainty, which brings about erroneous conclusion. In order to remedy such limitations, the objective of this research is to propose a comprehensive approach for supporting identification and evaluation of a number of soil and groundwater remediation technologies. Firstly, four different multi-attribute evaluation methods will be used to evaluate a series of alternative schemes and decisions on the basis of irrelevant and inconsistent rules. The problem of quantitative and qualitative description will be effectively solved. In this way, the assessment of remediation technologies will be transformed into a multi-attribute decision-making problem. Secondly, different multi-attribute evaluation methods will be integrated through mean ranking and Borda ranking methods to avoid the accidental nature of different MCDA methods. This represents an improvement upon stability and accuracy. Then, the developed evaluation method will be applied to various forms of pollution treatment technology. The results will be useful to the scheme selection problem in other cases. In this research, 18 technologies are included and four MCDA methods are used. The results of different MCDA methods are integrated through the introduction of mean ranking and Borda ranking methods to get the priority order. A desired solution will then be generated by giving the ranked results of each scheme related to remediation technologies.

2. Methodology

2.1. Development of Evaluation Indicators

A systematic and reasonable evaluation index system is desired in the evaluation of a large number of remediation technologies. Thus, evaluation indicators need to be identified and screened out. The indicators should cover pollution types, and intensity, geological survey as well as social and economic research. Therefore, the establishment of evaluation index system should use a variety of indicator selection methods. Indicators are used to describe the advantages and disadvantages of the methods in terms of cost, efficiency, application range, and technical maturity [19,20,21]. To carry out the selection of indicators and establish of index system, we must refer to certain principles [22,23,24,25,26,27,28]. The general principles of establishing index system include: (a) the indicator system should be scientifically based on concept and calculation method of the theory of sustainable development; (b) any developed index systems should include not only the index of technical applicability, but also the indexes that reflect the management cost, technology maturity, and efficiencies; there must be indicators that can reflect the degree of mutual coordination between the above system indicators; (c) because of the difference between the natural environment and social economy, the selection of indicators should be consistent with the regional characteristics and local conditions of the study area; (d) terminology, concepts, and calculation methods should be made as standard as possible to achieve comparability with other regional indicators; and (e) a combination of qualitative and quantitative indicators. Quantitative indicators should be selected as far as possible. Important indicators that are difficult to quantify can be described qualitatively. (f) Simplicity, i.e., the availability of data and the feasibility of statistical computation, should be taken into account. The index system should be easy to be understood and should be convenient to use through the adoption of certain mathematical evaluation models.

Therefore, to establish a scientific, reasonable and systematic evaluation index system for groundwater remediation technologies, based on the basic concept of water resources security and theoretical analysis method combined with expert consultation and system analysis, we scientifically select indicators to reflect the safety of groundwater, and establish an evaluation index system. We have collected a wide range of research results in recent years on water pollution, oil pollution, groundwater treatment and oil pollution control at home and abroad. Through theoretical analysis, we select indicators that can represent the features of petroleum and the associated products. The initially established evaluation index system contains a wide range of indicators and the correlation degree of some indexes is relatively large. Therefore, we need to choose certain indicators from all. Expert consultation method is a commonly used index screening method that is conducted by means of a questionnaire. We used a 0–1 scale design questionnaire from the “Oil Polluted Groundwater Remediation Technologies Evaluation Index System”. In the questionnaire, $0\le a_{ij}<0.5$. This means that j is more important than i, and the smaller a_ij is, the more important j is than i. We solicited the opinions of 18 domestic experts in the fields of water resources, water environment, ecological environment, oil pollution remediation, and other research areas and ensure that the indicators can fully reflect the views of the experts.

2.2. Uncertainties of Evaluation

Many uncertainties are associated with the evaluation process. For example, fuzzy judgments might be given for any criteria, which can be dealt with through the introduction of fuzzy sets theory. Normally, the first stage is fuzzy impact transformation, which includes two steps: (a) transformation of descriptive linguistic variables, which means transforming a descriptive language index into fuzzy sets; and (b) transforming the fuzzy sets into crisp values. The result of this stage is to generate a new index matrix that contains only numerical data. The second stage is to use the classical MCDA method to sort the various decision schemes. In the third stage, we use mean ranking and Borda ranking methods to integrate the results of MCDA methods to obtain a more accurate priority.

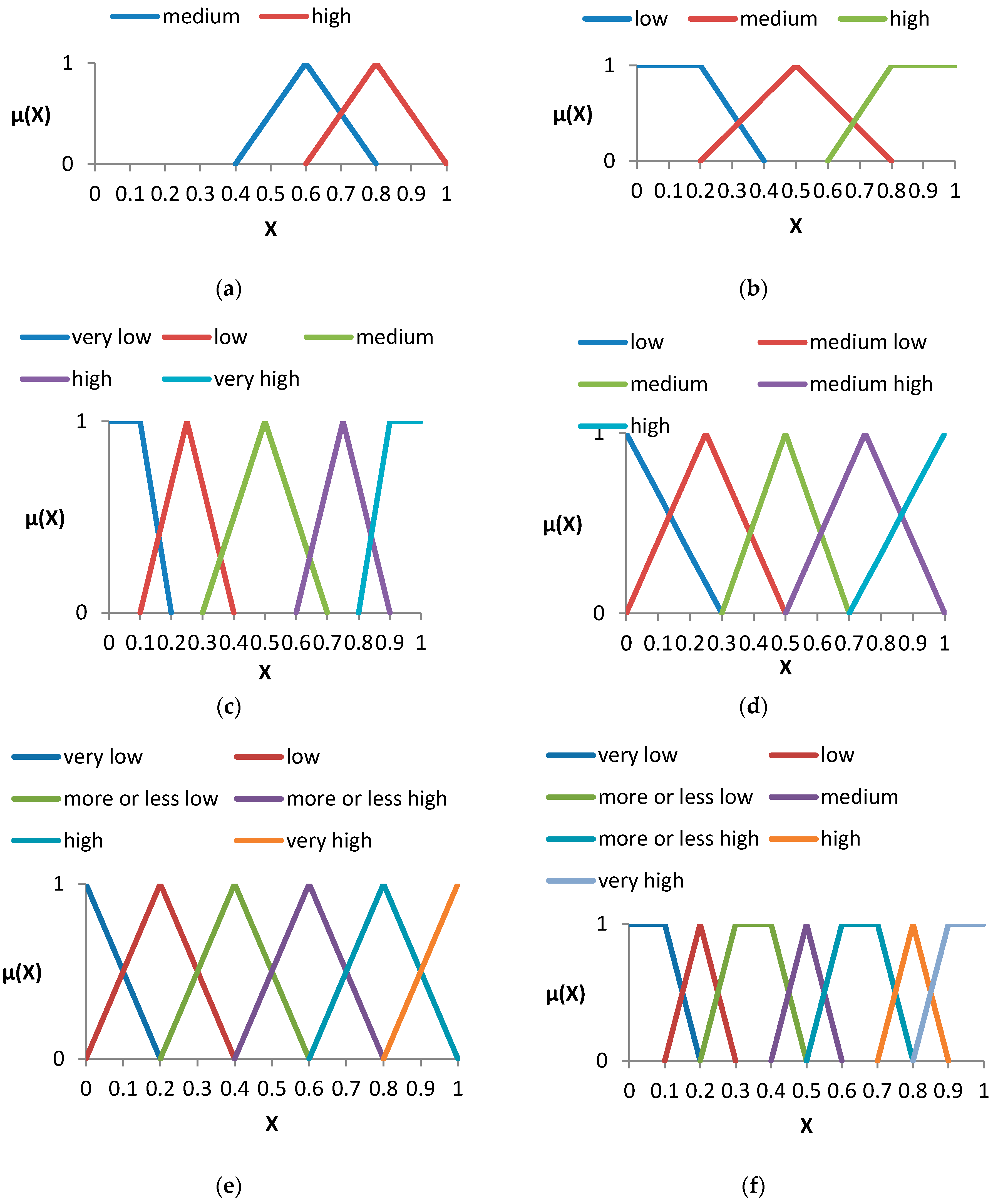
Chen proposed a numerical approximation system that can systematically convert linguistic variables into the corresponding fuzzy sets [29]. According to Chen, this transformation required eight conversion scales, as shown in Figure 1a–h. These conversion scales were presented in the synthesis and modification of Baas (1977), Bonissone (1982), Chen (1988), Efstathiou (1979, 1982), Kerre (1982) and Wenstop (1976) [30,31,32,33,34,35,36] and applied widely by Wang (2016), Xue (2016), Mardani (2016), and Karsak (2015) [37,38,39,40]. In general, the scale given in the graph is sufficient to cover all the representations of each feature, “high” and “low”. When given a specific variable representation, one of them can be used to analyze. Even if the same variable is used as the “high”, the membership functions are not the same in the different graphs. Chen argued that this phenomenon was caused by the fact that the same linguistic variables were expressed differently in different situations [29]. We used the membership function set to express the meaning of language data. For example, in Figure 1a, the red peak indicates the membership degree of “high”; the farther away it is from 0.8, the less it belongs to “high”.

The second step in the transformation of fuzzy variables is to convert the fuzzy values into crisp values. A lot of scholars have made relevant research such as Hipel (1982) [41] and Cheng (2000) [42]. Generally speaking, this kind of conversion can be regarded as a method to calculate the fuzzy average value. The fuzzy mean value is not necessarily the highest degree of membership. A left–right scoring approach based on Jain (1977) [43] and Chen (1985) [44] was used. The score of fuzzy sets M can be obtained through the following steps. In order to get the score value, fuzzy sets need to be compared with the maximum fuzzy sets (fuzzy maximum) and the minimum fuzzy sets (fuzzy minimum). These two fuzzy sets can be defined as:

$${\mu }_{\max }(x)=\{\begin{array}{c}x,\\ 0,\end{array}\begin{array}{c}0\le x\le 1\\ otherwise\end{array}$$

(1a)

$${\mu }_{\min }(x)=\{\begin{array}{c}1-x,\\ 0,\end{array}\begin{array}{c}0\le x\le 1\\ otherwise\end{array}.$$

(1b)

The score on the right is obtained by the intersection of fuzzy sets M and fuzzy maximum. The right score can be obtained by the following equation:

$${\mu }_R(M)={\sup }_x[{\mu }_M(x)\wedge {\mu }_{\max }(x)].$$

(2a)

Similarly, M left score can be calculated by using the following formula:

$${\mu }_L(M)={\sup }_x[{\mu }_M(x)\wedge {\mu }_{\min }(x)].$$

(2b)

The total score of M can be calculated by left and right scores:

$${\mu }_T(M)=[{\mu }_R(M)+1-{\mu }_L(M)]/2.$$

(2c)

As shown in Figure 2, ${\mu }_{\max }$ and ${\mu }_{\min }$ are the intersection points of the two diagonal with the membership function respectively, and the membership functions are as follows:

$${\mu }_{M_1}(x)=\frac{0.3-x}{0.3} ,0\le x\le 0.3$$

(3a)

$${\mu }_{M_2}(x)=\{\begin{array}{c}4x,\\ \frac{0.5-x.}{0.25},\end{array}\begin{array}{c}0\le x<0.25\\ 0.25\le x\le 0.5\end{array}$$

(3b)

$${\mu }_{M_3}(x)=\{\begin{array}{c}\frac{x-\mathrm{0.3.}}{0.2},\\ \frac{0.7-x}{0.2},\end{array}\begin{array}{c}0.3\le x<0.5\\ 0.5\le x\le 0.7\end{array}$$

(3c)

$${\mu }_{M_4}(x)=\{\begin{array}{c}4x-2,\\ \frac{1-x}{0.25},\end{array}\begin{array}{c}0.5\le x<0.75\\ 0.75\le x\le 1\end{array}$$

(3d)

$${\mu }_{M_5}(x)=\frac{x-0.7}{0.3}, 0.7\le x\le 1.$$

(3e)

Then, using Equations (1)–(3), we can get the total score. They can be used instead of the original language to describe the data. As shown in

Table 1. Determination of μ_total.

i	μR (Mi)	μL (Mi)	μT (Mi)
1	0.2308	1.0000	0.1154
2	0.6667	0.8000	0.4334
3	0.5833	0.5833	0.5000
4	0.8000	0.4000	0.7000
5	1.0000	0.2308	0.8846

, 0.8846, 0.7000, 0.5000, 0.4333, and 0.1154 take the place of “high”, “medium high”, “medium”, “medium low”, and “low”.

2.3. Multi-Criteria Decision Analysis

Multi-criteria decision analysis (MCDA) is a batch of methods that can evaluate a series of alternatives on the basis of irrelevant and inconsistent rules to identify the desired decision alternatives. It has the characteristics of flexibility and clear judgment of the correlation between indicators. Over the past 20 years, MCDA methods have become a powerful tool for decision analysis, and developed rapidly in management, engineering, and other fields. More recently, MCDA has been applied to many research areas such as environmental resource management. Hipel (1982), for example, introduced a fuzzy MCDA model in a sludge management (SWM) problem [41]. In order to broaden its scope of application, decision support systems (DSS) and MCDA methods were combined in the 1980s to form an integrated system, which has been applied in a variety of areas [45]. In Finland, PROMETHEE were used as an assistant decision method to solve landfill site selection problems [46]. Maniezzo (1998) applied it to the site selection of industrial waste management facilities in Italy [47]. Haastrup (1998) developed a decision support system that combined optimization algorithms to solve facility location problems [48]. Cheng (2000) established a DSS and applied it to support urban solid waste management problems [49]. Normally, MCDA is a method for decision makers to evaluate the merits and demerits of several schemes containing many attributes. In this research, four MCDA methods are introduced. These four methods are selected because they can deal with the same type of data (the index value and the weight).

(1) Simple Weighted Addition Method (SWA)

Simple Weighted Addition Method is believed to be the simplest MCDA method. Because it is relatively easy for decision makers to understand, it is widely used in various fields. For each scheme, the utility value of the index is obtained by the product of the normalized index value and the weight of each index, and the sum of the scheme can be obtained:

$$U_j={\displaystyle \sum _{i=1}^n{w}_i{r}_{ij}},j=1,2,\dots ,m.$$

(4)

In the formula, $w_i$ is the weight of the index I, $r_{ij}$ is the index value after standardization. After calculating the U_j, the scheme with the maximum value is the most desirable scheme for the decision maker.

A basic assumption of the SWA method is that it is independent of the index. Therefore, the weight of the index will not be affected by the weight of other indexes. Simplicity is the biggest advantage of SWA, but its disadvantages are also obvious: there is usually contact or complementarity between indicators. The basic assumption is not easy to accept, while ignoring the relevance between the indexes may lead to incorrect results.

(2) Weighted Product Method (WP)

The weighted product method has been in use for a long time. The SWA method needs to first standardize indicators of data to remove the impact of the unit, but the WP method does not have to standardize the data. When the index value is multiplied, the index weight is the power of the index value, and the U_j of each scheme is:

$$U_j={\displaystyle \prod _{i=1}^n{x}_{ij}^{w_j}},j=1,2,\dots ,m.$$

(5)

In the formula, $w_j$ is the weight of the index of number i. Forward index weights are positive in power. Backward index weights are negative in power. When adopting this method, the scheme with the maximum U_j is the most desirable for decision makers. Theoretically, due to the characteristic of the product, the value may be infinite. The purpose of WP is to screen out the scheme with the smallest U_j, and the difference between the largest and the second largest values is larger than that given by the SWA method. WP has reasonable logic and a simple calculation method, but it has not been widely used.

(3) Technique for Order Preference by Similarity to Ideal Solution (TOPSIS)

Technique for Order Preference by Similarity to Ideal Solution is proposed by Chen [29]. This author proposes that a MCDA problem can be regarded as a collection system. The m schemes with n indicators that need to be evaluated are equivalent to m points in the n-dimensional space. Therefore, the most desirable program should meet the “shortest distance” to the best scheme and the “longest distance” to the worst scheme. Compared to the CGT, in which only the worst solution is considered, MCDA can give more comprehensive consideration of the data when solving the TOPSIS problem.

The specific process is as follows:

(a) The data need to be standardized; the dimensional effects need to be removed and thus it is more convenient to make the comparison among the indicators. According to the given weight, the index value matrix with weight needs to be calculated.

$$v_{ij}=w_i{r}_{ij},i=1,2,\dots ,n;j=1,2,\dots ,m.$$

(6)

In the formula, $w_i$ is the weight of the index i.

(b) After $v_{ij}$ is calculated, the best scheme $A^{*}$ and the worst scheme $A^{-}$ is defined as follows:

$$A^{*}=\{({\max }_j{v}_{ij}|i\in I),({\min }_j{v}_{ij}{|i\in I}^{\text{'}})|j=1,2,\dots ,m\}=\{v_1^{*},v_2^{*},\dots ,v_i^{*},\dots ,v_n^{*}\}$$

(7a)

$$A^{-}=\{({\min }_j{v}_{ij}|i\in I),({\max }_j{v}_{ij}{|i\in I}^{\text{'}})|j=1,2,\dots ,m\}=\{v_1^{-},v_2^{-},\dots ,v_i^{-},\dots ,v_n^{-}\},$$

(7b)

where I represents the number of positive indicators and I’ represents the number of reverse indicators.

(c) Calculate the value of each scheme, that is, the relative closeness of the best scheme.

$$S_j^{*}=\sqrt{{\displaystyle \sum _{i=1}^n{(v_{ij}-v_j^{*})}^2}},j=1,2,\dots ,m$$

(8a)

$$S_j^{-}=\sqrt{{\displaystyle \sum _{i=1}^n{(v_{ij}-v_j^{-})}^2}},j=1,2,\dots ,m$$

(8b)

$$U_j=S_j^{-}/(S_j^{*}+S_j^{-}),j=1,2,\dots ,m$$

(8c)

In the formula, $S_j^{*}$ is the distance between the number j scheme and the best scheme. $S_j^{-}$ is the distance between the number j scheme and the worst scheme. At the same time, $0<U_j^{*}<1$.

Finally, we can sort all the schemes by the value of $U_j$. The scheme that has the biggest $U_j$ is the most desirable. The advantages of this method are the same as for SWP. It is easy to understand, but in a situation, it cannot point to a clear decision. If an MCDA problem involves only two indicators, it can be considered as a geometric problem of a two-dimensional space; the optimal and the worst scheme are defined as $P^{*}$ and $P^{-}$, assuming there are two schemes ($P_1$ and $P_2$) and they have the same U_j. In this case, they are considered to be the same and there is no more desirable scheme. The decision makers can only select a scheme based on their own judgment.

(4) Cooperative Game Theory (CGT)

Cooperative game theory is similar to the WP method and can also be considered as a combination of WP and TOPSIS. It can also enlarge the distance among the schemes. So decision makers can choose the scheme with the longest distance to the worst scheme. The method is designed to help decision makers choose the scheme that has the maximum geometric distance to the worst case. To define the worst scheme, the decision maker first defines a minimal acceptable set of indicator values. However, not all of the indicators have a minimum acceptable level. For example, it is difficult to determine the minimum cost to a decision maker, and when the cost is an indicator that must be considered in the MCDA problem-solving process, the decision maker must give the minimum value. Therefore, in order to avoid this situation, we can select the minimum value of the index before calculating. When a set of decision schemes is given, the worst index set $A^{-}$ is defined as:

$$A^{-}=\left\{({\min }_j{x}_{ij}|i\in I),({\max }_j{x}_{ij}|i\in I^{*})|j=1,2,\cdots ,m\right\}=\left\{x_1^{-},x_2^{-},\dots ,x_i^{-},\dots x_n^{-}\right\}$$

(9)

Among them, x_ij is the value of the index i; $x_i^{-}$ is the minimum value (the worst level) of the index i in all the schemes. Therefore, the $U_j$ of each index can be calculated by the following formula [49]:

$$U_j={\displaystyle \prod _{i=1}^n{\left|x_{ij}-x_i^{-}\right|}^{w_i}},j=1,2,\dots ,m,$$

(10)

in which $w_i$ is the weight of each index. The most desirable scheme is the one with the maximum $U_i$. At the same time, each program can be sorted by $U_i$.

It is not uncommon to solve the MCDA problem by Cooperative Game Theory. Lau believes that CGT can produce scheme selection system with more security and less risk [50]. In fact, the scheme sorting given by CGT is conservative for policy makers, and there are also some problems. Since any number multiplied by 0 equals 0, the CGT method will automatically exclude all programs that contain at least one minimum value (the worst level). They are not considered, even if the other indicators of these schemes are larger (better level).

(5) Integration of MCDA Approaches

To avoid the accidental nature of different methods, two integration methods, mean ranking and Borda Ranking, are used. The mean ranking method is one of the simplest methods. This method is based on the concept and theory of statistical computation. According to the ranking of technologies obtained by each MCDA method, we carry out mean ranking and get the final rank of each technology. Based on the voting theory, the Borda method is used to construct the N × N matrix by comparing every scheme to another. For each pair of schemes $A_j$ and $A_{j\text{'}}$ , the number of votes is defined as the number of support. For example, the first two rows in the table can determine the number of $A_j$ and $A_{j\text{'}}$ votes. According to $M_2$ and $M_4$, $A_1$ is better than $A_2$. However, according to $M_1$ and $M_3$, $A_1$ is worse than $A_2$. Thus, compared to $A_2$,$A_1$ gets two votes by $\{M_2,M_4\}$. Similarly, compared to , $A_1$, $A_2$ also gets two votes by $\{M_1,M_3\}$. So an N × N matrix X is established, and: $x_{jj\text{'}}=1$, which means that $A_j$ gets more votes than $A_{j\text{'}}$; $x_{jj\text{'}}=0$, and vice versa.

As

Table 2. N × N matrix used in the Borda ranking method.

Scheme	A1	A2	A3	A4	A5	Sj
A1	0	0	0	1	0	1
A2	0	0	1	1	0	2
A3	1	1	0	1	1	4
A4	0	0	0	0	0	0
A5	0	1	0	1	0	2
S’j	1	2	1	4	1

shows, $A_1$ and $A_2$ get the same number of votes. Thus, $x_{12}$ and $x_{21}$ both equal 0. The last column $S_j$ indicates the degree to which $A_j$ is better than other scheme, which is the sum of the same row. In this way, the scheme with the largest value of $S_j$ is considered the best and most desirable scheme. For example, this sorting result is $A_3>（A_2,A_5）>A_1>A_4$, and the most desirable scheme is $A_3$.

Thus, an integrated approach is proposed based on the combination of the abovementioned indicator system, as well as uncertainty expression and MCDA methods. Also, in order to reflect the uncertainties associated with weights for the evaluation, a fuzzy analytical hierarchy process (FAHP) [51] is used. Therefore, a fuzzy multi-criteria decision analysis (FMCDA) system is established.

3. Application for Evaluation of Technologies

3.1. Overview of the Case Study

The northern oil fields of Shengli are located in the Yellow River Delta region and cover an area of 8600 km², including Hekou, Lijin in Dongying, Bincheng, Zhanhua and Wuli in Binzhou, Linyi in Dezhou, Shanghe, and Jiyang in Ji’nan and other counties.

The study area is the main production area of Shengli oilfield. There are many oil wells. In the process of drilling and production, some of the crude oil will be scattered. During oil transportation, due to unreasonable design, incorrect installation, and material failure, the pipeline will rupture, causing oil leakage. A crude oil pipeline is generally buried 1 m deep or so, will be a direct threat to the nearby shallow groundwater and soil. According to the distribution of organic compounds, chlorinated organic compounds have the highest detectable rate of 72.7%, followed by halogenated hydrocarbons and aromatic hydrocarbons, with detectable rates of 14.8% and 12.5% respectively.

In order to quantify subjective feelings, the fuzzy analytical hierarchy process (FAHP) is used to calculate the weight of indicators. First, the priority relation matrix is established. It is then transformed into a fuzzy consistent matrix. After priority relation ranking, we get the weight of the indicators [51]. The comparison value of importance between every two indicators is given in

Table 3. Precedence relation matrix.

Indicator	I1	I2	I3	I4	I5	I6	I7
Aquifer depth (I1)	0.5	0.5	0.5	0.5	1	1	1
Permeability of aquifer (I2)	0.5	0.5	0.5	0.5	1	1	1
Applicable scope of pollution (I3)	0.5	0.5	0.5	0.5	1	1	1
Applicable pollution level (I4)	0.5	0.5	0.5	0.5	1	1	1
Technology maturity (I5)	0	0	0	0	0.5	0	0
Governance cost (I6)	0	0	0	0	1	0.5	1
Pollutant removal rate (I7)	0	0	0	0	1	0	0.5

.

In this research, FAHP is used to transfer the precedence relation matrix into a fuzzy consistent judgment matrix, as shown in

Table 4. Fuzzy consistent judgment matrix and weight list of evaluation indicators.

Indicator	I1	I2	I3	I4	I5	I6	I7	Weight
Aquifer depth (I1)	0.5000	0.5000	0.5000	0.5000	0.8214	0.6786	0.7500	0.1735
Permeability of aquifer (I2)	0.5000	0.5000	0.5000	0.5000	0.8214	0.6786	0.7500	0.1735
Applicable scope of pollution (I3)	0.5000	0.5000	0.5000	0.5000	0.8214	0.6786	0.7500	0.1735
Applicable pollution level (I4)	0.5000	0.5000	0.5000	0.5000	0.8214	0.6786	0.7500	0.1735
Technology maturity (I5)	0.1786	0.1786	0.1786	0.1786	0.5000	0.3571	0.4286	0.0816
Governance cost (I6)	0.3214	0.3214	0.3214	0.3214	0.6429	0.5000	0.5714	−0.1225
Pollutant removal rate (I7)	0.2500	0.2500	0.2500	0.2500	0.5714	0.4286	0.5000	0.1020

.

Table 5. The description of indicators in natural language. (Aquifer depth: A—4.6 m; B—4.6~15.2 m; C—15.2~30.5 m; D—>30.5 m. Permeability of aquifer: a—better; b—good; c—bad; d—worse.)

Remediation Technology	Aquifer Depth	Permeability of Aquifer	Applicable Scope of Pollution	Applicable Pollution Level	Technology Maturity	Governance Cost	Pollutant Removal Rate
Passive Collection Method (A1)	A, B	c, d	small	heavier	applied widely	general	high
Shielding Method (A2)	A, B	a, b, c, d	smaller	heavier	applied widely	higher	/
Hydrodynamic and Control (A3)	A, B, C, D	a, b	bigger	heavier	applied little	general	general
Pump and Treat (A4)	A, B, C, D	a, b, c	bigger	heavier	applied widely	higher	high
Light Non-Aqueous Phase Liquid Recovery (A5)	A, B, C, D	a, b, c	bigger	heavier	applied widely	general	high
In Situ Air Sparging (A6)	A, B, C, D	b, c, d	small	light	applied widely	low	higher
Enhanced Bioremediation (A7)	A, B, C, D	a, b, c	all	light	applied widely	lower	higher
Permeable Reactive Barrier (A8)	A, B	a, b, c, d	small	all	applied widely	low	higher
In Situ Chemical Oxidation (A9)	A, B, C, D	a, b, c, d	all	all	applied widely	low	higher
Organic Clay (A10)	A, B, C, D	d	all	heavy	average	low	higher
Electrochemical Dynamics (A11)	A, B, C, D	a, b, c, d	smaller	all	average	low	higher
Groundwater Circulation Well (A12)	A, B, C, D	a, b	big	all	average	general	higher
Monitoring Natural Attenuation (A13)	A, B, C, D	a, b, c, d	all	lighter	applied widely	lower	higher
Soil Vapor Extraction and In Situ Aeration (A14)	A, B, C, D	b, c	small	all	applied little	high	higher
Biological Aeration In Situ Aeration (A15)	A, B, C, D	a, b, c	small	all	average	high	higher
Dual Phase Extraction Single Pump System (A16)	A, B, C, D	c, d	bigger	heavier	applied little	higher	high
Dual Phase Extraction Double Pump System (A17)	A, B, C, D	a, b, c	bigger	heavier	applied little	higher	high
Surfactant Enhanced Remediation (A18)	A, B, C, D	a, b, c	bigger	heavier	average	low	higher

shows the description of indicators in natural language. As shown in

Table 6. The description of indicators in mathematical language.

Remediation Technology	Aquifer Depth	Permeability of Aquifer	Applicable Scope of Pollution	Applicable Pollution Level	Technology Maturity	Governance Cost	Pollutant Removal Rate
Passive Collection Method (A1)	0.1154	0.5000	0.4333	0.8846	0.8846	0.5000	0.7000
Shielding Method (A2)	0.1154	0.8846	0.1154	0.8846	0.8846	0.8846	0.1154
Hydrodynamic and Control (A3)	0.7000	0.5000	0.8846	0.8846	0.1154	0.5000	0.5000
Pump and Treat (A4)	0.7000	0.7000	0.8846	0.8846	0.8846	0.8846	0.7000
Light Non-Aqueous Phase Liquid Recovery (A5)	0.7000	0.7000	0.8846	0.8846	0.8846	0.5000	0.7000
In Situ Air Sparging (A6)	0.7000	0.7000	0.4333	0.4333	0.8846	0.4333	0.8846
Enhanced Bioremediation (A7)	0.7000	0.7000	0.5000	0.4333	0.8846	0.1154	0.8846
Permeable Reactive Barrier (A8)	0.1154	0.8846	0.4333	0.5000	0.8846	0.4333	0.8846
In Situ Chemical Oxidation (A9)	0.7000	0.8846	0.5000	0.5000	0.8846	0.4333	0.8846
Organic Clay (A10)	0.7000	0.1154	0.5000	0.7000	0.5000	0.4333	0.8846
Electrochemical Dynamics (A11)	0.7000	0.8846	0.1154	0.5000	0.5000	0.4333	0.8846
Groundwater Circulation Well (A12)	0.7000	0.5000	0.7000	0.5000	0.5000	0.5000	0.8846
Monitoring Natural Attenuation (A13)	0.7000	0.8846	0.5000	0.1154	0.8846	0.1154	0.8846
Soil Vapor Extraction and In Situ Aeration (A14)	0.7000	0.5000	0.4333	0.5000	0.1154	0.7000	0.8846
Biological Aeration In Situ Aeration (A15)	0.7000	0.7000	0.4333	0.5000	0.5000	0.7000	0.8846
Dual Phase Extraction Single Pump System (A16)	0.7000	0.5000	0.8846	0.8846	0.1154	0.8846	0.7000
Dual Phase Extraction Double Pump System (A17)	0.7000	0.7000	0.8846	0.8846	0.1154	0.8846	0.7000
Surfactant Enhanced Remediation (A18)	0.7000	0.7000	0.8846	0.8846	0.5000	0.4333	0.8846

, we transfer them into mathematical language using the rules in Table 1.

3.2. Result Analysis

Based on the weight of indicators and standardized indicator data of different technologies, results of SWA can be obtained via Equation (4).

Table 7. Ranking results of the Simple Weighted Addition, Weighted Product, Cooperative Game Theory, and Technique for Order Preference by Similarity to Ideal Solution methods.

Remediation Technology	SWA		WP		CGT		TOPSIS
	Uj	Ranking	Uj	Ranking	Uj	Ranking	Uj	Ranking
Passive Collection Method (A1)	0.139008	16	0.536495	17	0.093818	17	0.53	16
Shielding Method (A2)	0.104581	18	0.365298	18	0.020821	18	0.47	18
Hydrodynamic and Control (A3)	0.177789	7	0.679240	10	0.280765	11	0.68	4
Pump and Treat (A4)	0.198598	3	0.820635	4	2.875641	1	0.69	3
Light Non-Aqueous Phase Liquid Recovery (A5)	0.217416	1	0.880015	1	0.789412	4	0.8	2
In Situ Air Sparging (A6)	0.170366	9	0.716045	6	0.585903	9	0.61	10
Enhanced Bioremediation (A7)	0.190247	4	0.863145	3	0.567308	10	0.67	6
Permeable Reactive Barrier (A8)	0.147914	14	0.559180	14	0.094611	16	0.55	14
In Situ Chemical Oxidation (A9)	0.189545	5	0.783693	5	0.656443	6	0.68	5
Organic Clay (A10)	0.144997	15	0.556964	15	0.094752	15	0.54	15
Electrochemical Dynamics (A11)	0.153728	12	0.580043	13	0.099372	13	0.55	13
Groundwater Circulation Well (A12)	0.165646	10	0.705785	8	0.603190	8	0.63	8
Monitoring Natural Attenuation (A13)	0.182401	6	0.714569	7	0.098510	14	0.61	11
Soil Vapor Extraction and In Situ Aeration (A14)	0.127692	17	0.552921	16	0.250788	12	0.51	17
Biological Aeration In Situ Aeration (A15)	0.150386	13	0.660682	11	0.638466	7	0.57	12
Dual Phase Extraction Single Pump System (A16)	0.165036	11	0.655532	12	1.067405	3	0.63	9
Dual Phase Extraction Double Pump System (A17)	0.176863	8	0.694933	9	1.147820	2	0.66	7
Surfactant Enhanced Remediation (A18)	0.215410	2	0.875487	2	0.752292	5	0.81	1

shows the results obtained by the SWA method. Light non-aqueous phase liquid recovery, surfactant enhanced remediation, and pump and treat are the first three technologies according to this method.

Similarly, based on the weight of indicators and standardized indicator data of different technologies, results of WP can be obtained by Equation (5). Table 7 shows the results obtained by the WP method. Compared with the SWA method, WP increases the distance between every two technologies. The results are a little different. Liquid recovery, surfactant enhanced remediation, and enhanced bioremediation are the first three technologies according to this method.

The results of TOPSIS are obtained based on the weight of indicators and standardized indicator data of different technologies and Equations (6) to (8). Table 7 shows the results obtained by the TOPSIS method. The first three technologies are surfactant enhanced remediation, light non-aqueous phase liquid recovery, and pump and treat according to this method.

As to the CGT method, based on the weight of indicators and standardized indicator data of different technologies, the results of CGT can be obtained by Equations (9) and (10). Table 7 shows the results obtained by the CGT method. CGT also increases the distance between every two technologies. Because the minimum of indicators is from the value of one technology, there will be some invalid values. To avoid invalid values, we make the positive indicator 0.00001 smaller and the negative indicator 0.00001 larger in the worst sample. This will not influence the sorting result. The first three technologies are Pump and Treat, Dual Phase Extraction Double Pump System, and Dual Phase Extraction Single Pump System according to this method. Table 6 shows the results obtained by the CGT method.

3.3. MCDA Aggregation

The MCDA method aims to sort the given scheme. There are two ways to further integrate the results: the mean ranking method and the Borda ranking method. The mean ranking method sorts the schemes according to the average value, and the Borda ranking is given by comparing every two technologies.

The results are shown in

Table 8. Results of mean ranking method.

Remediation Technology	MCDA Methods				Mean Rankings
	SWA	WP	CGT	TOPSIS
Passive Collection Method (A1)	16	17	17	16	16.5	17
Shielding Method (A2)	18	18	18	18	18	18
Hydrodynamic and Control (A3)	7	10	11	4	8	7
Pump and Treat (A4)	3	4	1	3	2.75	3
Light Non-Aqueous Phase Liquid Recovery (A5)	1	1	4	2	2	1
In Situ Air Sparging (A6)	9	6	9	10	8.5	8
Enhanced Bioremediation (A7)	4	3	10	6	5.75	5
Permeable Reactive Barrier (A8)	14	14	16	14	14.5	14
In Situ Chemical Oxidation (A9)	5	5	6	5	5.25	4
Organic Clay (A10)	15	15	15	15	15	15
Electrochemical Dynamics (A11)	12	13	13	13	12.75	13
Groundwater Circulation Well (A12)	10	8	8	8	8.5	8
Monitoring Natural Attenuation (A13)	6	7	14	11	9.5	11
Soil Vapor Extraction and In Situ Aeration (A14)	17	16	12	17	15.5	16
Biological Aeration In Situ Aeration (A15)	13	11	7	12	10.75	12
Dual Phase Extraction Single Pump System (A16)	11	12	3	9	8.75	10
Dual Phase Extraction Double Pump System (A17)	8	9	2	7	6.5	6
Surfactant Enhanced Remediation (A18)	2	2	5	1	2.5	2

. This table shows the scheme sorting index and final average value of sorting. According to the final average sorting value, we can produce a final scheme order, that is: A5 > A18 > A4 > A9 > A7 > A17 > A3 > (A6, A12) > A16 > A13 > A15 > A11 > A8 > A10 > A14 > A1 > A2. The two in brackets have the same sorting value.

The matrix is given in

Table 9. N × N matrix used in Borda ranking method.

Technologies	A1	A2	A3	A4	A5	A6	A7	A8	A9	A10	A11	A12	A13	A14	A15	A16	A17	A18	Sj’
A1	0	0	1	1	1	1	1	1	1	1	1	1	1	0	1	1	1	1	15
A2	1	0	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	17
A3	0	0	0	1	1	0	1	0	1	0	0	0	0	0	0	0	0	1	5
A4	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	0	1	2
A5	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
A6	0	0	0	1	1	0	1	0	1	0	0	0	0	0	0	0	1	1	6
A7	0	0	0	1	1	0	0	0	0	0	0	0	0	0	0	0	0	1	3
A8	0	0	1	1	1	1	1	0	1	0	1	1	1	0	1	1	1	1	13
A9	0	0	0	1	1	0	0	0	0	0	0	0	0	0	0	0	0	1	3
A10	0	0	1	1	1	1	1	1	1	0	1	1	1	0	1	1	1	1	14
A11	0	0	1	1	1	1	1	0	1	0	0	1	1	0	1	1	1	1	12
A12	0	0	0	1	1	0	1	0	1	0	0	0	0	0	0	0	1	1	6
A13	0	0	0	1	1	1	1	0	1	0	0	0	0	0	0	0	0	1	6
A14	0	0	1	1	1	1	1	1	1	1	1	1	1	0	1	1	1	1	15
A15	0	0	1	1	1	1	1	0	1	0	0	1	1	0	0	1	1	1	11
A16	0	0	1	1	1	0	1	0	1	0	0	1	0	0	0	0	1	1	8
A17	0	0	0	1	1	0	1	0	1	0	0	0	0	0	0	0	0	1	5
A18	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	0	0	1
Sj	1	0	8	15	17	8	13	4	13	3	5	8	7	1	6	7	10	16

, and Sj is the votes the schedules get. As shown in

Table 10. Results of Borda ranking method.

Remediation Technology	Votes	Borda Rankings
Passive Collection Method (A1)	1	16
Shielding Method (A2)	0	18
Hydrodynamic and Control (A3)	8	7
Pump and Treat (A4)	15	3
Light Non-Aqueous Phase Liquid Recovery (A5)	17	1
In Situ Air Sparging (A6)	8	7
Enhanced Bioremediation (A7)	13	4
Permeable Reactive Barrier (A8)	4	14
In Situ Chemical Oxidation (A9)	13	5
Organic Clay (A10)	3	15
Electrochemical Dynamics (A11)	5	13
Groundwater Circulation Well (A12)	8	7
Monitoring Natural Attenuation (A13)	7	10
Soil Vapor Extraction and In Situ Aeration (A14)	1	16
Biological Aeration In Situ Aeration (A15)	6	12
Dual Phase Extraction Single Pump System (A16)	7	10
Dual Phase Extraction Double Pump System (A17)	10	6
Surfactant Enhanced Remediation (A18)	16	2

, the results are a little different from mean ranking: A5 > A18 > A4 > A7 > A9 > A17 > (A3, A6, A12) > (A13, A16) > A15 > A11 > A8 > A10 > (A1, A14) > A2. The results of the mean ranking and Borda ranking methods are conflated as following: A5 > A18 > A4 > (A7, A9) > A17 > (A3, A6, A12) > (A13, A16) > A15 > A11 > A8 > A10 > (A1, A14) > A2. The two in brackets have the same sorting value.

As shown in Figure 3, every method gives a priority order for each technology. When put into a quadrangle graph, the more every quadrangle looks like a regular quadrangle, the more stable the four methods are. The technologies with the highest and lowest ranking are more stable and have better consistency among WP, SWA and TOPSIS. When it comes to CGT methods, there is a sharp change. This is due to the fact that the application of CGT automatically removes all of the schemes with minimum indicator values. Even if the other indicators are large (better), they will not be considered.

A simple linear weighting method cannot avoid the impact of the results of the correlation between the indicators; a weighted product method will enlarge the characteristics of indicators, and may lead to results being affected by individual indicators. TOPSIS will miss schemes containing very poor indicators. The integration method avoids the shortcomings of the four programs to a certain extent. The ranking of options based on a simple weighted addition method is Light Non-Aqueous Phase Liquid Recovery, Surfactant Enhanced Remediation, Pump and Treat; the ranking of options based on a weighted product method is Light Non-Aqueous Phase Liquid Recovery, Surfactant Enhanced Remediation, Enhanced Bioremediation; the ranking of options based on cooperative game theory is Pump and Treat, Dual Phase Extraction Double Pump System, and Dual Phase Extraction Single Pump System; and the ranking of options based on TOPSIS is Surfactant Enhanced Remediation, Light Non-Aqueous Phase Liquid Recovery, and Pump and Treat. Based on the four MCDA methods, the 18 kinds of repair technology in the order of priority are as follows: Light Non-Aqueous Phase Liquid Recovery (A5) > Surfactant Enhanced Remediation (A18) > Pump and Treat (A4) > [Enhanced Bioremediation (A7), In Situ Chemical Oxidation (A9)] > Dual Phase Extraction Double Pump System (A17) > [Hydrodynamic and Control (A3), In Situ Air Sparging (A6), Groundwater Circulation Well (A12)] > [Monitoring Natural Attenuation (A13), Dual Phase Extraction Single Pump System (A16)]> Biological Aeration In Situ Aeration (A15) > Electrochemical Dynamics (A11) > Permeable Reactive Barrier (A8) > Organic Clay (A10) > [Passive Collection Method (A1), Soil Vapor Extraction and In Situ Aeration (A14)] > Shielding Method (A2). Technologies in square brackets have the same priority.

4. Conclusions

In this paper, a fuzzy multi-criteria decision analysis (FMCDA) system was established based on the integration of a set of indicators, fuzzy sets theory, multi-criteria decision analysis (MCDA), and fuzzy analytical hierarchy process (FAHP). The innovation of this research mainly comprised: (a) ranking results were obtained according to various indicators of 18 technologies, reflecting compromising and conflicting features among the technologies in terms of the proposed seven dimensions of evaluation indicators, and (b) uncertainties not only associated with weights for evaluation indicators, but also for the evaluation process of MCDA methods were introduced, improving the robustness of the evaluation procedure and the results obtained. The proposed FMCDA includes three stages based on the evaluation scheme. The first stage is the fuzzy impact transformation, which includes two steps: (a) the change of the descriptive language variables into fuzzy sets, and (b) the fuzzy sets were transformed into a single value. The results of this stage were to generate a new index matrix that contains only digital data. In the second stage, classical MCDA methods were used to sort all kinds of decision alternatives. In the third stage, the results of MCDA methods were integrated with different integration methods to get a more accurate result. The evaluation of groundwater remediation technologies based on fuzzy multi-criteria decision analysis approaches indicated that the method used in this research could reduce subjectivity and uncertainty, leading to a more robust and defensible remedy selection, and as many remediation technologies are involved as possible. This method can be applied to other areas for decision makers to select the best scheme among different choices.