Model of Suspended Solids Removal in the Primary Sedimentation Tanks for the Treatment of Urban Wastewater
Abstract
:1. Introduction
2. Materials and Methods
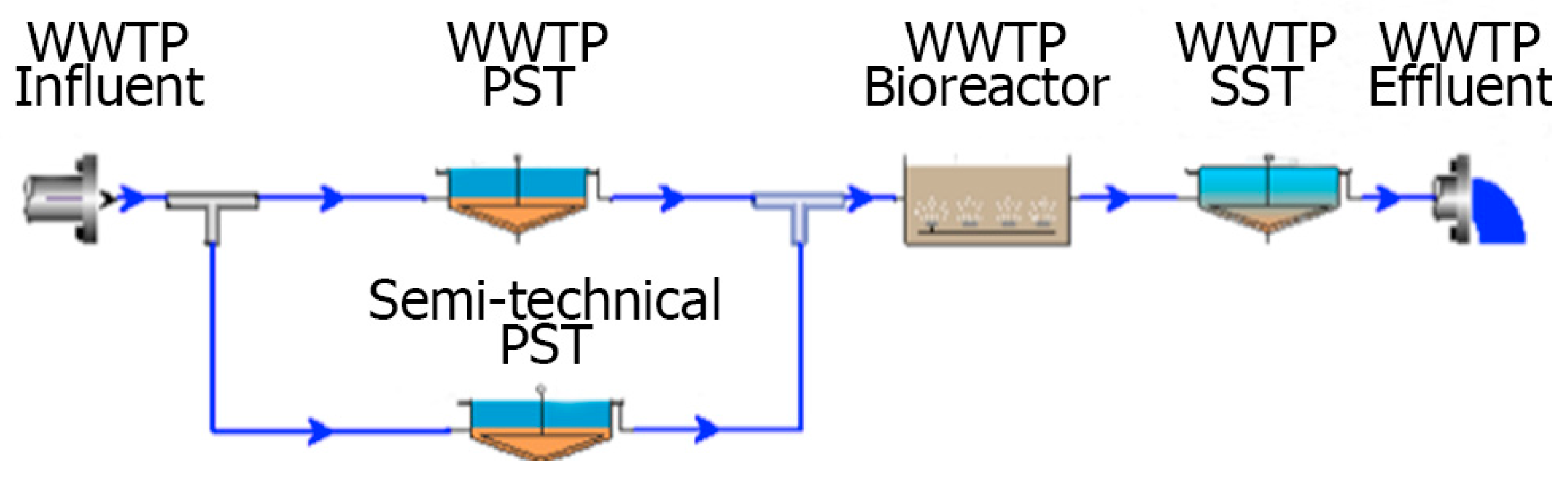
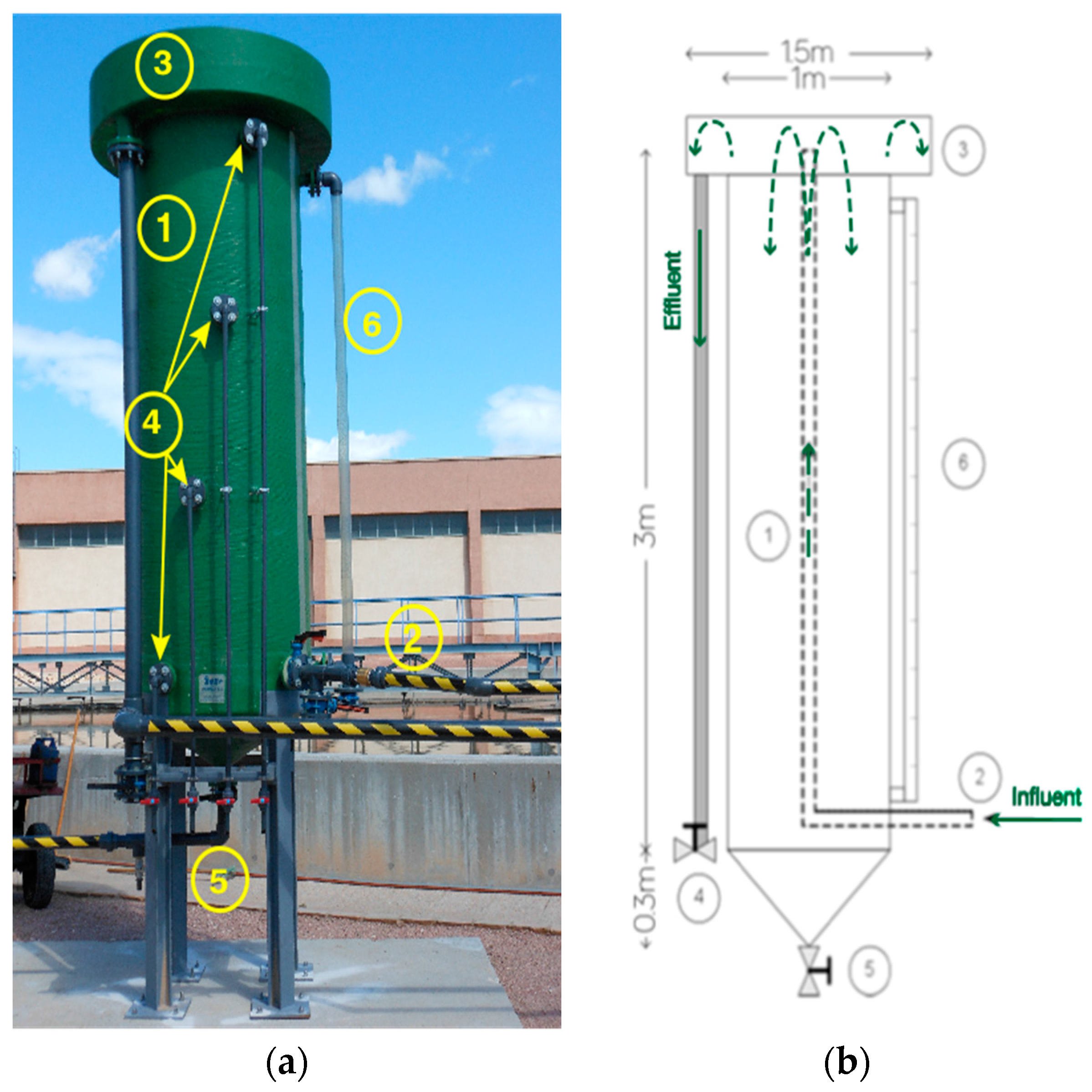
2.1. Semi-Technical PST
2.2. Experimental Procedure
2.3. Analytical Method
2.3.1. Physical and Chemical Determination
2.3.2. Statistical Analysis
2.4. Mathematical Model
3. Results
3.1. Influent Characteristics
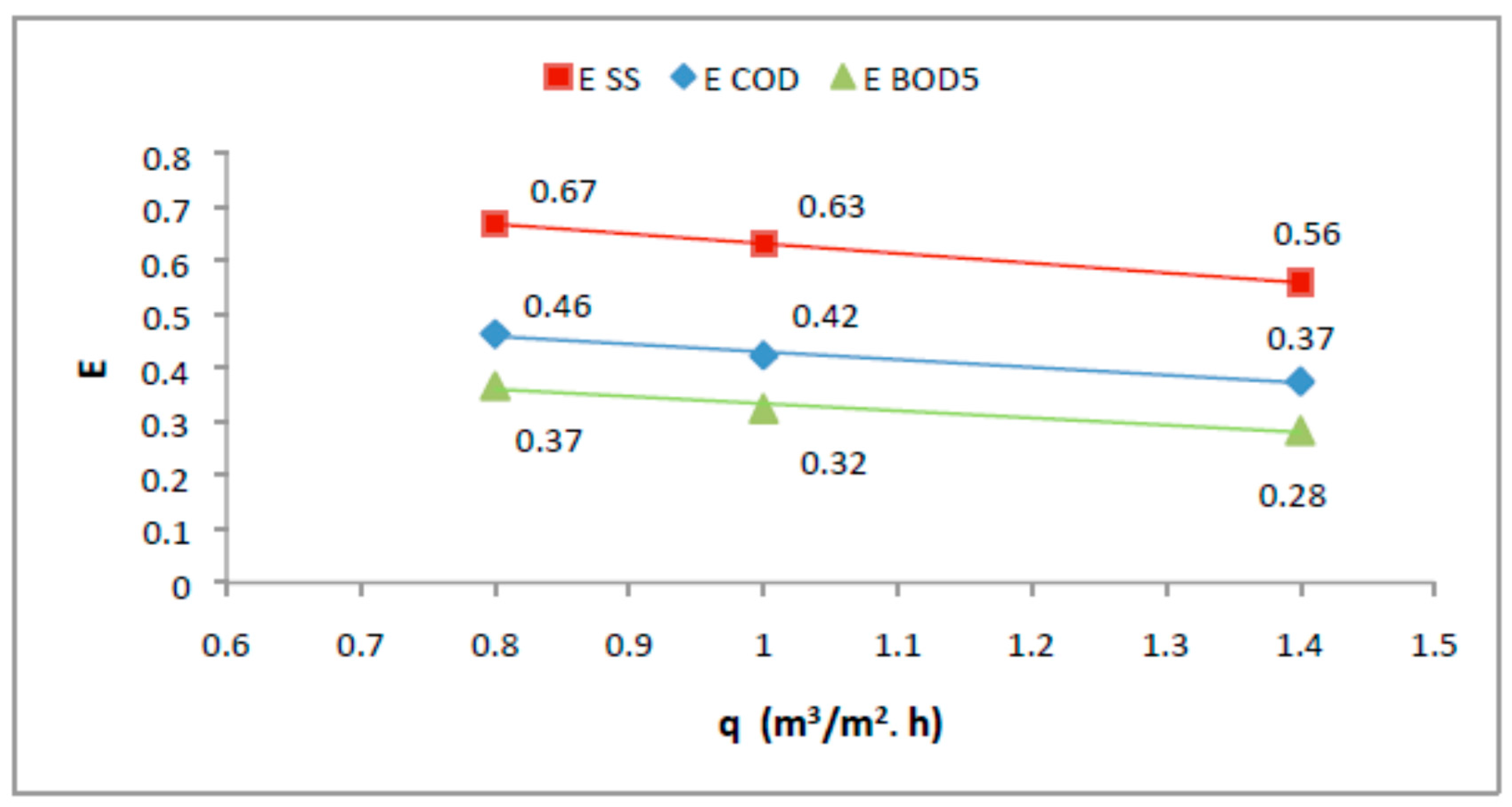
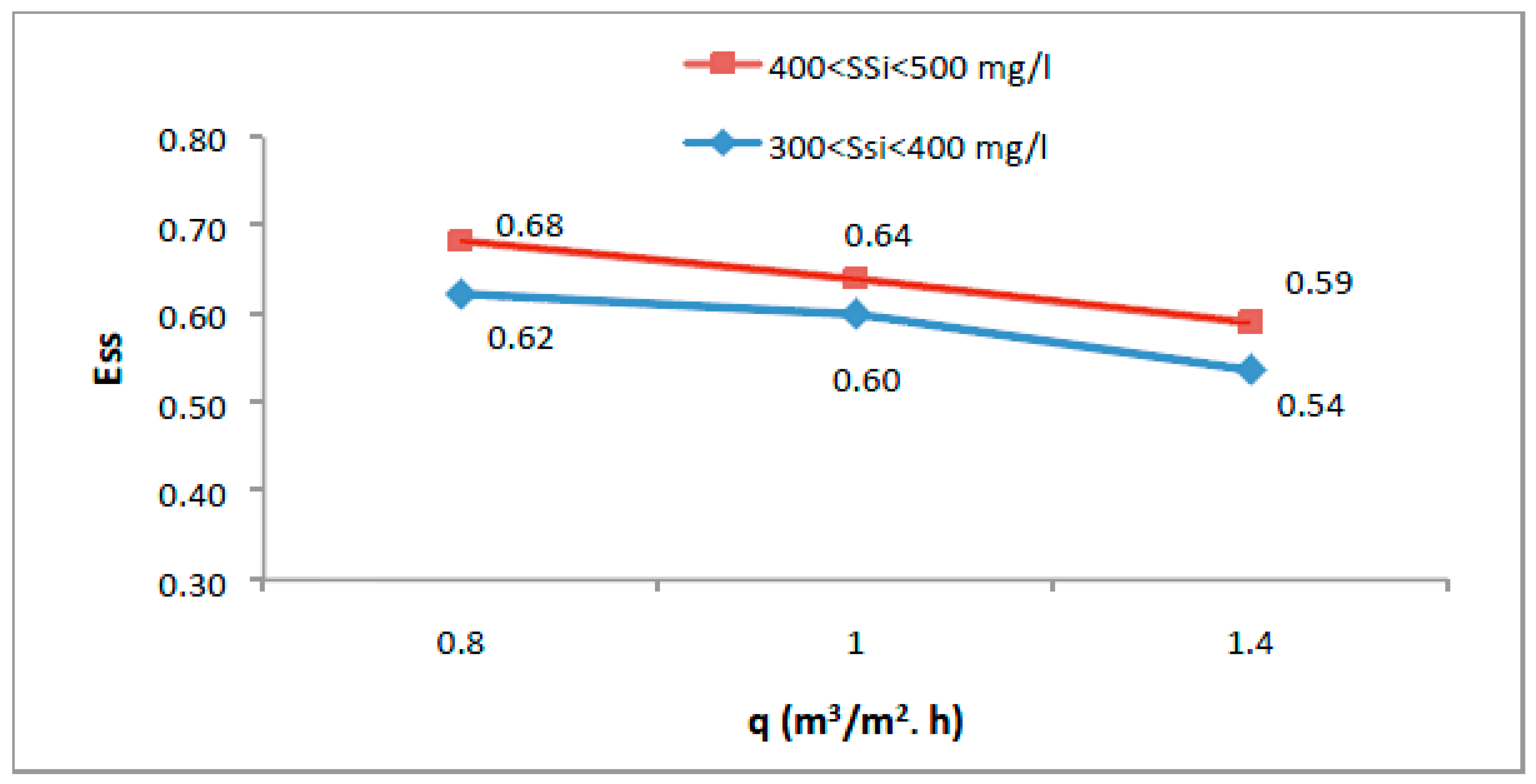
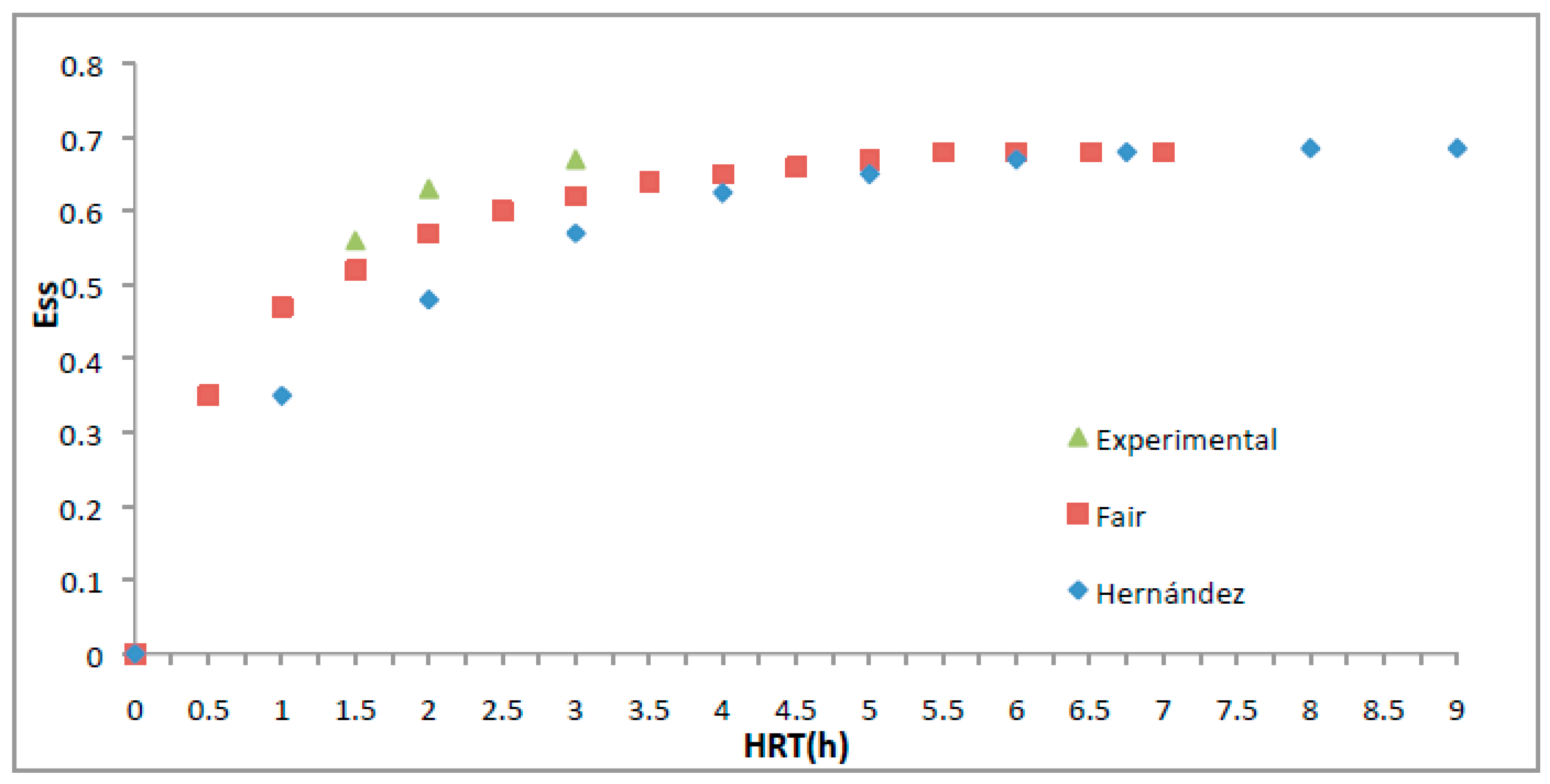
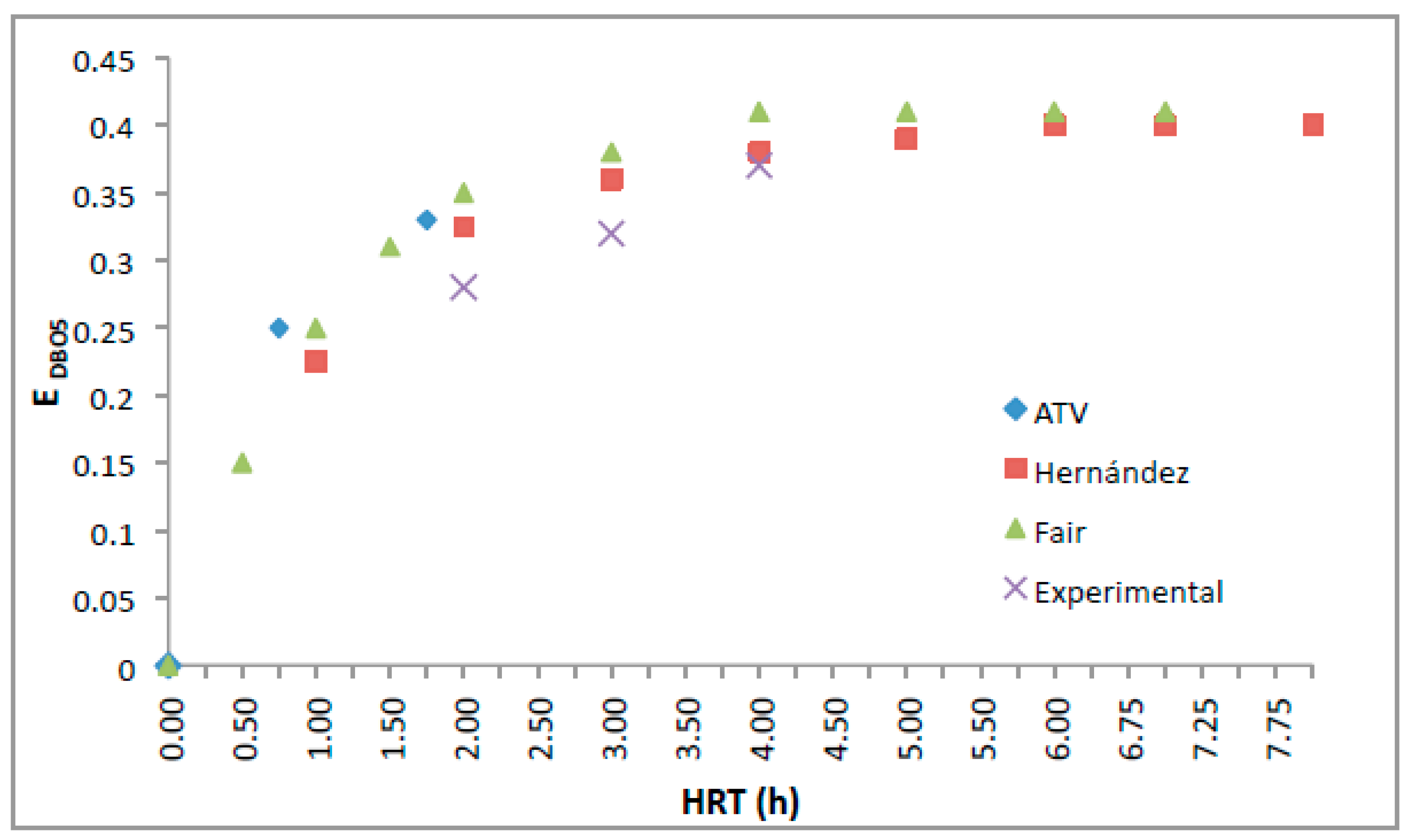
3.2. Removal Efficiency
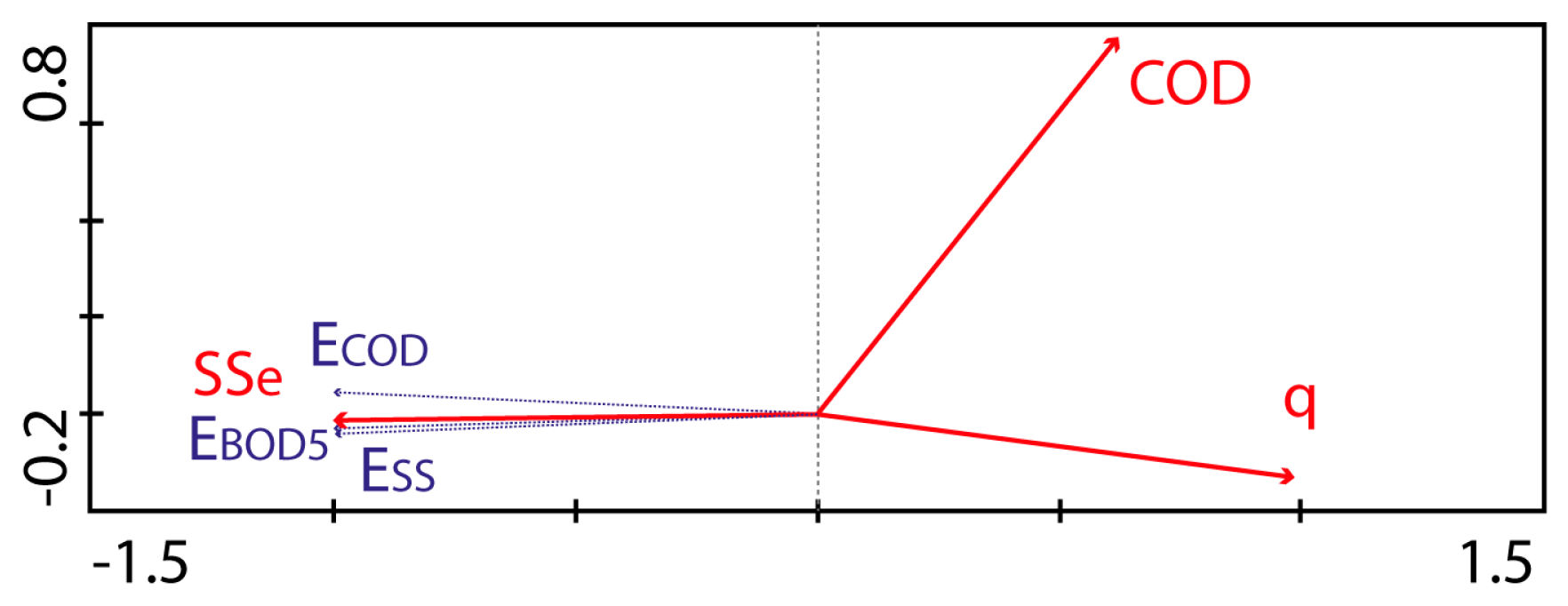
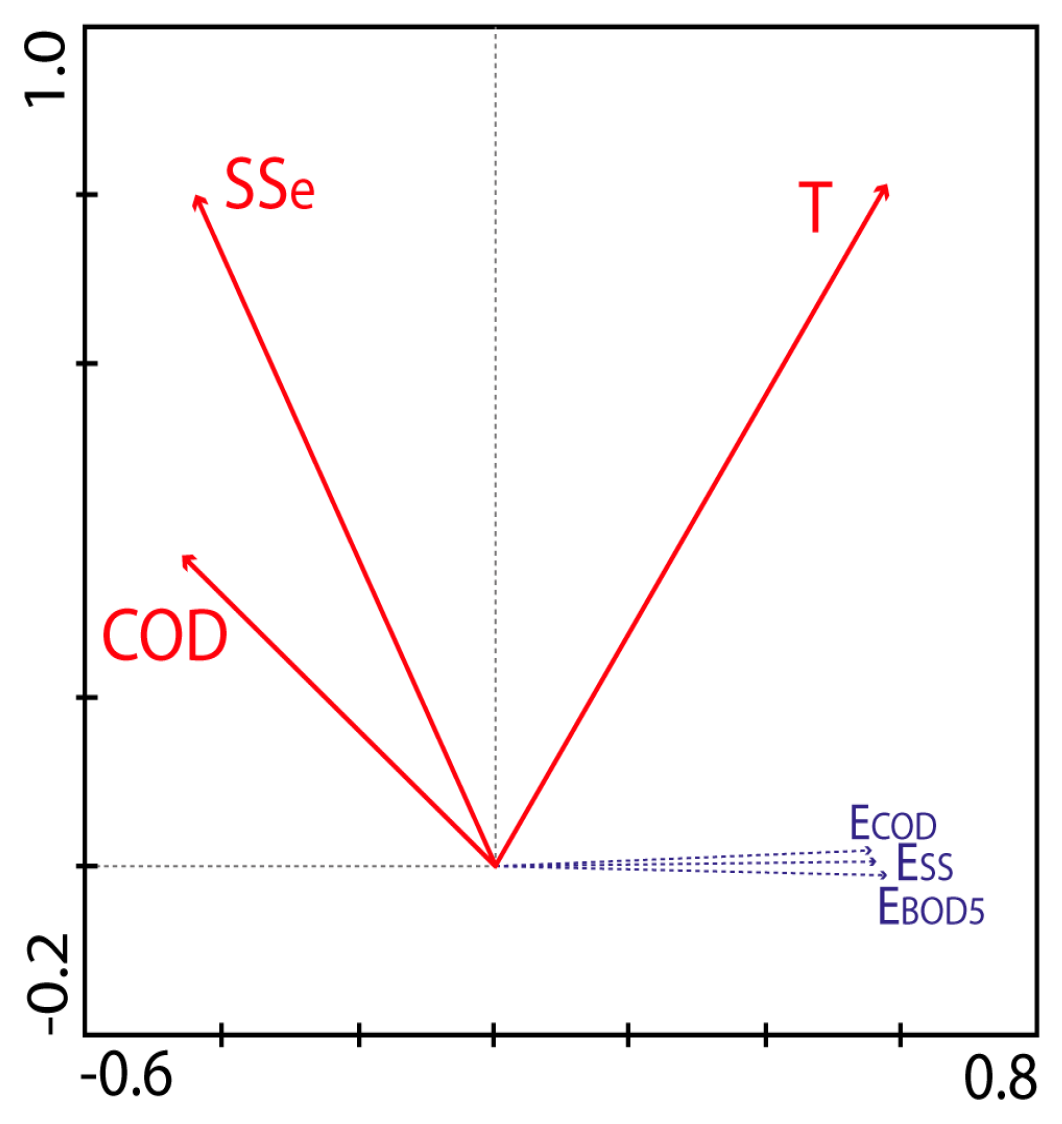
3.3. Combined Multivariate Analysis
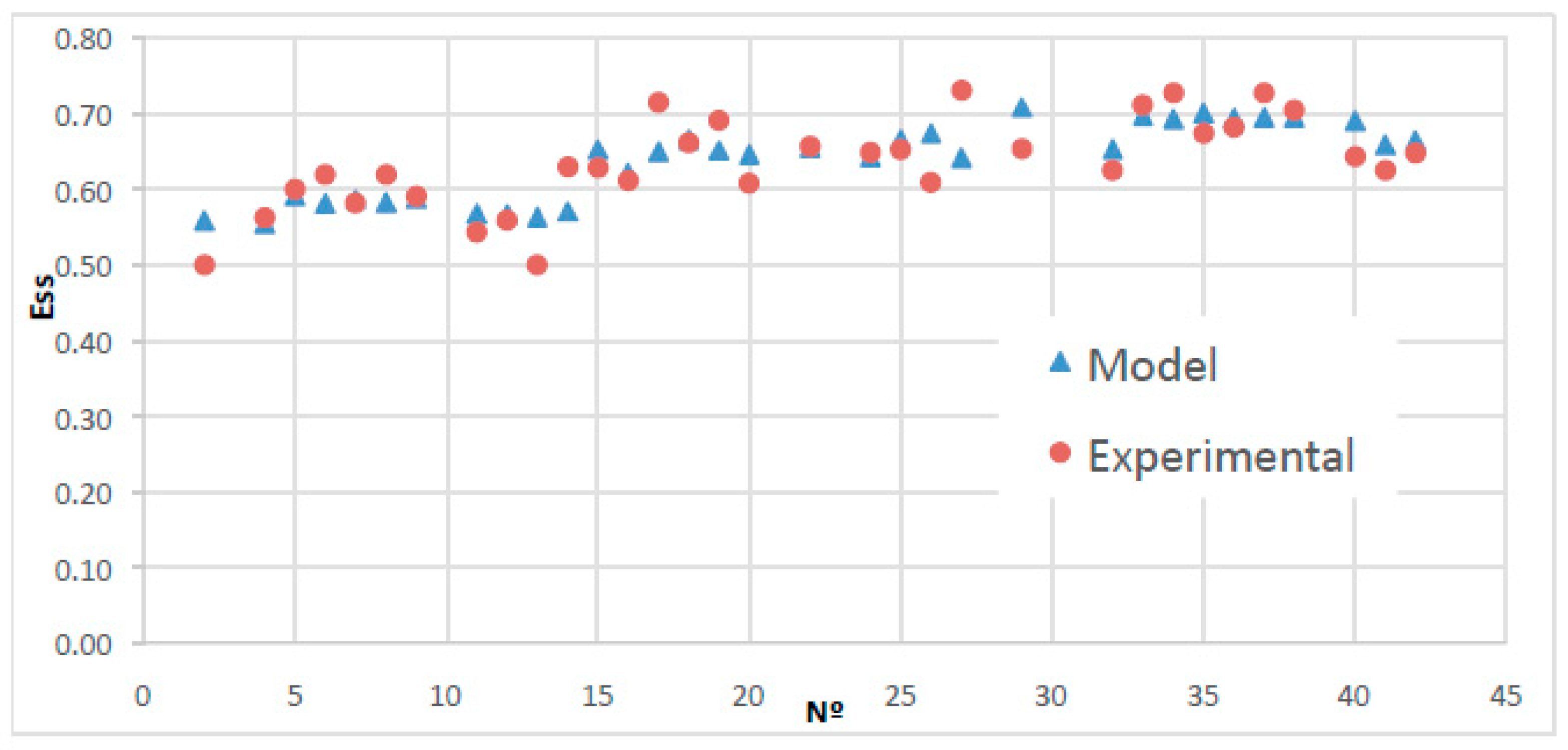
3.4. Empirical Model
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Christoulas, D.G.; Yannakopoulos, P.H.; Andreadakis, A.D. An empirical model for primary sedimentation of sewage. Environ. Int. 1998, 24, 925–934. [Google Scholar] [CrossRef]
- Patziger, M.; Günthert, F.W.; Jardin, N.; Kainz, H.; Londong, J. On the design and operation of primary settling tanks in state of the art wastewater treatment and water resources recovery. Water Sci. Technol. 2016. [Google Scholar] [CrossRef] [PubMed]
- Patziger, M.; Kiss, K. Towards a hydrodynamically enhanced design and operation of primary settling tanks—Results of a long term in situ measurement investigation program. Water Environ. J. 2015, 29, 338–345. [Google Scholar] [CrossRef]
- Bustos, M.C.; Concha, F.; Bürger, R.; Tory, E.M. Sedimentation and thickening. In Phenomenological Foundation and Mathematical Theory; Kluwer Academic: Dordrecht, The Netherlands, 1990; pp. 150–210. [Google Scholar]
- Concha, F.; Bürger, R. A century of research in sedimentation and thickening. KONA Powder Part. J. 2002, 20, 38–70. [Google Scholar] [CrossRef]
- Martínez-González, G.; Loría-Molina, H.; Taboada-López, D.; Ramírez-Rodríguez, F.; Navarrete-Bolaños, J.L.; Jiménez-Islas, H. Approximate method for designing a primary settling tank for wastewater treatment. Ind. Eng. Chem. Res. 2009, 48, 7842–7846. [Google Scholar] [CrossRef]
- Diehl, S. Operating charts for continous sedimentation I: Control of steady states. J. Eng. Math. 2001, 41, 117–144. [Google Scholar] [CrossRef]
- Je, C.H.; Chang, S. Simple approach to estimate flocculent settling velocity in a dilute suspension. Environ. Geol. 2004, 45, 1002–1009. [Google Scholar] [CrossRef]
- Mazzolani, C.; Pirozzi, F.; D’Antonoi, G. A generalized settling approach in the numerical modeling of sedimentation tanks. Water Sci. Technol. 1998, 38, 95–102. [Google Scholar] [CrossRef]
- Lindeborg, C.; Wiberg, N.; Seyf, A. Studies of the dynamic behaviour of a primary sedimentation tank. Water Sci. Technol. 1996, 34, 213–222. [Google Scholar] [CrossRef]
- Razmi, A.; Firoozabadi, B.; Ahmadi, G. Experimental and numerical approach to enlargement of performance of primary settling tanks. J. Appl. Fluid Mech. 2009, 2, 1–12. [Google Scholar]
- Camnasio, E.; Erpicum, S.; Orsi, E.; Pirotton, M.; Schleiss, A.J.; Dewals, B. Coupling between flow and sediment deposition in rectangular shallow reservoirs. J. Hydraul. Res. 2013, 51, 535–547. [Google Scholar] [CrossRef]
- Dufresne, M.; Dewals, B.; Erpicum, S.; Archambeau, P.; Pirotton, M. Flow patterns and sediment deposition in rectangular shallow reservoirs. Water Environ. J. 2012, 26, 504–510. [Google Scholar] [CrossRef]
- Dufresne, M.; Dewals, B.J.; Erpicum, S.; Archambeau, P.; Pirotton, M. Numerical investigation of flow patterns in rectangular shallow reservoirs. Eng. Appl. Comput. Fluid Mech. 2011, 5, 247–258. [Google Scholar] [CrossRef]
- Dufresne, M.; Dewals, B.J.; Erpicum, S.; Archambeau, P.; Pirotton, M. Experimental investigation of flow pattern and sediment deposition in rectangular shallow reservoirs. Int. J. Sediment Res. 2010, 25, 258–270. [Google Scholar] [CrossRef]
- Patziger, M.; Kiss, K. Analysis of suspended solids transport processes in primary settling tanks. Water Sci. Technol. 2015, 72, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Gong, M.; Xanthos, S.; Ramalingam, K.; Fillos, J.; Beckmann, K.; Deur, A.; McCorquodale, J.A. Development of a flocculation sub-model for a 3-D CFD model based on rectangular settling tanks. Water Sci. Technol. 2011, 63, 213–219. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Garcia, M.H. Computational Fluid Dynamics Modeling for the Design of Large Primary Settling Tanks. J. Hydraul. Eng. 2011, 137, 343–355. [Google Scholar] [CrossRef]
- Rostami, F.; Shahrokhi, M.; Said, M.A.M.; Abdullah, R. Numerical modeling on inlet aperture effects on flow pattern in primary settling tanks. Appl. Math. Model. 2011, 35, 3012–3020. [Google Scholar] [CrossRef]
- Shahrokhi, M.; Rostami, F.; Said, M.A.M.; Yazdi, S.R.S.; Syafalni, S. Computational investigations of baffle configuration effects on the performance of primary sedimentation tanks. Water Environ. J. 2013, 27, 484–494. [Google Scholar] [CrossRef]
- Shahrokhi, M.; Rostami, F.; Said, M.A.M.; Yazdi, S.R.S.; Syafalni, S.; Abdullah, R. The effect of baffle angle on primary sedimentation tank efficiency. Can. J. Civ. Eng. 2012, 39, 293–303. [Google Scholar] [CrossRef]
- Shahrokhi, M.; Rostami, F.; Said, M.A.M.; Yazdi, S.R.S. The effect of number of baffles on the improvement efficiency of primary sedimentation tanks. Appl. Math. Model. 2012, 36, 3725–3735. [Google Scholar] [CrossRef]
- Shahrokhi, M.; Rostami, F.; Said, M.A.M.; Yazdi, S.R.S. Numerical modeling of baffle location effects on the flow pattern of primary sedimentation tanks. Appl. Math. Model. 2013, 37, 4486–4496. [Google Scholar] [CrossRef]
- Kiss, K.; Patziger, M. Novel measurements in primary settling tanks of large municipal wastewater treatment plants. YBL J. Built Environ. 2013, 1. [Google Scholar] [CrossRef]
- Fair, G.M.; Geyer, J.C.; Okun, D.A. Elements of Water Supply and Waste Water Disposal; Wiley: Hoboken, NJ, USA, 1971. [Google Scholar]
- DWA (German Association for Water, Wastewater and Waste). ATV-DVWK-A 131: Dimensioning of Single-Stage Activated Sludge Plants; DWA: Hennef, Germany, 2000. [Google Scholar]
- Metcalf & Eddy Inc.; Tchobanoglous, G.; Burton, F.L.; Stensel, H.D. Wastewater Engineering: Treatment and Resource Recovery; McGraw-Hill: London, UK, 2003. [Google Scholar]
- Yoo, C.K.; Villez, K.; Van Hulle, S.W.H.; Vanrolleghem, P.A. Enhanced process monitoring for wastewater treatment systems. Envirometrics 2008, 19, 602–617. [Google Scholar] [CrossRef]
- Puig, S.; Van Loosdrecht, M.C.M.; Flameling, A.G.; Colprim, J.; Meijer, S.C.F. The effect of primary sedimentation on full-scale WWTP nutrient removal performance. Water Res. 2010, 44, 3375–3384. [Google Scholar] [CrossRef] [PubMed]
- Somlyódy, L.; Patziger, M. Urban wastewater development in Central and Eastern Europe. Water Sci. Technol. 2012, 66, 1081–1087. [Google Scholar] [CrossRef] [PubMed]
- Chiang, C.F.; Tsai, C.T.; Lo, H.M.; Chao, K.P.; Pai, T.Y. Analyzing the design criteria of primary settlers of small sewage treatment systems: A national survey in Taiwan. J. Hazard. Mater. 2010, 175, 915–919. [Google Scholar] [CrossRef] [PubMed]
- Tebbutt, T.H.Y.; Christoulas, D.G. Performance relationships for primary sedimentation. Water Res. 1975, 9, 347–356. [Google Scholar] [CrossRef]
- Tebbutt, T.H.Y. Primary Sedimentation of wastewater. Water Pollut. Control Fed. 1979, 51, 2858–2867. [Google Scholar]
- Annesini, M.C.; Beccari, M.; Mininni, G. Solids removal efficiency of primary settling tanks in municipal wastewater treatment plants. Water Air Soil Pollut. 1979, 12, 441–447. [Google Scholar] [CrossRef]
- Huang, J.; Jin, Y.C. Numerical modeling of Type I circular sedimentation tank. J. Environ. Eng. 2011, 137, 196–204. [Google Scholar] [CrossRef]
- Bridgewater, L.; American Public Health Association; American Water Works Association; Water Environment Federation. Standard Methods for the Examination of Water and Wastewater; American Public Health Association: Washington, DC, USA, 2012. [Google Scholar]
- Lepš, J.; Šmilauer, P. Multivariate Analysis of Ecological Data; Faculty of Biological Sciences, University of South Bohemia: České Budějovice, Czech Republic, 1999. [Google Scholar]
- Yetis, Ü.; Tarlan, E. improvement for primary settling performance with activated sludge. Environ. Technol. 2002, 23, 363–372. [Google Scholar] [CrossRef] [PubMed]
- Hernández, A. Depuración y Desinfección de Aguas Residuales; Colegio de Ingenieros de Caminos, Canales y Puertos: Madrid, Spain, 2001. [Google Scholar]


| Influent Characteristics | Stage 1 | Stage 2 | Stage 3 |
|---|---|---|---|
| q (m3/m2·h) | 1.4 | 1.0 | 0.8 |
| HRT (h) | 2 | 3 | 4 |
| tª (°C) | 23.64 ±2.00 | 23.10 ± 2.22 | 21.70 ± 2.00 |
| SSi (mg/L) | 382.14 ± 54.66 | 415.43 ± 40.99 | 418.57 ± 67.01 |
| CODi (mg/L) | 835.07 ± 102.91 | 862.29 ± 84.67 | 836.86 ± 91.01 |
| BOD5i (mg/L) | 396.64 ± 42.46 | 428.16 ± 42.12 | 405.23 ± 40.11 |
| pH | 8.30 ± 0.24 | 8.13 ± 0.21 | 8.20 ± 0.17 |
| Conductiv. (μS/cm) | 2517.14 ± 465.48 | 2530.71 ± 260.87 | 2771.07 ± 246.69 |
| Effluent Characteristics | Stage 1 | Stage 2 | Stage 3 |
|---|---|---|---|
| q (m3/m2·h) | 1.4 | 1.0 | 0.8 |
| HRT (h) | 2 | 3 | 4 |
| tª (°C) | 25.00 ± 3.50 | 23.00 ± 3.60 | 20.60 ± 3.30 |
| SSe (mg/L) | 165.00 ± 26.53 a | 155.00 ± 28.76 a,b | 138.57 ± 20.33 b |
| CODe (mg/L) | 521.57 ± 75.32 a | 493.93 ± 45.19 a,b | 449.07 ± 62.57 b |
| BOD5e (mg/L) | 283.92 ± 31.19 a,b | 288.08 ± 24.51 a | 256.80 ± 34.22 b |
| pH | 7.93 ± 0.24 | 7.83 ± 0.32 | 7.83 ± 0.14 |
| Conductiv. (μS/cm) | 2424.21 ± 274.7 | 2747.14 ± 235.84 | 2650.79 ± 330.9 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jover-Smet, M.; Martín-Pascual, J.; Trapote, A. Model of Suspended Solids Removal in the Primary Sedimentation Tanks for the Treatment of Urban Wastewater. Water 2017, 9, 448. https://doi.org/10.3390/w9060448
Jover-Smet M, Martín-Pascual J, Trapote A. Model of Suspended Solids Removal in the Primary Sedimentation Tanks for the Treatment of Urban Wastewater. Water. 2017; 9(6):448. https://doi.org/10.3390/w9060448
Chicago/Turabian StyleJover-Smet, Margarita, Jaime Martín-Pascual, and Arturo Trapote. 2017. "Model of Suspended Solids Removal in the Primary Sedimentation Tanks for the Treatment of Urban Wastewater" Water 9, no. 6: 448. https://doi.org/10.3390/w9060448
APA StyleJover-Smet, M., Martín-Pascual, J., & Trapote, A. (2017). Model of Suspended Solids Removal in the Primary Sedimentation Tanks for the Treatment of Urban Wastewater. Water, 9(6), 448. https://doi.org/10.3390/w9060448





