Dual-Control of Autothermal Thermophilic Aerobic Digestion Using Aeration and Solid Retention Time
Abstract
:1. Introduction
2. Materials and Methods
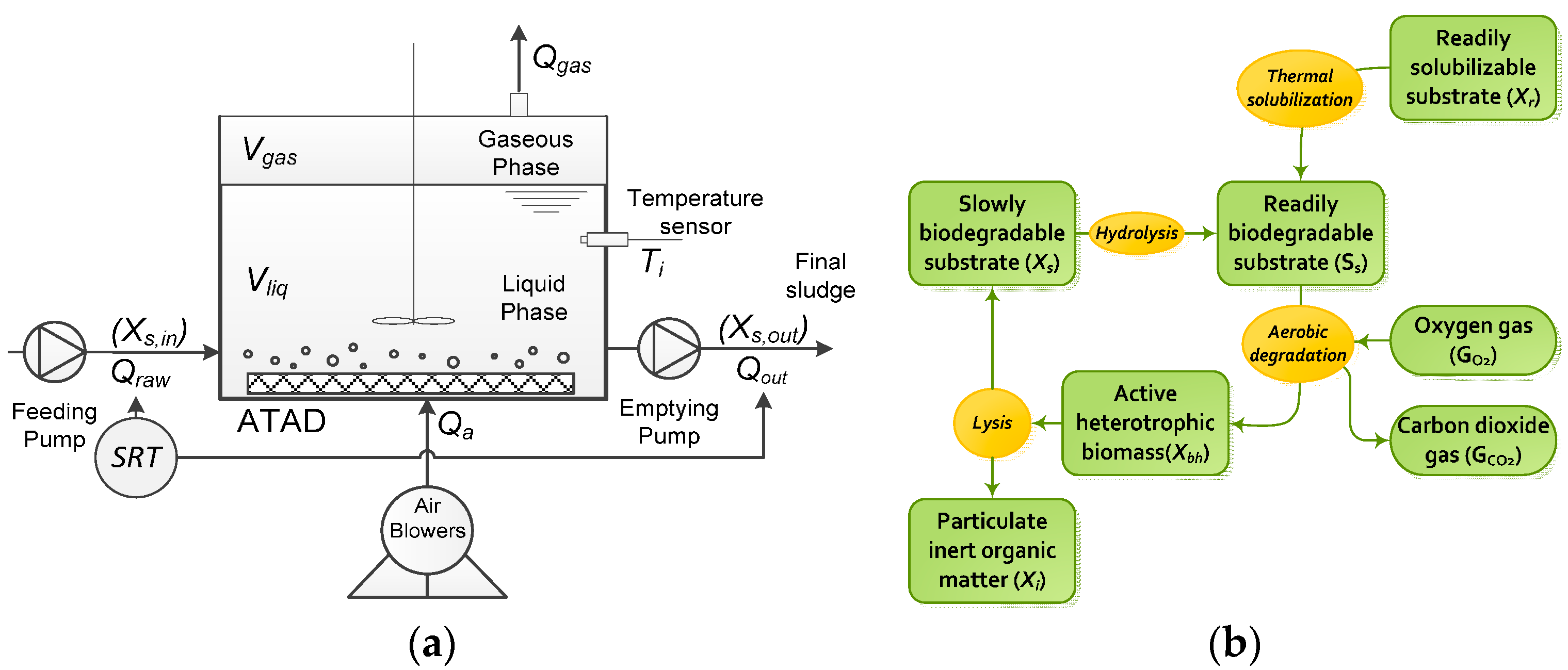
2.1. Steady-State Analysis of the ATAD
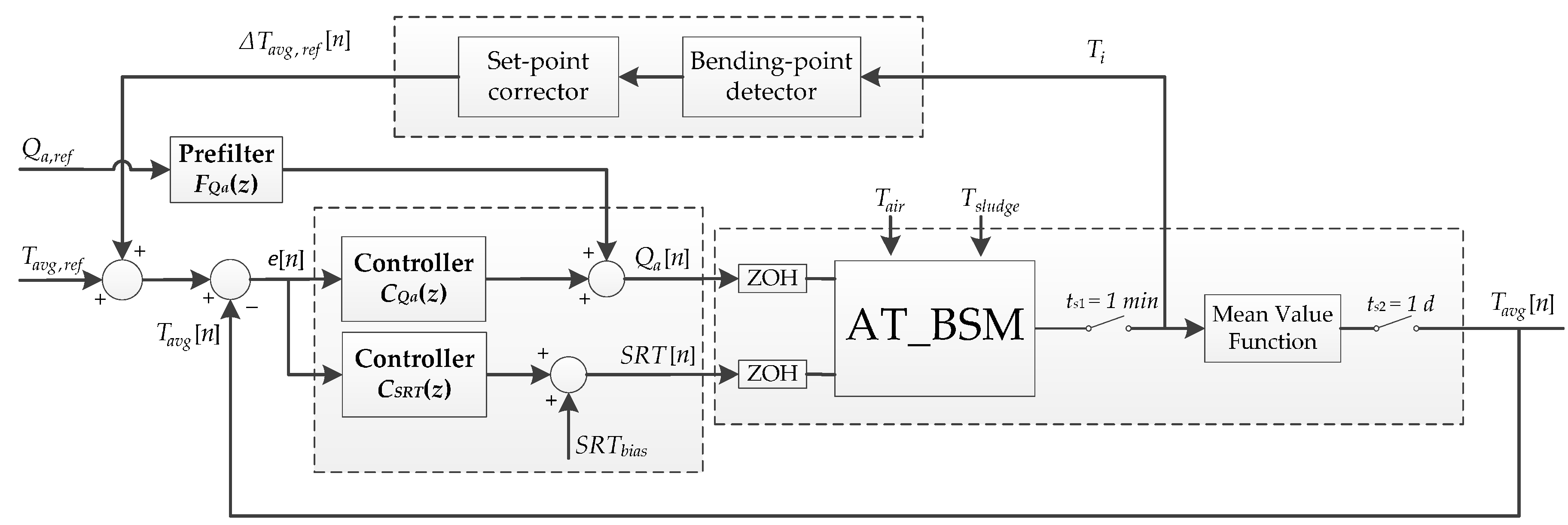
2.2. Dual-Control System of the ATAD
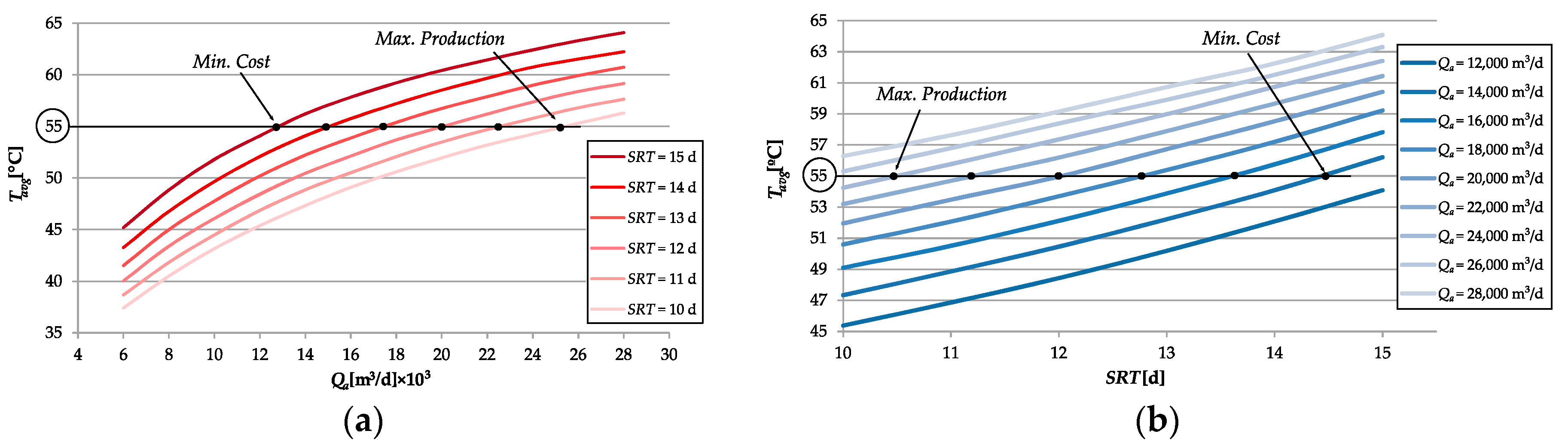
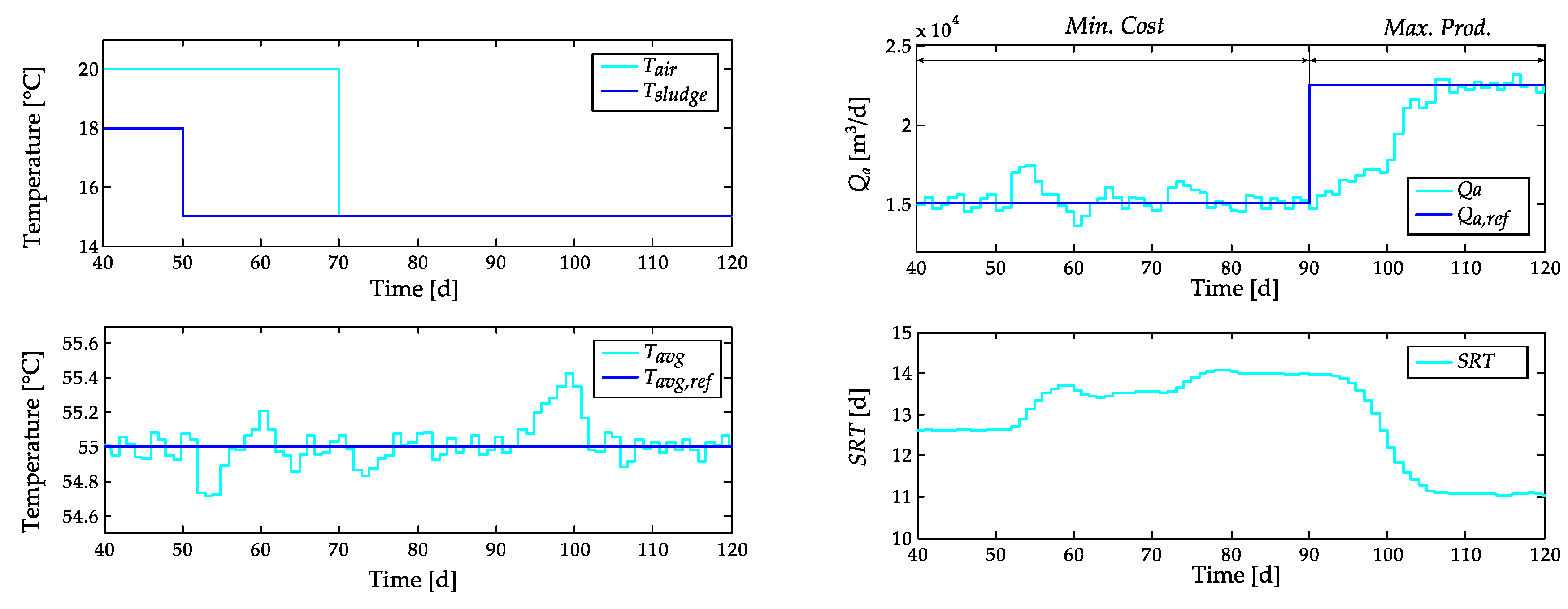
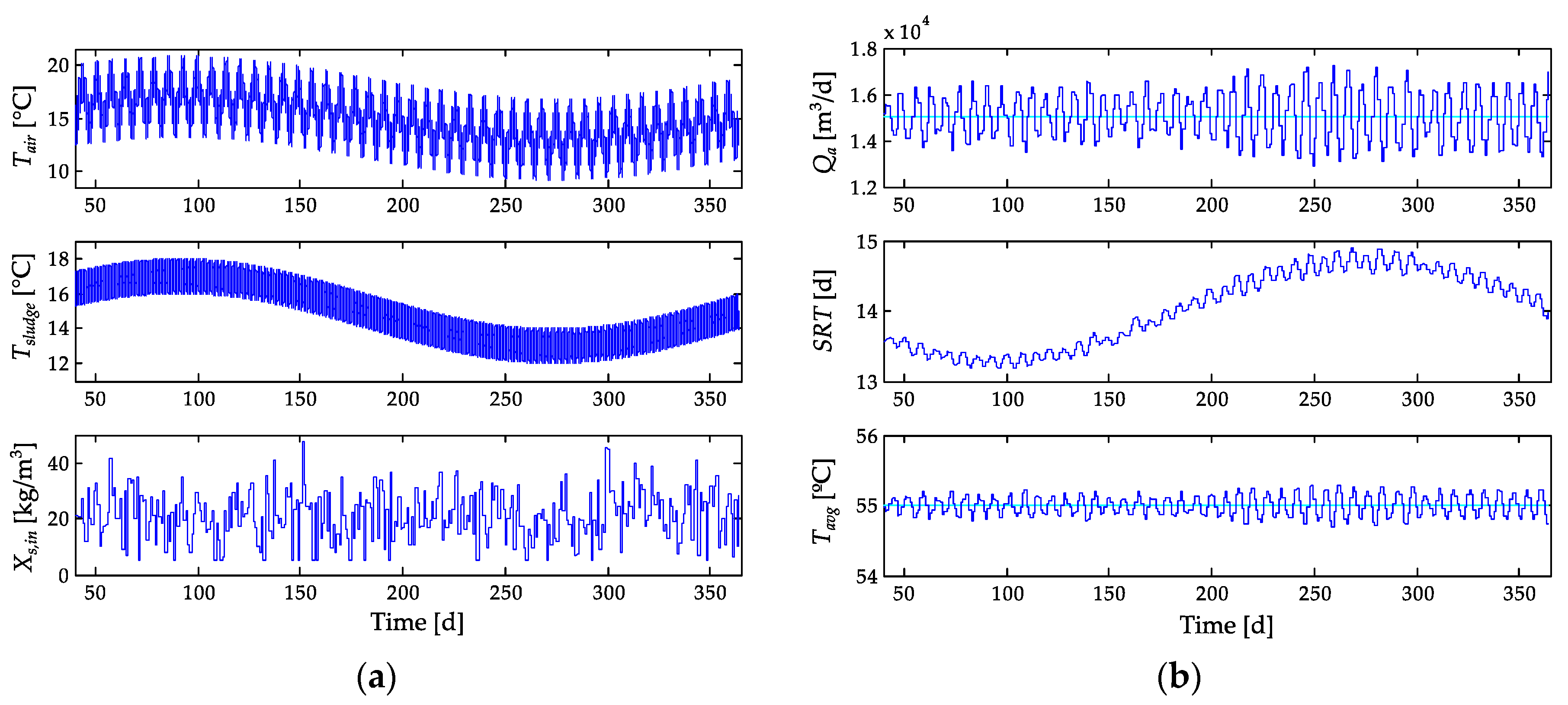
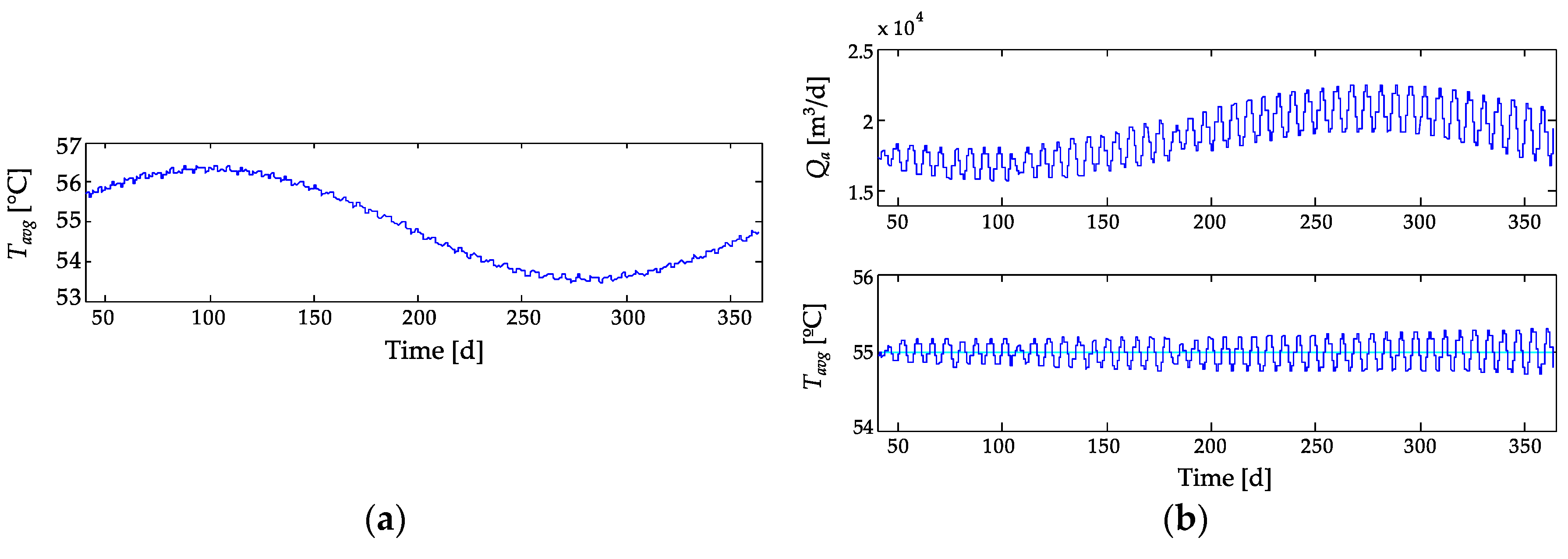
3. Results and Discussion
- (i)
- Pasteurization USEPA Index—IQPUSEPA (%) quantifies the quality of pasteurization as per USEPA guidelines [4,8]:where ts1 = 6.94 × 10−4 d is the sampling time of intra-batch Ti–temperature records, Ni = 1440 is the number of Ti–samples in a batch, and D(i) (Equation (2)) is the minimum time required at Ti–temperature. An IQPUSEPA index value equal to 100% meant strict agreement with the regulation. IQPUSEPA greater than 100% was safer, but revealed worthless expenses.
- (ii)
- Pasteurization EU Index—IQPEU (%) computed the percentage of treated-sludge that met the EU recommendation (55 °C for at least 20 h) [9]:where PTime(j) (h) represents the total time in which the sludge has been at a temperature greater than 55 °C during the aerated reaction phase of the j-th batch. One hundred percent corresponds to the maximum IQPEU value that was attainable. IQPEU values smaller than 100% indicated that some batch violated the EU regulation.
- (iii)
- Cost Index—IC (%) considers the aeration and pumping energies employed per unit of treated sludge volume. The index is normalized as a percentage of an average energy requirement (Eref = 12 kWh/m3 sludge) extracted from USEPA [8]:where EQa is the aeration energy; Epump is the pumping energy; and tbatch is the batch-time (1 day).
- (iv)
- Production Index − IP (%) is expressed as a ratio between the treated sludge flow and the maximum flow that could be treated:
4. Conclusions
Acknowledgments
Author Contributions
Conflict of Interest
Appendix A. Design of MISO Robust Control for ATAD
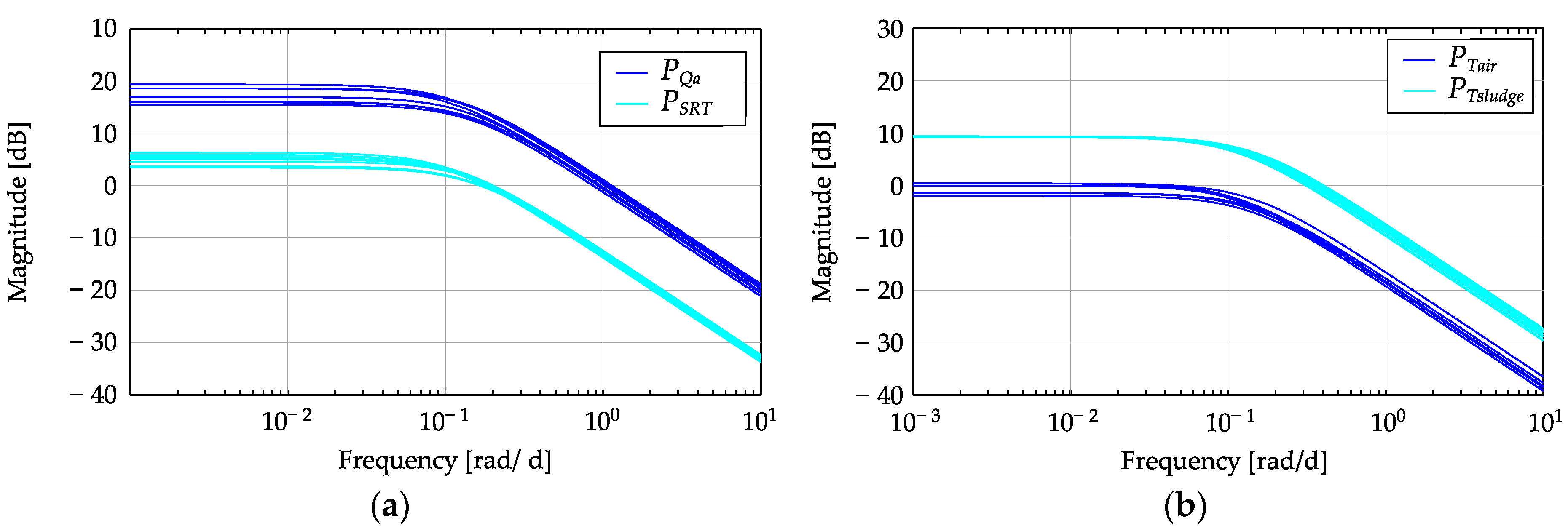
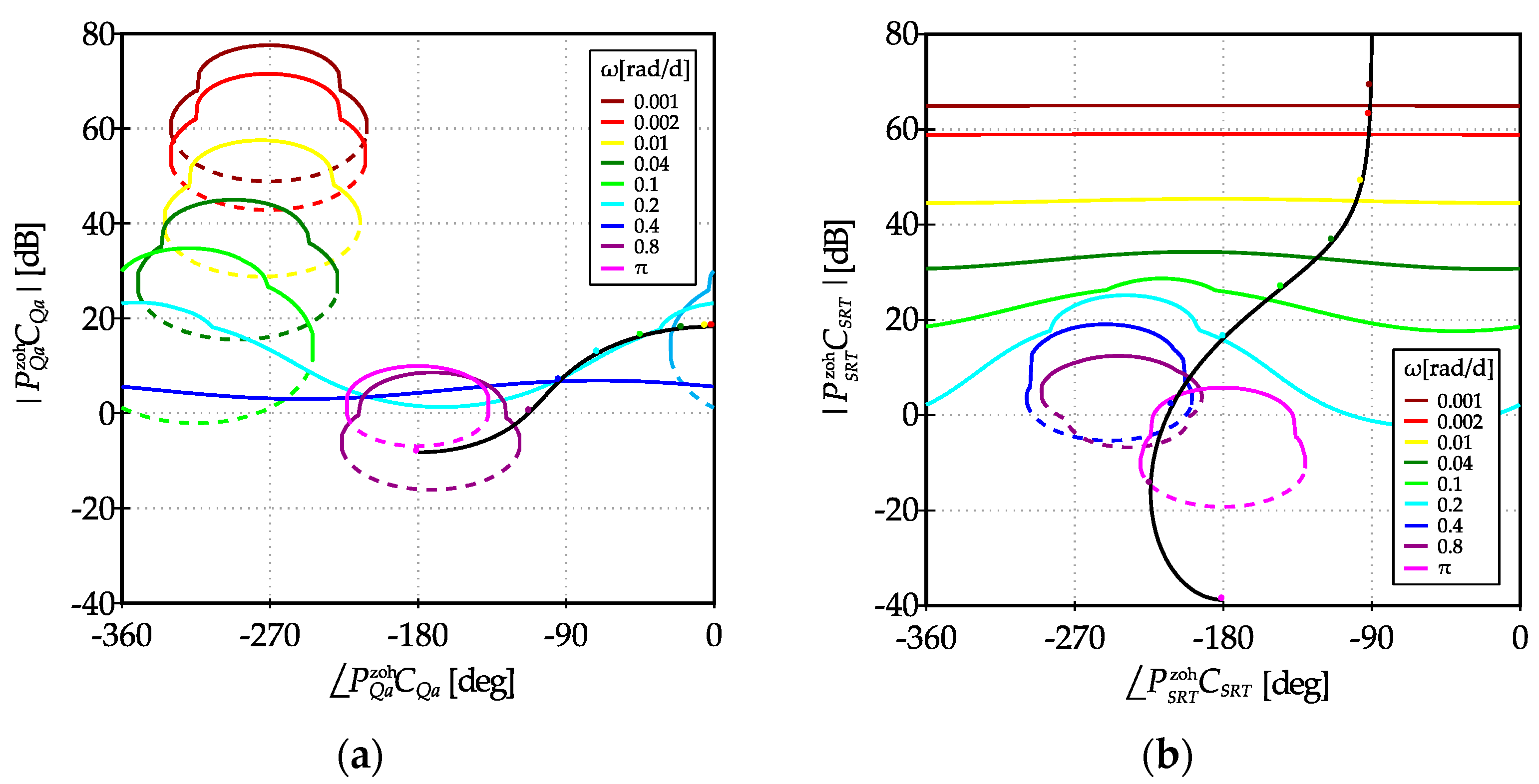
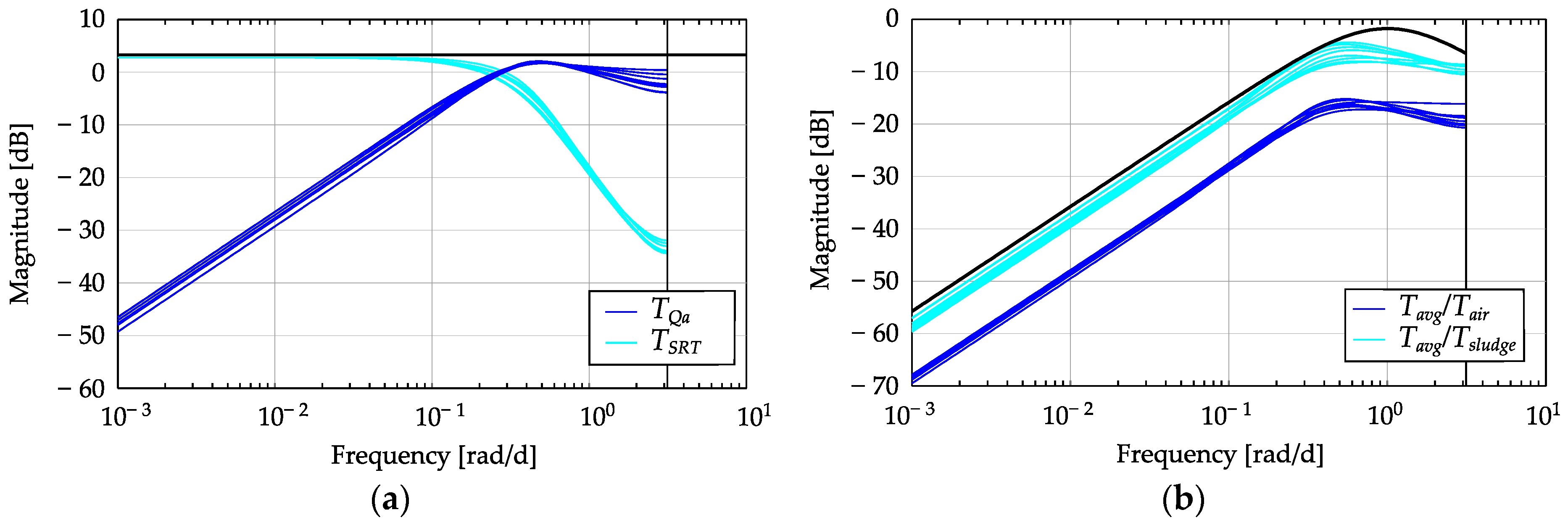
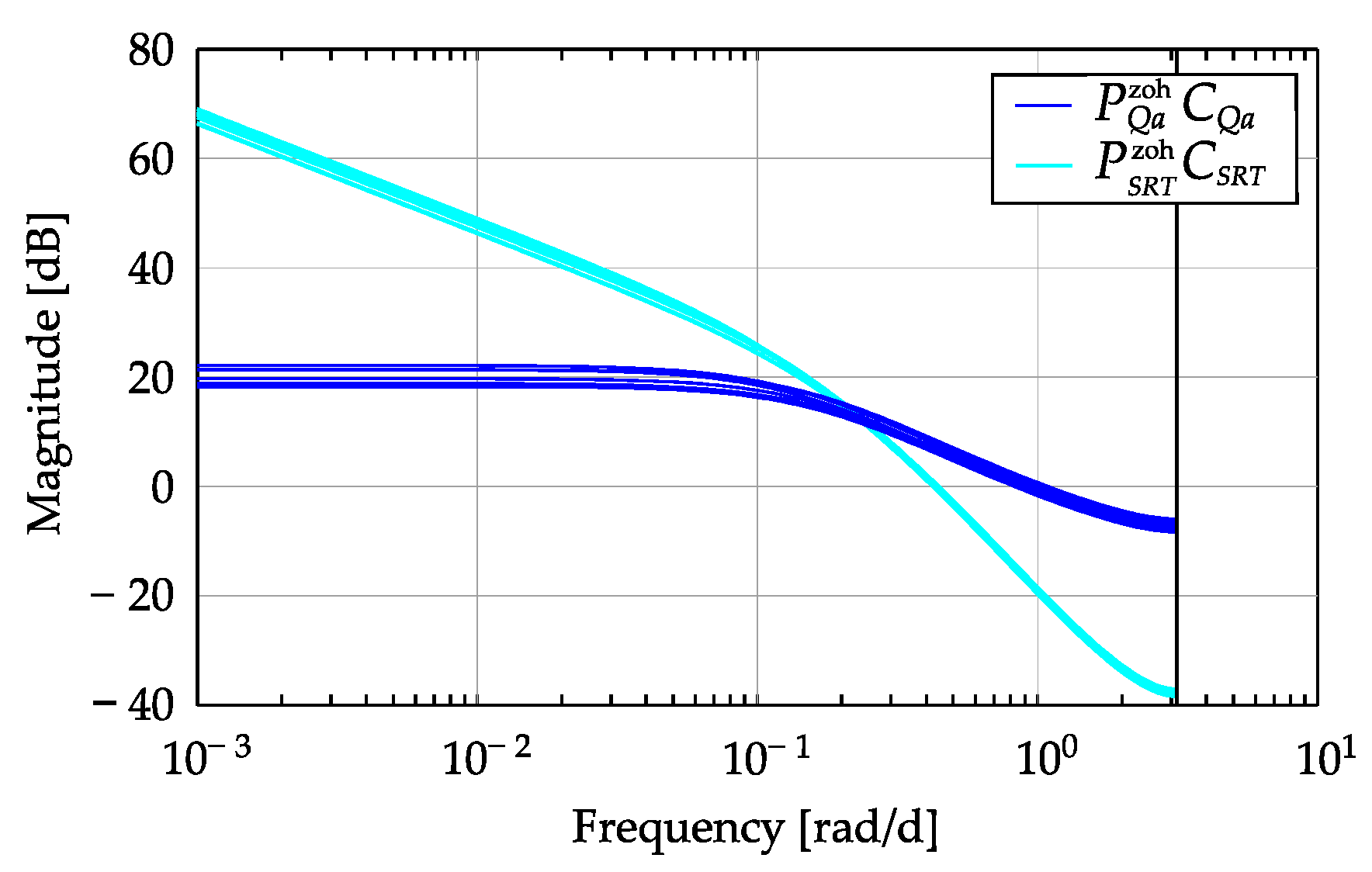
References
- Giffin, T. ATAD Process for the Treatment of Biosolids for Beneficial Re-Use. In Proceedings of the 72nd Annual Water Industry Engineers and Operators Conference, Bendigo Exhibition Centre, Bendigo, Australia, 1–3 September 2009. [Google Scholar]
- Lapara, T.M.; Alleman, J.E. Thermophilic aerobic biological wastewater treatment. Water Res. 1999, 33, 895–908. [Google Scholar] [CrossRef]
- Staton, K.L.; Alleman, J.E.; Pressley, R.L.; Eloff, J. 2nd Generation Autothermal Thermophilic Aerobic Digestion: Conceptual Issues and Process Advancements. In Proceedings of the WEF/AWWA/CWEA Joint Residuals and Biosolids Management Conference, San Diego, CA, USA, 21–24 February 2001. [Google Scholar]
- U.S. Environmental Protection Agency (USEPA). Environmental Regulations and Technology: Control of Pathogens and Vector Attraction in Sewage Sludge; EPA/625/R-92/013; U.S. Environmental Protection Agency, Office of Research and Development: Washington, DC, USA, 1992.
- Layden, N.M. An evaluation of autothermal thermophilic aerobic digestion (ATAD) of municipal sludge in Ireland. J. Environ. Eng. Sci. 2007, 6, 19–29. [Google Scholar] [CrossRef]
- Trim, B.C. Sludge Stabilization and Disinfection by means of Autothermal Aerobic Digestion using Oxygen. In Proceedings of the IWPC Biennal Conference, Durban, South Africa, 27–30 May 1984. [Google Scholar]
- Piterina, A.V.; Bartlett, J.; Pembroke, T.J. Evaluation of the Removal of Indicator Bacteria from Domestic Sludge Processed by Autothermal Thermophilic Aerobic Digestion (ATAD). Int. J. Environ. Res. Public Health 2010, 7, 3422–3441. [Google Scholar] [CrossRef] [PubMed]
- U.S. Environmental Protection Agency (USEPA). Environmental Regulations and Technology: Autothermal Thermophilic Aerobic Digestion of Municipal Wastewater Sludge; Technical Report; EPA/625/10-90/007; U.S. Environmental Protection Agency, Office of Research and Development: Washington, DC, USA, 1990.
- European Commission. Working Document on Sludge—3rd Draft; ENV.E.3/LM; European Union Commission: Brussels, Belgium, 27 April 2000. [Google Scholar]
- Breider, E.J.; Drnevich, R.F. Control of Sludge Temperature in Autothermal Sludge Digestion. U.S. Patent 4,276,174, 30 June 1981. [Google Scholar]
- Kim, Y.K.; Oh, B.K. Aeration Control of Thermophilic Aerobic Digestion Using Fluorescence Monitoring. J. Microbiol. Biotechnol. 2009, 19, 93–98. [Google Scholar] [PubMed]
- Wareham, D.G.; Mavinic, D.S.; Hall, K.J. Sludge Digestion Using ORP-Regulated Aerobic-Anoxic Cycles. Water Res. 1994, 28, 373–384. [Google Scholar] [CrossRef]
- Zambrano, J.A. Autothermal Thermophilic Aerobic Digestion: Design of Controllers and Benchmarking Validation. Ph.D. Thesis, Universidad de Navarra, San Sebastian, Spain, 2011. [Google Scholar]
- Nájera, S.; Zambrano, J.A.; Gil-Martínez, M. Improvements in ATAD using Quantitative Feedback Control and Nonlinear Generator of Optimal Operating Points. Chem. Eng. Sci. 2013, 102, 613–621. [Google Scholar] [CrossRef]
- García, J.; Gomez, J.; Lasheras, A.; Huete, E.; Echeverría, N.; García-Heras, J.L. Advancing with ATAD. Water Sci. Technol. 2007, 19, 48–55. [Google Scholar]
- Nájera, S.; Gil-Martínez, M.; Zambrano, J. ATAD control goals through the analysis of process variables and evaluation of quality, production and cost. Water Sci. Technol. 2015, 71, 717–724. [Google Scholar] [CrossRef] [PubMed]
- Scisson, J.P. ATAD, the Next Generation: Design, construction, start-up and operation of the first municipal 2nd generation ATAD. In Proceedings of the WEF/AWWA/CWEA Joint Residuals and Biosolids Management Conference and Exhibition, Baltimore, MD, USA, 19–22 February 2003. [Google Scholar]
- Velut, S.; de Mare, L.; Hagander, P. Bioreactor control using a probing feeding strategy and mid-ranging control. Control Eng. Pract. 2007, 15, 135–147. [Google Scholar] [CrossRef]
- Haugwitz, S.; Hagander, P.; Norén, T. Modeling and control of a novel heat exchange reactor, the open plate reactor. Control Eng. Pract. 2007, 15, 779–792. [Google Scholar] [CrossRef]
- Prado-Rubio, O.; Jörgensen, S.; Jonsson, G. pH control structure design for a periodically operated membrane separation process. Comp. Chem. Eng. 2012, 43, 120–129. [Google Scholar] [CrossRef]
- Johnsson, O.; Sahlin, D.; Linde, J.; Lidén, G.; Hägglund, T. A midranging control strategy for non-stationary processes and its application to dissolved oxygen control in a bioprocess. Control Eng. Pract. 2015, 42, 89–94. [Google Scholar] [CrossRef]
- Alferes, J.; Irizar, I. Combination of extremum-seeking algorithms with effective hydraulic handling of equalization tanks to control anaerobic digesters. Water Sci. Technol. 2010, 61, 2825–2834. [Google Scholar] [CrossRef] [PubMed]
- Houpis, C.H.; Rasmussen, S.J.; García-Sanz, M. Quantitative Feedback Theory, Fundamentals and Applications; Taylor and Francis: Boca Raton, FL, USA, 2006. [Google Scholar]
- Rico-Azagra, J.; Gil-Martínez, M.; Elso, J. Quantitative Feedback Control of Multiple Input Single Output Systems. Math. Probl. Eng. 2014, 2014, 1–17. [Google Scholar] [CrossRef]
- Zambrano, J.A.; Gil-Martinez, M.; García-Sanz, M.; Irizar, I. Benchmarking of control strategies for ATAD technology: A first approach to the automatic control of sludge treatment systems. Water Sci. Technol. 2009, 60, 409–417. [Google Scholar] [CrossRef] [PubMed]
- Jeppsson, U.; Pons, M.N.; Nopens, I.; Alex, J.; Coop, J.B.; Gernaey, K.V.; Rosen, C.; Steyer, J.P.; Vanrolleghem, P. Benchmark simulation model no 2: General protocol and exploratory case studies. Water Sci. Technol. 2007, 56, 67–78. [Google Scholar] [CrossRef] [PubMed]
- Gómez, J.; de Gracia, M.; Ayesa, E.; Garcia-Heras, J.L. Mathematical modelling of autothermal thermophilic aerobic digesters. Water Res. 2007, 41, 959–968. [Google Scholar] [CrossRef] [PubMed]
- Vrecko, D.; Gernaey, K.V.; Rosen, C.; Jeppsson, U. Benchmark Simulation Model Nº 2 in Matlab-Simulink: Towards plant-wide WWTP control strategy evaluation. Water Sci. Technol. 2006, 54, 65–72. [Google Scholar] [CrossRef]
- Fuchs, L.; Fuchs, M. Process for the Disinfection and Aerobic Stabilization of Sewage Sludge; U.S. Patent 4,983,298, 8 January 1991. [Google Scholar]
- Dorf, R.C.; Bishop, R.H. Modern Control System, 12th ed.; Pearson Prentice Hall: Upper Saddle River, NJ, USA, 2011. [Google Scholar]
- Yaniv, O. Quantitative Feedback Design of Linear and Nonlinear Control Systems; Kluwer Academic Publishers: Norwell, MA, USA, 1999. [Google Scholar]
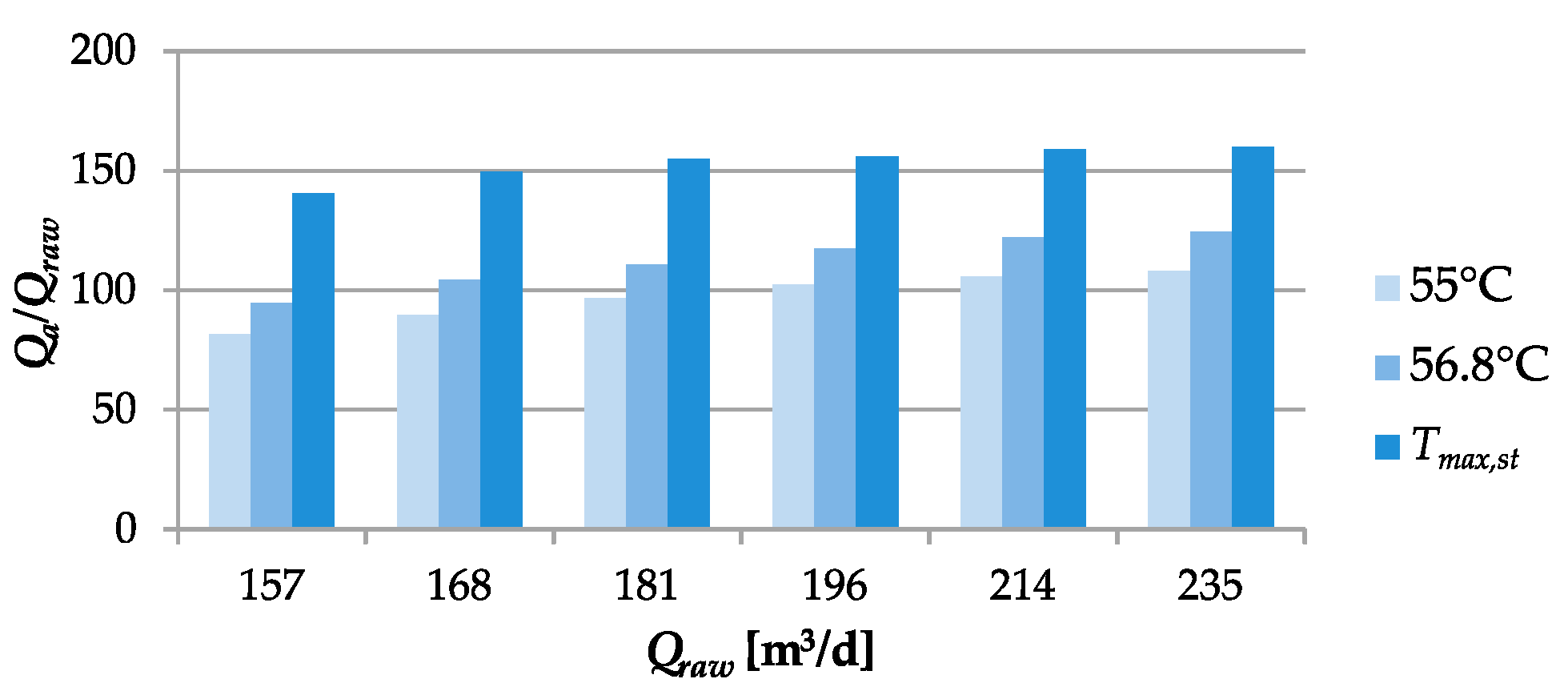
| Control Strategy | Regulated Variables Inside Feedback Control Structure (Figure 4) | Label | ||
|---|---|---|---|---|
| Quality | Aeration Cost | Production Rate | ||
| Strictly pasteurization (Goal) | Higher (Side effect) | Highest (Goal) | USEPA: Tavg,ref = 55 °C, Qa,ref = 22,524 m3/d EU: Tavg,ref = 56.8 °C, Qa,ref = 26,100 m3/d | MISO PROD |
| Lowest (Goal) | Lower (Side effect) | USEPA: Tavg,ref = 55 °C, Qa,ref = 15,053 m3/d EU: Tavg,ref = 56.8 °C, Qa,ref = 17,500 m3/d | MISO COST | |
| SRT (d) | 11 | 12 | 13 | 14 |
|---|---|---|---|---|
| Qa (m3/d) (Tavg,ref = 55 °C) | 22,524 | 20,025 | 17,426 | 15,053 |
| Qa (m3/d) (Tavg,ref = 56.8 °C) | 26,100 | 23,000 | 20,000 | 17,500 |
| OL | SISO | MISO STD | MISO COST | MISO PROD | |
|---|---|---|---|---|---|
| Qa (m3/d) | 18,750 (USEPA) 21,500 (EU) | Free feedback regulated | Feedback regulated to Qa,ref = 18,750 (USEPA) or to Qa,ref = 21,500 (EU) | Feedback regulated to Qa,ref in Table 1 | Feedback regulated to Qa,ref in Table 1 |
| SRT (d) | 12.5 | 12.5 | Free feedback regulated | Free feedback regulated | Free feedback regulated |
| Tavg = 55 °C (USEPA) | Tavg = 56.8 °C (EU) | |||||||
|---|---|---|---|---|---|---|---|---|
| IQPUSEPA (%) | IQPEU (%) | IC (%) | IP (%) | IQPUSEPA (%) | IQPEU (%) | IC (%) | IP (%) | |
| OL | 100.61 | 7.17 | 34.28 | 74.75 | 175.92 | 44.9 | 39.12 | 74.91 |
| SISO | 106.62 (5.97%) | 0 | 35.18 (2.63%) | 74.76 (0.01%) | 191.32 (8.75%) | 100 | 40.37 (3.20%) | 74.96 (0.07%) |
| MISO STD | 106.42 (5.77%) | 0 | 34.83 (1.70%) | 73.66 (−1.46%) | 190.99 (8.57%) | 100 | 39.89 (1.97%) | 73.53 (−1.84%) |
| MISO COST | 105.08 (4.44%) | 0 | 32.32 (−5.72%) | 63.93 (−14.47%) | 188.55 (7.18%) | 100 | 37.18 (−4.96%) | 64.39 (−14.04%) |
| MISO PROD | 107.81 (7.16%) | 0 | 37.04 (8.05%) | 82.93 (10.94%) | 193.9 (10.22%) | 100 | 42.54 (8.74%) | 83.42 (11.36%) |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nájera, S.; Gil-Martínez, M.; Rico-Azagra, J. Dual-Control of Autothermal Thermophilic Aerobic Digestion Using Aeration and Solid Retention Time. Water 2017, 9, 426. https://doi.org/10.3390/w9060426
Nájera S, Gil-Martínez M, Rico-Azagra J. Dual-Control of Autothermal Thermophilic Aerobic Digestion Using Aeration and Solid Retention Time. Water. 2017; 9(6):426. https://doi.org/10.3390/w9060426
Chicago/Turabian StyleNájera, Silvano, Montserrat Gil-Martínez, and Javier Rico-Azagra. 2017. "Dual-Control of Autothermal Thermophilic Aerobic Digestion Using Aeration and Solid Retention Time" Water 9, no. 6: 426. https://doi.org/10.3390/w9060426
APA StyleNájera, S., Gil-Martínez, M., & Rico-Azagra, J. (2017). Dual-Control of Autothermal Thermophilic Aerobic Digestion Using Aeration and Solid Retention Time. Water, 9(6), 426. https://doi.org/10.3390/w9060426









