3.1. Network Architecture
A three-layer, feedforward MLP network architecture was selected with 2 input variables and 1 output variable. A coupled method was used to determine the optimum n
H and the percentage of data for each of the training, validation and testing subsets. Sample results of the proposed method are shown in
Figure 2.
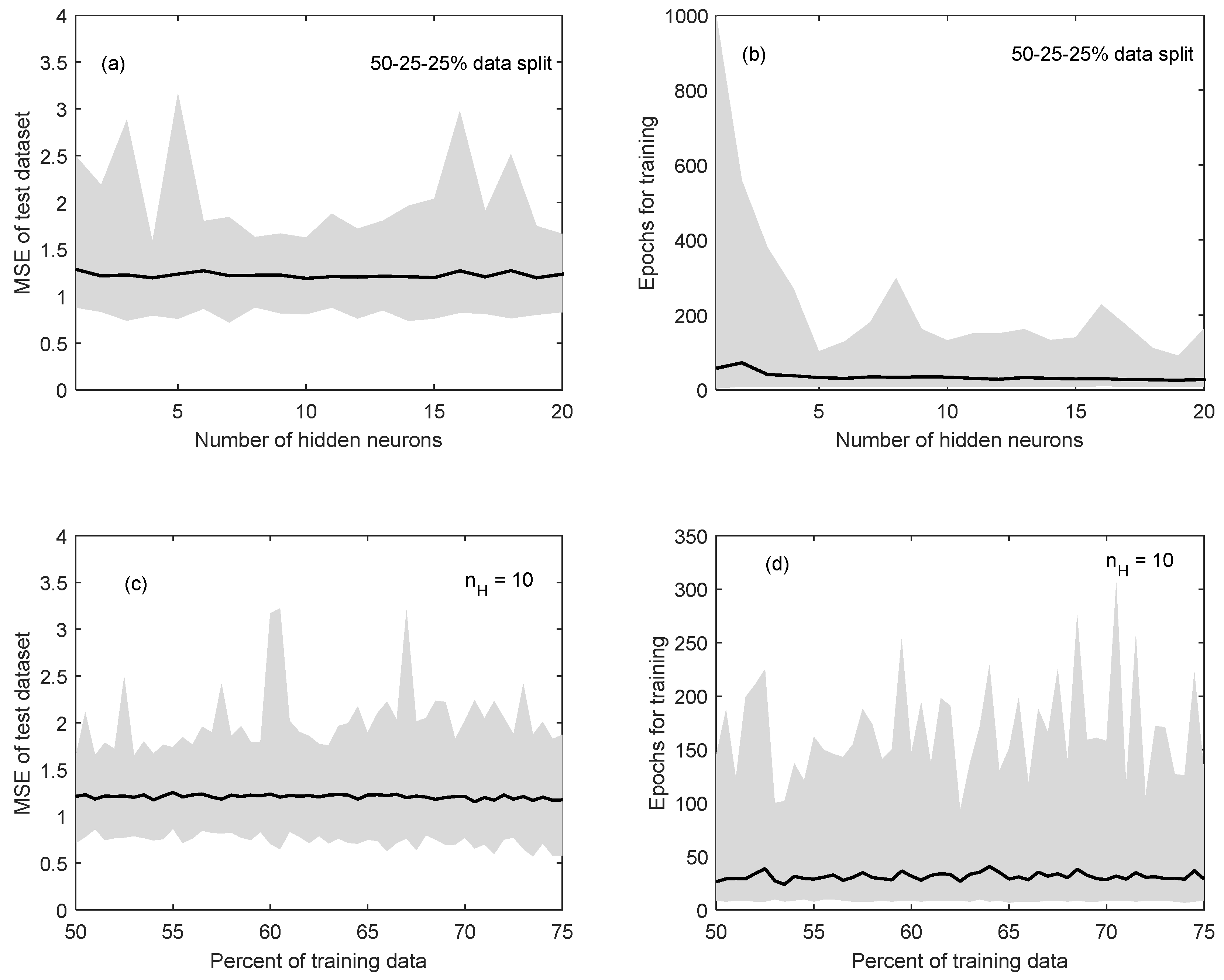
Figure 2a shows the mean MSE (solid black line) of the test dataset for the initial 50%:25%:25% data-division scenario, with n
H varying between 1 and 20 neurons. This simulation was repeated 100 times to account for the random selection of data and the upper and lower limits of MSE for each of these simulations are shown in grey. This figure demonstrates that the number of neurons did not have a noticeable impact on the MSE for this configuration. The most significant outcome of this process is that the variability (the difference between the upper and lower limits) of the performance seems to decrease after n
H = 6 and increases again after n
H = 12, with the lowest MSE at n
H = 10. This result has two important implications: first, increasing the model complexity results in limited improvement of model performance, suggesting that a simpler model structure may be more suitable to describe the system. Second, the variability in performance indicates that the initial selection of data in each training subset can highly influence the performance of the test dataset, especially at the lower (i.e., n
H < 6) and higher (i.e., n
H > 12) ends of the spectrum of the proposed number of neurons. This suggests that an optimum selection of hidden neurons lies within this range (6 < n
H < 12).
Figure 2b shows the change in the mean (solid black line) and the variability (in grey) of the number of epochs needed to train the network for the initial data-division scenario, as n
H increases from 1 to 20. While the mean value does not show a notable change, the variability of the time needed for training (i.e., the number of epochs) drastically decreases as n
H increases from 1 to 5. This means that a simpler model structure may require more time to train, and the performance of these simpler architectures (n
H = 1 to 5) is more variable. This is likely because the initial dataset selection has a higher impact on the final model performance for less complex models. The lowest number of mean epochs for this analysis occurred at n
H = 19, with 26 epochs. However, note that the variability of MSE at n
H = 19 (in
Figure 2a) is high, and that n
H = 19 falls outside the range 6 < n
H < 12, identified above.
The impact of changing the amount of data used for training, validation and testing on the model performance (MSE) was generally inconclusive as the amount of data used for training was increased from 50% to 75% at 0.5% intervals.
Figure 2c shows sample results for the n
H = 10 scenario, which was the best performing scenario, i.e., had the lowest mean MSE for each data-division scenarios when compared to other n
H values. However, the subplot illustrates that the MSE for the test dataset does not show a major trend as the amount of data for training is increased from the initial 50%. This means that for this scenario (n
H = 10) increasing the amount of data used for training has minimal impact on model performance, indicating that using the least amount of data for training (and thus having a higher fraction available for validating and testing) would be ideal. Note that the mean MSE values were generally higher for all data-division scenarios when the selected n
H was between 1 and 5 (follow the example shown in
Figure 2a).
The number of epochs needed for training the network at different data-division scenarios was inconclusive.
Figure 2d shows sample results for the n
H = 10 case, which demonstrates that the mean and the variability of the number of epochs does not demonstrate a clear trend, as the amount of data used for training is increased. The significance of this analysis is that the amount of computational effort (or time) does not necessarily decrease as a larger fraction of data is used for training. Given this result, the least amount of training data (50%) is the preferred choice for the number of neurons that result in the lowest MSE, which is n
H = 10 as described above. For the n
H = 10 case, the overall mean number of epochs for each data-division scenario is low ranging between 24 and 40 epochs.
Based on these results, nH = 10 with a 50%:25%:25% data-division was selected as the optimum architecture for this research. The fact that the mean and the variability of MSE was the lowest at nH = 10 makes it a preferred option over the nH = 19 case, which as a lower number of mean epochs but had higher variability in MSE. In other words, higher model performance was selected over model training speed (mean epochs at nH = 10 ranged between 9 and 122 for the 50%:25%:25% data-division scenario). Secondly no significant trend was seen as the amount of data used for training, validation and testing was altered, however lower MSE values were seen at nH = 10 compared to other at nH values. Thus, the option that guarantees the largest amount of independent data for validation and training is preferred. Given the fact that the mean MSE for the testing dataset does not show a significant change as the per cent of training data is increased from 50% to 75%, the initial 50%:25%:25% division is maintained as the final selection.
The overall outcome of this component of this research was that that instead of using the typical trial-and-error based approach to selecting neural network architecture parameters, the proposed method can provide objective results. Specifically, systematically exploring different numbers of hidden layers and fraction of training data can help select a model with the highest performance, whilst accounting for the randomness in data selection. Once these neural network architecture parameters were identified, subsequent training of the FNN was completed. The results of the training and optimisation are presented in the next section.
3.2. Network Coefficients
First, the network was trained at μ = 1 using the network structure outlined in the previous section. The crisp, abiotic inputs (Q and T) were used to estimate the values of each weight and bias in the network. This amounted to 20 weights (10 for each input) and 10 biases between the input and hidden layer, and 10 weights and 1 bias in the final layer. The MSE and the Nash–Sutcliffe model efficiency coefficient (NSE; [
59]) for the training, validation and testing scenarios for the μ = 1 case are shown in
Table 1 below.
The MSE for each dataset is low, approximately between 10% and 18% of the mean annual minimum DO seen in the Bow River for the study period. The NSE values are greater than 0.5 for each subset, which is higher than NSE values for most water quality parameters (when modelled daily) reported in the literature [
60] and is considered “satisfactory” using the ranking system proposed by Moriasi et al. [
60]. These two model performance metrics highlight that predicting minimum DO using abiotic inputs and a data-driven approach is an effective technique. Note that compared to results reported in [
19], the present modelling approach (with the optimised network architecture) produces similar performance metrics (i.e., “satisfactory”). However, note that in the present case the network architecture selection is selected using an explicit and transparent algorithm, rather than in an ad hoc manner as in [
19]. While both methods use the same dataset, the network architecture (number of neurons) is different for both methods, resulting in minor discrepancies between the model performance metrics. Additionally, some results in [
19] are derived from fuzzy inputs rather than crisp inputs (as is the case in the present work). Additional advantages of the proposed approach are seen when the fuzzy component of the results are analysed.
Once the crisp network was trained, a top down approach was taken to train the remaining intervals, starting at μ = 0.8 where 20% of the observations should be captured within the corresponding predicted output interval, and continuing to μ = 0 where 99.5% of the observations should be captured within the predicted output intervals. Each set of optimisation (both the SCE-UA and
fmincon algorithms) for each of the five remaining membership levels (μ = 0, 0.2, 0.4, 0.6 and 0.8) took approximately 2 h using a 2.40 GHz Intel
® Xeon microprocessor (with 4 GB RAM). The results of this optimisation are summarised in
Table 2, which shows the amount of data captured within the resulting α-cut intervals after each optimisation.
For the training dataset, the coupled algorithm was able to capture the exact amount of data it was required to. Similar results can be seen for the validation and testing datasets, where the amount of data captured are close to the constraints posed. For the two independent datasets, the amount of coverage decreases (i.e., lower performance) as the membership level increases, which is unavoidable when the width of the uncertainty bands decrease. Similar results were seen for the testing dataset in [
29]. These results are similar to those published in [
19] for both the fuzzy and crisp input case, with the only marked differences are: at the µ = 0.4 level where the present model captures a lower percentage of data than the crisp case in the previous method; and at the µ = 0.2 and 0.8 levels where the present model captures data closer to the assigned constraints as compared to the fuzzy inputs case in [
19].
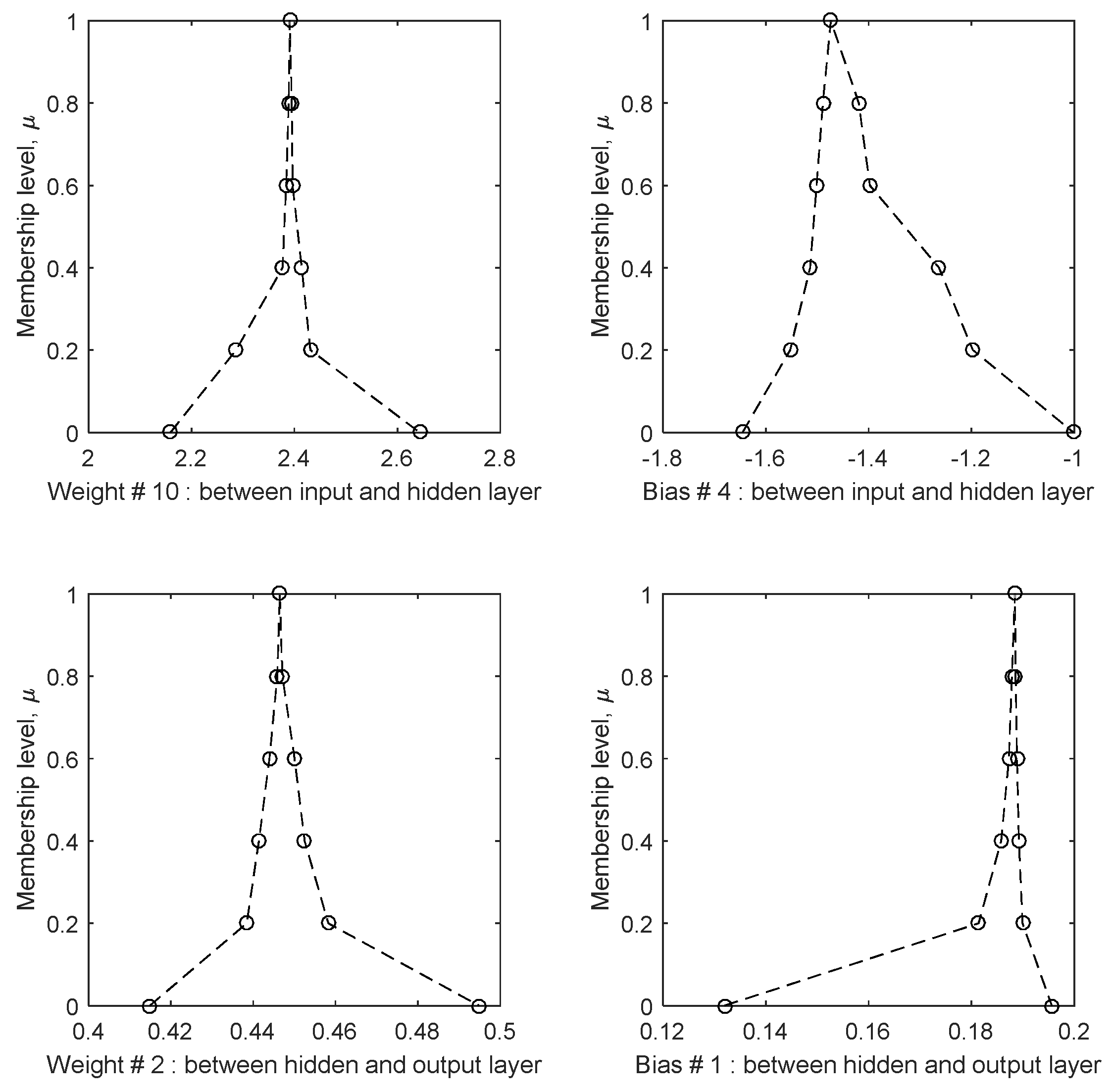
The result of this optimisation was the calibrated values of the fuzzy weights and biases; sample membership functions for four weights and biases are shown in
Figure 3. The figure illustrates that the shapes of all membership functions were convex, a consequence of the top-down calibration approach, where the interval at lower membership levels is constrained to include the entire interval at higher membership levels. In other words, since lower membership levels include a higher amount of data, the corresponding interval to that level is wider than at higher membership levels. Furthermore, since the crisp network was used at μ = 1, there is at least one element in each fuzzy number with μ = 1, meaning that each weight and bias is a normal fuzzy set.
The membership functions of the weights and biases are assumed to be piecewise linear following the assumption made in [
5,
14,
19,
29]. This means that enough α-cut levels need to be selected to completely define the shape of the membership functions. In this research six levels were selected to equally span, and to give a full spectrum of possibilities, between 0 and 1. Overall, the results of the weights and biases in the figure demonstrate that indeed enough levels were selected to define the shape of the membership function. If a smaller number of levels were selected, e.g., two levels, one at μ = 0 and one at μ = 1, the fuzzy number collapses to a triangular fuzzy number. This type of fuzzy number does not provide a full description of the uncertainty and how it changes in relation to the membership level. Thus, intermediate intervals are necessary and the results demonstrate that the functions are in fact not triangular shaped functions and not necessarily symmetric about the modal value (at μ = 1). A consequence of this is that the decrease in size of the intervals does not follow a linear relationship with the membership level. Similarly, a higher number of intervals than the six selected for this research could be used, e.g., 100 intervals, equally spaced between 0 and 1. The risk in selecting many intervals is that as the membership level increases (closer to 1) the intervals become narrower as a consequence of convexity. This will result in numerous closely spaced intervals, with essentially equal upper and lower bounds, making the extra information redundant. This is demonstrated in the sample membership functions for WIH = 10 in
Figure 3, where increasing the number of membership levels between 0.4 and 1.0 would not improve the shape or description of the membership function. This is because the existing intervals are already quite narrow. Defining more uncertainty bands between the existing levels would not add more detail but would merely replicate the information already calculated.
Table 2 and
Figure 3 demonstrate the overall success of the proposed approach to calibrate an FNN model. Whereas in many fuzzy set applications the membership function is not defined or selected based on a consistent, transparent or objective method [
30,
46,
47], or is selected arbitrarily (as noted in [
29]), the method proposed in this research is based on possibility theory and provides an objective method to create membership functions. The results of the process show that the method is capable in creating fuzzy number weights and biases that are convex and normal, and capture the required percentage of data within each interval.
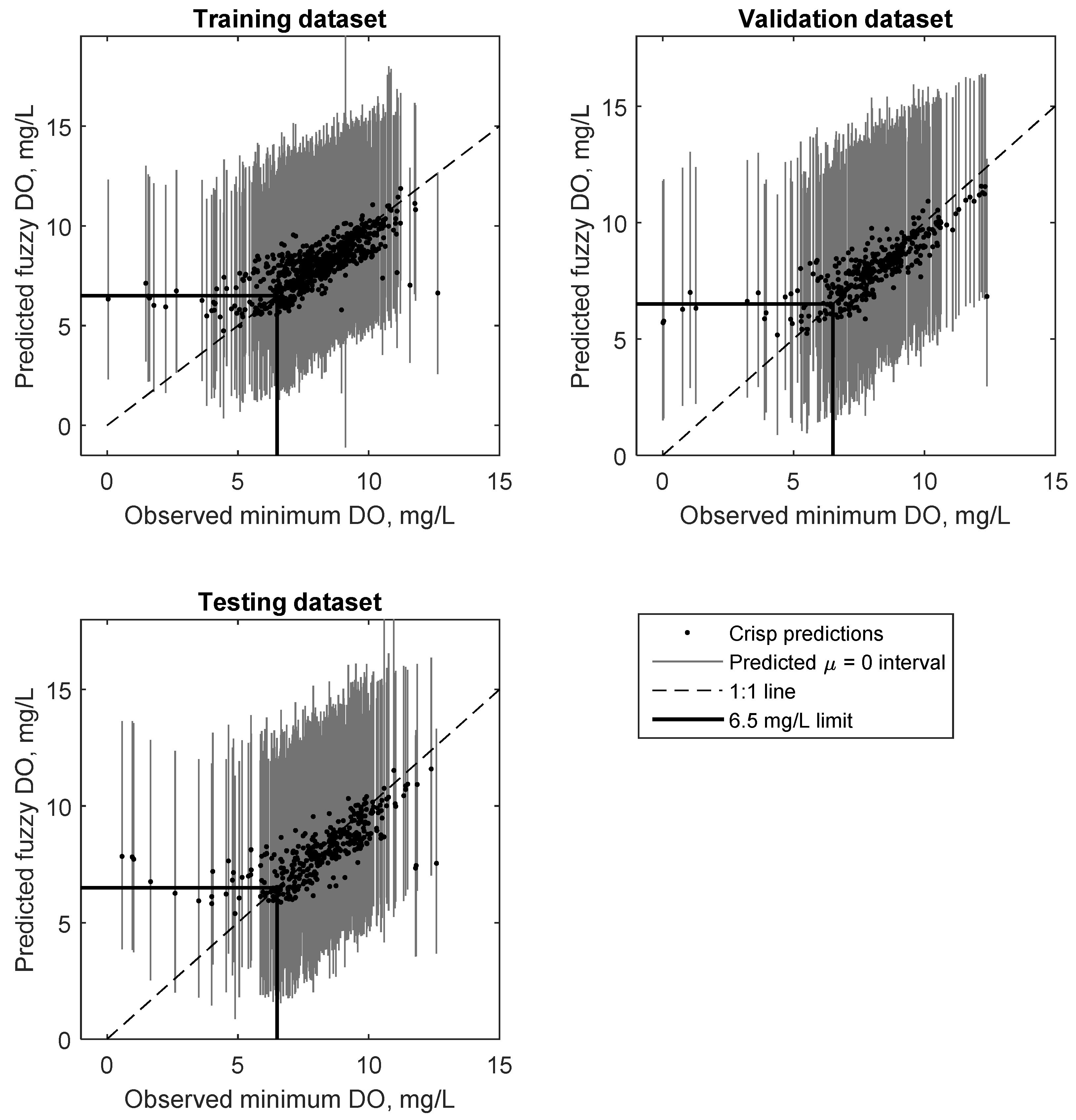
Figure 4 shows the results of observed versus crisp predictions (black dots) and fuzzy predictions (black line) of minimum DO at the membership level μ = 0 for the three different data subsets. The figure illustrates that nearly all (i.e., ~99.5%) of the observations fall within the α-cut interval defined at μ = 0 since the black dots are enveloped by the grey high-low lines of the fuzzy interval. The figure also demonstrates the advantage of the FNN over a simple ANN: while some of the crisp predictions veer away from the 1:1 line (especially at low DO, defined to be less than 6.5 mg/L here), nearly-all (i.e., ~99.5%) of the fuzzy predictions intersect the 1:1 line. This also illustrates that the NSE values reported in
Table 1 (which were calculated for the crisp case at μ = 1 only) are not representative of the NSE values of the fuzzy number predictions, and that there is a need to develop an equivalent performance metric when comparing crisp observations to fuzzy number predictions.
Lastly, the figure demonstrates the superiority of the FNN to be able to predict more of the low DO events compared to the crisp method. The low DO range (at DO = 6.5 mg/L) is highlighted in
Figure 4, and it is apparent that within this window both models tend to over predict minimum DO as they fall above the 1:1 line. However, the fuzzy intervals (grey lines) predicted by the FNN intersect the 1:1 line for the majority of low DO events, and hence predict some possibility (even if it is a low probability) at any μ of the low DO events, whereas the crisp do not predict any possibility at all. Thus, generally speaking the ability of the FNN to capture 99.5% of the data within its predicted intervals guarantees that most of the low DO events are successfully predicted. This is a major improvement over conventional methods used to predict low DO. Comparing
Figure 4 to similar results reported in [
19] demonstrate that the proposed approach in the present research has improved model performance. Specifically, the predicted intervals at µ = 0 are centred on the output rather than skewed. An outcome of this is that there are a lower number of “false alarms” (i.e., predicting low DO event when observed DO was not low) compared to [
19]. This is discussed in more detail below. This suggests that by using an optimised algorithm for the network, low DO prediction is improved, at the expense of a predicting high DO events (i.e., the upper limit of the predicted intervals). However, high DO values are of less interest and importance to most operators.
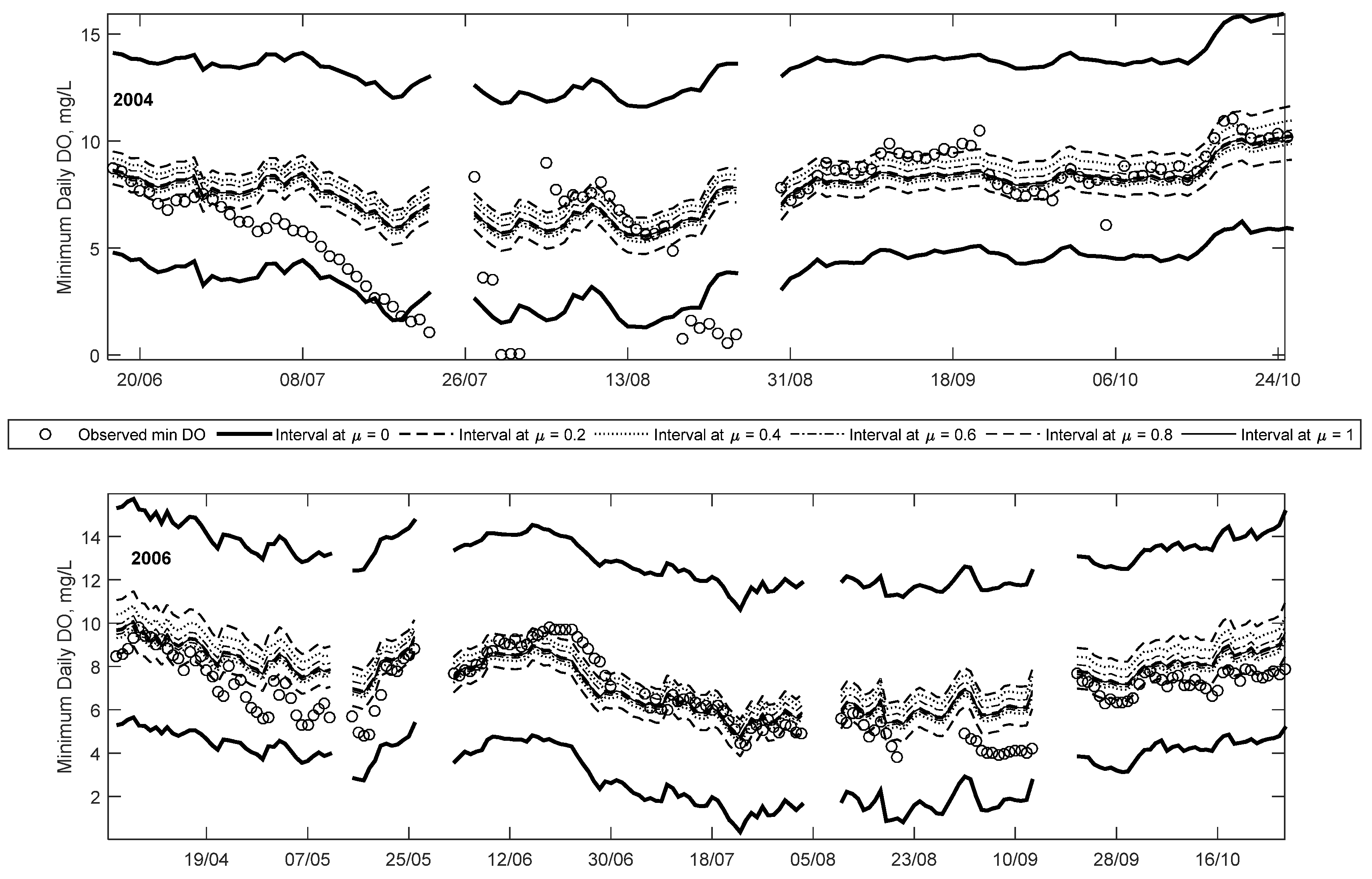
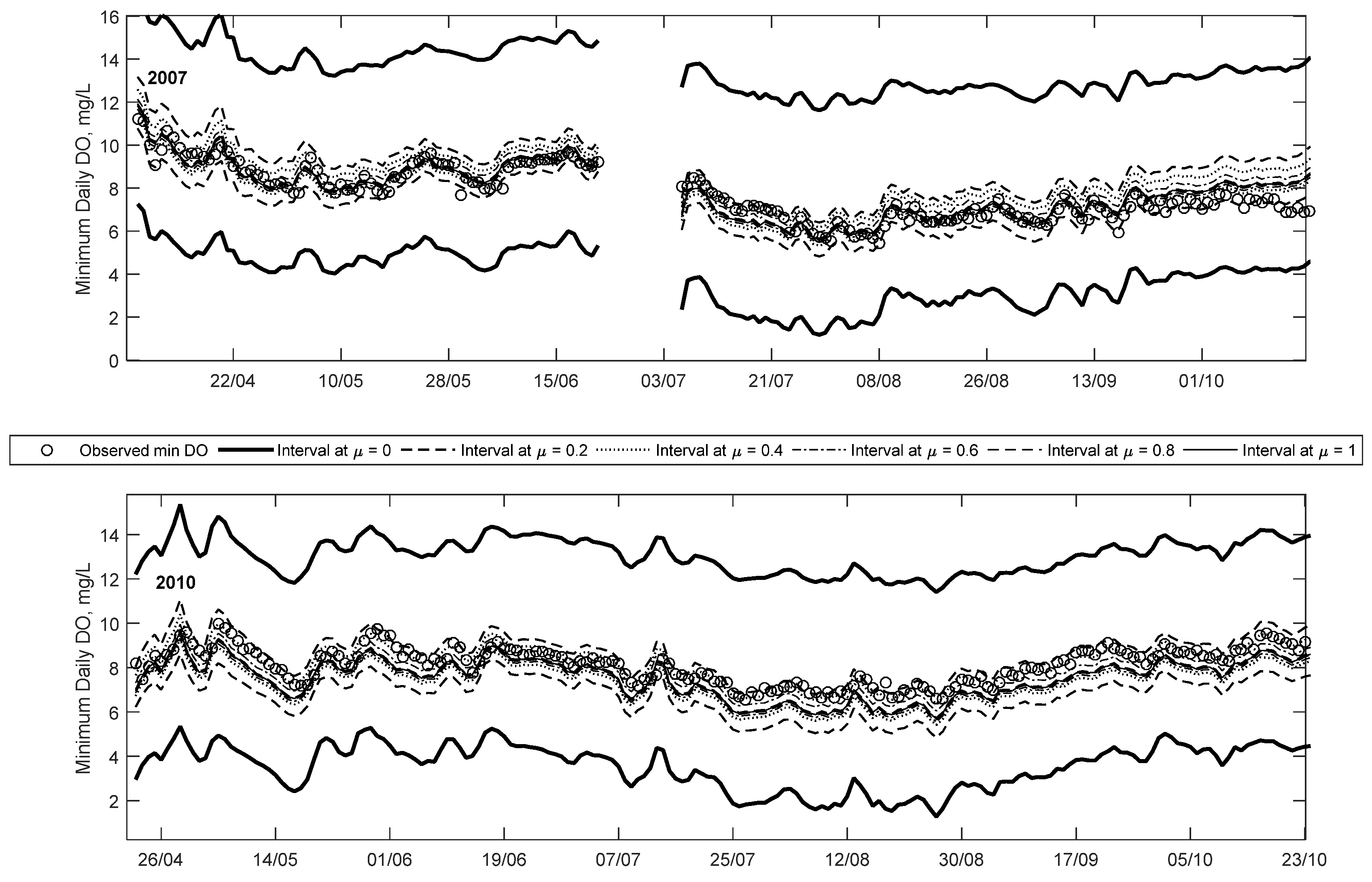
Figure 5 and
Figure 6 show trend plots of observed minimum DO and predicted fuzzy minimum DO for the years 2004, 2006, 2007 and 2010. These particular years were selected due to the high number of low DO occurrences in each year, and, thus, are intended to highlight the utility of the proposed method. Note that, for each year shown, approximately 50% of the data constitute training data, while the other 50% constitute a combination of validation and testing data. However, for clarity, this difference is not explicitly shown in these figures.
The most number of days where minimum daily DO was below the 5 mg/L guideline was observed in 2004 and 2006, with 25 days in each year. The year 2007 had the third most (after 2006 and 2004, respectively) number of days below the 6.5 mg/L guideline, with 27 days. Lastly, 2010 had the second most number of days below the 9.5 mg/L guideline with 180 days (after 2007 which had 182) below the guideline. Thus, these four years collectively represent the years with the lowest minimum daily DO during the study period. It is noteworthy that even though minimum DO was observed to be below 5 mg/L on several occasions in 2004 and 2006, the DO was below on 9.5 mg/L only 107 and 164 days, respectively, for these years. In contrast, in 2007 and 2010, no observations below 5 mg/L were seen, however 182 and 180 days, respectively, below the 9.5 mg/L were seen for those years. This indicates that even if no observations of DO < 5 mg/L are seen, it is not a good indicator of a healthy ecosystem, since the overall mean DO of the year might be low (e.g., a majority of days below the 9.5 mg/L). The implication of this is that only using one guideline is not a good indicator of overall aquatic ecosystem health.
In
Figure 5 and
Figure 6, the predicted minimum DO at equivalent membership levels (e.g., 0
L or 0
R) at different times steps are joined together creating bands representative of the predicted fuzzy numbers calculated at each time step. Note that the superscripts L and R define the lower bound and upper bounds of the interval at a membership level of 0, respectively. In doing so, it is apparent that all the observed values fall within the μ = 0 interval for the years 2006, 2007 and 2010, and nearly all observations in 2004. This difference in 2004 is because the per cent of data included within the μ = 0 interval was selected to be 99.5% rather than 100% to prevent over-fitting; the optimisation algorithm was designed to eliminate the outliers first to minimise the predicted interval. The low DO values in 2004 are the lowest of the study period, and thus are not captured by the FNN.
The width of each band corresponds to the amount of uncertainty associated with each membership level, for example, the bands are the widest at μ = 0, meaning the results have the most vagueness associated with it. Narrower band are seen as the membership level increases until μ = 1, which gives crisp results. This reflects the decrease in vagueness, increase in credibility, or less uncertainty of the predicted value. In each of the years shown, note that the observations fall closer to the higher credibility bands, except for some of the low DO events. This means that the low DO events are mostly captured with less certainty or credibility (typically between the 0L and 0.2L levels) compared to the higher DO events. However, it should be noted that compared to a crisp ANN, the proposed method provides some possibility of low DO, whereas the former only predicts a crisp result without a possibility of low DO. Thus, the ability to capture the full array of minimum DO within different intervals is an advantaged of the proposed method over existing methods.
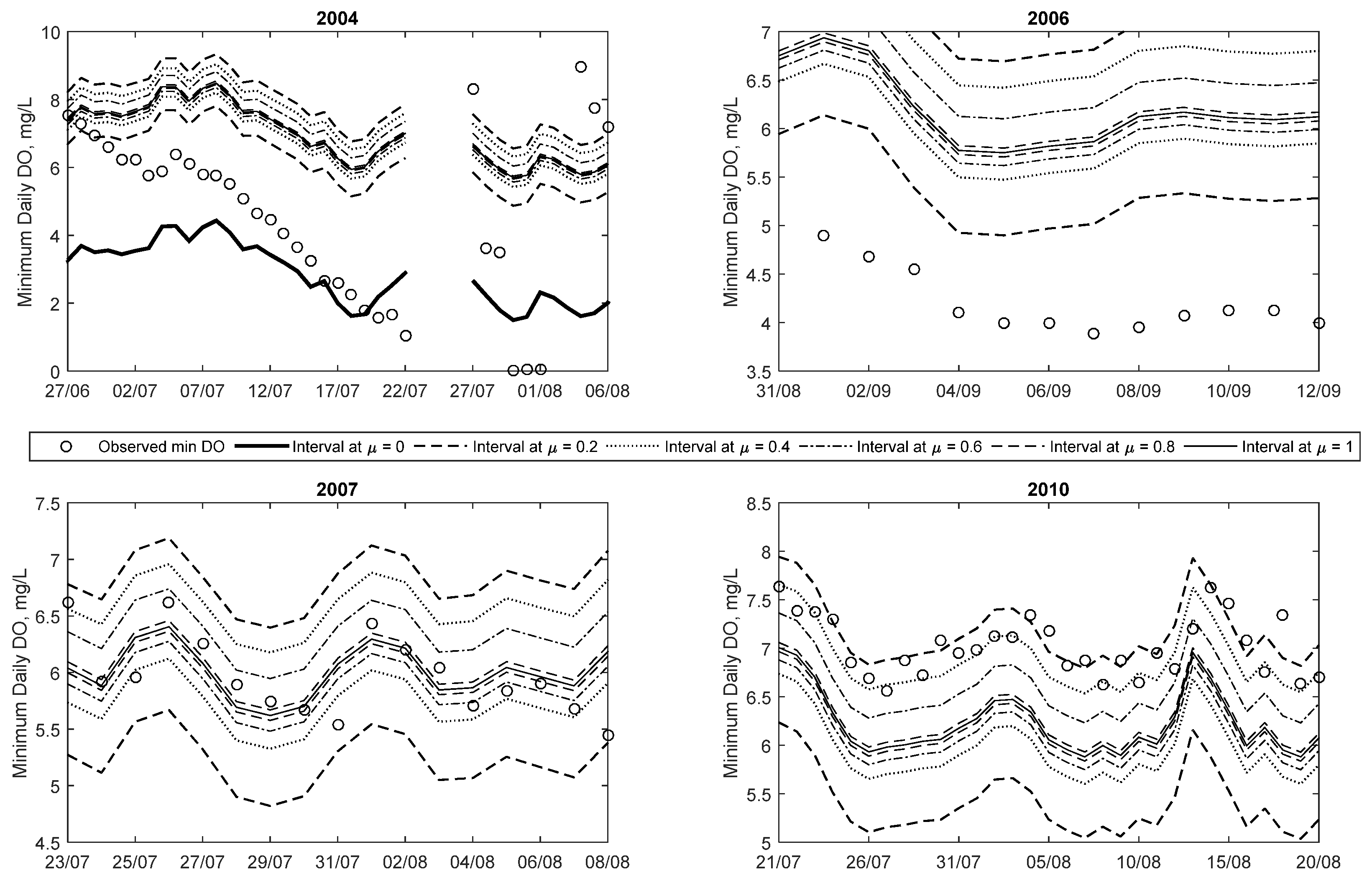
Results from 2004 show that minimum DO decreases rapidly starting in late June and continuing until late July, followed by a few days of missing data and near-zero measurements, before increasing to higher DO concentration. Details of this trend are shown in
Figure 7. The reason for this rapid decrease is unclear and may be an issue with the monitoring device. However, it demonstrates that the efficacy of data-driven methods is dependent on the quality of the data. One of the advantages of the proposed method is that while it is able to capture nearly all of the observations (including outliers) within the least certainty band (at μ = 0), other observations are mostly captured within higher certainty bands (μ > 0). As the data length increases (i.e., the addition of more data and the FNN is updated), the number of outliers included with the μ = 0 band will decrease because the optimisation algorithm searches for the smallest width of the interval whilst including 99.5% of the data. Thus, with more data, the 0.5% not included in the interval will be the type of outliers seen in 2004.
The time series plot for 2006 shows that all the observations fall within the predicted intervals. The majority of the 25 low DO (i.e., less than 5 mg/L) occur starting in mid-July and continuing occasionally until mid-September. Unlike in 2004, all of these low DO events are captured within both the μ = 0.2 and 0 intervals. This suggests that the model predicts these low DO events with more credibility than in the 2004 case. Details of some of the low DO events are also plotted in
Figure 7 (for September). This plot shows that the low DO events are captured between μ = 0 and 0.2 intervals. Even though the membership level is low, the general trend profile of the observed minimum daily DO is captured by the modelled results.
Figure 6 illustrates the time series predictions for 2007, and it clearly demonstrates that most of the observations are captured at higher membership levels, unlike the 2004 and 2006 examples, i.e., only a limited number of observations are seen between the μ = 0 and 0.2 intervals for the entire year. In addition to this, 26 out of the 27 low DO observations (in this case below 6.5 mg/L) for this year are captured within the predicted membership levels (between μ = 0 and 0.2).
Figure 7 shows details of a low DO period in 2007 in July and August, which shows that the observations are evenly scattered around the μ = 1 line.
The trend plot for 2010 is shown
Figure 6 and it is clear that nearly all observations for the year are below 10 mg/L, and about 87% of all observations are below the 9.5 mg/L guideline. As with the 2007 case, the bulk of the observations are captured within high credibility intervals, owing to the lack of extremely low DO (i.e., below 6.5 or 5 mg/L). The trend plot illustrates that the FNN generally reproduces the overall trend of observed minimum DO. This can be seen in a period in early May where DO falls from a high of 10 mg/L to a low of 7 mg/L, and all the predicted intervals replicate the trend. This is an indication that the two abiotic input parameters are suitable parameters for predicting minimum DO in this urbanised watershed.
Figure 7 shows details of a low DO (below 9.5 mg/L) event in 2010 in late July through late August. The bulk of low DO events are captured between the μ = 0.6 and 0.2 intervals—demonstrating that these values are predicted with higher credibility than the low DO cases (<5 mg/L) in 2004 and 2006. Some of the low DO (<9.5 mg/L) events highlighted in this plot are underestimated by the crisp ANN method. This means that in general the crisp method tends to over-predict extremely low DO events (i.e., those less than 5 mg/L) while under-predicting the less than 9.5 mg/L events. In both cases, the fuzzy method is able to capture the observations within its predicted intervals.
Comparing these trend plots (using crisp inputs) to those presented in [
19] using fuzzy inputs, highlights some important differences between the two approaches. In the present case, the fuzzy predictions tend to be less skewed than those shown in [
19]; a direct consequence of not including input uncertainty (i.e., fuzzy inputs) in the analysis. In addition to this, the predicted intervals are general narrower in comparison, suggesting lower uncertainty. However, this is to be expected since the input uncertainty was not considered in the present study. A consequence of this is that some of the extremely low DO events (e.g., in 2004) are not captured in the current model. However, it also means the amount of “false alarms” (predicting a possibility of low DO when none occurred) is lower in the current state.
The analysis of the trend plots for these four sample years show that the proposed FNN method is extremely versatile in capturing the observed daily minimum DO in the Bow River using abiotic (Q and T) inputs. The crisp case (at μ = 1) cannot capture the low DO events (as shown in
Figure 4 and
Figure 5), while the FNN is able to capture these events within some membership level. The top-down training method selected for the FNN has been successful in creating nested-intervals to represent the predicted fuzzy numbers. The width of the predicted intervals corresponds to the certainty of the predictions (i.e., larger intervals for more uncertainty). The utility of this method is further demonstrated in the proceeding section, where a risk analysis tool for low DO events in the Bow River is presented.
3.3. Risk Analysis
Daily minimum DO was observed to be below 5 mg/L on 51 occasions in the Bow River for the study period between 2004 and 2012. The FNN method predicted DO be less than 5 mg/L on each of the 51 occasions (at some possibility level), giving a 100% success rate, whereas the crisp ANN only correctly predicted one of these events, a 2% success rate. Similarly, for the 6.5 mg/L guideline, the FNN was able to correctly identify all 184 occasions where minimum daily DO was less than the threshold. The crisp ANN only predicted 52%, i.e., 96 out of 184 occasions of these low DO events. Lastly, of the 1151 occasions where the daily minimum DO was observed to be less than 9.5 mg/L, the FNN identified low DO events for each of these days, whereas the crisp method predicted 97% of these events. To summarise, the FNN method is able to predict all the low DO events, and performs significantly better compared to the crisp case for the most extreme low DO guideline (i.e., at the 5 mg/L).
Figure 8 shows sample plots of observed and predicted fuzzy minimum DO, corresponding to the lowest DO concentration observed for each year for the study period. As with the weights and biases shown in
Figure 3, the intervals are the largest at μ = 0, which decreases in size as the membership level increases. The shape of the membership functions are not triangularly shaped as assumed in many fuzzy set based applications. This is of significance because it shows that the amount of uncertainty (or credibility) does not change linearly with the magnitude of DO, which has important implications regarding the risk of low DO, discussed in detail below.
Comparing the crisp results at μ = 1 to fuzzy number predictions, it is apparent that on a number of occasions (e.g., 2006, 2005 and 2004) when the observed DO is below 5 mg/L, the crisp prediction does not predict low DO while the fuzzy number predicts a possibility of DO to be below 5 mg/L, (between μ = 0 and 0.2 for the illustrated examples). Even in the 2004 case, where both the crisp and fuzzy predictions over predict the observed DO, the fuzzy prediction still predicts some possibility of low DO, whereas the crisp results do not. These examples illustrate that low DO prediction using the FNN is superior to the crisp case.
As demonstrated in the above figures, the FNN model predicts some possibility (i.e., μ = 0) of low DO (e.g., 5 mg/L) even on days when the observed data are not below this limit (i.e., a false positive). It is important to note that the data used for this model have been filtered (as described above) to only include observations from April through October each year, and thus, the analysis is conducted during the period most susceptible to low DO. The consistency principle (see [
19] for more details) implies that something must be possible before it is probable; therefore, a low possibility of low DO prediction means that the probability must necessarily be low. For this dataset, the model predicted DO to be below 5 mg/L when it was observed to be above this limit on 1051 occasions (lower than what is reported in [
19]). However, on average, the probability of low DO for these events was 3.46% compared to the average probability of the 51 low DO events of 8.59%. Overall, for 98% of the false positive outcomes (20 out of 1051) the probability of low DO was much lower than the actual low DO events. These results are similar to those reported in [
19] with respect to overall rate of false positives; though the present method predicts a smaller number of false positives. Similar results were seen for the 6.5 mg/L (93%) and 9 mg/L (95%) cases. This shows that while the model may predict a possibility of low DO events, the vast majority of them have a very low probability of occurrence, owing to their skewed predicted membership functions. The calibrated FNN model was used to create a low DO risk tool where the risk (i.e., probability) of low DO was calculated from the fuzzy DO using the inverse transformation described in Equations (1) and (2). First, values of Q and T were selected to represent average conditions in the Bow River. The flow rate selected was between 40 and 220 m
3/s at 2 m
3/s intervals, and water temperature was between 0 and 25 °C at 0.2 °C intervals. For each combination of Q and T, the fuzzy DO was calculated using the FNN. The inverse transformation was used to calculate the probability of predicted DO to be below 5 mg/L for each combination of inputs.
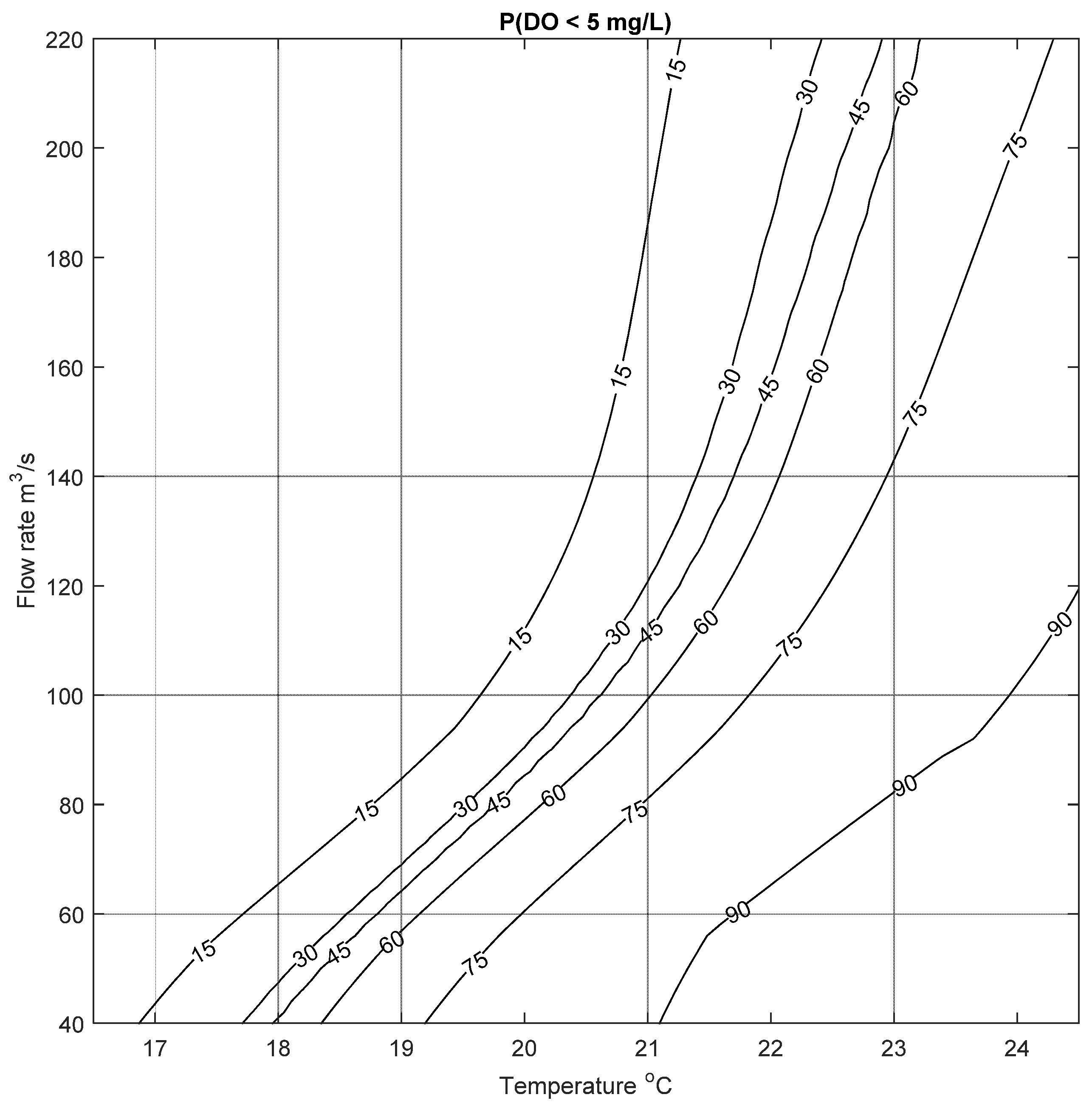
The results of this analysis are illustrated in
Figure 9, which shows the change in probability of low DO for different inputs. Generally the figure correctly recreates the conditions that lead to low DO events in the Bow River: low flow rates and high water temperature. The highest risk of low DO is when T ranges from 21 to 24 °C and Q ranges from 40 to 100 m
3/s: the probability of low DO is more than 90%. The risk of low DO decreases with higher flow rate and lower temperature. The utility of this method is that a water-resource manager can use forecasted water temperature data and expected flow rates to quantify the risk of low DO events in the Bow River, and can plan accordingly. For example, if the risk of low DO reaches a specified numerical threshold or trigger, different actions or strategies (e.g., increasing flow rate in the river by controlled release from the upstream dams) can be implemented. The quantification of the risk to specific probabilities means that the severity of the response can be tuned to the severity of the calculated risk.
It is worth highlighting here that this demarcation of probabilities for different inputs would not have been possible if only two membership levels (at μ = 0 and 1) were used to construct the fuzzy number weights, biases and output. This is because using only two membership levels would result in triangular membership functions which would show a linear change in probabilities with the change in magnitude of inputs. However, as the results in the previous section have shown, the change in the width of the intervals versus the change in membership levels is not linear. This is also highlighted in
Figure 9, where there is no linear change in the risk of low DO with the inputs.
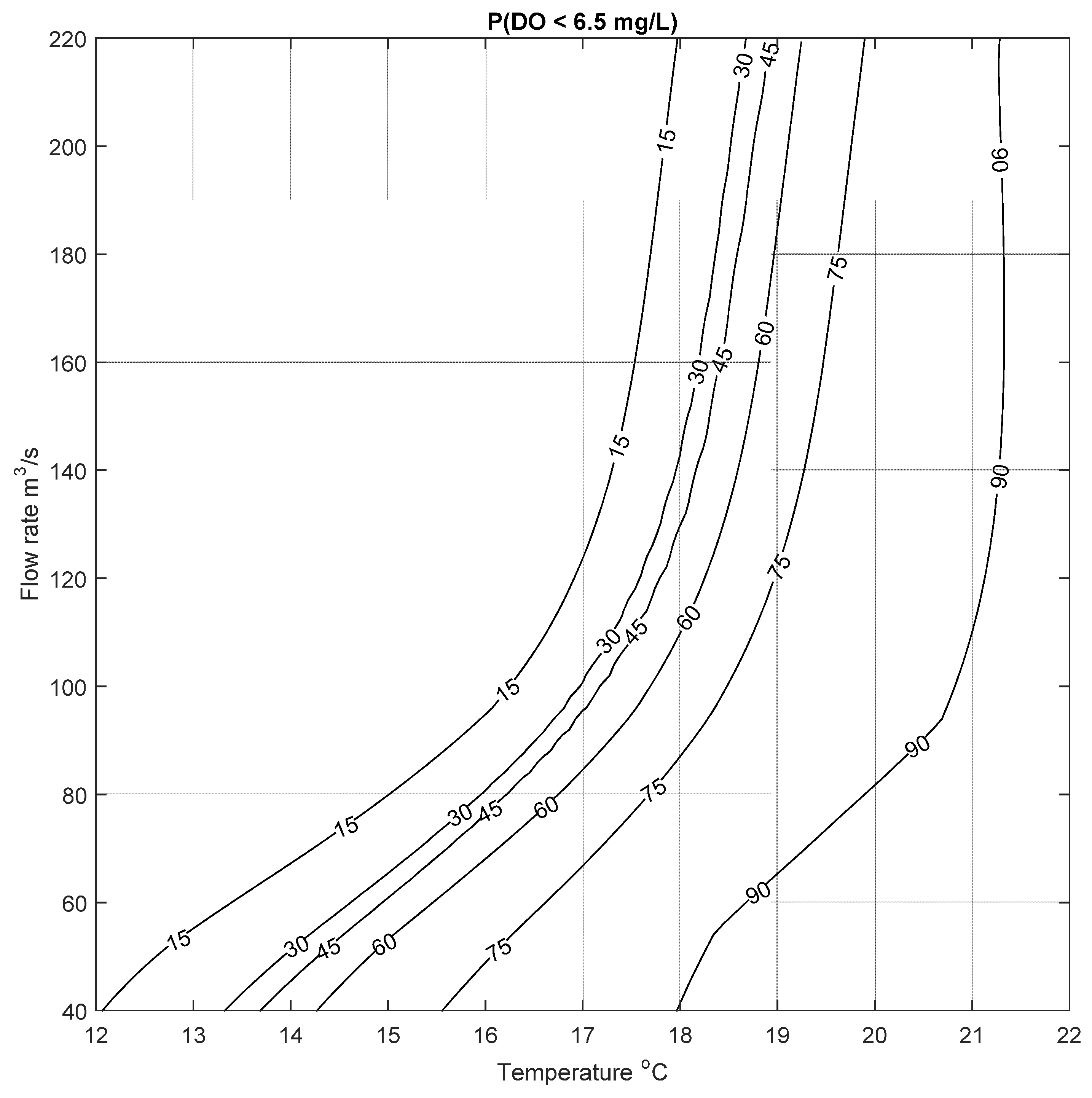
This process was repeated for two more cases to calculate the probability of low DO to be below 6.5 mg/L and 9.5 mg/L; the resulting risk of low DO are shown in
Figure 10 and
Figure 11. Similar results can be seen for these two cases, where the risk of low DO increases with increasing temperature and decreasing flow rate, as expected. These figures demonstrate that the probability of low DO is generally high for the type of conditions seen in the Bow River. The mean annual water temperature and flow rate for the study period was between 9.23 and 13.2 °C, and 75 and 146 m
3/s, respectively. For these conditions, the probability of DO to be less than 9.5 mg/L ranges between ~50% to more than 90% (based on results presented in
Figure 11). This risk increases in the summer months where the average daily water temperature in the Bow River is usually above 10 °C; under this condition there is a high risk of low DO even at high flow rates, as seen in
Figure 11. In contrast to this,
Figure 10 shows that there is a relatively higher risk of low DO (below 6.5 mg/L) in the spring (April and May) and late summer (September), when flow rate can be as low as 50 m
3/s, and the water temperature varies between 10 to 15 °C, resulting in a risk of low DO of about ~60%. These examples are meant to illustrate the potential utility of the data-driven and abiotic input parameter DO model, that can be used to assess the risk of low DO. Given that it is a data-driven approach, the model can be continually updated as more data become available, further refining the predictions.