Application of GIS-Interval Rough AHP Methodology for Flood Hazard Mapping in Urban Areas
Abstract
:1. Introduction
2. Study Area
3. Methodology
3.1. Methodological Background
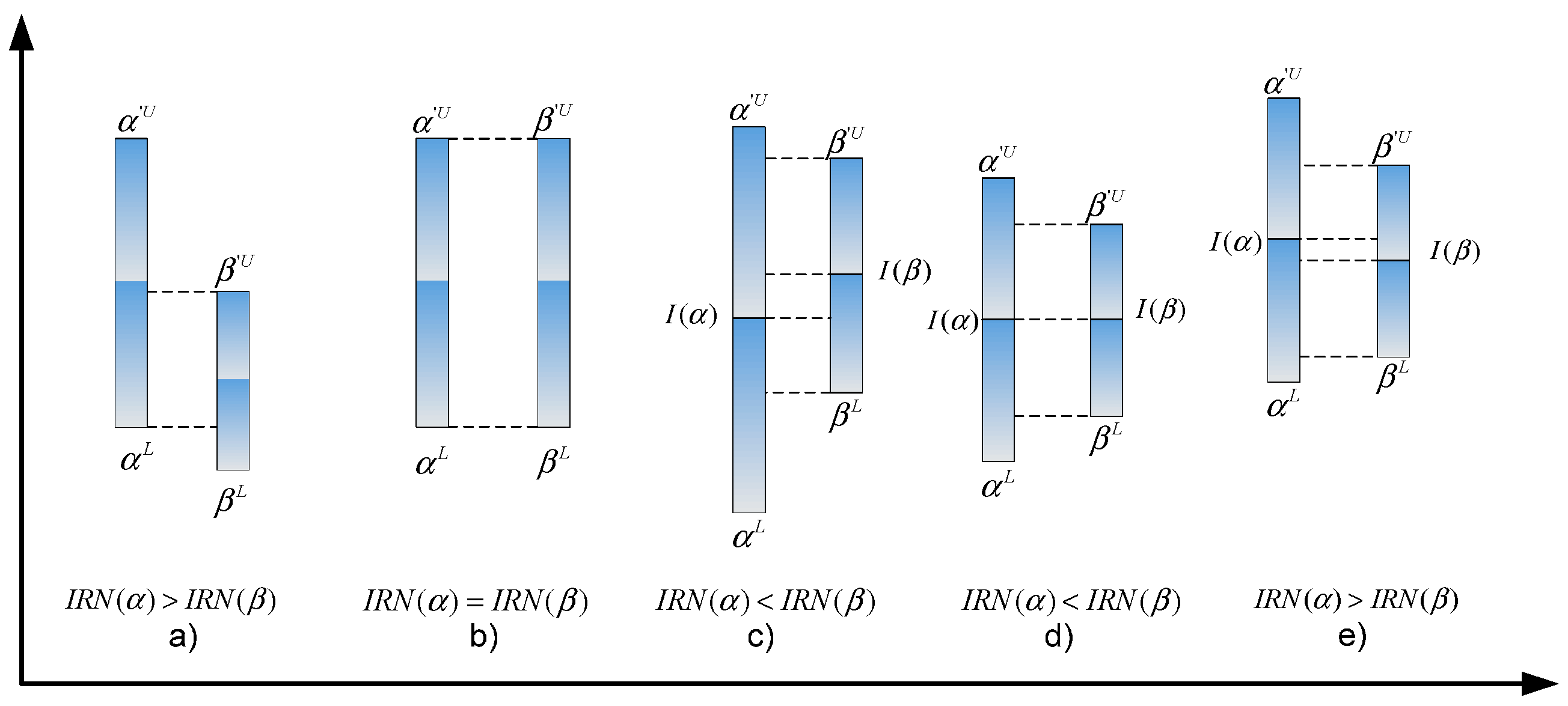
3.2. Interval Rough Numbers
3.3. IR’AHP Mathematical Model
4. Estimation of Flood-Prone Areas in Palilula Municipality
4.1. Criteria Selection
4.2. GIS-MCDA
4.3. Aggregation of Weighted Linear Combination
5. Results-Discussions
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
- (1)
- Adding of IRN“+”
- (2)
- Subtraction of IRN“−”
- (3)
- Multiplication of IRN“×”
- (4)
- Dividing of IRN“/”
- (5)
- Scalar multiplication of IRN where
- (1)
- If the intervals of IRN are not strictly bounded by other intervals, then:
- (2)
- If the intervals of IRN and are strictly bounded by other intervals, then it is necessary to find intersection points and of IRN and . Then, if this is satisfied, and .
References
- Duan, W.; He, B.; Takara, K.; Luo, P.; Nover, D.; Yamashiki, Y.; Huang, W. Anomalous atmospheric events leading to Kyushu’s flash floods, 11–14 July 2012. Nat. Hazards 2014, 73, 1255–1267. [Google Scholar] [CrossRef]
- Aronica, G.T.; Brigandí, G.; Morey, N. Flash floods and debris flow in the city area of Messina, north-east part of Sicily, Italy in October 2009: The case of the Giampilieri catchment. Nat. Hazards Earth Syst. 2012, 12, 1295–1309. [Google Scholar] [CrossRef]
- Forkuo, E.K. Flood Hazard Mapping using Aster Image data with GIS. Int. J. Geomat. Geosci. 2011, 1, 19. [Google Scholar]
- Yahaya, S.; Ahmad, N.; Abdalla, R.F. Multi-criteria analysis for flood vulnerable areas in Hadejia-Jama’are River basin, Nigeria. Eur. J. Sci. Res. 2010, 42, 71–83. [Google Scholar]
- Tsakiris, G. Flood risk assessment: Concepts, modelling, applications. Nat. Hazards Earth Syst. 2014, 14, 1361–1369. [Google Scholar] [CrossRef]
- Chen, J.; Hill, A.A.; Urbano, L.D. A GIS-based model for urban flood inundation. J. Hydrol. 2009, 373, 184–192. [Google Scholar] [CrossRef]
- Huong, H.T.L.; Pathirana, A. Urbanization and climate change impacts on future urban flooding in Can Tho city, Vietnam. Hydrol. Earth Syst. Sci. 2013, 17, 379–394. [Google Scholar] [CrossRef]
- Sowmya, K.; John, C.M.; Shrivasthava, N.K. Urban flood vulnerability zoning of Cochin City, southwest coast of India, using remote sensing and GIS. Nat. Hazards 2015, 75, 1271–1286. [Google Scholar] [CrossRef]
- Fernández, D.S.; Lutz, M.A. Urban flood hazard zoning in Tucumán Province, Argentina, using GIS and multicriteria decision analysis. Eng. Geol. 2010, 111, 90–98. [Google Scholar] [CrossRef]
- Yang, W.; Sun, X.; Deng, W.; Zhang, C.; Liao, Q. Fourier Locally Linear Soft Constrained MACE for facial landmark localization. CAAI Trans. Intell. Technol. 2016, 1, 241–248. [Google Scholar] [CrossRef]
- Brigandì, G.; Bonaccorso, B.; Aronica, G.T.; Gueli, R.; Basile, G. Flood and Landslide Warning based on rainfall thresholds and soil moisture indexes: The SyS Alert model for Sicily. In Proceedings of the 15th Risks Plinius Conference, Giardini Naxos, Italy, 8–11 June2016. [Google Scholar]
- Directive 2007/60/EC of the European Parliament and of the Council of 23 October 2007 on the Assessment and Management of Flood Risks; Official Journal of the European Union L288 on 6.11.2007; European Union: Brussels, Belgium, 2007; pp. 27–34.
- Büchele, B.; Kreibich, H.; Kron, A.; Thieken, A.; Ihringer, J.; Oberle, P.; Merz, B.; Nestmann, F. Flood-risk mapping: Contributions towards an enhanced assessment of extreme events and associated risks. Nat. Hazards Earth Syst. Sci. 2006, 6, 485–503. [Google Scholar] [CrossRef]
- Zerger, A. Examining GIS decision utility for natural hazard risk modelling. Environ. Model. Softw. 2002, 17, 287–294. [Google Scholar] [CrossRef]
- Wang, Y.; Li, Z.; Tang, Z.; Zeng, G. A GIS-based spatial multi-criteria approach for flood risk assessment in the Dongting Lake Region, Hunan, Central China. Water Resour. Manag. 2011, 25, 3465–3484. [Google Scholar] [CrossRef]
- Vahidnia, M.H.; Alesheikh, A.A.; Alimohammadi, A.; Hosseinali, F. A GIS-based neurofuzzy procedure for integrating knowledge and data in landslide susceptibility mapping. Comput. Geosci. 2010, 36, 1101–1114. [Google Scholar] [CrossRef]
- Patel, D.P.; Srivastava, P.K. Flood hazards mitigation analysis using remote sensing and GIS: Correspondence with town planning scheme. Water Resour. Manag. 2013, 27, 2353–2368. [Google Scholar] [CrossRef]
- Jaafari, A.; Najafi, A.; Pourghasemi, H.R.; Rezaeian, J.; Sattarian, A. GIS-based frequency ratio and index of entropy models for landslide susceptibility assessment in the Caspian forest, northern Iran. Int. J. Environ. Sci. Technol. 2014, 11, 909–926. [Google Scholar] [CrossRef]
- Strobl, R.O.; Forte, F.; Lonigro, T. Comparison of the feasibility of three flood-risk extent delineation techniques using Geographic Information System: Case study in Tavolieredelle Puglie, Italy. Flood Risk Manag. 2012, 5, 245–257. [Google Scholar] [CrossRef]
- Gong, M.; Wang, S.; Liu, W.; Yan, J.; Jiao, L. Evolutionary computation in China: A literature survey. CAAI Trans. Intell. Technol. 2016, 1, 334–354. [Google Scholar] [CrossRef]
- Pradhan, B.; Hagemann, U.; Tehrany, M.S.; Prechtel, N. An easy to use ArcMap based texture analysis program for extraction of flooded areas from TerraSAR-X satellite image. Comput. Geosci. 2014, 63, 34–43. [Google Scholar] [CrossRef]
- Bathrellos, G.D.; Gaki-Papanastassiou, K.; Skilodimou, H.D.; Papanastassiou, D.; Chousianitis, K.G. Potential suitability for urban planning and industry development by using natural hazard maps and geological-geomorphological parameters. Environ. Earth 2012, 66, 537–548. [Google Scholar] [CrossRef]
- Bathrellos, G.D.; Skilodimou, H.D.; Chousianitis, K.; Youssef, A.M.; Pradhan, B. Suitability estimation for urban development using multi-hazard assessment map. Sci. Total Environ. 2017, 575, 119–134. [Google Scholar] [CrossRef] [PubMed]
- Tehrany, M.S.; Pradhan, B.; Jebur, M.N. Spatial prediction of flood susceptible areas using rule based decision tree (DT) and a novel ensemble bivariate and multivariate statistical models in GIS. J. Hydrol. 2013, 504, 69–79. [Google Scholar] [CrossRef]
- Hammond, M.J.; Chen, A.S.; Djordjevic, S.; Butler, D.; Mark, O. Urban flood impact assessment: A stateoftheart review. Urban Water J. 2015, 12, 14–29. [Google Scholar] [CrossRef]
- Djordjevic, S.; Vojinovic, Z.; Dawson, R.; Savic, D.A. Uncertainties in flood modelling in urban areas. In Applied Uncertainty Analysis for Flood Risk Management; World Scientific: Singapore, 2014; pp. 297–334. [Google Scholar]
- Malczewski, J. GIS-based multicriteria decision analysis: A survey of the literature. Int. J. Geogr. Inf. Sci. 2006, 20, 703–726. [Google Scholar] [CrossRef]
- Rahmati, O.; Zeinivand, H.; Besharat, M. Flood hazard zoning in Yasooj region, Iran, using GIS and multi-criteria decision analysis, Geomatics. Nat. Hazards Risk 2016, 7, 1000–1017. [Google Scholar] [CrossRef]
- Gigović, L.; Pamučar, D.; Božanić, D.; Ljubojević, S. Application of the GIS-DANP-MABAC multi-criteria model for selecting the location of wind farms: A case study of Vojvodina. Renew. Energy 2017, 103, 501–521. [Google Scholar] [CrossRef]
- Zhong, Q.B.; Chen, F. Trajectory planning for biped robot walking on uneven terrain—Taking stepping as an example. CAAI Trans. Intell. Technol. 2016, 1, 197–209. [Google Scholar] [CrossRef]
- Gigović, L.; Pamučar, D.; Bajić, Z.; Milićević, M. The Combination of Expert Judgment and GIS-MAIRCA Analysis for the Selection of Sites for Ammunition Depots. Sustainability 2016, 8, 372. [Google Scholar] [CrossRef]
- Gigović, L.; Pamučar, D.; Lukić, D.; Marković, S. Application of the GIS—Fuzzy DEMATEL MCDA model for ecotourism development site evaluation: A case study of “Dunavskiključ”, Serbia. Land Use Policy 2016, 58, 348–365. [Google Scholar] [CrossRef]
- Gerl, T.; Bochow, M.; Kreibich, H. Flood Damage Modeling on the Basis of Urban Structure Mapping Using High-Resolution Remote Sensing Data. Water 2014, 6, 2367–2393. [Google Scholar] [CrossRef]
- Chau, V.N.; Holland, J.; Cassells, S.; Tuohy, M. Using GIS to map impacts upon agriculture from extreme floods in Vietnam. Appl. Geogr. 2013, 41, 65–74. [Google Scholar] [CrossRef]
- Kazakis, N.; Kougias, I.; Patsialis, T. Assessment of flood hazard areas at a regional scale using an index-based approach and analytical hierarchy process: Application in Rhodope–Evros region Greece. Sci. Total Environ. 2015, 538, 555–563. [Google Scholar] [CrossRef] [PubMed]
- Papaioannou, G.; Vasiliades, L.; Loukas, A. Multi-criteria analysis framework for potential flood prone areas mapping. Water Resour. Manag. 2015, 29, 399–418. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, W.; Jin, Q. Manifold alignment using discrete surface Ricci flow. CAAI Trans. Intell. Technol. 2016, 1, 285–292. [Google Scholar] [CrossRef]
- Kannan, M.; Saranathan, E.; Anbalagan, R. Comparative analysis in GIS-based landslide hazard zonation—A case study in Bodi—BodimettuGhat section, Theni District, Tamil Nadu, India. Arab. J. Geosci. 2014, 8, 691–699. [Google Scholar] [CrossRef]
- Kritikos, T.; Davies, T.R.H. GIS-based multi-criteria decision analysis for landslide susceptibility mapping at northern Evia, Greece. Z. Dt. Ges. Geowiss. 2011, 162, 421–434. [Google Scholar]
- Meyer, V.; Scheuer, S.; Haase, D. A multicriteria approach for flood risk mapping exemplified at the Mulderiver, Germany. Nat. Hazards 2009, 48, 17–39. [Google Scholar] [CrossRef]
- Tehrany, M.S.; Pradhan, B.; Mansor, S.; Ahmad, N. Flood susceptibility assessment using GIS-based support vector machine model with different kernel types. Catena 2015, 125, 91–101. [Google Scholar] [CrossRef]
- Gong, M.; Li, H.; Jiang, X. A multi-objective optimization framework for ill-posed inverse problems. CAAI Trans. Intell. Technol. 2016, 1, 225–240. [Google Scholar] [CrossRef]
- Pradhan, B. Flood susceptible mapping and risk area delineation using logistic regression, GIS and remote sensing. J. Spat. Hydrol. 2010, 9, 1–18. [Google Scholar]
- Kia, M.B.; Pirasteh, S.; Pradhan, B.; Rodzi, M.A.; Sulaiman, W.N.A.; Moradi, A. An artificial neural network model for flood simulation using GIS: Johor River Basin, Malaysia. Environ. Earth Sci. 2012, 67, 251–264. [Google Scholar] [CrossRef]
- Lohani, A.K.; Goel, N.K.; Bhatia, K.K.S. Improving real time flood forecasting using fuzzy inference system. J. Hydrol. 2014, 509, 25–41. [Google Scholar] [CrossRef]
- Saaty, T.L. The Analytic Hierarchy Process: Planning, Priority Setting, Resource Allocation; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Chandio, I.A.; Matori, A.N.B.; Yusof, K.B.W.; Talpur, M.A.H.; Balogun, A.L.; Lawal, D.U. GIS-based analytic hierarchy process as a multicriteria decision analysis instrument: A review. Arab. J. Geosci. 2013, 6, 3059–3066. [Google Scholar] [CrossRef]
- Siddayao, G.P.; Valdez, S.E.; Fernandez, P.L. Analytic hierarchy process (AHP) in spatial modeling for flood plain risk assessment. Int. J. Mach. Learn. Comput. 2014, 4, 450. [Google Scholar] [CrossRef]
- Stefanidis, S.; Stathis, D. Assessment of flood hazard based on natural and anthropogenic factors using analytic hierarchy process (AHP). Nat. Hazards 2013, 68, 569–585. [Google Scholar] [CrossRef]
- Chakraborty, A.; Joshi, P.K. Mapping disaster vulnerability in India using analytical hierarchy process. Geomat. Nat. Hazards Risk 2014, 7, 308–325. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Pradhan, B.; Gokceoglu, C. Application of fuzzy logic and analytical hierarchy process (AHP) to landslide susceptibility mapping at Haraz watershed, Iran. Nat. Hazards 2012, 63, 965–996. [Google Scholar] [CrossRef]
- Liu, H.; Tang, H.; Xiao, W.; Guo, Z.Y.; Tian, L.; Gao, Y. Sequential Bag-of-Words model for human action classification. CAAI Trans. Intell. Technol. 2016, 1, 125–136. [Google Scholar] [CrossRef]
- Rozos, D.; Bathrellos, G.D.; Skillodimou, H.D. Comparison of the implementation of rock engineering system and analytic hierarchy process methods, upon landslide susceptibility mapping, using GIS: A case study from the Eastern Achaia County of Peloponnesus, Greece. Environ. Earth Sci. 2011, 63, 49–63. [Google Scholar] [CrossRef]
- Ouma, Y.O.; Tateishi, R. Urban Flood Vulnerability and Risk Mapping Using Integrated Multi-Parametric AHP and GIS: Methodological Overview and Case Study Assessment. Water 2014, 6, 1515–1545. [Google Scholar] [CrossRef]
- Bathrellos, G.D.; Karymbalis, E.; Skilodimou, H.D.; Gaki-Papanastassiou, K.; Baltas, E.A. Urban flood hazard assessment in the basin of Athens Metropolitan city, Greece. Environ. Earth Sci. 2016, 75, 319. [Google Scholar] [CrossRef]
- Liu, H.; Wang, C.; Gao, Y. Scene-adaptive hierarchical data association and depth-invariant part-based appearance model for in door multiple objects tracking. CAAI Trans. Intell. Technol. 2016, 1, 210–224. [Google Scholar] [CrossRef]
- Moel, H.D.; Vliet, M.V.; Aerts, J.C.J.H. Evaluating the effect of flood damage-reducing measures: A case study of the unembanked area of Rotterdam, the Netherlands. Reg. Environ. Chang. 2014, 14, 895–908. [Google Scholar]
- Zhu, G.N.; Hu, J.; Qi, J.; Gu, C.C.; Peng, J.H. An integrated AHP and VIKOR for design concept evaluation based on rough number. Adv. Eng. Inform. 2015, 29, 408–418. [Google Scholar] [CrossRef]
- Song, W.; Ming, X.; Wu, Z. An integrated rough number-based approach to design concept evaluation under subjective environments. J. Eng. Des. 2013, 24, 320–341. [Google Scholar] [CrossRef]
- Statistical Office of the Republic of Serbia. 2011 Census of Population, Households and Dwellings in the Republic of Serbia; Book 20, Comparative overview of the number of population in 1948–2011. Data by settlements, Belgrade; Statistical Office of the Republic of Serbia: Krajevo, Serbia, 2014.
- Republic Hydrometeorological Institute of Serbia. Available online: http://www.hidmet.gov.rs/ciril/meteorologija/klimatologija_padav_rezim.php (accessed on 24 January 2017).
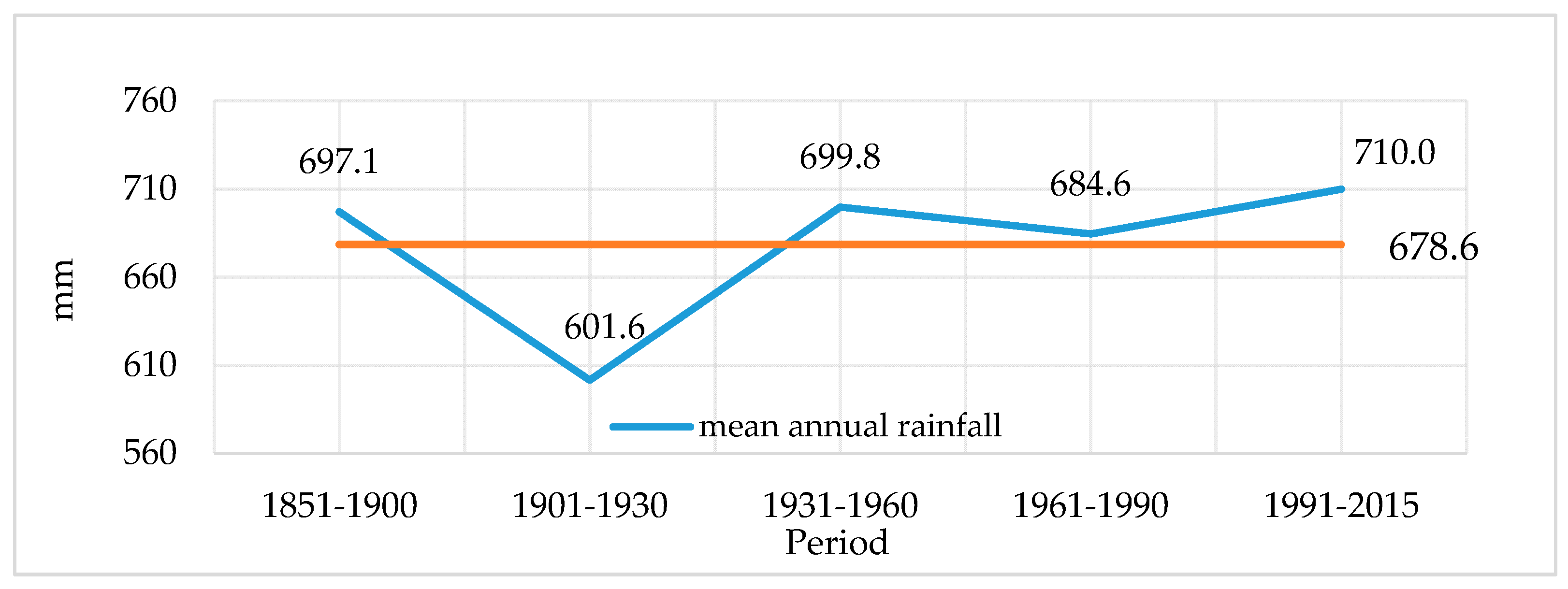
- Đorđević, V.S. Temperature and Precipitation Trends in Belgrade and Indicators of Changing Extremes for Serbia. Geogr. Pannon. 2008, 12, 62–68. [Google Scholar]
- Unkašević, M.; Tošić, I. A statistical analysis of the daily precipitation over Serbia: Trends and indices. Theor. Appl. Climatol. 2011, 106, 69–78. [Google Scholar] [CrossRef]
- Zeshui, X.; Qingli, D. The possibility of interval number sequence method and its application. J. Syst. Eng. 2003, 18, 67–70. [Google Scholar]
- Shuping, W. Interval multi-attribute decision-making of attitude indicator method. Control Decis. Mak. 2009, 24, 35–38. [Google Scholar]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Xu, X.; Law, R.; Chen, W.; Tang, L. Forecasting tourism demand by extracting fuzzy Takagi-Sugeno rules from trained SVMs. CAAI Trans. Intell. Technol. 2016, 1, 30–42. [Google Scholar] [CrossRef]
- Pamučar, D.; Ćirović, G. The selection of transport and handling resources in logistics centres using Multi-Attributive Border Approximation area Comparison (MABAC). Expert Syst. Appl. 2015, 42, 3016–3028. [Google Scholar] [CrossRef]
- Song, W.; Ming, X.; Wu, Z.; Zhu, B. A rough TOPSIS approach for failure mode and effects analysis in uncertain environments. Qual. Reliab. Eng. Int. 2014, 30, 473–486. [Google Scholar] [CrossRef]
- Zhang, Q.; Xie, Q.; Wang, G. A survey on rough set theory and its applications. CAAI Trans. Intell. Technol. 2016, 1, 323–333. [Google Scholar] [CrossRef]
- Arce, M.E.; Saavedra, A.; Míguez, J.L.; Granada, E. The use of grey-based methods in multi-criteria decision analysis for the evaluation of sustainable energy systems: A review. Sustain. Energy Rev. 2015, 47, 924–932. [Google Scholar] [CrossRef]
- Ji, W.; Tang, L.; Li, D.; Yang, W.; Liao, Q. Video-based construction vehicles detection and its application in intelligent monitoring system. CAAI Trans. Intell. Technol. 2016, 1, 162–172. [Google Scholar] [CrossRef]
- Kuang, H.; Kilgour, D.M.; Hipel, K.W. Grey-based PROMETHEE II with application to evaluation of source water protection strategies. Inf. Sci. 2015, 294, 376–389. [Google Scholar] [CrossRef]
- Vahdani, B.; Tavakkoli-Moghaddam, R.; Meysam, M.S. Soft computing based on new interval-valued fuzzy modified multi-criteria decision-making method. Appl. Soft Comput. 2013, 13, 165–172. [Google Scholar] [CrossRef]
- Sizong, G.; Tao, S. Interval-Valued Fuzzy Number and Its Expression Based on Structured Element. Adv. Intell. Soft Comput. 2016, 62, 1417–1425. [Google Scholar]
- Zywica, P.; Stachowiak, A.; Wygralak, M. An algorithmic study of relative cardinalities for interval-valued fuzzy sets. Fuzzy Sets Syst. 2016, 294, 105–124. [Google Scholar] [CrossRef]
- Nayagama, V.L.G.; Jeevaraja, S.; Sivaraman, G. Complete Ranking of Intuitionistic Fuzzy Numbers. Fuzzy Inf. Eng. 2016, 8, 237–254. [Google Scholar]
- Wang, H.; Yang, B.; Chen, W. Unknown constrained mechanisms operation based on dynamic interactive control. CAAI Trans. Intell. Technol. 2016, 1, 259–271. [Google Scholar] [CrossRef]
- Nguyen, H. A new interval-value d knowledge measure for interval-valued intuitionistic fuzzy sets and application in decision making. Expert Syst. Appl. 2016, 56, 143–155. [Google Scholar] [CrossRef]
- Zheng, P.; Xu, X.; Xie, S.Q. A weighted interval rough number based method to determine relative importance ratings of customer requirements in QFD product planning. J. Intell. Manuf. 2016, 1–14. [Google Scholar] [CrossRef]
- Kang, R.; Zhang, T.; Tang, H.; Zhao, W. Adaptive Region Boosting method with biased entropy for path planning in changing environment. CAAI Trans. Intell. Technol. 2016, 1, 179–188. [Google Scholar] [CrossRef]
- Pawlak, Z. Rough sets. Int. J. Comput. Inf. Sci. 1982, 11, 341–356. [Google Scholar] [CrossRef]
- Duntsch, I.; Gediga, G. The rough set engine GROBIAN. In Proceedings of the 15th IMACS World Congress, Berlin, Germany, 24–29 August 1997; Sydow, A., Ed.; Wissenschaft und Technik Verlag: Berlin, Germany, 1997; Volume 4, pp. 613–618. [Google Scholar]
- Khoo, L.P.; Zhai, L.Y. A prototype genetic algorithm enhanced rough set-based rule induction system. Comput. Ind. 2001, 46, 95–106. [Google Scholar] [CrossRef]
- Saaty, T.L.; Vargas, L.G. Models, Methods, Concepts and Applications of the Analytic Hierarchy Process; Springer Science and Business, Media: Berlin, Germany, 2012. [Google Scholar]
- Saaty, T.L. A scaling method for priorities in hierarchical structures. J. Math. Psychol. 1977, 15, 234–281. [Google Scholar] [CrossRef]
- Stieglitz, M.; Rind, D.; Famiglietti, J.; Rosenzweig, C. An efficient approach to modeling the topographic control of surface hydrology for regional and global climate modeling. J. Clim. 1997, 10, 118–137. [Google Scholar] [CrossRef]
- Youssef, A.M.; Pradhan, B.; Hassan, A.M. Flash flood risk estimation along the St. Katherine road, southern Sinai, Egypt using GIS based morphometry and satellite imagery. Environ. Earth Sci. 2011, 62, 611–623. [Google Scholar] [CrossRef]
- Regmi, N.R.; Giardino, J.R.; Vitek, J.D. Modeling susceptibility to landslides using the weight of evidence approach: Western Colorado, USA. Geomorphology 2010, 115, 172–187. [Google Scholar] [CrossRef]
- Glenn, E.; Morino, K.; Nagler, P.; Murray, R.; Pearlstein, S.; Hultine, K. Roles of Saltcedar (Tamarix spp.) and capillary rise in salinizing a non-flooding terrace on a flow-regulated desert river. J. Arid Environ. 2012, 79, 56–65. [Google Scholar] [CrossRef]
- Kourgialas, N.N.; Karatzas, G.P. A flood risk decision making approach for Mediterranean tree crops using GIS; climate change effects and flood-tolerant species. Environ. Sci. Policy 2016, 63, 132–142. [Google Scholar] [CrossRef]
- OpenStreetMap. Available online: https://www.openstreetmap.org/#map=11/44.9123/20.5197 (accessed on 27 January 2017).
- Retaei, J.; Fahim, P.B.M.; Tavasszy, L. Supplier selection in the airline retail industry using a funnel methodology: Conjunctive screening method and fuzzy AHP. Expert Syst. Appl. 2014, 41, 8165–8179. [Google Scholar]
- John, A.; Paraskevadakis, D.; Bury, A.; Yang, Z.; Riahi, R. An integrated fuzzy risk assessment for seaport operations. Saf. Sci. 2014, 68, 180–194. [Google Scholar] [CrossRef]
- BalBeşikçi, E.; Kececi, T.; Arslan, O.; Turan, O. An application of fuzzy-AHP to ship operational energy efficiency measures. Ocean Eng. 2016, 121, 392–402. [Google Scholar] [CrossRef]
- Aşchilean, I.; Badea, G.; Giurca, I.; Naghiu, G.S.; Iloaie, F.G. Choosing the optimal technology to rehabilitate the pipes in water distribution systems using the AHP method. Energy Procedia 2017, 112, 19–26. [Google Scholar] [CrossRef]




| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| RI | 0.00 | 0.00 | 0.52 | 0.89 | 1.11 | 1.25 | 1.35 | 1.40 | 1.45 | 1.49 |
| Criteria | Fuzzy Membership Function | Control Points/Value Points | Final Utility |
|---|---|---|---|
| Elevation (C1) | Linear monotonically decreasing | c = 50 m; d = 300 m | 0–50 m equal to 1, 50–300 m between 1 and 0, more than 300 m equal to 0 |
| Slope (C2) | Linear monotonically decreasing | c = 1°; d = 35° | 0°–1° equal to 1, 1°–30° between 1 and 0, more than 35° equal to 0 |
| Distance from drainage network (C3) | Linear monotonically decreasing | c = 100 m; d = 2000 m | 0–100 m equal to 1, 100–2000 m between 1 and 0, more than 2000 m equal to 0 |
| Distance from water surfaces (C4) | Linear monotonically decreasing | c = 100 m; d = 2000 m | 0–100 m equal to 1, 100–2000 m between 1 and 0, more than 2000 m equal to 0 |
| Water table(C5) | Linear monotonically decreasing | c = 100 cm; d = 5000 cm | 0–100 cm equal to 1, 100–4000 cm between 1 and 0, more than 5000 cm equal to 0 |
| Land cover use (C6) | Discrete categorical data | Water areas equal 1; wetlands equal 0.9; urbanized areas equal 0.8; industrial areas equal 0.7; agriculture equals 0.5; land covered with sparse vegetation equals 0.4; grass and parks equal 0.2; forests equal 0.1 | |
| Expert 1 | ||||||
| C1 | C2 | C3 | C4 | C5 | C6 | |
| C1 | (1.00;1.00) | (0.13;0.14) | (5;7) | (0.2;0.25) | (4;5) | (0.13;0.14) |
| C2 | (8;7) | (1.00;1.00) | (9;9) | (2;3) | (9;9) | (1.00;1.00) |
| C3 | (0.2;0.14) | (0.11;0.11) | (1.00;1.00) | (0.11;0.13) | (0.25;0.33) | (0.11;0.11) |
| C4 | (5;4) | (0.5;0.33) | (9;8) | (1.00;1.00) | (7;8) | (0.25;0.33) |
| C5 | (0.25;0.2) | (0.11;0.11) | (4;3) | (0.14;0.13) | (1.00;1.00) | (0.11;0.13) |
| C6 | (8;7) | (1.00;1.00) | (9;9) | (4;3) | (9;8) | (1.00;1.00) |
| … | ||||||
| Expert 10 | ||||||
| C1 | C2 | C3 | C4 | C5 | C6 | |
| C1 | (1.00;1.00) | (0.14;0.11) | (1.00;1.00) | (0.2;0.25) | (6;7) | (0.14;0.11) |
| C2 | (7;9) | (1.00;1.00) | (7;8) | (3;4) | (9;9) | (1;2) |
| C3 | (1.00;1.00) | (0.14;0.13) | (1.00;1.00) | (0.2;0.25) | (7;8) | (0.14;0.13) |
| C4 | (5;4) | (0.33;0.25) | (5;4) | (1.00;1.00) | (9;8) | (0.33;0.25) |
| C5 | (0.14;0.17) | (0.11;0.11) | (0.14;0.13) | (0.11;0.13) | (1.00;1.00) | (0.11;0.13) |
| C6 | (7;9) | (1;0.5) | (7;8) | (3;4) | (9;8) | (1.00;1.00) |
| Expert | CRe | CRe' | CRe | wke |
|---|---|---|---|---|
| E 1 | 0.022 | 0.088 | 0.055 | 0.102 |
| E 2 | 0.071 | 0.087 | 0.079 | 0.071 |
| E 3 | 0.035 | 0.064 | 0.049 | 0.114 |
| E 4 | 0.081 | 0.067 | 0.074 | 0.076 |
| E 5 | 0.022 | 0.051 | 0.036 | 0.155 |
| E 6 | 0.083 | 0.067 | 0.075 | 0.075 |
| E 7 | 0.037 | 0.071 | 0.054 | 0.105 |
| E 8 | 0.031 | 0.065 | 0.048 | 0.118 |
| E 9 | 0.044 | 0.057 | 0.050 | 0.112 |
| E 10 | 0.092 | 0.067 | 0.079 | 0.071 |
| C1 | C2 | C3 | ... | C6 | |
|---|---|---|---|---|---|
| C1 | ([1.00,1.00],[1.00,1.00]) | ([0.59,4.41],[0.50,3.69]) | ([0.26,1.08],[0.26,1.34]) | ... | ([0.29,1.84],[0.29,2.43]) |
| C2 | ([0.27,1.89],[0.28,2.27]) | ([1.00,1.00],[1.00,1.00]) | ([4.79,6.87],[4.74,6.72]) | ([0.28,2.48],[0.36,2.77]) | |
| C3 | ([0.12,0.16],[0.13,0.19]) | ([0.31,2.06],[0.27,2.29]) | ([1.00,1.00],[1.00,1.00]) | ([1.23,6.30],[1.37,6.47]) | |
| C4 | ([4.79,6.87],[4.74,6.72]) | ([3.16,7.00],[3.82,7.13]) | ([6.36,8.31],[5.51,7.62]) | ([0.16,0.43],[0.15,0.32]) | |
| C5 | ([0.16,0.43],[0.15,0.32]) | ([0.72,5.73],[0.71,6.00]) | ([1.57,4.45],[1.42,4.86]) | ([0.41,4.01],[0.37,4.01]) | |
| C6 | ([0.25,1.63],[0.22,1.85]) | ([0.68,6.23],[0.65,5.88]) | ([1.04,5.02],[0.86,5.31]) | ([0.68,6.23],[0.65,5.88]) | |
| C7 | ([0.61,1.76],[0.45,1.41]) | ([1.67,6.96],[1.31,6.45]) | ([4.94,8.18],[4.36,7.69]) | ([1.00,1.00],[1.00,1.00]) |
| C1 | C2 | C3 | … | C6 | |
|---|---|---|---|---|---|
| C1 | ([0.05,0.24],[0.04,0.26]) | ([0.02,0.09],[0.02,0.09]) | ([0.02,0.53],[0.02,0.45]) | … | ([0.01,0.51],[0.02,0.51]) |
| C2 | ([0.06,0.3],[0.05,0.36]) | ([0.04,0.74],[0.04,0.94]) | ([0.02,0.69],[0.02,0.74]) | ([0.03,0.58],[0.04,0.73]) | |
| C3 | ([0.03,0.05],[0.03,0.06]) | ([0.02,0.06],[0.02,0.08]) | ([0.01,0.25],[0.01,0.28]) | ([0.01,0.11],[0.01,0.18]) | |
| C4 | ([0.16,0.4],[0.14,0.43]) | ([0.14,0.39],[0.14,0.42]) | ([0.09,0.85],[0.12,0.88]) | ([0.05,1.22],[0.06,1.27]) | |
| C5 | ([0.04,0.22],[0.04,0.27]) | ([0.02,0.17],[0.02,0.13]) | ([0.03,0.12],[0.03,0.12]) | ([0.02,0.78],[0.02,0.79]) | |
| C6 | ([0.06,0.31],[0.05,0.37]) | ([0.03,0.64],[0.03,0.77]) | ([0.02,0.75],[0.02,0.72]) | ([0.04,0.19],[0.04,0.2]) | |
| C7 | ([0.13,0.4],[0.11,0.43]) | ([0.08,0.69],[0.06,0.59]) | ([0.05,0.84],[0.04,0.79]) | ([0.05,1.08],[0.04,1.07]) |
| Criteria | Interval Rough Approach | Fuzzy Approach | Crisp Approach | |||
|---|---|---|---|---|---|---|
| IRN(wj) | Rank | Fuzzy (wj) | Rank | Crisp (wj) | Rank | |
| C1 | ([0.02,0.27],[0.02,0.3]) | 5 | (0.08,0.12,0.16) | 5 | 0.122 | 5 |
| C2 | ([0.03,0.43],[0.04,0.5]) | 2 | (0.11,0.19,0.21) | 2 | 0.203 | 2 |
| C4 | ([0.09,0.68],[0.09,0.7]) | 6 | (0.04,0.08,0.07) | 6 | 0.259 | 6 |
| C5 | ([0.01,0.1],[0.01,0.12]) | 1 | (0.25,0.32,0.55) | 1 | 0.120 | 1 |
| C6 | ([0.02,0.34],[0.02,0.35]) | 4 | (0.07,0.14,0.15) | 4 | 0.137 | 4 |
| C7 | ([0.03,0.42],[0.03,0.43]) | 3 | (0.12,0.15,0.19) | 3 | 0.159 | 3 |
| Definition | Crisp Scale | Fuzzy Scale |
|---|---|---|
| Equal importance | 1 | (1,1,1) |
| Somewhat more important | 3 | (2,3,4) |
| Much more important | 5 | (4,5,6) |
| Very much more important | 7 | (6,7,8) |
| Absolutely more important | 9 | (8,9,9) |
| Intermediate values | 2, 4, 6, 8 | (x − 1, x, x+1) |
| Flood Hazard Index | Scenario 1 IR’AHP | Scenario 2 F’AHP | Scenario 3 Crisp AHP | ||||
|---|---|---|---|---|---|---|---|
| (km2) | % | (km2) | % | (km2) | % | ||
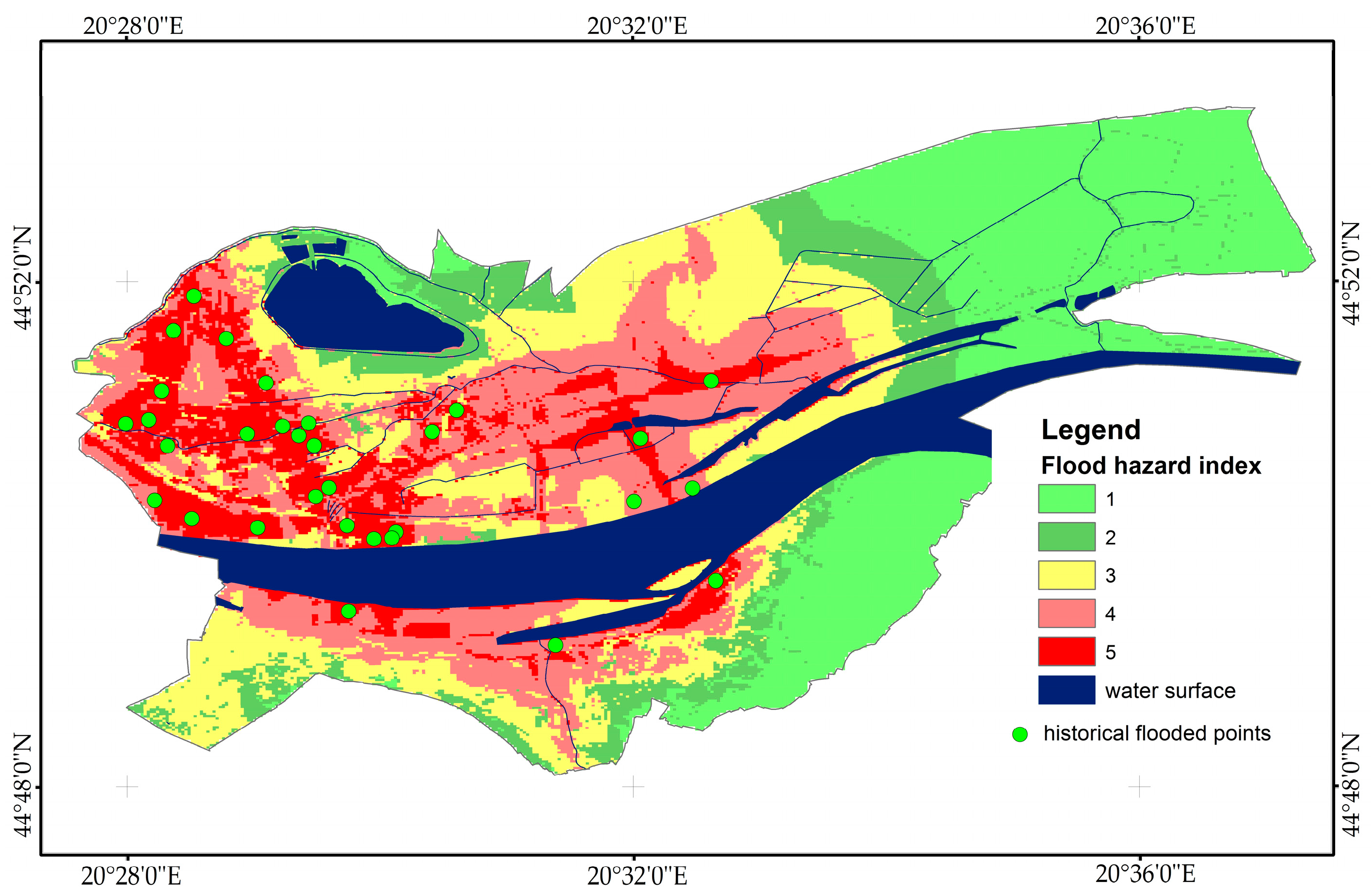
| FHI 5 | Very high | 12.9 | 18.5 | 8.8 | 12.6 | 7.8 | 11.2 |
| FHI 4 | High | 16.2 | 23.2 | 20.7 | 29.6 | 24.9 | 35.6 |
| FHI 3 | Moderate | 15.1 | 21.6 | 17.2 | 24.6 | 15.3 | 21.9 |
| FHI 2 | Low | 8.5 | 12.2 | 14.7 | 21.0 | 12.2 | 17.5 |
| FHI 1 | Very low | 17.2 | 24.6 | 8.5 | 12.2 | 9.7 | 13.9 |
| Scenarios | Historically-Flooded Points | Flood Hazard Index (FHI) | ||||
|---|---|---|---|---|---|---|
| 5 | 4 | 3 | 2 | 1 | ||
| 1 IR’AHP | 31 | 27 (87.1%) | 4 (12.9%) | 0 | 0 | 0 |
| 2 F’AHP | 31 | 21 (67.7%) | 9 (29.0%) | 1(3.2%) | 0 | 0 |
| 3 AHP (crisp) | 31 | 17 (54.8%) | 10 (32.3%) | 4 (12.9%) | 0 | 0 |
| Land Cover/Infrastructure | Unit | Flood Hazard Index | ||||
|---|---|---|---|---|---|---|
| 5 | 4 | 3 | 2 | 1 | ||
| Urban areas | km2 | 7.85 | 6.42 | 3.90 | 12.84 | 0.57 |
| Grassland | km2 | 0.12 | 0.32 | 0.53 | 0.60 | 0.96 |
| Forests | km2 | 0.24 | 0.63 | 1.69 | 0.81 | 2.38 |
| Scrub | km2 | 0.17 | 0.29 | 0.31 | 0.18 | 0.12 |
| Arable land | km2 | 2.06 | 7.85 | 6.42 | 3.90 | 12.84 |
| Industrial areas | km2 | 0.34 | 0.99 | 0.45 | 0 | 0 |
| Parks | km2 | 0.009 | 0.45 | 0.086 | 0.107 | 0.003 |
| Marshes | km2 | 0.92 | 0.22 | 0.02 | 0 | 0 |
| Schools and universities | No. | 11 | 17 | 9 | 6 | 0 |
| Kindergartens | No. | 9 | 8 | 5 | 2 | 0 |
| Residential buildings | No. | 540 | 407 | 449 | 114 | 25 |
| Industrial buildings | No. | 11 | 13 | 6 | 0 | 0 |
| Medical facilities | No. | 4 | 1 | 1 | 0 | 0 |
| Roads | km | 36.77 | 38.54 | 32.30 | 16.94 | 20.80 |
| Railroads | km | 0.64 | 2.26 | 3.44 | 0.74 | 0.83 |
| Population | thousands | 41,565 | 31,108 | 18,568 | 11,540 | 7856 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gigović, L.; Pamučar, D.; Bajić, Z.; Drobnjak, S. Application of GIS-Interval Rough AHP Methodology for Flood Hazard Mapping in Urban Areas. Water 2017, 9, 360. https://doi.org/10.3390/w9060360
Gigović L, Pamučar D, Bajić Z, Drobnjak S. Application of GIS-Interval Rough AHP Methodology for Flood Hazard Mapping in Urban Areas. Water. 2017; 9(6):360. https://doi.org/10.3390/w9060360
Chicago/Turabian StyleGigović, Ljubomir, Dragan Pamučar, Zoran Bajić, and Siniša Drobnjak. 2017. "Application of GIS-Interval Rough AHP Methodology for Flood Hazard Mapping in Urban Areas" Water 9, no. 6: 360. https://doi.org/10.3390/w9060360
APA StyleGigović, L., Pamučar, D., Bajić, Z., & Drobnjak, S. (2017). Application of GIS-Interval Rough AHP Methodology for Flood Hazard Mapping in Urban Areas. Water, 9(6), 360. https://doi.org/10.3390/w9060360








