A Study on Coastal Flooding and Risk Assessment under Climate Change in the Mid-Western Coast of Taiwan
Abstract
:1. Introduction
2. Methodology
2.1. Coastal Risk Assessment
2.2. Integrated Coastal Watershed Models
3. Application Area, Future Scenarios, and Results
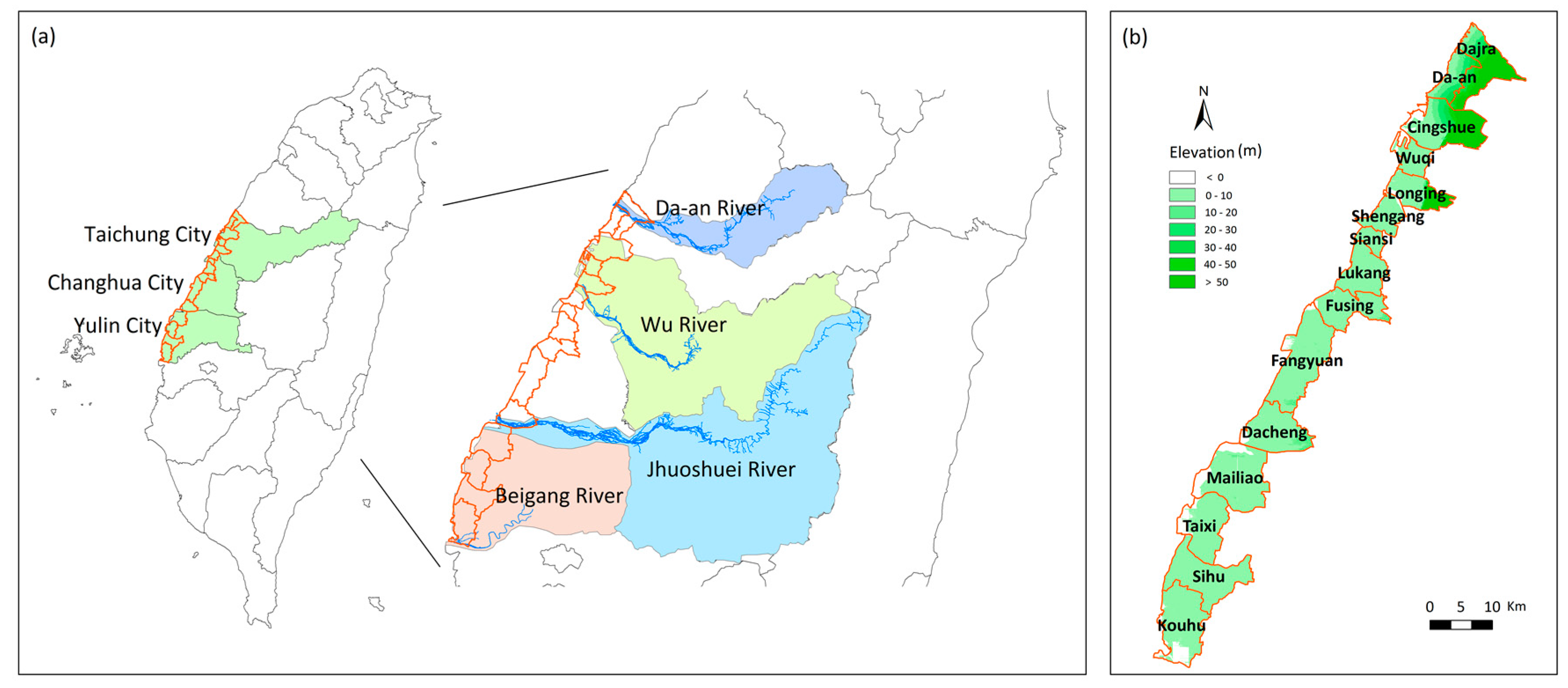
3.1. Application Area
3.2. Coastal Assessment under Climate Changes
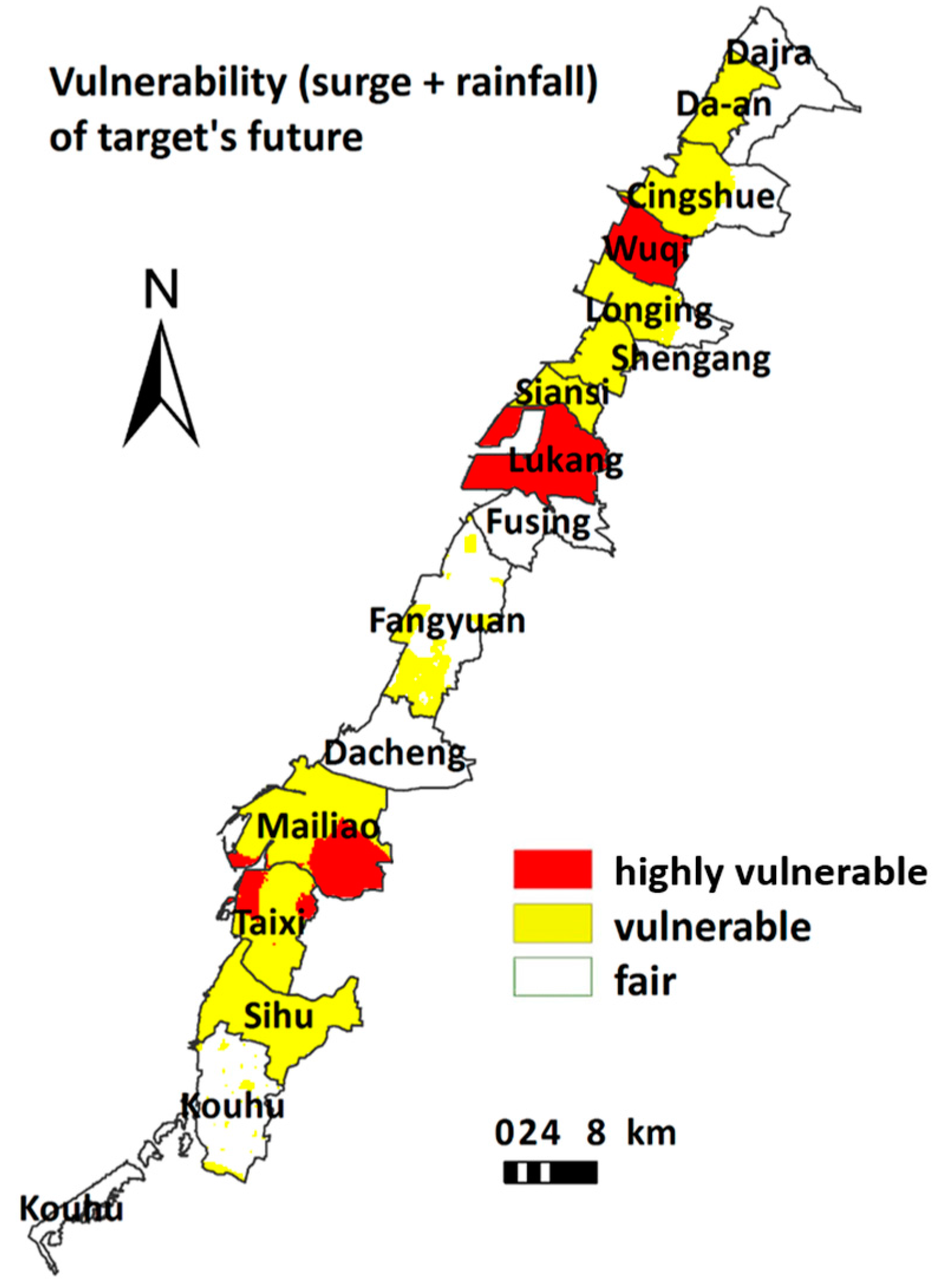
3.3. Discussions of Risk Map
4. Conclusions
- An approach using integrated coastal watershed models (POM-WWM-WASH123D) combined with a risk assessment method (AHP) is proposed to develop a methodology to investigate the impact resulting from coastal disasters under climate change.
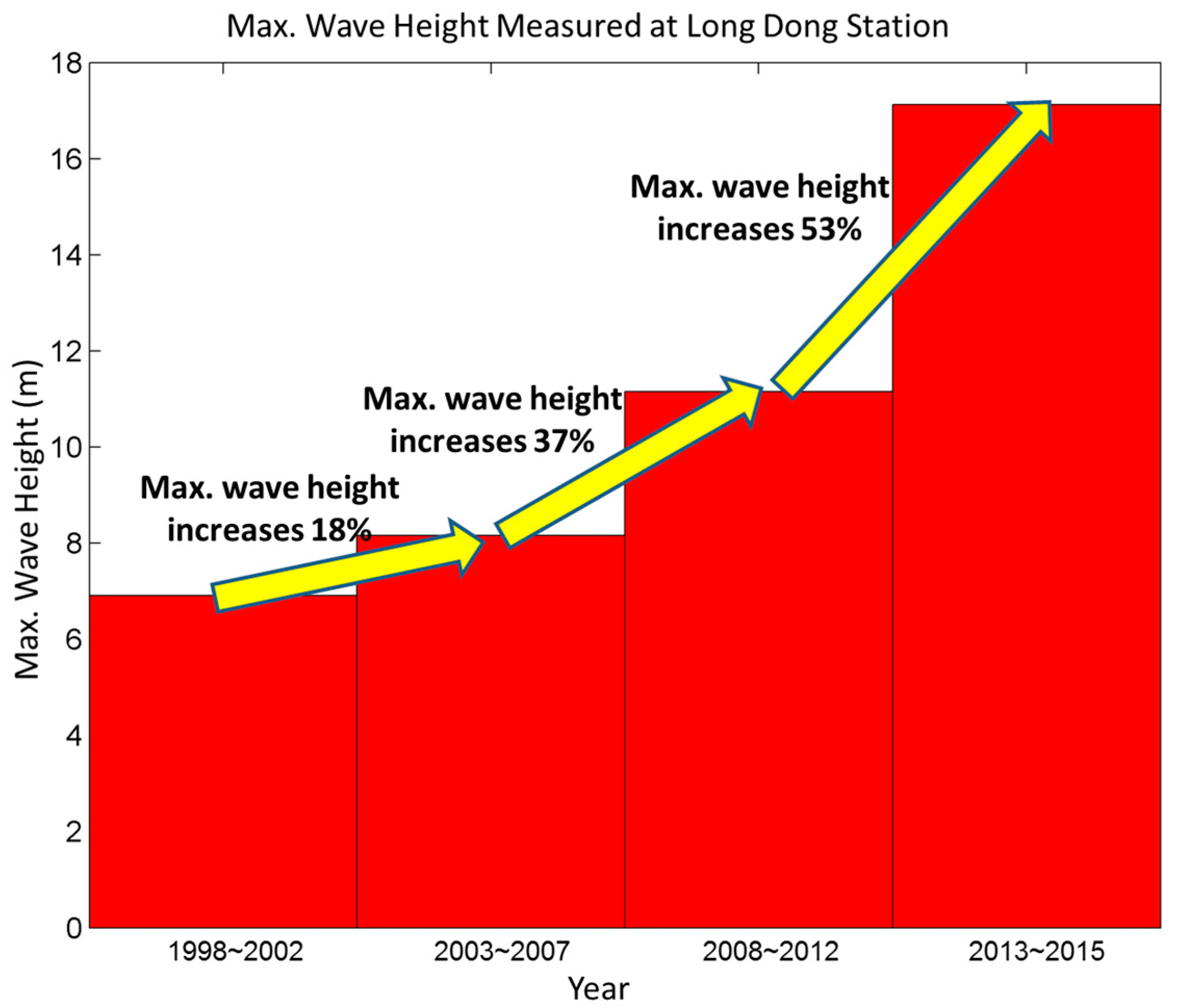
- Simulation results indicate that the sea level at the mid-western coast of Taiwan will rise on average by 5.8 cm from 2020 to 2039, equivalent to a rising velocity of 2.8 mm/year. The maximum typhoon-induced wave height will increase by about 35.98% and the maximum typhoon surge deviation will increase by 29.15% as compared to the status quo situation.
- To assess coastal disaster risks under climate change using the AHP weighting mode, the Wuqi, Lukang, Mailiao, and Taixi counties reach the high-risk level. Results also showed that climate change has a significant impact on the study area.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Intergovernmental Panel on Climate Change. Fifth Assessment Report (AR5). Available online: https://www.ipcc.ch/report/ar5/ (accessed on 20 May 2016).
- IPCC. Summary for Policymakers. In Climate Change 2014, Mitigation of Climate Change, Contribution of Working Group III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Edenhofer, O., Pichs-Madruga, R., Sokona, Y., Farahani, E., Kadner, S., Seyboth, K., Adler, A., Baum, I., Brunner, S., Eickemeier, P., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2014. [Google Scholar]
- Martínez-Graña, A.M.; Boski, T.; Goy, J.L.; Zazo, C.; Dabrio, C.J. Coastal-flood risk management in central Algarve: Vulnerability and flood risk indices (South Portugal). Ecol. Indic. 2016, 71, 302–316. [Google Scholar] [CrossRef]
- Hallegatte, S.; Green, C.; Nicholls, R.J.; Corfee-Morlot, J. Future flood losses in major coastal cities. Nat. Clim. Chang. 2013, 3, 802–806. [Google Scholar] [CrossRef]
- Déqué, M.; Rowell, D.P.; Lüthi, D.; Giorgi, F.; Christensen, J.H.; Rockel, B.; Jacob, D.; Kjellström, E.; de Castro, M.; van den Hurk, B. An intercomparison of regional climate simulations for Europe: Assessing uncertainties in model projections. Clim. Chang. 2007, 81, 53–70. [Google Scholar] [CrossRef]
- Menzel, L.; Thieken, A.H.; Schwandt, D.; Bürger, G. Impact of climate change on the Regional hydrology—Scenario-based modelling studies in the German Rhine catchment. Nat. Hazards 2006, 38, 45–61. [Google Scholar] [CrossRef]
- Minville, M.; Brissette, F.; Leconte, R. Uncertainty of the impact of climate change on the hydrology of a Nordic watershed. J. Hydrol. 2008, 358, 70–83. [Google Scholar] [CrossRef]
- Prudhomme, C.; Davies, H. Assessing uncertainties in climate change impact analyses on the river flow regimes in the UK. Part 2: Future climate. Clim. Chang. 2008, 93, 177–195. [Google Scholar] [CrossRef]
- Akhtar, M.; Ahmad, N.; Booij, M.J. The impact of climate change on water resources of Hindukush–Karakorum-Himalaya region under different glacier coverage scenarios. J. Hydrol. 2008, 355, 148–163. [Google Scholar] [CrossRef]
- Arnell, N.W.; Gosling, S.N. The impacts of climate change on river flow regimes at the global scale. J. Hydrol. 2013, 486, 351–364. [Google Scholar] [CrossRef]
- Guo, S.L.; Wang, J.X.; Xiong, L.H.; Ying, A.W.; Li, D.F. A macro-scale and semi-distributed monthly water balance model to predict climate change impacts in China. J. Hydrol. 2002, 268, 1–15. [Google Scholar] [CrossRef]
- Kling, H.; Stanzel, P.; Preishuber, M. Impact modelling of water resources development and climate scenarios on Zambezi River discharge. J. Hydrol. Reg. Stud. 2014, 1, 17–43. [Google Scholar] [CrossRef]
- Easterling, D.R.; Meehl, G.A.; Parmesan, C.; Changnon, S.A.; Karl, T.R.; Mearns, L.O. Climate extremes: Observations, modeling, and impacts. Science 2000, 289, 2068–2074. [Google Scholar] [CrossRef] [PubMed]
- Hay, L.E.; Markstrom, S.L.; Ward-Garrison, C. Watershed-scale response to climate change through the twenty-first century for selected basins across the United States. Earth Interact. 2011, 15, 1–37. [Google Scholar] [CrossRef]
- Hovenga, P.A.; Wang, D.; Medeiros, S.C.; Hagen, S.C.; Alizad, K.A. The response of runoff and sediment loading in the Apalachicola River, Florida to climate and land use land cover change. Earths Future 2016, 4, 124–142. [Google Scholar] [CrossRef]
- Acreman, M.; Sinclair, C. Classification of drainage basins according to their physical characteristics; and application for flood frequency analysis in Scotland. J. Hydrol. 1986, 84, 365–380. [Google Scholar] [CrossRef]
- Beven, K.; Wood, E.; Sivapalan, M. On hydrological heterogeneity—Catchment morphology and catchment response. J. Hydrol. 1988, 100, 353–375. [Google Scholar] [CrossRef]
- Veijalainen, H.; Lotsari, E.; Alho, P.; Vehviläinen, B.; Käyhkö, J. National scale assessment ofclimatechangeimpacts onfloodingin Finland. J. Hydrol. 2010, 391, 333–350. [Google Scholar] [CrossRef]
- Yan, D.; Werners, S.E.; Ludwig, F.; Huang, H.Q. Hydrological response to climate change: The Pearl River, China under different RCP scenarios. J. Hydrol. 2015, 4, 228–245. [Google Scholar] [CrossRef]
- Cayan, D.R.; Bromirski, P.D.; Hayhoe, K.; Tyree, M.; Dettinger, M.D.; Flick, R.E. Climate change projections of sea level extremes along the California coast. Clim. Chang. 2008, 87, S57–S73. [Google Scholar] [CrossRef]
- Mastrandrea, M.D.; Luers, A.L. Climate change in California: Scenarios and approaches for adaptation. Clim. Chang. 2012, 111, 5–16. [Google Scholar] [CrossRef]
- Rahmstorf, S. A Semi-Empirical Approach to Projecting Future Sea-Level Rise. Science 2007, 315, 368–370. [Google Scholar] [CrossRef] [PubMed]
- Scavia, D.; Field, J.C.; Boesch, D.F.; Buddemeier, R.W.; Burkett, V.; Cayan, D.R.; Fogarty, M.; Harwell, M.A.; Howarth, R.W.; Mason, C.; et al. Climate Change Impacts on US Coastal and Marine Ecosystems. Estuaries 2002, 25, 149–164. [Google Scholar] [CrossRef]
- Bilskie, M.V.; Hagen, S.C.; Medeiros, S.C.; Passeri, D.L. Dynamics of sea level rise and coastal flooding on a changing landscape. Geophys. Res. Lett. 2014, 41, 1–8. [Google Scholar] [CrossRef]
- Bilskie, M.V.; Hagen, S.C.; Alizad, K.; Medeiros, S.C.; Passeri, D.L.; Needham, H.; Cox, A. Dynamic simulation of numerical analysis of hurricane storm surge under sea level rise along the northern Gulf of Mexico. Earths Future 2016, 4, 177–193. [Google Scholar] [CrossRef]
- Passeri, D.L.; Hagen, S.C.; Medeiros, S.C.; Bilskie, M.V.; Alizad, K.; Wang, D. The dynamic effects of sea level rise on low-gradient coastal landscapes: A review. Earths Future 2015, 3, 159–181. [Google Scholar] [CrossRef]
- Passeri, D.L.; Hagen, S.C.; Plant, N.G.; Bilskie, M.V.; Medeiros, S.C.; Alizad, K. Tidal hydrodynamics under future sea level rise and coastal morphology in the Northern Gulf of Mexico. Earths Future 2016, 4, 159–176. [Google Scholar] [CrossRef]
- Nicholls, R.J. Analysis of global impacts of sea-level rise: A case study of flooding. Phys. Chem. Earth 2002, 27, 1455–1466. [Google Scholar] [CrossRef]
- Chen, X.; Alizad, K.; Wang, D.; Hagen, S.C. Climate change impact on runoff and sediment loads to the Apalachicola River at seasonal and event scales. J. Coast. Res. 2014, 68, 35–42. [Google Scholar] [CrossRef]
- Beckley, B.D.; Lemoine, F.G.; Luthcke, S.B.; Ray, R.D.; Zelensky, N.P. A reassessment of global and regional mean sea level trends from TOPEX and Jason-1 altimetry based on revised reference frame and orbits. Geophys. Res. Lett. 2007, 34, L14608. [Google Scholar] [CrossRef]
- Wu, L.C.; Kao, C.C.; Hsu, T.W.; Jao, K.C.; Wang, Y.F. Ensemble empirical mode decomposition on storm surge separation from sea level data. Coast. Eng. J. 2011, 53, 223–243. [Google Scholar] [CrossRef]
- Hsu, T.W.; Shih, D.S.; Chen, W.J. Destructive Flooding Induced by Broken Embankments along Linbian Creek, Taiwan, during Typhoon Morakot. J. Hydrol. Eng. ASCE 2015, 20, 05014025. [Google Scholar] [CrossRef]
- Stefanidis, S.; Stathis, D. Assessment of flood hazard based on natural and anthropogenic factors using analytic hierarchy process (AHP). Nat. Hazards 2013, 68, 569–585. [Google Scholar] [CrossRef]
- Tehrany, M.S.; Pradhan, B.; Jebur, M.N. Flood susceptibility mapping using a novel ensemble weights-of-evidence and support vector machine models in GIS. J. Hydrol. 2014, 512, 332–343. [Google Scholar] [CrossRef]
- Small, C.; Nicholls, R.J. A global analysis of human settlement in coastal zones. J. Coast. Res. 2003, 19, 584–599. [Google Scholar]
- Small, C.; Gornitz, V.; Cohen, J.E. Coastal hazards and the global distribution of human population. Environ. Geosci. 2000, 7, 3–12. [Google Scholar] [CrossRef]
- Nicholls, R.J. Coastal flooding and wetland loss in the 21st century: Changes under the SRES climate and socio-economic scenarios. Glob. Environ. Chang. 2004, 14, 69–86. [Google Scholar] [CrossRef]
- Veleda, V.; Martínez-Graña, A.M.; Santos-Francés, F.; Sánchez-San Roman, J.; Criado, M. Analysis of the Hazard, Vulnerability, and Exposure to the Risk of Flooding (Alba de Yeltes, Salamanca, Spain). Appl. Sci. 2017, 7, 157. [Google Scholar] [CrossRef]
- Nicholls, R.J.; Hoozemans, F.M.J.; Marchand, M. Increasing flood risk and wetland losses due to global sea-level rise: Regional and global analyses. Glob. Environ. Chang. 1999, 9, S69–S87. [Google Scholar] [CrossRef]
- United Nations Disaster Relief Co-ordinator (UNDRO). Natural Disasters and Vulnerability Analysis: Report of Expert Group Meeting (9–12 July 1979); United Nations Disaster Relief Co-ordinator: Geneva, Switzerland, 1980. [Google Scholar]
- Saaty, T.L. The Analytic Hierarchy Process; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Lin, S.C.; Tang, T.Y. Factor Assessment of the Environmental Impact for Tainan Technology Industry Area in Taiwan. In Ecosystems and Sustainable Development; Tiezzi, E., Brebbia, C.A., Uso, J.L., Eds.; WIT Press: Boston, MA, USA, 2003; Volume I, pp. 219–229. [Google Scholar]
- Lan, Y.J.; Hsu, T.W.; Lin, Y.C.; Huang, C.J. An Adaptation Due to Climate Change in Southwest Coast of Taiwan. Coast. Manag. 2013, 41, 172–189. [Google Scholar] [CrossRef]
- IPPC-CZM. The Seven Steps to the Vulnerability Assessment of Coastal Areas to Sea-Level Rise—Guideline for Case Studies; IPCC: Hague, The Netherlands, 1991; p. 46. [Google Scholar]
- Doukakis, E. Coastal vulnerability and risk parameters. Eur. Water 2005, 11, 3–7. [Google Scholar]
- United Nations Environment Programme Report (UNEP). Assessing Coastal Vulnerability: Developing a Global Index for Measuring Risk. Available online: http://www.unep.org/ (accessed on 20 May 2016).
- Hong, H.; Cui, S.; Zhang, L. A coastal vulnerability index and its application in Xiamen, China. Aquat. Ecosyst. Health Manag. 2006, 9, 333–337. [Google Scholar] [CrossRef]
- Kavi Kumar, K.S.; Tholkappian, S. Relative vulnerability of Indian coastal districts to sea-level rise and climate extremes. Int. Rev. Environ. Strateg. 2006, 6, 3–22. [Google Scholar]
- Holland, G.J. An analytical model of the wind and pressure profiles in hurricanes. Mon. Weather Rev. 1980, 108, 1212–1218. [Google Scholar] [CrossRef]
- Hsu, T.W.; Ou, S.H.; Liau, J.M. Hindcasting nearshore wind waves using a FEM code for SWAN. Coast. Eng. 2005, 52, 177–195. [Google Scholar] [CrossRef]
- Shih, D.S.; Hsu, T.W.; Chang, K.C.; Juan, H.L. Implementing Coastal Inundation Data with an Integrated Wind Wave Model and Hydrological Watershed Simulations. Terr. Atmos. Ocean. Sci. 2012, 23, 513–525. [Google Scholar] [CrossRef]
- Blumberg, A.F.; Mellor, G.L. A description of a three-dimensional coastal ocean circulation model. In Three-Dimensional Coastal Ocean Models; Heaps, N., Ed.; American Geophysical Union: Washington, DC, USA, 1987; Volume 4, p. 208. [Google Scholar]
- Mellor, G.L. Users Guide for a Three-Dimensional, Primitive Equation, Numerical Ocean Model; Princeton University: Princeton, NJ, USA, 1998. [Google Scholar]
- Hsu, T.W.; Liau, K.M.; Lin, J.G.; Zheng, J.; Ou, S.H. Sequential assimilation in the wind wave model for simulations of typhoon events around Taiwan Island. Ocean Eng. 2011, 38, 456–467. [Google Scholar] [CrossRef]
- Yeh, G.T.; Huang, G.B.; Zhang, F.; Cheng, H.P.; Lin, H.C. WASH123D: A Numerical Model of Flow, Thermal Transport, and Salinity, Sediment, and Water Quality Transport in WAterSHed Systems of 1-D Stream-River Network, 2-D Overland Regime, and 3-D Subsurface Media. In Technical Report Submitted to EPA; Department of Civil and Environmental Engineering, University of Central Florida: Orlando, FL, USA, 2006. [Google Scholar]
- Yeh, G.T.; Shih, D.S.; Cheng, J.R.C. An Integrated Media, Integrated Processes Watershed Model. Comput. Fluids 2011, 45, 2–13. [Google Scholar] [CrossRef]
- Taiwan Climate Change Projection and Information Platform Project (TCCIP). Available online: http://tccip.ncdr.nat.gov.tw/v2/index_en.aspx (accessed on 24 June 2015).
- Harbor and Marine Technology Center, Ministry of Transportation and Communications. Long-Term Marine Meteorological Observations of Taiwan’s Major Harbor Sea Areas and Application of the Data Characteristics ¼; Harbor and Marine Technology Center, Ministry of Transportation and Communications: Taipei, Taiwan, 2010. (In Chinese) [Google Scholar]
- National Center for Atmospheric Research Staff (Ed.) The Climate Data Guide: AVISO: Satellite derived Sea Surface Height above Geoid. Available online: https://climatedataguide.ucar.edu/climate-data/aviso-satellite-derived-sea-surface-height-above-geoid (accessed on 21 March 2016).

| Aspect | Construction | Index | |||
|---|---|---|---|---|---|
| Aspect | Weight | Construction | Weight | Index | Weight |
| Hazzard potential | 0.404 | Hazard factors | 1.000 | The range of flooding overflow | 0.384 |
| The depth of flooding overflow | 0.271 | ||||
| The range of surging tide overflow | 0.159 | ||||
| The depth of surging tide overflow | 0.186 | ||||
| Vulnerability | 0.596 | Artificial facilities | 0.327 | Seawall relative length | 0.257 |
| Seawall relative height | 0.499 | ||||
| Tidal gate relative comparison | 0.244 | ||||
| Environmental geography | 0.548 | Elevation | 0.139 | ||
| Slope | 0.098 | ||||
| Tide range | 0.086 | ||||
| Coastal erosion rate | 0.226 | ||||
| Land subsidence rate | 0.359 | ||||
| Land use | 0.093 | ||||
| Social economy | 0.125 | Population density | 0.415 | ||
| Education background | 0.223 | ||||
| Dependency ratio | 0.166 | ||||
| Enterprise return | 0.196 | ||||
| Return Period of Typhoon Wind Waves (in Years) | Status Quo (2014) | Target Year (2020–2039) | |||||
|---|---|---|---|---|---|---|---|
| Coastal Areas (Longitude, Latitude) | 50-Year | 100-Year | 200-Year | 50-Year | 100-Year | 200-Year | |
| Da-an River (120.5604°, 24.4193°) | 6.99 | 6.90 | 7.10 | 8.94 | 9.43 | 9.48 | |
| Taichung (Taichung Harbor) (120.4719°, 24.29778°) | 6.82 | 7.02 | 7.20 | 9.16 | 9.65 | 9.67 | |
| Wu River (120.3859°, 24.2151°) | 6.79 | 7.00 | 7.19 | 9.68 | 10.10 | 10.34 | |
| Changhua (south side of Chabnghua Coastal Industrial Park) (120.2761°, 24.06278°) | 7.09 | 7.34 | 7.57 | 9.45 | 10.01 | 10.09 | |
| Jhuoshuei River (120.1514°, 23.8818°) | 7.40 | 7.91 | 8.42 | 10.38 | 11.35 | 12.08 | |
| Yulin (Shantiaolun) (120.0594°, 23.70583°) | 6.79 | 6.99 | 7.17 | 8.52 | 8.82 | 9.55 | |
| Beigang River (119.9902°, 23.5403°) | 7.20 | 7.47 | 7.80 | 9.67 | 10.27 | 10.59 | |
| Return Period of Typhoon Wind Waves (in Years) | Status Quo (2014) | Target Year (2020–2039) | |||||
|---|---|---|---|---|---|---|---|
| Coastal Areas (Longitude, Latitude) | 50-Year | 100-Year | 200-Year | 50-Year | 100-Year | 200-Year | |
| Da-an River (120.5604°, 24.4193°) | 1.27 | 1.37 | 1.45 | 1.52 | 1.62 | 1.65 | |
| Taichung (Taichung Harbor) (120.4719°, 24.29778°) | 1.14 | 1.22 | 1.29 | 1.41 | 1.49 | 1.55 | |
| Wu River (120.3859°, 24.2151°) | 1.00 | 1.07 | 1.13 | 1.28 | 1.37 | 1.36 | |
| Changhua (south side of Chabnghua Coastal Industrial Park) (120.2761°, 24.06278°) | 1.00 | 1.05 | 1.09 | 1.29 | 1.30 | 1.44 | |
| Jhuoshuei River (120.1514°, 23.8818°) | 1.05 | 1.13 | 1.19 | 1.32 | 1.45 | 1.46 | |
| Yulin (Shantiaolun) (120.0594°, 23.70583°) | 0.90 | 0.99 | 1.09 | 1.17 | 1.37 | 1.4 | |
| Beigang River (119.9902°, 23.5403°) | 0.76 | 0.84 | 0.92 | 1.04 | 1.15 | 1.24 | |
| Seawalls | Target Year (2020−2039) | ||||
|---|---|---|---|---|---|
| 5-Year | 50-Year | 100-Year | 200-Year | 250-Year | |
| The Dinggueike seawall at Da-an District, Taichung City | 0.000 | 0.020 | 0.031 | 0.040 | 0.057 |
| The Shinjie seawall at Fangyuan Township, Changhua County | 0.000 | 0.010 | 0.015 | 0.025 | 0.030 |
| The Dacheng seawall at Dacheng Township, Changhua County | 0.000 | 0.000 | 0.001 | 0.003 | 0.004 |
| The Lintsouliao seawall at Sihu Township, Yulin County | 0.000 | 0.011 | 0.026 | 0.039 | 0.059 |
| Tidal Gauge Station | Analysis Base Period (Year) | Fourier Analysis | Ensemble Empirical Model Decomposition (EEMD) | Average Amount of Change |
|---|---|---|---|---|
| Taichung Harbor (120.25° E, 24.25° N) | 1980–1999 | 40 | 68 | 54 |
| Jiayi Dongshi (119.75° E, 23.25° N) | 1992–2013 | 43 | 81 | 62 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hsu, T.-W.; Shih, D.-S.; Li, C.-Y.; Lan, Y.-J.; Lin, Y.-C. A Study on Coastal Flooding and Risk Assessment under Climate Change in the Mid-Western Coast of Taiwan. Water 2017, 9, 390. https://doi.org/10.3390/w9060390
Hsu T-W, Shih D-S, Li C-Y, Lan Y-J, Lin Y-C. A Study on Coastal Flooding and Risk Assessment under Climate Change in the Mid-Western Coast of Taiwan. Water. 2017; 9(6):390. https://doi.org/10.3390/w9060390
Chicago/Turabian StyleHsu, Tai-Wen, Dong-Sin Shih, Chi-Yu Li, Yuan-Jyh Lan, and Yu-Chen Lin. 2017. "A Study on Coastal Flooding and Risk Assessment under Climate Change in the Mid-Western Coast of Taiwan" Water 9, no. 6: 390. https://doi.org/10.3390/w9060390
APA StyleHsu, T.-W., Shih, D.-S., Li, C.-Y., Lan, Y.-J., & Lin, Y.-C. (2017). A Study on Coastal Flooding and Risk Assessment under Climate Change in the Mid-Western Coast of Taiwan. Water, 9(6), 390. https://doi.org/10.3390/w9060390








