Quantitative Spatio-Temporal Characterization of Scour at the Base of a Cylinder
Abstract
:1. Introduction
2. Experimental Set Up and Data Collection
3. Results
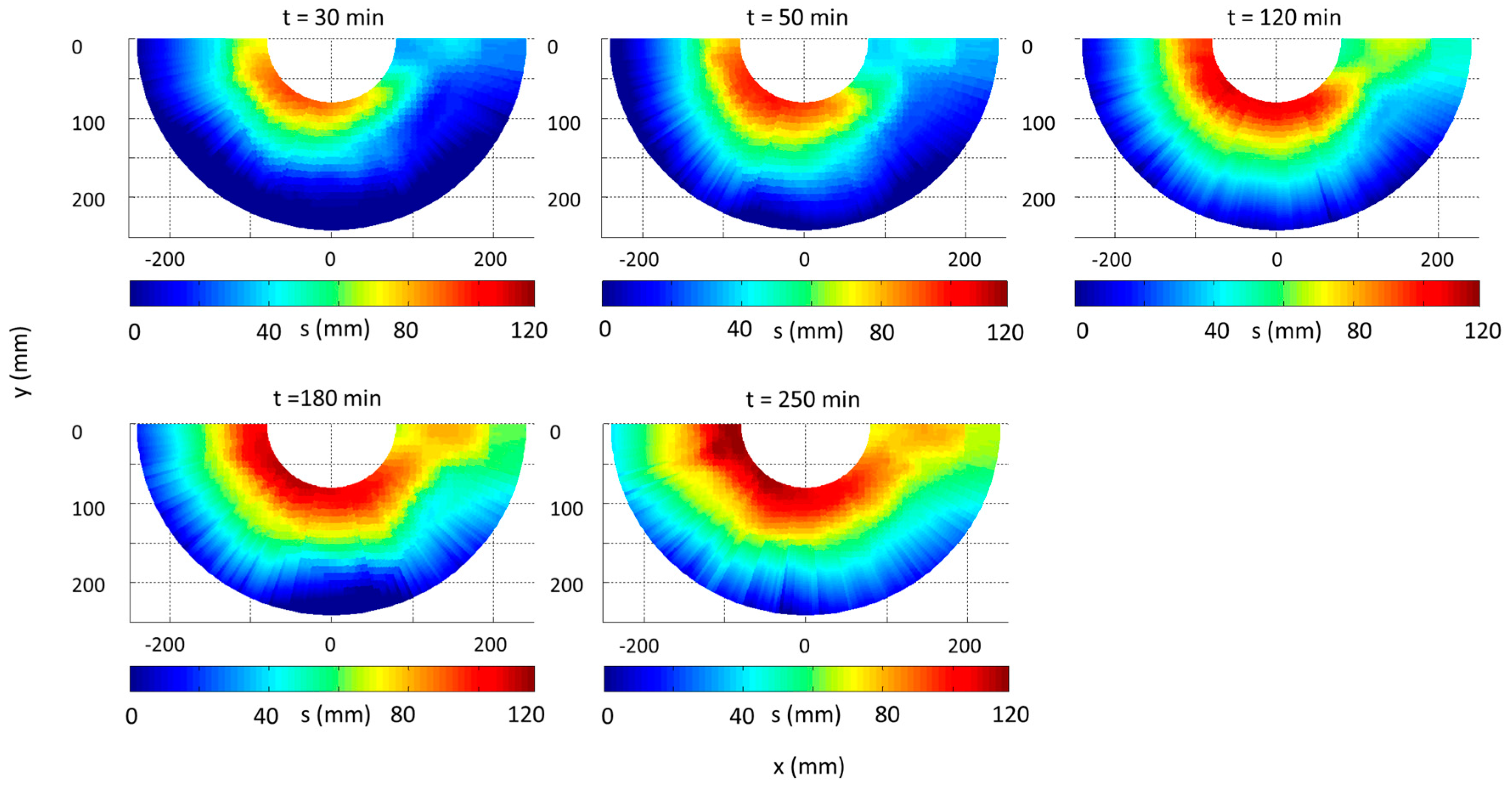
3.1. Overview of the Scour Hole Evolution
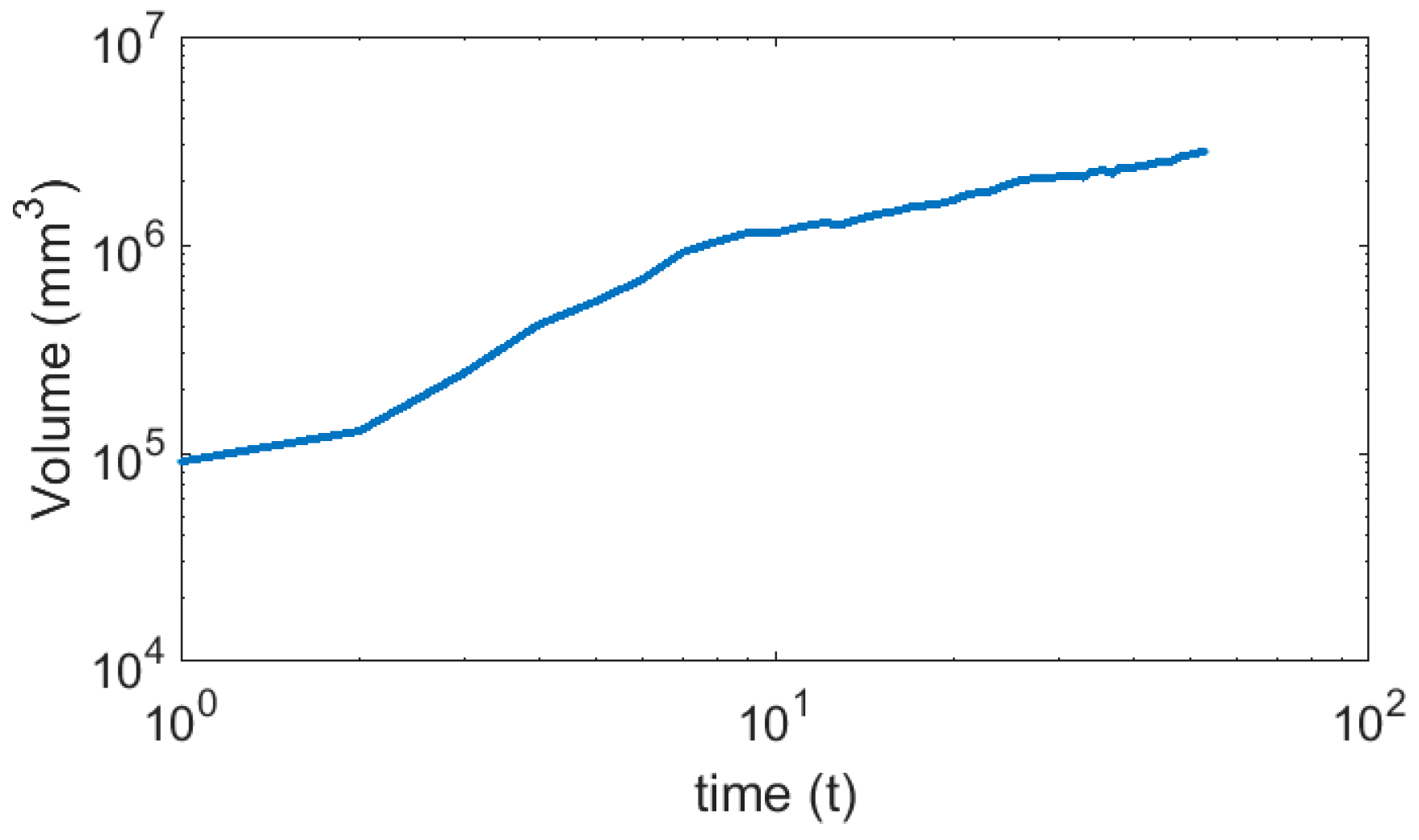
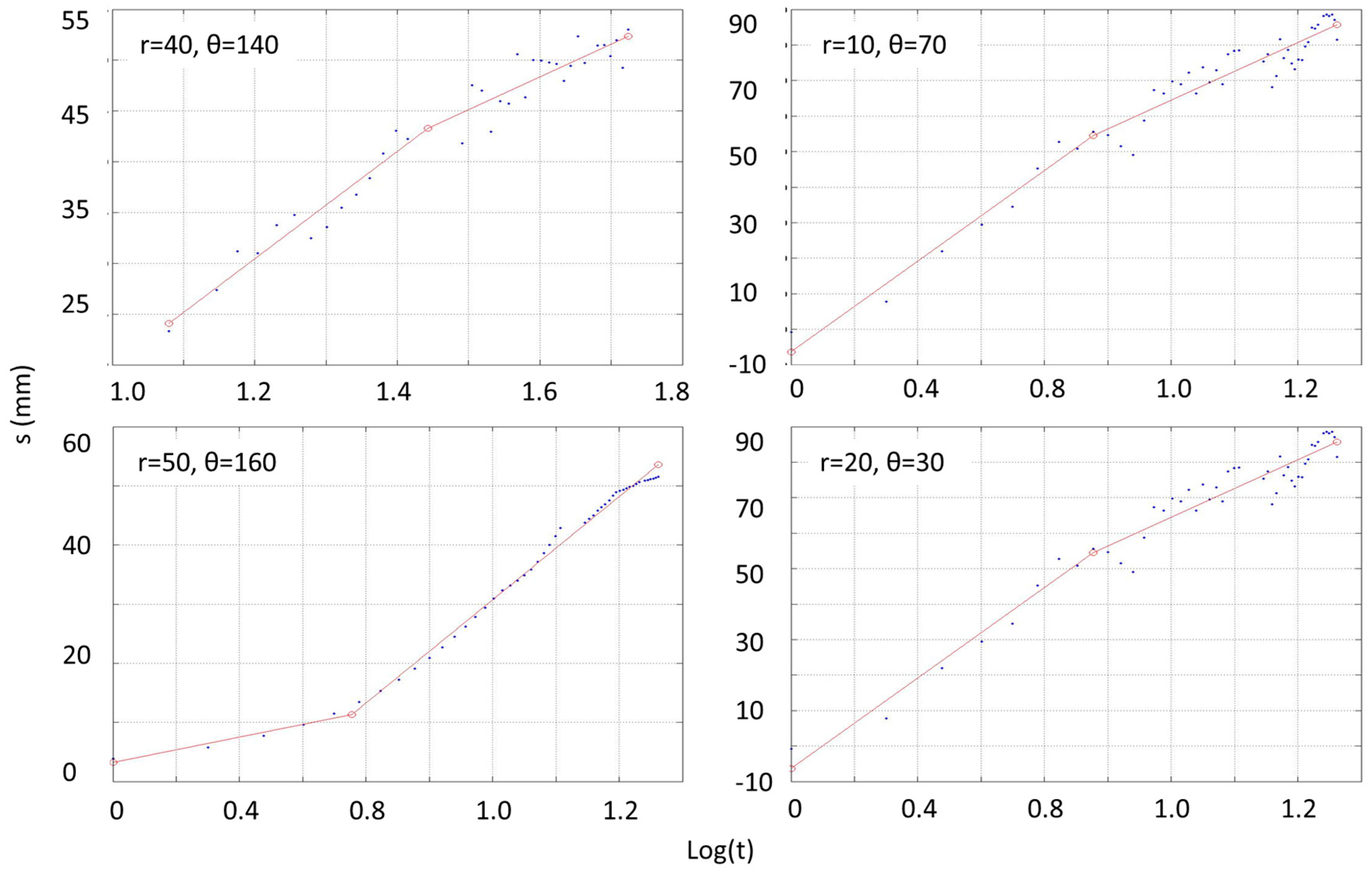
3.2. Overview of the Scour Rate Evolution and Distribution
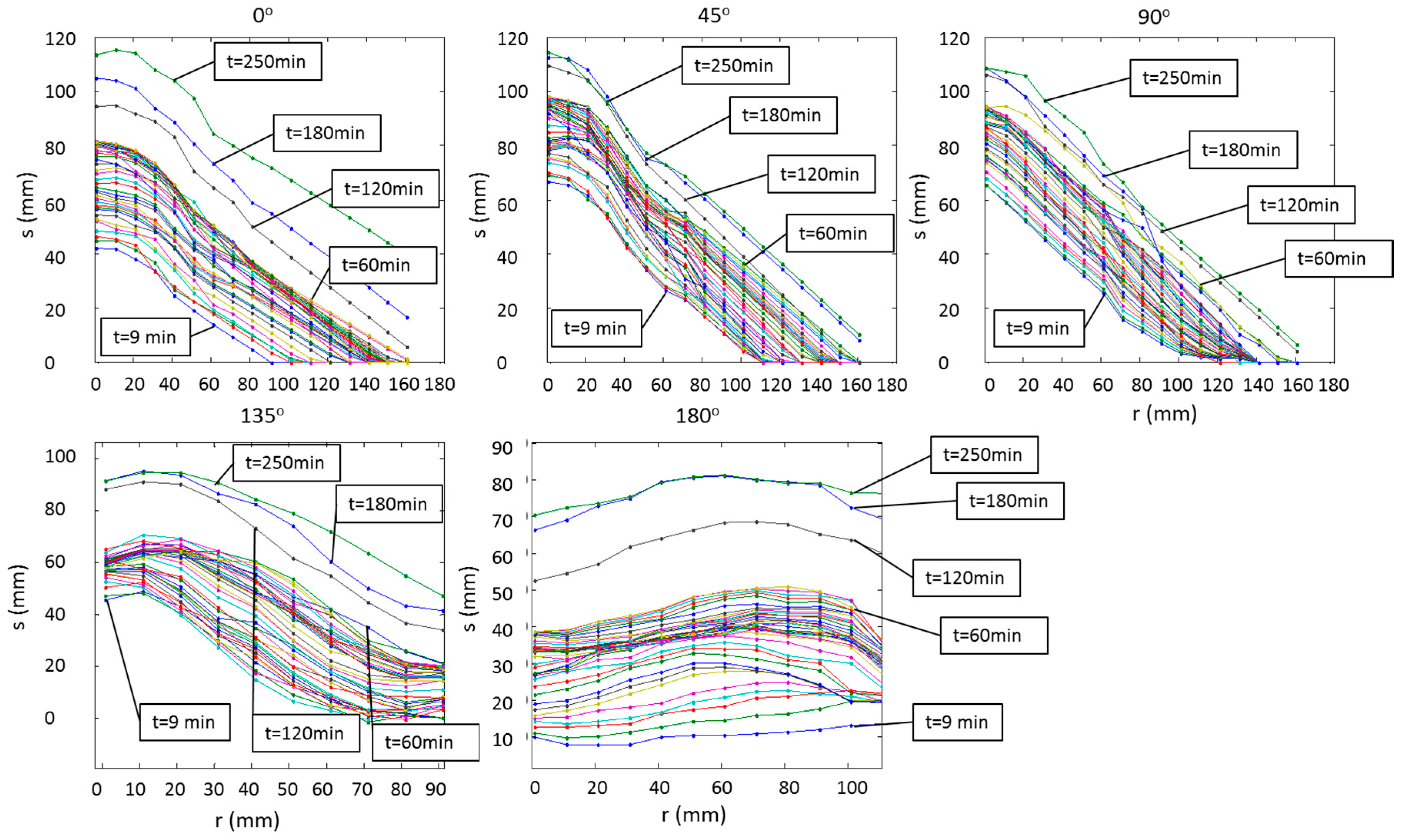
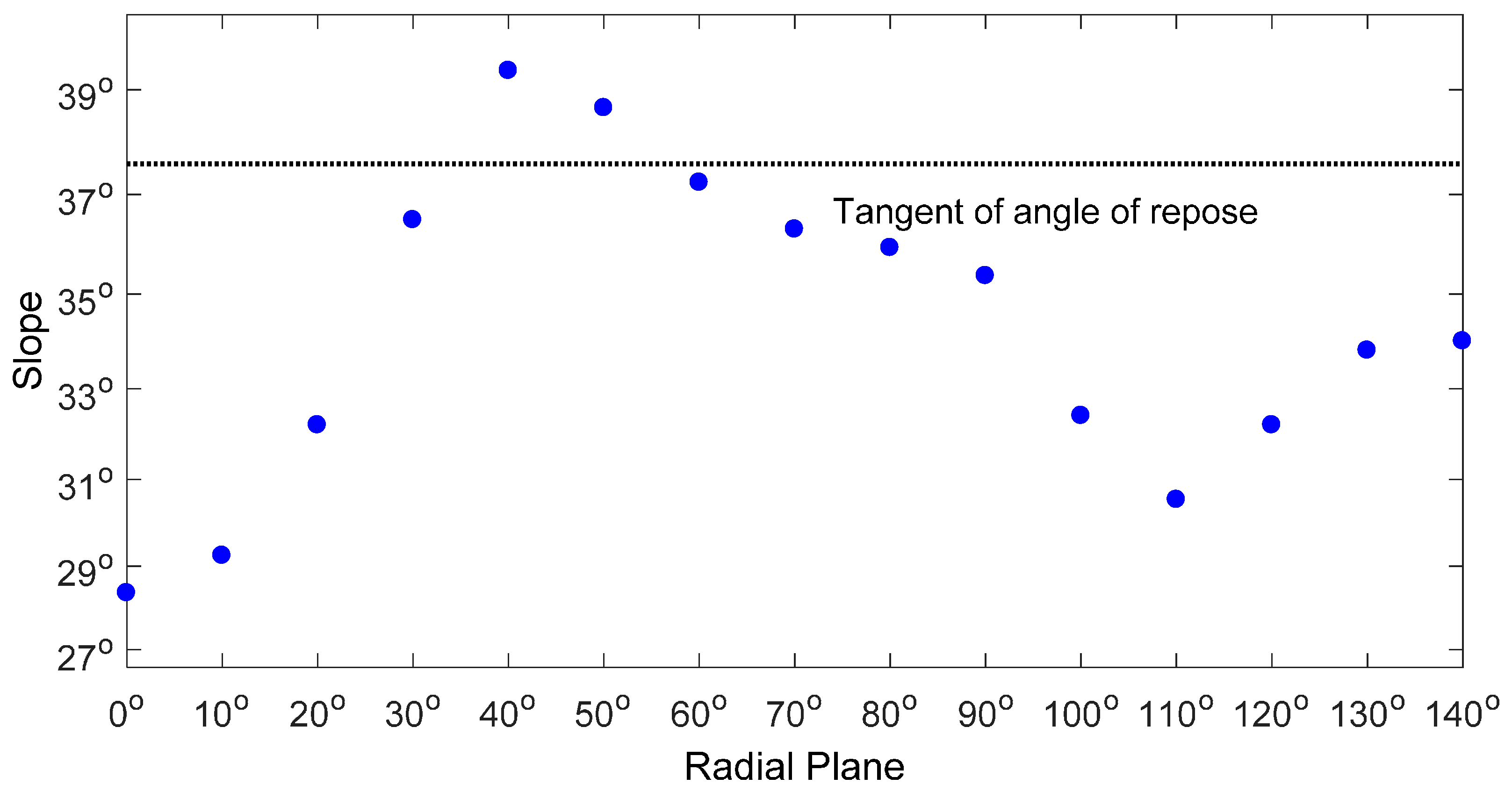
3.3. Dependence of Scour Depth on Location and Time
4. Discussion
4.1. Interpretation of the Results
4.2. Evaluation of the Measurements
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Johnson, P.A.; Jones, J.S. Merging laboratory and field data in bridge scour. J. Hydraul. Eng.-ASCE 1993, 119, 1176–1181. [Google Scholar] [CrossRef]
- Sheppard, D.M.; Demir, H.; Melville, B.W. Scour at Wide Piers and Long Skewed Piers; National Research Council (U.S.), Transportation Research Board, National Cooperative Highway Research Program, American Association of State Highway and Transportation Officials, and Federal Highway Administration: Washington, DC, USA, 2011. [Google Scholar]
- Baker, C.J. The Turbulent Horseshoe Vortex. J. Wind. Eng. Ind. Aerod. 1980, 6, 9–23. [Google Scholar] [CrossRef]
- Dargahi, B. The Turbulent-Flow Field around a Circular Cylinder. Exp. Fluids 1989, 8, 1–12. [Google Scholar] [CrossRef]
- Devenport, W.J.; Simpson, R.L. Time-dependent and time-averaged turbulence structure near the nose of a wing body junction. J. Fluid Mech. 1990, 210, 23–55. [Google Scholar] [CrossRef]
- Apsilidis, N.; Diplas, P.; Dancey, C.L.; Bouratsis, P. Time-resolved flow dynamics and Reynolds number effects at a wall-cylinder junction. J. Fluid Mech. 2015, 776, 475–511. [Google Scholar] [CrossRef]
- Paik, J.; Sotiropoulos, F. Numerical simulation of strongly swirling turbulent flows through an abrupt expansion. Int. J. Heat Fluid Flow 2010, 31, 390–400. [Google Scholar] [CrossRef]
- Escauriaza, C.; Sotiropoulos, F. Initial stages of erosion and bed form development in a turbulent flow around a cylindrical pier. J. Geophys. Res.-Earth 2011, 116. [Google Scholar] [CrossRef]
- Koken, M.; Constantinescu, G. An investigation of the dynamics of coherent structures in a turbulent channel flow with a vertical sidewall obstruction. Phys. Fluids 2009, 21, 085104. [Google Scholar] [CrossRef]
- Istiarto, I.; Graf, W.H. Experiments on flow around a cylinder in a scoured channel bed. Int. J. Sediment Res. 2001, 16, 431–444. [Google Scholar]
- Dey, S.; Raikar, R.V. Characteristics of horseshoe vortex in developing scour holes at piers. J. Hydraul. Eng.-ASCE 2007, 133, 399–413. [Google Scholar] [CrossRef]
- Debnath, K.; Manik, M.K.; Mazmder, B.S. Turbulence statistics of flow over scoured cohesive sediment bed around circular cylinder. Adv. Water Resour. 2012, 41, 18–28. [Google Scholar] [CrossRef]
- Kumar, A.; Kothyari, U.C.; Raju, K.G.R. Flow structure and scour around circular compound bridge piers—A review. J. Hydro-Environ. Res. 2012, 6, 251–265. [Google Scholar] [CrossRef]
- Beheshti, A.A.; Ataie-Ashtiani, B. Scour hole influence on turbulent flow field around complex bridge piers. Flow Turbul. Combust. 2016, 97, 451–474. [Google Scholar] [CrossRef]
- Melville, B.W.; Chiew, Y.M. Time scale for local scour at bridge piers. J. Hydraul. Eng.-ASCE 1999, 125, 59–65. [Google Scholar] [CrossRef]
- Kothyari, U.C.; Hager, W.H.; Oliveto, G. Generalized approach for clear-water scour at bridge foundation elements. J. Hydraul. Eng.-ASCE 2007, 133, 1229–1240. [Google Scholar] [CrossRef]
- Simarro, G.; Teixeira, L.; Cardoso, A.H. Closure to “Flow Intensity Parameter in Pier Scour Experiments” by Gonzalo Simarro, Luis Teixeira, and Antonio H. Cardoso. J. Hydraul. Eng.-ASCE 2009, 135, 155. [Google Scholar] [CrossRef]
- Link, O.; Castillo, C.; Pizarro, A.; Rojas, A.; Ettmer, B.; Escauriaza, C.; Manfreda, S. A model of bridge pier scour during flood waves. J. Hydraul. Res. 2016. [Google Scholar] [CrossRef]
- Oliveto, G.; Hager, W.H. Temporal evolution of clear-water pier and abutment scour. J. Hydraul. Eng.-ASCE 2002, 128, 811–820. [Google Scholar] [CrossRef]
- Lu, J.Y.; Shi, Z.Z.; Hong, J.H.; Lee, J.J.; Raikar, R.V. Temporal Variation of Scour Depth at Nonuniform Cylindrical Piers. J. Hydraul. Eng.-ASCE 2011, 137, 45–56. [Google Scholar] [CrossRef]
- Umeda, S.; Yamazaki, T.; Ishida, H. Time evolution of scour and deposition around a cylindrical pier in steady flow. In Proceedings of the International Conference on Scour and Erosion, Tokyo, Japan, 5–7 November 2008; pp. 140–146.
- Dodaro, G.; Tafarojnoruz, A.; Sciortino, G.; Adduce, C.; Calomino, F.; Gaudio, R. Modified Einstein sediment transport to simulate the local scour evolution downstream a rigid bed. J. Hydraul. Eng.-ASCE 2016, 142. [Google Scholar] [CrossRef]
- Radice, A.; Porta, G.; Franzetti, S. Analysis of the time-averaged properties of sediment motion in a local scour process. Water Resour. Res. 2009, 45, 12. [Google Scholar] [CrossRef]
- Radice, A.; Tran, C.K. Study of sediment motion in scour hole of a circular pier. J. Hydraul. Res. 2012, 50, 44–51. [Google Scholar] [CrossRef]
- Link, O.; Pfleger, F.; Zanke, U. Characteristics of developing scour-holes at a sand-embedded cylinder. Int. J. Sediment Res. 2008, 23, 258–266. [Google Scholar] [CrossRef]
- Dargahi, B. Controlling Mechanism of Local Scouring. J. Hydraul. Eng.-ASCE 1990, 116, 1197–1214. [Google Scholar] [CrossRef]
- Kirkil, G.; Constantinescu, G. Flow and turbulence structure around an in-stream rectangular cylinder with scour hole. Water Resour. Res. 2010, 46, W11549. [Google Scholar] [CrossRef]
- Escauriaza, C.; Sotiropoulos, F. Reynolds Number Effects on the Coherent Dynamics of the Turbulent Horseshoe Vortex System. Flow Turbul. Combust. 2011, 86, 231–262. [Google Scholar] [CrossRef]
- Khosronejad, A.; Kang, S.; Sotiropoulos, F. Experimental and computational investigation of local scour around bridge piers. Adv. Water Resour. 2012, 37, 73–85. [Google Scholar] [CrossRef]
- Bouratsis, P.; Diplas, P.; Dancey, C.L.; Apsilidis, N. High-resolution 3-D monitoring of evolving sediment beds. Water Resour. Res. 2013, 49, 977–992. [Google Scholar] [CrossRef]
- Sabersky, R.H.; Acosta, A.J.; Hauptmann, E.G. Fluid Flow: A First Course in Fluid Mechanics, 3rd ed.; Collier Macmillan: New York, NY, USA, 1989. [Google Scholar]
- Diplas, P.; Dancey, C.L.; Celik, A.O.; Valyrakis, M.; Greer, K.; Akar, T. The role of impulse on the initiation of particle movement under turbulent flow conditions. Science 2008, 322, 717–720. [Google Scholar] [CrossRef] [PubMed]
- Mia, F.; Nago, H. Design method of time-dependent local scour at circular bridge pier. J. Hydraul. Eng.-ASCE 2003, 129, 420–427. [Google Scholar] [CrossRef]
- Yanmaz, A.M.; Kose, O. A semi-empirical model for clear-water scour evolution at bridge abutments. J. Hydraul. Res. 2011, 47, 110–118. [Google Scholar]
- Guo, J. Semi-analytical model for temporal clear-water scour at prototype piers. J. Hydraul. Res. 2014, 52, 366–374. [Google Scholar] [CrossRef]
- Dey, S. Clear Water Scour around Circular Bridge Piers: A Model; Department of Civil Engineering, Indian Institute of Technology: Kharagpur, India, 1991. [Google Scholar]
- Euler, T.; Herget, J. Controls on local scour and deposition induced by obstacles in fluvial environments. Catena 2012, 91, 35–46. [Google Scholar] [CrossRef]
- Roulund, A.; Sumer, B.M.; Fredsoe, J.; Michelsen, J. Numerical and experimental investigation of flow and scour around a circular pile. J. Fluid Mech. 2005, 534, 351–401. [Google Scholar] [CrossRef]
- Breusers, H.N.C.; Raudkivi, A.J. Scouring; International Association for Hydraulic Research: Rotterdam, The Netherlands, 1991. [Google Scholar]
- Kirkil, G.; Constantinescu, G.; Ettema, R. Detached Eddy Simulation Investigation of Turbulence at a Circular Pier with Scour Hole. J. Hydraul. Eng.-ASCE 2009, 135, 888–901. [Google Scholar] [CrossRef]
- Apsilidis, N.; Diplas, P.; Dancey, C.L.; Bouratsis, P. Effects of wall roughness on turbulent junction flow characteristics. Ex Fluid 2016, 57. [Google Scholar] [CrossRef]
- Melville, B.W.; Raudkivi, A.J. Flow characteristics in local scour at bridge piers. J. Hydraul. Res. 1997, 15, 373–380. [Google Scholar] [CrossRef]
- Melville, B. Pier and Abutment Scour: Integrated Approach. J. Hydraul. Eng.-ASCE 1997, 123, 125–136. [Google Scholar] [CrossRef]
- Sheppard, D.M.; Melville, B.; Demir, H. Evaluation of Existing Equations for Local Scour at Bridge Piers. J. Hydraul. Eng.-ASCE 2014, 140, 14–23. [Google Scholar] [CrossRef]







| Initial Scour Phase | Development Scour Phase | |||||
|---|---|---|---|---|---|---|
| (0 min ≤ t < 9 min) | (9 min ≤ t ≤ 250 min) | |||||
| Front | Side | Wake | Front | Side | Wake | |
| (0 ≤ θ ≤ 20) | (20 < θ < 130) | (130 ≤ θ < 180) | (0 ≤ θ ≤ 20) | (20 < θ < 130) | (130 ≤ θ < 180) | |
| Terminal scour depth (mm) | 46.0 | 70.8 | 23.9 | 116.2 | 114.2 | 80.5 |
| Location of max scour depth (θ, r) | (20, 30) | (60, 30) | (175, 180) | (0, 20) | (60, 5) | (175, 100) |
| Terminal eroded volume (mm3) | 1.14 × 106 | 4.76 × 106 | ||||
| Scour (s) vs. Time (t) | s = tc1 | s = tc1 + c2 | Undefined | s = tc1 | s = tc1 + c2 | Undefined |
| Scour (s) vs. Angular Plane (θ) | Undefined | s = c3sin(c4θ) + c5 | ||||
| Scour (s) vs. radial distance (r) | s = c5r + c6 | s = c7r3 + c8r2 + c9r + c10 | s = c5r + c6 | s = c7r3 + c8r2 + c9r + c10 | ||
| Eroded Volume (V) vs. Time (t) | V = tc11 | V = tc11 + c12 | ||||
| Slope of the angular profile (Z) vs. Angular Plane (θ) | Undefined | Z = c13sin(c14θ) + c15 | Undefined | |||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bouratsis, P.; Diplas, P.; Dancey, C.L.; Apsilidis, N. Quantitative Spatio-Temporal Characterization of Scour at the Base of a Cylinder. Water 2017, 9, 227. https://doi.org/10.3390/w9030227
Bouratsis P, Diplas P, Dancey CL, Apsilidis N. Quantitative Spatio-Temporal Characterization of Scour at the Base of a Cylinder. Water. 2017; 9(3):227. https://doi.org/10.3390/w9030227
Chicago/Turabian StyleBouratsis, Pol, Panayiotis Diplas, Clinton L. Dancey, and Nikolaos Apsilidis. 2017. "Quantitative Spatio-Temporal Characterization of Scour at the Base of a Cylinder" Water 9, no. 3: 227. https://doi.org/10.3390/w9030227
APA StyleBouratsis, P., Diplas, P., Dancey, C. L., & Apsilidis, N. (2017). Quantitative Spatio-Temporal Characterization of Scour at the Base of a Cylinder. Water, 9(3), 227. https://doi.org/10.3390/w9030227







