Full Spectrum Analytical Channel Design with the Capacity/Supply Ratio (CSR)
Abstract
:1. Introduction
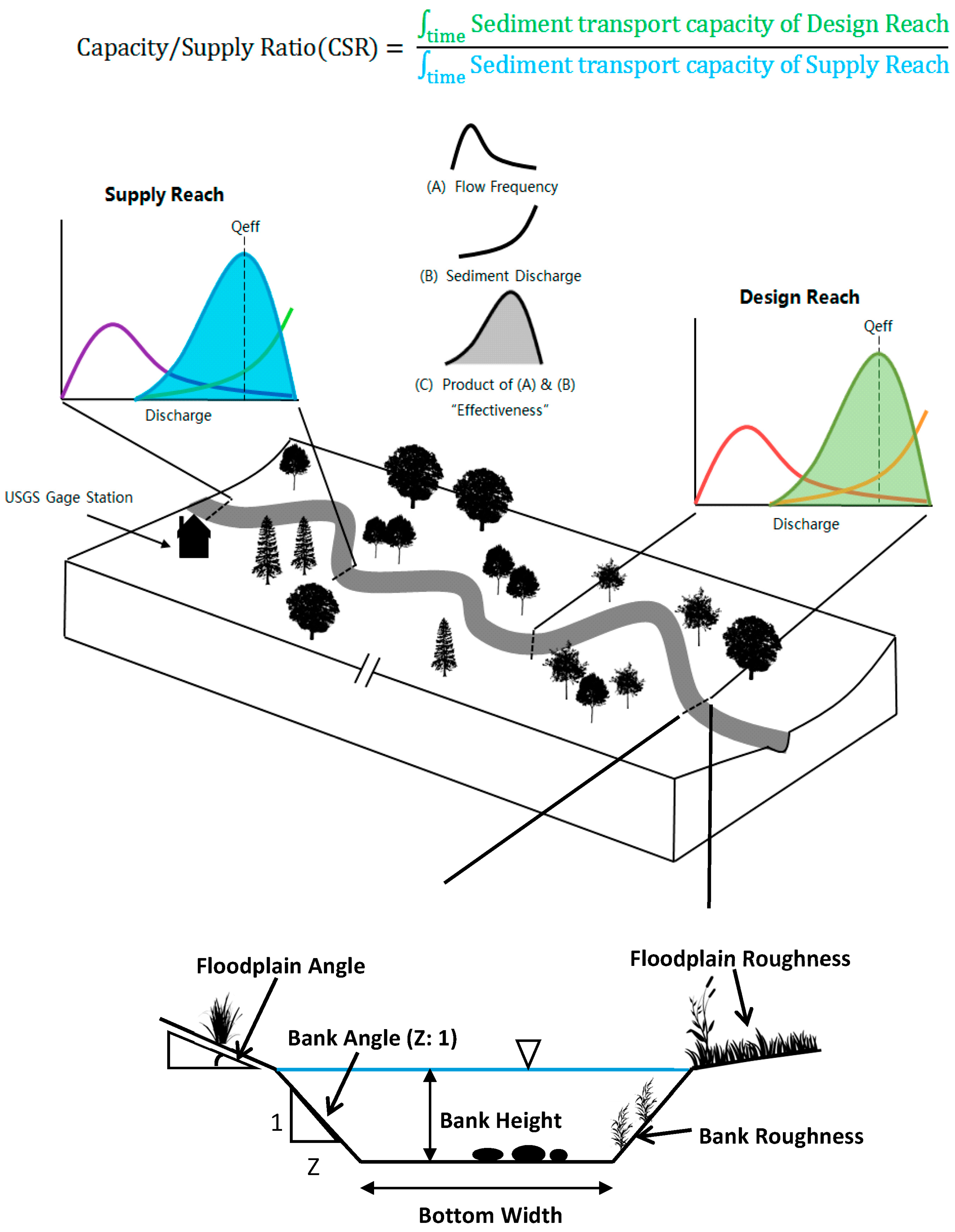
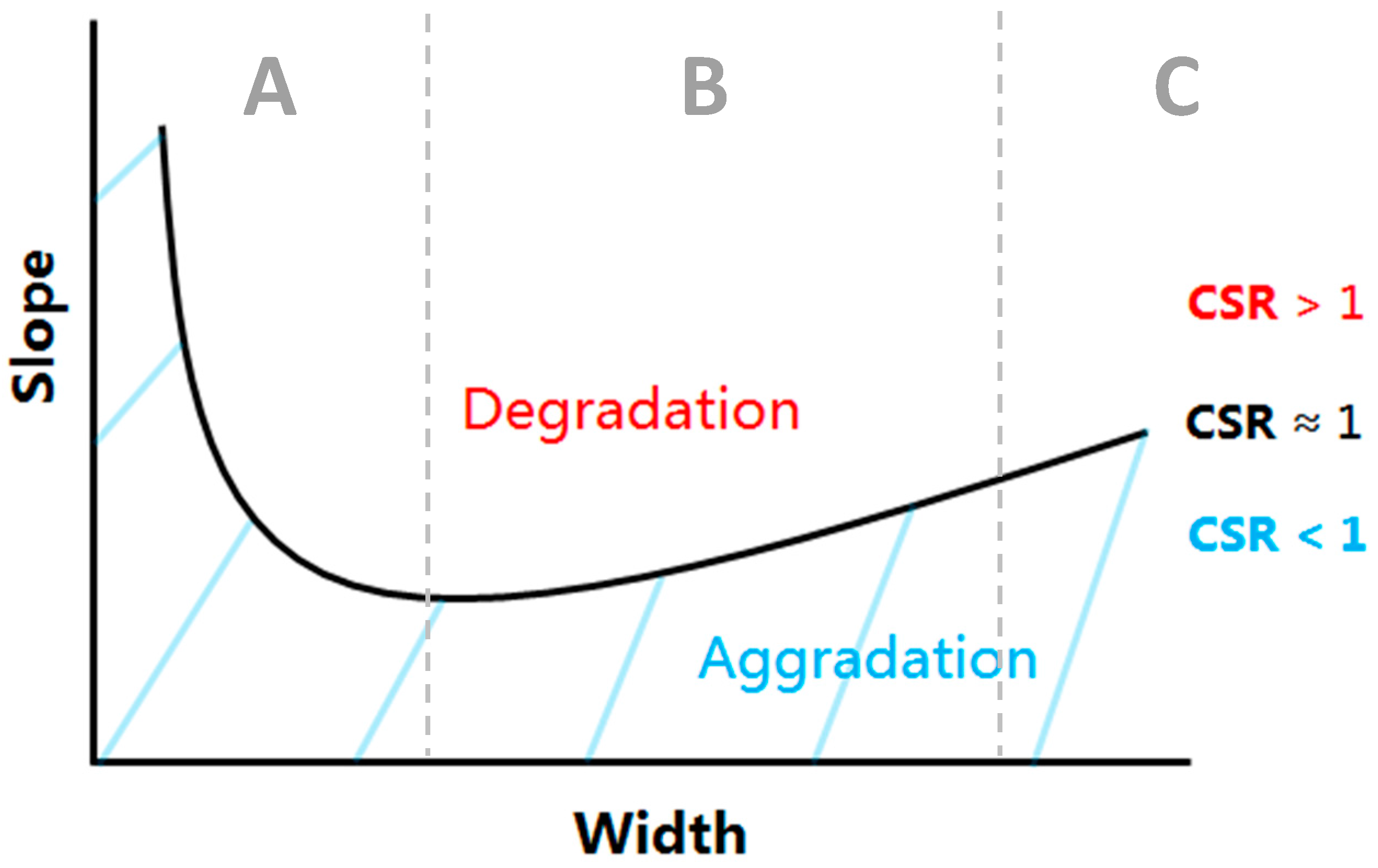
2. The Capacity/Supply Ratio
3. Methods
3.1. CSR Tool
3.1.1. Channel Partitioning
3.1.2. Hydrology Calculations
3.1.3. Sediment Transport Calculations
3.2. Sand-Bed Examples
4. Results
CSR Designs versus Single-Discharge Designs
5. Discussion
5.1. Strengths and Weaknesses of the CSR Tool Model
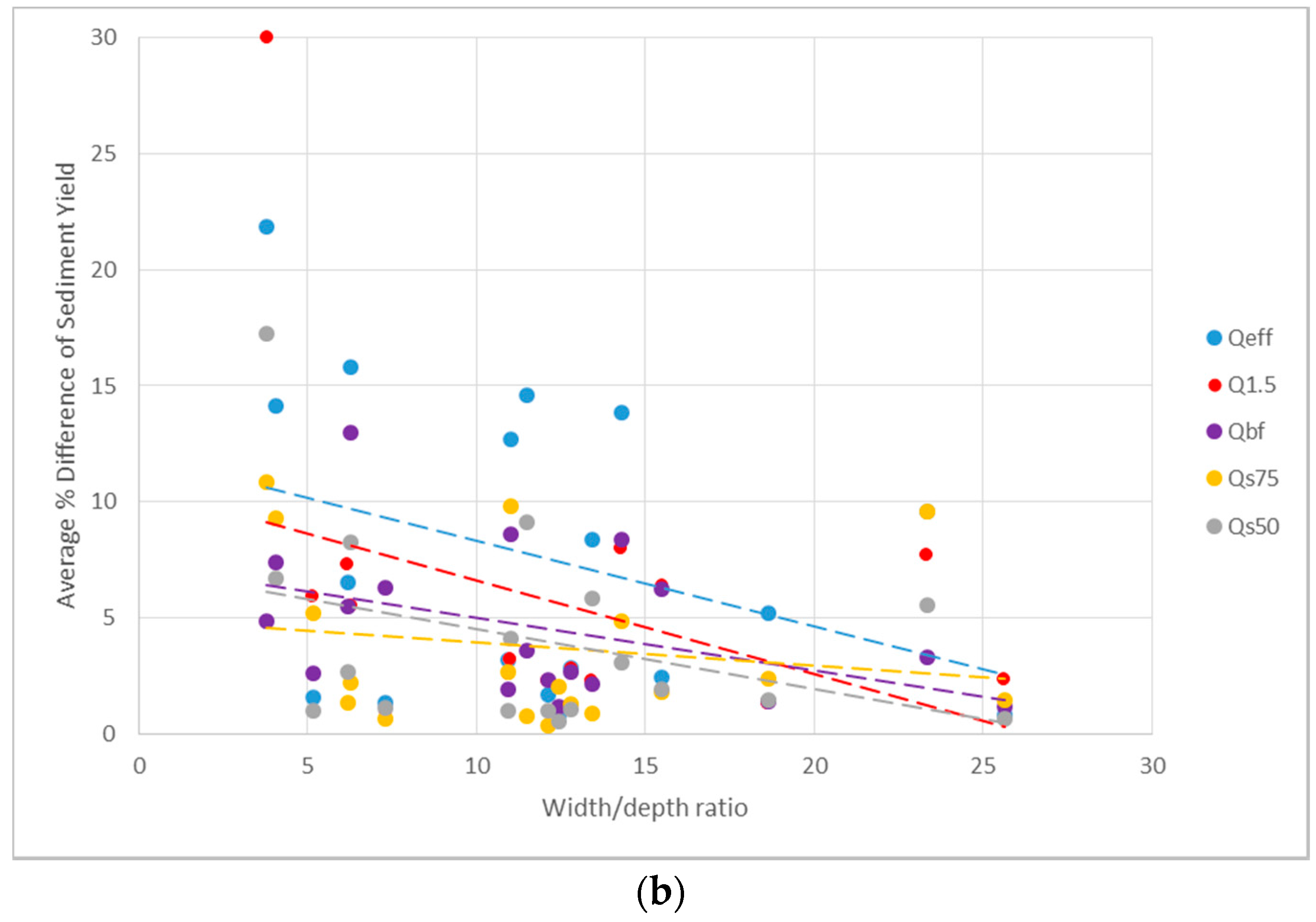
5.2. What Are the Most Important Influences on the Deviation of Single-Discharge Designs from the CSR Output?
5.3. Is the CSR Analysis Needed and, If So, When Is It Most Important to Use over a Single-Discharge Design?
5.4. What Single-Discharge Design Matches the CSR Output the Closest?
6. Conclusions
Author Contributions
Conflicts of Interest
References
- U.S. Environmental Protection Agency (EPA). National Water Quality Inventory: Report to Congress: 2004 Reporting Cycle; EPA Publication 841-R-08-001; EPA: Washington, DC, USA, 2009; p. 37. Available online: https://www.epa.gov/sites/production/files/2015-09/documents/2009_01_22_305b_2004report_2004_305breport.pdf (accessed on 15 June 2016).
- Ricciardi, A.; Rasmussen, J.B. Extinction rates of North American freshwater fauna. Conserv. Biol. 1999, 13, 1220–1222. [Google Scholar] [CrossRef]
- Strayer, D.L.; Dudgeon, D. Freshwater biodiversity conservation: Recent progress and future challenges. J. N. Am. Benthol. Soc. 2010, 29, 344–358. [Google Scholar] [CrossRef]
- Hawley, R.J.; Bledsoe, B.P.; Stein, E.D.; Haines, B.E. Channel evolution model of semiarid stream response to urban-induced hydromodification. J. Am. Water Resour. Assoc. 2012, 48, 722–744. [Google Scholar] [CrossRef]
- Trimble, S.W. Contribution of stream channel erosion to sediment yield from an urbanizing watershed. Science 1997, 278, 1442–1444. [Google Scholar] [CrossRef] [PubMed]
- Piégay, H.; Cuaz, M.; Javelle, E.; Mandier, P. Bank erosion management based on geomorphological, ecological and economic criteria on the Galaure River, France. Regul. Rivers Res. Manag. 1997, 13, 433–448. [Google Scholar] [CrossRef]
- Wohl, E.; Bledsoe, B.P.; Jacobson, R.B.; Poff, N.L.; Rathburn, S.L.; Walters, D.M.; Wilcox, A.C. The natural sediment regime in rivers: Broadening the foundation for ecosystem management. Bioscience 2015, 65, 358–371. [Google Scholar] [CrossRef]
- Soar, P.J.; Thorne, C.R. Design discharge for river restoration. In Stream Restoration in Dynamic Fluvial Systems: Scientific Approaches, Analyses, and Tools; Simon, A., Bennett, S.J., Castro, J.M., Eds.; Geophysical Monograph Series, 194; American Geophysical Union; Geopress: Washington, DC, USA, 2013; pp. 123–150. [Google Scholar]
- Shields, F.D., Jr.; Copeland, R.R.; Klingeman, P.C.; Doyle, M.W.; Simon, A. Design for stream restoration. J. Hydraul. Eng. 2003, 129, 575–584. [Google Scholar] [CrossRef]
- McCandless, T.L.; Starr, R.R.; Harman, W.A. Bankfull regional curves for the Alleghany Plateau/Valley and Ridge, Piedmont, and Coastal Plain regions of Maryland. J. Am. Water Resour. Assoc. 2015, 51, 1568–1580. [Google Scholar] [CrossRef]
- Doyle, M.W.; Shields, D.; Boyd, K.F.; Skidmore, P.B.; Dominick, D. Channel-forming discharge selection in river restoration design. J. Hydraul. Eng. 2007, 133, 831–837. [Google Scholar] [CrossRef]
- Bain, D.J.; Copeland, E.M.; Divers, M.T.; Hecht, M.; Hopkins, K.G.; Hynicka, J.; Koryak, M.; Kostalos, M.; Brown, L.; Elliott, E.M.; et al. Characterizing a major urban stream restoration project: Nine Mile Run (Pittsburgh, Pennsylvania, USA). J. Am. Water Resour. Assoc. 2014, 50, 1608–1621. [Google Scholar] [CrossRef]
- Vietz, G.J.; Walsh, C.J.; Fletcher, T.D. Urban hydrogeomorphology and the urban stream syndrome: Treating the symptoms and causes of geomorphic change. Prog. Phys. Geogr. 2016, 40, 480–492. [Google Scholar] [CrossRef]
- Bledsoe, B.P.; Baker, D.; Nelson, P.A.; Rosburg, T.; Sholtes, J.; Stroth, T.R. Design Hydrology for Stream Restoration and Channel Stability at Stream Crossings; Report, National Cooperative Highway Research Program (NCHRP) Project 24-40; National Cooperative Highway Research Program (NCHRP): Washington, DC, USA, 2017. [Google Scholar]
- Elkins, E.M.; Pasternack, G.B.; Merz, J.E. Use of slope creation for rehabilitating incised, regulated, gravel bed rivers. Water Resour. Res. 2007, 43, W05432. [Google Scholar] [CrossRef]
- Pasternack, G.B.; Brown, R.A. Ecohydraulic design of riffle-pool relief and morphological-unit geometry in support of regulated gravel-bed river rehabilitation. In Ecohydraulics: An Integrated Approach; Maddock, I., Harby, A., Kemp, P., Wood, P., Eds.; John Wiley & Sons, Ltd.: Chichester, UK, 2013. [Google Scholar]
- Brown, R.A.; Pasternack, G.B.; Lin, T. The topographic design of river channels for form-process linkages. Environ. Manag. 2016, 57, 929–942. [Google Scholar] [CrossRef] [PubMed]
- Skidmore, P.B.; Shields, F.D.; Doyle, M.W.; Miller, D.E. A categorization of approaches to natural channel design. In Proceedings of the 2001 Wetlands Engineering and River Restoration Conference, Reno, NV, USA, 27–31 August 2001; Hays, D.F., Ed.; American Society of Civil Engineers: Reston, VA, USA, 2001; pp. 1–12. [Google Scholar]
- Beechie, T.J.; Sear, D.A.; Olden, J.D.; Pess, G.R.; Buffington, J.M.; Moir, H.; Roni, P.; Pollock, M.M. Process-based principles for restoring river ecosystems. BioScience 2010, 60, 209–222. [Google Scholar] [CrossRef]
- Brunner, G.W. HEC-RAS River Analysis System, User’s Manual; Report No. CPD-68, Version 4.1; U.S. Army Corps of Engineers, Hydrologic Engineering Center: Davis, CA, USA, 2010; p. 790. Available online: http://www.hec.usace.army.mil/software/hec-ras/documentation/HEC-RAS_4.1_Users_Manual.pdf (accessed on 14 May 2015).
- Copeland, R.R. Application of Channel Stability Methods Case Studies; Technical Report HL-94-11; U.S. Army Corps of Engineers, Waterways Experiment Station: Vicksburg, MS, USA, September 1994; p. 60. Available online: http://www.dtic.mil/dtic/tr/fulltext/u2/a285625.pdf (accessed on 11 June 2015).
- Soar, P.J.; Thorne, C.R. Channel Restoration Design for Meandering Rivers; Technical Report No. ERDC/CHL CR-01-1; Coastal and Hydraulics Laboratory, U.S. Army, Engineer Research and Development Center: Vicksburg, MS, USA, 2001. Available online: http://www.nrcs.usda.gov/Internet/FSE_DOCUMENTS/stelprdb1043218.pdf (accessed on 9 March 2015).
- Sholtes, J.S.; Bledsoe, B.P. Half-yield discharge: Process-based predictor of bankfull discharge. J. Hydraul. Eng. 2016, 142. [Google Scholar] [CrossRef]
- Copeland, R.R.; McComas, D.N.; Thorne, C.R.; Soar, P.J.; Jonas, M.M.; Fripp, J.B. Hydraulic Design of Stream Restoration Projects; Technical Report No. ERDC/CHL-TR-01-28; Engineer Research and Development Center, Coastal and Hydraulics Laboratory: Vicksburg, MS, USA, 2001. Available online: http://www.nrcs.usda.gov/Internet/FSE_DOCUMENTS/stelprdb1043219.pdf (accessed on 10 November 2015).
- Church, M. Bed material transport and the morphology of alluvial river channels. Annu. Rev. Earth Planet. Sci. 2006, 34, 325–354. [Google Scholar] [CrossRef]
- Baker, D.B.; Richards, R.P.; Loftus, T.T.; Kramer, J.W. A new flashiness index: Characteristics and applications to Midwestern rivers and streams. J. Am. Water Resour. Assoc. 2004, 40, 503–522. [Google Scholar] [CrossRef]
- Vogel, R.M.; Stedinger, J.R.; Hooper, R.P. Discharge indices for water quality loads. Water Resour. Res. 2003, 39. [Google Scholar] [CrossRef]
- Andrews, E.D. Effective and bankfull discharges of streams in the Yampa River Basin, Colorado and Wyoming. J. Hydrol. 1980, 46, 311–330. [Google Scholar] [CrossRef]
- Emmett, W.W.; Wolman, M.G. Effective discharge and gravel-bed rivers. Earth Surf. Process. Landf. 2001, 26, 1369–1380. [Google Scholar] [CrossRef]
- Biedenharn, D.S.; Copeland, R.R.; Thorne, C.R.; Soar, P.J.; Hey, R.D.; Watson, C.C. Effective Discharge Calculation: A Practical Guide; Technical Report No. ERDC/CHL TR-00-15; U.S. Army Corps of Engineers, Engineer Research and Development Center: Vicksburg, MS, USA, 2000; p. 60. [Google Scholar]
- National Cooperative Highway Research Program. NCHRP Reports. Available online: http://www.trb.org/Publications/PubsNCHRPProjectReports.aspx (accessed on 1 March 2017).
- Einstein, H.A. The Bed-Load Function for Sediment Transportation in Open Channel Flows; Technical Bulletin No. 1026; U.S. Department of Agriculture, Soil Conservation Service: Washington, DC, USA, September 1950; p. 74. Available online: https://naldc.nal.usda.gov/download/CAT86201017/PDF (accessed on 9 July 2015).
- Brownlie, W.R. Prediction of Flow Depth and Sediment Discharge in Open-Channels; Report No. KH-R-43A; California Institute of Technology, W.M. Keck Laboratory of Hydraulics and Water Resources: Pasadena, CA, USA, November 1981; p. 246. Available online: http://authors.library.caltech.edu/25957/1/KH-R-43A.pdf (accessed on 23 June 2015).
- Parker, G. Surface-based bedload transport relation for gravel rivers. J. Hydraul. Res. 1990, 28, 417–436. [Google Scholar] [CrossRef]
- Wilcock, P.R.; Crowe, J.C. Surface-based transport model for mixed-size sediment. J. Hydraul. Eng. 2003, 129, 120–128. [Google Scholar] [CrossRef]
- Limerinos, J.T. Determination of the Manning Coefficient from Measured Bed Roughness in Natural Channels; U.S. Geological Survey Water-Supply Paper 1898-B; U.S. Government Printing Office: Washington, DC, USA, 1970; p. 47. Available online: http://pubs.usgs.gov/wsp/1898b/report.pdf (accessed on 7 October 2015).
- Rendell, H.; Alexander, D. Note on some spatial and temporal variations in ephemeral channel form. Geol. Soc. Am. Bull. 1979, 90, 761–772. [Google Scholar] [CrossRef]
- Brown, R.A.; Pasternack, G.B. Bed and width oscillations form coherent patterns in a partially confined, regulated gravel–cobble-bedded river adjusting to anthropogenic disturbances. Earth Surf. Dyn. 2017, 5, 1–20. [Google Scholar] [CrossRef]
- Wolman, M.G.; Miller, J.P. Magnitude and frequency of forces in geomorphic processes. J. Geol. 1960, 68, 54–74. [Google Scholar] [CrossRef]
- Bunte, K.; Swingle, K.W.; Abt, S.R.; Cenderelli, D. Steep Gravel Bedload Rating Curves Obtained from Bedload Traps Shift Effective Discharge to Flows Much Higher than “Bankfull”; ePoster EP41A-0774; American Geophysical Union: San Francisco, CA, USA, 2012. [Google Scholar]
- Rosburg, T.T.; Nelson, P.A.; Sholtes, J.S.; Bledsoe, B.P. The effect of flow data resolution on sediment yield estimation and channel design. J. Hydrol. 2016, 538, 429–439. [Google Scholar] [CrossRef]
- Hey, R.D. Design discharge for natural channels. In Science, Technology and Environmental Management; Hey, R.D., Davies, T.D., Eds.; Saxon House: Farnborough, UK, 1975; pp. 73–88. [Google Scholar]


| Stream Name | Site Location | USGS a Gage | Flow Days | Top Width (m) | Depth (m) | D50 (mm) | Bed Slope | Sinuosity |
|---|---|---|---|---|---|---|---|---|
| Big Raccoon Creek | Coxville, IN | 03341300 | 14,256 | 39.4 | 2.61 | 0.50 | 0.00054 | 1.2 |
| St. Joseph River | near Newville, IN | 04178000 | 18,882 | 58.4 | 2.04 | 0.61 | 0.00019 | 2.0 |
| Tallahala Creek | near Runnelstown, MS | 02474500 | 15,706 | 42.6 | 2.69 | 0.33 | 0.00058 | 1.4 |
| Fishing Creek | near Enfield, NC | 02083000 | 24,472 | 43.3 | 3.09 | 1.07 | 0.00017 | 2.0 |
| Licking River | Farmers, KY | 03249500 | 6848 | 43.2 | 4.19 | 1.38 | 0.00025 | 2.9 |
| Rough River | near Dundee, KY | 03319000 | 8309 | 37.5 | 4.60 | 0.15 | 0.00011 | 2.1 |
| South River | near Parkersburg, NC | 02107000 | 12,789 | 19.8 | 1.25 | 0.53 | 0.00027 | 1.5 |
| Mud Creek | near Lewsburg, KY | 03316000 | 12,054 | 16.3 | 2.69 | 0.14 | 0.00028 | 2.1 |
| Cahaba River | near Sprott, AL | 02424500 | 11,323 | 61.0 | 6.58 | 0.30 | 0.00041 | 1.4 |
| East Nishnabotna River | Red Oak, IA | 06809500 | 22,805 | 58.6 | 3.17 | 0.43 | 0.00060 | 1.4 |
| Buttahatchee River | near Sulligent, AL | 02439000 | 7519 | 21.7 | 3.49 | 0.28 | 0.00044 | 1.7 |
| Wolf River | Rossville, TN | 07030500 | 15,524 | 29.3 | 2.02 | 0.35 | 0.00045 | 1.6 |
| Big Sioux River | Akron, IA | 06485500 | 25,600 | 58.3 | 3.55 | 0.59 | 0.00025 | 1.7 |
| Cossatot River | near Dequeen, AR | 07340500 | 15,524 | 49.5 | 3.55 | 0.12 | 0.00079 | 1.7 |
| Rock River | near Rock Valley, IA | 06483500 | 18,407 | 54.3 | 2.51 | 0.50 | 0.00051 | 1.8 |
| Red River | Clay City, KY | 03283500 | 21,128 | 35.2 | 3.83 | 1.60 | 0.00040 | 1.7 |
| Sugar Creek | near Edinburgh, IN | 03362500 | 20,208 | 35.1 | 2.03 | 1.34 | 0.00040 | 1.2 |
| Washita River | Anadarko, OK | 07326500 | 25,639 | 55.1 | 2.09 | 0.29 | 0.00043 | 1.4 |
| Stream Name | CSR Slope | Qeff/CSR | Qbf/CSR | Qs50/CSR | Qs75/CSR | Q1.5/CSR |
|---|---|---|---|---|---|---|
| Big Raccoon Creek | 0.000532 | 1.01 | 1.01 | 1.00 | 1.00 | 1.01 |
| St. Joseph River | 0.00018 | 0.99 | 1.01 | 0.99 | 1.01 | 1.01 |
| Tallahala Creek | 0.000577 | 1.00 | 1.00 | 1.00 | 1.01 | 1.00 |
| Fishing Creek | 0.000162 | 0.94 | 1.04 | 0.99 | 1.05 | 1.01 |
| Licking River | 0.00026 | 0.99 | 0.95 | 0.99 | 1.00 | 0.99 |
| Rough River | 0.00011 | 1.00 | 1.00 | 1.00 | 1.04 | 1.00 |
| South River | 0.000272 | 1.01 | 0.99 | 1.00 | 0.99 | 0.99 |
| Mud Creek | 0.000275 | 1.09 | 1.05 | 1.04 | 1.01 | 0.75 |
| Cahaba River | 0.000446 | 1.07 | 0.92 | 1.04 | 1.01 | 0.97 |
| East Nishnabotna River | 0.000696 | 1.03 | 0.96 | 0.99 | 1.00 | 0.96 |
| Buttahatchee River | 0.000411 | 1.15 | 0.97 | 1.12 | 1.08 | 0.52 |
| Wolf River | 0.000462 | 0.91 | 0.97 | 0.94 | 1.00 | 1.18 |
| Big Sioux River | 0.000267 | 1.06 | 1.01 | 1.04 | 1.00 | 1.01 |
| Cossatot River | 0.000809 | 1.02 | 0.99 | 1.00 | 0.98 | 0.98 |
| Rock River | 0.000556 | 1.03 | 0.99 | 1.00 | 0.98 | 0.99 |
| Red River | 0.000411 | 1.04 | 0.96 | 1.01 | 0.99 | 0.95 |
| Sugar Creek | 0.000413 | 1.08 | 1.05 | 1.02 | 0.97 | 0.96 |
| Washita River | 0.00045 | 0.98 | 1.02 | 1.00 | 0.98 | 0.99 |
| Comparison Metric | Qeff | Qbf | Qs50 | Qs75 | Q1.5 |
|---|---|---|---|---|---|
| Number of times closest to CSR | 0 | 2 | 7 | 7 | 2 |
| Average % difference | 7.6% | 4.6% | 4.0% | 3.8% | 10.5% |
| Number of times (<5%) | 8 | 10 | 12 | 13 | 9 |
| Number of times (5% to 10%) | 4 | 7 | 5 | 4 | 6 |
| Number of times (>10%) | 6 | 1 | 1 | 1 | 3 |
| Stream Name | Single-Design Discharge | Average % Difference | Incoming Sediment Yield (tons/Day) | Erosion/Deposition (m/Year) |
|---|---|---|---|---|
| Sugar Creek | Qs75 | 4.9 | 93 | 0.03 |
| Buttahatchee River | Qbf | 4.9 | 1013 | 0.8 |
| Washita River | Qs50 | 5.6 | 13,588 | 2.6 |
| Sugar Creek | Qbf | 9.8 | 93 | 0.06 |
| Buttahatchee River | Qs75 | 10.9 | 1013 | 1.9 |
| Washita River | Qs75 | 9.6 | 13,588 | 5.8 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stroth, T.R.; Bledsoe, B.P.; Nelson, P.A. Full Spectrum Analytical Channel Design with the Capacity/Supply Ratio (CSR). Water 2017, 9, 271. https://doi.org/10.3390/w9040271
Stroth TR, Bledsoe BP, Nelson PA. Full Spectrum Analytical Channel Design with the Capacity/Supply Ratio (CSR). Water. 2017; 9(4):271. https://doi.org/10.3390/w9040271
Chicago/Turabian StyleStroth, Travis R., Brian P. Bledsoe, and Peter A. Nelson. 2017. "Full Spectrum Analytical Channel Design with the Capacity/Supply Ratio (CSR)" Water 9, no. 4: 271. https://doi.org/10.3390/w9040271
APA StyleStroth, T. R., Bledsoe, B. P., & Nelson, P. A. (2017). Full Spectrum Analytical Channel Design with the Capacity/Supply Ratio (CSR). Water, 9(4), 271. https://doi.org/10.3390/w9040271





