Modeling the Influence of River Cross-Section Data on a River Stage Using a Two-Dimensional/Three-Dimensional Hydrodynamic Model
Abstract
:1. Introduction
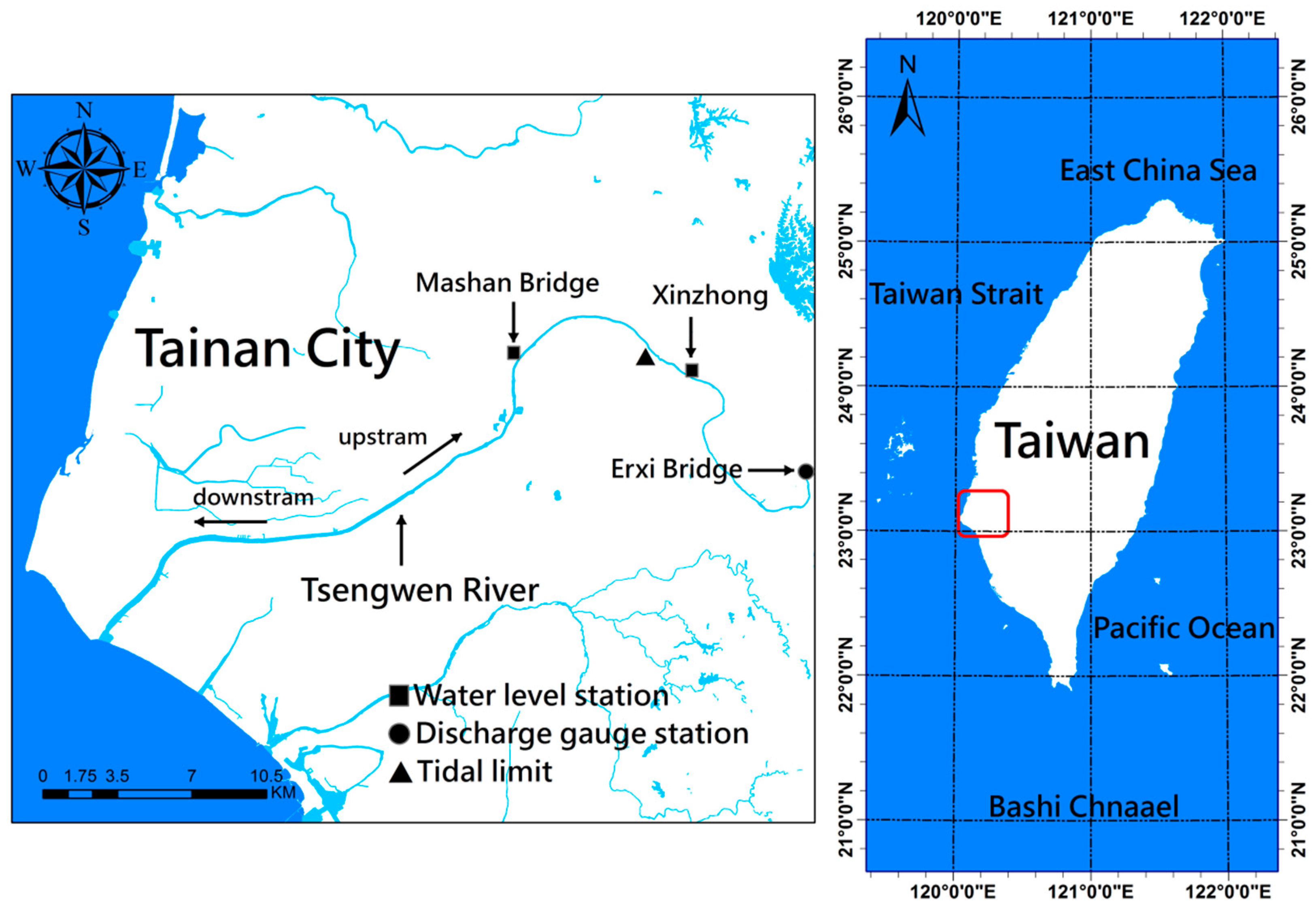
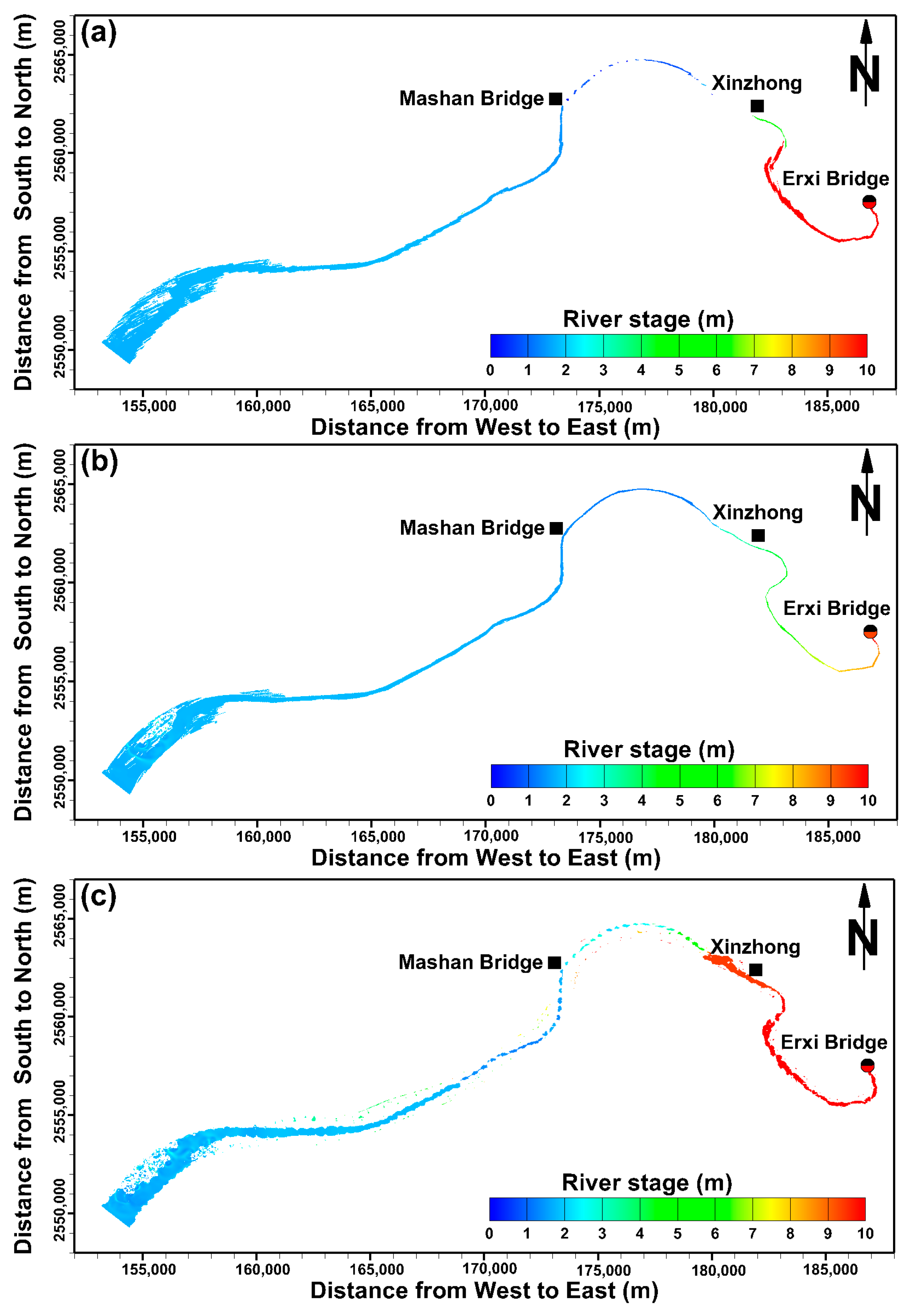
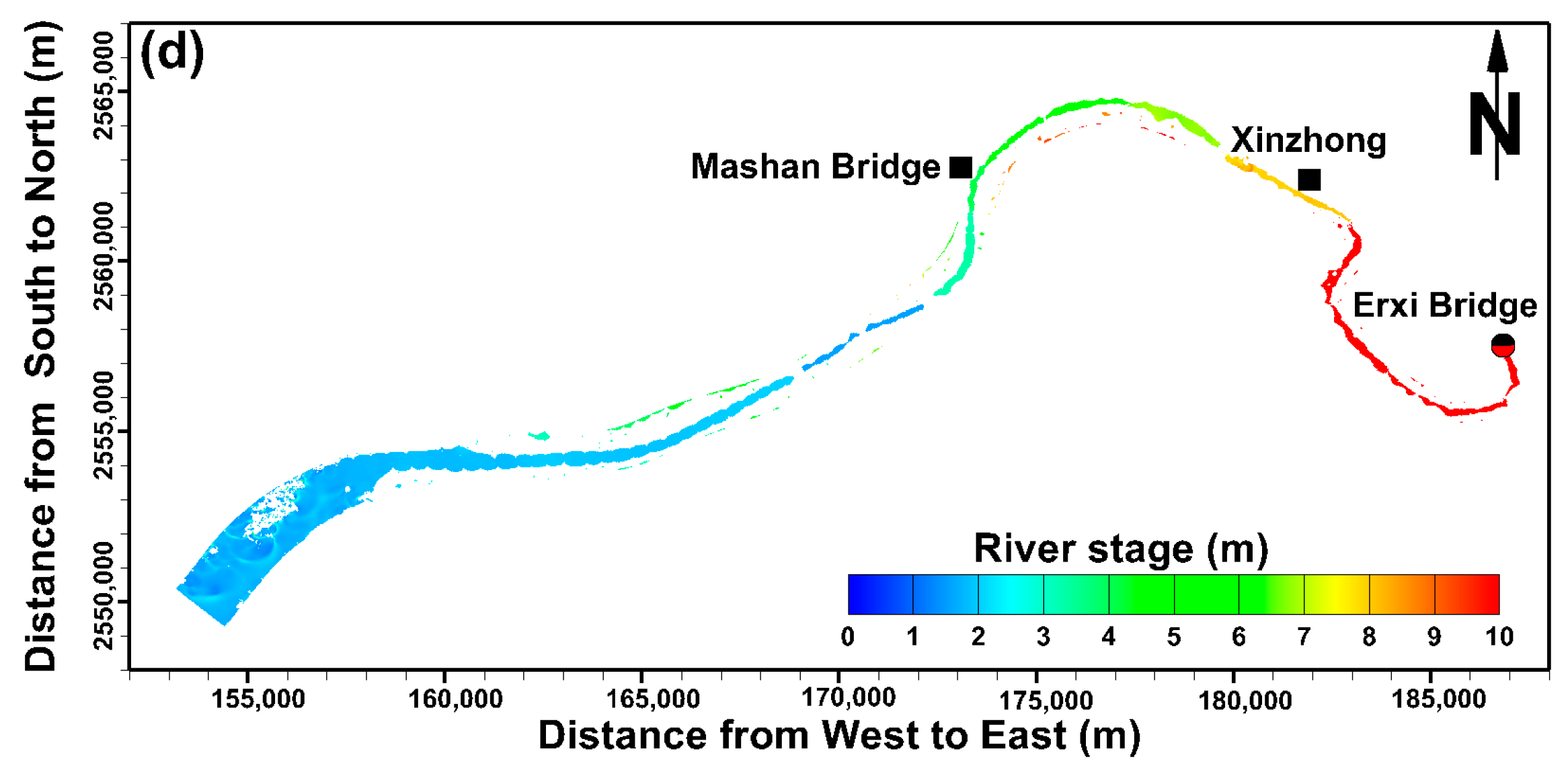
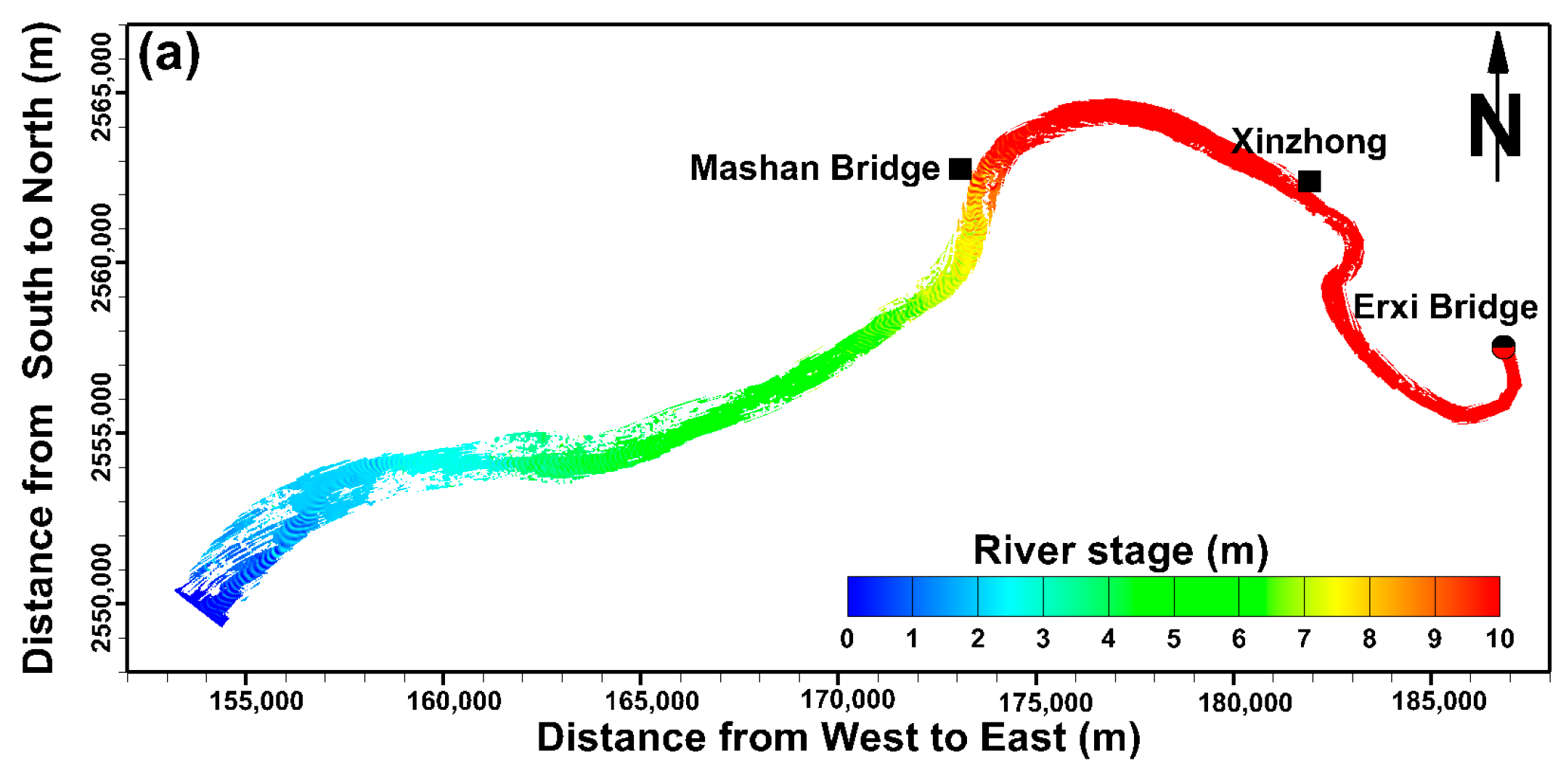
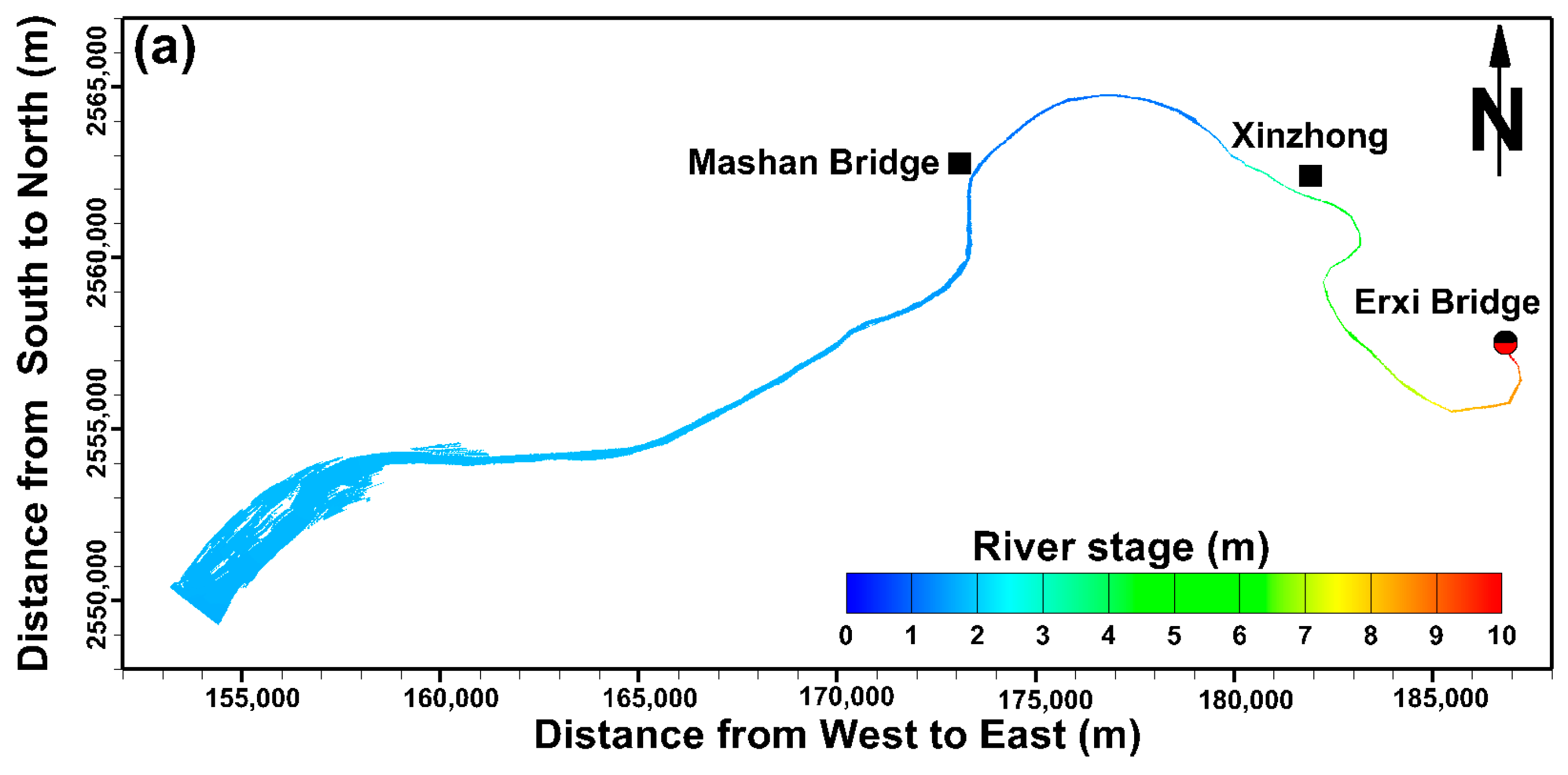
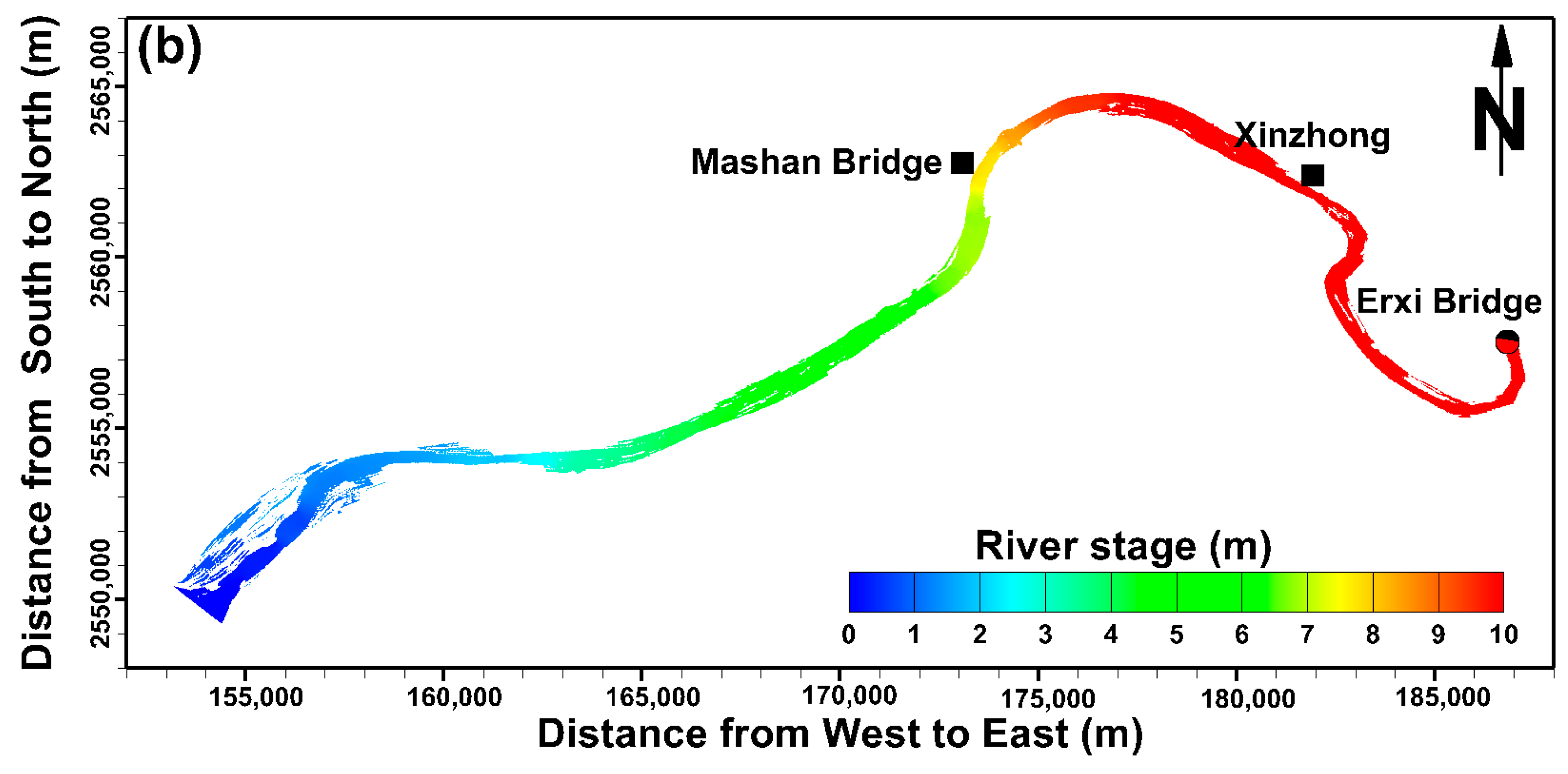
2. Description of Study Area
3. Materials and Methods
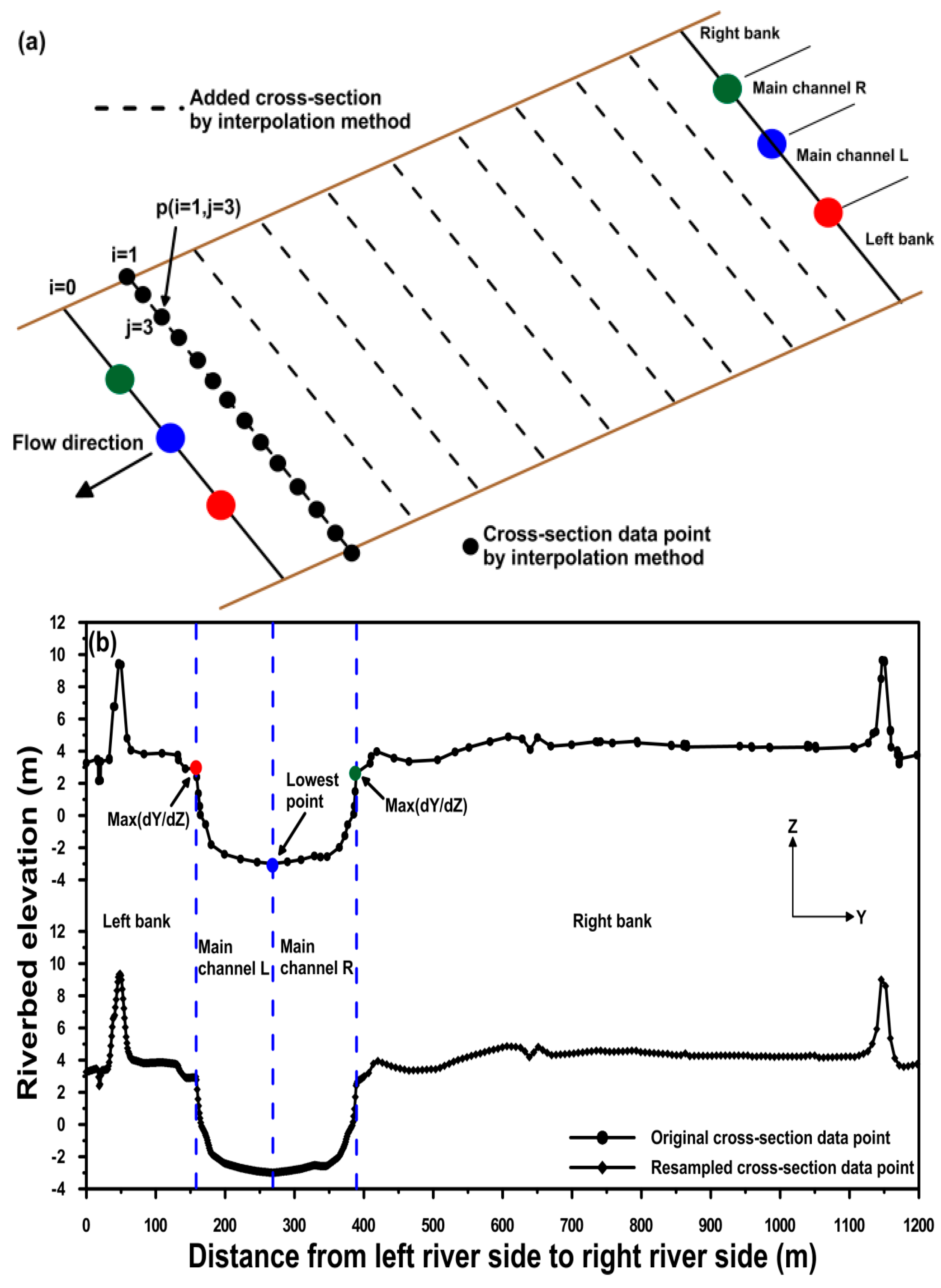
3.1. Methods for Resampling River Cross-Section Data
3.2. Interpolation Methods
3.2.1. Linear Interpolation
3.2.2. Inverse Distance Weighting (IDW)
3.2.3. Natural Neighbor (NN)
3.3. Three-Dimensional (3D) Hydrodynamic Model
3.4. Two-Dimensional (2D) Hydrodynamic Model
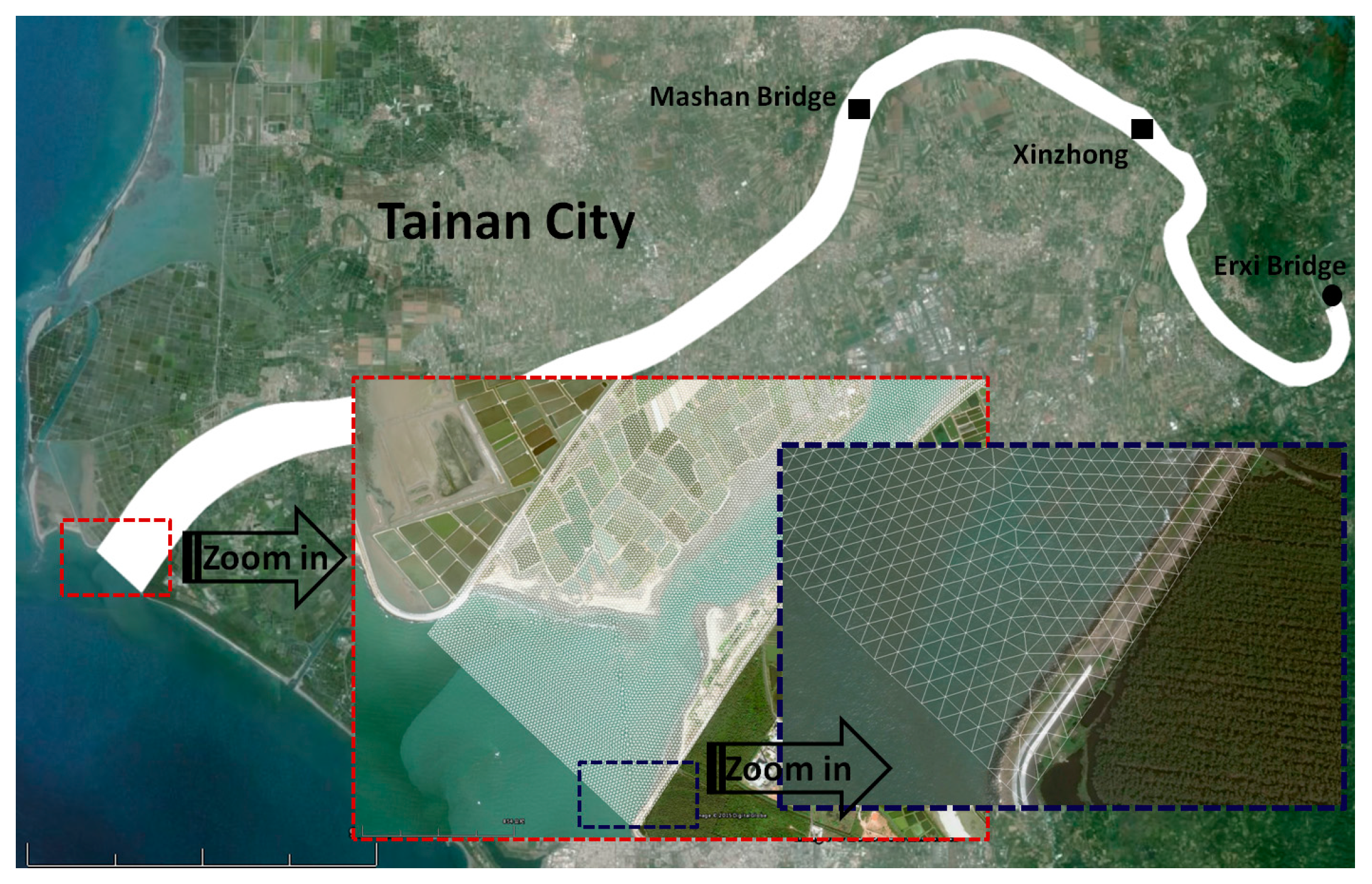
3.5. Model Implementation
3.6. Assessment of the Model Performance
4. Results
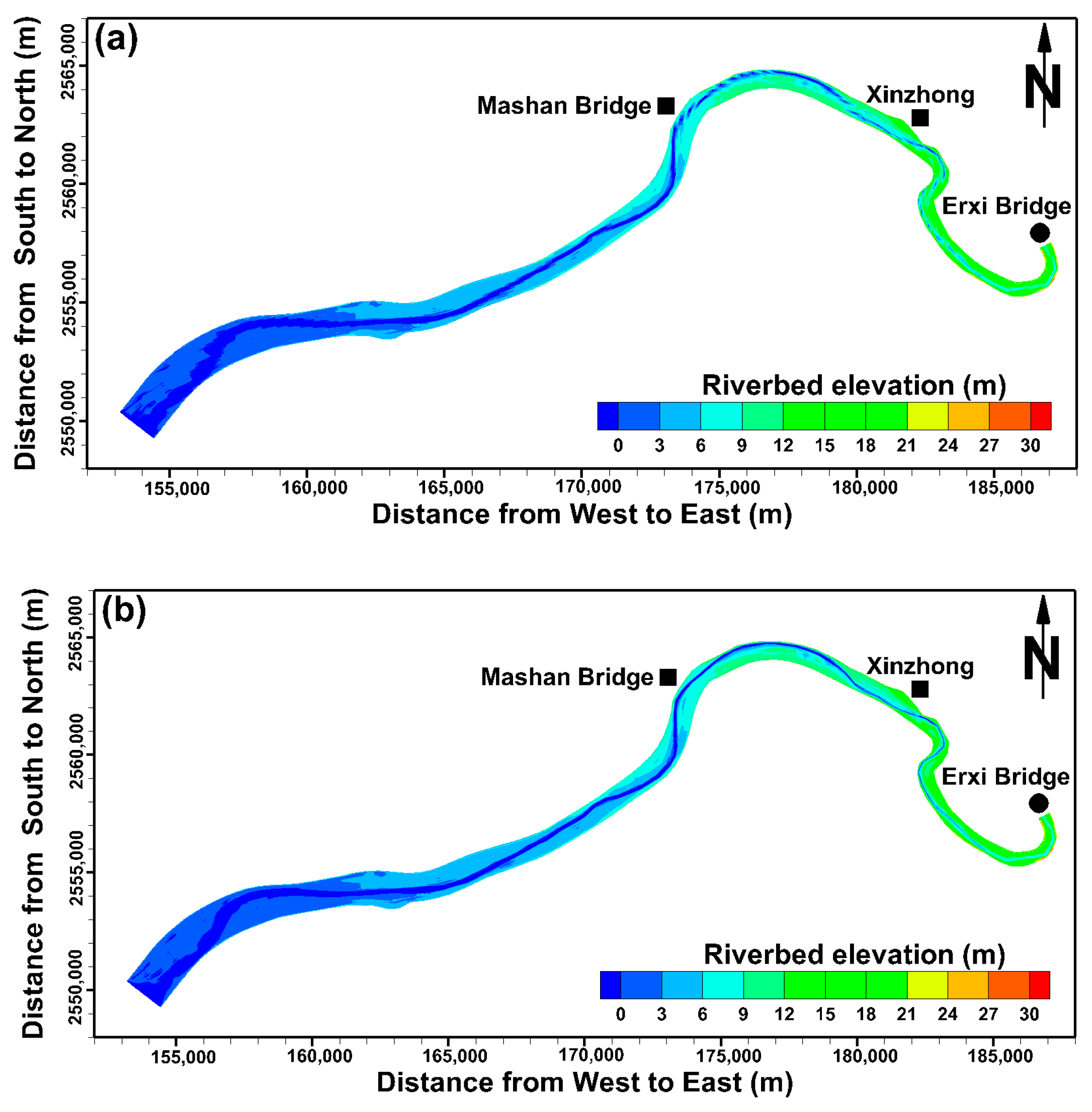
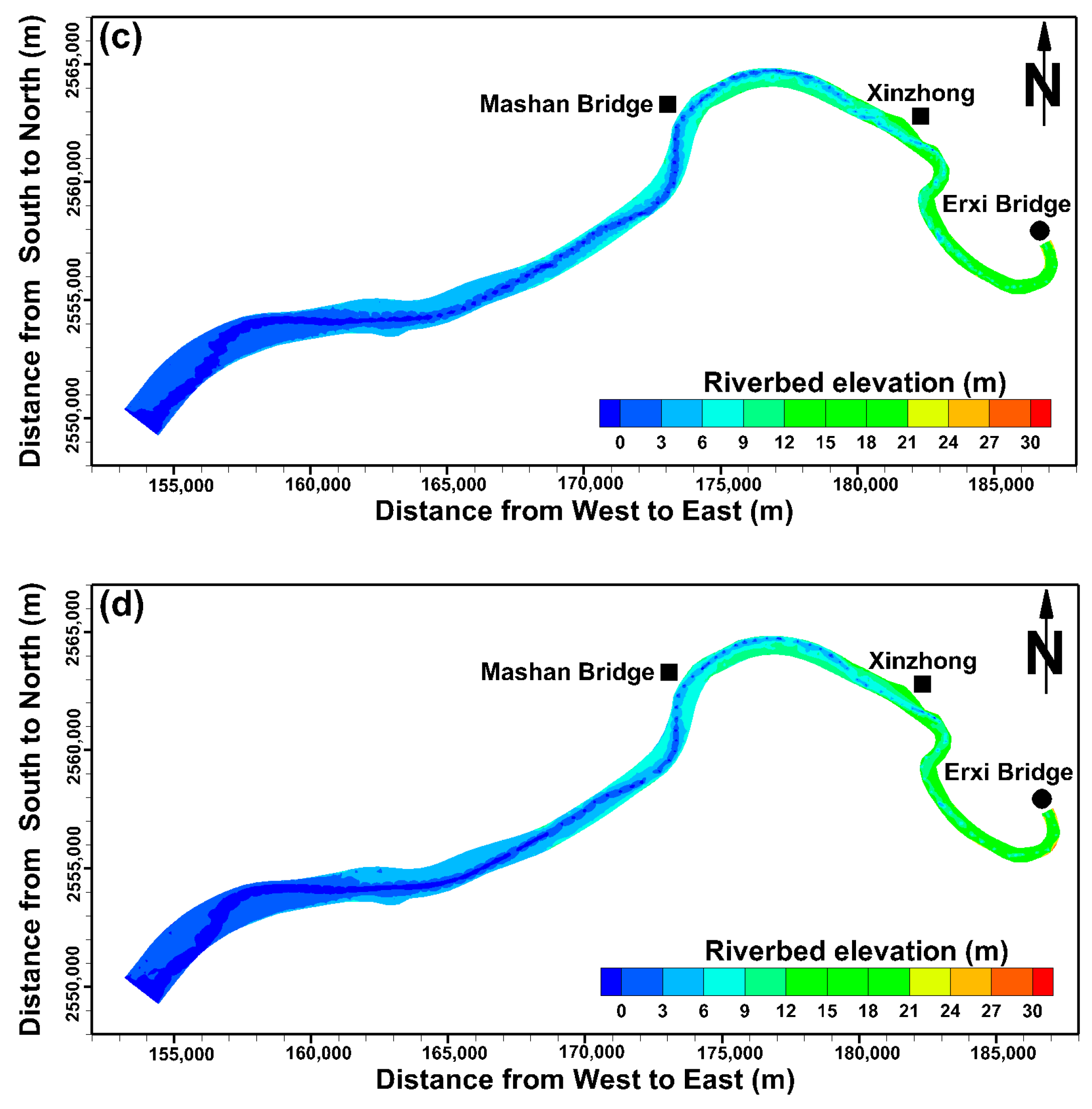
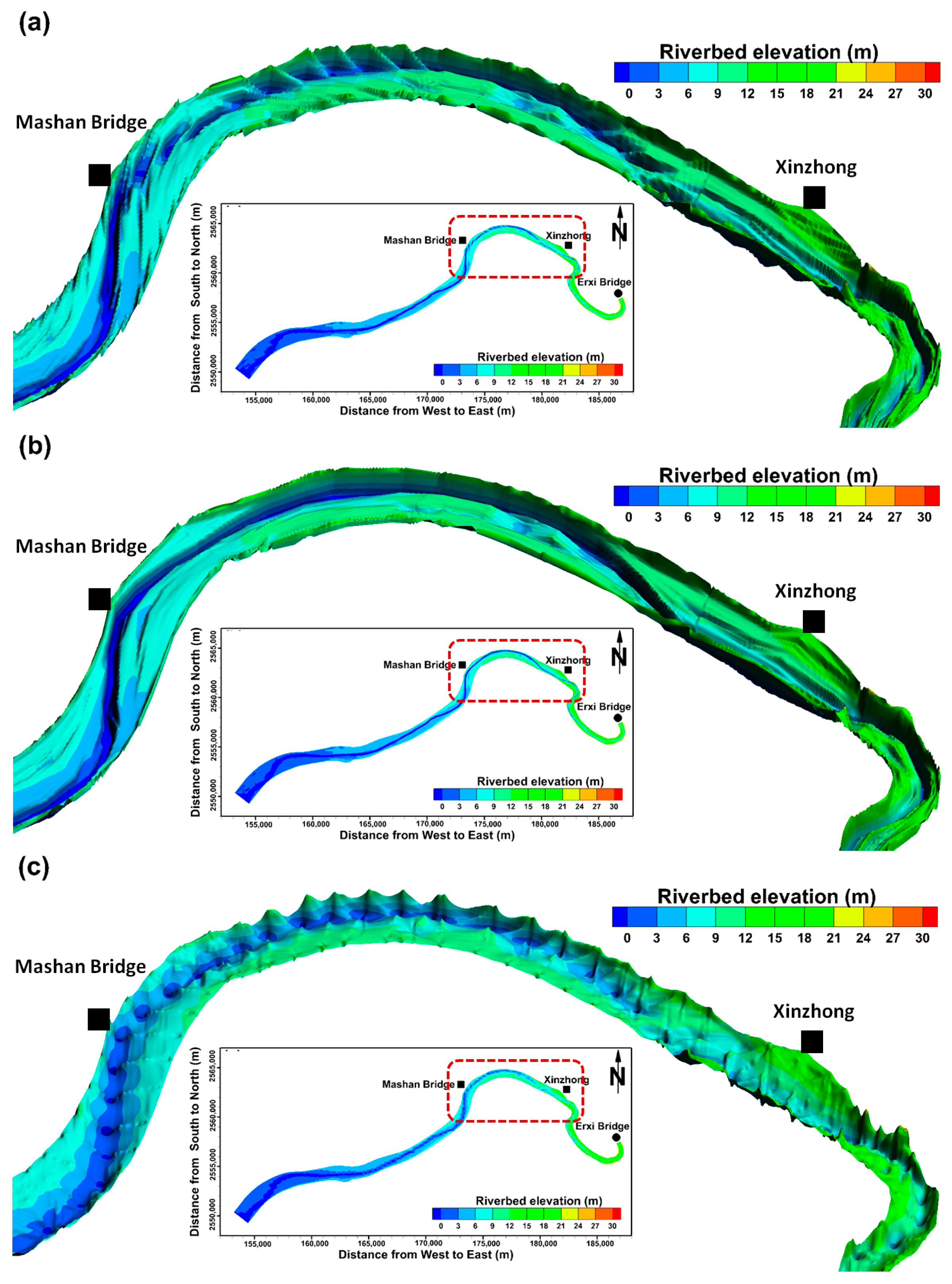
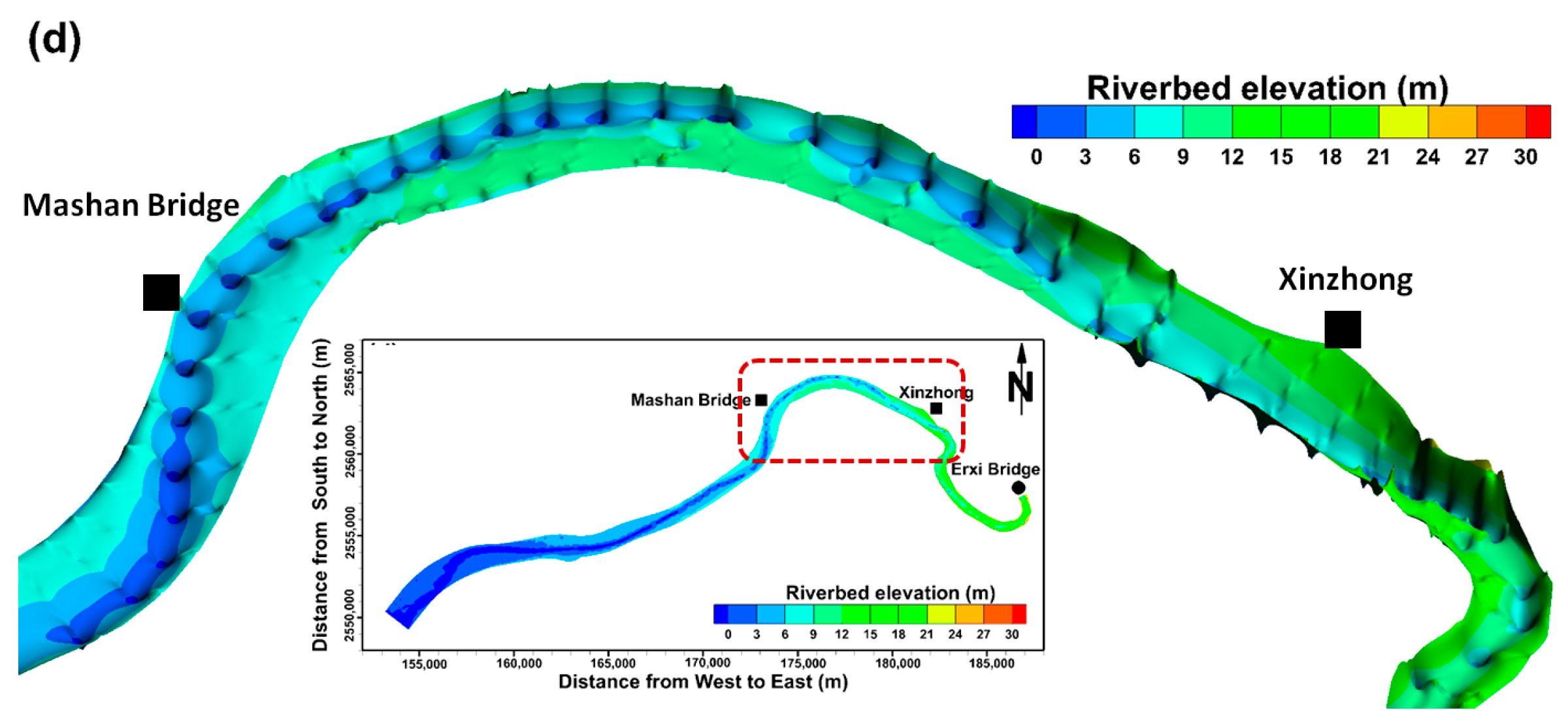
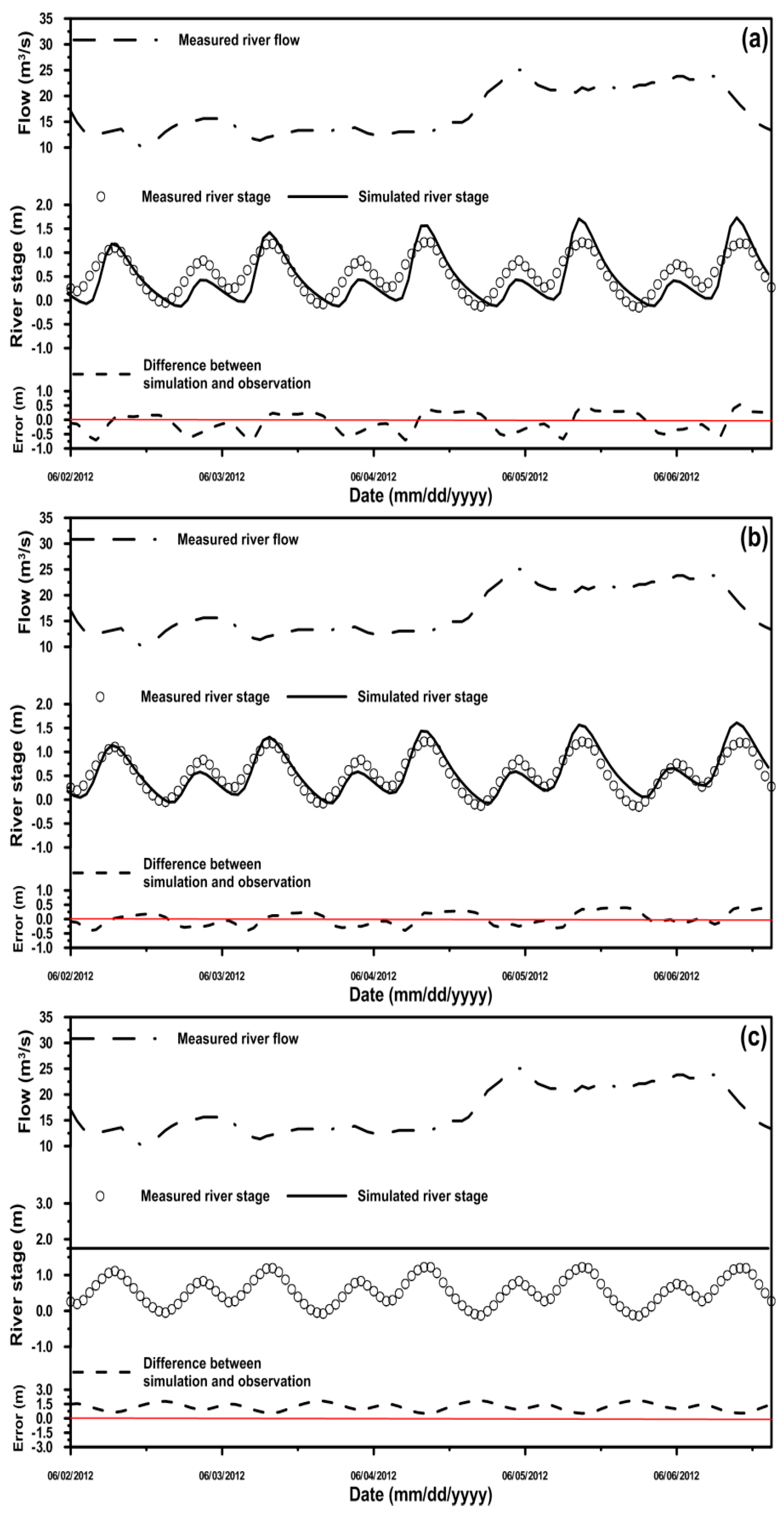
4.1. Simulation of the River Stage Using Different Cross-Section Data
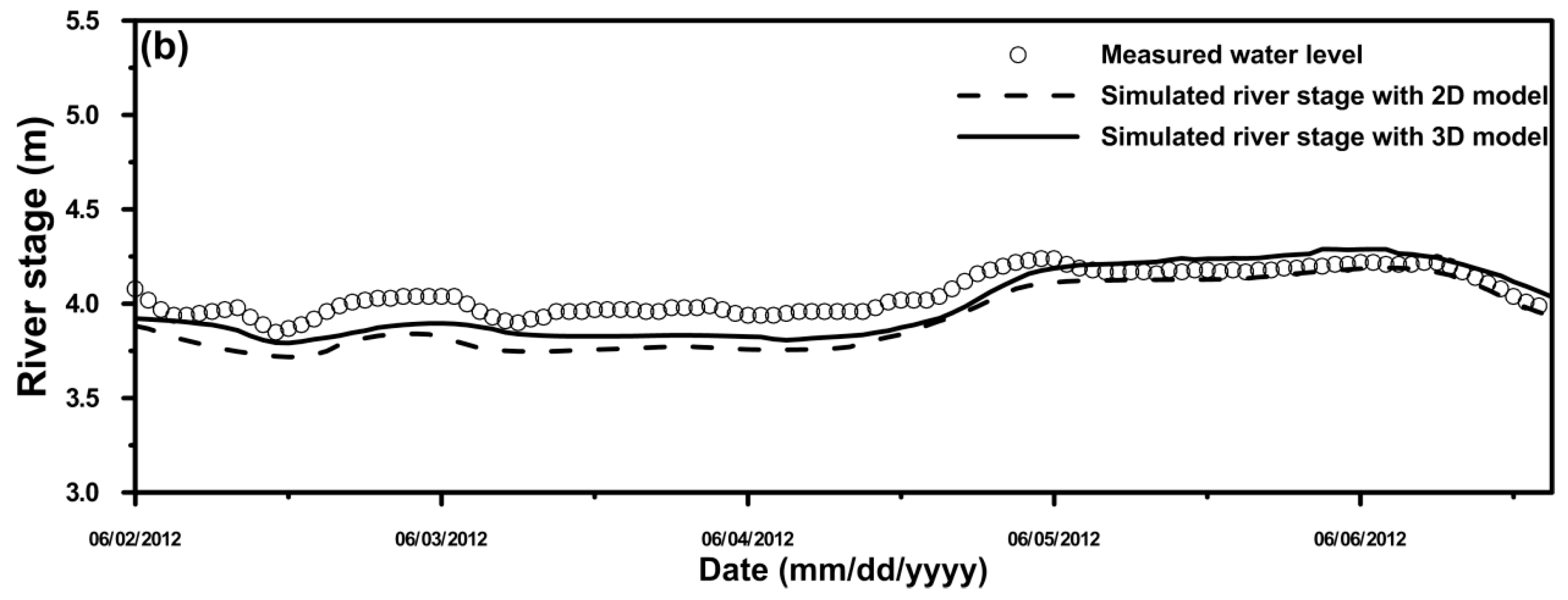
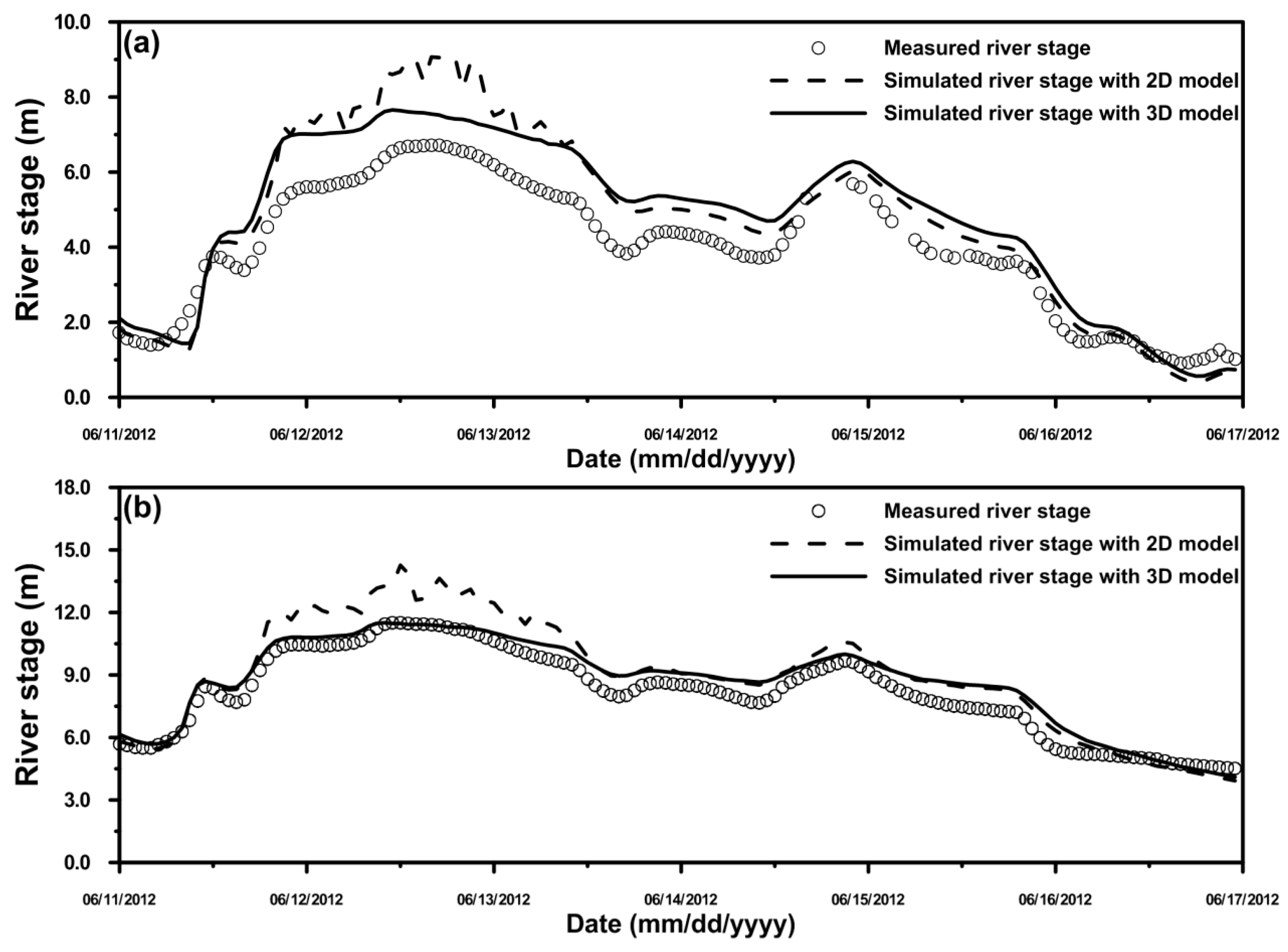
4.2. Comparison of the Simulated River Stage Using the 2D and 3D Models
4.3. Model Sensitivity
5. Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
Appendix B
References
- Yoshida, H.; Dittrich, A. 1D unsteady-state flow simulation of a section of the upper Rhine. J. Hydrol. 2002, 269, 78–88. [Google Scholar] [CrossRef]
- Juez, C.; Lacasta, A.; Murillo, J.; Garcia-Navarro, P. An efficient GPU implementation for a faster simulation of unsteady bed-load transport. J. Hydraul. Res. 2016, 54, 275–288. [Google Scholar] [CrossRef]
- Caviedes-Voullieme, D.; Morales-Hernandez, M.; Lopez-Marijuan, I.; García-Navarro, P. Reconstruction of 2D river beds by appropriate interpolation of 1D cross-sectional information for flood simulation. Environ. Model. Softw. 2014, 61, 206–228. [Google Scholar] [CrossRef]
- Merwade, V.M.; Cook, A.; Coonrod, J. GIS techniques for creating river terrain models for hydrodynamic modeling and flood inundation mapping. Environ. Model. Softw. 2008, 23, 1300–1311. [Google Scholar] [CrossRef]
- Chen, W.B.; Liu, W.C.; Wu, C.Y. Coupling of a one-dimensional river routing model and a three-dimensional ocean model to predict overbank flows in a complex river-ocean system. Appl. Math. Model. 2013, 37, 6163–6176. [Google Scholar] [CrossRef]
- Kasvi, E.; Alho, P.; Lotsari, E.; Wang, Y.S.; Kukko, A.; Hyyppa, H.; Hyppa, J. Two-dimensional and three-dimensional computational models in hydrodynamic and morphodynamic reconstructions of a river bend: Sensitivity and functionality. Hydrol. Process. 2015, 29, 1604–1629. [Google Scholar] [CrossRef]
- Horritt, M.S.; Bates, P.D.; Mattinson, M.J. Effects of mesh resolution and topographic representation in 2D finite volume models of shallow water fluvial flow. J. Hydrol. 2006, 329, 306–314. [Google Scholar] [CrossRef]
- Casas, A.; Benito, G.; Thorndycraft, V.; Rico, M. The topographic data source of digital terrain models. Earth Surf. Process. Landf. 2006, 31, 444–456. [Google Scholar] [CrossRef]
- Flanagin, M.; Grenotton, A.; Ratcliff, J.; Shaw, K.B.; Sample, J.; Abdelguerfi, M. Hydraulic splines-a hybrid approach to modeling river channel geometries. Comput. Sci. Eng. 2007, 9, 4–15. [Google Scholar] [CrossRef]
- Jha, S.K.; Mariethoz, G.; Kelly, B.F. Bathymetry fusion using multiple-point geostatistics: Novelty and challenges in representing non-stationary bedforms. Environ. Model. Softw. 2013, 50, 66–76. [Google Scholar] [CrossRef]
- Tomczak, M. Spatial interpolation and it uncertainty using automated anisotropic inverse distance weighting (IDW)-cross-validation/Jackknife approach. J. Geogr. Inform. Decis. Anal. 1998, 2, 18–30. [Google Scholar]
- Schappi, B.; Perona, P.; Schneider, P.; Burlando, P. Integrating river cross section measurements with digital terrain models for improved flow modeling applications. Comput. Geosci. 2010, 36, 707–716. [Google Scholar] [CrossRef]
- Legleiter, C.J.; Kyriakidis, P.C. Spatial prediction of river channel topography by kriging. Earth Surf. Process. Landf. 2008, 33, 841–867. [Google Scholar] [CrossRef]
- Cook, A.; Merwade, V. Effect of topographic data, geometric configuration and modeling approach on flood inundation mapping. J. Hydrol. 2009, 377, 131–142. [Google Scholar] [CrossRef]
- Horritt, M.S.; Bates, P.D. Effects of spatial resolution on a raster based model of flood flow. J. Hydrol. 2001, 253, 239–249. [Google Scholar] [CrossRef]
- Liu, X. Airborne LiDAR for DEM generation: Some critical issues. Prog. Phys. Geogr. 2008, 32, 31–49. [Google Scholar]
- Wang, C.K.; Philpot, W.D. Using airborne bathymetric Lidar to detect bottom type variation in shallow waters. Remote Sens. Environ. 2007, 106, 123–135. [Google Scholar] [CrossRef]
- Dal Cin, C.; Moens, L.; Dierickx, P.; Bastin, G.; Zech, Y. An integrated approach for realtime floodmap forecasting on the Belgian Meuse River. Nat. Hazards 2005, 36, 237–256. [Google Scholar]
- Merwade, V. Effect of spatial trends on interpolation of river bathymetry. J. Hydrol. 2009, 371, 169–181. [Google Scholar] [CrossRef]
- Zhang, Y.; Xian, C.; Chen, H.; Grieneisen, M.L.; Liu, J.; Zhang, M. Spatial interpolation of river channel topography using the shortest temporal distance. J. Hydrol. 2016, 542, 450–462. [Google Scholar] [CrossRef]
- Dyer, K.R. Estuaries: A Physical Introduction; Wiley: New York, NY, USA, 1997. [Google Scholar]
- Chen, W.B.; Liu, W.C. Modeling flood inundation induced by river flow and storm surge over a river basin. Water 2014, 6, 3182–3199. [Google Scholar] [CrossRef]
- Wei, H.P.; Yeh, K.C.; Liou, J.J.; Chen, Y.M.; Cheng, C.T. Estimating the risk of river flow under climate change in the Tsengwen River Basin. Water 2016, 8, 81. [Google Scholar] [CrossRef]
- Isaaks, E.H.; Srivastava, R.M. Applied Geostatistics; Oxford University Press: New York, NY, USA, 1989; pp. 257–258. [Google Scholar]
- Sibson, R. A brief description of natural neighbor interpolation. In Interpreting Multivariate Data; Barnett, V., Ed.; John Wiley and Sons: New York, NY, USA, 1981; Volume 21, pp. 21–36. [Google Scholar]
- Zhang, Y.; Baptisa, A.M. SELFE: A semi-implicit Eulerian-Lagrangian finite-element model for cross-scale ocean circulation. Ocean Model. 2008, 21, 71–96. [Google Scholar] [CrossRef]
- Zhang, Y.J.; Witter, R.C.; Priest, G.R. Tsunami-tide interaction in 1964 Prince William Sound tsunami. Ocean Model. 2011, 40, 246–259. [Google Scholar] [CrossRef]
- Zhang, Y.; Ye, F.; Stanev, E.V.; Grashorn, S. Seamless cross-scale modeling with SCHISM. Ocean Model. 2016, 102, 64–81. [Google Scholar] [CrossRef]
- Juez, C.; Murillo, J.; Garcia-Navarro, P. 2D simulation of granular flow over irregular steep slopes using global and local coordinates. J. Comput. Phys. 2013, 255, 166–204. [Google Scholar] [CrossRef]
- Langendoen, E.J.; Mendoza, A.; Abad, J.D.; Tassi, P.; Wang, D.; Ata, R.; Kadi Abederrezzak, E.K.; Hevouet, J.M. Improved numerical modeling of morphodynamics of rivers with steep banks. Adv. Water Resour. 2016, 93, 4–14. [Google Scholar] [CrossRef]
- Zu, T.; Gana, J.; Erofeevac, S.Y. Numerical study of the tide 456 and tidal dynamics in the South China Sea. Deep Sea Res. Part I 2008, 55, 137–154. [Google Scholar] [CrossRef]
- Prandle, D. The influence of bed friction and vertical eddy viscosity on tidal propagation. Cont. Shelf Res. 1997, 17, 1367–1374. [Google Scholar] [CrossRef]
- Kim, T.B.; Choi, S. Depth-averaged modeling of vegetated open-channel flows using finite element method. In Advances in Water Resources and Hydraulic Engineering, Proceedings of the 16th IAHR-APD Congress and 3rd Symposium of IAHR-ISHS; Spring: Berlin/Heidelberg, Germany, 2008; Volume 2, pp. 411–416. [Google Scholar]
- Dean, R.G.; Dalrymple, R.A. Coastal Processes with Engineering Applications; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Miller, A.J.; Cluer, B.L. Modeling considerations for simulation of flow in bedrock channels. In Rivers over Rock: Fluvial Processes in Bedrock Channels; Tinkler, K.J., Wohl, B.L., Eds.; Geophysical Monograph Series; American Geophysical Union: Washington, DC, USA, 2013; Volume 107, pp. 61–104. [Google Scholar]
- Large, W.G.; Pond, S. Open ocean momentum flux measurements in moderate to strong winds. J. Phys. Oceanogr. 1981, 11, 324–336. [Google Scholar] [CrossRef]
- Powell, M.D.; Vickery, P.J.; Reinhold, T.A. Reduced drag coefficient for high wind speeds in tropical cyclones. Nature 2003, 422, 279–283. [Google Scholar] [CrossRef] [PubMed]

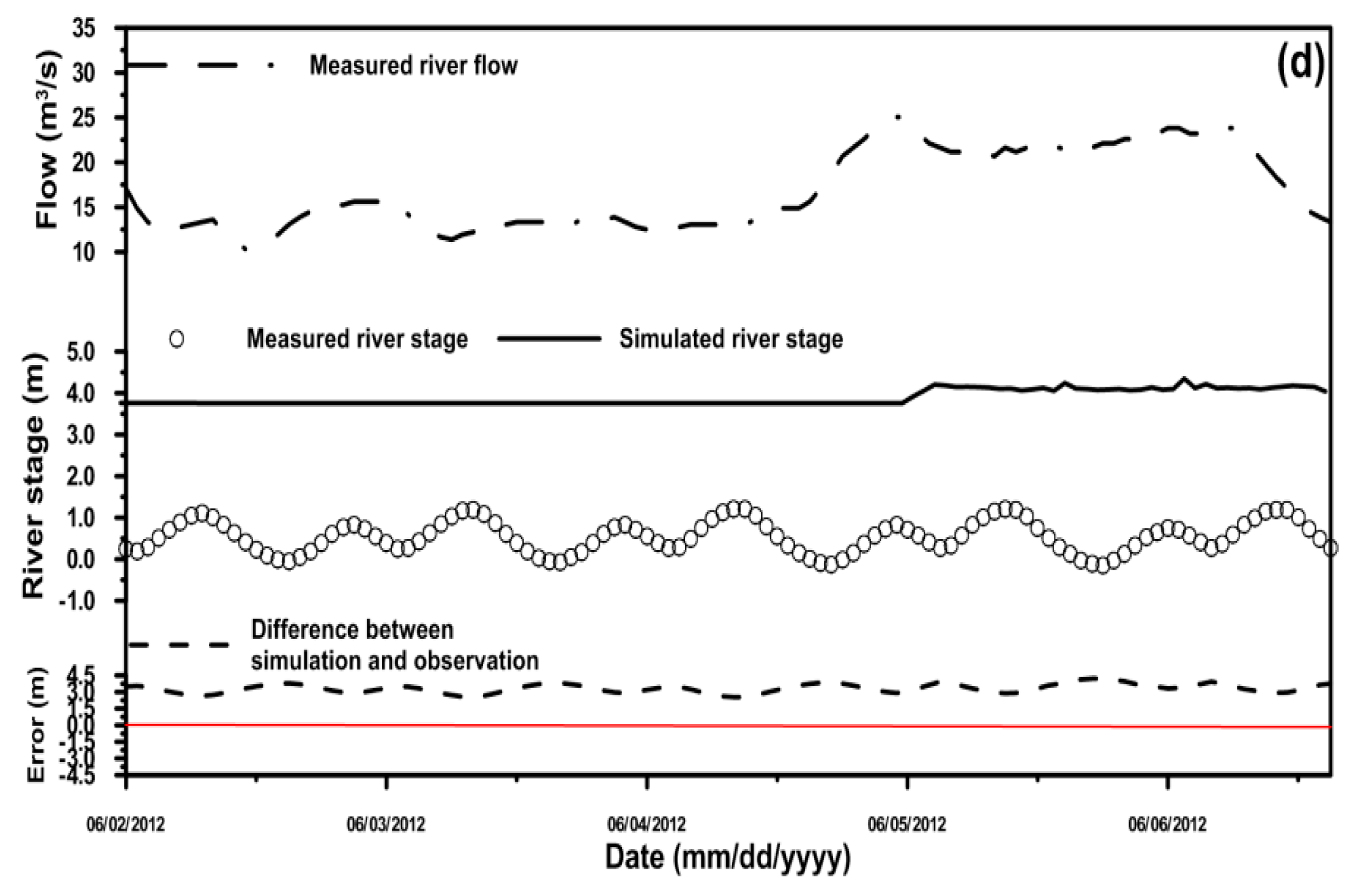
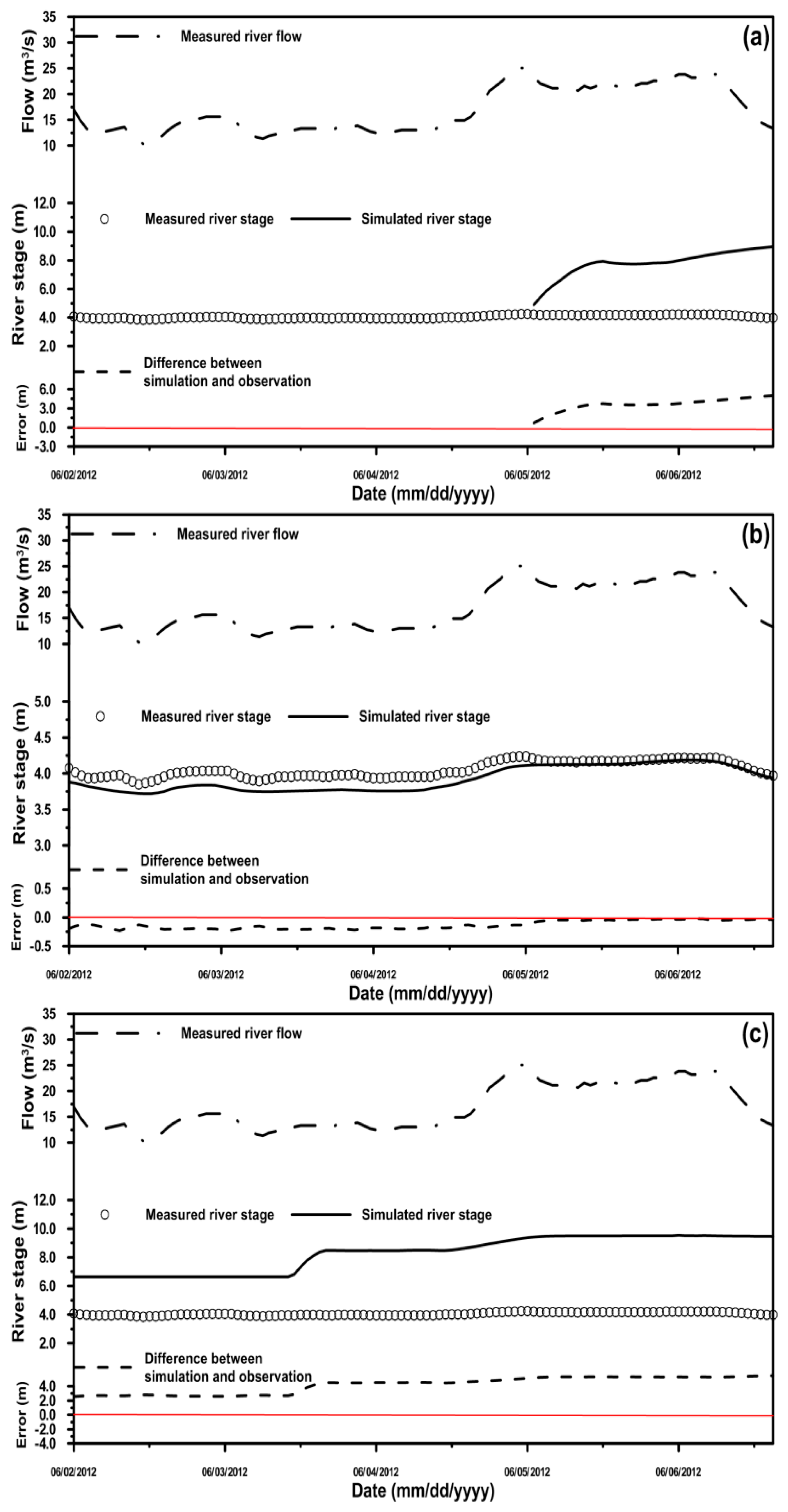
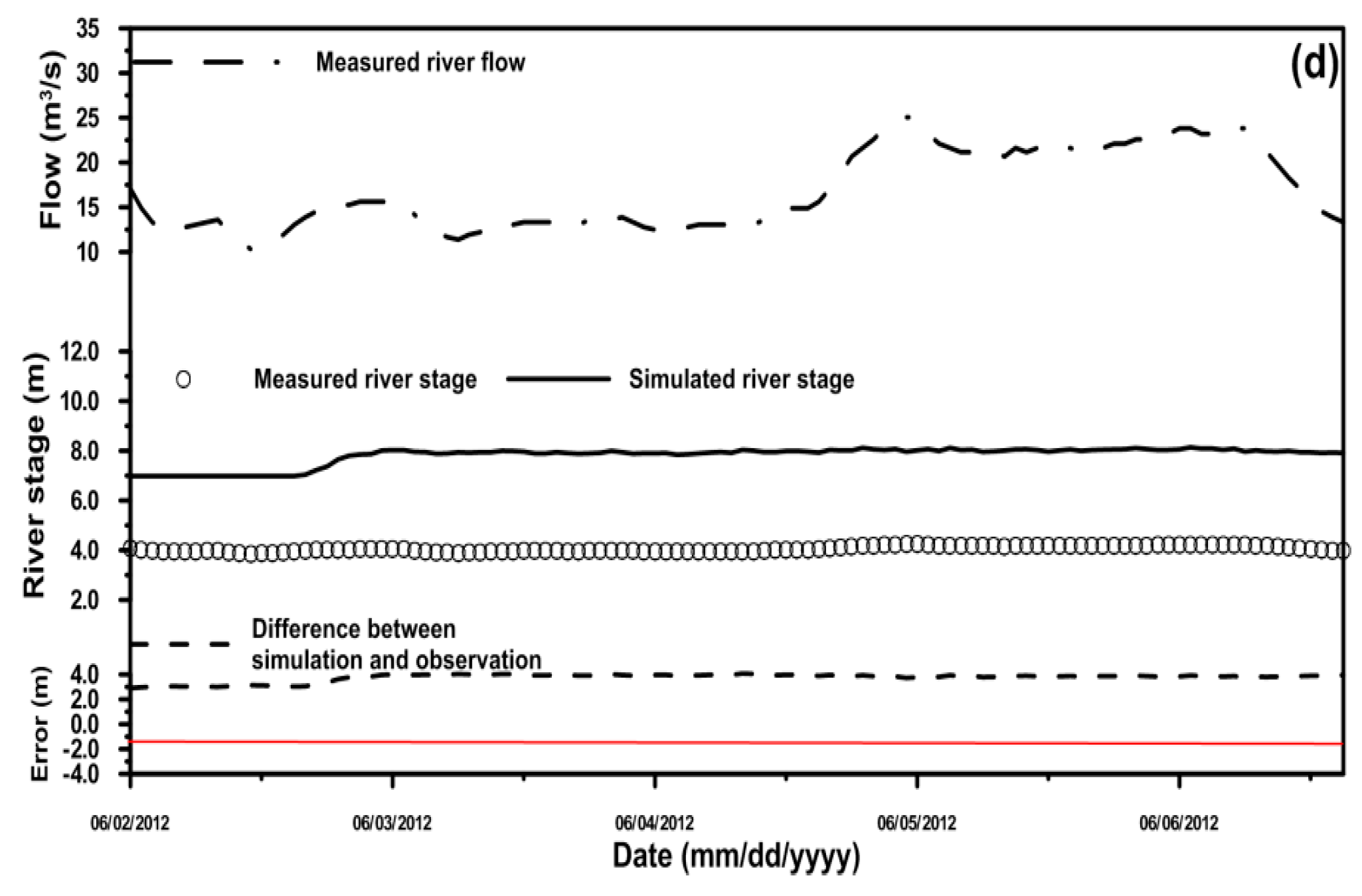
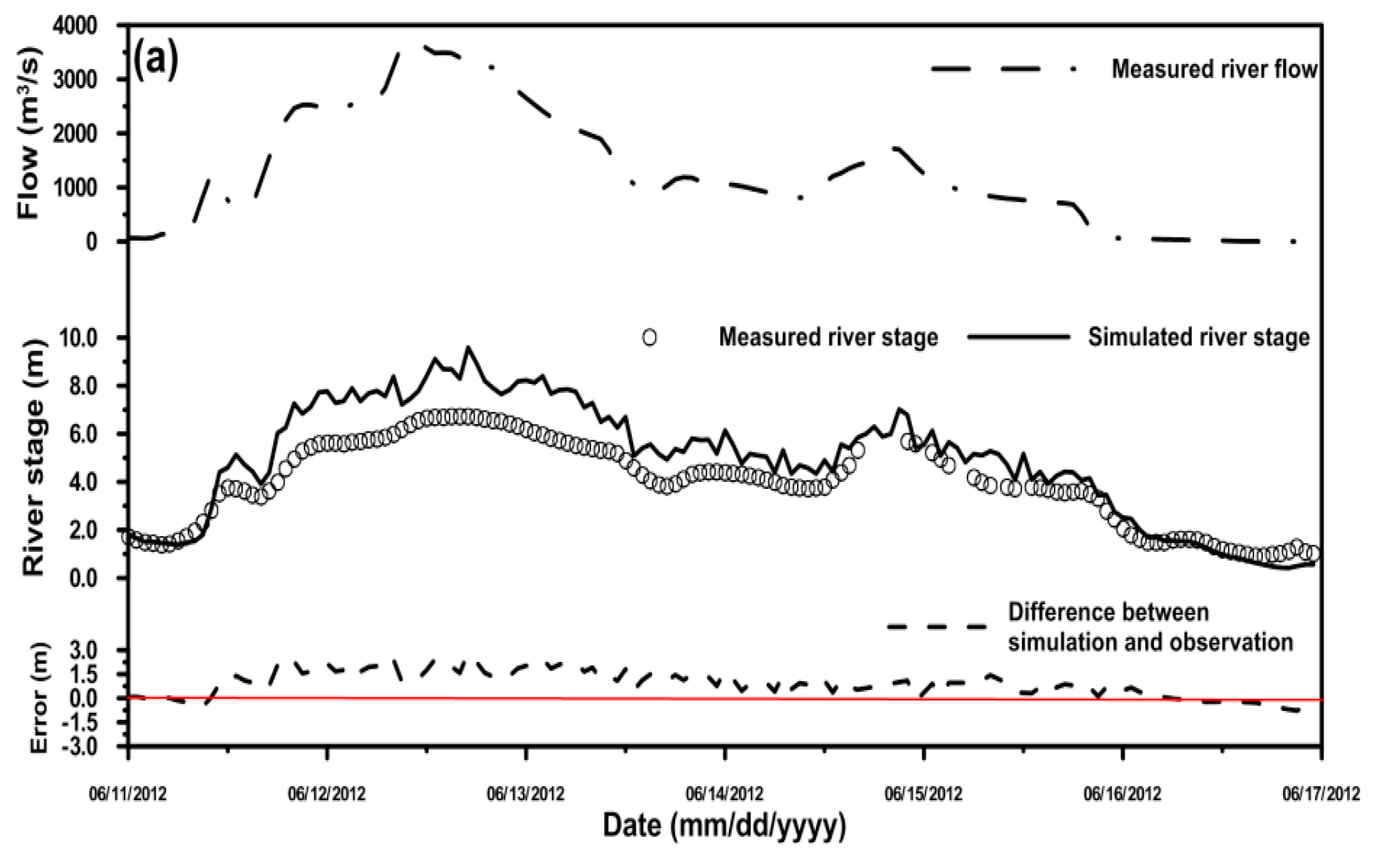
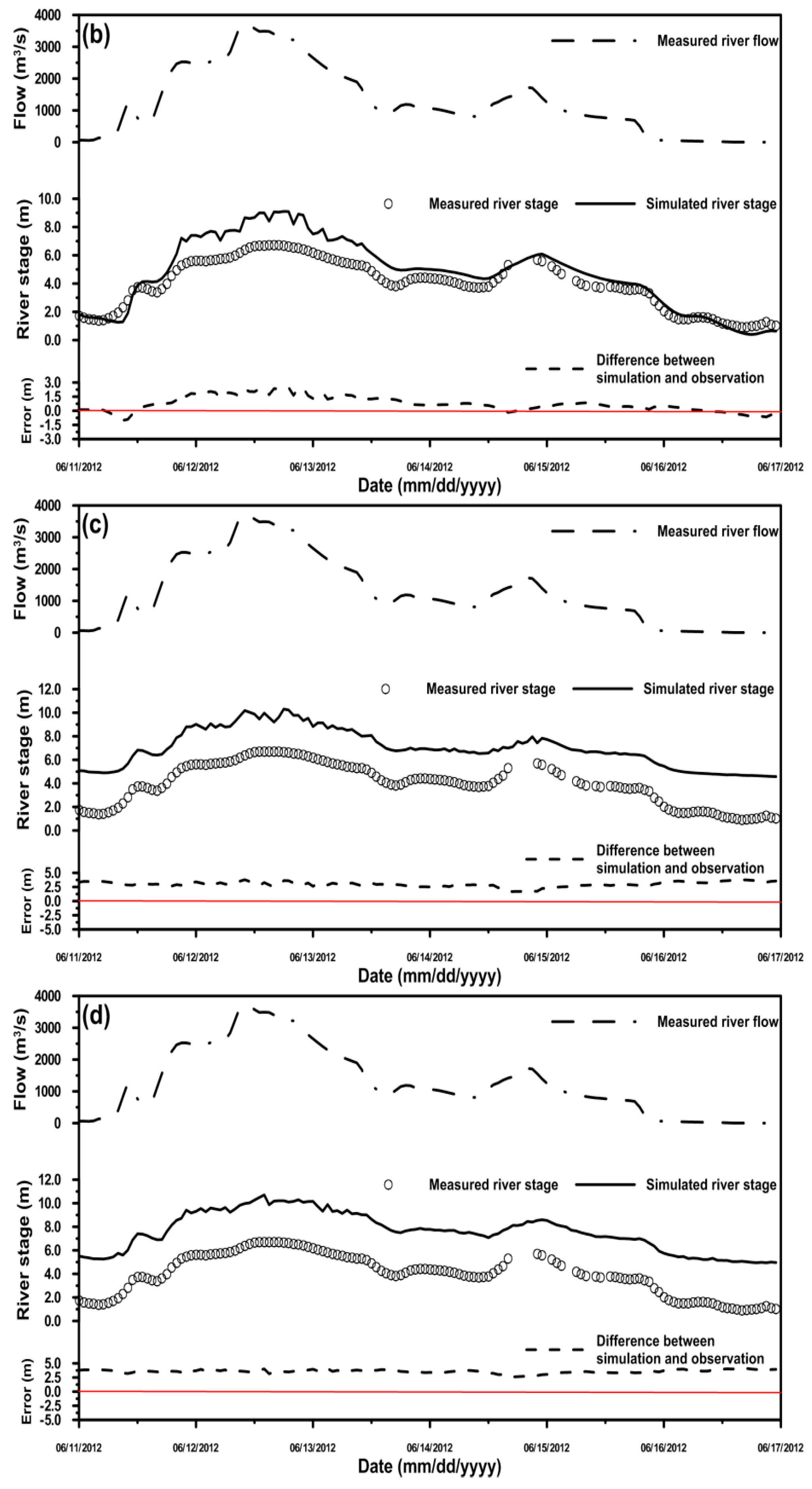
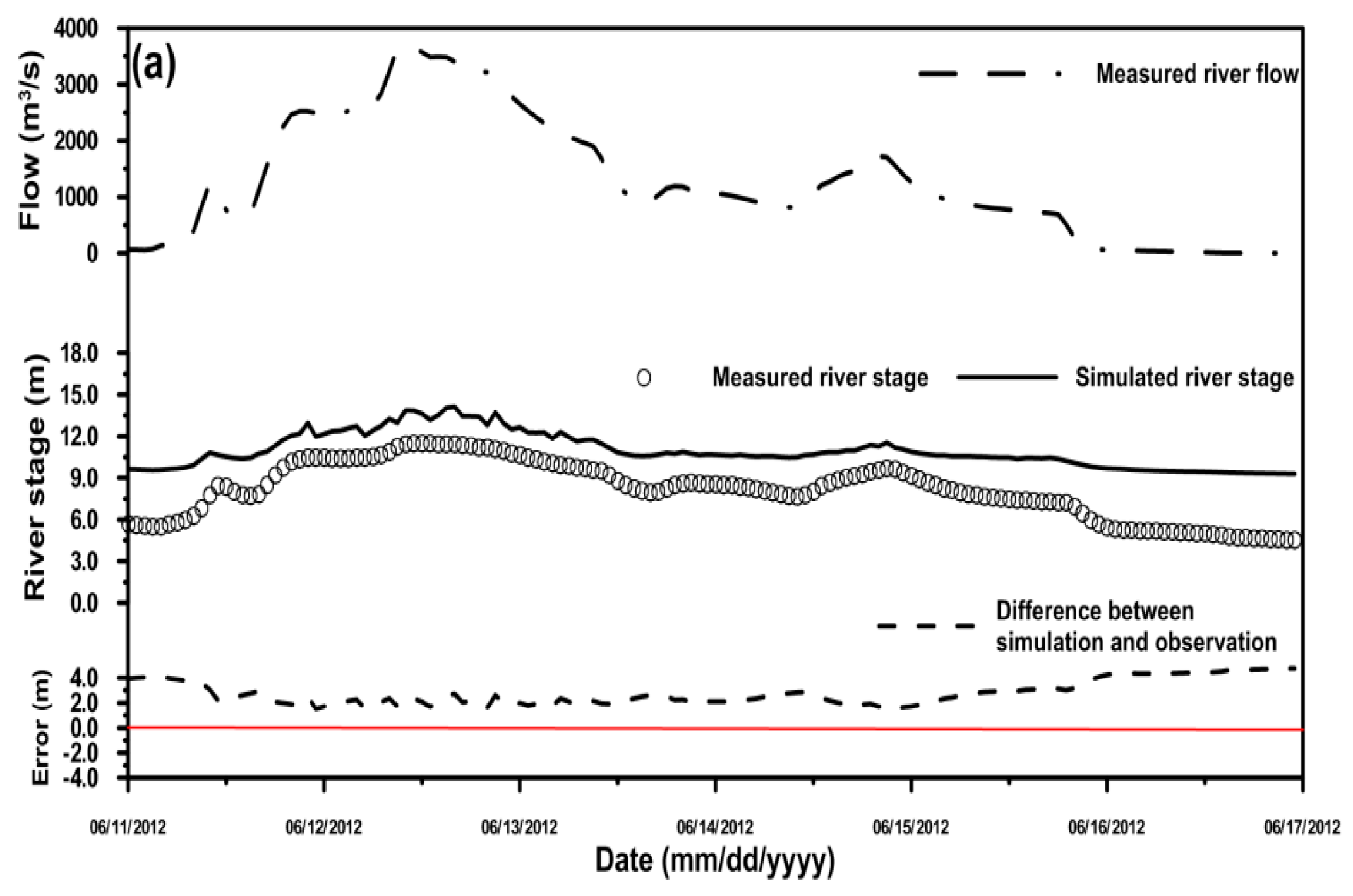
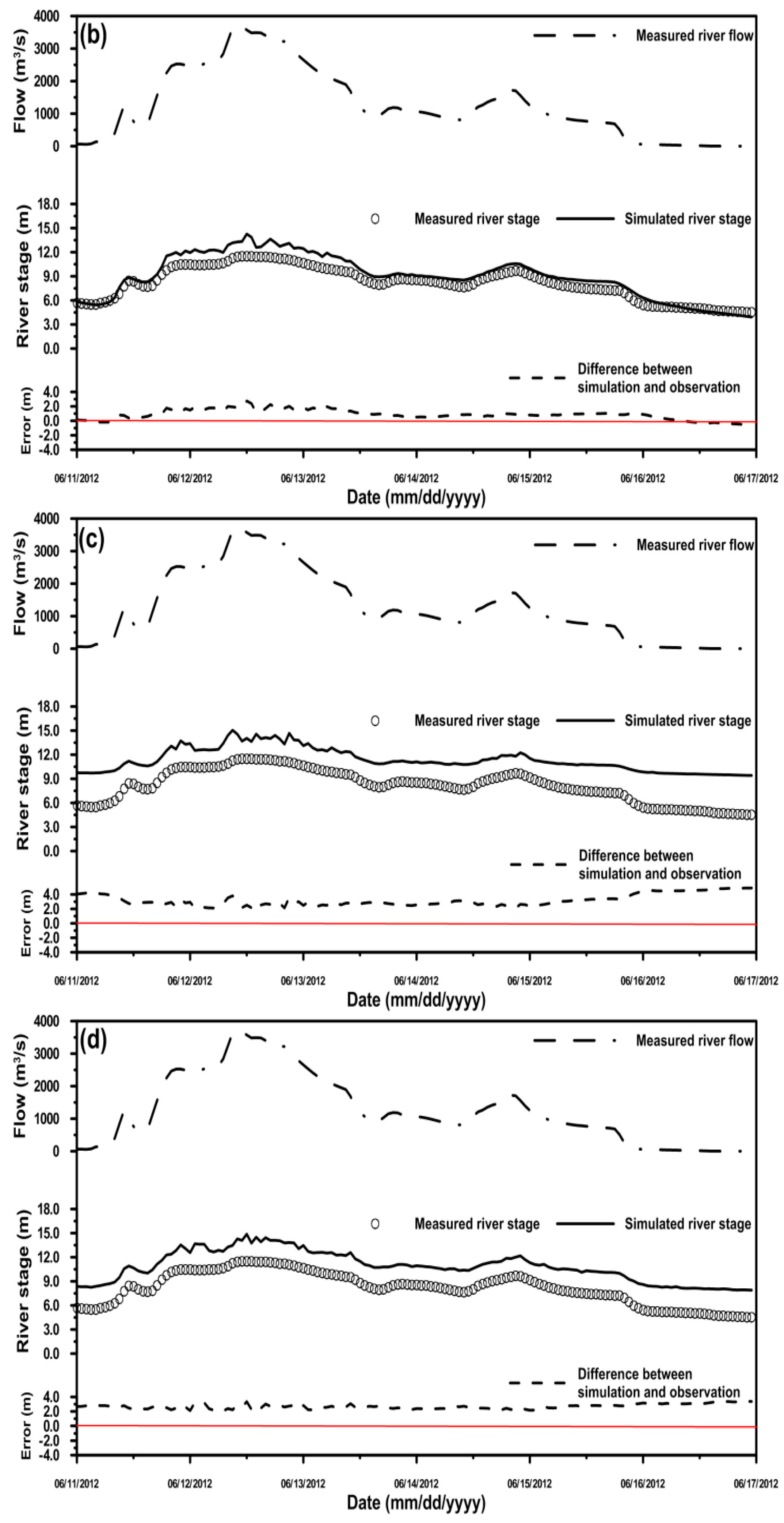
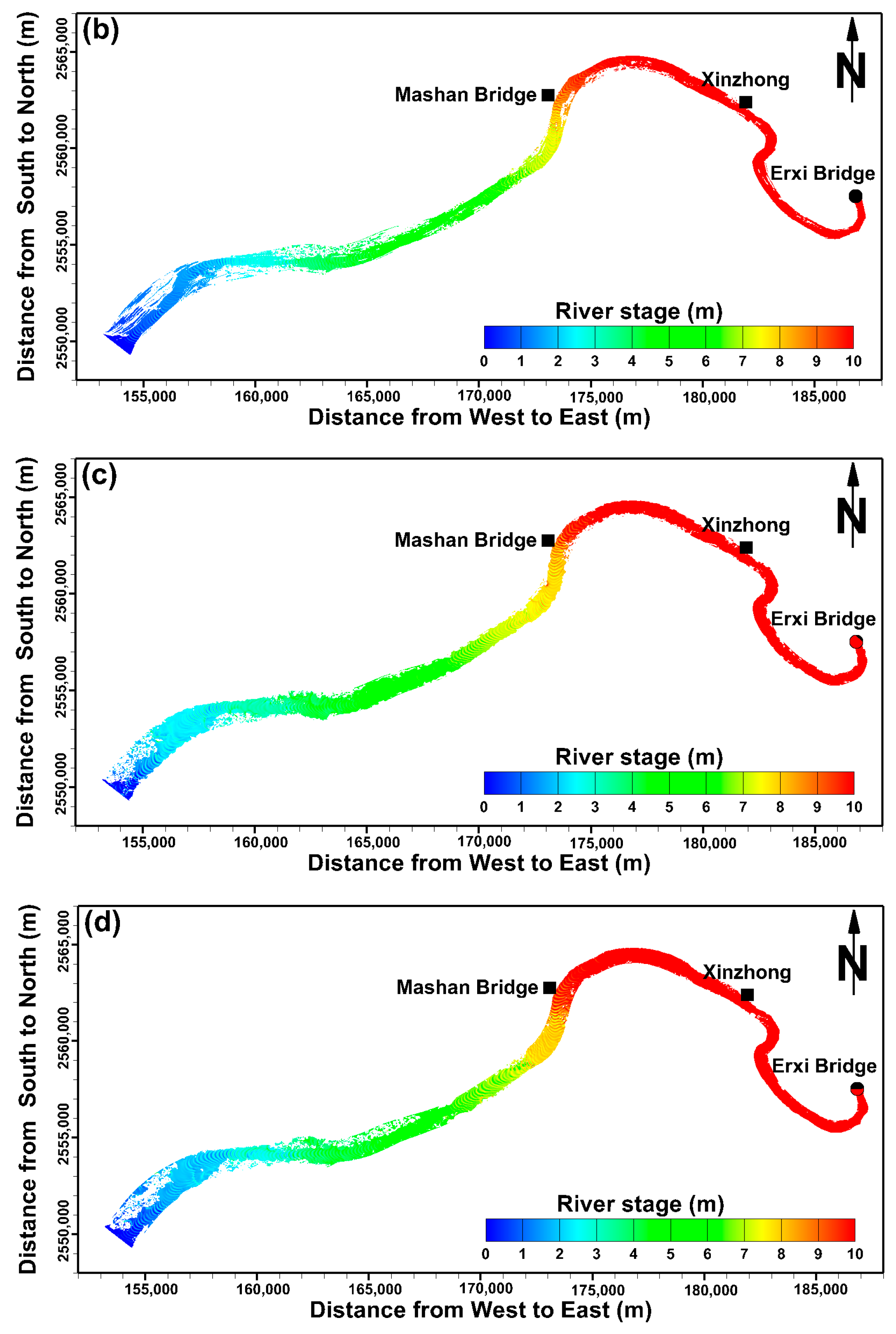
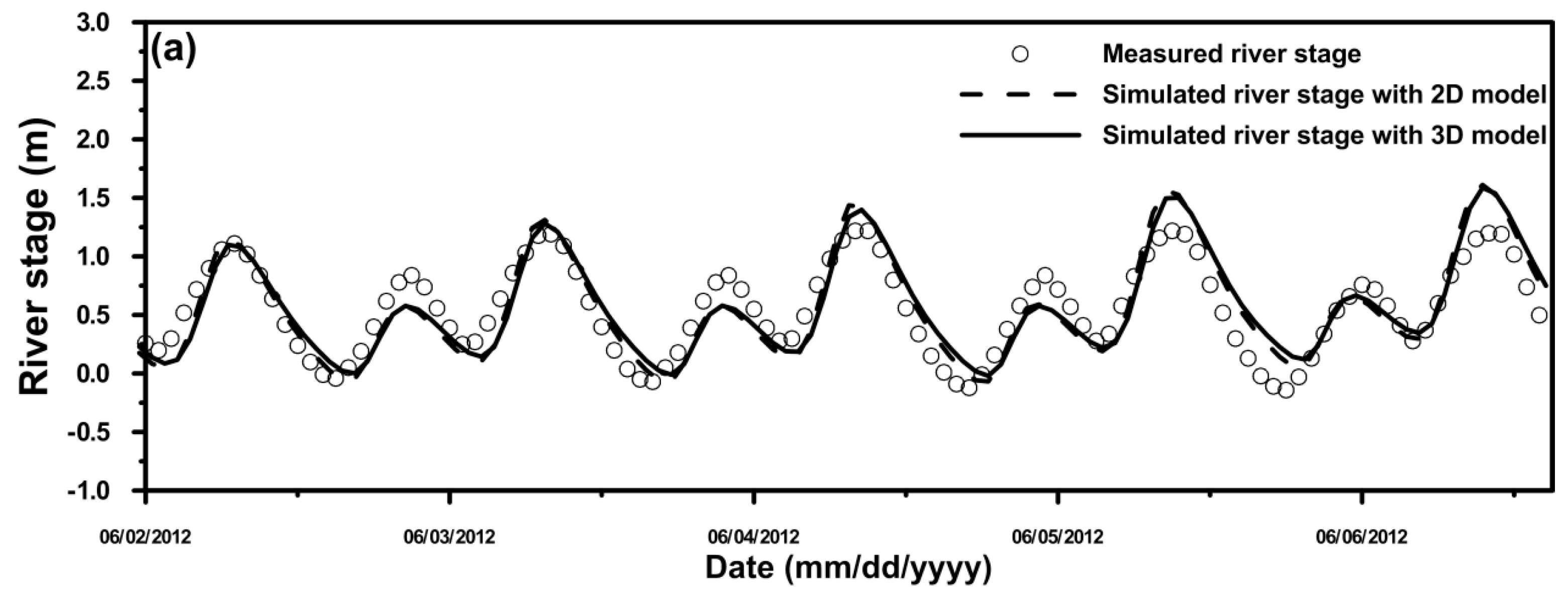
| Condition | Station | MAE (m) | RMSE (m) | PBIAS (%) |
|---|---|---|---|---|
| 2D modeling with original cross-section data | Mashan Bridge | 0.304 | 0.346 | −17.13 |
| Xinzhong | 3.627 | 3.750 | 87.090 | |
| 2D modeling with the linear interpolation method | Mashan Bridge | 0.203 | 0.232 | 1.229 |
| Xinzhong | 0.133 | 0.151 | −3.285 | |
| 2D modeling with the IDW method | Mashan Bridge | 1.190 | 1.250 | 214.385 |
| Xinzhong | 4.220 | 4.367 | 104.055 | |
| 2D modeling with the NN method | Mashan Bridge | 3.328 | 3.353 | 599.405 |
| Xinzhong | 3.760 | 3.774 | 92.715 | |
| 3D modeling with the linear interpolation method | Mashan Bridge | 0.216 | 0.253 | 3.390 |
| Xinzhong | 0.096 | 0.105 | −1.404 |
| Condition | Station | MAE (m) | RMSE (m) | PBIAS (%) |
|---|---|---|---|---|
| 2D modeling with original cross-section data | Mashan Bridge | 1.018 | 1.238 | 22.981 |
| Xinzhong | 2.794 | 2.956 | 34.254 | |
| 2D modeling with the linear interpolation method | Mashan Bridge | 0.911 | 1.135 | 19.670 |
| Xinzhong | 0.934 | 1.093 | 10.499 | |
| 2D modeling with the IDW method | Mashan Bridge | 3.038 | 3.063 | 77.010 |
| Xinzhong | 3.192 | 3.293 | 39.133 | |
| 2D modeling with the NN method | Mashan Bridge | 3.613 | 3.623 | 91.595 |
| Xinzhong | 2.690 | 2.711 | 32.978 | |
| 3D modeling with the linear interpolation method | Mashan Bridge | 0.858 | 0.950 | 19.428 |
| Xinzhong | 0.546 | 0.645 | 6.267 |
| Condition | Station | Maximum Rate of River Stage (%) |
|---|---|---|
| 2D modeling with increasing 50% BDC | Mashan Bridge | 0.615 |
| Xinzhong | 0.081 | |
| 2D modeling with decreasing 50% BDC | Mashan Bridge | −1.037 |
| Xinzhong | −0.069 | |
| 3D modeling with increasing 50% BDC | Mashan Bridge | 0.208 |
| Xinzhong | 0.002 | |
| 3D modeling with decreasing 50% BDC | Mashan Bridge | −0.353 |
| Xinzhong | −0.005 | |
| 3D modeling with increasing 50% VEV | Mashan Bridge | 0.001 |
| Xinzhong | 0.009 | |
| 3D modeling with decreasing 50% VEV | Mashan Bridge | −0.006 |
| Xinzhong | −0.007 |
| Condition | Station | Maximum Rate of River Stage (%) |
|---|---|---|
| 2D modeling with increasing 50% BDC | Mashan Bridge | 2.612 |
| Xinzhong | 5.960 | |
| 2D modeling with decreasing 50% BDC | Mashan Bridge | −0.267 |
| Xinzhong | −4.217 | |
| 3D modeling with increasing 50% BDC | Mashan Bridge | 1.309 |
| Xinzhong | 0.329 | |
| 3D modeling with decreasing 50% BDC | Mashan Bridge | −0.0003 |
| Xinzhong | −0.0001 | |
| 3D modeling with increasing 50% VEV | Mashan Bridge | 0.943 |
| Xinzhong | 0.506 | |
| 3D modeling with decreasing 50% VEV | Mashan Bridge | −0.945 |
| Xinzhong | −0.508 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, W.-B.; Liu, W.-C. Modeling the Influence of River Cross-Section Data on a River Stage Using a Two-Dimensional/Three-Dimensional Hydrodynamic Model. Water 2017, 9, 203. https://doi.org/10.3390/w9030203
Chen W-B, Liu W-C. Modeling the Influence of River Cross-Section Data on a River Stage Using a Two-Dimensional/Three-Dimensional Hydrodynamic Model. Water. 2017; 9(3):203. https://doi.org/10.3390/w9030203
Chicago/Turabian StyleChen, Wei-Bo, and Wen-Cheng Liu. 2017. "Modeling the Influence of River Cross-Section Data on a River Stage Using a Two-Dimensional/Three-Dimensional Hydrodynamic Model" Water 9, no. 3: 203. https://doi.org/10.3390/w9030203
APA StyleChen, W.-B., & Liu, W.-C. (2017). Modeling the Influence of River Cross-Section Data on a River Stage Using a Two-Dimensional/Three-Dimensional Hydrodynamic Model. Water, 9(3), 203. https://doi.org/10.3390/w9030203







