An Approach to Predict Debris Flow Average Velocity
Abstract
:1. Introduction
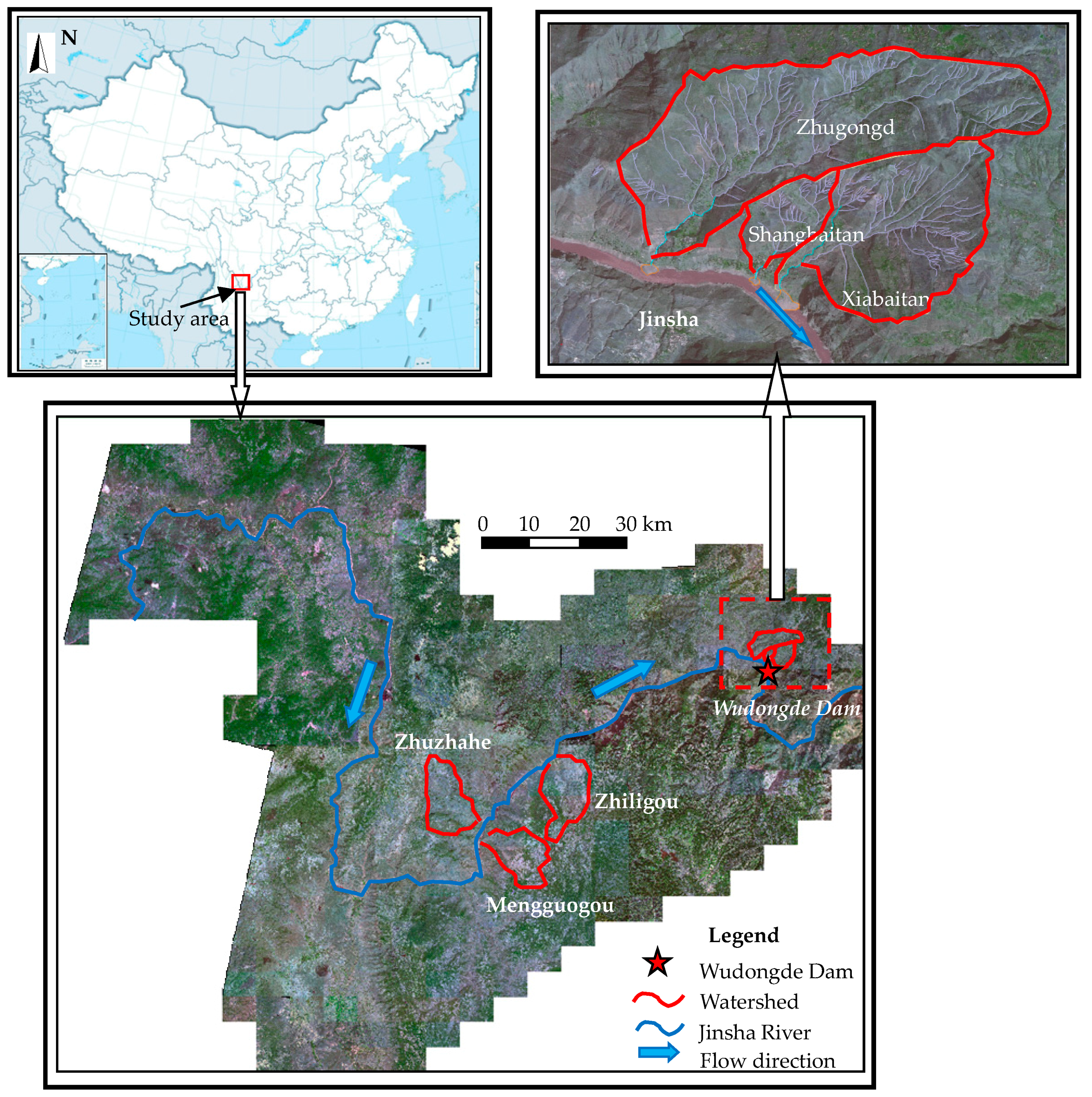
2. Study Area
3. Data Acquisition
4. Methodology
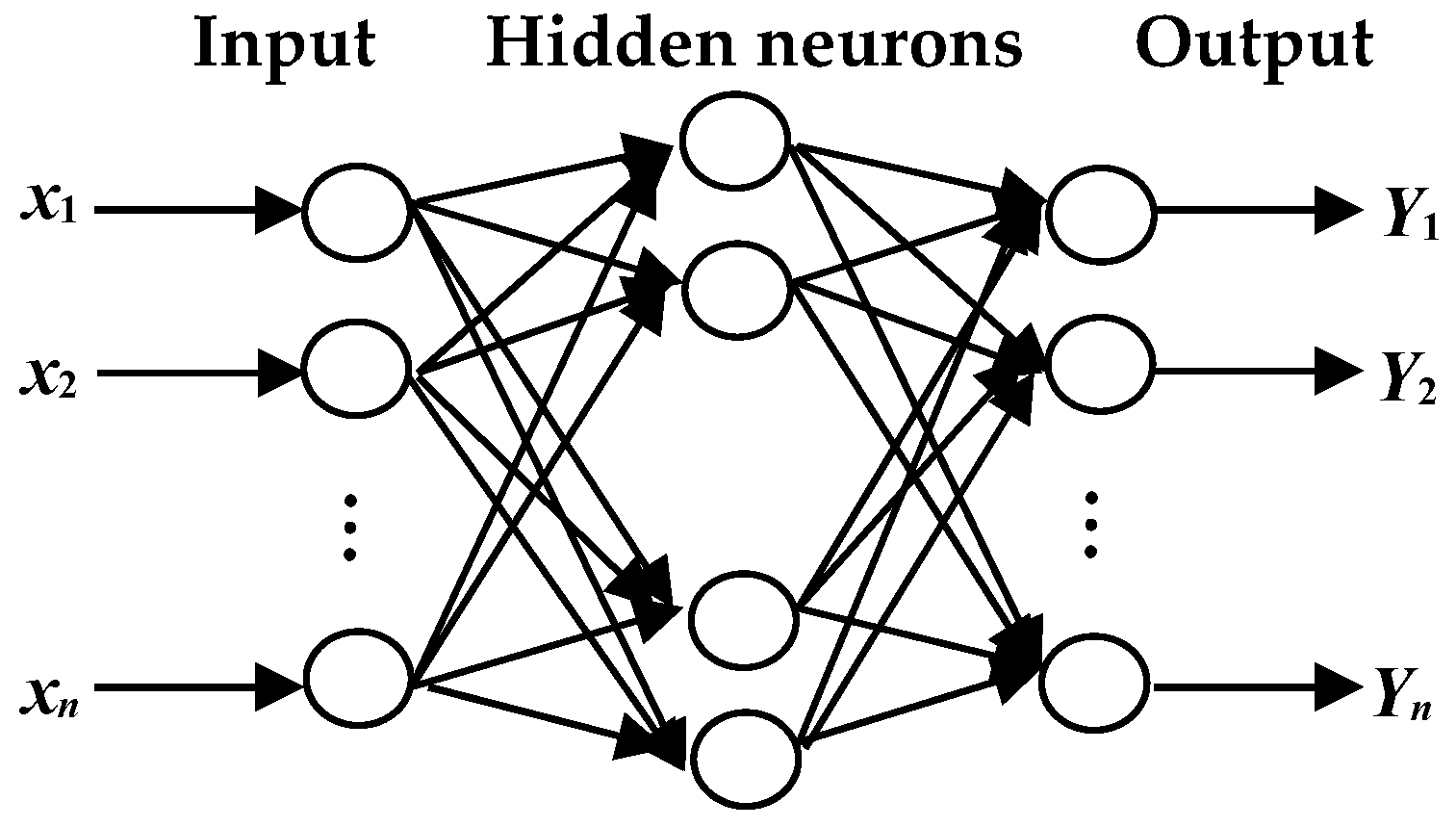
4.1. Radial Basis Function Neural Network
- Step 1. Initialize the weights randomly
- Step 2. Calculate the output vector Y by the equation:where Wi is the weight of the ith hidden neuron to the output node.
- Step 3. Calculate the error εi for each neuron in the output by the equation:where is the desired output of the ith neuron in the output layer.
- Step 4. Based on the least squares method, determine the weights between the hidden neurons and the output nodes:where cmax is the maximum distance between the selected centers.
- Step 5. Update the weights until the error meets the requirement:where W′ij is the updated weight and μ is learning rate. When the network clustering center Ci and weight Wi are determined, we can conduct the predictions with the training model.
4.2. The Gravitational Search Algorithm
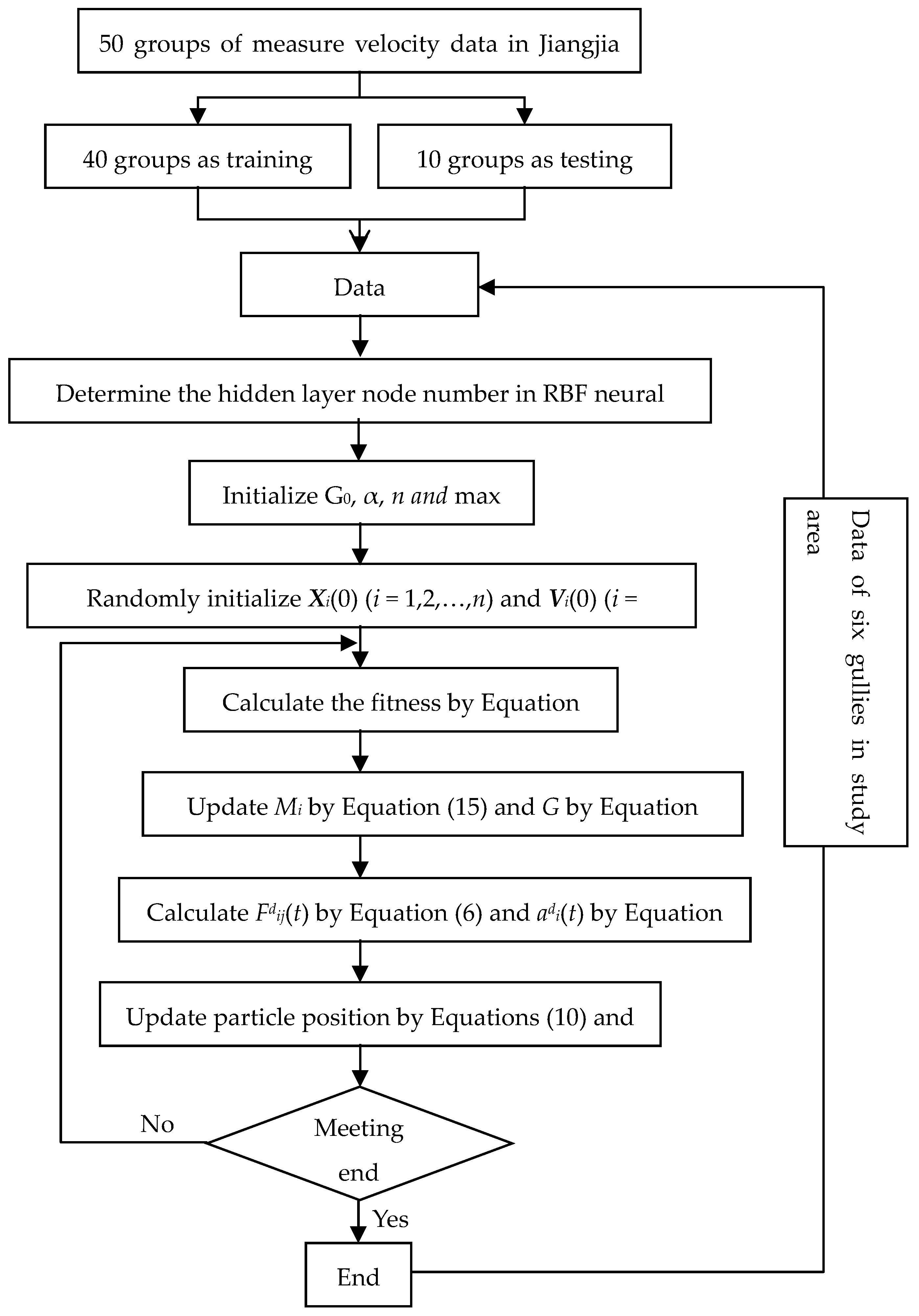
4.3. The Proposed GSA-RBF Method
4.4. The Modified Dongchuan Empirical Equation
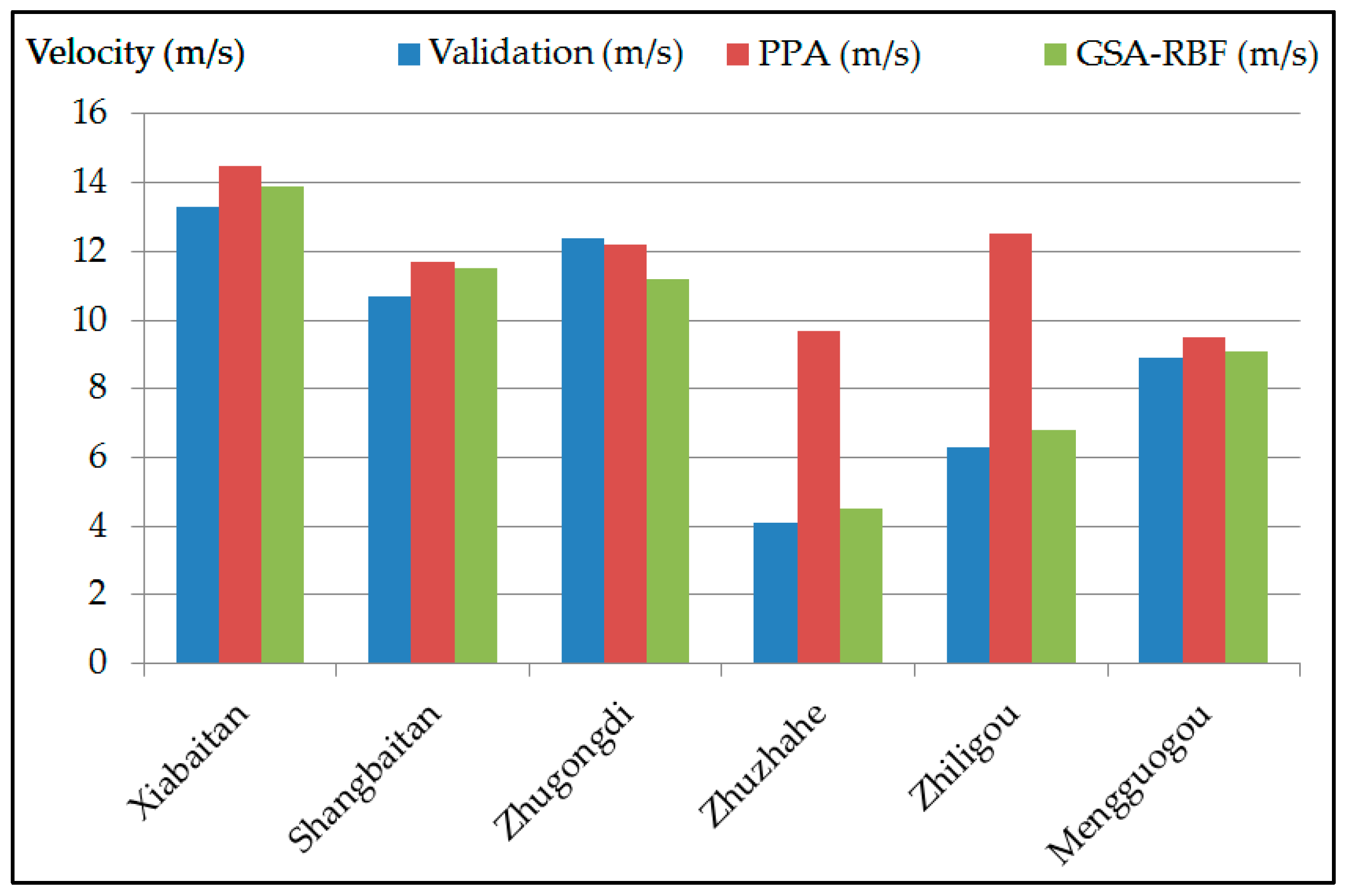
5. Results and Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Cao, C.; Xu, P.; Chen, J.; Zheng, L.; Niu, C. Hazard assessment of debris-flow along the baicha river in heshigten banner, inner mongolia, china. Int. J. Environ. Res. Public Health 2016, 14, 30. [Google Scholar] [CrossRef] [PubMed]
- Tang, C.; Zhu, J.; Li, W.L.; Liang, J.T. Rainfall-Triggered debris flows following the wenchuan earthquake. B Eng. Geol. Environ. 2009, 68, 187–194. [Google Scholar] [CrossRef]
- Cui, P.; Zhu, Y.-Y.; Han, Y.-S.; Chen, X.-Q.; Zhuang, J.-Q. The 12 may wenchuan earthquake-induced landslide lakes: Distribution and preliminary risk evaluation. Landslides 2009, 6, 209–223. [Google Scholar] [CrossRef]
- Cui, P.; Chen, X.Q.; Zhu, Y.Y.; Su, F.H.; Wei, F.Q.; Han, Y.S.; Liu, H.J.; Zhuang, J.Q. The wenchuan earthquake (May 12, 2008), sichuan province, china, and resulting geohazards. Nat. Hazards 2011, 56, 19–36. [Google Scholar] [CrossRef]
- Hu, K.H.; Wei, F.Q.; Li, Y. Real-Time measurement and preliminary analysis of debris-flow impact force at jiangjia ravine, china. Earth Surf. Proc. Land 2011, 36, 1268–1278. [Google Scholar] [CrossRef]
- Li, Y.; Liu, J.J.; Hu, K.H.; Su, P.C. Probability distribution of measured debris-flow velocity in jiangjia gully, yunnan province, china. Nat. Hazards 2012, 60, 689–701. [Google Scholar]
- Cascini, L.; Cuomo, S.; Pastor, M. Inception of debris avalanches: Remarks on geomechanical modelling. Landslides 2013, 10, 701–711. [Google Scholar] [CrossRef]
- Bugnion, L.; McArdell, B.W.; Bartelt, P.; Wendeler, C. Measurements of hillslope debris flow impact pressure on obstacles. Landslides 2012, 9, 179–187. [Google Scholar] [CrossRef]
- Scheidl, C.; Chiari, M.; Kaitna, R.; Mullegger, M.; Krawtschuk, A.; Zimmermann, T.; Proske, D. Analysing debris-flow impact models, based on a small scale modelling approach. Surv. Geophys. 2013, 34, 121–140. [Google Scholar] [CrossRef]
- Johnson, C.G.; Kokelaar, B.P.; Iverson, R.M.; Logan, M.; LaHusen, R.G.; Gray, J.M.N.T. Grain-Size segregation and levee formation in geophysical mass flows. J. Geophys. Res.-Earth 2012, 117. [Google Scholar] [CrossRef]
- Murakawa, Y.; Hara, M.; Oguchi, H.; Hamate, Y.; Kuwano, H. Surface acoustic wave based sensors employing ionic liquid for hydrogen sulfide gas detection. Microsyst. Technol. 2013, 19, 1255–1259. [Google Scholar] [CrossRef]
- Berti, M.; Genevois, R.; LaHusen, R.; Simoni, A.; Tecca, P.R. Debris flow monitoring in the acquabona watershed on the dolomites (Italian alps). Phys. Chem. Earth Part B 2000, 25, 707–715. [Google Scholar] [CrossRef]
- Hurlimann, M.; Rickenmann, D.; Graf, C. Field and monitoring data of debris-flow events in the swiss alps. Can. Geotech. J. 2003, 40, 161–175. [Google Scholar] [CrossRef]
- Uddin, M.S.; Inaba, H.; Itakura, Y.; Yoshida, Y.; Kasahara, M. Adaptive computer-based spatial-filtering method for more accurate estimation of the surface velocity of debris flow. Appl. Opt. 1999, 38, 6714–6721. [Google Scholar] [CrossRef] [PubMed]
- Han, Z.; Chen, G.; Li, Y.; Xu, L.; Zheng, L.; Zhang, Y. A new approach for analyzing the velocity distribution of debris flows at typical cross-sections. Nat. Hazards 2014, 74, 2053–2070. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, W.J.; Xu, Q.; Xie, P.; Hao, L. Run-Out analysis of flow-like landslides triggered by the ms 8.0 2008 wenchuan earthquake using smoothed particle hydrodynamics. Landslides 2012, 9, 275–283. [Google Scholar] [CrossRef]
- Cascini, L.; Cuomo, S.; Pastor, M.; Sorbino, G.; Piciullo, L. Sph run-out modelling of channelised landslides of the flow type. Geomorphology 2014, 214, 502–513. [Google Scholar] [CrossRef]
- Armanini, A.; Capart, H.; Fraccarollo, L.; Larcher, M. Rheological stratification in experimental free-surface flows of granular-liquid mixtures. J. Fluid Mech. 2005, 532, 269–319. [Google Scholar] [CrossRef]
- Hotta, N. Basal interstitial water pressure in laboratory debris flows over a rigid bed in an open channel. Natl. Hazards Earth Syst. Sci. 2012, 12, 2499–2505. [Google Scholar] [CrossRef]
- Iverson, R.M.; Logan, M.; LaHusen, R.G.; Berti, M. The perfect debris flow? Aggregated results from 28 large-scale experiments. J. Geophys. Res.-Earth 2010, 115. [Google Scholar] [CrossRef]
- Stancanelli, L.M.; Lanzoni, S.; Foti, E. Mutual interference of two debris flow deposits delivered in a downstream river reach. J. Mt. Sci.-Engl. 2014, 11, 1385–1395. [Google Scholar] [CrossRef]
- Stancanelli, L.M.; Lanzoni, S.; Foti, E. Propagation and deposition of stony debris flows at channel confluences. Water Resour. Res. 2015, 51, 5100–5116. [Google Scholar] [CrossRef]
- Takahashi, T. Debris Flow: Mechanics, Prediction and Countermeasures; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Egashira, S.; MIYAMOTO, K.; Itoh, T. Constitutive equations of debris flow and their applicability. In Proceedings of the First International Conference Water Resources Engineering Division/ASCE, San Francisco, CA, USA, 2–6 September 2001; pp. 340–349.
- Yang, H.J.; Wei, F.Q.; Hu, K.H. Mean velocity estimation of viscous debris flows. J. Earth Sci.-China 2014, 25, 771–778. [Google Scholar] [CrossRef]
- Prochaska, A.B.; Santi, P.M.; Higgins, J.D. Relationships between size and velocity for particles within debris flows. Can. Geotech. J. 2008, 45, 1778–1783. [Google Scholar] [CrossRef]
- Cagnoli, B.; Romano, G.P. Granular pressure at the base of dry flows of angular rock fragments as a function of grain size and flow volume: A relationship from laboratory experiments. J. Geophys. Res. Solid Earth 2012, 117. [Google Scholar] [CrossRef]
- Julien, P.Y.; Paris, A. Mean velocity of mudflows and debris flows. J. Hydraul. Eng.-Asce 2010, 136, 676–679. [Google Scholar] [CrossRef]
- Chen, G. Prevention and Control of Debris Flow; China Railway Press: Beijing, China, 1983. [Google Scholar]
- Koch, T. Testing various constitutive equations for debris flow modelling. IAHS Publ.-Ser. Proc. Rep.-Intern Assoc. Hydrol. Sci. 1998, 248, 249–258. [Google Scholar]
- Rickenmann, D. Empirical relationships for debris flows. Nat. Hazards 1999, 19, 47–77. [Google Scholar] [CrossRef]
- Huang, R. Model Building and Calculation of the Debris Flow Rate in Dam Site of Wudongde Hydropower Station Based on Ppa. Ph.D. Dessertation, Jilin University, Changchun, China, 2011. [Google Scholar]
- Riverol-Canizares, C.; Pilipovik, V. The use of radial basis function networks (rbfn) to predict critical water parameters in desalination plants. Expert Syst. Appl. 2010, 37, 7285–7287. [Google Scholar] [CrossRef]
- Khodaveisi, J.; Dadfarnia, S.; Shabani, A.M.H.; Moghadam, M.R.; Hormozi-Nezhad, M.R. Artificial neural network assisted kinetic spectrophotometric technique for simultaneous determination of paracetamol and p-aminophenol in pharmaceutical samples using localized surface plasmon resonance band of silver nanoparticles. Spectrochim. Acta A 2015, 138, 474–480. [Google Scholar] [CrossRef] [PubMed]
- Rasouli, Z.; Hassanzadeh, Z.; Ghavami, R. Application of a new version of ga-rbf neural network for simultaneous spectrophotometric determination of zn(ii), fe(ii), co(ii) and cu(ii) in real samples: An exploratory study of their complexation abilities toward mtb. Talanta 2016, 160, 86–98. [Google Scholar] [CrossRef] [PubMed]
- Xu, L.; Wang, Q.; Chen, J. Forcast for average velocity of debris flow based on bp neural network. J. Jilin Univ. (Earth Sci. Ed.) 2013, 43, 186–191. [Google Scholar]
- Wang, Q.; Kong, Y.Y.; Zhang, W.; Chen, J.P.; Xu, P.H.; Li, H.Z.; Xue, Y.G.; Yuan, X.Q.; Zhan, J.W.; Zhu, Y.J. Regional debris flow susceptibility analysis based on principal component analysis and self-organizing map: A case study in southwest china. Arab. J. Geosci. 2016, 9, 718. [Google Scholar] [CrossRef]
- Poggio, T.; Girosi, F. Networks for approximation and learning. Proc. IEEE 1990, 78, 1481–1497. [Google Scholar] [CrossRef]
- Yu, G.; Zhang, M.; Wang, G. Application and comparison of prediction models of support vector machines and back-propagation artificial neural network for debris flow average velocity. J. Hydraul. Eng. 2012, 43, 105–110. [Google Scholar]
- Zhang, W.; Li, H.-Z.; Chen, J.-P.; Zhang, C.; Xu, L.-M.; Sang, W.-F. Comprehensive hazard assessment and protection of debris flows along jinsha river close to the wudongde dam site in china. Nat. Hazards 2011, 58, 459–477. [Google Scholar] [CrossRef]
- Niu, C.; Wang, Q.; Chen, J.; Zhang, W.; Xu, L.; Wang, K. Hazard assessment of debris flows in the reservoir region of wudongde hydropower station in china. Sustainability 2015, 7, 15099–15118. [Google Scholar] [CrossRef]
- Dal Sasso, S.F.; Sole, A.; Pascale, S.; Sdao, F.; Pinzon, A.B.; Medina, V. Assessment methodology for the prediction of landslide dam hazard. Nat. Hazards Earth Syst. Sci. 2014, 14, 557–567. [Google Scholar] [CrossRef]
- Dang, C.; Cui, P.; Cheng, Z.L. The formation and failure of debris flow-dams, background, key factors and model tests: Case studies from china. Environ. Geol. 2009, 57, 1901–1910. [Google Scholar] [CrossRef]
- Ermini, L.; Casagli, N.; Farina, P. Landslide dams: Analysis of case histories and new perspectives from the application of remote sensing monitoring techniques to hazard and risk assessment. Ital. J. Eng. Geol. Environ. 2006, 1, 45–52. [Google Scholar]
- Chen, J.; He, Y.; Wei, F. Debris flow erosion and deposition in jiangjia gully, yunnan, china. Environ. Geol. 2005, 48, 771–777. [Google Scholar] [CrossRef]
- Cui, P.; Chen, X.; Waqng, Y.; Hu, K.; Li, Y. Jiangjia ravine debris flows in south-western china. In Debris-Flow Hazards and Related Phenomena; Springer: New York, NY, USA, 2005; pp. 565–594. [Google Scholar]
- Tiranti, D.; Bonetto, S.; Mandrone, G. Quantitative basin characterisation to refine debris-flow triggering criteria and processes: An example from the italian western alps. Landslides 2008, 5, 45–57. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-Pour, H.; Saryazdi, S. Gsa: A gravitational search algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Xu, Y.N. Study on Flow Mechanism for Avalanche Soils and Scour and Silting Characteristics of Debris Flows. Ph.D. Dessertation, Institute of Water Conservancy and Hydroelectric Power Research, Beijing, China, 2001. [Google Scholar]
- Liu, H.J.; Tang, C.; Cui, P. Gis-Based criticality zoning of debris flow in dongchuan district. Arid Land Geogr. 2005, 28, 445–449. [Google Scholar]
- Specification of Geological Investigation for Debris Flow Stabilization dz/t 0220-2006; China Standard Press: Beijing, China, 2006.
- Gregoretti, C.; Fontana, G.D. The triggering of debris flow due to channel-bed failure in some alpine headwater basins of the dolomites: Analyses of critical runoff. Hydrol. Process 2008, 22, 2248–2263. [Google Scholar] [CrossRef]
- Wolman, M.G. A method of sampling coarse river-bed material. EOS Trans. Am. Geophys. Union 1954, 35, 951–956. [Google Scholar] [CrossRef]





| y | x1 | x2 | x3 | x4 | y | x1 | x2 | x3 | x4 |
|---|---|---|---|---|---|---|---|---|---|
| 8.8 | 150 | 6.3 | 2200 | 1.1 | 3.7 | 40 | 6.3 | 2020 | 0.1 |
| 7.8 | 140 | 6.3 | 1950 | 0.6 | 4.1 | 70 | 5.8 | 1800 | 0.2 |
| 3.8 | 40 | 6.3 | 1850 | 0.1 | 3.5 | 50 | 5.8 | 1760 | 0.2 |
| 6.9 | 202 | 5.5 | 2270 | 1.7 | 8.2 | 130 | 6.6 | 2200 | 0.7 |
| 7.5 | 168 | 5.5 | 2280 | 1.6 | 4.8 | 93 | 5.8 | 1920 | 0.3 |
| 8.9 | 175 | 6.3 | 2080 | 0.8 | 9.2 | 372 | 6.6 | 2210 | 1.2 |
| 7.4 | 200 | 6.3 | 2210 | 1.7 | 9.6 | 220 | 6.6 | 2290 | 1.5 |
| 7.3 | 90 | 6.3 | 2210 | 1 | 5.8 | 107 | 5.5 | 2290 | 1.2 |
| 6.6 | 70 | 6.3 | 2190 | 1.2 | 3.9 | 55 | 5.8 | 2070 | 0.8 |
| 9.4 | 210 | 6.6 | 2210 | 1.2 | 5.6 | 70 | 5.5 | 1920 | 0.3 |
| 4 | 40 | 6.3 | 2040 | 0.3 | 3.9 | 60 | 5.5 | 1830 | 0.1 |
| 7.4 | 145 | 5.5 | 2250 | 1.1 | 6.9 | 122 | 5.5 | 2210 | 1 |
| 5.8 | 103 | 5.5 | 2210 | 0.8 | 9.6 | 275 | 6.6 | 2210 | 1.6 |
| 4.7 | 60 | 5.5 | 1970 | 0.5 | 5 | 65 | 5.5 | 2240 | 1.1 |
| 7.7 | 161 | 5.5 | 2250 | 1 | 3.7 | 55 | 5.8 | 1800 | 0.1 |
| 7.7 | 177 | 5.5 | 2240 | 1.1 | 8.1 | 160 | 6.6 | 2220 | 1.2 |
| 7.9 | 200 | 6.3 | 2250 | 1.4 | 6.6 | 226 | 5.5 | 2130 | 1.1 |
| 8.4 | 210 | 6.6 | 2200 | 0.8 | 7.4 | 55 | 6.3 | 2250 | 0.9 |
| 9.3 | 210 | 6.3 | 2290 | 1 | 7.5 | 170 | 6.6 | 2190 | 1.1 |
| 3.6 | 58 | 5.8 | 1690 | 0.2 | 6.4 | 109 | 5.5 | 2250 | 1.1 |
| 10 | 95 | 6.3 | 2160 | 0.6 | 9.3 | 210 | 6.3 | 2210 | 1.1 |
| 7.6 | 125 | 6.3 | 2100 | 0.6 | 6.9 | 250 | 5.5 | 2220 | 0.9 |
| 7.6 | 11 | 6.3 | 2070 | 0.7 | 6 | 120 | 5.5 | 2200 | 0.8 |
| 7.6 | 100 | 6.3 | 2190 | 0.9 | 4.9 | 60 | 5.5 | 1990 | 0.6 |
| 8.5 | 200 | 6.3 | 2300 | 1.5 | 3.6 | 52 | 5.8 | 1700 | 0.1 |
| Gully | x1 (cm) | x2 (%) | x3 (kg·m−3) | x4 (cm) |
|---|---|---|---|---|
| Xiabaitan | 200 | 40.7 | 2250 | 3.23 |
| Shangbaitan | 150 | 35.8 | 2110 | 3.08 |
| Zhugongdi | 180 | 41.8 | 2040 | 2.97 |
| Zhuzhahe | 180 | 5.0 | 2120 | 2.15 |
| Zhiligou | 170 | 10.2 | 2320 | 3.23 |
| Mengguogou | 180 | 5.6 | 2100 | 3.06 |
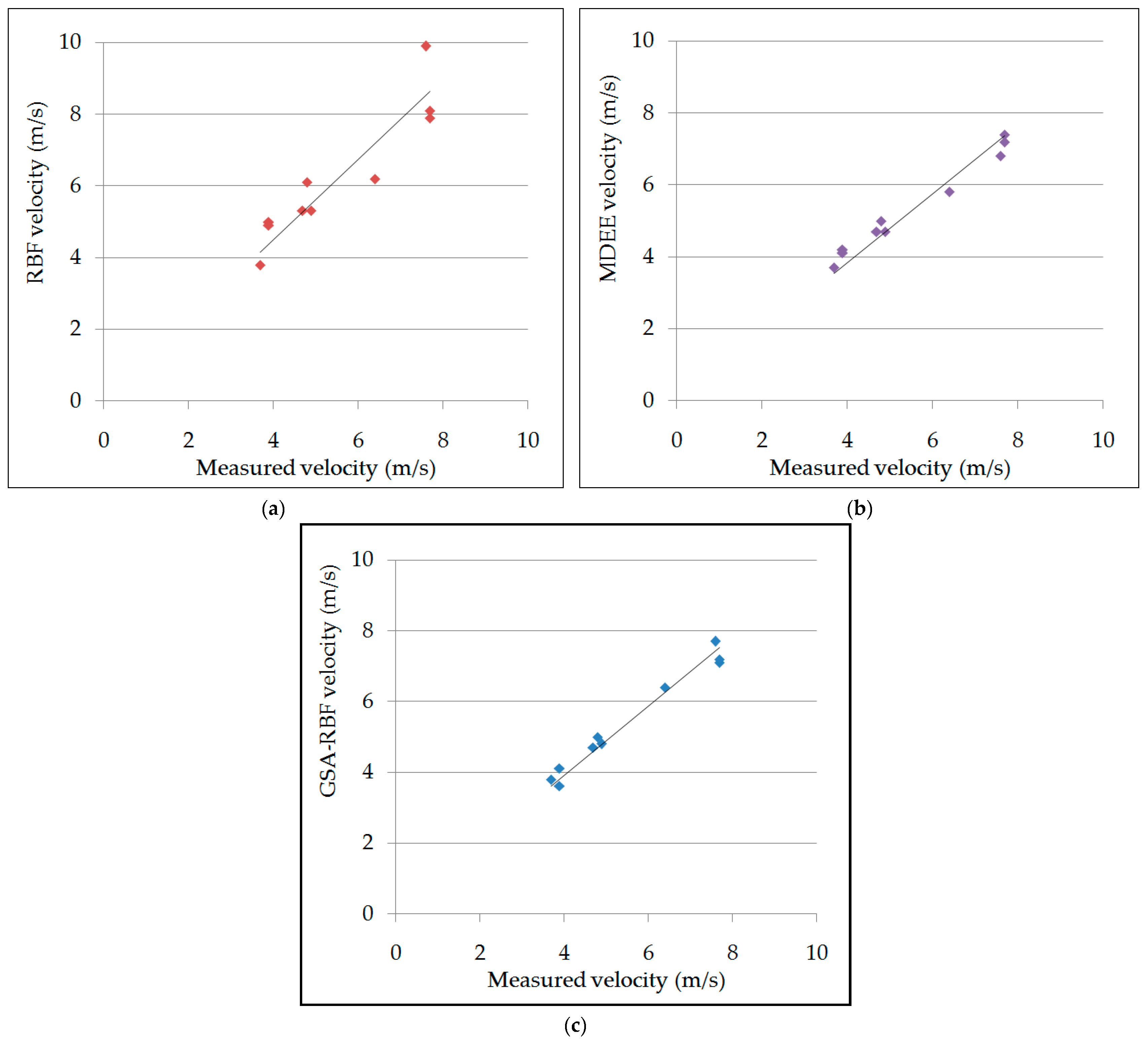
| Measured Value (m/s) | RBF | MDEE | GSA-RBF | |||
|---|---|---|---|---|---|---|
| Value (m/s) | Relative Error (%) | Value (m/s) | Relative Error (%) | Value (m/s) | Relative Error (%) | |
| 4.8 | 6.1 | 27.1 | 5.0 | 3.6 | 5.0 | 4.2 |
| 4.9 | 5.3 | 8.2 | 4.7 | 3.6 | 4.8 | 2.0 |
| 4.7 | 5.3 | 12.8 | 4.7 | 0.5 | 4.7 | 0.0 |
| 7.7 | 7.9 | 2.6 | 7.2 | 6.3 | 7.1 | 7.8 |
| 7.7 | 8.1 | 5.2 | 7.4 | 3.3 | 7.2 | 6.5 |
| 3.9 | 5.0 | 28.2 | 4.2 | 7.0 | 3.6 | 7.7 |
| 3.9 | 4.9 | 25.6 | 4.2 | 9.0 | 4.1 | 5.1 |
| 6.4 | 6.2 | 3.1 | 5.8 | 10.0 | 6.4 | 0.0 |
| 3.7 | 3.8 | 2.7 | 3.7 | 0.2 | 3.8 | 2.7 |
| 7.6 | 9.9 | 30.3 | 6.8 | 10.3 | 7.7 | 1.3 |
| Average error | - | 14.6 | - | 5.4 | - | 3.7 |
| Maximum error | - | 30.3 | - | 10.3 | - | 7.8 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, C.; Song, S.; Chen, J.; Zheng, L.; Kong, Y. An Approach to Predict Debris Flow Average Velocity. Water 2017, 9, 205. https://doi.org/10.3390/w9030205
Cao C, Song S, Chen J, Zheng L, Kong Y. An Approach to Predict Debris Flow Average Velocity. Water. 2017; 9(3):205. https://doi.org/10.3390/w9030205
Chicago/Turabian StyleCao, Chen, Shengyuan Song, Jianping Chen, Lianjing Zheng, and Yuanyuan Kong. 2017. "An Approach to Predict Debris Flow Average Velocity" Water 9, no. 3: 205. https://doi.org/10.3390/w9030205
APA StyleCao, C., Song, S., Chen, J., Zheng, L., & Kong, Y. (2017). An Approach to Predict Debris Flow Average Velocity. Water, 9(3), 205. https://doi.org/10.3390/w9030205







