In this study, two different approaches are proposed to evaluate the four proxy variables for runoff prediction by measuring the remotely sensed soil moisture. The first approach assesses the initial condition-derived soil moisture with validation sets of rainfall events, and the second approach assesses the error analysis of the estimated runoff prediction with the evaluation set of rainfall events.
3.2.1. Proxy Variables of IWC
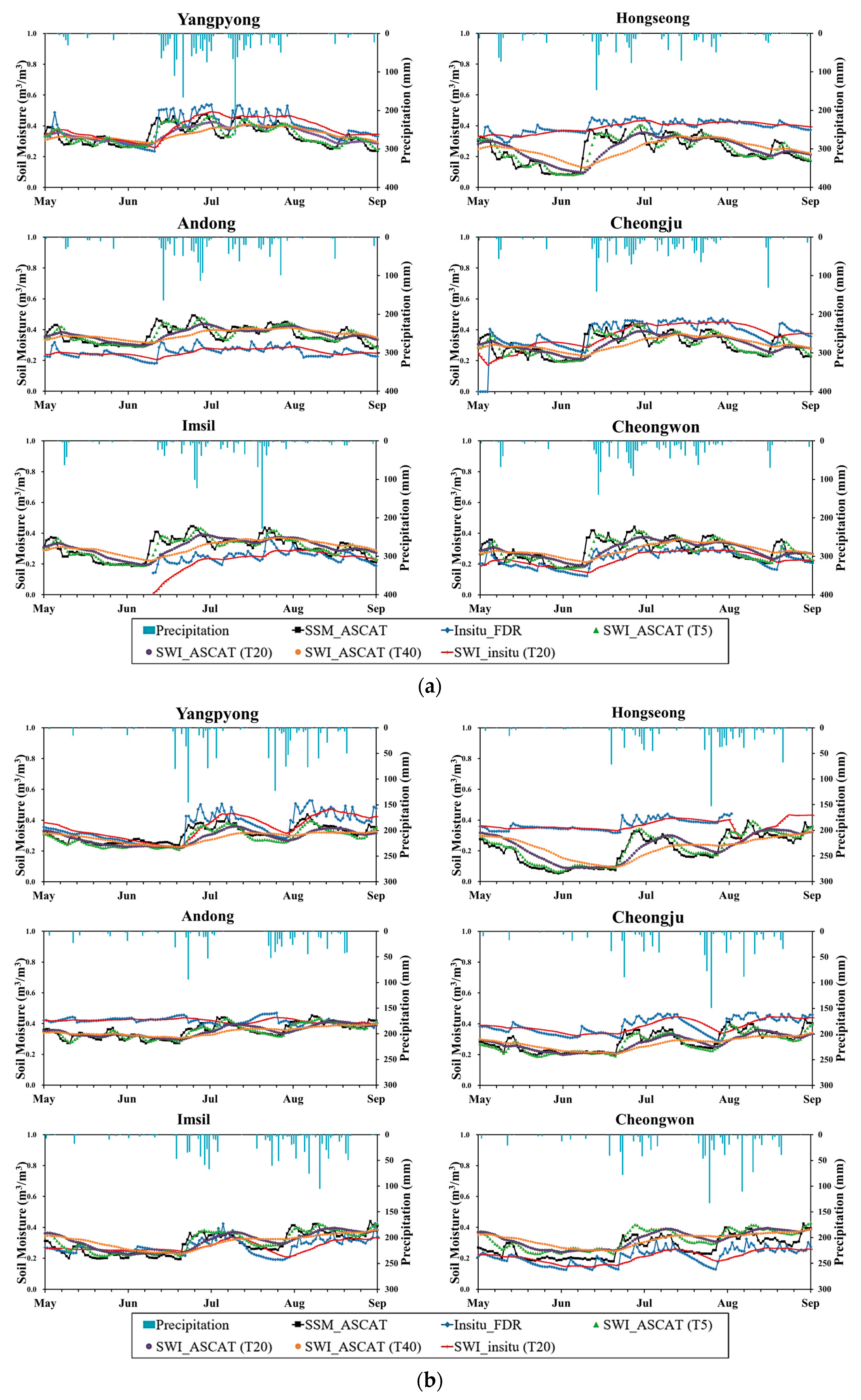
The analysis of the ASCAT soil moisture was performed for both the surface and root zone layers. We selected the rainfall–runoff events objectively, along with the criteria at each of the validation sites. As previously stated, this study conducts validation of the four proxy variables of IWC to improve the accuracy of the initial conditions in the rainfall–runoff simulation. The four proxy variables were assessed using an event-based runoff model, the SCS-CN method, which is widely used for runoff prediction because it is known as one of the most robust approaches [
3,
9,
10]. The set of rainfall events (
Table 4) characterized by a mean rainfall depth greater than 10 mm/day and no rainfall event in the previous one or two days was selected to efficiently capture a relatively dry soil condition [
10,
20]. The total rainfall depth
P was calculated using the Thiessen polygon method, and the direct runoff depth
Q was determined using the base flow separation method.
The correlation coefficients for the IWC proxy variables were calculated in relation to the value of the maximum potential water retention,
Sobs. The maximum potential water retention capacity can be explained by the mean soil water deficit of the catchment having an inverse linear relationship with the wetness condition and degree of saturation. Considering the effect of the SSM and RZSM, the
T value was counted as a calibration parameter ranging from 1 to 150 days.
Table 5 shows the results of the correlation coefficient for each site along with the optimal value of
T parameters determined for minimizing the error. As shown in the table, the API
5 value ranged from −0.151 to 0.179; SSM
insitu ranged from −0.327 to 0.579; SSM ranged from −0.14 to 0.897, and SWI ranged from −0.516 to −0.769. The SWI derived from the RZSM had higher inverse correlation values than the other IWC proxy variables, with an average correlation of −0.67. The API
5 value derived from the antecedent five-day rainfall was found to have a lower reliability for estimating the potential maximum retention, as the average
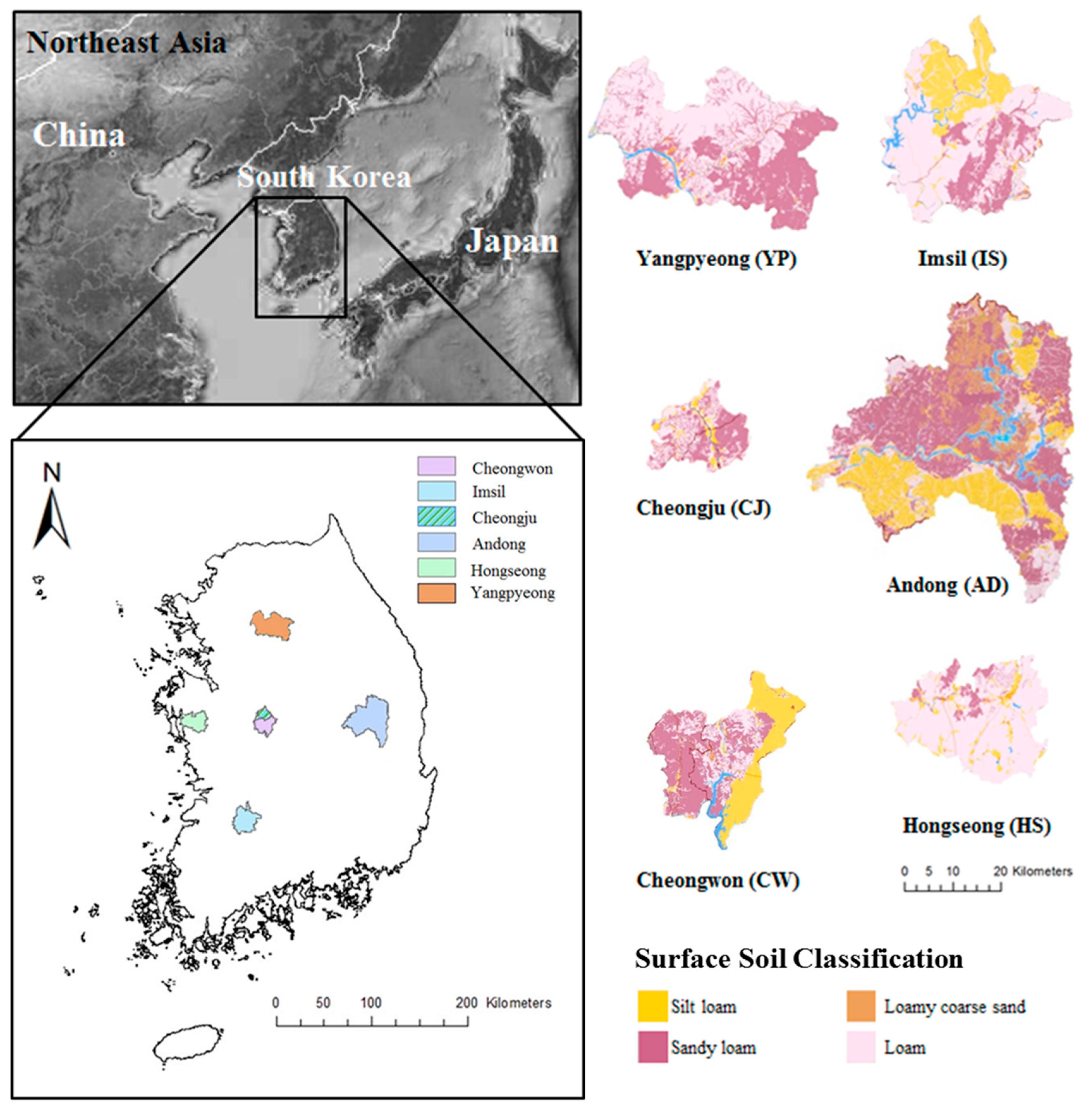
R value was 0.019. This may be explained by the spatial heterogeneity of surface soil type compared with other sites (
Table 1). The diverse soil types could be the cause of erroneous results, and the quality of the soil moisture was influenced by the spatial heterogeneity in a pixel [
40,
41]. The IWC proxy variables, API
5, SSM
insitu, and SSM, representing the surface soil moisture or cumulative precipitation during the short term, showed a poor regression performance with
Sobs. In particular, API
5, as a classical indicator of the SCS-CN approach, was not suitable for the IWC proxy variable with a correlation value close to zero. These results correspond to those of Brocca et al. [
10] and Jacobs et al. [
17]. The ASCAT SWI can be considered more reliable in the estimation of the IWC, providing a more accurate runoff prediction.
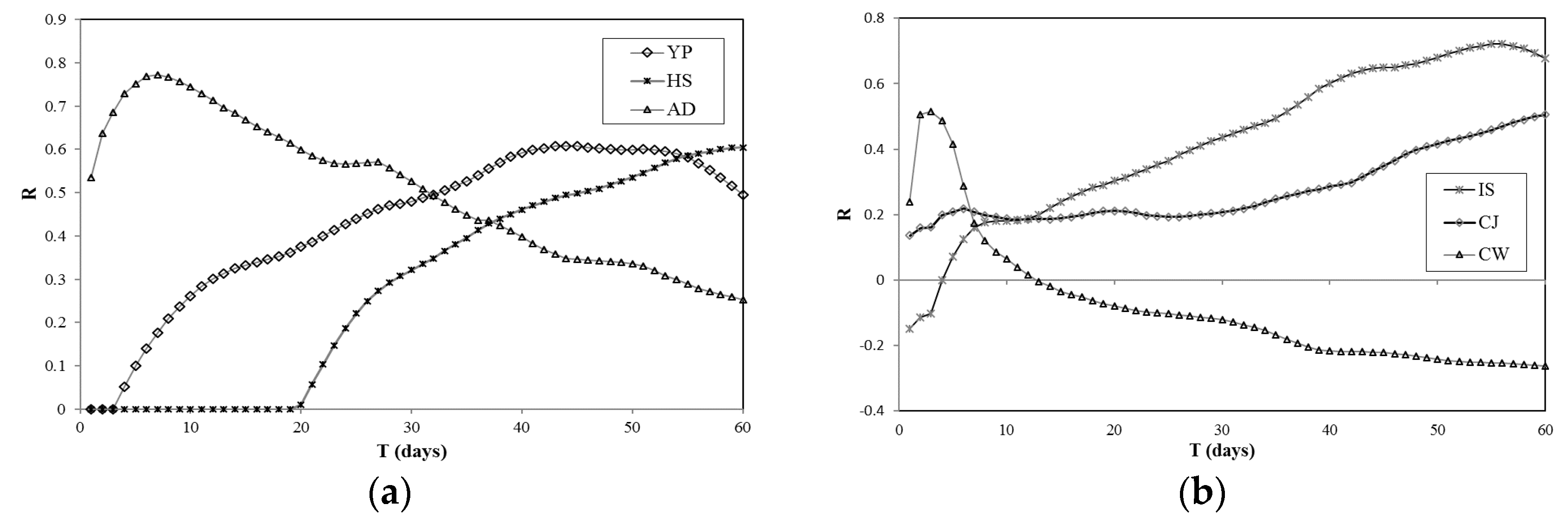
Figure 3 shows the correlation coefficient of the linear regression between the SWI proxy variable and S
obs values according to the characteristic time length parameter,
T, for the six validation sites. The optimal
T value was determined for a
T 1 to 150 days, and optimal
T value for sites YP, HS, AD, CJ, and IS was estimated as 45, 64, 59, 100, and 59 days, respectively; the optimal
T value for site CW was estimated as three days. According to previous studies [
10,
44,
47], the optimal
T value ranges from 30 to 90 days. In
Figure 3,
T was set to range from 1 to 60 days because it is difficult to explain that remotely sensed soil moisture before two months (60 days) can affect to the infiltration of the next rainfall events. However, in the CJ correlation coefficient increased continuously with the
T value and reached a maximum at
T = 100 days. The reason for the differences in
T value is due to the investigated soil layer thickness. The lower
T value for site CW was obtained from the fast-responding catchment influenced by a thin soil layer. A higher
T value suggests that a deeper soil layer influences the rainfall–runoff transformation process. The differences in topography and land cover could explain the variation in
T value. To obtain the optimal
T value, further examination should be conducted by considering a larger number of study sites.
3.2.2. Estimated Runoff Model Comparison
This study proposed several approaches to improve event-based rainfall–runoff modeling using the SSM and SWI derived from the ASCAT satellite. Based on the runoff data availability, evaluation sets of rainfall–runoff events were selected, and the main characteristics, such as total rainfall (mm), measured runoff data (mm), AMC, ASCAT SSM, and
CN (
P) calculated from the
CN–
P relationship, are shown in
Table 6. The estimated runoff for each event was determined by four different
CN parameters to define the initial conditions, representing the IWC (
Table 7). In the first approach, the
QCNP values were predicted using the
CN–
P relationship obtained from the exponential regression for each site, as shown with the standard response in
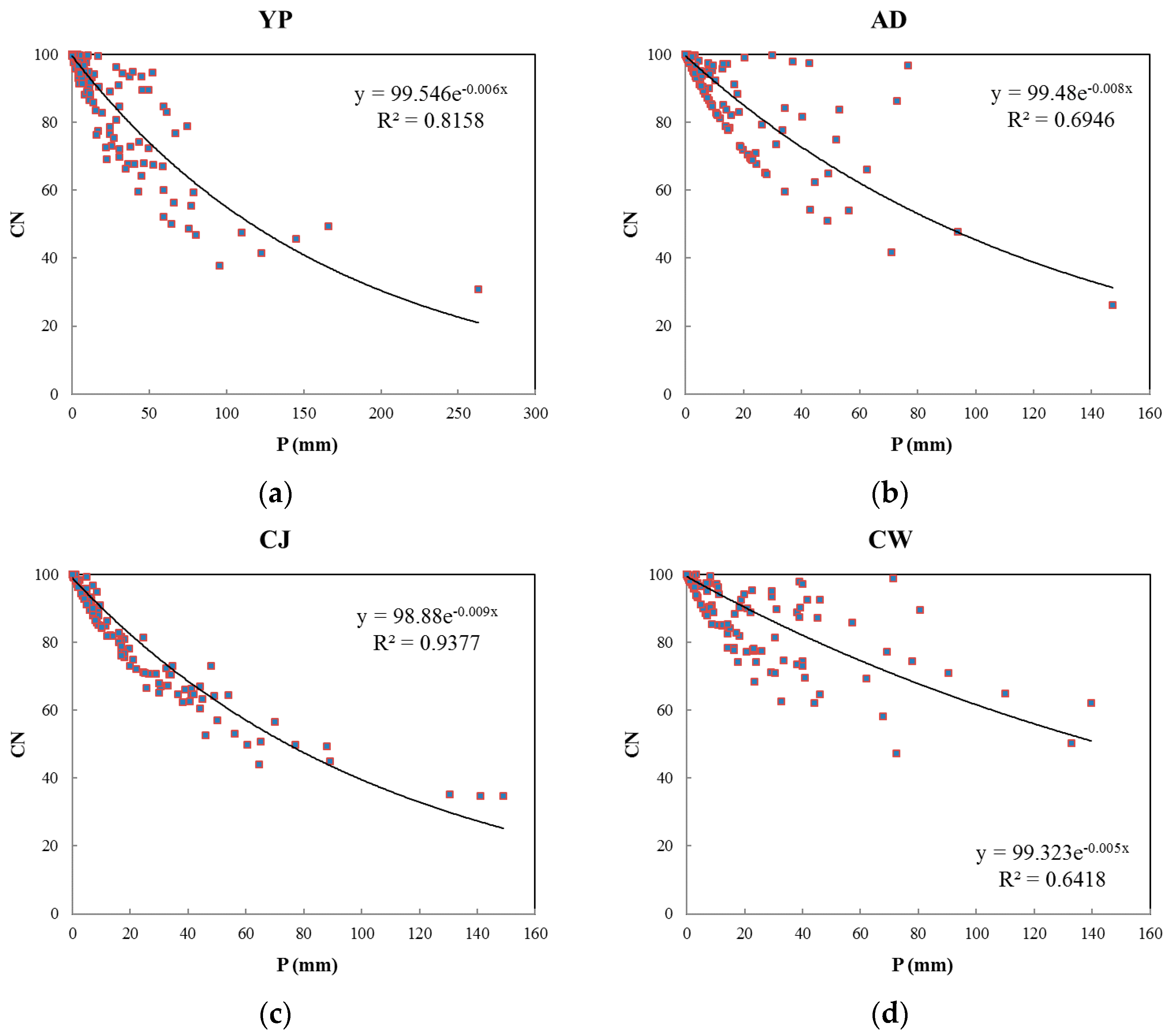
Figure 4. These were greater than the asymptotic
CN values. Equations (7)–(10) are fitted functions and represent the values of the coefficient of determination for sites YP, AD, CJ, and CW, respectively, as follows:
Figure 4 shows a standard behavior characterized by constant
CN values with increasing rainfall depth. In most of these cases, when the
CN values calculated using Equation (5) were plotted against rainfall depth (
P), they decreased steadily with increasing
P. A strong relationship between
P and
CN was detected from the standard behavior. Thus, the maximum potential retention
S increases as
P increases until it reaches a constant value. The variation of the standard form is clearly described by [
33,
36].
In the second approach,
QAMC was predicted using the
CN value estimated from the adjusted
CN (
P) corresponding to the antecedent moisture condition (API
5) using Equation (5). In the third approach,
QSSM was predicted using the linear relationship between the rescaled
CN value (
CN*) and the ASCAT SSM. The
CN* value was obtained from the calculated
CN value divided by
CN (
P) to indicate the relationship between the dry and wet condition-influenced rainfall depth [
20]. A larger
CN* value represents a greater wetness condition that has less potential for storage. Similarly, a lower
CN* value represents a drier soil condition with increased infiltration capacity.
In the last approach,
QSWI was predicted from the estimated
CN value using the linear relationship between
CN* and the ASCAT SWI data at
T = 5, 10, 20, and 40 days to consider the variability of the infiltration effect. The overall adequacy of the initial conditions on runoff prediction was quantified by calculating the
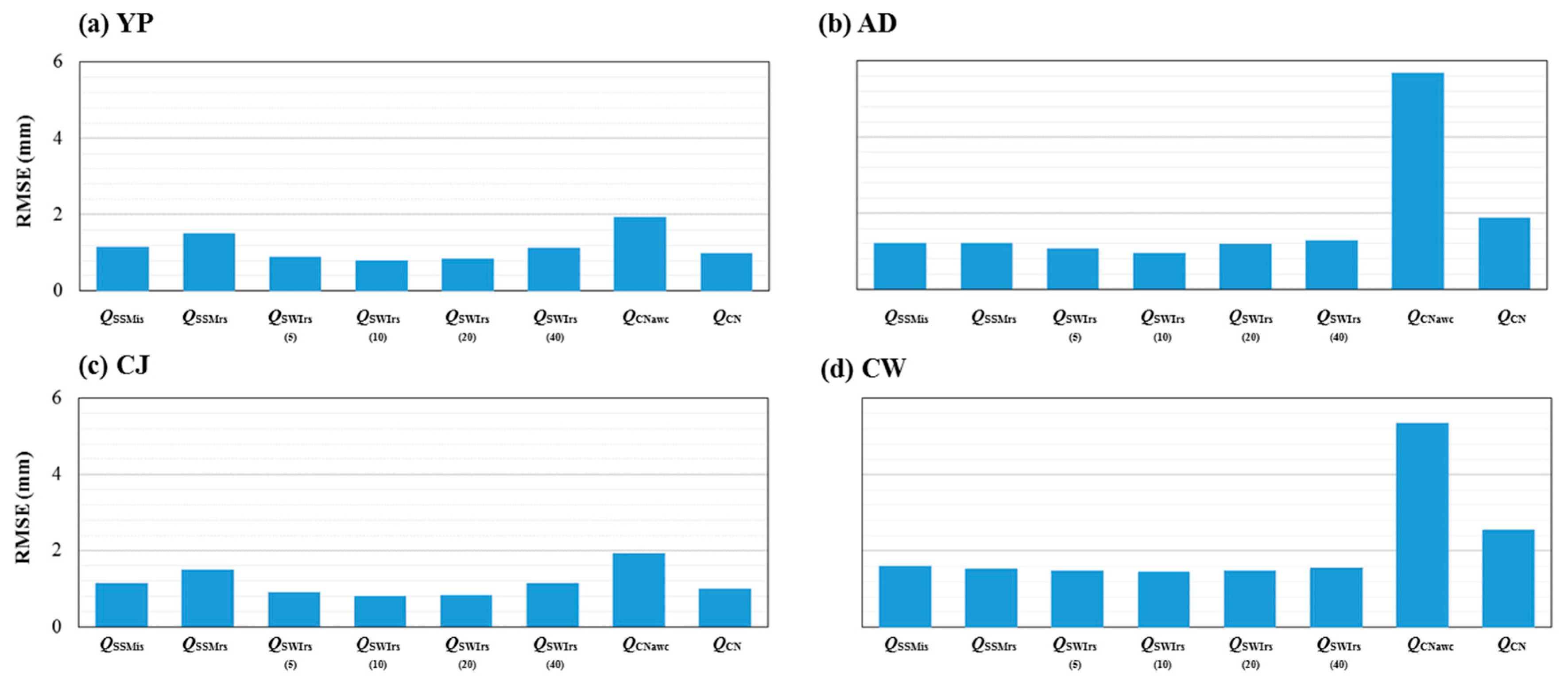
RMSE values for the four sites (
Table 7). The model performance was also determined using the Nash–Sutcliffe coefficient (
NSe) [
48]. The
RMSE values for the site YP ranged from 3.33 to 4.83 mm when compared with the measured runoff data; the estimated runoff derived by the ASCAT SSM showed a smaller error in comparison. The
RMSE value for the site AD presented lower overall values, with the exception of one case: the error of the second approach using the adjusted AMC condition, which was high. The
RMSE value for site CJ ranged from 0.81 to 1.93 mm, and the average
RMSE value in the case of the ASCAT SWI was 0.93 mm. For site CW, the average
RMSE was lower than 1.50 mm for
QSWI, and
QAWC was the highest at 5.35 mm. Thus, the estimated runoff derived from the ASCAT SWI values showed outstanding results, and the small errors could be inferred from the catchment size. The predicted runoff using the ASCAT SSM and SWI (
T = 10) showed high
NSe values (YP: 0.71, AD: 0.48, CJ: 0.74, and CW: 0.48). Therefore, the runoff prediction values using the remotely sensed soil moisture indicated potentially reliable statistical results for assessing the goodness of fit of the rainfall–runoff model. The runoff prediction scheme applying the remotely sensed soil moisture, meeting the reliable goodness of fit criteria, provided an enhanced framework for the rainfall–runoff model.
This suggests that modeling uncertainties can be reduced using more accurate initial condition parameters based on remotely sensed soil moisture. In addition, these results agree with the observation of Kustas and Goodrich [
49] that a medium-sized catchment was adequate for runoff prediction. For these evaluated rainfall events, the remotely sensed soil moisture reduced the overall error in the runoff prediction by approximately 70% compared to the reference amount of runoff obtained the traditional SCS-CN approach. Site YP exhibited the highest reduction rate among the four sites with a value of 80%, along with 68% for site AD and 22% for CW in the case of runoff prediction using the
CN–
P relationship. Subsequently, the SSM and SWI data also significantly reduced the error with improved runoff prediction at 88% for site YP, 92% for AD, and 60% for CW. On the other hand, for site CJ, the
CN–
P relationship did not improve the runoff prediction, and the error reduction was 35% for both SSM and SWI. This could be due to the pattern of land use, i.e., grassland < 10%, mixed forest < 33%, and cropland > 30%, as well as the surface soil type.
The estimated runoff,
QCN-Table, predicted using the tabulated
CN values, has the largest error for the measured runoff depth (
Figure 5). It is difficult to select an accurate
CN value from handbook tables because the calculated runoff is more sensitive to the selected
CN than the recorded rainfall data [
36,
49] The error in runoff prediction patterns at the four sites exhibited a considerable difference owing to the variation of
CN parameters (
Figure 6). The variability and differences between SSM (
Figure 6c) and SWI (
T = 40) considering RZSM (
Figure 6d) appeared smaller for all sites compared with the
CN–
P relationships (
Figure 6a,b). It is likely that this is due to the differences between the real soil moisture data and synthetic initial condition data to simulate the runoff depth. Moreover, this may indicate a shortcoming of the event-based model in the absence of accurate IWC information. It is worthwhile to note that the remotely sensed soil moisture provides the required reliability for the simulation of runoff prediction.
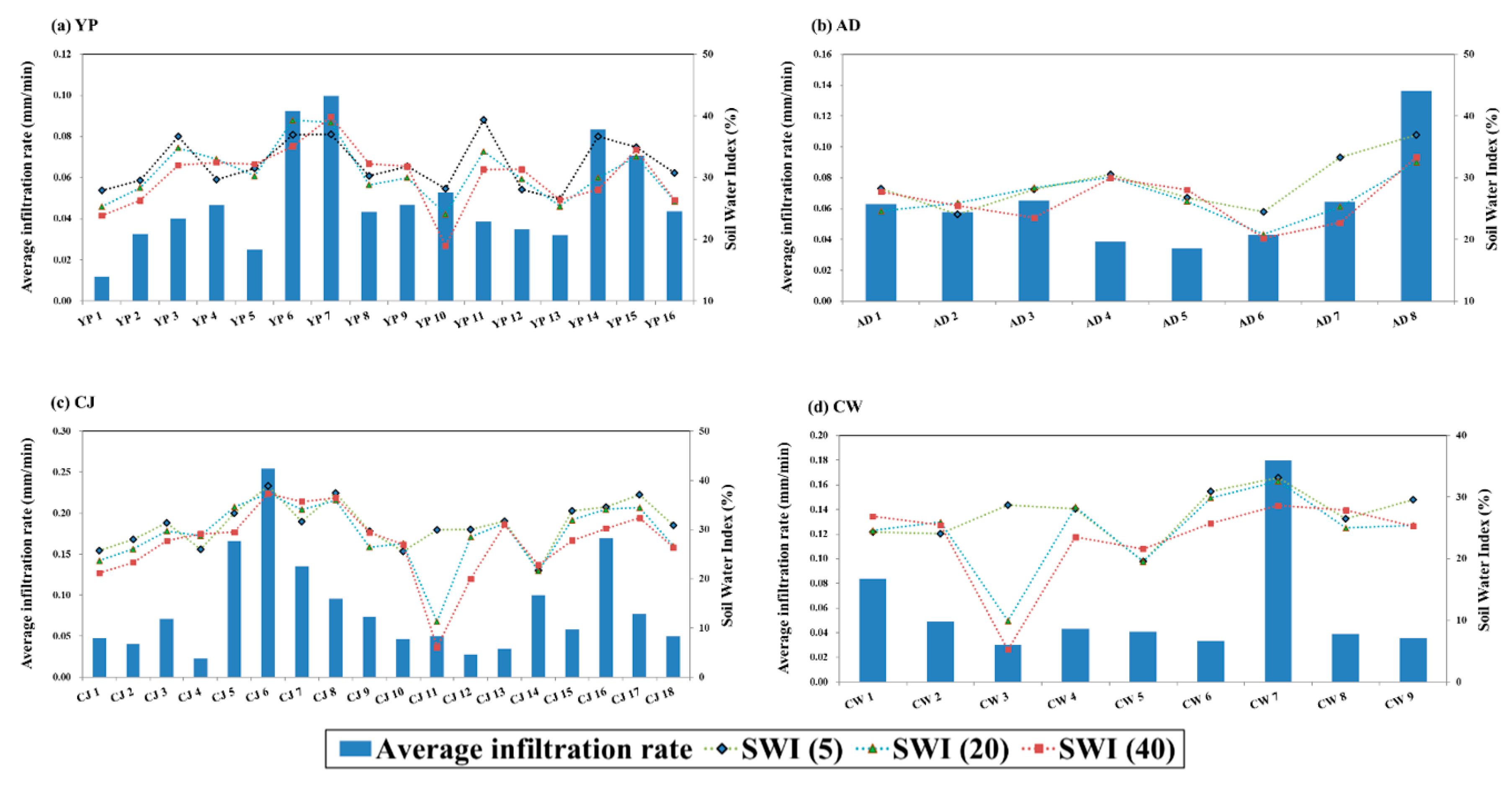
To describe the rainfall distribution in runoff prediction, the average infiltration rates after runoff response were calculated as follows:
where
Ii is the average infiltration after the generation of surface flow (mm/min),
α is the slope gradient (°), and
t is the rainfall duration (min). As shown in
Figure 7, the changing trend of the average infiltration rate and soil moisture with the SWI values (at
T = 5, 20, and 40) exhibited a good agreement in general, and the consistency of the SWI (at
T = 5) was generally higher than in the other cases. This also explains that the main cause of the difference in SWI values is that the infiltrated soil moisture was collected gradually and formed a lateral flow along the impermeable base according to the topographical features. Moreover, the differences in the average infiltration rate for each site were caused by the differences in the dominant land cover. The results of this study show that the remotely sensed soil moisture considering the infiltration effect can provide a reasonable initial condition to predict the runoff for a range of catchments. However, they should be used with caution according to the regional conditions.