Extreme Precipitation Frequency Analysis Using a Minimum Density Power Divergence Estimator
Abstract
:1. Introduction
2. Methodology
2.1. Decadal Changes in Extreme Rainfall in South Korea
2.2. MDPDE
3. Results and Discussion
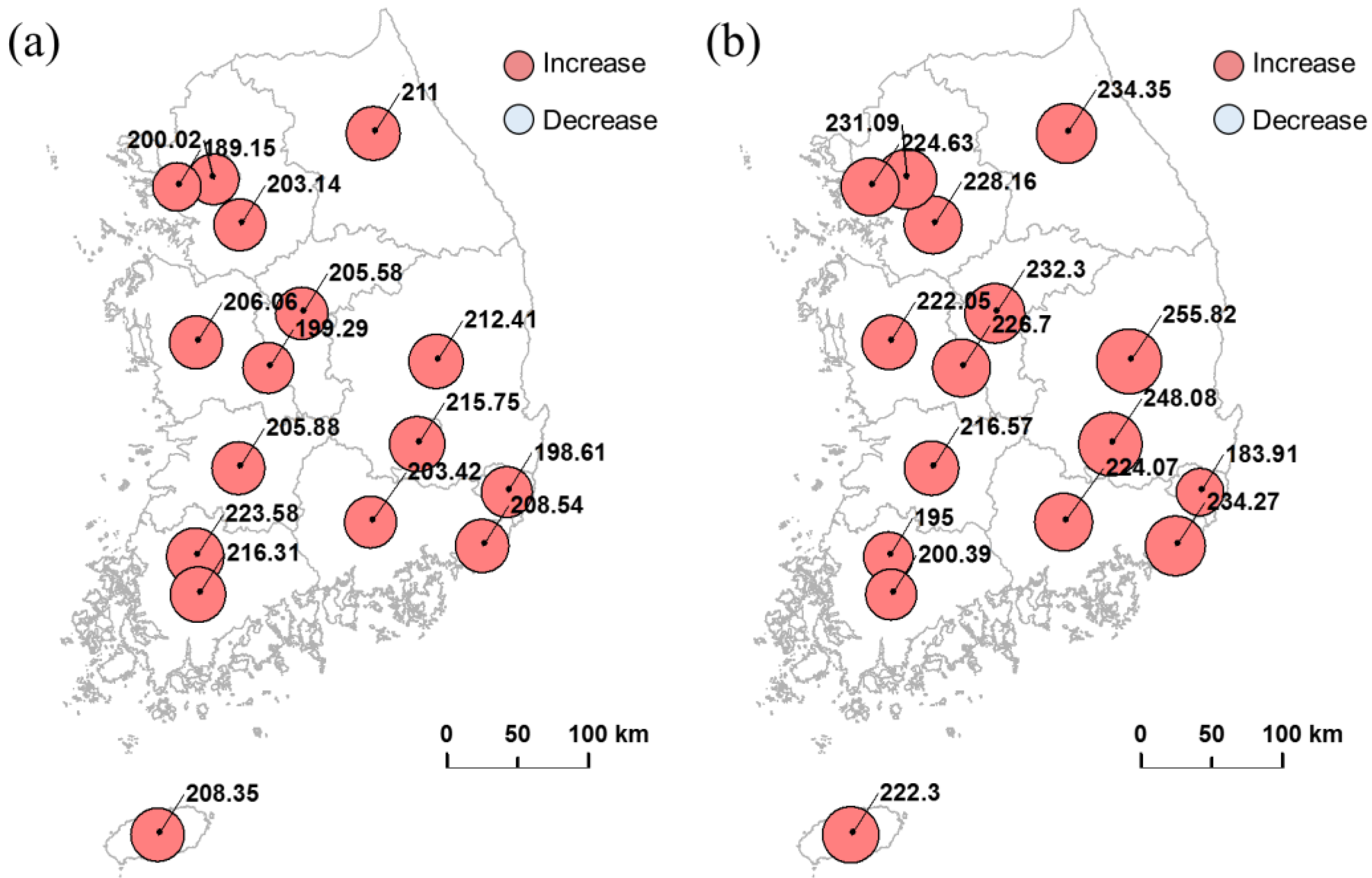
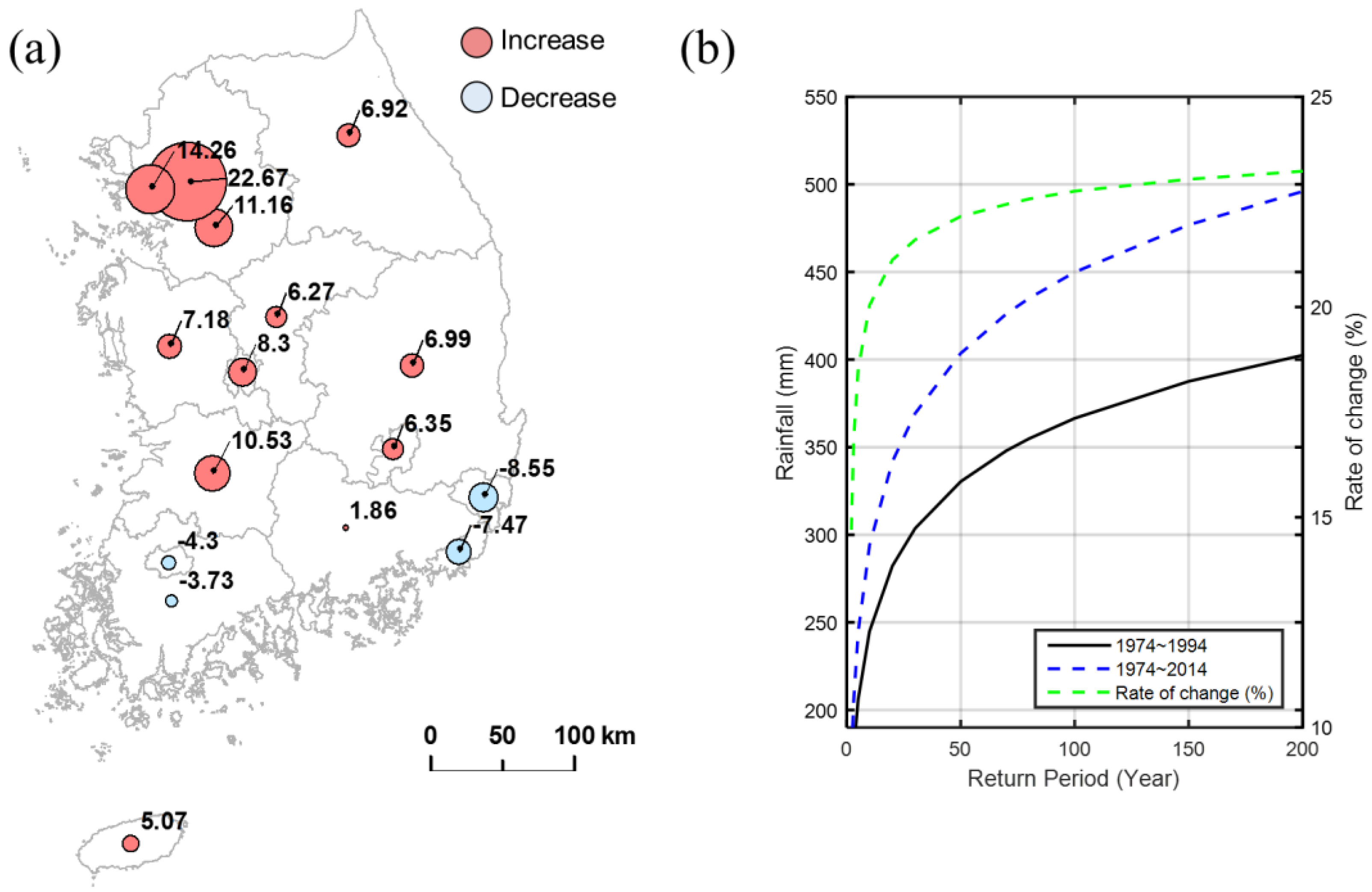
3.1. Decadal Changes in Extreme Rainfall in South Korea
3.2. Physical Mechanism Behind the Changes of Extreme Events
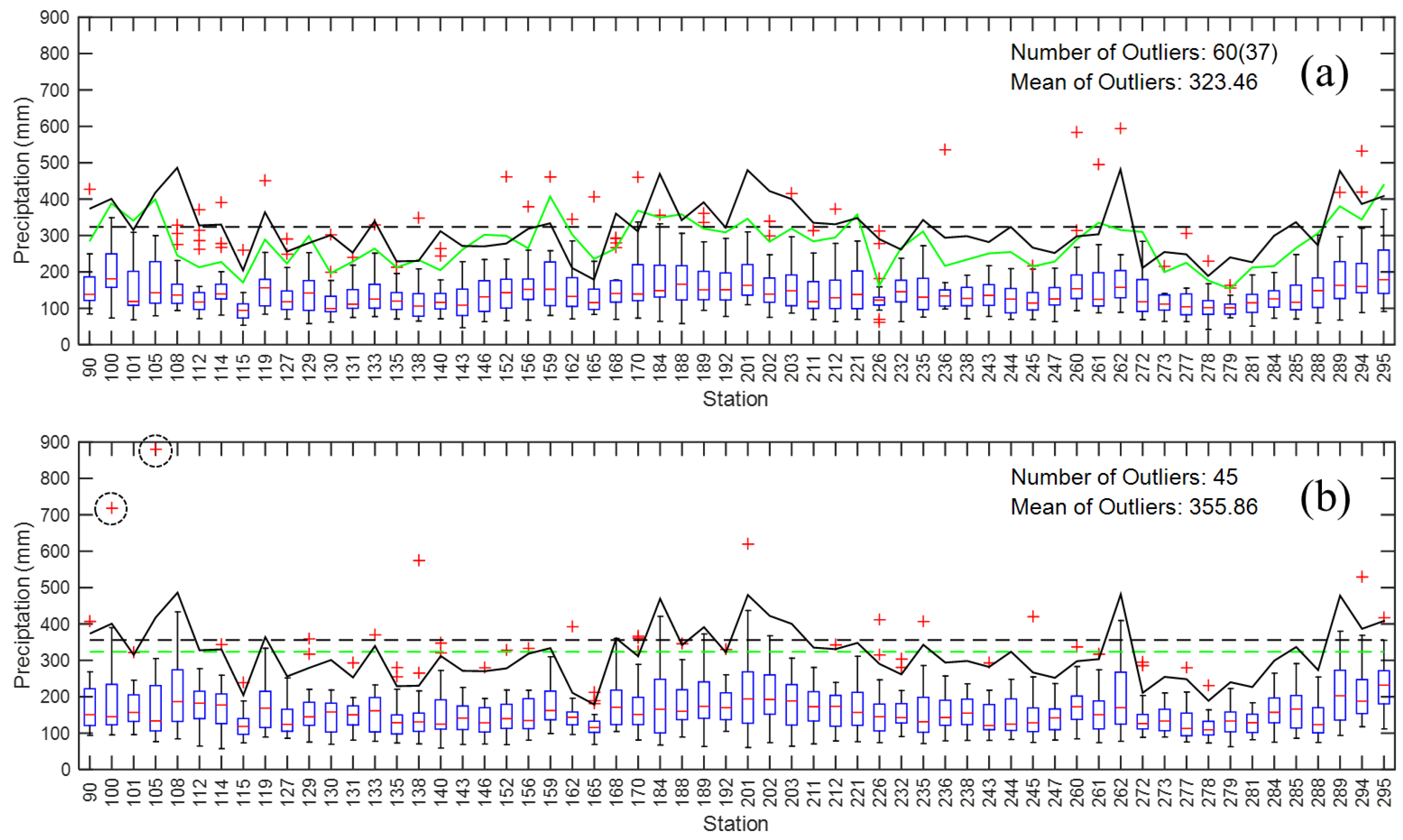
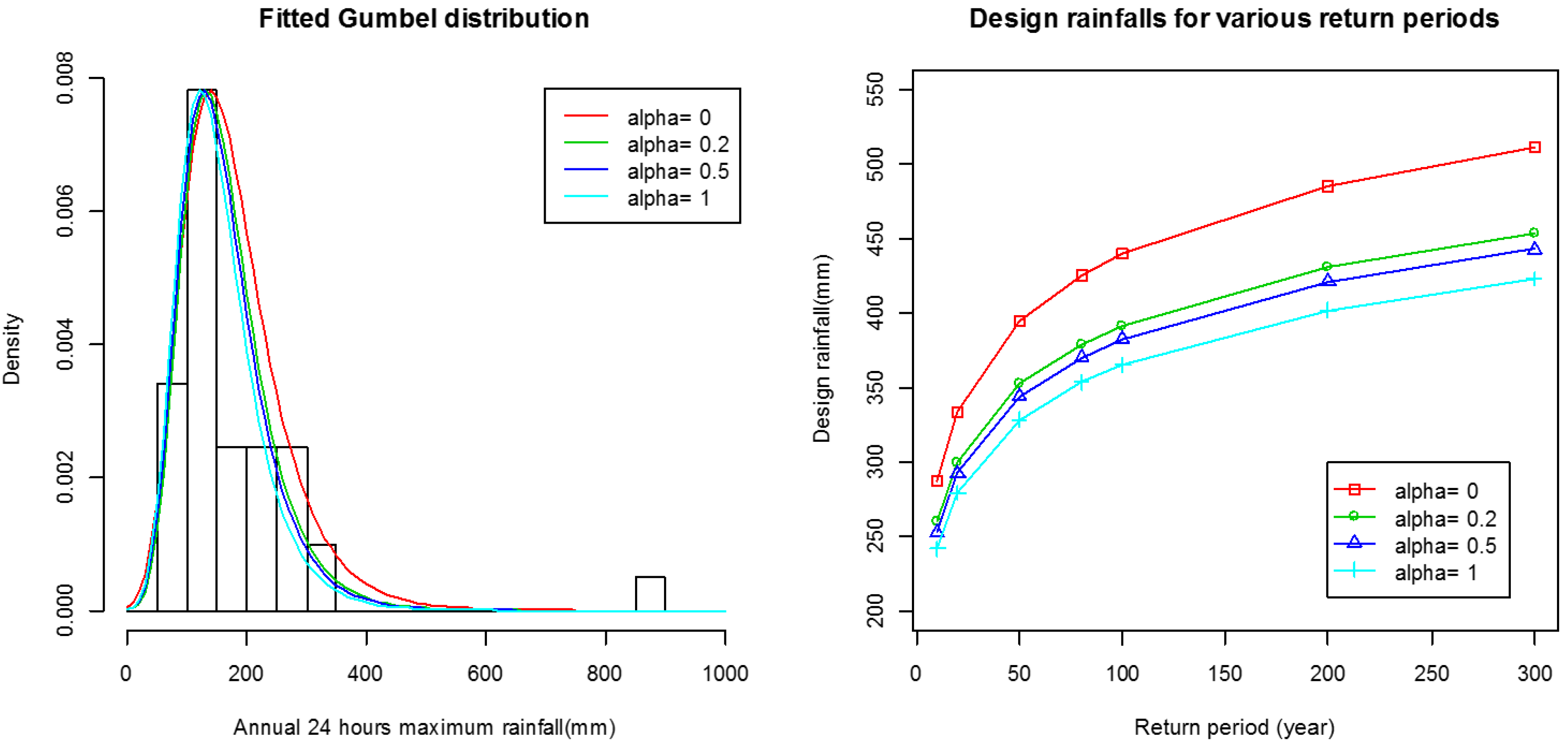
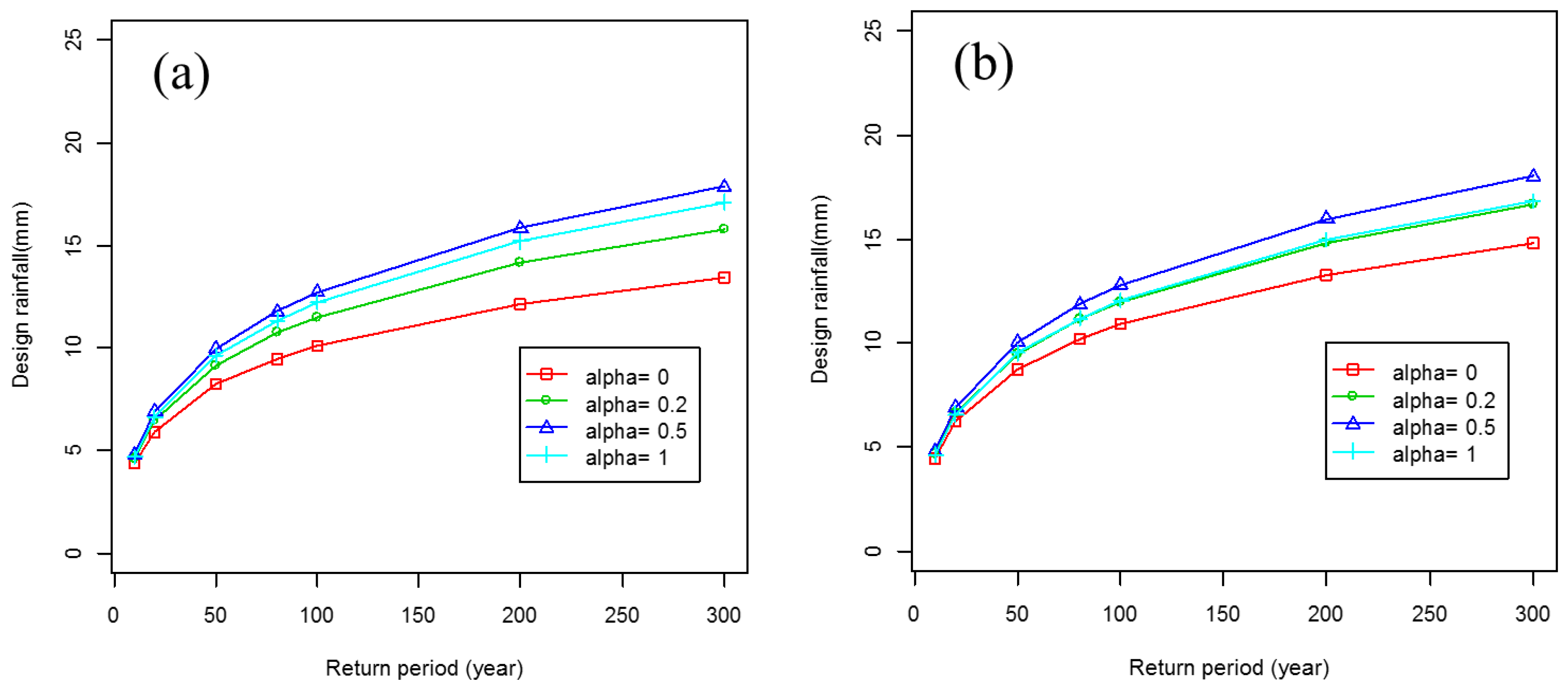
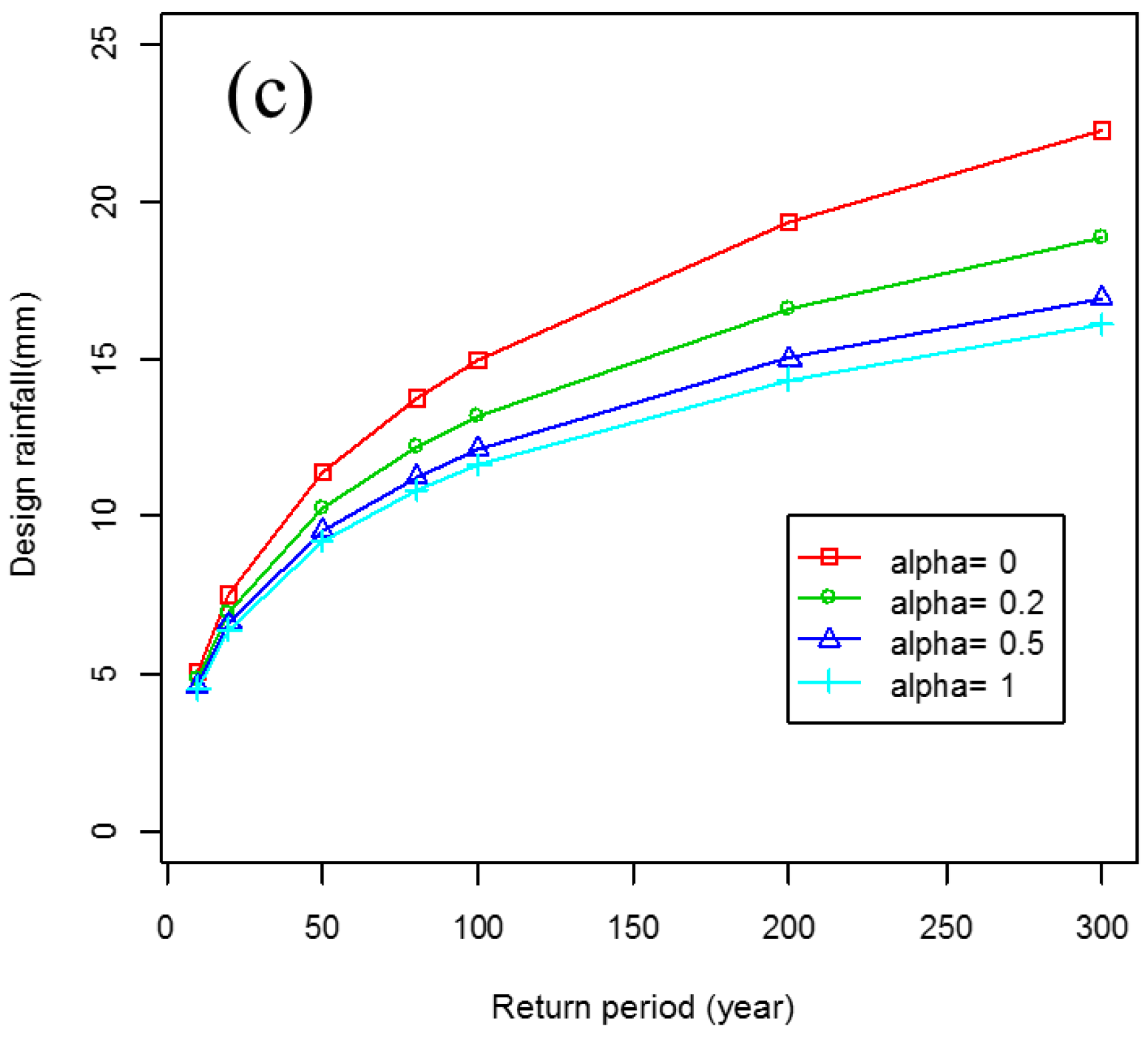
3.3. Performance of MDPDE with the Gumbel Distribution
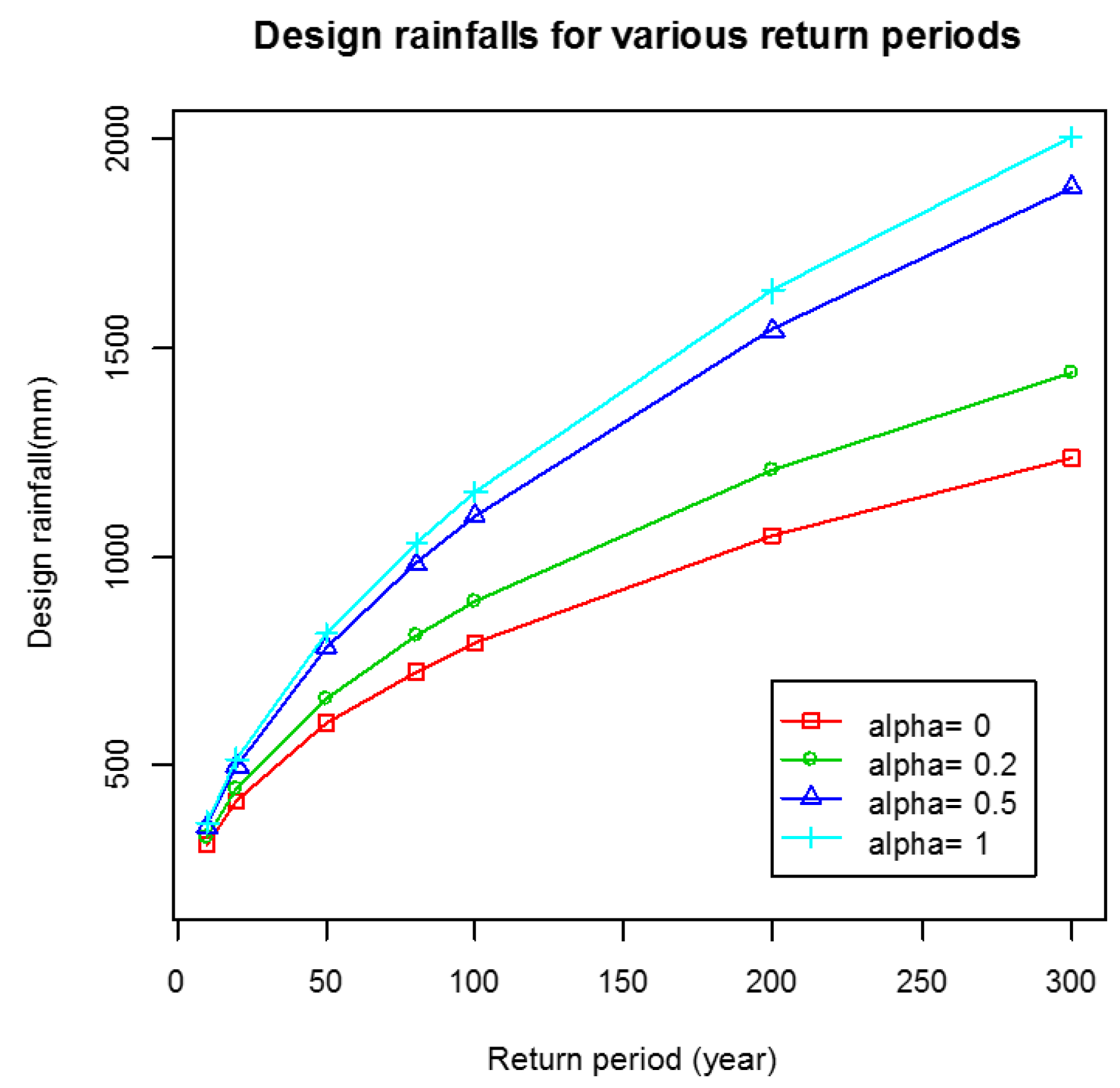
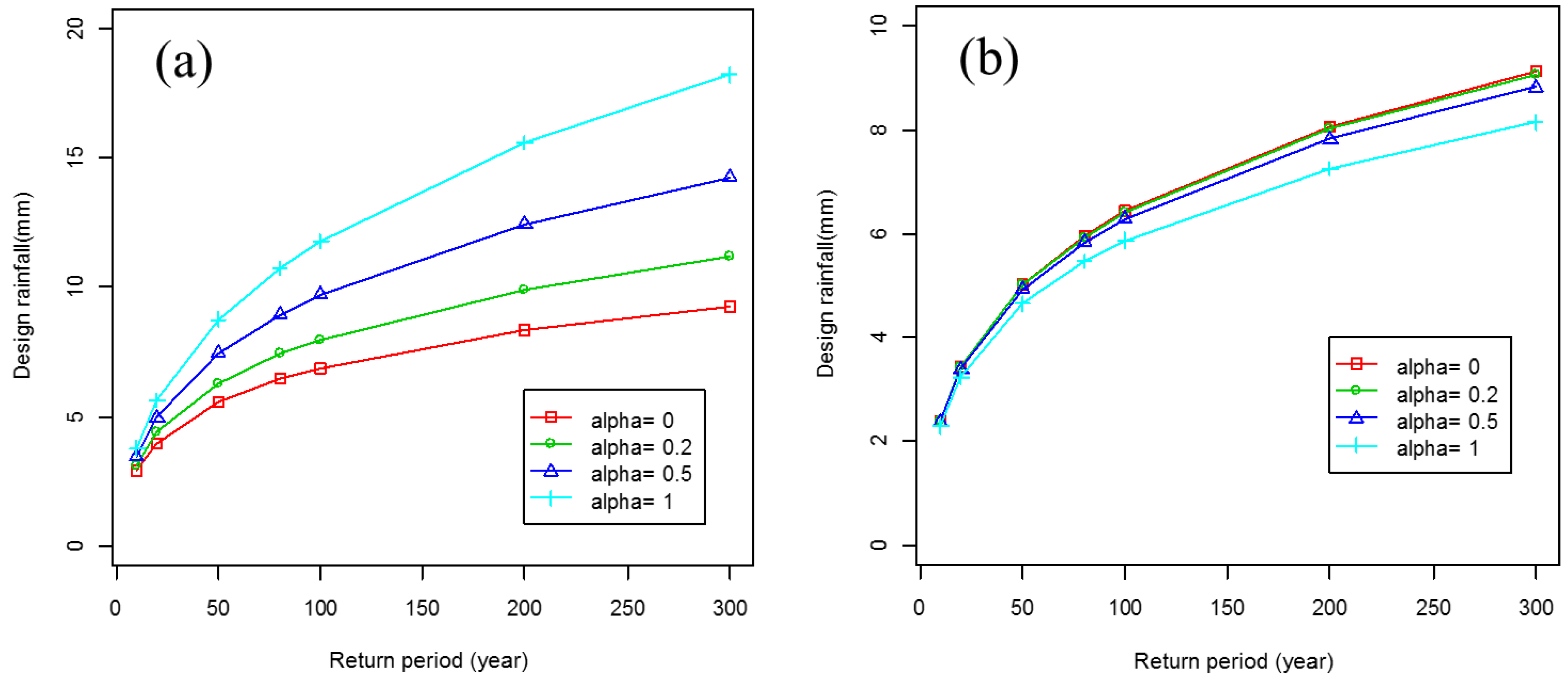
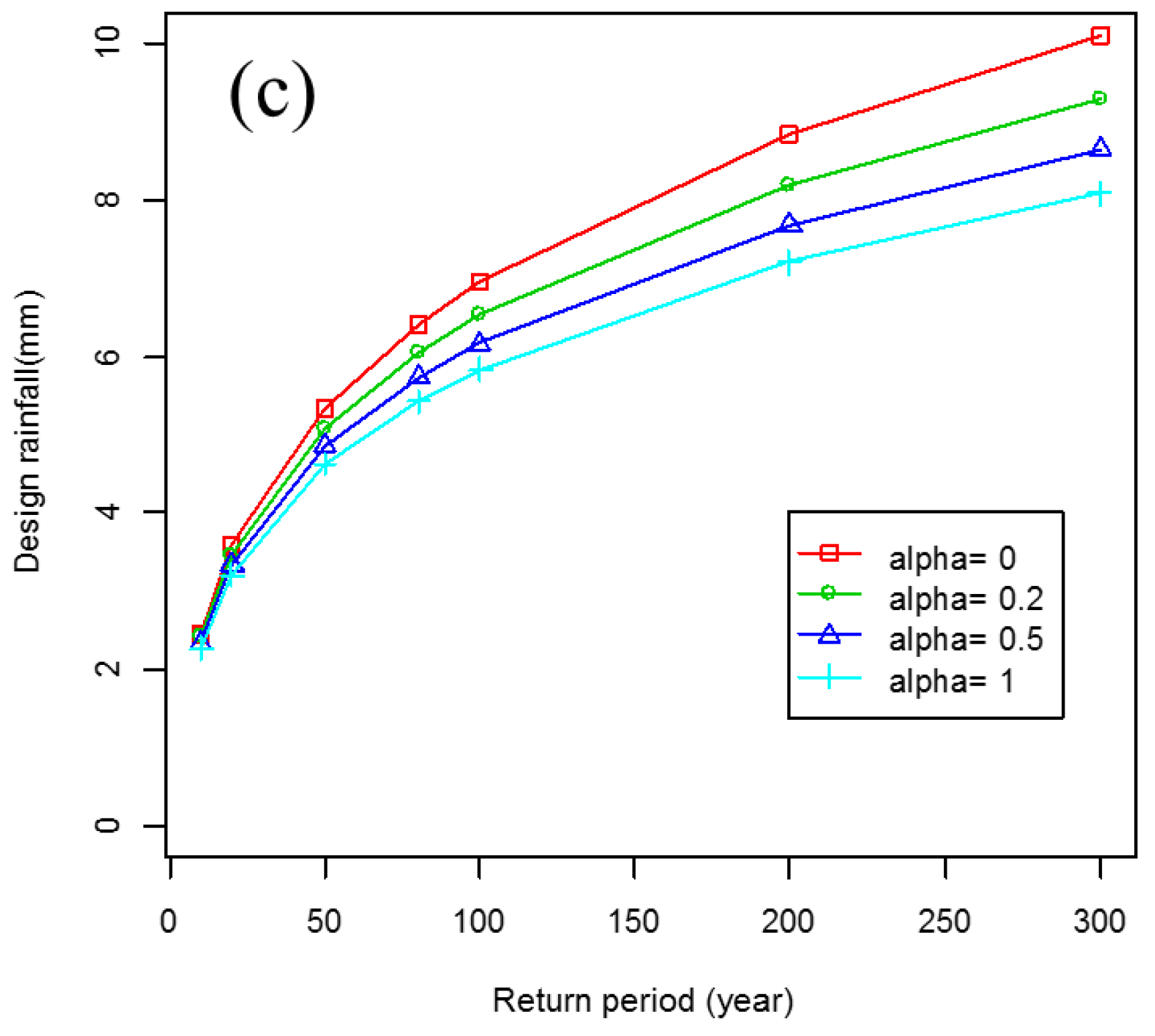
3.4. Balance between Robustness and Asymptotic Efficiency Based on the Optimal Value of
3.5. Performance of the MDPDE with GEV Depending on the Magnitude of the Extremes
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Park, S.K.; Lee, E. Synoptic features of orographically enhanced heavy rainfall on the east coast of Korea associated with typhoon Rusa (2002). Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Lee, D.K.; Choi, S.J. Observation and numerical prediction of torrential rainfall over Korea caused by typhoon Rusa (2002). J. Geophys. Res. Atmos. 2010, 115. [Google Scholar] [CrossRef]
- Kim, N.W.; Won, Y.S.; Chung, I.M. The scale of typhoon Rusa. Hydrol. Earth Syst. Sci. Discuss. 2006, 3, 3147–3182. [Google Scholar] [CrossRef]
- Franks, S.W.; Kuczera, G. Flood frequency analysis: Evidence and implications of secular climate variability, New South Wales. Water Resour. Res. 2002. [Google Scholar] [CrossRef]
- Alexander, L.V.; Zhang, X.; Peterson, T.C.; Caesar, J.; Gleason, B.; Tank, A.M.G.K.; Haylock, M.; Collins, D.; Trewin, B.; Rahimzadeh, F.; et al. Global observed changes in daily climate extremes of temperature and precipitation. J. Geophys. Res. Atmos. 2006, 111. [Google Scholar] [CrossRef]
- Madsen, H.; Lawrence, D.; Lang, M.; Martinkova, M.; Kjeldsen, T.R. Review of trend analysis and climate change projections of extreme precipitation and floods in Europe. J. Hydrol. 2014, 519, 3634–3650. [Google Scholar] [CrossRef]
- Trenberth, K.E. Changes in precipitation with climate change. Clim. Res. 2011, 47, 123–138. [Google Scholar] [CrossRef]
- Intergovernmental Panel on Climate Change (IPCC). Climate Change 2014: Synthesis Report. Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; IPCC: Geneva, Switzerland, 2014; p. 151.
- Prosdocimi, I.; Kjeldsen, T.R.; Miller, J.D. Detection and attribution of urbanization effect on flood extremes using nonstationary flood-frequency models. Water Resour. Res. 2015, 51, 4244–4262. [Google Scholar] [CrossRef] [PubMed]
- Coles, S.; Pericchi, L.R.; Sisson, S. A fully probabilistic approach to extreme rainfall modeling. J. Hydrol. 2003, 273, 35–50. [Google Scholar] [CrossRef]
- Strupezewski, W.G.; Kochanek, K.; Weglarczyk, S.; Singh, V.P. On robustness of large quantile estimates of log-Gumbel and log-logistic distributions to largest element of the observation series: Monte Carlo results vs. first order approximation. Stoch. Environ. Res. Risk Assess. 2005, 19, 280–291. [Google Scholar] [CrossRef]
- Strupczewski, W.G.; Kochanek, K.; Weglarczyk, S.; Singh, V.P. On robustness of large quantile estimates to largest elements of the observation series. Hydrol. Process. 2007, 21, 1328–1344. [Google Scholar] [CrossRef]
- Cunnane, C. Factors affecting choice of distribution for flood series. Hydrol. Sci. J. 1985, 30, 25–36. [Google Scholar] [CrossRef]
- Mutua, F.M. The use of the akaike information criterion in the identification of an optimum flood frequency model. Hydrol. Sci. J. 1994, 39, 235–244. [Google Scholar] [CrossRef]
- Neykov, N.; Filzmoser, P.; Dimova, R.; Neytchev, P. Robust fitting of mixtures using the trimmed likelihood estimator. Comput. Stat. Data Anal. 2007, 52, 299–308. [Google Scholar] [CrossRef]
- Singh, V.P. Hydrologic Frequency Modeling. In Proceedings of the International Symposium on Flood Frequency and Risk Analyses, Baton Rouge, LA, USA, 14–17 May 1986; Springer Netherlands: Dordrecht, The Netherlands, 1987; p. 645. [Google Scholar]
- Smith, R.L. Extreme value theory based on the r largest annual events. J. Hydrol. 1986, 86, 27–43. [Google Scholar] [CrossRef]
- Strupczewski, W.G.; Kochanek, K.; Singh, V.P. On the informative value of the largest sample element of log-gumbel distribution. Acta Geophys. 2007, 55, 652–678. [Google Scholar] [CrossRef]
- Basu, A.; Harris, I.R.; Hjort, N.L.; Jones, M.C. Robust and efficient estimation by minimising a density power divergence. Biometrika 1998, 85, 549–559. [Google Scholar] [CrossRef]
- Beran, R. Minimum hellinger distance estimates for parametric models. Ann. Stat. 1977, 5, 445–463. [Google Scholar] [CrossRef]
- Tamura, R.N.; Boos, D.D. Minimum hellinger distance estimation for multivariate location and covariance. J. Am. Stat. Assoc. 1986, 81, 223–229. [Google Scholar] [CrossRef]
- Simpson, D.G. Minimum hellinger distance estimation for the analysis of count data. J. Am. Stat. Assoc. 1987, 82, 802–807. [Google Scholar] [CrossRef]
- Basu, A.; Lindsay, B. Minimum disparity estimation for continuous models: Efficiency, distributions and robustness. Ann. Inst. Stat. Math. 1994, 46, 683–705. [Google Scholar] [CrossRef]
- Cao, R.; Cuevas, A.; Fraiman, R. Minimum distance density-based estimation. Comput. Stat. Data Anal. 1995, 20, 611–631. [Google Scholar] [CrossRef]
- Mihoko, M.; Eguchi, S. Robust blind source separation by beta divergence. Neural Comput. 2002, 14, 1859–1886. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.; Song, J. Minimum density power divergence estimator for garch models. Test 2009, 18, 316–341. [Google Scholar] [CrossRef]
- Kim, B.; Lee, S. Robust estimation for the covariance matrix of multivariate time series based on normal mixtures. Comput. Stat. Data Anal. 2013, 57, 125–140. [Google Scholar] [CrossRef]
- Karl, T.R.; Knight, R.W.; Easterling, D.R.; Quayle, R.G. Indices of climate change for the United States. Bull. Am. Meteorol. Soc. 1996, 77, 279–292. [Google Scholar] [CrossRef]
- Groisman, P.Y.; Karl, T.R.; Easterling, D.R.; Knight, R.W.; Jamason, P.F.; Hennessy, K.J.; Suppiah, R.; Page, C.M.; Wibig, J.; Fortuniak, K.; et al. Changes in the probability of heavy precipitation: Important indicators of climatic change. Clim. Chang. 1999, 42, 243–283. [Google Scholar] [CrossRef]
- Kunkel, K.E.; Andsager, K.; Easterling, D.R. Long-term trends in extreme precipitation events over the conterminous United States and Canada. J. Clim. 1999, 12, 2515–2527. [Google Scholar] [CrossRef]
- Groisman, P.Y.; Knight, R.W.; Karl, T.R. Heavy precipitation and high streamflow in the contiguous United States: Trends in the twentieth century. Bull. Am. Meteorol. Soc. 2001, 82, 219–246. [Google Scholar] [CrossRef]
- Chu, P.S.; Chen, Y.R.; Schroeder, T.A. Changes in precipitation extremes in the Hawaiian Islands in a warming climate. J. Clim. 2010, 23, 4881–4900. [Google Scholar] [CrossRef]
- Spierre, S.G.; Wake, C. Trends in Extreme Precipitation Events for the Northeastern United States 1948–2007; University of New Hampshire: Durham, NH, USA, 2010. [Google Scholar]
- Korea Meteorological Administration (KMA). Open Portal for Meteorological Data in South Korea. Available online: https://data.kma.go.kr/cmmn/main.do (accessed on 10 September 2016).
- Yen, B.C.; Tung, Y.-K.; American Society of Civil Engineers. Subcommittee on Uncertainty and Reliability Analysis in Design of Hydraulic Structures. In Reliability and Uncertainty Analyses in Hydraulic Design: A Report; American Society of Civil Engineers: New York, NY, USA, 1993; p. 291. [Google Scholar]
- Korea Meteorological Administration (KMA). Fact Book of Climate Change in Korea; Korea Meteorological Administration: Seoul, Korea, 2011; p. 117.
- Korea Meteorological Administration (KMA). Learning from Recent Events in 20 Years: Top 10 Severe Rainfall Events; Korea Meteorological Administration: Seoul, Korea, 2012; p. 48.
- Choi, K.-S.; Park, K.-J.; Kim, J.-Y.; Kim, B.-J. Synoptic analysis on the trend of northward movement of tropical cyclone with maximum intensity. J. Korean Earth Sci. Soc. 2015, 36, 171–180. [Google Scholar] [CrossRef]
- Choi, K.S.; Moon, I.J. Changes in tropical cyclone activity that has affected Korea since 1999. Nat. Hazards 2012, 62, 971–989. [Google Scholar] [CrossRef]
- Oh, S.M.; Moon, I.J. Typhoon and storm surge intensity changes in a warming climate around the Korean peninsula. Nat. Hazards 2013, 66, 1405–1429. [Google Scholar] [CrossRef]
- Fujisawa, H.; Eguchi, S. Robust estimation in the normal mixture model. J. Stat. Plan. Inference 2006, 136, 3989–4011. [Google Scholar] [CrossRef]



| Methods | Description |
|---|---|
| Actual rainfall amounts | Heavy rainfall: an event with precipitation above 50.8 mm (2 in) Very heavy rainfall: an event with precipitation above 101.6 mm (4 in) |
| Specific thresholds | Heavy rainfall: an event with precipitation above 90th percentiles Very heavy rainfall: an event with precipitation above 99th percentiles |
| Return periods | Heavy rainfall event: an event with 24-h precipitation above the 20 year return period Very heavy rainfall: an event with 24-h precipitation above the 100 year return period |
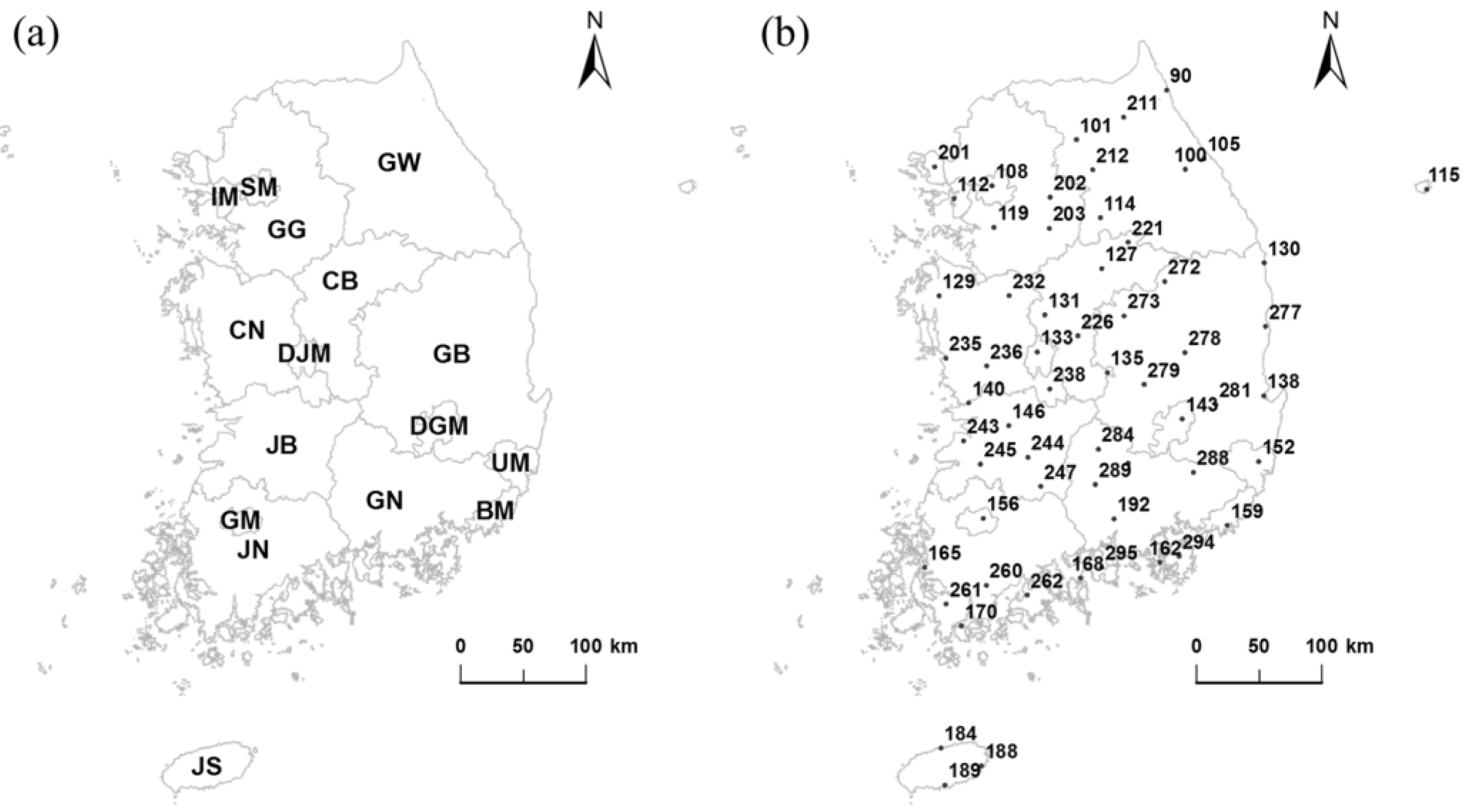
| No. | Province | Abbreviation | Rain Gauges |
|---|---|---|---|
| 1 | Seoul Metropolitan City | SM | 108 |
| 2 | Incheon Metropolitan City | IM | 112 |
| 3 | Gyeonggi-do | GG | 119, 201, 202, 203 |
| 4 | Gangwon-do | GW | 90, 100, 101, 105, 114, 211, 212 |
| 5 | Chungcheongbuk-do | CB | 127, 131, 226 |
| 6 | Chungcheongnam-do | CN | 129, 135, 140, 232, 235, 236 |
| 7 | Daejeon Metropolitan City | DJM | 133 |
| 8 | Gyeongsangbuk-do | GB | 115, 130, 138, 272, 273, 277, 279, 281 |
| 9 | Gyeongsangnam-do | GN | 162, 192, 284, 288, 289, 295 |
| 10 | Daegu Metropolitan City | DGM | 143 |
| 11 | Ulsan Metropolitan City | UM | 152 |
| 12 | Busan Metropolitan City | BM | 159 |
| 13 | Jeolabuk-do | JB | 146, 243, 244, 245, 247 |
| 14 | Jeolanam-do | JN | 165, 170, 260, 261, 262 |
| 15 | Gwangju Metropolitan City | GM | 156 |
| 16 | Jeju Island | JS | 184, 188, 189 |
| 0 | 0.2 | 0.5 | 1 | 0.092 | |
| 139.413 | 132.468 | 128.227 | 122.340 | 135.257 | |
| 65.360 | 56.354 | 55.286 | 52.815 | 59.122 |
| 0 | 0.2 | 0.5 | 1 | |
| 126.380 | 126.453 | 126.705 | 126.461 | |
| 49.747 | 51.759 | 54.615 | 56.341 | |
| 0.404 | 0.438 | 0.497 | 0.506 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Seo, Y.; Hwang, J.; Kim, B. Extreme Precipitation Frequency Analysis Using a Minimum Density Power Divergence Estimator. Water 2017, 9, 81. https://doi.org/10.3390/w9020081
Seo Y, Hwang J, Kim B. Extreme Precipitation Frequency Analysis Using a Minimum Density Power Divergence Estimator. Water. 2017; 9(2):81. https://doi.org/10.3390/w9020081
Chicago/Turabian StyleSeo, Yongwon, Junshik Hwang, and Byungsoo Kim. 2017. "Extreme Precipitation Frequency Analysis Using a Minimum Density Power Divergence Estimator" Water 9, no. 2: 81. https://doi.org/10.3390/w9020081
APA StyleSeo, Y., Hwang, J., & Kim, B. (2017). Extreme Precipitation Frequency Analysis Using a Minimum Density Power Divergence Estimator. Water, 9(2), 81. https://doi.org/10.3390/w9020081






