Integrating Local Scale Drainage Measures in Meso Scale Catchment Modelling
Abstract
:1. Introduction
1.1. Numerical Model Review
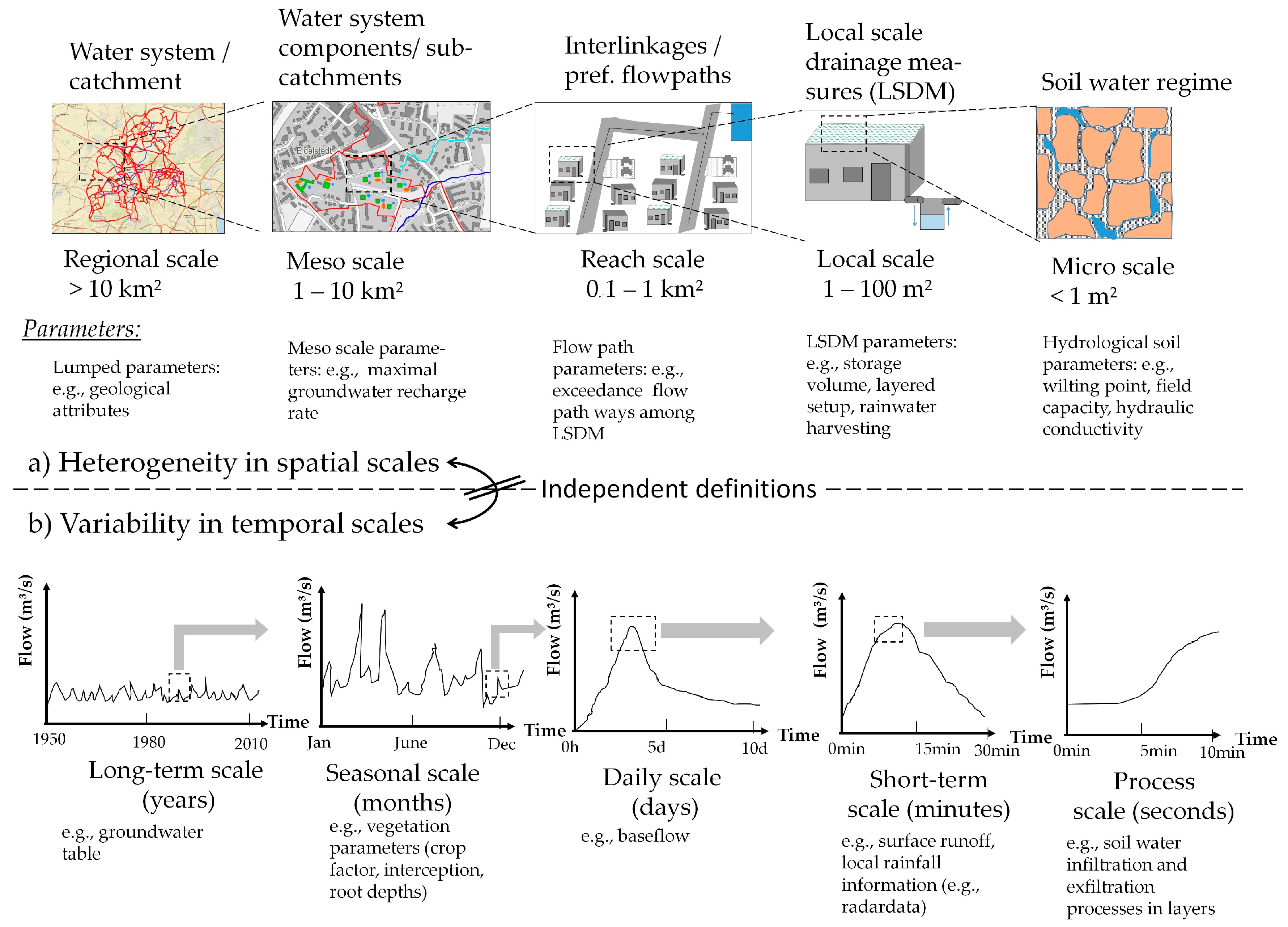
1.2. The Scale Issue in Numerical Models
1.3. The Example of Local Scale Drainage Measures and the Deficits in Numerical Models
1.4. Outline
2. Theoretical Approach
2.1. Multiscale Modelling
2.2. Features to Integrate LSDM in Catchment Models
- (1)
- Spatial micro scale and temporal process scale features:
- (a)
- Physical process features on the micro scale: e.g., interception, infiltration, evaporation, transpiration, soil pore space storage, water retention and detention, vertical and lateral water flow in layers.
- (b)
- Interaction and feedback features: Backwater effect and exceedance flow generation in coupled layers.
- (c)
- Material features: Supporting the use of hydrological parameters of material tested in laboratories and physical model tests.
- (2)
- Spatial local scale and temporal short-term scale features:
- (a)
- Spatial features: Geographic defined local scale areas realized with GIS data import and data processing functions to enable multiple type definitions, e.g., different green roof types per meso scale sub-catchment.
- (b)
- Variable design features: Supporting a flexible setup of drainage measures with multiple layers to model new designs.
- (c)
- Rainwater harvesting features: Modelling the water withdrawal of local measures.
- (3)
- Spatial local scale and temporal seasonal scale features:
- (a)
- Vegetative features: Parameterisation of vegetation systems according to seasonal changes for different vegetation types (e.g., interception storage, root depth, crop factor).
- (4)
- Spatial reach scale and temporal short-term scale features:
- (a)
- Real-time control features: Water control and drainage functions according to local rainfall forecasts (e.g., predrainage of cisterns or retention roofs). Integrating radar-based precipitation forecasting techniques.
- (b)
- Water redistribution features: Water storage and hydrological processes depending on interactions among linked individual elements. Modelling exceedance flow control in a cascade of local measures on the reach scale.
- (5)
- Spatial meso scale and temporal short-term scale features:
- (a)
- Adoption of meso scale features: Relevant preset parameters of meso scale features are adopted for local scale measures (e.g., geological attributes defined on the sub-catchment scale).
- (b)
- Backwater effect features: Backwater effects between local scale and meso scale elements (e.g., when the capacity of retention measures is exceeded) or backwater effects derived on the meso scale by external forces (e.g., tidal effect or increased groundwater level).
- (6)
- Spatial regional scale and long-term scale features:
- (a)
- Enabling the simulation of prewetting and initial water storage conditions on the basis of continuous water balance simulations.
3. Methodology
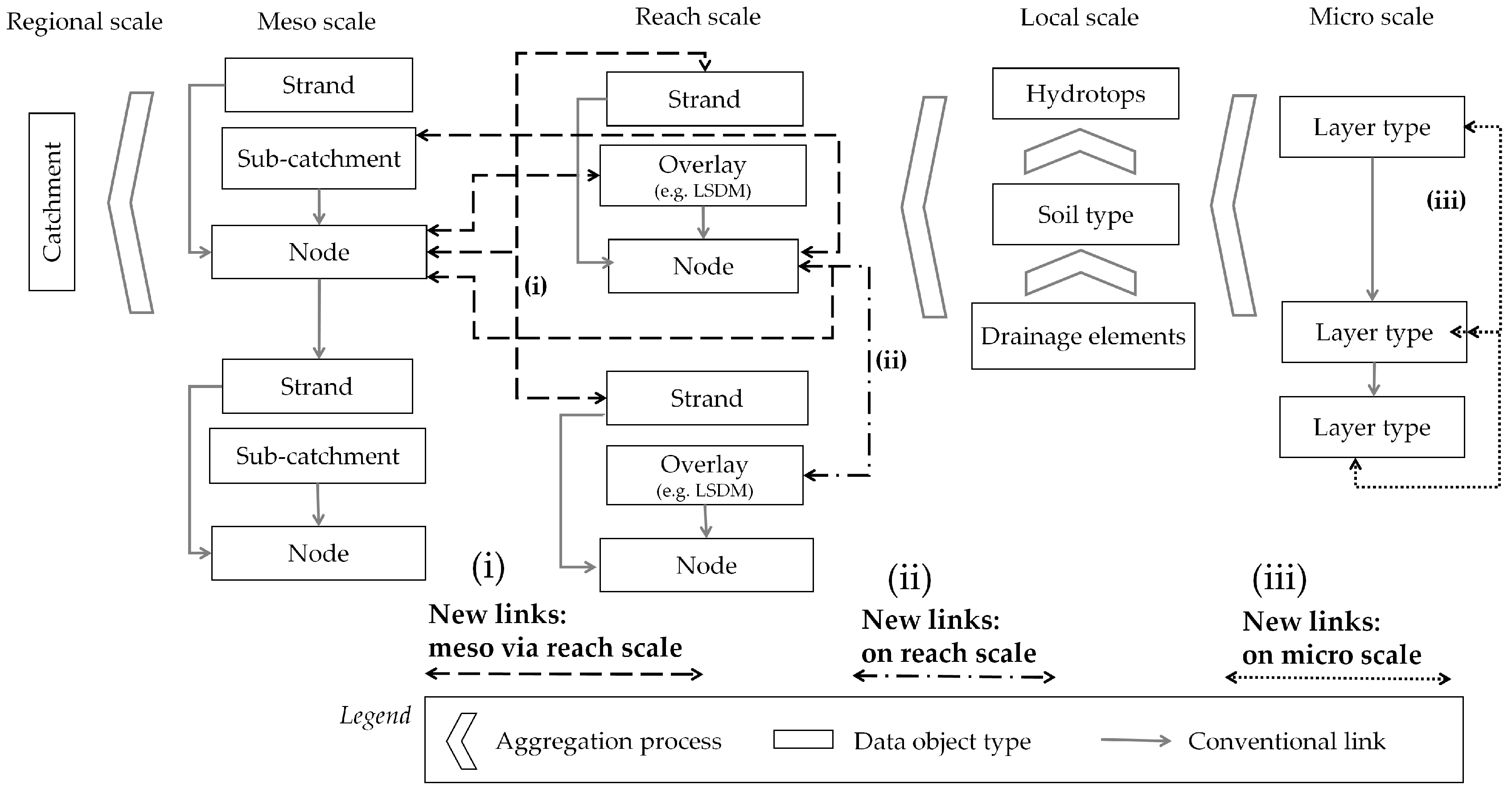
3.1. Data Mapping with “Overlay” Data Objects
3.2. Interlinked Multiple Scale Data Objects
3.3. Multiple Interlinked Micro Scale Layers
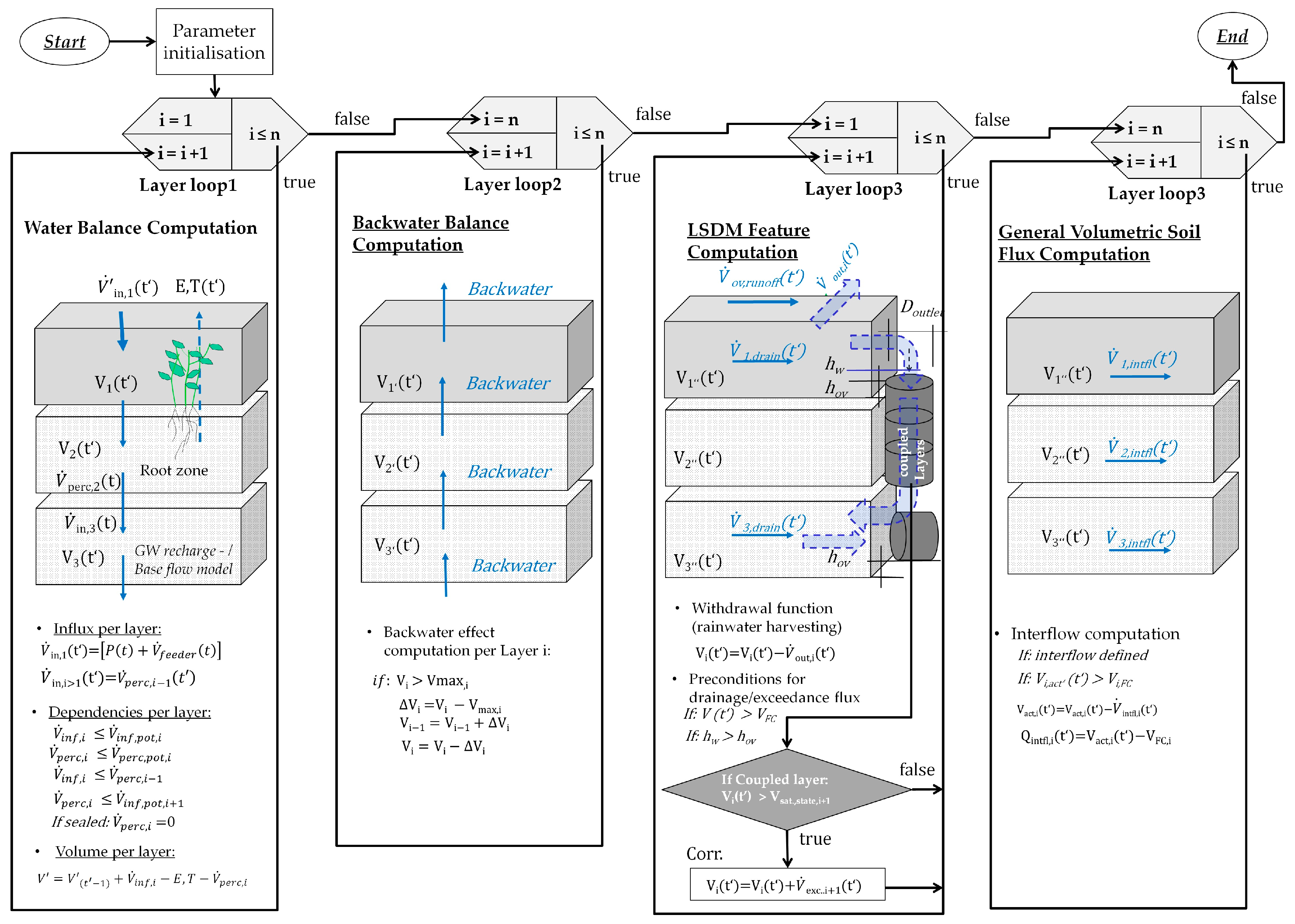
3.3.1. Integration of the Concept in the Overall Computation Procedure
3.3.2. The Water Balance Computation
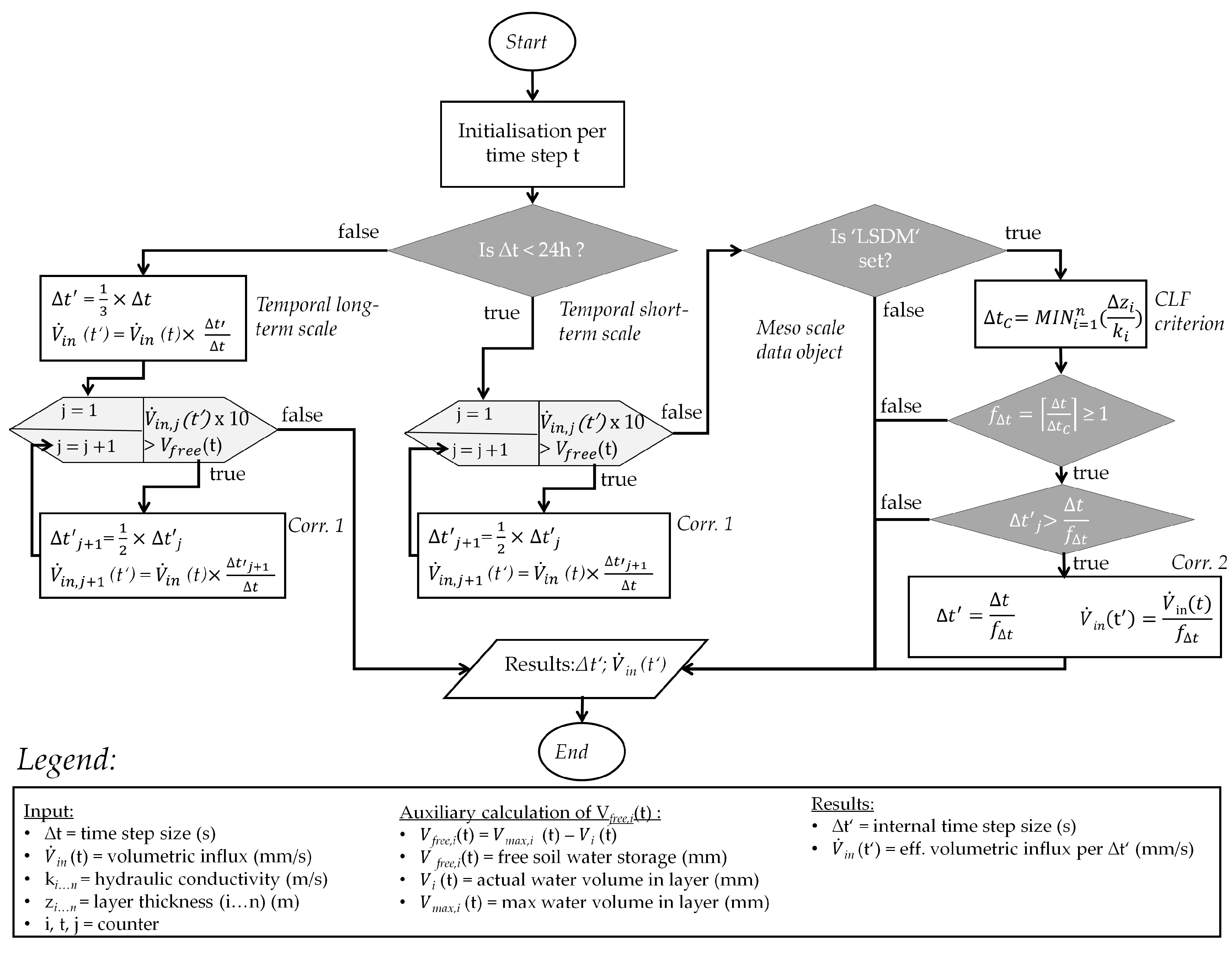
3.3.3. The Dynamic Time Step Size Module
3.3.4. Computation Procedure for Multiple Interlinked Micro Scale Layers
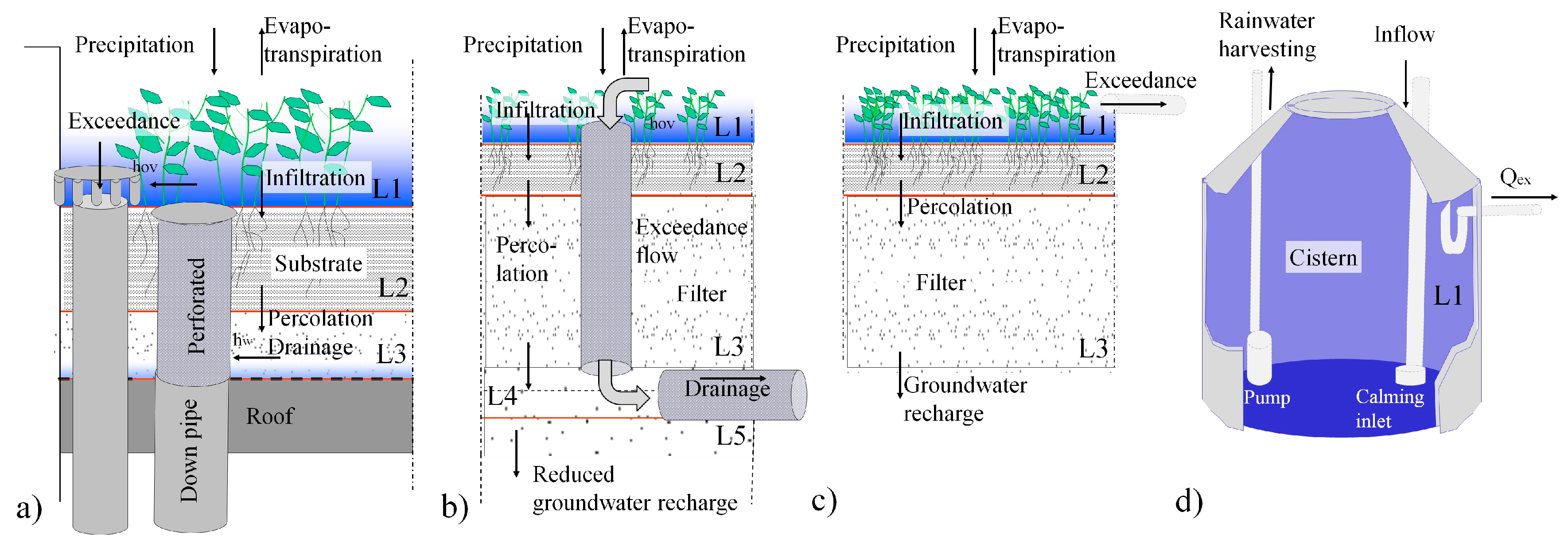
3.3.5. Design Examples of Local Scale Drainage Measures
4. Implementation
5. Validation of the Method of Multiple Interlinked Micro Scale Layers
5.1. Laboratory Physical Model Setup
5.2. Numerical Model Setup and Input Parameters
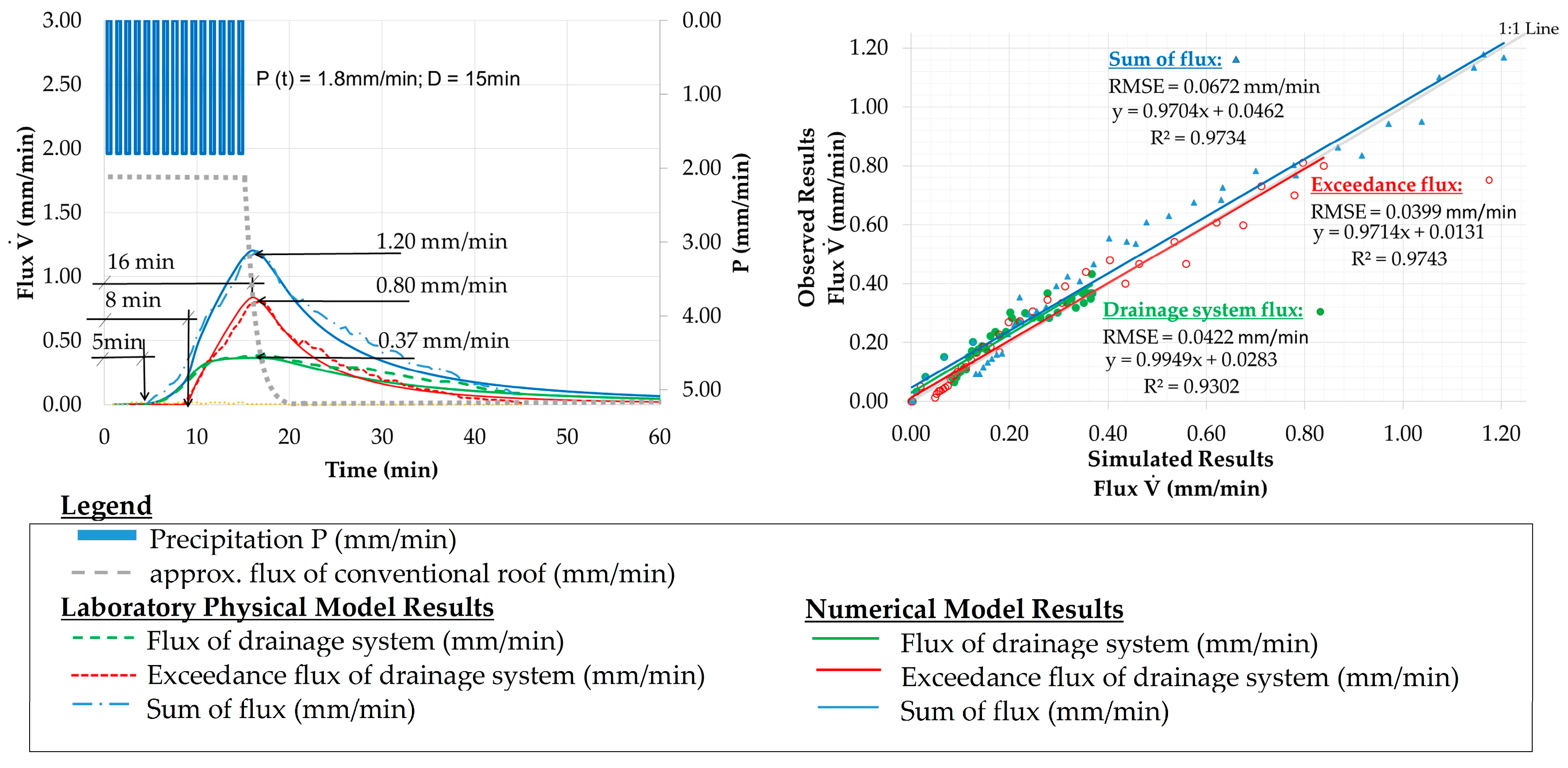
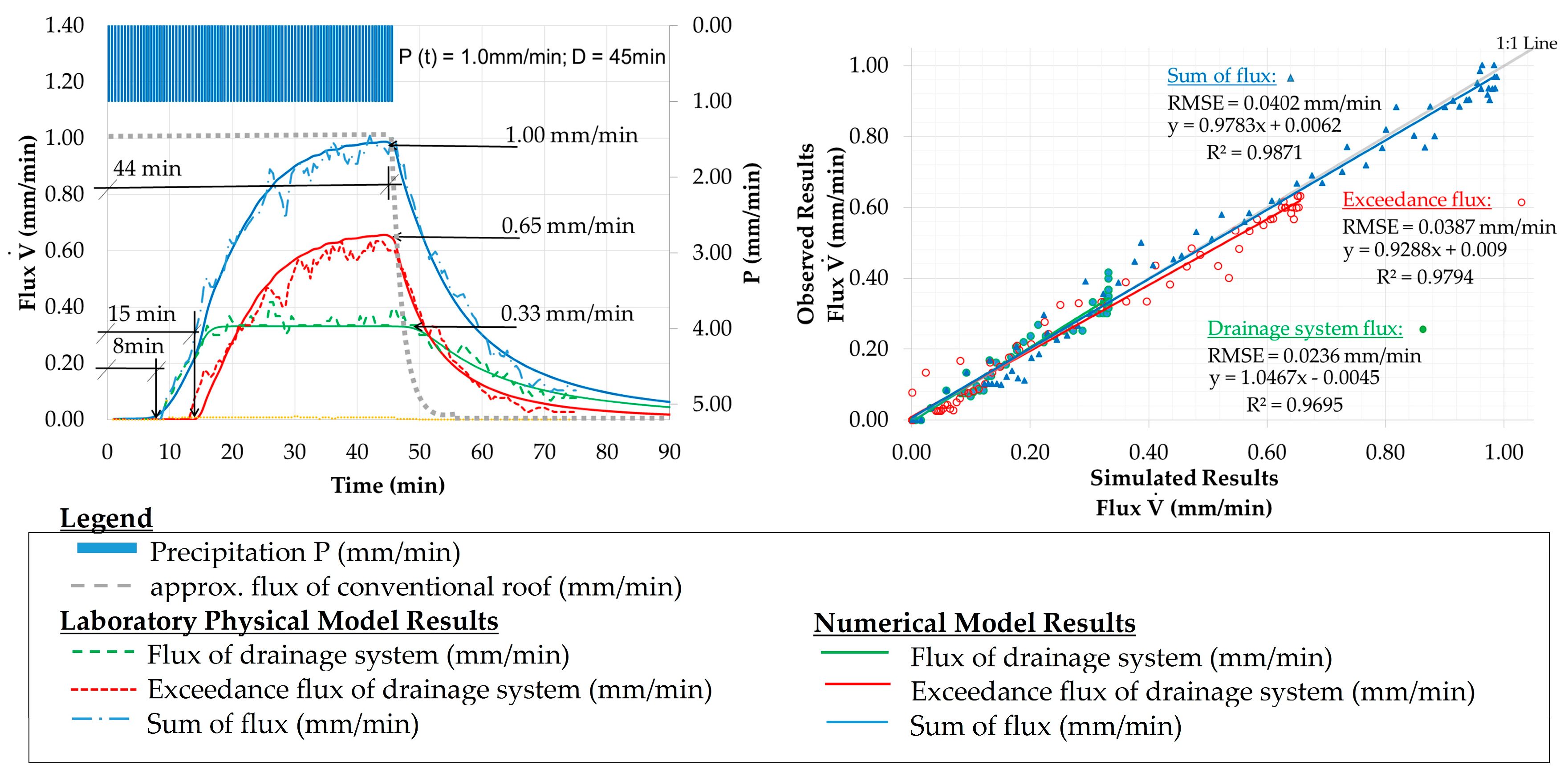
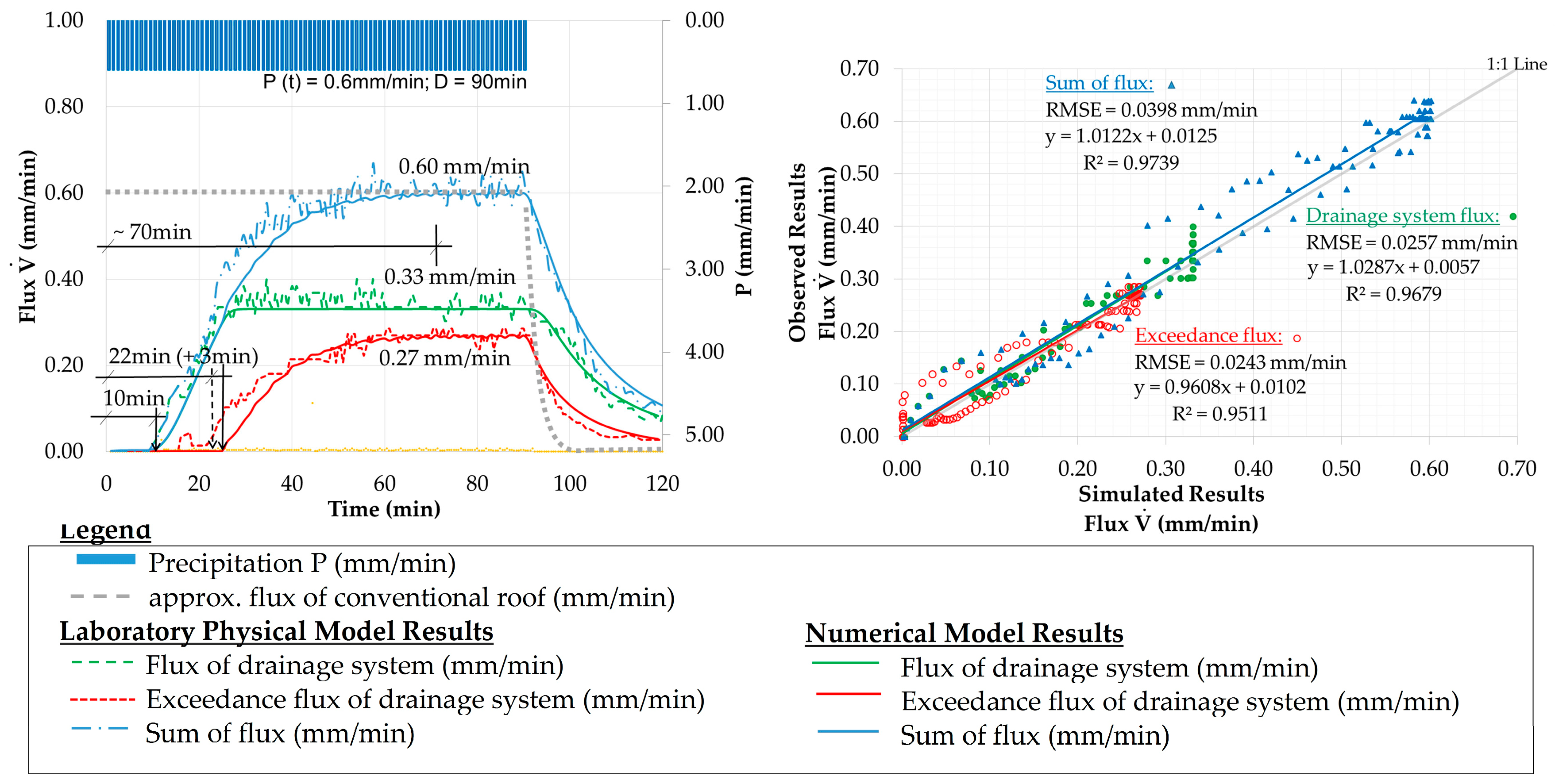
5.3. Calibration Procedure and Results
5.4. Validation Results
5.5. Summary of Calibration and Validation Results
6. Application Studies of the Catchment Model
7. Discussion and Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- United Nations Department of Economic and Social Affairs. Population Division (2014). World Urbanization Prospects: The 2014 Revision, Highlights; (ST/ESA/SER.A/352); United Nations Department of Economic and Social Affairs: New York, NY, USA, 2014. [Google Scholar]
- Liebscher, H.G.; Mendel, H.G. Vom Empirischen Modellansatz zum Komplexen Hydrologischen Flussgebietsmodell—Rückblick und Perspektiven; Bundesanstalt für Gewässerkunde: Koblenz, Germany, 2010. [Google Scholar]
- Vaze, J.; Jordan, P.; Beecham, R.; Frost, A.; Summerell, G. Guidelines for Rainfall-Runoff Modelling: Towards Best Practice Model Application. 2011. Available online: http://ewater.org.au/uploads/files/eWater-Modelling-Guidelines-RRM-%28v1-Mar-2012%29.pdf (accessed on 10 September 2016).
- Bach, P.M.; Rauch, W.; Mikkelsen, P.S.; McCarthy, D.T.; Deletic, A. A critical review of integrated urban water modelling—Urban drainage and beyond. Environ. Model. Softw. 2014, 54, 88–107. [Google Scholar] [CrossRef]
- Todini, E. Hydrological catchment modelling: Past, present and future. Hydrol. Earth Syst. Sci. 2007, 11, 468–482. [Google Scholar] [CrossRef]
- Burton, G.A.; Pitt, R.E. Stormwater Effects Handbook: A Toolbox for Watershed Managers, Scientists, and Engineers; Lewis Publishers: Boca Raton, FL, USA, 2002. [Google Scholar]
- Urbonas, B. Stormwater Runoff Modeling; Is It as Accurate as We Think? In Proceedings of the International Conference on Urban Runoff Modeling: Intelligent Modeling to Improve Stormwater Management, Arcata, CA, USA, 22–27 July 2007.
- Paniconi, C.; Putti, M. Physically based modeling in catchment hydrology at 50: Survey and outlook. Water Resour. Res. 2015, 51, 7090–7129. [Google Scholar] [CrossRef]
- Messal, H.E.E. Rückkopplungen und Rückwirkungen in der Hydrologischen Modellierung am Beispiel von Kontinuierlichen Niederschlag-Abfluß-Simulationen und Hochwasservorhersagen. Ph.D. Thesis, Technische Universität Berlin, Berlin, Germany, 2000. [Google Scholar]
- Liu, C.; Chen, Y. Application of geographic information system in hydrological models. In From Headwaters to the Ocean: Hydrological Change and Water Management—Hydrochange 2008; Fukushima, Y., Burnett, W., Taniguchi, M., Haigh, M., Umezawa, Y., Eds.; CRC Press: Kyoto, Japan, 2008; pp. 217–222. [Google Scholar]
- Blöschl, G.; Sivapalan, M. Scale issues in hydrological modelling: A review. Hydrol. Process. 1995, 1995, 251–290. [Google Scholar]
- Gentine, P.; Troy, T.J.; Lintner, B.R.; Findell, K.L. Scaling in surface hydrology: Progress and challenges. J. Contemp. Water Res. Educ. 2012, 147, 28–40. [Google Scholar] [CrossRef]
- Gleeson, T.; Paszkowski, D. Perceptions of scale in hydrology: What do you mean by regional scale? Hydrol. Sci. J. 2013, 59, 99–107. [Google Scholar] [CrossRef]
- Viglione, A.; Merz, B.; Viet Dung, N.; Parajka, J.; Nester, T.; Blöschl, G. Attribution of regional flood changes based on scaling fingerprints. Water Resour. Res. 2016, 52, 5322–5340. [Google Scholar] [CrossRef] [PubMed]
- Fletcher, T.D.; Shuster, W.; Hunt, W.F.; Ashley, R.; Butler, D.; Arthur, S.; Trowsdale, S.; Barraud, S.; Semadeni-Davies, A.; Bertrand-Krajewski, J.-L.; et al. SUDS, LID, BMPs, WSUD and more—The evolution and application of terminology surrounding urban drainage. Urban Water J. 2014, 12, 525–542. [Google Scholar] [CrossRef]
- Geiger, W.F.; Dreiseitl, H. Neue Wege für das Regenwasser: Handbuch zum Rückhalt und zur Versickerung von Regenwasser in Baugebieten; Oldenbourg: München, Germany, 1995. [Google Scholar]
- Elliott, A.H.; Trowsdale, S.A. A review of models for low impact urban stormwater drainage. Environ. Model. Softw. 2007, 22, 394–405. [Google Scholar] [CrossRef]
- Jato-Espino, D.; Charlesworth, S.M.; Bayon, J.R.; Warwick, F. Rainfall-runoff simulations to assess the potential of SuDS for mitigating flooding in highly urbanized catchments. Int. J. Environ. Res. Public Health 2016, 13, 149. [Google Scholar] [CrossRef] [PubMed]
- Ahiablame, L.M.; Engel, B.A.; Chaubey, I. Effectiveness of low impact development practices: Literature review and suggestions for future research. Water Air Soil Pollut. 2012, 223, 4253–4273. [Google Scholar] [CrossRef]
- Sharma, A.; Pezzaniti, D.; Myers, B.; Cook, S.; Tjandraatmadja, G.; Chacko, P.; Chavoshi, S.; Kemp, D.; Leonard, R.; Koth, B.; et al. Water sensitive urban design: An investigation of current systems, implementation drivers, community perceptions and potential to supplement urban water services. Water 2016, 8, 272. [Google Scholar] [CrossRef]
- Bach, P.M.; Deletic, A.; Urich, C.; Sitzenfrei, R.; Kleidorfer, M.; Rauch, W.; McCarthy, D.T. Modelling interactions between lot-scale decentralised water infrastructure and urban form—A case study on infiltration systems. Water Resour. Manag. 2013, 27, 4845–4863. [Google Scholar] [CrossRef]
- Bach, P.M.; Eisenstein, W.; McCarthy, D.T.; Hatt, B.; Sedlak, D.; Deletic, A. Australian water sensitive planning in the San Francisco Bay Area: Challenges and implications for model transferability. In Proceedings of the 2016 International Low Impact Development Conference, Portland, ME, USA, 29–31 August 2016.
- Woods Ballard, B.; Wilson, S.; Updale-Clarke, H.; Illman, S.; Scott, T.; Ashley, R.; Kellagher, R. The SuDS Manual (C753). 2015. Available online: https://ciria.sharefile.com/share?#/view/6b7cd338f8a640aa (accessed on 7 August 2016).
- Zhang, X.; Drake, N.A.; Wainwright, J. Spatial Modelling and Scaling Issues. In Environmental Modelling: Finding Simplicity in Complexity, 2nd ed.; Muzlligan, M., Wainwright, J., Eds.; John Wiley & Sons, Ltd.: Chichester, UK, 2013; Chapter 5; pp. 69–90. [Google Scholar]
- Petrucci, G.; Bonhomme, C. The dilemma of spatial representation for urban hydrology semi-distributed modelling: Trade-offs among complexity, calibration and geographical data. J. Hydrol. 2014, 517, 997–1007. [Google Scholar] [CrossRef]
- Leavesley, G.H.; Lichty, R.W.; Troutman, B.M.; Saindon, L.G. Precipitation-Runoff Modeling System—Users Manual; Water-Resources Investigation Report; United States Department of the Interior: Denver, CO, USA, 1983.
- Klawitter, A. Ein Modellkonzept zur Integrativen Betrachtung von Urban- und Ruralhydrologie auf Einzugsgebietsebene. Ph.D. Thesis, Institut für Wasserbau und Wasserwirtschaft, Technische Universität Darmstadt, Darmstadt, Germany, 2006. [Google Scholar]
- Sverdlova, L. Reference Values to Estimate the Efficiency of Sustainable Drainage Systems—Development by Using Hydrological Modeling. Master’s Thesis, Hamburg University of Technology, Hamburg, Germany, 2015. [Google Scholar]
- Shreve, R.L. Infinite topologically random channel networks. J. Geol. 1967, 1967, 178–186. [Google Scholar] [CrossRef]
- Deutscher Verband für Wasserwirtschaft und Kulturbau e.V. (DVWK). Ermittlung der Verdunstung von Land- und Wasserflächen; DVWK, Wirtschafts- und Verlagsgesellschaft Gas und Wasser: Bonn, Germany, 1996. [Google Scholar]
- Courant, R.; Friedrichs, K.; Lewy, H. Über die partiellen Differenzengleichungen der mathematischen Physik. Math. Ann. 1928, 100, 32–74. [Google Scholar] [CrossRef]
- Pinder, G.F. Groundwater Modeling Using Geographical Information Systems; Wiley: New York, NY, USA, 2002. [Google Scholar]
- Hellmers, S. Abbildbarkeit mehrfach vernetzter heterogener dezentraler Maßnahmen in NA-Modellen. In Räumliche Heterogenität—Erkennen, Abbilden, Validieren oder Ignorieren? Casper, M., Gronz, O., Eds.; Forum für Hydrologie und Wasserbewirtschaftung: Trier, Germany, 2016; Volume 36.16, pp. 75–84. [Google Scholar]
- Bund der Ingenieure für Wasserwirtschaft, Abfallwirtschaft und Kulturbau e.V. (BWK). Hydraulische Berechnung von Naturnahen Fließgewässern—Teil 1, Stationäre Berechnung der Wasserspiegellinie unter Besonderer Berücksichtigung von Bewuchs- und Bauwerkseinflüssen, 3rd ed.; BWK, Frauenhofer IRB Verlag: Sindelfingen, Germany, 2009. [Google Scholar]
- Palmaricciotti, G.; Patzke, J.; Hellmers, S.; Manojlović, N.; Fröhle, P. Entwicklung und Umsetzung des Regensimulators “RS-TUHH”. In Aktuelle Herausforderungen im Flussgebiets- und Hochwassermanagement; Evers, M., Diekkrüger, B., Eds.; Forum für Hydrologie und Wasserwirtschaft: Bonn, Germany, 2015; Volume 35.15, pp. 101–110. [Google Scholar]
- Palmaricciotti, G.; Patzke, J.; Hellmers, S.; Manojlović, N.; Fröhle, P. Rainfall Simulator TUHH (RS-TUHH)—Planning, Construction and Use. In Proceedings of the 11th International Conference on Hydroscience & Engineering, Hamburg, Germany, 28 September–2 October 2014.
- OptiGreen LTD. Retention Roof Meander 30. 2015. Available online: http://www.optigreen.co.uk/system-solutions/retention-roof/meander-30/ (accessed on 1 September 2016).
- Hellmers, S.; Manojlović, N.; Palmaricciotti, G.; Kurzbach, S.; Fröhle, P. Multiple linked sustainable drainage systems in hydrological modelling for urban drainage and flood risk management. J. Flood Risk Manag. 2015. [Google Scholar] [CrossRef]
- Locatelli, L.; Mark, O.; Mikkelsen, P.S.; Arnbjerg-Nielsen, K.; Bergen Jensen, M.; Binning, P.J. Modelling of green roof hydrological performance for urban drainage applications. J. Hydrol. 2014, 519, 3237–3248. [Google Scholar] [CrossRef]
- Kasmin, H.; Stovin, V.R.; Hathway, E.A. Towards a generic rainfall-runoff model for green roofs. Water Sci. Technol. 2010, 62, 898–905. [Google Scholar] [CrossRef] [PubMed]





| Cali- and Validation Runs 1 | Drainage System Criteria | Exceedance System Criteria | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | (1) | (2) | (3) | (4) | (5) | |
| Δ in Time Delay (min) | Δ in Time to Peak Flux (min) | Δ in Peak Flux (%) | Δ in Volume (%) | RMSE (mm/min) | Δ in Time Delay (min) | Δ in Time to Peak Flux (min) | Δ in Peak Flux (%) | Δ in Volume (%) | RMSE (mm/min) | |
| Cal. 1 | <1 min | <1 min | 7.5% | <10% | 0.0422 | <1 min | <1 min | 4.5% | <10% | 0.0399 |
| Val. 1 | <1 min | <1 min | 10.0% | <10% | 0.0236 | <1 min | <1 min | 3.0% | <10% | 0.0387 |
| Val. 2 | <1 min | <1 min | 3.5% | <10% | 0.0257 | ~3 min | <1 min | 10.0% | <10% | 0.0243 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hellmers, S.; Fröhle, P. Integrating Local Scale Drainage Measures in Meso Scale Catchment Modelling. Water 2017, 9, 71. https://doi.org/10.3390/w9020071
Hellmers S, Fröhle P. Integrating Local Scale Drainage Measures in Meso Scale Catchment Modelling. Water. 2017; 9(2):71. https://doi.org/10.3390/w9020071
Chicago/Turabian StyleHellmers, Sandra, and Peter Fröhle. 2017. "Integrating Local Scale Drainage Measures in Meso Scale Catchment Modelling" Water 9, no. 2: 71. https://doi.org/10.3390/w9020071
APA StyleHellmers, S., & Fröhle, P. (2017). Integrating Local Scale Drainage Measures in Meso Scale Catchment Modelling. Water, 9(2), 71. https://doi.org/10.3390/w9020071






