1. Introduction
Nowadays, water utility managers often choose to perform active pressure control in their water distribution networks (WDNs) due to the many associated benefits [
1], which include leakage and pipe burst reduction and the extension of network infrastructure useful life [
2]. Another benefit of pressure control lies in the possibility of recovering energy from the WDN through turbines or similar devices [
3,
4]. After the WDN is subdivided in pressure zones [
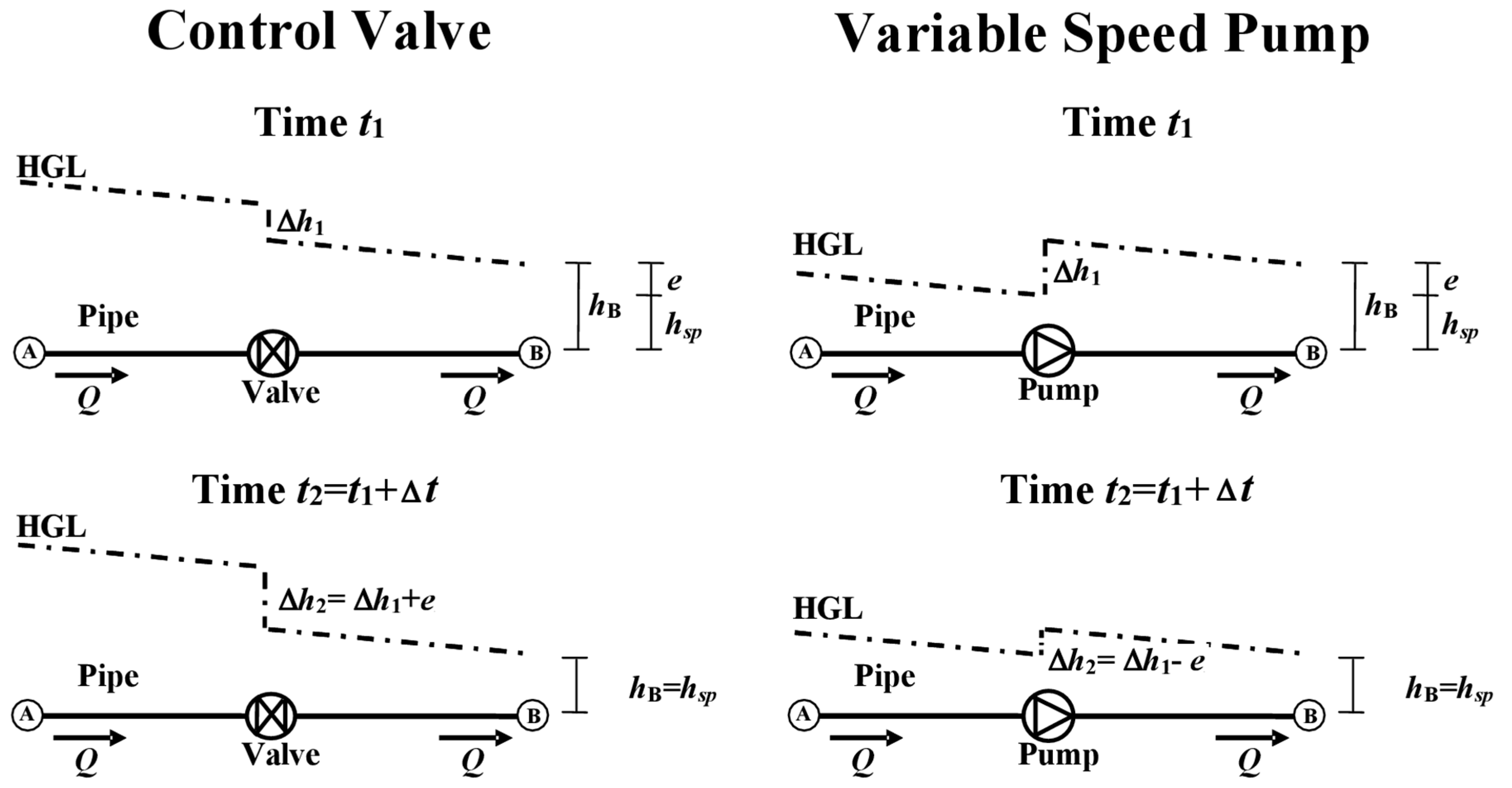
5], active pressure control requires a suitable pressure control device to be installed in the pipe(s) connecting each pressure zone to its source(s). Recent studies have proven that active pressure control can be more cost effective when the device setting is controlled in real time, in order to meet WDN demand variations in time [
6]. In this context, the device controlled in real time can be a pressure control valve [
7] or a variable speed pump [
8], depending on whether the source node is under pressure surplus or deficit conditions compared to the pressure zone it feeds.
Remote real time control (RTC) is a kind of control in which the pressure head is monitored at remote critical node(s) in the WDN. By making use of suitable algorithms operating on the pressure head measurements, a programmable logic controller sets the new suitable device setting to maintain the minimum desired pressure at the remote node(s). In the scientific literature of WDNs, the first study on service pressure RTC was carried out by Campisano et al. [
9], followed by many others [
10,
11,
12,
13,
14,
15]. Whereas the proportional algorithms of Campisano et al. [
9,
10,
12] only used the pressure head measurement at the critical node, Creaco and Franchini [
11] set up a more effective algorithm that also makes use of the water discharge measurement in the pipe fitted with the control device. Like the algorithm used by Campisano et al. [
9,
10,
12], the algorithm of Creaco and Franchini [
11] has a parameter that needs to be tuned to ensure the maximum regulation performance. Later, a parameter-less algorithm with only slightly worse performance than the algorithm of Creaco and Franchini [
11] was proposed for the RTC of control valves [
13] and variable speed pumps [
14]. The algorithm of Page et al. [
13,
14] has the novel aspect of making use of the water discharge prediction in the pipe fitted with the control device. The prediction is carried out through water discharge measurements at small temporal steps (smaller than the RTC temporal step, which has order of magnitude of some minutes). However, a limit of this approach lies in the fact that it is effective only if the water discharge trend is smooth.
In this work, the water discharge prediction is implemented in a refined version of the algorithm of Creaco and Franchini [
11]. Unlike the work of Page et al. [
13,
14], the prediction method operates on larger temporal steps than the control temporal step. Therefore, it is able to cope with the irregular trend of the pipe water discharge at fine temporal scale, due to the random nature of demand [
15,
16]. To show this, a stochastic bottom-up approach is used for nodal demand reconstruction in the applications, which concern the numerical simulation of RTC in a WDN.
3. Results
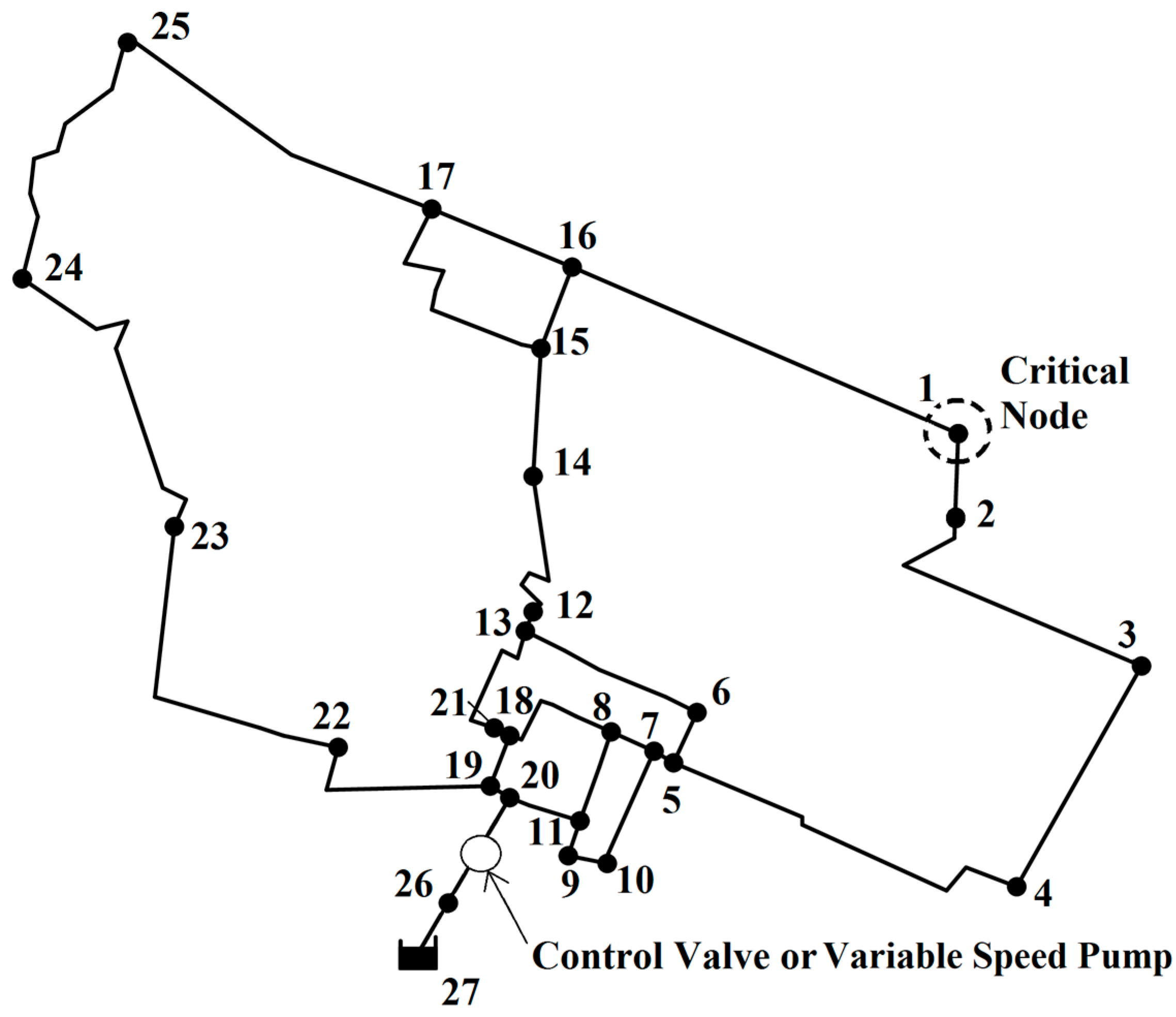
The applications concerned the numerical simulation of a network in Northern Italy, which serves about 30,000 inhabitants and has already been used for research in the field of pressure control [
6,
11,
15]. The skeletonized layout is reported in
Figure 3.
The network has a single source node, 26 demanding nodes with ground elevation of 0 m a.s.l. and 32 pipes. The uniform ground elevation and the size make the network eligible for being considered as a single pressure zone.
More details about characteristics of the pipes, in terms of pipes and length, can be found in the referenced work.
Two scenarios were considered hereinafter. In scenario 1, the source node is considered to have a constant head of 40 m a.s.l. Furthermore, a DN350 plunger control valve is inserted in pipe 26-11, which connects the source node to the rest of the network. The valve curve
ξ(
α) considered for the plunger valve has the following form [
10]:
where
c1 = 0.75 and
c2 = 3.25 are the coefficients calculated to best fit the data provided by a valve manufacturer. In Equation (14),
α was allowed to range from 0 (fully open) to 0.95 (almost fully closed).
In scenario 2, the source node is considered to have a constant head of 1 m a.s.l. and a variable speed pump is inserted in pipe 26-11. The curve used for this device is the following:
with
β allowed to range from 0.5 (minimum speed) to 1 (maximum speed).
In both scenarios, the critical node of the network, which features the lowest pressure head values along the day, is node 1. Therefore, node 1 was selected as control node. The RTC of the control valve and of the variable speed pump, in scenarios 1 and 2, respectively, was carried out to bring the pressure head at the control node to set point value hsp = 25 m.
For each node, the demand trend was obtained through the bottom-up approach by applying the methodology described in [
15,
16], which is based on demand pulse generation through the Poisson model. In the present work, the same pulse features as those associated with Dutch households with two to three inhabitants (reported in [
16]), in terms of duration, intensity, and duration/intensity correlation, were considered. After being generated for five consecutive days and for all the network nodes, the demand pulses were aggregated over Δ
t = 180 s long temporal steps, to correspond to the temporal step adopted for RTC and for the extended period simulation [
18] of the network. At this stage, a remark must be made about the choice of Δ
t = 180 s as control temporal step for RTC. In fact, this choice was made based on the findings in [
15], which proved that 180 s guarantees the best trade-off between closeness of the controlled variable to the set point and number of actuator setting variations in this case study.
Each instant of network operation was simulated through the global gradient algorithm [
19]. Incidentally, the combination of extended period simulation with nodal demands reconstructed with the bottom-up approach at medium temporal steps represents the best combination to simulate the behavior of RTC [
15] and WDNs [
16] in real time, in the trade-off between accuracy of the results and computational efficiency.
At each node and at each instant of simulation, the outflow to the users was evaluated with the pressure-driven approach through the Wagner et al. [
20] formula, taking
hsp as the pressure head for full demand satisfaction at all nodes. Furthermore, leakage
qleak (m
3/s) was related to the nodal pressure head
h through the Tucciarelli et al. [
21] formula:
where
∑L (m) is the total length of the pipes connected to the node. Furthermore,
αleak (m
2−γ/s) and
γ (-) are the leakage coefficient and exponent, respectively. While
γ depends on pipe material and leak opening shape [
22],
αleak depends on the number of leak openings along the pipe and then grows with pipe age. In this work, these parameters were assumed uniform over the network.
γ was set to 1 (typical value for plastic pipes) while
αleak was set to 9.4 × 10
−9 m/s in order to have in the first scenario a leakage percentage rate close to 20% of the total outflow from the source, in the case of fully open control valve.
The total network demand
D (L/s) trend at the Δ
t = 180 s temporal scale obtained with the bottom-up reconstruction is reported in graph a) in
Figure 4 and
Figure 5 for the five consecutive days of network operation. These graphs show that, despite the spatial and temporal aggregation, demand random fluctuations are still present, especially under low demand conditions. Furthermore, each daily trend of demand is slightly different from the others. These aspects are due to the stochastic method used for demand generation, which obtains nodal demands as the superimposition of demand pulses [
15,
16], consistently with real WDNs.
For analyzing the performance of RTC, two indices were used. The former, indicated as mean|
e|, concerns the closeness of the controlled variable at the generic
i-th time, that is the pressure head
hi at the control node, to the set point value
hsp. It is calculated as:
where
Ntot = 2400 is the number of temporal steps Δ
t in the five days of simulation.
The latter index, indicated as ∑|Δ
α| and ∑|Δ
β| for the control valve and for the variable speed pump, respectively, is representative of the total variations of the device setting. In the two scenarios, it is calculated as:
where
αi and
β i are the values of valve setting
α and pump setting
β, respectively, at the generic
i-th time. Generally speaking, a good controller is expected to keep the controlled variable close to the set point with small device setting variations, to avoid the wear of the control device. Therefore, it will feature a low value of both indices.
For both control valves (Equation (5)) and pumps (Equation (10)), the coefficient K of the logic controller was calibrated in such a way as to minimize mean|e|.
Globally, 4 simulations were carried out: simulations 1a and 1b, associated with scenario 1, and simulations 2a and 2b, associated with scenario 2. Simulations 1a and 2a were carried out considering the original RTC algorithm of Creaco and Franchini [
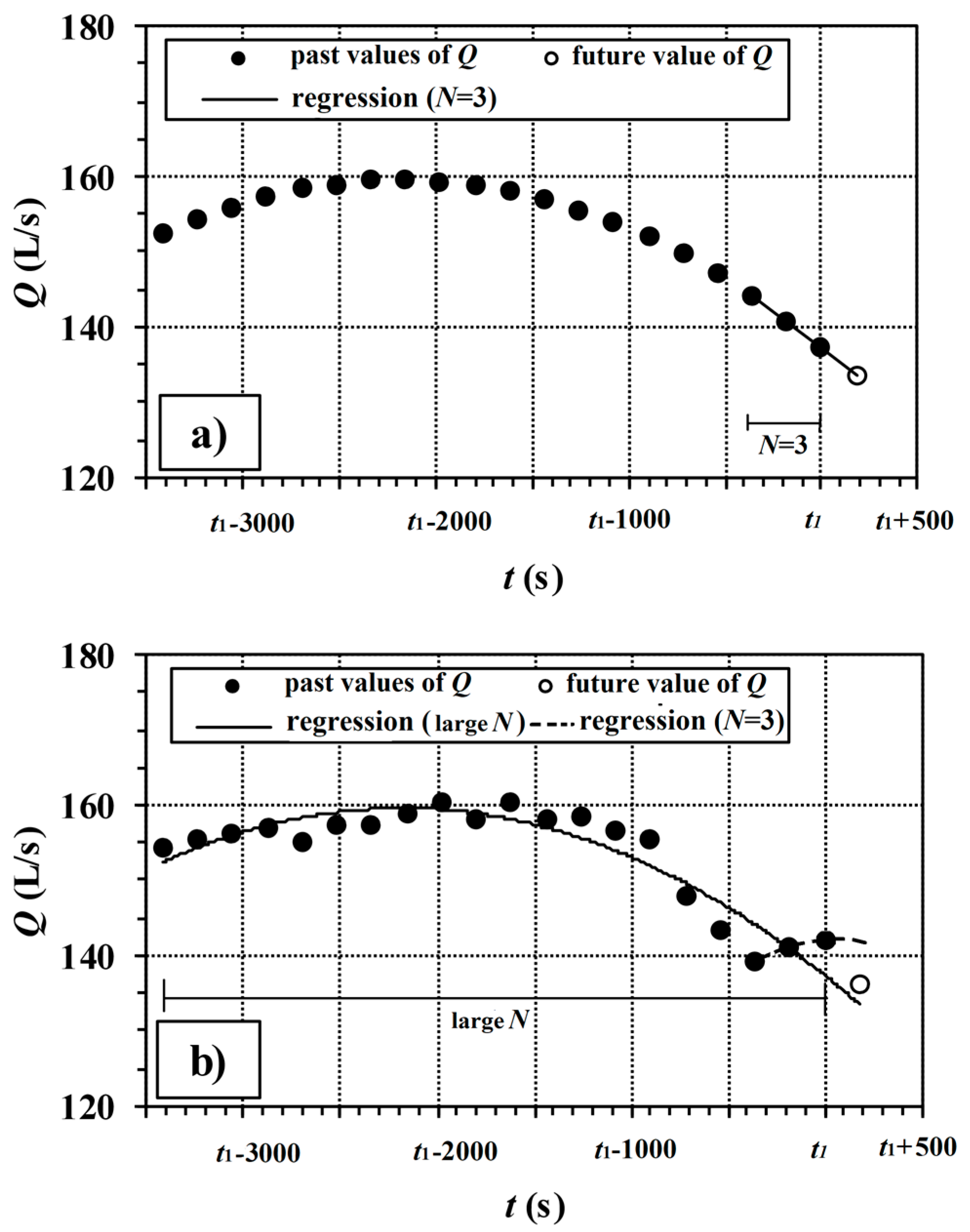
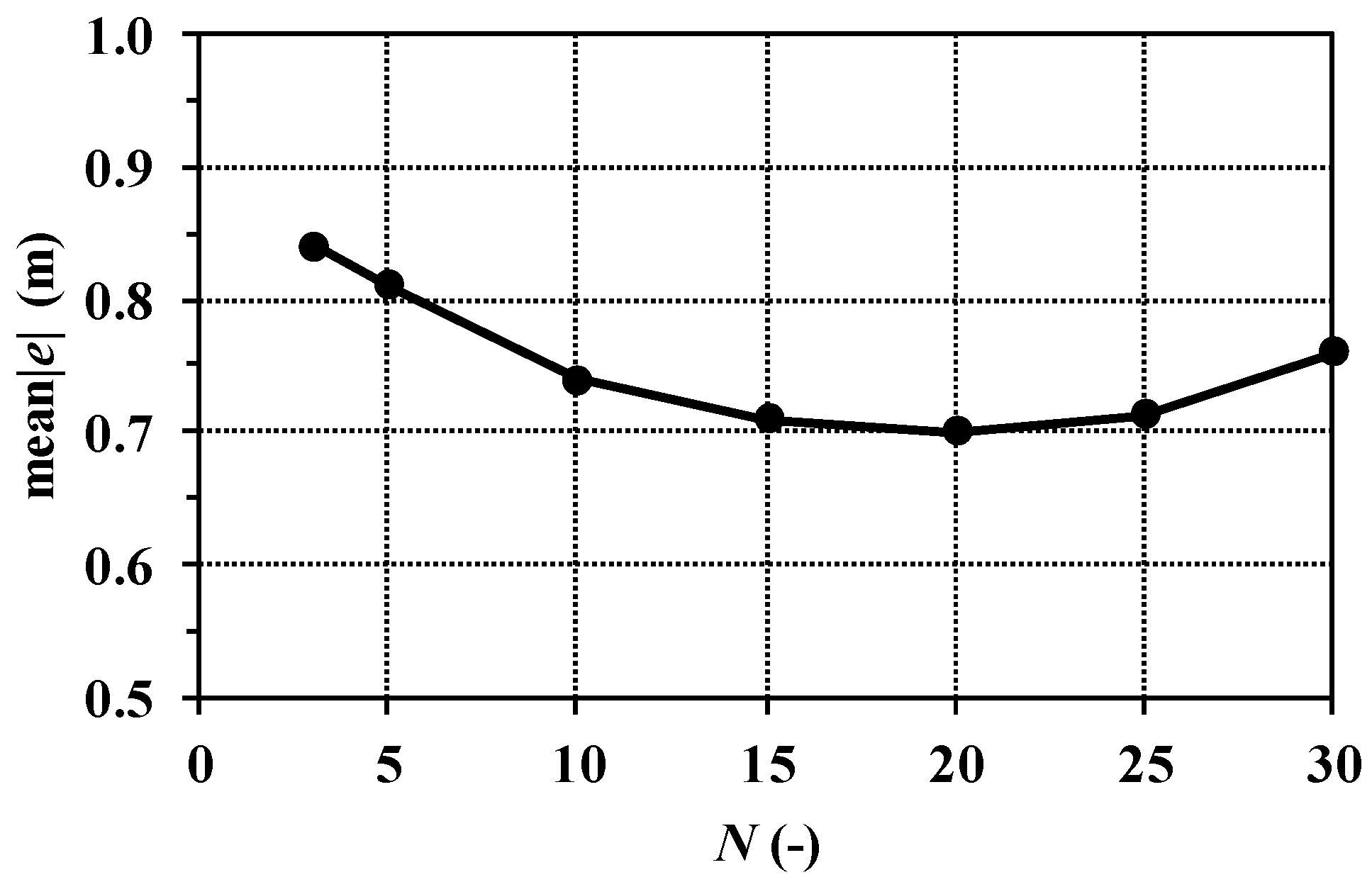
11] with no water discharge prediction, hereinafter indicated as LCa (logic controller a). In simulations 1b and 2b, the refined RTC algorithm fitted with the water discharge prediction, hereinafter indicated as LCb (logic controller b), was used. In the application, the polynomial regression useful for the demand prediction was carried out on
N = 20 time instants, following a preliminary analysis the results of which are reported in
Appendix A.
The setting variation speed of both the control valve and the variable speed pump was set in such a way as to allow the maximum setting variation (0–0.95 and 0.5–1 for the former and the latter device, respectively) inside the control temporal step Δt = 180 s.
The results of the simulations in terms of optimal
K, mean
|e| and ∑|Δ
α| are reported in
Table 1 and
Table 2 for the control valve and the variable speed pump, respectively.
The results in
Table 1 highlight, for the control valve controlled in real time, the superiority of LCb, in terms of both mean
|e| and ∑|Δ
α|. In fact, accounting for the water discharge prediction enabled the controlled variable to stay, on average, closer to the set point with smaller control valve setting variations.
The results in
Table 2 highlights, also for the variable speed pump controlled in real time, the better performance of LCb.
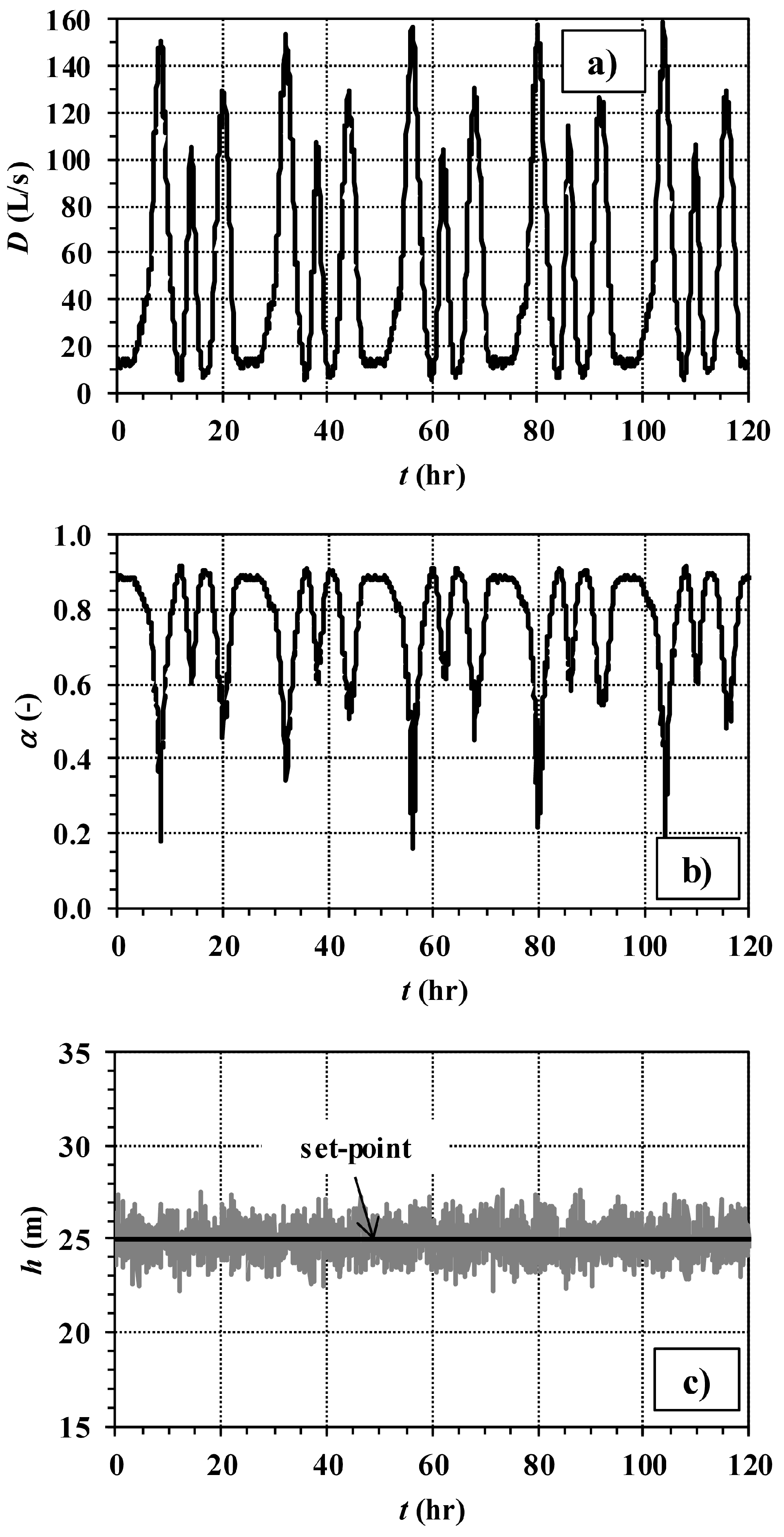
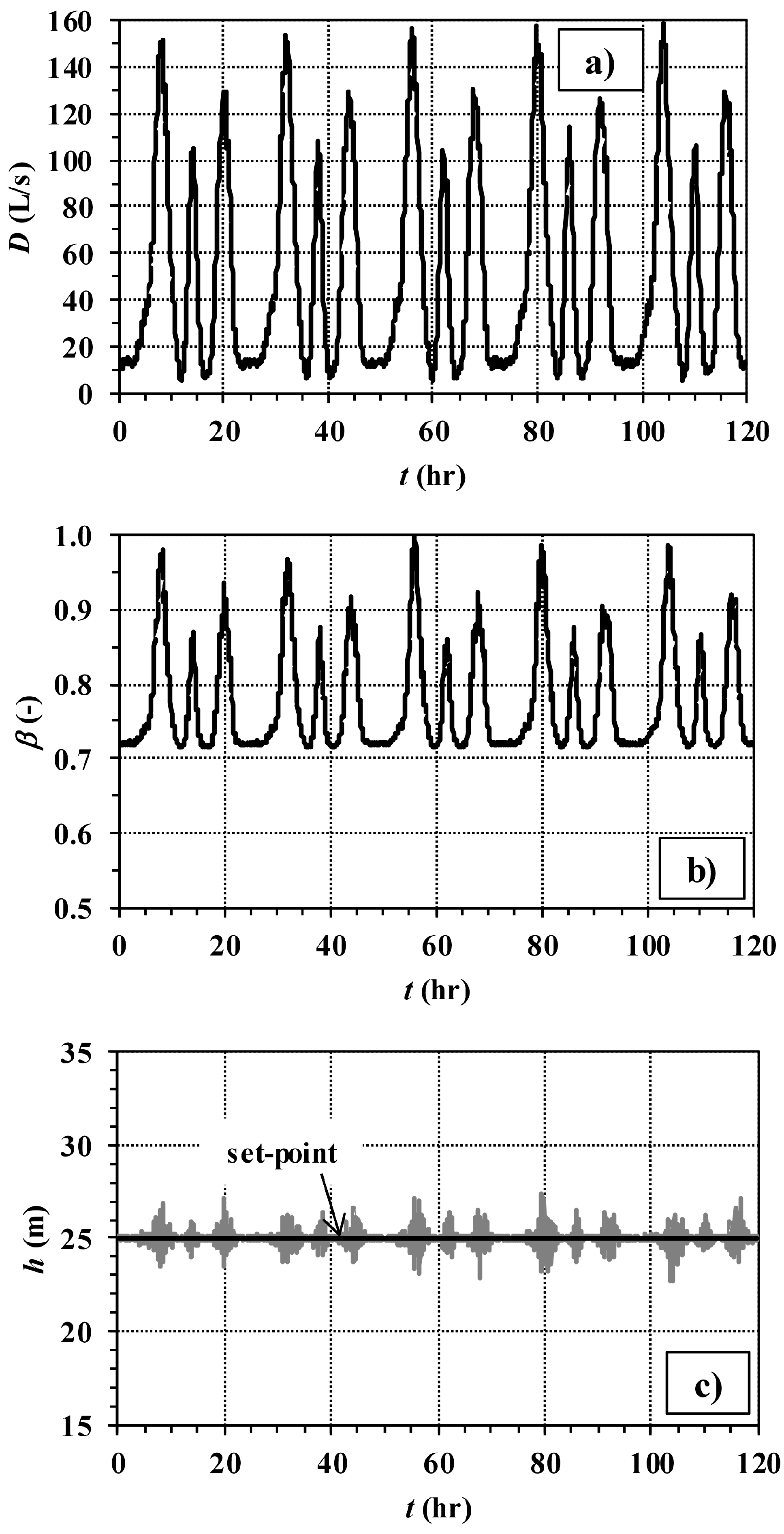
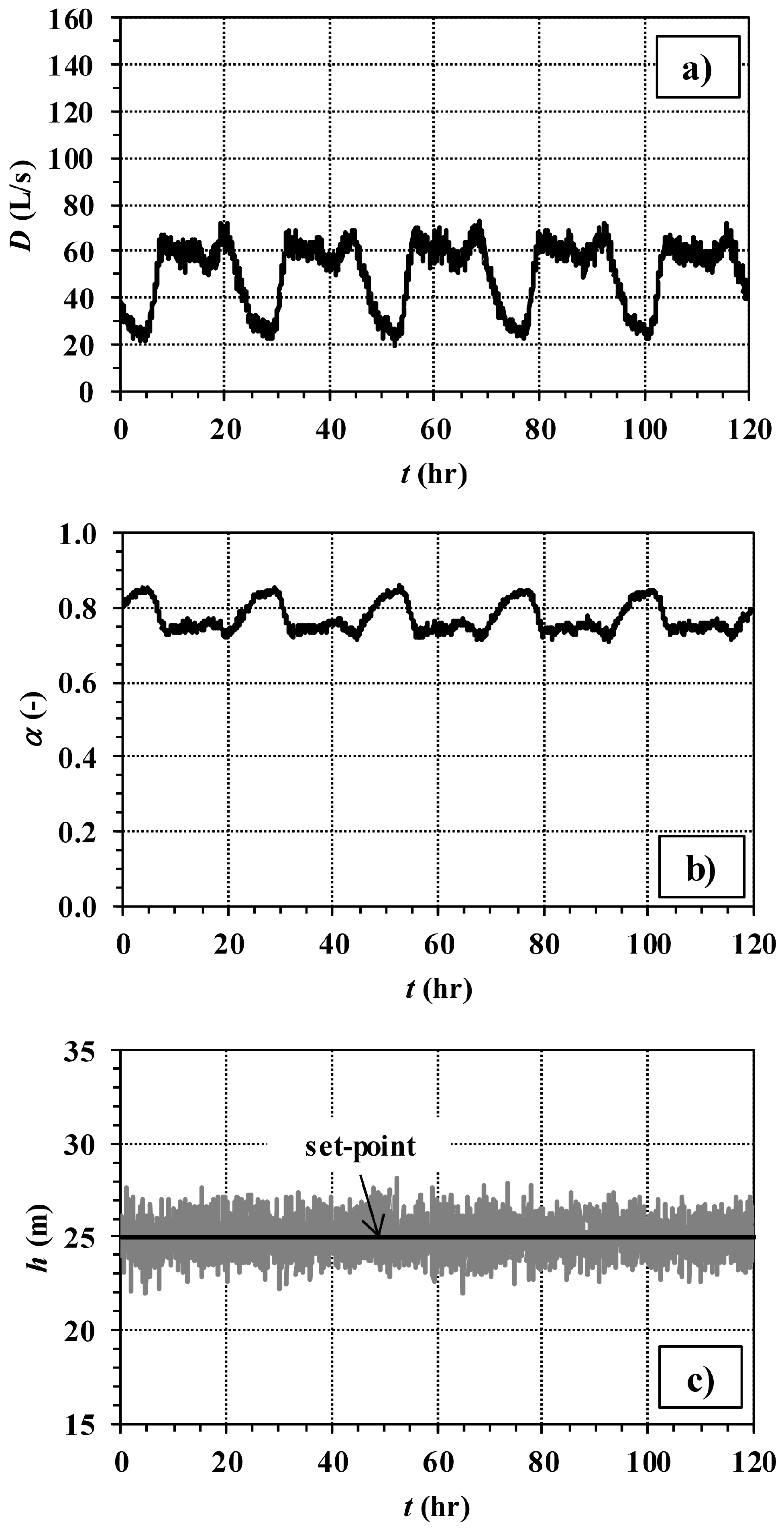
Other results of simulations 1b and 2b (with LCb) are reported in
Figure 4 and
Figure 5, respectively. In either Figure, graphs b and c report the trend of the device setting and of the controlled pressure head, respectively. Graph b) in
Figure 4 shows, as expected, that the control valve tends to open (lower values of
α, down to about 0.2) in correspondence to the morning, midday and evening demand peaks. Outside the peaks, instead, the control valve tends to close (higher values of
α, up to about 0.9), in order to cause larger local head losses. Only minor oscillations are observed in the valve setting trend. Graph c shows that
h is, on average, always close to the set point. However, up to 2.5 m large overshooting and undershooting are remarked. These oscillations take place due to the imperfect effectiveness of the prediction method. In fact, as was remarked above with reference to
Figure 2b, the prediction method is not able to catch the random fluctuations of the water discharge, though being able to detect its overall trend.
In this context, it has to be stressed that it is unfeasible to totally eliminate the random oscillations of the pressure head at a remote node. In fact, this would require the prediction/time step to be reduced. However, the control time step cannot be reduced below a threshold value, which accounts for signal propagation from the control node to the valve, as was stated in [
15].
The graphs in
Figure 5 show that, contrary to
α, the pump speed ratio
β tends to increase during demand peaks and to decrease under low demand conditions. Furthermore, in the case of the variable speed pump, the oscillations of the controlled variable are smaller, especially under low demand conditions. This can be explained as follows. If we consider, for an assigned value of water discharge
Q, the device settings bringing the controlled pressure head to the set point, a variation in
Q, like that associated with a demand fluctuation, tends to produce a smaller change in terms of Δ
h for the pump (Equation (6)) than for the valve (Equation (1)). In other words, the pump tends to dampen the effects of water discharge variations better than the valve, especially under low-demand conditions (which require high valve closures and low pump speeds).
A sensitivity analysis is then carried out to investigate if the superiority of LCb persists when other values are used for the parameters in the bottom-up generation of nodal pulsed demands. In new simulations performed with the control valve, the pulse parameters associated with the Milford households [
23] were used (see [
16] for more details on the values of these parameters). Furthermore, a flatter trend was considered for the demand pattern throughout the day, leading to the total demand
D shown in
Figure 6a, where demand fluctuations are more evident than in
Figure 4a and
Figure 5a. The optimization of parameter
K yielded, for both LCa and LCb, the optimal value of 0.3, in correspondence to which the two algorithms produce an almost identical value of mean|
e| = 0.8. However, LCb is still superior in terms of ∑|Δ
α| (9.42 for LCb vs. 11.09 for LCa). Graphs b and c in
Figure 6 show the trend of the valve closure setting and of the controlled pressure head for LCb under conditions of modified demand.
Overall, the advantages of LCb are less evident in the case of the modified pulse parameter values, due to the more evident presence of random fluctuations, uncaptured by the water discharge prediction method (see
Figure 2), in the total network demand (compare
Figure 6a with
Figure 4a and
Figure 5a). This entails that, ceteribus paribus, the benefits of LCb will be more evident when the random fluctuations of demand are small compared to its hourly variations. Otherwise, the benefits of LCb will decrease due to the worse effectiveness of the prediction.