Changes in Extreme Precipitation: A Case Study in the Middle and Lower Reaches of the Yangtze River in China
Abstract
1. Introduction
2. Study Area and Data Preprocessing
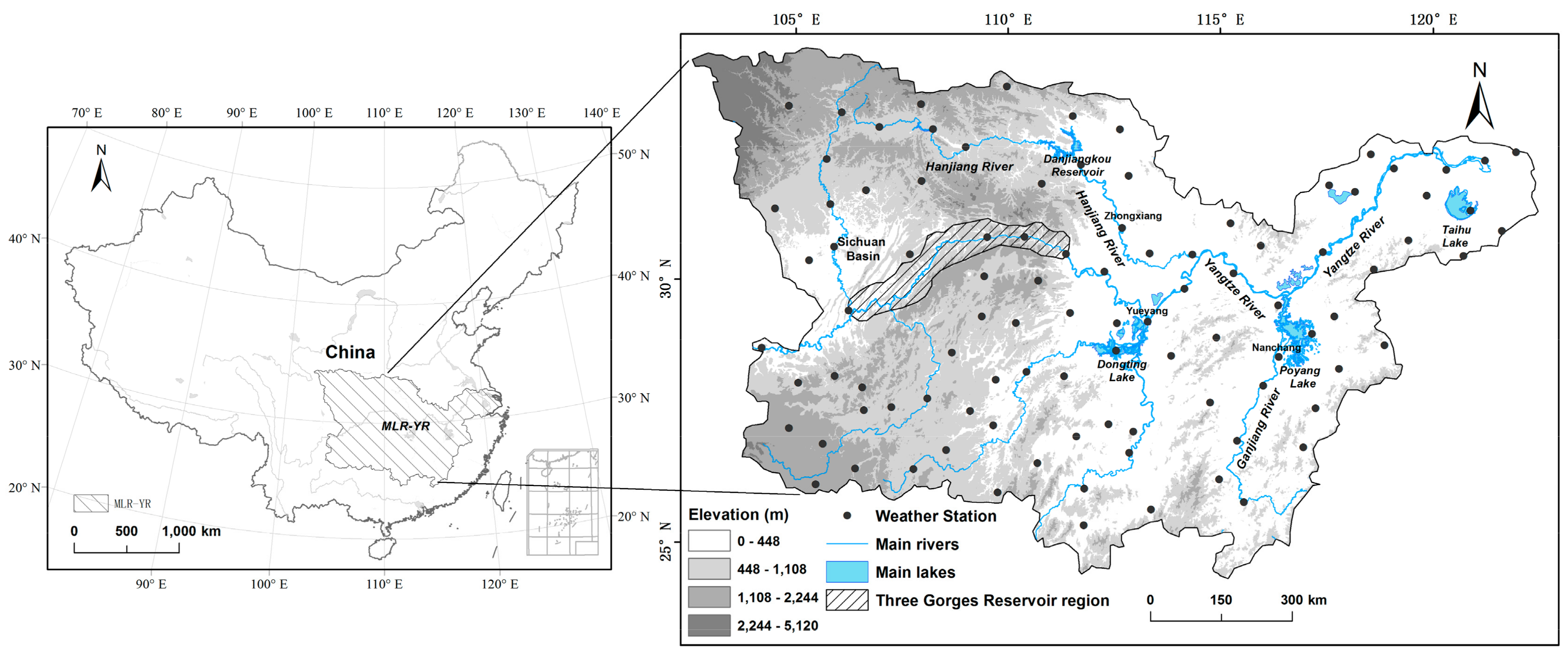
2.1. Study Area
2.2. Data and Preprocessing
3. Methods
3.1. Peaks-Over-Threshold Approach with Poisson Arrival Rate to Examine the Occurrence of Extreme Daily Precipitation Events
3.1.1. Peaks-Over-Threshold Approach
3.1.2. Poisson Distribution Validation
3.2. The to Analyze Extreme Precipitation Frequency and Its Trends
3.3. The to Analyze Extreme Precipitation Intensity and Trend Analysis
3.4. Attribution of Changes in Extreme Daily Precipitation Events
4. Results
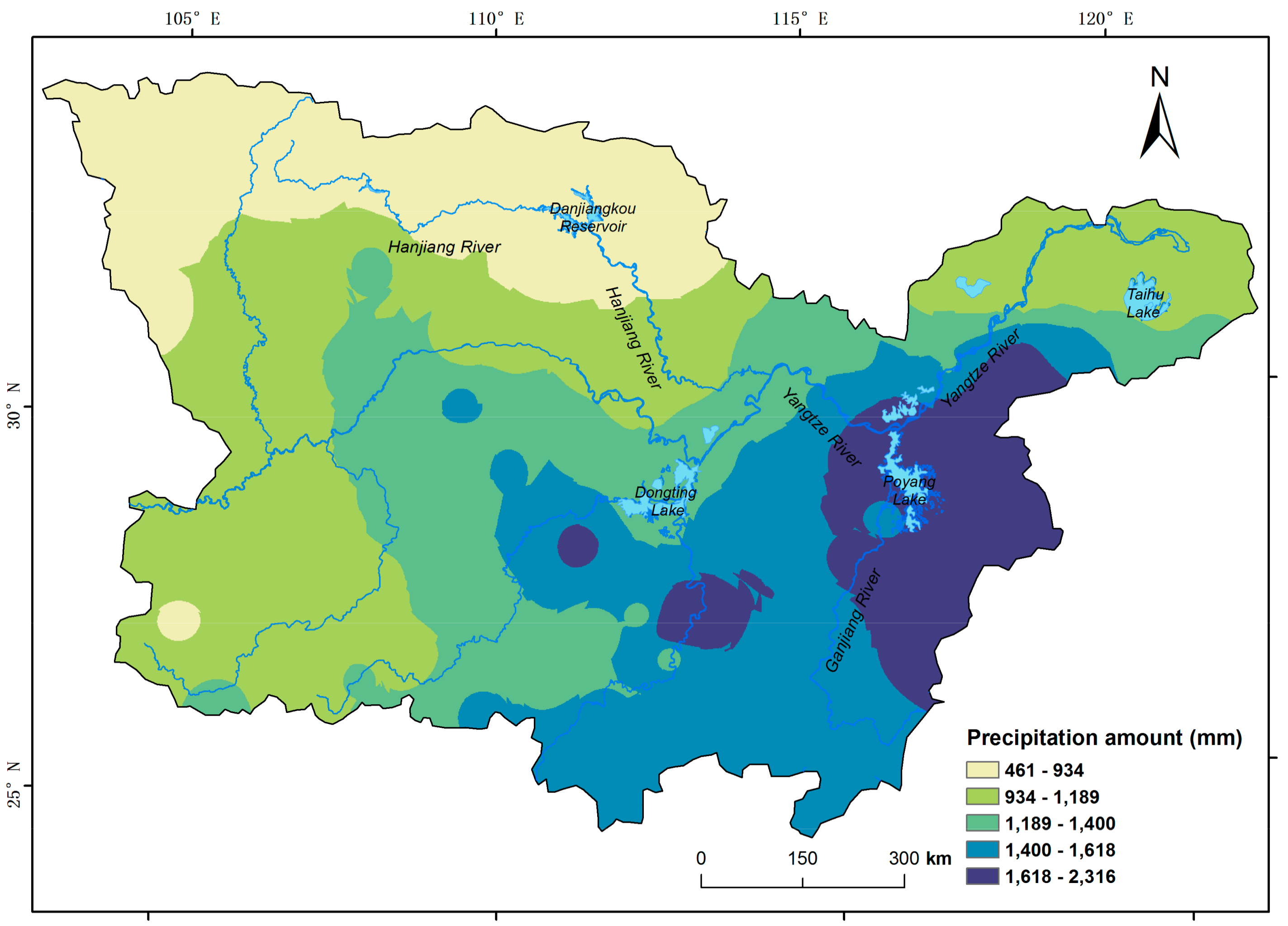
4.1. Long-Time Average Annual Precipitation in the MLR-YR from 1961 to 2012
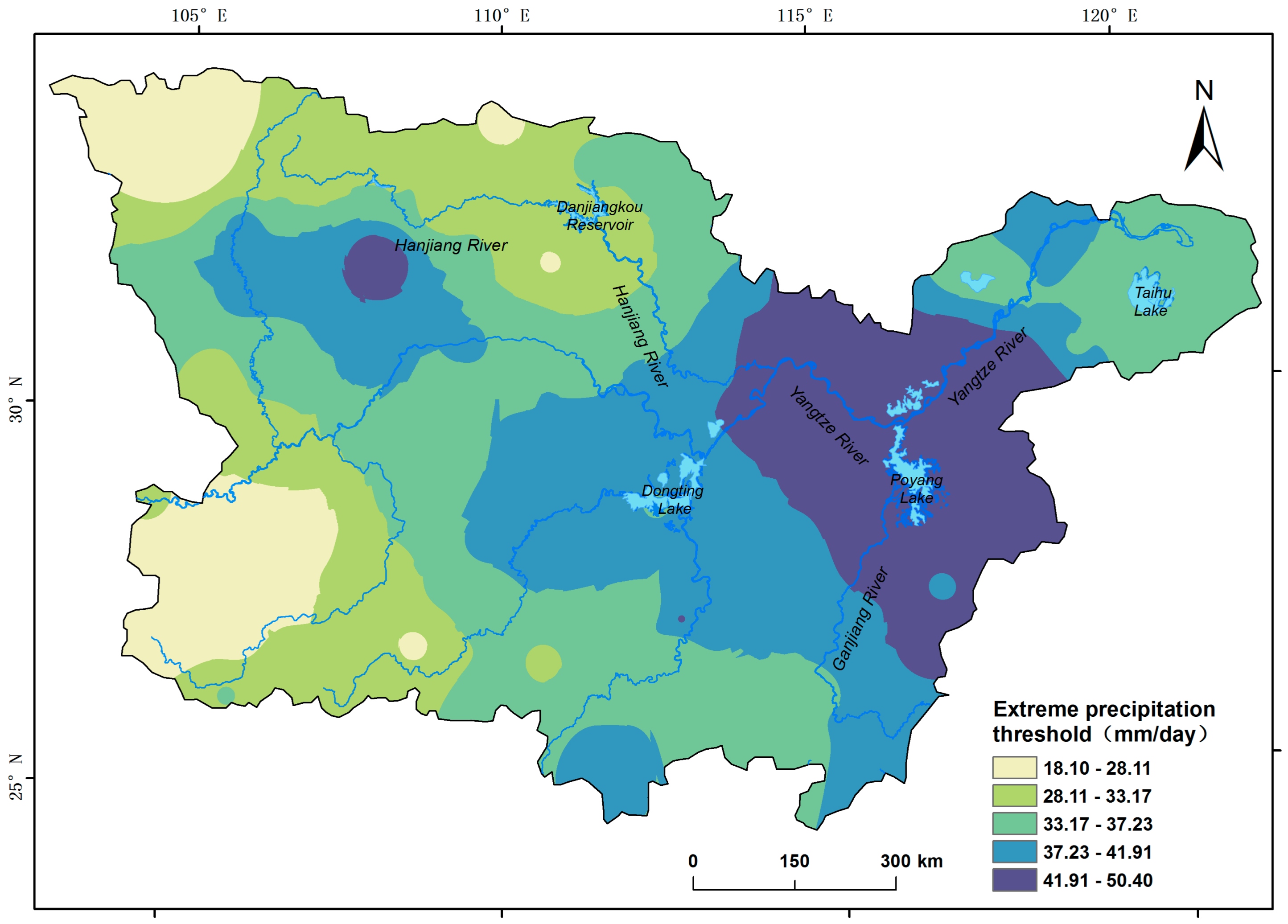
4.2. Threshold Selection of Extreme Daily Precipitation in the MLR-YR
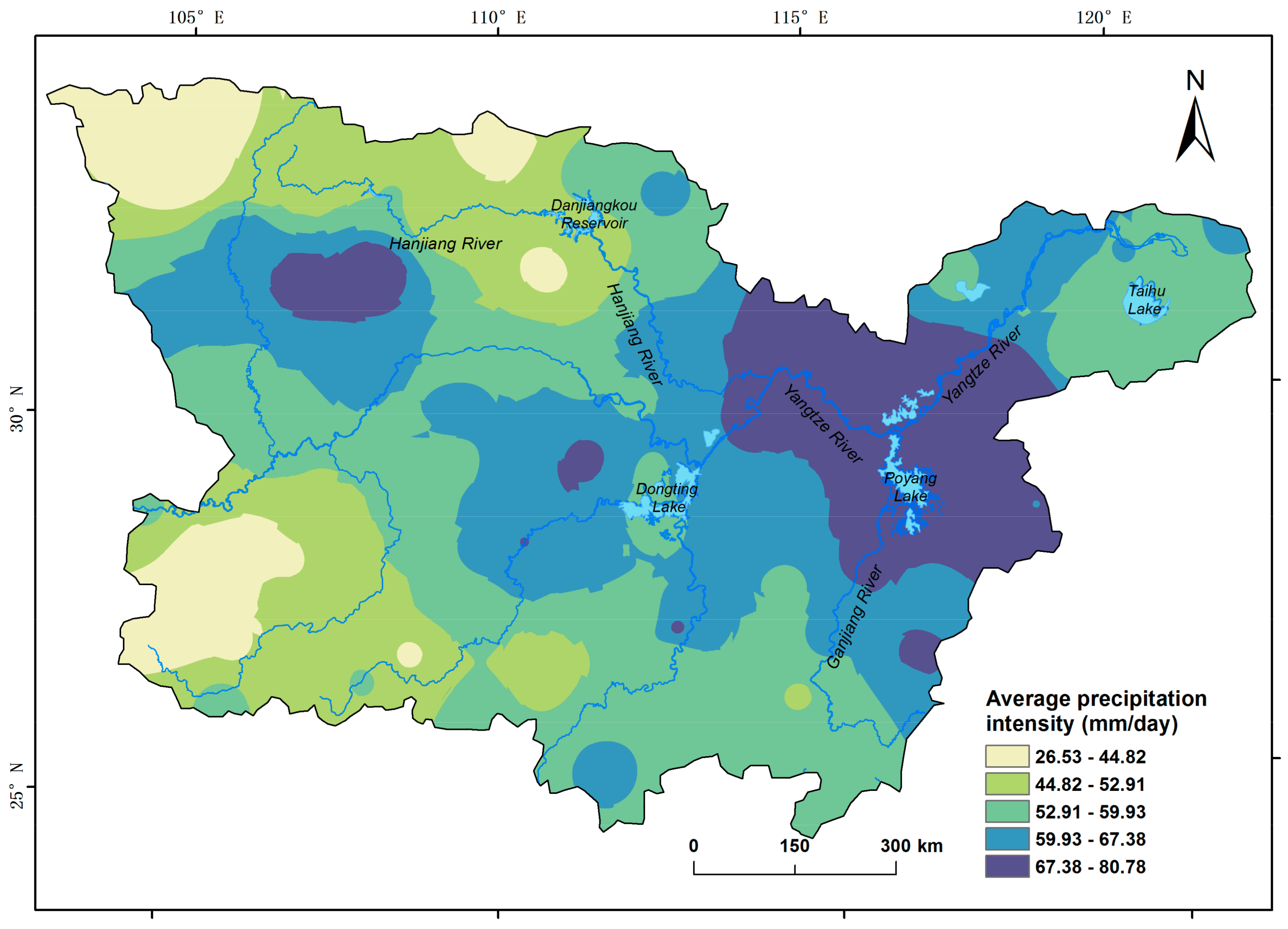
4.3. Average Intensity of Extreme Daily Precipitation
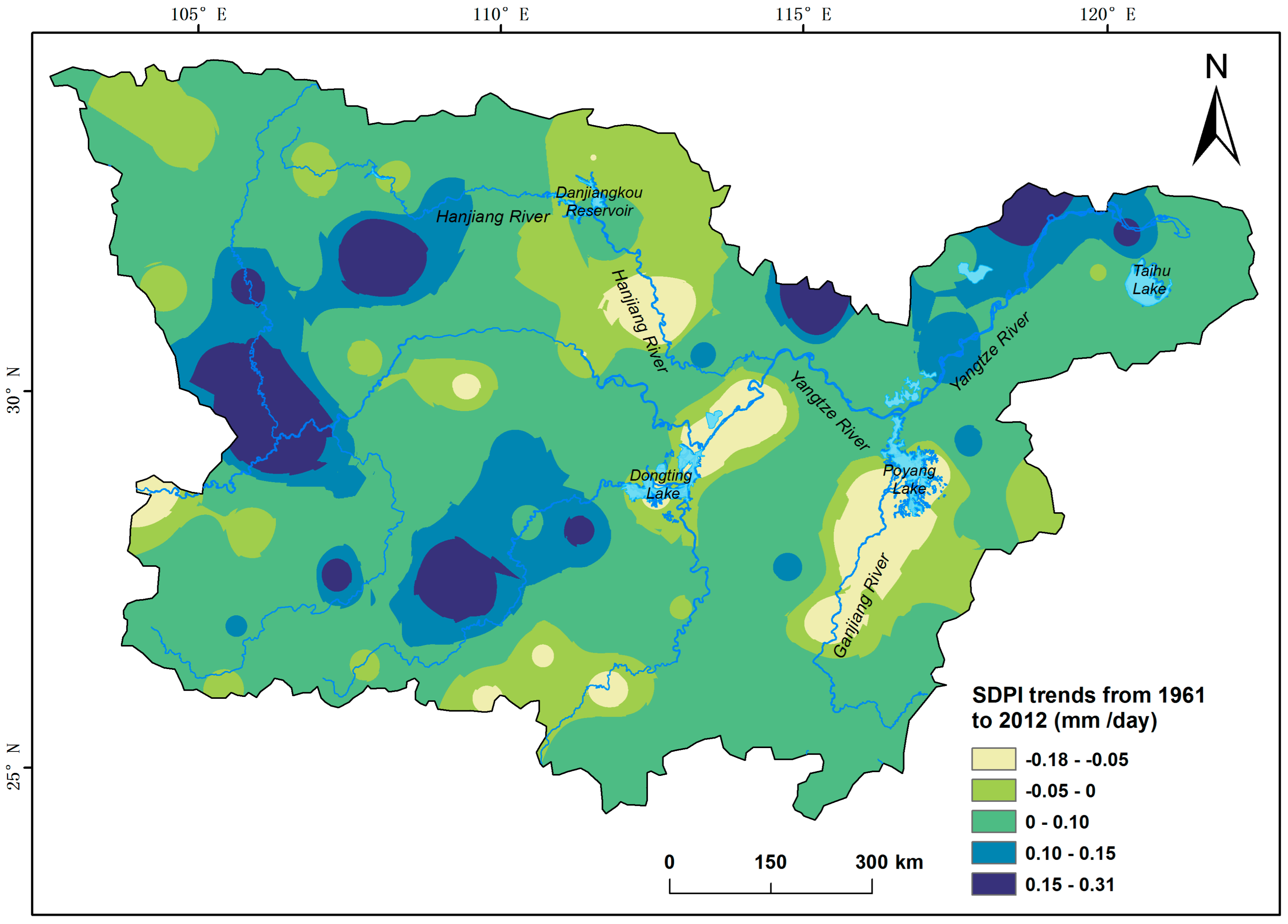
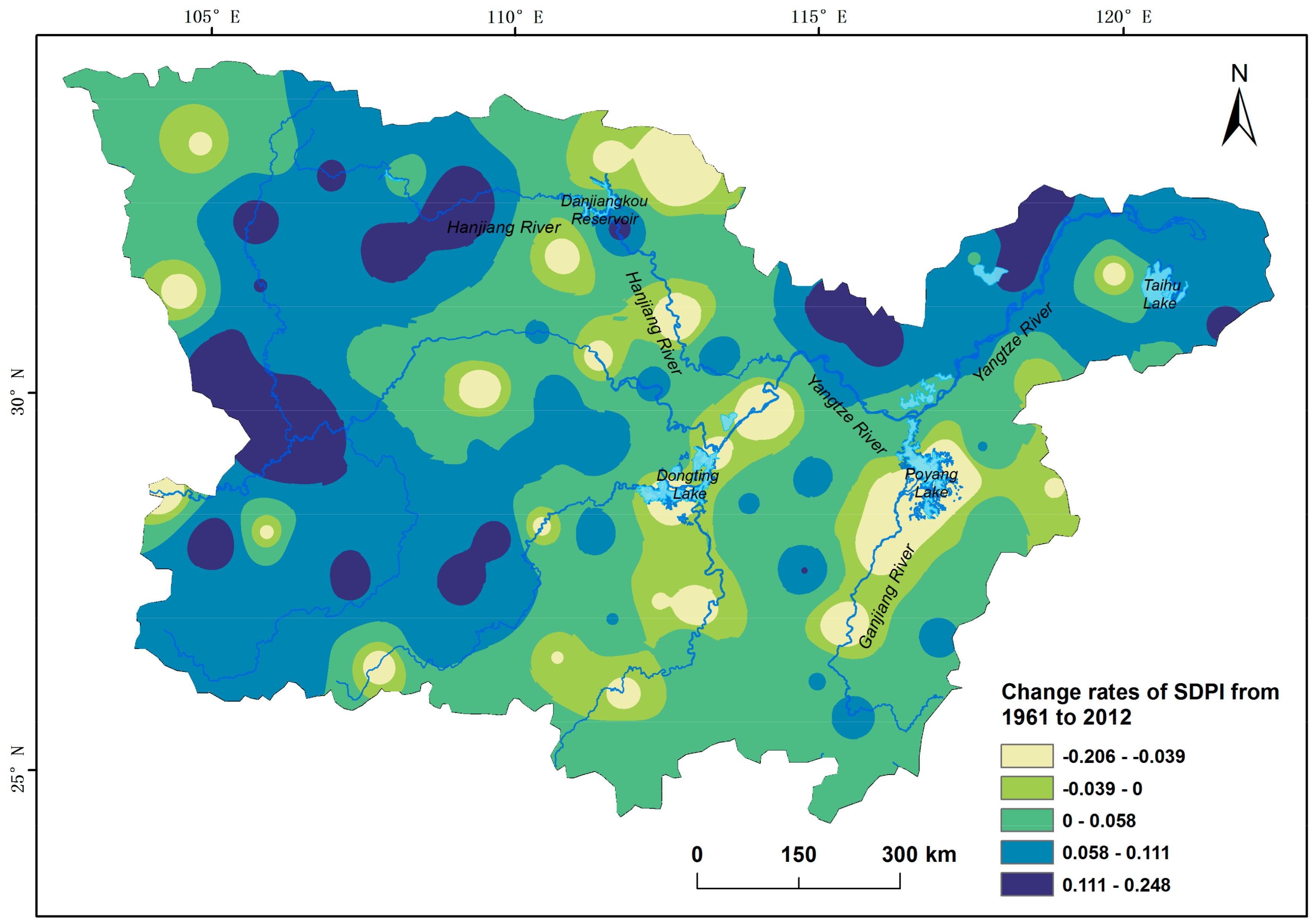
4.4. Trends in Extreme Daily Precipitation in the MLR-YR from 1961–2012
4.4.1. Frequency of Extreme Daily Precipitation Events
4.4.2. Intensity of Extreme Daily Precipitation
5. Discussions
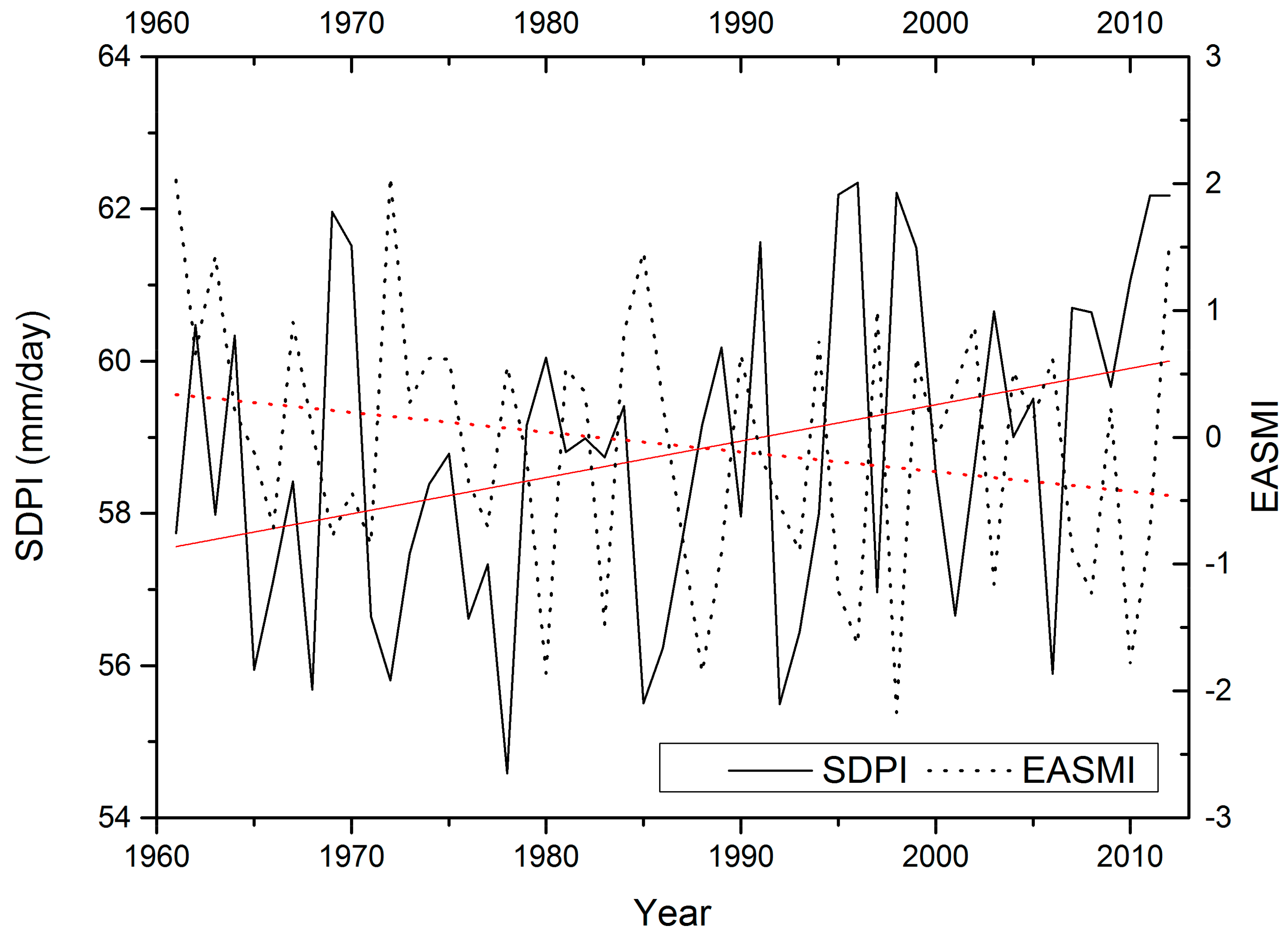
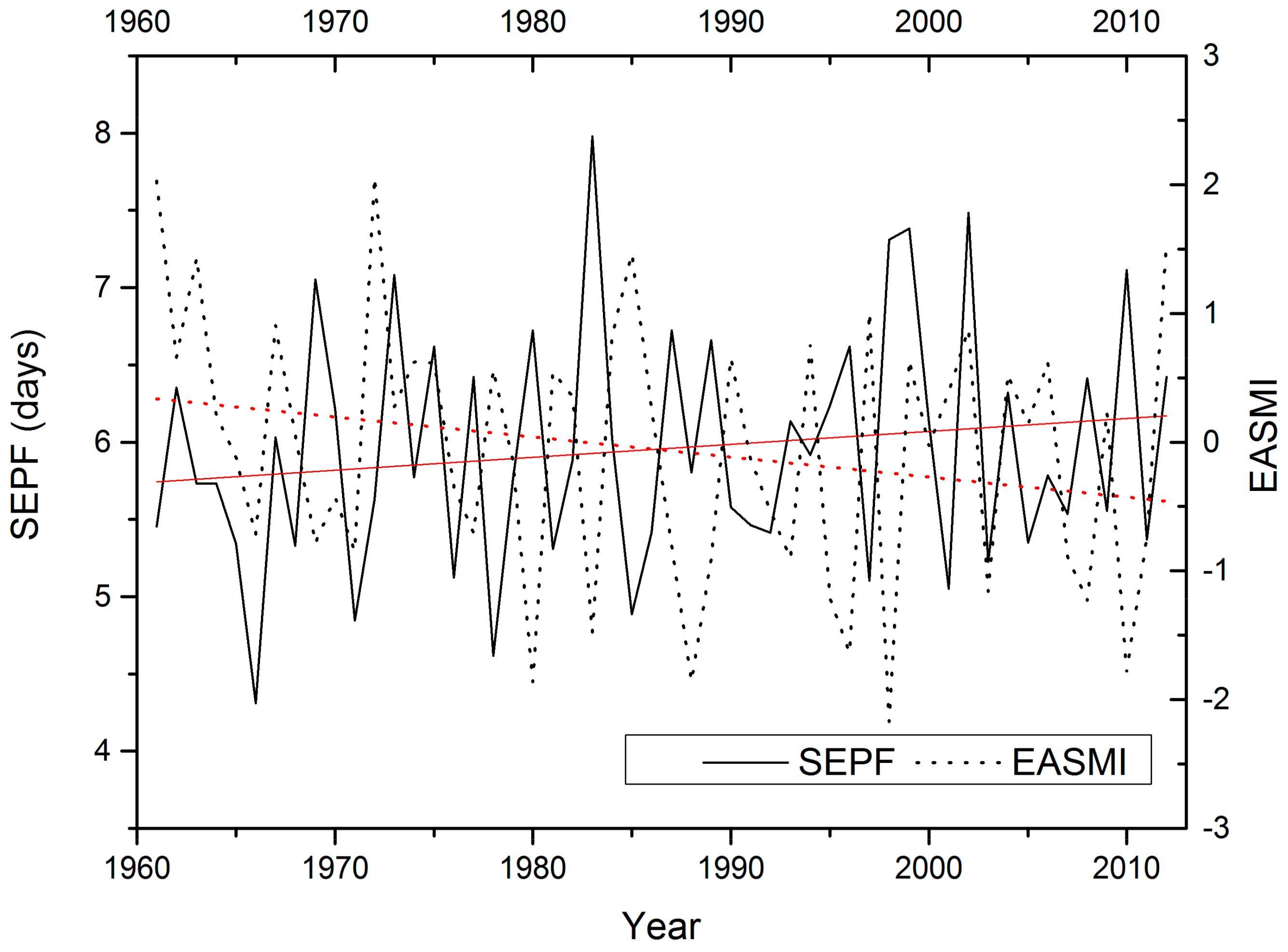
5.1. Impacts of East Asian Summer Monsoon on Extreme Daily Precipitation Events
5.2. Relationships between Extreme Daily Precipitation and Several Local Factors
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Solomon, S.; Qin, D.; Manning, M.; Chen, Z.; Marquis, M.; Averyt, K.B.; Tignor, M.; Miller, H.L. Contribution of Working Group I to the Fourth Assessment Report. In Climate Change 2007: The Physical Science Basis; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2007. [Google Scholar]
- Houghton, J.T.; Ding, Y.; Griggs, D.J.; Noguer, M.; van der Linden, P.J.; Dal, X.; Maskell, K.; Jonhson, C.A. Climate Change 2001: The Scientific Basis. Contribution of Working Group I to the Third Assessment Report of the International Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2001. [Google Scholar]
- Intergovernmental Panel on Climate Change (IPCC). Climate change 2007: Synthesis report. In Contribution of Working Groups I, II and III to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Bernstein, L., Reisinger, A., Riahi, K., Bosch, P., Eds.; IPCC: Geneva, Switzerland, 2007; p. 53. [Google Scholar]
- Cai, W.; Borlace, S.; Lengaigne, M.; van Rensch, P.; Collins, M.; Vecchi, G.; Timmermann, A.; Santoso, A.; McPhaden, M.J.; Wu, L.; et al. Increasing frequency of extreme El Nino events due to greenhouse warming. Nat. Clim. Chang. 2014, 4, 111–116. [Google Scholar] [CrossRef]
- Intergovernmental Panel on Climate Change (IPCC). Managing the Risks of Extreme Events and Disasters to Advance Climate Change Adaptation: Special Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2012. [Google Scholar]
- Heisler White, J.L.; Blair, J.M.; Kelly, E.F.; Harmoney, K.; Knapp, A.K. Contingent productivity responses to more extreme rainfall regimes across a grassland biome. Glob. Chang. Biol. 2009, 15, 2894–2904. [Google Scholar] [CrossRef]
- Taylor, R.G.; Todd, M.C.; Kongola, L.; Maurice, L.; Nahozya, E.; Sanga, H.; MacDonald, A.M. Evidence of the dependence of groundwater resources on extreme rainfall in East Africa. Nat. Clim. Chang. 2013, 3, 374–378. [Google Scholar] [CrossRef]
- Pei, F.; Wu, C.; Liu, X.; Li, X.; Yang, K.; Zhou, Y.; Wang, K.; Xu, L.; Xia, G. Monitoring the vegetation activity in China using vegetation health indices. Agr. For. Meteorol. 2018, 248, 215–227. [Google Scholar] [CrossRef]
- O’Gorman, P.A.; Schneider, T. The physical basis for increases in precipitation extremes in simulations of 21st-century climate change. Proc. Natl. Acad. Sci. USA 2009, 106, 14773–14777. [Google Scholar] [CrossRef] [PubMed]
- Scoccimarro, E.; Gualdi, S.; Bellucci, A.; Zampieri, M.; Navarra, A. Heavy precipitation events in a warmer climate: Results from CMIP5 models. J. Clim. 2013, 26, 7902–7911. [Google Scholar] [CrossRef]
- Moore, T.R.; Matthews, H.D.; Simmons, C.; Leduc, M. Quantifying changes in extreme weather events in response to warmer global temperature. Atmos. Ocean 2015, 53, 1–14. [Google Scholar] [CrossRef]
- Sarhadi, A.; Soulis, E.D. Time-varying extreme rainfall intensity-duration-frequency curves in a changing climate. Geophys. Res. Lett. 2017, 5, 2454–2463. [Google Scholar] [CrossRef]
- Alexander, L.V.; Zhang, X.; Peterson, T.C.; Caesar, J.; Gleason, B.; Klein Tank, A.M.G.; Haylock, M.; Collins, D.; Trewin, B.; Rahimzadeh, F.; et al. Global observed changes in daily climate extremes of temperature and precipitation. J. Geophys. Res. Atmos. 2006, 111, D05109. [Google Scholar] [CrossRef]
- Orlowsky, B.; Seneviratne, S.I. Global changes in extreme events: Regional and seasonal dimension. Clim. Chang. 2012, 110, 669–696. [Google Scholar] [CrossRef]
- Kunkel, K.E.; Frankson, R.M. Global land surface extremes of precipitation: Data limitations and trends. J. Extrem. Events 2015, 2, 1550004. [Google Scholar] [CrossRef]
- Singh, D.; Tsiang, M.; Rajaratnam, B.; Diffenbaugh, N.S. Precipitation extremes over the continental United States in a transient, high-resolution, ensemble climate model experiment. J. Geophys. Res. 2013, 118, 7063–7086. [Google Scholar] [CrossRef]
- Rajczak, J.; Schaer, C.; Pall, P. Projections of extreme precipitation events in regional climate; simulations for Europe and the Alpine Region. J. Geophys. Res. 2013, 118, 3610–3626. [Google Scholar] [CrossRef]
- Ghosh, S.; Das, D.; Kao, S.; Ganguly, A.R. Lack of uniform trends but increasing spatial variability in observed Indian rainfall extremes. Nat. Clim. Chang. 2012, 2, 86–91. [Google Scholar] [CrossRef]
- Wu, F.T.; Wang, S.Y.; Fu, C.B.; Qian, Y.; Gao, Y.; Lee, D.K.; Cha, D.H.; Tang, J.P.; Hong, S. Evaluation and projection of summer extreme precipitation over East Asia in the Regional Model Inter-comparison Project. Clim. Res. 2016, 69, 45–48. [Google Scholar] [CrossRef]
- Zong, Y.; Chen, X. The 1998 flood on the Yangtze, China. Nat. Hazards 2000, 22, 165–184. [Google Scholar] [CrossRef]
- Shen, H.; Kuang, Y.; Li, Z.I. Genesis of 2010 storm-flood in Yangtze River Basin and its comparison with 1998 flood. Yangtze River 2011, 42, 11–14. (In Chinese) [Google Scholar]
- Su, B.; Gemmer, M.; Jiang, T. Spatial and temporal variation of extreme precipitation over the Yangtze River Basin. Q. Int. 2008, 186, 22–31. [Google Scholar] [CrossRef]
- Chen, Y.D.; Zhang, Q.; Xiao, M.; Singh, V.P.; Leung, Y.; Jiang, L. Precipitation extremes in the Yangtze River Basin, China: Regional frequency and spatial–temporal patterns. Theor. Appl. Climatol. 2014, 116, 447–461. [Google Scholar] [CrossRef]
- Guo, J.; Guo, S.; Li, Y.; Chen, H.; Li, T. Spatial and temporal variation of extreme precipitation indices in the Yangtze River basin, China. Stoch. Environ. Res. Risk Assess. 2013, 27, 459–475. [Google Scholar] [CrossRef]
- Ehsanzadeh, E.; Ouarda, T.B.M.J.; Saley, H.M. A simultaneous analysis of gradual and abrupt changes in Canadian low streamflows. Hydrol. Process. 2015, 25, 727–739. [Google Scholar] [CrossRef]
- Karl, T.R.; Nicholls, N.; Ghazi, A. CLIVAR/GCOS/WMO workshop on indices and indicators for climate extremes: Workshop summary. Clim. Chang. 1999, 42, 3–7. [Google Scholar] [CrossRef]
- Peterson, T.; Folland, C.; Gruza, G.; Hogg, W.; Mokssit, A.; Plummer, N. Report on the Activities of the Working Group on Climate Change Detection and Related Rapporteurs; World Meteorological Organization: Geneva, Switzerland, 2001; p. 143. [Google Scholar]
- China Meteorological Administration (CMA). Surface Meteorological Observation Standards; China Meteorological Press: Beijing, China, 1979; pp. 167–192. (In Chinese) [Google Scholar]
- Li, J.; Zeng, Q. A unified monsoon index. Geophys. Res. Lett. 2002, 29, 111–115. [Google Scholar] [CrossRef]
- Pandey, M.D.; Van Gelder, P.; Vrijling, J.K. Bootstrap simulations for evaluating the uncertainty associated with peaks-over-threshold estimates of extreme wind velocity. Environmetrics 2003, 14, 27–43. [Google Scholar] [CrossRef]
- Acero, F.J.; García, J.A.; Gallego, M.C. Peaks-over-threshold study of trends in extreme rainfall over the Iberian Peninsula. J. Clim. 2011, 24, 1089–1105. [Google Scholar] [CrossRef]
- Thiombiano, A.N.; Adlouni, S.E.; St-Hilaire, A.; Ouarda, T.B.M.J.; El-Jabi, N. Nonstationary frequency analysis of extreme daily precipitation amounts in Southeastern Canada using a peaks-over-threshold approach. Theor. Appl. Climatol. 2016, 129, 1–14. [Google Scholar] [CrossRef]
- Lang, M.; Ouarda, T.; Bobée, B. Towards operational guidelines for over-threshold modeling. J. Hydrol. 1999, 225, 103–117. [Google Scholar] [CrossRef]
- Pandey, M.D.; Van Gelder, P.; Vrijling, J.K. The estimation of extreme percentiles of wind velocity using L-moments in the peaks-over-threshold approach. Struct. Saf. 2001, 23, 179–192. [Google Scholar] [CrossRef]
- Coles, S.; Bawa, J.; Trenner, L.; Dorazio, P. An Introduction to Statistical Modeling of Extreme Values; Springer: London, UK, 2001. [Google Scholar]
- Pickands, J., III. Statistical inference using extreme order statistics. Ann. Stat. 1975, 3, 119–131. [Google Scholar]
- Wang, Q.J. The POT model described by the generalized Pareto distribution with Poisson arrival rate. J. Hydrol. 1991, 129, 263–280. [Google Scholar] [CrossRef]
- Donegan, S.P.; Tucker, J.C.; Rollett, A.D.; Barmak, K.; Groeber, M. Extreme value analysis of tail departure from log-normality in experimental and simulated grain size distributions. Acta Mater. 2013, 61, 5595. [Google Scholar] [CrossRef]
- Cunnane, C. A particular comparison of annual maxima and partial duration series methods of flood frequency prediction. J. Hydrol. 1973, 18, 257–271. [Google Scholar] [CrossRef]
- Cameron, A.C.; Trivedi, P.K. Regression-based tests for overdispersion in the Poisson model. J. Econ. 1990, 46, 347–364. [Google Scholar] [CrossRef]
- Faraway, J.J. Extending the Linear Model with R: Generalized Linear, Mixed Effects and Nonparametric Regression Models; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Villarini, G.; Smith, J.A.; Baeck, M.L.; Vitolo, R.; Stephenson, D.B.; Krajewski, W.F. On the frequency of extreme rainfall for the Midwest of the United States. J. Hydrol. 2011, 400, 103–120. [Google Scholar] [CrossRef]
- Beguería, S.; Angulo-Martínez, M.; Vicente-Serrano, S.M.; El Kenawy, A.M.; López-Moreno, J.I. Assessing trends in extreme precipitation events intensity and magnitude using non-stationary peaks-over-threshold analysis: A case study in northeast Spain from 1930 to 2006. Int. J. Clim. 2011, 31, 2102–2114. [Google Scholar] [CrossRef]
- Zhai, P.; Zhang, X.; Wan, H.; Pan, X. Trends in total precipitation and frequency of daily precipitation extremes over China. J. Clim. 2005, 18, 1096–1108. [Google Scholar] [CrossRef]
- Kim, J.; Jain, S. Precipitation trends over the Korean peninsula: Typhoon-induced changes and a typology for characterizing climate-related risk. Environ. Res. Lett. 2011, 6, 034033. [Google Scholar] [CrossRef]
- Villarini, G.; Smith, J.A.; Vecchi, G.A. Changing frequency of extreme rainfall over the central United States. J. Clim. 2013, 26, 351–357. [Google Scholar] [CrossRef]
- Dickey, D.A.; Brillinger, D.R. Time series: Data analysis and theory. Signal Process. Mag. IEEE 1982, 77, 214. [Google Scholar] [CrossRef]
- Pettitt, A.N. A Non-parametric approach to the change-point problem. J. R. Stat. Soc. 1979, 28, 126–135. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2016; Available online: https://www.R-project.org/ (accessed on 2 December 2017).
- Wang, B.; Wu, Z.; Li, J.; Liu, J.; Chang, C.P.; Ding, Y.; Wu, G. How to measure the strength of the East Asian summer monsoon. J. Clim. 2008, 21, 4449–4463. [Google Scholar] [CrossRef]
- Li, J.P.; Wu, Z.W.; Jiang, Z.H.; He, J.H. Can global warming strengthen the East Asian summer monsoon? J. Clim. 2010, 23, 6696–6705. [Google Scholar] [CrossRef]
- Hossain, F. Empirical relationship between large dams and the alteration in extreme precipitation. Nat. Hazards Rev. 2010, 11, 97–101. [Google Scholar] [CrossRef]
- Li, K.; Zhu, C.; Huang, L. Problems caused by the Three Gorges Dam construction in the Yangtze River basin: A review. Environ. Rev. 2013, 21, 127–135. [Google Scholar] [CrossRef]
- Wu, L.; Zhang, Q.; Jiang, Z. Three Gorges Dam affects regional precipitation. Geophys. Res. Lett. 2006, 331, 338–345. [Google Scholar] [CrossRef]
- Wu, W.; Liu, T. Possible role of the “Holocene Event 3” on the collapse of Neolithic Cultures around the Central Plain of China. Quat. Int. 2004, 117, 153–166. [Google Scholar]
- Shi, X.; Wang, Y.; Xu, X. Effect of mesoscale topography over the Tibetan Plateau on summer precipitation in China: A regional model study. Geophys. Res. Lett. 2008, 35, 19707. [Google Scholar] [CrossRef]
- Hu, D.; Li, Y. Spatial and temporal variations of nocturnal precipitation in Sichuan over the Eastern Tibetan Plateau. Chin. J. Atmos. Sci. 2015, 39, 161–179. [Google Scholar]
- Ding, Y.; Wang, Z.; Sun, Y. Inter-decadal variation of the summer precipitation in East China and its association with decreasing Asian summer monsoon. Part I: Observed evidences. Int. J. Climatol. 2008, 28, 1139–1161. [Google Scholar] [CrossRef]
- Lu, G.; Liu, Y.; Zou, X.; Zou, Z.; Cai, T. Impact of Danjiangkou reservoir on flow regime in the middle and lower reaches of the Hanjiang River. Resour. Environ. Yangtze Basin 2009, 18, 959–963. [Google Scholar]
- Zinke, P.; Bogen, J. Effect of water level regulation on gradients and levee deposits in the Lake Øyeren delta, Norway. Hydrol. Res. 2013, 44, 523–537. [Google Scholar] [CrossRef]
- Jin, X.; Wu, T.; Li, L. The quasi-stationary feature of nocturnal precipitation in the Sichuan Basin and the role of the Tibetan Plateau. Clim. Dynam. 2012, 41, 977–994. [Google Scholar] [CrossRef]
- Xue, Y.; Bai, A.; Li, D. Analysis and numerical simulation of diurnal variation of precipitation in Sichuan Basin. Adv. Earth Sci. 2012, 27, 885–894. [Google Scholar]
- Yilmaz, A.G.; Hossain, I.; Perera, B.J.C. Effect of climate change and variability on extreme rainfall intensity-frequency-duration relationships: A case study of Melbourne. Hydrol. Earth Syst. Sci. Discuss. 2014, 11, 4065–4076. [Google Scholar] [CrossRef]

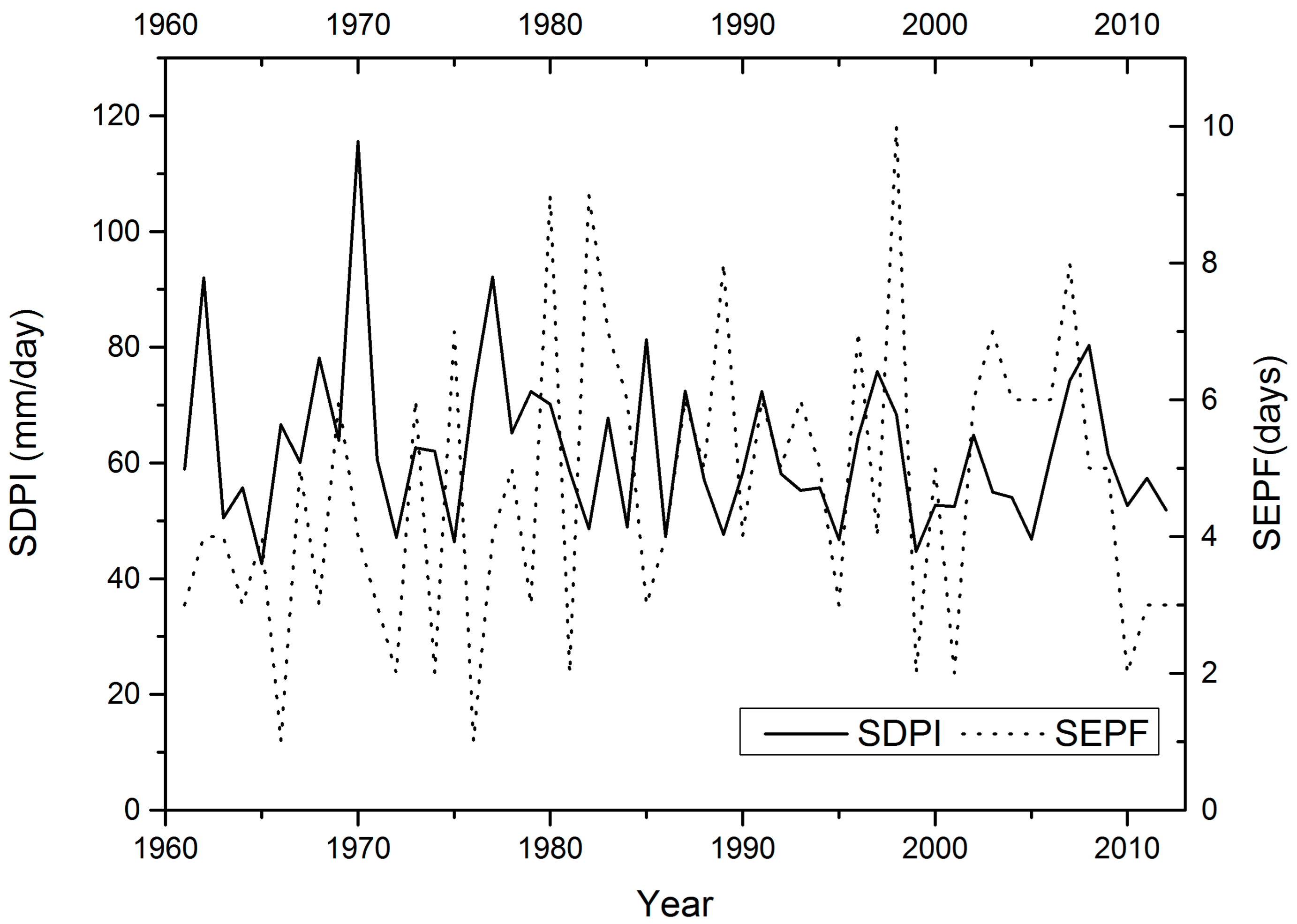
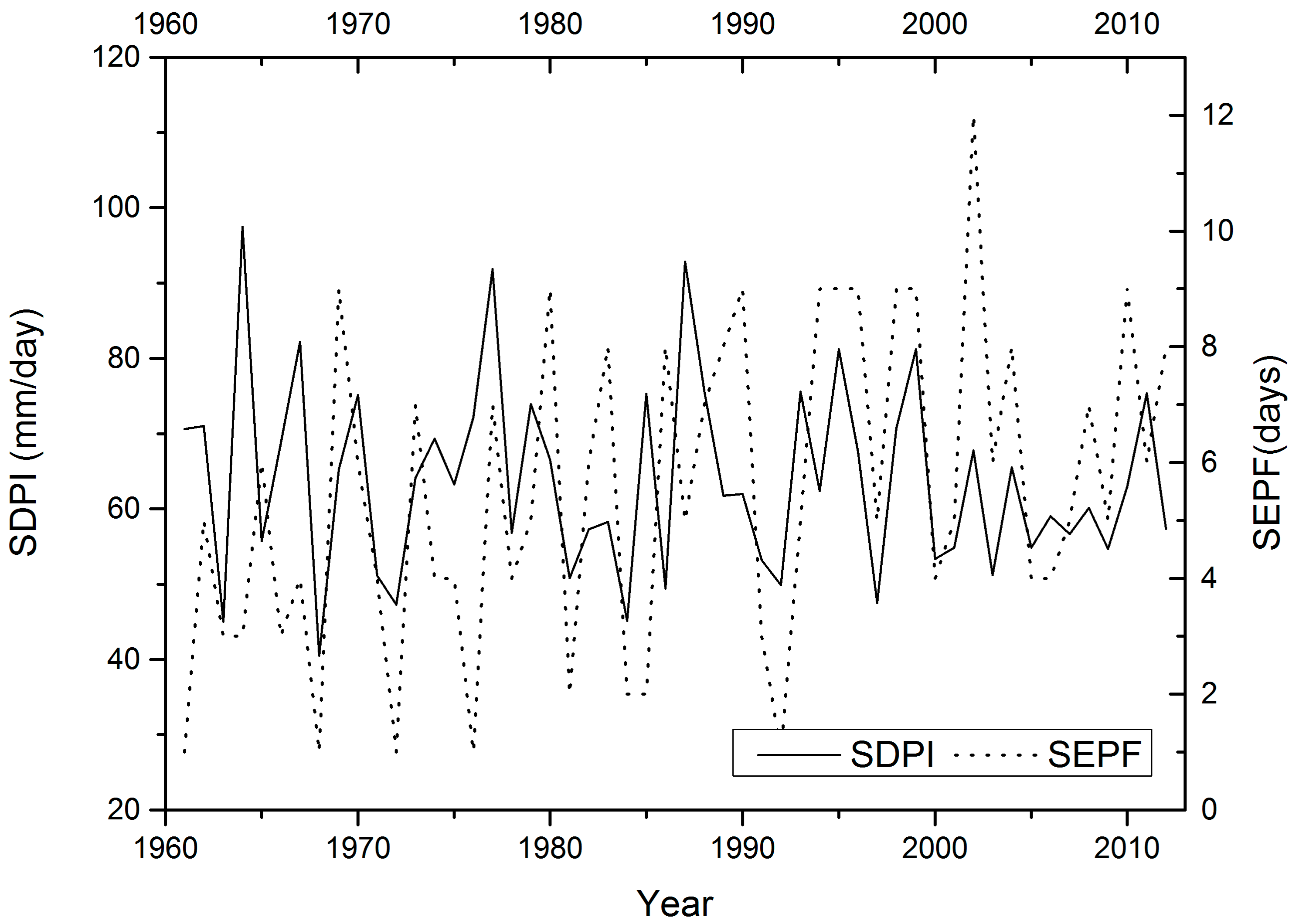
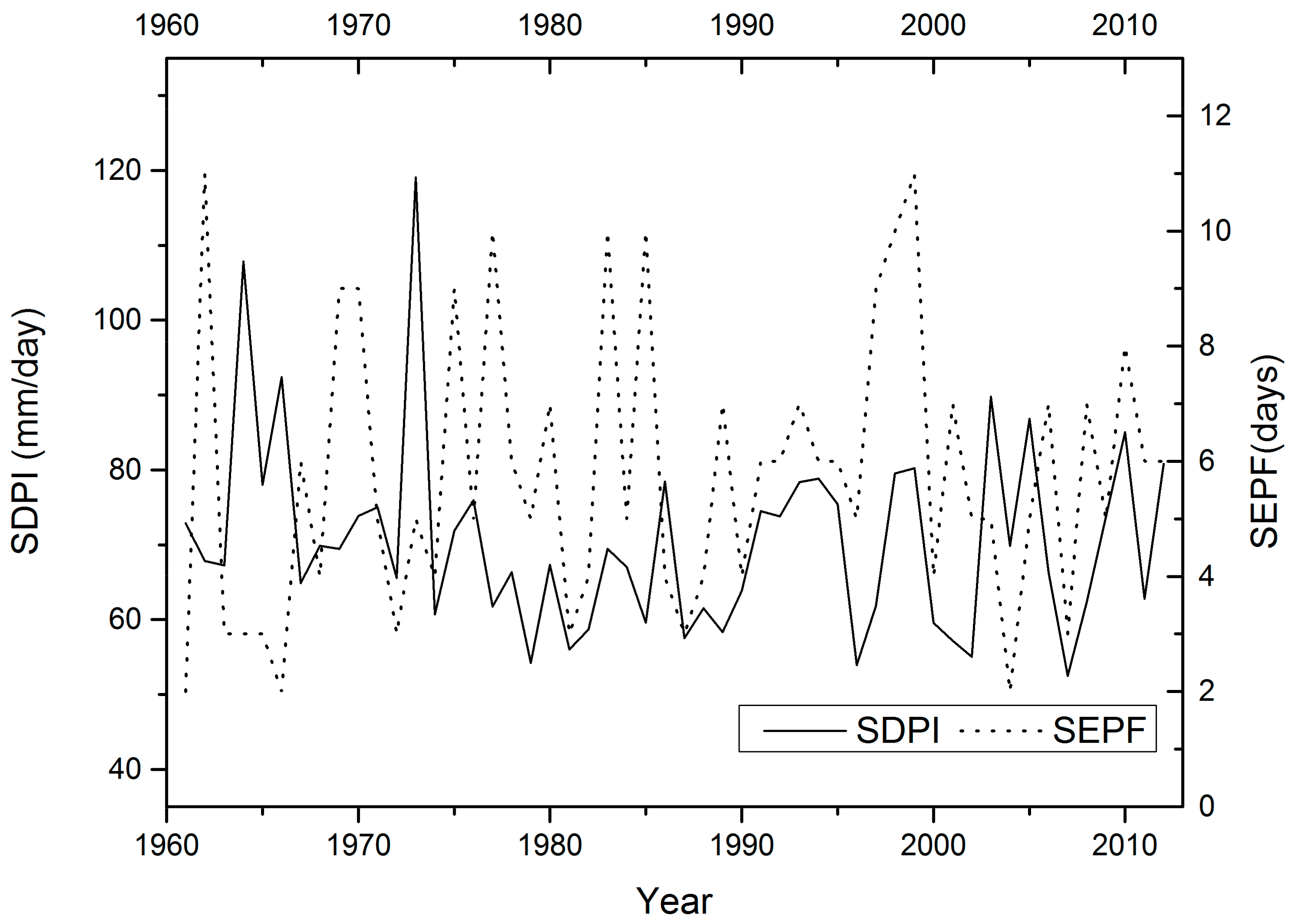
| Precipitation Features | 90th | 95th | 99th |
|---|---|---|---|
| Threshold (mm/day) | 23.97 4.41 | 36.43 6.10 | 72.14 12.22 |
| Occurrence rate (days) | 11.05 1.76 | 5.96 1.01 | 1.31 0.22 |
| Dispersion coefficients | 0.78 0.18 | 0.91 0.19 | 0.96 0.18 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pei, F.; Wu, C.; Qu, A.; Xia, Y.; Wang, K.; Zhou, Y. Changes in Extreme Precipitation: A Case Study in the Middle and Lower Reaches of the Yangtze River in China. Water 2017, 9, 943. https://doi.org/10.3390/w9120943
Pei F, Wu C, Qu A, Xia Y, Wang K, Zhou Y. Changes in Extreme Precipitation: A Case Study in the Middle and Lower Reaches of the Yangtze River in China. Water. 2017; 9(12):943. https://doi.org/10.3390/w9120943
Chicago/Turabian StylePei, Fengsong, Changjiang Wu, Aixue Qu, Yan Xia, Kun Wang, and Yi Zhou. 2017. "Changes in Extreme Precipitation: A Case Study in the Middle and Lower Reaches of the Yangtze River in China" Water 9, no. 12: 943. https://doi.org/10.3390/w9120943
APA StylePei, F., Wu, C., Qu, A., Xia, Y., Wang, K., & Zhou, Y. (2017). Changes in Extreme Precipitation: A Case Study in the Middle and Lower Reaches of the Yangtze River in China. Water, 9(12), 943. https://doi.org/10.3390/w9120943





