Overview, Comparative Assessment and Recommendations of Forecasting Models for Short-Term Water Demand Prediction
Abstract
:1. Introduction
- explaining day-to-day demand variations
- minimising the operating cost of pumping stations
- pinpointing possible network failures (e.g., water leaks and pipe bursts)
- helping utilities plan and manage water demands for near-term events
- optimizing daily operations of the infrastructure (e.g., pump scheduling, control of reservoirs volume, pressure management, and water conservation program)
2. Overview of STWD Forecasting Methods
2.1. UTS Forecasting Methods
2.2. Time Series Regression (TSR) Forecasting Methods
2.3. Artificial Neural Network (ANN) Forecasting Methods
2.4. Hybrid Forecasting Methods
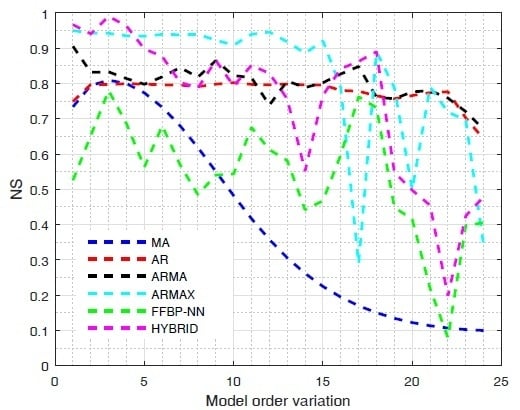
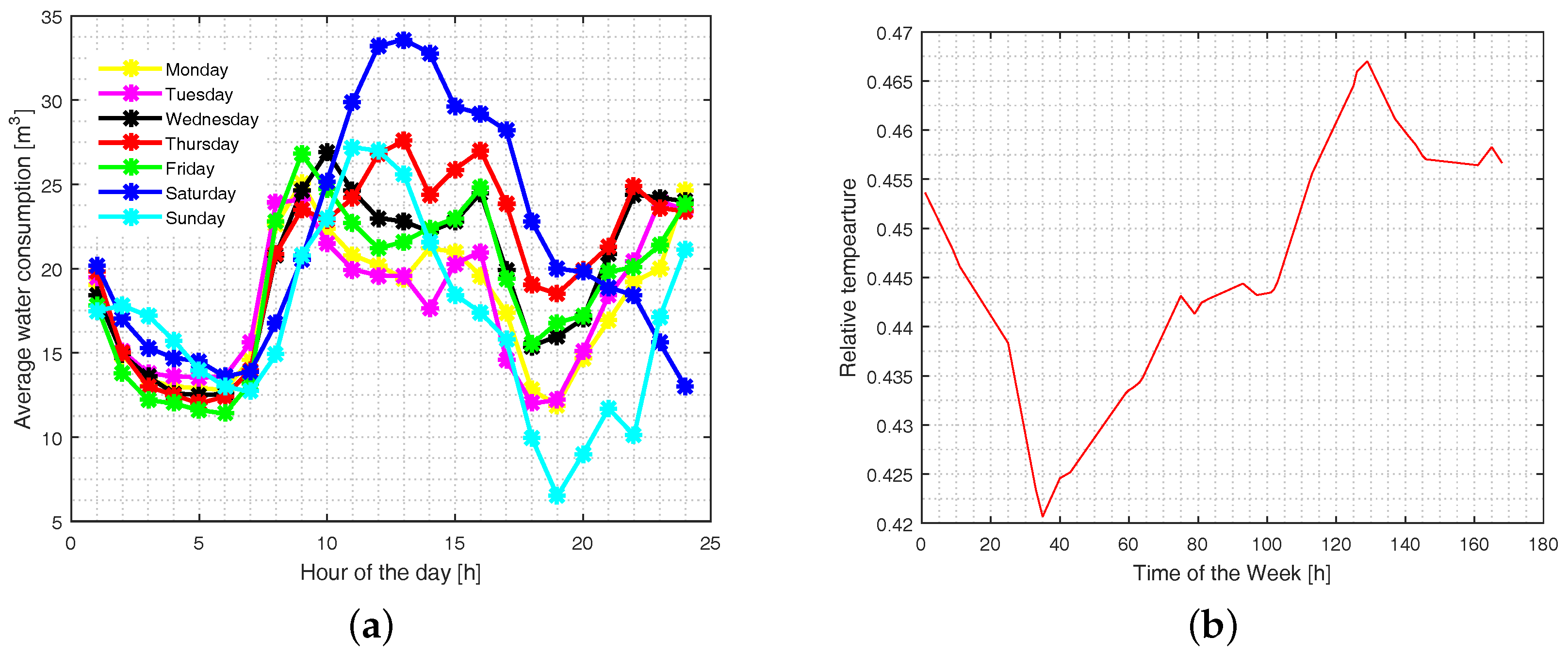
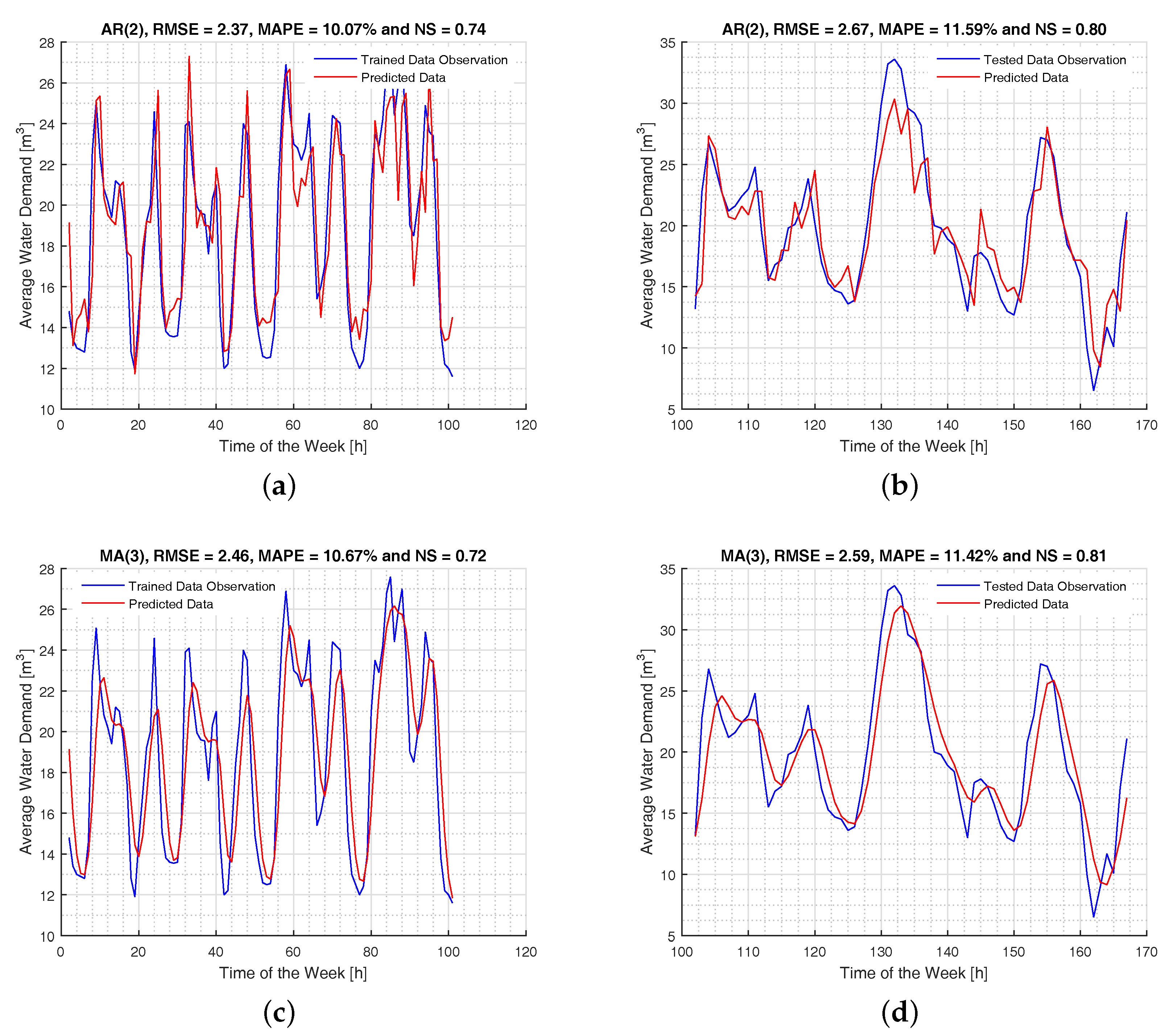
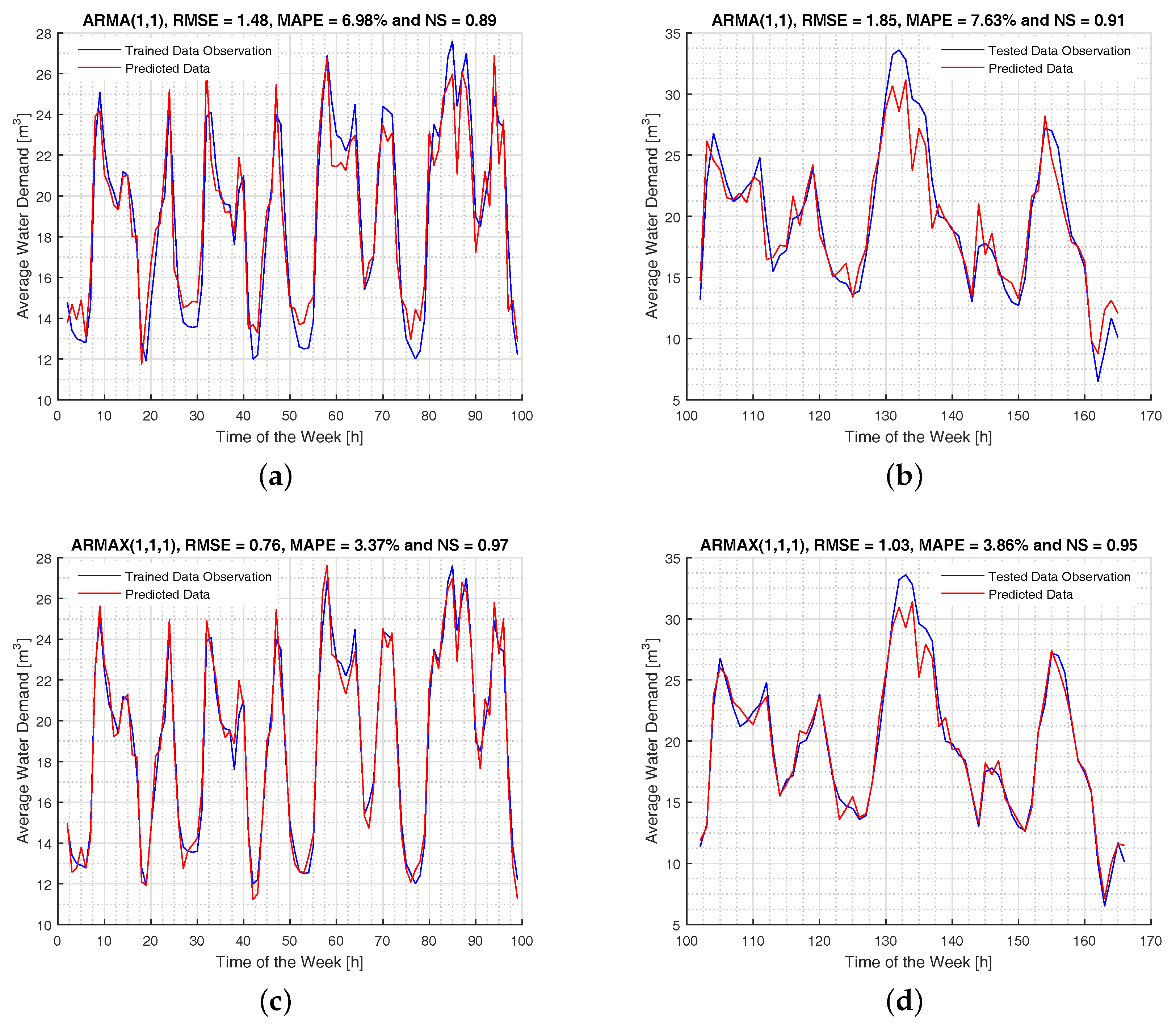
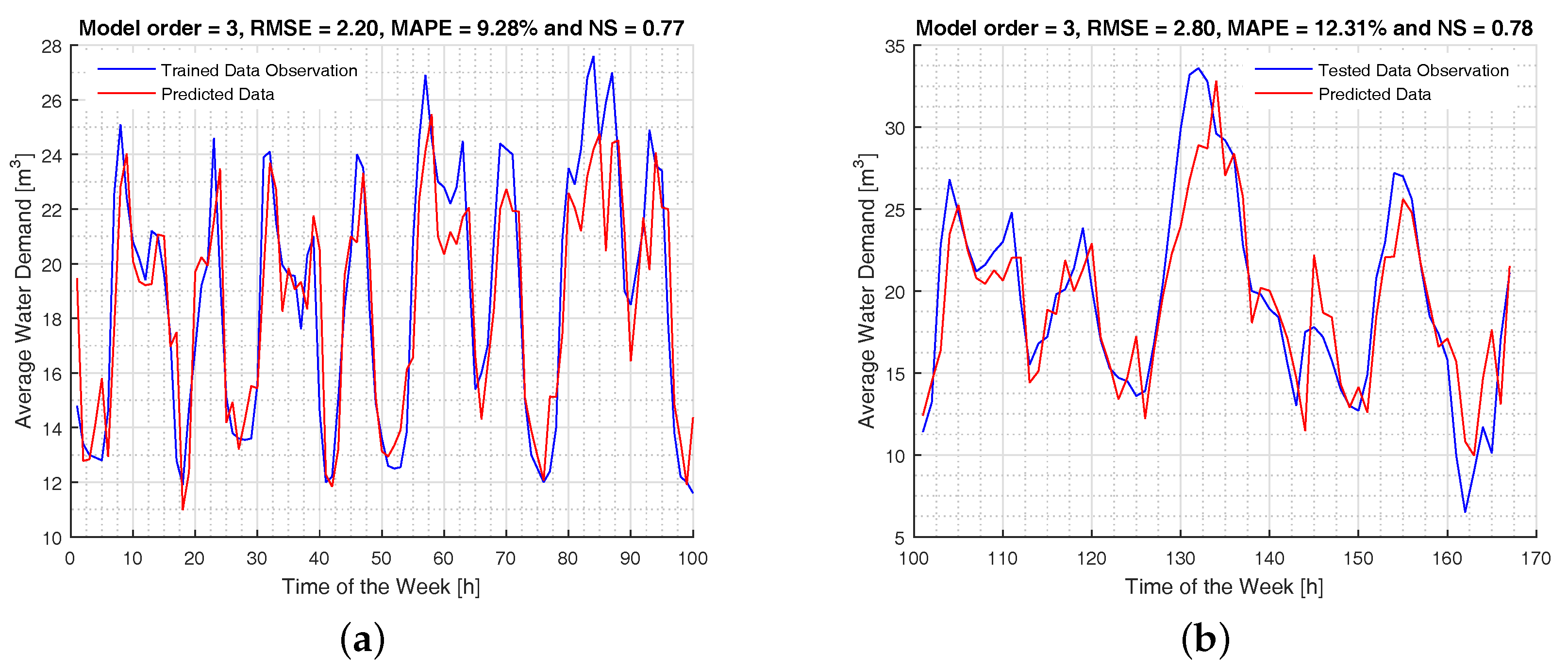
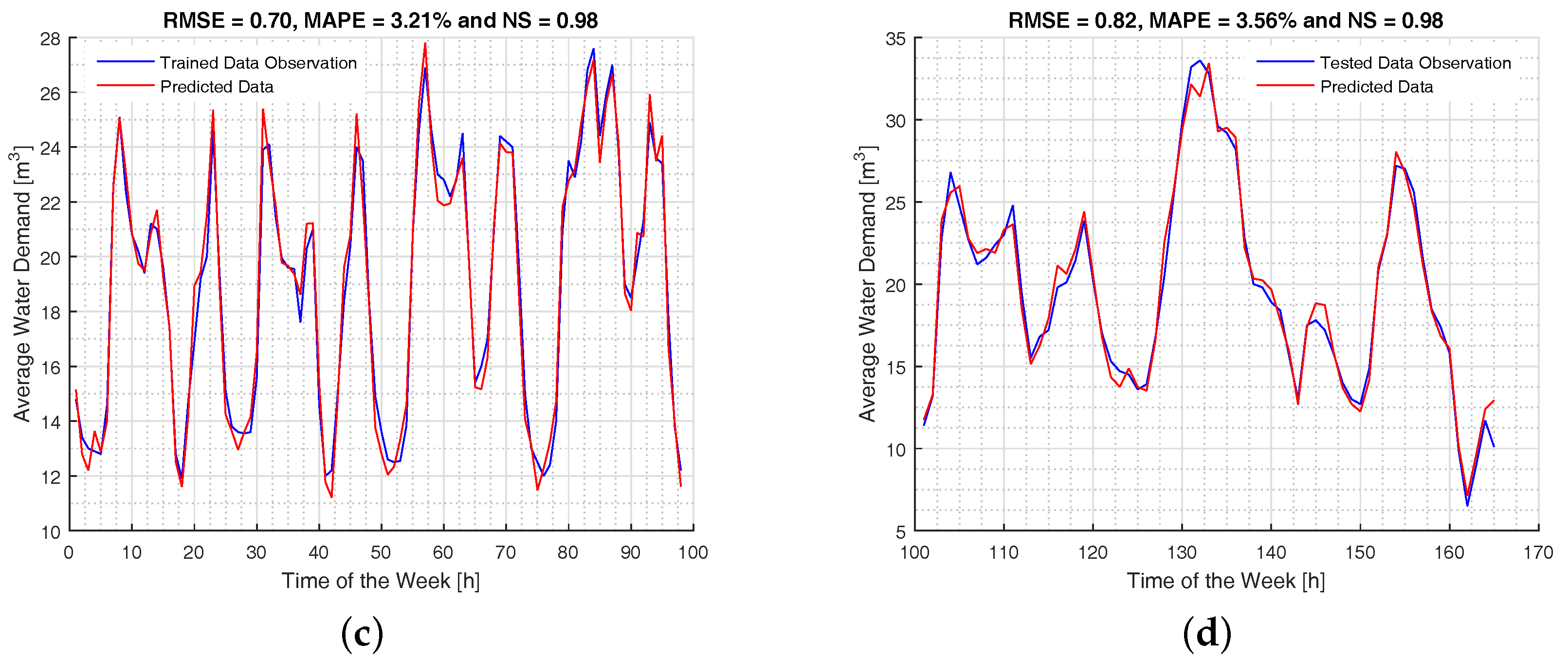
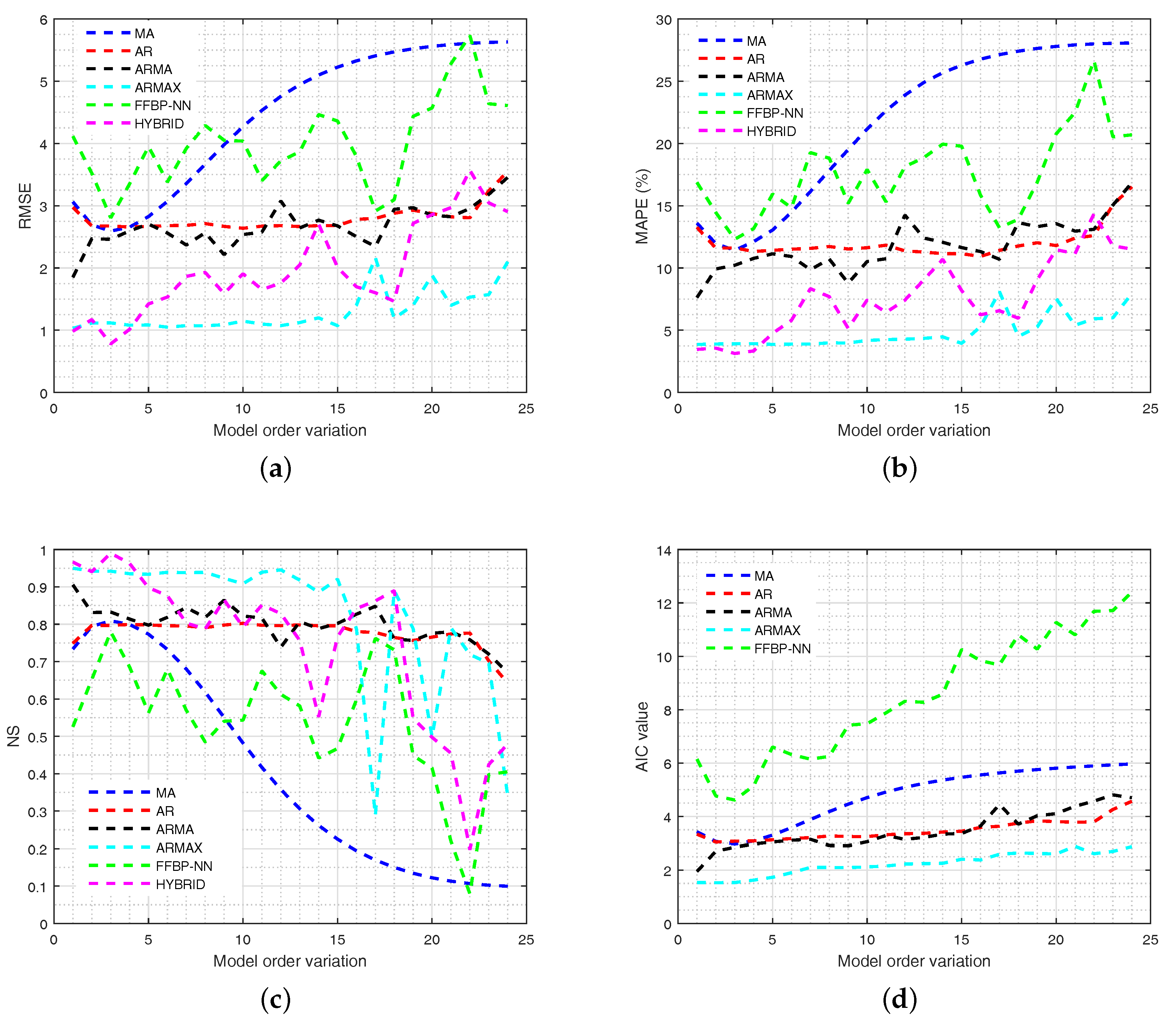
3. Presentation and Discussion of Results
4. Recommendations of STWD Forecasting Models and Future Work
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Herrera, M.; Torgo, L.; Izquierdo, J.; Pérez-García, R. Predictive models for forecasting hourly urban water demand. J. Hydrol. 2010, 387, 141–150. [Google Scholar] [CrossRef]
- Gharun, M.; Azmi, M.; Adams, M.A. Short-term forecasting of water yield from forested catchments after Bushfire: A case study from southeast Australia. Water 2015, 7, 599–614. [Google Scholar] [CrossRef]
- Abu-Mahfouz, A.M.; Hamam, Y.; Page, P.R.; Djouani, K.; Kurien, A. Real-time dynamic hydraulic model for potable water loss reduction. Procedia Eng. 2016, 154, 99–106. [Google Scholar] [CrossRef]
- Pacchin, E.; Alvisi, S.; Franchini, M. A Short-Term Water Demand Forecasting Model Using a Moving Window on Previously Observed Data. Water 2017, 9, 172. [Google Scholar] [CrossRef]
- Jain, A.; Ormsbee, L.E. Short-term water demand forecast modeling techniques—Conventional methods versus AI. J. Am. Water Works Assoc. 2002, 94, 64–72. [Google Scholar]
- Alvisi, S.; Franchini, M.; Marinelli, A. A short-term, pattern-based model for water-demand forecasting. J. Hydroinf. 2007, 9, 39–50. [Google Scholar] [CrossRef]
- Khatri, K.; Vairavamoorthy, K. Water Demand Forecasting for the City of the Future Against the Uncertainties and the Global Change Pressures: Case of Birmingham. In Proceedings of the World Environmental and Water Resources Congress, Kansas, MO, USA, 17–21 May 2009; pp. 17–21. [Google Scholar]
- Hamam, Y.M.; Hindi, K.S. Optimised on-Line Leakage Minimisation in Water Piping Networks Using Neural Nets. In Proceedings of the IFIP Working Conference, Dagschul, Germany, 28 September–1 October 1992; pp. 57–64. [Google Scholar]
- Hindi, K.; Hamam, Y. Locating pressure control elements for leakage minimization in water supply networks: An optimization model. Eng. Opt. 1991, 17, 281–291. [Google Scholar] [CrossRef]
- Hindi, K.; Hamam, Y. Pressure control for leakage minimization in water supply networks Part 1: Single period models. Int. J. Syst. Sci. 1991, 22, 1573–1585. [Google Scholar] [CrossRef]
- Donkor, E.A.; Mazzuchi, T.A.; Soyer, R.; Alan Roberson, J. Urban water demand forecasting: Review of methods and models. J. Water Resour. Plan. Manag. 2012, 140, 146–159. [Google Scholar] [CrossRef]
- Veiga, V.B.; Hassan, Q.K.; He, J. Development of Flow Forecasting Models in the Bow River at Calgary, Alberta, Canada. Water 2014, 7, 99–115. [Google Scholar] [CrossRef]
- Arampatzis, G.; Perdikeas, N.; Kampragou, E.; Scaloubakas, P.; Assimacopoulos, D. A Water Demand Forecasting Methodology for Supporting Day-to-Day Management of Water Distribution Systems. In Proceedings of the 12th International Conference “Protection & Restoration of the Environment”, Skiathos, Greece, 29 June–3 July 2014. [Google Scholar]
- Amponsah, S.; Otoo, D.; Todoko, C. Time series analysis of water consumption in the Hohoe municipality of the Volta region, Ghana. Int. J. Appl. Math. Res. 2015, 4, 393–403. [Google Scholar] [CrossRef]
- Alvisi, S.; Franchini, M. Assessment of predictive uncertainty within the framework of water demand forecasting using the Model Conditional Processor (MCP). Urban Water J. 2015, 14, 1–10. [Google Scholar] [CrossRef]
- Gagliardi, F.; Alvisi, S.; Kapelan, Z.; Franchini, M. A Probabilistic Short-Term Water Demand Forecasting Model Based on the Markov Chain. Water 2017, 9, 507. [Google Scholar] [CrossRef]
- Box, G.; Jenkins, G. Time Series Analysis: Forecasting and Control; Holden-Day: San Franciso, CA, USA, 1970. [Google Scholar]
- Billings, R.B.; Jones, C.V. Forecasting Urban Water Demand; American Water Works Association: Denver, CO, USA, 2011. [Google Scholar]
- Polebitski, A.S.; Palmer, R.N.; Waddell, P. Evaluating water demands under climate change and transitions in the urban environment. J. Water Resour. Plan. Manag. 2010, 137, 249–257. [Google Scholar] [CrossRef]
- Qi, G.; Hamam, Y.; Van Wyk, B.J.; Du, S. Model-free Prediction based on Tracking Theory and Newton Form of Polynomial. World Acad. Sci. Eng. Technol. 2011, 5, 882–889. [Google Scholar]
- Candelieri, A. Clustering and Support Vector Regression for Water Demand Forecasting and Anomaly Detection. Water 2017, 9, 224. [Google Scholar] [CrossRef]
- Rosenblatt, F. The perceptron: A probabilistic model for information storage and organization in the brain. Psychol. Rev. 1958, 65, 386. [Google Scholar] [CrossRef] [PubMed]
- Hindi, K.; Hamam, Y. Locating pressure control elements for leakage minimisation in water supply networks by genetic algorithms. In Artificial Neural Nets and Genetic Algorithms; Springer: Vienna, Austria, 1993; pp. 583–587. [Google Scholar]
- Jentgen, L.; Kidder, H.; Hill, R.; Conrad, S. Energy management strategies use short-term water consumption forecasting to minimize cost of pumping operations. J. Am. Water Works Assoc. 2007, 99, 86. [Google Scholar]
- Cutore, P.; Campisano, A.; Kapelan, Z.; Modica, C.; Savic, D. Probabilistic prediction of urban water consumption using the SCEM-UA algorithm. Urban Water J. 2008, 5, 125–132. [Google Scholar] [CrossRef]
- Adamowski, J.; Karapataki, C. Comparison of multivariate regression and artificial neural networks for peak urban water-demand forecasting: evaluation of different ANN learning algorithms. J. Hydrol. Eng. 2010, 15, 729–743. [Google Scholar] [CrossRef]
- Ghiassi, M.; Zimbra, D.K.; Saidane, H. Urban water demand forecasting with a dynamic artificial neural network model. J. Water Resour. Plan. Manag. 2008, 134, 138–146. [Google Scholar] [CrossRef]
- Jain, A.; Varshney, A.K.; Joshi, U.C. Short-term water demand forecast modelling at IIT Kanpur using artificial neural networks. Water Resour. Manag. 2001, 15, 299–321. [Google Scholar] [CrossRef]
- Bougadis, J.; Adamowski, K.; Diduch, R. Short-term municipal water demand forecasting. Hydrol. Process. 2005, 19, 137–148. [Google Scholar] [CrossRef]
- Hamam, Y.; Brameller, A. Hybrid method for the solution of piping networks. Proc. Inst. Electr. Eng. IET 1971, 118, 1607–1612. [Google Scholar] [CrossRef]
- Zhou, S.L.; McMahon, T.A.; Walton, A.; Lewis, J. Forecasting daily urban water demand: A case study of Melbourne. J. Hydrol. 2000, 236, 153–164. [Google Scholar] [CrossRef]
- Gato, S.; Jayasuriya, N.; Roberts, P. Temperature and rainfall thresholds for base use urban water demand modelling. J. Hydrol. 2007, 337, 364–376. [Google Scholar] [CrossRef]
- Wang, X.; Sun, Y.; Song, L.; Mei, C. An eco-environmental water demand based model for optimising water resources using hybrid genetic simulated annealing algorithms. Part I. Model development. J. Environ. Manag. 2009, 90, 2628–2635. [Google Scholar] [CrossRef] [PubMed]
- Brentan, B.M.; Luvizotto, E., Jr.; Herrera, M.; Izquierdo, J.; Pérez-García, R. Hybrid regression model for near real-time urban water demand forecasting. J. Comput. Appl. Math. 2017, 309, 532–541. [Google Scholar] [CrossRef]
- Tiwari, M.; Adamowski, J.; Adamowski, K. Water demand forecasting using extreme learning machines. J. Water Land Dev. 2016, 28, 37–52. [Google Scholar] [CrossRef]
- Aly, A.H.; Wanakule, N. Short-term forecasting for urban water consumption. J. Water Resour. Plan. Manag. 2004, 130, 405–410. [Google Scholar] [CrossRef]
- Caiado, J. Performance of combined double seasonal univariate time series models for forecasting water demand. J. Hydrol. Eng. 2009, 15, 215–222. [Google Scholar] [CrossRef]
- Altunkaynak, A.; Özger, M.; Çakmakci, M. Water consumption prediction of Istanbul city by using fuzzy logic approach. Water Resour. Manag. 2005, 19, 641–654. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Todini, E. Using phase-state modelling for inferring forecasting uncertainty in nonlinear stochastic decision schemes. J. Hydroinf. 1999, 1, 75–82. [Google Scholar]
- Todini, E. A model conditional processor to assess predictive uncertainty in flood forecasting. Int. J. River Basin Manag. 2008, 6, 123–137. [Google Scholar] [CrossRef]
- Anele, A.; Hamam, Y.; Todini, E.; Abu-Mahfouz, A. Predictive uncertainty estimation in water demand forecasting using the model conditional processor. Water Resour. Manag. 2007. under review. [Google Scholar]
- Coccia, G.; Todini, E. Recent developments in predictive uncertainty assessment based on the model conditional processor approach. Hydrol. Earth Syst. Sci. 2011, 15, 3253–3274. [Google Scholar] [CrossRef]
- Todini, E. The role of predictive uncertainty in the operational management of reservoirs. In Proceedings of the ICWRS2014—Evolving Water Resources Systems: Understanding, Predicting and Managing Water-Society Interactions, Bologna, Italy, 16 September 2014; pp. 4–6. [Google Scholar]
- Barbetta, S.; Coccia, G.; Moramarco, T.; Todini, E. Case study: A real-time flood forecasting system with predictive uncertainty estimation for the Godavari River, India. Water 2016, 8, 463. [Google Scholar] [CrossRef]
- Reggiani, P.; Coccia, G.; Mukhopadhyay, B. Predictive Uncertainty Estimation on a Precipitation and Temperature Reanalysis Ensemble for Shigar Basin, Central Karakoram. Water 2016, 8, 263. [Google Scholar] [CrossRef]
| Forecasting Methods and Models | Quantitative Assessment of Forecast Accuracy | Forecast Purpose |
|---|---|---|
| UTS models [18,27,29]: MA, AR, ARIMA, exponential smoothing, ARMA, SARIMA | It can exhibit more complex profiles. However, it does not account for the effect of exogenous variables (e.g., weather data or price) [11]. | Useful for short-term operational forecasts (i.e., to minimise the operating cost of pumping stations, etc.) |
| TSR models [1,25,26]: MNLR, ARMAX, MLR and ARIMAX | TSR models produce forecasts on the basis of the relationship between water demand and its determinants (e.g., weather data, income, demographics) [19]. | Useful for better prediction of daily water demand [24]. Relevant for setting water rates, revenue forecasting, and financial planning exercises. |
| ANN models: FFBP-NN, GRNN, RBNN, DAN2 [5,35] | Used with TSR models [1,24,25,26,27], with UTS models [27], or with both UTS and TSR models [5,28,29]. According to [11], ANN outperforms UTS and TSR models. However, the results of [24,25] were inconclusive. | Useful for a better prediction of peak daily water demand. To inform optimal operating policy as well as pumping and maintenance scheduling. |
| Hybrid models: FFBP-NN and AR [36], Holt–Winters, ARIMA, and GARCH [37], Fuzzy logic and AR [38] | Different forecasting models are able to capture different aspects of the information available for prediction [11]. As a result, leading to better forecasting performance [33,36] | Useful for real-time, near-optimal control of water distribution systems (WDS) [6]. Necessary for operational purposes [33,36]. |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anele, A.O.; Hamam, Y.; Abu-Mahfouz, A.M.; Todini, E. Overview, Comparative Assessment and Recommendations of Forecasting Models for Short-Term Water Demand Prediction. Water 2017, 9, 887. https://doi.org/10.3390/w9110887
Anele AO, Hamam Y, Abu-Mahfouz AM, Todini E. Overview, Comparative Assessment and Recommendations of Forecasting Models for Short-Term Water Demand Prediction. Water. 2017; 9(11):887. https://doi.org/10.3390/w9110887
Chicago/Turabian StyleAnele, Amos O., Yskandar Hamam, Adnan M. Abu-Mahfouz, and Ezio Todini. 2017. "Overview, Comparative Assessment and Recommendations of Forecasting Models for Short-Term Water Demand Prediction" Water 9, no. 11: 887. https://doi.org/10.3390/w9110887
APA StyleAnele, A. O., Hamam, Y., Abu-Mahfouz, A. M., & Todini, E. (2017). Overview, Comparative Assessment and Recommendations of Forecasting Models for Short-Term Water Demand Prediction. Water, 9(11), 887. https://doi.org/10.3390/w9110887