Modeling of Mixed Crop Field Water Demand and a Smart Irrigation System
Abstract
1. Introduction
2. Methodology
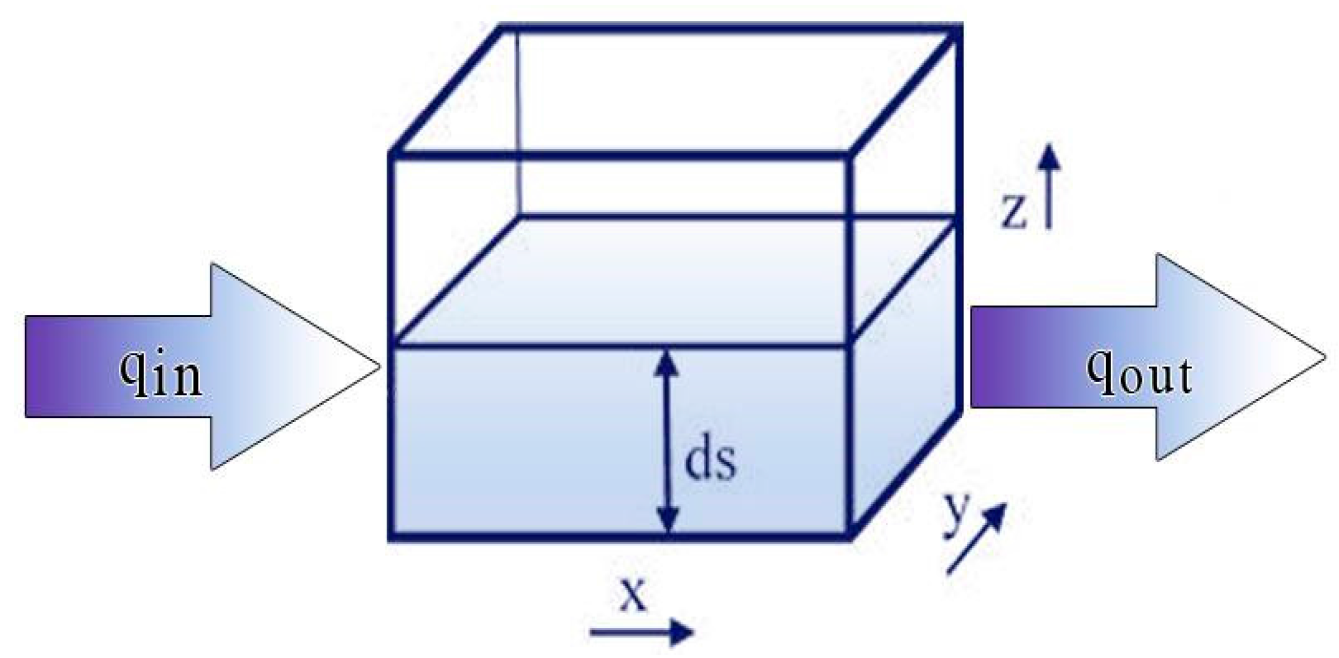
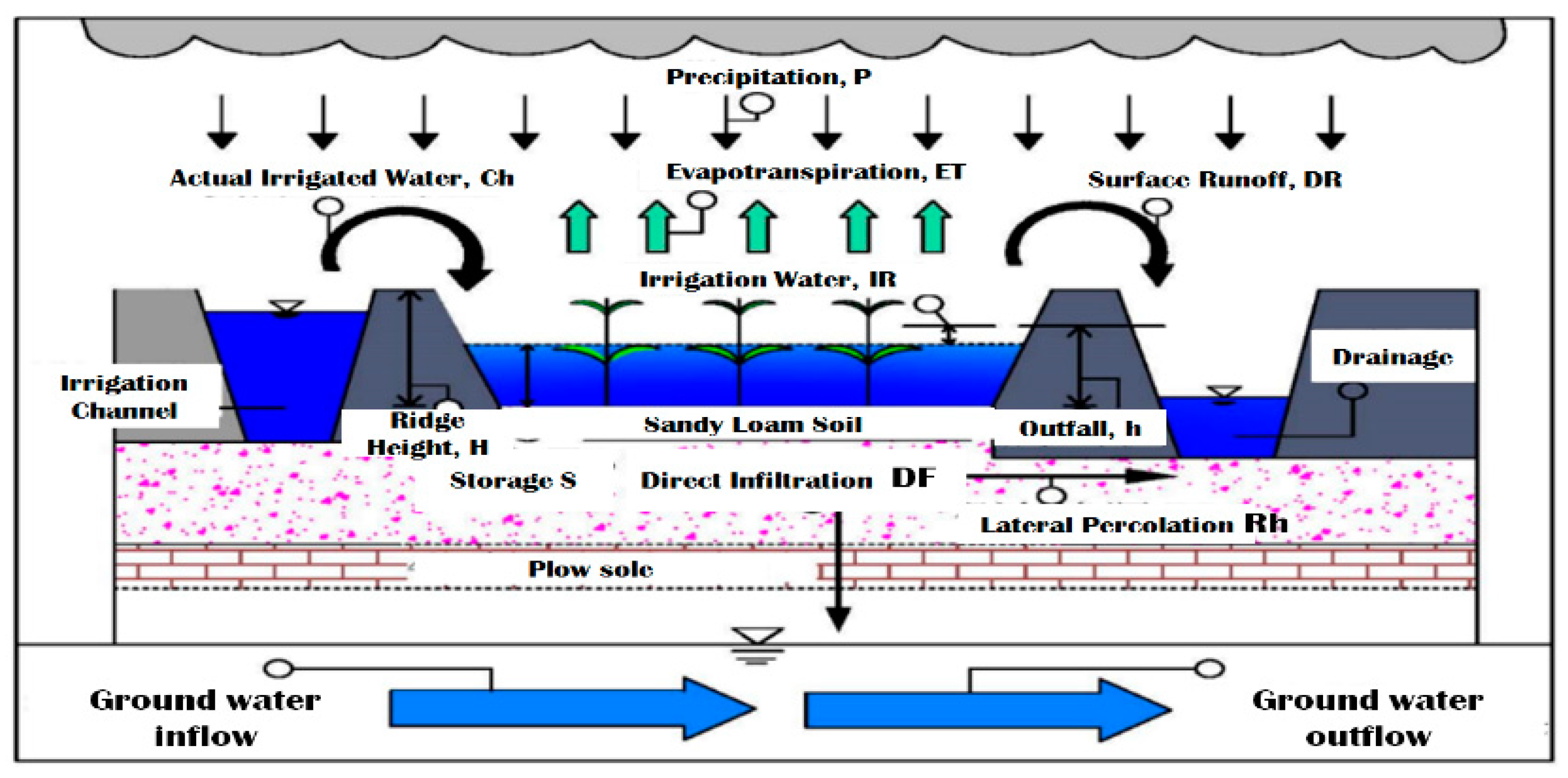
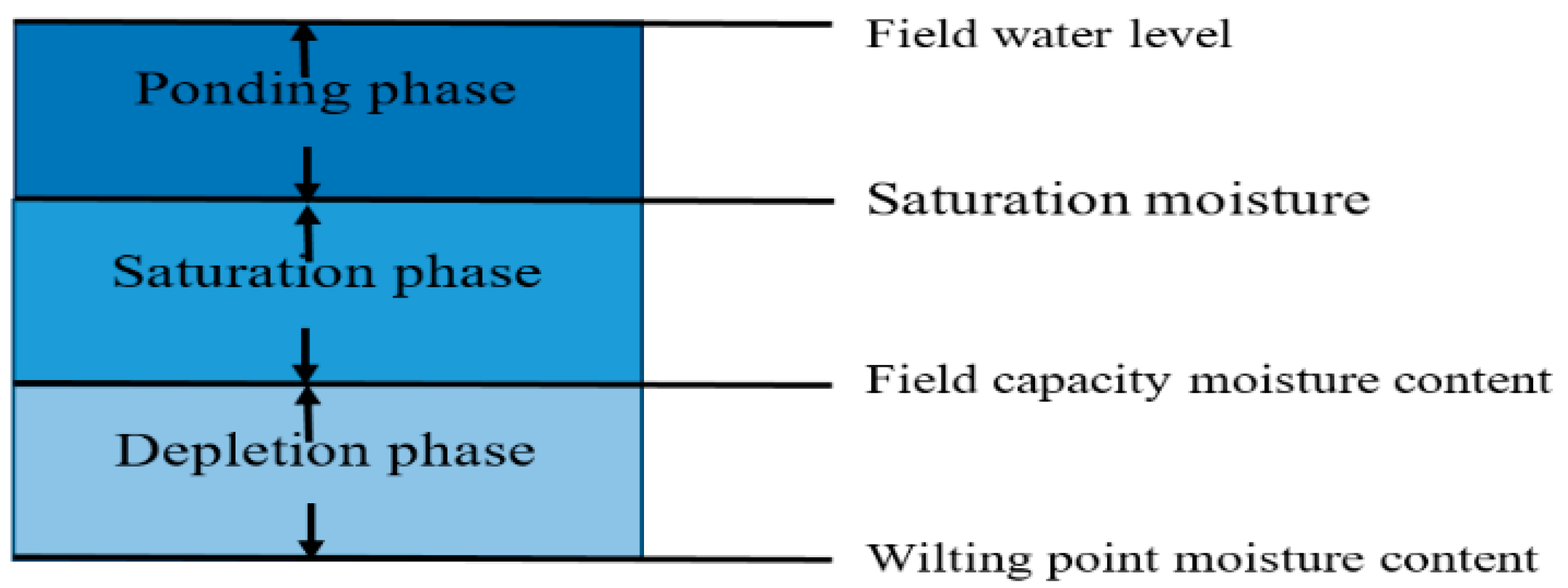
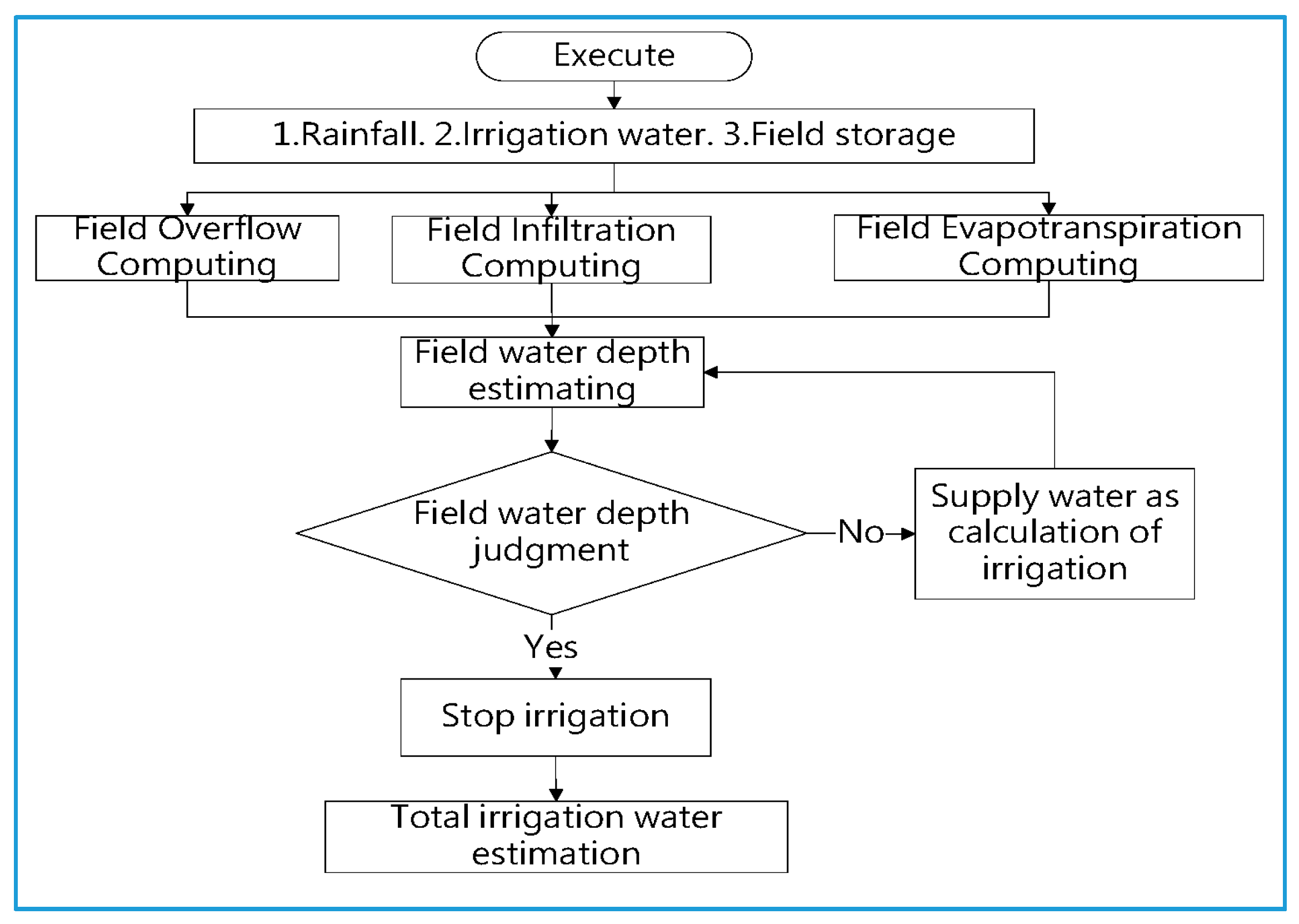
2.1. Field Water Balance Method
2.2. Crop Evapotranspiration
2.3. Irrigation Water Demand
2.4. Percolation Calculation
2.4.1. Vertical Percolation
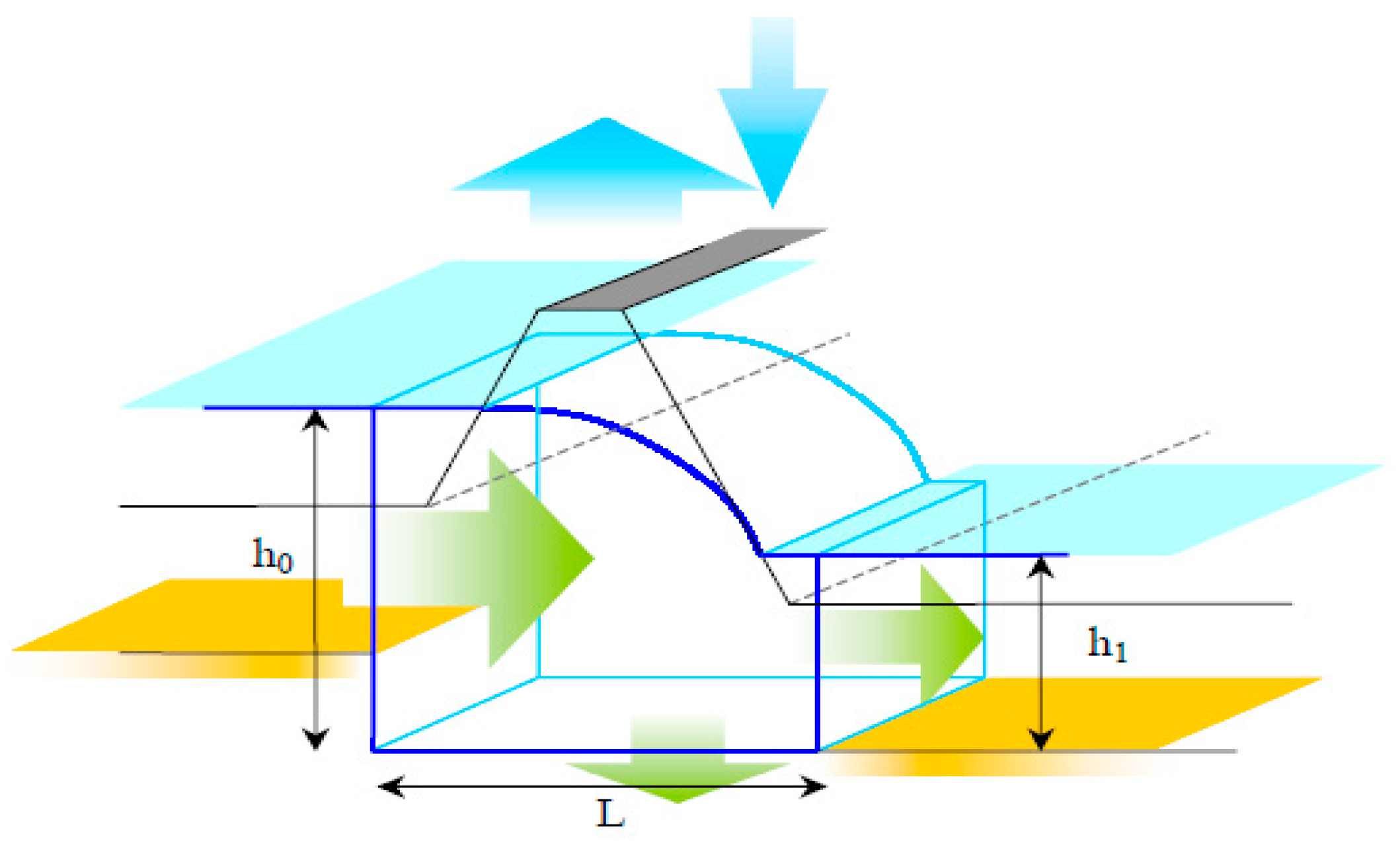
2.4.2. Lateral Seepage
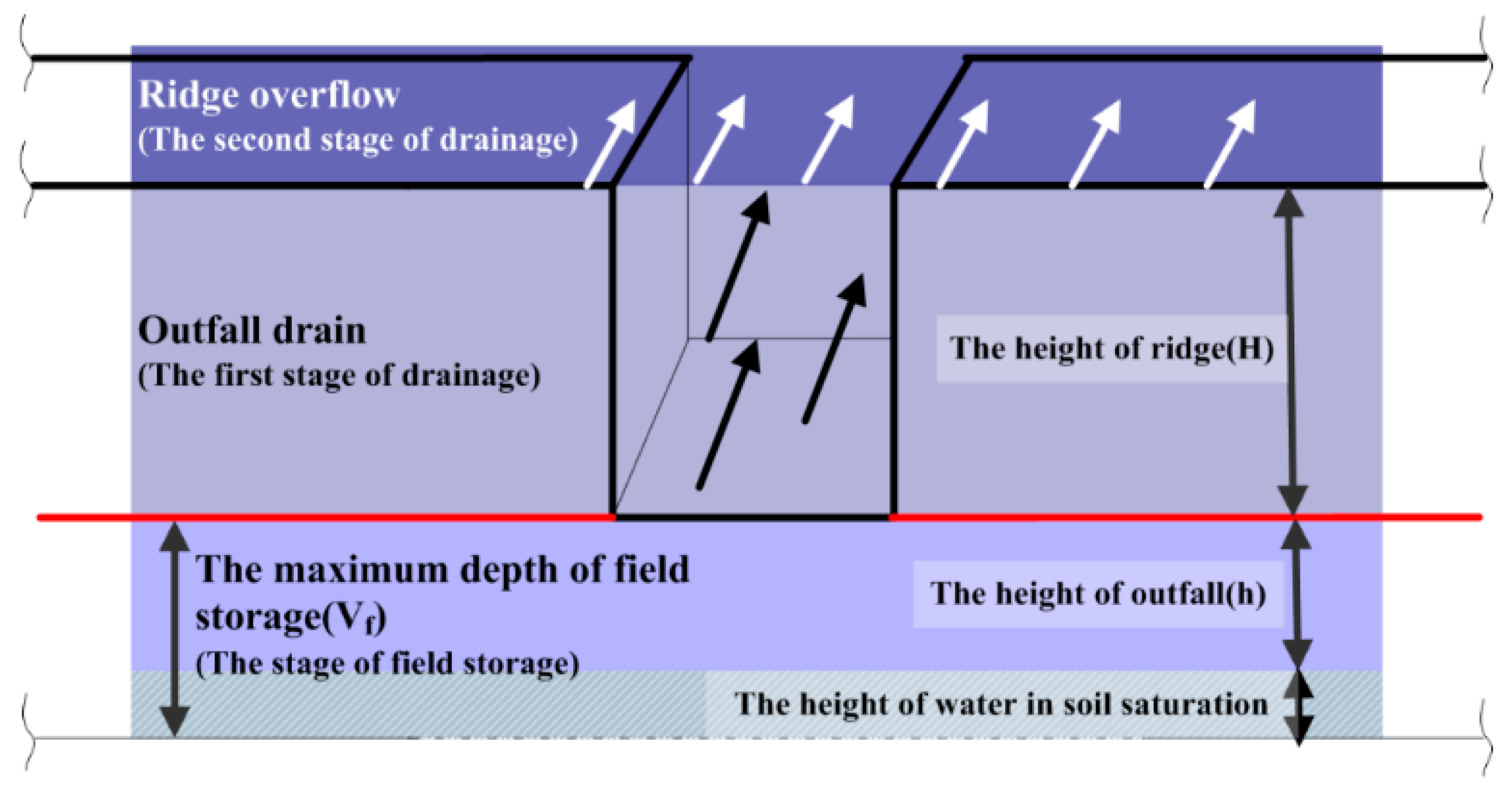
2.5. Field Surface Runoff Calculation
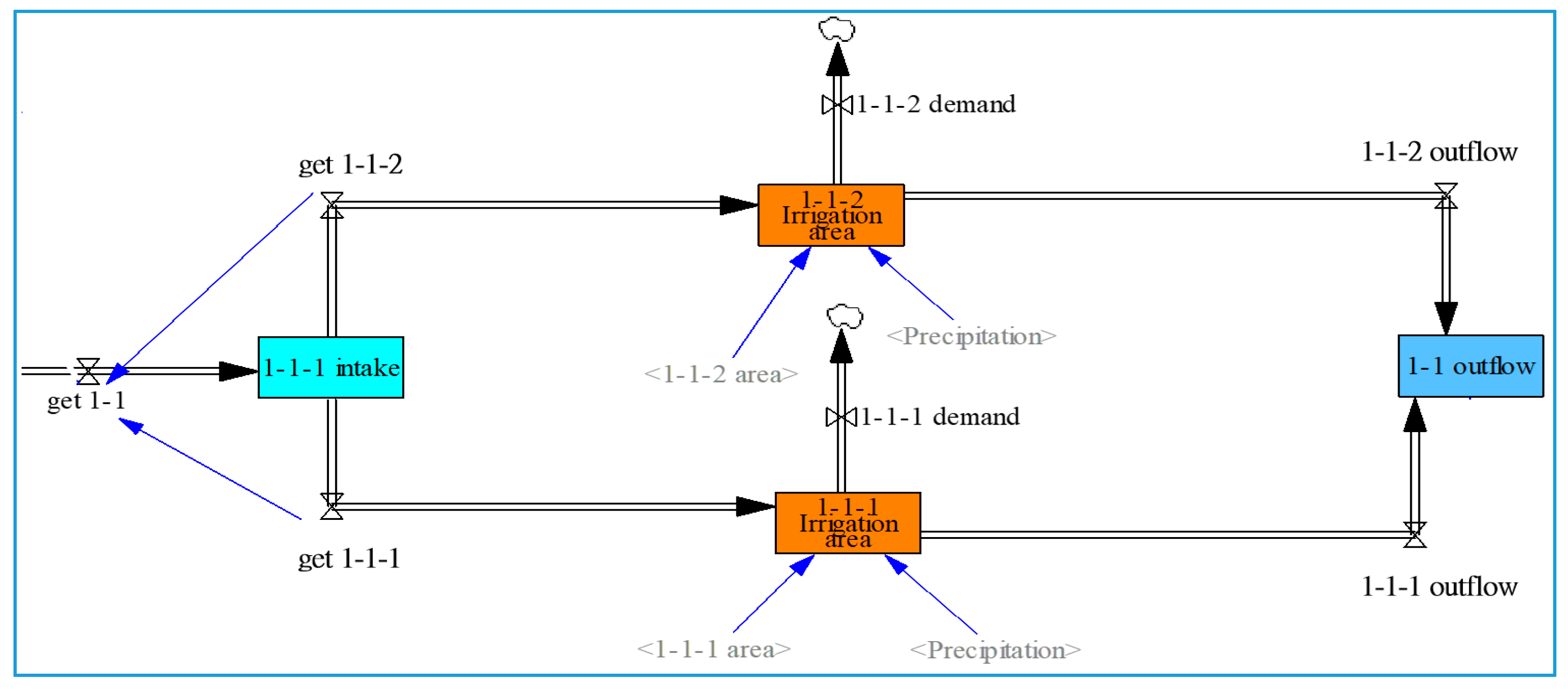
3. System Dynamic Model: VENSIM
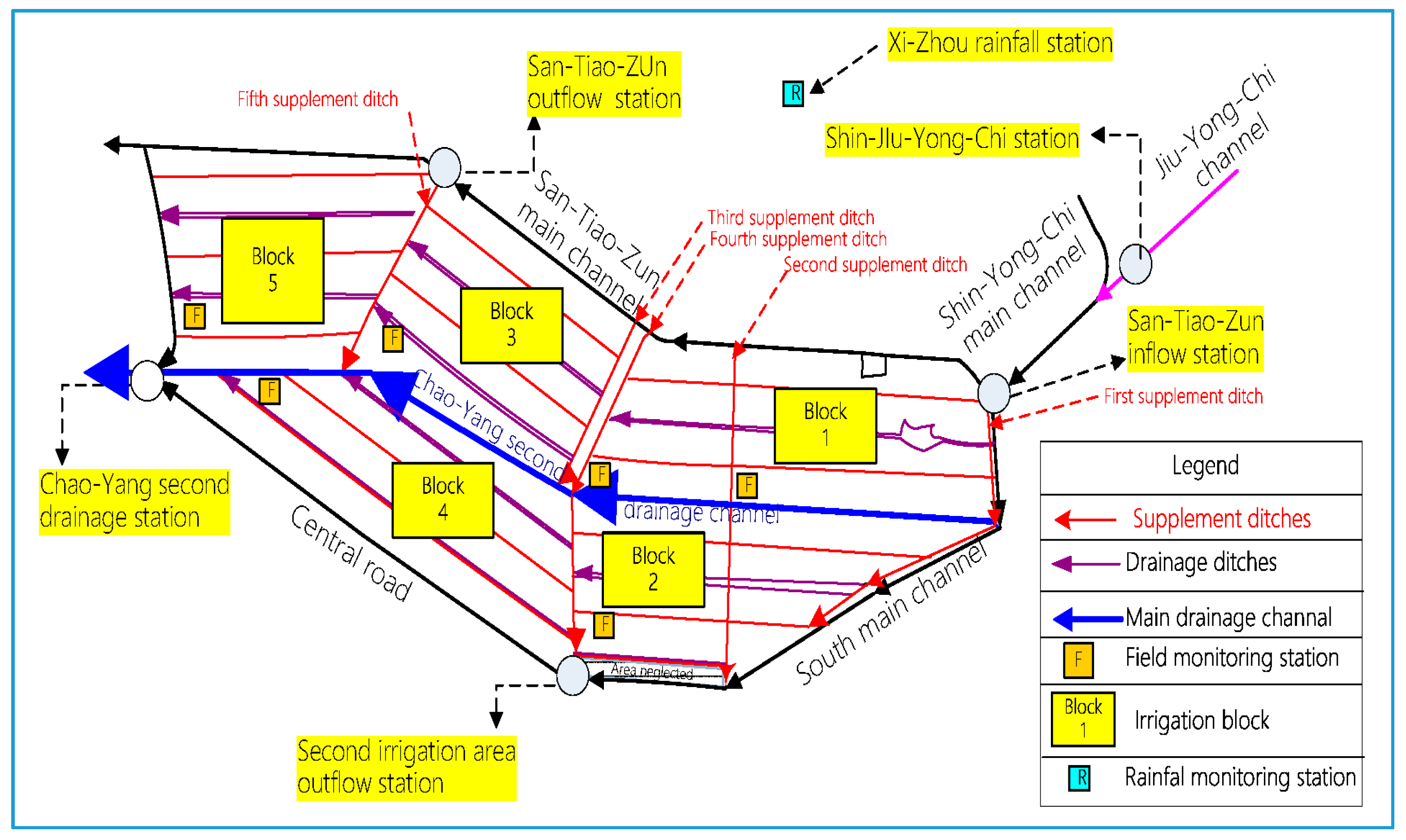
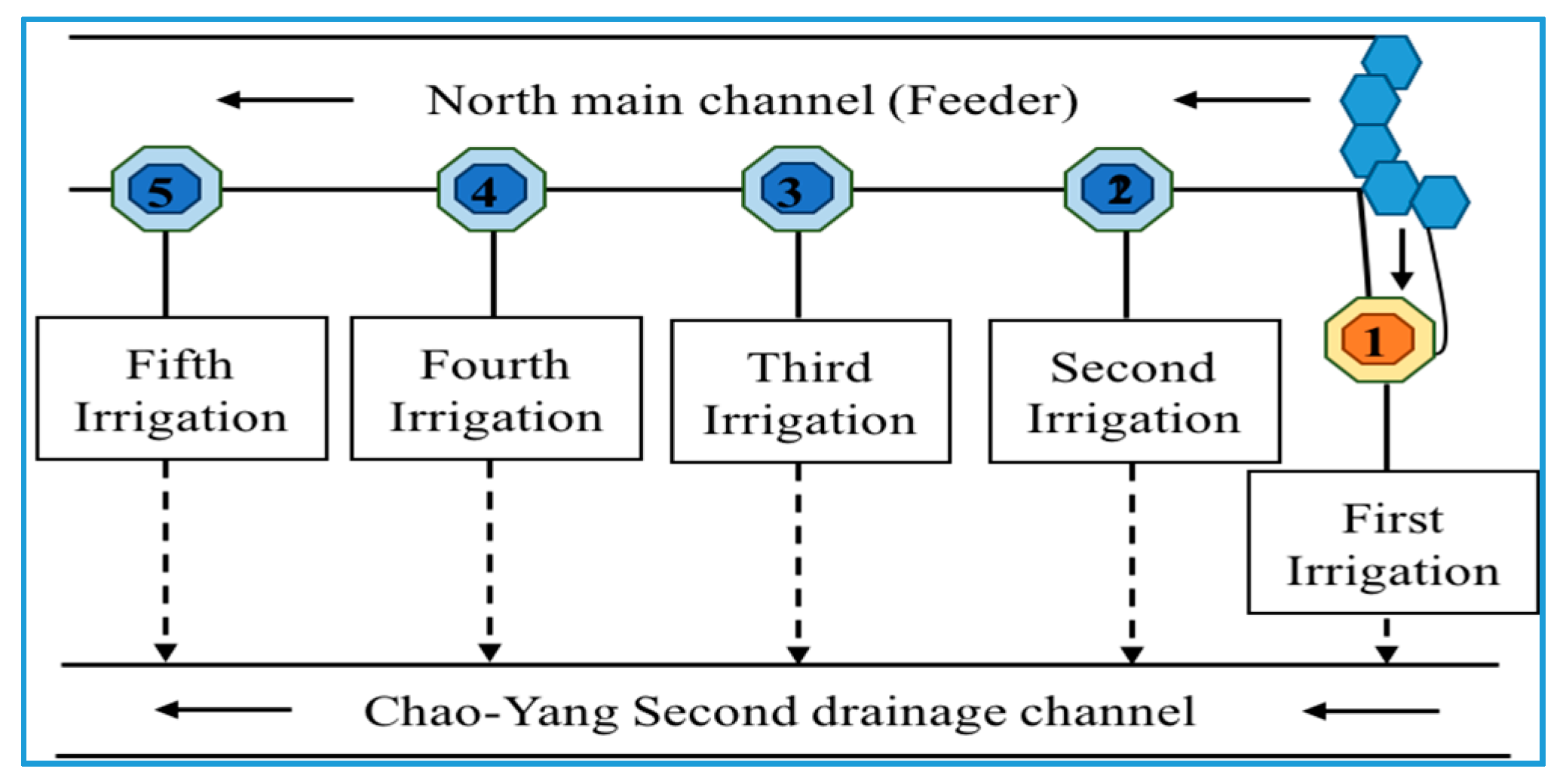
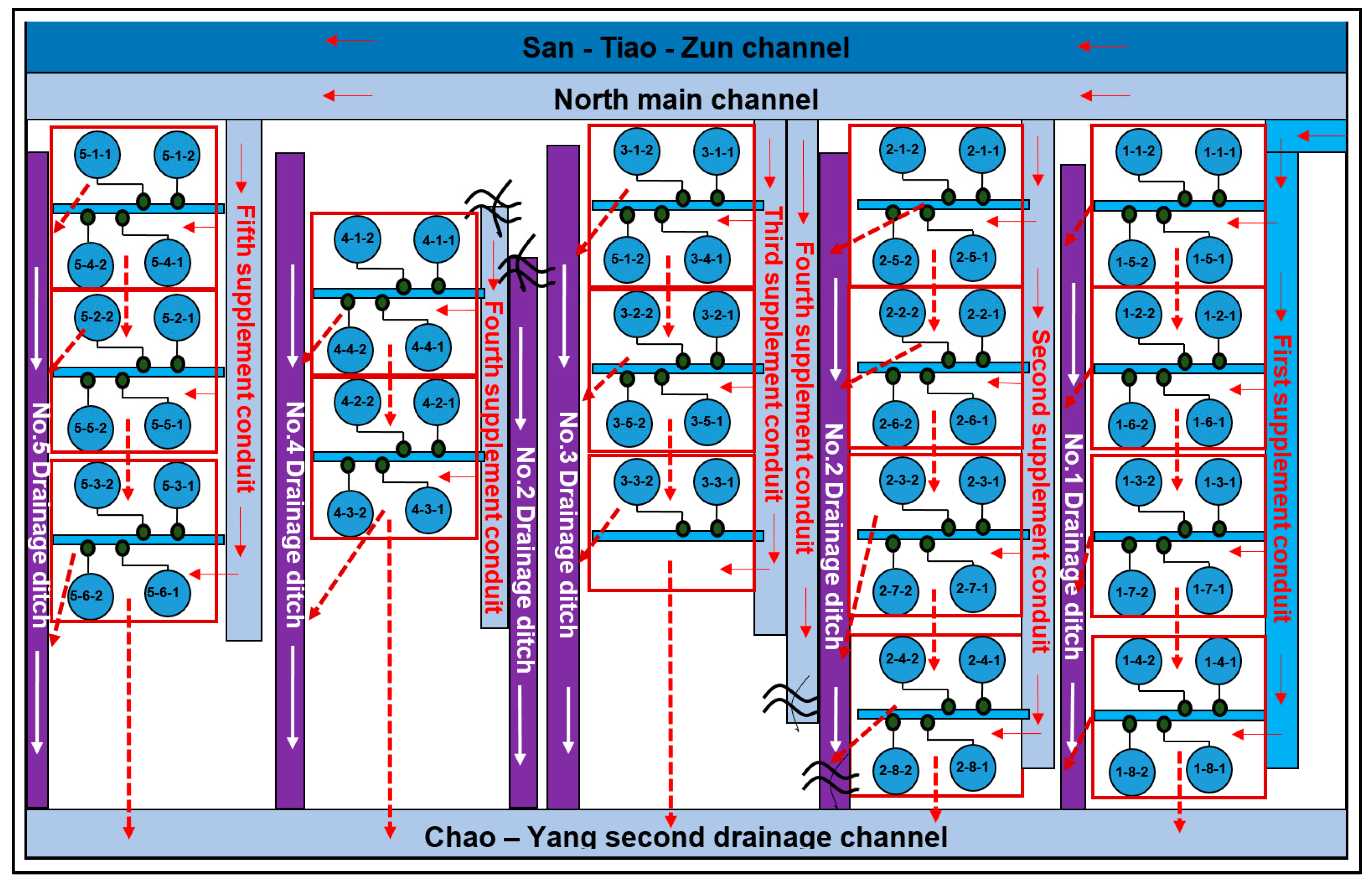
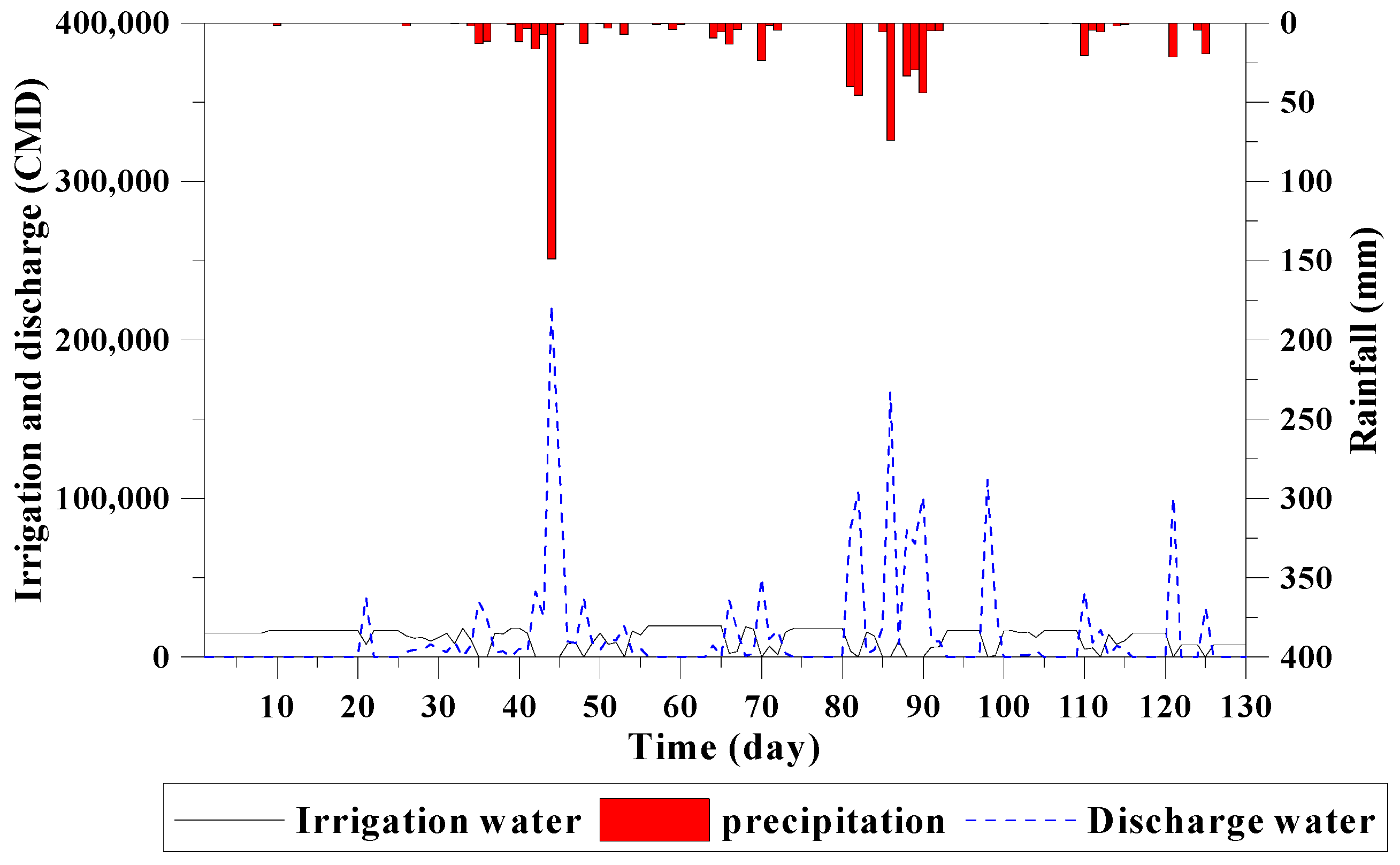
3.1. Study Area Overview
3.2. Model Establishment
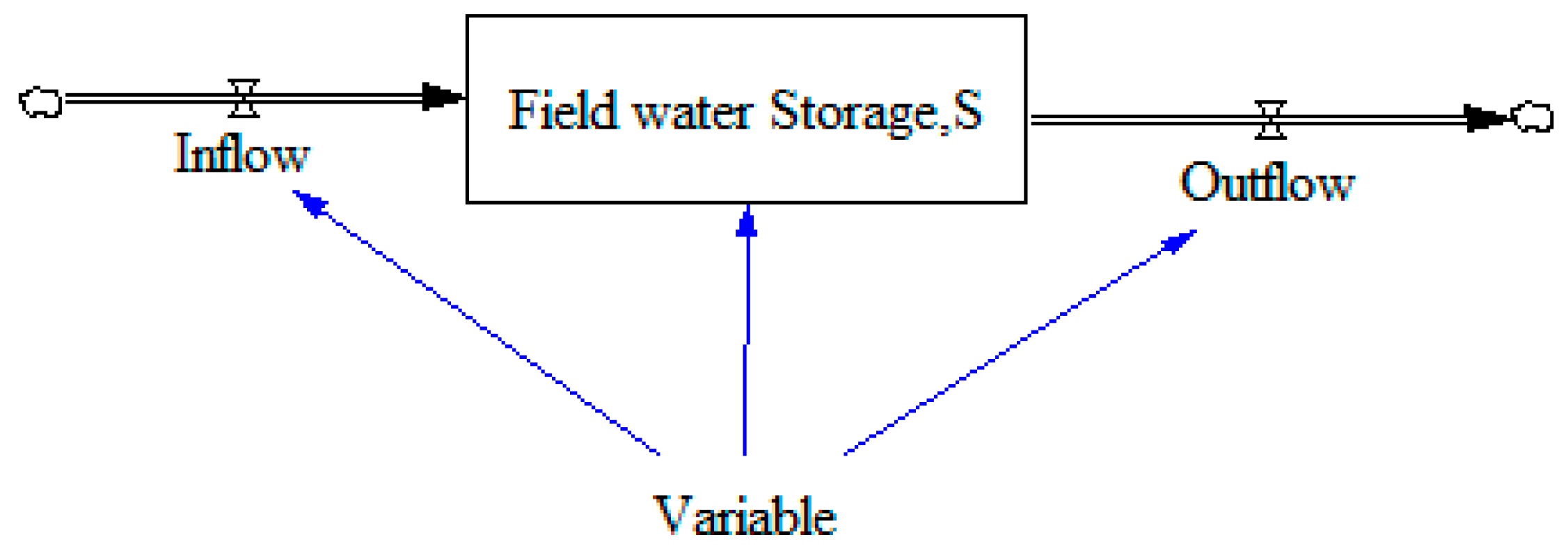
- Level: Also called accumulated amount, the accumulation of flow inside the system, which indicates the variable’s situation in a moment, for example, field storage; integral calculus in mathematics.
- Rate: Also called rate amount, which implies the in or out storage flow. The value is obtained by function calculation; differential calculus in mathematics.
- Auxiliary: Its main function is to describe the relation between Level and Rate, and makes the system structure more clear. Another function is that of test value or test function.
- Arrow: It is used to connect auxiliary and flow formula.
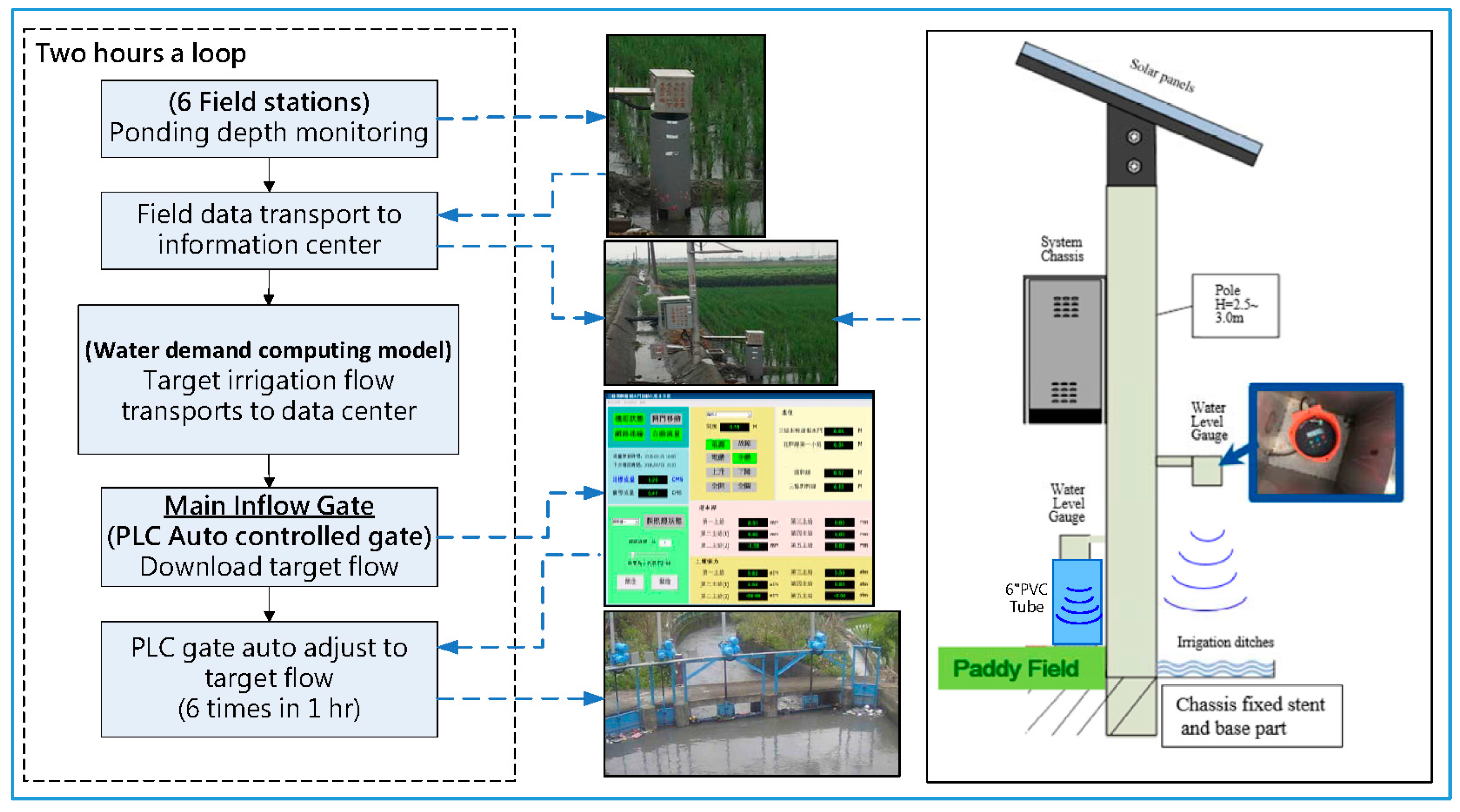
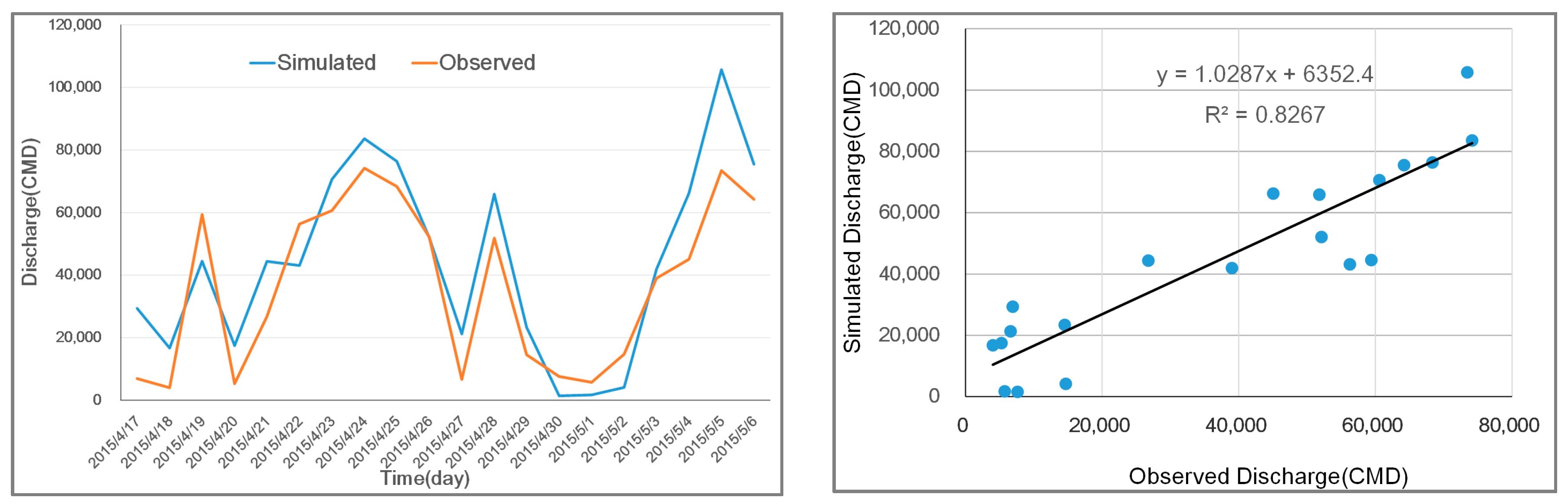
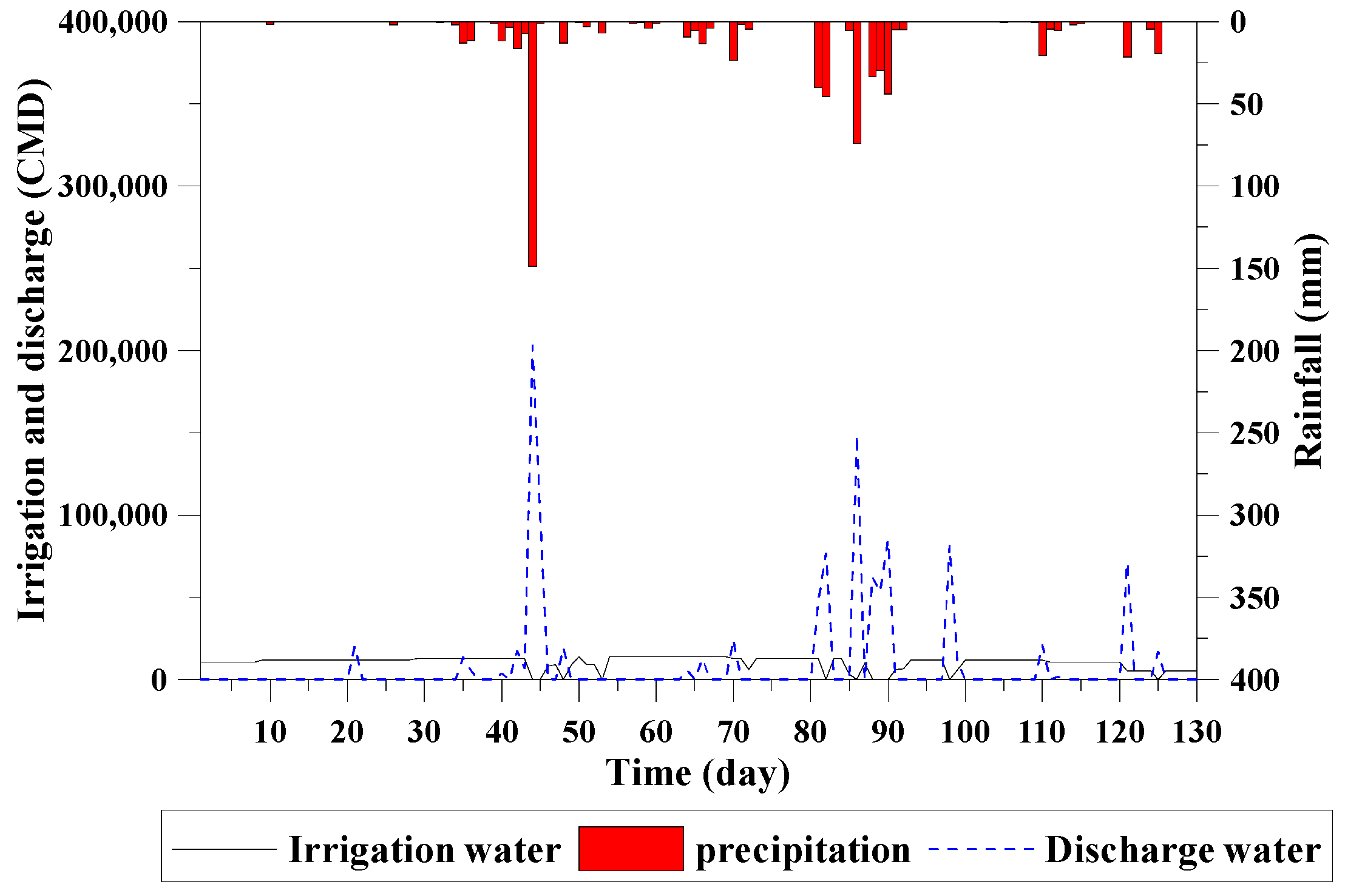
3.3. Model Verification
4. Results and Discussion
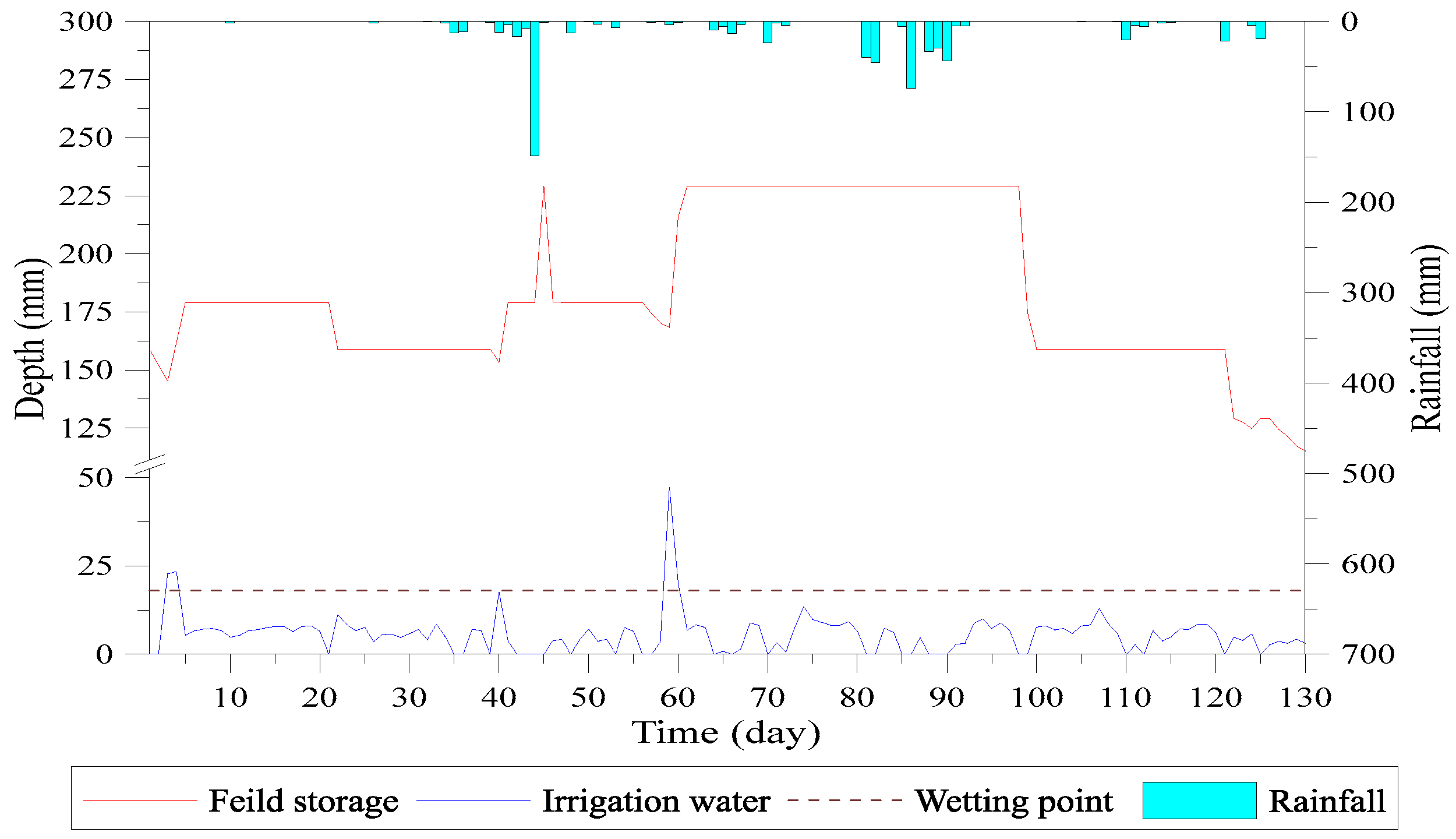
4.1. Scenario 1: 30% Reduction of Planned Irrigation Water
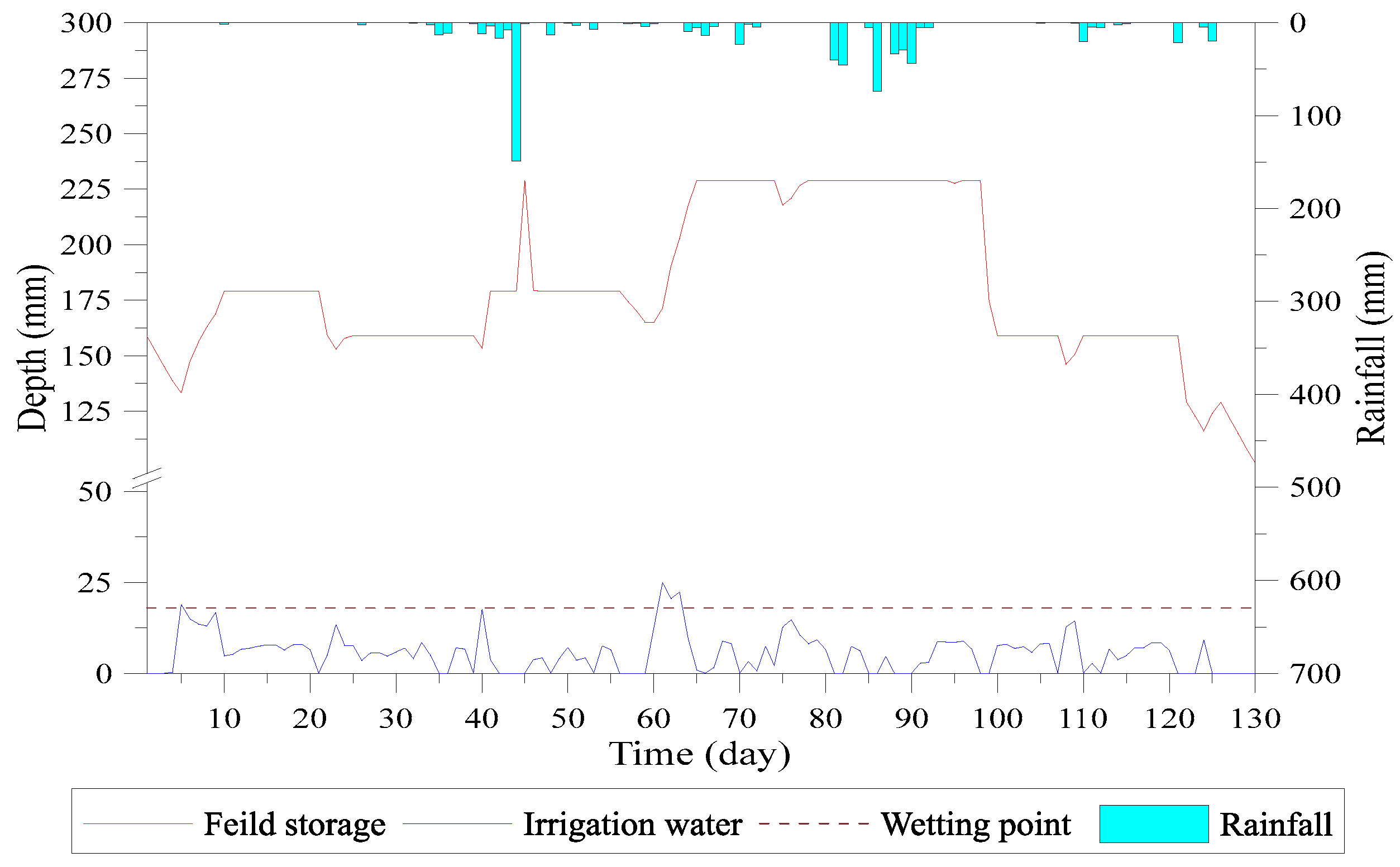
4.2. Scenario 2: 50% Discount of Planned Irrigation Water
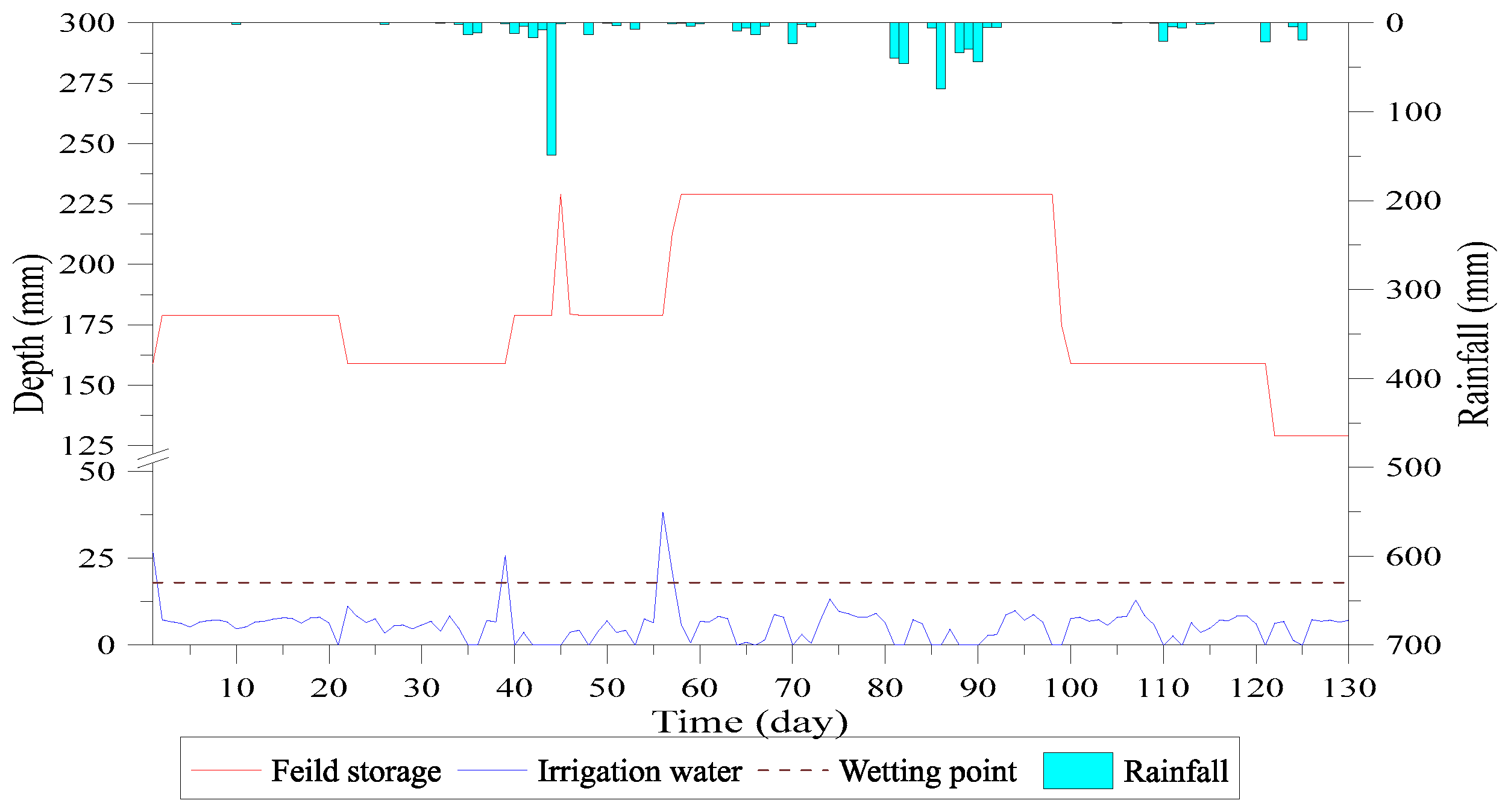
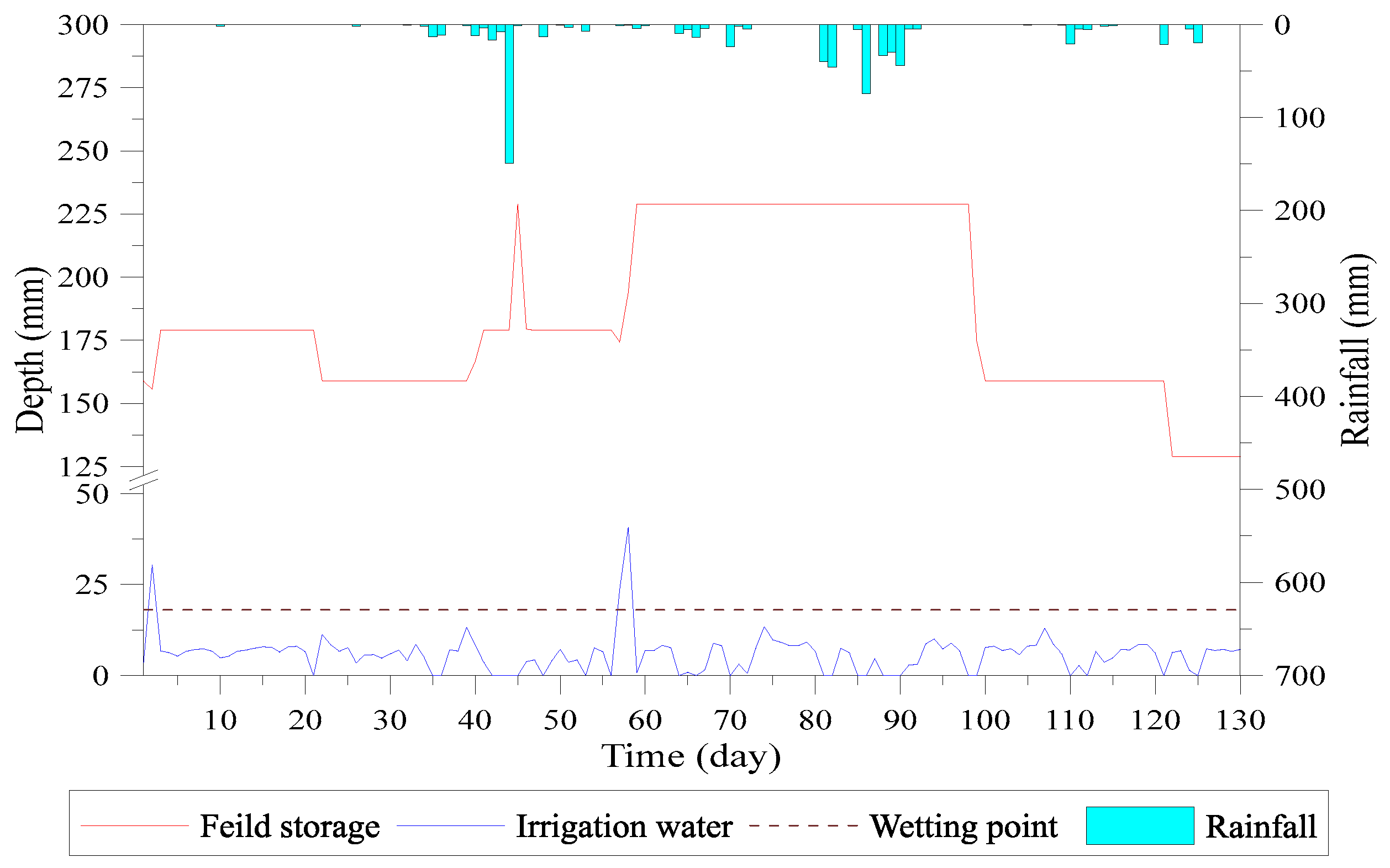
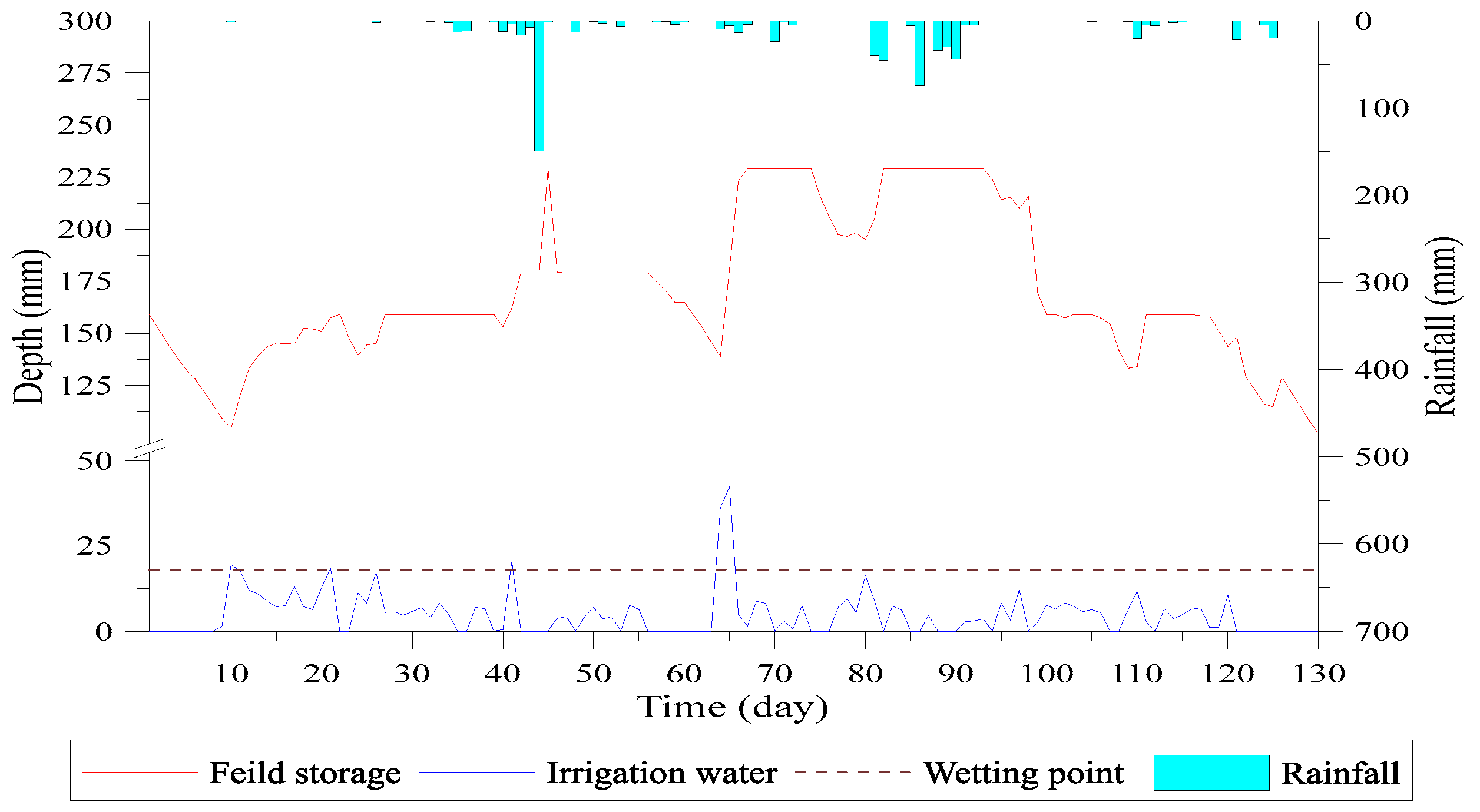
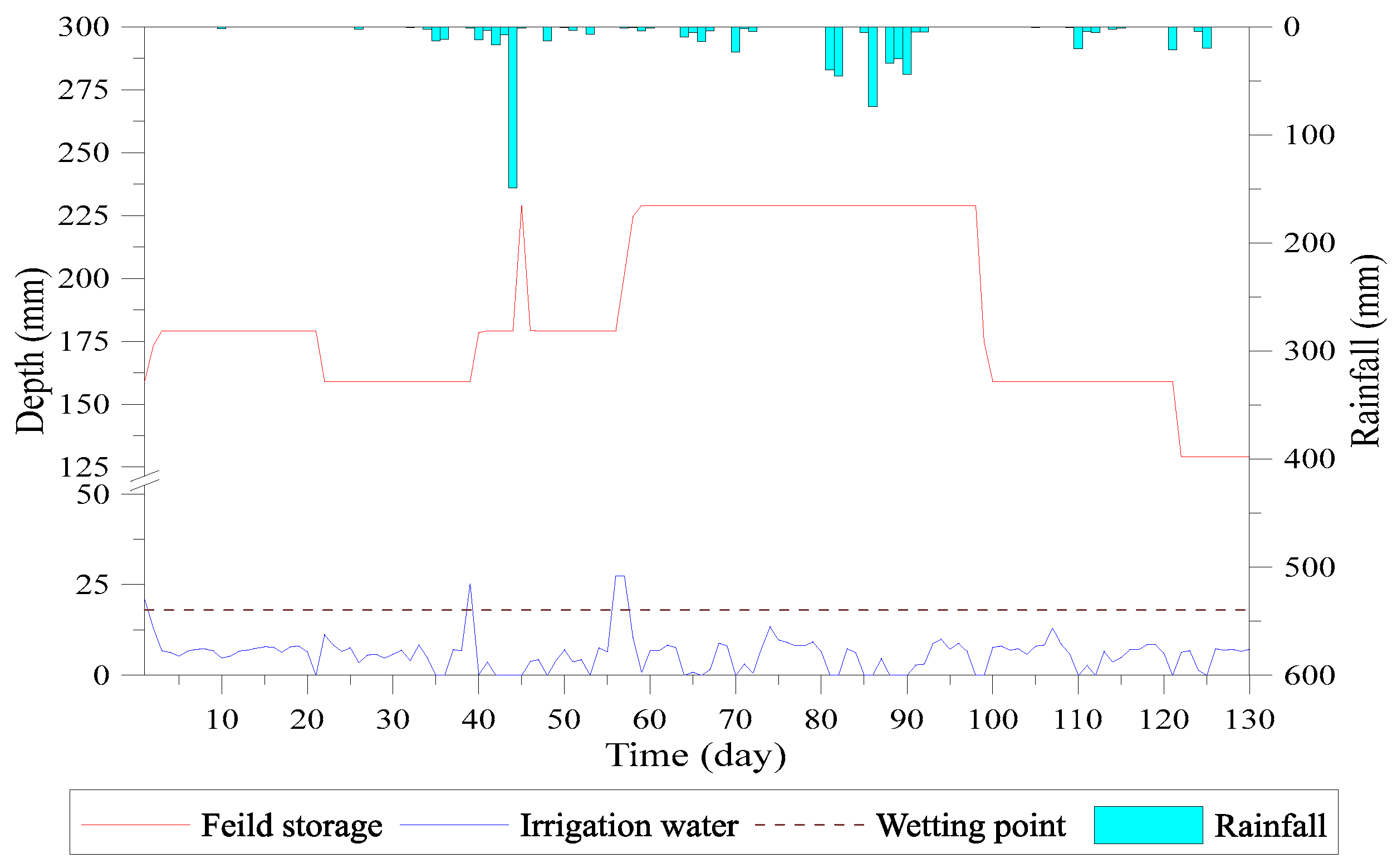
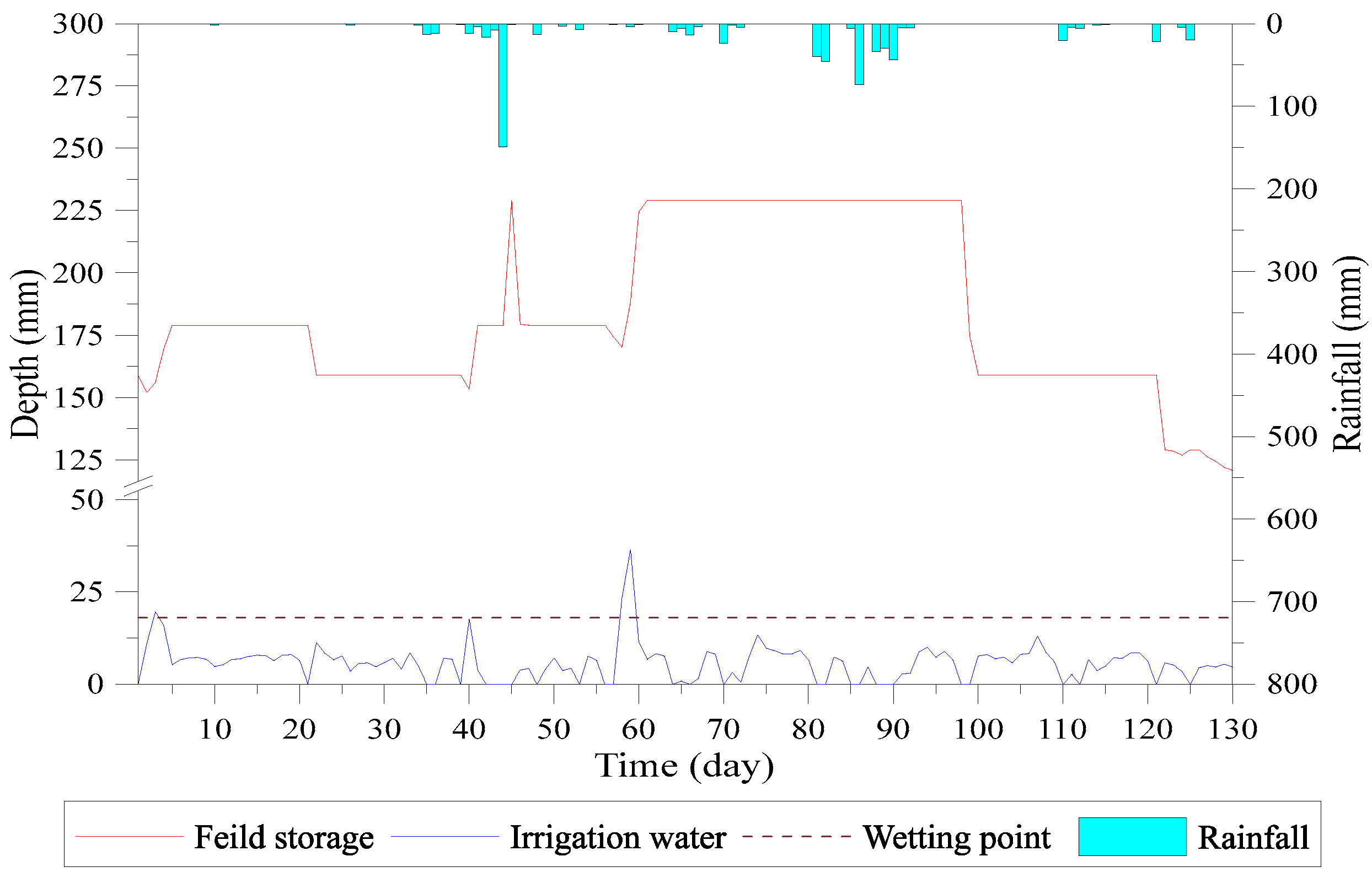
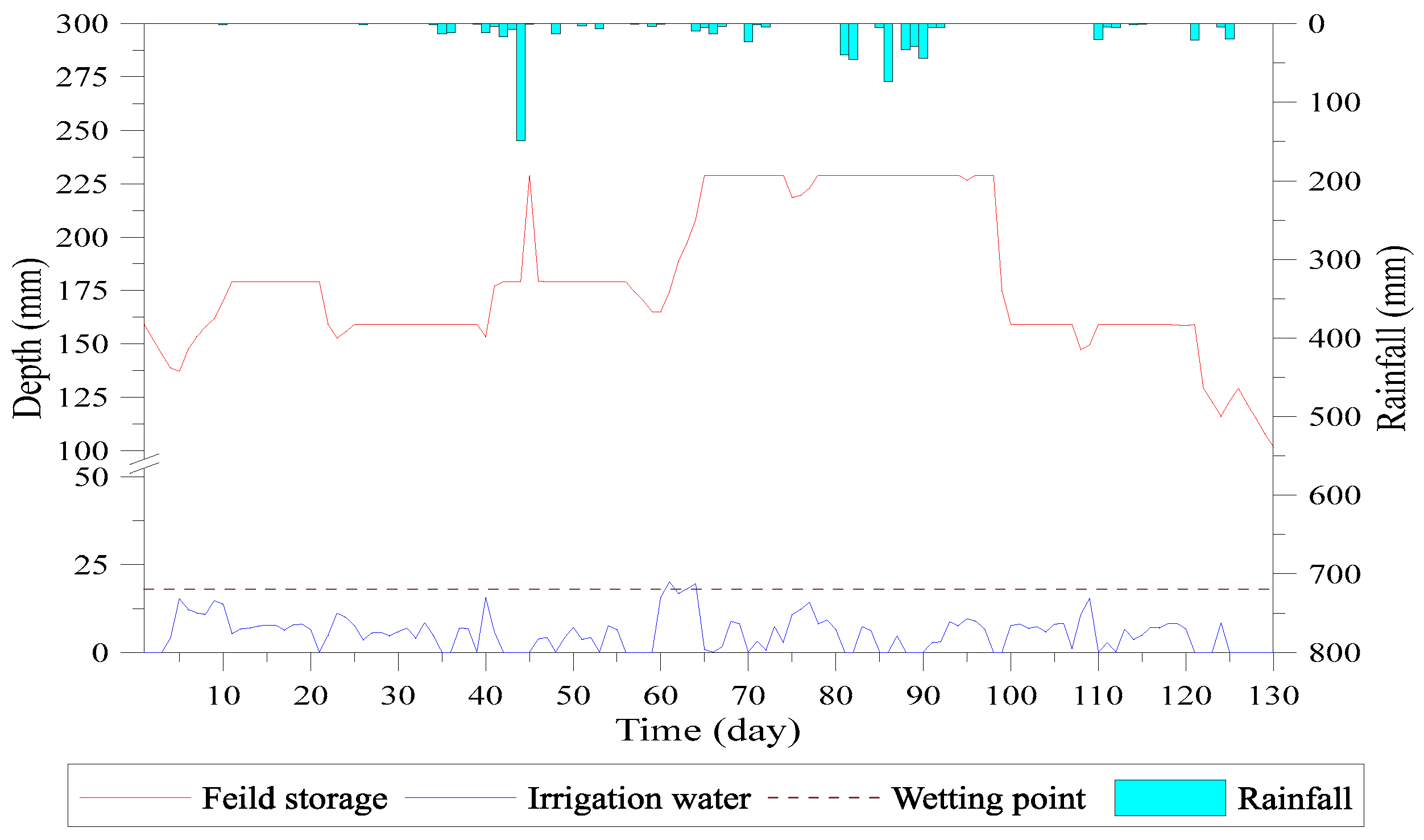
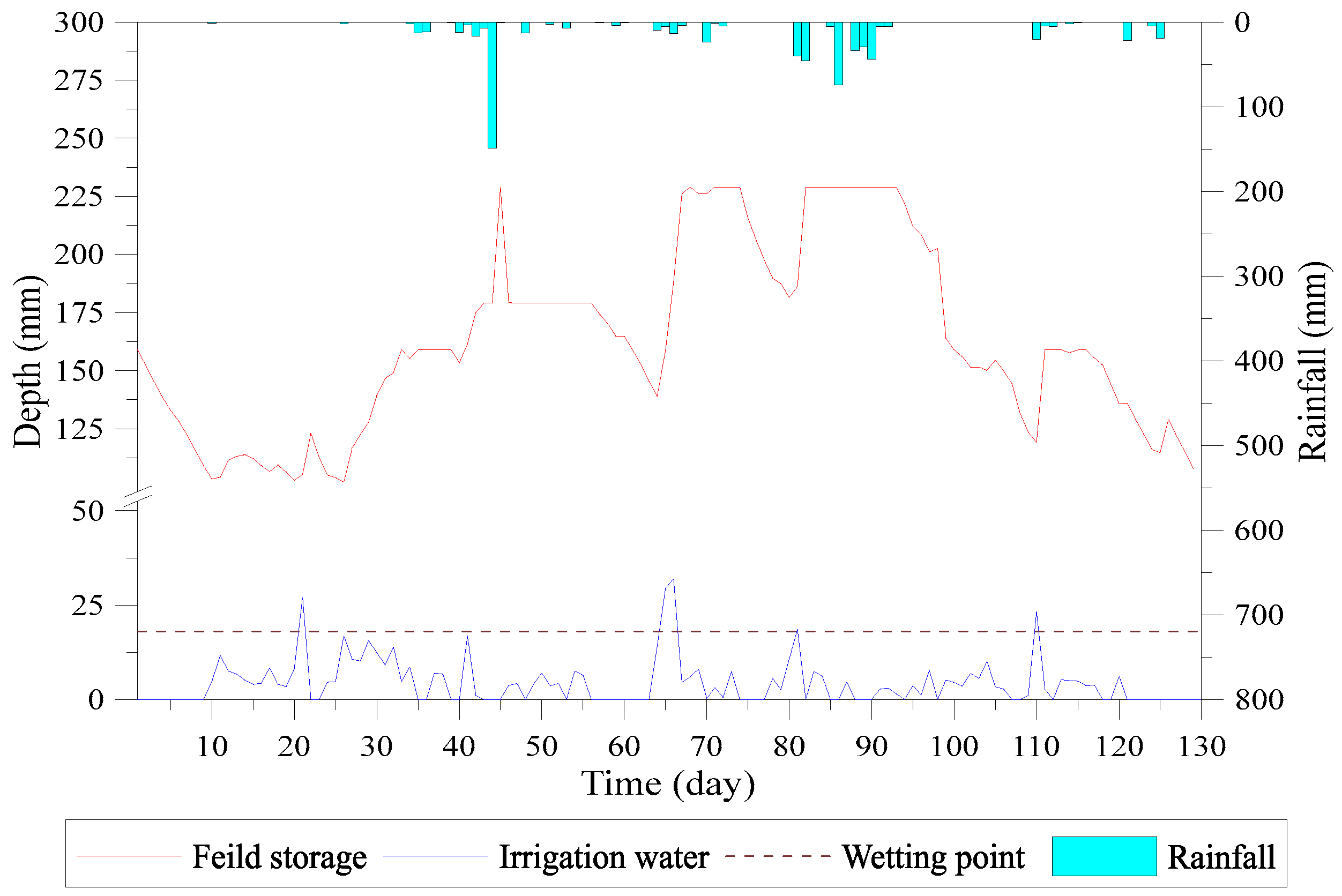
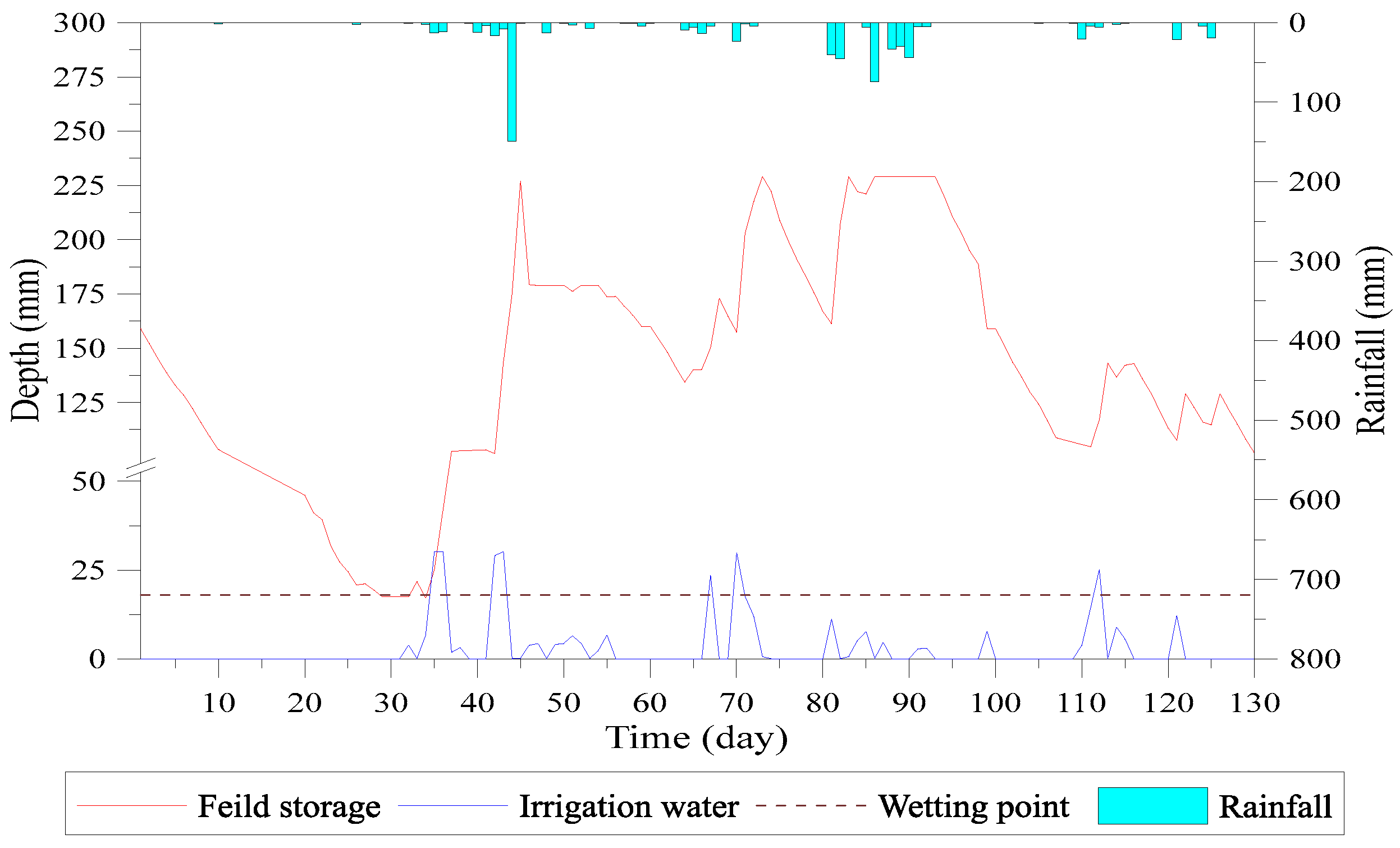
- The target ponding depth is 5 cm for the 1st day to 20th day cropping period. Blocks 1–3 reach this depth within 11 days, while block 4 reaches the target depth on the 34th day. The irrigation started in a sequence from upstream to downstream and reduces the issue of lack of water. The upstream fields receive the targeted depth irrigation and then transfer the water to downstream fields. The simulation results of targeted water depth of blocks 1–4 are shown in Figure 21, Figure 22, Figure 23 and Figure 24.
- The water depth of block 5 dropped below the saturated soil moisture curve on the 6th day due to lack of water. On the 21st day, the field storage turns lower than field capacity and the vertical percolation stopped. Up to the 29th day, the decrease in field storage continued and reached to the wilting point, also stopping the evapotranspiration, as shown in Figure 25.
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- National Science Council. Climate Change in Taiwan: Scientific Report 2011; Taiwan Climate Change Projection and Information Platform Project; National Science Council: Taipei, Taiwan, 2011. Available online: https://tccip.ncdr.nat.gov.tw/v2/upload/book/20150410100030.pdf (accessed on 1 November 2017).
- Wilhite, D.A.; Glantz, M.H. Understanding: The drought phenomenon: The role of definitions. Water Int. 1985, 10, 111–120. [Google Scholar] [CrossRef]
- Niu, F.X.; Hua, X.X.; Guo, X.D. Studies on several physiological indexes of drought resistance of sweet potato and its comprehensive evaluation. Acta Agron. Sin. 1996, 22, 392–398. [Google Scholar]
- Shao, H.B.; Liang, Z.S.; Shao, M.A.; Wang, B.C. Impacts of PEG-6000 pretreatment for barely (Hordeum vulgare L.) seeds on the effect of their mature embryo in vitro culture and primary investigation on its physiological mechanism. Colloids Surf. B Biointerfaces 2005, 41, 73–77. [Google Scholar]
- Morison, J.I.; Baker, N.R.; Mullineaux, P.M.; Davies, W.J. Improving water use in crop production. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2008, 12, 639–658. [Google Scholar] [CrossRef] [PubMed]
- Passioura, J. Increasing the crop productivity when water is scarce—From breeding to field management. Agric. Water Manag. 2006, 80, 176–196. [Google Scholar] [CrossRef]
- Viets, F.G. Fertilizers and the efficient use of water. Adv. Agron. 1962, 14, 233–264. [Google Scholar]
- Yeh, W.W.G. Reservoir management and operations models—A state-of-the-art review. Water Resour. Res. 1985, 21, 1797–1818. [Google Scholar] [CrossRef]
- Ventana Systems, Inc. Vensim PLE Software. 2006. Available online: http://vensim.com/ (accessed on 30 May 2008).
- Sathish, K.R.; Raghavendra, L. Smart System in Irrigation Field. Int. J. Comput. Appl. 2015, 2, 19–21. [Google Scholar]
- Forrester, J.W. Industrial Dynamics; MIT Press: Cambridge, MA, USA, 1961. [Google Scholar]
- Sehlke, G.; Jacobson, J. System dynamics modeling of transboundary systems: The Bear River basin model. Ground Water 2005, 43, 722–730. [Google Scholar] [CrossRef] [PubMed]
- Winz, I.; Brierley, G.; Trowsdale, S. The use of system dynamics simulation in water resources management. Water Resour. Manag. 2009, 23, 1301–1323. [Google Scholar] [CrossRef]
- Tidwell, V.C.; Passell, H.D.; Conrad, S.H.; Thomas, R.P. System dynamics modeling for community based water planning: Application to the middle Rio Grande. Aquat. Sci. 2004, 66, 357–372. [Google Scholar] [CrossRef]
- Simonovic, S.P.; Fahmy, H. A new modeling approach for water resources policy analysis. Water Resour. Res. 1999, 35, 295–304. [Google Scholar] [CrossRef]
- Xu, Z.X.; Takeuchi, K.; Ishidaira, H.; Zhang, X.W. Sustainability analysis for yellow river water resources using the system dynamics approach. Water Resour. Manag. 2002, 16, 239–261. [Google Scholar] [CrossRef]
- Guo, H.C.; Liu, L.; Huang, G.H.; Fuller, G.A.; Zou, R.; Yin, Y.Y.A. System dynamics approach for regional environmental planning and management: A study for the Lake Erhai Basin. J. Environ. Manag. 2001, 61, 93–111. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, S.; Simonovic, S. An intelligent decision support system for management of floods. Water Resour. Manag. 2006, 20, 391–410. [Google Scholar] [CrossRef]
- Khan, S.; Luo, Y.F.; Ahmad, A. Analysing complex behaviour of hydrological systems through a system dynamics approach. Environ. Model. Softw. 2009, 24, 1363–1372. [Google Scholar] [CrossRef]
- Graham, M.; Turner, G.M.; Baynes, T.M.; McInnis, B.C. A water accounting system for strategic water management. Water Resour. Manag. 2009, 24, 513–545. [Google Scholar]
- Jesús, R.; Gastélum, J.R.; Valdés, J.B.; Stewart, S. A decision support system to improve water resources management in the Conchos basin. Water Resour. Manag. 2009, 23, 1519–1548. [Google Scholar]
- Wu, R.-S.; Liu, J.S.; Chang, J.S. Modeling Irrigation System for Water Management of a Companion and Inter Cropping Field in Central Taiwan. In Proceedings of the 2nd World Irrigation Forum, Chiang Mai, Thailand, 6–8 November 2016. [Google Scholar]
- Elmahdi, A.; Malano, H.; Etchells, T. System Dynamics Optimization Approach to Irrigation Demand Management; From the Selected Works of Amgad Elmahdi; Department of Civil and Environment Engineering, The University of Melbourne: Parkville, Australia, 2005. [Google Scholar]
- Luo, Y.; Khan, S.; Cui, Y. Application of system dynamics approach for time varying water balance in aerobic paddy fields. Paddy Water Environ. 2009, 7, 1–9. [Google Scholar] [CrossRef]
- Miller, G.R.; Cable, J.M.; McDonald, A.K.; Bond, B.; Franz, T.E.; Wang, L.X.; Gou, S.; Tyler, A.P.; Zou, C.B.; Scott, R.L. Understanding ecohydrological connectivity in savannas: A system dynamics modelling approach. Ecohydrology 2012, 5, 200–220. [Google Scholar] [CrossRef]
- Yang, C.C.; Chang, L.C.; Ho, C.C. Application of system dynamics with impact analysis to solve the problem of water shortages in Taiwan. Water Resour. Manag. 2008, 22, 1561–1577. [Google Scholar] [CrossRef]
- Ali, M.H. Field Water Balance. In Fundamentals of Irrigation and On-farm Water Management; Springer: New York, NY, USA, 2010. [Google Scholar]
- Panigrahi, B.; Panda, S.N.; Mull, R. Simulation of water harvesting potential in rainfed rice lands using water balance model. Agric. Water Manag. 2001, 69, 165–182. [Google Scholar]
- Odhiambo, L.O.; Murty, V.V.N. Modeling water balance components in relation to field layout in lowland paddy fields. II: Model application. Agric. Water Manag. 1996, 30, 201–216. [Google Scholar] [CrossRef]
- Brown, K.W.; Turner, F.T.; Thomas, J.C.; Deuel, L.E.; Keener, M.E. Water balance of flooded rice paddies. Agric. Water Manag. 1978, 1, 277–291. [Google Scholar] [CrossRef]
- Agrawal, M.K.; Panda, S.N.; Panigrahi, B. Modeling water balance parameters for rainfed rice. J. Irrig. Drain. Eng. 2004, 130, 129–139. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration: Guidelines for Computing Crop Water Requirements; FAO Irrigation and Drainage Paper 56; Food and Agriculture Organization (FAO): Rome, Italy, 1998; p. D05109. [Google Scholar]
- Yao, M.H.; Chen, S.H. Measurement of Evapotranspiration and Crop Parameters in Paddy Field by Eddy Correlation. In Proceedings of the Conference on Paddy Farming Multi-Functionality, Tai-Chung, Taiwan, 25 May 2005; pp. 227–240. (In Chinese). [Google Scholar]
- Smith, M.; Allen, R.; Monteith, J.L.; Perrier, A.; Santos Pereira, L.; Segeren, A. Expert Consultation on Revision of FAO Methodologies for Crop Water Requirements; Land and Water Development Division: Rome, Italy, 1992. [Google Scholar]
- Chen, S.K.; Chen, W.L. Analysis of water movement in paddy rice fields (I) experimental studies. J. Hydrol. 2002, 260, 206–215. [Google Scholar] [CrossRef]
- Sharma, P.K.; De Datta, S.K. Effects of Puddling on Soil Physical Properties and Processes. In Soil Physics and Rice; International Rice Research Institute (IRRI): Laguna, Philippines, 1985; pp. 217–234. [Google Scholar]
- Bhadra, A.; Bandyopadhyay, A.; Singh, R. Development of a user friendly water balance model for paddy. Paddy Water Environ. 2013, 11, 331–441. [Google Scholar] [CrossRef]
- Khepar, S.D.; Yadav, A.K.; Sondhi, S.K.; Siag, M. Water balance model for paddy fields under intermittent irrigation practices. Irrig. Sci. 2000, 19, 199–208. [Google Scholar] [CrossRef]
- Huang, H.C.; Liu, C.W.; Chen, S.K.; Chen, J.S. Analysis of percolation and seepage through paddy bunds. J. Hydrol. 2003, 284, 13–25. [Google Scholar] [CrossRef]
- Bouman, B.A.M.; Wopereis, M.C.S.; Kropff, M.J.; ten Berge, H.F.M.; Tuong, T.P. Water use efficiency of flooded rice fields. (II) Percolation and seepage losses. Agric. Water Manag. 1994, 26, 291–304. [Google Scholar] [CrossRef]
- Tuong, T.P.; Wopereis, M.C.S.; Marquez, J.A.; Kropff, M.J. Mechanisms and control of percolation losses in irrigated puddle rice fields. Soil Sci. Soc. Am. J. 1994, 58, 1794–1803. [Google Scholar] [CrossRef]
- Walker, S.H.; Rushton, K.R. Verification of lateral percolation losses from irrigated rice fields by a numerical model. J. Hydrol. 1984, 71, 335–351. [Google Scholar] [CrossRef]
- Wickham, T.H.; Singh, V.P. Water movement through wet soils. In Soils and Rice; International Rice Research Institute: Los Banos, PA, USA, 1978. [Google Scholar]
- Chen, R.S.; Pi, L.C.; Huang, Y.H. Analysis of rainfall-runoff relation in paddy fields by diffusive tank model. Hydrol. Process. 2003, 17, 2541–2553. [Google Scholar] [CrossRef]
- Wu, R.-S.; Sue, W.-R.; Chien, C.-B.; Chen, C.-H.; Chang, J.-S.; Liu, K.-M. Simulation Model for Investigating the Effects of Rice Paddy Fields on the Runoff System. Math. Comput. Model. 2001, 33, 649–658. [Google Scholar] [CrossRef]
| Growth Days | Growth Stage | Growth Degree | Crop Season | |
|---|---|---|---|---|
| 1st Crop | 2nd Crop | |||
| — | Ground | — | — | — |
| 1~15 | Seedling | 185 | 0.92 | 1.01 |
| 16~30 | Early tillering | 381 | 1.00 | 1.11 |
| 31~45 | End of tillering | 589 | 1.00 | 1.11 |
| 46~60 | Early flowering | 808 | 1.13 | 1.23 |
| 61~75 | End of flowering | 1032 | 1.13 | 1.23 |
| 76~90 | Early ripening | 1259 | 0.89 | 0.93 |
| 91~105 | Middle of ripening | 1487 | 0.89 | 0.93 |
| 106~120 | End of ripening | 1715 | 0.89 | 0.93 |
| Conveyance Loss (%) | Block 1 | Block 2 | Block 3 | Block 4 | Block 5 | |
|---|---|---|---|---|---|---|
| Sub-Block | ||||||
| No. 1 | 8.15 | 13.15 | 20.23 | 21.16 | 28.5 | |
| No. 2 | 8.15 | 13.15 | 20.23 | 24.93 | 28.5 | |
| No. 3 | 10.45 | 11.9 | 22.01 | 24.93 | 29.33 | |
| No. 4 | 10.45 | 11.9 | 22.01 | 33.33 | 29.33 | |
| No. 5 | 11.71 | 19.08 | 22.85 | — | 30.38 | |
| No. 6 | 11.71 | 19.08 | — | — | 30.38 | |
| No. 7 | 12.74 | 21 | — | — | — | |
| No. 8 | 12.74 | 21 | — | — | — | |
| Growth Stages | Seedling | Start of Tillering | End of Tillering | Young Panicle Differentiation | Young Panicle Formation | Booting Stage | Heading | Milk Ripe | Mature | Reaping | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| The day after transplanting | 1 | 16 | 25 | 30 | 48 | 50 | 65 | 77 | 92 | 107 | 120 | 130 |
| Date | 3/4 | 3/19 | 3/28 | 4/2 | 4/20 | 4/22 | 5/7 | 5/19 | 6/3 | 6/18 | 7/1 | 7/11 |
| Ponding depth (cm) | 5 | 5 | 5 | 5 | 5 | 5 | 10 | 10 | 10 | 3 | 3 | 0 |
| Symbol | Variable Definition | Component Description | Remark |
|---|---|---|---|
 | Storage in the system | Storage | Initial value |
| Components | |||
 | Flow rate or storage rate | Flow Rate | Figures, tables, functions or logics are acceptable |
| Components | |||
 | The assistant variables between storage and flow | Auxiliary | |
 | The connection of information and function in the system | Assistant | Connection |
| Components | |||
 | The system boundary | — | — |
| Block | 30% Discount of Planned Irrigation Water | Total Irrigated Water | Rainfall | Infiltration | Discharge | Crop Evapotranspiration | ||
|---|---|---|---|---|---|---|---|---|
| 1 | 1003.2 | 762.1 | 675 | 537.2 | 858.8 | 336.3 | 1.272 | 1.127 |
| 2 | 756.6 | 675 | 535.9 | 336.3 | 1.135 | |||
| 3 | 732.7 | 675 | 533.5 | 336.3 | 1.172 | |||
| 4 | 704.5 | 675 | 528.4 | 336.3 | 1.219 | |||
| 5 | 624.7 | 675 | 513.4 | 336.3 | 1.374 |
| Block | 50% Discount of Planned Irrigation Water | Total Irrigated Water | Rainfall | Infiltration | Discharge | Crop Evapotranspiration | ||
|---|---|---|---|---|---|---|---|---|
| 1 | 716.6 | 761.5 | 675 | 537.3 | 516.0 | 336.3 | 0.764 | 0.678 |
| 2 | 740.7 | 675 | 534.7 | 336.3 | 0.697 | |||
| 3 | 703.7 | 675 | 528.3 | 336.3 | 0.733 | |||
| 4 | 558.0 | 675 | 498.4 | 336.3 | 0.925 | |||
| 5 | 366.6 | 675 | 420.4 | 325.5 | 1.408 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, R.-S.; Liu, J.-S.; Chang, S.-Y.; Hussain, F. Modeling of Mixed Crop Field Water Demand and a Smart Irrigation System. Water 2017, 9, 885. https://doi.org/10.3390/w9110885
Wu R-S, Liu J-S, Chang S-Y, Hussain F. Modeling of Mixed Crop Field Water Demand and a Smart Irrigation System. Water. 2017; 9(11):885. https://doi.org/10.3390/w9110885
Chicago/Turabian StyleWu, Ray-Shyan, Jih-Shun Liu, Sheng-Yu Chang, and Fiaz Hussain. 2017. "Modeling of Mixed Crop Field Water Demand and a Smart Irrigation System" Water 9, no. 11: 885. https://doi.org/10.3390/w9110885
APA StyleWu, R.-S., Liu, J.-S., Chang, S.-Y., & Hussain, F. (2017). Modeling of Mixed Crop Field Water Demand and a Smart Irrigation System. Water, 9(11), 885. https://doi.org/10.3390/w9110885







