Evaluation of Maximum a Posteriori Estimation as Data Assimilation Method for Forecasting Infiltration-Inflow Affected Urban Runoff with Radar Rainfall Input
Abstract
:1. Introduction
2. Theory and Methods
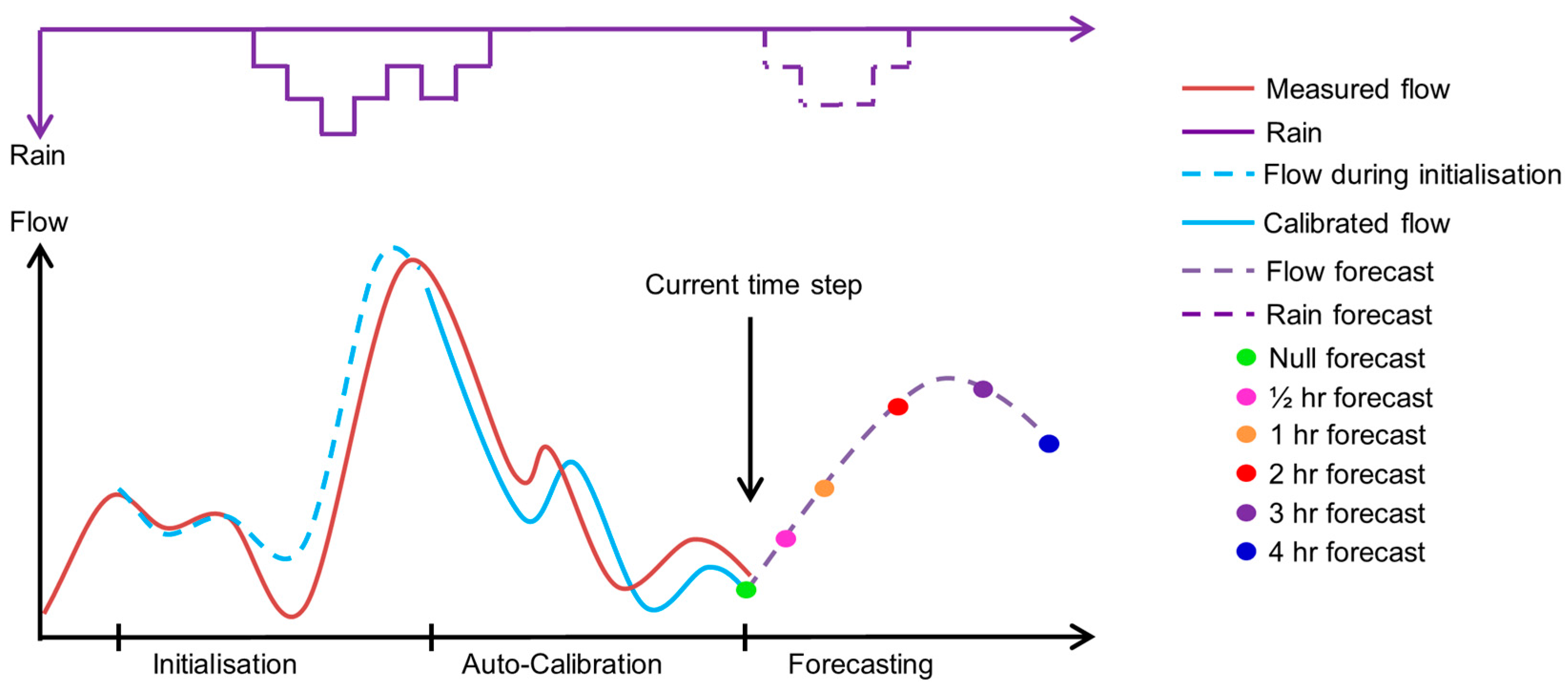
2.1. Online Flow Forecasting Workflow
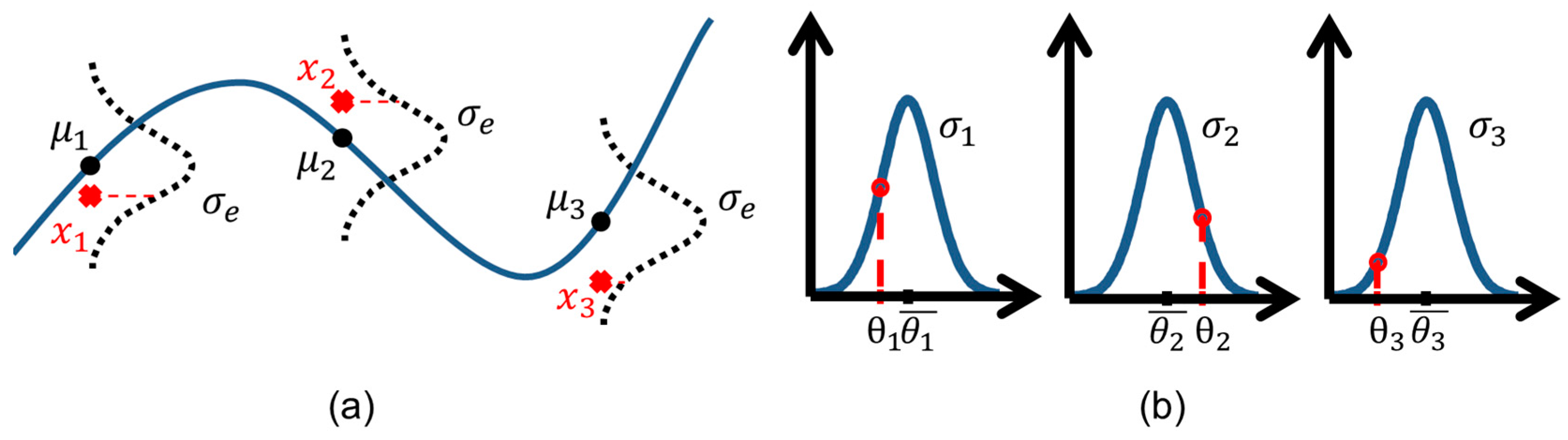
2.2. Data Assimilation with Auto-Calibration of Parameters
2.3. Modelling Tool and Implementation of MAP
2.4. Modelling Approach
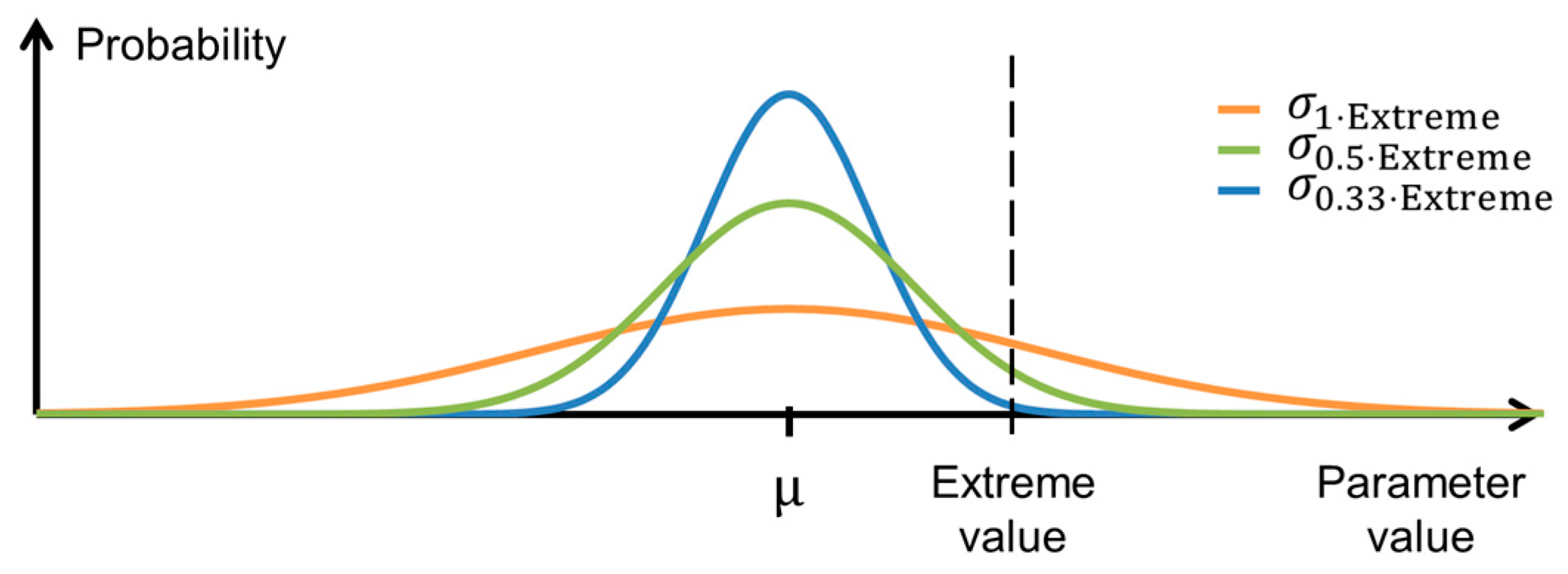
2.5. Setup of the MAP Auto-Calibration
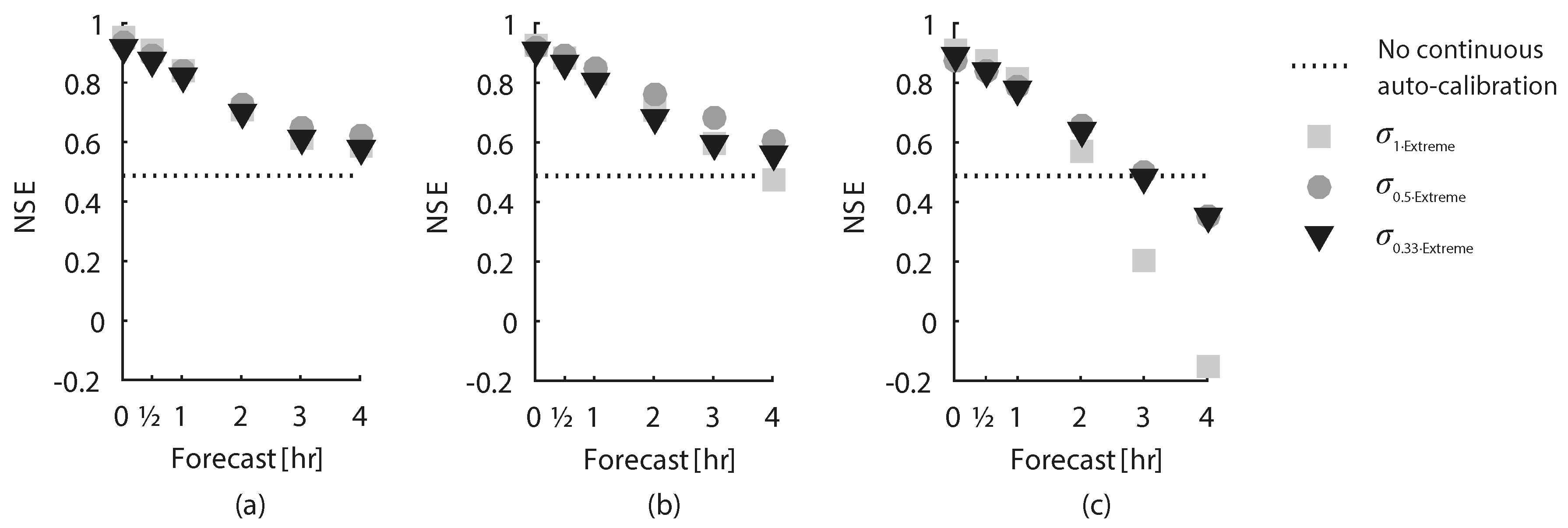
2.6. Evaluation of Forecasting Performance
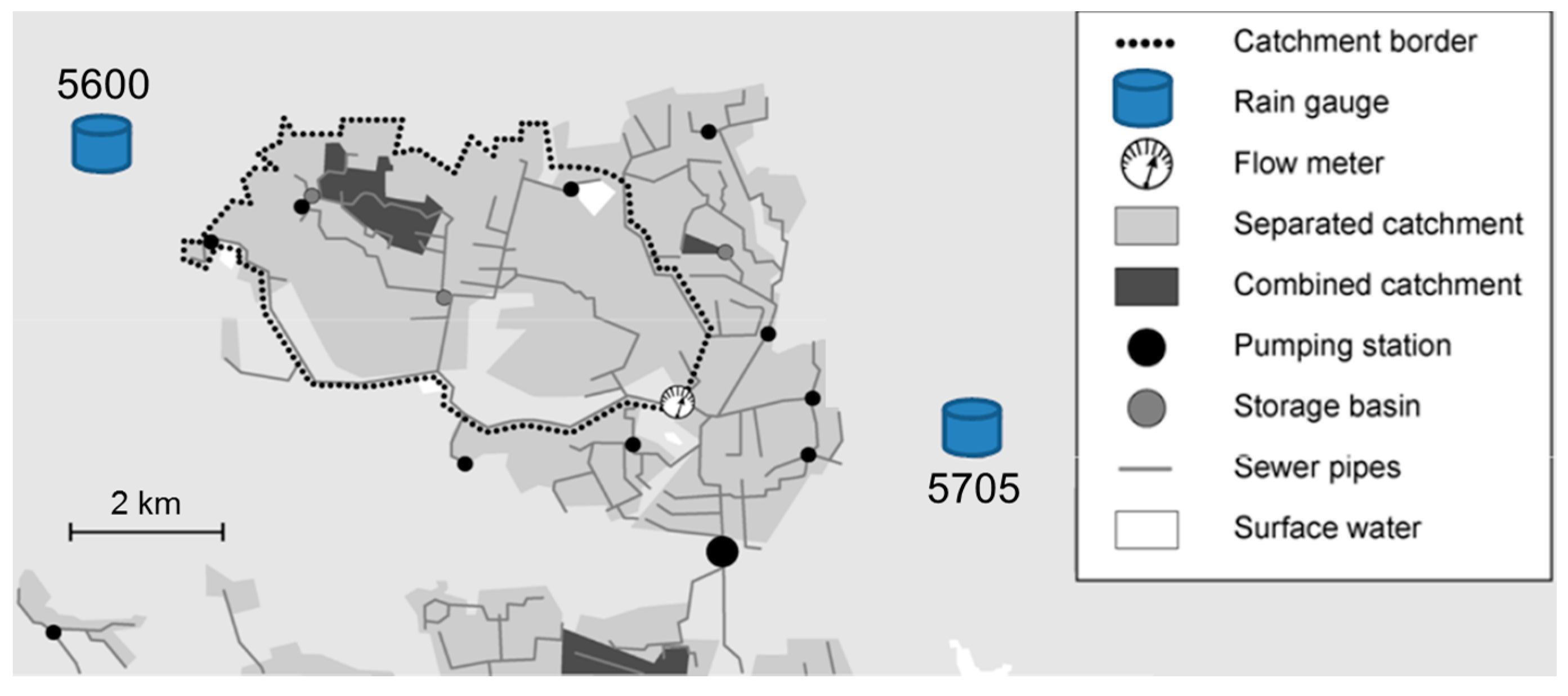
3. Case Study
4. Results and Discussion
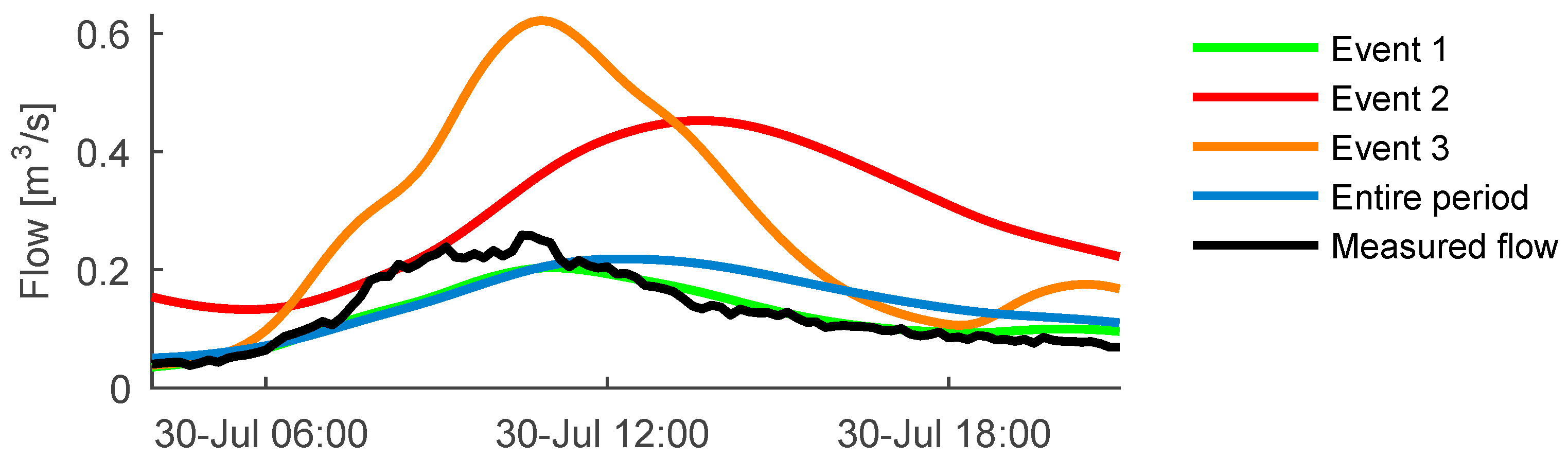
4.1. Prior Parameter Distributions, DWF Equation and Choice of Auto-Calibration Periods
4.2. Effects of Applying Different -Scenarios and Different Lengths of Auto-Calibration Period
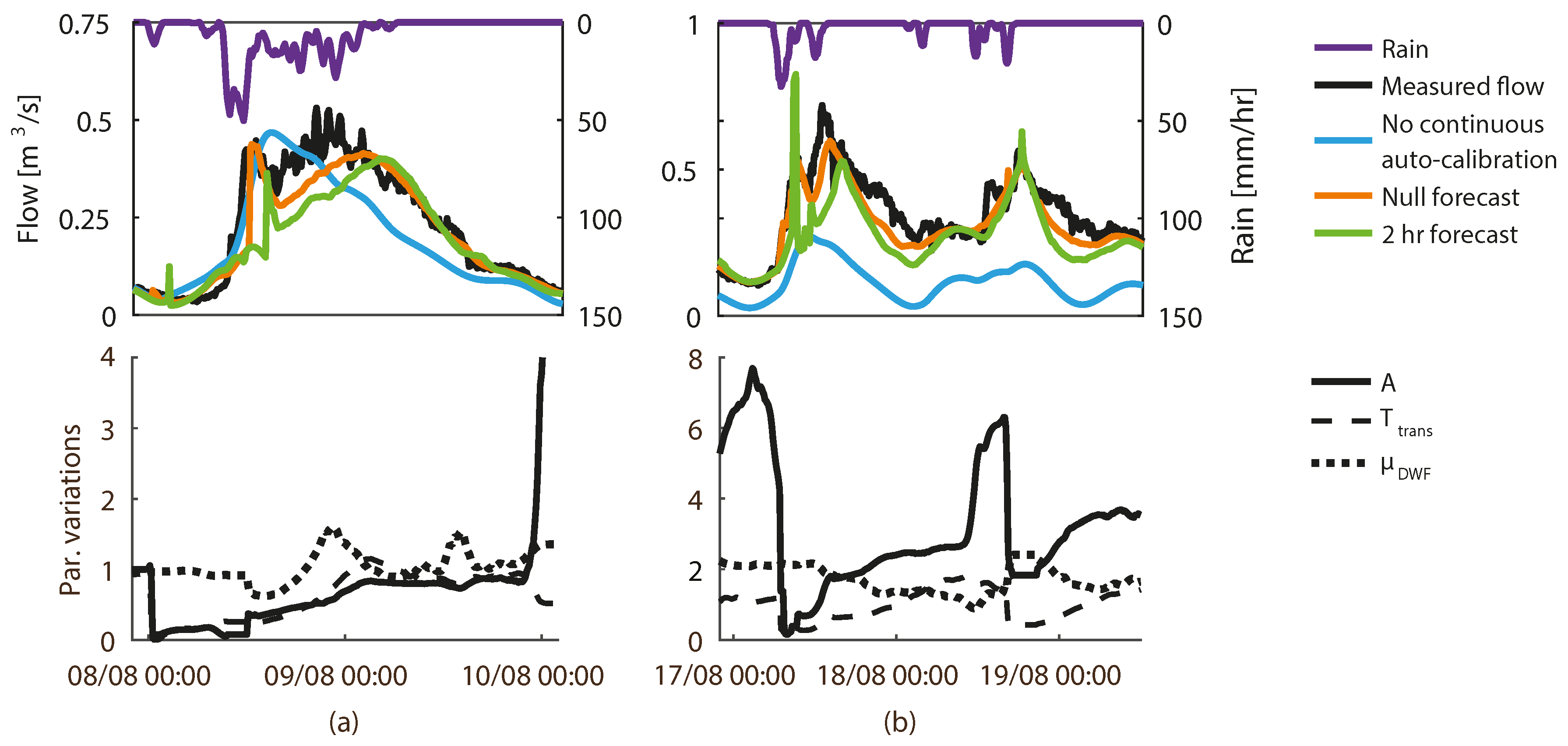
4.3. Visual Representation of Forecast Abilities and Parameter Variations
4.4. Benefits and Challenges When Using MAP for Auto-Calibration
4.5. Guidance for Practical Implementation
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Grum, M.; Thornberg, D.; Christensen, M.L.; Shididi, S.A.; Thirsing, C. Full-scale real time control demonstration project in Copenhagen’s largest urban drainage catchments. In Proceedings of the 12th International Conference on Urban Drainage, Porto Alegre, Brazil, 11–16 September 2011.
- Fradet, O.; Pleau, M.; Marcoux, C. Reducing CSOs and giving the river back to the public: Innovative combined sewer overflow control and riverbanks restoration of the St. Charles River in Quebec City. Water Sci. Technol. 2011, 63, 331–338. [Google Scholar] [CrossRef] [PubMed]
- Pabst, M.; Alex, J.; Beier, M.; Niclas, C.; Ogurek, M.; Peikert, D.; Schütze, M. ADESBA—A new general global control system applied to the Hildesheim sewage system. In Proceedings of the 12th International Conference on Urban Drainage, Porto Alegre, Brazil, 11–16 September 2011.
- Puig, V.; Cembrano, G.; Romera, J.; Quevedo, J.; Aznar, B.; Ramón, G.; Cabot, J. Predictive optimal control of sewer networks using CORAL tool: Application to Riera Blanca catchment in Barcelona. Water Sci. Technol. 2009, 60, 869–878. [Google Scholar] [CrossRef] [PubMed]
- Seggelke, K.; Löwe, R.; Beeneken, T.; Fuchs, L. Implementation of an integrated real-time control system of sewer system and waste water treatment plant in the city of Wilhelmshaven. Urban Water J. 2013, 10, 330–341. [Google Scholar] [CrossRef]
- Harremoës, P.; Madsen, H. Fiction and reality in the modelling world-Balance between simplicity and complexity, calibration and identifiability, verification and falsification. Water Sci. Technol. 1999, 39, 1–8. [Google Scholar] [CrossRef]
- Schilling, W.; Fuchs, L. Errors in stormwater modeling—A quantitative assessment. J. Hydraul. Eng. 1986, 112, 111–123. [Google Scholar] [CrossRef]
- Schellart, A.N.A.; Liguori, S.; Krämer, S.; Saul, A.J.; Rico-Ramirez, M.A. Comparing quantitative precipitation forecast methods for prediction of sewer flows in a small urban area. Hydrol. Sci. J. 2014, 59, 1418–1436. [Google Scholar] [CrossRef]
- Liguori, S.; Rico-Ramirez, M.A.; Schellart, A.N.A.; Saul, A.J. Using probabilistic radar rainfall nowcasts and NWP forecasts for flow prediction in urban catchments. Atmos. Res. 2012, 103, 80–95. [Google Scholar] [CrossRef]
- Rico-Ramirez, M.A.; Liguori, S.; Schellart, A.N.A. Quantifying radar rainfall uncertainties in urban drainage flow modelling. J. Hydrol. 2015, 528, 17–28. [Google Scholar] [CrossRef]
- Hutton, C.J.; Vamvakeridou-Lyroudia, L.S.; Kapelan, Z.; Savic, D.A. Real-Time Modelling and Data Assimilation Techniques for Improving the Accuracy of Model Predictions: Scientific Report. Available online: https://emps.exeter.ac.uk/media/universityofexeter/emps/research/cws/downloads/PREPARED_Deliverable_3_6_2_Final.pdf (accessed on 30 August 2016).
- Hutton, C.J.; Kapelan, Z.; Vamvakeridou-Lyroudia, L.S.; Savic, D.A. Real-time data assimilation in urban rainfall-runoff models. Procedia Eng. 2014, 70, 843–852. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Weerts, A.; Clark, M.P.; Hendricks Franssen, H.J.; Kumar, S.; Moradkhani, H.; Seo, D.J.; Schwanenberg, D.; Smith, P.J.; Van Dijk, A.I.J.M.; et al. Advancing data assimilation in operational hydrologic forecasting: Progresses, challenges, and emerging opportunities. Hydrol. Earth Syst. Sci. 2012, 16, 3863–3887. [Google Scholar] [CrossRef]
- Hansen, L.S.; Borup, M.; Møller, A.; Mikkelsen, P.S. Flow forecasting using deterministic updating of water levels in distributed hydrodynamic urban drainage models. Water 2014, 6, 2195–2211. [Google Scholar] [CrossRef] [Green Version]
- Ho, J.Y.; Lee, K.T. Grey forecast rainfall with flow updating algorithm for real-time flood forecasting. Water 2015, 7, 1840–1865. [Google Scholar] [CrossRef]
- Breinholt, A.; Møller, J.K.; Madsen, H.; Mikkelsen, P.S. A formal statistical approach to representing uncertainty in rainfall-runoff modelling with focus on residual analysis and probabilistic output evaluation—Distinguishing simulation and prediction. J. Hydrol. 2012, 472–473, 36–52. [Google Scholar] [CrossRef]
- Borup, M.; Grum, M.; Madsen, H.; Mikkelsen, P.S. A Partial Ensemble Kalman Filtering approach to enable use of range limited observations. Stoch. Environ. Res. Risk Assess. 2015, 29, 119–129. [Google Scholar] [CrossRef] [Green Version]
- Vrugt, J.A.; Gupta, H.V.; Nualláin, B.; Bouten, W. Real-Time Data Assimilation for Operational Ensemble Streamflow Forecasting. J. HydRometeorol. 2006, 7, 548–565. [Google Scholar] [CrossRef]
- Madsen, H.; Skotner, C. Adaptive state updating in real-time river flow forecasting—A combined filtering and error forecasting procedure. J. Hydrol. 2005, 308, 302–312. [Google Scholar] [CrossRef]
- Shamseldin, A.Y.; O’Connor, K.M. A non-linear neural network technique for updating of river flow forecasts. Hydrol. Earth Syst. Sci. 2001, 5, 577–598. [Google Scholar] [CrossRef]
- Moradkhani, H.; Sorooshian, S.; Gupta, H.V.; Houser, P.R. Dual state-parameter estimation of hydrological models using ensemble Kalman filter. Adv. Water Resour. 2005, 28, 135–147. [Google Scholar] [CrossRef]
- Dumedah, G.; Coulibaly, P. Evaluating forecasting performance for data assimilation methods: The ensemble Kalman filter, the particle filter, and the evolutionary-based assimilation. Adv. Water Resour. 2013, 60, 47–63. [Google Scholar] [CrossRef]
- Todini, E. Rainfall-Runoff Models for Real-Time Forecasting. In Encyclopedia of Hydrological Sciences; John Wiley & Sons, Inc.: New York, NY, USA, 2005; pp. 1869–1896. [Google Scholar]
- Kowalsky, M.B.; Finsterle, S.; Rubin, Y. Estimating flow parameter distributions using ground-penetrating radar and hydrological measurements during transient flow in the vadose zone. Adv. Water Resour. 2004, 27, 583–599. [Google Scholar] [CrossRef]
- Hsu, K.L.; Moradkhani, H.; Sorooshian, S. A sequential Bayesian approach for hydrologic model selection and prediction. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Thorndahl, S.; Poulsen, T.S.; Bøvith, T.; Borup, M.; Ahm, M.; Nielsen, J.E.; Grum, M.; Rasmussen, M.R.; Gill, R.; Mikkelsen, P.S. Comparison of short-term rainfall forecasts for model based flow prediction in urban drainage systems. Water Sci. Technol. 2013, 68, 472–478. [Google Scholar] [CrossRef] [PubMed]
- Thorndahl, S.; Rasmussen, M.R. Short-term forecasting of urban storm water runoff in real-time using extrapolated radar rainfall data. J. Hydroinform. 2013, 15, 897–912. [Google Scholar] [CrossRef]
- Lund, N.S.V.; Pedersen, J.W.; Borup, M.; Grum, M.; Mikkelsen, P.S. Auto-calibration for data assimilation in linear reservoir models used in flow forecasting of urban runoff. In Proceedings of the 13th International Conference on Urban Drainage, Kuching, Sarawak, Malaysia, 7–12 September 2014.
- Beven, K.; Young, P. A guide to good practice in modeling semantics for authors and referees. Water Resour. Res. 2013, 49, 5092–5098. [Google Scholar] [CrossRef] [Green Version]
- Bernardo, J.M.; Smith, A.F.M. Bayesian Theory; John Wiley & Sons, Inc.: New York, NY, USA, 2008. [Google Scholar]
- Grum, M.; Longin, E.; Linde, J.J. A flexible and extensible open source tool for urban drainage modelling: www.WaterAspects.org. In Proceedings of the 6th International Conference on Urban Drainage Modelling, Dresden, Germany, 15–17 September 2004.
- Fletcher, R. Practical Methods of Optimization, 2nd ed.; John Wiley & Sons, Inc.: New York, NY, USA, 1987. [Google Scholar]
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Applied Hydrology; McGraw-Hill, Inc.: New York, NY, USA, 1988. [Google Scholar]
- Butler, D.; Davies, J.W. Urban Drainage, 3rd ed.; Spon Press: London, UK, 2011; pp. 215–218. [Google Scholar]
- Velickov, S. Nonlinear Dynamics and Chaos with Applications to Hydrodynamics and Hydrological Modelling; CRC Press: Leiden, The Netherlands, 2004. [Google Scholar]
- Borup, M.; Grum, M.; Mikkelsen, P.S. Real time adjustment of slow changing flow components in distributed urban runoff models. In Proceedings of the 12th International Conference on Urban Drainage, Porte Allegre, Brazil, 11–16 September 2011.
- Breinholt, A.; Grum, M.; Madsen, H.; Thordarson, F.Ö.; Mikkelsen, P.S. Informal uncertainty analysis (GLUE) of continuous flow simulation in a hybrid sewer system with infiltration inflow—Consistency of containment ratios in calibration and validation? Hydrol. Earth Syst. Sci. 2013, 17, 4159–4176. [Google Scholar] [CrossRef]
- Löwe, R.; Thorndahl, S.; Mikkelsen, P.S.; Rasmussen, M.R.; Madsen, H. Probabilistic online runoff forecasting for urban catchments using inputs from rain gauges as well as statically and dynamically adjusted weather radar. J. Hydrol. 2014, 512, 397–407. [Google Scholar] [CrossRef]
- Löwe, R.; Mikkelsen, P.S.; Madsen, H. Stochastic rainfall-runoff forecasting: Parameter estimation, multi-step prediction, and evaluation of overflow risk. Stoch. Environ. Res. Risk Assess. 2014, 28, 505–516. [Google Scholar] [CrossRef] [Green Version]
- Del Giudice, D.; Löwe, R.; Madsen, H.; Mikkelsen, P.S.; Rieckermann, J. Comparing two stochastic techniques for reliable urban runoff predictions by modeling systematic errors. Water Resour. Res. 2015, 51, 5004–5022. [Google Scholar] [CrossRef]
- Jørgensen, H.K.; Rosenørn, S.; Madsen, H.; Mikkelsen, P.S. Quality control of rain data used for urban runoff systems. Water Sci. Technol. 1998, 37, 113–120. [Google Scholar] [CrossRef]
- Thorndahl, S.; Rasmussen, M.R.; Neve, S.; Poulsen, T.S.; Grum, M. Vejrradarbaseret Styring af Spildevandsanlæg; DCE Technical Report 95; Aalborg University: Aalborg, Denmark, 2010. [Google Scholar]
- Beven, K. A philosophical diversion. In Environmental Modelling: An Uncertain Future? An Introduction to Techniques for Uncertainty Estimation in Environmental Prediction; Routledge: London, UK, 2009; pp. 31–48. [Google Scholar]
- Borup, M.; Grum, M.; Mikkelsen, P.S. Comparing the impact of time displaced and biased precipitation estimates for on-line updated urban runoff models. Water Sci. Technol. 2012, 68, 109–116. [Google Scholar] [CrossRef] [PubMed]

| Parameter | Unit | Mean Value | Mean Value Calibrated on | Standard Deviation | ||
|---|---|---|---|---|---|---|
| α1 | m3/s | −0.0322 | A dry weather period | |||
| α2 | m3/s | −0.0165 | ||||
| ω1 | — | 1.17 | ||||
| ω2 | — | −0.0391 | ||||
| μDWF | m3/s | 0.074 | 0.029 | 0.015 | 0.0097 | |
| A | m2 | 113,125 | The entire dataset | 280,721 | 140,361 | 93,574 |
| Ttrans | h | 9.36 | 6.54 | 3.27 | 2.18 | |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pedersen, J.W.; Lund, N.S.V.; Borup, M.; Löwe, R.; Poulsen, T.S.; Mikkelsen, P.S.; Grum, M. Evaluation of Maximum a Posteriori Estimation as Data Assimilation Method for Forecasting Infiltration-Inflow Affected Urban Runoff with Radar Rainfall Input. Water 2016, 8, 381. https://doi.org/10.3390/w8090381
Pedersen JW, Lund NSV, Borup M, Löwe R, Poulsen TS, Mikkelsen PS, Grum M. Evaluation of Maximum a Posteriori Estimation as Data Assimilation Method for Forecasting Infiltration-Inflow Affected Urban Runoff with Radar Rainfall Input. Water. 2016; 8(9):381. https://doi.org/10.3390/w8090381
Chicago/Turabian StylePedersen, Jonas W., Nadia S. V. Lund, Morten Borup, Roland Löwe, Troels S. Poulsen, Peter S. Mikkelsen, and Morten Grum. 2016. "Evaluation of Maximum a Posteriori Estimation as Data Assimilation Method for Forecasting Infiltration-Inflow Affected Urban Runoff with Radar Rainfall Input" Water 8, no. 9: 381. https://doi.org/10.3390/w8090381
APA StylePedersen, J. W., Lund, N. S. V., Borup, M., Löwe, R., Poulsen, T. S., Mikkelsen, P. S., & Grum, M. (2016). Evaluation of Maximum a Posteriori Estimation as Data Assimilation Method for Forecasting Infiltration-Inflow Affected Urban Runoff with Radar Rainfall Input. Water, 8(9), 381. https://doi.org/10.3390/w8090381






