Sea Level Acceleration in the China Seas
Abstract
:1. Introduction
2. Data and Methods
2.1. Data
2.2. EMD Analysis
2.3. Least Squares Fitting Method
3. Results
3.1. Effects of Lunar Nodal Cycle on Sea Level Acceleration Estimation
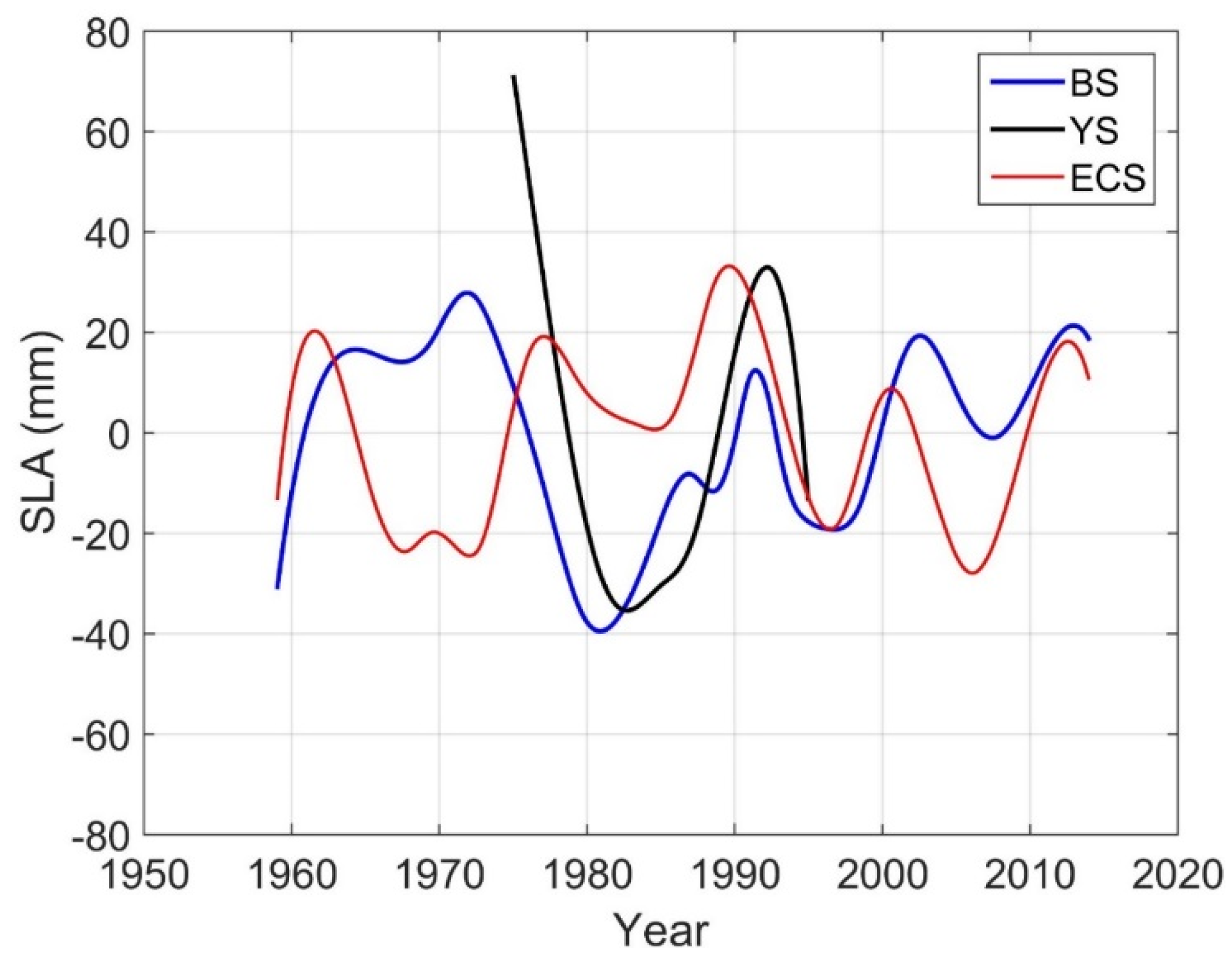
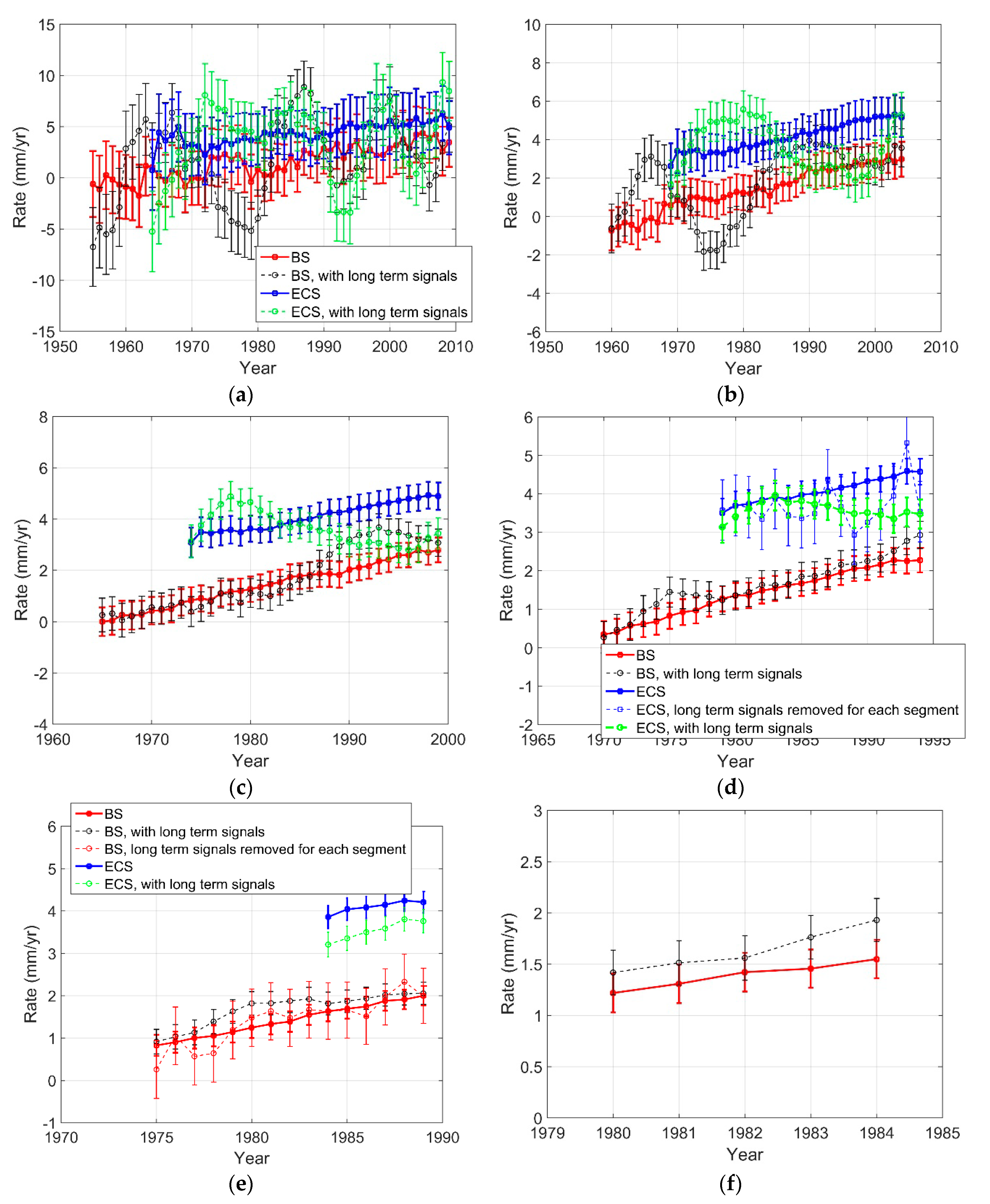
3.2. Effects of Long-Term Sea Level Variability
3.2.1. On Sea Level Acceleration Estimation
3.2.2. On Sea Level Rise Rate Estimation
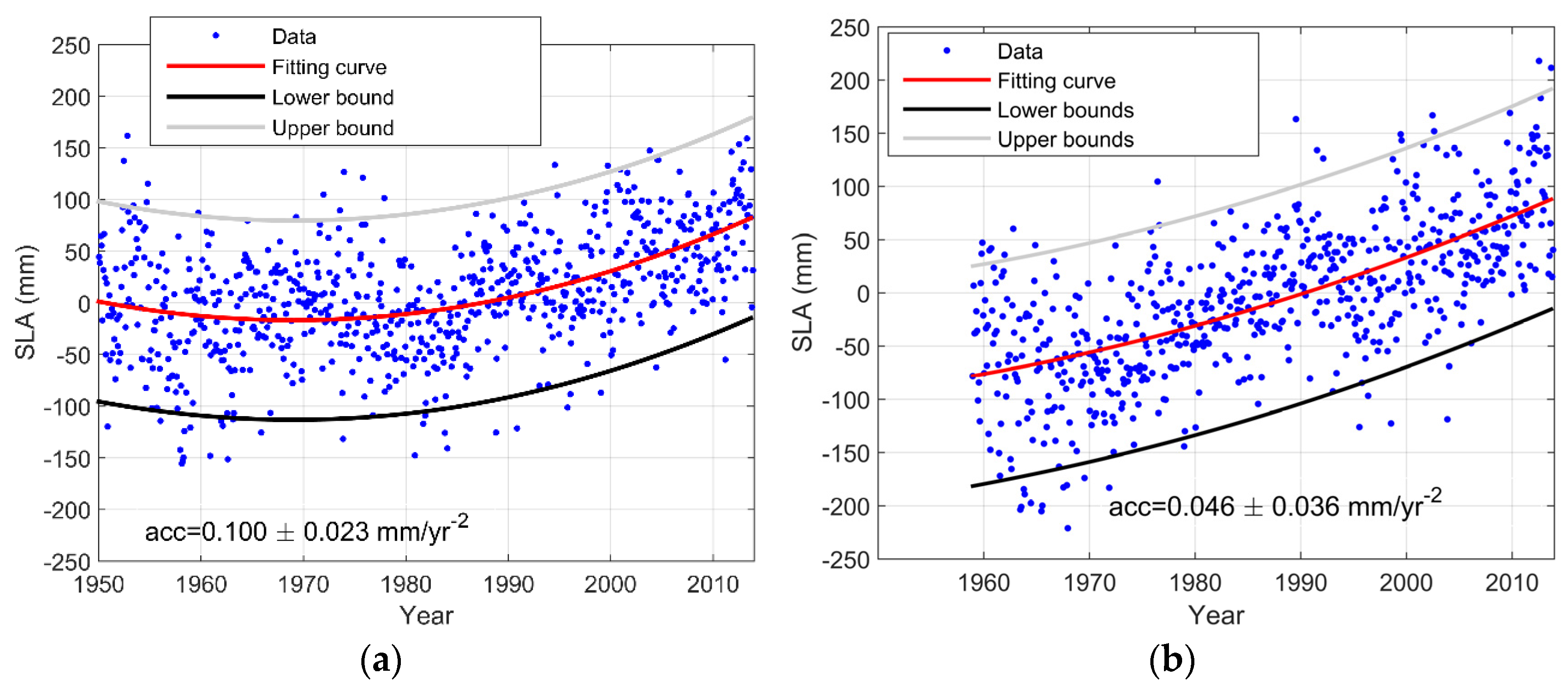
3.3. Sea Level Acceleration Estimated with Evolution of Sea Level Rise Trend Approach
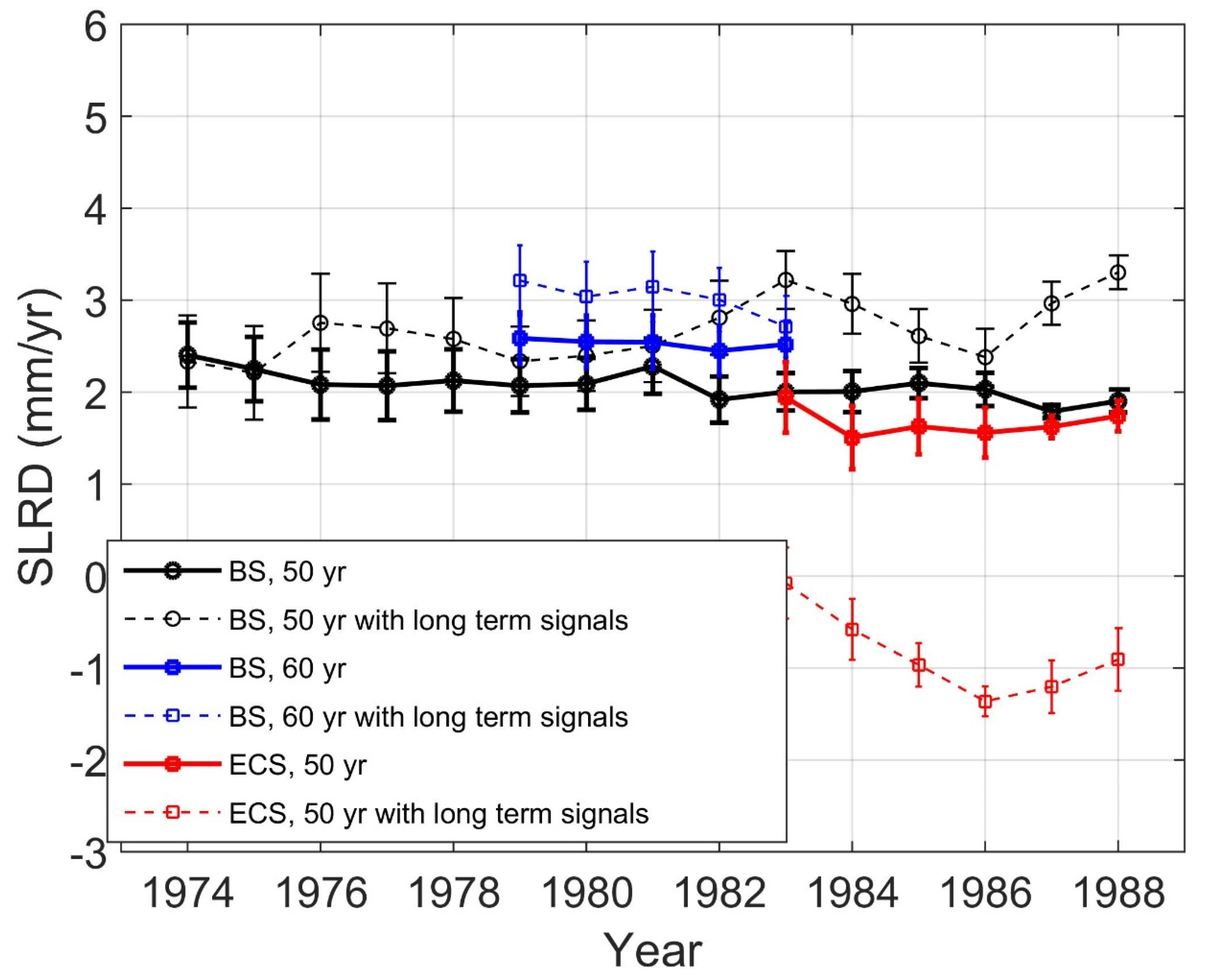
3.4. Sea Level Acceleration Estimated with the SLRD Approach
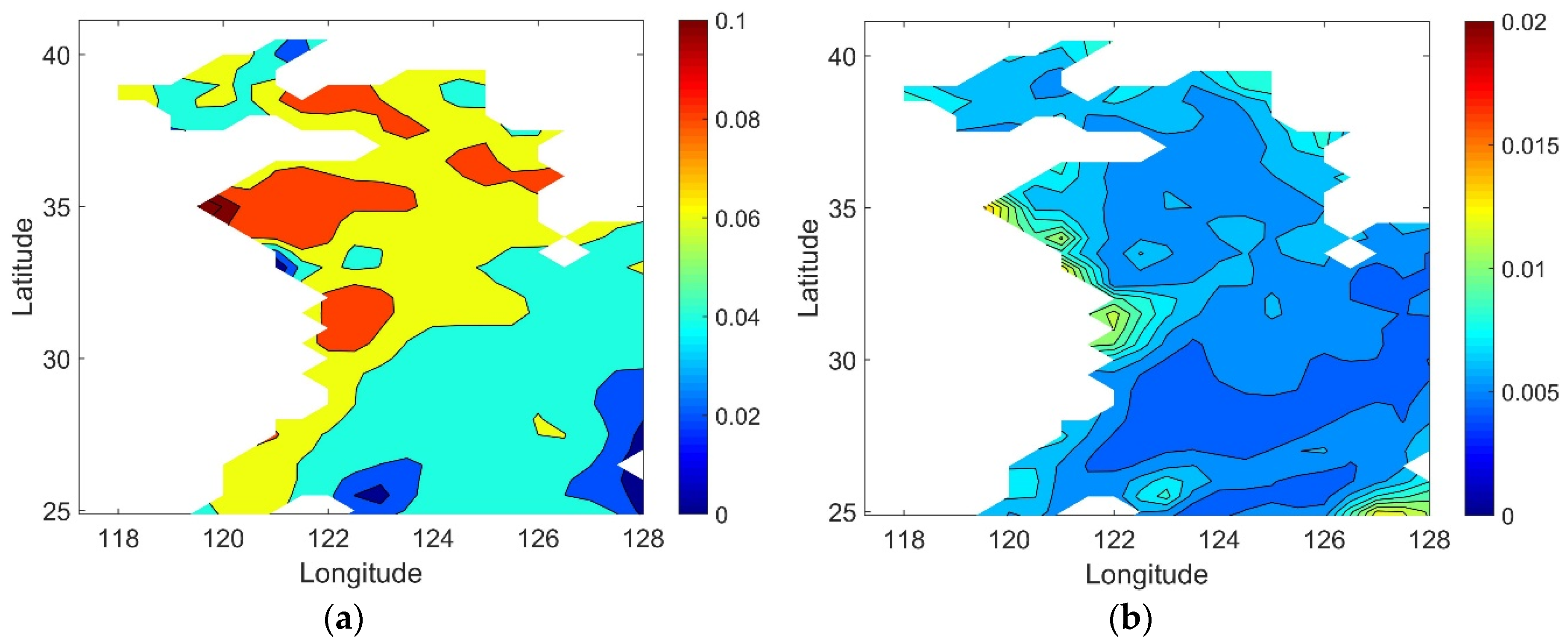
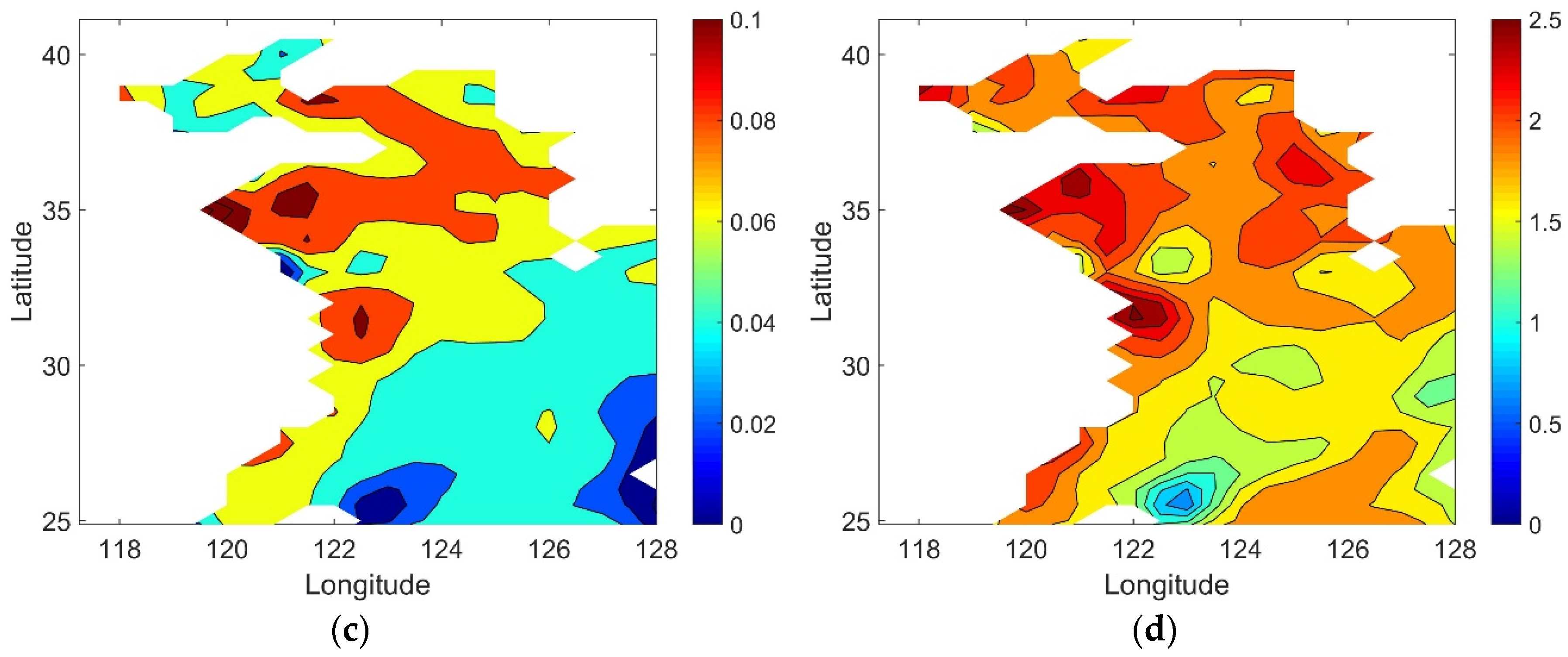
3.5. Spatial Pattern of Sea Level Acceleration
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Nicholls, R.J.; Cazenave, A. Sea-Level Rise and Its Impact on Coastal Zones. Science 2010, 328, 1517–1520. [Google Scholar] [CrossRef] [PubMed]
- Hallegatte, S.; Green, C.; Nicholls, R.J.; Corfee-Morlot, J. Future flood losses in major coastal cities. Nat. Clim. Chang. 2013, 3, 802–806. [Google Scholar] [CrossRef]
- Holgate, S.J.; Matthews, A.; Woodworth, P.L.; Rickards, L.J.; Tamisiea, M.E.; Bradshaw, E.; Foden, P.R.; Gordon, K.M.; Jevrejeva, S.; Pugh, J. New data systems and products at the permanent service for mean sea level. J. Coast. Res. 2013, 29, 493–504. [Google Scholar] [CrossRef]
- Chen, C.; Zuo, J.; Chen, M.; Gao, Z.; Shum, C.K. Sea level change under IPCC-A2 scenario in Bohai, Yellow and East China Seas. Water Sci. Eng. 2014, 7, 446–456. [Google Scholar]
- Marcos, M.; Tsimplis, M.N.; Calafat, F.M. Inter-annual and decadal sea level variations in the north-western Pacific marginal seas. Prog. Oceanogr. 2012, 105, 4–21. [Google Scholar] [CrossRef]
- Guo, J.; Hu, Z.; Wang, J.; Chang, X.; Li, G. Sea level changes of China seas and neighboring ocean based on satellite altimeter missions from 1993 to 2012. J. Coast. Res. 2015, 73, 17–21. [Google Scholar] [CrossRef]
- Rietbroek, R.; Brunnabend, S.E.; Kusche, J.; Schröter, J.; Dahle, C. Revisiting the contemporary sea-level budget on global and regional scales. Proc. Natl. Acad. Sci. USA 2016, 113, 1504–1509. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Gao, W.; Xu, S.; Yu, L. Evaluation of the combined risk of sea level rise, land subsidence, and storm surges on the coastal areas of Shanghai, China. Clim. Chang. 2012, 115, 537–558. [Google Scholar] [CrossRef]
- Zhao, C.; Ge, J.; Ding, P. Impact of Sea Level Rise on Storm Surges around the Changjiang Estuary. J. Coast. Res. 2014, 68, 27–34. [Google Scholar] [CrossRef]
- Wang, G.; Kang, J.; Yan, G.; Han, G.; Han, Q. Spatio-Temporal Variability of Sea Level in the East China Sea. J. Coast. Res. 2015, 73, 40–47. [Google Scholar] [CrossRef]
- Feng, X.; Tsimplis, M.N. Sea level extremes at the coasts of China. J. Geophys. Res. Oceans 2014, 119, 1593–1608. [Google Scholar] [CrossRef]
- Zhang, W.; Yan, Y.; Zheng, J.; Li, L.; Dong, X.; Cai, H. Temporal and spatial variability of annual extreme water level in the Pearl River Delta region, China. Glob. Planet. Chang. 2009, 69, 35–47. [Google Scholar] [CrossRef]
- Pelling, H.E.; Uehara, K.; Green, J.A.M. The impact of rapid coastline changes and sea level rise on the tides in the Bohai Sea, China. J. Geophys. Res. 2013, 118, 3462–3472. [Google Scholar] [CrossRef]
- He, Q.; Bertness, M.D.; Bruno, J.F.; Li, B.; Chen, G.; Goverdale, T.C.; Altieri, A.H.; Bai, J.; Sun, T.; Pennings, S.C.; et al. Economic development and coastal ecosystem change in China. Sci. Rep. 2014, 4, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Woodworth, P.L. A search for accelerations in records of European mean sea level. Int. J. Climatol. 1990, 10, 129–143. [Google Scholar] [CrossRef]
- Ezer, T. Sea level rise, spatially uneven and temporally unsteady: Why the U.S. East Coast, the global tide gauge record, and the global altimeter data show different trends. Geophys. Res. Lett. 2013, 40, 5439–5444. [Google Scholar] [CrossRef]
- Ezer, T.; Atkinson, L.P.; Corlett, W.B.; Blanco, J.L. Gulf Stream’s induced sea level rise and variability along the U.S. mid-Atlantic coast. J. Geophys. Res. 2013, 118, 685–697. [Google Scholar] [CrossRef]
- Ezer, T.; Haigh, I.D.; Woodworth, P.L. Nonlinear sea-level trends and long-term variability on Western European Coasts. J. Coast. Res. 2015. [Google Scholar] [CrossRef]
- Boon, J.D.; Mitchell, M. Nonlinear change in sea-level observed at North American tide stations. J. Coast. Res. 2015, 31, 1295–1305. [Google Scholar] [CrossRef]
- Haigh, I.D.; Wahl, T.; Rohling, E.J.; Price, R.M.; Pattiaratchi, C.B.; Calafat, F.M.; Dangendorf, S. Timescales for detecting a significant acceleration in sea level rise. Nat. Commun. 2014, 5, 3635. [Google Scholar] [CrossRef] [PubMed]
- Spada, G.; Olivieri, M.; Galassi, G. A heuristic evaluation of long-term global sea level acceleration. Geophys. Res. Lett. 2015, 42, 4166–4172. [Google Scholar] [CrossRef]
- State Oceanic Administration (SOA). Report of Sea Level Rise at Chinese Coast in 2014; State Oceanic Administration People’s Republic of China: Beijing, China, 2015. (In Chinese)
- Church, J.A.; White, N.J. Sea-level rise from the late 19th to the early 21st century. Surv. Geophys. 2011, 32, 585–602. [Google Scholar] [CrossRef]
- Woodworth, P.L.; White, N.J.; Jevrejeva, S.; Holgate, S.J.; Church, J.A.; Gehrels, W.R. Evidence for the accelerations of sea level on multi-decade and century timescales. Int. J. Climatol. 2009, 29, 777–789. [Google Scholar] [CrossRef]
- Jevrejeva, S.; Moore, J.C.; Grinsted, A.; Matthews, A.P.; Spada, G. Trends and acceleration in global and regional sea levels since 1807. Glob. Planet. Chang. 2014, 113, 11–22. [Google Scholar] [CrossRef]
- Jevrejeva, S.; Moore, J.C.; Grinsted, A.; Woodworth, P.L. Recent global sea level acceleration started over 200 years ago? Geophys. Res. Lett. 2008, 35, L08715. [Google Scholar] [CrossRef]
- Gehrels, W.R.; Woodworth, P.L. When did modern rates of sea-level rise start? Glob. Planet. Chang. 2013, 100, 263–277. [Google Scholar] [CrossRef]
- Kopp, R.E.; Kemp, A.C.; Bittermann, K.; Horton, B.P.; Donnelly, J.P.; Gehrels, W.R.; Hay, C.C.; Mitrovica, J.X.; Morrow, E.D.; Rahmstorf, S. Temperature-driven global sea-level variability in the Common Era. Proc. Natl. Acad. Sci. USA 2016, 113, E1434–E1441. [Google Scholar] [CrossRef] [PubMed]
- Calafat, F.M.; Chambers, D.P. Quantifying recent acceleration in sea level unrelated to internal climate variability. Geophys. Res. Lett. 2013, 40, 3661–3666. [Google Scholar] [CrossRef]
- Kenigson, J.S.; Han, W. Detecting and understanding the accelerated sea level rise along the east coast of the United States during recent decades. J. Geophys. Res. 2014, 119, 8749–8766. [Google Scholar] [CrossRef]
- Church, J.A.; White, N.J. A 20th century acceleration in global sea-level rise. Geophys. Res. Lett. 2006, 33, L01602. [Google Scholar] [CrossRef]
- Ren, M.-E. Relative sea-level changes in China over the last 80 years. J. Coast. Res. 1993, 9, 229–241. [Google Scholar]
- Visser, H.; Dangendorf, S.; Petersen, A.C. A review of trend models applied to sea level data with reference to the acceleration-deceleration debate. J. Geophys. Res. 2015, 120, 3873–3895. [Google Scholar] [CrossRef]
- Sallenger, A.H.; Doran, K.S.; Howd, P. Hotspot of accelerated sea-level rise on the Atlantic coast of North America. Nat. Clim. Chang. 2012, 2, 884–888. [Google Scholar] [CrossRef]
- Kalnay, E.; Kanamitsu, M.; Kistler, R.; Collins, W.; Deaven, D.; Gandin, L.; Iredell, M.; Saha, S.; White, G.; Woollen, J.; et al. The NCEP/NCAR 40-year reanalysis project. Bull. Am. Meteorol. Soc. 1996, 77, 437–471. [Google Scholar] [CrossRef]
- Peltier, W.R. Global Glacial Isostasy and the Surface of the Ice-Age Earth: The ICE-5G (VM2) model and GRACE. Ann. Rev. Earth Planet Sci. 2004, 32, 111–149. [Google Scholar] [CrossRef]
- Cheng, Y.C.; Plag, H.P.; Hamlington, B.D.; Xu, Q.; He, Y.J. Regional sea level variability in the Bohai Sea, Yellow Sea, and East China Sea. Conti. Shelf Res. 2015, 111, 95–107. [Google Scholar] [CrossRef]
- Olivieri, M.; Spada, G. Intermittent sea-level acceleration. Glob. Planet. Chang. 2013, 109, 64–72. [Google Scholar] [CrossRef]
- Scafetta, N. Multi-scale dynamical analysis (MSDA) of sea level records versus PDO, AMO, and NAO indexes. Clim. Dyn. 2014, 43, 175–192. [Google Scholar] [CrossRef]
- Hamlington, B.D.; Leben, R.R.; Nerem, R.S.; Han, W.; Kim, K.Y. Reconstructing sea level using cyclostationary empirical orthogonal functions. J. Geophys. Res. 2011, 116, C12015. [Google Scholar] [CrossRef]
- Hamlington, B.D.; Leben, R.R.; Nerem, R.S.; Kim, K.Y. The effect of signal-to-noise ratio on the study of sea level trends. J. Clim. 2011, 24, 1396–1408. [Google Scholar] [CrossRef]
- Hamlington, B.D.; Leben, R.R.; Kim, K.Y. Improving sea level reconstructions using non-sea level measurements. J. Geophys. Res. 2012, 117, C10025. [Google Scholar] [CrossRef]
- Hamlington, B.D.; Leben, R.R.; Strassburg, M.W.; Kim, K.Y. Cyclostationary empirical orthogonal function sea-level reconstruction. Geosci. Data J. 2014, 1, 13–19. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, E.H.; Zheng, Q.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for non-stationary time series analysis. Proc. R. Soc. Lond. Ser. A 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Huang, N.E.; Wu, Z. A review on Hilbert-Huang transform: The method and its applications on geophysical studies. Rev. Geophys. 2008, 46, RG2006. [Google Scholar] [CrossRef]
- Ezer, T.; Corlett, W.B. Is sea level rise accelerating in the Chesapeake Bay? A demonstration of a novel new approach for analyzing sea level data. Geophys. Res. Lett. 2012, 39, L19605. [Google Scholar] [CrossRef]
- Chambers, D.P. Evaluation of empirical mode decomposition for quantifying multi-decadal variations and acceleration in sea-level records. Nonlinear Process. Geophys. 2015, 22, 157–166. [Google Scholar] [CrossRef]
- Haigh, I.D.; Eliot, M.; Pattiaratchi, C. Global influences of the 18.61 year nodal cycle and 8.85 year cycle of lunar perigee on high tidal levels. J. Geophys. Res. 2011, 116, C06025. [Google Scholar] [CrossRef]
- Baart, F.; Gelder, P.H.A.J.M.; Ronde, J.; Koningsveld, M.; Wouters, B. The effect of the 18.6-year lunar nodal cycle on regional sea-level rise estimates. J. Coast. Res. 2012, 28, 511–516. [Google Scholar] [CrossRef]
- Woodworth, P.L. A note on the nodal tide in sea level records. J. Coast. Res. 2012, 28, 316–323. [Google Scholar] [CrossRef]
- Feng, X.; Tsimplis, M.N.; Woodworth, P.L. Nodal variations and long-term changes in the main tides on the coasts of China. J. Geophys. Res. 2015, 120, 1215–1232. [Google Scholar] [CrossRef]
- Douglas, B.C. Global sea level acceleration. J. Geophys. Res. 1992, 97, 12699–12706. [Google Scholar] [CrossRef]
- Cazenave, A.; Nerem, R.S. Present-day sea level change: Observations and causes. Rev. Geophys. 2004, 42, RG3001. [Google Scholar] [CrossRef]
- Han, G.; Huang, W. Pacific Decadal Oscillation and Sea Level Variability in the Bohai, Yellow, and East China Seas. J. Phys. Oceanogr. 2008, 38, 2772–2783. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, X.W.; Cao, Y.; Zhang, L.; Shao, C.; Sun, C.; Wu, X.; Fu, H.; Xuan, X. Climate modulation on sea surface height in China seas. Chin. J. Oceanol. Limnol. 2015, 33, 1245–1255. [Google Scholar] [CrossRef]
- Dangendorf, S.; Rybski, D.; Mudersbach, C.; Muller, A.; Kaufmann, E.; Zorita, E.; Jensen, J. Evidence for long-term memory in sea level. Geophys. Res. Lett. 2014, 41, 5530–5537. [Google Scholar] [CrossRef]
- Liu, S.; Chen, C.; Liu, K.; Mu, L.; Wang, H.; Wu, X.; Gao, J. Vertical motions of tide gauge stations near the Bohai Sea and Yellow Sea. Sci. China Earth Sci. 2015, 58, 2279–2288. [Google Scholar] [CrossRef]
- Zhang, S.; Du, L.; Wang, H.; Jiang, H. Regional sea level variation on interannual timescale in the East China Sea. Int. J. Geosci. 2014, 5, 1405–1414. [Google Scholar] [CrossRef]
- Li, Y.; Zuo, J.; Lu, Q.; Zhang, H.; Chen, M. Impacts of wind forcing on sea level variations in the East China Sea: Local and remote effects. J. Mar. Syst. 2016, 154, 172–180. [Google Scholar] [CrossRef]
- Liu, X.Y.; Liu, Y.G.; Guo, L.; Rong, Z.R.; Gu, Y.Z.; Liu, Y.H. Interannual changes of sea level in the two regions of East China Sea and different response to ENSO. Glob. Planet. Chang. 2010, 72, 215–226. [Google Scholar] [CrossRef]
- Andres, M.; Park, J.H.; Wimbush, M.; Zhu, X.H.; Nakamura, H.; Kim, K.; Chang, K.I. Manifestation of the pacific decadal oscillation in the kuroshio. Geophys. Res. Lett. 2009, 36, L16602. [Google Scholar] [CrossRef]
- Chambers, D.P.; Merrifield, M.A.; Nerem, R.S. Is there a 60-year oscillation in global mean sea level? Geophys. Res. Lett. 2012, 39, L18607. [Google Scholar] [CrossRef]
- Jordà, G. Detection time for global and regional sea level trends and accelerations. J. Geophys. Res. 2014, 119, 7164–7174. [Google Scholar] [CrossRef]
- Woodruff, J.D.; Irish, J.L.; Camargo, S.J. Coastal flooding by tropical cyclones and sea-level rise. Nature 2013, 504, 44–52. [Google Scholar] [CrossRef] [PubMed]
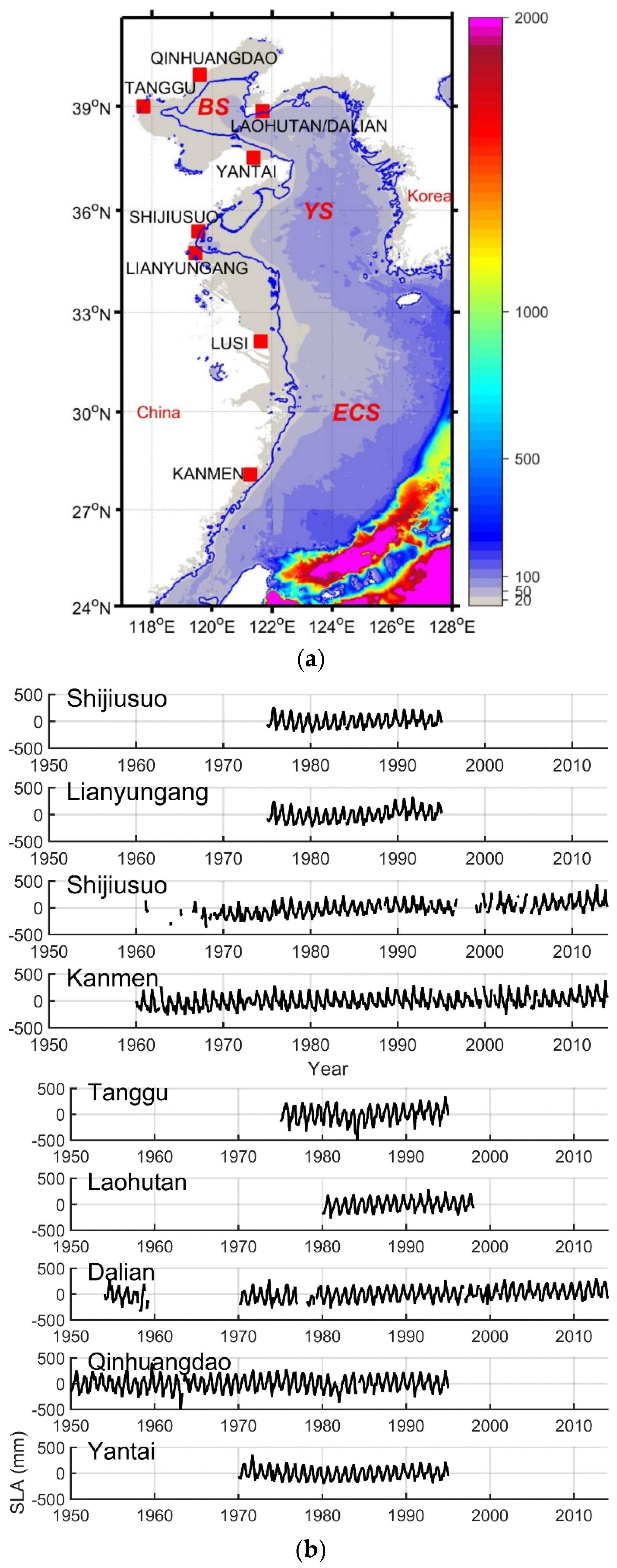
| ID | GIA | Time Span | Data Completeness | Correlations |
|---|---|---|---|---|
| Bohai Sea (1950–2013) | ||||
| TANGGU | −0.36 | 1975–1994 | 100% | 0.85 |
| LAOHUTAN | −0.31 | 1980–1997 | 100% | 0.97 |
| QINHUANGDAO | −0.33 | 1950–1994 | 99% | 0.86 |
| DALIAN | −0.31 | 1954–2013 | 79% | – |
| YANTAI * | −0.28 | 1954–1994 | 100% | 0.89 |
| Yellow Sea (1975–1994) | ||||
| SHIJIUSUO | −0.37 | 1975–1994 | 100% | 1.00 |
| LIANYUNGANG | −0.39 | 1975–1994 | 100% | – |
| East China Sea (1959–2013) | ||||
| KANMEN | −0.37 | 1959–2013 | 99% | 0.73 |
| LUSI * | −0.41 | 1961–2013 | 83% | – |
| Time Span | 1950–2013 | 1975–1994 | 1959–2013 |
|---|---|---|---|
| Bohai Sea | 0.086 ± 0.024 (0.100 ± 0.023 *) | 0.305 ± 1.116 (0.719 ± 0.381 *) | 0.098 ± 0.031 (0.097 ± 0.031 *) |
| East China Sea | – | −0.410 ± 1.103 (−0.059 ± 0.372 *) | 0.044 ± 0.036 (0.046 ± 0.036 *) |
| Yellow Sea | – | 0.364 ± 1.049 (0.577 ± 0.384 *) | – |
| Time Span | 1950–2013 | 1959–2013 |
|---|---|---|
| Bohai Sea | 0.085 ± 0.020 (0.081 ± 0.021 1 0.085 ± 0.008 2) | 0.075 ± 0.028 |
| East China Sea | – | 0.074 ± 0.032 (0.070 ± 0.038 1 0.073 ± 0.010 2) |
| Yellow Sea (1975–1994) | −0.022 ± 0.337 | – |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, Y.; Ezer, T.; Hamlington, B.D. Sea Level Acceleration in the China Seas. Water 2016, 8, 293. https://doi.org/10.3390/w8070293
Cheng Y, Ezer T, Hamlington BD. Sea Level Acceleration in the China Seas. Water. 2016; 8(7):293. https://doi.org/10.3390/w8070293
Chicago/Turabian StyleCheng, Yongcun, Tal Ezer, and Benjamin D. Hamlington. 2016. "Sea Level Acceleration in the China Seas" Water 8, no. 7: 293. https://doi.org/10.3390/w8070293
APA StyleCheng, Y., Ezer, T., & Hamlington, B. D. (2016). Sea Level Acceleration in the China Seas. Water, 8(7), 293. https://doi.org/10.3390/w8070293






