3.2.1. Influence of Rainfall Hyetograph
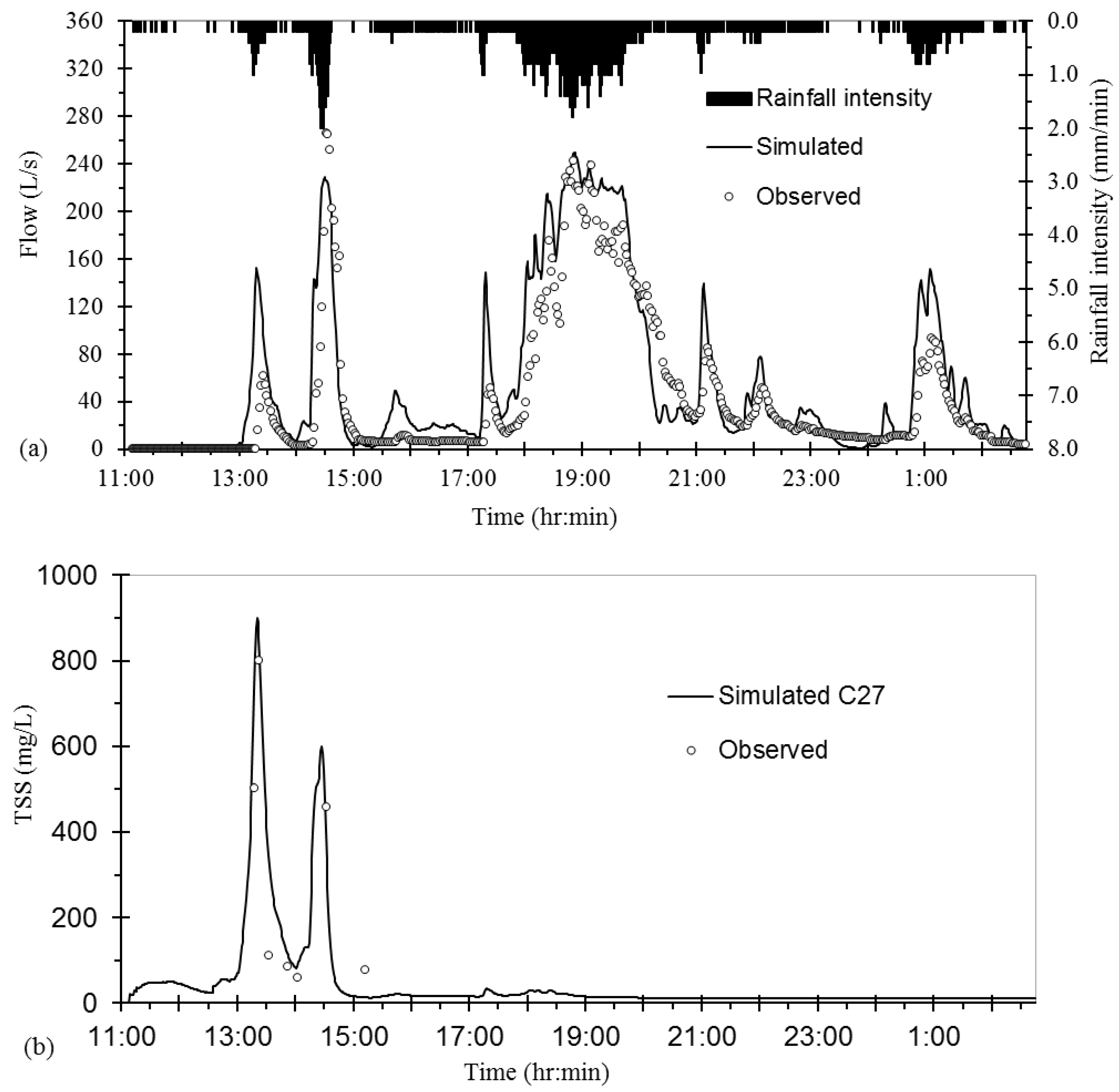
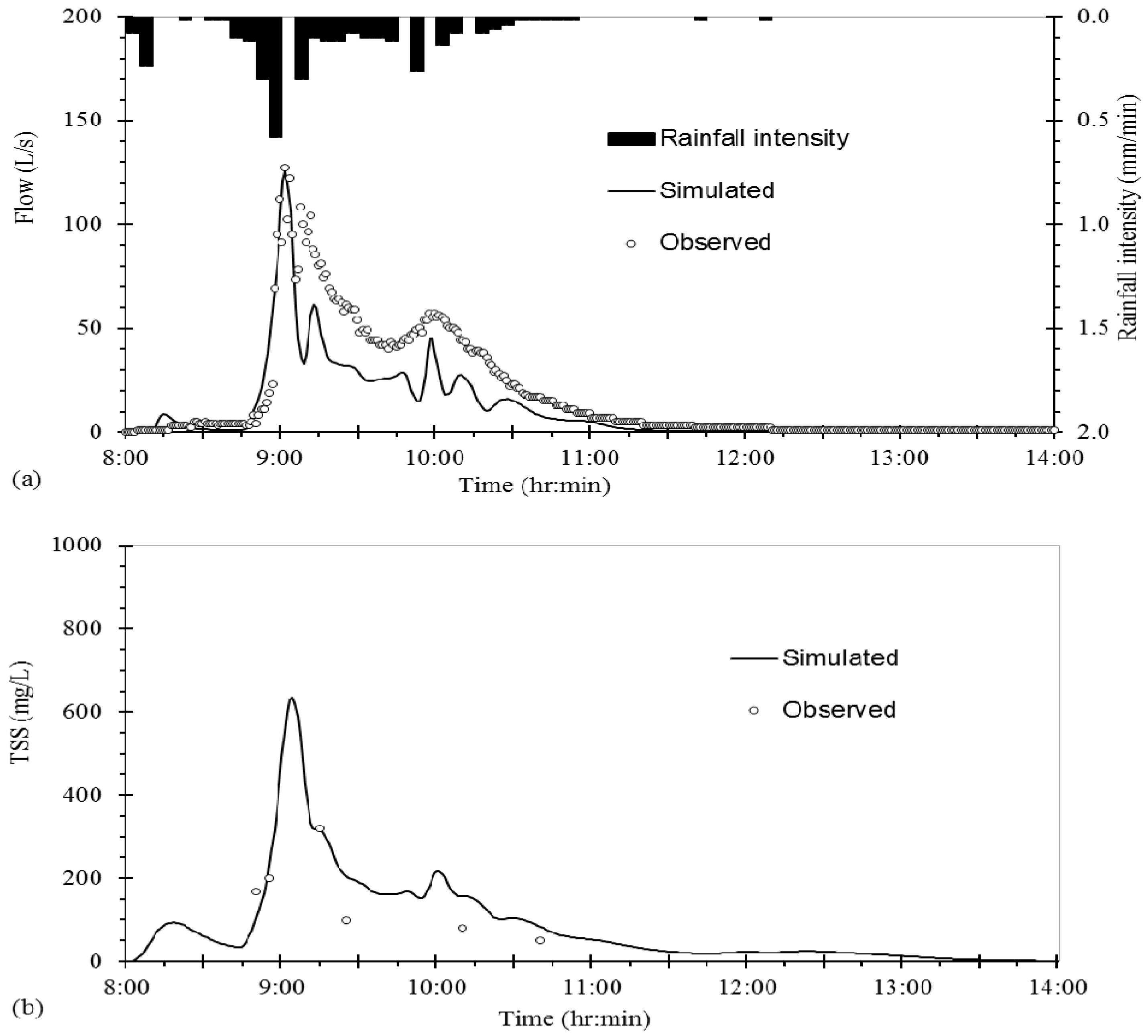
Pollutographs of TSS at the catchment outlet (
Outfall in
Figure 1) resulting from three different design rainfall distributions are shown in
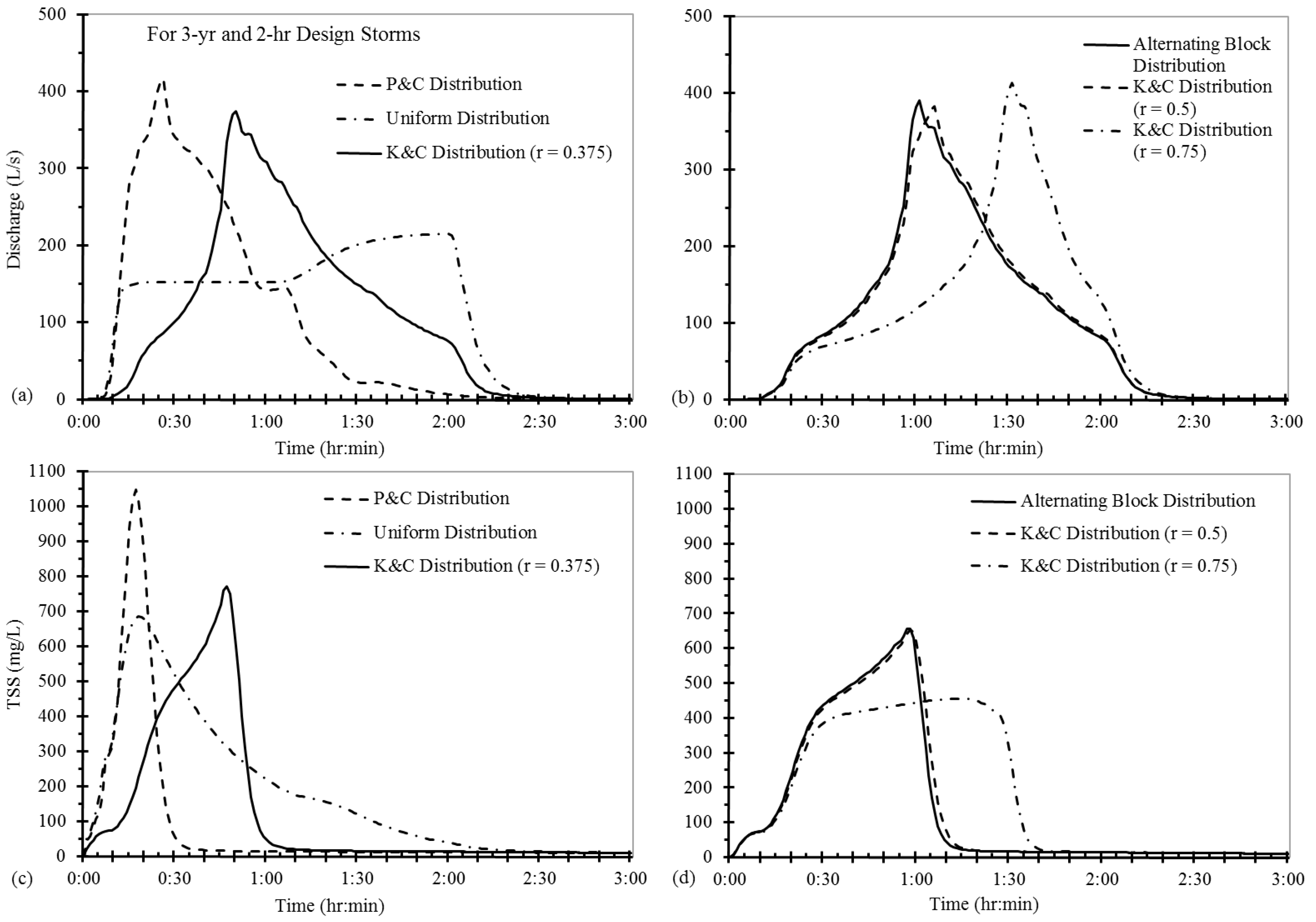
Figure 8, each under the assumption of five antecedent dry days. The initial buildup of TSS is 327.0 kg determined using Equation (1), and the three-year, 2-h storm delivers 24.2 kg of TSS from the wet deposition; therefore, total TSS available for washoff for each design rainfall in
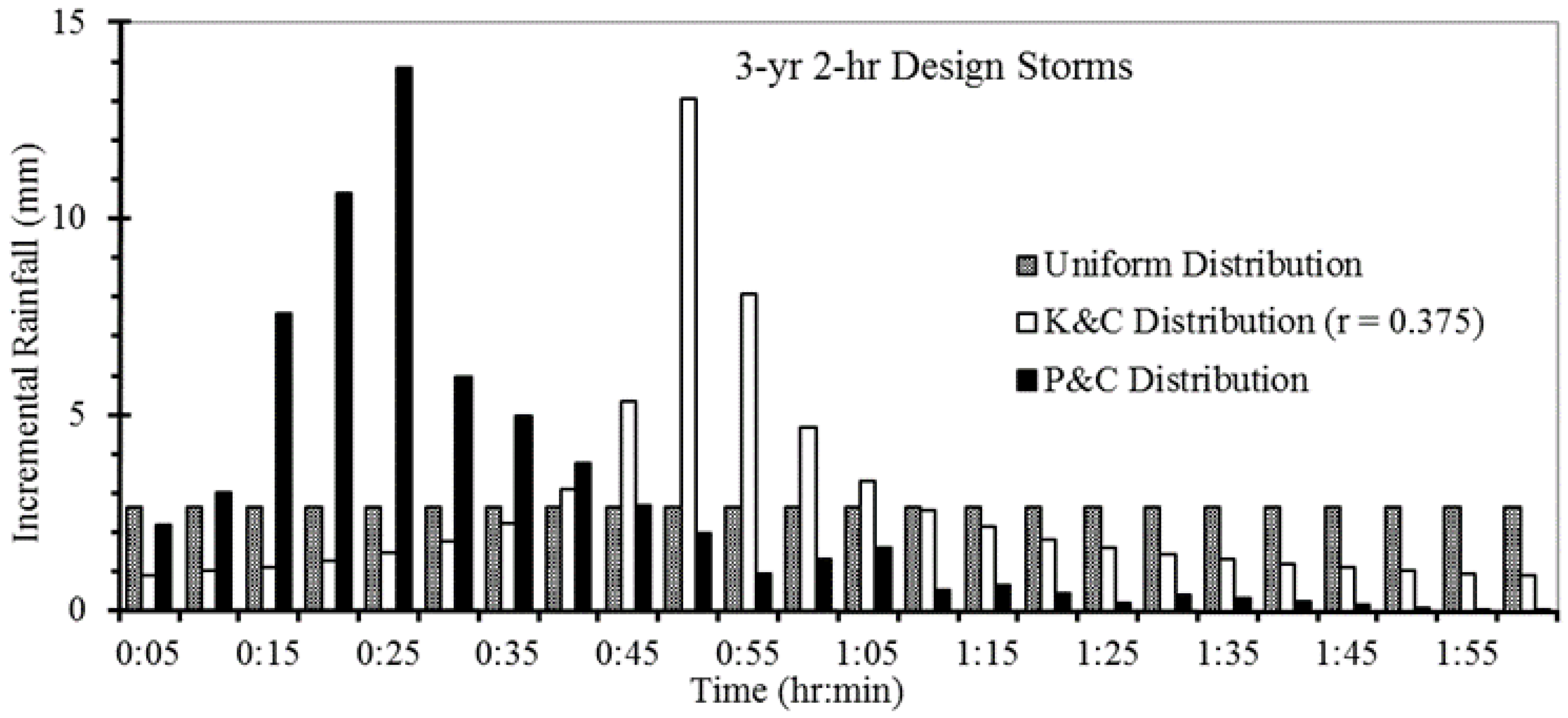
Figure 8 is 351.2 kg. For the same rainfall depth (63.4 mm), the peak concentration of TSS and the time of its appearance depend on the timing of peak rainfall (
Figure 8), which is related to rainfall pattern (i.e., choice of hyetograph). The washoff load of TSS is a function of runoff and the amount of buildup remaining (Equation (2)). With the increase of discharge due to the increase (continuation) of rainfall over time, TSS concentration first increases with time and reaches a peak value, then decreases with time because the amount of previously accumulated pollutant that is remaining for washoff decreases with time. After the TSS concentration reaches its peak (
Figure 8), it begins to decrease and eventually reaches a stable, low concentration (approximately 10 mg/L), which is the background rainfall TSS concentration.
Table 5 summarizes
Qp and TSS characteristics for the three-year, 2-h design rainfall distributed according to the different hyetographs. As a result of all but the uniform rainfall distributions, the TSS concentration reaches a peak value that precedes the peak discharge (
Qp) by 3 min to 18 min (
Table 5) and decreases rapidly after the peak (
Figure 8); this is the same behavior observed by Luo et al. [
42]. The uniform rainfall distribution has no rainfall peak and results in a TSS peak concentration of 686.3 mg/L at 18 min (
Table 5), followed by a gradual decrease of TSS concentration (
Figure 8b). For the uniform rainfall distribution, the peak discharge of 214.9 L/s is lower than the peak discharges resulting from other rainfall distributions, and occurs at a much later time (120 min). Although all hyetographs produce the same rainfall depth, the simulated TSS peak concentration at the outfall is the highest for the P&C rainfall distribution because it results in the largest
Qp (415.9 L/s) at the earliest time (26 min), followed in descending order by the K&C distribution (with
r = 0.375) and the uniform rainfall distribution. This result occurs because the P&C distribution has higher rainfall intensity in the first 25 min than the other two distributions (
Figure 2), and because TSS concentration increases with an increase in initial rainfall intensity. The washoff ability of the P&C rainfall pattern is stronger than the K&C distribution and uniform rainfall distribution in the first 25 min. Once a large proportion of accumulated TSS has been washed off by runoff, TSS concentration decreases rapidly with time after the TSS concentration reaches its peak, a pattern that results from all design rainfall distributions except the uniform distribution (
Figure 8). In contrast to other distributions, the uniform design rainfall results in smaller runoff discharges and no (or minimal) increase in runoff from 0:10 to 2:10; thus, TSS concentration gradually decreases with time after reaching its peak concentration.
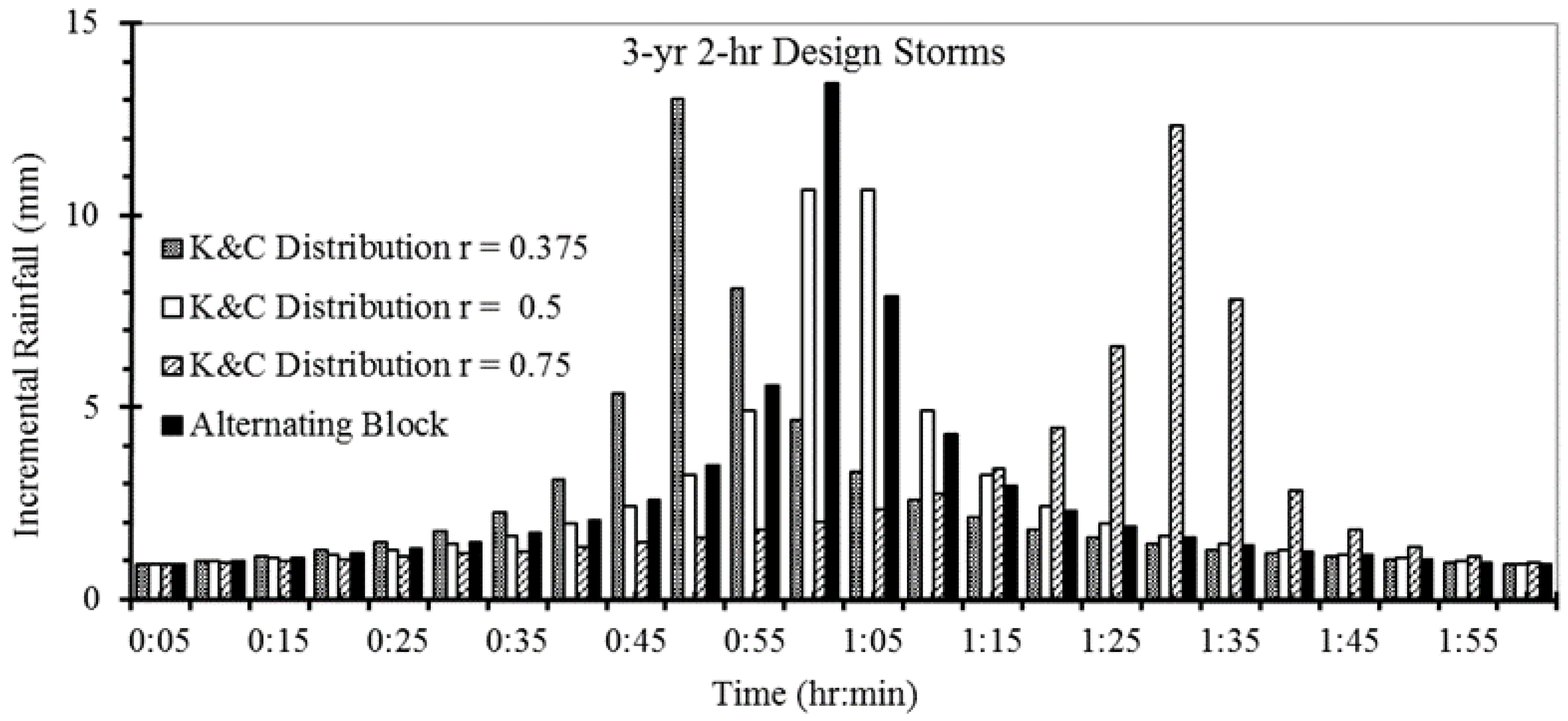
TSS concentrations resulting from the K&C rainfall distribution with the constant
r equal to 0.5 were almost the same as those resulting from the alternating block rainfall distribution because these two rainfall distributions are very similar (
Figure 3). Comparatively, however, the K&C distribution with the constant
r equal to 0.75 has a later rainfall peak (148.1 mm/h at 85 min), which results in a gradual increase of TSS concentration that peaks at 455.4 mg/L (73 min). TSS concentrations resulting from the K&C distributions with the constant
r equal to 0.375 and 0.5 are very similar, but when
r was 0.375, the peak TSS concentration was 18% larger and occurred 10 min earlier than when
r was 0.5 (
Table 5). When the peak location constant
r in the K&C distribution increases (0.375, 0.5, and 0.75), which ultimately results in a third-quartile storm, peak runoff discharge increases and peak TSS concentration decreases (
Table 5). Nevertheless, both the outlet TSS load and event mean concentration (EMC) increase because the TSS flood loss decreases as
r increases.
The EMC is commonly used to quantify the overall pollutant load of stormwater runoff and is defined as the event load divided by the event water volume [
43]. The EMC in this study was calculated at the outfall of the catchment; therefore, it is equal to the outlet TSS load divided by the runoff volume integrated from the outlet hydrograph (
Figure 8). As shown in
Table 5, the EMC of TSS ranged from 211.3 mg/L to 242.6 mg/L (with both extremes resulting from K&C rainfall distributions). The P&C distribution, alternating block distribution and uniform distribution of the design rainfall results in outlet EMCs of 213.2 mg/L, 219.8 mg/L, and 226.6 mg/L, respectively. The differences in the EMCs from different rainfall distributions are much smaller than the differences in the TSS peaks that result from the distributions (
Table 5).
The time bases of TSS pollutographs are given in
Table 5 and range from 32 min (for the P&C distribution) to 125 min (for the uniform distribution), which were 26.7% to 104.2% of the rainfall duration. The TSS time bases for K&C distributions and alternating blocking distributions are similar (64–98 min). The TSS time base is larger when the rainfall distribution is more uniform and when the rainfall peak occurs later (e.g., a third-quartile storm represented by the K&C distribution with
r = 0.75).
Table 5 also gives TSS load at the outlet (calculated using the flow and TSS distributions) and surface runoff TSS mass (kg) for each design rainfall distribution. The surface runoff TSS mass ranged from 310.2 kg to 319.4 kg, which was 88.3%–91.0% of the 351.2 kg total available TSS (
Table 5). The resulting runoff from three-year, 2-h storms has adequate washoff capability to transport TSS; therefore, the surface runoff TSS loads for all hyetographs are similar (317.0 ± 3.4 kg) because the washoff is limited by available sediments from initial buildup and wet deposition, not by the transport capacity of the runoff. For the uniform, K&C (
r = 0.375) and P&C rainfall distributions, the outlet TSS loads are calculated as 284.5 kg, 248.4 kg and 216.4 kg, respectively. The outlet TSS loads are 67.7%–91.8% of the surface runoff TSS, indicating that surface flooding deposits a certain amount of TSS above ground after flooding. The TSS “loss” due to flooding as a percentage of the total TSS transport by surface runoff range from 8.2% for the uniform rainfall distribution to 32.3% for the P&C distribution (last row of
Table 5). The P&C rainfall distribution produces the earliest and highest peak discharge among all six rainfall distributions; therefore, the resulting outlet TSS load is the smallest (216.4 kg) because the surface flooding lasts approximately 58 min and has the largest overflow (flood) volume (614 m
3). The uniform rainfall distribution results in the largest outlet TSS load (284.8 kg) because this distribution produces the smallest flooding volume (210 m
3). However, the flooding duration (115 min) at junction J16 under the uniform rainfall distribution is longer than that from the P&C rainfall distribution because the runoff simulated from uniform rainfall has a slower and longer increase before reaching the peak than that from other distributions. The flood volume as a percentage of total surface runoff ranges from 14.3% for uniform rainfall to 37.7% for the P&C rainfall distribution (
Table 5). As shown in
Table 5, the total runoff volumes simulated for the six rainfall distributions are almost identical, with only 3.5% standard deviation (1568.7 ± 54.4 m
3).
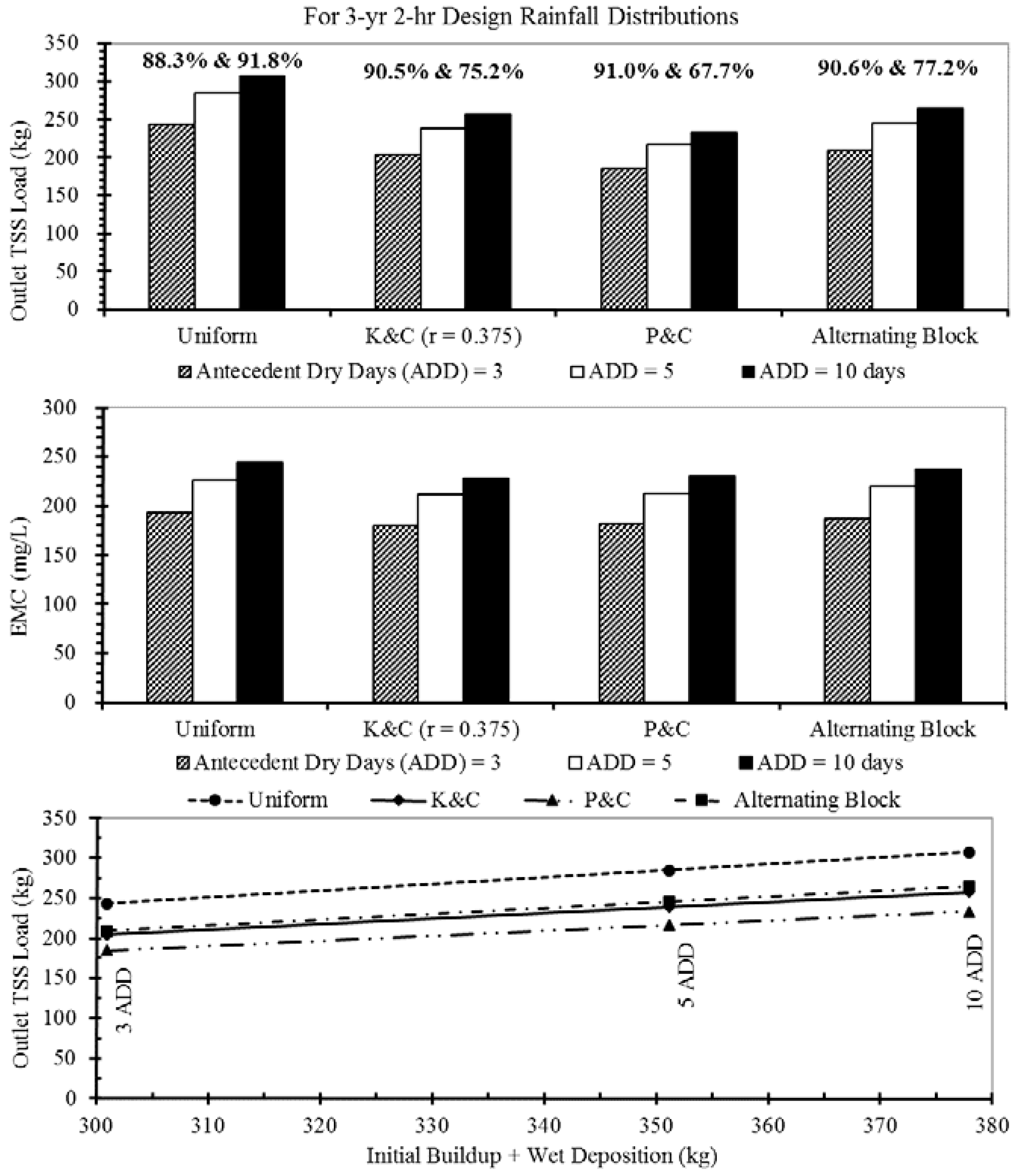
Results presented in
Figure 8 and
Table 5 were developed under the assumption of five antecedent dry days for all design storms in SWMM modeling. A sensitivity analysis was conducted using four design rainfall distributions to examine the effect of antecedent dry days (three days and 10 days); comparative results of the simulated outlet TSS loads and EMCs are given in
Figure 9. As described in
Section 3.1, the three-day and 10-day antecedent dry periods were happened for the 7 June 2013 model-validation event and the 21 July 2012 model-calibration event. The three and 10 dry days result in initial buildups of 276.8 kg and 353.8 kg TSS, respectively (
Table 4). Because the volume of rainfall is the same for the four distributions, so is the mass of TSS in wet deposition (24.1 kg). Both the outlet TSS load and EMC have perfect linear correlations with the available sediment for transport (initial buildup plus wet deposition); this result can be explained using Equation (2) when discharges produced by the design rainfall are the same for three sensitivity model runs and assuming three antecedent dry days. In
Figure 9, two percentages are given above the bars of the outlet TSS load for each design rainfall distribution. The first of these percentages is surface runoff TSS as a percentage of total available sediment for washoff or transport. The second percentage is the outlet TSS load as a percentage of surface runoff TSS. These two percentages for an assumption of five antecedent dry days are given in
Table 4. Data shown in
Figure 9 and
Table 4 reveal that the two percentages are exactly the same for all three antecedent dry-day periods. The product of these two percentages gives the outlet TSS load as the percentage of total available sediment. Of the four rainfall distributions, the uniform design storm transported the highest percentage (81.1% = 88.3% × 91.8%) of total sediment because it yields the lowest TSS flood loss (8.2%), although runoff from the uniform rainfall has the lowest capability (88.3%) to wash off sediment. The P&C design storm transports the lowest percentage of total sediment (61.6%) because 32.3% of TSS load (i.e., 100%–67.7%) is trapped by surface flooding.
In summary, six design rainfall distributions (hyetographs) with the same return period (3 year) and duration (2-h) were examined using SWMM. The choice of hyetograph can significantly affect the shape and peak value of the resulting runoff hydrograph and thus the TSS pollutograph (
Figure 8). The P&C rainfall distribution is a first-quartile storm (the most severe) and results in the highest peak discharge and TSS concentration at the outlet, but the lowest outlet TSS load because of the highest TSS loss due to flood deposition (32.3%). The uniform rainfall distribution results in the lowest peak discharge and the latest time to peak and the highest outlet TSS load, not because it has the highest washoff capability, but rather because it produces the smallest TSS loss due to flooding (8.2%). Fang et al. [
44] also confirmed that the rainfall hyetograph is a major determinant of runoff pollution load. Huang and Nie [
45] pointed out that the position of the rainfall peak in an event had a certain influence on urban NPS pollution. Others have shown that the removal of pollutants from pervious surfaces depends heavily on the rainfall hyetograph [
46].
3.2.2. Influences of Rainfall Depth or Intensity
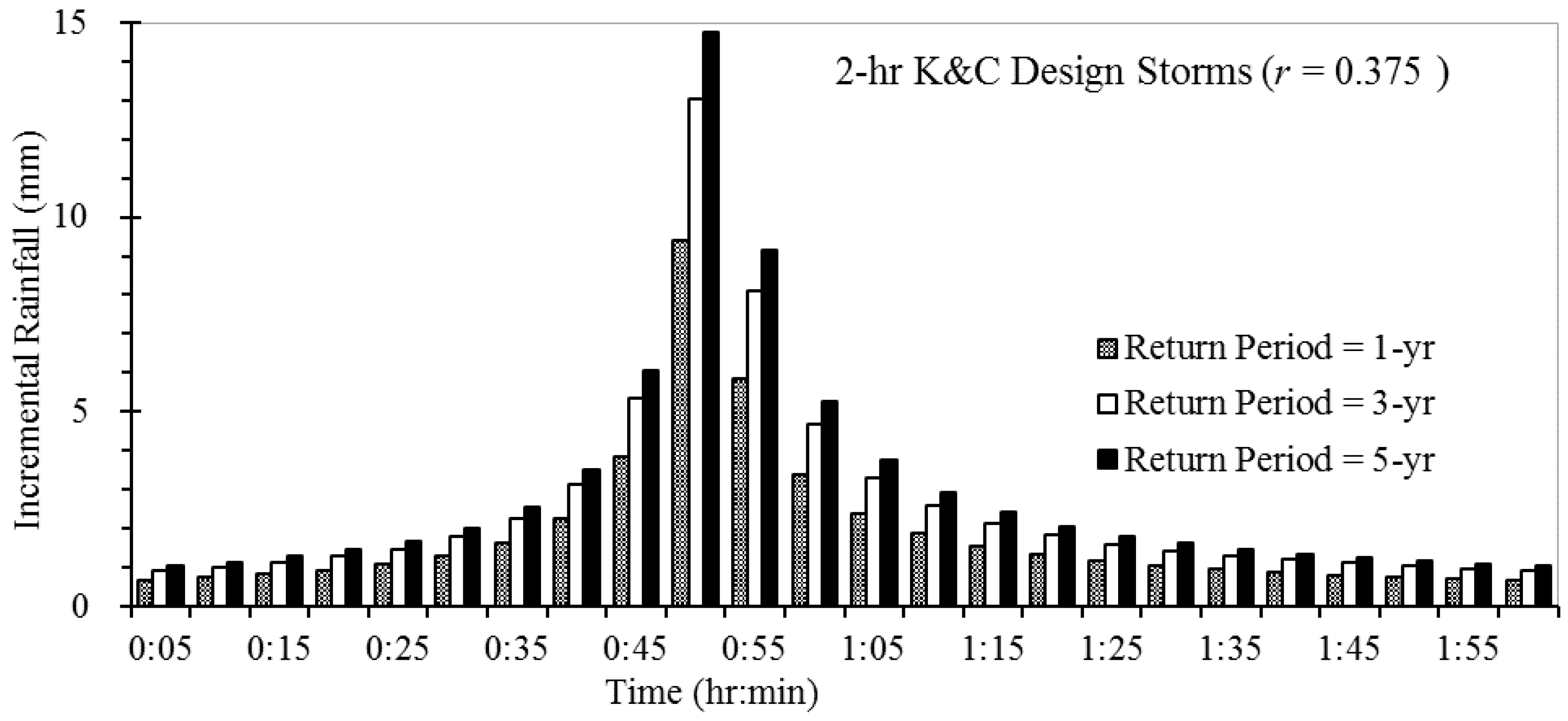
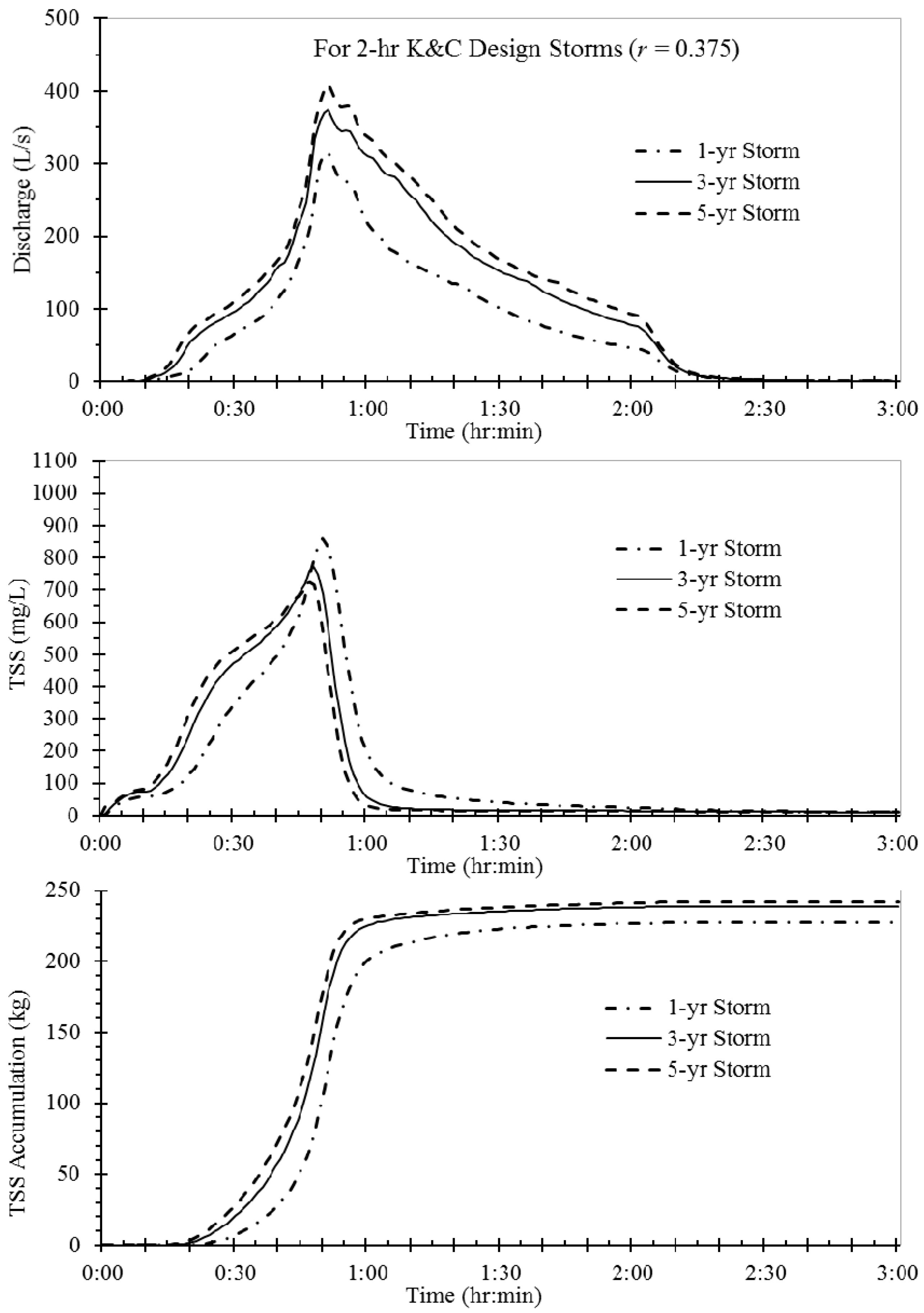
TSS resulted from different rainfall intensities are shown in
Figure 10 using the 2-h K&C design storms (
r = 0.375) having one-, three-, and five-year return periods. When the return period changes from one-year to five-year, total rainfall increases from 45.8 mm to 71.7 mm (
Table 2); likewise, the 5-min peak rainfall intensity increases from 100.3 mm/h to 176.9 mm/h, but occurs at the same time (during 45–50 min,
Table 1 and
Table 4). The resulting peak discharges at the outlet are 341.2 L/s, 374.1 L/s, and 408.9 L/s with the same time to peak (51 min) for one-, three-, and five-year storms, respectively. For all SWMM simulations in this study, design rainfalls for 5-min intervals were used as model input, but outflow and TSS were predicted and reported at 1-min intervals. The results indicated that rainfall intensity has a certain impact on TSS concentration and total TSS load. However, the TSS accumulation processes are similar for rainfalls of different rainfall depths and intensities, and the TSS washed off by runoff mainly concentrates from 10 min to 55 min after the rainfall starts (
Figure 10).
The TSS peak concentrations at the outlet for one-, three-, and five-year return periods are 859.4 mg/L, 772.9 mg/L, and 725.9 mg/L, respectively; and occur at 47 min to 50 min after the rainfall begins. Surface runoff volumes for one-, three-, and five-year design storms range from 942 m
3 to 1582 m
3 for the study catchment, but TSS due to initial build-up is constant (327.0 kg) owing to the use of a common antecedent dry period in all simulations. Tiefenthaler and Schiff [
47] found that a greater runoff volume resulting from larger rainfall depth would dilute the concentration of a pollutant in runoff, reducing, for example, the TSS peak concentration.
The simulated total pollutant loads of TSS for the K&C design storms having one-, three-, and five-year return periods are 227.4 kg, 238.8 kg and 242.0 kg, respectively (
Table 6). The results suggest that pollutant load at the outfall has a positive correlation (
R2 = 0.95) with rainfall depth and intensity, while the outlet EMC decreases from 290.8 mg/L for a one-year storm to 191.9 mg/L for a five-year storm (
Table 6) because of the dilution effect. The one-year storm produces a larger TSS time base (104 min) because the TSS peak occurs slightly later and the smaller discharges makes TSS decrease slowly to the 30-mg/L cutoff limit when TSS < 100 mg/L (
Figure 10). When the return period increases, the total pollution loads of TSS from the outlet also increases. Gnecco et al. [
48] reported that there is a strong correlation between the EMC of TSS and the maximum rainfall intensity because rainfall intensity determines the surface pollutants washoff portion. Other studies have also shown that the amount of accumulated pollutant load washed off during rainfall event is dependent on rainfall and runoff characteristics [
9]. As the return period increases, so too does rainfall intensity. Thus, in this study, as return period increases, the sediment in surface runoff gradually increases, and the resulting NPS pollution load increases. However, because the mass of contaminants available for wash off was limited, the increased rainfall intensity results in a decreasing trend in the amplitude of increases in the pollutant load.
The data analysis shows that, under the same rainfall hyetograph, simulated peak discharge and outlet TSS load are positively correlated (R2 = 0.95) to the rainfall depth as a function of the return period, while peak TSS concentration and the outlet EMC have the negative correlation (R2 = 0.95).
3.2.3. Influence of Rainfall Duration
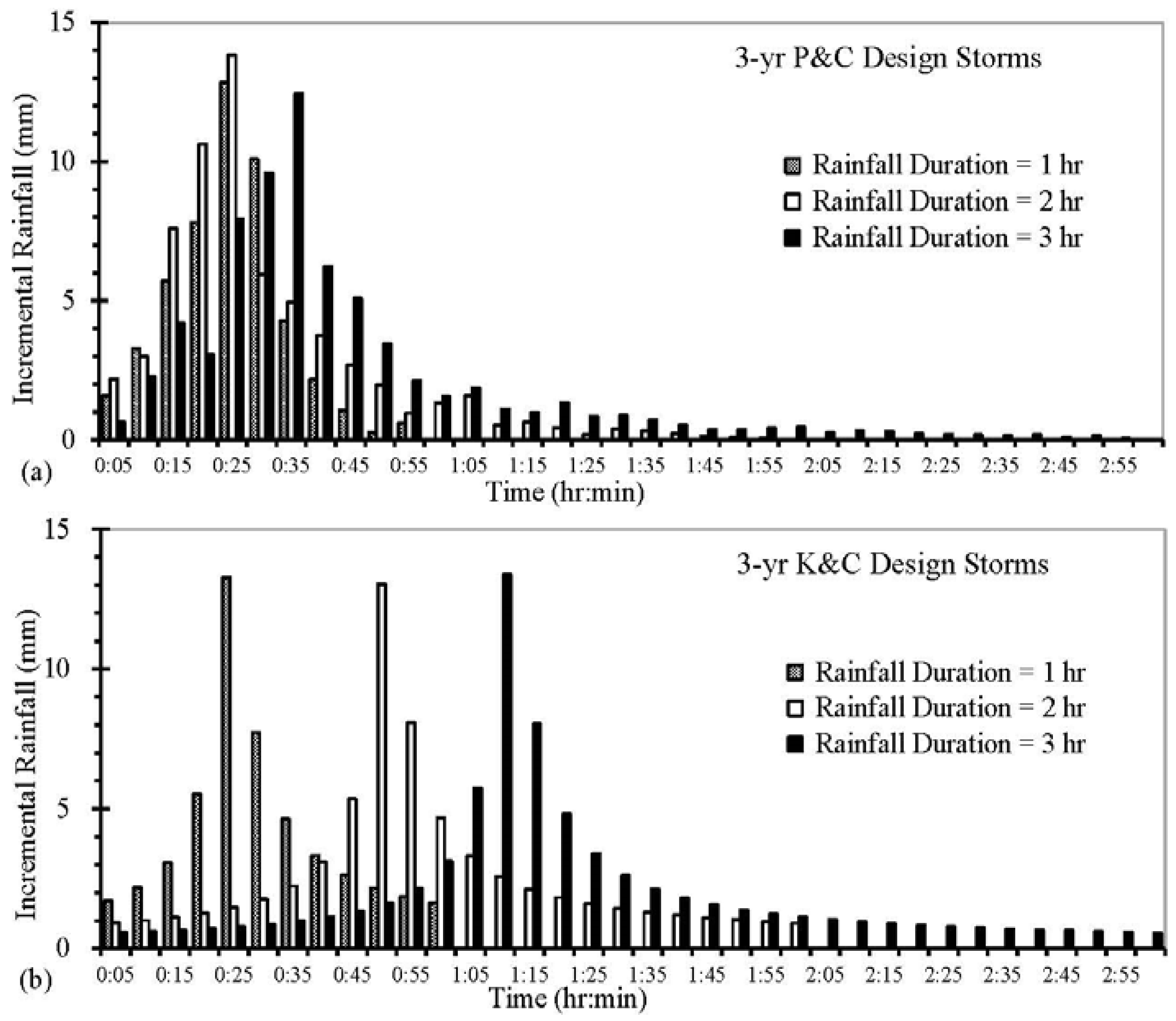
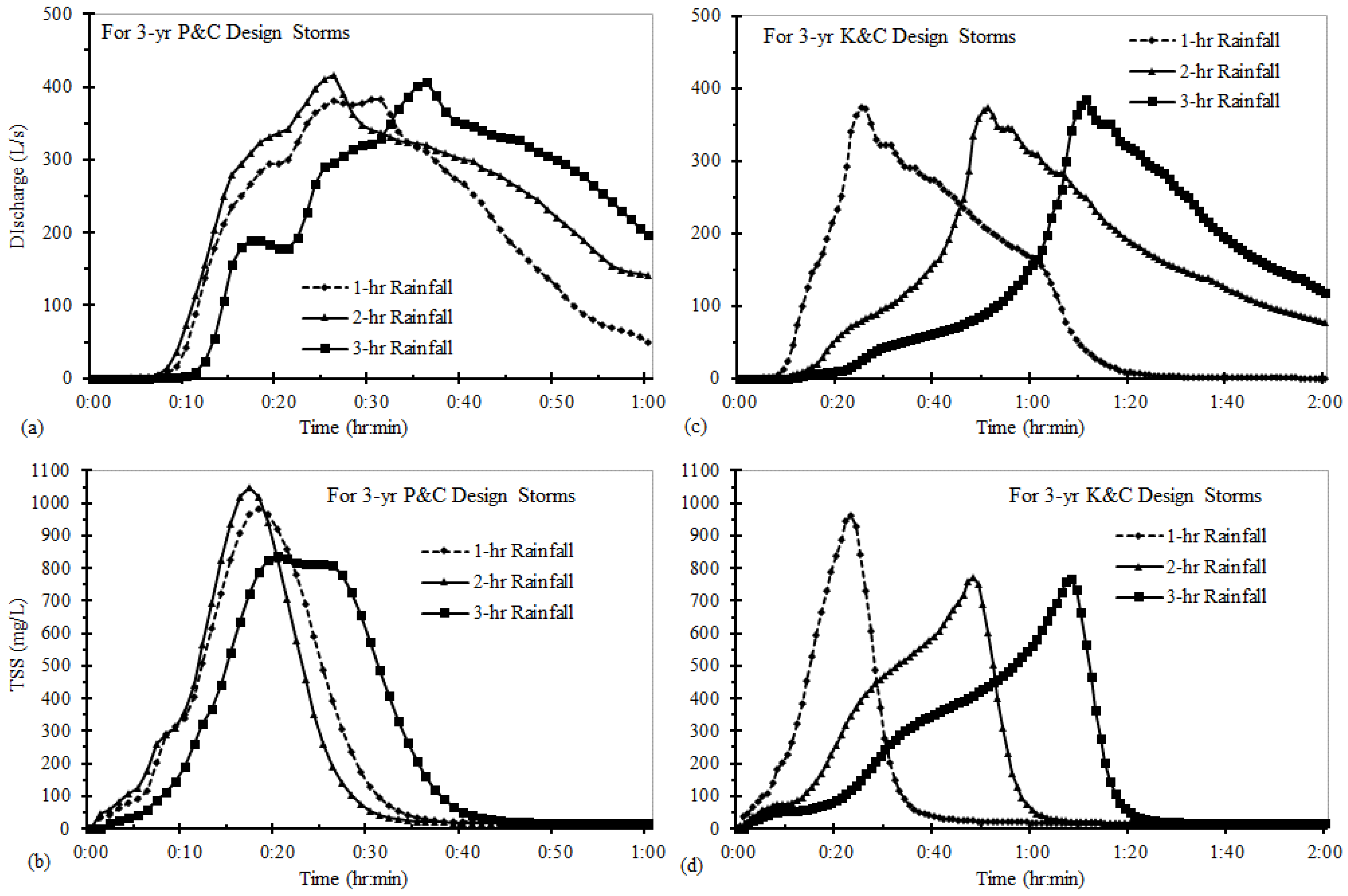
TSS resulted from different rainfall durations are shown in
Figure 11 using three P&C design rainfall distributions, which were based on observed long-term heavy rainfall events in Beijing central districts [
32], and three K&C rainfall distributions based on Beijing IDF curves. The P&C distributions have periods in which incremental rainfall during successive intervals can be either lower or higher than in the previous interval (
Figure 5). The P&C distributions were different from the K&C distributions and the alternating block distribution (
Figure 2,
Figure 3 and
Figure 4) in which the 5-min incremental rainfalls gradually increased to the peak rainfall and then gradually decreased. The results indicate that for the same total rainfall depth, the rainfall duration was a major factor of the urban NPS pollutant loads. Pollutographs in
Figure 11 show that the TSS peak concentrations at the outlet for the 60-, 120- and 180-min rainfall durations were 983.7 mg/L, 1047.8 mg/L and 838.1 mg/L, respectively, for three-year P&C design rainfall distributions. Even though the average rainfall intensity of a short-duration rainfall event is greater than that of a long-duration event, incremental 5-min rainfall (or rainfall intensity) of the 2-h P&C distribution during the first 25 min is larger than for both the 1-h and 3-h P&C design storm rainfall distributions (
Figure 5). Therefore, simulated discharge and TSS concentration at the outlet for the 2-h storm increase faster and reach higher peaks at earlier times than do these measures for 1-h and 3-h storm durations (
Figure 11 and
Table 7). For the 3-h P&C design storm distribution, lower rainfall at 15–20 min results in small decreases of discharge (17–21 min) prior to the occurrence of
Qp as well as in TSS concentration (838.1–807.8 mg/L at 21–26 min) after the TSS peak (at 21 min). The TSS time base for the 3-h storm is 41 min, which is only slightly larger than that for the 1- and 2-h storms (35 and 32 min, respectively;
Table 7). For the period after the TSS time base, even though discharges at the outfall remain large (
Figure 11), TSS concentrations are less than 30 mg/L because most of initial TSS buildup has already been washed off and transported through the outlet. Such is the case for the other scenarios shown in
Figure 8 and
Figure 10.
The resulting hydrographs and TSS pollutographs for 1-, 2-, and 3-h K&C distributions of rainfall from a three-year design storm has consistent patterns. Peak discharges and outlet TSS loads increase while peak TSS concentrations and the outlet EMCs decrease as the storm duration increases (
Table 7). Likewise, the TSS time base increases from 42 to 81 min as design storm duration increases from 1 h to 3 h because these K&C distributions (
Figure 5) have the same peak location constant (
r = 0.375) and are similar second-quartile storms. For P&C distributions of three durations, the peak location with respect to total rainfall duration is not constant; therefore, simulated hydrographs and TSS pollutographs are not similar from one duration to another of P&C distributions.
Total pollution loads of TSS at the catchment outlet are 221.9 kg, 216.4 kg and 234.5 kg for the 60-, 120- and 180-min rainfall durations, respectively. The outlet TSS load from 3-h duration rainfall is slightly larger than loads from 1- and 2-h rainfall, perhaps because the pollutant load is related to rainfall flushing time of the pollutant washoff process. For any given rainfall volume, long-duration rainfall implies a long pollutant washing time, which in turn will wash away more pollutants than rainfall of a shorter duration.
As indicated by the above conclusions, there are close relationships between TSS concentration in runoff and rainfall characteristics (rainfall patterns, rainfall intensity and rainfall duration). Among these rainfall characteristics, rainfall intensity and duration are the two dominant factors that control the hydrologic response, an observation corroborates by others [
49,
50].