Abstract
Water markets have been used by Australian irrigators as a way to reduce risk and uncertainty in times of low water allocations and rainfall. However, little is known about how irrigators’ bidding trading behavior in water markets compares to other markets, nor is it known what role uncertainty and a lack of water in a variable and changing climate plays in influencing behavior. This paper studies irrigator behavior in Victorian water markets over a decade (a time period that included a severe drought). In particular, it studies the evidence for price clustering (when water bids/offers end mostly around particular numbers), a common phenomenon present in other established markets. We found that clustering in bid/offer prices in Victorian water allocation markets was influenced by uncertainty and strategic behavior. Water traders evaluate the costs and benefits of clustering and act according to their risk aversion levels. Water market buyer clustering behavior was mostly explained by increased market uncertainty (in particular, hotter and drier conditions), while seller-clustering behavior is mostly explained by strategic behavioral factors which evaluate the costs and benefits of clustering.
1. Introduction
Water scarcity has emerged in many semi-arid regions of the world. This requires the development of mechanisms to efficiently reallocate available resources between competing extractive as well as in-stream uses. Water markets have been promoted as an efficient way of facilitating this process in a number of jurisdictions, such as Australia, USA and Chile [1,2,3] and more recently in Canada [4] and Spain [5]. As scarcity intensifies, demand for, and participation in, water markets is likely to increase. A continual review of market mechanisms will help to improve and facilitate greater market efficiency, through reducing transaction costs, improving product choice or reducing barriers to trade. Adoption of water market trading (where available) will represent one potential adaptation strategy for many irrigators in the face of climate change. Modeling by Adamson, Mallawaarachchi and Quiggin [6] demonstrates that adaptation will partially offset the adverse impact of climate change and suggests that improvements in the function of water markets could support adaptation.
In order to provide greater insights into how to best improve water market mechanisms and water management in general, a better understanding of irrigators’ behavior in such markets and how this compares to behavior in other financial markets is necessary. In the Murray-Darling Basin (MDB) of Australia, irrigators’ participation in the water market has been growing over the past two decades and this provides a unique opportunity to study irrigators’ water market behavior. Two major forms of water markets exist in the MDB: the water allocation market (also known as temporary water markets, which involve the short-term right to use of water) and the water entitlement market (also known as permanent water markets involving the long-term right to access water—see Wheeler et al. [7] for more detail). This paper focuses on the water allocation market.
Since the Council of Australian Governments water reform agenda in 1994, water markets have played a central role in allowing farmers to deal with increased volatility, risk and adjustment pressures by permitting them to alter their short and long-term access to water resources as well as allowing them to exit out of irrigation while realizing their water assets [8,9]. In 2011, the Murray-Darling Basin Authority (MDBA) released the MDB Plan, with a target of 2750 GL to be returned from consumptive to environmental use [10]. Water entitlements are to be sourced from willing sellers, and are bought by the Commonwealth of Australia. Increasingly, there are arguments that governments should also consider buying water from the allocation market (otherwise known as temporary water available in one season) to provide environmental flows [11]. The rationale for government utilizing the water allocation market is that benefits of carry-over, lower water allocation prices, and temporal demand can provide a more efficient and flexible supply of water to meet stochastic environmental flow requirements since the timing of entitlement releases does not correspond well with the volume and timing of water applications required to achieve environmental objectives [3,12].
In light of these policy arguments regarding government intervention in the allocation market, a more thorough understanding of irrigators’ trading behavior in that market, particularly how they bid and offer for water, is needed. In particular, we need to understand how variability in climate conditions impacts on water market trading behavior. One way of analyzing water market trader behavior is to analyze the extent to which irrigator bids or offers exhibit price clustering (that is, the extent they cluster around particular numbers). The existence of clustering is important as it identifies a possible dead-weight loss that exists in water allocation markets. Utilizing bid and offer data also allows us to understand how differently buyers and sellers act in the water market, something that is difficult to do in other water market analysis. It also offers continuing insights into how irrigators behave in water markets, and how similar (or dissimilar) their behavior is to participation in financial markets. Understanding the similarity between irrigator bidding and offering behavior in a water market and a trader in a stock market may also offer insights into how well introducing other water market products (for example: option trading) will be received. For instance, Heaney et al. [13] discuss how missing options markets in storage and delivery might impact water trading. Addressing these issues is a function of market design. Hence, undertaking analysis on price clustering is informative for water management policies aiming to improve the efficiency and flexibility of resource allocation.
Price clustering in financial markets has been well documented in the literature (e.g., Chung and Chiang [14]). Clustering is found when indicative quotes for currencies end mostly around particular numbers, for example, those with either “zero” or “five”. Round numbers are disproportionately represented in bid-ask spreads for major currencies. Typically, the economics and psychological literature identify different reasons for clustering. In economics, clustering is considered a rational response to trading impediments. In psychology, clustering is thought to occur due to a human bias for prominent numbers, such as zero and one. There have been very few studies that have analyzed clustering in other non-financial product markets. There are a number of similarities between financial markets and water markets, but there are also fundamental differences because water markets are dealing with common property resource issues. In addition there is an issue as to whether recent events in financial markets during the global financial crisis make such markets an appropriate benchmark for comparison of resource markets. The issue of the efficient markets hypothesis (EMH) and the global financial crisis (GFC) is discussed by Ball [15] and Brown [16] who suggests that the failure to predict the bursting of the real estate bubble-that lead to the GFC-is in fact consistent with the central idea in the EMH. This paper analyzes clustering in the water allocation market over the past decade. In doing so, we will be able to determine (a) the extent of price clustering in this market and (b) given the constraints that prevent traders having a precise valuation of water, whether clustering behavior is a response to uncertainty (either weather or policy changes) or a strategic behavior.
The only other paper that has examined price clustering in water markets [17] found robust evidence of clustering in the water market in northern Victoria from 2002 to 2007. Its’ econometric modeling suggested uncertainty faced by irrigators is a major reason for clustering. This paper extends the work by Brooks, Harris and Joymungul [17] in four ways. First, a longer time span is used covering 10 trading seasons in the northern Victorian water market. Much of this data is not publicly available. Second, alternative price clustering definitions are employed to check the robustness of the findings. Third, a variety of other data are included to identify specific factors associated with irrigators’ risk awareness that in turn influence the extent of price clustering. In particular, we are interested in assessing how government water policy changes, rainfall and evaporation influence bid and offer behavior in the water market. Finally, the extent to which price clustering is a result of traders’ response to uncertainty and/or strategic behavior is examined.
2. Study Area
The Goulburn Murray Irrigation District (GMID) is Australia’s largest irrigation district, located in northern Victoria, along the River Murray. It has one of Australia’s longest running water markets with the bulk of trading taking place in three trading zones. The most active trading zone is Greater Goulburn, which provides the data source for this paper. Water allocations and entitlements have been traded since the early 1990s and irrigators are increasingly adopting water trading (in particular water allocation trading) over time [18]. Given that the majority of trades, especially bids and offers for water, are in the water allocations market, this is the market we chose to focus on for a study on price clustering in water markets. Dairy, fruit and, grape producers are the most significant buyers in the allocation market, whereas cereal, grazing and mixed farmers are the main sellers [19]. Over the past decade, MDB irrigators have faced considerable changes to their water allocation levels (which conversely influence the amount of land irrigated). An allocation level refers to the percentage of water entitlements that is available for the entitlement holder to use throughout a season. The resource manager manages seasonal allocation levels on behalf of all entitlement holders and regularly reviews the water budget calculations in the GMID. For example, Goulburn water allocation levels dropped from a consistently secure 200% in the early 1990s to around 30% in the mid 2000s. As a result, uncertainty for irrigators has increased considerably with opening allocations of 0% in eight consecutive years from 2002 and below 100% since 1998 and with closing allocations below 100% for five out of eight years from 2002 to 2010 [18]. In 2010 and 2011 higher than expected rainfall increased water allocations, this in turn increased the amount of land irrigated. Furthermore, water policy changes add to the climate uncertainties experienced by irrigators. There have been many government and institutional changes that impact on water markets in Australia over the time-period studied. This paper considers three of the most major ones that occurred, namely: (a) the lifting of the Cap (in 1994 the Victorian Government restricted the volume of water access entitlements that could be traded out of each irrigation district in Northern Victoria to no more than 2% annually of the volume of entitlement held in the district at the start of the irrigation season. On 1 July 2006 this was increased to 4%); (b) introduction of unbundling (this occurred on 1 July 2007 in northern Victoria and it is the legal separation of rights to land and rights to access water, have water delivered, use water on land or operate water infrastructure, all of which can be traded separately) and (c) the times when the Australian Government is conducting a tender in buying back water entitlements (the Federal government began a decade long policy of buying back water entitlements from willing sellers in February 2008 in order to return water from a consumptive to an environmental use—see [7,8] for more detail).
3. Price Clustering Literature and Applications to Water Markets
3.1. Price Clustering Theories
Empirical studies in the finance literature find that the degree of clustering in any market is a function of market structure, uncertainty, resolution costs and human preferences [14]. Several hypotheses have been developed to better understand why clustering occurs. These include: the negotiation hypothesis; the price resolution hypothesis (uncertainty); the attraction hypothesis and strategic behavior. We discuss briefly each of these hypotheses and their relevance in the context of the Australian water market.
A market’s structure may bring about clustering and Harris [20] developed the negotiation hypothesis to explain these effects, arguing that regulatory restrictions can reduce negotiation costs for traders. These restrictions require quotes and transaction prices to be stated as some multiple of a minimum price variation, or trading tick. Negotiation costs fall because restrictions create a discrete price set around which traders bid and offer. In the absence of these restrictions, the number of possible offers and counter-offers widens so that negotiation time also increases, creating higher price risks for participants [21]. A discrete price set reduces the amount of information exchanged, leading price to converge more quickly than would otherwise occur. As a result, transactions costs are reduced. The bid prices in the Australian water market analyzed are not required to be some multiple of a trading tick greater than one cent. Therefore, the degree of clustering is expected to be small because irrigators bid on a continuous price set.
The method of trading can also influence the degree of clustering observed. For example, the use of electronic trade compared with floor trade (in person) alters the costs associated with precise valuation and, therefore, clustering. Chung and Chiang [14] found extreme clustering occurred on floor-traded futures compared with those traded electronically. Floor trade made precise valuation more costly because it takes more time to call out information to the accuracy of several digits and there is a wider margin for error in doing so [21]. The mechanism for water trading in the GMID creates a pool price that tends to decrease the costs associated with precise valuation, so a finer grid of numbers may be expected. However, a uniform pool price each trading week may also decrease the benefits of a precise valuation and the weekly trading frequency may be too long for traders to place more precise bids. Nevertheless, Brooks, Harris and Joymungul [17] found evidence of clustering on bid prices in the GMID water market.
The price resolution hypothesis contends that prices may be evenly clustered at particular points if valuation is indecisive [22]. Loomes [23] and Butler and Loomes [24] argued that economic decision makers do not measure utilities exactly but act in a sphere of haziness, which represents the degree of difficulty in precise valuation. In other words, the risk of taking certain actions increases with uncertainty. A greater sphere of haziness implies a higher clustering propensity due to people’s risk aversion behavior. When uncertainty and volatility are high, precision valuation is costly, leading to greater clustering [25].
In the case of the water market, water availability uncertainty can be brought about by several factors, including rainfall variation, water allocations, demand fluctuations, government policy changes, and climate change [7,19,26]. Variable and unpredictable rainfall in the MDB system can be on a range of time scales and intra-season variations, making it difficult to forecast final closing allocations. Allocations are announced fortnightly during the water season, and as discussed often have started at 0%. Uncertainty in allocations can lead to miscalculations regarding seasonal allocations by irrigators at the time of planting decisions. If an irrigator overestimates what their expected allocations will be at the time of planting a crop, they may have to buy additional water later. Alternatively, if an irrigator underestimates the final allocations they will receive, they may have surplus temporary water available that can be sold in the market at a later point in the season or be carried forward into the next season (depending on storage availability). Climate information only becomes available as the season progresses, so depending on how accurate irrigators were in their water expectations and the watering requirements of their permanent or annual crops, changes (or lack of changes) in monthly seasonal allocations may cause relatively high price volatility in the market. Government intervention in water markets has increased considerably over the first decade of the 21st century [27]. Government intervention affects short- and medium-term price expectations, thereby increasing costs of precise valuations.
Ikenberry and Weston [28] demonstrate that clustering of U.S. stock price also stems from the psychological preferences of market participants. This is broadly referred to as the attraction hypothesis and it suggests that clustering is the result of behavioral idiosyncrasies (heuristics). Tversky and Kahneman [29] argued that individuals often rely on a number of heuristic principles that reduce complex tasks, such as valuation to simpler or even non-optimal judgment operations.
Brooks, Harris and Joymungul [17] use variables representing the price resolution hypothesis to explain price clustering in the GMID water market. Their results indicate a large proportion of the variation in price clustering cannot be explained by the price resolution hypothesis (the largest adjusted R2 in their regression models is 0.61). Therefore, the attraction hypothesis is very likely to be able to explain some of the variation in price clustering that cannot be explained by the models of Brooks, Harris and Joymungul [17]. Unfortunately, it is almost impossible to collect data on testable variables representing the attraction hypothesis.
An alternative explanation for clustering is that its existence is the result of strategic behavior—where people estimate the net benefits of their action [30]. Specifically, they weigh the benefits of increasing the precision of their bid/offer relative to the loss of value resulting from an imprecise estimate. In Victoria, the benefits of precise valuation are not obvious for individual traders on the water market because the water exchange Watermove used a pool price. Watermove was a trading organization in the GMID that conducted water exchanges within MDB trading zones, it operated by telephone and online. It closed down in August 2012, but still remains a valuable source of historical data, especially bid and offer data, and is used in the analysis here. Table 1 presents an example of how the Watermove exchange worked. For example, in the week of 8 September 2011, there were 35 sale offers with the offering price ranging from $14 to $100 and a total volume for sale of 4724.8 ML; and 21 buy bids ranging from $10 to $26.38 with a total volume for purchase of 5841 ML. A pool price of $21.15 (the average price of the last fulfilled sale offer, $20, and buy bid, $22.3—which is calculated after all bids and offers are received for the week) was found for the week in order to maximize the volume traded, namely 1441.5 ML. As a result, the last fulfilled buy bid had bought only 80.5 ML, instead of the full amount, 200 ML. This exchange mechanism results in the potential for price clustering to create a deadweight loss. The size of the deadweight loss depends on the pool price, the last fulfilled sale offer and buy bid prices and the amount of unsatisfied volume to sell or buy. It can be evident that the pool price could be quite different from their offer prices, which is likely to be caused by the weekly trading frequency. In this setting, the cost of rounding will be the lower likelihood of their orders being executed and the cost of not rounding will be the extra expenditure paid by buyers or the reduced revenue for sellers. A strategic bidder, therefore, would evaluate whether the cost of rounding outweighs the cost of not rounding in order to decide the bid price.

Table 1.
An example of Watermove weekly exchange bids and offers.
| Seller Offer Price ($/ML) | Volume for Sale | Total Volume in Exchange | Buyer Bid Price ($/ML) | Volume for Purchase | Total Volume in Exchange |
|---|---|---|---|---|---|
| 14.00 | 200 | 200 | 26.38 | 200 | 200 |
| 15.00 | 103 | 303 | 25.50 | 200 | 400 |
| 15.00 | 18.2 | 321.2 | 25.00 | 400 | 800 |
| 15.00 | 60 | 381.2 | 25.00 | 11 | 811 |
| 17.00 | 80 | 461.2 | 25.00 | 200 | 1011 |
| 18.00 | 55 | 516.2 | 25.00 | 150 | 1161 |
| 19.00 | 320 | 836.2 | 23.38 | 200 | 1361 |
| 19.90 | 100 | 936.2 | 22.30 | 200 | 1561 |
| 20.00 | 100 | 1036.2 | 22.00 | 20 | 1581 |
| 20.00 | 150 | 1186.2 | 20.38 | 200 | 1781 |
| 20.00 | 120 | 1306.2 | 20.00 | 100 | 1881 |
| 20.00 | 59 | 1365.2 | 20.00 | 100 | 1981 |
| 20.00 | 24.3 | 1389.5 | 19.85 | 1500 | 3481 |
| 20.00 | 52 | 1441.5 | 18.00 | 500 | 3981 |
| 28.00 | 50 | 1491.5 | 18.00 | 200 | 4181 |
| 28.00 | 210 | 1701.5 | 15.88 | 200 | 4381 |
| 29.00 | 92 | 1793.5 | 15.00 | 200 | 4581 |
| 30.00 | 379 | 2172.5 | 15.00 | 10 | 4591 |
| 30.00 | 150 | 2322.5 | 14.22 | 500 | 5091 |
| 30.00 | 150 | 2472.5 | 12.88 | 500 | 5591 |
| 30.00 | 60 | 2532.5 | 10.00 | 250 | 5841 |
| 30.99 | 300 | 2832.5 | Date: 8 September 2011 Pool price: $21.15/ML Total volume traded: 1441.5 ML (The shaded bids and offer orders were executed, with the buy order indicated by asterisk only fulfilled by 80.5 ML) | ||
| 30.99 | 140 | 2972.5 | |||
| 35.00 | 500 | 3472.5 | |||
| 42.38 | 490.7 | 3963.2 | |||
| 42.38 | 192.6 | 4155.8 | |||
| 45.00 | 68 | 4223.8 | |||
| 45.00 | 20 | 4243.8 | |||
| 45.00 | 100 | 4343.8 | |||
| 50.00 | 20 | 4363.8 | |||
| 50.00 | 70 | 4433.8 | |||
| 58.00 | 100 | 4533.8 | |||
| 60.00 | 50 | 4583.8 | |||
| 60.25 | 46 | 4629.8 | |||
| 100.00 | 95 | 4724.8 | |||
Traders who expect natural clustering can easily change their offer prices by a cent (penny) to avoid cluster points thereby increasing the probability of their offers being executed, described as the “pennying behavior” by Jennings [31] and also documented in Edwards and Harris [32]. This behavior is evident in the water market as demonstrated in Section 4.2. First, price clustering would decrease when traders seek a higher probability of their orders being executed. On the buyers’ side, traders would require a higher probability of their orders being filled if they had overestimated seasonal allocations and therefore have experienced a deficit in available water. Assuming crop loss is a distinct possibility in this case; traders would avoid clustering to increase the likelihood that they will obtain water. On the sellers’ side, greater precision could be used if surplus water could be sold at a premium price; for example, during times of protracted drought. The high returns available during these periods would encourage a greater determination for offers to be executed. Second, when buyers (sellers) consider the extra dollar expenditure (revenue) as more significant, that is, the costs of not rounding as considerable, price clustering is expected to increase. It is difficult to identify which of these effects will dominate strategic behavior in the water market, as this will depend on the market and biophysical conditions at specific times. The analysis here will investigate the effects of those conditions on the potential for strategic clustering.
3.2. Overall Water Market Clustering Hypothesis
In summary, we propose the reasons for price-clustering behavior in the water allocation market as: (1) attraction; (2) price resolution (or uncertainty); and (3) strategic behavior. Attraction suggests traders prefer certain price points to others for psychological reasons, which is discussed in Section 3.1. Price resolution proposes that traders are more likely to cluster when they perceive uncertainty in water markets is higher. We expect the following variables will be important influences on uncertainty: trading volume, water allocation price, water entitlement price, bid-ask spreads, water allocation level, climate conditions, seasonal factors, and government policy changes. Strategic behavior explanations for price clustering (where water traders will evaluate the cost and benefits of clustering, or the costs of rounding and not rounding) would also be influenced by many of these same factors. Farmers decide to trade one more unit of water allocations if the cost (revenue) from the trade is smaller (greater) than the value of the marginal product of their additional water using activities. Hence, the bid and offer prices are likely to reflect the farming enterprises and the associated risk levels for the farming enterprises if there is water scarcity. Since price clustering is measured for the whole Greater Goulburn region, we cannot consider farming enterprise variables. This question is left for future research that needs access to data across a variety of regions or access to bid and offer individual survey records (either entitlement or allocation records).
The following sections identify evidence that support the attraction hypothesis, as well as determining the extent to which price resolution and strategic behavior can explain price clustering in the water market.
4. Price Clustering Evidence in the Greater Goulburn Water Allocation Market
Before analyzing the drivers of clustering behavior in the water market, we first determined if there was evidence of clustering. We collected weekly data from Watermove on all individual buy and sell bids, including the volumes and prices of each bid for the period August 2001 to May 2011 for Greater Goulburn in Victoria—the most active trading zone. Most of these time series data are not publicly available. The data include quite a few weeks where the total number of orders is less than 20. In order to have a sufficiently large base of bids, we calculated price clustering at monthly intervals. Orders are fewer both at the start and toward the end of each season. The analysis covers ten years, and our monthly clustering series includes 100 observations, sufficient for the subsequent regression analyses. June and July are not included as there is usually no, or very scarce, trading in those two months. For the whole dollar amount clustering series of sell offers within the 10% range of the pool price, the number of sell offers is smaller than 30 for most of the months in the 2010/2011 season. This small number of observations makes the clustering calculation unreliable. Therefore, there are 90 months instead of 100 for this clustering series.
4.1. Evidence of Price Clustering
Table 2 provides an overview of the existence of price clustering in the Greater Goulburn water allocation market. We first examined the extent of clustering at whole dollar amounts, versus amounts at particular cents. Over the time period being considered, 80% of all water allocation buy bids and 96% of all sell bids were placed at whole dollar amounts. Moreover, Table 2 also illustrates that if percentages are weighted by the volume associated with each order, whole dollar clustering decreases to 73% and 92% for the buy and sell orders respectively.

Table 2.
Water allocation price clustering (%) at whole dollars.
| Water Trade Type | All | Within 10% of Pool Price | Within 5% of Pool Price | |||
|---|---|---|---|---|---|---|
| Number | ML | Number | ML | Number | ML | |
| Buy bids | 79.59 | 72.74 | 78.39 | 70.77 | 78.43 | 71.11 |
| Sell offers | 96.47 | 91.69 | 95.92 | 91.08 | 95.84 | 91.20 |
By including orders where prices are too distant from the pool price the extent of price clustering may be biased upward because it is less costly to be precise if a price offering is likely to be far away from the pool price. As a result, it is possible for an irrigator to be acting in a greater sphere of haziness. Therefore, we calculate the clustering at whole dollar amounts again but use only those orders whose prices are within 10% of the pool price range and then only within 5% of the pool price range. As expected, Table 2 indicates the extent of price clustering decreases when orders are constrained in a narrower range around the pool price. However, the decrease appears to be small and insignificant.
Table 3 explores the extent of clustering at specific whole dollar digits of the buy and sell offers. For buy offers that are whole dollar amounts, Table 3 shows more than half of them ended in zero, while about a fifth end in five. Results are similar if the percentages are weighted by the order volumes or if only those orders within 10% or 5% of the pool price range are used.
The extent of clustering at whole dollar amounts and at specific whole dollar digits is similar to what is found for the Greater Goulburn trading zone in Brooks, Harris and Joymungul [17], where the authors use data from 2002 to 2007. Similar to Brooks, Harris and Joymungul [16], we used Chi-squared and HHI (Herfindahl-Hirschman Index) to test the significance of price clustering in our data. The results, which are available upon request, indicate the presence of significant price clustering. To further investigate price clustering over time, we present the buy and sell offer series for clustering at whole dollar amounts in Figure 1 and for clustering at the specific whole dollar digit zero in Figure 2. Figure 1 demonstrates that neither series exhibits a clear time trend but the buy offer series appears to have a greater variation over time. An augmented Dickey-Fuller unit root test indicates the absence of a unit root for both series. In Figure 2, both series appear to vary within a wider range, especially for the sell offers, compared to the results in Figure 1. The time series of clustering at the specific whole dollar digit zero also exhibits no clear time trend and does not have a unit root.

Table 3.
Water allocation price clustering at whole dollar digits (%).
| Whole Dollar Digits | All | Within 10% of Pool Price | Within 5% of Pool Price | |||
|---|---|---|---|---|---|---|
| Number | ML | Number | ML | Number | ML | |
| Buy offers | ||||||
| 0 | 54.17 | 44.82 | 52.14 | 44.53 | 51.61 | 42.99 |
| 1 | 9.87 | 11.21 | 10.63 | 11.86 | 11.24 | 11.66 |
| 2 | 4.58 | 8.64 | 5.32 | 5.39 | 5.83 | 6.60 |
| 3 | 1.89 | 2.42 | 2.16 | 2.57 | 2.09 | 2.59 |
| 4 | 0.76 | 0.88 | 0.94 | 1.20 | 0.83 | 1.19 |
| 5 | 20.01 | 20.64 | 18.94 | 20.65 | 17.97 | 20.61 |
| 6 | 3.99 | 5.08 | 4.27 | 5.61 | 4.22 | 4.88 |
| 7 | 2.13 | 2.78 | 2.06 | 2.88 | 2.11 | 3.24 |
| 8 | 1.74 | 2.62 | 2.39 | 3.97 | 2.92 | 4.94 |
| 9 | 0.87 | 0.91 | 1.14 | 1.34 | 1.18 | 1.29 |
| Sell offers | ||||||
| 0 | 71.38 | 59.16 | 67.28 | 56.02 | 67.02 | 55.00 |
| 1 | 0.48 | 0.84 | 0.53 | 0.86 | 0.49 | 0.74 |
| 2 | 0.87 | 1.81 | 0.96 | 1.78 | 1.01 | 1.80 |
| 3 | 0.66 | 1.32 | 0.87 | 1.36 | 1.05 | 1.78 |
| 4 | 1.36 | 2.63 | 1.75 | 2.66 | 1.60 | 2.48 |
| 5 | 14.52 | 19.76 | 16.54 | 21.00 | 15.86 | 20.31 |
| 6 | 0.57 | 1.07 | 0.76 | 1.29 | 0.84 | 1.30 |
| 7 | 1.04 | 1.67 | 1.16 | 1.68 | 1.27 | 1.77 |
| 8 | 3.12 | 4.77 | 3.54 | 4.91 | 4.36 | 6.36 |
| 9 | 6.01 | 6.96 | 6.62 | 8.44 | 6.50 | 8.46 |
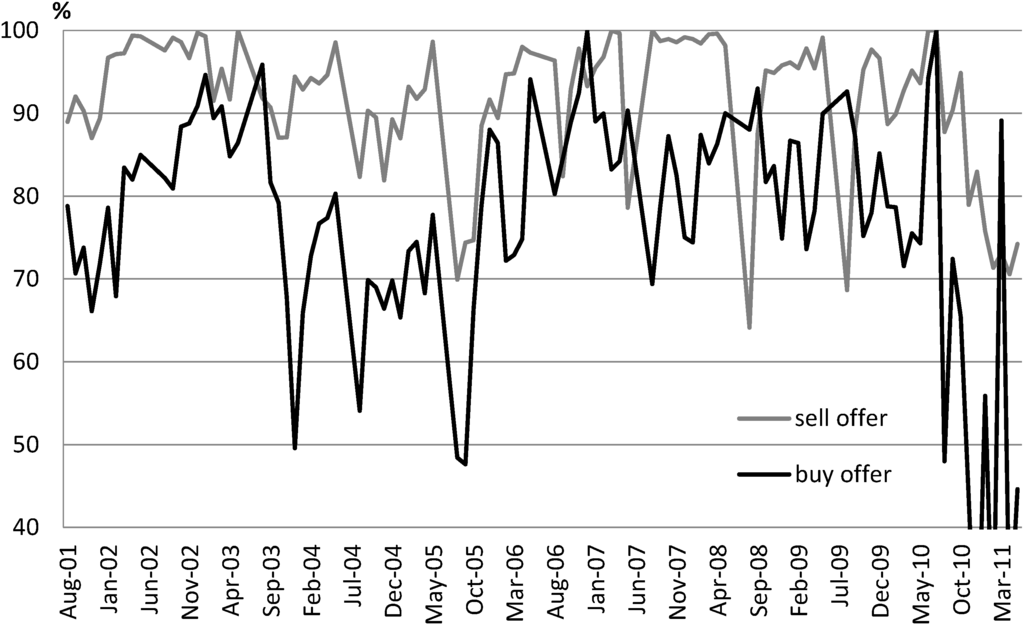
Figure 1.
Water allocation price clustering at whole dollar amounts (all offers).
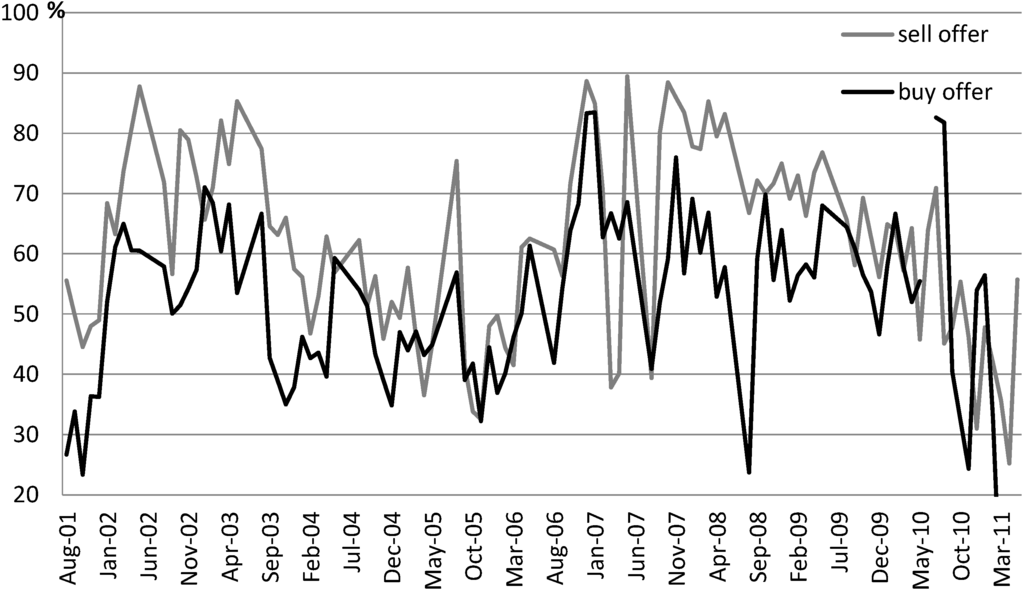
Figure 2.
Water allocation price clustering at whole dollar digit ending in zero (all offers).
4.2. Evidence of Strategic Price Clustering Behavior
Niederhoffer [33] argues that asymmetry between ask and bid quotes around integer prices could exist because of strategic behavior where the intention is to exploit opportunities resulting from price clustering. Aşçıoğlu, Comerton-Forde and McInish [34] show that investors submit orders with one tick better than zero and five to avoid queuing orders at prices ending in these digits. Given prices cluster on round numbers, a water trader who places a bid and wants a higher probability of execution than a bid at the clustered price will tend to place the bid one cent away from the clustered price. Figure 3 and Figure 4 investigate the evidence of strategic price-clustering behavior.
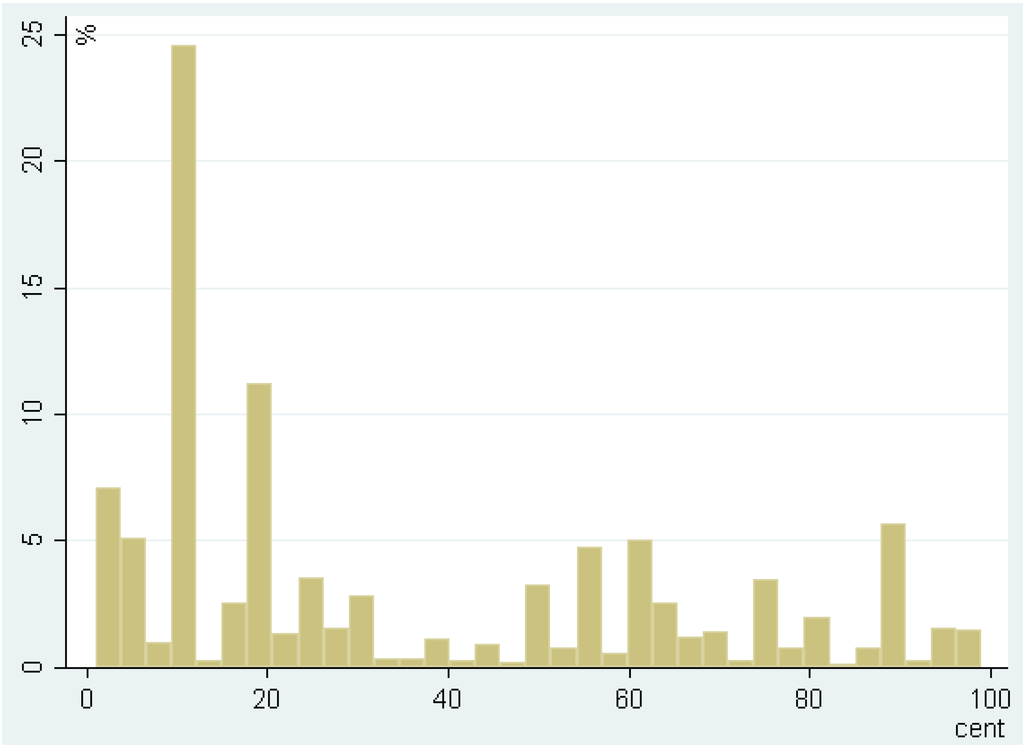
Figure 3.
Distribution of buy offers not ending in whole or half dollar amounts.
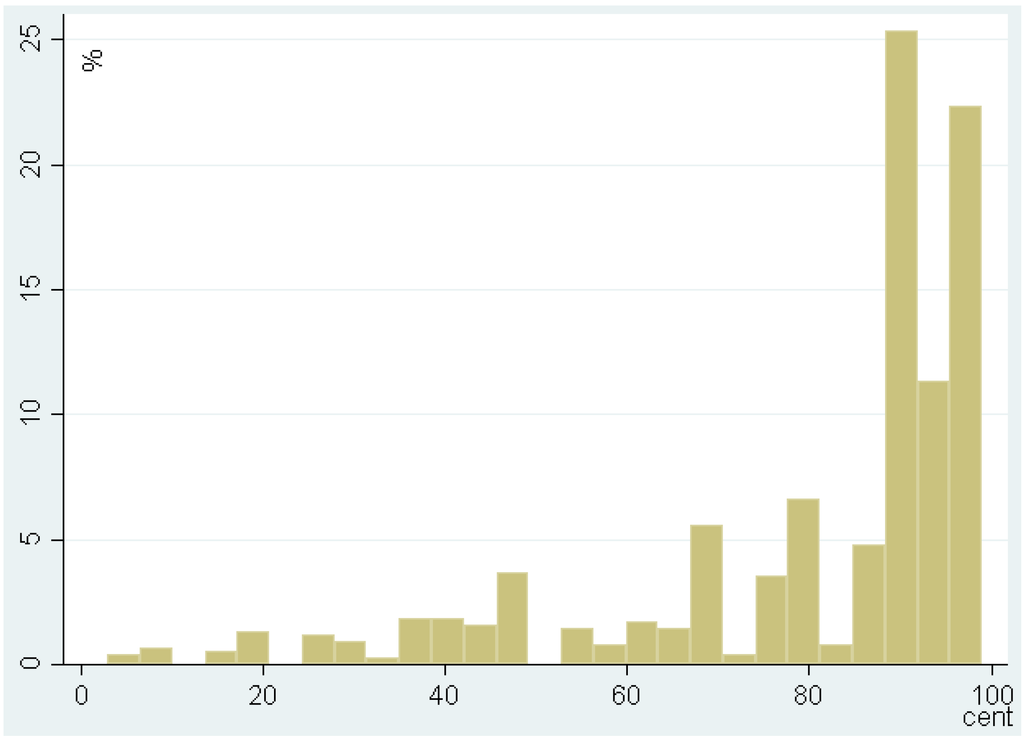
Figure 4.
Distribution of sell offers not ending in whole or half dollar amounts.
The figures respectively show the distribution of buy and sell offers that are not ended in whole or half dollar amounts. Clustering at half dollar amounts is also evident and much greater than its expected clustering. It is evident that the non-whole and half-dollar buy bids are most likely to be slightly greater than the price cluster, while the non-whole and half-dollar sell offers are mostly present slightly less than the price cluster. For those offers of whole-dollar, ending in other than zero or five, Figure 5 and Figure 6 display the distribution across the remaining eight digits. If expecting clustering happens at zero, a buyer is most likely to place a bid with just one extra dollar. In fact, the probability of a buy bid ended in one is about 0.38˗well above the probability of any other seven digits. On the sell side, a seller expecting clustering at zero is most likely to place a bid ended in nine. The probability of a sell bid ended in nine is about 0.43, well above the probability of any other seven digits.
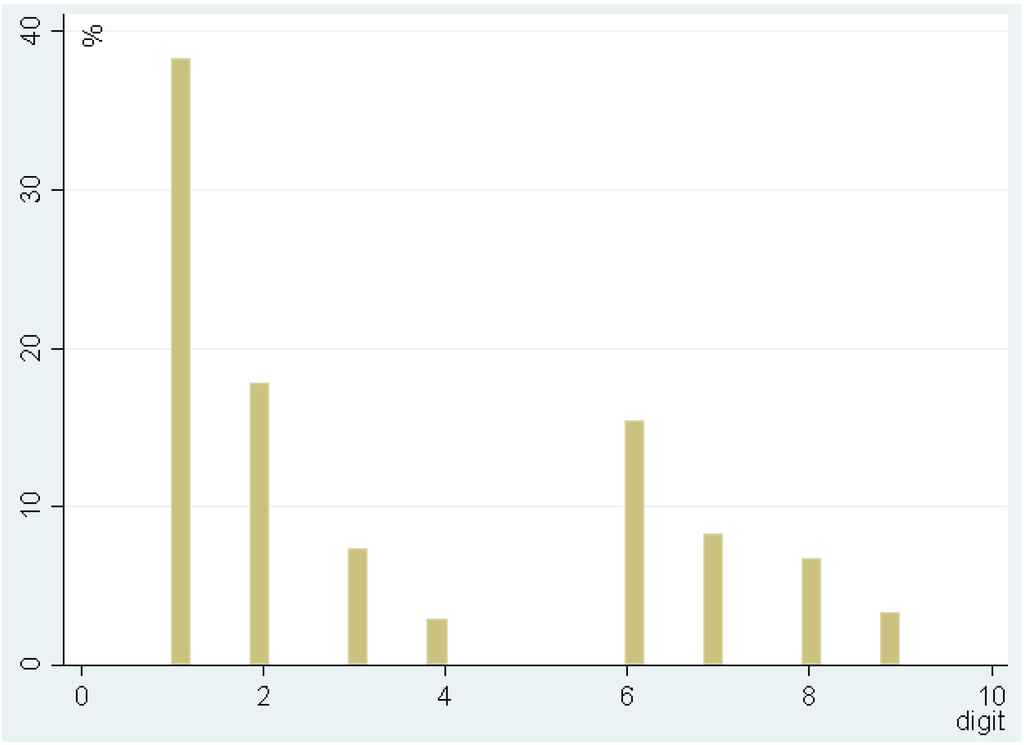
Figure 5.
Distribution of buy offers across eight digits.
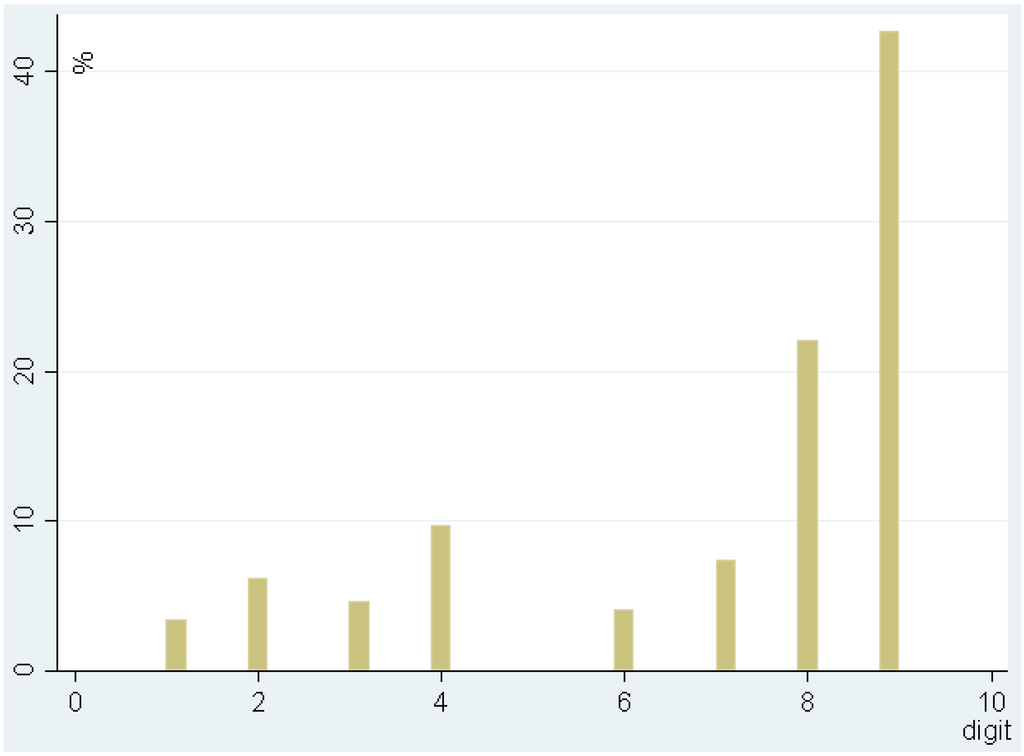
Figure 6.
Distribution of sell offers across eight digits.
5. Methodology
Having observed substantial price clustering in the water allocation market, especially on the sell side, we now investigate the extent to which price clustering is driven by uncertainty and/or strategic behavior and if buyers and sellers’ price-clustering behavior are influenced in the same way. The dependent variable, observed price clustering in a month, is defined as a proportion, which is bounded between 0 and 1. A linear probability model may not be appropriate as it can generate predictions outside the 0 and 1 interval. One way to take account of the bounded nature is the logit transformation and thus the fractional logit model, first used by Papke and Wooldridge [35]. The regression equation used was:
where yt is the observed price clustering in month t, Xt is a vector of regressors that potentially influence the dependent variable, and μt is the disturbance. The logit transformation of yt results in a latent variable yt*, as a linear function of a set of regressors, Xt. The fractional logit model was executed by Stata 13’s generalized linear model (GLM) command with the logit link function. We also used the type of standard error option that is heteroskedasticity- and autocorrelation-consistent to account for any heteroskedasticity and autocorrelation in the disturbance term μt.
yt adopts two types of clustering weighted by order volume, namely: (1) clustering at whole dollar amounts versus fractions; and (2) clustering at whole dollar amounts ending in zero versus the remaining nine digits. For the first definition, the calculation is based on all offers and offers within the 10% range of the pool price. The clustering calculation based on offers within the 5% range of the pool price is not modeled as there is no significant difference in clustering between the 5% and 10% pool price range. For the second definition, the calculation is based on all offers since offers within the 10% range of the pool price in some months do not have enough observations to calculate a reliable clustering percentage.
Independent Variables
Table 4 lists the detailed definitions of the independent and dependent variables that were used in the price clustering models.

Table 4.
Variable definitions.
| Variable Name | Variable Definition |
|---|---|
| WholeBuy | Percentages of buy offers that are whole dollars in each month |
| WholeBuy_10 | Percentage of buy offers that are whole dollars out of those within the plus and minus 10% range of pool price in each month |
| WholeSell | Percentages of sell offers that are whole dollars in each month |
| WholeSell_10 | Percentage of sell offers that are whole dollars out of those within the plus and minus 10% range of pool price in each month |
| ZeroBuy | Percentage of buy offers that end in zero out of buy offers in whole dollars in each month |
| ZeroSell | Percentage of sell offers that end in zero out of sell offers in whole dollars in each month |
| Watervolume | Natural logarithm of volume traded for water allocations in Greater Goulburn in each month |
| Waterallocprice | Natural logarithm of average monthly price ($/ML) for water allocations in Greater Goulburn |
| Waterentprice | Natural logarithm of average monthly price ($/ML) for water entitlements in Greater Goulburn |
| Ln_spread | Natural logarithm of the spread between the last outstanding buyer and seller offering water allocation prices |
| Allocationlevel | Allocation level for Goulburn at the beginning of each month (%) |
| Evapminusrainfall | Monthly evaporation minus rainfall at Kerang station (mm) |
| Feedbarley | Natural logarithm of export price for feed barley ($/ton) |
| Wholemilkprice | Natural logarithm of export price for whole milk powder ($/kg) |
| Cattleprice | Natural logarithm of export price for cattle ($cent/kg) |
| Carryover % | Percentage of water entitlement allowed for carryover (note for 2010/11 season all the allocation in linked Allocation Bank Account on 30 June 2011 is eligible for carryover—there is no maximum) |
| Govpolicy | 1 for the months when major water market policies were introduced/ongoing in the GMID (namely the lifting of the Cap, introduction of unbundling and the times when the Government is conducting a tender in buying back water). For Cap and unbundling introduction, the dummy is coded for the first three months after policy introduction |
| Govpolicy10/11 | Interaction variable between Govpolicy variable and season 2010/11 |
| Monthindex | Monthly index from 1 to 10 for August to May, respectively |
| Monthindexsqrd | Monthly index squared |
Note: The first six variables are the respective dependent variables for the six regression models presented in Table 5.
Our final choice of independent variables was influenced by other studies that have studied influences on water market trade (e.g., Wheeler et al. [19] and Brooks et al. [17]). It was also determined by statistical issues, such as serious multicollinearity (discussed in Section 6). There are a number of potential relationships our independent variables could have with price clustering, and these impacts will vary depending on whether we are looking at buyer or seller behavior. For example, weather, measured by net evaporation in millimeters, may be positively related to price clustering according to the price resolution (uncertainty) hypothesis. Net evaporation is calculated as total evaporation minus total rainfall for the month in question. Ceteris paribus, drier weather increases water prices and, in turn, increases the uncertainty perceived by irrigators who are trying to buy water, resulting in a higher level of price-clustering behavior in the water market. However, drier weather presents a greater need for water in general. In turn, at the margin some buyers will have a greater need to have their orders executed, and therefore act more strategically in the market. This will reduce price clustering overall. Alternatively, as water prices increase sellers’ risk decreases so there is less need for strategic behavior to sell their water. As a result, the overall effect of weather on price clustering depends on whether water buyers or sellers are behaving more risk aversely or strategically. Other independent variables that may be influenced by the price resolution (uncertainty) hypothesis for both buyers and sellers include water allocation and water entitlement prices, trading volume, the spread between the offer prices, feed barley prices, carryover level and government policy. Our government policy variable represents either (a) a time of uncertainty, namely three months after major policy changes, such as unbundling of land and water and the changing water trade restriction policies; and/or (b) a time when the government is purchasing water entitlements in the market. Victoria has had annual restrictions on the amount of entitlement trade allowed out of a district for years. In January 2006, the cap on entitlement trade was eased from 2% to 4%. The unbundling of land and water occurred in the GMID on 1 July 2007. Unbundling reduced the transaction costs associated with trading water, and allowed irrigators to own shares in different rivers (reducing risks). The unbundling aimed to facilitate trading in water entitlement and allocation and make trading more efficient.
Variables that may be influenced primarily by the strategic behavior hypothesis include whole-milk powder prices, cattle prices and water allocations received by irrigators, but risk averse behavior may also play a part in influencing price clustering. Whole-milk powder represents a production output of dairy farmers, feed barley represents an input substitute for watering pasture for dairy production, and cattle represents an alternative output production substitute. The overall influence of each variable will be determined by the strength of each hypothesis in determining behavior. Wherever model statistics allow, we have included all the same independent variables in every model to examine whether there are any differences between the influences on buying and selling clustering behavior.
6. Results and Discussion
Results for our buy and sell price clustering models in the Greater Goulburn water allocation market are presented in Table 5. Since the coefficient results produced by the fractional logit model are not practically meaningful, we report the marginal effect estimates. Multicollinearity was an issue in some of the models, with the variance inflation factors (VIFs) of water allocation price, water entitlement price, spread, allocation level and government policy variables being greater than five. The potential consequence is to make the variables involved insignificant where they should be significant. In order to verify whether collinearity caused this problem, we dropped the variables with insignificant coefficients one by one and checked whether the coefficients of the remaining variables became significant. If this was the case, the involved insignificant variables were dropped. However, if it was not the case they were kept in order to minimize omitted variable bias.

Table 5.
Buy and sell offer monthly water allocation price clustering.
| Variable | WholeBuy | WholeBuy_10 | ZeroBuy | WholeSell | WholeSell_10 | ZeroSell |
|---|---|---|---|---|---|---|
| Watervolume | −0.003 | −0.034 | −0.035 *** | 0.016 *** | 0.026 | −0.032 * |
| Waterallocprice | 0.016 | 0.033 | - | −0.005 | - | 0.045 |
| Waterentprice | 0.067 | 0.079 | - | −0.165 *** | - | - |
| Ln_spread | −0.015 | −0.096 *** | 0.050 *** | 0.046 *** | - | 0.063 *** |
| Allocationlevel | 0.001 | 0.002 | - | −0.0002 | - | - |
| Evapminusrainfall | 0.001 *** | 0.001 *** | 0.0003 | 0.00004 | −0.0001 | 0.00002 |
| Feedbarley | 0.240 *** | 0.377 *** | 0.090 | −0.010 | 0.052 | −0.020 |
| Wholemilkprice | −0.122 | −0.225 * | −0.130 ** | 0.094 *** | 0.026 | 0.179 ** |
| Cattleprice | −0.059 | 0.011 | −0.039 | −0.363 *** | −0.478 *** | −0.389 * |
| Monthindex | −0.055 ** | −0.128 *** | 0.016 *** | 0.009 *** | - | 0.015 *** |
| Monthindexsqrd | 0.005 ** | 0.011 *** | - | - | - | - |
| Carryover | −0.001 | 0.000 | 0.0002 | −0.0003 | −0.001 | −0.001 ** |
| Govpolicy | 0.076 * | 0.135 ** | 0.008 | −0.028 | −0.070 ** | −0.090 |
| Govpolicy10/11 | −0.255 *** | −0.248 *** | −0.277 *** | −0.029 | - | 0.075 |
| Observations | 100 | 94 | 100 | 100 | 90 | 100 |
| Log likelihood | −35.80 | −32.66 | −44.52 | −19.34 | −18.89 | −42.65 |
| BIC | −386.85 | −356.94 | −405.79 | −393.45 | −360.68 | −401.31 |
Note: Marginal effects are reported. * p < 0.1; ** p < 0.05; *** p < 0.01 indicate significance at the 10%, 5% and 1% levels, respectively.
6.1. Buy Offer Price Clustering
Positive coefficients for net evaporation, feed barley price and the government policy dummy suggest that uncertainty (from the price resolution hypothesis) is able to explain clustering by buyers in the water market. Higher net evaporation loss increases water uncertainty and increases clustering. Higher feed barley prices augment water demand because it is an input substitute for on-farm feed production. In turn, as feed barley prices rise dairy farmers will find it more costly to replace water to grow their own pasture with purchased feed. This increases water market demand, and the costs of precise bids thereby causing greater clustering in buy offers.
The government policy dummy represented periods of uncertainty and significant government intervention in the market (e.g., the first three months following significant government changes) and is associated with greater uncertainty in water prices; especially in the short-term after the policy introduction. For two of three buy models; periods of policy uncertainty were positively and significantly associated with price clustering. This implies that water allocation buyers are using price clustering as a response to policies that add to market uncertainty. In times of change; irrigators will be operating in a greater sphere of haziness; with higher levels of uncertainty and volatility being experienced; so buyers exhibit a higher clustering propensity.
A surprising finding regarding the government policy variable is the result of its interaction with season 2010/11, when water was plentiful due to the record rainfall during the season, when prices dropped accordingly. Contrary to the positive impact of government policy on price clustering observed for previous seasons, government policy had a significantly negative impact in 2010/2011. Two influences (government intervention and rainfall) may explain this result. The Commonwealth was in the market buying entitlement water from November 2010 to May 2011, which was a time of flooding and falling water prices. The flooding reduced irrigator buyers’ risk and their water demand, thereby reducing their clustering.
The price resolution hypothesis also predicts that the trade volume is negatively associated with price clustering, while price is positively related to price clustering. Our results, however, only offer a very weak support for this. The volume of trade has a significantly negative impact on clustering in the zero buy model, while a negative but insignificant impact on clustering at whole dollar. Neither water allocation nor entitlement prices have significant impact on clustering although their impacts are estimated as positive.
The coefficients of our time variable—months in the year (and its squared term)—suggests buyer price clustering generally decreases from the start of the season (August) until the month of January and then increases until the end of the season. Brennan [27] argued irrigators are generally risk averse and will hold more water than required at the start of a season when climate and allocation information is yet to be revealed, creating price premiums. As a result, some buyers may be more concerned with having their orders executed, increasing the costs of rounding. If, in the aggregate, all buyers behave this way, clustering will fall over the season. This result could also be explained by buyers’ aversion to the sequential resolution of uncertainty suggesting a preference for uncertainty to be resolved all at one time rather than sequentially [36]. Hence, facing limited and uncertain climate information at the beginning of the season, buyers intend to secure the water they need at one time rather than through multiple orders as the season progresses. Later in the season (e.g., January onwards in our results) when climate and allocation information are revealed, uncertainty will diminish, the costs of rounding will decrease and therefore, clustering will increase again. The results presented in Table 5 demonstrate this outcome for most of the buy models, whereas in the sell models the opposite is true: clustering tends to increase throughout the water season.
The results that suggest strategic behavior as a reason for clustering by water buyers include the negative coefficient for whole milk powder price. When the milk powder price increases, irrigators have greater incentive to produce milk to take advantage of the higher returns. In turn, they are more determined to have their buy offers executed, so the costs of rounding increases thereby decreasing price clustering. We would expect to see the opposite effect on clustering if the price resolution hypothesis applied in this case.
But overall, it appears that buyer bid behavior in water markets is most influenced by price resolution (uncertainty) rather than strategic behavior. In light of the fact that our data-set includes years during which irrigators were learning how to use the new water market, it is not surprising that, on balance, uncertainty would create costs associated with precision thereby leading to greater clustering. The continuing tendency for clustering on the buyers’ side of the market may well reflect the ongoing uncertainty caused by the combined effects of Australia’s highly variable climate and changes in government policy.
6.2. Sell Offers Price Clustering
Both the price resolution hypothesis and strategic behavior can also be identified from significant variables in our seller price clustering models. The results for volume could support either hypothesis with positive coefficients in the WholeSell models and negative coefficients for the ZeroSell model. An increase in clustering in the whole sell models reflects strategic behavior where the costs of rounding are low because sellers may be less determined to have their trades executed. The price resolution hypothesis better explains the decrease in clustering in the ZeroSell model because greater trade intensity creates higher liquidity levels and produces more information with regard to value, allowing for greater precision. In combination, these factors reduce volatility and clustering. Alternatively, these mixed signs could suggest that the attraction hypothesis better explains the effects of volume on clustering for water sellers and that these traders are simply drawn to particular numbers.
The positive significant coefficients for spread lend support to the price resolution hypothesis because a wider bid-ask spread indicates precise valuations are more difficult. This adds to market volatility, so clustering will increase. The negative and significant coefficient on cattle prices is also consistent with the price resolution hypothesis. An increase in cattle prices (which is a dryland output substitute for irrigated production) would lead to a reduction in water demand and price. Falling water prices increase the costs of rounding thereby causing the clustering levels to fall also.
Water entitlement price is significantly negative in the WholeSell model, which suggests that strategic behavior, rather than the price resolution hypothesis, explains price clustering at whole dollars. When some buyers replace water entitlements with water allocations due to increasing water entitlement prices, the demand for water allocations increases and this pushes up water allocation prices. Water allocation sellers may consider the loss in revenue from pennying behavior is compensated by the higher allocation price and a greater chance of offer execution. Hence price clustering decreases and pennying behavior increases.
A positive impact of whole milk powder price, or a negative impact of carry-over level on price clustering, would suggest that strategic behavior may be playing a role in seller behavior. Our results support these hypotheses. Whole milk powder price has a positive estimate in all sell models and significant in the WholeSell and ZeroSell models, while carry-over level has a negative estimate in all sell models but is only significant in the ZeroSell model. As whole milk powder price rises, demand for water also increases so that higher returns from selling water accrue and sellers may expect to trade a higher volume. This magnifies the extra dollar per megaliter from clustering at whole dollars ending in zero, indicating strategic behavior may be utilized by sellers in these situations.
A higher carry-over percentage potentially increases the demand for water allocations in the market, especially later in the season, as risk-averse farmers can carry-over water that they have not used, and buy extra supplies to cover potential shortfalls the following season. This is a more dynamic explanation of the impact of carry-over in the water market, where irrigators are adjusting their practices over seasons. Water allocation prices are therefore higher than otherwise and price clustering decreases.
The government policy variable had a significant negative impact on price clustering in the WholeSell_10 model. In general, periods of policy uncertainty decrease price-clustering behavior by sellers, indicating that perhaps price increases are expected, there is a lower risk of entering the market for sellers and hence price-clustering behavior falls.
The relationship between most of the variables and clustering outcomes on the sellers’ side of the market runs in the opposite direction to that which would be expected under the price resolution hypothesis. Therefore, it appears that strategic behavior influences seller bid behavior more than buyer bid behavior.
7. Conclusions
This paper has provided evidence to show there are a range of influences impacting buyer and sellers’ water allocation market behavior in the Greater Goulburn trading zone in Victoria. While there are similarities between irrigators’ behavior in the water market and general investors’ behavior in the financial product markets, such as strong evidence of price clustering present in both markets, differences between two markets exist in terms of the explanations for price clustering, which we have investigated in the current study. Understanding irrigators’ water market clustering behavior allows us to gain a range of possible insights about how buyers and sellers may respond to uncertainty and policy changes in the market. These insights are useful for achieving more efficient resource allocation. Our analyses indicate that buyer-clustering behavior is for the most part explained by the price resolution hypothesis—where uncertainty tends to increase risks and decrease the costs of rounding. The cost of precision valuation increases when water allocation prices are difficult to predict and are volatile. For buyers, times of severe climate conditions (e.g., hotter and drier conditions), commodity price volatility, and government policy introduction increases the risk associated with trading and, thereby, their price-clustering behavior.
Conversely, the models’ results seem to reflect that sellers’ clustering behavior is more reflective of strategic behavior than uncertainty. Strategic behavior in water markets prevails when the benefit of clustering does not outweigh its cost. These costs may include a reduction in the chance of order execution; an increase in the purchase cost for buyers; or an associated loss of sale revenue for water sellers. Correspondingly, the cost of unsuccessful sale offers is high if buyers are in greater need of water or if sellers keenly anticipate the revenue from water sales. Under such circumstances of high costs, traders are likely to consider carefully the cost of clustering and bid/offer strategically, which our results suggested happened the most in the seller clustering models. Hence, our results suggest sellers are acting in a more sophisticated manner in water markets than water buyers, and most of the costs of clustering are therefore borne by buyers.
In terms of policy implications from this research, it is clear that there is a need, wherever possible, for governments to attempt to reduce irrigator uncertainty. This will be of most importance for buyers. More effective farmer adaptation to external impacts, such as water variability is driven by timely and useful information. Water price, climate, commodity forecasts, allocation information and certainty in government policy are all important influences of water market strategies. Incomplete and fragmented information, as well as uncertain policy, decreases farmers’ ability to manage their water needs.
Acknowledgments
This research was supported by an Australian Research Council Discovery Project DP140103946.
Author Contributions
Alec Zuo conducted the majority of the analysis, and wrote the paper with Sarah Wheeler. Robert Brooks and Edwyna Harris provided the original idea for the paper, and Henning Bjornlund provided historical water market data.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bjornlund, H.; McKay, J. Aspects of water markets for developing countries—Experiences from Australia, Chile and the US. Environ. Dev. Econ. 2002, 7, 767–793. [Google Scholar] [CrossRef]
- Grafton, R.Q.; Libecap, G.; McGlennon, S.; Landry, C.; O’Brien, B. An integrated assessment of water markets: A cross-country comparison. Rev. Environ. Econ. Policy 2011, 5, 219–239. [Google Scholar] [CrossRef]
- Wheeler, S.; Garrick, D.; Loch, A.; Bjornlund, H. Evaluating water market products to acquire water for the environment in Australia. Land Use Policy 2013, 30, 427–436. [Google Scholar] [CrossRef]
- Nicol, L.; Klein, K.; Bjornlund, H. Permanent transfers of water rights: A study of the southern Alberta market. Prairie Forum 2008, 33, 341–356. [Google Scholar]
- Giannoccaro, G.; Pedraza, V.; Berbel, J. Analysis of stakeholders’ attitudes towards water markets in Southern Spain. Water 2013, 5, 1517–1532. [Google Scholar] [CrossRef]
- Adamson, D.; Mallawaarachchi, T.; Quiggin, J. Declining inflows and more frequent droughts in the Murray-Darling Basin: Climate change, impacts and adaptation. Aust. J. Agric. Resour. Econ. 2009, 53, 345–366. [Google Scholar] [CrossRef]
- Wheeler, S.; Loch, A.; Zuo, A.; Bjornlund, H. Reviewing the adoption and impact of water markets in the Murray-Darling Basin, Australia. J. Hydrol. 2014, 518, 28–41. [Google Scholar] [CrossRef]
- Crase, L.; Pagan, P.; Dollery, B. Water markets as a vehicle for reforming water resource allocation in the Murray-Darling Basin. Water Resour. Res. 2004, 40, 1–10. [Google Scholar] [CrossRef]
- National Water Commission. Impacts of Water Trading in the Southern Murray—Darling Basin Between 2006–07 and 2010–11; Commonwealth of Australia: Canberra, Australia, 2012. [Google Scholar]
- Murray-Darling Basin Authority (MDBA). Proposed Basin Plan; MDBA: Canberra, Australia, 2011. [Google Scholar]
- Market Mechanisms for Recovering Water in the Murray-Darling Basin; Final Report for Productivity Commission: Canberra, Australia, 2010.
- Loch, A.; Bjornlund, H.; Wheeler, S.; Connor, J. Trading in allocation water in Australia: A qualitative understanding of irrigator motives and behavior. Aust. J. Agric. Resour. Econ. 2012, 56, 42–60. [Google Scholar] [CrossRef]
- Heaney, A.; Dwyer, G.; Beare, S.; Peterson, D.; Pechey, L. Third-party effects of water trading and potential policy responses. Aust. J. Agric. Resour. Econ. 2006, 50, 277–293. [Google Scholar] [CrossRef]
- Chung, H.; Chiang, S. Price clustering in E-mini and floor-traded index futures. J. Futur. Mark. 2006, 26, 269–295. [Google Scholar] [CrossRef]
- Ball, R. The global financial crisis and the efficient markets hypothesis: What have we learned? J. Appl. Corp. Financ. 2009, 21, 8–16. [Google Scholar] [CrossRef]
- Brown, S. The efficient markets hypothesis: The demise of the demon of chance? Account. Financ. 2011, 51, 79–95. [Google Scholar]
- Brooks, R.; Harris, E.; Joymungul, Y. Price clustering in Australian water markets. Appl. Econ. 2013, 45, 677–685. [Google Scholar] [CrossRef]
- Bjornlund, H.; Wheeler, S.; Rossini, P. Water Markets and Their Environmental, Social and Economic Impact in Australia. In Water Trading and Global Water Scarcity: International Perspectives; Maestu, J., Ed.; Francis Taylor: Gloucester, UK, 2013; pp. 68–93. [Google Scholar]
- Wheeler, S.; Bjornlund, H.; Shanahan, M.; Zuo, A. Price elasticity of allocations water demand in the Goulburn-Murray irrigation district of Victoria, Australia. Aust. J. Agric. Resour. Econ. 2008, 52, 37–55. [Google Scholar] [CrossRef]
- Harris, L. Stock price clustering and discreteness. Rev. Financ. Stud. 1991, 4, 389–415. [Google Scholar] [CrossRef]
- Grossman, S.; Miller, M.; Cone, K.; Fischel, D.; Ross, D. Clustering and competition in asset markets. J. Law Econ. 1997, 40, 23–60. [Google Scholar] [CrossRef]
- Ball, C.; Torous, W.; Tschoegl, A. The degree of price resolution: The case of the gold market. J. Futur. Mark. 1985, 5, 29–43. [Google Scholar] [CrossRef]
- Loomes, G. Different experimental procedures for obtaining valuations of risky actions: Implications for utility theory. Theory Decis. 1988, 25, 1–23. [Google Scholar] [CrossRef]
- Butler, D.; Loomes, G. Decision difficulty and imprecise preferences. Acta Psycholog. 1988, 68, 183–196. [Google Scholar] [CrossRef]
- Capelle-Blanchard, G.; Chaudhury, M. Price clustering in the CAC 40 index options market. Appl. Financ. Econ. 2007, 17, 1201–1210. [Google Scholar] [CrossRef]
- Mallawaarachchi, T.; McClintock, A.; Adamson, D.; Quiggin, J. Investment as an Adaptation Response to Water Scarcity. In Water Policy Reform: Lessons in Sustainability from the Murray-Darling Basin; Quiggin, J., Mallawaarachchi, T., Chambers, S., Eds.; Edward Elgar: Cheltenham, UK, 2012; pp. 101–126. [Google Scholar]
- Brennan, D. Water policy reform in Australia: Lessons from the Victorian seasonal water market. Aust. J. Agric. Resour. Econ. 2006, 50, 403–423. [Google Scholar] [CrossRef]
- Ikenberry, D.L.; Weston, J.P. Clustering in US stock prices after decimalisation. Eur. Financ. Manag. 2008, 14, 30–54. [Google Scholar]
- Tversky, A.; Kahneman, D. Judgement under uncertainty: Heuristics and biases. Science 1974, 185, 1124–1131. [Google Scholar] [CrossRef] [PubMed]
- Mitchell, J. Clustering and psychological barriers: The importance of numbers. J. Futur. Mark. 2001, 21, 395–428. [Google Scholar] [CrossRef]
- Jennings, R. Getting “pennied”: The effect of decimalization on traders’ willingness to lean on the limit order book at the New York Stock Exchange. NNYSE Doc. 2001, 1, 1–24. [Google Scholar]
- Edwards, A.; Harris, J. Stepping Ahead of the Book; Securities and Exchange Commission: Washington, DC, USA, 2002. [Google Scholar]
- Niederhoffer, V. Clustering of stock prices. Oper. Res. 1965, 13, 258–265. [Google Scholar] [CrossRef]
- Aşçıoğlu, A.; Comerton-Forde, C.; McInish, T.H. Price clustering on the Tokyo Stock Exchange. Financ. Rev. 2007, 42, 289–301. [Google Scholar] [CrossRef]
- Papke, L.E.; Wooldridge, J.M. Econometric methods for fractional response variables with an application to 401(K) plan participation rates. J. Appl. Econ. 1996, 11, 619–632. [Google Scholar] [CrossRef]
- Palacios-Huerta, I. The aversion to sequential resolution of uncertainty. J. Risk Uncertain. 1999, 18, 249–269. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).