Can a Century Old Experiment Reveal Hidden Properties of Water?
Abstract
:1. Introduction: Water Properties and Structure
2. Explanatory Models: Interaction with Magnetic and Electric Fields

2.1. Dielectrophoresis/Electrospray

2.2. Quantum Mechanical/Quantumelectrodynamical Viewpoint
3. Investigated Properties and Features
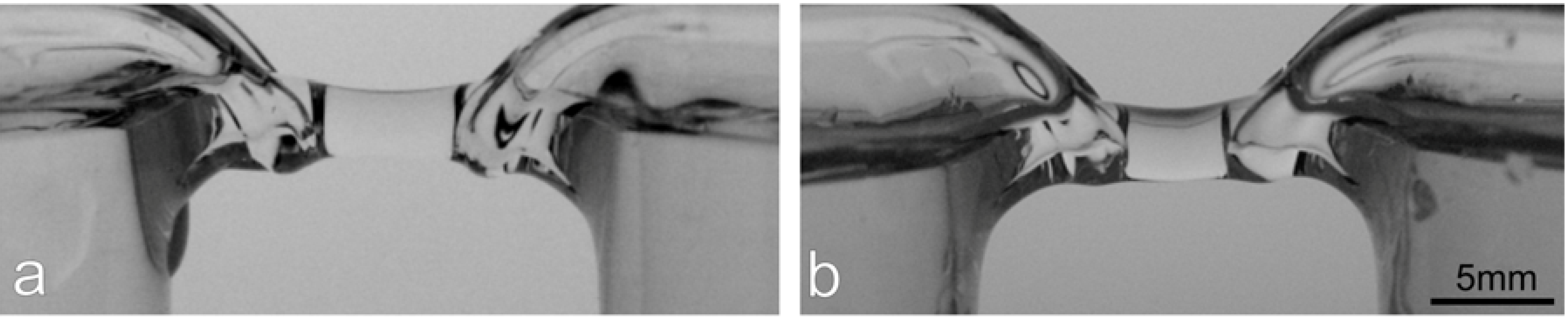
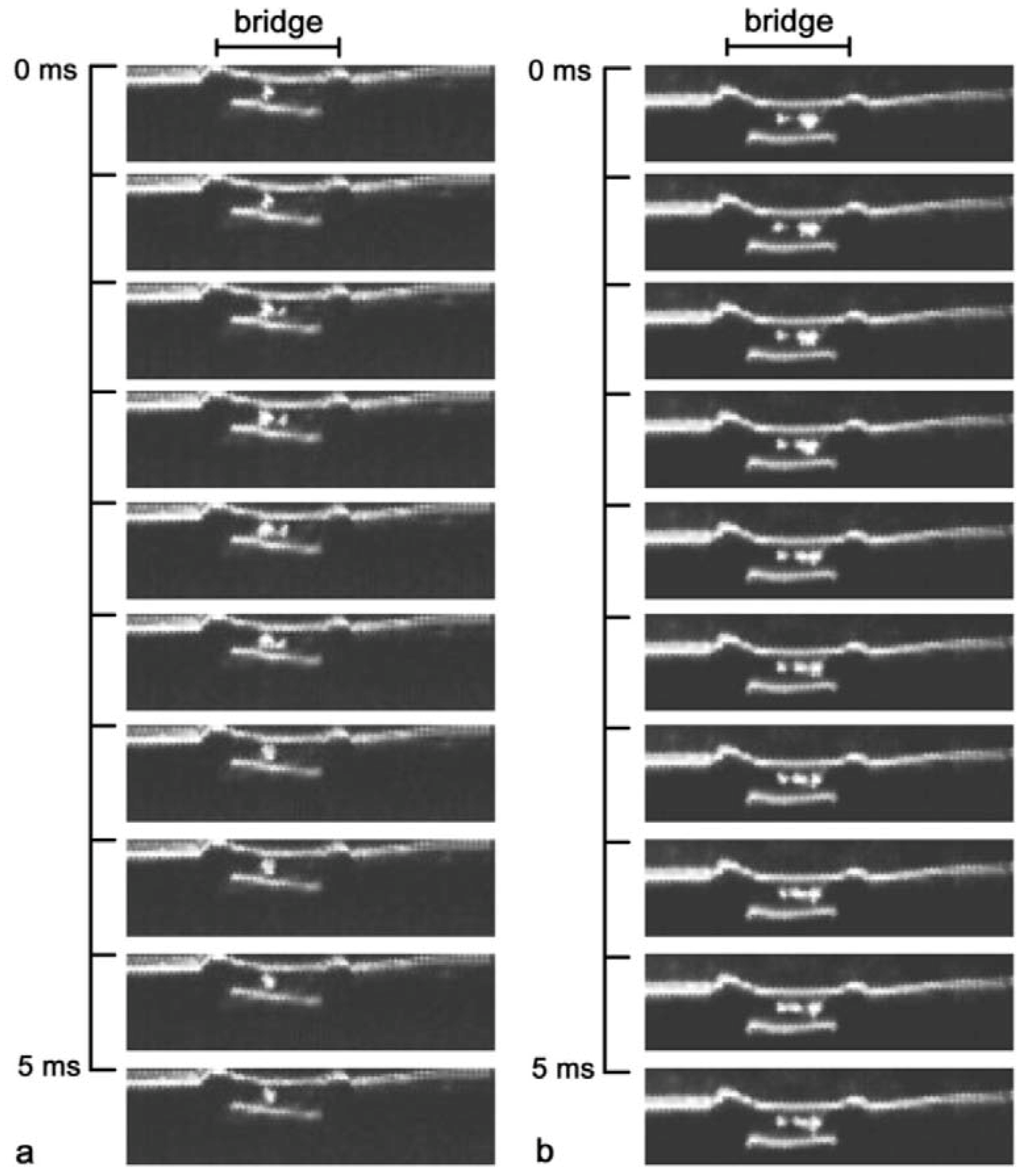
3.1. Bridge Formation




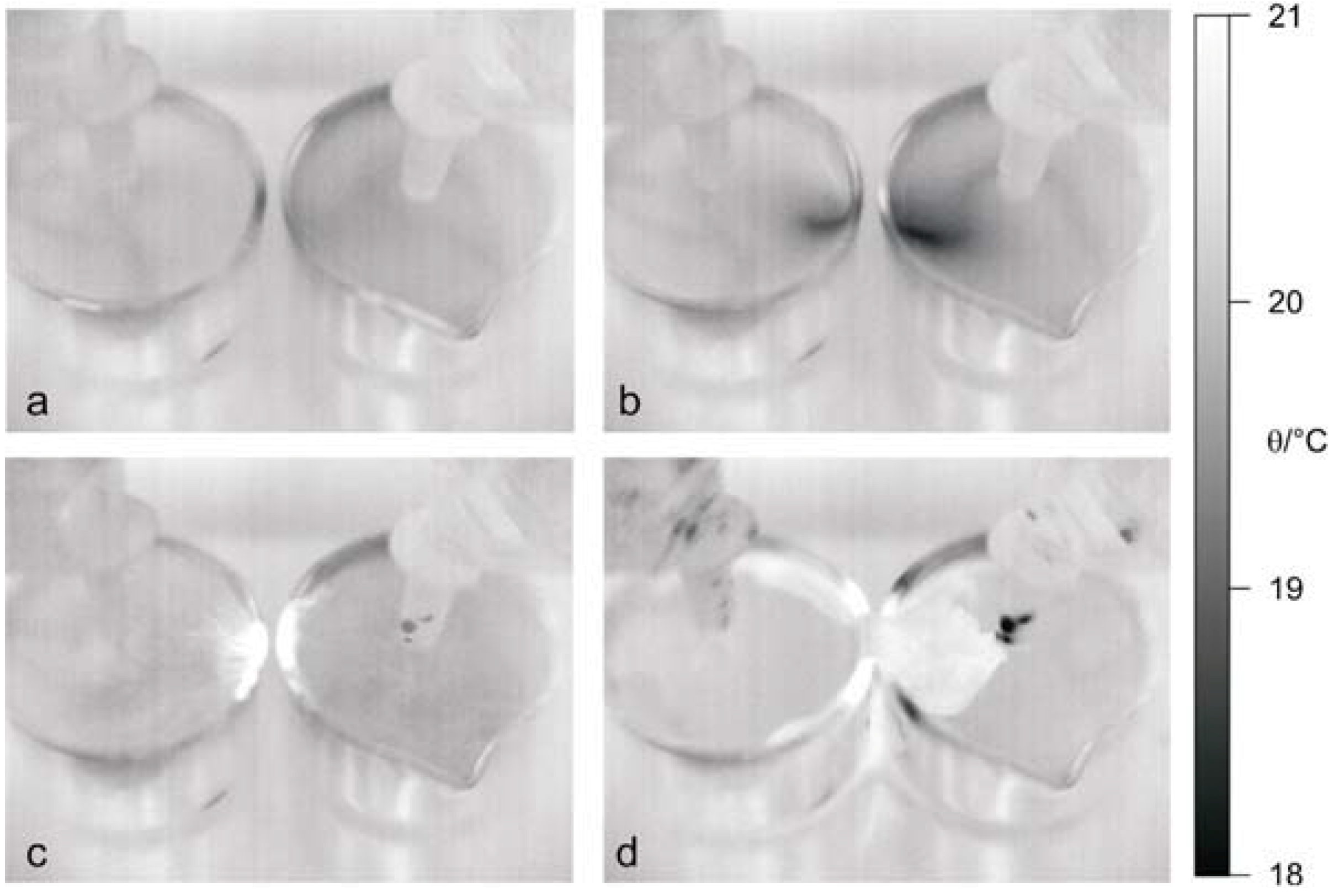
3.2. Bridge Properties
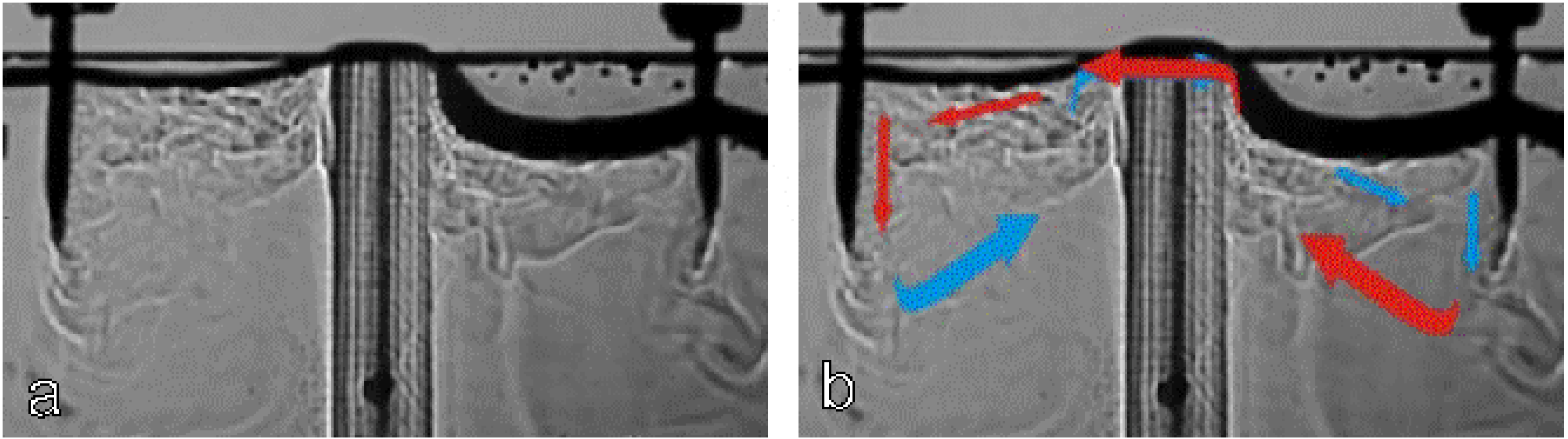
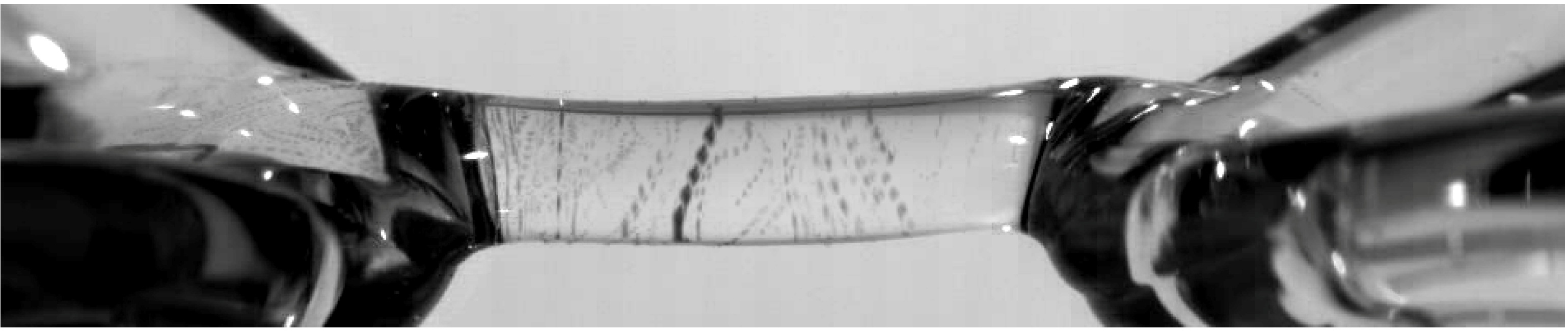
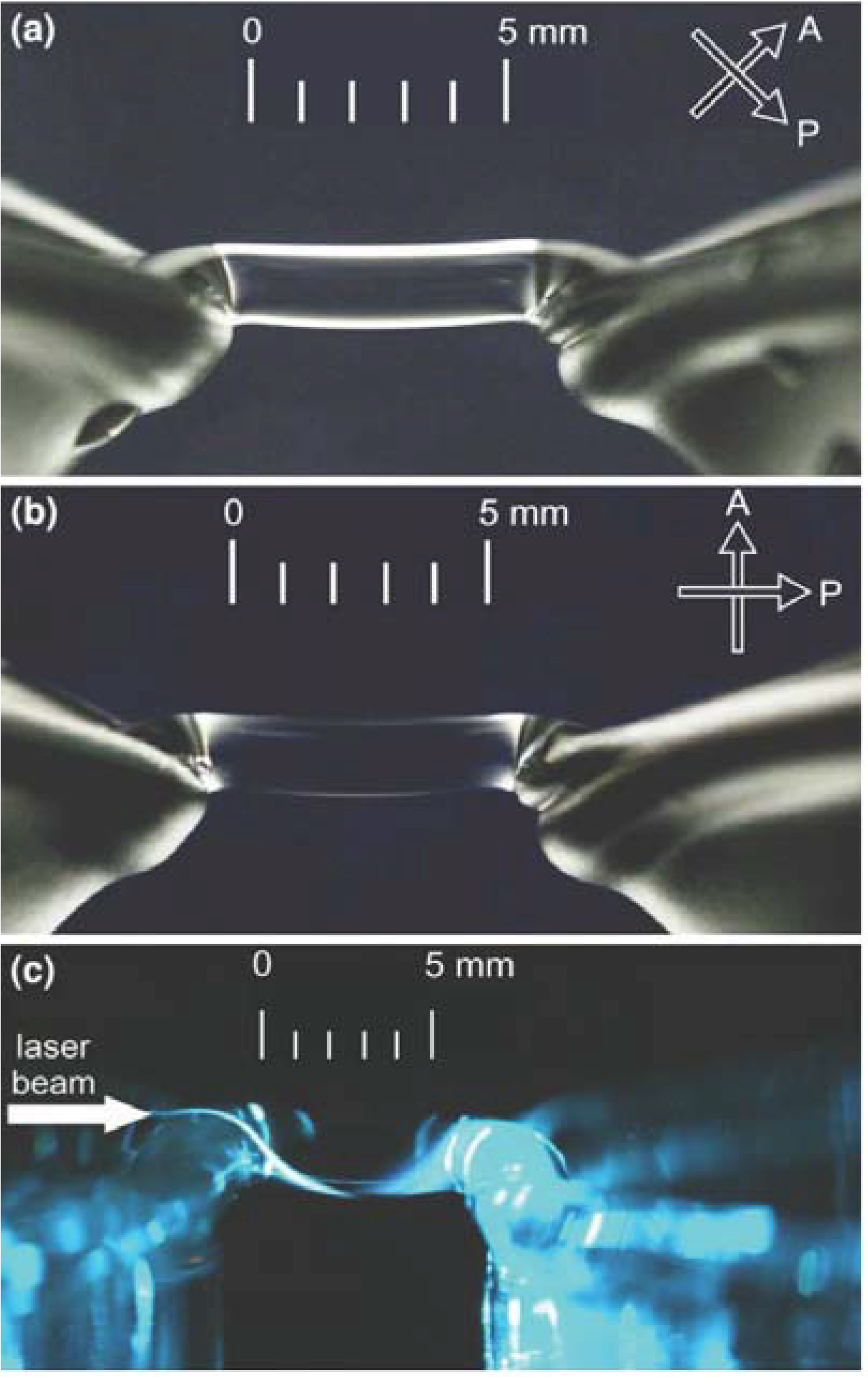
3.3. Spectroscopic Investigations
3.4. Chemical Investigations



4. Conclusions
Acknowledgments
References
- Eisenberg, D.; Kauzman, W. The Structure and Properties of Water; Clarendon Press: Oxford, UK, 1969. [Google Scholar]
- Franks, F. Water: A Comprehensive Treatise; Plenum: New York, NY, USA; pp. 1972–1982.
- Ball, P. Life’s Matrix: a Biography of Water; Farrar, Straus, and Giroux: New York, NY, USA, 1999. [Google Scholar]
- Ball, P. Water: Water—an enduring mystery. Nature 2008, 452, 291–292. [Google Scholar]
- Ball, P. Water as an Active Constituent in Cell Biology. Chem. Rev. 2008, 108, 74. [Google Scholar]
- Chaplin, M.F. Thirty eight anomalies of water Part 1. Homeopath. Med. Panorama 2003, 11, 12–19. [Google Scholar]
- Chaplin, M.F. Thirty eight anomalies of water Part II. Homeopath. Med. Panorama 2003, 11, 22–28. [Google Scholar]
- Cho, C.H.; Singh, S.; Robinson, G.W. Understanding all of water's anomalies with a nonlocal potential. J. Chem. Phys. 1997, 107, 7979–7988. [Google Scholar] [CrossRef]
- The Hydrogen Bond: Recent Developments in Theory and Experiments; Schuster, P.; Zundel, G.; Sandorfy, C. (Eds.) North-Holland: Amsterdam, The Netherlands, 1976; Vols. I-III.
- Xantheas, S.S. Cooperativity and hydrogen bonding network in water clusters. Chem. Phys. 2000, 258, 225–231. [Google Scholar]
- Stanley, H.E. Liquid water: A very complex fluid. Pramana-J. Phys. 1999, 53, 53–83. [Google Scholar] [CrossRef]
- Reed, A.E.; Weinhold, F.; Curtiss, L.A.; Pochatko, D.J. Natural bond orbital analysis of molecular interactions: Theoretical studies of binary complexes of HF, H2O, NH3, N2, O2, F2, CO, and CO2 with HF, H2O, and NH3. J. Chem. Phys. 1986, 84, 5687–5705. [Google Scholar] [CrossRef]
- Ojamäe, L.; Hermansson, K. Ab Initio Study of Cooperativity in Water Chains: Binding Energies and Anharmonic Frequencies. J. Phys. Chem. 1994, 98, 4271–4282. [Google Scholar] [CrossRef]
- Pedulla, J. M.; Vila, F.; Jordan, K. D. Binding energy of the ring form of (H2O)6: Comparison of the predictions of conventional and localized‐orbital MP2 calculations. J. Chem. Phys. 1996, 105, 11091–11099. [Google Scholar] [CrossRef]
- Kumar, R.; Skinner, J.L. Water Simulation Model with Explicit Three-Molecule Interactions. J. Phys. Chem. 2008, 112, 8311–8318. [Google Scholar] [CrossRef]
- Reed, A.E.; Curtiss, L.A.; Weinhold, F. Intermolecular interactions from a natural bond orbital, donor-acceptor viewpoint. Chem. Rev. 1988, 88, 899–926. [Google Scholar] [CrossRef]
- Car, R.; Parrinello, M. Unified approach for molecular dynamics and density-functional theory. Phys. Rev. Lett. 1985, 55, 2471–2474. [Google Scholar] [CrossRef] [PubMed]
- Izvekov, S.; Voth, G.A. Car-Parrinello molecular dynamics simulation of liquid water: New results. J. Chem. Phys. 2002, 116, 10372–10376. [Google Scholar] [CrossRef]
- Lee, H.-S.; Tuckerman, M.E. Dynamical properties of liquid water from ab initio molecular dynamics performed in the complete basis set limit. J. Chem. Phys. 2007, 126, 164501–164516. [Google Scholar] [CrossRef] [PubMed]
- Schwegler, E.; Grossman, J.C.; Gygi, F.; Galli, G. Towards an assessment of the accuracy of density functional theory for first principles simulations of water. II. J. Chem. Phys. 2004, 121, 5400–5409. [Google Scholar] [CrossRef] [PubMed]
- Mantz, Y.A.; Chen, B.; Martyna, G.J. Structural Correlations and Motifs in Liquid Water at Selected Temperatures: Ab Initio and Empirical Model Predictions. J. Phys. Chem. B 2006, 110, 3540–3554. [Google Scholar] [CrossRef] [PubMed]
- Todorova, T.; Seitsonen, A.P.; Hutter, J.; Kuo, I.-F.W.; Mundy, C.J. Molecular Dynamics Simulation of Liquid Water: Hybrid Density Functionals. J. Phys Chem. B 2006, 110, 3685–3691. [Google Scholar] [CrossRef] [PubMed]
- van de Vondele, J.; Mohamed, F.; Krack, M.; Hutter, J.; Sprik, M.; Parrinello, M. The influence of temperature and density functional models in ab initio molecular dynamics simulation of liquid water. J. Chem. Phys. 2005, 122, 14515. [Google Scholar] [CrossRef] [PubMed]
- Bukowski, R.; Szalewicz, K.; Groenenboom, G.C.; van der Avoird, A. Predictions of the properties of water from first principles. Science 2007, 315, 1249–1252. [Google Scholar] [CrossRef] [PubMed]
- Fanourgakis, G.S.; Xantheas, S.S. The Flexible, Polarizable, Thole-Type Interaction Potential for Water (TTM2-F) Revisited. J. Phys. Chem. A 2006, 110, 4100–4106. [Google Scholar] [CrossRef] [PubMed]
- Tuckerman, M.; Laasonen, K.; Sprik, M.; Parrinello, M. Ab Initio Molecular Dynamics Simulation of the Solvation and Transport of H3O+ and OH− Ions in Water. J. Phys. Chem. 1995, 99, 5749–5752. [Google Scholar] [CrossRef]
- Hofer, T.S.; Tran, H.T.; Schwenk, C.F.; Rode, B.M. Characterization of dynamics and reactivities of solvated ions by ab initio simulations. J. Comput. Chem. 2004, 25, 211–217. [Google Scholar] [CrossRef] [PubMed]
- Kuharski, R.A.; Rossky, P.J. A quantum mechanical study of structure in liquid H2O and D2O. J. Chem. Phys. 1985, 82, 5164–5177. [Google Scholar] [CrossRef]
- Poulsen, J.A.; Nyman, G.; Rossky, P.J. Feynman-Kleinert Linearized Path Integral (FK-LPI) Algorithms for Quantum Molecular Dynamics, with Application to Water and He(4). J. Chem. Theory Comput. 2006, 2, 1482–1491. [Google Scholar] [CrossRef]
- Stern, H.A.; Rittner, F.; Berne, B.J.; Friesner, R.A. Combined fluctuating charge and polarizable dipole models: Application to a five-site water potential function. J. Chem. Phys. 2001, 115, 2237–2251. [Google Scholar] [CrossRef]
- Paesani, F.; Iuchi, S.; Voth, G.A. Quantum effects in liquid water from an ab initio-based polarizable force field. J. Chem. Phys. 2007, 127, 074506–074514. [Google Scholar] [CrossRef] [PubMed]
- de la Peña, L.H.; Kusalik, P.G. Quantum effects in light and heavy liquid water: A rigid-body centroid molecular dynamics study. J. Chem. Phys. 2004, 121, 5992–6002. [Google Scholar] [CrossRef] [PubMed]
- Paesani, F.; Voth, G.A. The Properties of Water: Insights from Quantum Simulations. J. Phys. Chem. B 2009, 113, 5702–5719. [Google Scholar] [CrossRef] [PubMed]
- Hadju, F.; Lengyel, S.; Pálinkás, G. X-ray scattering and radial distribution function of liquid water. J. Appl. Cryst. 1976, 9, 134–138. [Google Scholar] [CrossRef]
- Hadju, F. A Model of liquid water—Tetragonal Clusters: Description and determination of parameters. Acta Chim. 1977, 93, 371–394. [Google Scholar]
- Hadju, F. The structural model of water II—the structure of amorphous ice and structural relations between water and some ice polymorphs on the basis of the tetragonal cluster model. Acta Chim. Acad. Sci. Hung. 1978, 96, 355–371. [Google Scholar]
- Teixeira, J.; Luzar, A. Physics of Liquid Water. Structure and Dynamics. In Hydration Processes in Biology: Theoretical and Experimental Approaches (NATO ASI series A); Bellissent-Funel, M.C., Ed.; IOS Press: Amsterdam, The Netherlands, 1999; pp. 35–65. [Google Scholar]
- Soper, A.K. An asymmetric model for water structure. J. Phys. Condens. Matter 2005, 17, S3273–S3282. [Google Scholar] [CrossRef]
- Soper, A.K. Joint structure refinement of X-ray and neutron diffraction data on disordered materials: application to liquid water. J. Phys. Condens. Matter 2007, 19, 335206:1–335206:18. [Google Scholar]
- Stanley, H.E.; Buldyrev, S.V.; Franzese, G.; Giovambattista, N.; Starr, F.W. Static and dynamic heterogeneitities in water. Phil. Trans. R. Soc. A 2005, 363, 509–523. [Google Scholar] [CrossRef] [PubMed]
- Stanley, H.E.; Teixeira, J. Interpretation of the unusual behavior of H2O and D2O at low temperature: tests of a percolation model. J. Chem. Phys. 1980, 73, 3404–3422. [Google Scholar] [CrossRef]
- Stanley, H.E.; Teixeira, J.; Geiger, A.; Blumberg, R.L. Interpretation of the unusual behavior of H2O and D2O at low temperature: Are concepts of percolation relevant to the “puzzle of liquid water”? Phyisca 1981, 106, 260–277. [Google Scholar]
- Mishima, O.; Stanley, H.E. The relationship between liquid, supercooled and glassy water. Nature 1998, 396, 329–335. [Google Scholar]
- Yamada, M.; Mossa, S.; Stanley, H.E.; Sciortino, F. Interplay between time-temperature transformation and the liquid-liquid phase transition in water. PRL 2002, 88, 195701–195704. [Google Scholar] [CrossRef]
- Leetmaa, M.; Ljungberg, M.; Ogasawara, H.; Odelius, M.; Näslund, L.-Å.; Nilsson, A.; Pettersson, L.G.M. Are recent water models obtained by fitting diffraction data consistent with infrared/Raman and x-ray absorption spectra? J. Chem. Phys. 2006, 125, 244510:1–244510:12. [Google Scholar] [CrossRef]
- Leetmaa, M.; Wikfeldt, K.T.; Ljungberg, M.P.; Odelius, M.; Swenson, J.; Nilsson, A.; Pettersson, L.G.M. Diffraction and IR/Raman data do not prove tetrahedral water. J. Chem. Phys. 2008, 129, 084502:1–084502:13. [Google Scholar] [CrossRef]
- Chumaevskii, N.A.; Rodnikova, M.N. Some peculiarities of liquid water structure. J. Mol. Liquids 2003, 106, 167–177. [Google Scholar] [CrossRef]
- Bakker, H.J.; Skinner, J.L. Vibrational Spectroscopy as a Probe of Structure and Dynamics in Liquid Water. Chem. Rev. 2010, 110, 1498–1517. [Google Scholar] [CrossRef]
- Molinero, V.; Moore, E.B. Water Modeled As an Intermediate Element between Carbon and Silicon. J. Phys. Chem. B 2009, 113, 4008–4016. [Google Scholar] [CrossRef] [PubMed]
- Miyazaki, M.; Fujii, A.; Ebata, T.; Mikami, N. Infrared spectroscopic evidence for protonated water clusters forming nanoscale cages. Science 2004, 304, 1134–1137. [Google Scholar] [CrossRef] [PubMed]
- Shin, J.-W.; Hammer, N.I.; Diken, E.G.; Johnson, M.A.; Walters, R.S.; Jaeger, T.D.; Duncan, M.A.; Christie, R.A.; Jordan, K.D. Infrared Signature of Structures Associated with the H+(H2O)n (n = 6 to 27) Clusters. Science 2004, 304, 1137–1140. [Google Scholar] [CrossRef] [PubMed]
- Nibbering, E.T.J.; Elsaesser, T. Ultrafast Vibrational Dynamics of Hydrogen Bonds in the Condensed Phase. Chem. Rev. 2004, 104, 1887–1914. [Google Scholar] [CrossRef] [PubMed]
- Wernet, Ph.; Nordlund, D.; Bergmann, U.; Cavalleri, M.; Odelius, M.; Ogasawara, H.; Näslund, L.-Å.; Hirsch, T. K.; Ojamäe, L.; Glatzel, P.; Pettersson, L.G.M.; Nilsson, A. The structure of the first coordination shell in liquid water. Science 2004, 304, 995–999. [Google Scholar] [CrossRef] [PubMed]
- Odelius, M.; Cavalleri, M.; Nilsson, A.; Pettersson, L.G.M. X-ray absorption spectrum of liquid water from molecular dynamics simulations: Asymmetric model. Phys. Rev. B 2006, 73, 024205:1–024205:6. [Google Scholar] [CrossRef]
- Smith, J.D.; Cappa, C.D.; Wilson, K.R.; Messer, B.M.; Cohen, R.C.; Saykally, R.J. Energetics of Hydrogen Bond Network Rearrangements in Liquid Water. Science 2004, 306, 851–853. [Google Scholar] [CrossRef] [PubMed]
- Head-Gordon, T.; Johnson, M.E. Tetrahedral structure or chains for liquid water. PNAS 2006, 103, 7973–7977. [Google Scholar] [CrossRef] [PubMed]
- Tse, J.S.; Shaw, D.M.; Klug, D.D.; Patchkovskii, S.; Vankó, G.; Monaco, G.; Krisch, M. X-Ray Raman Spectroscopic Study of Water in the Condensed Phases. Phys. Rev. Lett. 2008, 100, 095502:1–095502:4. [Google Scholar] [CrossRef]
- Lin, I.J.; Yotvat, J. Exposure of irrigation and drinking water to a magnetic field with controlled power and direction. J. Magn. Magn. Mater. 1990, 83, 525–526. [Google Scholar] [CrossRef]
- Sisken, B.; Walker, J. Therapeutic aspects of electromagnetic fields for soft tissue healing. In Electromagnetic Fields: Biological Interactions and Mechanisms; Blank, M., Ed.; American Chemical Society: Washington, DC, USA, 1995. [Google Scholar]
- Basset, C.A. Bioelectromagnetics in the service of medicine. In Electromagnetic Fields: Biological Interactions and Mechanisms; Blank, M., Ed.; American Chemical Society: Washington, DC, USA, 1995. [Google Scholar]
- Walleczek, J. Magnetokinetic effects on radical pairs: A paradigm for magnetic field interactions with biologic systems at lower than thermal energy. In Electromagnetic Fields: Biological Interactions and Mechanisms; Blank, M., Ed.; American Chemical Society: Washington, DC, USA, 1995. [Google Scholar]
- Colic, M.; Morse, D. The elusive mechanism of the magnetic ‘memory’ of water. Colloid. Surfaces A 1999, 154, 167–174. [Google Scholar] [CrossRef]
- Alimi, F.; Tlili, M.; Amor, M.B.; Gabrielli, C.; Maurin, G. Influence of magnetic field on calcium carbonate precipitation. Desalination 2007, 206, 163–168. [Google Scholar] [CrossRef]
- Higashitani, K.; Kage, A.; Katamura, S.; Imai, K.; Hatade, A. Effects of a Magnetic Field on the Formation of CaCO3 Particles. J. Colloid Interf. Sci. 1993, 156, 90–95. [Google Scholar] [CrossRef]
- Pach, L.; Duncan, S.; Roy, R.; Komarneni, S. Effects of a magnetic field on the precipitation of calcium carbonate. J. Materials Sci. Letters 1996, 15, 613–615. [Google Scholar] [CrossRef]
- Roy, R.; Tiller, W.A.; Bell, I.; Hoover, M.R. The structure of liquid water; novel insights from materials research; potential relevance to homeopathy. Mater. Res. Innov. 2005, 9, 577–608. [Google Scholar]
- Cowan, M.L.; Bruner, B.D.; Huse, N.; Dwyer, J.R.; Chugh, B.; Nibbering, E.T.J.; Elsaesser, T.; Miller, R.J.D. Ultrafast memory loss and energy redistribution in the hydrogen bond network of liquid H2O. Nature 2005, 434, 199–202. [Google Scholar] [CrossRef] [PubMed]
- Juraschek, R.; Röllgen, F.W. Pulsation phenomena during electrospray ionization. Int. J. Mass. Spectrom. 1998, 177, 1–15. [Google Scholar] [CrossRef]
- Yu, J.H.; Fridrikh, S.V.; Rutledge, G.C. The role of elasticity in the formation of electrospun fibers. Polymer 2006, 47, 4789–4797. [Google Scholar] [CrossRef]
- He, J.-H.; Wan, Y.-Q.; Yu, J.-Y. Critical length of straight jet in electrospinning. Polymer 2005, 46, 12637–12640. [Google Scholar] [CrossRef]
- Spivak, A.E.; Dzenis, Y.A.; Reneker, D.H. A model of steady state jet in the electrospinning process. Mech. Res. Commun. 2000, 27, 37–42. [Google Scholar] [CrossRef]
- Feng, J. Stretching of a straight electrically charged viscoelastic jet. J. Non-Newtonian Fluid Mech. 2003, 116, 55–70. [Google Scholar] [CrossRef]
- Marginean, I.; Parvin, L.; Heffernan, L.; Vertes, A. Flexing the electrified meniscus: the birth of a jet in electrosprays. Anal. Chem. 2004, 76, 4202–4207. [Google Scholar] [CrossRef] [PubMed]
- Gañán-Calvo, A.M. On the theory of electrohydrodynamically driven capillary jets. J. Fluid Mech. 1997, 335, 165–188. [Google Scholar] [CrossRef]
- Jaworek, A.; Krupa, A. Classification of the modes of EHD spraying. J. Aerosol Sci. 1999, 30, 873–893. [Google Scholar] [CrossRef]
- Cherney, L.T. Electrohydrodynamics of electrified liquid menisci and emitted jets. J. Aerosol Sci. 1999, 30, 851–862. [Google Scholar] [CrossRef]
- Yan, F.; Farouk, B.; Ko, F. Numerical modeling of an electrostatically driven liquid meniscus in the cone-jet mode. J. Aerosol Sci. 2003, 34, 99–116. [Google Scholar] [CrossRef]
- Lopez-Herrera, J. M.; Gañán-Calvo, A.M.; Perez-Saborid, M. One-dimensional simulation of the breakup of capillary jets of conducting liquids. Application to E.H.D. spraying. J. Aerosol Sci. 1999, 30, 895–912. [Google Scholar]
- He, J.-H.; Wan, Y.-Q.; Yu, J.-Y. Scaling law in electrospinning: relationship between electric current and solution flow rate. Polymer 2005, 46, 2799–2801. [Google Scholar] [CrossRef]
- Wei, J.; Shui, W.; Zhou, F.; Lu, Y.; Chen, K.; Xu, G.; Yang, P. Naturally and externally pulsed electrospray. Mass Spectrometry Rev. 2002, 2, 148–162. [Google Scholar] [CrossRef]
- Hartman, R.P.A.; Brunner, D.J.; Camelot, D.M.A.; Marijnissen, J.C.M.; Scarlett, B. Jet break-up in electrohydrodynamic atomization in the cone-jet mode. J. Aerosol Sci. 2000, 31, 65–95. [Google Scholar] [CrossRef]
- Hartman, R.P.A.; Brunner, D.J.; Camelot, D.M.A.; Marijnissen, J.C.M.; Scarlett, B. Electrohydrodynamic atomization in the cone-jet mode. Physical modelling of the liquid cone and jet. J. Aerosol Sci. 1999, 30, 823–849. [Google Scholar] [CrossRef]
- Hartman, R.P.A.; Borra, J.-P.; Brunner, D.J.; Marijnissen, J.C.M.; Scarlett, B. The evolution of electrohydrodynamic sprays produced in the cone-jet mode, a physical model. J. Electrostat. 1999, 47, 143–170. [Google Scholar] [CrossRef]
- Gunji, M.; Washizu, M. Self-propulsion of a water droplet in an electric field. J. Phys.-D-Appl. Phys. 2005, 38, 2417–2423. [Google Scholar] [CrossRef]
- Armstrong, Lord W. Electrical Phenomena. The Electrical Engineer 1893, 10 February, 154–155. [Google Scholar]
- Uhlig, W.; Laboratory of Inorganic Chemistry, ETH Hönggerberg—HCI, Zürich, Switzerland. Personal communication, 2005.
- Fuchs, E.C.; Woisetschläger, J.; Gatterer, K.; Maier, E.; Pecnik, R.; Holler, G.; Eisenkölbl, H. The floating water bridge. J. Phys.-D-Appl. Phys. 2007, 40, 6112–6114. [Google Scholar] [CrossRef]
- Hand, E. Water doesn’t mind the gap. Nature 2007, 449, 517. [Google Scholar] [CrossRef] [PubMed]
- Fuchs, E.C.; Gatterer, K.; Holler, G.; Woisetschläger, J. Dynamics of the floating water bridge. J. Phys.-D-Appl. Phys. 2008, 41, 185502–185507. [Google Scholar] [CrossRef]
- Fuchs, E.C.; Bitschnau, B.; Woisetschläger, J.; Maier, E.; Beuneu, B.; Teixeira, J. Neutron Scattering of a Floating Heavy Water Bridge. J. Phys.-D-Appl. Phys. 2009, 42, 065502:1–065502:4. [Google Scholar] [CrossRef]
- Fuchs, E.C.; Baroni, P.; Bitschnau, B.; Noirez, L. Two-Dimensional Neutron Scattering in a Floating Heavy Water Bridge. J. Phys.-D-Appl. Phys. 2010, 43, 105502:1–105502:5. [Google Scholar] [CrossRef]
- Woisetschläger, J.; Gatterer, K.; Fuchs, E.C. Experiments in a floating water bridge. Exp. Fluids 2010, 48-1, 121–131. [Google Scholar]
- Del Giudice, E.; Fuchs, E.C.; Vitiello, G. Collective molecular dynamics of a floating water bridge. Water(Seattle) 2010, 2, 69–82. [Google Scholar]
- Nishiumi, H.; Honda, F. Effects of Electrolyte on Floating Water Bridge. Res. Let. Phys. Chem. 2009, 2009, 371650:1–371650:3. [Google Scholar]
- Ponterio, R.C.; Pochylski, M.; Aliotta, F.; Vasi, C.; Fontanella, M. E.; Saija, F. Raman scattering measurements on a floating water bridge. J. Phys.-D-Appl. Phys. 2010, 43, 175405:1–175405:8. [Google Scholar] [CrossRef]
- Widom, A.; Swain, J.; Silverberg, J.; Sivasubramanian, S.; Srivastava, Y.N. Theory of the Maxwell pressure tensor and the tension in a water bridge. Phys. Rev. E 2009, 80, 016301:1–016301:7. [Google Scholar] [CrossRef]
- Fuchs, E.C.; Eisenhut, M.; Agostinho, L.L.F.; Woisetschläger, J. Mass and Charge Transfer within a Floating Water Bridge. In SPIE Conference Proceedings of the XII. International Conference on Laser Applications in Life Sciences, Oulu, Finland, June 2010. submitted.
- Castellanos, A. Electrohydrodynamics: No. 380 (Courses and Lectures); Springer: Vienna, Austria, 1998. [Google Scholar]
- Sumoto, I. An interesting Phenomenon Observed on Some Dielectrics. J. Phys. Soc. Jpn. 1955, 10, 494. [Google Scholar] [CrossRef]
- Pohl, H.A. Some effects of nonuniform fields on dielectrics. J. Appl. Phys. 1958, 29, 1182–1188. [Google Scholar] [CrossRef]
- Parmar, D.S.; Jalaluddin, A.K. Dielectrophoretic forces in liquids. Jpn. J. Appl. Phys. 1974, 13, 793–798. [Google Scholar] [CrossRef]
- Pickard, W.F. Electrical force effects in dielectric liquids. In Progress in Dielectrics Vol. 6; Birks, J.B., Hart, J., Eds.; Academic Press: New York, NY, USA, 1965; pp. 1–39. [Google Scholar]
- Krasucki, Z. Breakdown of liquid dielectrics. Proc. Roy. Soc. London Ser. A. 1966, 294, 393–404. [Google Scholar] [CrossRef]
- Maxwell, J.C. A Treatise on Electricity and Magnetism, 3rd ed.; Clarendon Press: Oxford, UK, 1891; Vol. 1, Chapter V; pp. 159–162. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Electrodynamics of Continuous Media; Pergamon Press: Oxford, UK, 1960; Chapter II; pp. 66–67. [Google Scholar]
- Parmar, D.S.; Labroo, B. Dielectrophoretic transients effects on liquid stability. Pramana-J. Phys. 1985, 25, 81–94. [Google Scholar] [CrossRef]
- Hughes, M.P.; Pething, R.; Wang, X.-B. Dielectrophoretic forces on particles in travelling electric fields. J. Phys.-D-Appl. Phys. 1996, 29, 474–482. [Google Scholar] [CrossRef]
- Techaumnat, B.; Eua-arporn, B.; Takuma, B. Calculation of electric field and dielectrophoretic force on spherical particles in chain. J. Appl. Phys. 2004, 95, 1586–1593. [Google Scholar] [CrossRef]
- Cloupeau, M.; Prunet-Foch, B. Electrostatic spraying of liquids in cone-jet mode. J. Electrostatics 1989, 22, 135–159. [Google Scholar] [CrossRef]
- Gomez, A.; Tang, K. Charge and fission of droplets in electrostatic sprays. Phys. Fluids 1994, 6, 404–414. [Google Scholar] [CrossRef]
- Chen, D.-R.; Pui, D.Y.H.; Kaufman, S.L. Electrospraying of conducting liquids for monodisperse aerosol generation in the 4 nm to 1.8 µm diameter range. J. Aerosol Sci. 1995, 26, 963–977. [Google Scholar] [CrossRef]
- Agostinho, L.L.F.; Wetsus Centre of Excellence for Sustainable Water Technology, Agora 1, 8900 CC Leeuwarden, the Netherlands. Personal communication, 2010.
- Hartman, R.P.A.; Marijnissen, J.C.M.; Scarlett, B. Electrohydrodynamic atomization in the cone-jet mode. A physical model of the liquid cone and jet. J. Aerosol Sci. 1997, 28, S527–S528. [Google Scholar] [CrossRef]
- Gomez, A.; Tang, K. Atomization and dispersion of quasi-monodisperse electrostatic sprays of heptane. In Proceedings of the 5th International Conference on Liquid Atomization and Spray Systems, 15–18 July, 1991; US Department of Commerce, National Institute of Standards and Technology: Gaithersburg, MD, USA, 1991; pp. 805–812. [Google Scholar]
- Rayleigh, L.F. On the instability of jets. Proc. London Math. Soc. 1878, 11, 4–13. [Google Scholar] [CrossRef]
- Weber, C. Zum Zerfall eines Flüssigkeitsstrahles. Z. Für Angew. Math. und Mech. 1931, 11, 136. [Google Scholar] [CrossRef]
- Yuen, M.C. Non-linear capillary instability of a liquid jet. J. Fluid Mech. 1968, 33, 151–163. [Google Scholar] [CrossRef]
- Rutland, D.F.; Jameson, G.J. Theoretical prediction of the sizes of drops formed in the break-up of capillary jets. Chem. Eng. Sci. 1970, 25, 1689–1698. [Google Scholar] [CrossRef]
- Melcher, J.R. Field-Coupled Surface Waves; MIT Press: Cambridge, MA, USA, 1963. [Google Scholar]
- Parkin, C.S. The Production of Droplets from Liquid Jets by Capillary and Electrohydrodynamic Instabilities. PhD Thesis, Loughborough University of Technology, Leicestershire, UK, 1973. [Google Scholar]
- Turnbull, R.J. On the instability of an electrostatically sprayed liquid jet. IEEE Trans. Ind. Appl. 1992, 28, 1432–1438. [Google Scholar] [CrossRef]
- Jones, T.B. On the relationship of dielectrophoresis and electrowetting. Langmuir 2002, 18, 4437–4443. [Google Scholar] [CrossRef]
- Mugele, F.; Baret, J.-C. Electrowetting: from basics to applications. J. Phys. Condens. Matter 2005, 17, R705–R774. [Google Scholar] [CrossRef]
- Saville, D.A. ELECTROHYDRODYNAMICS: The Taylor-Melcher Leaky Dielectric Model. Annu. Rev. Fluid Mech. 1997, 29, 27–64. [Google Scholar] [CrossRef]
- Schneider, J.M.; Lindblad, N.R.; Hendricks, C.D.; Crowley, J.M. Stability of an electrified liquid jet. J. Appl. Phys. 1967, 38, 2599–2605. [Google Scholar] [CrossRef]
- Neukermans, A. Stability criteria of an electrified liquid jet. J. Appl. Phys. 1973, 44, 4769–4770. [Google Scholar] [CrossRef]
- Fernández de la Mora, J.; Loscertales, I.G. The current emitted by highly conducting Taylor cones. J. Fluid Mech. 1994, 260, 155–184. [Google Scholar] [CrossRef]
- Gañán-Calvo, A.M. Cone-jet analytical extension of Taylor's electrostatic solution and the asymptotic universal scaling laws in electrospraying. Phys. Rev. Lett. 1997, 79, 217–220. [Google Scholar] [CrossRef]
- Gañán-Calvo, A.M.; Dávila, J.; Barrero, A. Current and droplet size in the electrospraying of liquids. Scaling Laws. J. Aerosol Sci. 1997, 28, 249–275. [Google Scholar] [CrossRef]
- Kuli, M.E.; Abrahams, J.P.; Marijnissen, J.C.M. Nano-dispensing by electrospray for biotechnology. Biotechnol. J. 2006, 1, 969–975. [Google Scholar] [CrossRef] [PubMed]
- Xie, J.; Marijnissen, J.C.M.; Wang, C.-H. Microparticles developed by electrodydrodynamic atomization for the local delivery of anticancer drug to treat C6 glioma in vitro. Biomaterials 2006, 27, 3321–3332. [Google Scholar] [CrossRef] [PubMed]
- Sugiyama, H.; Ogura, H.; Otsubo, Y. Development of EHD Motor of Water Solution Utilizing Electrohydrodynamics. In Proceedings of the XV International Congress on Rheology: The Society of Rheology 80th Annual Meeting, Monterey, CA, USA, 3–8 August 2008; Co, A., Leal, G., Colby, R., Giacomin, A.J., Eds.; American Institute of Physics: New York, NY, USA, 2008; pp. 1453–1455. [Google Scholar]
- Ohyama, R.; Kumeta, M.; Ueda, A.; Watson, A.; Chang, J.S. A fundamental characteristic and image analysis of liquid flow in an AW type EHD pump. J. Visualization 2005, 8, 339–346. [Google Scholar] [CrossRef]
- Burcham, C.L.; Saville, D.A. The electrohydrodynamic stability of a liquid bridge: microgravity experiments on a bridge suspended in a dielectric gas. J. Fluid Mech. 2000, 405, 37–56. [Google Scholar] [CrossRef]
- Rai, D.; Kulkarni, A.D.; Gejji, S.P.; Pathak, R.K. Water clusters (H2O)n, n = 6–8, in external electric fields. J. Chem. Phys. 2008, 128, 34310:1–34310:14. [Google Scholar] [CrossRef]
- Choi, Y.C.; Pak, C.; Kim, K.S. Electric field effects on water clusters (n = 3–5): Systematic ab initio study of structures, energetics, and transition states. J. Chem. Phys. 2006, 124, 94308:1–94308:4. [Google Scholar]
- Del Giudice, E.; Istituto Nazionale Fisica Nucleare (INFN), Via Celoria 16, 20133 Milano, Italy. Personal communication, 2008.
- Chatzidimitriou-Dreismann, C.A.; Krieger, U.K.; Möller, A.; Stern, M. Evidence of Quantum Correlation Effects of Protons and Deuterons in the Raman Spectra of Liquid H2O-D2O. Phys. Rev. Lett. 1995, 75, 3008–3011. [Google Scholar] [CrossRef] [PubMed]
- Chatzidimitriou-Dreismann, C.A.; Redah, T.A.; Streffer, R.M.F.; Mayers, J. Anomaleous deep inelastic neutron scattering from liquid H2O–D2O: evidence of nuclear quantum entanglement. Phys. Rev. Lett. 1997, 79, 2839–2842. [Google Scholar] [CrossRef]
- Torii, H. Comment on “Evidence of Quantum Correlation Effects of Protons and Deuterons in Raman Spectra of Liquid H2O-D2O”. Phys. Rev. Lett. 2000, 84, 5236. [Google Scholar] [CrossRef] [PubMed]
- Chatzidimitriou-Dreismann, C.A.; Abdul-Redah, T.; Kolaric, B.; Juranic, I. Reply to Comment on “Evidence of Quantum Correlation Effects of Protons and Deuterons in Raman Spectra of Liquid H2O-D2O”. Phys. Rev. Lett. 2000, 84, 5237. [Google Scholar] [CrossRef] [PubMed]
- Cyrot, M. Ginzburg-Landau theory for superconductors. Rep. Prog. Phys. 1973, 36, 103–158. [Google Scholar] [CrossRef]
- Hendricks, R.W.; Mardon, P.G.; Schaffer, L.B. X-ray zero-angle scattering cross section of water. J. Chem. Phys. 1974, 61, 319–322. [Google Scholar] [CrossRef]
- Bosio, L.; Teixeira, J.; Stanley, H.E. Enhanced density fluctuations in supercooled H2O, D2O, and ethanol-water solutions: evidence from small-angle X-ray scattering. Phys. Rev. Lett. 1981, 46, 597–600. [Google Scholar] [CrossRef]
- Huang, C.; Wikfeldt, K.T.; Tokushima, T.; Nordlund, D.; Harada, Y.; Bergmann, U.; Niebuhr, M.; Weiss, T.M.; Horikawa, Y.; Leetmaa, M.; Ljungberg, M.P.; Takahashi, O.; Lenz, A.; Ojamäe, L.; Lyubartsev, A.P.; Shin, S.; Pettersson, L.G.M.; Nilsson, A. The inhomogeneous structure of water at ambient conditions. PNAS 2009, 106, 15214–15216. [Google Scholar] [CrossRef] [PubMed]
- Yinnon, C.A.; Yinnon, T.A. Domains in aqueous solutions: theory and experimental evidence. Mod. Phys. Lett. B 2009, 23, 1959–1973. [Google Scholar] [CrossRef]
- Arani, R.; Bono, I.; Del Giudice, E.; Preparata, G. QED Coherence and the thermodynamics of water. Int. J. Mod. Phys. B 1995, 9, 1813–1841. [Google Scholar] [CrossRef]
- Del Giudice, E.; Preparata, G.; Vitiello, G. Water as a free electric dipole laser. Phys. Rev. Let. 1988, 61, 1085–1088. [Google Scholar] [CrossRef]
- Del Giudice, E.; Vitiello, G. Role of the electromagnetic field in the formation of domains in the process of symmetry-breaking phase transitions. Phys. Rev. A 2006, 74, 022105:1–022105:9. [Google Scholar]
- Yanga, M.; Skinner, J.L. Signatures of coherent vibrational energy transfer in IR and Raman line shapes for liquid water. Phys. Chem. Chem. Phys. 2010, 12, 982–991. [Google Scholar] [CrossRef] [PubMed]
- Jones, T.B.; Wang, K.L.; Yao, D.J. Frequency-dependent electromechanics of aqueous liquids: Electrowetting and dielectrophoresis. Langmuir 2004, 20, 2813–2818. [Google Scholar] [CrossRef]
- Del Giudice, E.; Preparata, G. A new QED picture of water. In Macroscopic Quantum Coherence; Sassaroli, E., Srivasta, Y., Swain, J., Widom, A., Eds.; World Scientific: Singapore, 1998; pp. 108–129. [Google Scholar]
- Zheng, J.-M.; Chin, W.-C.; Khijniak, E.; Khijniak, E., Jr.; Pollack, G.H. Surfaces and interfacial water: Evidence that hydrophilic surfaces have long-range impact. Ad. Colloid. Interface Sci. 2006, 23, 19–27. [Google Scholar] [CrossRef]
- Henniker, J.C. The depth of the surface zone of a liquid. Rev. Mod. Phys. 1949, 21, 322–341. [Google Scholar] [CrossRef]
- Del Giudice, E.; Tedeschi, A. Water and Autocatalysis in Living Matter. Electromagn. Biol. Med. 2009, 28, 46–52. [Google Scholar] [CrossRef] [PubMed]
- Katsir, Y.; Miller, L.; Aharonov, Y.; Ben Jacob, E. The effect of rf-irradiation on electrochemical deposition and its stabilization by nanoparticle doping. J. Electrochem. Soc. 2007, 154, D249–D259. [Google Scholar] [CrossRef]
- Ben Jacob, E.; Aharonov, Y.; Shapira, Y. Bacteria harnessing complexity. Biofilms 2004, 1, 239–263. [Google Scholar] [CrossRef]
- Woisetschläger, J.; Fuchs, E.C. Nonaqueous floating bridges. unpublished. 2010. [Google Scholar]
- Chen, X.B.; Xi, J.T.; Jiang, T.; Jin, Y.X. Research and development of an accurate 3D shape measurement system based on fringe projection: model analysis and performance evaluation. Precision Eng. 2008, 32, 215–221. [Google Scholar] [CrossRef]
- Taylor, F.R.S. Disintegration of water drops in an electric field. Proc. Roy. Soc. London Ser. A 1964, 280, 383–397. [Google Scholar] [CrossRef]
- Gañán-Calvo, A.M; Montanero, J. Revision of capillary cone-jet physics: Electrospray and flow focusing. Phys. Rev. E. 2009, 79, 066305:1–066305:18. [Google Scholar]
- Merzkirch, W. Flow Visualization, 2nd ed.; Academic Press: Orlando, FL, USA, 1987. [Google Scholar]
- Albrecht, H.-W.; Borys, M.; Damaschke, N.; Tropea, C. Laser Doppler and phase Doppler measurement techniques; Springer: Heidelberg, Germany, 2003. [Google Scholar]
- Musso, M.; Giorgini, M. G.; Torii, H. The effect of microscopic inhomogeneities in acetone/methanol binary liquid mixtures observed through the Raman spectroscopic noncoincidence effect. J. Mol. Liquids 2009, 147, 37–44. [Google Scholar] [CrossRef]
- Zahn, M.; Takada, T. High voltage electric field and space charge distributions in highly purified water. J. Appl. Phys. 1983, 54, 4762–4775. [Google Scholar] [CrossRef]
- Woisetschläger, J.; Institute for Thermal Turbomachinery and Machine Dynamics, Graz University of Technology, Inffeldgasse 25A, 8010 Graz, Austria. Personal communication, 2008.
- Fuchs, E.C.; Woisetschläger, J. The properties of a luminol solution in a floating bridge set-up. unpublished. 2007. [Google Scholar]
- Ovchinnikova, K.; Pollack, G.H. Can Water Store Charge? Langmuir 2009, 25, 542–547. [Google Scholar] [CrossRef]
- Corti, H.R. Do Concentration Cells Store Charge in Water? Comment on: Can Water Store Charge? Langmuir 2009, 25, 6587–6589. [Google Scholar] [CrossRef] [PubMed]
- Ovchinnikova, K.; Pollack, G.H. Reply to: Comment on: Can Water Store Charge? Langmuir 2009, 25, 11202. [Google Scholar] [CrossRef] [PubMed]
- Corti, H.R. Response to: Reply to: Comment on: Can Water Store Charge? Langmuir 2009, 25, 11203. [Google Scholar] [CrossRef]
© 2010 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Fuchs, E.C. Can a Century Old Experiment Reveal Hidden Properties of Water? Water 2010, 2, 381-410. https://doi.org/10.3390/w2030381
Fuchs EC. Can a Century Old Experiment Reveal Hidden Properties of Water? Water. 2010; 2(3):381-410. https://doi.org/10.3390/w2030381
Chicago/Turabian StyleFuchs, Elmar C. 2010. "Can a Century Old Experiment Reveal Hidden Properties of Water?" Water 2, no. 3: 381-410. https://doi.org/10.3390/w2030381
APA StyleFuchs, E. C. (2010). Can a Century Old Experiment Reveal Hidden Properties of Water? Water, 2(3), 381-410. https://doi.org/10.3390/w2030381




