Urban Flood Prediction Model Based on Transformer-LSTM-Sparrow Search Algorithm
Abstract
1. Introduction
2. Materials and Methods
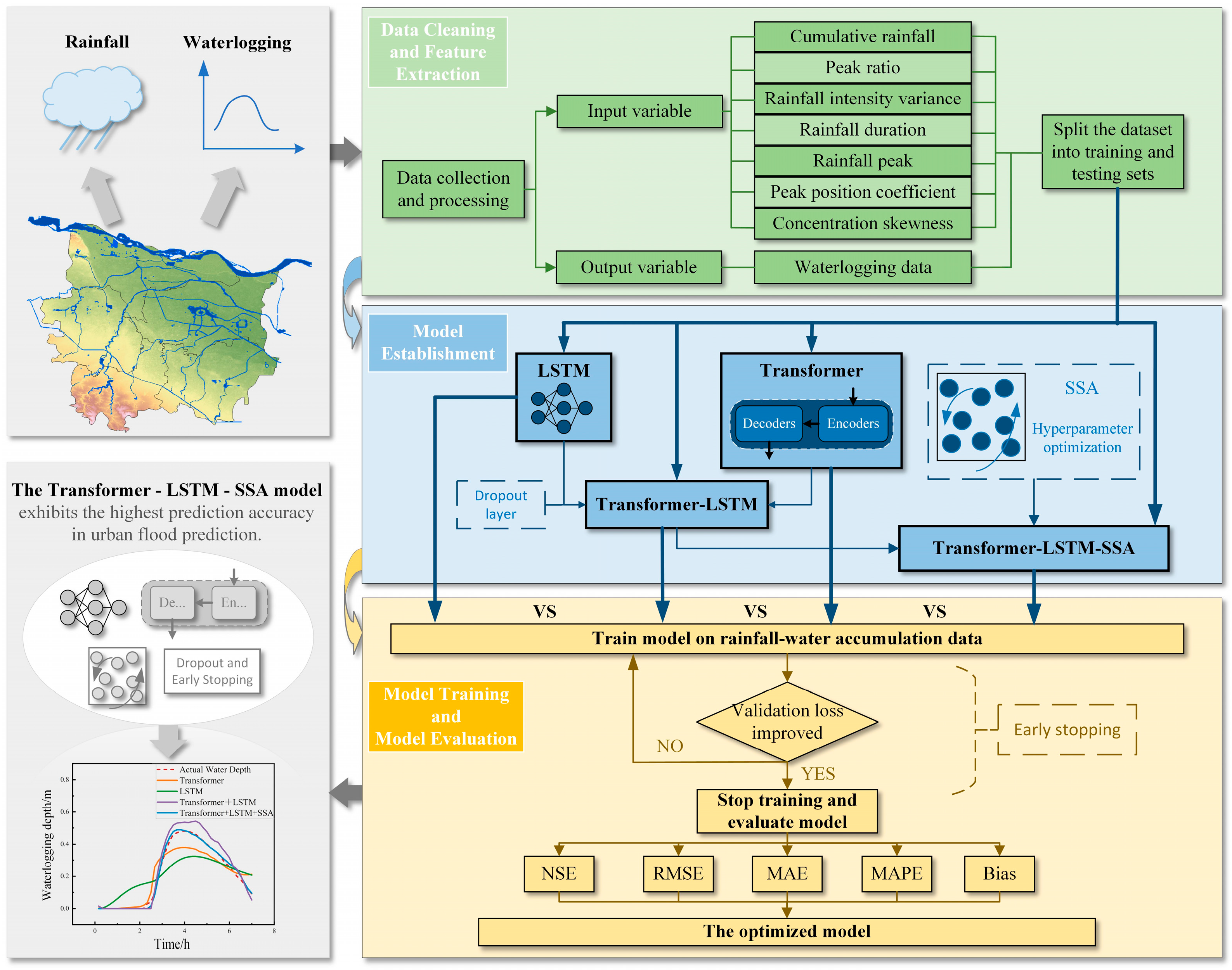
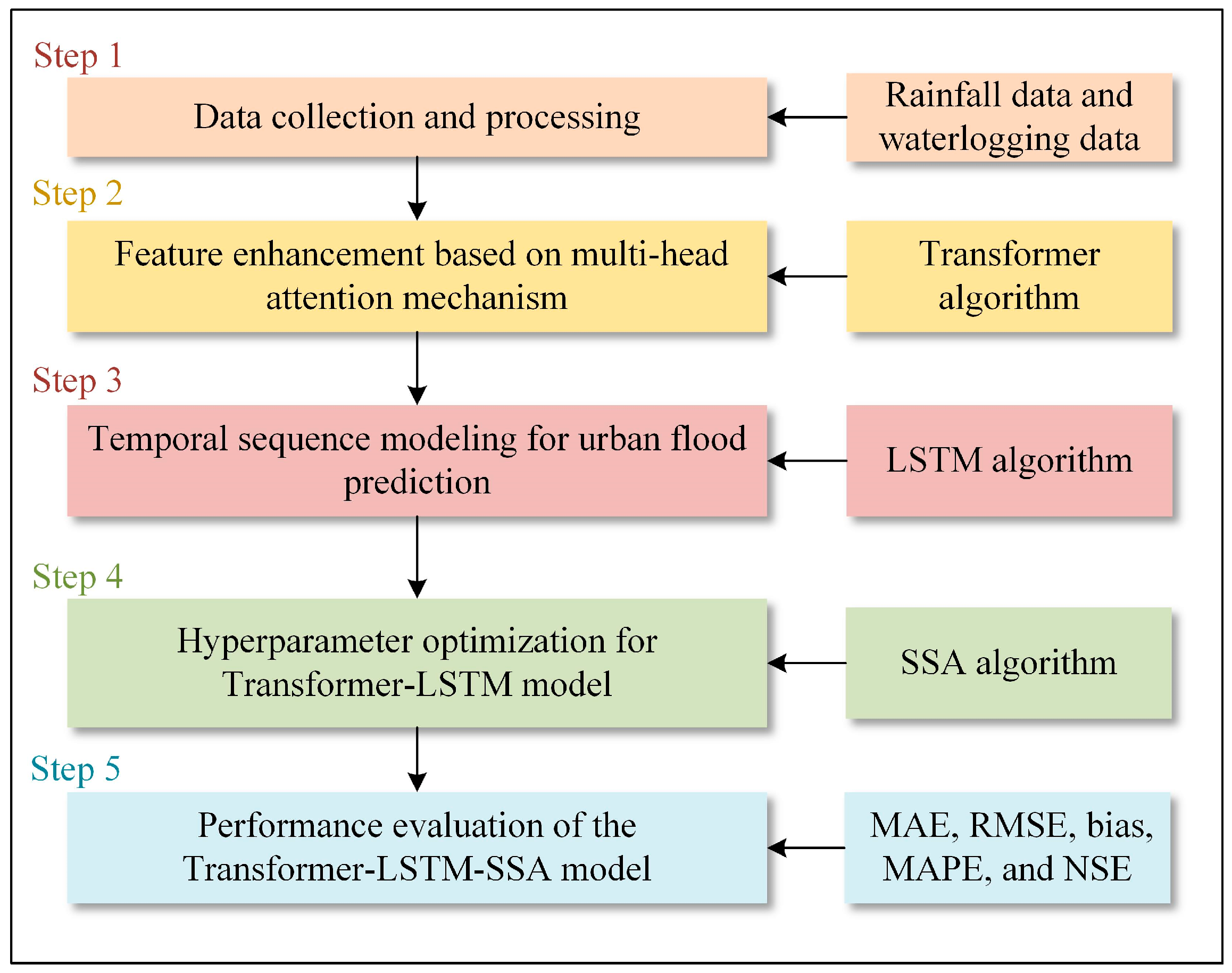
2.1. Overall Framework
2.2. Urban Flood Prediction Model Based on Transformer-LSTM-SSA
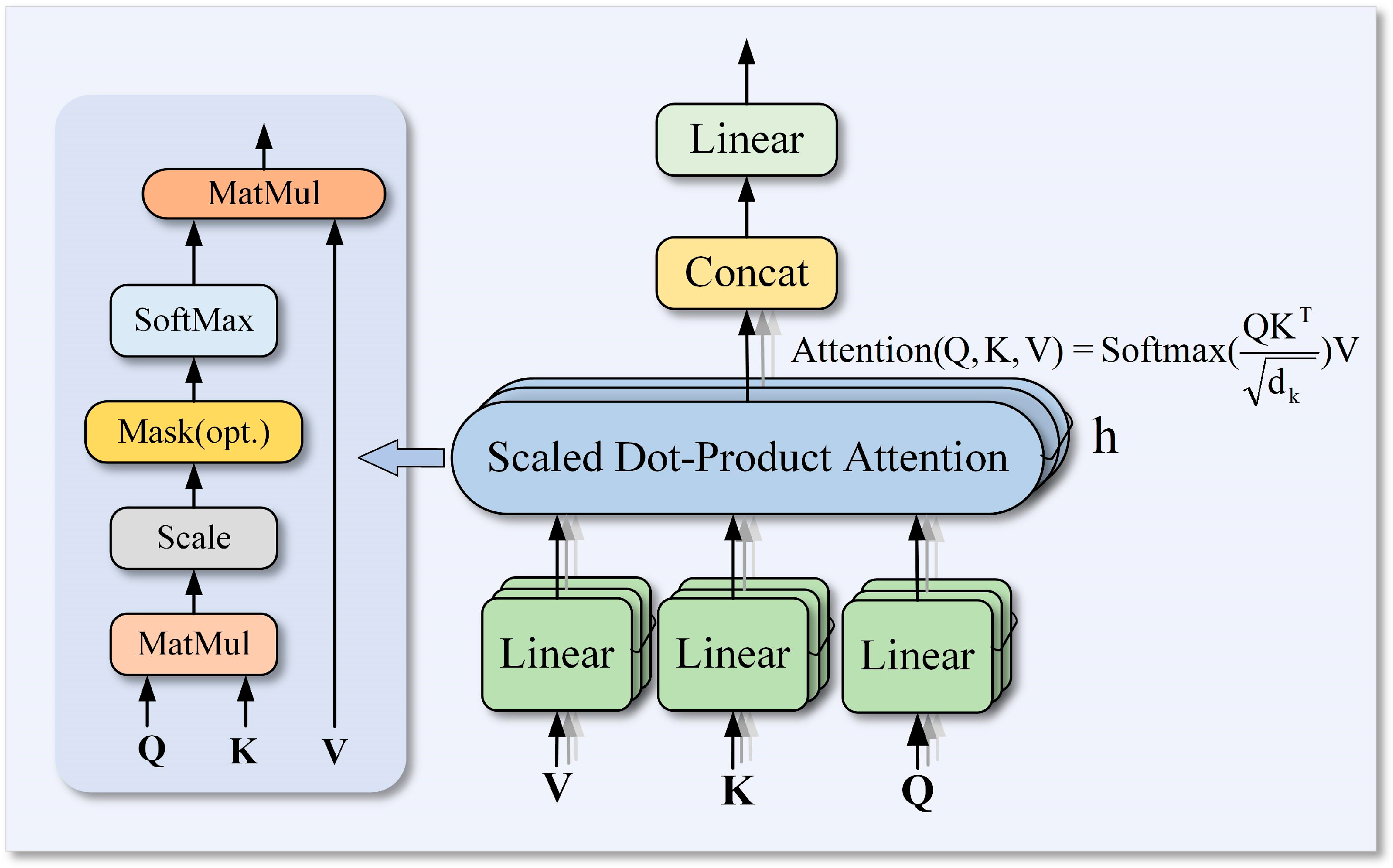
2.2.1. Transformer-LSTM Algorithm
- (1)
- Encoder-only architecture of the Transformer
- (2)
- LSTM temporal modeling module
2.2.2. Sparrow Search Algorithm for Hyperparameter Optimization
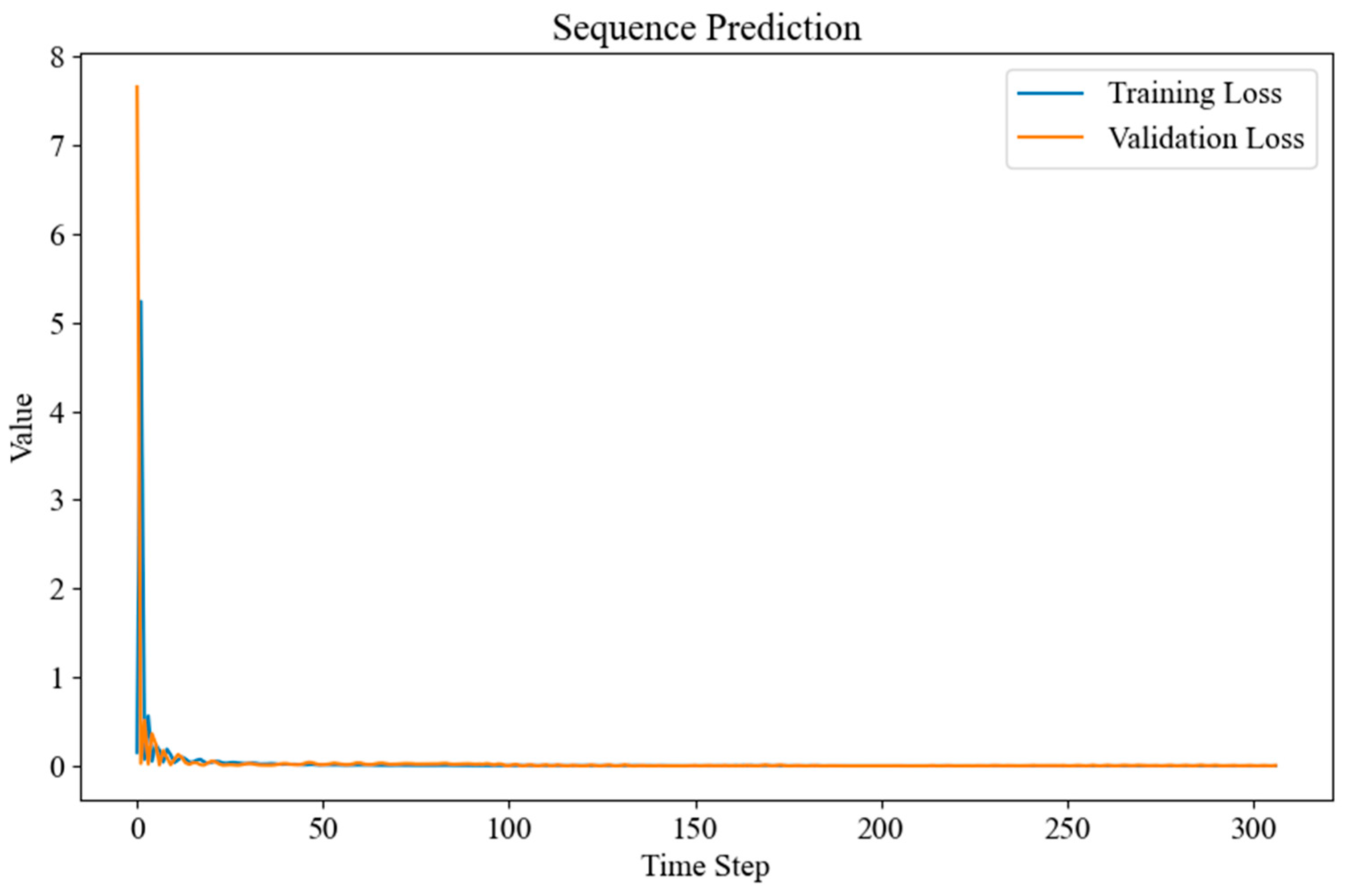
2.2.3. Overfitting Control of the Transformer-LSTM-SSA Model
2.2.4. Model Performance Evaluation
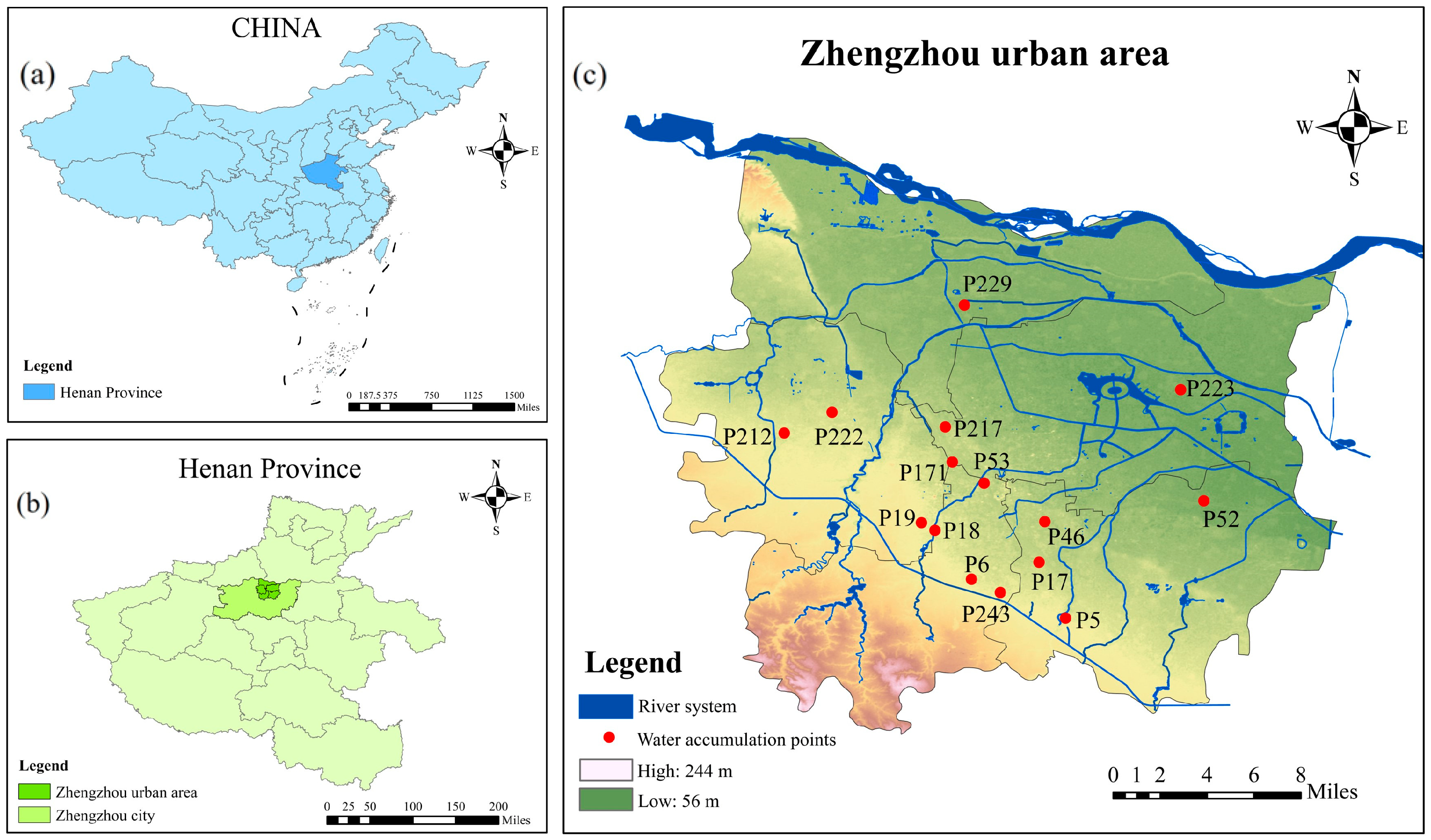
2.3. Study Area and Data
3. Results
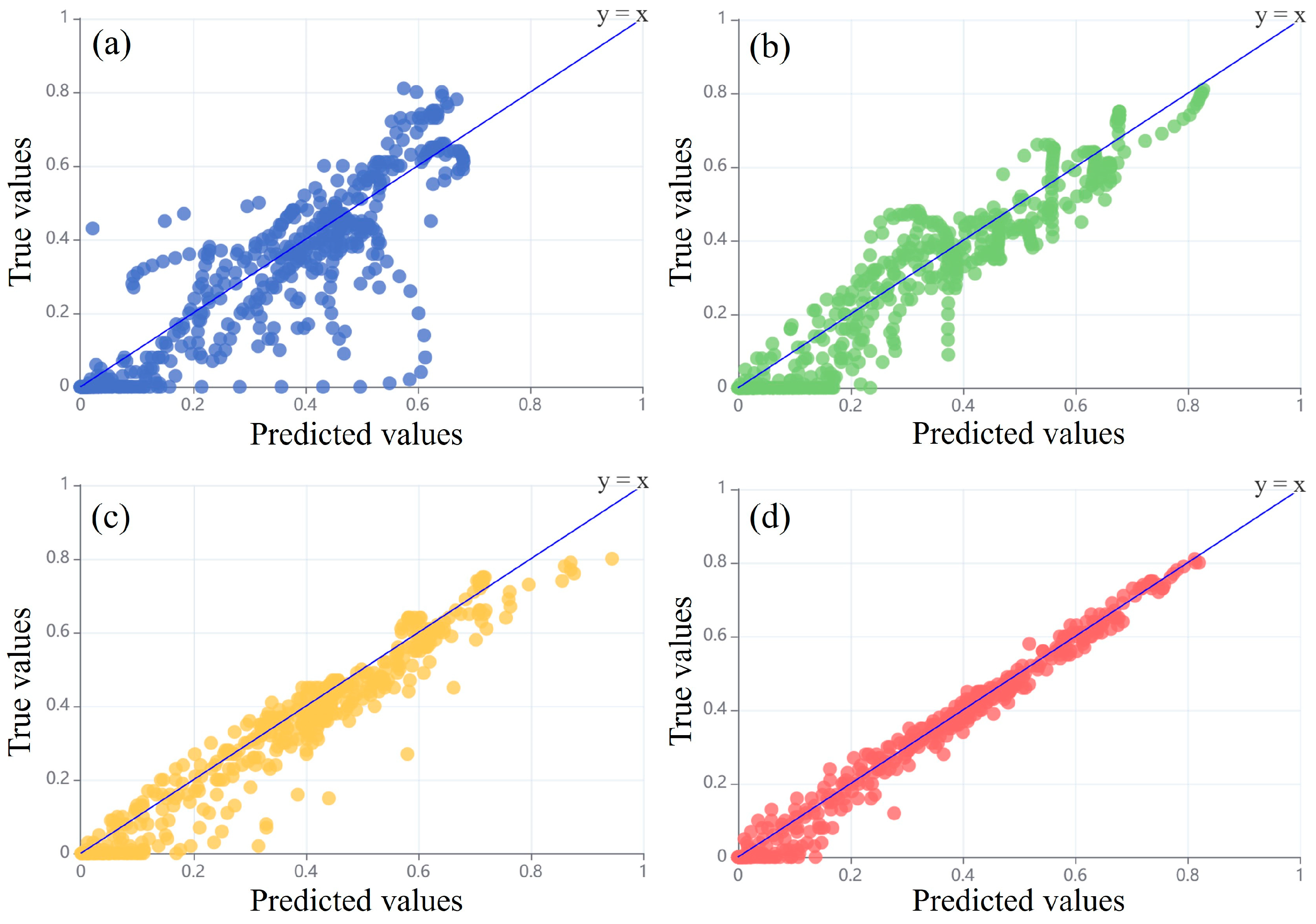
3.1. Urban Flood Prediction Model Based on Transformer-LSTM Algorithm
3.2. Hyperparameter Optimization Based on SSA
3.3. Performance Evaluation of Transformer-LSTM-SSA Model for Urban Flood Prediction
4. Discussion
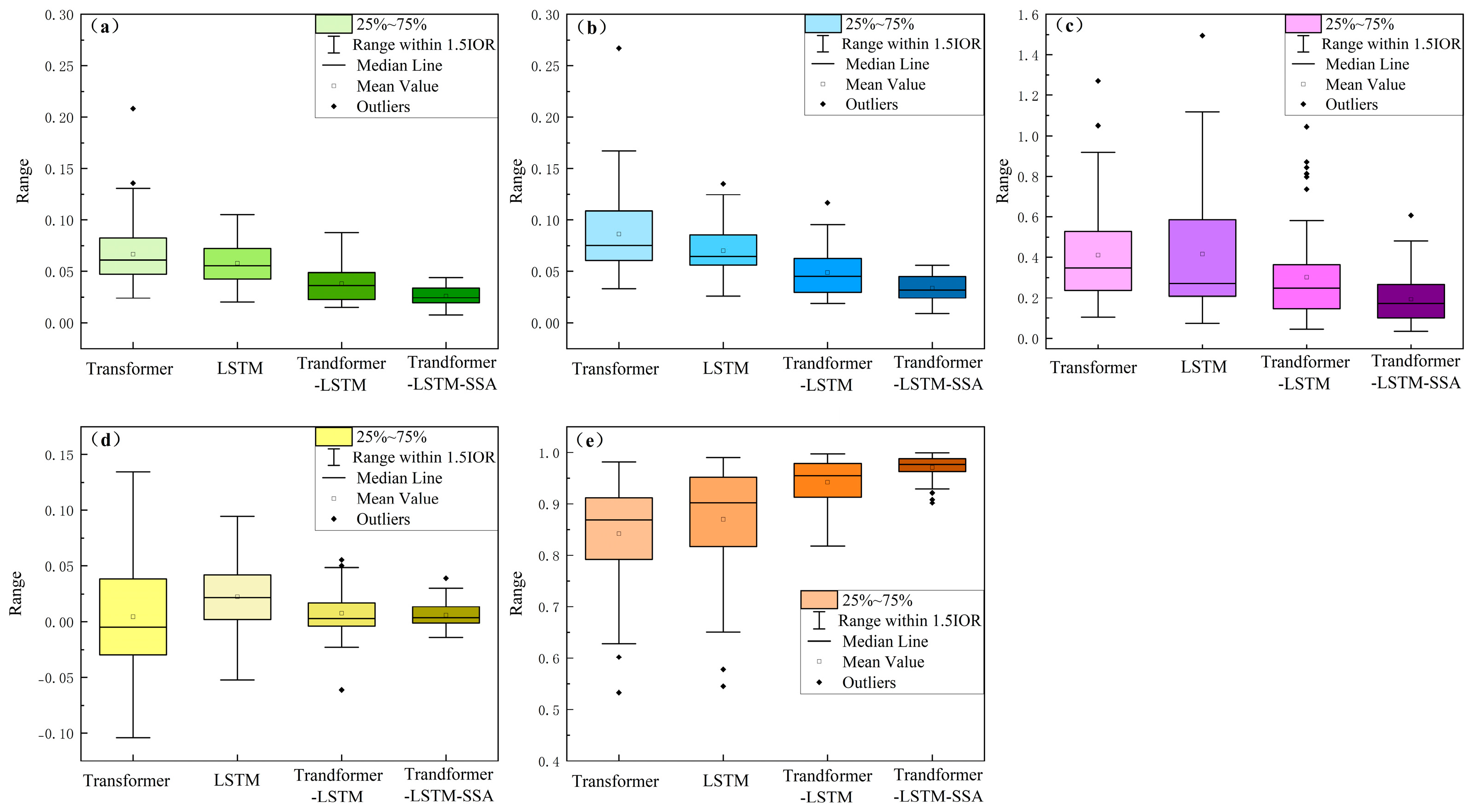
4.1. Comparative Performance of Different Models for Urban Flood Prediction
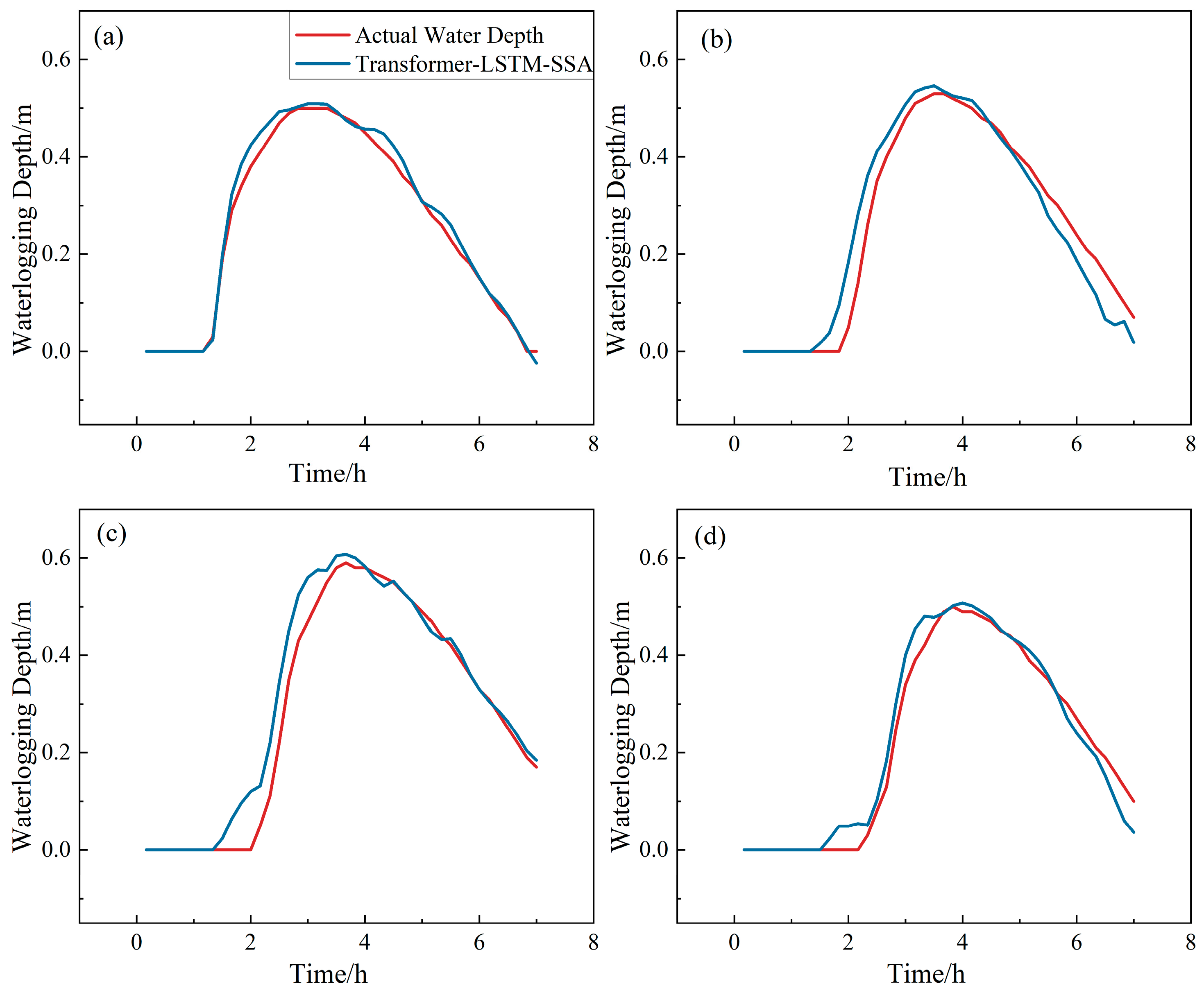
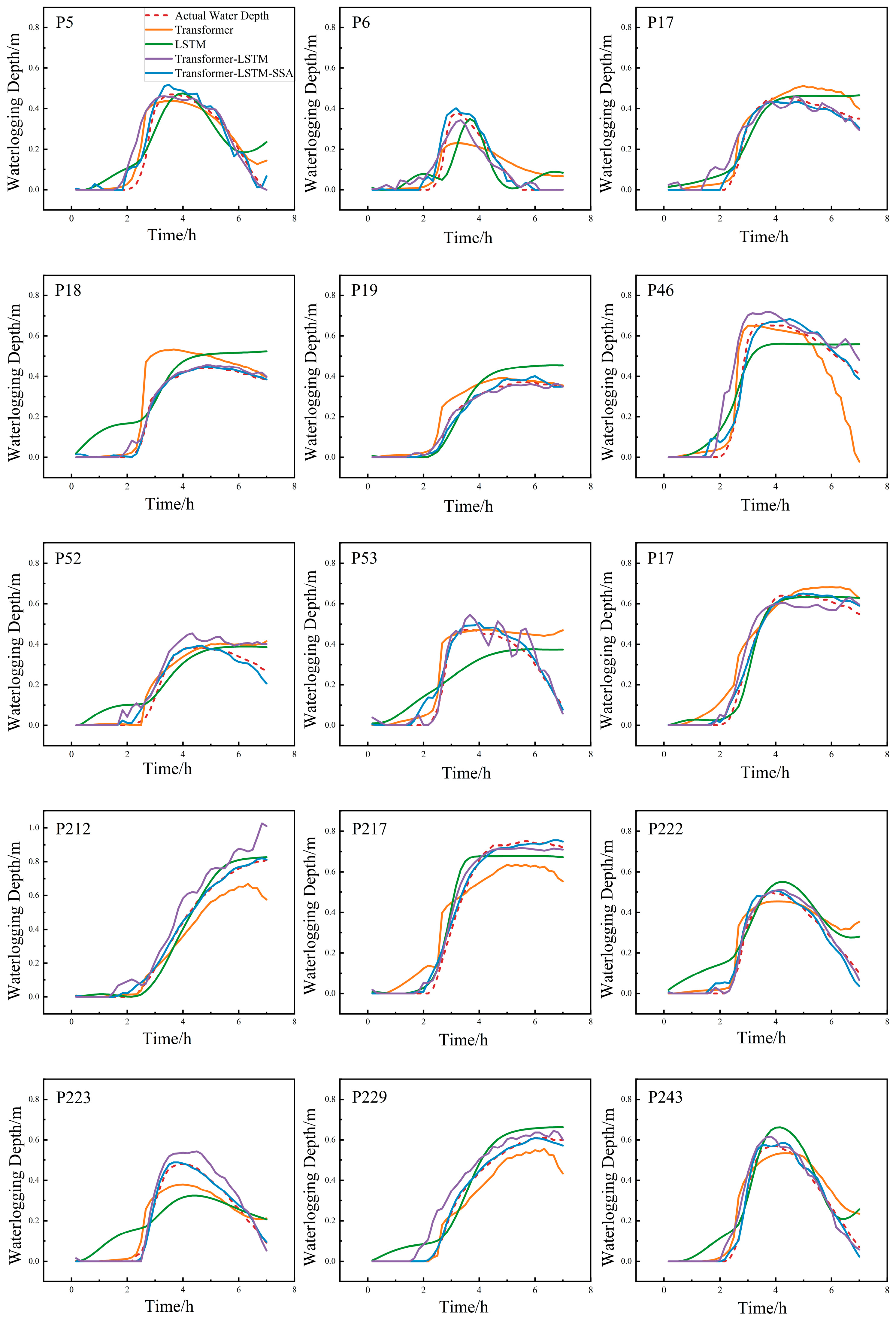
4.2. Waterlogging Process Prediction of Different Models
4.3. Impact of Overfitting Control on Prediction Efficiency
4.4. Limitations and Future Perspectives
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| LSTM | Long Short-Term Memory |
| SSA | Sparrow Search Algorithm |
References
- Kundzewicz, Z.W.; Kanae, S.; Seneviratne, S.I.; Handmer, J.; Nicholls, N.; Peduzzi, P.; Mechler, R.; Bouwer, L.M.; Arnell, N.; Mach, K.; et al. Flood risk and climate change: Global and regional perspectives. Hydrol. Sci. J. 2013, 59, 1–28. [Google Scholar] [CrossRef]
- Hammond, M.J.; Chen, A.S.; Djordjević, S.; Butler, D.; Mark, O. Urban flood impact assessment: A state-of-the-art review. Urban Water J. 2013, 12, 14–29. [Google Scholar] [CrossRef]
- Guan, X.; Yu, F.; Xu, H.; Li, C.; Guan, Y. Flood risk assessment of urban metro system using random forest algorithm and triangular fuzzy number based analytical hierarchy process approach. Sustain. Cities Soc. 2024, 109, 105546. [Google Scholar] [CrossRef]
- Wang, W.; Yuan, X. Climate change and La Niña increase the likelihood of the ‘7·20’ extraordinary typhoon-rainstorm in Zhengzhou, China. Int. J. Climatol. 2024, 44, 1355–1370. [Google Scholar] [CrossRef]
- Xu, T.; Xie, Z.; Zhao, F.; Li, Y.; Yang, S.; Zhang, Y.; Yin, S.; Chen, S.; Li, X.; Zhao, S.; et al. Permeability control and flood risk assessment of urban underlying surface: A case study of Runcheng south area, Kunming. Nat. Hazards 2022, 111, 661–686. [Google Scholar] [CrossRef]
- Teng, J.; Jakeman, A.J.; Vaze, J.; Croke, B.F.; Dutta, D.; Kim, S. Flood inundation modelling: A review of methods, recent advances and uncertainty analysis. Environ. Model. Softw. 2017, 90, 201–216. [Google Scholar] [CrossRef]
- Neal, J.; Schumann, G.; Fewtrell, T.; Budimir, M.; Bates, P.; Mason, D. Evaluating a new LISFLOOD-FP formulation with data from the summer 2007 floods in Tewkesbury, UK. J. Flood Risk Manag. 2011, 4, 88–95. [Google Scholar] [CrossRef]
- Alfieri, L.; Salamon, P.; Pappenberger, F.; Wetterhall, F.; Thielen, J. Operational early warning systems for water-related hazards in Europe. Environ. Sci. Policy. 2012, 21, 35–49. [Google Scholar] [CrossRef]
- Lei, X.; Chen, W.; Panahi, M.; Falah, F.; Rahmati, O.; Uuemaa, E.; Kalantari, Z.; Ferreira, C.S.S.; Rezaie, F.; Tiefenbacher, J.P.; et al. Urban flood modeling using deep-learning approaches in Seoul, South Korea. J. Hydrol. 2021, 601, 126684. [Google Scholar] [CrossRef]
- Reichstein, M.; Camps-Valls, G.; Stevens, B.; Jung, M.; Denzler, J.; Carvalhais, N.; Prabhat, F. Deep learning and process understanding for data-driven Earth system science. Nature 2019, 566, 195–204. [Google Scholar] [CrossRef]
- Wang, H.; Xu, S.; Xu, H.; Wu, Z.; Wang, T.; Ma, C. Rapid prediction of urban flood based on disaster-breeding environment clustering and Bayesian optimized deep learning model in the coastal city. Sustain. Cities Soc. 2023, 99, 104898. [Google Scholar] [CrossRef]
- Li, J.; Meng, Z.; Zhang, J.; Chen, Y.; Yao, J.; Li, X.; Qin, P.; Liu, X.; Cheng, C. Prediction of Seawater Intrusion Run-Up Distance Based on K-Means Clustering and ANN Model. J. Mar. Sci. Eng. 2025, 13, 377. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Brenner, C.; Schulz, K.; Herrnegger, M. Rainfall–runoff modelling using Long Short-Term Memory (LSTM) networks. Hydrol. Earth Syst. Sci. 2018, 22, 6005–6022. [Google Scholar] [CrossRef]
- Zhang, J.F.; Zhu, Y.; Zhang, X.P.; Ye, M.; Yang, J.Z. Developing a Long Short-Term Memory (LSTM) based model for predicting water table depth in agricultural areas. J. Hydrol. 2018, 561, 918–929. [Google Scholar] [CrossRef]
- Chen, J.; Li, Y.W.; Zhang, S.J. Fast Prediction of Urban Flooding Water Depth Based on CNN−LSTM. Water 2013, 15, 1397. [Google Scholar] [CrossRef]
- Zhang, C.; Xu, T.; Wang, T.; Zhao, Y. Spatial-temporal evolution of influencing mechanism of urban flooding in the Guangdong Hong Kong Macao greater bay area, China. Front. Earth Sci. 2023, 10, 1113997. [Google Scholar] [CrossRef]
- Zhou, Q.; Leng, G.; Su, J.; Ren, Y. Comparison of urbanization and climate change impacts on urban flood volumes: Importance of urban planning and drainage adaptation. Sci. Total Environ. 2019, 658, 24–33. [Google Scholar] [CrossRef]
- Li, B.; Li, R.; Sun, T.; Gong, A.; Tian, F.; Khan, M.Y.A.; Ni, G. Improving LSTM hydrological modeling with spatiotemporal deep learning and multi-task learning: A case study of three mountainous areas on the Tibetan Plateau. J. Hydrol. 2023, 620, 129401. [Google Scholar] [CrossRef]
- Yin, H.; Guo, Z.; Zhang, X.; Chen, J.; Zhang, Y. RR-Former: Rainfall-runoff modeling based on Transformer. J. Hydrol. 2022, 609, 127781. [Google Scholar] [CrossRef]
- Liu, C.; Liu, D.; Mu, L. Improved transformer model for enhanced monthly streamflow predictions of the Yangtze River. IEEE Access 2022, 10, 58240–58253. [Google Scholar] [CrossRef]
- Bahdanau, D.; Cho, K.; Bengio, Y. Neural Machine Translation by Jointly Learning to Align and Translate. arXiv 2014, arXiv:1409.0473. [Google Scholar]
- Cao, K.; Zhang, T.; Huang, J. Advanced hybrid LSTM-transformer architecture for real-time multi-task prediction in engineering systems. Sci. Rep. 2024, 14, 4890. [Google Scholar] [CrossRef]
- Li, W.; Liu, C.; Xu, Y.; Niu, C.; Li, R.; Li, M.; Hu, C.; Tian, L. An interpretable hybrid deep learning model for flood forecasting based on Transformer and LSTM. J. Hydrol. Reg. Stud. 2024, 54, 101873. [Google Scholar] [CrossRef]
- Guo, S.; Wen, Y.; Zhang, X.; Chen, H. Monthly runoff prediction using the VMD-LSTM-Transformer hybrid model: A case study of the Miyun Reservoir in Beijing. J. Water Clim. Change 2023, 14, 3221–3236. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Oyelade, O.N.; Ezugwu, A.E.S.; Mohamed, T.I.; Abualigah, L. Ebola optimization search algorithm: A new nature-inspired metaheuristic optimization algorithm. IEEE Access 2022, 10, 16150–16177. [Google Scholar] [CrossRef]
- Gharehchopogh, F.S.; Namazi, M.; Ebrahimi, L.; Abdollahzadeh, B. Advances in Sparrow Search Algorithm: A Comprehensive Survey. Arch. Comput. Methods Eng. 2023, 30, 427–455. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. A novel swarm intelligence optimization approach: Sparrow search algorithm. Syst. Sci. Control Eng. 2020, 8, 22–34. [Google Scholar] [CrossRef]
- Paul, V.; Ramesh, R.; Sreeja, P.; Jarin, T.; Kumar, P.S.S.; Ansar, S.; Ashraf, G.A.; Pandey, S.; Said, Z. Hybridization of long short-term memory with Sparrow Search Optimization model for water quality index prediction. Chemosphere 2022, 307, 135762. [Google Scholar] [CrossRef]
- Xue, Y. An overview of overfitting and its solutions. J. Phys. Conf. Ser. 2019, 1168, 022022. [Google Scholar] [CrossRef]
- Prechelt, L. Early stop-but when? In Neural Networks: Tricks of the Trade; Springer: Berlin/Heidelberg, Germany, 2002; pp. 55–69. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Proceedings of the 31st International Conference on Neural Information Processing Systems (NIPS), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Nair, V.; Hinton, G.E. Rectified linear units improve restricted Boltzmann machines. In Proceedings of the 27th International Conference on Machine Learning (ICML), Haifa, Israel, 21–24 June 2010; pp. 807–814. [Google Scholar]
- Kratzert, F.; Klotz, D.; Shalev, G.; Klambauer, G.; Hochreiter, S.; Nearing, G. Towards learning universal, regional, and local hydrological behaviors via machine learning applied to large-sample datasets. Hydrol. Earth Syst. Sci. 2019, 23, 5089–5110. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Gers, F.A.; Schmidhuber, J.; Cummins, F. Learning to forget: Continual prediction with LSTM. Neural Comput. 2000, 12, 2451–2471. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, H.; Guan, X.; Meng, Y.; Xu, H. Urban flood depth prediction and visualization based on the XGBoost-SHAP model. Water Resour. Manag. 2024, 39, 1353–1375. [Google Scholar] [CrossRef]
- Miller, J.D.; Kim, H.; Kjeldsen, T.R.; Packman, J.; Grebby, S.; Dearden, R. Assessing the impact of urbanization on storm run-off in a peri-urban catchment using historical change in impervious cover. J. Hydrol. 2014, 515, 59–70. [Google Scholar] [CrossRef]
- Zhao, H.; Zhang, H.; Miao, C.; Ye, X.; Min, M. Linking Heat Source–Sink Landscape Patterns with Analysis of Urban Heat Islands: Study on the Fast-Growing Zhengzhou City in Central China. Remote Sens. 2018, 10, 1268. [Google Scholar] [CrossRef]
- Wang, H.; Guan, X.; Meng, Y.; Wang, H.; Xu, H.; Liu, Y.; Liu, M.; Wu, Z. Risk prediction based on oversampling technology and ensemble model optimized by tree-structured parzed estimator. Int. J. Disaster Risk Reduct. 2024, 111, 104753. [Google Scholar] [CrossRef]
- Wei, P.; Xu, X.; Xue, M.; Zhang, C.; Wang, Y.; Zhao, K.; Zhou, A.; Zhang, S.; Zhu, K. On the key dynamical processes supporting the 21.7 Zhengzhou record-breaking hourly rainfall in China. Adv. Atmos. Sci. 2023, 40, 337–349. [Google Scholar] [CrossRef]
- Guo, X.; Cheng, J.; Yin, C.; Li, Q.; Chen, R.; Fang, J. The extraordinary Zhengzhou flood of 7/20, 2021: How extreme weather and human response compounding to the disaster. Cities 2023, 134, 104168. [Google Scholar] [CrossRef]
- Wu, Z.; Zhou, Y.; Wang, H.; Jiang, Z. Depth prediction of urban flood under different rainfall return periods based on deep learning and data warehouse. Sci. Total Environ. 2020, 716, 137077. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Wu, Z.; Xu, H.; Yan, D.; Jiang, M.; Zhang, X.; Wang, H. Adaptive selection and optimal combination scheme of candidate models for real-time integrated prediction of urban flood. J. Hydrol. 2023, 626, 130152. [Google Scholar] [CrossRef]
- Längkvist, M.; Karlsson, L.; Loutfi, A. A review of unsupervised feature learning and deep learning for time-series modeling. Pattern Recognit. Lett. 2014, 42, 11–24. [Google Scholar] [CrossRef]
- Zhou, Y.; Wu, Z.; Jiang, M.; Xu, H.; Yan, D.; Wang, H.; Zhang, X. Real-time prediction and ponding process early warning method at urban flood points based on different deep learning methods. J. Flood Risk Manag. 2024, 17, e12964. [Google Scholar] [CrossRef]
- Yue, Y.; Cao, L.; Lu, D.; Hu, Z.; Xu, M.; Wang, S.; Li, B.; Ding, H. Review and empirical analysis of sparrow search algorithm. Artif. Intell. Rev. 2023, 56, 10867–10919. [Google Scholar] [CrossRef]




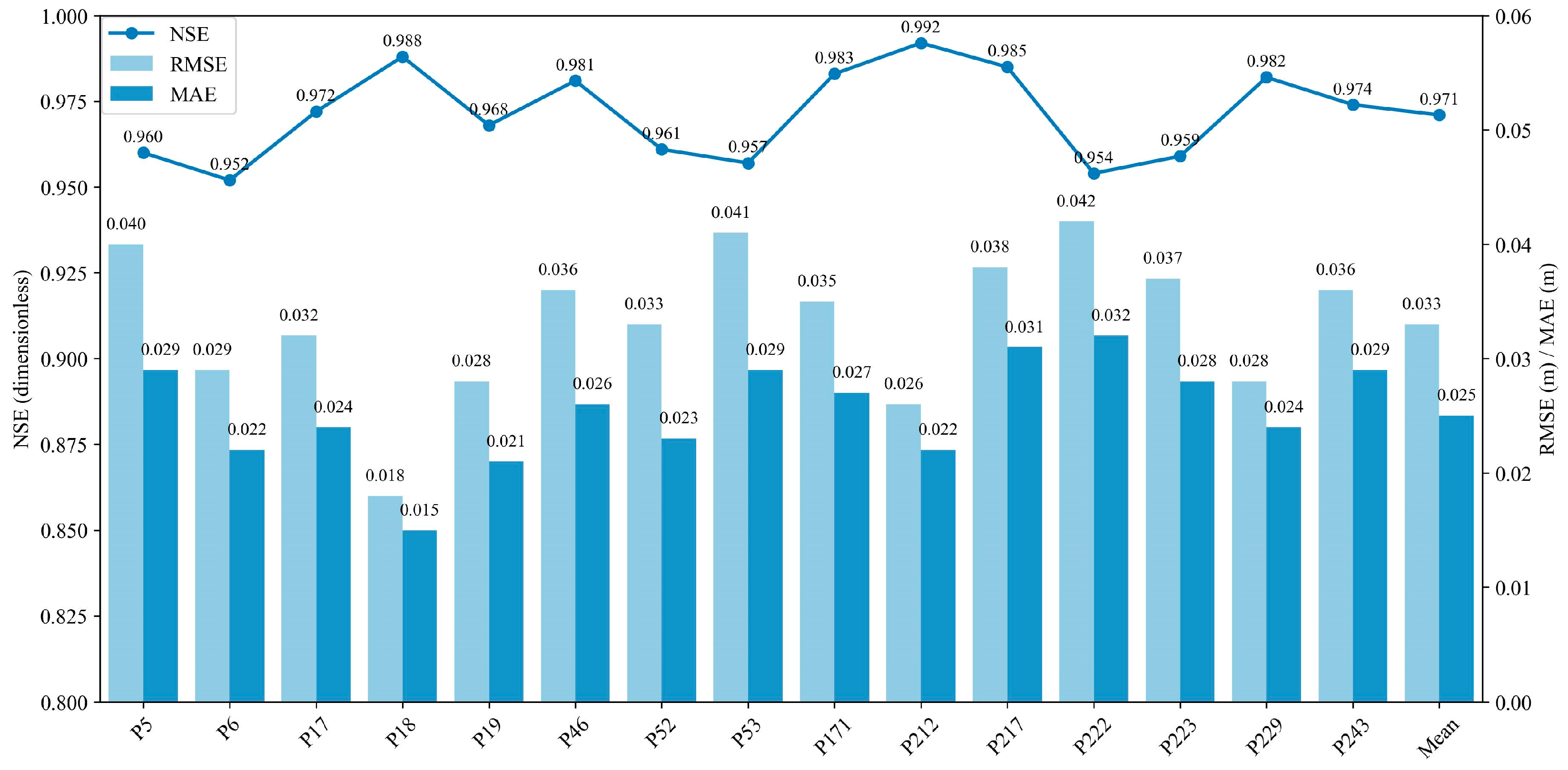

| Rainfall Events | Rainfall 1 | Rainfall 2 | Rainfall 3 | Rainfall 4 | Mean |
|---|---|---|---|---|---|
| RMSE (m) | 0.052 | 0.046 | 0.043 | 0.056 | 0.049 |
| MAE (m) | 0.043 | 0.033 | 0.032 | 0.045 | 0.038 |
| MAPE (%) | 20.60 | 25.15 | 30.77 | 44.44 | 30.24 |
| Bias (m) | 0.007 | 0.008 | −0.003 | 0.017 | 0.007 |
| NSE | 0.936 | 0.947 | 0.963 | 0.922 | 0.942 |
| Number | Attention Heads | Encoder Layers | Hidden-Layers 1 | Dropout Rate | Hidden-Layers 2 |
|---|---|---|---|---|---|
| Range | 1–10 | 1–10 | 64,128,256 | 0–0.5 | 64,128,256 |
| Optimized parameters | 6 | 3 | 128 | 0.16 | 256 |
| Model | Transformer | LSTM | Transformer-LSTM | Transformer-LSTM-SSA |
|---|---|---|---|---|
| RMSE (m) | 0.086 | 0.070 | 0.049 | 0.033 |
| MAE (m) | 0.066 | 0.058 | 0.038 | 0.025 |
| MAPE (%) | 41.04 | 41.55 | 30.24 | 19.35 |
| Bias (m) | 0.004 | 0.022 | 0.007 | 0.005 |
| NSE | 0.842 | 0.870 | 0.942 | 0.971 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, Z.; Zhang, J.; Chen, Y.; Xu, H. Urban Flood Prediction Model Based on Transformer-LSTM-Sparrow Search Algorithm. Water 2025, 17, 1404. https://doi.org/10.3390/w17091404
Fan Z, Zhang J, Chen Y, Xu H. Urban Flood Prediction Model Based on Transformer-LSTM-Sparrow Search Algorithm. Water. 2025; 17(9):1404. https://doi.org/10.3390/w17091404
Chicago/Turabian StyleFan, Zixuan, Jinping Zhang, Yanpo Chen, and Hongshi Xu. 2025. "Urban Flood Prediction Model Based on Transformer-LSTM-Sparrow Search Algorithm" Water 17, no. 9: 1404. https://doi.org/10.3390/w17091404
APA StyleFan, Z., Zhang, J., Chen, Y., & Xu, H. (2025). Urban Flood Prediction Model Based on Transformer-LSTM-Sparrow Search Algorithm. Water, 17(9), 1404. https://doi.org/10.3390/w17091404







