Optimized Filtrations for Stormwater Quality Improvement by Porous Media–Biochar Applications: Column Experiments and Inverse Modeling
Abstract
1. Introduction
2. Materials and Methods
2.1. Column Experiment and Water Quality Assessment
2.2. Model Simulation
3. Results and Discussion
3.1. Soil–Biochar Hydraulic Parameter Characteristics
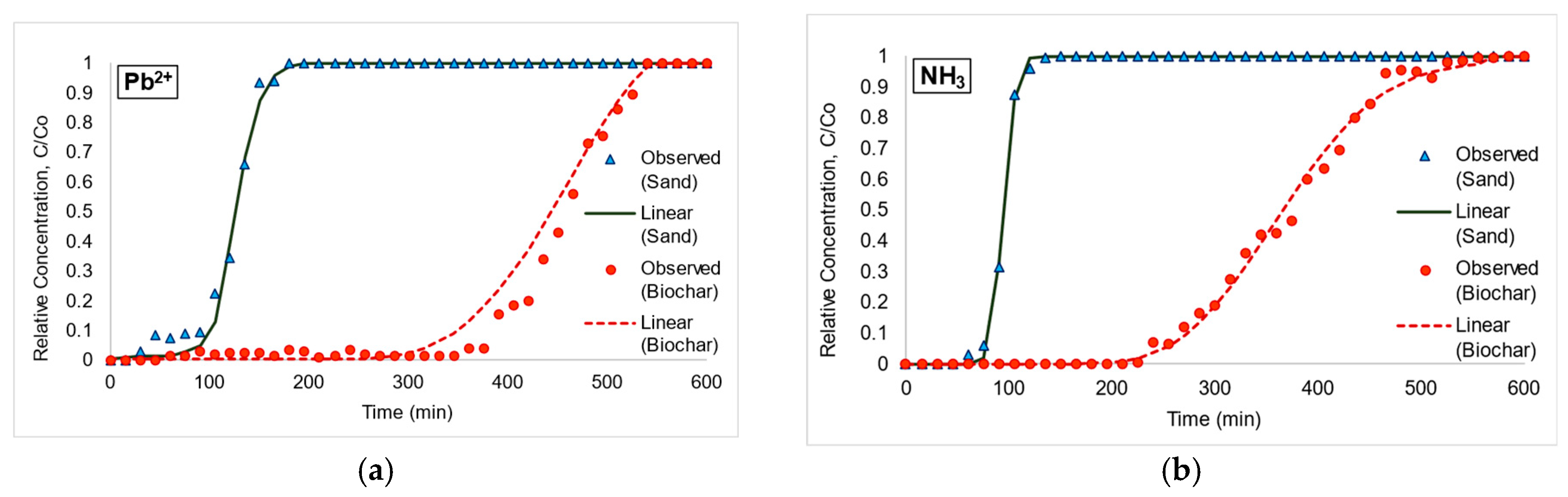
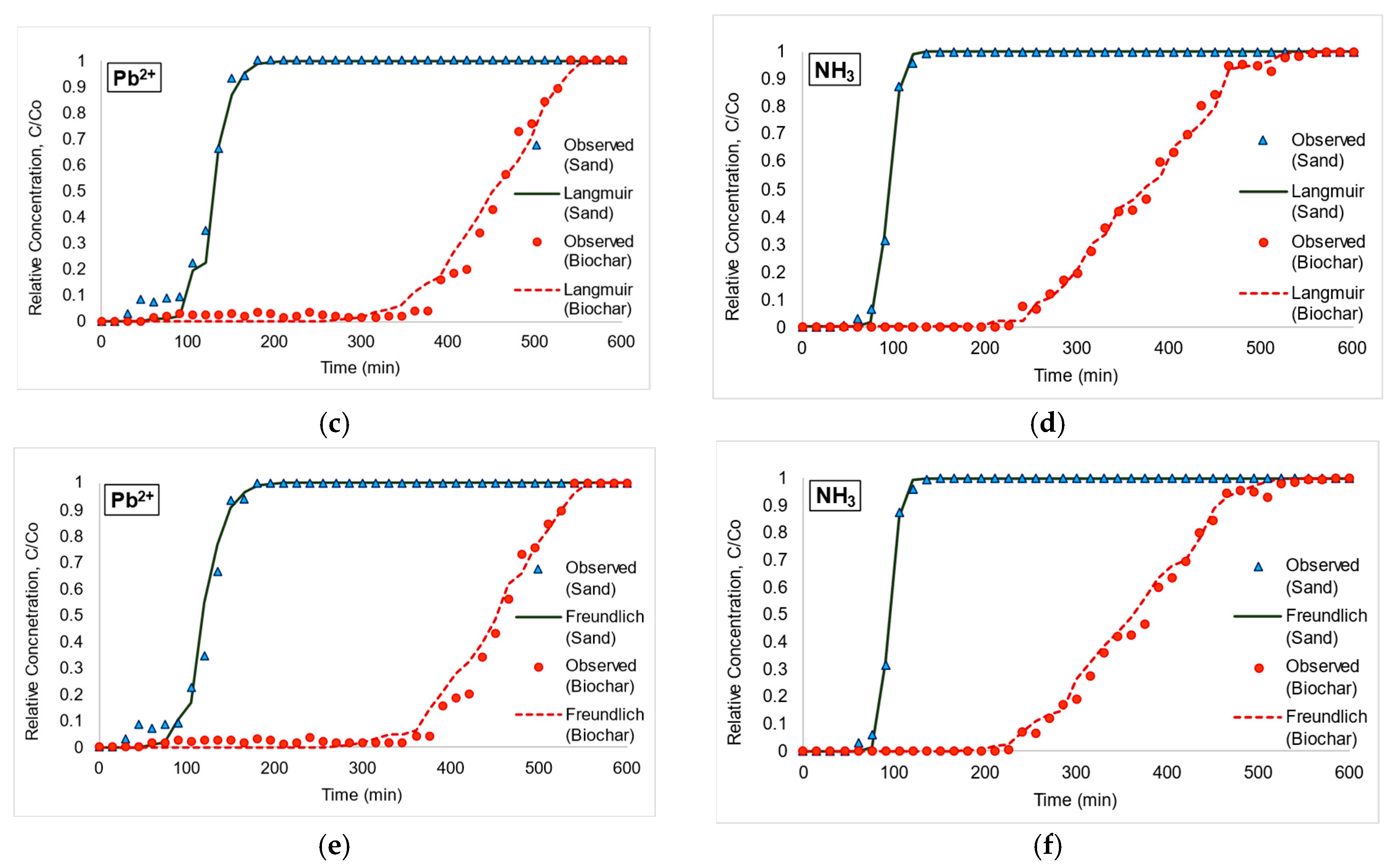
3.2. Adsorption Isotherms from Column Experiment and Inverse Model Simulation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BMP | Best Management Practice |
| Flood-MAR | Flood-Managed Aquifer Recharge |
| HYPROP | Hydraulic Property Analyzer |
| PFAS | Perfluoroalkyl and Polyfluoroalkyl Substances |
| RH | Rice Husk |
| SWRC | Soil Water Retention Curve |
References
- California Department of Water Resources Flood-Managed Aquifer Recharge (Flood-MAR). Available online: https://water.ca.gov/programs/all-programs/flood-mar (accessed on 20 January 2025).
- Mumberg, T.; Ahrens, L.; Wanner, P. Managed Aquifer Recharge as a Potential Pathway of Contaminants of Emerging Concern into Groundwater Systems—A Systematic Review. Chemosphere 2024, 364, 143030. [Google Scholar] [CrossRef]
- Imig, A.; Szabó, Z.; Halytsia, O.; Vrachioli, M.; Kleinert, V.; Rein, A. A Review on Risk Assessment in Managed Aquifer Recharge. Integr. Environ. Assess. Manag. 2022, 18, 1513–1529. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.S.; Holman, R.E.; Dorney, J.R. Systematic Evaluation of Pollutant Removal by Urban Wet Detention Ponds. J. Environ. Eng. 1996, 122, 983–988. [Google Scholar] [CrossRef]
- Wu, J.S.; Allan, C.J.; Saunders, W.L.; Evett, J.B. Characterization and Pollutant Loading Estimation for Highway Runoff. J. Environ. Eng. 1998, 124, 584–592. [Google Scholar] [CrossRef]
- Davis, A.P.; Shokouhian, M.; Ni, S. Loading Estimates of Lead, Copper, Cadmium, and Zinc in Urban Runoff from Specific Sources. Chemosphere 2001, 44, 997–1009. [Google Scholar] [CrossRef]
- Barrett, M.E.; Irish, L.B.; Malina, J.F.; Charbeneau, R.J. Characterization of Highway Runoff in Austin, Texas, Area. J. Environ. Eng. 1998, 124, 131–137. [Google Scholar] [CrossRef]
- Sansalone, J.J.; Buchberger, S.G. Partitioning and First Flush of Metals in Urban Roadway Storm Water. J. Environ. Eng. 1997, 123, 134–143. [Google Scholar] [CrossRef]
- TCEQ. Surface Water Quality Web Reporting Tool. Available online: https://www80.tceq.texas.gov/SwqmisPublic/index.htm (accessed on 25 February 2025).
- Maliva, R.G. MAR Pretreatment. In Anthropogenic Aquifer Recharge; Springer: Cham, Switzerland, 2020; Volume 5, pp. 343–379. [Google Scholar]
- Idelovitch, E.; Icekson-Tal, N.; Avraham, O.; Michail, M. The Long-Term Performance of Soil Aquifer Treatment (SAT) for Effluent Reuse. Water Supply 2003, 3, 239–246. [Google Scholar] [CrossRef]
- Sharma, S.K.; Kennedy, M.D. Soil Aquifer Treatment for Wastewater Treatment and Reuse. Int. Biodeterior. Biodegrad. 2017, 119, 671–677. [Google Scholar] [CrossRef]
- Selintung, M.; Mangarengi, N.A.P.; Zubair, A. The Reduction of Heavy Metals Cd and Cr Levels in Wastewater Using Bagasse Charcoal as an Adsorbent. IOP Conf. Ser. Earth Environ. Sci. 2020, 419, 012171. [Google Scholar] [CrossRef]
- Vamvuka, D.; Loupasis, E.; Chamilaki, E.; Sdoukou, E. Adsorption of Ammonium from Wastewaters by an Almond Kernel Derived Biochar Modified by Potassium Hydroxide or Dolomite and Activated by Steam. Environ. Adv. 2024, 15, 100465. [Google Scholar] [CrossRef]
- Poo, K.-M.; Son, E.-B.; Chang, J.-S.; Ren, X.; Choi, Y.-J.; Chae, K.-J. Biochars Derived from Wasted Marine Macro-Algae (Saccharina Japonica and Sargassum Fusiforme) and Their Potential for Heavy Metal Removal in Aqueous Solution. J. Environ. Manag. 2018, 206, 364–372. [Google Scholar] [CrossRef]
- Batool, S.; Idrees, M.; Hussain, Q.; Kong, J. Adsorption of Copper (II) by Using Derived-Farmyard and Poultry Manure Biochars: Efficiency and Mechanism. Chem. Phys. Lett. 2017, 689, 190–198. [Google Scholar] [CrossRef]
- Chen, X.; Chen, G.; Chen, L.; Chen, Y.; Lehmann, J.; McBride, M.B.; Hay, A.G. Adsorption of Copper and Zinc by Biochars Produced from Pyrolysis of Hardwood and Corn Straw in Aqueous Solution. Bioresour. Technol. 2011, 102, 8877–8884. [Google Scholar] [CrossRef] [PubMed]
- Wijeyawardana, P.; Nanayakkara, N.; Gunasekara, C.; Karunarathna, A.; Law, D.; Pramanik, B.K. Removal of Cu, Pb and Zn from Stormwater Using an Industrially Manufactured Sawdust and Paddy Husk Derived Biochar. Environ. Technol. Innov. 2022, 28, 102640. [Google Scholar] [CrossRef]
- Silvani, L.; Cornelissen, G.; Botnen Smebye, A.; Zhang, Y.; Okkenhaug, G.; Zimmerman, A.R.; Thune, G.; Sævarsson, H.; Hale, S.E. Can Biochar and Designer Biochar Be Used to Remediate Per- and Polyfluorinated Alkyl Substances (PFAS) and Lead and Antimony Contaminated Soils? Sci. Total Environ. 2019, 694, 133693. [Google Scholar] [CrossRef]
- Hasan, M.S.; Vasquez, R.; Geza, M. Application of Biochar in Stormwater Treatment: Experimental and Modeling Investigation. Processes 2021, 9, 860. [Google Scholar] [CrossRef]
- Liang, B.; Lehmann, J.; Solomon, D.; Kinyangi, J.; Grossman, J.; O’Neill, B.; Skjemstad, J.O.; Thies, J.; Luizão, F.J.; Petersen, J.; et al. Black Carbon Increases Cation Exchange Capacity in Soils. Soil Sci. Soc. Am. J. 2006, 70, 1719–1730. [Google Scholar] [CrossRef]
- Ahmad, M.; Rajapaksha, A.U.; Lim, J.E.; Zhang, M.; Bolan, N.; Mohan, D.; Vithanage, M.; Lee, S.S.; Ok, Y.S. Biochar as a Sorbent for Contaminant Management in Soil and Water: A Review. Chemosphere 2014, 99, 19–33. [Google Scholar] [CrossRef]
- Rahmat, A.; Nissa, R.C.; Nuraini, L.; Nurtanto, M.; Ramadhani, W.S. Analysis of Rice Husk Biochar Characteristics under Different Pyrolysis Temperature. IOP Conf. Ser. Earth Environ. Sci. 2023, 1201, 012095. [Google Scholar] [CrossRef]
- Wang, J.; Guo, X. Adsorption Isotherm Models: Classification, Physical Meaning, Application and Solving Method. Chemosphere 2020, 258, 127279. [Google Scholar] [CrossRef]
- Guo, X.; Wang, J. The Phenomenological Mass Transfer Kinetics Model for Sr2+ Sorption onto Spheroids Primary Microplastics. Environ. Pollut. 2019, 250, 737–745. [Google Scholar] [CrossRef] [PubMed]
- Guo, X.; Wang, J. Comparison of Linearization Methods for Modeling the Langmuir Adsorption Isotherm. J. Mol. Liq. 2019, 296, 111850. [Google Scholar] [CrossRef]
- Langmuir, I. The Adsorption of Gases on Plane Surfaces of Glass, Mica and Platinum. J. Am. Chem. Soc. 1918, 40, 1361–1403. [Google Scholar] [CrossRef]
- Langmuir, I. The Constitution and Fundamental Properties of Solids and Liquids. Part I. Solids. J. Am. Chem. Soc. 1916, 38, 2221–2295. [Google Scholar] [CrossRef]
- Freundlich, H. Über Die Adsorption in Lösungen. Z. Phys. Chemie 1907, 57U, 385–470. [Google Scholar] [CrossRef]
- Zaheer, Z.; AL-Asfar, A.; Aazam, E.S. Adsorption of Methyl Red on Biogenic Ag@Fe Nanocomposite Adsorbent: Isotherms, Kinetics and Mechanisms. J. Mol. Liq. 2019, 283, 287–298. [Google Scholar] [CrossRef]
- Wang, F.; Shih, K. Adsorption of Perfluorooctanesulfonate (PFOS) and Perfluorooctanoate (PFOA) on Alumina: Influence of Solution PH and Cations. Water Res. 2011, 45, 2925–2930. [Google Scholar] [CrossRef]
- PC-PROGRESS Engineering Software Developer. The HYDRUS 1D Description. Available online: https://www.pc-progress.com/en/Default.aspx?h1d-description (accessed on 4 February 2025).
- PC-PROGRESS Engineering Software Developer. HYDRUS 3D Help Inverse Solution. Available online: https://www.pc-progress.com/en/OnlineHelp/HYDRUS3/Hydrus.html?InverseSolution.html (accessed on 28 January 2025).
- Vrugt, J.A.; Stauffer, P.H.; Wöhling, T.; Robinson, B.A.; Vesselinov, V.V. Inverse Modeling of Subsurface Flow and Transport Properties: A Review with New Developments. Vadose Zone J. 2008, 7, 843–864. [Google Scholar] [CrossRef]
- Pal, S.; Mukherjee, S.; Ghosh, S. Application of HYDRUS 1D Model for Assessment of Phenol–Soil Adsorption Dynamics. Environ. Sci. Pollut. Res. 2014, 21, 5249–5261. [Google Scholar] [CrossRef]
- do Nascimento, Í.V.; de Assis Júnior, R.N.; de Araújo, J.C.; de Alencar, T.L.; Freire, A.G.; Lobato, M.G.R.; da Silva, C.P.; Mota, J.C.A.; do Nascimento, C.D.V. Estimation of van Genuchten Equation Parameters in Laboratory and through Inverse Modeling with Hydrus-1D. J. Agric. Sci. 2018, 10, 102. [Google Scholar] [CrossRef]
- Šimůnek, J.; van Genuchten, M.T. Modeling Nonequilibrium Flow and Transport Processes Using HYDRUS. Vadose Zone J. 2008, 7, 782–797. [Google Scholar] [CrossRef]
- Emerson, K.; Russo, R.C.; Lund, R.E.; Thurston, R.V. Aqueous Ammonia Equilibrium Calculations: Effect of PH and Temperature. J. Fish. Res. Board Can. 1975, 32, 2379–2383. [Google Scholar] [CrossRef]
- Russo, R.C. Ammonia, Nitrite, and Nitrate. In Fundamentals of Aquatic Toxicology and Chemistry; Rand, G.M., Petrocelli, S.R., Eds.; Hemisphere Publishing Corp.: Washington, DC, USA, 1985; pp. 455–471. [Google Scholar]
- Amazon SAYOYO Horticultural Charcoal—Natural Biochar Soil Amendment, Rice Husk Charcoal for Plants, Activated Charcoal for Terrariums 0.6 Lbs. Available online: https://a.co/d/cm0Y1Hk (accessed on 2 February 2025).
- Leng, L.; Xiong, Q.; Yang, L.; Li, H.; Zhou, Y.; Zhang, W.; Jiang, S.; Li, H.; Huang, H. An Overview on Engineering the Surface Area and Porosity of Biochar. Sci. Total Environ. 2021, 763, 144204. [Google Scholar] [CrossRef] [PubMed]
- Richards, L.A. Capillary Conduction of Liquids Through Porous Mediums. Physics 1931, 1, 318–333. [Google Scholar] [CrossRef]
- van Genuchten, M.T. A Closed-form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Simunek and Sejna HYDRUS Soil Hydraulic Models. Available online: https://www.pc-progress.com/en/OnlineHelp/HYDRUS3/Hydrus.html?SoilHydraulicModels.html (accessed on 29 January 2025).
- Shokrana, M.S.B.; Ghane, E. Measurement of Soil Water Characteristic Curve Using HYPROP2. MethodsX 2020, 7, 100840. [Google Scholar] [CrossRef]
- Freeze, R.A.; Cherry, J.A. Groundwater; Prentice-Hall: Englewood Cliffs, NJ, USA, 1979. [Google Scholar]
- Devereux, R.C.; Sturrock, C.J.; Mooney, S.J. The Effects of Biochar on Soil Physical Properties and Winter Wheat Growth. Earth Environ. Sci. Trans. R. Soc. Edinb. 2012, 103, 13–18. [Google Scholar] [CrossRef]
- Omondi, M.O.; Xia, X.; Nahayo, A.; Liu, X.; Korai, P.K.; Pan, G. Quantification of Biochar Effects on Soil Hydrological Properties Using Meta-Analysis of Literature Data. Geoderma 2016, 274, 28–34. [Google Scholar] [CrossRef]
- Huang, C.; Chen, Y.; Jin, L.; Yang, B. Properties of Biochars Derived from Different Straw at 500 °C Pyrolytic Temperature: Implications for Their Use to Improving Acidic Soil Water Retention. Agric. Water Manag. 2024, 301, 108953. [Google Scholar] [CrossRef]
- Minnesota Pollution Control Agency Determining Soil Infiltration Rates. Available online: http://stormwater.pca.state.mn.us/index.php/Determining_soil_infiltration_rates (accessed on 1 February 2025).
- USEPA. Stormwater Best Management Practice Infiltration Basin; USEPA: Washington, DC, USA, 2021. [Google Scholar]
- Nguyen, K.T.; Ahmed, M.B.; Mojiri, A.; Huang, Y.; Zhou, J.L.; Li, D. Advances in As Contamination and Adsorption in Soil for Effective Management. J. Environ. Manag. 2021, 296, 113274. [Google Scholar] [CrossRef] [PubMed]
- Ghosal, P.S.; Gupta, A.K. Development of a Generalized Adsorption Isotherm Model at Solid-Liquid Interface: A Novel Approach. J. Mol. Liq. 2017, 240, 21–24. [Google Scholar] [CrossRef]
- Mobasherpour, I.; Salahi, E.; Pazouki, M. Comparative of the Removal of Pb2+, Cd2+ and Ni2+ by Nano Crystallite Hydroxyapatite from Aqueous Solutions: Adsorption Isotherm Study. Arab. J. Chem. 2012, 5, 439–446. [Google Scholar] [CrossRef]
- Sidey, V. On the Effective Ionic Radii for Ammonium. Acta Crystallogr. B Struct. Sci. Cryst. Eng. Mater. 2016, 72, 626–633. [Google Scholar] [CrossRef]
- Jaffrezic-Renault, N.; Dzyadevych, S.V. Conductometric Microbiosensors for Environmental Monitoring. Sensors 2008, 8, 2569–2588. [Google Scholar] [CrossRef] [PubMed]
- Severo, F.F.; da Silva, L.S.; Moscôso, J.S.C.; Sarfaraz, Q.; Rodrigues Júnior, L.F.; Lopes, A.F.; Marzari, L.B.; Molin, G.D. Chemical and Physical Characterization of Rice Husk Biochar and Ashes and Their Iron Adsorption Capacity. SN Appl. Sci. 2020, 2, 1286. [Google Scholar] [CrossRef]
- Persson, I. Hydrated Metal Ions in Aqueous Solution: How Regular Are Their Structures? Pure Appl. Chem. 2010, 82, 1901–1917. [Google Scholar] [CrossRef]
- Pye, C.C.; Gunasekara, C.M. An Ab Initio Investigation of the Hydration of Lead(II). Liquids 2022, 2, 39–49. [Google Scholar] [CrossRef]
- Babiaczyk, W.I.; Bonella, S.; Guidoni, L.; Ciccotti, G. Hydration Structure of the Quaternary Ammonium Cations. J. Phys. Chem. B 2010, 114, 15018–15028. [Google Scholar] [CrossRef]
- Granados, P.; Mireles, S.; Pereira, E.; Cheng, C.-L.; Kang, J.J. Effects of Biochar Production Methods and Biomass Types on Lead Removal from Aqueous Solution. Appl. Sci. 2022, 12, 5040. [Google Scholar] [CrossRef]
- Cheng, C.-L.; Perfect, E.; Mills, R.T. Forward Prediction of Height-Averaged Capillary Pressure–Saturation Parameters Using the BC-vG Upscaler. Vadose Zone J. 2013, 12, vzj2012-0174. [Google Scholar] [CrossRef]
- Cropper, S.C.; Perfect, E.; Cheng, C.-L.; McKay, L.; Kang, M. Evaluation of TrueCell Program for Estimating Point Capillary Pressure—Saturation Parameters for Flint Sand. Geoderma 2017, 287, 90–97. [Google Scholar] [CrossRef]

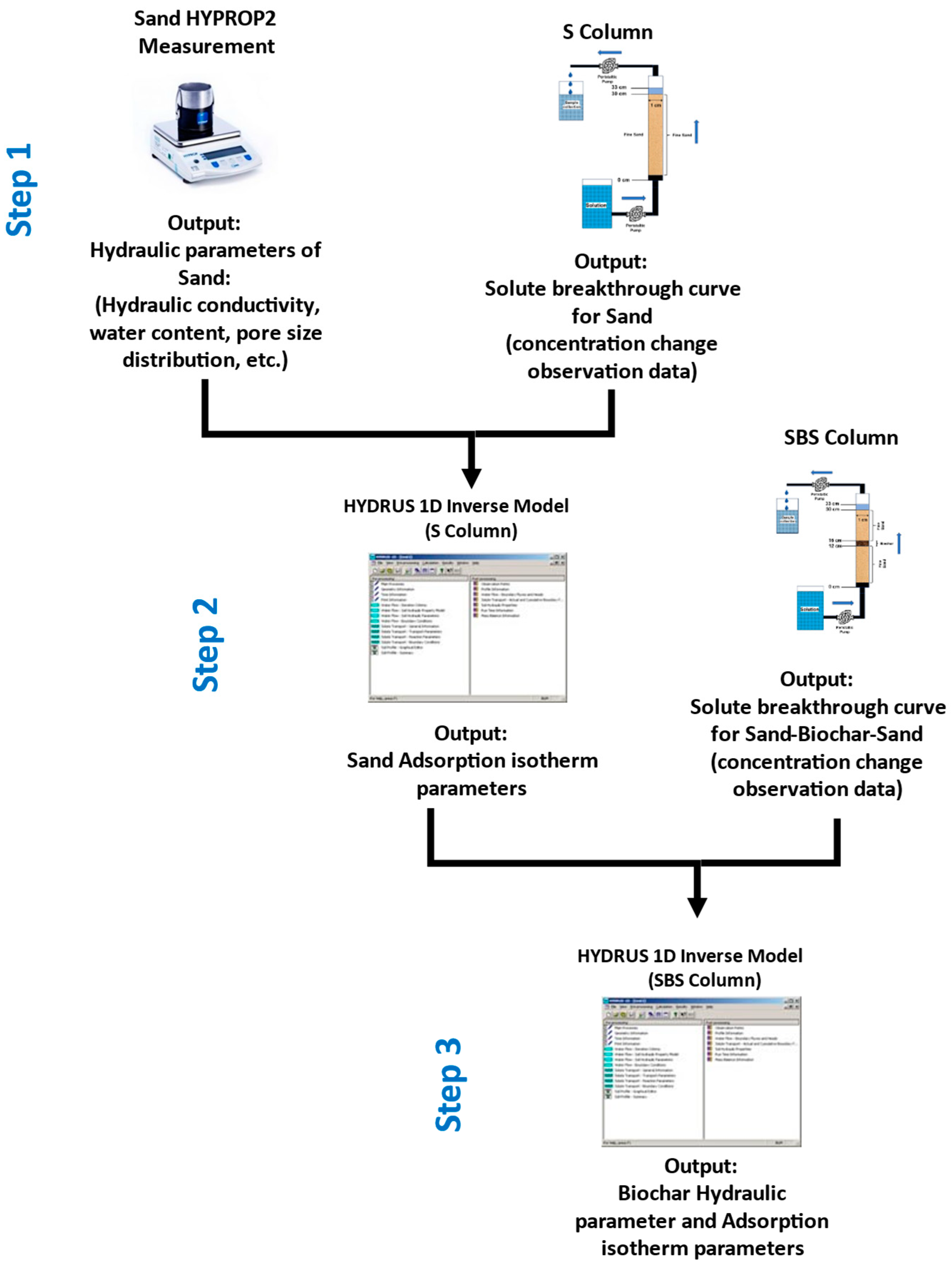
| Material | Residual Soil Water Content Θr - | Saturated Soil Water Content Θs - | Inverse of the Air-Entry Pressure α (1/cm) | Pore Size Distribution n - | Hydraulic Conductivity K (cm/min) |
|---|---|---|---|---|---|
| Sand (HYPROP2) | 0.045 | 0.439 | 0.0725 | 1.1 | 0.14 |
| RH Biochar (Optimized) | 0.213 | 0.728 | 0.0777 | 2.913 | 0.008753 |
| Adsorbent | Adsorbate | Model | Kd (cm3/mg) | η (cm3/mg) | β (-) | R2 (-) | RMSE (mg/L) | AIC (-) | Sorption, s (mg/g) |
|---|---|---|---|---|---|---|---|---|---|
| Sand | Pb2+ | Linear | 0.05845 | - | - | 0.99316 | 0.07824 | −62.29 | 0.117 |
| Langmuir * | 0.05916 | 0.000048 | - | 0.99354 | 0.0801 | −65.37 | 0.118 | ||
| Freundlich | 0.03728 | - | 1.133 | 0.97468 | 0.1312 | −49.85 | 0.033 | ||
| NH3 | Linear | 0.00169 | - | - | 0.74425 | 1.229 | 81.26 | 0.084 | |
| Langmuir * | 0.002082 | 0.005016 | - | 0.74437 | 1.229 | 66.37 | 0.104 | ||
| Freundlich | 0.002001 | - | 1.037 | 0.74503 | 1.229 | 83.26 | 0.090 | ||
| Biochar | Pb2+ | Linear | 1.99 | - | - | 0.76631 | 0.1793 | −28.44 | 3.980 |
| Langmuir | 1.9589 | 0.000321 | - | 0.76751 | 0.1765 | −26.67 | 3.918 | ||
| Freundlich * | 2.4216 | - | 1.001 | 0.7681 | 0.1768 | −28.65 | 4.813 | ||
| NH3 | Linear | 0.1467 | - | - | 0.80646 | 1.063 | 100.2 | 7.335 | |
| Langmuir | 0.1563 | 0.0001 | - | 0.80652 | 1.067 | 102.4 | 7.812 | ||
| Freundlich * | 0.167 | - | 1.1 | 0.80672 | 1.042 | 100.2 | 6.188 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Preota, S.A.; Cheng, C.-L.; Hwangbo, M.; Kim, J. Optimized Filtrations for Stormwater Quality Improvement by Porous Media–Biochar Applications: Column Experiments and Inverse Modeling. Water 2025, 17, 1372. https://doi.org/10.3390/w17091372
Preota SA, Cheng C-L, Hwangbo M, Kim J. Optimized Filtrations for Stormwater Quality Improvement by Porous Media–Biochar Applications: Column Experiments and Inverse Modeling. Water. 2025; 17(9):1372. https://doi.org/10.3390/w17091372
Chicago/Turabian StylePreota, Sumiaya Amin, Chu-Lin Cheng, Myung Hwangbo, and Jongsun Kim. 2025. "Optimized Filtrations for Stormwater Quality Improvement by Porous Media–Biochar Applications: Column Experiments and Inverse Modeling" Water 17, no. 9: 1372. https://doi.org/10.3390/w17091372
APA StylePreota, S. A., Cheng, C.-L., Hwangbo, M., & Kim, J. (2025). Optimized Filtrations for Stormwater Quality Improvement by Porous Media–Biochar Applications: Column Experiments and Inverse Modeling. Water, 17(9), 1372. https://doi.org/10.3390/w17091372










