Abstract
Under the context of global climate change, floods are one of the major challenges facing urban development. Based on resilience theory, this study proposed an evaluation method to accurately assess the resilience of urban flooding prevention and control systems (FPCs), integrating both attribute resilience (AR) and functional resilience (FR). First, the method organized FPC attributes from the perspective of the waterlogging generation and elimination processes using foundational data from the study area, and it established a resilience indicator system. The Entropy Weight Method (EWM) was applied to calculate indicator weights, and the Technique for Order Preference by Similarity to Ideal Solution (TOPSIS) was used to calculate indicator values, ultimately deriving the attribute resilience (AR). Subsequently, functional performance during actual operations was evaluated using scenario simulation based on hydrodynamic model results, and the FR was determined. Finally, spatial correlation analysis of the AR and FR was conducted to identify areas with weak resilience. This study developed an evaluation method that considers both system attributes and functional performance using the central urban area of Beijing as a case study to assess flood resilience. The results indicated that the most influential factors affecting the AR of the FPC are the green space percentage (GSP), average slope, and drainage capacity (DC), with their weights calculated as 0.17, 0.137, and 0.205, respectively. Among resistance, absorption, and recovery, absorption had the greatest influence, with a weight of 0.447. The Moran’s I indices for the AR and FR were 0.66 and 0.49, respectively, indicating spatial clustering, although the clustering locations differed. There was spatial correlation between the AR and FR, enabling more precise identification of areas with high and low flood resilience. However, the trends of the AR and FR were not entirely consistent across different types of sub-districts due to differences in evaluation methods and the influence of various indicators.
1. Introduction
With global climate change, the frequency of extreme weather events has increased in recent years [1]. Additionally, urban development has led to an expansion of impervious surfaces, reducing natural rainwater infiltration capacity and exacerbating urban flood problems [2,3]. Urban flooding disrupts transportation, electricity, and communication systems, affecting residents’ daily lives, damaging infrastructure, and posing threats to property and life safety [4,5]. Urban flood prevention and control systems (FPCs) play a critical role in mitigating flood disasters and reducing associated losses [6,7]. In the increasingly complex context of disaster risks, the evaluation of urban flood resilience has become a focal topic [8]. Investigating FPC resilience under heavy rainfall and urban flooding focuses on comprehensive capacity of city. This capacity covers the entire flooding process, including disaster resistance, absorption during the event, and recovery after the event [9,10]. Assessing FPC resilience can provide decision makers with valuable guidance. It enhances the scientific basis for urban spatial planning and strengthens flood response capacities.
Several studies have explored methods to assess the resilience of FPCs in response to storm and flood disasters. Some researchers have developed evaluation systems for flood resilience by constructing indicator systems, a method widely used in resilience assessments related to climate change [11,12]. Ali et al. [13] developed a community resilience index system for flood-prone areas. The system includes evaluation criteria spanning social, economic, political, health, communication, education, and infrastructure dimensions. Tayyab et al. [14] combined GIS and remote sensing data to propose a resilience assessment framework based on four dimensions: flood hazard, exposure, vulnerability, and adaptive capacity. Kotzee et al. [15] integrated flood-related social, ecological, infrastructure, and economic indicators using principal component analysis to derive resilience indices and map their spatial distribution. Wang et al. [16] combined Bayesian networks (BNs) and geographic information systems (GISs) to identify key drivers of urban flood resilience. They developed an indicator system covering key factors such as inundation risk, population risk, and flood mitigation to evaluate urban flood resilience. These studies constructed indicator systems based on various attributes of the drainage system’s environment to assess urban flood resilience, which is referred to as attribute resilience (AR). While AR effectively quantifies the impact of multiple attributes on resilience, the selection of indicators involves a degree of subjectivity. However, urban floods occur due to insufficient drainage system capacity, where rainwater overflows from the system to the surface during drainage, resulting in waterlogging. Therefore, when assessing flood resilience, it is also essential to consider the operational performance of the drainage system during rainfall events.
In flood resilience studies, researchers have built hydrological models to simulate storm and flood scenarios. These models were used to analyze FPC resilience under storm conditions based on drainage system performance. Bisht et al. [17] utilized SWMM and MIKE models to study flood processes under extreme precipitation events in a region of West Bengal, India. Wang et al. [18] utilized the Cellular Automata Dual-DraInagE Simulation (CADDIES) model to develop a two-dimensional flood model. This model simulates surface waterlogging distribution and measures flood resilience using the proportion of inundated grid cells. Zhang et al. [19] combined a GIS and SWMM software to simulate flood scenarios and used drainage efficiency as a performance indicator to assess the resilience of drainage systems. Wang et al. [20] constructed a drainage network model for the study area using SWMM and proposed a new resilience indicator based on resilience profile graphs. This method was used to evaluate the resilience of urban drainage systems under synthetic short-duration storms and real continuous rainfall conditions. These methods evaluate resilience by analyzing urban drainage functional performance during rainfall, which can accurately identify areas with weak resilience. The resilience results derived from these methods are referred to as functional resilience (FR). However, these models can only capture the surface types and drainage network capacities of cities, overlooking the emergency measures deployed during storm events. Furthermore, such evaluation methods cannot identify the specific causes of low resilience, limiting their ability to guide subsequent improvement efforts.
The two aforementioned evaluation methods have their respective advantages. The main gaps of previous studies are the following: (a) The evaluation of AR only ignores the physical process, which is subjective. The evaluation results may be biased from the results of actual flood conditions. (b) The evaluation of FR relies heavily on hydrodynamic models but insufficiently considers non-hydrodynamic factors and other contributors to flooding. Evaluating FR relies heavily on hydrodynamic models but insufficiently considers non-hydrodynamic factors and other contributors to flooding. (c) The lack of spatial correlation feature analysis of the AR and FR cannot provide an accurate reference for toughness improvement strategies.
To address these limitations, this study proposes a comprehensive framework for evaluating the AR and FR of urban FPCs. The primary objectives of this study were (a) to establish an indicator system for assessing the AR of the FPC; (b) to evaluate the FR of the FPC under actual rainfall scenarios using a model; and (c) to conduct spatial correlation analysis of the AR and FR to guide resilience enhancement strategies. Using the central urban area of Beijing as a case study, the framework selects AR evaluation indicators. These indicators are based on the three dimensions of resilience: resistance, absorption, and recovery corresponding to different stages of resilience during storm events. Indicator values at this scale are obtained, and the entropy weight method (EWM) is used to determine indicator weights, while TOPSIS is applied to derive the AR. Subsequently, a one-dimensional pipe network and two-dimensional surface coupling model are constructed, and the FR is calculated using the proportion of waterlogged area as an indicator. Finally, spatial correlation analysis of the two types of resilience is conducted to identify their shared spatial distribution characteristics and key influencing factors. The novelties of this study were grounded on the following: (a) an integrated evaluation of AR and FR, which provides a more comprehensive reflection of the complexity and dynamics of urban flood resilience; and (b) the use of spatial correlation analysis to identify the spatial distribution characteristics of AR and FR, offering a more scientific basis for resilience enhancement.
2. Methodology
2.1. Study Area
Beijing, located in northern China, serves as the country’s political, cultural, international exchange, and technological innovation center. The city has a temperate semi-arid continental climate characterized by cold and dry winters and hot, rainy summers. The annual average rainfall is 698.4 mm, with 75–80% concentrated between June and September. With the development of urbanization and the increasing frequency of storm events caused by extreme weather, flood disasters have become increasingly severe in the city. During the “7·21” storm event in 2012, Beijing experienced the most intense storm and flood disaster in 61 years, with an average daily rainfall of 190.3 mm across the city. This resulted in severe urban flooding, causing significant disruption to transportation, considerable economic losses, and casualties. The disaster affected 1.602 million people, caused 79 deaths, and led to the emergency relocation of 97,000 people. The direct economic losses amounted to 11.64 billion RMB [21]. From 29 July to 2 August 2023, Beijing experienced an extreme storm event. Fangshan District suffered extensive damage, including 21,500 collapsed or damaged houses. Over 60,000 rooms were destroyed, and 6300 vehicles were submerged. Additionally, 200,000 mu of farmland was flooded, with 81,000 mu experiencing reduced yields. Additionally, flooding destroyed multiple sections of National Highway 108, leaving several villages with damaged roads, interrupted communication, and disrupted water supply [22]. These incidents highlight the severe flood impacts in Beijing. Therefore, this study selected the central urban area of Beijing as the research region (Figure 1), covering a total area of 740.2 km2. The study area includes Dongcheng and Xicheng districts, as well as parts of Chaoyang, Haidian, Shijingshan, Fengtai, and Daxing districts.
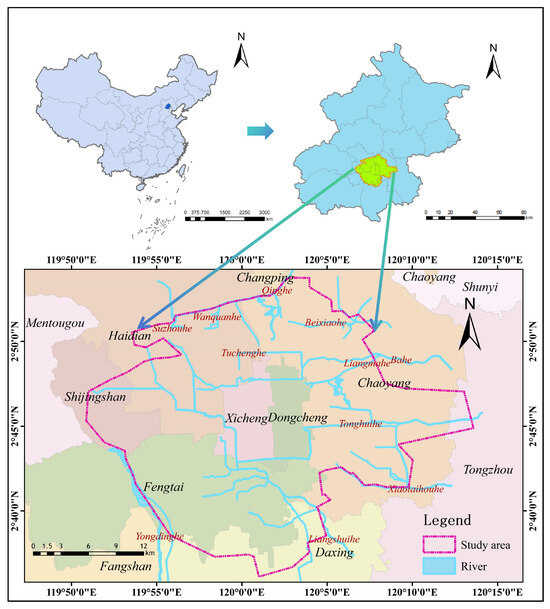
Figure 1.
Location of study area.
2.2. Resilience Assessment Framework of FPC
Resilience refers to the ability of a system to return to a normal state after being disrupted by an event. AR is a descriptive type of resilience that evaluates whether a system possesses the foundational conditions necessary to meet specific requirements. It is also referred to as design resilience. Urban flooding occurs when intense or continuous rainfall within a certain area exceeds the capacity of stormwater facilities, resulting in surface water accumulation. FPC refers to the combination of engineering and non-engineering measures designed to prevent and address urban flooding. It includes natural and artificial facilities, as well as management measures, for stormwater infiltration, collection, conveyance, storage, discharge, treatment, and reuse. During storm events, FPC plays a critical role in safeguarding property, ensuring life safety, and maintaining normal living and production activities.
Resilience is a process of responding to external disturbances and recovering from them. The AR level of FPC depends on the process from the decline of system performance to its recovery. This process corresponds to the period from the onset of water accumulation on the surface to its dissipation. Studying resilience as a process helps to understand system performance at different stages and provides targeted recommendations for improvement [23]. This study used the impact process of a storm on the drainage system as a timeline, as illustrated in Figure 2 [24]. During a specific storm event, the initial system performance is set to 1. In the first stage (t0–t1), source reduction facilities of FPC control stormwater runoff through infiltration, purification, and detention, reducing peak flow rates. This corresponds to the resistance of FPC. When rainfall intensity exceeds the drainage capacity of the system, flood accumulation begins. The system is impacted, and its performance starts to decline until reaching the lowest point. In the second stage (t1–t3), drainage and storage facilities transfer accumulated water to water bodies to alleviate flooding, corresponding to the absorption capacity of FPC. After the rainfall peak ends, system performance gradually recovers to its initial state. In the third stage (t2–t4), emergency drainage facilities are used to quickly remove accumulated water and eliminate flooding hazards, corresponding to the recovery capacity of FPC. In this process, analyzing the resilience of FPC in response to flood disasters requires describing the system ability to maintain performance under external disturbances. It also requires describing its ability to mitigate disaster impacts during decline and recovery process to the original state. Flood disasters are divided into three stages (resistance, absorption, and recovery) corresponding to the three dimensions of resilience [25,26]. These dimensions encompass the system’s capacities at each stage, aiding in the understanding of overall system resilience.
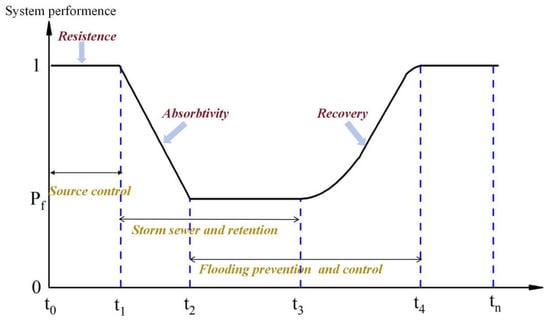
Figure 2.
The change process of urban flood prevention and control systems (FPC) system performance during storm.
In this study, the disturbance process caused by storms is divided into different stages of system performance change (resistance, absorption, and recovery stages). From the perspective of flood prevention and control, resilience can be evaluated based on three objectives. These objectives are source reduction, drainage and storage, and emergency drainage. They correspond to the three capacities of the system: resistance, absorption, and recovery. Resistance reflects the ability to resist external disturbances and reduce flood risk of system. Absorption reflects the ability to absorb external disturbances without completely losing functionality of system. Recovery reflects the ability to return to its original state of system, allowing it to recover within a certain time.
2.3. Evaluation System of AR
2.3.1. Construction of Evaluation Index System for AR
Based on the different stages of system performance shown in Figure 2, an indicator system for evaluating AR is established from the perspective of water accumulation and dissipation, reflecting changes in system performance under disturbance. Table 1 presents the 12 secondary indicators included in this evaluation system and the rationale for their selection, with their attribution to AR classified as either “+” or “-”, denoting the positive or negative correlation with AR, respectively.

Table 1.
Index system of attribute resilience (AR).
During the resistance stage, when no surface water accumulation occurs, source reduction facilities are used to prevent flooding. This involves measures such as infiltration and detention during the formation of stormwater runoff on underlying surfaces, reducing the volume of runoff entering municipal drainage systems. Factors affecting the resistance of the system include the intensity of external disturbances and the system’s ability to maintain its original state. In this stage, the runoff generated by rainfall serves as the premise for disrupting the system’s equilibrium. Indicators such as average elevation, average slope, green space percentage (GSP), impervious surface percentage (ISP), and impervious surface percentage (RP) are used to evaluate the system resistance [3].
During the absorption stage, when surface water begins to accumulate and gradually increases, drainage and storage facilities are utilized to mitigate flooding. The key to system absorption lies in its ability to maintain normal functioning under high-intensity rainfall. The construction of municipal drainage facilities is critical for evaluating system absorption. In this stage, the greater the capacity of the system to absorb external disturbances, the lower the severity of the disaster, leading to higher resilience. From the perspective of system performance changes, absorption is related to the absorption duration and robustness. A longer absorption stage and higher robustness indicate stronger absorption capacity. Drainage facilities associated with the volume of runoff absorbed by the system should be used as indicators for evaluating absorption. Indicators such as drainage capacity (DC), detention and retention facilities (DRFs) density, pump station density (PSD), and emergency stormwater conveyance (ESC) length are selected to evaluate absorption [27].
In the recovery stage, emergency drainage facilities are employed to restore the system to normal conditions as quickly as possible. This occurs after system performance has declined to its lowest point. Recovery is primarily influenced by the spatial distribution of emergency resources and reflects a city’s ability to respond to and manage storm-induced flooding. It is a key factor in enabling cities to recover rapidly from disasters. Indicators such as fire service coverage (FSC), professional staffing (PS), and flood-fighting materials (FFMs) are selected to evaluate recovery [28].
In this study, the central urban area of Beijing was divided into 100 m × 100 m grid units, resulting in a total of 73,123 grid units. For GSP and ISP, land use data were used to extract green space and impervious surfaces, and the proportions of different surface types were calculated for each grid unit. For elevation and slope, the average elevation of each grid unit was determined using a digital elevation model. For DC of the pipe network, the Manning formula was applied to calculate the drainage capacity of each concrete pipe under full-flow conditions. A kernel density analysis was performed on the pipe network to produce a spatial distribution map of urban drainage capacity. For RP, proximity analysis was conducted to calculate the shortest distance from each grid unit to the nearest water body. For ESC density, DRF density, PSD, FSC, PS, and FFM, kernel density analysis was used to obtain the values of these indicators. Figure 3 illustrates the spatial distribution of these factors.
where Q is the flow rate, and n is Manning’s roughness coefficient, taken as 0.013. R is the hydraulic radius (cross-sectional area/wetted perimeter), which reflects the influence of channel shape on flow velocity. i is the channel slope (elevation difference/length), which reflects the impact of channel slope on flow velocity.
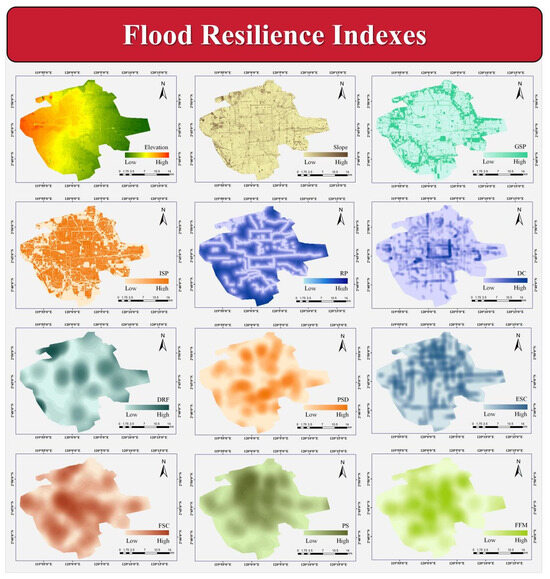
Figure 3.
Spatial distribution of AR index of FPC.
2.3.2. Calculation Method of AR Based on EWM-TOPSIS
EWM is an approach that uses the amount of information provided by entropy to calculate indicator weights [29]. It measures the contribution of each attribute to the decision-making process, with larger information entropy corresponding to smaller weights. EWM determines weights based on the characteristics of the data themselves, avoiding biases caused by subjective judgments. In this study, EWM was used to calculate the weights of indicators. The basic steps were as follows: first, data standardization was performed. Then, the proportion of each indicator was calculated to represent the importance of different facilities to resilience. Next, the information entropy of each indicator was computed to evaluate the amount of effective information it carries. Finally, by normalizing the difference coefficients, the weights of each indicator were obtained. The weight of a primary indicator is the sum of the weights of its secondary indicators.
TOPSIS (Technique for Order Preference by Similarity to Ideal Solution) is a multi-attribute decision analysis method [30]. It ranks evaluation objects by calculating their proximity to an idealized target, conducting a comprehensive assessment of the objective. The main calculation steps are as follows: First, the indicator data are standardized to eliminate the influence of different dimensions and scales. Then, the positive ideal solution and the negative ideal solution are determined. The positive ideal solution is a set of the optimal values of all indicators, representing the highest standard for urban flood resilience evaluation. The negative ideal solution is a set of the worst values of all indicators, representing the lowest standard. Subsequently, the Euclidean distance between each grid unit’s indicator values and the positive and negative ideal solutions are calculated. A smaller distance indicates that the grid is closer to the ideal state. Finally, the closeness coefficients for resistance, absorption, and recovery are calculated for each grid unit. A higher closeness coefficient indicates stronger resilience in the corresponding grid unit.
The AR value for each grid unit is obtained by multiplying the primary indicator values by their corresponding weights and summing them. The calculation of AR is as follows:
where Res, Abs, and Rec represent the relative proximity of resistance, absorption, and recovery to the optimal solution, and , , and are the weights of resistance, absorption, and recovery, respectively.
2.4. Evaluation Method of FR for FPC
2.4.1. Construction of Urban Flood Hydrodynamic Model
This study evaluated FR by constructing an urban flood hydrodynamic model and simulating the operation of the drainage system under rainfall scenarios. Currently, InfoWorks ICM (Version 9.5) is widely used to build complex models that integrate one-dimensional and two-dimensional simulations for urban flood modeling [31]. In this study, data on the drainage pipe network system (Figure 4) and land use (Figure 5) in the central urban area of Beijing were collected to establish a one-dimensional model using InfoWorks ICM. Elevation data were then used to construct a DEM, and triangular grids were created within the study area to develop a two-dimensional overland flow model. Finally, the one-dimensional pipe network was coupled with the two-dimensional topography and calibrated and validated. The Nash efficiency coefficient (NSE) was used as the evaluation metric for model calibration and validation [32,33].
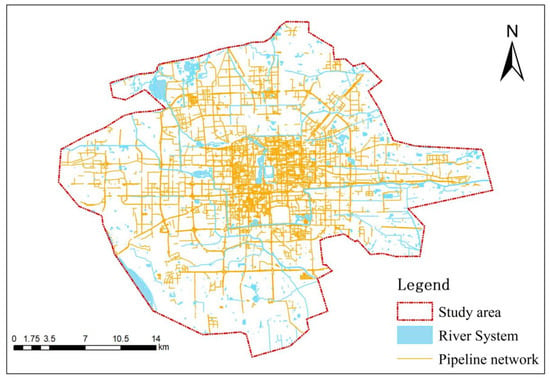
Figure 4.
Drainage network data.
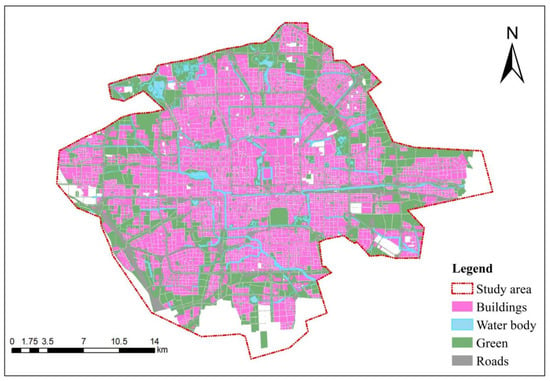
Figure 5.
Land use data.
2.4.2. Calculation Method of FR
FR refers to the system’s ability to limit the duration and scale of failures when subjected to specific threats. FR is typically goal-oriented, focusing on the system’s actual performance under disturbances and assessing whether system performance meets practical needs. In this study, the scenario simulation method was applied. Based on the constructed flood model, simulations were conducted. These simulations analyzed water accumulation in the central urban area of Beijing during a 50-year return period 24-h rainfall event (Figure 6). The data were sourced from the Technical Specification for Construction and Application of Mathematical Models for Urban Drainage and Flood Prevention Systems [Beijing Local Standard]. The design rainfall was calculated using the formula of rainstorm intensity in the second district of Beijing (Formula (3)). When the return period is 50 years and the rainfall duration is 24 h, the total rainfall amount is 268.19 mm. When water depths exceed 15 cm, traffic and building safety are significantly affected. Therefore, in the grid resilience evaluation, a water depth of 15 cm was used as the inundation threshold. The ratio of the non-inundated area to the total area of the study region was used to represent system performance [18].
where q is the design rainstorm intensity, t is the design rainfall duration, and P is the design return period.
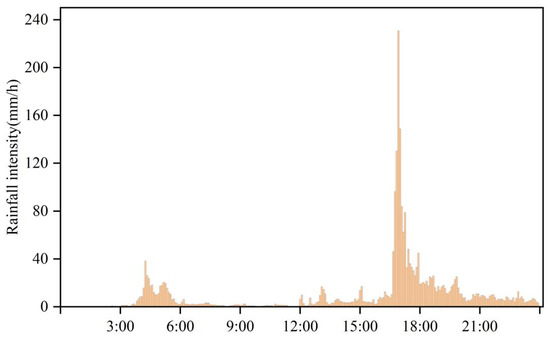
Figure 6.
Design rainfall time series with a return period of 50 years and rainfall duration of 24 h (50 years).
The system performance at time t is represented by p(t), where F(t) denotes the total area with water depths exceeding 15 cm at time t, and F represents the total area of the grid unit.
The FR represents system performance throughout the simulation process.
FR represents the functional resilience of the urban flood prevention and control system, corresponding to the total simulation duration.
2.5. AR and FR Spatial Autocorrelation Analysis
To identify low-resilience clustering areas, spatial autocorrelation analysis was applied to examine whether variables exhibited spatial distribution associations. Positive spatial autocorrelation occurs when adjacent locations tend to be similar, while negative spatial autocorrelation occurs when adjacent locations tend to differ. In studying the spatial distribution of resilience, spatial autocorrelation analysis helps determine whether low-resilience areas are clustered, allowing targeted measures to improve resilience in these areas [34,35].
2.5.1. Univariate Spatial Autocorrelation
Spatial autocorrelation includes global autocorrelation and local autocorrelation, which are represented by the global Moran’s I and local Moran’s I, respectively. The global Moran’s I is a coefficient ranging from −1 to 1. A global Moran’s I close to 1 indicates positive spatial autocorrelation, meaning similar values are spatially clustered. A value close to −1 indicates negative spatial autocorrelation, where dissimilar values are spatially clustered. A value near 0 suggests that the variable is randomly distributed in space, with no significant correlation [35]. The formula is as follows:
where represents the deviation between the attribute value of spatial unit i and the average value, is the weight between spatial element i and j, n is the total number of spatial units, and S0 is the sum of the weights of all spatial elements.
The local Moran’s I can identify clustering areas and visually represent “hotspots” (high-high clustering) and “coldspots” (low-low clustering) in spatial data [36]. The results can be categorized into five types: High-high clustering: The AR of a sub-district and its surrounding sub-districts is significantly higher than the average. Low-low clustering: The AR of a sub-district and its surrounding sub-districts is significantly lower than the average. Low-high clustering: The AR of a grid is significantly lower than average, while the surrounding grids have relatively higher flood risks or values. High-low clustering: The AR of a grid is significantly higher than average, while the surrounding grids have relatively lower flood risks or values. Not significant: Indicates no significant spatial correlation between the grid and its surrounding environment. The formula for local Moran’s I is as follows:
where is the number of samples; and denote the observed values of geographic attributes for regions and , respectively; is the mean number of observations; is the sample variance; and is the spatial proximity weight matrix based on distance.
This study used the global Moran’s I to assess whether resilience exhibited spatial clustering and the local Moran’s I to analyze the spatial distribution characteristics of AR and FR.
2.5.2. Bivariate Spatial Autocorrelation
Bivariate spatial autocorrelation analysis was applied to examine the spatial association between two variables [36]. Bivariate spatial autocorrelation can produce a bivariate LISA (Local Indicators of Spatial Association) map, revealing spatial “hotspots” and “coldspots” of interaction. In this study, AR and FR assessments each exhibited unique spatial distributions with certain differences. Bivariate spatial autocorrelation analysis was used to identify the relationships between the two. First, global bivariate spatial autocorrelation analysis was conducted to evaluate the correlation between AR and FR, with higher values indicating stronger correlations. Then, local Moran’s I analysis was performed to reveal the local spatial clustering characteristics of AR and FR, focusing on identifying areas with low AR and low-FR clusters to determine regions of weak resilience. The formula is as follows:
where Isf and are the global and local bivariate Moran’s I. N is the total number of grid units; Wij is the spatial weight matrix for the unit i and unit j. is the urban value of the grid unit i; is the resilience of the grid unit j.
3. Result
3.1. Evaluation Results of AR of Urban FPC Based on EWM-TOPSIS
3.1.1. Weight of Resilience Evaluation Indicators
Table 2 presents the weights of each indicator calculated using the EWM. A higher weight indicates a greater impact of the indicator on resilience. Among the three components, absorption accounts for the largest proportion, followed by resistance, with recovery being the smallest. From the perspective of resistance, it accounts for 0.39 of the total weight. Among its indicators, the GSP and average slope have a significant influence on flood resilience, while the effects of topography and water bodies are relatively smaller. This highlights the importance of increasing the GSP to effectively mitigate flood occurrence. For absorption, the total weight is 0.447, making it the most influential among the three stages. DC contributes the largest share of this weight, playing a critical role in enhancing absorption. Regarding recovery, PS and FFM are the most important factors influencing this stage.

Table 2.
The weight of criterion layer and index layer of AR evaluation system.
3.1.2. Evaluation Results of AR
The drainage system of Beijing is managed at the sub-district level, and the study area includes 119 sub-districts. Figure 7 shows the results of resistance, absorption, and recovery calculating by TOPSIS, as well as the AR derived from Equation (2). The natural breaks classification method was used to divide the resistance, absorption, and recovery evaluations into five levels: I, II, III, IV, and V, representing very low, low, medium, high, and very high levels, respectively. The results reveal that resistance, absorption, and recovery are relatively concentrated. Resistance shows low values primarily in the central areas, while high values are distributed around the periphery. In contrast, absorption and recovery exhibit opposite patterns, with low values concentrated around the periphery. The AR is relatively dispersed, showing a trend of higher values in the central areas and lower values in the surrounding regions. This suggests that, despite the high resistance in peripheral areas due to favorable natural geographic conditions, the lack of infrastructure development and resource allocation results in the overall resilience being lower than in other areas.
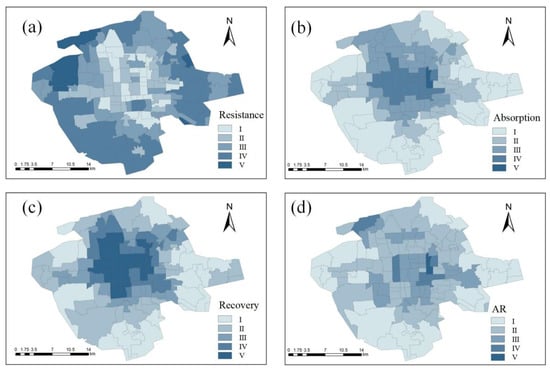
Figure 7.
Spatial distribution map of resistance (a), absorption (b), recovery (c), and AR (d).
Table 3 summarizes the number of sub-districts at different levels of resistance, absorption, recovery, and AR. For resistance, absorption, and overall resilience, very high-level sub-districts are rare. However, 23.5% of the sub-districts have very high recovery levels. Most sub-districts exhibit medium-level resistance, accounting for 26.9%. In contrast, 42.9% of the sub-districts show low absorption levels. Additionally, 30.3% of the sub-districts have medium-level resilience.

Table 3.
The number of sub-districts with resistance, absorption, recovery, and resilience in five levels.
Figure 8 compares the resistance, absorption, recovery, and AR of the 119 sub-districts. The figure indicates that as resilience increases, recovery shows the most significant upward trend, while resistance remains relatively unchanged, and absorption lies in between. This demonstrates that differences in resilience across sub-districts are primarily reflected in variations in the recovery levels. Furthermore, sub-districts with low resilience, resistance, absorption, and recovery do not show significant differences. However, as resilience reaches its maximum, clear distinctions begin to emerge: recovery becomes the highest, followed by absorption, with resistance being the lowest. For the two sub-districts with the highest resilience, absorption reaches the highest level and is classified as very high. Therefore, improving system absorption is essential for enhancing resilience.
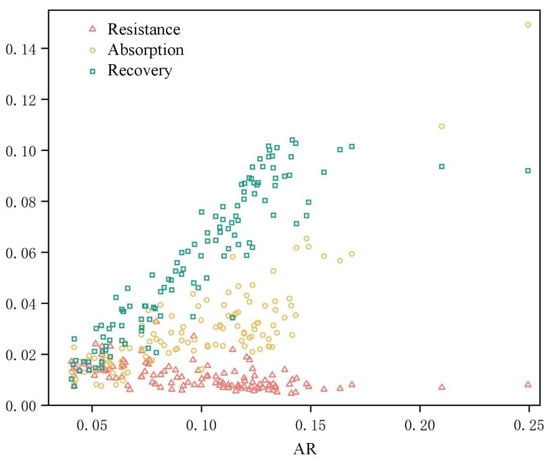
Figure 8.
Distribution of resistance, absorption, and recovery in AR.
3.2. FR Based on Hydrodynamic Model
3.2.1. Result of Flood Risk
Model accuracy is fundamental to simulation. Water level data from three nodes were used for calibration and validation (Figure 9). Discrepancies between the simulated and observed data stemmed from model parameters, including runoff generation, confluence parameters, and pipe network roughness. The complexity of actual infiltration and confluence processes limited the model’s ability to fully replicate real-world conditions. However, parameter adjustments can align simulations with reality, supporting further analysis. Studies indicate that an NSE exceeding 0.6 signifies high reliability for analysis and application [32]. The calibration and validation results indicate that all NSE values exceeded 0.6. This demonstrates that the model meets the accuracy requirements. The model is suitable for hydrological and hydraulic simulations to calculate subsequent FR.
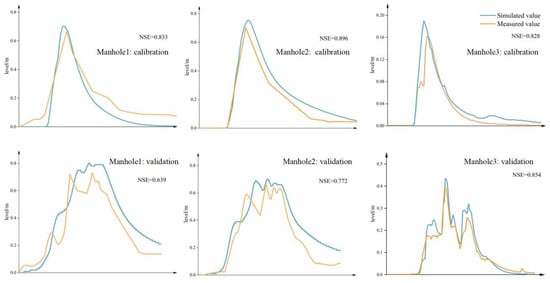
Figure 9.
Comparison of simulated values and measured values for model calibration and verification.
The flood simulation results provided data on water inundation, including the maximum flood depth and flood duration for each grid. These values were classified into five levels according to the degree of the impact of the flood on social activities and infrastructure. Figure 10 illustrates the spatial distribution of the maximum flood depth and flood duration across the levels. The total inundated area reached 242.1 km2, accounting for 32.7% of the study area. The total flood area (where the maximum flood depth exceeds 0.15 m) was 165.5 km2, representing 22.4% of the study area. As shown in the figure, the most severely inundated areas were concentrated in the southern region. Grids with a maximum flood depth exceeding 1 m covered a total area of 2.28 km2, accounting for 0.31% of the study area. Most inundated grids experienced flood durations of more than 3 h, covering a total area of 167.8 km2, which is 22.7% of the study area.
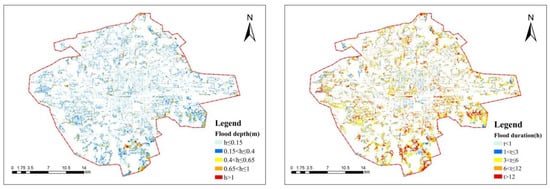
Figure 10.
Spatial distribution result of flood depth and flood duration.
3.2.2. Spatial Distribution of FR
Based on the hydrodynamic model simulation results, the FR of each sub-district was calculated and classified into five categories using the natural breaks classification method. Figure 11 illustrates the spatial distribution of the FR in the study area. The results show that the FR is higher in the southwest region and lower in the northeast, differing somewhat from the spatial distribution of the AR. Sub-districts with very low FR values are all located in the northeast, covering a total area of 70.6 km2, which represents 9.5% of the study area. In contrast, 46 sub-districts exhibit very high FR values, covering a total area of 241.1 km2 accounting for 32.6% of the study area.
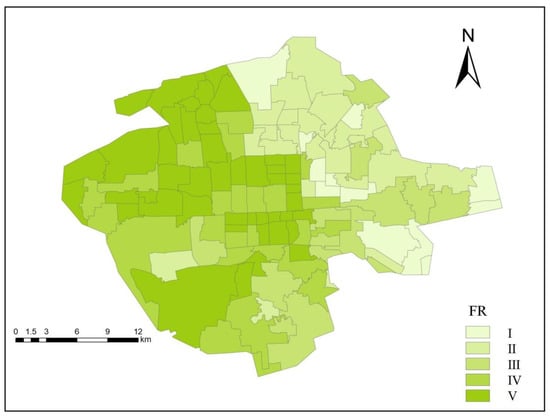
Figure 11.
Spatial distribution of functional resilience (FR) for five categories by the natural breaks classification method.
3.3. Spatial Correlation Analysis of Flood Resilience
3.3.1. Univariate Spatial Autocorrelation Analysis of Resilience
To reveal the spatial clustering characteristics of the AR and FR, global autocorrelation analysis was performed separately for the AR and FR to determine whether their spatial distributions exhibited correlations. The global Moran’s I was calculated using Equation (5), with the results shown in Table 4.

Table 4.
Moran’s I index, z-score, and p-value for AR and FR.
The results show that the global Moran’s I for the AR and FR came out to 0.66 and 0.49, respectively, indicating spatial clustering in their distributions. The z-scores and p-values reflect the confidence level of this distribution pattern. When z > 2.58 and p < 0.01, the confidence level is 99%. This suggests that the probability of the AR and FR being randomly distributed is only 1%, confirming that their spatial distributions are correlated and the analysis is meaningful.
To visualize the clustering areas, a local autocorrelation analysis was further conducted for the AR and FR. The results include five types: high-high (HH), low-high (LH), high-low (HL), low-low (LL), and not significant (NS). This analysis identified high-resilience and low-resilience clustering areas, and corresponding spatial clustering maps for the AR and FR were created (Figure 12). For the AR, three types of clustering were observed: HH, LL, and LH. Most central regions showed HH clustering, with 40 sub-districts covering a total area of 123.7 km2, accounting for 16.7% of the study area. LL clustering was distributed in the eastern, southern, and western peripheral regions, with 21 sub-districts covering 183.3 km2, which accounts for 24.8% of the study area. For the FR, only HH and LL clustering were observed, indicating a more distinct and homogeneous spatial clustering pattern. HH clustering was concentrated in the western region, covering 46 sub-districts and a total area of 186.2 km2, or 25.2% of the study area. LL clustering was located in the eastern region, with 26 sub-districts covering 151.4 km2, accounting for 20.5% of the study area.
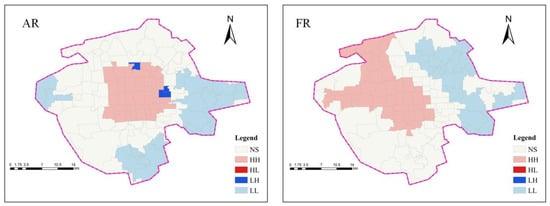
Figure 12.
Distribution of local autocorrelation analysis; 5-type results for AR and FR.
3.3.2. Bivariate Spatial Autocorrelation Analysis of AR and FR
Based on the AR and FR results, a bivariate global Moran’s I was calculated to analyze the spatial association between the AR and FR. The global Moran’s I for the AR and FR was 0.289, indicating a positive correlation between the two. This suggests that areas with high AR also tend to have high FR, while areas with low AR are often accompanied by low FR.
To further identify key areas in the central urban region of Beijing with low AR and low FR (LL clustering areas), a local Moran’s I analysis was conducted. Sub-districts were categorized into high AR–high FR (HA-HF), low AR–low FR (LA-LF), low AR–high FR (LA-HF), high AR–low FR (HA-LF), and non-significant (NS) regions. The results are shown in the Figure 13. HA-HF clusters were primarily distributed in the central region, including 21 sub-districts covering a total area of 70.2 km2, accounting for 9.5% of the study area. LA-LF clusters were mainly concentrated in the northeastern region, with 17 sub-districts covering a total area of 121 km2, or 16.3% of the study area.
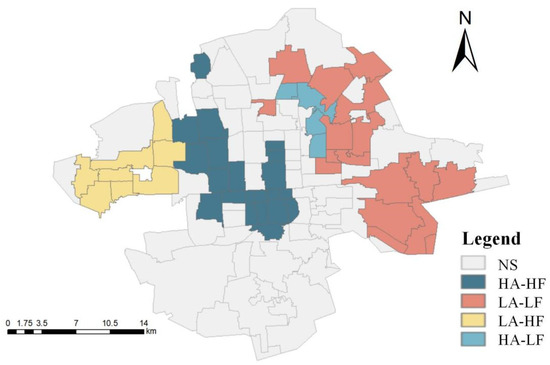
Figure 13.
Bivariate spatial autocorrelation LISA distribution of AR and FR.
Table 5 presents the differences in the areas of HA-HF and LA-LF areas compared to the HH and LL clusters of AR and FR. For the HA-HF region, the area decreased by 19 sub-districts and 53.5 km2 compared to the HH clusters of AR and by 25 sub-districts and 116 km2 compared to the HH clusters of FR. For the LA-LF region, the area decreased by four sub-districts and 62.3 km2 relative to the LL clusters of AR and by nine sub-districts and 30.4 km2 compared to the LL clusters of FR. The results indicate that, in terms of total clustering area, the FR is larger than the AR. The LL area of AR is greater, whereas the HH area of FR is larger. Considering the spatial correlation between the AR and FR, the identified HH area was reduced more significantly compared to analyzing individual resilience indicators alone.

Table 5.
Agglomeration area comparison of AR, FR, and bivariate spatial autocorrelation analysis results.
4. Discussion
Analyzing the impact of different factors on the AR can reveal the characteristics of low-resilience areas. The weights of various indicators were calculated by the EWM, identifying the GSP (0.17), average slope (0.137), and DC (0.205) as the three most important factors. This indicates that areas with low GSP, low average slope, and low DC tend to have lower levels of resilience. Analyzing the impact of different factors on the AR can reveal the characteristics of low-resilience areas. Using the entropy weight method, the weights of various indicators were calculated, identifying the GSP (0.17), average slope (0.137), and DC (0.205) as the three most important factors. This indicates that areas with low GSP, low average slope, and low DC tend to have lower levels of resilience.
The final evaluation of grid units showed the thresholds for resistance, absorption, and recovery as 0.004–0.93, 0.002–0.8, and 0.02–0.67, respectively, while the AR threshold ranged from 0.02 to 0.48. After aggregating the results by sub-districts, the AR threshold narrowed to 0.04–0.25. This indicates spatial inconsistency among the evaluation indicators. Sub-districts with very high resistance are located in peripheral areas, those with very high absorption are limited to only two, and areas with very high recovery are concentrated in the central region. As a result, the overall AR evaluation is relatively low. The FR evaluation reflects the functional performance of the urban drainage system under actual rainfall conditions, with weak resilience areas identified in the northeastern region. Regions with very high FR cover an area of 241.1 km2, while regions with very high AR account for only 4.27 km2. Regions with very low FR cover 70.6 km2, while very low AR regions account for only 3.38 km2. This suggests that FR evaluation results are generally higher than those of AR.
The spatial autocorrelation analysis results indicate that the AR and FR exhibit significant spatial clustering, suggesting that low-resilience areas are often surrounded by other low-resilience areas. However, the clustering locations differ: AR weak areas are distributed in the eastern and southern regions, while FR weak areas are concentrated in the northeastern region. A bivariate spatial autocorrelation analysis of AR and FR identified four types of regions: HA-HF, HA-LF, LA-HF, and LA-LF. To analyze the influencing factors of these results, the distribution of indicator values for different types of sub-districts was further examined, as shown in Figure A1 (in Appendix A). The results indicate that HA-HF and LA-LF sub-districts are more prevalent, while HA-LF and LA-HF sub-districts are less common, reflecting the spatial correlation between the AR and FR. In practice, the indicator data for resistance and absorption are part of the FR model calculation, which explains the relationship between the FR and these two components. However, the differences between the AR and FR are attributable to factors such as the absence of emergency resource distribution in the FR evaluation and the influence of drainage network distribution. When assessing the AR, denser drainage networks and higher DC result in higher AR. However, for the FR, sub-districts with sparse drainage networks may experience less overflow and inundation, leading to higher FR. Therefore, analyzing the reasons behind these differences across sub-district types is critical to providing guidance for improving urban resilience.
For the HA-HF sub-districts, as the AR increases, the FR does not show a corresponding upward trend, indicating inconsistencies between the two. The two sub-districts with the highest AR mainly exhibited high GSP, ISP, and elevation values. For the HA-LF sub-districts, the AR is high, but the actual operational FR is low, and the FR decreases as the AR increases. This may be due to dense drainage networks and severe inundation. Improving DC in these areas should be prioritized. Compared to the HA-HF sub-districts, the HA-LF sub-districts have lower slope, DRF, DC, and FSC values, while other indicators are evenly distributed. Enhancements could focus on the ESC, PSD, DRF, DC, and FSC indicators. Measures such as improving drainage capacity, adding pump stations and storage facilities in flood-prone areas, and deploying emergency drainage vehicles can help increase FR. For the LA-HF sub-districts, the FR remains stable. These sub-districts are clustered in the western region, where drainage networks are sparse, and overflow is not severe. To further improve resilience, efforts could focus on ESC and FSC. Urban road planning could direct runoff along ESCs to water bodies, and emergency drainage vehicles could be deployed in low-lying flood-prone areas. The LA-LF sub-districts are the key resilience-weak areas requiring attention. These sub-districts are located at the urban periphery, where infrastructure and emergency resource coverage are limited, though population and critical infrastructure are still significant. Enhancing resilience in these areas is necessary. In these sub-districts, the FR fluctuates significantly as the AR increases. For sub-districts with particularly low FR, most indicators, except for the GSP and ISP, are low, especially the DRF. Therefore, it is recommended to develop targeted improvement strategies based on the specific weaknesses of each sub-district to enhance their overall resilience. This study presents results that differ from previous research, primarily in the following aspects. First, a resilience indicator system covering resistance, absorption, and recovery was developed, aligning closely with urban flooding processes. Second, precise clusters of low- and high-resilience areas were identified, enabling targeted interventions. Third, differentiated measures for LH (low AR–high FR) and HL (high AR–low FR) zones were proposed, supporting optimized resource allocation and enhancing urban flood resilience.
This study proposes differentiated resilience improvement strategies for sub-districts in these categories. For the HA-HF sub-districts, the infrastructure is well-developed, and the DC is strong, resulting in good performance during rainfall events. Efforts can focus on further enhancing management practices and exploring intelligent and precise flood prevention measures. For the LA-LF sub-districts, significant shortcomings exist in flood prevention, and these areas face a high risk of flooding. Resilience can be improved by implementing sponge facilities such as permeable pavements and rain gardens, retrofitting drainage networks, and adding rainwater storage facilities to first enhance the AR. For the HA-LF sub-districts, the AR is high, but the FR is low, indicating good infrastructure conditions but sub-optimal performance during actual flood events. These areas should prioritize inspecting drainage systems to evaluate operational efficiency and identify potential issues, such as aging network infrastructure. Targeted optimization and retrofitting of problematic drainage facilities can improve functional performance during rainfall events. For the LA-HF sub-districts, the AR is low, but the FR is high, suggesting poor infrastructure conditions but relatively good performance during actual flood events. On one hand, the reasons for their good performance during flood events should be analyzed to summarize effective practices. On the other hand, efforts should focus on strengthening risk warnings and emergency preparedness to mitigate the potential risks associated with inadequate infrastructure.
5. Conclusions
This research used quantitative analysis and spatial autocorrelation analysis to reveal the characteristics and influencing factors of resilience-weak areas in an urban FPC. The results underscore the importance of a combined evaluation of AR and FR. This provides a theoretical basis and practical reference for improving the resilience of urban FPCs. The main conclusions are as follows:
- (1)
- The AR analysis identifies key factors influencing the FPC. Using the EWM, this study determined that the GSP, average slope, and DC are the critical factors affecting AR. In areas with a low GSP, small slope, and insufficient DC, the AR is generally low due to high runoff and limited drainage capacity. Further analysis shows that among the three dimensions of AR (resistance, absorption, and recovery), absorption has the most significant impact, with a weight of 0.447. This indicates that drainage and storage facilities play a crucial role in enhancing the AR. Future strategies for improving flood resilience should prioritize GSP development, slope optimization, and the enhancement of drainage capacity while focusing on improving absorption and recovery to achieve a more balanced resilience distribution.
- (2)
- This study evaluated urban AR and FR, revealing that the AR has an uneven spatial distribution and generally low levels. Sub-districts with high resistance are mainly located in peripheral regions, high recovery areas are concentrated in central regions, and sub-districts with high absorption are rare. In contrast, the FR exhibits higher levels overall, with resilience-weak areas predominantly distributed in the northeastern region. Future efforts should target these resilience-weak areas, optimizing spatial layouts and improving the coordination of resistance, absorption, and recovery to enhance overall urban flood resilience
- (3)
- The Moran’s I indices for the AR and FR were calculated as 0.66 and 0.49, respectively, indicating significant spatial clustering, though the clustering locations differ. The spatial autocorrelation analysis demonstrated a strong spatial correlation between the AR and FR. A combined evaluation of the AR and FR allowed for a more accurate identification of high- and low-resilience areas, wherein the area of high-resilience areas significantly reduced. This suggests that evaluating AR or FR independently may lead to an overestimation of high- or low-resilience areas. Combining AR and FR provides a more precise identification of resilience patterns.
- (4)
- Across various sub-district types (HA-HF, HA-LF, LA-HF, LA-LF), the trends of AR and FR are not entirely consistent primarily due to differences in the influencing mechanisms of certain indicators. On the one hand, the evaluation of FR does not consider the role of emergency resources. On the other hand, the drainage network infrastructure positively impacted AR but negatively affects FR. Therefore, integrating AR and FR in flood resilience evaluation is essential. For different sub-district types, an in-depth analysis of resilience characteristics is required to provide guidance for improving urban flood resilience.
The study utilized correlation analysis to identify the relationship between AR and FR, but it did not quantify specific correlation values. While this method can preliminarily reveal the relationship between the two, it lacks quantitative support. The absence of quantified correlation values may lead to results that fail to accurately reflect the actual contributions of AR and FR to resilience assessment, thus affecting the scientific validity and practical applicability of the evaluation outcomes. In future research, more precise quantitative methods (e.g., regression analysis, structural equation modeling, etc.) can be introduced to calculate the correlation values between AR and FR, thereby improving the accuracy and reliability of resilience evaluation. The current study did not incorporate climate change factors into the resilience assessment framework. As climate change intensifies, the frequency and intensity of extreme rainfall events may increase significantly, posing greater challenges to urban flood resilience. Ignoring climate change factors might result in resilience assessment outcomes that fail to account for future potential risks. In subsequent research, future climate scenarios (e.g., RCP4.5, RCP8.5, etc.) can be integrated to simulate the impacts of climate change on urban flooding, and climate change factors can be incorporated into the resilience.
Author Contributions
Data curation, M.L.; Formal analysis, X.Z.; Funding acquisition, J.Z. and H.W.; Investigation, X.Z. and J.Z.; Methodology, M.L.; Project administration, H.W.; Resources, H.W.; Software, Z.W.; Supervision, J.Z.; Validation, Z.W.; Visualization, M.L.; Writing—original draft, M.L.; Writing—review and editing, H.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Beijing Natural Science Foundation, grant number: 8242003, the Major Science and Technology Innovation Pilot Project for Water Resources Protection and Integrated-Saving Utilization in the Yellow River Basin of Inner Mongolia Autonomous Region, grant number: 2023JBGS0007, and the National Natural Science Foundation of China General Project, grant number: 72373011. And The APC was funded by 2023JBGS0007.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to privacy.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
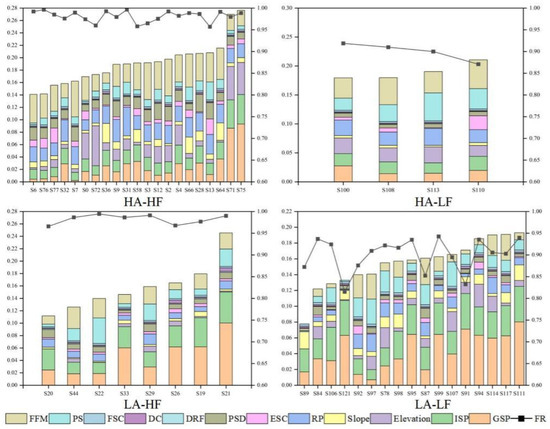
Figure A1.
Distribution of three levels of index of sub-districts.
References
- Yin, J.; Yu, D.; Wilby, R. Modelling the impact of land subsidence on urban pluvial flooding: A case study of downtown Shanghai, China. Sci. Total Environ. 2016, 544, 744–753. [Google Scholar] [CrossRef] [PubMed]
- Tellman, B.; Sullivan, J.A.; Kuhn, C.; Kettner, A.J.; Doyle, C.S.; Brakenridge, G.R.; Erickson, T.A.; Slayback, D.A. Satellite imaging reveals increased proportion of population exposed to floods. Nature 2021, 596, 80–86. [Google Scholar] [CrossRef] [PubMed]
- Li, P.; Zhuang, L.; Lin, K.; She, D.; Wang, Q.; Luo, W.; He, J.; Xia, J. Impact on nonlinear runoff of LID facilities and parameter response in the TVGM model. J. Hydrol. 2025, 653, 132780. [Google Scholar] [CrossRef]
- Huang, H.; Liao, W.; Lei, X.; Wang, C.; Cai, Z.; Wang, H. An urban DEM reconstruction method based on multisource data fusion for urban pluvial flooding simulation. J. Hydrol. 2023, 617, 128825. [Google Scholar] [CrossRef]
- Lin, J.; He, P.; Yang, L.; He, X.; Lu, S.; Liu, D. Predicting future urban waterlogging-prone areas by coupling the maximum entropy and FLUS model. Sustain. Cities Soc. 2022, 80, 103812. [Google Scholar] [CrossRef]
- Monachese, A.P.; Gómez-Villarino, M.T.; López-Santiago, J.; Sanz, E.; Almeida-Ñauñay, A.F.; Zubelzu, S. Challenges and Innovations in Urban Drainage Systems: Sustainable Drainage Systems Focus. Water 2025, 17, 76. [Google Scholar] [CrossRef]
- Charlesworth, S.M. A review of the adaptation and mitigation of global climate change using sustainable drainage in cities. J. Water Clim. Change 2010, 1, 165–180. [Google Scholar] [CrossRef]
- Liao, K. A Theory on Urban Resilience to Floods—A Basis for Alternative Planning Practices. Ecol. Soc. 2012, 17, 15. [Google Scholar] [CrossRef]
- Azadgar, A.; Nyka, L.; Salata, S. Advancing Urban Flood Resilience: A Systematic Review of Urban Flood Risk Mitigation Model, Research Trends, and Future Directions. Land 2024, 13, 2138. [Google Scholar] [CrossRef]
- Salata, S.; Ronchi, S.; Giaimo, C.; Arcidiacono, A.; Pantaloni, G.G. Performance-Based Planning to Reduce Flooding Vulnerability Insights from the Case of Turin (North-West Italy). Sustainability 2021, 13, 5697. [Google Scholar] [CrossRef]
- Adnan, S.; Ullah, K. Development of drought hazard index for vulnerability assessment in Pakistan. Nat. Hazards 2020, 103, 2989–3010. [Google Scholar] [CrossRef]
- Ning, X.; Xueqin, L.; Shuai, Y.; Yuxian, M.; Wenqi, S.; Weibin, C. Sea ice disaster risk assessment index system based on the life cycle of marine engineering. Nat. Hazards 2019, 95, 445–462. [Google Scholar] [CrossRef]
- Ali, S.; George, A. Modelling a community resilience index for urban flood-prone areas of Kerala, India (CRIF). Nat. Hazards 2022, 113, 261–286. [Google Scholar] [CrossRef]
- Tayyab, M.; Zhang, J.; Hussain, M.; Ullah, S.; Liu, X.; Khan, S.N.; Baig, M.A.; Hassan, W.; Al-Shaibah, B. GIS-Based Urban Flood Resilience Assessment Using Urban Flood Resilience Model: A Case Study of Peshawar City, Khyber Pakhtunkhwa, Pakistan. Remote Sens. 2021, 13, 1864. [Google Scholar] [CrossRef]
- Kotzee, I.; Reyers, B. Piloting a social-ecological index for measuring flood resilience: A composite index approach. Ecol. Indic. 2016, 60, 45–53. [Google Scholar] [CrossRef]
- Wang, Y.; Xie, Y.; Chen, L.; Zhang, P. Identifying key drivers of urban flood resilience for effective management: Insights and implications. Geogr. Sustain. 2025, 6, 100278. [Google Scholar] [CrossRef]
- Bisht, D.S.; Chatterjee, C.; Kalakoti, S.; Upadhyay, P.; Sahoo, M.; Panda, A. Modeling urban floods and drainage using SWMM and MIKE URBAN: A case study. Nat. Hazards 2016, 84, 749–776. [Google Scholar] [CrossRef]
- Wang, Y.; Meng, F.; Liu, H.; Zhang, C.; Fu, G. Assessing catchment scale flood resilience of urban areas using a grid cell based metric. Water Res. 2019, 163, 114852. [Google Scholar] [CrossRef]
- Zhang, X.; Kang, A.; Lei, X.; Wang, H. Urban drainage efficiency evaluation and flood simulation using integrated SWMM and terrain structural analysis. Sci. Total Environ. 2024, 957, 177442. [Google Scholar] [CrossRef]
- Wang, S.; Fu, J.; Wang, H. Unified and rapid assessment of climate resilience of urban drainage system by means of resilience profile graphs for synthetic and real (persistent) rains. Water Res. 2019, 162, 11–21. [Google Scholar] [CrossRef]
- Wu, X.; Guo, J. Comprehensive Economic Loss Assessment of Disaster Based on CGE Model and IO model—A Case Study on Beijing “7.21 Rainstorm”. In Economic Impacts and Emergency Management of Disasters in China; Wu, X., Guo, J., Eds.; Springer Nature: Singapore, 2021; pp. 105–136. [Google Scholar]
- Chen, S. Flood and Waterlogging Risk Assessment and Countermeasures for the 2023 Beijing Heavy Rainfall. Available online: https://news.cctv.com/2023/08/09/ARTI2lSDqRVIwH2GueKKhn30230809.shtml (accessed on 22 March 2025).
- Yu, S.; Kong, X.; Wang, Q.; Yang, Z.; Peng, J. A new approach of Robustness-Resistance-Recovery (3Rs) to assessing flood resilience: A case study in Dongting Lake Basin. Landsc. Urban Plan 2023, 230, 104605. [Google Scholar] [CrossRef]
- Mugume, S.N.; Gomez, D.E.; Fu, G.; Farmani, R.; Butler, D. A global analysis approach for investigating structural resilience in urban drainage systems. Water Res. 2015, 81, 15–26. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Burian, S.J. Evaluating real-time control of stormwater drainage network and green stormwater infrastructure for enhancing flooding resilience under future rainfall projections. Resour. Conserv. Recycl. 2023, 198, 107123. [Google Scholar] [CrossRef]
- Xu, F.; Fang, D.; Chen, B.; Wang, H. Resilience assessment of subway system to waterlogging disaster. Sustain. Cities Soc. 2024, 113, 105710. [Google Scholar] [CrossRef]
- Liu, K.; Li, J.; Xia, J.; Gao, X.; Gao, J.; Jiang, C. Study on LID Facilities Comprehensive Effect Evaluation: A case in Campus. Ecohydrol. Hydrobiol. 2022, 22, 530–540. [Google Scholar] [CrossRef]
- Jiang, C.; Han, Q.; Li, J. Optimization model of storage detention tanks based on nonlinear time-varying process of surface runoff under low impact development mode. J. Hydrol. 2025, 656, 133019. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, D.; Zhang, L.; Guo, H.; Ma, J.; Gao, W. Flood risk assessment of Wuhan, China, using a multi-criteria analysis model with the improved AHP-Entropy method. Environ. Sci. Pollut. Res. 2023, 30, 96001–96018. [Google Scholar] [CrossRef]
- Assari, A.; Mahesh, T.; Assari, E. Role of public participation in sustainability of historical city: Usage of TOPSIS method. Indian J. Sci. Technol. 2012, 5, 2289–2294. [Google Scholar]
- Yang, T. Research on Waterlogging Prevention and Control in Jinzhong Street Old Town Based on InfoWorks. J. Munic. Technol. 2024, 42, 189–196. [Google Scholar] [CrossRef]
- Debebe, D.; Seyoum, T.; Tessema, N.; Ayele, G.T. Modeling rainfall-runoff estimation and assessing water harvesting zone for irrigation practices in Keleta watershed, Awash river basin, Ethiopia. Geocarto. Int. 2023, 38, 1–24. [Google Scholar] [CrossRef]
- Uddin, M.G.; Jackson, A.; Nash, S.; Rahman, A.; Olbert, A.I. Comparison between the WFD approaches and newly developed water quality model for monitoring transitional and coastal water quality in Northern Ireland. Sci. Total Environ. 2023, 901, 165960. [Google Scholar] [CrossRef] [PubMed]
- Rahimi, F.; Sadeghi-Niaraki, A.; Ghodousi, M.; Choi, S. Spatial-temporal modeling of urban resilience and risk to earthquakes. Sci. Rep. 2025, 15, 8321. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Lv, W.; Liu, G.; Wang, Y. Multidimensional spatiotemporal autocorrelation analysis theory based on Multi-observation spatiotemporal Moran’s I and its application in resource allocation. Earth Sci. Inf. 2024, 18, 36. [Google Scholar] [CrossRef]
- Fotheringham, A.; Rogerson, P.; Fortin, M.E.; Dale, M.R.T. Spatial Autocorrelation; SAGE Publications, Ltd.: London, UK, 2009. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).