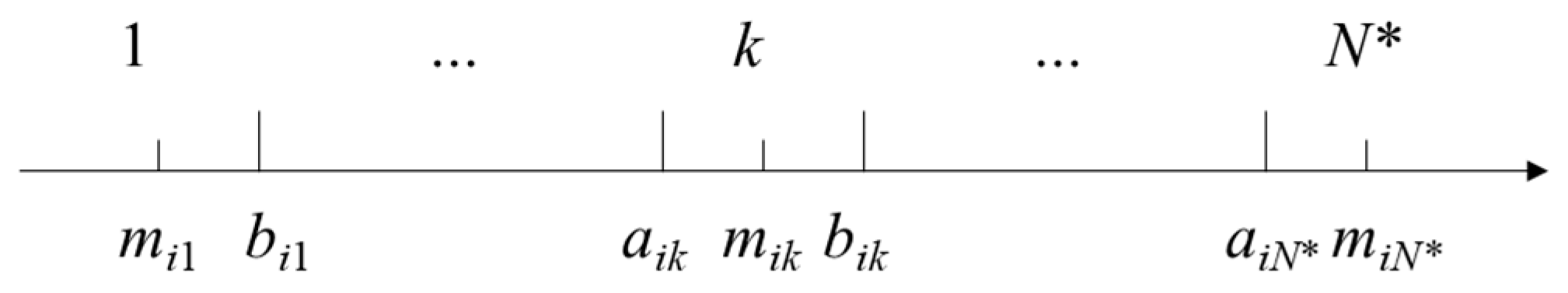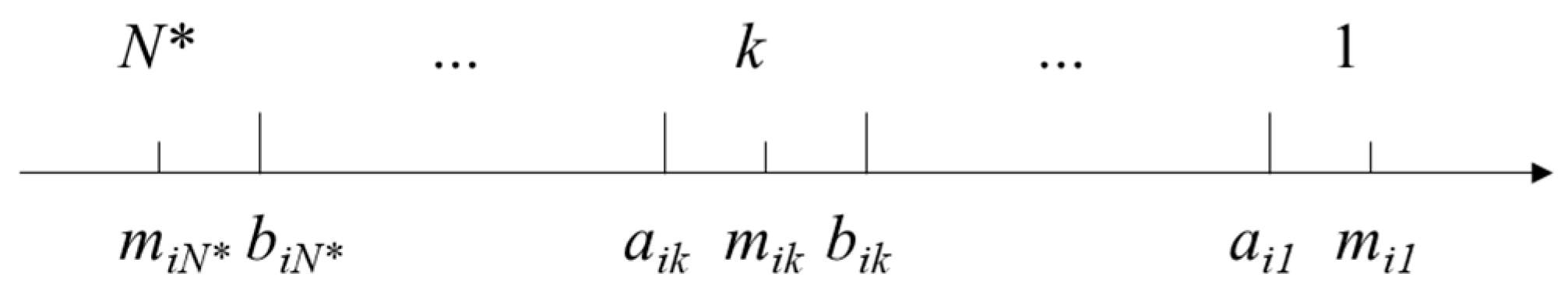An Improved Entropy Weight Method Mitigating Grade Distortion in Water Quality Assessment

Abstract

The Entropy Weight Method (EWM) is a prevalent and objective technique for assigning weights in water quality assessment. However, engineering practice has shown that distortion phenomena occur in water quality assessment results based on the EWM. This study reveals EWM’s distortion in grade discrimination via theory and case studies. To address this, we developed an improved entropy weight model (I-EWM) based on fuzzy variable set theory, which determines weights by incorporating both pollution degree and grade discrimination capacity. We quantify an indicator’s grade discrimination level and pollution degree using the fuzzy entropy and first-order moment of its average membership vector, respectively. A specific water quality assessment example was used to demonstrate the effectiveness of the I-EWM. The I-EWM significantly altered the weight allocation: the weights for COD_Mn, NH₃-N, and TP shifted from (0.687, 0.185, 0.127) to (0.191, 0.428, 0.381). When applied to the five monitoring points, the I-EWM produced markedly different results from the EWM. The water quality grades shifted from a pattern of (“Good”, “Good”, “Good”, “Good”, “Medium”) to a more conservative and realistic assessment of (“Medium”, “Medium”, “Poor”, “Poor”, “Poor”). Theoretical analysis demonstrates that the I-EWM provides more reasonable water quality assessments and effectively addresses the grade discrimination distortion inherent in the EWM.

1. Introduction

Water is a natural resource that humans rely on for survival and development. Due to rapid industrialization and continuous population growth, water pollution has become increasingly serious, and water environmental problems have become a widely concerning issue worldwide [1]. To ensure the rational development and utilization of water resources, it is necessary to scientifically plan and manage the water environment [2]. Water quality assessment is an important means of water environment supervision and management. In recent years, the scientific effectiveness of water quality assessment methods has been a hot topic in the field of the water environment.

Water quality assessment encompasses a variety of approaches, with widely used methods including the comprehensive index method, fuzzy comprehensive evaluation method, principal component analysis, machine learning techniques, and multi-criteria decision-making [3,4,5]. The comprehensive index method evaluates water quality through an integrated water quality index, offering straightforward implementation and interpretable results, yet its accuracy is heavily influenced by the weighting of pollutant indicators [6,7]. Fuzzy comprehensive evaluation introduces membership functions to address the inherent ambiguity in water quality classification boundaries, though the definition of these functions involves a degree of subjectivity. Principal component analysis is suitable for handling high-dimensional pollution data, but the resulting principal components often lack clear physical interpretation [8]. Machine learning methods such as artificial neural networks can establish predictive black-box models, yet their decision-making processes remain opaque and lack physical explicability [9]. Thus, while these diverse methods provide adaptable solutions for different scenarios, each carries inherent limitations that require careful selection and adjustment based on specific practical needs.

In recent years, water quality assessment models have shown a trend of shifting from single methods to hybrid models. By coupling models based on different principles, their strengths can be combined to achieve more robust and accurate comprehensive evaluations. For instance, Wang Wenchuan et al. integrated the Fuzzy Binary Comparison Method (FBCM) with Variable Fuzzy Sets (VFS) theory to propose a Variable Fuzzy Evaluation Model (VFEM) for river water quality assessment [4]. Applied to the Three Gorges Reservoir and Tseng-Wen River, this model effectively handles grading standards in interval form. Wu Guozheng et al. employed a coupled Principal Component Analysis (PCA) and Self-Organizing Map (SOM) artificial neural network model to evaluate the eutrophication status of Ulansuhai Lake [10]. This approach objectively classified samples and calculated evaluation weights, avoiding the subjectivity and arbitrariness inherent in selecting evaluation indicators. Peng Qi et al. combined an optimized TOPSIS model with Hasse diagram technique to analyze groundwater samples from villages around an industrial site in Beijing. The results demonstrated a more refined assessment compared to those obtained using the traditional TOPSIS model for water quality evaluation [11].

These hybrid approaches underscore a fundamental principle: whether in a single water quality assessment model or a coupled water quality assessment model, the determination of weights plays a decisive role in the accuracy of evaluation results. The precision of weight assignment directly governs the model’s effectiveness—even within complex coupled water quality assessment frameworks, this challenge remains a central methodological concern [12].

In comprehensive water quality assessment, weights reflect the importance of indicators and are one of the most important parameters [1]. The earliest weighting methods were subjective methods, such as expert scoring and the Analytic Hierarchy Process [13]. The subjective weighting method can intuitively explain the differences in the importance of indicators, but it cannot guarantee the uniqueness of the weighting results, which can cause uncertainty in the water quality assessment results [14].

To ensure the uniqueness of water quality assessment results, objective weighting methods have been developed, among which the Entropy Weight Method (EWM) proposed by is a prominent representative. EWM assigns weights based on the information content of pollutant indicators. The higher the information content of the indicators, the greater the corresponding weight; vice versa [15]. Compared with subjective methods, EWM eliminates human interference and ensures the uniqueness of the weighted results. Therefore, it has been widely used in water quality assessment [16]. For example, Agossou and Yang [17] used EWM to evaluate the vulnerability and contamination of groundwater in the south of Benin, West Africa. Md. Yousuf Mia et al. [18] applied a combined approach of explainable artificial intelligence (XAI) and the entropy weight method to identify the key influencing factors of drinking water quality from a hydrochemical perspective in the Haor region. Soumya S. Singha et al. [19] evaluated the groundwater quality status in the Arang Block of Chhattisgarh, India, through the integration of the entropy weight method and the PROMETHEE II (Preference Ranking Organization METHod for Enrichment of Evaluations II) method, achieving results with high accuracy.

However, the wide application of EWM has also revealed several limitations. Scholars have found that the weighting results of EWM may not always align with environmental realities. For example, Yan et al. [20] pointed out that when monitoring data are highly concentrated, EWM fails to reflect the true importance of pollutants. Bao, Qian et al. [21] found that data with excessive zero values can lead to distorted results. Additionally, Wang et al. [14] reported that in dynamic assessments, EWM might even cause the evaluation trend to contradict the actual pollution trend. These issues indicate that the purely data-driven nature of EWM can sometimes lead to biased assessments in practice.

Particularly, through extensive practice, in addition to the problems discovered by Feng, Bao, and Zhe, the authors found another abnormal phenomenon in the EWM in water quality assessment. When there is a significant difference in the threshold division of different indicators, the weighting results of the EWM cannot reflect the difference in indicator grades correctly, resulting in distorted evaluation results.

The objectives of this study are threefold: (i) to intuitively reveal the distortion phenomenon of the EWM in grade discrimination through theoretical derivation and evaluation examples; (ii) to develop an improved entropy weight model (I-EWM) based on fuzzy set theory to effectively mitigate this issue; and (iii) to validate the effectiveness and superiority of the proposed I-EWM through a concrete case study in water quality assessment.

2. Materials and Methods

2.1. Water Quality Index (WQI)

The Water Quality Index (WQI) serves as a structured approach for assessing the overall quality of water [22]. Since Horton established the first WQI in 1965, numerous variants have been developed to suit specific environmental contexts, including those by Bhargava, the Oregon Index, and the Weighted Arithmetic WQI [23]. Among these, the Weighted Arithmetic WQI is the most widely adopted method for comprehensive water quality evaluation in China [24].

According to the Chinese national criteria for surface water environmental quality (China 2002) [25], the standard limits for basic parameters are categorized into five grades: excellent, good, medium, poor, and bad. The specific thresholds are presented in

Table 1. Threshold values of pollutants (mg/L).

Indicators	Excellent	Good	Medium	Poor	Bad
CODMn	[0, 2]	(2, 4]	(4, 6]	(6, 10]	(10, 15]
NH3-N	[0, 0.15]	(0.15, 0.5]	(0.5, 1]	(1, 1.5]	(1.5, 2]
TP	[0, 0.02]	(0.02, 0.1]	(0.1, 0.2]	(0.2, 0.3]	(0.3, 0.4]

. In this section, we selected three pollutant indicators, including permanganate index (COD_Mn), ammonia nitrogen (NH₃-N), and total phosphorus (TP), as the research subjects, with a total of five monitoring stations.

The monitoring value of the i-th indicator of the j-th station is recorded as x_ij. There are m indicators and n stations. The WQI of the i-th indicator of the j-th station is recorded as q_ij.

Following the method of Yan et al. [26], who established that for these indicators, smaller values correspond to better water quality, q_ij is calculated using the following formula:

$$q_{ij}=\left\{\begin{array}{cc}100& x_{ij}\le l_{i1}\\ 80+20·{\displaystyle \frac{s_{i1}-x_{ij}}{s_{i1}-l_{i1}}}& l_{i1}<x_{ij}\le s_{i1}\\ 60+20·{\displaystyle \frac{s_{i2}-x_{ij}}{s_{i2}-l_{i2}}}& l_{i2}<x_{ij}\le s_{i2}\\ 40+20·{\displaystyle \frac{s_{i3}-x_{ij}}{s_{i3}-l_{i3}}}& l_{i3}<x_{ij}\le s_{i3}\\ 20+20·{\displaystyle \frac{s_{i4}-x_{ij}}{s_{i4}-l_{i4}}}& l_{i4}<x_{ij}\le s_{i4}\\ 20·{\displaystyle \frac{s_{i5}-x_{ij}}{s_{i5}-l_{i5}}}& l_{i5}<x_{ij}\le s_{i5}\\ 0& s_{i5}<x_{ij}\end{array}\right.$$

(1)

Accordingly, q_ij is calculated with the following formula (for the case where a larger value is better):

$$q_{ij}=\left\{\begin{array}{cc}100& x_{ij}>s_{i1}\\ 80+20·{\displaystyle \frac{x_{ij}-l_{i1}}{s_{i1}-l_{i1}}}& l_{i1}<x_{ij}\le s_{i1}\\ 60+20·{\displaystyle \frac{x_{ij}-l_{i2}}{s_{i2}-l_{i2}}}& l_{i2}<x_{ij}\le s_{i2}\\ 40+20·{\displaystyle \frac{x_{ij}-l_{i3}}{s_{i3}-l_{i3}}}& l_{i3}<x_{ij}\le s_{i3}\\ 20+20·{\displaystyle \frac{x_{ij}-l_{i4}}{s_{i4}-l_{i4}}}& l_{i4}<x_{ij}\le s_{i4}\\ 20·{\displaystyle \frac{x_{ij}-l_{i5}}{s_{i5}-l_{i5}}}& l_{i5}<x_{ij}\le s_{i5}\\ 0& x_{ij}\le l_{i5}\end{array}\right.$$

(2)

where s_ik and l_ik are the maximum and minimum of the k-th grade of the i-th indicator, respectively. The comprehensive water quality index (CWQI_j) of the j-th station can be generated as follows:

$$CWQ{I}_j={\displaystyle \sum _{i=1}^m{w}_i·}{q}_{ij}$$

(3)

where w_i represents the weight assigned to the i-th indicator, with its assessment categories of “excellent”, “good”, “medium”, “poor”, and “bad” corresponding to the ranges [80, 100], [60, 80), [40, 60), [20, 40), and [0, 20), respectively.

2.2. Entropy Weight Method (EWM)

The Entropy Weight Method (EWM) is an objective technique for assigning weights based on information entropy theory, and it is extensively applied in water quality assessment [15]. The EWM determines weights according to the information significance of each indicator. A greater degree of dispersion for an indicator corresponds to a higher information content and, consequently, a greater assigned weight; conversely, lower dispersion results in a lower weight. The standard procedure of the EWM is as follows:

Step 1: Data Standardization

The initial step involves standardizing the raw monitoring matrix. The specific formula is selected based on the pollutant indicator’s attribute:

For “the larger, the better” indicators:

$$y_{ij}={\displaystyle \frac{x_{ij}-\underset{j=1,2,\dots ,n}{\min }{x}_{ij}}{\underset{j=1,2,\dots ,n}{\max }{x}_{ij}-\underset{j=1,2,\dots ,n}{\min }{x}_{ij}}}$$

(4)

For “the smaller, the better” indicators:

$$y_{ij}={\displaystyle \frac{\underset{j=1,2,\dots ,n}{\max }{x}_{ij}-x_{ij}}{\underset{j=1,2,\dots ,n}{\max }{x}_{ij}-\underset{j=1,2,\dots ,n}{\min }{x}_{ij}}}$$

(5)

y_ij is the standardized value of the monitoring value of the i-th indicator at the j-th monitoring station, with a value range of [0, 1]; Although the domain of y_ij is [0, 1], the sum of y_ij is not 1. Therefore, in order to calculate the entropy value, it is necessary to normalize y_ij.

Step 1: Data Normalization

$$p_{ij}={\displaystyle \frac{y_{ij}}{{\displaystyle {\sum }_{j=1}^n{y}_{ij}}}}$$

(6)

where p_ij is the normalized value of y_ij, the domain of p_ij is [0, 1], and the sum of p_ij is 1.

Step 3: Calculate the Entropy Value

The entropy value H_i for the i-th indicator is calculated as follows:

$$H_i=-{\displaystyle \frac{1}{\ln n}}·{\displaystyle \sum _{j=1}^n\left(p_{ij}·\ln p_{ij}\right)}$$

(7)

where H_i ranges from 0 to 1. A larger H_i indicates less variability in the data for the i-th indicator and, consequently, a lower information content. Conversely, a smaller H_i signifies greater variability and higher information content. By convention, if p_ij = 0, the term p_ij⋅ln p_ij is defined as 0 to ensure the calculation remains valid [27].

Step 4: Determine the Indicator Weight

The weight w_i is calculated as follows:

$$w_i={\displaystyle \frac{1-H_i}{m-{\displaystyle \sum _{i=1}^m{H}_i}}}$$

(8)

w_i represents the weight value assigned to the i-th indicator in the water quality assessment model, and its value range is [0, 1].

It should be noted that the EWM assigns weights according to the degree of dispersion, namely the numerical discrimination of indicators but not the grade discrimination of indicators [5]. The grade discrimination and the numerical discrimination of indicators are not the same thing, the grade discrimination of indicators is the parameter that we truly want to reflect the information content of water quality. For example, when the monitoring values of COD_Mn and TP at the five stations are 0.015, 0.025, 0.15, 0.25, and 0.35, the numerical discrimination of the two indicators is the same. However, referencing Table 1, it can be found that the water quality grade of COD_Mn at all 5 stations is “excellent”, without any grade discrimination, while the grade of TP at the five stations is “excellent”, “good”, “medium”, “poor”, and “bad”. The grade discrimination of TP is much higher than that of COD_Mn, which means that the information content of TP is much higher, but the EWM cannot accurately reflect this difference.

2.3. Improved Entropy Weight Model (I-EWM) Based on Fuzzy Variable Set Theory

2.3.1. Fuzzy Variable Set Theory and the Relative Membership Degree

Fuzzy variable set theory, initially introduced by Chen as a method for uncertainty analysis, has been subsequently utilized in water resource management studies, as demonstrated by Chunqing, Duan et al. [28]. According to Section 2.1, it can be seen that each water quality grade indicator has an accurate threshold. However, when the monitoring value of the indicator falls within the threshold range of the k-th water quality grade, it cannot be guaranteed that the water quality definitely belongs to that water quality grade or other water quality grades [29]. In other words, when the monitoring value of the indicator falls within the threshold range of the k-th water quality grade, the water quality grade belonging to the k-th grade is a fuzzy concept [30,31].

The monitoring value of the i-th indicator at the j-th station is denoted as x_ij. The possibility that a water sample belongs to the k-th water quality grade is represented by the relative membership degree μ(x_ij)_k, which ranges from 0 to 1 [32]. A higher value of μ(x_ij)_k indicates a greater likelihood that the water quality grade is k. Specifically, when μ(x_ij)_k = 1, it indicates definite membership to the k-th grade, while μ(x_ij)_k = 0, indicates definite non-membership.

As established in Section 2.2, the information content of water quality is derived from the grade discrimination of indicators rather than their numerical values. To quantify this grade discrimination, the distribution of an indicator across the various quality grades must be determined [32].

For a specific monitoring value x_ij, its membership to the k-th water quality grade is a fuzzy concept; thus, the grade distribution cannot be directly inferred from x_ij alone. However, the relative membership degree μ(x_ij)_k provides a precise quantitative measure of this distribution. The grade discrimination—and consequently, the information content of water quality—can be quantified by calculating the dispersion (e.g., entropy or standard deviation) of the membership vector μ(x_ij)_k, across all grades k [33]. In other words, the grade discrimination of monitoring values can be indirectly quantified by calculating the information entropy of the relative membership degrees—that is, the fuzzy entropy.

2.3.2. Improved Entropy Weight Model (I-EWM)

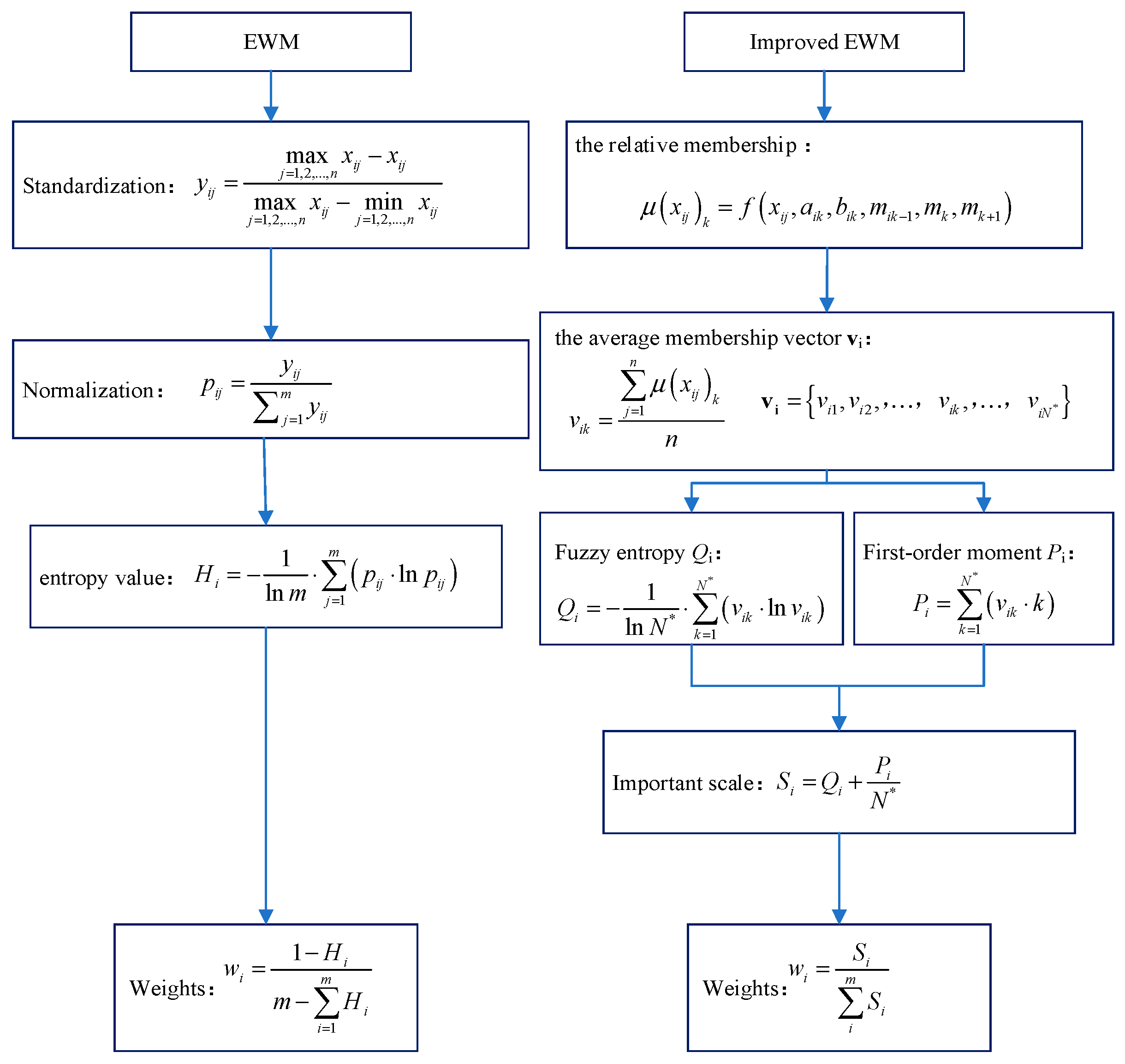
The Improved Entropy Weight Method (I-EWM) attempts to calculate the information content of water quality grade distribution using fuzzy entropy. The basic approach of this method is to first compute the relative membership degree matrix and the fuzzy entropy of indicator monitoring values, and then determine the weights based on the informational significance of each indicator’s relative membership degrees. The greater the dispersion of an indicator’s monitoring values in terms of relative membership degrees, the higher the information content of that indicator, and thus the larger the weight assigned to it; conversely, the smaller the dispersion, the lower the weight.

Assuming there are m pollutant indicators and n monitoring stations, the thresholds for the i-th indicator are defined in Figure 1 and Figure 2, where the N*-th grade represents the highest water quality level. For the k-th grade:

a_ik denotes the lower limit of the threshold,

b_ik denotes the upper limit,

m_ik denotes the median value,

and general β = 1 [34,35].

The weighting procedure of the Improved Entropy Membership Weight (I-EMW) method comprises the following steps.

Step 1: Calculate the relative membership degree μ(x_ij)_k:

The membership degree vector serves as the primary carrier of information. Therefore, a scientific analysis of this vector is a prerequisite for conducting grade evaluation and identifying limiting factors. Common principles for such evaluation include the maximum membership degree principle, the proximity principle, and the weighted average principle [36]. Building upon the weighted average principle, this paper calculates the relative membership degree and the average membership degree of the indicators.

For a “smaller-is-better” indicator, μ(x_ij)_k is calculated as follows:

When k = 1;

$$\left\{\begin{array}{l}\mu {\left(x_{ij}\right)}_k=1,\hspace{1em}\hspace{1em}{x}_{ij}<m_{ik}\\ \mu {\left(x_{ij}\right)}_k=0.5\times \left(1+{\left({\displaystyle \frac{x_{ij}-b_{ik}}{m_{ik}-b_{ik}}}\right)}^{\beta }\right), \hspace{1em}{x}_{ij}\in \left[m_{ik}, b_{ik}\right) \\ \mu {\left(x_{ij}\right)}_k=0.5\times \left(1-{\left({\displaystyle \frac{x_{ij}-b_{ik}}{{\mathrm{m}}_{ik+1}-b_{ik}}}\right)}^{\beta }\right),\hspace{1em}{x}_{ij}\in \left[b_{ik},{ \mathrm{m}}_{ik+1}\right)\\ \mu {\left(x_{ij}\right)}_k=0,\hspace{1em}\hspace{1em}{x}_{ij}\ge m_{ik+1}\end{array}\right.$$

(9)

When N* > k > 1;

$$\left\{\begin{array}{l}\mu {\left(x_{ij}\right)}_k=0,\hspace{1em}\hspace{1em}{x}_{ij}<m_{ik-1}\\ \mu {\left(x_{ij}\right)}_k=0.5\times \left(1-{\left({\displaystyle \frac{x_{ij}-a_{ik}}{m_{ik-1}-a_{ik}}}\right)}^{\beta }\right), \hspace{1em}{x}_{ij}\in \left[m_{ik-1}, a_{ik}\right)\\ \mu {\left(x_{ij}\right)}_k=0.5\times \left(1+{\left({\displaystyle \frac{x_{ij}-a_{ik}}{m_{ik}-a_{ik}}}\right)}^{\beta }\right), \hspace{1em}{x}_{ij}\in \left[a_{ik}, m_{ik}\right)\\ \mu {\left(x_{ij}\right)}_k=0.5\times \left(1+{\left({\displaystyle \frac{x_{ij}-b_{ik}}{m_{ik}-b_{ik}}}\right)}^{\beta }\right), \hspace{1em}{x}_{ij}\in \left[m_{ik}, b_{ik}\right) \\ \mu {\left(x_{ij}\right)}_k=0.5\times \left(1-{\left({\displaystyle \frac{x_{ij}-b_{ik}}{{\mathrm{m}}_{ik+1}-b_{ik}}}\right)}^{\beta }\right), \hspace{1em}{x}_{ij}\in \left[b_{ik},{ \mathrm{m}}_{ik+1}\right)\\ \mu {\left(x_{ij}\right)}_k=0,\hspace{1em}\hspace{1em}{x}_{ij}\ge m_{ik+1}\end{array}\right.$$

(10)

When k = N*,

$$\left\{\begin{array}{l}\mu {\left(x_{ij}\right)}_k=0,\hspace{1em}\hspace{1em}{x}_{ij}<m_{ik-1}\\ \mu {\left(x_{ij}\right)}_k=0.5\times \left(1-{\left({\displaystyle \frac{x_{ij}-a_{ik}}{m_{ik-1}-a_{ik}}}\right)}^{\beta }\right), x_{ij}\in \left[m_{ik-1}, a_{ik}\right)\\ \mu {\left(x_{ij}\right)}_k=0.5\times \left(1+{\left({\displaystyle \frac{x_{ij}-a_{ik}}{m_{ik}-a_{ik}}}\right)}^{\beta }\right), x_{ij}\in \left[a_{ik}, m_{ik}\right)\\ \mu {\left(x_{ij}\right)}_k=1,\hspace{1em}\hspace{1em}{x}_{ij}\ge m_{ik}\end{array}\right.$$

(11)

For a “larger-is-better” indicator, μ(x_ij)_k is calculated as follows:

When k = 1;

$$\left\{\begin{array}{l}\mu {\left(x_{ij}\right)}_k=1,\hspace{1em}\hspace{1em}{x}_{ij}>m_{ik}\\ \mu {\left(x_{ij}\right)}_k=0.5\times \left(1+{\left({\displaystyle \frac{x_{ij}-a_{ik}}{m_{ik}-a_{ik}}}\right)}^{\beta }\right), x_{ij}\in \left(a_{ik},m_{ik}\right]\\ \mu {\left(x_{ij}\right)}_k=0.5\times \left(1-{\left({\displaystyle \frac{x_{ij}-a_{ik}}{{\mathrm{m}}_{ik+1}-a_{ik}}}\right)}^{\beta }\right), x_{ij}\in \left({\mathrm{m}}_{ik+1},a_{ik}\right]\\ \mu {\left(x_{ij}\right)}_k=0,\hspace{1em}\hspace{1em}{x}_{ij}\le m_{ik+1}\end{array}\right.$$

(12)

When N* > k > 1;

$$\left\{\begin{array}{l}\mu {\left(x_{ij}\right)}_k=0,\hspace{1em}\hspace{1em}{x}_{ij}>m_{ik-1}\\ \mu {\left(x_{ij}\right)}_k=0.5\times \left(1-{\left({\displaystyle \frac{x_{ij}-b_{ik}}{m_{ik-1}-b_{ik}}}\right)}^{\beta }\right), x_{ij}\in \left(b_{ik},m_{ik-1}\right]\\ \mu {\left(x_{ij}\right)}_k=0.5\times \left(1+{\left({\displaystyle \frac{x_{ij}-b_{ik}}{m_{ik}-b_{ik}}}\right)}^{\beta }\right), x_{ij}\in \left(m_{ik},b_{ik}\right]\\ \mu {\left(x_{ij}\right)}_k=0.5\times \left(1+{\left({\displaystyle \frac{x_{ij}-a_{ik}}{m_{ik}-a_{ik}}}\right)}^{\beta }\right), x_{ij}\in \left(a_{ik},m_{ik}\right] \\ \mu {\left(x_{ij}\right)}_k=0.5\times \left(1-{\left({\displaystyle \frac{x_{ij}-a_{ik}}{{\mathrm{m}}_{ik+1}-a_{ik}}}\right)}^{\beta }\right), x_{ij}\in \left({\mathrm{m}}_{ik+1},a_{ik}\right]\\ \mu {\left(x_{ij}\right)}_k=0,\hspace{1em}\hspace{1em}{x}_{ij}\le m_{ik+1}\end{array}\right.$$

(13)

When k = N*,

$$\left\{\begin{array}{l}\mu {\left(x_{ij}\right)}_k=0,\hspace{1em}\hspace{1em}{x}_{ij}>m_{ik-1}\\ \mu {\left(x_{ij}\right)}_k=0.5\times \left(1-{\left({\displaystyle \frac{x_{ij}-b_{ik}}{m_{ik-1}-b_{ik}}}\right)}^{\beta }\right), x_{ij}\in \left(b_{ik},m_{ik-1}\right]\\ \mu {\left(x_{ij}\right)}_k=0.5\times \left(1+{\left({\displaystyle \frac{x_{ij}-b_{ik}}{m_{ik}-b_{ik}}}\right)}^{\beta }\right), x_{ij}\in \left(m_{ik},b_{ik}\right]\\ \mu {\left(x_{ij}\right)}_k=1,\hspace{1em}\hspace{1em}{x}_{ij}\le m_{ik}\end{array}\right.$$

(14)

Step 2: Calculate the average membership vector of indicators.

The relative membership degrees for all grades constitute the relative membership vector of the monitoring value x_ij, denoted as u_ij = {μ(x_ij)₁, μ(x_ij)₂, …, μ(x_ij)_k, …, μ(x_ij)_N*}. It is easy to find that each element of the relative membership vector u_ij satisfies the following conditions:

$$\left\{\begin{array}{l}0\le \mu {\left(x_{ij}\right)}_k\le 1\\ {\displaystyle \sum _{k=1}^{N^{*}}\mu {\left(x_{ij}\right)}_k}=1\end{array}\right.$$

(15)

To comprehensively represent the environmental characteristics of the i-th indicator across all monitoring stations, we define its average membership vector v_i = {v_i1, v_i2, …, v_ik, …, v_iN*}. This vector is obtained by averaging the membership vectors u_ij from all n stations:

$$v_{ik}={\displaystyle \frac{{\displaystyle \sum _{j=1}^n\mu {\left(x_{ij}\right)}_k}}{n}}$$

(16)

where v_ik represents the average extent to which the i-th indicator belongs to the k-th grade across the entire study area.

$$\left\{\begin{array}{l}0\le v_{ik}\le 1\\ {\displaystyle \sum _{k=1}^{N^{*}}{v}_{ik}}=1\end{array}\right.$$

(17)

Step 3: Calculate the fuzzy entropy and the first-order moments.

The basic calculation formula for fuzzy entropy is derived from Shannon’s information entropy theory. After more than a century of development, the concept of entropy has expanded beyond its narrow physical origins, with its definition, formulas, and laws undergoing varying degrees of transformation—particularly in the expressions used to calculate entropy. In this paper, the fuzzy entropy formula is computed by treating the average membership vector as a discrete variable [37].

The fuzzy entropy Q_i for the i-th indicator is introduced to quantify the uncertainty (or information content) inherent in its grade discrimination. It is calculated based on the average membership vector v_i as follows:

$$Q_i=-{\displaystyle \frac{1}{\ln N^{*}}}·{\displaystyle \sum _{k=1}^{N^{*}}\left(v_{ik}·\ln v_{ik}\right)}$$

(18)

The fuzzy entropy Q_i reflects the grade discrimination level of the i-th indicator, with a value range of [0, 1]. A higher Q_i value indicates a greater grade discrimination level and, consequently, a greater importance of the indicator in the evaluation system. Specifically:

When Q_i = 1, the grade discrimination and information content of the indicator are maximized, signifying the highest importance.

When Q_i = 0, the indicator possesses no grade discrimination or information content, rendering it unimportant.

However, in water quality assessment, the practical significance of heavily polluted indicators often outweighs that of clean indicators. To account for this, I-EMW incorporates the pollution degree into the weighting process. This is quantified by the first-order moment P_i, which is defined as the expected (average) water quality grade for the i-th indicator across all monitoring stations. It is calculated as follows:

$$P_i={\displaystyle \sum _{k=1}^{N^{*}}\left(v_{ik}·k\right)}$$

(19)

where k is the grade number (e.g., 1, 2, …, N*), and v_ik is the average membership degree of the i-th indicator to the k-th grade from Equation (16). A higher P_i value indicates a worse overall pollution state for the indicator.

As established, P_i reflects the pollution degree, while Q_i quantifies the grade discrimination level of the i-th indicator. The I-EMW integrates these two dimensions to assign weights, adhering to the following principles [14]:

For indicators with an identical pollution degree (P_i), a higher grade discrimination level (Q_i) confers greater importance and thus a higher weight.

For indicators with an identical grade discrimination level (Q_i), a higher pollution degree (P_i) confers greater importance and thus a higher weight.

Step 4: Calculate the importance scale.

To integrate the pollution degree P_i and the grade discrimination level Q_i into a composite measure, the importance scale S_i for the i-th indicator is defined by their weighted sum:

$$S_i=Q_i+{\displaystyle \frac{P_i}{N^{*}}}$$

(20)

This additive form ensures that both dimensions contribute independently and additively to the overall importance, preventing the scenario where a low value in one dimension nullifies the contribution of the other.

The value range of S_i is [1/N*, 2], which is derived from the lower and upper bounds of its components (Q_i ∈ [1/N*, 2], P_i/N* ∈ [1/N*, 1]). This signifies:

When S_i = 2, both the pollution degree and the grade discrimination level are maximized (Q_i = 1, P_i = N*), signifying the greatest importance.

When S_i = 1/N*, both dimensions are minimized (Q_i = 0, P_i = 1), signifying the least importance.

Step 5: Calculate the final weights.

The final weight w_i for the i-th indicator is obtained by normalizing the importance scale S_i across all m indicators to ensure their sum equals unity, fulfilling the fundamental constraint of weight assignment:

$$w_i={\displaystyle \frac{S_i}{{\displaystyle \sum _i^m{S}_i}}}$$

(21)

2.4. Compared with the EWM and I-EWM

2.4.1. Benchmark Methods for Comparison

To more convincingly demonstrate the advantages and applicability of the I-EWM, this study selects two additional mainstream weighting methods—Principal Component Analysis (PCA) and the AHP-Entropy Weight combination method—as benchmarks for a comprehensive comparative analysis. As widely adopted approaches in integrated water quality assessment, they are frequently used in conjunction with comprehensive water quality indices and are considered well-represented in the field.

2.4.2. Comparative Analysis of Weighting Logic and Procedure

A comparison of the EWM and I-EWM reveals distinct weighting logics. The EWM assigns weights based on entropy values derived from the numerical discrimination of raw monitoring data. According to this logic, a lower entropy value results in a higher weight. Thus, the weight in EWM fundamentally reflects the statistical characteristics of the data. In contrast, the I-EWM determines weights by integrating fuzzy entropy and the first-order moment. Here, higher values of both fuzzy entropy and the first-order moment lead to a higher weight. The fuzzy entropy is calculated from the dispersion of the “grade membership distribution”, while the first-order moment is computed based on the expected (average) water quality grade for each indicator. Consequently, the weight in I-EWM essentially represents a measure of grade-discriminatory power.

As shown in Figure 3, a comparison of the calculation procedures for the Entropy Weight Method (EWM) and the Improved Entropy Weight Method (I-EWM) can be made based on the content in Section 2.2 and Section 2.3.

A procedural comparison reveals that I-EWM, while involving more steps than the classic EWM, does not incur a substantial computational penalty. The EWM process requires data standardization, normalization, entropy calculation, and weighting. In contrast, I-EWM replaces the preprocessing steps with a fuzzy transformation (calculating relative and average membership degrees) and introduces the calculation of a dual-parameter set (fuzzy entropy and first-order moment) along with an importance scale. Although this adds to the step count, each new operation is mathematically straightforward and common in fuzzy evaluation. The additional computational cost is marginal and justified, as it enables the model to capture the critical information needed for grade-based discrimination, which is the core improvement over EWM.

When comparing the applicability of the Entropy Weight Method (EWM) and the Improved Entropy Weight Method (I-EWM), EWM shows a strong dependence on the overall distribution of raw data. As a purely statistical analysis-based method, it can objectively and efficiently identify the most discriminative dimensions within a dataset and is therefore suitable for scenarios where evaluation indicators lack predefined grading standards or exhibit insignificant differences in decision thresholds. In contrast, the weights derived from I-EWM are more robust. This method relies on predefined and relatively stable grading standards, making it insensitive to occasional extreme values in the data, and is thus particularly applicable to situations where indicator thresholds differ significantly. From a theoretical perspective, I-EWM provides a more solid theoretical foundation and better aligns with the purpose of assigning weights based on the information content pertaining to water quality grades in water quality assessment.

3. Results and Discussion

3.1. Statistical Characteristics of Monitoring

To validate the effectiveness of the method proposed in this study, a water quality monitoring scenario was simulated for a typical section of a river. Five sampling points were set up along this section, and a one-time simultaneous sampling was conducted. The monitoring indicators selected were key pollution parameters from the Environmental Quality Standards for Surface Water (GB 3838-2002) [25]: permanganate index (COD_Mn), ammonia nitrogen (NH₃-N), and total phosphorus (TP). The concentration data for each indicator are shown in

Table 2. Monitoring values of indicators.

Stations	Concentrations (mg/L)			Grades
	CODMn	NH3-N	TP	CODMn	NH3-N	TP
1#	0.7	0.88	0.26	excellent	medium	poor
2#	1.84	0.91	0.29	excellent	medium	poor
3#	1.82	1.21	0.28	excellent	poor	poor
4#	1.86	1.62	0.31	excellent	bad	bad
5#	1.84	1.80	0.38	excellent	bad	bad

Note: # denotes the monitoring site location (or sampling site number).

, aiming to construct a typical scenario with significant differences in thresholds among indicators (e.g., wide thresholds for COD_Mn and narrow thresholds for NH₃-N), thereby highlighting the limitations of the traditional entropy weight method.

As shown in Table 2, the monitoring values of COD_Mn for the five stations are 0.7 mg/L, 1.84 mg/L, 1.82 mg/L, 1.86 mg/L, and 1.84 mg/L; referencing Table 1, all monitoring values are in the “excellent” grade, indicating that the water quality at all five stations is good and not polluted. It is easy to see that the monitoring values of COD_Mn range from 0.7 to 1.84 mg/L, with water quality grades concentrated in the “excellent” grade, which does not have grade discrimination. From a grade perspective, the information content of COD_Mn is low.

The monitoring values of NH₃-N for the five stations are 0.88 mg/L, 0.91 mg/L, 1.21 mg/L, 1.62 mg/L, and 1.80 mg/L; referencing Table 1, it can be seen that the monitoring values are in the “medium”, “medium”, “poor”, “bad”, and “bad” grades, respectively. This indicates that the water quality at all five stations has been polluted to varying degrees. It is easy to see that the monitoring values of NH₃-N range from 0.88 to 1.80 mg/L, with water quality grades distributed in the “medium”, “poor”, and “bad” grades, indicating significant grade discrimination. From a grade perspective, the information content of NH₃-N is high.

The monitoring values of TP for the five stations are 0.26 mg/L, 0.29 mg/L, 0.28 mg/L, 0.31 mg/L, and 0.38 mg/L; referencing Table 1, the monitoring values are in “poor”, “poor”, “poor”, “bad”, and “bad” grades, respectively. This indicates that the water quality at all five stations has been significantly polluted. It is easy to see that the monitoring values of TP range from 0.26 to 0.38 mg/L, with water quality grades distributed in the “poor” and “bad” grades, indicating some grade discrimination. From a grade perspective, the information content is relatively high.

It should be noted that, referencing Table 1 and Table 2, among the three indicators, COD_Mn has the largest numerical discrimination but the smallest grade discrimination. This is because all monitoring values of COD_Mn are distributed in one water quality grade, while all monitoring values of NH₃-N are distributed in three water quality grades, and TP is distributed in two water quality grades. Although the numerical discrimination of monitoring values of COD_Mn is the largest, all monitoring values of COD_Mn are actually in the same grade. Although the numerical discrimination of monitoring values of NH₃-N and TP is smaller, the monitoring values of NH₃-N and TP are distributed in different grades. From the perspective of water resource management, NH₃-N and TP provide more information than COD_Mn.

In addition, the monitoring values of indicators are not concentrated in seriously polluted grades, so there is no distortion phenomenon as described by [20]. There are also no monitoring values of 0, so there is no distortion phenomenon as described by Bao et al. [21]. This water quality assessment is not a dynamic evaluation, so there is no distortion phenomenon as described by Wang et al. [14].

3.2. Weight Results of the EWM

The weight results of the EWM introduced in Section 2.1 are shown in

Table 3. Weight results of the EWM.

Indicators	CODMn	NH3-N	TP
Stations	Normalized Values
1#	0.936	0.356	0.316
2#	0.016	0.345	0.237
3#	0.032	0.229	0.263
4#	0.000	0.070	0.184
5#	0.016	0.000	0.000
Hj	0.190	0.782	0.850
1 − Hj	0.810	0.218	0.150
wi	0.687	0.185	0.127

Note: # denotes the monitoring site location (or sampling site number).

.

As shown in Table 3, the weight results of COD_Mn, NH₃-N, and TP are 0.687, 0.185, and 0.127, respectively, indicating that the rank of the weight parameters generated by the EWM is COD_Mn > NH₃-N > TP. Referencing Table 2, the difference in monitoring values between COD_Mn is the largest, NH₃-N is the second largest, and TP is the smallest, indicating that the numerical discrimination of COD_Mn is the largest, followed by NH₃-N and then TP. Therefore, the weight results of the EWM can correctly reflect the dispersion degree of indicators and data information content.

Referencing Table 2, the water quality grades of COD_Mn are all “excellent” grades, while the water quality grades of NH₃-N are “medium”, “poor”, or “bad” grade, and the water quality grades of TP are “poor” or “bad”. According to the grade distribution of indicators, NH₃-N has the largest information content, followed by TP, and COD_Mn has the smallest information content. Therefore, the rank of weight parameters should be NH₃-N > TP > COD_Mn. However, based on the weight results of the EWM the weight parameters of COD_Mn, which has the smallest grade discrimination, are much larger than those of NH₃-N and TP, which have higher grade discrimination. This is clearly unreasonable.

Furthermore, referencing Table 2, TP has the highest degree of pollution, NH₃-N has the second highest, and COD_Mn has the lowest. Therefore, the rank of weight parameters should be TP > NH₃-N > COD_Mn. However, the weight parameters of COD_Mn, which has a lower pollution degree, are much larger than those of NH₃-N and TP, which have high pollution degrees. The weight results of the EWM are clearly unreasonable because the EWM does not consider the importance of heavy pollution indicators.

Based on the above content, the weight results of the EWM cannot correctly reflect the importance of indicators in water quality assessment. The reason for this phenomenon is that EWM is weighted based on the numerical discrimination of indicators, rather than the grade discrimination of indicators. The grade discrimination of indicators can only reflect the information content of indicators, and the numerical discrimination of indicators cannot. Furthermore, EWM neglects the importance of heavy pollution indicators in the weighting process, which leads to distorted weighting results of EWM. How to obtain information entropy based on the grade discrimination of indicators while considering the importance of heavily polluting indicators is the research content of this article.

3.3. Weight Results of I-EWM

The weight results of I-EWM introduced in Section 2.3 are shown in

Table 4. Weight results of I-EWM.

Indicators	CODMn	NH3-N	TP
Stations	uij
1#	(1.00, 0.00, 0.00, 0.00, 0.00)	(0.00, 0.00, 0.74, 0.26, 0.00)	(0.00, 0.00, 0.00, 0.90, 0.10)
2#	(0.58, 0.42, 0.00, 0.00, 0.00)	(0.00, 0.00, 0.68, 0.32, 0.00)	(0.00, 0.00, 0.00, 0.60, 0.40)
3#	(0.59, 0.41, 0.00, 0.00, 0.00)	(0.00, 0.00, 0.08, 0.92, 0.00)	(0.00, 0.00, 0.00, 0.70, 0.30)
4#	(0.57, 0.43, 0.00, 0.00, 0.00)	(0.00, 0.00, 0.00, 0.26, 0.74)	(0.00, 0.00, 0.00, 0.40, 0.60)
5#	(0.58, 0.42, 0.00, 0.00, 0.00)	(0.00, 0.00, 0.00, 0.00, 1.00)	(0.00, 0.00, 0.00, 0.00, 1.00)
vi	(0.664, 0.336, 0.000, 0.000, 0.000)	(0.00, 0.00, 0.300, 0.352, 0.348)	(0.00, 0.00, 0.00, 0.520, 0.480)
Qi	0.397	0.681	0.430
Pi	1.336	4.048	4.480
wi	0.191	0.428	0.381

Note: # denotes the monitoring site location (or sampling site number).

.

As shown in Table 4, the fuzzy entropies of COD_Mn, NH₃-N, and TP are 0.397, 0.681, and 0.430, respectively. The larger the fuzzy entropy of the indicator is, the higher the level of grade discrimination of the indicator is, the greater the information content of the indicator is and the greater the importance of the indicator is. Therefore, NH₃-N has the greatest level of grade discrimination, that of TP is second, and that of COD_Mn is the smallest. Referencing Table 2, COD_Mn does not have a level of grade discrimination, NH₃-N is distributed in three water quality grades, and TP is distributed in two water quality grades, which is consistent with the analysis results in Section 3.1.

As shown in Table 4, the first-order moments of COD_Mn, NH₃-N, and TP are 0.267, 0.810, and 0.896, respectively. The larger the first-order moment of the indicator is, the higher the degree of pollution of the indicator is and the greater the importance of the indicator is. Therefore, the degree of pollution and the importance of TP and NH₃-N are greater than those of COD_Mn. Referencing Table 2, according to the TP and NH₃-N of the five stations, the water quality has been polluted to varying degrees, while according to COD_Mn, the water quality is not polluted, which is consistent with the analysis results in Section 3.1.

The weights of COD_Mn, NH₃-N, and TP are 0.191, 0.428, and 0.381, respectively, indicating that the rank of weight parameters generated by the I-EWM is NH₃-N > TP > COD_Mn. The I-EWM assigns weights based on fuzzy entropy and the first-order moment of the indicator, where the larger the fuzzy entropy and the first-order moment are, the greater the weight is. Comparing COD_Mn, NH₃-N, and TP, the first-order moments of NH₃-N and TP are greater than that of COD_Mn, and the fuzzy entropies of NH₃-N and TP are also greater than that of COD_Mn, so the weights of NH₃-N and TP are greater than that of COD_Mn. Comparing NH₃-N and TP, the first-order moments of NH₃-N and TP are equivalent, and the fuzzy entropy of NH₃-N is greater than that of TP, so the weight of NH₃-N is greater than that of TP. Based on the above content, NH₃-N has the highest weight, followed by TP, and COD_Mn has the lowest weight.

Comparing the weight results of the I-EWM and that of the EWM, the weight of COD_Mn is significantly reduced, while the weights of NH₃-N and TP are significantly increased. This is because the numerical discrimination of COD_Mn is greater than that of NH₃-N and TP, but the level of grade discrimination and the pollution degree of COD_Mn are smaller than those of NH₃-N and TP. The EWM assigns weights based on the numerical discrimination of indicators; COD_Mn with high numerical discrimination is assigned larger weights, while NH₃-N and TP, with low numerical discrimination, are assigned smaller weights. The I-EWM assigns weights based on the level of grade discrimination and pollution degree of indicators, COD_Mn, without grade discrimination and with a low pollution degree are assigned smaller weights, while NH₃-N and TP with higher grade discrimination and higher pollution degree are assigned larger weights.

3.4. Comprehensive Evaluation Results of Water Quality

The comprehensive WQI results using the weights generated by the EWM are shown in

Table 5. Comprehensive WQI results based on EWM weights.

Indicators	CODMn	NH3-N	TP	CWQIj	Grades
wi	0.687	0.185	0.127
1#	93.0	44.8	28.0	75.79	good
2#	81.6	43.6	22.0	66.97	good
3#	81.8	31.6	24.0	65.14	good
4#	81.4	15.2	18.0	61.06	good
5#	81.6	8.0	4.0	58.08	medium

Note: # denotes the monitoring site location (or sampling site number).

, and the comprehensive WQI results using the weights generated by the I-EWM are shown in

Table 6. Comprehensive WQI results using the weights generated by I-EWM.

Indicators	CODMn	NH3-N	TP	CWQIj	Grades
wi	0.191	0.428	0.381
1#	93.0	44.8	28.0	47.59	medium
2#	81.6	43.6	22.0	42.62	medium
3#	81.8	31.6	24.0	38.28	poor
4#	81.4	15.2	18.0	28.89	poor
5#	81.6	8.0	4.0	20.51	poor

Note: # denotes the monitoring site location (or sampling site number).

.

As shown in Table 5, according to the water quality assessment results of the EWM, the comprehensive WQI of stations #1, #2, #3, #4, and #5 are 75.79, 66.97, 65.14, 61.06, and 58.08, respectively. Correspondingly, the water quality grades of stations #1, #2, #3, and #4 are all “good”, while only that of station #5 is “medium”. According to the water quality assessment results of the EWM, the final water quality grades are mostly “good”, indicating that the overall water quality has not been polluted.

As shown in Table 6, according to the water quality assessment results of the I-EWM, the comprehensive WQI of stations #1, #2, #3, #4, and #5 are 47.59, 42.62, 38.28, 28.89, and 20.51, respectively. Correspondingly, the water quality grades of stations #1 and #2 are “medium”, while those of stations #3, #4, and #5 are “ poor”. According to the water quality assessment results of the I-EWM, the final water quality grades are “medium” and “poor”, indicating that the overall water quality pollution degree is high.

Comparing the water quality assessment results of the EWM and I-EWM, the water quality assessment results of the I-EWM are much worse than those of the EWM. Compared with the CWQI_j values of the EWM, the CWQI_j values of the I-EWM at stations #1, #2, #3, #4, and #5 are reduced by 28.20, 24.35, 26.86, 32.17, and 37.57, respectively. Compared with the water quality grades of the EWM, the water quality grades of the I-EWM at stations #1, #2, and #5 are reduced by one level, while the water quality grades of the I-EWM at stations #3 and #4 are reduced by two levels.

Why are the water quality assessment results of the EWM and I-EWM completely opposite? Referencing Table 5 and Table 6, this phenomenon is caused by the difference in weight assignment between the two methods. According to the EWM, the weight of COD_Mn is significantly higher than that of NH₃-N and TP, and the fact that COD_Mn is in the “excellent” grade plays a dominant role in the water quality assessment results, leading to optimistic water quality assessment results. According to the I-EWM, the weights of NH₃-N and TP were significantly higher than that of COD_Mn, with NH₃-N concentrated in the “medium”, “poor”, and “bad” grades and TP concentrated in the “poor” and “bad” grades. NH₃-N and TP played a dominant role in the water quality assessment results, resulting in poor water quality assessment results.

In summary, the water quality assignment results based on the I-EWM are more reasonable. The EWM assigns higher weights to COD_Mn with high numerical discrimination and low level of grade discrimination, while assigning smaller weights to NH₃-N and TP with low numerical discrimination and high level of grade discrimination, resulting in overly optimistic water quality evaluation results. The I-EWM assigned higher weights to NH₃-N and TP with high levels of grade discrimination and pollution degree, while smaller weights were assigned to COD_Mn with no grade discrimination and no pollution, resulting in more reasonable water quality assignment results.

3.5. Comparative Analysis of Weight Allocation

To more effectively validate the superiority of the Improved Entropy Weight Method (I-EWM), this study simultaneously introduced the Analytic Hierarchy Process-Entropy combination method (AHP-Entropy) and Principal Component Analysis (PCA) to compare their weighting results with those of I-EWM. As shown in

Table 7. Comparison of Weights from Four Weighting Methods.

Methods	CODMn	NH3-N	TP
EWM	0.687	0.185	0.127
PCA	0.332	0.336	0.332
AHP-Entropy	0.639	0.215	0.146
I-EWM	0.191	0.428	0.381

, although the AHP-Entropy method incorporates subjective adjustments, its weighting results remain predominantly influenced by COD_Mn. PCA assigns weights to the permanganate index (COD_Mn), ammonia nitrogen, and total phosphorus that are relatively equal in magnitude. As established in the preceding analysis, the weighting results of both methods fail to accurately reflect the information content pertaining to grade discriminability among the indicators. Consequently, they cannot serve as substitutes for I-EWM in addressing the weighting distortion related to grade discrimination inherent in the traditional EWM.

The water quality assessment results of the four weighting methods presented in

Table 8. Comparison of Water Quality Assessment Results Using Four Weighting Methods.

Methods	EWM	PCA	AHP-Entropy	I-EWM
1#	good	medium	good	medium
2#	good	medium	good	medium
3#	good	medium	good	poor
4#	good	poor	medium	poor
5#	medium	poor	medium	poor

Note: # denotes the monitoring site location (or sampling site number).

demonstrate the following: The results of the AHP-Entropy method are similar to those of the conventional EWM, both exhibiting an overly optimistic bias. Although the results of the PCA method are relatively closer to those of I-EWM, its water quality rating for Site 3# remains one grade higher than that of I-EWM, being rated as “Medium”. This discrepancy arises because the PCA weighting process assigns a comparatively high weight to the permanganate index, which consequently exerts a dominant influence on the water quality evaluation result for Site 3#.

4. Conclusions

4.1. Main Findings and Contributions

The weight results of the EWM cannot accurately reflect the importance of pollutants in actual water environment management. The EWM assigns weights based on the numerical discrimination of indicators rather than the grade discrimination of indicators. The numerical discrimination of indicators cannot reflect the information content of indicators, and grade discrimination can reflect the information content of indicators. When there are significant differences in the threshold division of different indicators, the EWM will give too much weight to indicators with high numerical discrimination and low level of grade discrimination and give too little weight to indicators with low numerical discrimination and high level of grade discrimination, resulting in distorted water quality evaluation results.

The I-EWM introduces fuzzy variable set theory and assigns weights based on the fuzzy entropy and first-order moment of the average membership vector of indicators. The fuzzy entropy reflects the water quality grade discrimination, and the first-order moment reflects the pollution degree of the indicator. The basic principle of weights assigned to the I-EWM is as follows: When the indicators have the same degree of pollution, the higher the level of grade discrimination of the indicators is, the greater the importance of the indicators is, and the higher the weights assigned are, and vice versa. When there is the same level of grade discrimination of indicators, the higher the degree of pollution is, the greater the importance of the indicators is, and the higher the weights assigned are, and vice versa. Through a specific water quality evaluation example, it is proven that the I-EWM can effectively improve the distortion phenomenon mentioned above in the EWM, and the water quality evaluation results are more reasonable.

4.2. Limitations and Applicability Discussion

In practical applications, the I-EWM weighting model has the following two limitations. Firstly, the method assumes equal importance between grade discrimination (fuzzy entropy) and pollution degree (first-order moment) in weight allocation. However, in practice, the influence of these two factors may differ significantly, requiring adjustments to the weighting formula based on specific conditions. Secondly, the advantage of I-EWM is most prominent in scenarios where there are significant differences in threshold divisions among evaluation indicators and where grade discrimination holds clear management significance. For ordinary datasets with uniformly distributed thresholds or ambiguous grade distinctions, its improvement may be limited, and the computational cost is slightly higher compared to the traditional EWM.

Nevertheless, I-EWM remains valuable in addressing the critical issue of traditional entropy weight methods neglecting grade discrimination. It is particularly suitable for hierarchical evaluation systems with significant threshold differences, thus demonstrating clear practical significance and potential for broader application.

4.3. Future Research Directions

To address the limitations of I-EWM in practical applications, future research should focus on integrating machine learning techniques to enhance the model’s adaptability and intelligence:

When significant differences exist in how grade discrimination and pollution degree influence weights, reinforcement learning or multi-objective optimization algorithms can be introduced. This enables the model to automatically adjust the proportional relationship between fuzzy entropy and first-order moment in weight calculations based on historical evaluation outcomes or managerial preferences, thereby improving the model’s adaptability across different application scenarios.

For conventional datasets with uniformly distributed thresholds or unclear grade discrimination, a lightweight hybrid model can be developed to balance performance and efficiency. Specifically, simple classifiers (e.g., decision trees) or rule-based criteria can be employed to pre-assess whether a dataset exhibits the characteristic of “significant threshold differences”. If this feature is present, the complete I-EWM model is activated; if the dataset is conventional, the system automatically switches to the more computationally efficient traditional EWM or other suitable models.