A New Fuzzy Preference Relation (FPR) Approach to Prioritizing Drinking Water Hazards: Ranking, Mapping, and Operational Guidance

Abstract

This paper presents a practical and auditable methodology for prioritizing drinking water hazards based on fuzzy preference relations (FPR). The method is based on additive pairwise comparisons of tap water quality parameters, which are aggregated (median) into a complete preference matrix. For each parameter, a Fuzzy Priority Index (FPI) was determined as the average “advantage” over the others. The FPI values were mapped to five fuzzy priority levels (very low–very high) using triangular/trapezoidal membership functions, followed by a defuzzification process using the centroid of singletons (COGS) method. The final step is to map the categories to operational actions, ensuring a clear transition from assessment to decision (from routine monitoring to immediate intervention). The method was demonstrated on nine parameters that are relevant for regulatory (WHO/DWD) and operational purposes: As, Pb, THM, NO₃⁻, Hg, Cr, Mn, Cu, Fe. Thirty-six pairwise assessments were determined, which, after aggregation, formed fuzzy relations. The resulting ranking (FPI) is: As (0.76) > Pb (0.70) > THM (0.64) > NO₃⁻ (0.56) > Hg (0.50) > Cr (0.43) > Mn (0.36) > Cu (0.30) > Fe (0.25). Fuzzy categorization assigned As, Pb, THM to the High level, NO₃⁻, Hg, Cr to Medium, and Mn, Cu, Fe to Low, with the Score reflecting the “proximity” of higher levels. The approach is transparent, replicable, and supports sensitivity analysis. The combination of FPI with fuzzy categorization and a decision map transforms expert knowledge and uncertainty into prioritized, actionable steps for water safety management.

1. Introduction

Access to safe and clean drinking water is one of the basic conditions for public health and social development. It is estimated that more than 2 billion people worldwide still use water that does not meet basic safety standards [1]. In developed countries, including Europe, thanks to extensive water supply infrastructure, the microbiological risk has been significantly reduced, but the importance of risks related to chemical parameters of water, such as heavy metals, nitrates or disinfection by-products, is growing [2,3]. The quality of drinking water is therefore a fundamental factor determining public health. Chemical and physicochemical contaminants present in water supply systems can contribute to chronic diseases, damage to the nervous system, developmental disorders in children and carcinogenic effects, even at low levels of exposure and long-term consumption [4,5]. The WHO Guidelines for Drinking-Water Quality emphasise that water quality standards should protect consumers from such health effects, and that risk-based approaches are key to managing water supply safety [6].

In the European Union, the legislative basis in this area is Directive (EU) 2020/2184 of the European Parliament and of the Council [7], which implements an integrated “source to tap” approach, expands the range of monitored parameters and imposes an obligation to inform consumers about water quality. This document establishes parametric values for substances such as nitrates (50 mg/L), arsenic (10 μg/L), lead (10 μg/L, with a target reduction to 5 μg/L), mercury (1 μg/L), chromium (50 μg/L), copper (2 mg/L) and total trihalomethanes (100 μg/L) [7]. In Poland, these regulations are transposed into national law, inter alia, through the Regulation of the Minister of Health of 2017 on the quality of water intended for consumption [8].

Despite the existence of regulations and numerous studies documenting the impact of selected water quality parameters on human health, comparing the risks posed by different substances remains a methodological challenge. This is due to a number of factors: differences in measurement units and toxicity, different dose-effect characteristics, diversity of particularly sensitive populations (children, pregnant women, the elderly), high variance in monitoring data, and different ways of interpreting exceedances of normative values (instantaneous exceedances, annual averages, cumulative exposure). These conditions make the creation of a uniform hierarchy of risks a complex task fraught with considerable interpretative uncertainty [9].

Despite the regulations in force, numerous cases in recent decades indicate that exceedances of chemical parameters in drinking water continue to pose a serious health problem:

-

Nitrates (NO₃⁻). In Central and Eastern Europe, the problem of nitrate pollution of water associated with intensive agriculture remains significant. Studies in Poland have shown that in some municipalities, concentrations in groundwater exceed 50 mg/L, increasing the risk of methemoglobinemia in infants (blue baby syndrome) [10]. Similar results have been reported in the Czech Republic and Hungary [11].

-

Lead (Pb). Lead contamination in drinking water is well documented, for example, in the Flint (USA) incident, where corrosion of old pipes led to neurotoxic exposure of thousands of children [12]. In Europe, the problem mainly concerns internal installations—studies in the United Kingdom have shown that in older buildings, Pb concentrations in water exceeded 10 μg/L [13].

-

Arsenic (As). The most well-known incidents of mass exposure concern Bangladesh and India, where tens of millions of people have been using groundwater with As concentrations reaching hundreds of μg/L for decades, resulting in an epidemic of skin and bladder cancer [14]. In Europe, the problem has been noted in southern Italy and Hungary, among other places, where geothermal waters naturally contain arsenic in concentrations above 10 μg/L [15,16].

-

Trihalomethanes (THMs). An analysis by Villanueva [17] covering 26 EU countries showed that approximately 6500 cases of bladder cancer per year (about 5% of the total) can be attributed to chronic exposure to THMs in drinking water, even in systems that comply with the 100 μg/L limit.

-

Manganese (Mn). Epidemiological studies in Canada and the USA have shown that chronic consumption of water with elevated manganese concentrations (above 100 μg/L) is associated with reduced cognitive ability in children [18].

-

Copper (Cu). Exceedances of acceptable values are recorded locally in highly corrosive water supply systems—chronic exposure can lead to hepatotoxicity and gastric problems [19].

-

Iron (Fe). In most cases, iron does not pose a health risk, but it is the cause of consumer complaints due to its colour, taste and sediment, and it can also promote the secondary growth of microorganisms in the network [6].

Comparing the risks posed by different quality parameters presents numerous methodological difficulties. These arise from different toxicity (acute vs. chronic), different mechanisms of action (methemoglobinemia vs. carcinogenicity), different routes of exposure (ingestion, THM inhalation, dermal contact), and varied spatial and temporal variability in the water supply network [9]. In addition, differences in particularly sensitive groups (infants, children, pregnant women) are important, as they react differently to the same concentrations.

There are several different methods in the literature for assessing the risks associated with water quality parameters:

-

Water Quality Index (WQI). Many studies use WQI, a multi-parameter index that aggregates various variables (chemical, physicochemical, biological) into a single index value, which facilitates communication of the overall water status. For example, Luo et al. [20] used WQI together with multidimensional analysis to assess 17 drinking water parameters in the city of Nanning (China), including metals such as arsenic, lead and mercury [20].

-

Statistical and probabilistic methods. Other studies use classification and comparison methods, such as ranking or aggregation approaches, as well as probabilistic risk measures. In a study of the Douro River Basin (Portugal), the authors used various risk measures (mean, variance, exceedance probability, value at risk, etc.) and then merged the ranking of monitoring stations on this basis [21].

-

WQI with uncertainty analysis. Methods combining the classic WQI with uncertainty analysis are becoming increasingly common. Critical studies of the arbitrariness in the selection of weights indicate that the choice of parameters and their weights can significantly affect the final result and interpretation of water status. An example of this is analyses that have shown that different weighting schemes lead to different quality assessments [22].

Despite the existence of these methods, there is still a need for a simple, transparent and practical tool that will allow for quick comparison of risks between water quality parameters—especially in local and water supply contexts. Complex methods, such as full epidemiological analysis or probabilistic simulations, require large amounts of data and specialised resources, which limit their applicability in the practice of water supply companies. This article proposes a ranking method that addresses this gap, enabling simple prioritisation of risks and supporting operational and regulatory decisions.

The aim of this article is to develop and present a practical ranking method for key water quality parameters. This method, based on toxicological, epidemiological and operational criteria and in light of WHO regulations and Directive (EU) 2020/2184 [1,6,7], allows each parameter to be assigned a risk weight and linked to clearly defined operating instructions. The methodological innovation of this study is the construction of a fuzzy decision pipeline based on additive preference matrices, using linguistically valid pairwise comparisons aggregated by the median. This matrix forms the basis for calculating the Fuzzy Priority Index (FPI), a normalized dominance score for each parameter. FPI values are then translated into fuzzy categories using simple, calibrated membership functions and defuzzied using the Centroid of Singletons (COGS) method. Unlike fuzzy AHP or WQI methods, which often rely on complex weight hierarchies or aggregated indices with limited transparency, the proposed approach is easy to audit, interpret, and directly linked to operational guidelines. The ranking model constructed in this way is a tool that supports the prioritization of actions in water supply companies and public administration, ensuring a balance between simplicity of use and reliability of assessment, and provides a basis for further research into the development of an innovative approach to the analysis of health risks resulting from exceedances of quality parameters for water intended for human consumption.

At the same time, this work should be framed not as a fundamental innovation in fuzzy theory, but as a practical and operational tool tailored to the needs of water utilities and public health services. The proposed approach offers a transparent, auditable, and implementable decision-support scheme that complements existing methodologies, such as WQI, fuzzy-WQI, and fuzzy-AHP. While traditional indices focus on aggregating data into a single score or rely on subjective weighting, our method eliminates the need for predefined weights or hierarchical structures, providing an accessible and repeatable mechanism for prioritizing actions based on expert judgments and regulatory relevance.

2. Materials and Methods

2.1. Basics of the Research Methodology

Fuzzy logic and preference relations in this application are part of the broad trend of multi-criteria decision-making and risk analysis, which are discussed and generalised in classic monographs and works on FPR in group decisions. The literature has repeatedly emphasised the usefulness of fuzzy techniques for prioritising environmental and health risks [23,24,25].

Fuzzy set theory [26] allows for the description of vague concepts—e.g., “high priority”, “more dangerous”—using membership degrees μ ∈ [0, 1] instead of sharp “yes/no” boundaries. Details of the design of fuzzy models and membership function variants are described in detail in monographs [27,28].

The proposed model uses trapezoidal and triangular functions. Both function shapes are linear segments, which ensures transparency (easy explanation of the classification logic) and calibrability (simple shifting of inflection points). The trapezoidal function is useful for extreme categories (e.g., to describe “Very low”, “Very high”), where an area of complete certainty with smooth transitions on the sides of the function is needed, so that minor fluctuations arising during the fuzzifying process do not cause immediate category jumps. In turn, the triangular function works best for intermediate categories (“Low”, “Medium”, “High”) when there is a natural “centre” of the category and symmetrical or controlled asymmetrical blurring towards adjacent levels is required.

The membership functions μA used in the methodology are described by Formulas (1) and (2) [26,27,28]:

-

trapezoidal function μ(x; a, b, c, d)

$${\mathsf{\mu }}_{\left(\mathrm{A}\right)}(\mathrm{x};\mathrm{a},\mathrm{b},\mathrm{c},\mathrm{d})=\left\{\begin{array}{cc}0,\hfill & \hfill \hspace{1em}\hspace{1em}\hspace{1em}\mathrm{x}\le \mathrm{a}\\ {\displaystyle \frac{\mathrm{x}-\mathrm{a}}{\mathrm{b}-\mathrm{a}}},\hfill & \hfill \hspace{1em}\hspace{1em}\hspace{1em}\mathrm{a}<\mathrm{x}<\mathrm{b}\\ 1,\hfill & \hfill \hspace{1em}\hspace{1em}\hspace{1em}\mathrm{b}\le \mathrm{x}\le \mathrm{c}\\ {\displaystyle \frac{\mathrm{d}-\mathrm{x}}{\mathrm{d}-\mathrm{c}}},\hfill & \hfill \hspace{1em}\hspace{1em}\hspace{1em}\mathrm{c}<\mathrm{x}<\mathrm{d}.\\ 0,\hfill & \hfill \hspace{1em}\hspace{1em}\hspace{1em}\mathrm{x}\ge \mathrm{d}\end{array}\right.$$

(1)

-

triangular function μ(x; a, b, c)

$${\mathsf{\mu }}_{\left(\mathrm{A}\right)}(\mathrm{x};\mathrm{a},\mathrm{b},\mathrm{c})=\left\{\begin{array}{cc}0,\hfill & \hfill \hspace{1em}\hspace{1em}\hspace{1em}\mathrm{x}\le \mathrm{a}\\ {\displaystyle \frac{\mathrm{x}-\mathrm{a}}{\mathrm{b}-\mathrm{a}}},\hfill & \hfill \hspace{1em}\hspace{1em}\hspace{1em}\mathrm{a}<\mathrm{x}<\mathrm{b}\\ {\displaystyle \frac{\mathrm{c}-\mathrm{x}}{\mathrm{c}-\mathrm{b}}},\hfill & \hfill \hspace{1em}\hspace{1em}\hspace{1em}\mathrm{b}<\mathrm{x}\le \mathrm{c}\\ 0,\hfill & \hfill \hspace{1em}\hspace{1em}\hspace{1em}\mathrm{x}\ge \mathrm{c}.\end{array}\right.$$

(2)

Furthermore, x = FPI ∈ [0, 1] (fuzzy priority index) was adopted; therefore, using Formulas (1) and (2) in the proposed research methodology, x = FPI was adopted as the function argument.

In order to order multiple elements relative to a single, combined criterion, a fuzzy preference relation was used. For each pair (i, j), a value a_ij ∈ [0, 1] was defined, interpreted as the extent to which parameter i is more dangerous than j. Additive reciprocity a_ii = 0.5 and a_ji = 1 − a_ij, assuming (i ≠ j). This relationship ensures consistency and interpretability of comparisons. The data source is expert opinions in the form of pairwise comparisons. Each expert creates a matrix A^(k), and the group matrix A = [a_ij] is obtained by aggregating parameter by parameter (in practice, by the median $\overline{{\mathrm{a}}_{\mathrm{i}\mathrm{j}}}$, which is resistant to extreme judgements) [29,30].

The final stage is the “defuzzification” process, used to obtain a single representative value (Score) and its “position” between levels. For this purpose, the singleton centroid method (COGS) was used, i.e., the weighted average of the fixed centroids of categories by their membership μ_(A). This method corresponds to the “centre of gravity” of the membership distribution and provides a stable, interpretable result for further comparison and sorting [31].

The final result is the presentation of the analysis results in the form of a “fuzzy queue graph”, where the nodes characterise the elements/parameters ordered in descending order according to the adopted methodology, while the edges between adjacent nodes can be additionally described as a(i → i + 1) from the created fuzzy preference matrix A. The value a(i → i + 1) from the fuzzy preference matrix A is placed on the edge of the graph, i.e., the degree to which parameter i is more dangerous than the next i + 1.

The fuzzy queue graph shows not only the order, but also the strength of the advantage of neighboring nodes of the examined parameters—this facilitates communication with stakeholders and identification of parts of the ranking where the order may change with slight fluctuations in expert assessments, and represents an innovative approach to presenting analysis results.

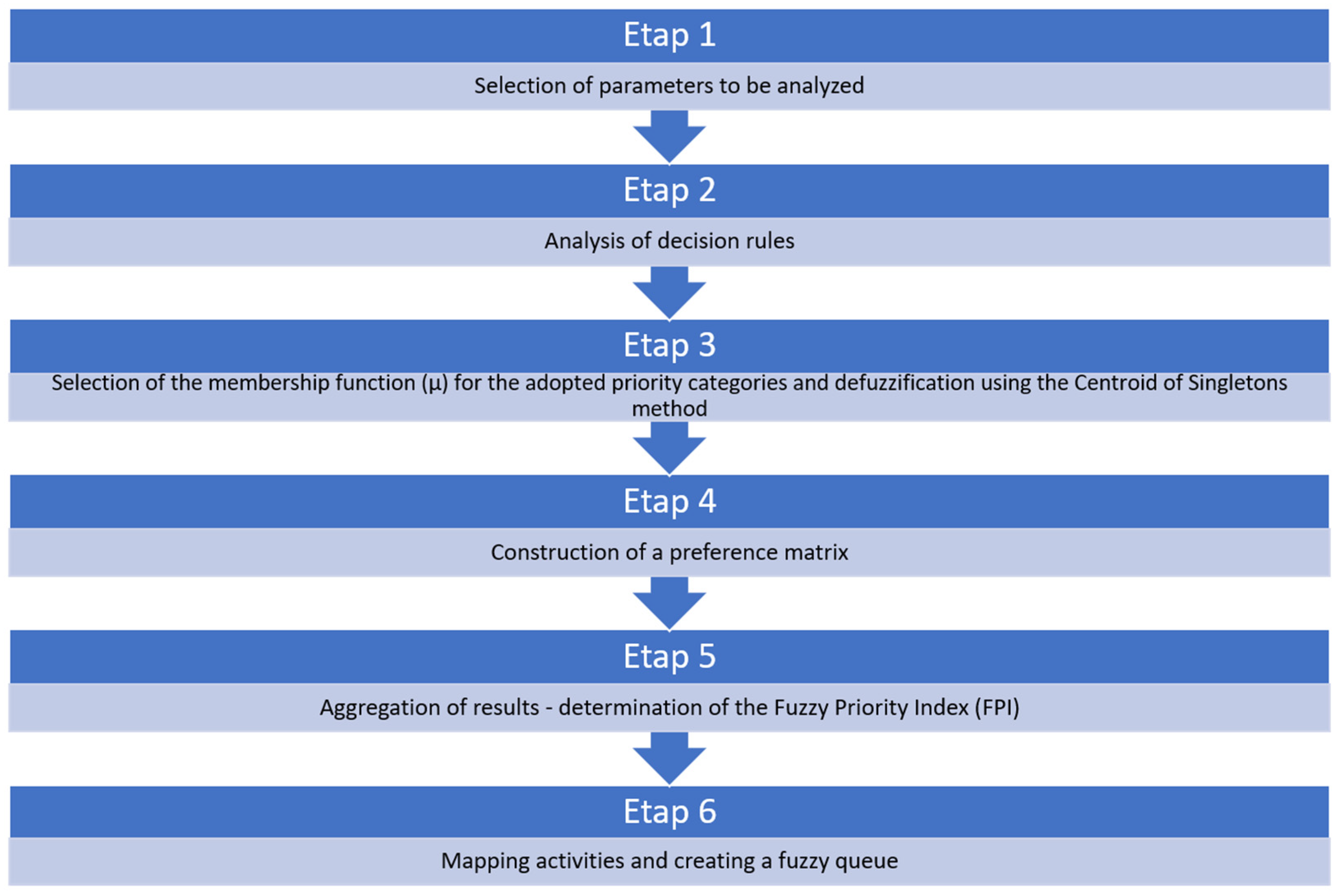
2.2. Prioritisation of Water Quality Parameters: Assumptions and Stages of the Method (FPR–FPI)

In the context of assessing the quality of water intended for consumption, fuzzy logic allows us to build a hierarchy of parameter priorities while taking into account the uncertainty and multi-criteria nature of the problem. In the proposed procedure, we integrate information on toxicity/epidemiology, frequency and severity of exceedances, as well as technological, operational and social conditions into a single combined (operational) criterion [32,33,34]. As a result, the ranking and fuzzy categorisation obtained are more transparent, auditable and resistant to subjective fluctuations than classical approaches based on rigid weights [35].

The methodology is based on fuzzy preference relations (FPR) obtained from pairwise comparisons performed by independent experts. From the aggregated (median) preference matrix, the Fuzzy Priority Index (FPI) was calculated for each parameter and then mapped to five priority levels (using triangular/trapezoidal membership functions, defined a priori on the x-axis = FPI ∈ [0, 1]. The final, one-dimensional measure for resolving borderline cases was obtained by defuzzification using the singleton centroid method (COGS), which allowed for consistent category assignment and mapping to operational instructions (monitoring, technological activities, etc.) [36].

In order to capture the uncertainty and multi-criteria nature of the proposed methodology, Figure 1 shows the individual stages of the procedure.

2.2.1. Stage 1. Selection of Parameters for Analysis

This stage involves selecting the quality parameters of tap water that are relevant from the point of view of both the water producer and the consumer. A set of elements is considered, defined by the relationship A = {a_i, …, a_n}, where a_i, …, a_n are the water quality parameters to be analysed. These may be quality parameters tested as part of monitoring carried out by water supply companies in accordance with the recommendations of the WFD [7,8] and national regulations.

Table 1. Proposed ranks for selected water quality parameters with instructions for action.

Parameter	Main Health Effects	Technological Criterion	Priority Level (Rank 1–5)	Justification	Action Map
Arsenic (As)	Highly carcinogenic (skin, bladder and lung cancer), skin lesions,	None	5	One of the most dangerous parameters, documented health effects with chronic exposure.	Immediate corrective action; suspension of supply or switching of source; implementation of advanced technologies (adsorption, membranes); priority monitoring and reporting.
Lead (Pb)	Neurotoxicity (children), developmental disorders, hypertension, nephrotoxicity	corrosion of installations	5	High toxicological significance, especially in sensitive groups.	Elimination of the source (replacement of lead installations, corrosion control); child health protection programmes; intensive monitoring and consumer information.
Mercury (Hg)	Neurotoxicity, kidney damage, foetal effects	None	4	Highly toxic, but rarely exceeds standards in water supplies.	Increased monitoring frequency; identification of the source of contamination; implementation of reduction technologies (e.g., ion exchange); notifications in case of exceedances.
THM (Trihalomethanes)	Cancer risk (bladder, intestine), inhalation and dermal effects	Disinfection by-product	4	Commonly found, risk signals even at concentrations below EU standards.	Optimization of the disinfection process (contact time, chloramination, DBP precursors); implementation of technologies limiting the formation of THM (GAC, ozone, biological filtration); monitoring at network points.
Nitrates (NO3−)	Methaemoglobinaemia (infants), possible links to stomach cancer	insignificant	4	Very important parameter in agriculture; high risk for infants.	Monitoring in agricultural areas; identification of sources of inflow (sewage, fertilisers); alternative water sources for infants; implementation of desalination/denitrification in treatment.
Chromium (Cr)	Carcinogenic (Cr(VI)), toxic to kidneys and liver	Industrial nature	3	Significant toxicologically, but exceedances in water supply systems are rare.	Periodic monitoring; testing of industrial sources; contingency plan in case of increased concentrations; implementation of reduction technologies (e.g., reduction of Cr(VI) to Cr(III) + coagulation).
Copper (Cu)	Diarrhoea, liver damage with chronic exposure	corrosion of installations	2	Significant mainly in the case of long-term exceedances in domestic installations.	Monitoring of internal installations (corrosion of copper pipes); operating recommendations (flushing of the network, pH control); measures to be taken in the event of long-term exceedances.
Manganese (Mn)	Neurotoxicity (children), developmental disorders	sediment, secondary contamination	2	Moderate health risk, more often an aesthetic and technological problem.	Regular rinsing of nets; use of filtration in treatment plants; measures mainly in the case of aesthetic problems and secondary contamination.
Iron (Fe)	No significant health effects (except for haemochromatosis in high doses)	colour, taste, sediment	1	Secondary parameter, more of a visual quality issue than a toxicological one.	Measures to reduce sediment and colour (iron removal, network flushing); response to consumer complaints; maintaining the

presents a proposal for numerical priority levels for nine selected water quality parameters, taking into account:

-

health significance (toxicity, carcinogenic potential, impact on sensitive groups),

-

frequency of occurrence in water supply systems,

-

technological/operational consequences (colour, sediments).

Based on the data and descriptions proposed in Table 1, the following interpretation was adopted

-

highest priority (rank 5): parameter with the highest priority due to carcinogenicity and neurotoxicity, with proven health effects even with chronic low exposure (e.g., arsenic, lead).

-

high priority (rank 4): parameter of high health significance, more frequently exceeded in monitoring or with a documented link to negative effects (e.g., nitrates, THM, mercury),

-

medium priority (rank 3): parameter of significant toxicological importance, but less frequently exceeding normative values (e.g., chromium),

-

low priority (rank 1–2): copper, manganese, iron—mainly local exceedances and aesthetic/technological problems, less toxicological and health significance.

The information and data contained in Table 1 are used for mapping the results (Stages 5–6).

Table 1 presents five priority levels (ranks 1–5) with corresponding action instructions. These levels serve as a decision dictionary and do not constitute input data for calculations. Later in the paper, the FPI values determined from the preference matrix are mapped to these levels using a membership function (Step 3) and then translated into actions presented in Step 6.

The main advantage of the method is its simplicity and transparency—each parameter is assigned a numerical value, which makes it easy to compare the entire set and rank the threats. Its disadvantage is a certain subjectivity in assigning weights, depending on the criteria adopted and the knowledge of the evaluator. Therefore, in the future, the authors plan to supplement the methodology with a quantitative risk assessment (HQ, HI, CR), which ensures greater reliability and comparability of results between different water supply systems.

2.2.2. Stage 2. Analysis of Decision Rules

In the second stage, the assessment criteria should be determined on the basis of as much data as possible and information on possible parameter exceedances, their negative impact on human health (toxicity, carcinogenicity, possible sensitive groups), frequency of occurrence in monitoring results, consequences of their presence in the water supply network and in internal building installations, technological and social effects (e.g., deposits, consumer complaints, operator costs). The criteria taken into account are presented in Table 1.

It is assumed that the set A = {a_i, a_j,…, a_n} is the set of analysed water quality parameters, and at this stage, at least three independent experts select the most dangerous parameter or rank them from the most dangerous to the least dangerous (a queue of parameters is established) based on the proposed criteria (Table 1—Stage 1). The decision-making experts compare the parameters in pairs, which is intended to reduce the possibility of error. For each expert k, an additive mutual fuzzy preference relation (FPR) is created in the form of a matrix.

In order to facilitate the formulation of preferences (a_ij) of one parameter in relation to another j, the following rating scale (linguistic description) in the range [0, 1] is proposed:

-

absolutely more dangerous (absolute preference): a_ij = 0.9

-

definitely more dangerous: a_ij = 0.80

-

significantly more dangerous: a_ij = 0.70

-

slightly more dangerous: a_ij = 0.55

-

equally dangerous: a_ij = 0.50

Additional mandatory assumptions for the model:

• The sum of preferences ai relative to a_j and a_j relative to a_i is equal to one, i.e., there is so-called additive reciprocity: (a_ij) + (a_ji) = 1 for all i ≠ j.
• Diagonal: a_ii = 0.5 for all i.
• Accepting the relationship (a_ji) = 1 − (a_ij) and (a_ii) = 0.5 creates a fuzzy relation (of preference) with the membership function μ_A (a_i, a_j).

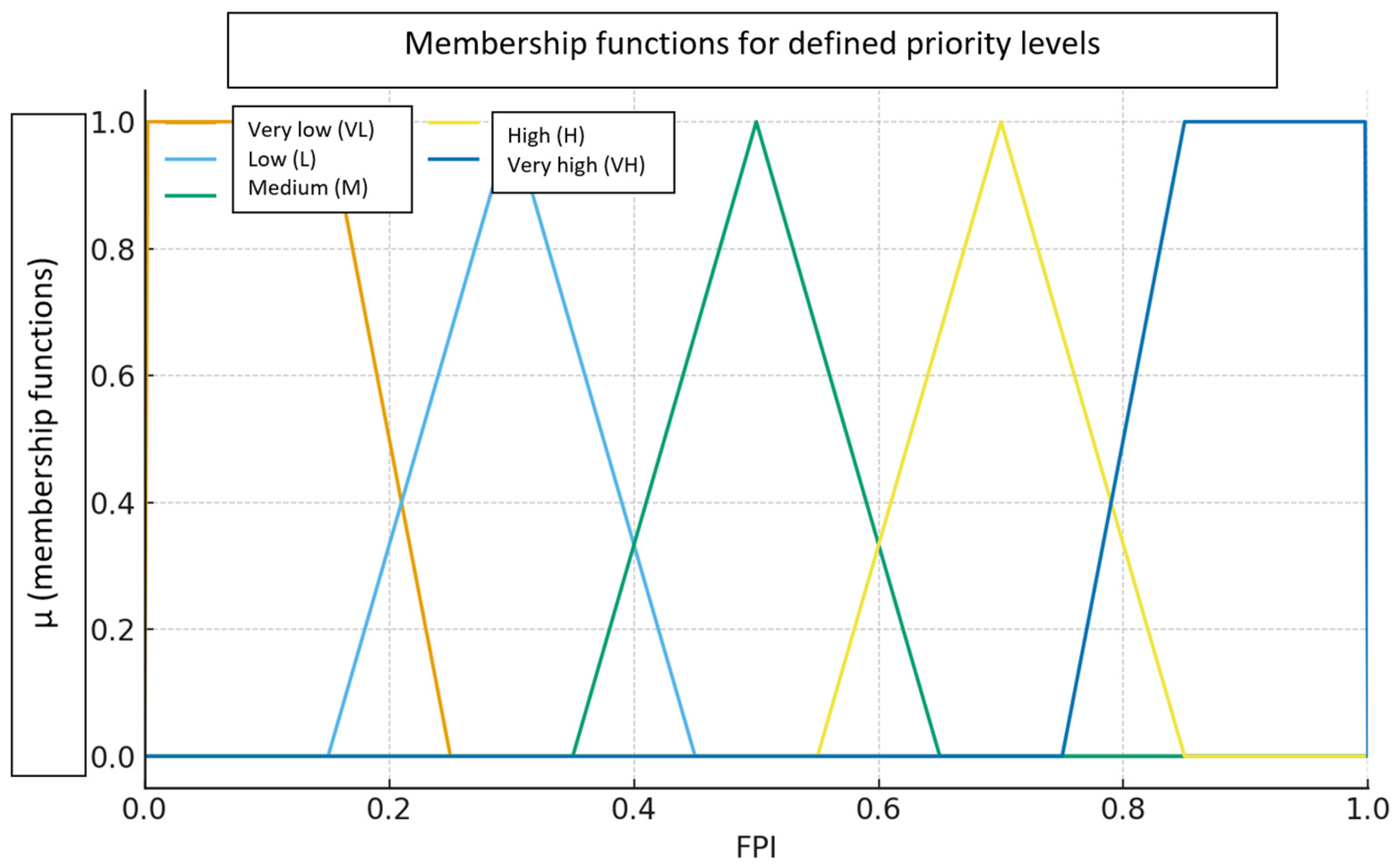
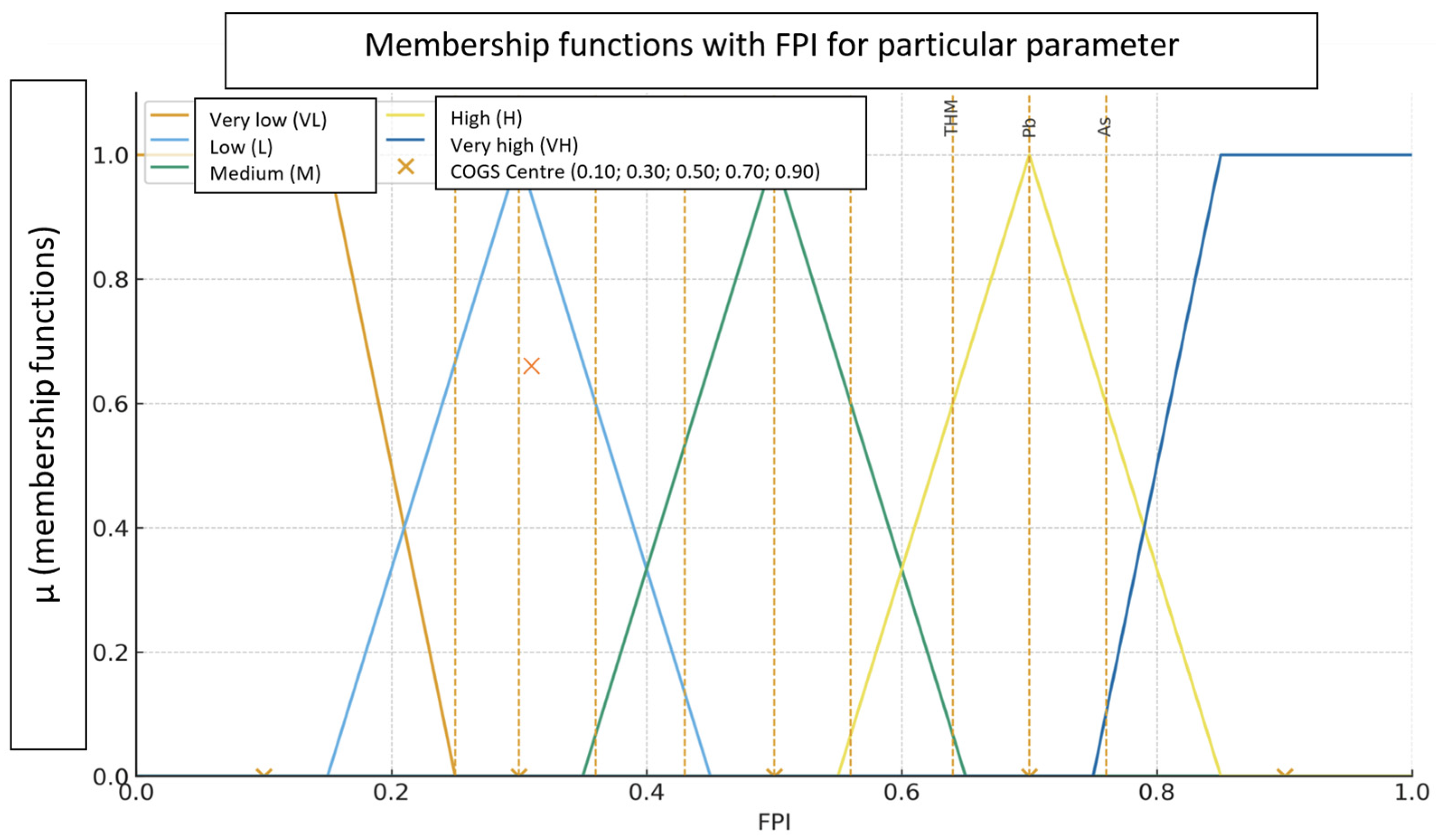
2.2.3. Stage 3. Selection of Membership Functions (μ) for the Adopted Priority Categories and Defuzzification Using the Centroid of Singletons Method (A Priori Calibration)

This stage involves determining a priori the membership function μ_A(x) for five priority levels A ∈ {VL, L, M, H, VH} on the x = FPI ∈ [0, 1] axis. The Formulas (1) and (2) for membership functions μ_A [26,27,28,29,30,31] were used.

The argument of the function was taken as x = FPI ∈ [0, 1] (fuzzy priority index).

The following membership functions were defined depending on the priority level:

-

Very low (VL)—trapezoidal ⟨a = 0.00, b = 0.00, c = 0.15, d = 0.25⟩, (centre C = 0.10)

-

Low (L)—triangular ⟨a = 0.15, b = 0.30, c = 0.45⟩, (centre C = 0.30)

-

Medium (M)—triangular ⟨a = 0.35, b = 0.50, c = 0.65⟩, (centre C = 0.50)

-

High (H)—triangular ⟨a = 0.55, b = 0.70, c = 0.85⟩, (centre C = 0.70)

-

Very high (VH)—trapezoidal ⟨a = 0.75, b = 0.85, c = 1.00, d = 1.00⟩, (centre C = 0.90).

Extreme levels are described by the arms of a trapezoidal function (stable full membership at very low/high FPI), and intermediate levels by a triangular function with vertices b = {0.30, 0.50, 0.70}. Care was taken to ensure overlap between adjacent functions and full coverage of the scale [0, 1], so that the boundary values could have non-zero membership in two adjacent levels.

Figure 2 shows the membership functions μ_A(x) for all priority levels on the axis x = FPI ∈ [0, 1].

In order to assign a parameter to a single, specific membership function and determine its position between levels, a defuzzification process using the singleton method (centroid for singletons—COGS) was applied. Each level A was assigned a fixed centroid C ∈ {0.10, 0.30, 0.50, 0.70, 0.90} (VL, L, M, H, VH, respectively). For parameter i with a given value FPI_(i), the Score was calculated according to the Formula (3) [26,27,28,31]:

$${\mathrm{S}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}}_{\mathrm{i}}={\displaystyle \frac{{\sum }_{\mathrm{A}}{\mathsf{\mu }}_{\mathrm{A}}\left({\mathrm{F}\mathrm{P}\mathrm{I}}_{\mathrm{i}}\right)·\mathrm{C}}{{\sum }_{\mathrm{A}}{\mathsf{\mu }}_{\mathrm{A}}\left({\mathrm{F}\mathrm{P}\mathrm{I}}_{\mathrm{i}}\right)}},$$

(3)

The sharpening process is not mandatory, but it is recommended to perform it so that the results obtained can be adapted to specific operational activities.

2.2.4. Stage 4. Construction of the Preference Matrix

A fuzzy relation is a set of pairs A = {(μ(_A) (a_i, a_j), (a_j, a_n))}, where μ_A is a membership function of a fuzzy relation, assigning each pair (a_i, a_j), a ∈ A, its degree of membership μ_A (a_i, a_j) ∈ [0, 1], which is a measure of the intensity of the fuzzy relation between i and j.

Based on the set of parameters, a preference matrix A = [a_ij] was created, where a_ij is the degree to which i has a higher priority than j. The matrix contains values in the range [0, 1]. A higher value in a row means that a given parameter has a higher priority than the column, the matrix is mutually complementary.

The construction of the preference matrix is presented in Formula (4) [26,27,28].

$$\mathrm{A}({\mathrm{a}}_{\mathrm{i}},{\mathrm{a}}_{\mathrm{j}})\left[\begin{array}{c}\begin{array}{cc}\begin{array}{cc}{\mathrm{a}}_{11}& {\mathrm{a}}_{12}\\ {\mathrm{a}}_{21}& {\mathrm{a}}_{22}\\ {\mathrm{a}}_{31}& {\mathrm{a}}_{32}\\ {\mathrm{a}}_{\mathrm{n}1}& \dots \end{array}& \begin{array}{cc}{\mathrm{a}}_{13}& {\mathrm{a}}_{1\mathrm{n}}\\ {\mathrm{a}}_{23}& \dots \\ {\mathrm{a}}_{33}& \dots \\ \dots & {\mathrm{a}}_{\mathrm{n}\mathrm{n}}\end{array}\end{array}\end{array}\right]$$

(4)

where i = 1, 2, …, n; j = 1, 2, …, n.

Experts fill in the upper triangle of the matrix (all pairs i < j). For each pair of elements (i, j), the three expert ratings are aggregated using the median, yielding a_ij. Then, reciprocity is created in the matrix based on: a_ji = 1 − a_ij and a_ii = 0.5. The result is an additively reciprocal matrix A = [a_ij], where a_ij ∈ [0, 1].

Table 2. Example of a preference matrix for selected comparisons of water quality parameters.

	As	Pb	THM	…
As	0.5	a12	a13	…
Pb	1 − a12	0.5	a23	…
THM	1 − a13	1 − a23	0.5	…
…	…	…	…	…

presents an example of the construction of a preference matrix for selected water quality parameters.

When, in the stage of evaluating the process of pairwise comparison of water quality parameters, we use more than one expert opinion (the method proposes 3 experts), sets of numbers {aije} are created for each pair (i, j). It is then necessary to use the median to create a single value $\overline{a_{\mathrm{i}\mathrm{j}}}$ (expert aggregation) according to Formula (5) [26,27,28]:

$$\overline{{\mathrm{a}}_{\mathrm{i}\mathrm{j}}}=\mathrm{m}\mathrm{e}\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{n}\mathrm{a}({\mathrm{a}}_{\mathrm{i}\mathrm{j}}^{\left(1\right)},\dots ,{\mathrm{a}}_{\mathrm{i}\mathrm{j}}^{\left(\mathrm{m}\right)})$$

(5)

where

• ${\mathrm{a}}_{\mathrm{i}\mathrm{j}}^{\mathrm{k}}$—expert assessment, e = 1, …, m:
• m—number of experts.

Determining the median prevents individual extreme opinions from “overturning” the result, increases confidence in the opinions of other experts, and provides a single, consistent input for determining the FPI.

2.2.5. Stage 5. Aggregation of Results—Determination of the Fuzzy Priority Index (FPI)

For each analysed water quality parameter (row i of the preference matrix A = [a_ij]), the “Fuzzy Priority Index” (FPI) value was determined as the average of its advantage over the other analysed parameters. This index provides a synthetic description of how high the priority of a given water quality parameter is in comparison with other parameters. The FPI result takes the form of a number in the range [0, 1]. In this method, it was assumed that the closer the FPI is to 1, the higher the priority.

The FPI is represented by formula (6), where n is the number of analysed parameters [32,33,34]:

$$\mathrm{F}\mathrm{P}\mathrm{I}={\displaystyle \frac{{\mathsf{\Sigma }}_{\mathrm{j}\ne \mathrm{i}}\overline{{\mathrm{a}}_{\mathrm{i}\mathrm{j}}}}{\mathrm{n}-1}}\in [0,1],$$

(6)

where n—number of parameters analysed.

Table 3. Priority categories for water quality parameters based on the FPI.

FPI Range	Priority Category
<0.20	Very low (VL)
0.20–0.40	Low (L)
0.40–0.60	Medium (M)
0.60–0.80	High (H)
≥0.80	Very high (VH)

proposes the following priority categories for water quality parameters based on the FPI value.

Due to the fact that the index is normalized to [0, 1], it is possible to perform comparative analyses for other water supply systems, trend analyses (temporal/seasonal) and benchmarking between cities.

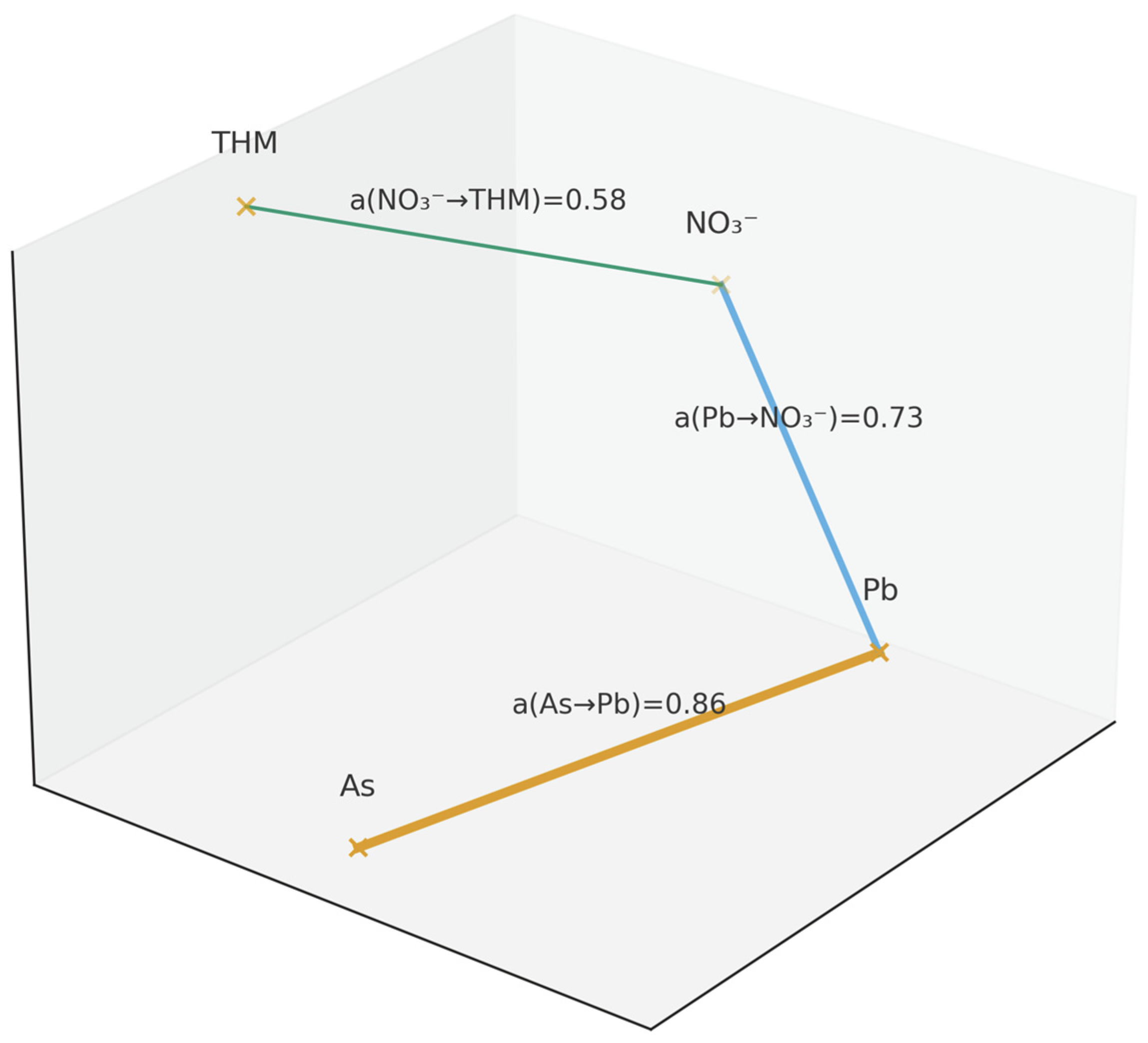
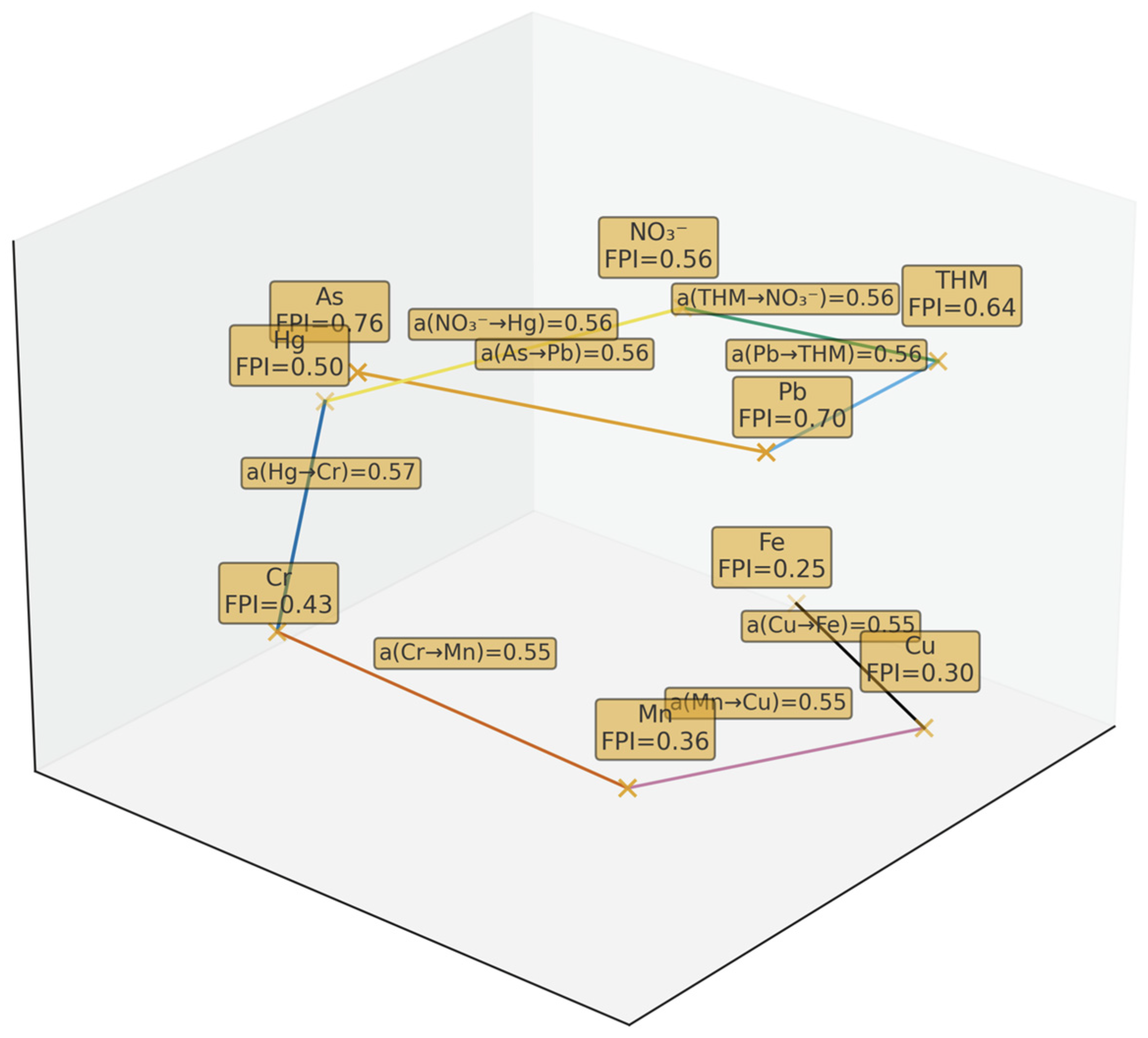
2.2.6. Stage 6. Mapping Actions and Creating a Fuzzy Queue of Water Quality Parameters

The final stage is the implementation of corrective action instructions depending on the FPI values obtained and the results of the priority categories.

The proposed FPI ranges and action instructions are presented in

Table 4. Proposed operational measures based on the FPI and water quality parameter priority categories.

FPI Range	Priority Category	Proposed Actions
<0.20	Very low (VL)	Routine monitoring; action only in response to complaints/aesthetic nuisances.
0.20–0.40	Low (L)	Planned monitoring; analysis in case of upward trends; local action.
0.40–0.60	Medium (M)	Periodic in-depth investigations; source analysis; targeted corrosion/precursor control.
0.60–0.80	High (H)	Increased monitoring frequency; optimisation/implementation of removal technologies (e.g., GAC, membranes, denitrification); notifications in case of exceedances.
≥0.80	Very high (VH)	Immediate corrective action; possible suspension of supply/switching of source; advanced technologies; priority reporting and supervision.

, created on the basis of Table 1 in Stage 1.

The methodology is complemented by the creation of a “fuzzy queue” graph ranking water quality parameters based on the proposed methodology.

Figure 3 shows an example of a fuzzy queue graph for selected water quality parameters (graphical visualizations were performed using Python v.3.11.).

Description for Figure 3:

-

The nodes (crosses with labels) are water quality parameters arranged in descending order according to FPI (from highest priority to lowest).

-

The edges connect neighbours in the ranking—they show how strong the local advantage of the previous parameter over the next one is.

-

The edge label is in the form a(i → j)—this is a value from the preference matrix: the degree to which parameter i is more important/dangerous than neighbouring parameter j (a ∈ [0, 1]; 0.50 ≈ tie).

-

The thickness of the line is proportional to the strength of the preference a(i → j): the thicker the line, the greater the advantage.

-

The colour of the line is used to visually distinguish between levels of strength (see legend); in the black and white version, line thickness + value label are used.

The result of Stage 6 is a map of operational activities assigned to specific parameters and a clear visualization of the queue showing both the order and strength of the local advantages of the analysed parameters—a result ready for reporting to decision-makers and for operational implementation.

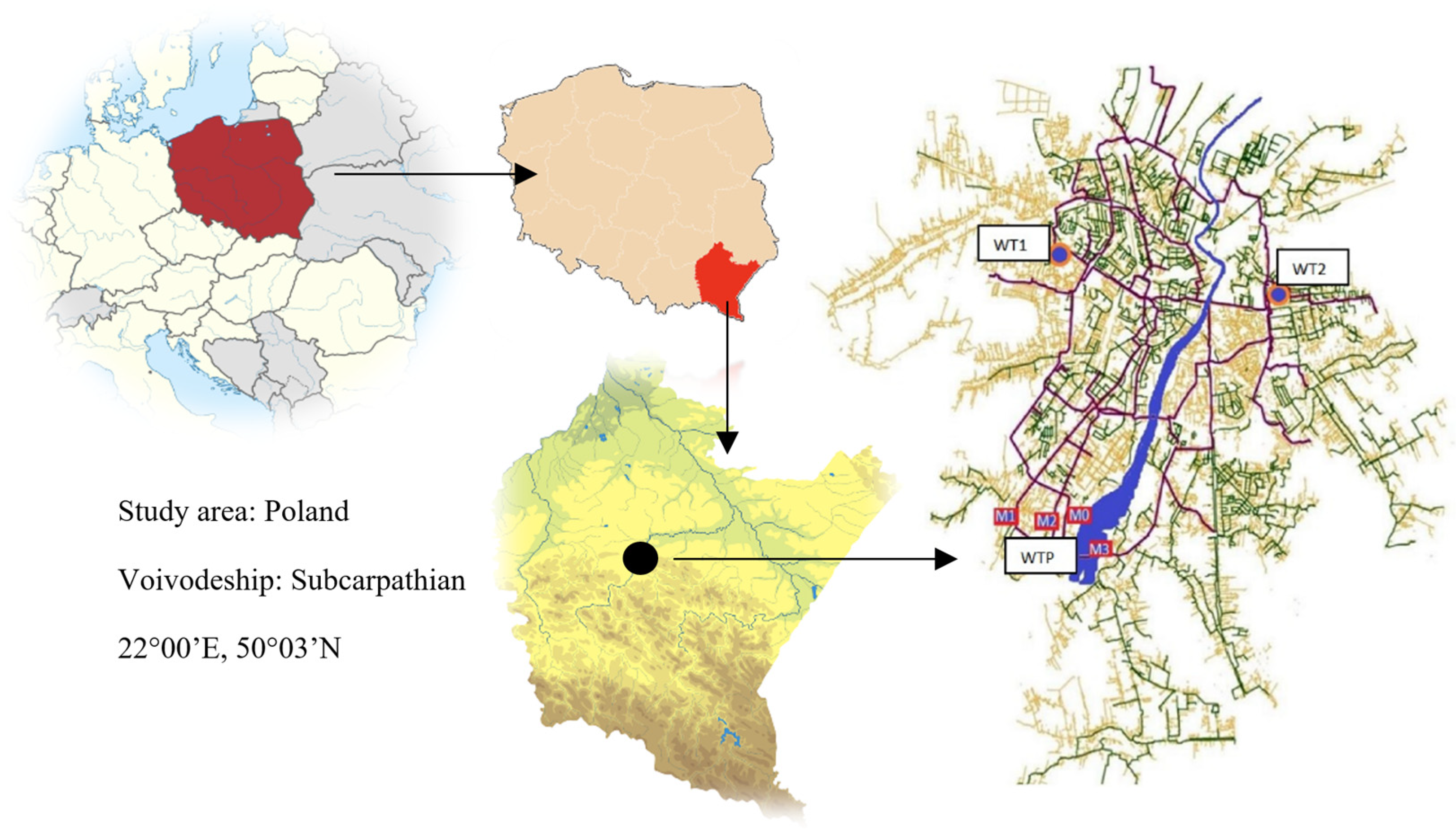
3. Characteristics of the Study Object

The study area is a voivodeship capital located in south-eastern Poland, within the Sandomierz Basin and the catchment of the Wisłok River—a left-bank tributary of the San River. The region’s hydrographic and geomorphological setting, combined with dynamic urban development, strongly influences the design, operation, and modernization of the city’s water supply infrastructure. According to the Central Statistical Office, the city’s population in 2024 was 198,317, with a clear upward trend driven by industrial growth, internal migration, and administrative boundary expansion. This growth increases water demand and necessitates continuous upgrades and extensions of the water supply system.

The collective water supply system (CWSS) is operated by a municipal utility responsible for the water and sewer networks across the city. The supply area is highly urbanized and features a diverse consumer profile, including public buildings (administration, schools, kindergartens, universities, hospitals and clinics), multi-family and single-family housing, hotels, and commercial/service facilities. Water is abstracted from a surface water intake on the river in the southern part of the city—a typical mountain river characterized by variable flows and water quality—and conveyed to two parallel treatment lines, Water Treatment Plant I (WTP I) and Water Treatment Plant II (WTP II), also located in the south. Together, the plants provide an average daily capacity of 84,000 m³/d (WTP I: 36,500 m³/d; WTP II: 47,500 m³/d) [37,38,39].

The treatment train is designed to meet European and national drinking-water requirements and currently comprises the following processes [37,38,39]:

(1)

Initial ozonation—oxidation of colour, taste, and odour compounds and initial disinfection (ozone generated from oxygen);

(2)

Coagulation (aluminium salts)—removal of colloids and poorly settling suspensions affecting turbidity and colour (e.g., humic substances, silica, organic pollutants);

(3)

Sedimentation in horizontal settling tanks—separation of flocs formed during coagulation;

(4)

Filtration through sand and anthracite–sand beds—removal of fine particulates;

(5)

Intermediate ozonation—further oxidation of residual colour/taste/odour compounds and reinforcement of disinfection;

(6)

Granular activated carbon (GAC) filtration—removal of dissolved organics and reduction of selected micro-pollutants;

(7)

UV pre-disinfection—enhancement of microbiological stability, improvement of organoleptic qualities, and reduction in chlorination doses;

(8)

Final disinfection with chlorine compounds (chlorine dioxide and chlorine gas)—ensuring sanitary quality in the distribution network; chlorine dioxide is produced in situ from sodium chlorite and chlorine gas;

(9)

pH correction using sodium carbonate (as needed)—mitigation of corrosivity in the distribution system.

From the WTPs, water is pumped into the municipal transmission and distribution network via a zoned pressure system stabilized by pump sets and strategically located retention reservoirs. This arrangement enables effective pressure and supply management across areas with varied topography and building heights. The mains include a primary “0” main (Φ1200–Φ800 mm) and mains no. “1–4” (Φ400 mm), with a total main length of ~98.4 km (cast iron and steel). The distribution network (cast iron, steel, PE, PVC) extends ~676.7 km, and service connections total ~341.8 km; combined network length with connections is about 1116.9 km. An alternative asset inventory (as of 31 December 2022) reports a total of 1140.66 km, comprising 99.11 km of mains, 705.48 km of distribution pipes, and 336.07 km of service lines. Pipes in new sections are predominantly plastic materials compliant with the Regulation of the Minister of Health of 7 December 2017 on the quality of materials in contact with drinking water [8] ensuring increased corrosion resistance, lower hydraulic losses, and longer service life.

The CWSS includes 43 pumping stations (hydrophores), 18 reservoirs with a total capacity of ~53,000 m³, 10 public street springs, and 179 emergency wells. The operator maintains an integrated water quality control system that covers raw-water monitoring at the intake and WTP (including a protective station safeguarding the intake against accidental contamination), comprehensive testing of treated water entering the network, and routine sampling at defined control points located throughout the distribution system and at network extremities.

Overall, the analysed network is an excellent example of a medium-sized urban water supply system that combines traditional infrastructure elements (e.g., cast-iron/steel trunk mains) with modern operational solutions (e.g., GAC, UV, ozonation, zoned pressure management). This makes it a valuable and highly representative research site for assessing distribution system reliability, analysing failure risks and associated environmental and social impacts, testing renovation strategies, including trenchless technologies, evaluating the carbon footprint of water and wastewater infrastructure modernization and implementing decision-support tools such as water-supply risk maps. The urban context, mounting climate-related stresses, and increasing network loads underscore the site’s relevance for studies on sustainable water management in medium-sized cities across Central and Eastern Europe.

Figure 4 presents the location of the study object.

4. Results

In order to present the operation of the proposed methodology, an application example was prepared based on nine water quality parameters: arsenic (As), lead (Pb), nitrates (NO₃⁻), total trihalomethanes (THM), mercury (Hg), chromium(VI) [Cr(VI)], manganese (Mn), copper (Cu) and iron (Fe). The set was selected to reflect key health risk mechanisms (As, Pb, Cr(VI), THM, Hg), frequent operational dilemmas (Mn, Fe, Cu) and real network conditions (NO₃⁻) encountered in medium-sized water supply systems. As a result, the study covers both parameters of high toxicological significance and those that clearly affect operation, communication with consumers and costs.

The input assessments for the preference matrix were obtained from three independent experts representing the areas of water quality, risk management and water supply networks. The experts did not communicate with each other, and their judgements were collected in a manner that ensured the independence of their opinions. Further steps—aggregation (median), enforcement of additive reciprocity, determination of the FPI, fuzzy categorisation and defuzzification—were carried out exactly according to the six-step methodology described in Section 2.2. The example was broken down into stages to ensure full consistency with the methodology and maximum clarity for the recipient (network operator, reviewer and decision-maker).

The application example analysed nine commonly reported water quality parameters: nitrates (NO₃⁻), lead (Pb), arsenic (As), mercury (Hg), chromium (Cr—including Cr(VI) toxicity), copper (Cu), manganese (Mn), iron (Fe), total trihalomethanes (THM).

The selection of these indicators was based on:

-

regulatory significance—all are included in the catalogue of parameters of Directive (EU) 2020/2184 [7], with specified parametric values (Part B—chemical parameters; Fe and Mn as indicator parameters in Part C) or monitoring guidelines.

-

the diversity of risk-creating mechanisms, which allows for reliable testing of the proposed prioritisation methodology:

• carcinogenicity (As, Cr(VI), part of DBP/THM),
• neurotoxicity and developmental effects (Pb, Hg, Mn),
• acute effects in infants (NO₃⁻),
• gastrointestinal effects and metallic taste (Cu),
• nuisances/secondary operational risks (Fe, Mn).

-

operational challenges in European water supply systems: corrosion and metal leaching from installations, water ageing, seasonal variability of NO₃⁻ parameters, prevailing hydraulic conditions.

-

availability of data from routine water quality monitoring programmes for water supply systems, which facilitates the use of the method in other cities.

Table 5. Set of selected analysed parameters.

Parameter	Risk Group	Health/Operational Justification	Regulatory Comments (WHO/DWD) [1,6,7,8]
Nitrates (NO3−)	Inorganic pollutants (agriculture)	Methaemoglobinaemia in infants; possible thyroid disorders; strong	WHO: 50 mg/L; DWD: 50 mg/L
Lead (Pb)	Heavy metal (installation materials)	Developmental neurotoxicity, increased cardiovascular RR; release from lead fittings and fixtures	DWD: 5 μg/L from 12 January 2036 (until then 10 μg/L; 5 μg/L when using new materials in internal installations).
Arsenic (As)	Metalloids (geogenic)	Carcinogen (skin, bladder, lungs); chronic exposure	WHO: 10 μg/L DWD: 10 μg/L
Chromium (Cr; toxicologically mainly Cr(VI))	Heavy metal	Caution regarding carcinogenicity	DWD: 25 μg/L from 2036 (until then 50 μg/L)
Copper (Cu)	Metal (installation materials)	Potential hepatotoxicity with chronic exposure; depends on pH/alkalinity and water stagnation in pipes	DWD: 2 mg/L
Manganese (Mn)	Metal (water supply network material)	Neurodevelopmental risk in children, sediment formation, discolouration; promotes biofilm formation	DWD: indicator value 50 μg/L (indicator parameter—operational significance)
Iron (Fe)	Metal (water supply network material)	Nuisance (colour, taste), deposits, risk of secondary quality degradation; significant impact on consumer complaints	WHO: parameter Aesthetic DWD: indicator 200 μg/L
THM—total	Disinfection by-products (DBPs)	Increased risk of bladder cancer (chronic exposure); dependent on water temperature and age	WHO: individual guidelines DWD: total 100 μg/L (chloroform, bromoform, dibromochloromethane, bromodichloromethane).

summarizes the water quality parameters included in the analysis, together with the reasons for their selection.

The next stage of the calculations involves the assessment of water quality parameters by three independent experts, taking into account the pairwise comparison scale and linguistic description proposed in point 2 of the Methodology. The expert panel consisted of three professionals with more than 20 years of experience in critical water infrastructure—design engineers, utility operators, and water sector managers. Their backgrounds combine academic, operational, and regulatory perspectives, covering expertise in water quality management, public health risk, and infrastructure operation. The expert panel was international and interdisciplinary, which enabled a comprehensive interpretation of priorities relevant to real-world systems. The assessment was based on potential health consequences (toxicology, epidemiology, vulnerable groups), exposure to a given parameter, professional practice of experts, operational activities (impact on treatment technology/water supply network operation, costs and corrective measures taken).

Pairwise comparisons were made based on the following assumptions:

-

a_ij ∈ [0, 1]—degree of preference of i over j.

-

additive reciprocity: a_ij + a_ji = 1 for i ≠ j

-

diagonal in the matrix: a_ii = 0.5 (no preference for i over i).

-

only ratings for pairs i < j (upper triangle) were collected. Values for j < i were automatically reconstructed based on the rule: a_ji = 1 − a_ij.

Table 6. Experts’ ratings for 36 comparison pairs for the analysed water quality parameters.

Comparison Pair Number	Parameter_i	Parameter_j	Expert Assessment 1	Expert Assessment 2	Expert Assessment 3	Median
P01	As	Pb	0.57	0.56	0.53	0.56
P02	As	THM	0.59	0.59	0.63	0.59
P03	As	NO3−	0.70	0.66	0.68	0.68
P04	As	Hg	0.77	0.76	0.76	0.76
P05	As	Cr	0.74	0.82	0.79	0.79
P06	As	Mn	0.82	0.88	0.86	0.86
P07	As	Cu	0.90	0.90	0.90	0.90
P08	As	Fe	0.90	0.90	0.90	0.90
P09	Pb	THM	0.56	0.56	0.57	0.56
P10	Pb	NO3−	0.59	0.63	0.60	0.60
P11	Pb	Hg	0.71	0.71	0.67	0.71
P12	Pb	Cr	0.76	0.75	0.73	0.75
P13	Pb	Mn	0.80	0.82	0.76	0.80
P14	Pb	Cu	0.89	0.86	0.87	0.87
P15	Pb	Fe	0.90	0.90	0.90	0.90
P16	THM	NO3−	0.53	0.58	0.56	0.56
P17	THM	Hg	0.63	0.58	0.63	0.63
P18	THM	Cr	0.65	0.67	0.69	0.67
P19	THM	Mn	0.77	0.73	0.76	0.76
P20	THM	Cu	0.80	0.78	0.80	0.80
P21	THM	Fe	0.85	0.85	0.85	0.85
P22	NO3−	Hg	0.54	0.60	0.56	0.56
P23	NO3−	Cr	0.66	0.59	0.57	0.59
P24	NO3−	Mn	0.68	0.71	0.64	0.68
P25	NO3−	Cu	0.73	0.69	0.70	0.70
P26	NO3−	Fe	0.79	0.79	0.77	0.79
P27	Hg	Cr	0.58	0.56	0.57	0.57
P28	Hg	Mn	0.63	0.64	0.59	0.63
P29	Hg	Cu	0.69	0.70	0.67	0.69
P30	Hg	Fe	0.75	0.76	0.78	0.76
P31	Cr	Mn	0.62	0.55	0.55	0.55
P32	Cr	Cu	0.61	0.61	0.64	0.61
P33	Cr	Fe	0.66	0.71	0.65	0.66
P34	Mn	Cu	0.54	0.55	0.55	0.55
P35	Mn	Fe	0.64	0.58	0.59	0.59
P36	Cu	Fe	0.59	0.53	0.55	0.55

presents expert assessments for 36 comparative pairs for the analysed water quality parameters.

Based on the results obtained, a complete preference matrix A was drawn up in accordance with Formula (1), as shown in

Table 7. Additively mutual fuzzy preference matrix A = [$\overline{{\mathrm{a}}_{\mathrm{i}\mathrm{j}}}$] after aggregation by the median of expert ratings.

	As	Pb	THM	NO3−	Hg	Cr	Mn	Cu	Fe
As	0.50	0.56	0.59	0.68	0.76	0.79	0.86	0.90	0.90
Pb	0.44	0.50	0.56	0.60	0.71	0.75	0.80	0.87	0.90
THM	0.41	0.44	0.50	0.56	0.63	0.67	0.76	0.8	0.85
NO3−	0.32	0.40	0.44	0.50	0.56	0.59	0.68	0.7	0.79
Hg	0.24	0.29	0.37	0.44	0.50	0.57	0.63	0.69	0.76
Cr	0.21	0.25	0.33	0.41	0.43	0.50	0.55	0.61	0.66
Mn	0.14	0.2	0.24	0.32	0.37	0.45	0.50	0.55	0.59
Cu	0.10	0.13	0.20	0.30	0.31	0.39	0.45	0.50	0.55
Fe	0.10	0.10	0.15	0.21	0.24	0.34	0.41	0.45	0.50

.

Based on the created preference matrix A = [$\overline{{\mathrm{a}}_{\mathrm{i}\mathrm{j}}}$], the numerical priority index FPI was determined (Formula (3)). Then, the parameters were ranked from the most to the least important based on the criteria proposed in Table 3, point 2.

Using Formulas (1), (2) and (6), the FPI was determined, the membership function values for each of the five priority categories were determined, and using Formula (3), the defuzzification process was carried out using the singleton method, which made it possible to refine the obtained results to the final values, which were related to the proposed priority category levels. The results are summarized in

Table 8. Membership function values for μ_A for the five priority levels adopted and the Score (COGS) defuzzification result for the analysed water quality parameters.

Parameter	FPI	μ(VL)	μ(L)	μ(M)	μ(H)	μ(VH)	Score (COGS)
As	0.76	0.00	0.00	0.00	0.60	0.10	0.73
Pb	0.70	0.00	0.00	0.00	1.00	0.00	0.70
THM	0.64	0.00	0.00	0.07	0.60	0.00	0.68
NO3−	0.56	0.00	0.00	0.60	0.07	0.00	0.52
Hg	0.50	0.00	0.00	1.00	0.00	0.00	0.50
Cr	0.43	0.00	0.13	0.53	0.00	0.00	0.46
Mn	0.36	0.00	0.60	0.07	0.00	0.00	0.32
Cu	0.30	0.00	1.00	0.00	0.00	0.00	0.30
Fe	0.25	0.00	0.67	0.00	0.00	0.00	0.30

.

Figure 5 shows the membership functions of five priority levels (VL, L, M, H, VH) over the FPI axis [0–1]: extreme sets—trapezoidal (VL, VH), middle sets—triangular (L, M, H). The crosses mark the COGS centres (0.10, 0.30, 0.50, 0.70, 0.90). Vertical dashed lines show FPI values for the analysed parameters (As 0.76; Pb 0.70; THM 0.64,; NO₃⁻ 0.56; Hg 0.50; Cr 0.43; Mn 0.36; Cu 0.30; Fe 0.25).

For borderline FPI values (e.g., FPI = 0.70), partial membership occurs in two adjacent categories (e.g., ‘High (H)’ and ‘Very High (VH)’), which is handled by defuzzification using the centroid of singletons method to assign the final label and operational guidance.

The designated FPI indicators, priority level categories and Score values were used in the decision mapping process.

Table 9. Decision-making process.

Parameter	FPI	Score	Priority Category	Operational Activities
As	0.76	0.72	High (H)	Immediate corrective action; suspension of supply or switching of source; implementation of advanced technologies (adsorption, membranes); priority monitoring and reporting.
Pb	0.7	0.7	High (H)	Elimination of the source (replacement of lead installations, corrosion control); child health protection programmes; intensive monitoring and consumer information.
THM (total)	0.64	0.68	High (H)	Optimization of the disinfection process (contact time, chloramination, DBP precursors); implementation of technologies limiting the formation of THM (GAC, ozone, biological filtration); monitoring at network points.
NO3−	0.56	0.52	Medium (M)	Monitoring in agricultural areas; identification of sources of inflow (sewage, fertilisers); alternative water sources for infants; implementation of desalination/denitrification in treatment.
Hg	0.5	0.50	Medium (M)	Increased monitoring frequency; identification of pollution sources; implementation of reduction technologies (e.g., ion exchange); notifications in case of exceedances.
Cr	0.43	0.46	Medium (M)	Periodic monitoring; testing of industrial sources; contingency plan in case of increased concentrations; implementation of reduction technologies (e.g., reduction of Cr(VI) to Cr(III) + coagulation).
Mn	0.36	0.32	Low (L)	Regular flushing of the network; use of filtration in treatment plants; measures mainly in the case of aesthetic problems and secondary contamination.
Cu	0.3	0.3	Low (L)	Monitoring of internal installations (corrosion of copper pipes); operational recommendations (flushing the network, pH control); measures in the event of prolonged exceedances.
Fe	0.25	0.3	Low (L)	Measures to reduce deposits and colour (iron removal, network flushing); response to consumer complaints; maintaining the aesthetics and acceptability of water.

presents a set of actions depending on the results obtained (the selection of examples of actions is in line with operational practice and can be modified based on the technological processes used and the prevailing hydraulic conditions in the water supply network in order to perform a comparative analysis of other water supply systems).

Table 9 presents the decision-making process: tested water quality parameter → priority category → operational actions (based on Stage 5).

Figure 6 shows a fuzzy queue graph of the nine analyzed water quality parameters depending on the prioritization process carried out.

5. Discussion

The resulting priority ranking is consistent with toxicological knowledge and operational experience. At the top of the list are parameters with proven serious health effects: arsenic (FPI 0.76), lead (0.70) and total THM (0.64). They are followed by nitrates (0.56), whose importance increases during agricultural seasons and with increased rainfall intensity. In the second half of the ranking, we have mercury (0.50) and chromium (0.43), and at the end manganese (0.36), copper (0.30) and iron (0.25)—parameters that are usually less hazardous to health in treated water, but important in terms of operation (colour, sediment, corrosion). The differences between neighbouring parameters in the ranking are moderate (usually 0.05–0.08), which indicates a systematic but not very “rapid” advantage of successive positions; in practice, this means that under certain local conditions, some places in the queue may change.

The fuzzy layer reflects this continuity well. The FPI of each substance was converted into a “soft” priority category (very low—very high) using triangular and trapezoidal membership functions, and then converted into a continuous value using the “Score” function (singleton centroid). As a result, the results were not classified in steps, but showed how close a given parameter actually is to the “higher end”. For example, arsenic (0.76) lies in the “High” area with a clear proximity to “Very high”, lead (0.70) is exactly at the top of “High”, and THM (0.64) is at the upper part of “High”. The “fuzzy graph” confirms this interpretation: the edges between neighbours have preference values of around 0.55–0.57 (a moderate but steady advantage), while extreme pairs (e.g., As vs. Fe) achieve high values, which clearly explains the position of the most dangerous and least dangerous parameters.

From the point of view of the water supply company’s operations, the conclusions are clear. For As, Pb and THM (category “High”), it is recommended to increase the frequency of testing and take specific technological measures: for arsenic—refinement of coagulation and/or adsorption, for lead—control of corrosivity and phosphates, together with measures on connections and installations inside buildings, for THM—reduction of precursors (DOC) and shortening of the “water age” in the network. Nitrates (“Medium”) require a seasonal approach and control of the combined condition with nitrites. Mercury and chromium (“Medium”) suggest vigilance and targeted testing (e.g., Cr speciation), while manganese, copper and iron (“Low”) suggest consistent system maintenance (flushing, sediment management, corrosivity), with readiness to intervene in the event of local problems.

Compared to popular index-based (FWQI, fuzzy-WQI) or weighting-based (fuzzy-AHP) approaches, the proposed solution stands out in that it is based on simple, direct pairwise comparisons in a fuzzy preference relationship. Instead of assuming fixed weights in advance, we use expert judgements in pairs and ensure mathematical consistency through additive reciprocity. The FPI is derived from these relationships as the “average advantage” of one parameter over others, which is clear, easy to explain and comparable between cities or systems. The fuzzy layer (categories + Score) bridges the gap between uncertainty and decision: from the numerical result, we move directly to the priority level and the assigned action instruction.

To compare the obtained FPI ranking with the classic index approach, a rank correlation analysis was performed with the traditional Water Quality Index (WQI). WQI values for the nine analysed parameters were calculated according to the methodology presented by WHO, using maximum allowable values as reference values. The obtained rankings were then compared using Spearman’s rank correlation coefficient (ρ). The analysis revealed a monotonic correlation between the FPI ranking and the classic WQI ranking (ρ = 0.78), confirming the consistency and validity of the proposed prioritization method in the context of classic index approaches.

The proposed methodology introduces an additive fuzzy preference relation (FPR) framework that eliminates the need for predefined criterion weights and complex hierarchical structures typical of fuzzy-AHP approaches. Mutual expert preference relations are applied in accordance with the principle of additive reciprocity, ensuring interpretability and mathematical consistency of pairwise comparisons. Unlike conventional fuzzy-WQI methods that aggregate water quality into a single index, the approach produces a hierarchical ranking of parameters, which is subsequently mapped to actionable operational strategies through a structured decision map. A distinctive feature of the method is the incorporation of a fuzzy queue graph, providing a clear and intuitive visualization of relationships between adjacent parameters and the strength of their relative preferences—an element absent in standard fuzzy-FMEA implementations. The methodology is auditable and robust against variability in individual expert judgments through median-based aggregation of pairwise assessments. The entire computational pipeline—FPR → FPI → fuzzy membership mapping → defuzzification via COGS → operational actions—is transparent, replicable, and optimized for practical implementation in water safety management.

The presented method indicates which parameters require immediate response, which translates into simple operating instructions, and at the same time remains simple enough to implement that it can be realistically applied in the company’s work cycle and the results communicated between stakeholders.

6. Conclusions

In contrast to the widespread index (FWQI, fuzzy-WQI) and weighting (fuzzy-AHP) approaches, this study uses direct, additive pairwise comparisons of water quality parameters in relation to fuzzy preferences (FPR) and proposes the FPI for constructing a ranking of threats to drinking water. Rather than proposing a fundamentally new mathematical model, this contribution should be understood as a structured and operational framework that allows water supply operators to integrate expert knowledge into an auditable, flexible, and reproducible pipeline for decision-making. The FPI results were mapped to five priority levels (membership functions) and then, after defuzzification using the singleton centroid method (COGS), transformed into specific operational instructions. The combination of elements into the sequence “FPI → fuzzy category → action” for drinking water quality parameters is a novelty with clear practical utility.

The proposed methodology provides a mathematically consistent, transparent and replicable prioritization procedure. The additive mutual preference relation provides a formal and data-efficient description of expert judgements, while FPI creates a stable and comparable hierarchy. The fuzzy layer (membership functions + centroid) enables a smooth transition from uncertainty to operational risk categories and their mapping to actions. The method is scalable (from one to many criteria), easy to calibrate to WHO/DWD requirements, and amenable to sensitivity analysis, making it a valuable tool for both research and implementation in water supply security management.

The novelty of the approach lies in the integration of FPI with fuzzy categorization and the creation of an operational action map. The index reduces subjectivity: instead of rigid weights of 1–5, we use pair-wise relationships, thus combining toxicology, frequency and scale of exceedances, and operational factors into a single result.

The method works for different sets of parameters and network layouts (just update the list of parameters and perform pairwise comparisons); it accepts different panel compositions and numbers of experts (≥3), and median aggregation increases resistance to extreme judgements, it allows calibration of membership functions and category thresholds to local safety policies, WHO/DWD limits and the needs of vulnerable groups, it is auditable—each a_ij has a clear interpretation, and FPI is a clear “average advantage” of one parameter over others, can be automated (spreadsheet/software) and repeated periodically, creating a “fuzzy queue” for planning research, technological activities and investments.

The Spearman correlation (ρ = 0.78) obtained between the FPI ranking and the classic WQI-based ranking confirms that the FPR/FPI method leads to similar conclusions to established indicator approaches. However, it also allows for more flexible consideration of expert knowledge, uncertainty, and dynamic safety thresholds. The high agreement between the approaches indicates the potential for their complementary use in water quality management practice.

The final ranking and fuzzy category assignments are largely consistent with current WHO and EU regulatory priorities, while also revealing practical differences shaped by expert experience and operational sensitivity—particularly for mid-priority parameters such as NO₃⁻, Hg, and Cr. This highlights the method’s value not only in confirming formal risk hierarchies but also in refining them based on real-world conditions.