Reliability Assessment of Long-Service Gravity Dams Based on Historical Water Level Monitoring Data

Abstract

This paper addresses the challenge of systemic extreme risk in long-service gravity dams under human-controlled operation. It is the first study to construct a Generalized Extreme Value (GEV) distribution model using long-term operational monitoring data. The model, validated by multiple statistical tests and engineering boundary conditions, is then applied within a Response Surface Method-Monte Carlo (RSM-MC) reliability framework. Results indicate that the historical GEV model accurately captures the high-water-level tail characteristics and significantly overcomes the risk underestimation inherent in the uniform distribution model. Compared to the Log-Pearson Type III (Log-P3) design condition model, the GEV model yields a significantly lower probability of failure, e.g., the probability of cracking at the dam heel, the most sensitive failure mode, is reduced by nearly six times. This quantitative difference fully demonstrates GEV’s ability to precisely quantify the effective risk reduction achieved by human control, establishing a more scientific and realistic foundation for risk assessment of long-service gravity dams.

1. Introduction

Reservoir water level is the core load for gravity dams, and its variation is crucial to structural reliability [1,2]. Traditional design loads are determined based on the statistical extremes of the original natural hydrological sequence. However, water levels in long-service dams are modified and influenced by human-controlled operation procedures, creating a unique sequence of systemic operational extremes. The probability distribution of this sequence is distinctly different from the original natural sequence [3,4], yet it directly reflects the actual load risk the structure is exposed to during real operation. Therefore, scientifically utilizing long-term historical monitoring data to infer the true water level load distribution during the operational period is a major challenge for accurate risk assessment [5]. For long-service hydraulic structures, accurate risk assessment also involves the precise detection and quantification of potential structural damage and defects [6,7], which is a rapidly developing field relying on advanced vision-guided and deep learning techniques [8,9].

To address this challenge, authoritative international organizations, such as the U.S. Bureau of Reclamation (USBR), emphasize in their risk analysis guidelines that the randomness and uncertainty of hydrological loads must be systematically quantified and managed based on historical operation data to enable scientific risk-informed decision-making [10].

In response to this demand for uncertainty-based risk decision-making, safety assessment methods for gravity dams have evolved and can be broadly divided into three levels: The first level primarily uses the traditional deterministic Factor of Safety method [11]. This approach simplifies loads and resistances to deterministic values, ignoring their inherent randomness and uncertainty, making it difficult to accurately assess the true safety level [12]. The second level is based on stochastic reliability theory, where critical loads and resistances are treated as random variables. Computational methods like the Response Surface Method (RSM) are used to solve for the partial reliability index [13,14,15]. These reliability methods heavily depend on the accuracy of structural response and material parameters. Significant research has focused on improving this accuracy, including advanced techniques for dam deformation data preprocessing and long-term parameter identification [16,17,18], alongside developing novel stochastic inverse approaches and explainable probabilistic models for health monitoring [19,20]. The third level, represented by Monte Carlo simulation (MCS) or stochastic finite element methods [21,22], directly computes the probability of failure at a low probability level through extensive random sampling.

Although the second and third levels of reliability methods have made significant progress in computational accuracy and efficiency [23,24,25], they remain limited by the accuracy of the load input random variables. Current research still exhibits limitations in handling the critical water level load: First, some studies continue the first-level approach by adopting the normal pool level or design flood level as deterministic parameters [26,27]. Second, in second- and third-level computations, simple uniform or normal distributions are often used as proxies for the actual systemic operational water level sequence [21,22]. Both simplifications fail to accurately reflect the extreme characteristics of the operational water level sequence in long-service dams under human control.

This paper aims to solve the problem of accurately quantifying the true load risk for the water level in long-service gravity dams. It systematically constructs and applies for the first time a GEV model based on long-term operational monitoring data to precisely quantify the systemic annual maximum water level extreme load, which combines natural randomness with human constraints. This load is then introduced as a core random variable into the reliability calculation framework. This research provides a new paradigm for operational recalibration of hydraulic structure risk, leading to a more scientific and realistic assessment of the safety level of long-service gravity dams.

2. Water Level Load Distribution Model

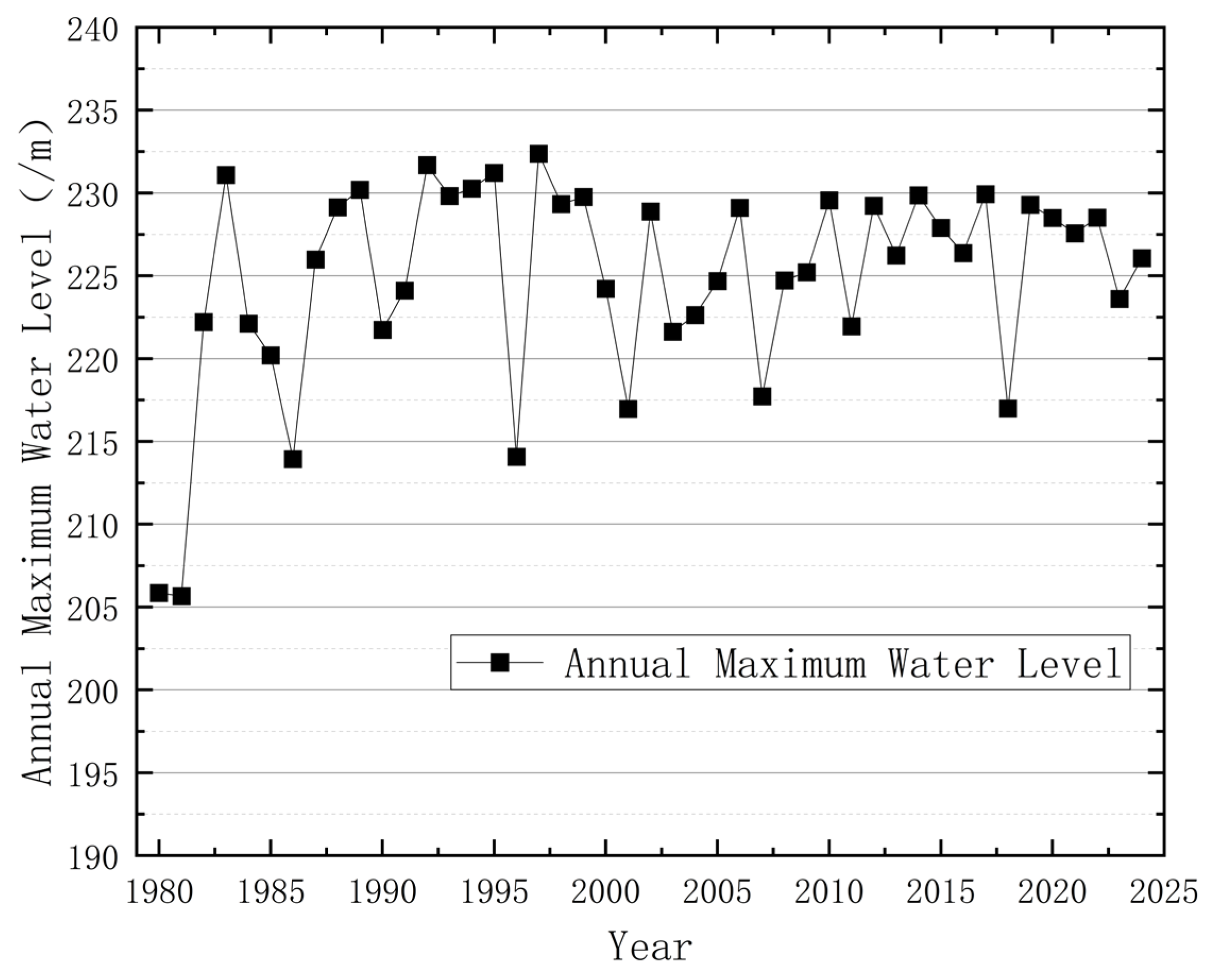
2.1. Historical Water Level Statistical Characteristic Model

Current reliability assessments often use engineering design characteristic water levels as deterministic parameters. However, the actual conditions after long-term operation are inevitably different from the original design parameters. Although the Code for Hydrological Computation of Water Resources and Hydropower Projects (SL44—2006) mandates periodic re-evaluation of characteristic floods [28], the establishment of the operational water level probability model has not been systematically incorporated into the project safety appraisal process.

Referencing the USBR risk analysis guidelines [10], this paper constructs an annual maximum exceedance probability curve using historical reservoir water level data to infer the probability of a given water level being exceeded. The specific procedure is as follows:

First, the annual maximum water level dataset is extracted from multiple years of daily or annual reservoir maximum water level records.

Next, a suitable probability distribution model must be selected and fitted to this dataset. The USBR guidelines recommend common distributions, including the Generalized Extreme Value (GEV) distribution, Log-Pearson Type III distribution, and Gumbel distribution. This paper adopts the Generalized Extreme Value (GEV) distribution, which is primarily determined by three parameters: location $\mu$, scale $\sigma$, and shape $\xi$. The Cumulative Distribution Function (CDF) for GEV is:

$$F(x;\mu ,\sigma ,\xi )=\exp \left\{-{\left[1+\xi \left({\displaystyle \frac{x-\mu }{\sigma }}\right)\right]}^{-1/\xi }\right\}$$

(1)

where $1+\xi (x-\mu )/\sigma >0$.

The GEV parameters are typically estimated using the Maximum Likelihood Estimation (MLE) method. Once the parameters are determined, the water level corresponding to a specific exceedance probability can be found by inverting the CDF. The formula is:

$$E_p=\mu -{\displaystyle \frac{\sigma }{\xi }}\left[1-{(-\ln (1-p))}^{-\xi }\right]$$

(2)

The preceding steps are repeated to ultimately obtain a smooth annual maximum exceedance probability curve. This curve provides a quantitative basis for the safety assessment of hydraulic structures and is a vital component of risk analysis.

2.2. Robustness and Uncertainty Validation for Model Parameter Estimation

To adhere to the USBR guideline’s requirement for quantifying hydrological load uncertainty, this paper employs the Bootstrap resampling method to quantitatively assess the prediction error introduced by GEV parameter estimation. The primary goal is to quantify and establish the statistical reliability of high-return period extrapolation results.

The statistical principle of Bootstrap validation for extrapolation is [29]: the empirical distribution of the observed sample is taken as the optimal approximation of the population distribution. By repeatedly drawing a large number ($B$) of “pseudo-samples” $X^{(b)}$ with replacement from the original dataset $X=\{X_1,X_2,\dots ,X_n\}$, the GEV parameters ${\widehat{\Theta }}^{(b)}=\{{\widehat{\mu }}^{(b)},{\widehat{\sigma }}^{(b)},{\widehat{\xi }}^{(b)}\}$ are re-estimated for each pseudo-sample, thus yielding the water level prediction ${\widehat{x}}_T^{(b)}$ corresponding to the return period $T$:

$${\widehat{x}}_T^{(b)}={\widehat{\mu }}^{(b)}-{\displaystyle \frac{{\widehat{\sigma }}^{(b)}}{{\widehat{\xi }}^{(b)}}}\left[1-\left(-\ln \left(1-{\displaystyle \frac{1}{T}}\right)\right)\right]$$

(3)

Through $B$ repetitions, an empirical distribution of $B$ estimated water levels for the return period $\{{\widehat{x}}_T^{(1)},\dots ,{\widehat{x}}_T^{(B)}\}$ is formed. This non-parametric method directly quantifies the impact of parameter estimation variability on the extrapolation prediction. Based on this empirical distribution, a confidence interval (CI) can be calculated using the percentile method:

$$C{I}_{1-\alpha }=\left[{\widehat{x}}_T^{*(\alpha /2)},{\widehat{x}}_T^{*(1-\alpha /2)}\right]$$

(4)

where ${\widehat{x}}_T^{*(q)}$ is the q-th quantile of the set of Bootstrap predicted values $\left\{{\widehat{x}}_T^{(b)}\right\}$. This CI provides quantifiable statistical reliability validation, strongly proving the robustness of the fitted GEV parameters and the reliability of the extrapolation.

However, traditional Maximum Likelihood Estimation (MLE) has inherent high variance and instability for the crucial shape parameter $\xi$ under small sample sizes [30,31]. The directly obtained CI is often overly wide. Therefore, to ensure the scientific and engineering validity of the extrapolation results, this paper adopts a prior information constraint practice commonly used in hydraulic engineering [32]: the Bootstrap fixed-shape parameter strategy. In each resampling, the shape parameter $\xi$ is fixed to the MLE estimate of the original dataset, and only the location $\mu$ and scale $\sigma$ parameters are re-estimated. Although fixing the shape parameter may introduce a certain bias, the primary engineering requirement for hydraulic risk assessment is ensuring the stability of extreme tail prediction and reducing the high variance associated with small sample sizes. This strategy effectively eliminates the uncertainty caused by fluctuation of $\xi$ under a small sample size, greatly enhancing the statistical robustness of the CI estimation. Therefore, this strategy maximizes the balance between statistical variance and engineering reliability requirements.

3. Gravity Dam Reliability Analysis Model

3.1. Failure Modes and Analysis Model

In gravity dam design, the core control indicators mainly include the stress state at the heel and toe of the dam and the sliding stability of the dam foundation. This paper uses the principles of reliability analysis to calculate the reliability index for three main failure modes: cracking at the dam heel, crushing at the dam toe, and sliding along the dam base. The failure criteria are determined by defining the limit state function $Z$ in accordance with the Design Specification for Concrete Gravity Dams (SL 319—2018) [33]. The structure is safe when $Z>0$, and failure occurs when $Z\le 0$.

1.

Failure by Cracking of the Plinth Heel:

The limit state function $Z_1$ is defined as the difference between the specified ultimate limit value for tensile strength of the plinth, $R_{\lim }$, and the vertical tensile stress in the plinth, $S_t$, under the load combination.

$$Z_1=R_{\lim }-S_t$$

(5)

where $R_{\lim }$ is the allowable tensile stress limit for the plinth as stipulated in standard SL319—2018. Based on the standard, this limit is 0.1 MPa, and it can be treated as a deterministic resistance threshold value. $S_t$ is the vertical tensile stress in the plinth under various load combinations.

2.

Failure by Crushing of the Plinth Toe:

The limit state function $Z_2$ is defined as the difference between the compressive strength of the concrete, $R_c$, and the maximum compressive stress in the plinth toe, $S_c$, under the load combination.

$$Z_2=R_c-S_c$$

(6)

where $R_c$ is the compressive strength of the concrete in the plinth body, and $S_c$ is the maximum compressive stress in the plinth toe under various load combinations.

3.

Failure by Sliding along the Foundation Plane:

The limit state function $Z_3$ is defined as the difference between the sliding resistance (Resistance $R$) and the sliding force (Load $S$).

$$Z_3=(f^{\prime }(W\cos \beta -U+P\sin \beta )+c^{\prime }A)-(P\cos \beta -W\sin \beta )$$

(7)

where $f^{\prime }$ and $c^{\prime }$ are the coefficient of sliding friction and the cohesion, respectively, along the plinth-foundation interface; $W$, $P$, and $U$ are, in order, the total vertical force on the plinth-foundation interface (excluding uplift pressure), the total horizontal force, and the uplift pressure. $A$ is the area of the plinth-foundation interface cross-section.

$W$ and $P$ are obtained by integrating the stresses acting on the foundation plane, based on the linear elastic finite element method.

3.2. Reliability Calculation Method

This paper adopts a reliability analysis framework combining the Response Surface Method (RSM) and Monte Carlo Simulation (MCS) to efficiently and accurately assess the probability of failure for the gravity dam.

The Response Surface Method is used for efficient approximation of the limit state function, aiming to solve the issue of low computational efficiency with the Finite Element Method. After multiple attempts, a 3rd-order polynomial with cross-terms is selected as the general response surface model, as shown below. Its advantage lies in its ability to capture high-order nonlinearity and coupled effects between multi-dimensional random variables.

$$Z(X)\approx c_0+{\displaystyle \sum _{i=1}^n{c}_i}{X}_i+{\displaystyle \sum _{i=1}^n{c}_{ii}}{X}_i^2+{\displaystyle \sum _{i=1}^n{c}_{iii}}{X}_i^3+{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=i+1}^n{c}_{ij}}}{X}_i{X}_j+{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=i+1}^n{\displaystyle \sum _{k=j+1}^n{c}_{ijk}}}}{X}_i{X}_j{X}_k$$

(8)

where $X=\{X_1,X_2,\dots ,X_n\}$ is the random variable vector composed of water level, material parameters, etc.; $n$ is the number of random variables; and c is the polynomial fitting coefficient. The accuracy of the response surface function will be measured and verified by the coefficient of determination $R^2$. The structural response values at the response surface sample points are computed using the self-developed Hstar_BA software from the research group, based on the linear elastic Finite Element Method.

After obtaining a high-precision response surface function, the Monte Carlo Simulation is used to calculate the structural probability of failure $P_f$ and the reliability index $\beta$. To improve computational efficiency and sample space coverage, Latin Hypercube Sampling (LHS) is chosen to generate random samples. LHS samples are converted through the Inverse Cumulative Distribution Function based on the probability distribution type of the random variables. Simultaneously, a re-sampling mechanism is employed for random variables with physical constraints, such as material strength, to ensure the physical validity of the samples. Finally, the generated $N$ sets of random samples are substituted into the response surface function $Z(X)$, and the probability of failure $P_f$ is calculated by counting the number of failed samples $N_f$ that satisfy $Z(X)\le 0$:

$$P_f={\displaystyle \frac{N_f}{N}}$$

(9)

Subsequently, the reliability index $\beta$ can be calculated from the probability of failure $P_f$:

$$\beta =-{\mathrm{\Phi }}^{-1}(P_f)$$

(10)

where ${\mathrm{\Phi }}^{-1}(·)$ is the inverse of the standard normal cumulative distribution function.

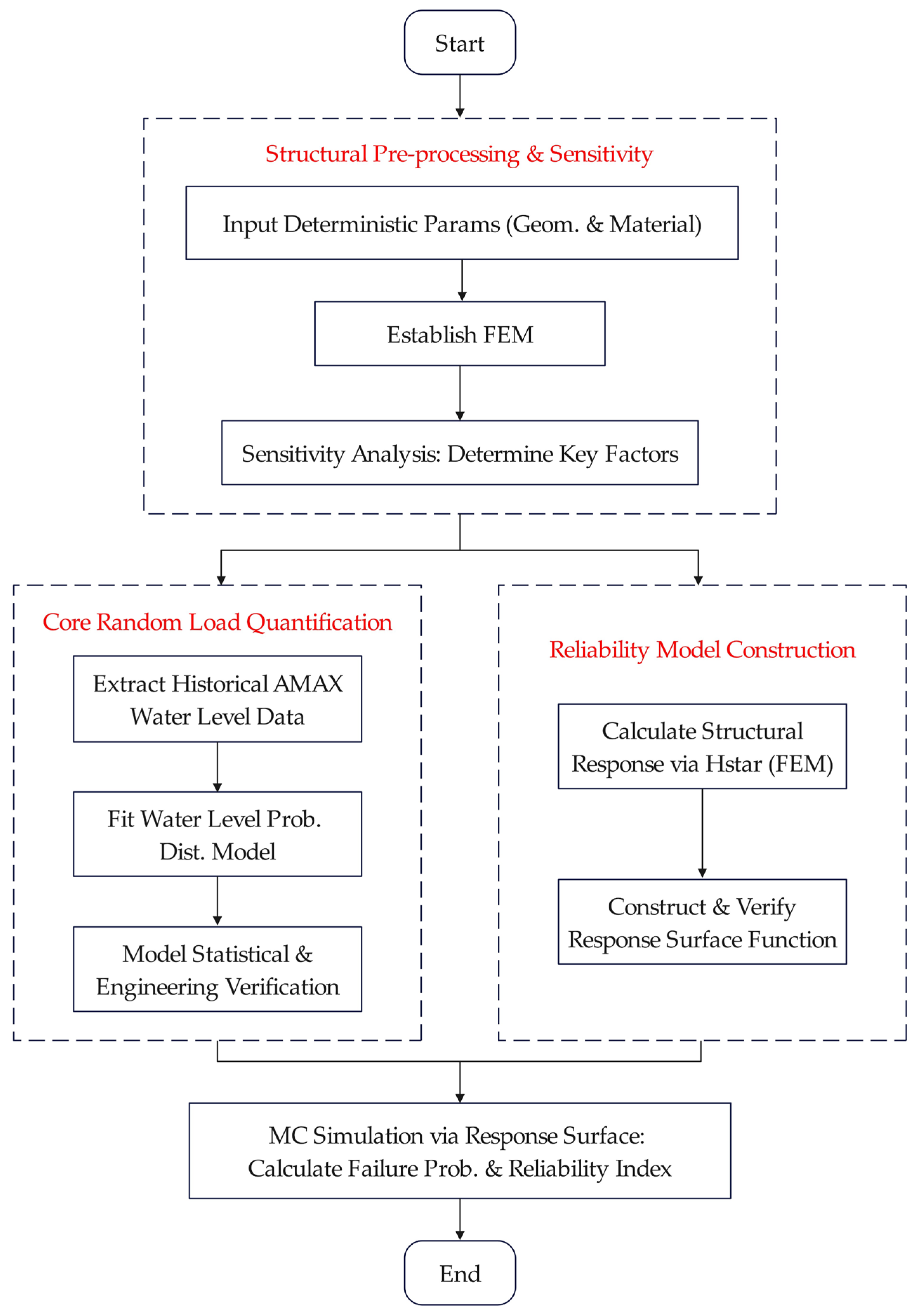
3.3. Integrated Reliability Analysis Framework Based on Historical Water Level Distribution

Based on the theories and methods described above, this paper establishes an integrated reliability assessment framework for long-service gravity dams based on historical water level distribution. The core process is shown in Figure 1.

This framework uses the historical GEV water level distribution quantified in Section 2 as the core random input, and employs the Response Surface Method and Monte Carlo Simulation from Section 3.2 to efficiently calculate the structural probability of failure under three limit states. This framework tightly couples hydrological analysis with structural reliability analysis, achieving a refined risk assessment based on actual operational loads.

4. Engineering Application

4.1. Project Overview

The Wuxijiang Hunan Town Hydropower Station is located in Quzhou City, Zhejiang Province, China, and serves as the first-tier power station on the upstream tributary of the Qiantang River. The project is classified as a Class I project, and the dam is a Grade 1 structure. Its primary function is power generation, while also providing comprehensive benefits such as flood control.

The reservoir’s dead water level is 190.0 m, the normal pool level is 230.0 m, the original design flood level is 238.0 m, and the check flood level is 240.25 m. The impounding dam is a concrete gravity buttress dam with a crest elevation of 242 m and a maximum height of 129 m.

4.2. Computational Model

This paper selects the #13 non-overflow dam section to establish a two-dimensional Finite Element (FE) model comprising the dam body and the dam foundation. The origin is chosen at the dam heel, with the x-axis pointing downstream as positive, and the y-axis pointing upward as positive. The foundation extends two times the dam height both to the base and to the upstream and downstream directions, as shown in Figure 2a. The model is partitioned into 8662 nodes and 8465 elements, as shown in Figure 2b. A vertical displacement constraint is applied to the bottom of the model, and horizontal displacement constraints are applied to both sides.

The computational model involves two materials: the dam body and the dam foundation, both treated as isotropic linear elastic materials. Based on project data, relevant literature [34], and preliminary parameter inversion results, the material parameters for calculation are tentatively set as shown in

Table 1. Preliminary material parameters table for dam body and foundation (linear elastic).

Material	Elastic Modulus (GPa)	Poisson’s Ratio	Unit Weight (kN/m3)
Dam Body	24	0.167	24
Dam Foundation	20	0.25	26

below:

The friction coefficient and cohesion between the dam body and dam foundation base surface are taken as 1 and 1058.4 kN/m², respectively, according to the engineering technical specification.

The selected calculation conditions are: The considered loads include self-weight, upstream and downstream water pressure, and dam base uplift pressure. Water pressure and uplift pressure are applied as surface forces. A vertical displacement constraint is applied to the bottom of the model, and horizontal displacement constraints are applied to both sides.

5. Discussion

5.1. Sensitivity Analysis

To identify the main factors affecting dam failure, this paper uses the Control Variable Method to perform stress and stability sensitivity analysis on the input parameters. The parameters considered include: unit weights, elastic moduli, and Poisson’s ratios of the dam body and foundation, as well as the upstream water level, friction coefficient, and cohesion.

The degree of influence of each parameter is quantified using a sensitivity index processed by a normalization formula, $(x-x_{min})/(x_{max}-x_{min})$. It is defined as the normalized change in structural response when a parameter changes from its minimum normalized value to its maximum normalized value. Since the change in structural response for each parameter is relatively smooth, it can be approximated by the secant slope.

The normalized sensitivity indices for each parameter under the three control criteria are shown in

Table 2. Normalized sensitivity indices for input parameters under three failure control criteria.

Control Indices	Unit Weight of Dam Body	Unit Weight of Dam Foundation	Elastic Modulus of Dam Body	Elastic Modulus of Dam Foundation	Poisson’s Ratio of Dam Body	Poisson’s Ratio of Dam Foundation	Upstream Water Level	Coefficient of Friction	Cohesion
Cracking at Plinth Heel	0.1380	0.0017	0.0586	−0.0704	0.0271	−0.0279	−0.7047	/	/
Crushing at Plinth Toe	0.0385	0.0019	0.0388	−0.0466	0.0140	−0.0150	0.3842	/	/
Sliding along Foundation Plane	0.0389	0.0012	−0.0047	0.0056	−0.0356	0.0118	−0.0921	0.3869	0.0003

below:

Selecting the parameters with significantly larger sensitivity indices as the main sensitive factors, the following is obtained: The primary sensitive factors for the cracking at the dam heel failure mode are the dam body unit weight and upstream water level; the primary sensitive factor for the crushing at the dam toe failure mode is the upstream water level; and the primary sensitive factor for the sliding along the dam base failure mode is the friction coefficient.

Therefore, the main sensitive factors for this dam are chosen as the dam body unit weight, upstream water level, and friction coefficient.

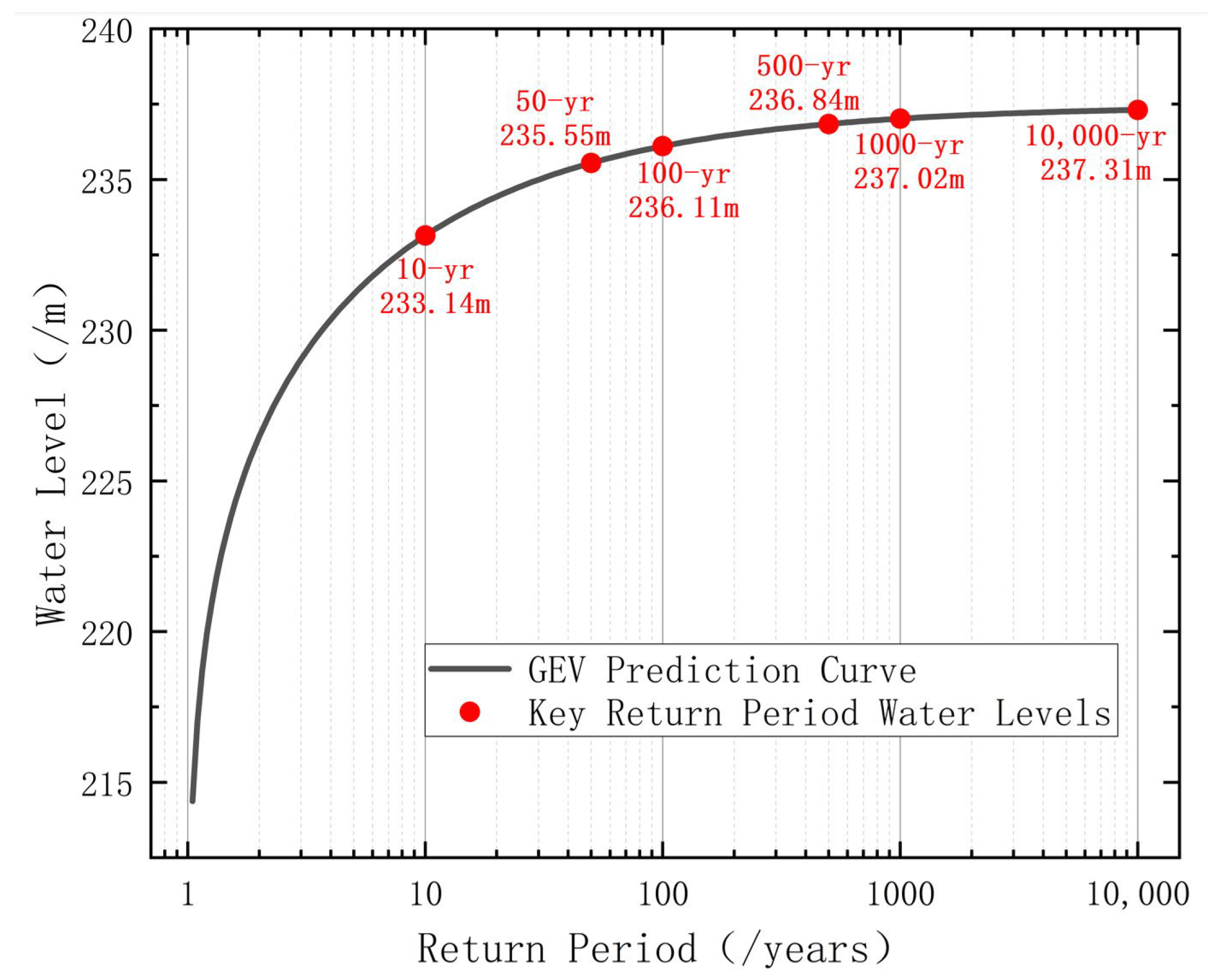
5.2. Historical Water Level Statistical Characteristic Analysis

The sensitivity analysis shows that the upstream water level is a primary sensitive factor, and its variation has a significant impact on the dam’s stress and stability reliability. Hence, this section aims to systematically construct and fit a reservoir water level probability distribution model using the long-term accumulated historical monitoring data to provide scientific and accurate random variable input for subsequent reliability analysis.

Figure 3 below displays the time series data of the annual maximum water level for the Wuxijiang Hunan Town Hydropower Station from 1980 to 2024, spanning 45 years.

Figure 3 reveals that the reservoir’s annual maximum water level exhibits significant randomness and volatility, indicating a high degree of uncertainty in the water level load borne by the dam during its long-term service. Therefore, incorporating the historical water level statistical model into the structural reliability assessment framework is highly necessary for achieving a more precise safety evaluation.

Following the USBR guidelines in Section 2.1, this paper performs an extreme value statistical analysis on the historical water level data. By using the Maximum Likelihood Estimation (MLE) method, multiple probability distribution models suitable for extreme value data are fitted, including Generalized Extreme Value (GEV), Gumbel, Log-Normal, Pearson Type III (Pearson3), and Log-Pearson Type III (Log-Pearson3). The fitting results are shown in Figure 4 below, where the blue discrete points represent the historical water level data, and the colored curves are the corresponding fitted distribution curves.

The Kolmogorov–Smirnov test (K-S test) is a non-parametric goodness-of-fit test used to assess the difference between the sample distribution and the theoretical distribution. Empirically, the fitting effect is considered good when the test statistic p-value is above 0.20 [35].

The p-values from the K-S test for the fitting effect of each distribution are shown in

Table 3. p-Values of the K-S test for different water level distribution models.

Model	p-Value
GEV	0.8246
Gumbel	0.0215
Log-Normal	0.2796
Pearson3	0.2841
Log-Pearson3	0.2876

below:

It is evident that the Generalized Extreme Value (GEV) distribution provides the best fit, effectively covering the overall trend of the historical water level data. Its three key Cumulative Distribution Function parameters are: location parameter $\mu$ = 224.2846, shape parameter $\xi$ = 0.5092, and scale parameter $\sigma$ = 6.5356. The annual maximum exceedance probability curve drawn from this is shown in Figure 5 below. This curve plots the predicted water level against the Return Period ($T$), where the Return Period ($T$) is the reciprocal of the Exceedance Probability ($P$), defined as $T=1/P$ (in years).

However, it should be noted that the K-S test statistic is primarily sensitive to the central body of the distribution and is generally less effective in verifying the fitting accuracy of the extreme tail, which is crucial for reliability analysis. Therefore, this study must further substantiate the rationality of its extreme value extrapolation through engineering and statistical validation in the following section.

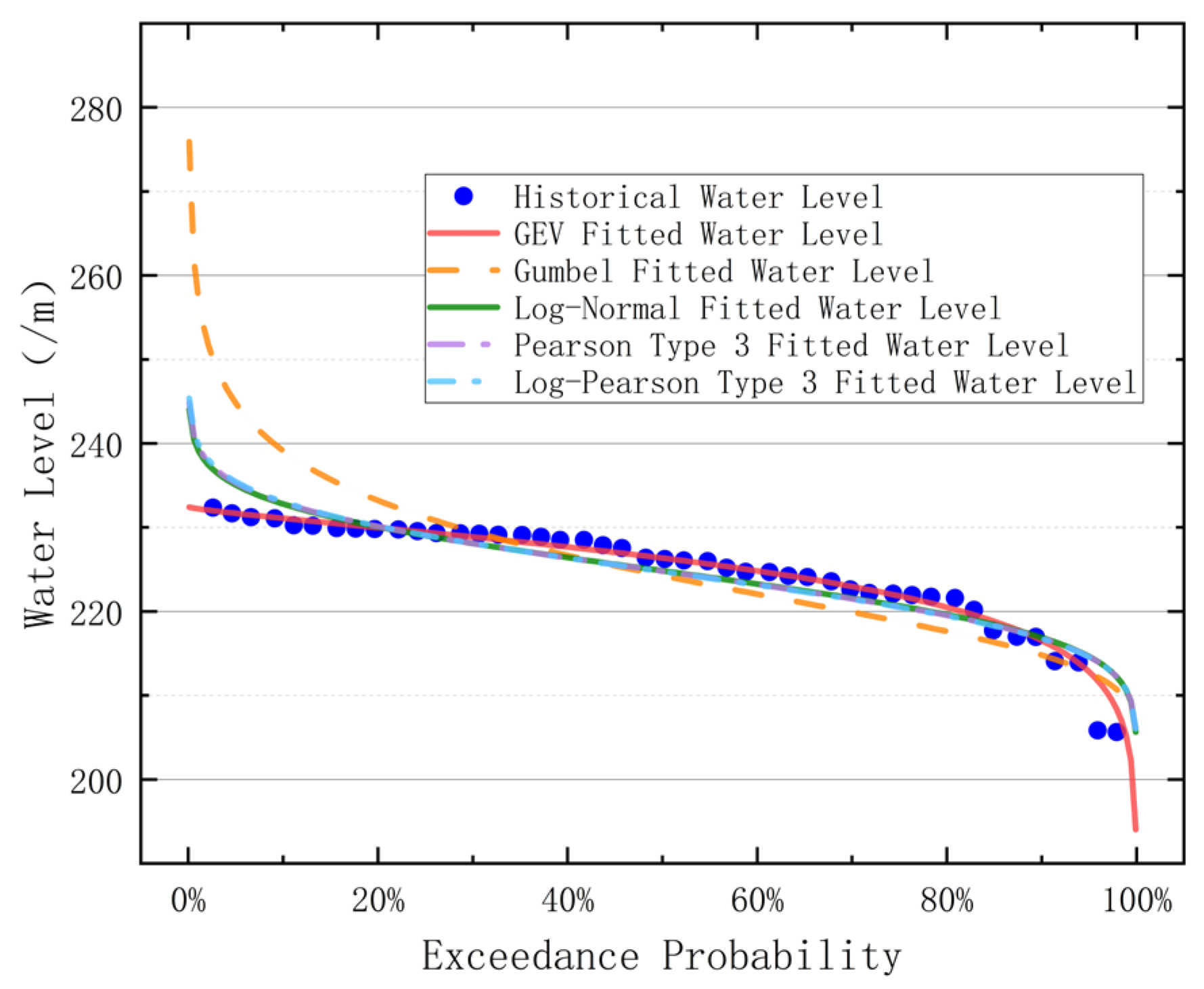
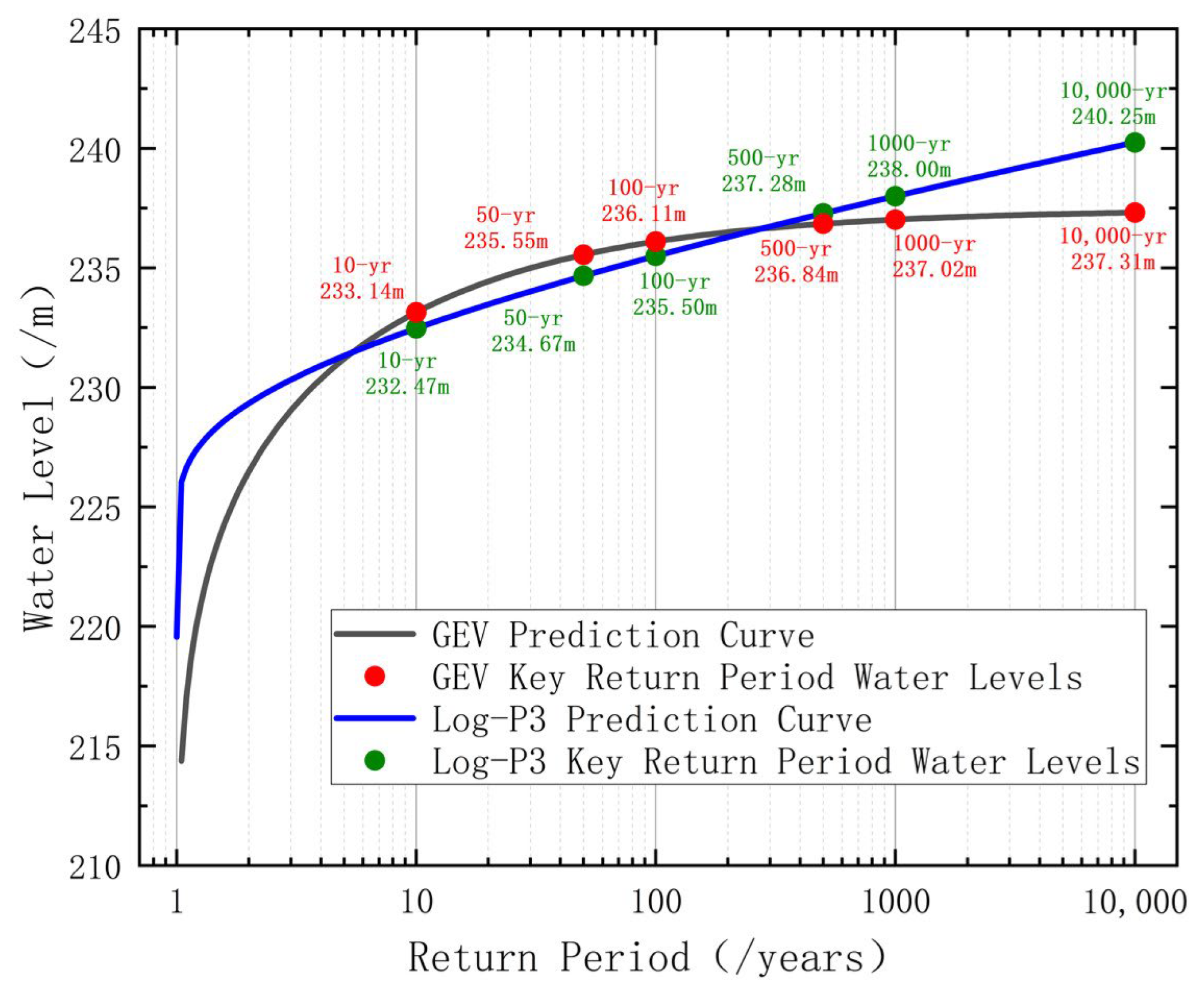
5.3. Rationale and Comparative Analysis of the GEV Water Level Model

Although the GEV model passed the K-S statistical test, the water level sequence of a long-service reservoir is significantly influenced by human control and operational procedures, so the rationality of extreme value extrapolation for the exceedance probability curve still requires demonstration.

This paper refers to the principles of the USBR guidelines to systematically demonstrate the effectiveness, uncertainty, and rationality of extreme value extrapolation based on historical water level data from the perspective of engineering system operation, thus ensuring its scientific validity as a load for reliability analysis.

1.

Engineering System Risk Positioning of Extreme Variables

The goal of risk assessment is to evaluate the probability of failure that may occur under the dam’s actual operational conditions, not the natural inflow itself. Therefore, the annual maximum water level in this study can be defined as the extreme load actually borne by the system under the stable constraint of the current reservoir operating rules and scheduling procedures. The GEV model here captures the probability distribution of the reservoir system’s operational extremes under the joint action of natural random input and human non-random intervention and the GEV model in this study relies on the stationarity assumption that reservoir operating rules have remained unchanged over the long term. Although the sequence is intervened, in the case of long-term service and unchanged operating rules, GEV is still considered the theoretical limit distribution model that describes this engineering system operational risk manifestation [6]. While climate change or management shifts could introduce non-stationarity, the assumption is reasonable for the current risk assessment due to the dam’s long service life and the absence of major operational regulation modifications. Future work will incorporate non-stationary analysis into the model to address these challenges.

2.

Robustness and Uncertainty Validation for GEV Model Parameter Estimation

Through the Bootstrap resampling method with the fixed shape parameter strategy from Section 2.2, a 95% confidence interval (CI) with high statistical reliability is calculated and shown in Figure 6 below. This confidence interval successfully quantifies the uncertainty of the prediction results. For example, the 95% CI for the 1000-year return period water level is [236.67, 237.77]. This result powerfully proves that, with the uncertainty of parameter estimation clearly quantified, the predicted extreme water levels remain constrained within a statistically reliable range, fully establishing the robustness of the parameter fitting and the scientific usability of the high-return period extrapolation results.

3.

Validation of Engineering Physical Boundary Constraints

The extreme value extrapolation results must be rational within the engineering design boundaries. Their rationality can be verified by comparing the GEV model extrapolation results with the original design water levels. For instance, the extrapolated 1000-year water level in this paper is 237.02 m, and the 10,000-year water level is 237.31 m. Both are distinctly lower than the reservoir’s original design flood level of 238 m and the check flood level of 240.25 m.

This result not only proves the engineering rationality of the extreme value extrapolation, but more crucially, it quantitatively refutes the idea that long-term operating procedures have an effective regulatory effect on extreme floods. This provides empirical support for evaluating and optimizing the dam’s actual operational management strategy, serving as positive feedback from historical operating data on the design safety margin. Therefore, the extrapolation results based on the system operational extremes are contained within the original design boundaries and are engineeringly acceptable.

To enable a quantitative comparison between the actual operational risk and the original design risk, this paper introduces the Log-Pearson Type III (Log-P3) distribution, a fundamental model in hydraulic engineering design codes, to represent the water level load under the original design conditions. The parameters of this model were fitted based on the natural hydrological sequence before the reservoir construction and are now inversely derived from the known design water levels for the dam, which are 235.50 m (100-year), 238.00 m (1000-year), and 240.25 m (10,000-year). Its Cumulative Distribution Function is as follows:

$$F(x)=I\left({\alpha }_g,{\displaystyle \frac{\ln (x)-{\xi }_g}{{\beta }_g}}\right)$$

(11)

where $I(·,·)$ is the normalized incomplete gamma function; and ${\alpha }_g$, ${\beta }_g$, and ${\xi }_g$ are the fitted parameters, which are 20.5205, 0.002163, and 5.3915, respectively.

Based on this model, the Log-P3 annual maximum exceedance probability curve for the design conditions is drawn and compared with the GEV annual maximum exceedance probability curve for the historical conditions, as shown in Figure 7 below:

The separation trend between the two curves clearly reveals the modifying effect of human control on different magnitudes of flood risk. In the low-return period region (10- to 100-year), the Log-P3 (natural sequence) water level is slightly higher than the GEV (actual operational sequence). This quantifies the effective constraint of routine operating procedures on small and medium floods, resulting in the reservoir system’s annual maximum water level being lower than the natural prediction value. As the return period increases, the two curves significantly separate, with the predicted water level of the Log-P3 model (representing original hydrological risk) being much higher than the GEV model. This high-return period difference powerfully reflects that the multiple systemic interventions, such as reservoir capacity regulation, flood discharge control, and emergency scheduling, have played a significant role in risk reduction for ultra-high return period floods. Therefore, the actual operational risk assessment based on the GEV model can more scientifically reflect the structure’s true safety level under long-term control.

In summary, this paper ultimately selects the Generalized Extreme Value (GEV) distribution as the core model for describing the randomness of the annual maximum water level at the Wuxijiang Hydropower Station. To systematically quantify the impact of different water level treatments on gravity dam reliability assessment, the subsequent analysis will compare the GEV model (fitted based on historical actual operational conditions) with the Log-P3 model (fitted based on design conditions) and the commonly used Uniform Distribution model. These three probability distribution forms will be used as the key random variables to fully reveal the differences in structural failure probability under different water level assumptions.

5.4. Reliability Analysis

Based on the parameter sensitivity analysis results, the main sensitive factors, dam body unit weight, upstream water level, and friction coefficient, are selected as random variables. For the upstream water level, the core random variable, the reliability calculation is performed separately using three probability distribution models: the Generalized Extreme Value distribution (fitted based on historical actual operational conditions), the Log-Pearson Type III distribution (fitted based on design conditions), and the commonly used Uniform distribution. The Uniform distribution uses the dead water level as the lower limit and the check flood level as the upper limit. The statistical characteristics of the other random variables are determined by combining on-site engineering survey data and relevant literature [36,37], and remain unchanged across the three water level distribution models. The specific statistical parameters are shown in

Table 4. Statistical characteristics of the main random variables in reliability analysis.

Random Variable	Unit	Distribution Type	Mean Value	Coefficient of Variation
Unit Weight of Dam Body	kN/m3	Normal Distribution	24	0.03
Coefficient of Friction	Dimensionless	Normal Distribution	1.2	0.22
Compressive Strength of Concrete	MPa	Normal Distribution	25	0.16

below:

The corresponding response values for the failure modes are obtained through 1000 calculations using the Stochastic Finite Element Method. 70% of the samples are used for response surface fitting, and the remaining 30% are used to verify the accuracy of the constructed response surface.

The functional expressions of the limit state functions for the three failure modes are as follows:

Failure by Cracking of the Plinth Heel:

$$Z_1=0.1-\left(\begin{array}{c}-374414.4503\\ +6644.5558H-631.8823\gamma \\ -50.3618H^2-0.0161{\gamma }^2-0.6019H\gamma \\ +1.4123H^3+0.0001H{\gamma }^2-0.0007H^2\gamma \end{array}\right)$$

(12)

Failure by Crushing of the Plinth Toe:

$$Z_2=R_c-\left(\begin{array}{c}-63266.2518\\ +845.7394H-161.8382\gamma \\ -44.3298H^2-0.0150{\gamma }^2+0.1847H\gamma \\ -0.4252H^3+0.0001H{\gamma }^2-0.0007H^2\gamma \end{array}\right)$$

(13)

Failure by Sliding along the Foundation Plane:

$$Z_3=\left(\begin{array}{c}-0.4658\\ +0.109966\gamma -0.014204H+2.187760f^{\prime }\\ -0.005801{\gamma }^2+0.000686\gamma H+0.035713\gamma f^{\prime }+0.000064H^2-0.014104H{f}^{\prime }-0.000640{(f^{\prime })}^2\\ +0.000091{\gamma }^3-0.000009{\gamma }^{2}H-0.000427{\gamma }^2{f}^{\prime }-0.000001\gamma H^2+0.000053\gamma H{f}^{\prime }-0.000873\gamma {(f^{\prime })}^2\\ -0.0000001H^3+0.000043H^2{f}^{\prime }-0.0000054H{(f^{\prime })}^2+0.008683{(f^{\prime })}^3\end{array}\right)-1$$

(14)

The fitting performance of each response surface function is represented by the coefficient of determination $R^2$, shown in

Table 5. Coefficient of determination ($R^2$) of the response surface function for each failure mode.

Failure by Cracking of the Plinth Heel	Failure by Crushing of the Plinth Toe	Failure by Sliding Along the Foundation Plane
0.99662	0.99878	0.99266

below:

It can be seen that the goodness-of-fit $R^2$ for all cases exceeds 0.99, indicating an ideal fitting effect.

Based on the constructed response surface functions, Monte Carlo Simulation is used to generate 10⁷ samples to calculate the probability of failure. The calculated probabilities of failure and reliability indices for the three failure modes under the three water level models are shown in

Table 6. Calculated probability of failure and reliability index for three water level models.

Water Level Model	Cracking at Plinth Heel			Crushing at Plinth Toe			Sliding Along Foundation Plane
	Number of Failures	Probability of Failure	Reliability Index	Number of Failures	Probability of Failure	Reliability Index	Number of Failures	Probability of Failure	Reliability Index
Uniform Distribution	45	4.5 × 10−6	4.44	5	5.0 × 10−7	4.89	23	2.3 × 10−6	4.55
Historical Data GEV	75	7.5 × 10−6	4.33	6	6.0 × 10−7	4.83	88	8.8 × 10−6	4.29
Design Condition Log-P3	432	4.3 × 10−5	3.93	6	6.0 × 10−7	4.83	89	8.9 × 10−6	4.28

below:

As shown in Table 6, the probability of failure calculated by the Uniform Distribution water level model is consistent in order of magnitude with data provided in relevant literature [11], and its result is lower than the other two models. In contrast, the probability of failure derived from the Historical Condition GEV model (reflecting actual operational risk) is clearly higher than the Uniform Distribution model, but much lower than the Design Condition Log-P3 model (representing original design risk). This difference illustrates the GEV model’s accurate capture of extreme risk and the effective risk reduction achieved by operational control on the design risk.

5.5. Reliability Result Analysis for Different Water Level Models

Based on the reliability calculation results, the following conclusions are drawn:

• Among all calculated conditions, cracking at the dam heel is the most sensitive to the water level load distribution, exhibiting the largest magnitude variation in its probability of failure, with the probability of failure differing by nearly six times between the Log-P3 model (4.3 × 10⁻⁵) and the GEV model (7.5 × 10⁻⁶). It should be noted that the current reliability assessment is based on the assumption of a linear elastic material model (Section 4.2). For the failure mode of cracking at the dam heel, which is controlled by a tensile limit state, the linear elastic assumption may potentially overestimate local tensile stresses compared to nonlinear fracture mechanics models. However, the use of a linear elastic model combined with the allowable tensile stress limit (0.1 MPa) specified in the code (SL319—2018) is a conservative practice widely adopted in preliminary reliability assessments of hydraulic structures. Future work will consider incorporating a nonlinear fracture model to further refine the tensile failure probability. While sliding along the dam base is primarily controlled by material properties such as the friction coefficient and cohesion; the crushing at the dam toe failure mode maintains an extremely low probability of failure across all models, which is due to the concrete’s compressive strength being much greater than its tensile strength, and a large safety margin being reserved in the design.
• The probability of failure calculated by the Uniform Distribution model is significantly lower than the other two models. This result quantitatively proves that the Uniform Distribution has an inherent statistical flaw due to its inability to accurately reflect the extreme characteristics of the annual maximum water level, leading to a severe underestimation of the high-water-level risk.
• The probability of failure for the GEV model (actual operational risk) is significantly lower than the Log-P3 model (design risk). This difference stems from the distinct characterization of the extreme value probability density by the models: The Log-P3 curve (natural sequence) has a steeper tail, assigning higher weight to high water levels that approach the structural limit state. Given that gravity dam failure occurs in the extremely small probability region of high water load, the conservative estimation of the dangerous tail by Log-P3 directly increases the number of failure samples. Therefore, the higher reliability index of the GEV model is rational, as it precisely reflects the risk reduction effect of human control. This strongly proves the scientific validity of the GEV model for assessing the true safety level of long-service dams under long-term control.
• Finally, it should be noted that this reliability analysis focuses on quantifying the uncertainty of the water level load. For other material parameters, although they were treated as random variables, a more complex probability density function (PDF) fitting was not performed. Future work will incorporate the uncertainty of material and geometric parameters more comprehensively to enhance the comprehensiveness of the system reliability assessment.

6. Conclusions

This paper aims to address the limitations of traditional methods in treating the water level load by proposing an integrated gravity dam reliability analysis method based on the historical water level Generalized Extreme Value (GEV) distribution. Through engineering application, the main conclusions are as follows:

• This study is the first to systematically utilize long-term operational monitoring data to construct a GEV model-based probability distribution of systemic operational extremes for human-controlled reservoirs. The model’s rationality and reliability are statistically proven through the K-S test and Bootstrap robustness analysis, providing a new paradigm for transforming long-term dam monitoring data into scientific risk input.
• By comparison with the commonly used Uniform Distribution model in engineering, the GEV model is confirmed to be able to more accurately capture high-water-level uncertainty, effectively overcoming the inherent risk underestimation problem of simple distributions, and providing a more refined basis for risk quantification.
• The probability of failure for the Historical Operational GEV model is significantly lower than the Design Code Log-P3 model. For the most sensitive failure mode (cracking at the dam heel), the GEV model’s probability of failure is approximately six times lower than that of the Log-P3 model. This quantitative result reveals that the Log-P3 model yields overly conservative assessment results due to its conservative estimation of the probability density of the extreme tail risk. The comparison powerfully demonstrates that the GEV model can precisely reflect the risk reduction effect of human control, providing a more scientific basis for true operational risk assessment of long-service gravity dams. From a practical standpoint, the GEV-RSM-MC framework established in this study offers decision support for operational management. It allows managers to perform an operational recalibration of the design safety margin based on actual running data, guiding more scientific risk prevention and resource allocation. For example, when the GEV model demonstrates that the actual risk is significantly lower than the design risk, it can inform the optimization of operating rules or maintenance budgets.