An Analytical Solution for the Stability Evaluation of Anti-Dip Layered Rock Slopes Under Water-Level Fluctuations in Reservoirs
Abstract
1. Introduction
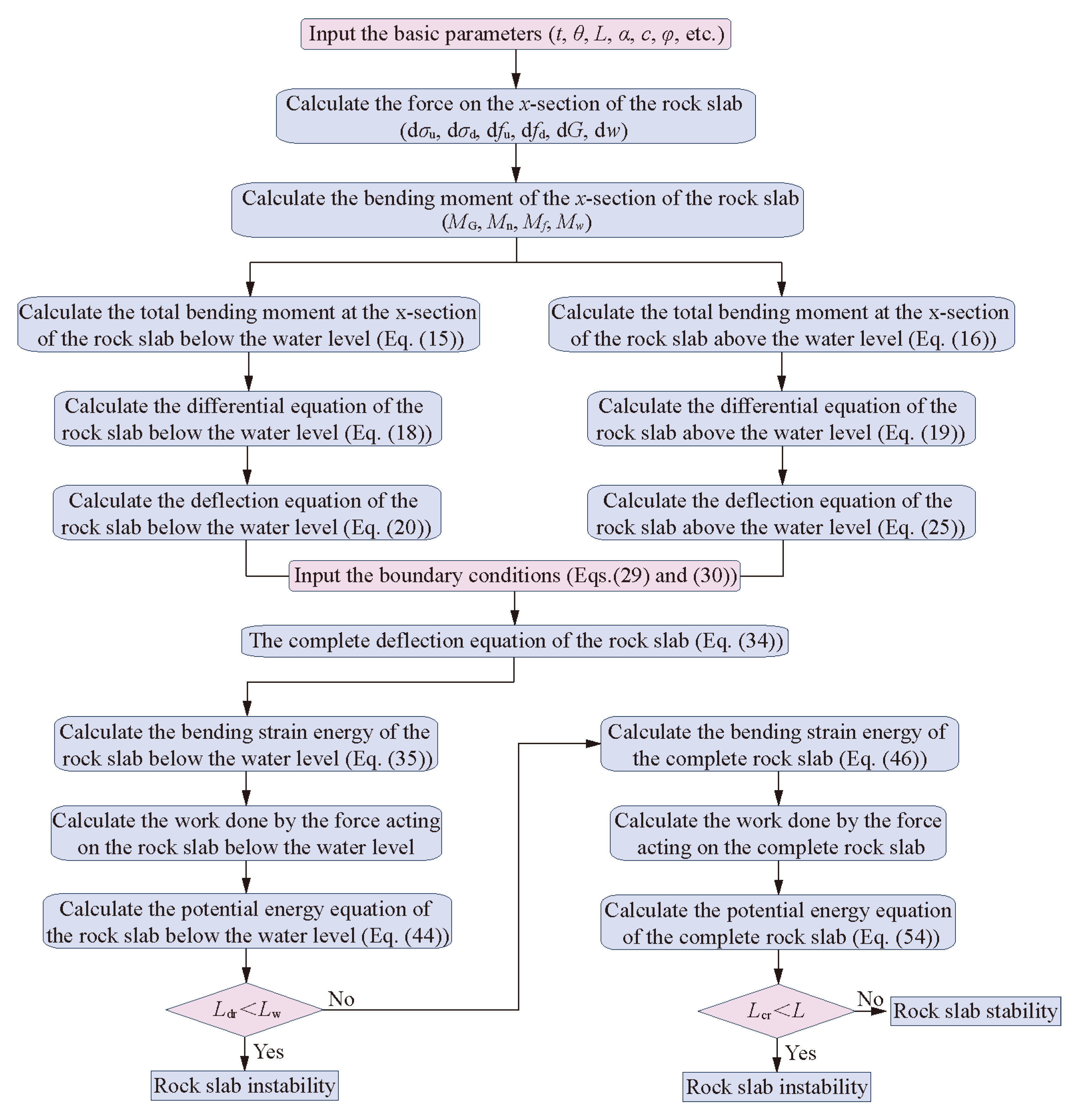
2. Theoretical Analyses
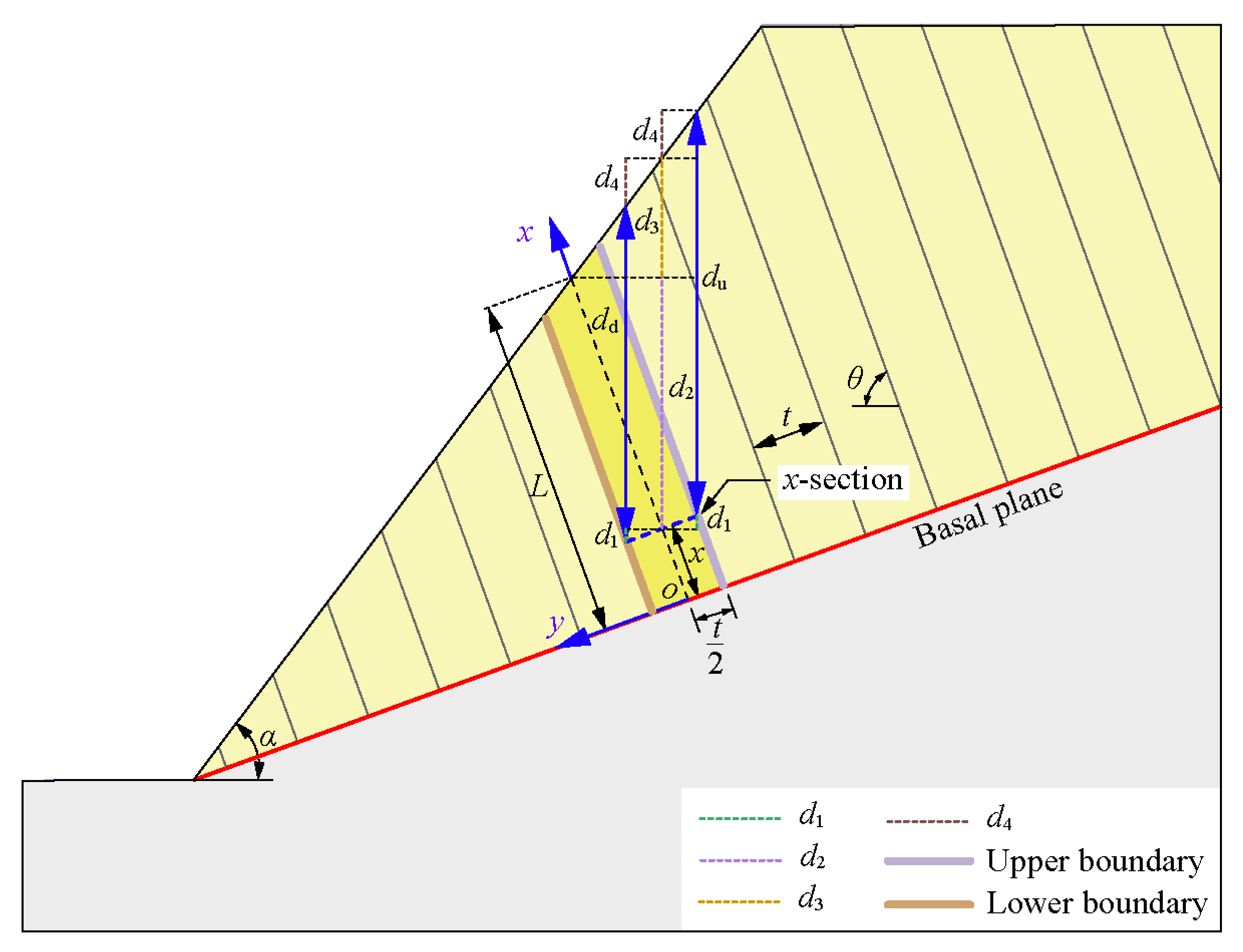
2.1. Mechanical Model
2.2. Deflection Equation
2.3. Critical Length
3. Parameter Analysis
3.1. Qualitative Discussion
3.2. Quantitative Discussion
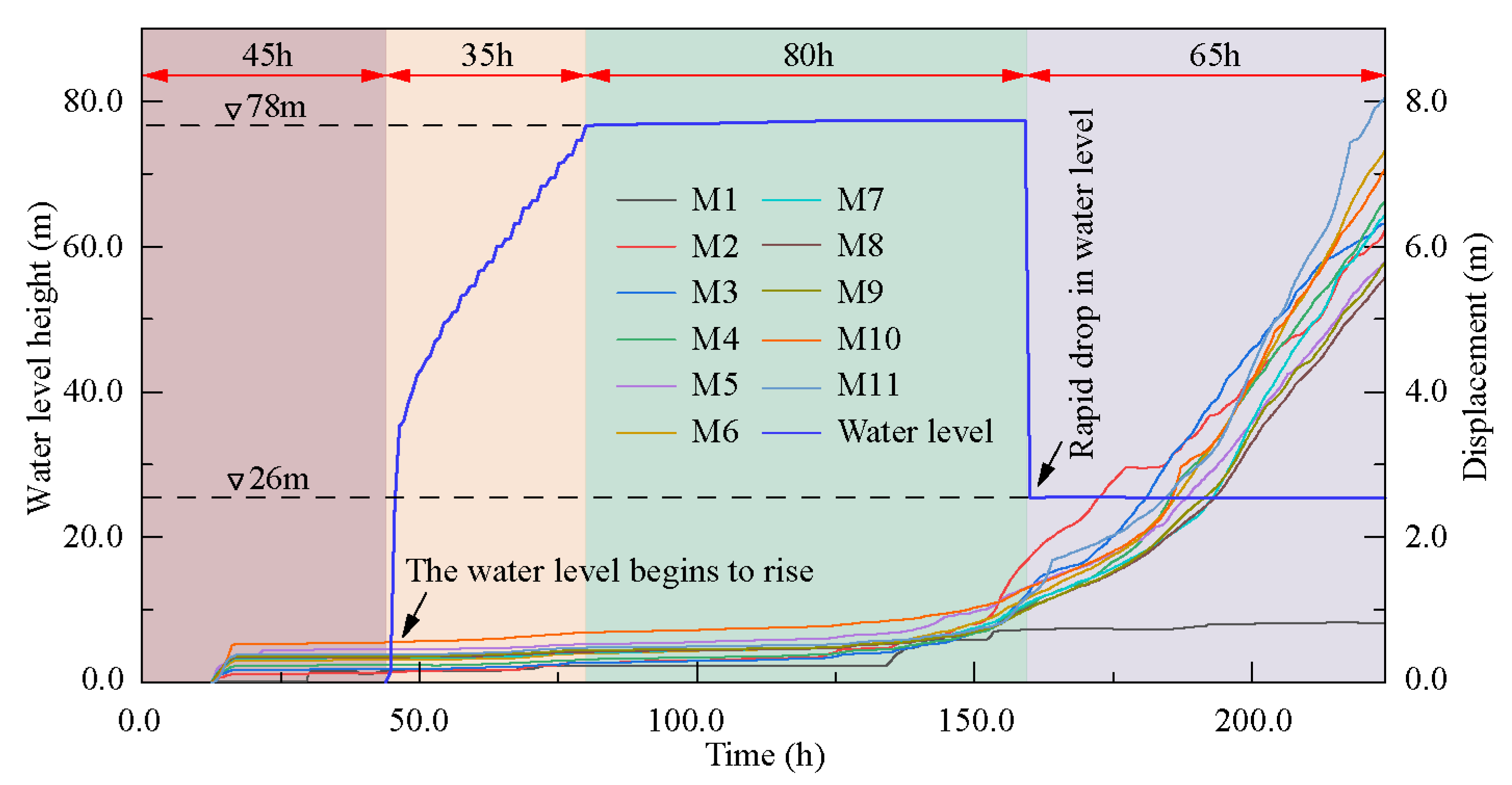
4. Numerical Simulation
4.1. Numerical Simulation Method
4.2. Numerical Model
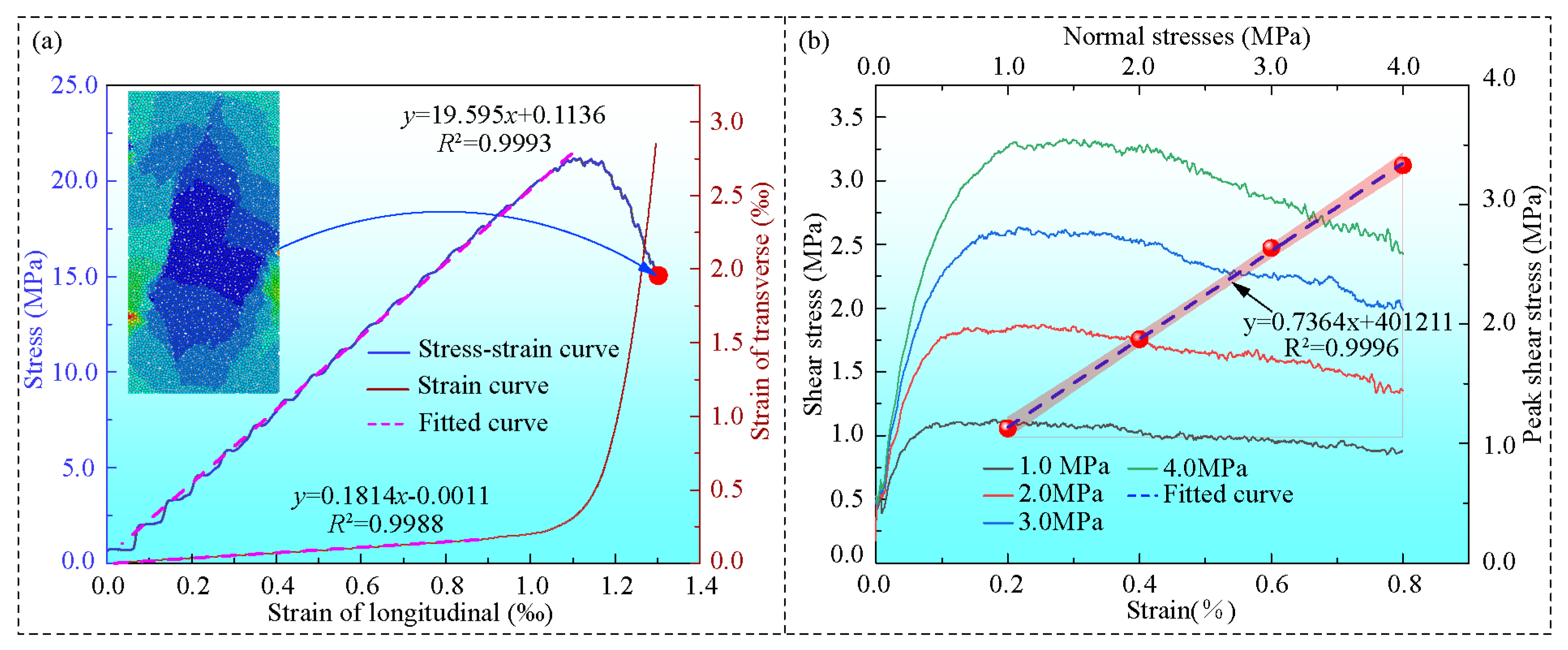
4.3. Parameter Calibration
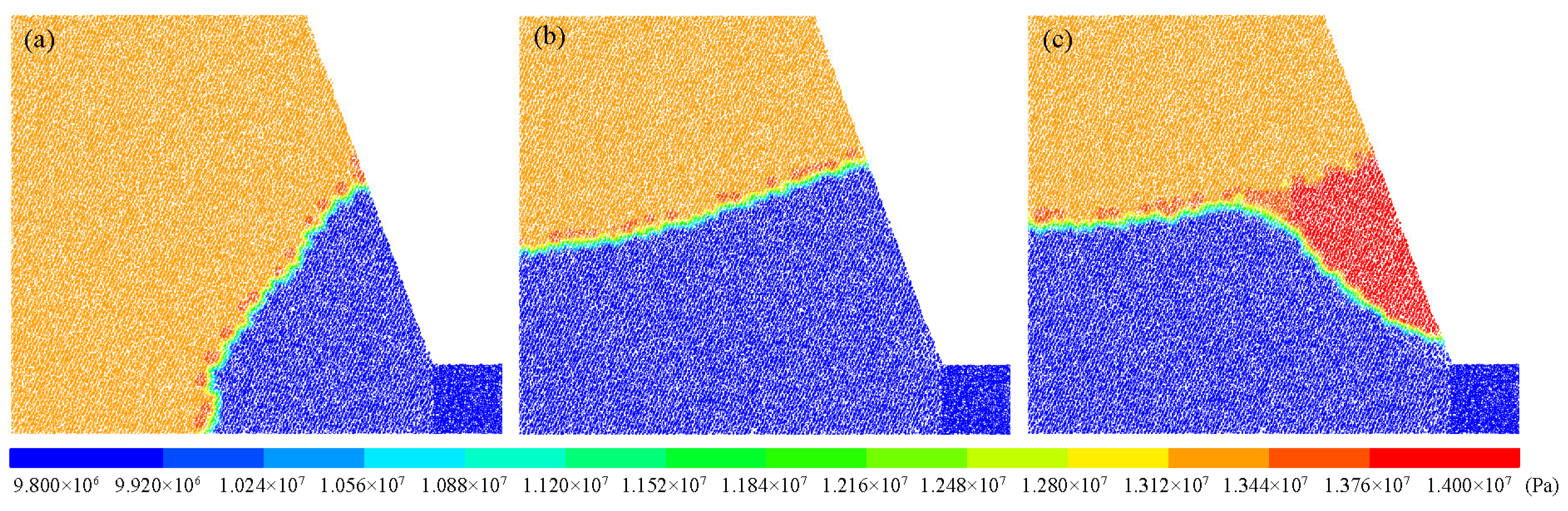
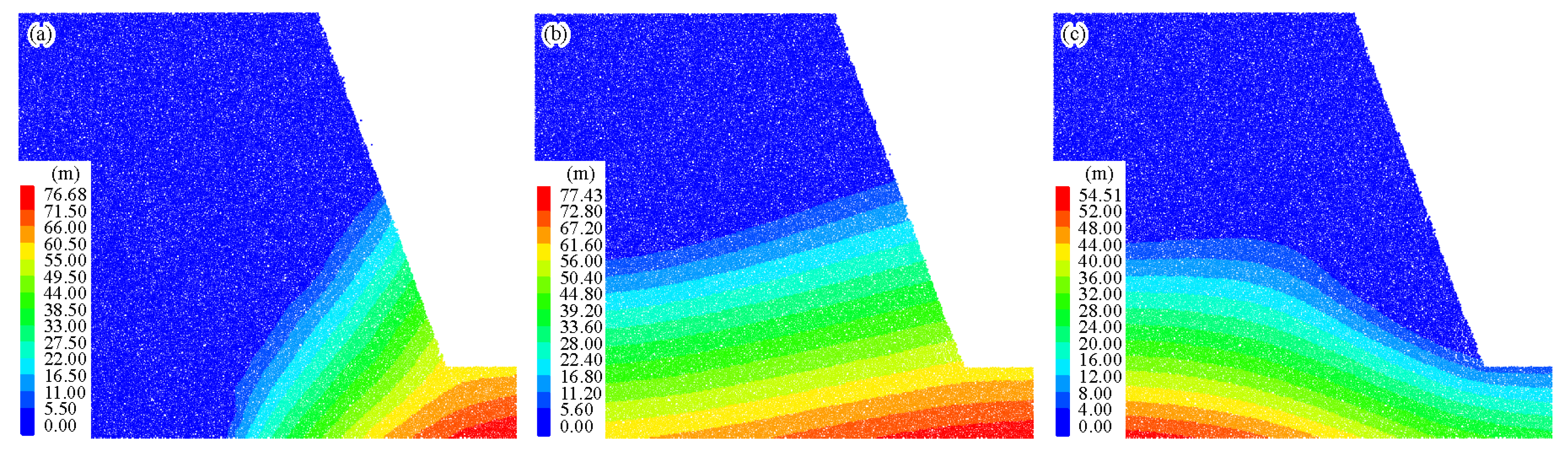
4.4. Simulated Results
5. Validation
5.1. Simulation Result Validation
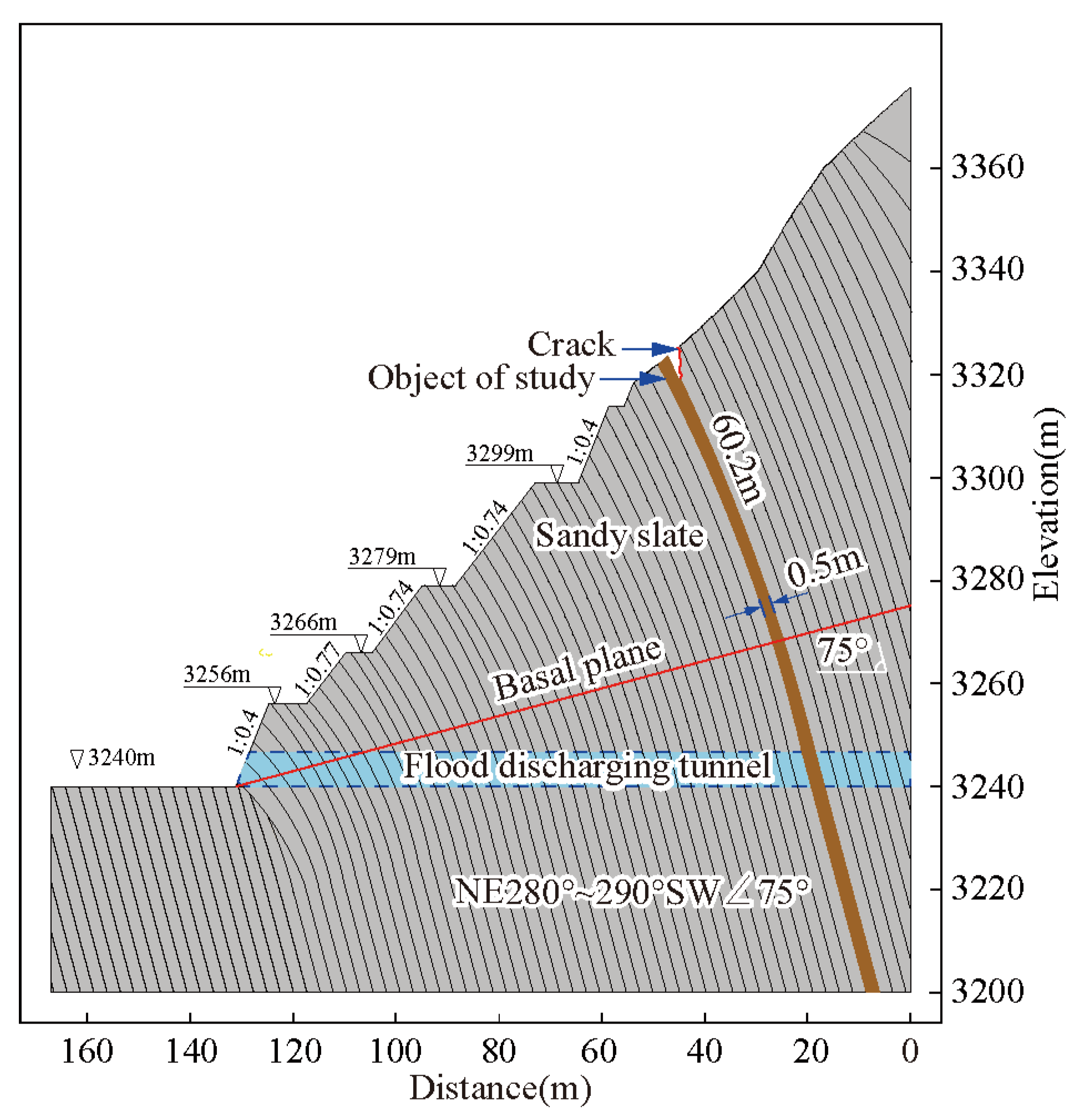
5.2. Laohuzui Slope
5.2.1. Engineering Settings
5.2.2. Calculation Results
5.2.3. Comparison Validation
6. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gong, Y.F.; Yao, A.J.; Li, Y.L.; Li, Y.Y.; Li, Y.N.; Sun, Y.T. Model test study on sliding-toppling composite deformation evolution of anti-dip layered rock slope. Bull. Eng. Geol. Environ. 2023, 82, 194. [Google Scholar] [CrossRef]
- Zheng, Y.; Wang, R.Q.; Chen, C.X.; Meng, F. Analysis of flexural toppling failure in rock slopes using discrete element method. Front. Earth Sci. 2021, 9, 773088. [Google Scholar] [CrossRef]
- Weng, M.C.; Peng, C.H.; Hung, W.Y.; Guo, Y.J. Exploring failure evolution of anti-dip slate slope using centrifuge test and discrete element method. Bull. Eng. Geol. Environ. 2024, 83, 457. [Google Scholar] [CrossRef]
- Ashby, J. Sliding and Toppling Modes of Failure in Models and Jointed Rock Slopes; Imperial College, University of London: London, UK, 1971. [Google Scholar]
- Goodman, R.E.; Bray, J.W. Toppling of rock slopes. In Proceedings of the ASCE Specialty Conference on Rock Engineering for Foundations and Slopes, Boulder, CO, USA, 15–18 August 1976; pp. 201–234. [Google Scholar]
- Beng, X.T.; Zhan, G.C.; Yang, Y.C.; Zhu, C.; Murat, K.; Wang, D.S. Flexural toppling characteristics of anti-dip soft rock slope with base friction test. Bull. Eng. Geol. Environ. 2023, 82, 21. [Google Scholar] [CrossRef]
- Yan, K.M.; Wang, G.H.; Nikitas, N.; Bao, N.; Doi, I.; Tao, Z.G. Time-frequency analysis on seismic response and pre-toppling damage evolution of anti-dip rock slope under earthquake sequences by shaking table tests. Eng. Geol. 2025, 355, 108220. [Google Scholar] [CrossRef]
- Liu, H.D.; Zhao, Y.W.; Dong, J.Y.; Wang, Z.F. Experimental study of the dynamic response and failure mode of anti-dip rock slopes. Bull. Eng. Geol. Environ. 2021, 80, 6583–6596. [Google Scholar] [CrossRef]
- Zhang, H.N.; Chen, C.X.; Zheng, Y.; Yu, Q.Q.; Zhang, W. Centrifuge modeling of layered rock slopes susceptible to block-flexure toppling failure. Bull. Eng. Geol. Environ. 2020, 79, 3815–3831. [Google Scholar] [CrossRef]
- Jin, L.L.; Dong, H.K.; Ye, F.; Wei, Y.F.; Liu, J.F.; Wang, C.K. Investigation of the block toppling evolution of a layered model slope by centrifuge test and discrete element modeling. J. Rock Mech. Geotech. 2024, 16, 112–122. [Google Scholar] [CrossRef]
- Lian, J.J.; Li, Q.; Deng, X.F.; Zhao, G.F.; Chen, Z.Y. A numerical study on toppling failure of a jointed rock slope by using the distinct lattice spring model. Rock Mech. Rock Eng. 2018, 51, 513–530. [Google Scholar] [CrossRef]
- Adhikary, D.P.; Dyskin, A.V. Modelling of progressive and instantaneous failures of foliated rock slopes. Rock Mech. Rock Eng. 2007, 40, 349–362. [Google Scholar] [CrossRef]
- Sarfaraz, H.; Amini, M. Numerical simulation of slide-toe-toppling failure using distinct element method and finite element method. Geotech. Geol. Eng. 2020, 38, 2199–2212. [Google Scholar] [CrossRef]
- Cui, Z.; Chen, P.Z.; Chu, W.J.; Zhou, Y.; Liu, N.; Sheng, Q. Deformation mechanism and reinforcement design for the flexural toppled slope of Miaowei HPP. Bull. Eng. Geol. Environ. 2023, 82, 39. [Google Scholar] [CrossRef]
- You, M.L.; Tong, D.F.; Tan, F.; Lv, J.H. Discrete element-based numerical simulation and failure mechanism analysis of anti-dip rock slopes. Bull. Eng. Geol. Environ. 2024, 83, 399. [Google Scholar] [CrossRef]
- Gong, W.J.; Tao, Z.G.; He, M.C.; Hou, H.J. Feasibility analysis on the support of rock slopes against flexural toppling failure using the DDA Method-A case study. KSCE J. Civ. Eng. 2022, 26, 3847–3862. [Google Scholar] [CrossRef]
- Aydan, O.; Kawamoto, T. The stability of slopes and underground openings against flexural toppling and their stabilization. Rock Mech. Rock Eng. 1992, 25, 143–165. [Google Scholar] [CrossRef]
- Azarafza, M.; Bonab, M.H.; Akgun, H. Numerical analysis and stability assessment of complex secondary toppling failures: A case study for the south pars special zone. Geomech. Eng. 2021, 27, 481–495. [Google Scholar] [CrossRef]
- Amini, M.; Majdi, A.; Aydan, Ö. Stability analysis and the stabilisation of flexural toppling failure. Rock Mech. Rock Eng. 2009, 42, 751–782. [Google Scholar] [CrossRef]
- Wang, R.Q.; Zheng, Y.; Chen, C.X.; Zhang, W. Theoretical and numerical analysis of flexural toppling failure in soft-hard interbedded anti-dip rock slopes. Eng. Geol. 2023, 312, 106923. [Google Scholar] [CrossRef]
- Majdi, A.; Amini, M. Analysis of geo-structural defects in flexural toppling failure. Int. J. Rock Mech. Min. 2011, 48, 175–186. [Google Scholar] [CrossRef]
- Zhang, G.C.; Wang, F.; Zhang, H.; Tang, H.M.; Li, X.H.; Zhong, Y. New stability calculation method for rock slopes subject to flexural toppling failure. Int. J. Rock Mech. Min. 2018, 106, 319–328. [Google Scholar] [CrossRef]
- Wang, D.J.; Tang, H.M.; Zhang, Y.Q.; Shen, P.W. Local failure probability of the anti-dip slope susceptible to flexural toppling. Stoch. Environ. Res. Risk A 2019, 33, 1187–1202. [Google Scholar] [CrossRef]
- Sarfaraz, H. Stability analysis of flexural toppling failure using the Sarma’s method. Geotech. Geol. Eng. 2020, 38, 3667–3682. [Google Scholar] [CrossRef]
- Li, A.; Dai, F.; Liu, Y.; Du, H.B.; Jiang, R.C. Dynamic stability evaluation of underground cavern sidewalls against flexural toppling considering excavation-induced damage. Tunn. Undergr. Space Technol. 2021, 112, 103903. [Google Scholar] [CrossRef]
- Zheng, Y.; Chen, C.X.; Liu, T.T.; Ren, Z.H. A new method of assessing the stability of anti-dip bedding rock slopes subjected to earthquake. Bull. Eng. Geol. Environ. 2021, 80, 3693–3710. [Google Scholar] [CrossRef]
- Jin, L.L.; Fu, W.X.; Wang, Y.; Xiao, Q.F.; Li, Y.J.; Ye, F. A novel method for evaluating stability and mechanism of flexural toppling based on energy conservation principle and numerical simulation. Int. J. Rock Mech. Min. 2024, 183, 105896. [Google Scholar] [CrossRef]
- Zhu, J.; Deng, J.H.; Chen, F.; Huang, Y.M.; Yu, Z.Q. Water saturation effects on mechanical and fracture behavior of marble. Int. J. Geomech. 2020, 20, 04020191. [Google Scholar] [CrossRef]
- Sun, Q.; Zhang, Y.L. Combined effects of salt, cyclic wetting and drying cycles on the physical and mechanical properties of sandstone. Eng. Geol. 2019, 248, 70–79. [Google Scholar] [CrossRef]
- Gratchev, I.; Pathiranagei, S.V.; Kim, D.H. Strength properties of fresh and weathered rocks subjected to wetting-drying cycles. Geomech. Geophys. Geo 2019, 5, 211–221. [Google Scholar] [CrossRef]
- Zhao, Y.B.; Yang, C.Q.; Qu, F.; Wu, Z.R.; Ding, K.J.; Liang, Z.S. Effect of wet-dry cycles on the mechanical performances and microstructure of pisha sandstone. Molecules 2025, 28, 2533. [Google Scholar] [CrossRef]
- He, L.P.; Yu, J.Y.; Hu, Q.J.; Cai, Q.J.; Qu, M.F.; He, T.J. Study on crack propagation and shear behavior of weak muddy intercalations submitted to wetting-drying cycles. Bull. Eng. Geol. Environ. 2020, 79, 4873–4889. [Google Scholar] [CrossRef]
- Teng, T.; Chen, Y.L.; Wang, S.G.; Jia, W.J.; Wang, Y.M.; Liu, K.; Li, Z.L. Water injection softening modeling of hard roof and application in Buertai coal mine. Environ. Earth Sci. 2025, 84, 54. [Google Scholar] [CrossRef]
- Cai, J.C.; Ju, N.P.; Huang, R.Q.; Zheng, D.; Zhao, W.H.; Li, L.Q.; Huang, J. Mechanism of toppling and deformation in hard rock slope: A case of bank slope of Hydropower Station, Qinghai Province, China. J. Mt. Sci. 2019, 16, 924–934. [Google Scholar] [CrossRef]
- Jin, L.L.; Wei, Y.F.; Ye, F.; Fu, W.X.; Liu, J.F.; Li, S.W. Large-scale toppling slope under water level fluctuation of reservoir: A case of Yunnan Province, China. J. Rock Mech. Geotech. 2024, 16, 3034–3046. [Google Scholar] [CrossRef]
- Pan, S.T.; Gao, W.; Hu, R.L. Physical modeling for large-scale landslide with chair-shaped bedrock surfaces under precipitation and reservoir water fluctuation conditions. Water 2022, 14, 984. [Google Scholar] [CrossRef]
- Shan, Z.G.; Lv, J.Q.; Zhang, F.M.; Chen, L.; Yin, F.; Dong, M.L. Different toppling bank slope failures under hydrodynamic action during impoundment of the Miaowei hydropower station reservoir. Water 2022, 14, 2126. [Google Scholar] [CrossRef]
- Roy, D.; Maheshwari, P. Probabilistic analysis of rock slopes against block toppling failure. Indian Geotech. J. 2018, 48, 484–497. [Google Scholar] [CrossRef]
- Bowa, V.M.; Gong, W.P. Analytical technique for stability analyses of the rock slope subjected to slide head toppling failure mechanisms considering groundwater and stabilization effects. Int. J. Geo-Eng. 2021, 12, 4. [Google Scholar] [CrossRef]
- Zhou, W.J.; Xu, W.Y.; Ning, Y.; Xiao, H.B.; Xie, W.C. Analytical method of stability analyses of toppling rock slopes subjected to flexural toppling failure damage. Eur. J. Environ. Civ. Eng. 2023, 27, 2373–2387. [Google Scholar] [CrossRef]
- Lin, Y.S.; Zhao, X.T.; Wu, Q.H.; Ding, G.Z.; Yang, R.T.; Wen, T. Calculation method for toppling stability of layered counter-tilt rock slope considering the effect of reservoir water and its application. In Applied Mathematics, Modeling and Computer Simulation; IOS Press: Amsterdam, The Nederland, 2023; Volume 42, pp. 1046–1056. [Google Scholar] [CrossRef]
- Chaudhary, N.; Metya, S.; Sharma, K.K. Influence of Hydraulic Distribution Pattern on the Rock Slope Stability under Block Toppling Failure. KSCE J. Civ. Eng. 2024, 28, 1253–1266. [Google Scholar] [CrossRef]
- Qin, S.; Jiao, J.J.; Wang, S. A cusp catastrophe model of instability of slip-buckling slope. Rock Mech. Rock Eng. 2001, 34, 119–134. [Google Scholar] [CrossRef]
- Zhou, Z.K.; Yao, X.; Li, R.J.; Jiang, S.; Zhao, X.M.; Ren, K.Y.; Zhu, Y.F. Deformation characteristics and mechanism of an impoundment-induced toppling landslide in Baihetan Reservoir based on multi-source remote sensing. J. Mt. Sci. 2023, 220, 3614–3630. [Google Scholar] [CrossRef]







| Parametric Classification | Parameter | Value |
|---|---|---|
| Linear Parallel Bond Model (Microscopic parameters) | Bond modulus (Pa) | 1.05 × 1010 |
| Normal-to-shear stiffness ratio (-) | 1.53 | |
| Friction coefficient (-) | 0.5 | |
| Normal critical damping ratio (-) | 0.2 | |
| Density (kg/m3) | 2600 | |
| Damping (Ns/m) | 0.7 | |
| contact gap (m) | 1 × 10−5 | |
| Tensile strength (Pa) | 6.5 × 106 | |
| Cohesion (Pa) | 1.4 × 107 | |
| Friction angle (°) | 45 | |
| Rock mass (Macroscopic parameters) | Modulus of deformation (GPa) | 19.595 |
| Poisson (-) | 0.1814 |
| Parametric Classification | Parameter | Value |
|---|---|---|
| Linear Model (Microscopic parameters) | Normal stiffness (N/m) | 1 × 108 |
| Shear stiffness (N/m) | 1 × 108 | |
| Normal critical damping ratio (-) | 0.5 | |
| Bedding plane (macroscopic parameters) | Cohesion (Pa) | 401,211 |
| Friction angle (°) | 36.37 |
| Parameter | Symbol | Unit | Value |
|---|---|---|---|
| Rock elastic modulus | E | GPa | 17.0 |
| Bedding plane friction angle | φ | ° | 38.0 |
| Rock slab thickness | t | m | 0.5 |
| Rock density | ρ | kg/m3 | 2750.0 |
| Rock layer dip angle | θ | ° | 75.0 |
| Bedding plane cohesion | c | MPa | 0.06 |
| Actual length of the rock slab | L | m | 60.2 |
| Poisson’s ratio | μ | / | 0.25 |
| Tensile strength of rock | σt | MPa | 7.4 |
| Friction angle of the rock | φ’ | ° | 52.0 |
| Cohesion of the rock | c’ | MPa | 2.33 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, N.; Yao, S.; Jin, L.; Fu, W.; Wang, Y.; Ye, F.; Wu, Z. An Analytical Solution for the Stability Evaluation of Anti-Dip Layered Rock Slopes Under Water-Level Fluctuations in Reservoirs. Water 2025, 17, 3375. https://doi.org/10.3390/w17233375
Sun N, Yao S, Jin L, Fu W, Wang Y, Ye F, Wu Z. An Analytical Solution for the Stability Evaluation of Anti-Dip Layered Rock Slopes Under Water-Level Fluctuations in Reservoirs. Water. 2025; 17(23):3375. https://doi.org/10.3390/w17233375
Chicago/Turabian StyleSun, Ning, Shuang Yao, Leilei Jin, Wenxi Fu, Yang Wang, Fei Ye, and Zhihao Wu. 2025. "An Analytical Solution for the Stability Evaluation of Anti-Dip Layered Rock Slopes Under Water-Level Fluctuations in Reservoirs" Water 17, no. 23: 3375. https://doi.org/10.3390/w17233375
APA StyleSun, N., Yao, S., Jin, L., Fu, W., Wang, Y., Ye, F., & Wu, Z. (2025). An Analytical Solution for the Stability Evaluation of Anti-Dip Layered Rock Slopes Under Water-Level Fluctuations in Reservoirs. Water, 17(23), 3375. https://doi.org/10.3390/w17233375





