Optimization Tool of Hybrid Energy Systems Toward a New Integrated Solution to Improve the Fish Sector’s Effectiveness

Abstract

A techno-economic-environmental assessment tool was tailored to a fish sector case study. The fish sector, combined with two renewable components (wind and hydro), was analysed, and sensitivity analyses were carried out to integrate other renewables in a specifically developed optimization model (i.e., HY4RES-AHS). The model used an evolutionary method and resulted in the following conclusions: Scenario 2 excels financially, with the highest IRR (42%), shortest payback (4 years), and lowest investment (EUR 14,500), though it suffers from high energy losses (27.4%) due to a limited grid feed-in (120 kW). Scenario 4 is the most sustainable, with the highest SSR (97.8%) and SCR (63.4%) and lowest grid emissions (12.83 t CO₂ eq.), supported by 600 kW PV and strong biomass use, but it has the lowest NPV (EUR 2241) and longest payback (25 years). Scenario 3 offers the best overall balance, achieving the highest NPV (EUR 741,293), solid IRR (20%), low energy losses (2.8%), and strong SSR (94%). Scenarios 5 and 7 prohibit grid feed-in, resulting in the highest energy losses (46.7% and 48.4%) and poor sustainability. Scenario 6 is financially strong (NPV EUR 602,280) but lacks biomass and biogas, reducing system resilience and autonomy. In summary, Scenario 2 is cost-efficient, Scenario 4 leads to sustainability, and Scenario 3 exhibits balanced performance.

1. Introduction

The increasing penetration of distributed energy resources has raised concerns regarding grid congestion [1]. Declining asset profitability has led grid operators to restrict or delay new connections [2]. Hybrid renewable energy systems (HRESs) are a potential solution [3]. Their integration of complementary renewable technologies and proximity to local demand centres enhance system self-sufficiency and reduce grid dependence [4]. Photovoltaic (PV) systems, battery energy storage systems (BESSs), and wind turbines are the most commonly investigated technologies [5]. Alternatives such as biomass gasifiers [6], internal combustion engine (ICE) units [7], small hydropower systems (SHPs) [8], and hydrogen electrolysers remain comparatively underexplored [9]. This gap highlights the need for further research into diversified configurations of HRES to improve both technical performance and economic viability [10].

The hybridization potential of rural areas, as well as water systems, is a strong tool that managers should analyse to implement, thereby reducing the carbon footprint of societal consumption [11]. The most promising system scenario includes wind turbines and solar PV systems, utilizing water reservoirs for irrigation as a pumped hydropower storage plant [12]. The optimum configuration for electrifying five villages to be disconnected from the grid was evaluated in Odisha (India) using renewable energy systems with high-interest-rate values [13]. Different optimization techniques for ports’ hybrid renewable energy systems were developed, and energy management strategies based on AI-driven forecasting were proposed [14]. Ref. [15] compared different hybrid systems and capacities to evaluate their availability, analysing 243 case studies with investment costs between EUR 45 k and EUR 2.1 M and net present values between EUR 18 k and EUR 600 k. Other optimization procedures were defined as particle swarm optimization (PSO) [16], colony optimization (ACO) [17], sine cosine algorithm [18], bacterial forging algorithm [19], grasshopper optimization algorithm [20], imperialist competitive algorithm [21], modified sine cosine algorithm [22], slap swarm algorithm [23], genetic algorithm [24], sooty terns optimization algorithm [25], or artificial gorilla troops optimizer [26], among others.

Hybrid renewable energy systems (HRESs) are complex due to the integration of multiple renewable technologies, loads, and storage, making optimization a central research topic [27]. For simple economic optimization, classical techniques such as linear programming (LP) or generalized reduced gradient (GRG) are used [28]. When problems involve multiple objectives and many decision variables, advanced methods like evolutionary strategies or genetic algorithms (GA) are applied [29]. Commercial tools such as HOMER Pro facilitate simulations with user-friendly interfaces, but they are limited in handling flexible loads [30]. HOMER Pro often relies on black-box approaches and only supports single-objective optimization [31]. To overcome these issues, customized models are increasingly developed using Python 3.12 or Solver [32]. Such models allow greater flexibility in addressing the diverse objectives of HRES optimization [33]. Nonetheless, results should always be compared against established tools like HOMER Pro to ensure reliability [34].

Optimal sizing of HRES components is frequently the central focus of research. Nevertheless, most studies address systems designed from scratch, without considering existing infrastructures [34]. For instance, ref. [35] compared the Giza Pyramid Construction (GPC) technique with particle swarm optimization (PSO) in an HRES composed of PV, wind, and BESS. Their findings indicate that GPC enhances the global optimum, achieving a reduction of EUR 165 in annual costs and an 8% decrease in simulation time. Aligned with this topic, ref. [36] combined a genetic algorithm with PSO to optimize a PV–wind–BESS HRES, obtaining an annual system cost of EUR 276,200 and a levelized cost of electricity (LCOE) of 0.0065 EUR/kWh. To fully exploit the potential of HRES, future research should prioritize their integration with existing infrastructures, as well as with commercial or community loads [37].

The fish sector has potential for the application of hybrid renewable power systems in its decarbonization, considering a carbon footprint equal to 179 million tonnes of CO₂-equivvalent [38]. The integration of renewable systems is essential to mitigate their impact on the global energy chain, requiring an effective balance between supply and demand within complex hybrid energy systems. Leveraging variable supply and demand patterns can enhance overall system performance and operational efficiency [39]. These objectives are pursued by optimizing the system to maximize cost savings and minimize emissions [40]. The integrated configuration includes a small hydropower plant, a wind turbine, a wastewater treatment unit, a wood-drying kiln, and two fish processing facilities [41].

This research develops a tailored model, HY4RES-AHS, for the aquaculture sector, applying evolutionary algorithms in Excel’s Solver to optimally size an extended H4YRES system. By integrating existing wind and hydropower assets with PV systems, a biomass gasifier, an ICE unit, and BESS, the study identifies optimal technology combinations and capacities. A techno-economic assessment and sensitivity analysis of key parameters are performed, and the best scenarios for the site are compared. This approach demonstrates a practical and improved strategy for hybrid energy integration in aquaculture systems.

2. Materials and Methods

2.1. Fish Sector Case Study

The case study observed for this research is located in the northwest of Ireland in County Donegal [10]. It comprises two aquaculture companies, Island Seafoods and Albatross Seafoods, each producing different value-added fish and seafood products. The water from the two processing facilities is treated in a wastewater treatment plant (WWTP) on-site. On the generation side, a wind turbine and an SHP are installed. Recently, it was decided to install a biomass drying kiln next to the wind turbine to utilize excess electricity that cannot be fed into the grid due to a power limitation for grid injection. Currently, the primary and secondary sites are separate systems, each connected individually to the power grid, due to regulatory restrictions. This is depicted in Figure 1 (yellow line connections). To analyse the viability of extending the system with other renewable energy technologies and storage, the system is considered as a single unit for this research development (Figure 1, showing yellow and orange connections in an optimised way).

Island Seafoods has collected 10 years of electricity generation and consumption data, which is available for this research project. This includes consumption data of the WWTP and generation data for the SHP plant.

2.2. Proposal of Developed Optimization Tool HY4RES-AHS

Taking into account the findings from previous analyses, local site interactions, and the limitations identified, a new simulation framework (HY4RES—Aquaculture Hybrid System (AHS)) was developed to address existing gaps and enhance the accuracy of the case study investigation. The objective of the tool is to enable a comprehensive techno-economic assessment of hybrid renewable energy systems while allowing detailed system expansion analysis and optimization through the integration of additional renewable technologies. The optimization objective was the maximization of the self-sufficiency ratio (SSR). The following paragraphs describe the input data considered, the structure of the technical and financial models, and the optimization techniques applied.

2.2.1. Input Data

Hourly load profiles of Island Seafoods and Albatross Seafoods for 2023 were obtained from their energy management system (EMS), the only year with available data. The WWTP load profile was not available due to inconsistent metering; therefore, its demand was estimated from a one-week monitoring campaign in winter 2023, yielding an average hourly consumption of 10.68 kWh and a peak load of 26 kW. A representative daily profile was derived from these values (

Table 1. Load profile for the WWTP, according to the metered peak demand and hourly average load.

Hour	${\mathit{P}}_{\mathit{W}\mathit{W}\mathit{T}\mathit{P}}$ kW	Hour	${\mathit{P}}_{\mathit{W}\mathit{W}\mathit{T}\mathit{P}}$ kW
1	4	13	22
2	4	14	26
3	4	15	22
4	4	16	16
5	6	17	14
6	8	18	11
7	10	19	9
8	11	20	8
9	12	21	6
10	14	22	4
11	16	23	4
12	18	24	4

) and extrapolated for the entire year. Finally, a combined hourly load profile of the three facilities was constructed and implemented in the model.

Raw roadside wood with a moisture content of 45–60% [42] is purchased from the local market. The wood-drying kiln reduces the moisture content of Sitka spruce chips to 20% [43], resulting in a lower heating value (LHV), $LH{V}_{wood}$, equal to 3811 kWh/t [44]. The installed kiln has a rated power, $P_{r,kiln}$, equal to 300 kW, and for simplification, its operation is assumed to range between 200 kW and 300 kW. Consequently, during any hour of the year, when excess renewable electricity above 200 kW is available, a corresponding amount of wood can be dried. The kiln’s operation is mathematically represented in Equation (1):

$$\begin{array}{l}\mathrm{if} { P}_{wind}+P_{SHP}+P_{PV}-P_{load},fixed\ge 200 \mathrm{kW}\to P_{kiln}=P_{wind}+P_{SHP}+P_{PV}-P_{loadfixed}\\ \mathrm{if} P_{wind}+P_{SHP}+P_{PV}-P_{load},fixed\ge 300 \mathrm{kW}\to P_{kiln}=300 \mathrm{kW}\\ \mathrm{else} P_{kiln}=0 \mathrm{kW}\end{array}$$

(1)

where each power P corresponds to a specific hour of the year in kW.

The dried wood output of the drying kiln is computed according to Equation (2):

$${\eta }_{wood,dried}={\displaystyle \frac{P_{kiln}}{2000\frac{\mathrm{kW}\mathrm{h}}{t}}}$$

(2)

where P_kiln corresponds to the power of the drying kiln at the hour observed.

An additional vector is defined, ${\eta }_{wood,dried}$, which sums all previous hours of the year to the current one. If desired, an initial amount of wood m_{wood,dried,t0}, left in storage from the previous year, can be added to this cumulative vector. It is assumed that m_{wood,dried,t0} = 0. Surplus production of dried wood is sold at the market price, which is considered in the cost and financial evaluation. The wood purchase and selling prices are adjusted with respect to the reduction in the moisture content. Hence, the wood cash-fow can directly be computed with the amount of dried wood not used in the BG.

2.2.2. Small Hydropower Plant

Generation data from the fixed PPA contract are available in 15 min time steps for the year 2023. As the total generation is not known and only the percentage of self-consumption of the SHP is available, this data is used as the total generation before feed-in. The 15 min data is consolidated into hourly values.

2.2.3. Wind Turbine

The parameters from

Table 2. Parameters of the Vestas V52850 wind turbine at the primary site.

Name	Value	Note
$P_r$	850 kW	Maximum operation at 500 kW due to current grid injection limitations
$h_{hub}$	44 m
$h_{alt}$	60 m	Above sea level
Latitude	54.673°
Longitude	−8.422°
Data	merra2	For 2023

are inserted into Renewables.Ninja’s wind simulation tool to obtain the hourly generation data for the same year under analysis [45]. No scaling of the generation output is carried out at this point.

2.2.4. Photovoltaic (PV) Systems

To simulate the PV system, PVGIS 5.3 [46] is used with the input displayed in

Table 3. Parameters of the rooftop PV System.

Name	Value	Note
$P_r$	120 kW	(C-Si)
$\beta$	42$°$	Slope
$\gamma$	0$°$	Azimuth
$f_{derate}$	14%	System losses
$h_{alt}$	46 m	Above sea level
Data	merra2	For 2023
Latitude	54.673$°$	System losses
Longitude	−8.422$°$
Data	merra2	For 2023

. PVGIS is run with 1 kW_p nominal power. Its generation is then scaled in the model by multiplying P_PV, which is set by the optimization technique, with the hourly generation vector from PVGIS. The approximation developed in [14] is used to limit the PV system to the roof of the seafood processing facilities, which can host up to 120 kW of installed power.

2.2.5. Biomass Generator

To utilize the dried wood available on site, the integration of a biomass gasifier (BG) is proposed. The optimization objective is to determine the appropriate rated power of the BG to support the renewable system as a continuous base load throughout the year. A gas-fired internal combustion engine (ICE) generator is selected due to its efficient conversion pathway and flexible sizing options, ranging from a few kilowatts to several hundred kilowatts. In the first stage, wood chips are gasified in a downdraft gasifier, and the resulting syngas is subsequently cleaned, cooled, and combusted in a gas engine [47].

A total wood-to-electricity conversion efficiency of ${\eta }_{BG}$ = 25% is assumed, in accordance with the simulation results reported in [48]. In terms of operation, renewable sources are given dispatch priority, while the BG is only activated when the load cannot be fully met by the wind turbine and small hydropower (SHP) generation, as defined in Equation (3). The BG’s wood consumption is constrained to the biomass dried on site, with no external purchase of wood chips considered. To maximize efficiency, the BG is assumed to operate exclusively at its rated power and is configured to only supply the fixed loads, excluding the flexible demand of the wood-drying kiln.

$$P_{wind}+P_{SHP}+P_{PV}<P_{load,fixed} {{}^{^}m}_{wood,dried.cum}\ge m_{wood,BG}$$

(3)

$m_{wood,BG}$ is the amount of wood needed to operate the BG at the defined power. It is computed according to Equation (4):

$$m_{wood,BG}={\displaystyle \frac{P_{BG}}{{\mathsf{\eta }}_{BG} LH{V}_{wood}}}$$

(4)

2.2.6. Battery Energy Storage System

A lithium-ion battery system is assumed as a battery energy storage system (BESS). The input parameters for the BESS are found in

Table 4. Parameters of the BESS.

Name	Value	Note
$\mathrm{E}\mathrm{P}\mathrm{R}$	4 kWh/kW	Equals 4 h storage duration
$SO{C}_{t0}$	0.25 $C_{BESS}$	Slope
${\eta }_{ch/dis}$	0.95	Same efficiency for charging and discharging is assumed
$SO{C}_{min}$	0.1 $C_{BESS}$	System losses

. The energy-to-power ratio (EPR) of the BESS is equal to a storage duration of 4 h [49]. Additionally, state-of-charge (SOC) limits are set to prevent deep discharge of the battery, with an initial charge defined at the first timestep of the simulation. The optimization technique sizes the BESS in terms of its capacity $C_{BESS}$ in kWh.

The charge/discharge power (P_BESS) of the battery is computed by expression (5). This is used to limit the amount of energy being charged and discharged at each hour and is also used to compute the CAPEX and OPEX of the BESS:

$$P_{BESS}={\displaystyle \frac{C_{BESS}}{EPR}}$$

(5)

The charge and discharge are found in Figure 2. It was carried out accordingly for each hour of the year. The resulting charge and discharge powers are considered from the system’s point of view: the power available to charge the battery and the power obtained from discharging it.

Hence, the power values do not represent the actual energy that is stored in the battery. $\eta ch/dis$ is only considered for the computation of the battery SOC. The latter is computed using Equation (6):

$$SO{C}^t={SOC}^{t-1}+P_{ch}^t {\eta }_{dis}-{\displaystyle \frac{P_{dis}^t}{{\eta }_{ch}}}$$

(6)

where $SO{C}^{t-1}$ is the SOC of the previous timestep. The SOC is generally given in kWh. Thanks to charge and discharge modelling, it never exceeds battery capacity $C_{BESS}$, nor does it reach a value below $SO{C}_{min}$.

Once the annual electricity charged and discharged is known, the number of full charge/discharge cycles can be computed according to Equation (7).

$$n_{BESS}={\displaystyle \frac{n_{BESS-cycles}}{5475}}$$

(7)

The corresponding number of years is computed by dividing the number of lifetime cycles from

Table 5. Cost parameters, financial parameters, and emission coefficients.

Data	Variable Name	Value	Source
Lifetime
System lifetime	n	25 years	[49]
BG lifetime	$n_{BG}$	25 years	[50]
PV modules lifetime	$n_{PV}$	25 years	[51]
PV converter lifetime	$n_{PV-c}$	15 years	[52]
BESS calendar life	$n_{cBESS}$	15 years	[50]
BESS cycle life	$n_{BESS}$	5475 cycles	[50]
Financial Data
General inflation rate	g	3%	[49]
Corporate tax rate	TR	12.5%	[53]
Discount rate	r	6%	[54]
PV converter inflation rate	$g_{PV}$	−5%	[55]
BESS inflation rate	$g_{P{V}_{BESS}}$	−5.7%	[50]
Capital Cost
BG capital cost	$IBG$	6000 EUR/kW	[14]
BG market value at end of life	$MVBG$	0.1·IBG	[56]
PV capital cost	$IPV$	1500 EUR/kW	[57]
PV market value at end of life	$MVPV$	0	[57]
PV converter capital cost	IPV-c	150 EUR/kW	[35]
PV converter market value at 15 years	MVPV-c	0	[57]
BESS capital cost power	IBESS	2749.83 EUR/kW	[50]
BESS market value at 15 years	MBESS	0	[50]
Fixed O&M Cost
BG fixed O&M costs	O&M, BG	0.12 EUR/kg	[58]
PV fixed O&M costs	O&M, PV	28.91 EUR/kW	[49]
BESS fixed O&M costs	O&M, BESS	0 EUR/kW	[59]
Variable O&M Cost
BG variable O&M costs (PBG ≤ 100 kW)	O&M, BG	0.18 EUR/kWh	[59]
BG variable O&M costs (PBG > 100 kW)	O&M, BG	0.12 EUR/kWh	[59]
Subsidies
PV investment grant (PPV ≤ 20 kW)	$spv$	300 EUR/kW	[53]
PV investment grant (PPV ≤ 200 kW)	$spv$	200 EUR/kW	[60]
PV investment grant (PPV ≤ 1000 kW)	$spv$	100 EUR/kW	[60]
Roadside
Roadside wood pulp price	praw, wood	40 EUR/t	[57]
Dried wood chips	pdried, wood	120 EUR/t	[57]
Grid financial data
SHP fixed PPA price	pSHP, PPA	0.0946 EUR/kWh	[50]
Carbon tax and Emission
Carbon tax on biomass conversion	pCarbon-tax	0 EUR/tCO2eq	[28,29]
Emissions from biomass conversion	mCO2eq., $BG$	69 gCO2eq/kWh	[61]
Emissions from grid electricity	mCO2eq. $Grid$	187 gCO2eq/kWh	[62]

by the actual number of cycles per year. The lifetime of the battery is then evaluated according to the shorter lifetime: either the one derived from the cycles or the calendar life from Table 5:

$$n_{BESS-cycles}={\displaystyle \frac{\sum E_{a,ch}+\sum E_{dis}}{2 C_{BESS}}}$$

(8)

The system is grid-connected, as depicted in Figure 1. However, due to grid capacity restrictions, this research assumed that the feed-in limitation can be overcome for the combined site and primary site in the near future to give more flexibility to the entire system. The SHP has an hourly feed-in tariff according to a fixed value. For electricity purchase prices, the facility has fixed night and day tariffs. Between 11:00 p.m. and 07:00 a.m., it is at 0.1477 EUR/kWh, while it remains at 0.2393 EUR/kWh for the rest of the day. These tariffs are obtained from the EMS of the site. For the primary site, the feed-in tariff is equal to the electricity purchase price and has the same hourly variation through the day. This variable feed-in tariff is also applied to the combined site.

2.2.7. Financial and Emission Parameters

All input parameters for the financial calculations are found in Table 5. The system lifetime is set to 25 years in the financial analysis according to similar studies [49]. Adhering to Irish tax rules, any renewable energy technology is depreciated linearly over 8 years, regardless of its lifetime [53].

2.3. Proposal Simulation for Technical and Financial Parameters

In this section, the methodology implemented in HY4RES-AHS for simulating energy flows and their corresponding financial assessment is described. The combined site was selected as the reference case, as it integrates all technologies considered in both the primary and secondary sites (Figure 1). An overview of the technical structure of the programming tool’s model is presented in Figure 3. At the initial stage, the hourly load profiles, along with the generation profiles of the wind turbine and the small hydropower plant (SHP), are introduced into the model. Subsequently, the required input parameters are inserted. The installed capacities of the photovoltaic (PV) and biogas (BG) systems, as well as the battery energy storage system (BESS), are either predefined or optimized through Solver. Based on the PV capacity defined, the hourly generation profile is calculated.

The total generation is then compared with the fixed-load profile. When an excess is identified and is sufficiently large to operate the wood-drying kiln, its load is deducted from the balance for the corresponding hour, and the amount of dried wood is subsequently determined. The operation of the BG unit is validated, and its generation is incorporated into the balance. In Figure 3, the dashed hexagons represent the decision variables for optimization.

Afterwards, the BESS operation is applied: Any remaining deficit is covered by electricity purchased from the grid, whereas any surplus exceeding the BESS charging capacity is exported at the hourly feed-in tariff. When this surpasses 120 kW, the value is inserted into the grid, and the remaining surplus can be technically absorbed by the power electronic converters of the wind turbine and PV system.

Once the hourly simulations are completed, annual performance indicators are calculated. Among them, the system’s self-sufficiency ratio (SSR) is emphasized as an indicator of the degree of grid independence achieved by the hybrid energy system. The SSR is determined according to the following expression:

$$SSR={\displaystyle \frac{E_{a,loads}+E_{a,kiln}-E_{a,fromgrid}}{E_{a,loads}+E_{a,kiln}}}$$

(9)

where $E_a$ denotes the annual electricity generated or consumed in kWh.

Additionally, the self-consumption ratio (SCR) of the system, indicating the amount of renewable generation directly consumed on site, is computed according to Equation (10). E_a,gen corresponds to the sum of the renewable energy generated on site during the whole year:

$$SCR={\displaystyle \frac{E_{a,loads}+E_{a,kiln}}{E_{a,gen}}}$$

(10)

An overview of the cash-flow simulation is given in Figure 4. Dashed hexagons represent the decision variables for optimization. Initially, based on the current situation, the system without the BG, PV, or BESS was considered. Hence, any differences in cash flows that occur due to the integration of new technologies are taken into account.

Investment cash flows (ICFs) are calculated for each of the 25 years according to Equation (11). The residual value (RV) of the asset after its lifetime is considered exclusively in the final year of the project or of the asset’s operational life. The initial investment is accounted for in the first year, while reinvestments are included whenever an asset reaches the end of its lifetime before the project is completed:

$$ICF=-I_{PV}+R{V}_{PV}-I_{PV,conv}+{RV}_{PV,conv}-I_{BG}+{RV}_{BG}-I_{BESS}+{RV}_{BESS}$$

(11)

and RV is computed according to Equation (12):

$$RV=MV-\left(MV-BV\right)TR$$

(12)

where MV stands for the market value of the asset at the end of the project’s lifetime, and BV stands for the book value of the same asset in the last year of the project or at the end of life of an asset. As the company profits from the higher market value, it has to pay corporate tax TR on the difference.

In the next step, the operating cash flows (OCFs) are calculated. With the resulting dried wood and electricity purchased from the grid and fed into the grid, the wood and grid cash flows are computed. The cash flow from wood drying and selling can be calculated according to Equation (13). In contrast, the grid cash flow is computed according to Equation (14). This is carried out once for the baseline and then for the optimized system, and the difference is then accounted for in the revenue calculation:

$${CF}_{wood} = \left(\right(m_{wood,dried} - m_{wood,BG})·p_{dried,wood}) - m_{wood,dried}·p_{raw,wood}$$

(13)

CF_grid = E_excess·p_grid,sell − E_deficit·p_grid,buy

(14)

Next, the cash-flow changes regarding electricity sales and wood sales are computed for the first year. In order to take inflation into account, the annual cash-flow results from the technical simulation are compounded with the inflation rate with respect to the corresponding year of the project according to

$$∆Revenue=∆Electricity sales+∆Woodsales$$

(15)

This calculates the change in revenue for the implementation of the BG, PV, and BESS. The same approach is taken for electricity purchased from the grid. The costs for purchasing wood are neglected, as the amount of wood dried does not change due to the implementation of the BG; only the amount sold changes. According to the optimal sizing of the PV, BESS, and BG, the fixed and variable O&M costs are computed for the first year. Afterwards, they are combined with the annual inflation rate with respect to the remaining years of the project’s lifetime. This leads to a change in the cash flows of expenses according to Equation (16):

$$∆Expenses=∆Elecricity purchased+C_{O\&M,BG}+c_{O\&M,BG}+C_{O\&M,BESS}+c_{O\&M,BESS}+C_{O\&M,PV}+c_{O\&M,PV}$$

(16)

The OCF can be computed according to Equation (17), in which depreciations are calculated according to IRIS rule, where any renewable energy technology is depreciated linearly over 8 years regardless of its lifetime [26]:

$$OCF=(EBITDA-Depreciations) \left(1-TR\right)+Depreciations$$

(17)

Here, EBITDA is defined as

$$EBITDA=∆Revenue-∆Expenses$$

(18)

Finally, the free cash flows (FCFs) can be computed via the following expression:

FCF = ICF + OCF

(19)

When the present day with discount rate (r) is discounted, the discounted cash flows (DCFs) can be evaluated. The sum of these cash flows gives the NPV, according to Equation (20), where t is the corresponding year. It is a fitting metric for assessing the viability of a project, as it discounts cash flows over the lifetime of the project with respect to the current date and enables evaluations on monetary terms in the present.

$$NPV=\sum _{t=0}^{25}{\displaystyle \frac{FCF}{{\left(1+r\right)}^t}}-\sum _{t=0}^{25}DFC$$

(20)

Additionally, the profitability index can be calculated according to

$$PI={\displaystyle \frac{NPV}{I}}$$

(21)

Other metrics are also computed, such as the payback period (PP), the LCOE, and the modified internal rate of return (MIRR). The MIRR is chosen instead of the internal rate of return (IRR), as it is more accurate for projects where reinvestments occur. It is computed according to the following expression:

$$MIRR=\sqrt[n]{{\displaystyle \frac{FVC{F}^{+}}{FVC{F}^{-}}}}$$

(22)

where $FVC{F}^{+}$ is the future value of all positive cash-flows, $FVC{F}^{-}$ is the present value of all negative cash-flows, and n is the year.

The LCOE value is calculated separately for each generation technology and derived from Equation (23):

$$LCOE={\displaystyle \frac{\sum _{t=0}^{25}\frac{C_{O\&M}+c_{O\&M}+I}{{\left(1+r\right)}^t}}{\sum _{t=0}^{25}\frac{E_a}{{\left(1+r\right)}^t}}}$$

(23)

In this formulation, the total costs incurred over the project’s lifetime are divided by the total energy generated by the corresponding technology over its lifetime, with both quantities discounted to their present values.

The computation of the PP is slightly more complex. It is defined as the period until the accumulated DCF turns positive, given in years. The corresponding mathematical description is given by Equation (24):

$$\begin{gathered} \mathrm{if} \sum _{t=0}^{p}DCF>0, t=min \\ PP=t\left(\sum _{t=0}^{p}DCF>0\right)+\left|{\displaystyle \frac{DC{F}_{p-1}}{DC{F}_p}}\right| \end{gathered}$$

(24)

For year p, the sum of DCF turns positive; p − 1 is the previous year to the year p.

2.4. Proposal of Optimization and Sensitive Analysis

The main objective of the proposed optimization can be to maximize the net present value (NPV) or the self-sufficiency ratio. The implementation of the optimization model in Excel through Solver restricts the available algorithms to a limited set. Specifically, simplex linear programming (SLP) is suitable for linear and continuous problems; however, it cannot be applied in this case due to the non-linear nature of the optimization problem. For non-linear cases, two alternatives are available: the evolutionary method, which relies on metaheuristics and can be applied to non-smooth and non-linear problems, and the generalized reduced gradient (GRG) algorithm, designed for non-linear but smooth problems. The GRG method exploits the derivatives of the objective function and iteratively adjusts input parameters by analysing the slope of the function. While effective, this approach is prone to converging to local optima, potentially neglecting the global optimum. To overcome this limitation, the multi-start option is incorporated, which initializes the algorithm from multiple starting points across the search space, enhancing the likelihood of identifying the global maximum.

Given that the NPV or SSR fitness function is non-linear but smooth, both the evolutionary method and GRG with multi-start are suitable approaches.

Table 6. Fitness function, decision variables, and optimization parameter for the evolutionary method and multi-start GRG.

Definition of Programming Setup
Objective Function	$\mathit{m}\mathit{a}\mathit{x}\mathit{N}\mathit{P}\mathit{V},\mathbf{max}\mathit{S}\mathit{S}\mathit{R}$
Decision variables	$P_{PV},{ C}_{BESS}\&P_{BG}$
Constraints on $P_{PV}$	$0\le P_{PV}\ge 120 \mathrm{kW};{ P}_{PV}=int$
Constraints on $P_{BG}$	$0\le P_{BG}\ge 500 \mathrm{kW};{ P}_{BG}=int$
Constraints on $C_{BESS}$	$0\le C_{BESS}\le 1000 \mathrm{kWh};{ C}_{BESS}=int$
Setup
Value	Evolutionary	GRG
Convergence	0.001	0.001
Mutation ratio	0.075
Population size	100	100
Random seed	5	5
Time limit without improvement	30 s
Require bound on variables	Yes	Yes
Derivatives		Forward
Multi-Start		Yes

summarizes the optimization setup, including input parameters, the objective function, and the decision variables. The upper boundary of 120 kWp for the PV system is determined by the physical constraint of available rooftop space, while the limits for the battery energy storage system (BESS) and the backup generator (BG) are defined by the validity range of the input parameters rather than site-specific restrictions.

Self-sufficiency ratio (SSR) maximization enables the evaluation of a configuration that achieves the highest degree of energy autonomy. The optimization procedure follows the same structure as the one described for NPV maximization. Figure 5 illustrates the workflow of the NPV optimization process, where the dashed-line hexagons denote the decision variables.

After the optimization found the optimal size of the BG, PV, and BESS, a sensitivity analysis was conducted on the most uncertain parameters. The same approach undertaken in [49] is chosen, where each parameter is changed, and a change in NPV and PP is observed. The main input parameters on which the sensitivity analysis is conducted are essentially the discount rate, each of the technology’s investment costs, the electricity feed-in price, the electricity purchase price, and the biomass gasifier ICE unit’s conversion efficiency.

3. Results of the Case Study

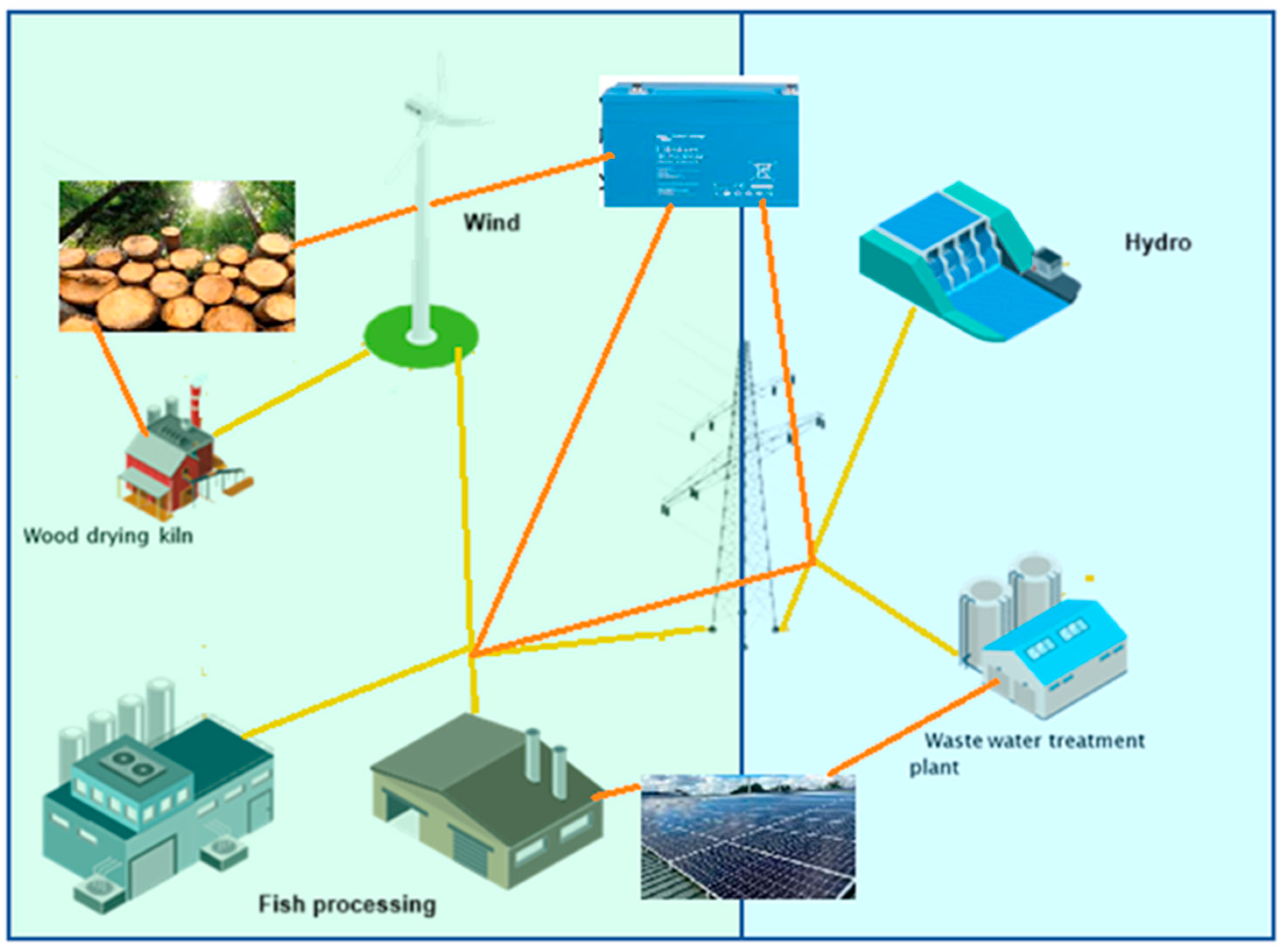
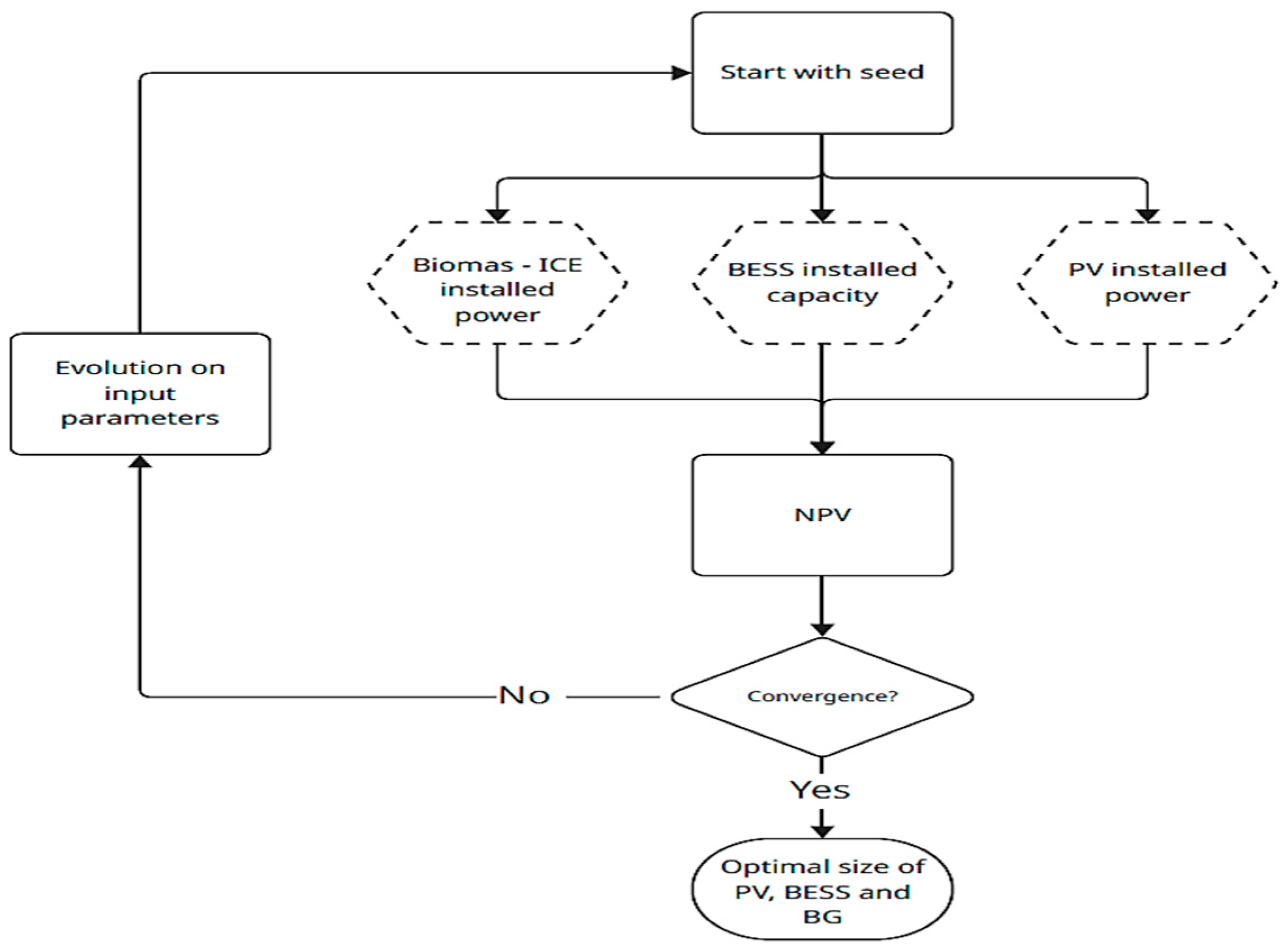
3.1. Input Data

The definition of several parameters is necessary for the simulations, such as those presented in

Table 7. Input data values considered.

System Parameters
Fixed Generation		General Financial Indicators
Parameter	Value	Parameter	Value
$P_{hydro}$/(kW)	380	Interest rate	0.0566
$P_{wind}$/(kW)	850	Inflation	0.03
Biomass drying kiln		Corporate tax rate	0.125
Parameter	Value	Discount rate	0.06
$P_{rated}$/(kW)	10	PV DC-DC converter inflation rate	−0.05
$P_{min}/$(kW)	5	BESS inflation rate	−0.057
$E_{BG}$/(kWh/t wood)	2000
Wood		Capital costs
Parameter	Value	Parameter	Value
Type	Sitka spruce	Wind Turbine/(EUR/unit)	500,000.00
$m_{wood,t_0}$/(t)	0	SHP/(EUR/unit)	100,000.00
LHV/(kWh/t)	3811	BG/(EUR/kW)	3000.00
Moisture content	0.2	PV/(EUR/kW)	1000.00
--	--	PV converter/(EUR/kWp)	150
--	--	BESS power capacity/(EUR/kW)	1000.00
Biomass gasifier ICE		Fixed O and M costs
Parameter	Value	Parameter	Value
Efficiency_wood-elec	0.25	Wind Turbine/(EUR/year)	25,782.00
Grid parameters		SHP/(EUR/year)	30,000.00
Parameter	Value	BG fraction of installed capacity	0.12
$P_{feed-in,limiy}$/(kW)	500	PV/(EUR/kW)	28.91
		BESS/(EUR/kW)	25
BESS		Emissions data
Parameter	Value	Parameter	Value
Initial SOC/(SOC/C)	0.25	BG emissions/(g CO2 eq./kWh)	69
Charge efficiency	0.95	Grid emissions/(g CO2 eq./kWh)	187
Discharge efficiency	0.95	Carbon tax/(EUR/t CO2 eq.)	-
$SO{C}_{min}$/(SOC/C)	0.1	Carbon tax growth rate	0.03
Energy to Power ratio	4
Financial indicators		Variable O&M costs
Parameter	Value	Parameter	Value
Wood chip purchase price/(EUR/t)	40	BG < 100 kW/(EUR/kWh)	0.15
Wood chip selling price/(EUR/t)	120	BG > 100 kW/(EUR/kWh)	0.1
System lifetime/(years)	25	Market value
BG lifetime/(years)	25	Parameter	Value
Depreciation duration/(years)	8	BG after life-time/%-CAPEX	0.1
Wind turbine lifetime/(years)	20	PV system (excl. converter)/(EUR/kW)	0
Wind turbine res lifetime/(years)	8	PV converter/(EUR/kW)	0
SHP lifetime/(years)	50	BESS/(EUR/kWh)	0
PV modules lifetime/(years)	25	Grid tariffs
PV DC-DC converter lifetime/(years)	15	Parameter	Value
BESS calendar life/(years)	15	Fixed feed-in tariff/(EUR)	0.0946
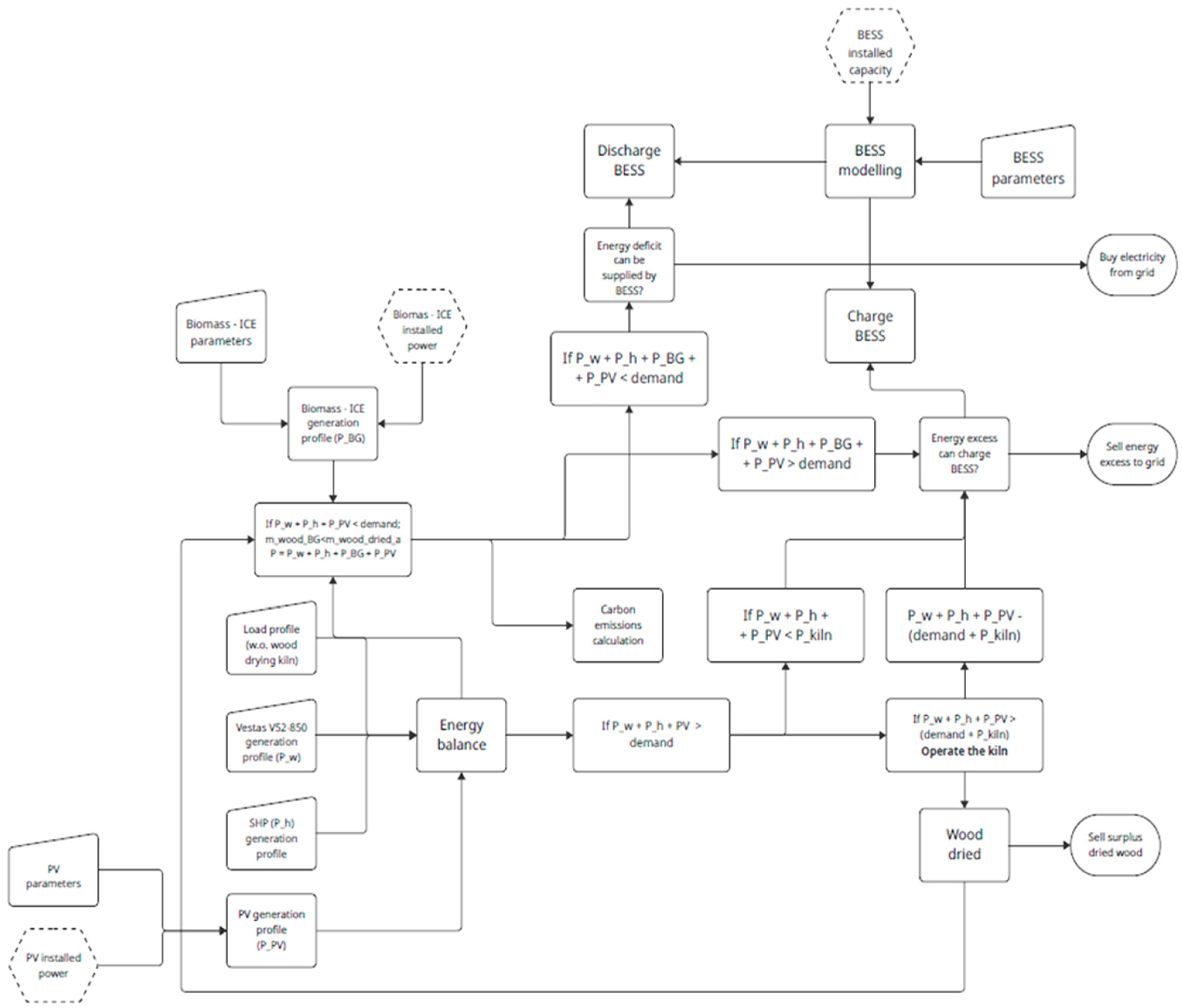
BESS cycle life/(cycles)	5475	Fixed purchase price/(EUR)	0.3808

. This table lists all variables corresponding to what is called scenario 1, illustrating the complexity of the simulation tool and hybrid energy platform developed for renewable energy optimization, which can be applied in different sectors.

The system integrates multiple renewable energy sources, including hydropower with a capacity of 380 kW, wind power at 850 kW, and a biomass gasifier producing 2000 kWh per ton of wood. The biomass used is Sitka spruce, with a lower heating value of 3811 kWh/t and a moisture content of 20%. The biomass-to-electricity conversion efficiency is 25%. Financially, the system operates under an interest rate of 5.66%, a discount rate of 6%, and an inflation rate of 3%. Corporate tax is set at 12.5%, while inflation rates for PV converters and BESS are negative at −5% and −5.7%, respectively. Capital costs include EUR 500,000 per wind turbine, EUR 100,000 per SHP unit, EUR 3000/kW for biomass gasifiers, EUR 1000/kW for PV systems, EUR 150/kWp for PV converters, and EUR 1000/kW for BESS power capacities. Fixed operation and maintenance costs are EUR 25,782/year for wind turbines, EUR 30,000/year for SHP, EUR 28.91/kW for PV, and EUR 25/kW for the BESS. The grid allows a feed-in limit of 500 kW, with biomass gasifiers representing 12% of installed capacity. Battery energy storage systems (BESSs) start with a state of charge (SOC) of 25%, operate with 95% charge/discharge efficiency, and maintain a minimum SOC of 10%. Their energy-to-power ratio is 4. Emission data show that biomass gasifiers emit 69 g CO₂/kWh, while grid electricity emits 187 g CO₂/kWh. Carbon tax is not defined, but its growth rate is set at 3%. Variable operating costs include EUR 40/t for wood chip purchases and EUR 120/t for sales. Biomass gasifiers under 100 kW incur EUR 0.15/kWh in O&M costs, while those over 100 kW cost EUR 0.10/kWh. The system and biomass gasifier lifetimes are 25 years, with wind turbines lasting 20 years and SHP up to 50 years. PV modules and converters last 25 and 15 years, respectively, while a BESS has a calendar life of 15 years and a cycle life of 5475 cycles. Depreciation is calculated over 8 years, and the residual value of biomass gasifiers after their lifetime is 10% of CAPEX. Market values for PV systems, converters, and BESSs are set to zero. Grid tariffs include a fixed feed-in rate of EUR 0.0946 and a fixed purchase price of EUR 0.3808.

3.2. Decision Variables

The energy system’s configuration is defined by a set of key decision variables that shape its performance and capacity. The installed biomass gasifier’s power (P_BG) is set at 20 kW, contributing to the renewable generation mix. The system’s battery energy storage capacity (C) is 1000 kWh, with an initial state of charge (SOC) of 25 kWh, ensuring readiness for load balancing and energy dispatch.

Solar energy plays a significant role, with a photovoltaic (PV) system capacity ($P_{PV}$) of 150 kW, providing clean electricity during daylight hours. To support energy storage and grid flexibility, the battery power capacity ($P_{BESS}$) is configured at 12 kW, enabling efficient charge and discharge cycles.

3.3. Technical Summary

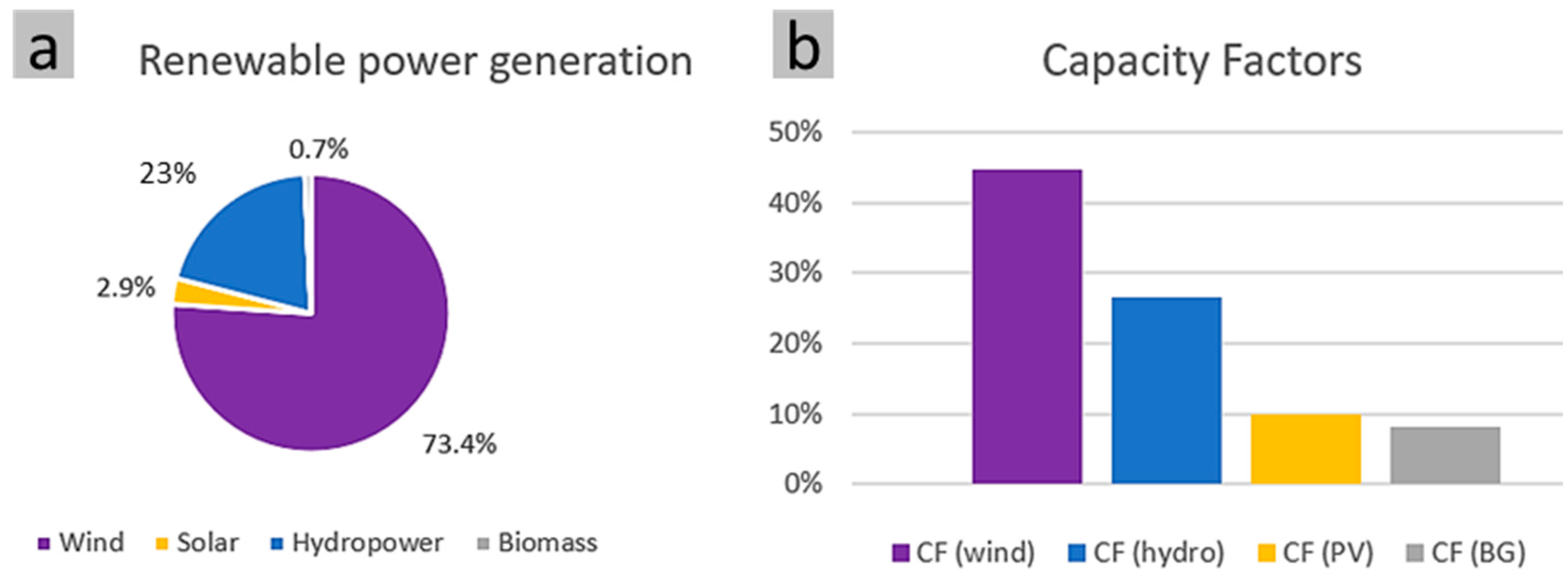
The energy system demonstrates a strong reliance on renewable sources (Figure 6), with wind energy contributing the largest share at 3,262,431 kWh, representing 73.1% of total generation (

Table 8. Main results of scenario 1.

Generation		Self-Sufficiency and Self-Consumption
Source	$E_a$/kWh [$E_i/E_{tot}$]	Metric	Value
Wind	3,323,431 [73.4%]	Self-sufficiency (SSR)	93.0% (2,335,896 kWh)
Solar	130,757 [2.9%]	Self-consumption (SCR)	53.70%
Hydropower	884,225 [19.5%]	Wood
Primary 4	0 [0.0%]	Metric	Value
Biomass	31,020 [0.7%]	$m_a$ (dried)/t eq.	35.73
Total generation	4,369,434 [96.5%]	$m_a$ (used)/t eq.	32.56 (91%)
From grid	161,012 [3.6%]	Carbon emissions
$E_{tot}$	4,530,446	Metric	Value
$E_{loss}$ (grid limit)/kWh	89,288 [2.0%]	$m_{a,grid}$/t CO2 eq.	35.56
Loss (grid limit)/EUR	18,276	$m_{a,grid}$/t CO2 eq.	32.89
Consumption		$m_{a,BIG}$/t CO2 eq.	0.99
Source	E_a/kWh	SUM	33.87
Load	2,440,296 (54.8%)	Utilization factor of generation
Drying kiln	71,461 (1.6%)	Source	h_a/h
Grid feed-in	1,943,697 (43.6%)	Wind	3910
Total	4,455,455	Hydro	2327
Storage		PV	872
Type	$E_a$/kWh	BG	716
BESS charge	15,836.48
BESS discharge	13,366.18
n_cycles	15
Lifetime (cycles)/years	375

). Solar and hydropower follow with 884,225 kWh (19.8%) and 884,225 kWh (6.1%), respectively, while biomass plays a minimal role at 3999 kWh (0.1%). Overall, renewable sources account for 95.5% of the total generation, amounting to 4,459,694 kWh.

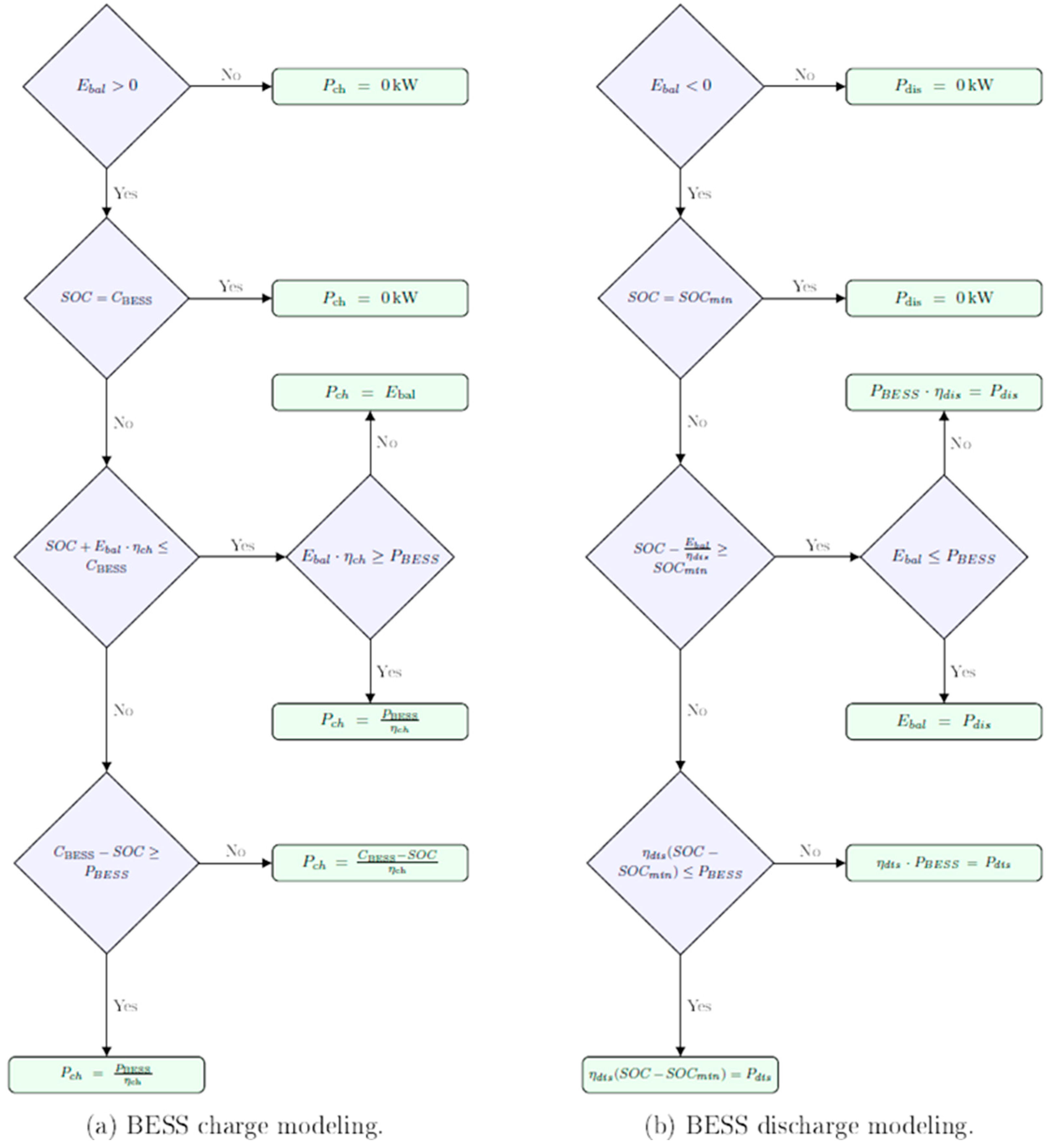
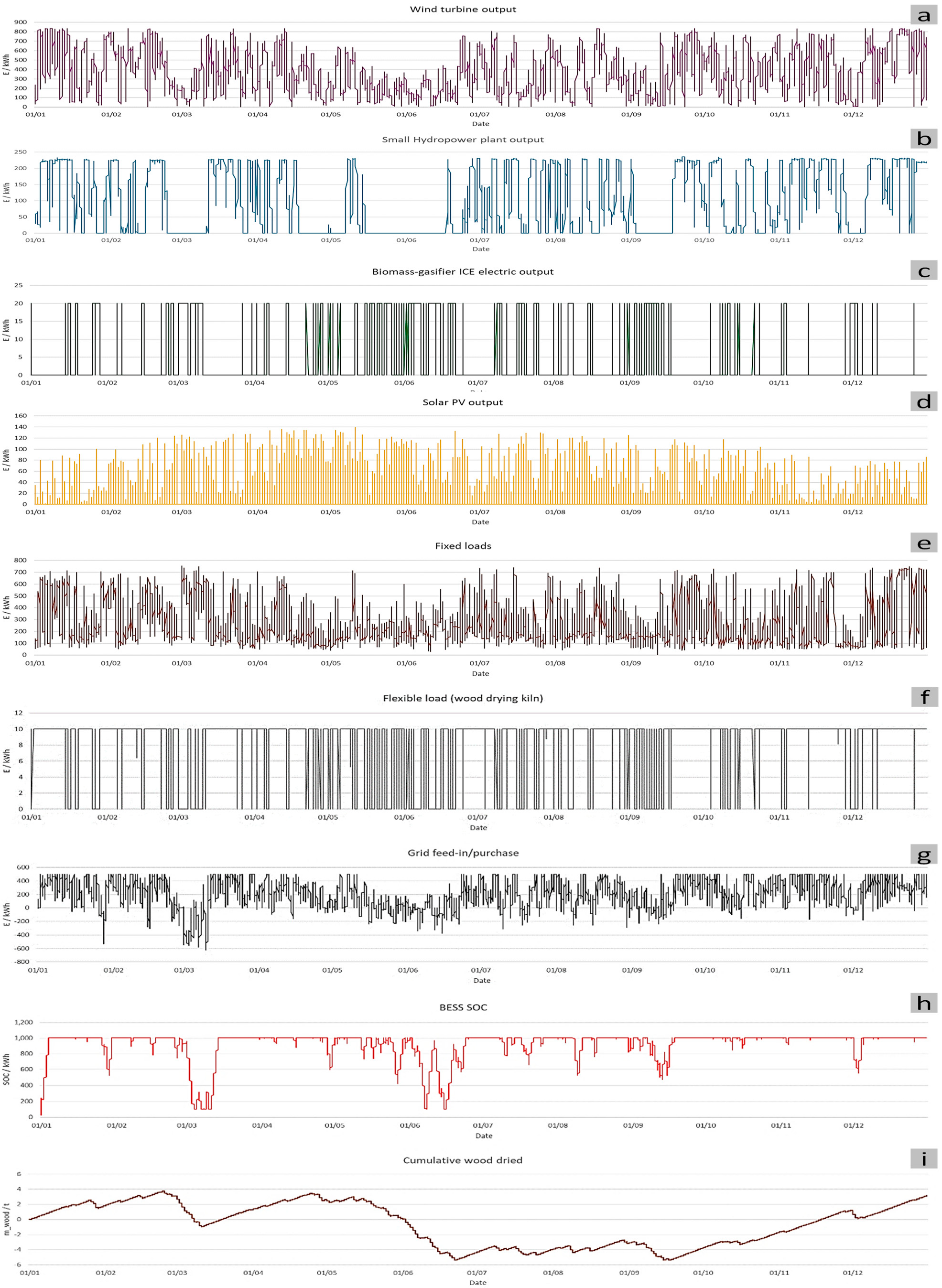
The system also imports 151,012 kWh from the grid, covering 3.2% of the energy demand. The contribution of each RES is shown in Figure 7a. Electricity consumption is dominated by the system’s load, totaling 4,681,866 kWh. No energy is allocated to the drying kiln, while 151,012 kWh is fed back into the grid. The battery energy storage system (BESS) supports grid flexibility with 13,986.48 kWh of both charge and discharge, operating over a cycle life of 5475 cycles and a calendar life of 15 years. The system achieves a high self-sufficiency rate of 96.8%, indicating minimal dependence on external energy sources. Its self-consumption rate stands at 50.7%, reflecting the efficient use of locally generated energy.

The technical summary highlights key performance metrics related to wood usage, carbon emissions, and generation efficiency. The system consumes 35.73 tons of wood, with 51% of it used in the gasification process. Carbon emissions from biomass gasification amount to 35.95 g CO₂ eq./kWh, while grid electricity contributes slightly less at 32.36 g CO₂ eq./kWh. The overall system emissions average 33.87 g CO₂ eq./kWh. In terms of utilization, wind energy shows the highest operational efficiency, with 3970 full-load hours, followed by hydropower at 2367 h. PV systems operate for 876 h, and biomass gasification operates for 682 h. The capacity factors reflect this trend, with wind at 45%, hydro at 27%, PV at 10%, and biomass gasification at 8%, indicating wind as the most productive source in the system (Figure 7b).

3.4. Financial Summary

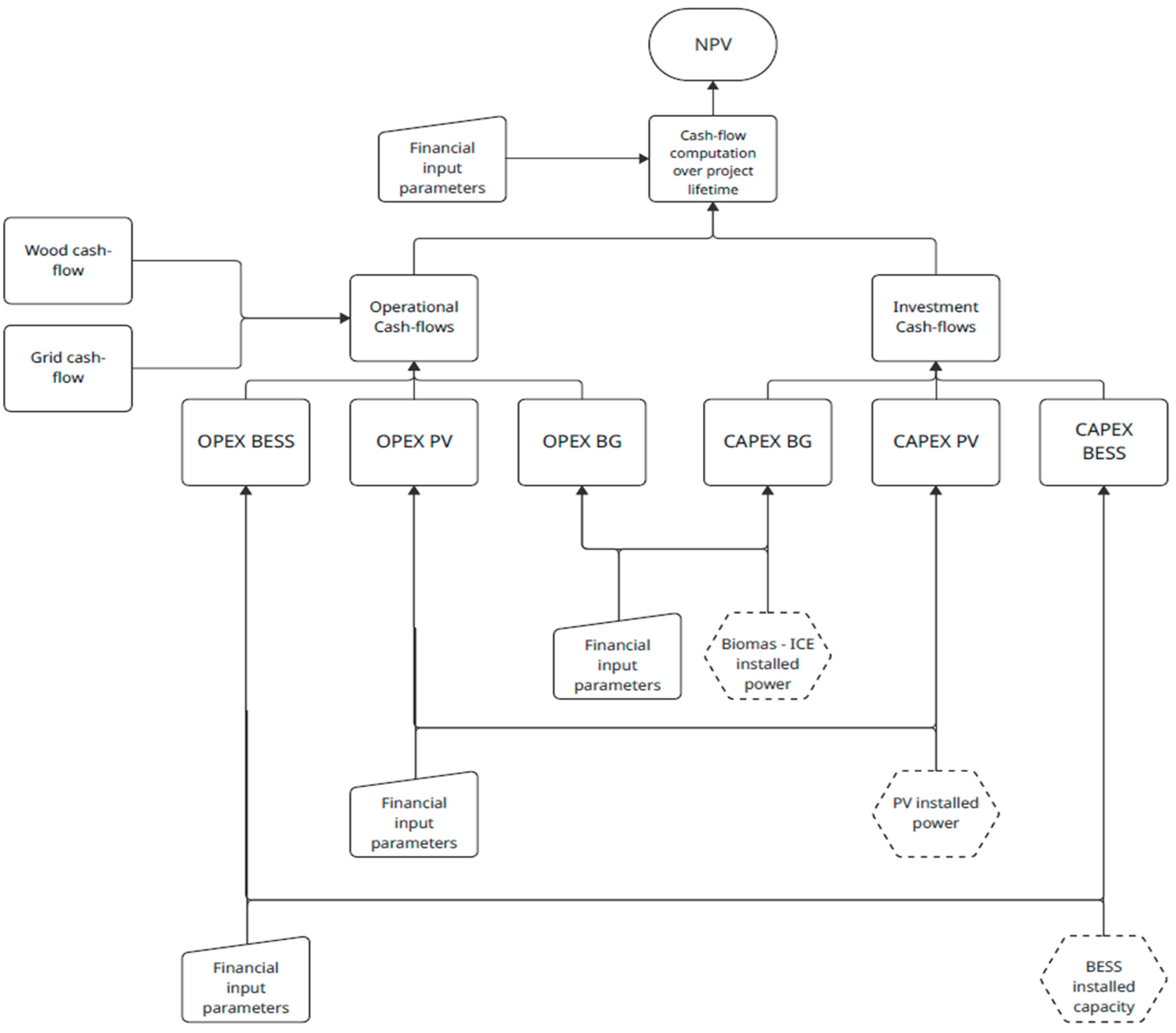
The financial results from scenario 1 indicate that the project is economically viable, with a net present value (NPV) of EUR 107,290.91, suggesting a positive return over its operational lifetime. The internal rate of return (IRR) stands at 12%, which is comfortably above typical discount rates, reinforcing the attractiveness of the investment. However, the modified internal rate of return (MIRR) is slightly lower at 8%, reflecting more conservative reinvestment assumptions. The total investment required is EUR 114,500, and the payback period is estimated at 16.05 years. While this is relatively long, it is not uncommon for renewable energy infrastructure projects of this type. In terms of energy cost efficiency, the levelized cost of energy (LCOE) for biomass gasification is notably high at EUR 1287/MWh, indicating that this technology is less cost-effective within the scenario. In contrast, photovoltaic generation offers a much lower LCOE of EUR 192/MWh, making it a more economically favourable option.

Table 9. Financial results of scenario 1.

Financial Results of Scenario 1
a	107,290.91
IRR	12%
MIRR	8%
PP/years	16.05
I_total/EUR	114,500.00
LCOE_BG/EUR/MWh	1287
LCOE_PV/EUR/MWh	192

presents a resume of financial investments with respect to Scenario 1, which is primarily driven by the performance of the PV system, while the high cost of biomass energy may allow reconsideration or optimization.

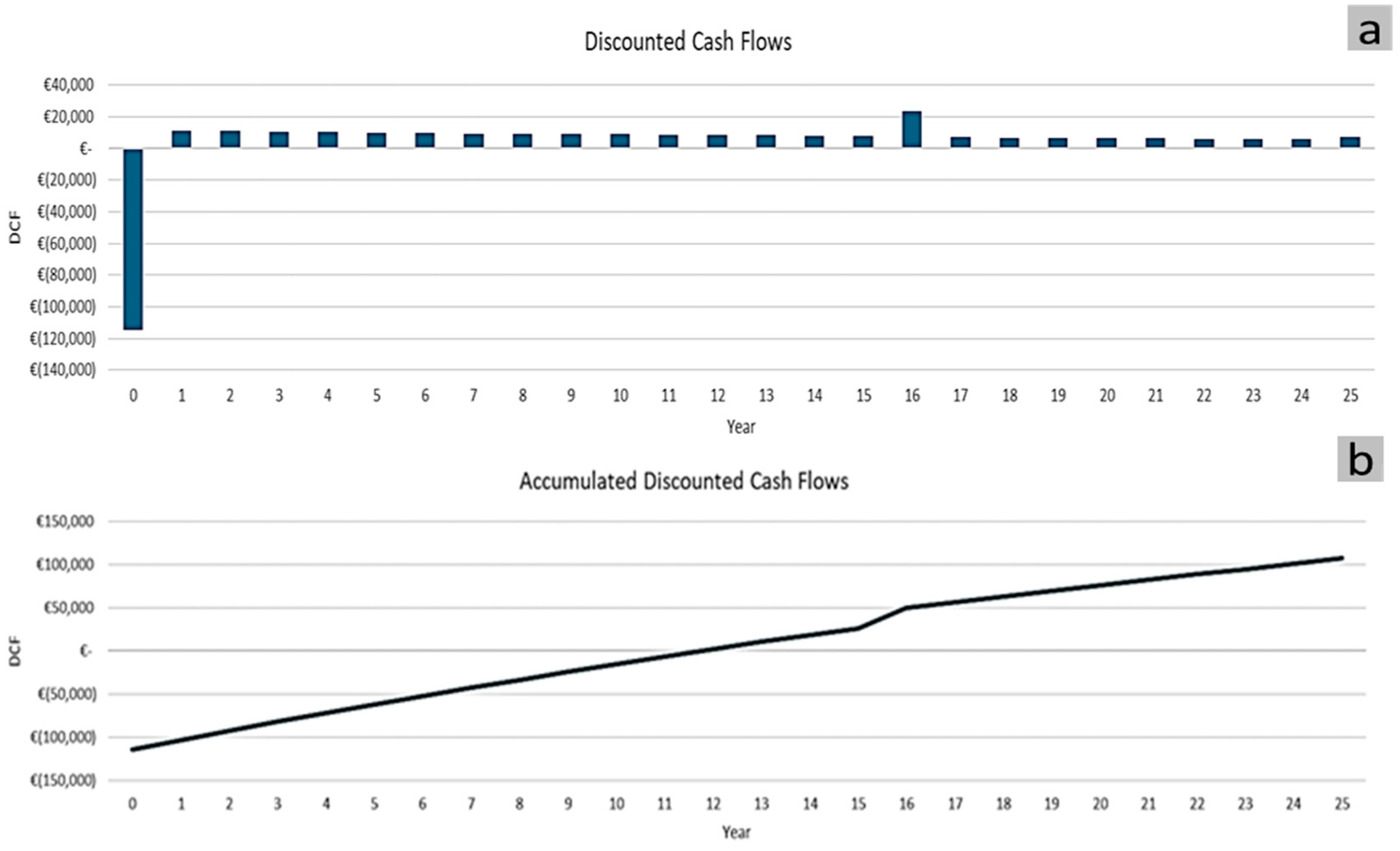
Figure 8a illustrates the discounted cash flows over a 25-year period for the project. It shows a significant initial investment in Year 0, represented by a large negative cash flow. Subsequent years exhibit relatively stable and modest positive returns, indicating consistent financial performance. Overall, the cash-flow trend supports a gradual return on investment, aligning with the long payback period observed in the financial results.

Figure 8b presents the accumulated discounted cash flows over 25 years, showing a steady upward trajectory after the initial investment. The curve crosses into positive territory around Year 16, confirming the payback period. A noticeable increase around Year 15 suggests a financial boost, possibly from asset recovery or reduced costs. Overall, the project demonstrates gradual capital recovery and long-term profitability, culminating in a positive net return by the end of its lifetime.

3.5. Sensitivity Analyses

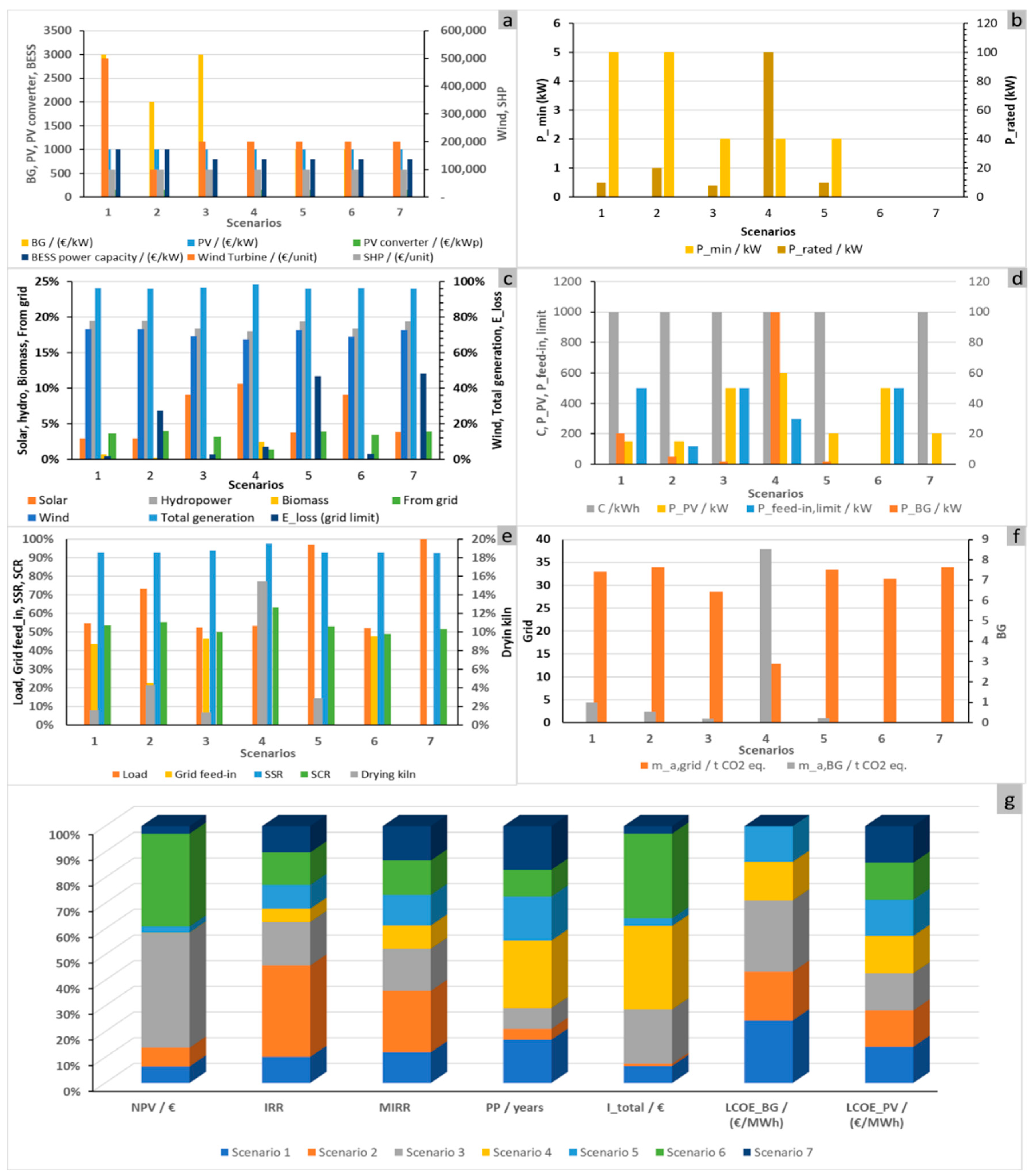
The developed analysis explores the techno-economic and environmental performance of these hybrid renewable energy systems, with a focus on biomass, solar, wind, small hydropower (SHP), and battery energy storage systems (BESSs), where the following results are presented in Figure 9.

From the seven scenarios (Sc1 to Sc7) modelled, the analysis explores techno-economic and environmental performances. Here is a breakdown of the key findings: In terms of technical configuration, with respect to the biomass drying kiln, the following conclusions are drawn: Only scenarios 1–5 include biomass kilns, with Sc4 having the highest rated power (100 kW). Sc6 and Sc7 exclude biomass entirely. Grid Feed-in Limits: These vary significantly from 0 kW (Sc5, Sc7) to 500 kW (Sc1, Sc3, and Sc6), influencing grid reliance and feed-in potential. Installed Capacities: PV ranges from 150 kW (Sc1, Sc2) to 600 kW (considering a future situation without this limitation) (Sc4). Biogas (BG) capacity peaks at 100 kW in Sc4, but it is zero in Sc6 and Sc7. With respect to storage performance, for BESS Usage, scenarios 1–5 utilize battery storage, with Sc2 showing the highest charge/discharge values. Sc6 and Sc7 omit BESSs, resulting in zero cycles and no storage contribution. Lifetime: Sc4’s BESS has the longest projected lifespan (861 cycles), likely due to its lower cycling intensity.

Based on the renewable generation mix by source and the type of scenarios, some highlights can be drawn: wind in Sc1, 2, 5, and 7 consistently presented high generation (~0.73). Solar in Sc4 has the highest share (10.6%). Hydropower is fairly stable at ~19% across all scenarios. Biomass in Sc4 presents the highest share (2.5%). Scenarios with higher renewable penetration show reduced grid reliance and emissions.

Regarding financial metrics, the NPV of Sc3 (EUR 741,293) has the stronger investment return. Sc2 exhibits fast payback and high profitability, with an IRR of 42%. For the payback period, Sc2 has 4 years and exhibits the quickest return on investment for all scenarios. Sc5 has the lowest biogas energy cost (LCOE_BG) of 734 EUR/MWh. Hence, Sc3 and Sc2 stand out financially, but Sc4 lags with a long payback (25 years) and low IRR (6%).

In terms of environmental impact and carbon emissions, scenario 4 (Sc4) achieves the lowest grid-related emissions (12.83 t CO₂ eq.) due to its high renewable penetration and limited grid dependence; however, it also records the highest biogas emissions as a result of its large biogas capacity. Nevertheless, Sc4 attains the highest values for both the self-sufficiency ratio (SSR, 97.8%), indicating strong grid independence, and self-consumption ratio (63.4%), positioning it as technically robust and environmentally advantageous, albeit financially, it is less favourable. By contrast, Sc2 delivers the strongest economic performance while maintaining acceptable environmental outcomes. Sc3 balances a high net present value (NPV) with moderate emissions and solid renewable integration, whereas Sc6 and Sc7, lacking biomass and storage, exhibit limited sustainability and resilience.

A comparative evaluation of the seven scenarios (Sc1–Sc7) highlights pronounced trade-offs among technical performance, environmental impact, and financial feasibility, as summarised in

Table 10. Main keynotes of the sensitivity analysis.

Scenario	NPV (EUR)	IRR (%)	Payback (Years)	SSR (%)	SCR (%)	Grid Emissions (t CO2)	Energy Loss (%)	Highlights
Sc1	107,291.0	12.0	16.0	93.0	53.7	32.89	2.0	Moderate performance; wind-dominated; modest financials
Sc2	121,835	42.0	4.0	93.0	55.2	33.89	27.4	Best financial viability; high losses
Sc3	741,293.0	20.0	7.7	94.0	50.0	28.52	2.8	Best NPV; balanced renewables; good autonomy
Sc4	2241.0	6.0	25.0	97.8	63.4	12.83	7.2	Technically strongest; lowest emissions; weak financials
Sc5	40,106.0	11.0	16.3	93.0	53.0	33.38	46.7	No grid feed-in; high losses; weak financials
Sc6	602,280.0	15.0	10.0	93.1	48.9	31.41	3.0	Strong NPV; no biomass; limited autonomy
Sc7	48,025.0	0.12	16.1	92.6	51.6	33.87	48.4	High losses; weak sustainability; poor financials

. Scenario 4 (Sc4) achieved the lowest grid-related carbon emissions, estimated at 12.83 t CO₂ equivalent, reflecting its strong renewable integration. However, this environmental advantage was offset by its limited financial viability, as evidenced by a minimal net present value (NPV) and a significantly prolonged payback period.

In contrast, Sc2 demonstrated outstanding financial feasibility, showing the highest IRR equal to 42% and the shortest payback, which was 4 years. Its technical efficiency was compromised by significant grid-related energy losses. Sc3 provided the most balanced outcome, combining the best NPV, which was equal to EUR 741,293, low emissions, and good renewable integration, defining moderate IRR and payback. Sc6 also performed strongly financially while maintaining low energy losses, but its lack of biomass and storage integration limited sustainability and autonomy. Scenarios 5 and 7, constrained by the absence of grid feed-in and/or biomass, show the highest energy losses (>45%), poor financial metrics, and weaker sustainability. Finally, Sc1 offered an intermediate pathway, with acceptable emissions, modest financial returns, and reasonable autonomy.

Hence, Sc3 showed the most balanced configuration, combining the highest NPV with moderate emissions and solid renewable integration. Unlike Sc2, which favoured financial returns at the expense of efficiency, or Sc4, which maximized environmental performance but suffered financially, Sc3 provided a practical, compromising solution. This balance makes it the most suitable scenario for real-world implementation within sustainable energy transition pathways.

3.6. Discussion

The comparative assessment of the seven modeled scenarios (Sc1–Sc7) reveals a complex interplay between technical configuration, financial viability, and environmental performance, underscoring the necessity of integrated evaluation frameworks for hybrid energy systems.

Technical and Environmental Trade-offs: Scenario 4 (Sc4) emerges as the technically strongest configuration, characterized by the highest rated biomass kiln power (100 kW), extensive renewable integration—particularly solar (10.6%) and biomass (2.5%)—and superior storage performance, with the longest battery lifespan (861 cycles). These attributes contribute to Sc4’s exceptional grid independence (SSR 97.8%) and lowest grid-related emissions (12.83 t CO₂ eq.). However, its elevated biogas emissions and limited financial returns (NPV EUR 2241; IRR 6%) highlight the environmental–financial trade-off inherent in highly renewable systems.

Financial Performance and Efficiency: Scenarios 2 and 3 (Sc2, Sc3) demonstrate strong financial metrics, with Sc2 offering the fastest payback (4 years) and highest IRR (42%), albeit with significant energy losses (27.4%). Sc3, by contrast, balances economic and environmental dimensions, achieving the highest NPV (EUR 741,293), moderate emissions (28.52 t CO₂ eq.), and robust renewable integration. This positions Sc3 as the most viable compromise between sustainability and profitability.

System Limitations and Design Implications: Scenarios 6 and 7, which exclude biomass and storage, exhibit constrained autonomy and sustainability. Sc6 performs well financially (NPV EUR 602,280) with low energy losses (3.0%), yet its lack of storage and biomass integration limits resilience. Sc7, with minimal IRR (0.12%) and high losses (48.4%), underscores the risks of under-investment in key system components. Similarly, Sc5’s absence of grid feed-in and high losses (46.7%) result in poor financial and environmental outcomes.

Strategic Insights for Implementation: The analysis confirms that no single scenario optimally satisfies all performance dimensions. Sc4 excels environmentally but lacks financial appeal; Sc2 maximizes returns but compromises efficiency; Sc3 offers a balanced configuration, making it the most suitable candidate for real-world deployment. These findings reinforce the value of multi-criteria decision analysis (MCDA) in guiding energy system design, where stakeholder priorities—be they environmental, economic, or technical—must be explicitly weighted.

4. Conclusions

This study introduces a tailored techno-economic–environmental assessment framework applied to a real-world case study in the fish processing sector, which is characterized by high energy demands and sensitivity to operational costs and environmental regulations. The analysis focuses on integrating two renewable energy sources—wind and hydropower—into the sector’s energy supply, using actual site-specific data and operational constraints. To support this evaluation, a dedicated optimization model named HY4RES-AHS (Hybrid for Renewable Energy Systems—Adaptive Hybrid Strategy) was developed. This model incorporates multi-criteria decision-making and adaptive scenario analysis to identify optimal hybrid configurations that balance cost-effectiveness, environmental performance, and operational reliability.

Across the seven analysed scenarios, distinct patterns emerge in terms of technical configuration, energy performance, environmental impact, and financial viability. Scenario 4 stands out as the most sustainable and autonomous configuration, featuring the highest self-sufficiency ratio (97.8%) and self-consumption ratio (63.4%), alongside the lowest grid carbon emissions (12.83 t CO₂ eq.). This is largely due to its robust integration of biomass and biogas systems, as well as having the highest photovoltaic capacity (600 kW). However, this technical excellence comes at a financial cost, showing the lowest net present value (EUR 2241), the longest payback period (25 years), and a modest internal rate of return (6%), making it the least attractive from an investment standpoint. In contrast, Scenario 2 offers the most compelling financial performance, with the highest IRR (42%), the shortest payback period (4 years), and the lowest total investment (EUR 14,500). Despite its economic appeal, it suffers from significant energy losses (27.4%) due to a restrictive grid feed-in limit (120 kW), which undermines its overall efficiency and sustainability. Scenario 3 presents a strong balance between financial and technical metrics. It achieves the highest NPV (EUR 741,293) and a solid IRR (20%), and it maintains low energy losses (2.8%) thanks to its generous grid feed-in capacity. Its renewable generation mix is well distributed, and it maintains a high self-sufficiency ratio (94%), making it a well-rounded option. Scenarios 5 and 7, which prohibit grid feed-in, experience the highest energy losses (46.7% and 48.4%, respectively), severely limiting their efficiency and sustainability. Scenario 6, while financially strong with an NPV of EUR 602,280, lacks biomass and biogas integration, resulting in zero emissions from those sources but also reduced system resilience and autonomy.

Overall, the analysis discloses that Scenario 4 is ideal for maximizing sustainability and energy independence, Scenario 2 excels in cost-efficiency, and Scenario 3 offers the best compromise between financial return and technical robustness. The remaining scenarios either suffer from grid constraints, a lack of renewable diversity, or poor economic performance, making them less favourable depending on the chosen priority.

In summary, Scenario 2 excels in cost-efficiency, Scenario 4 is ideal for maximizing sustainability and autonomy, and Scenario 3 offers the best overall balance across all key performance indicators.

While the comparative assessment across the seven scenarios provides valuable insights into the trade-offs between sustainability, autonomy, and financial viability, several limitations should be acknowledged. First, the analysis is based on static techno-economic parameters and assumes stable market conditions, which may not reflect future fluctuations in energy prices, technology costs, or policy incentives. Second, the grid feed-in constraints were modeled as fixed values, whereas in practice, these may vary dynamically or be subject to negotiation with grid operators. Third, the environmental impact assessment focused primarily on CO₂ emissions, without accounting for other relevant indicators such as land use, water footprint, or lifecycle emissions of renewable components. Additionally, the optimization framework did not incorporate the stochastic modeling of resource availability (e.g., wind and solar intermittency), which could affect system reliability and investment risk.

Future work should extend the modeling framework to include probabilistic scenarios and uncertainty quantification, enabling more robust decision-making under variable conditions. Incorporating demand-side management strategies and energy storage technologies could further enhance system flexibility and reduce energy losses, particularly in scenarios with restricted grid interaction. Moreover, expanding the environmental assessment to include multi-impact metrics and conducting stakeholder-informed evaluations would strengthen the applicability of the results to real-world planning contexts. Finally, replicating the methodology across different industrial sectors or geographic regions would help validate its generalizability and support the broader adoption of hybrid renewable energy systems.