Evaluation of Priority Queues in the Priority Flood Algorithm for Hydrological Modelling
Abstract
1. Introduction
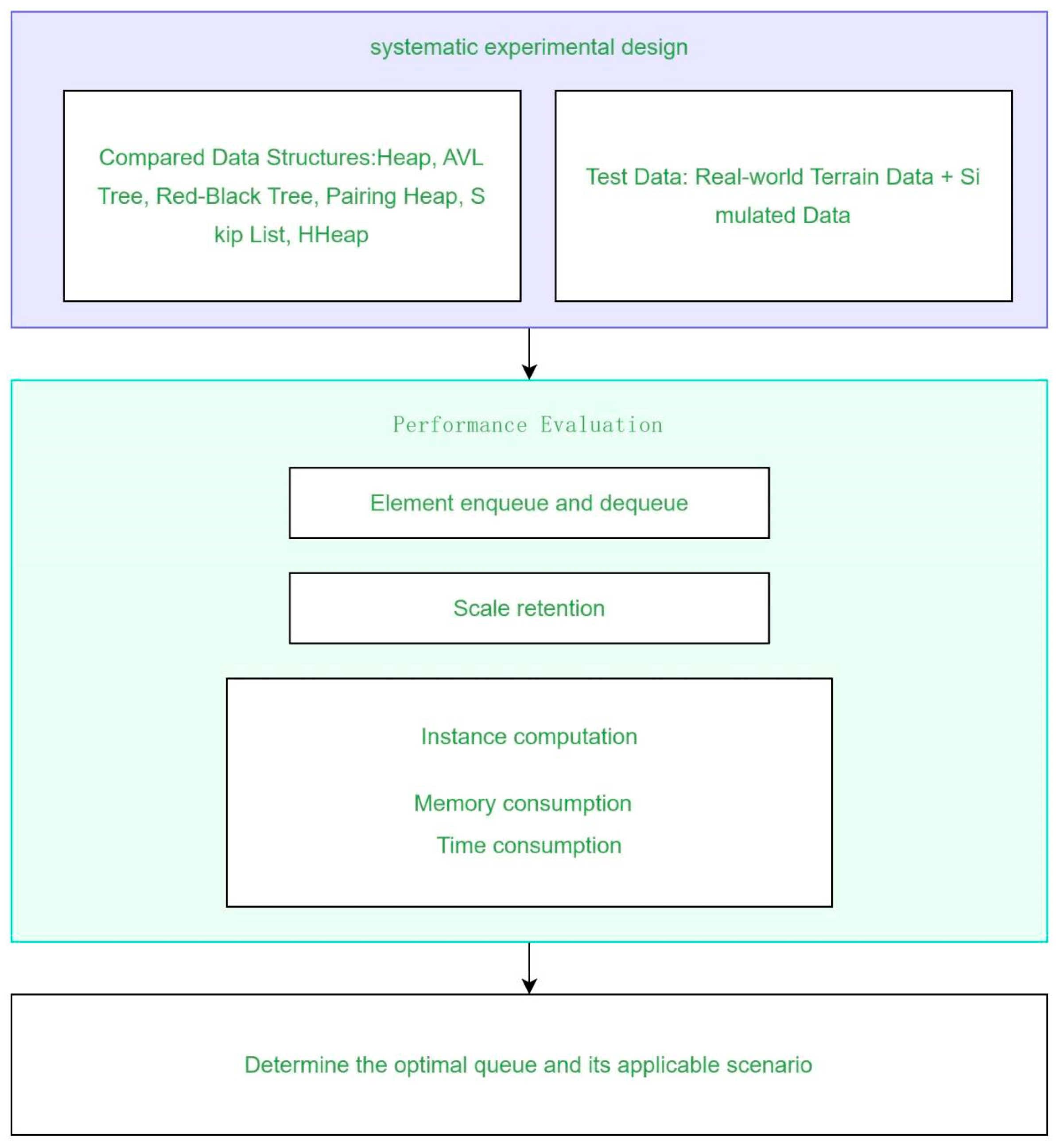
2. Materials and Methods
2.1. Data
2.1.1. Dataset
2.1.2. Test Plan
2.2. Algorithm
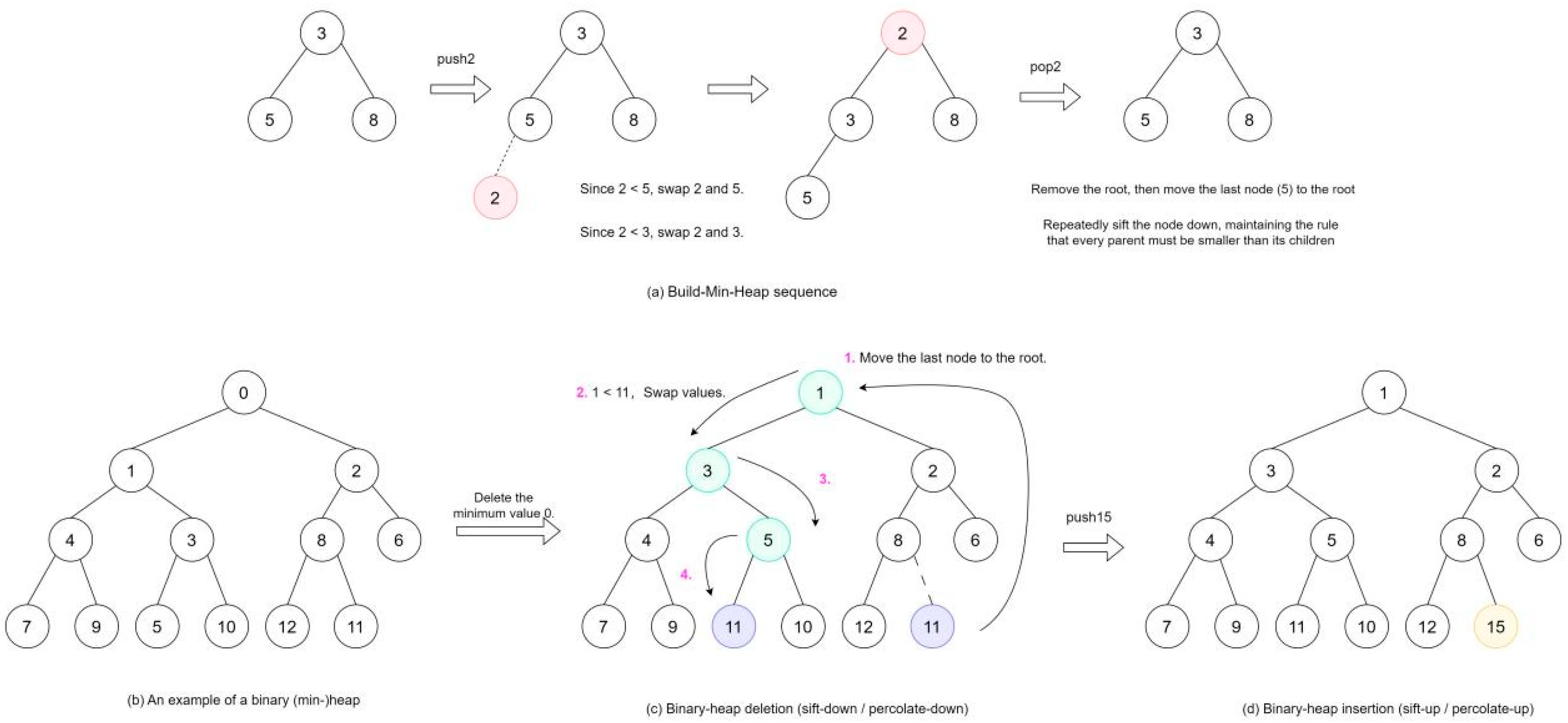
2.2.1. Heap
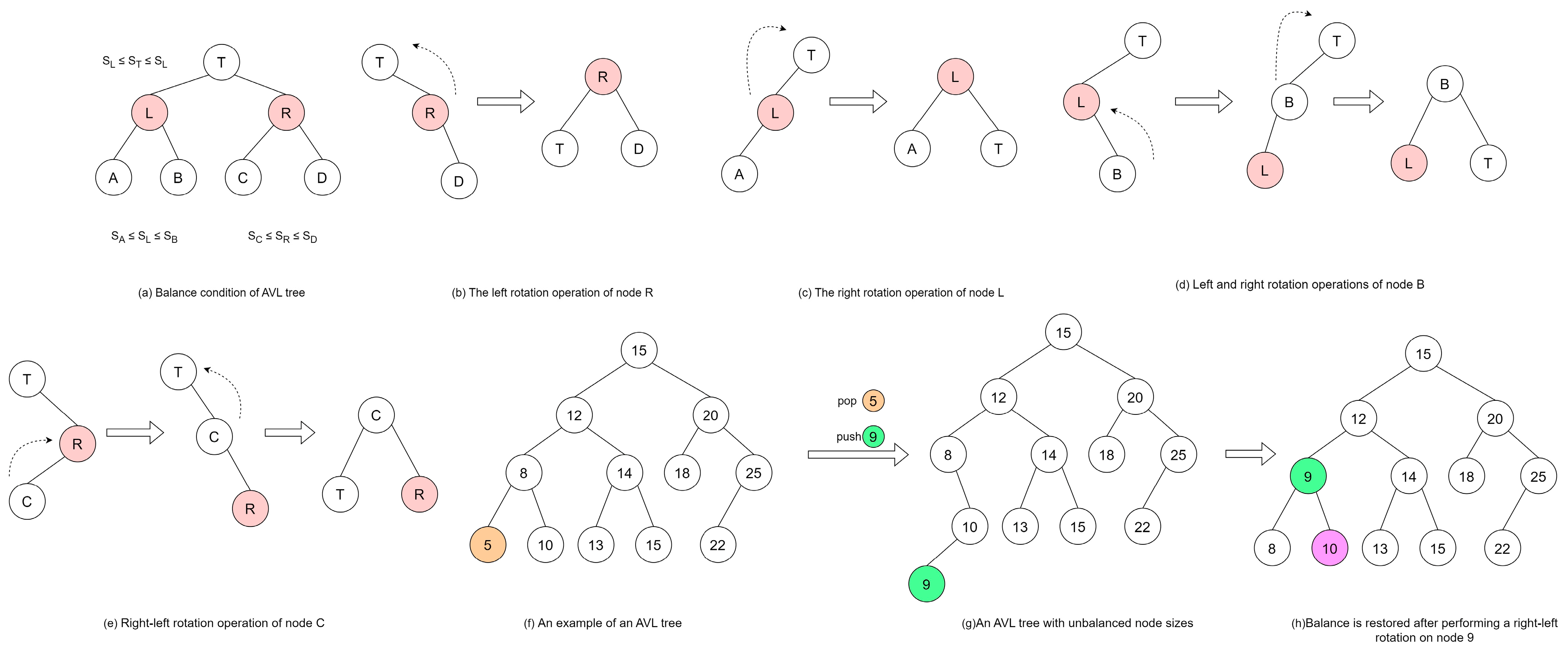
2.2.2. AVL Tree
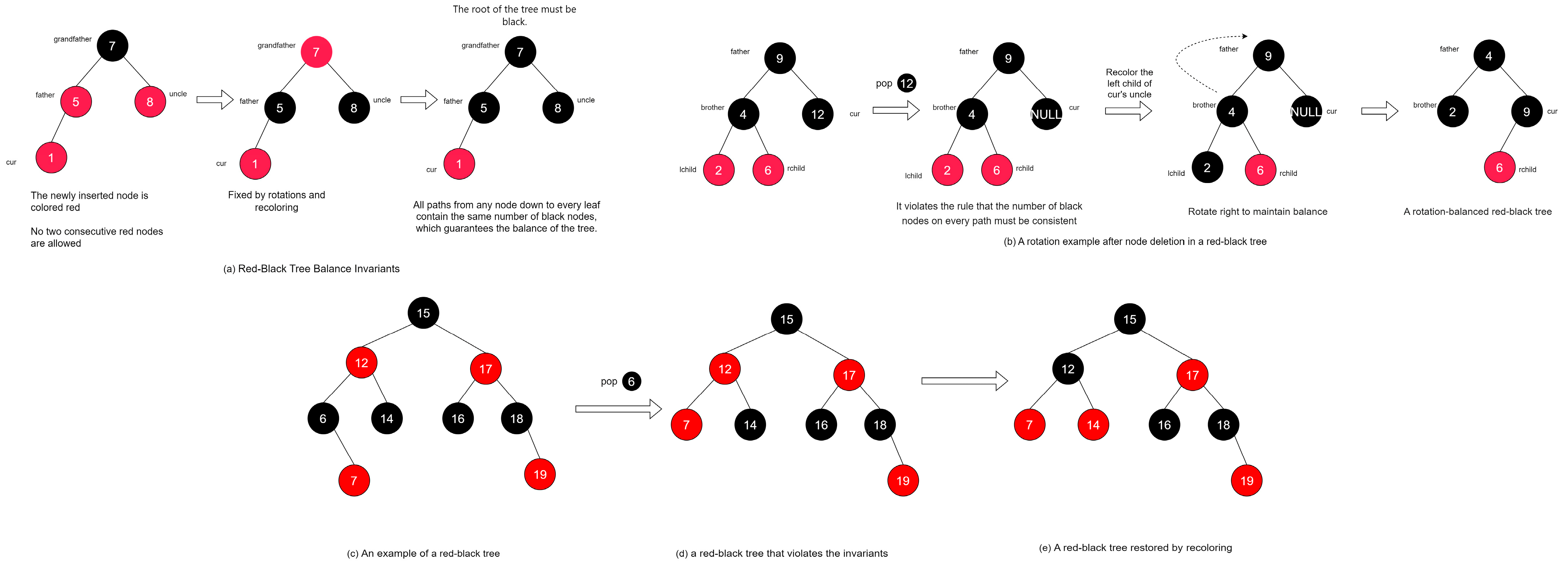
2.2.3. RBTree
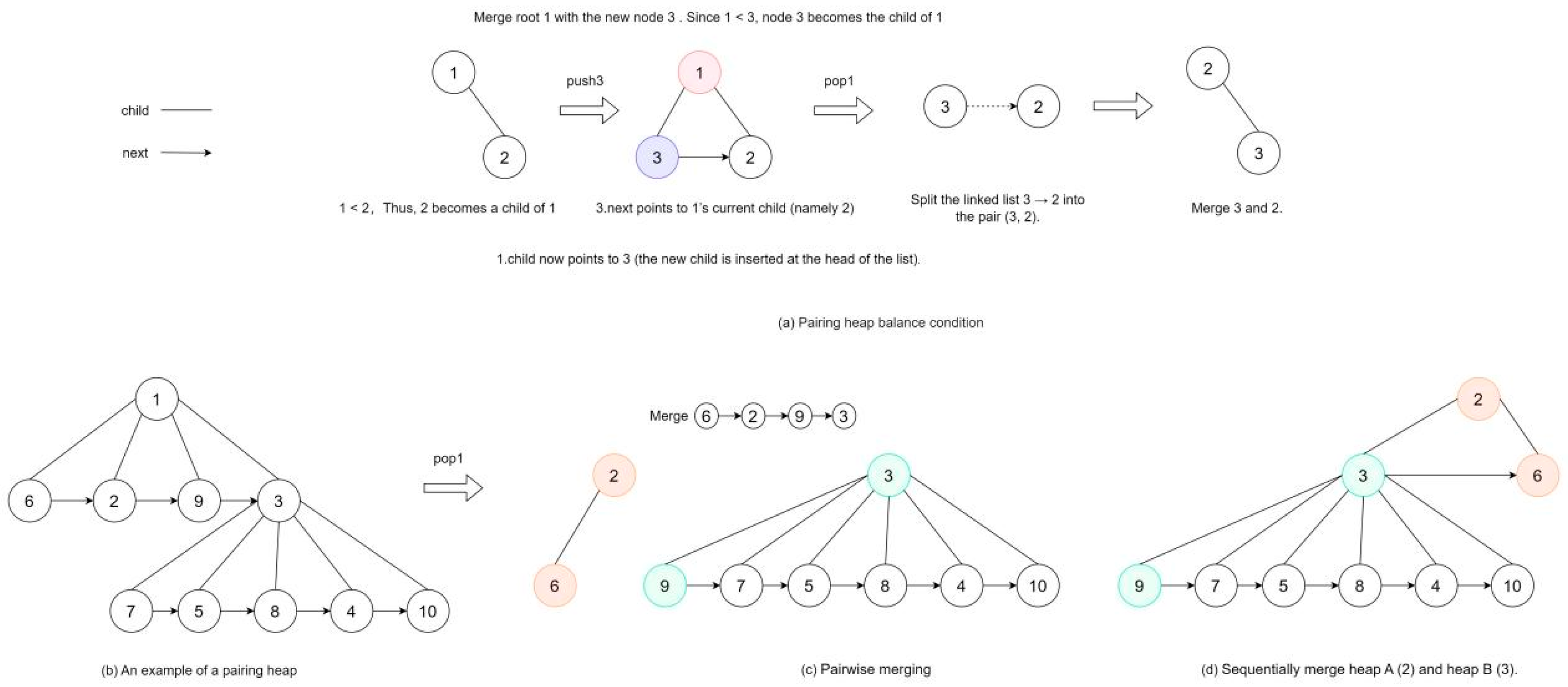
2.2.4. Pairing Heap
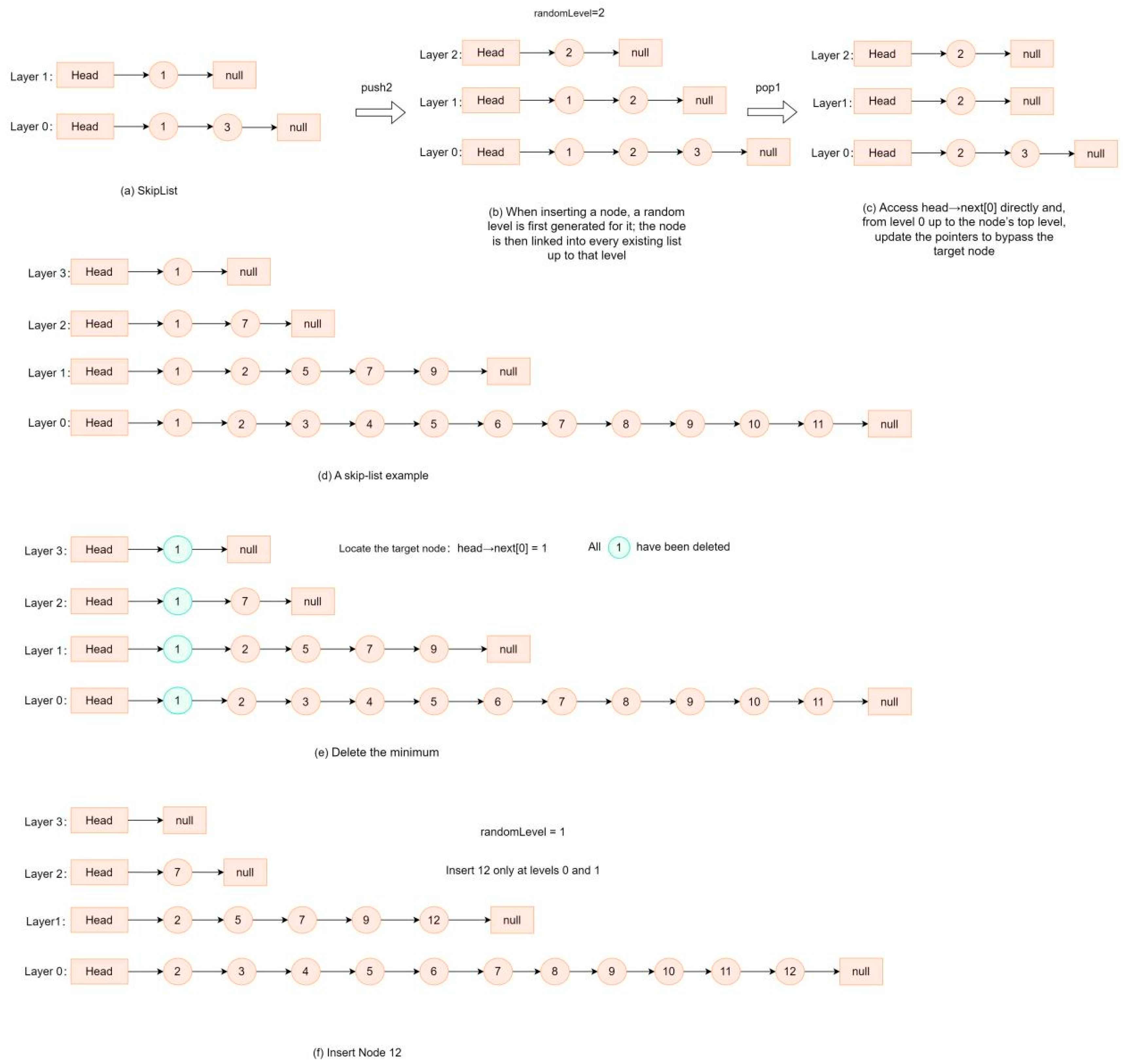
2.2.5. Skip List
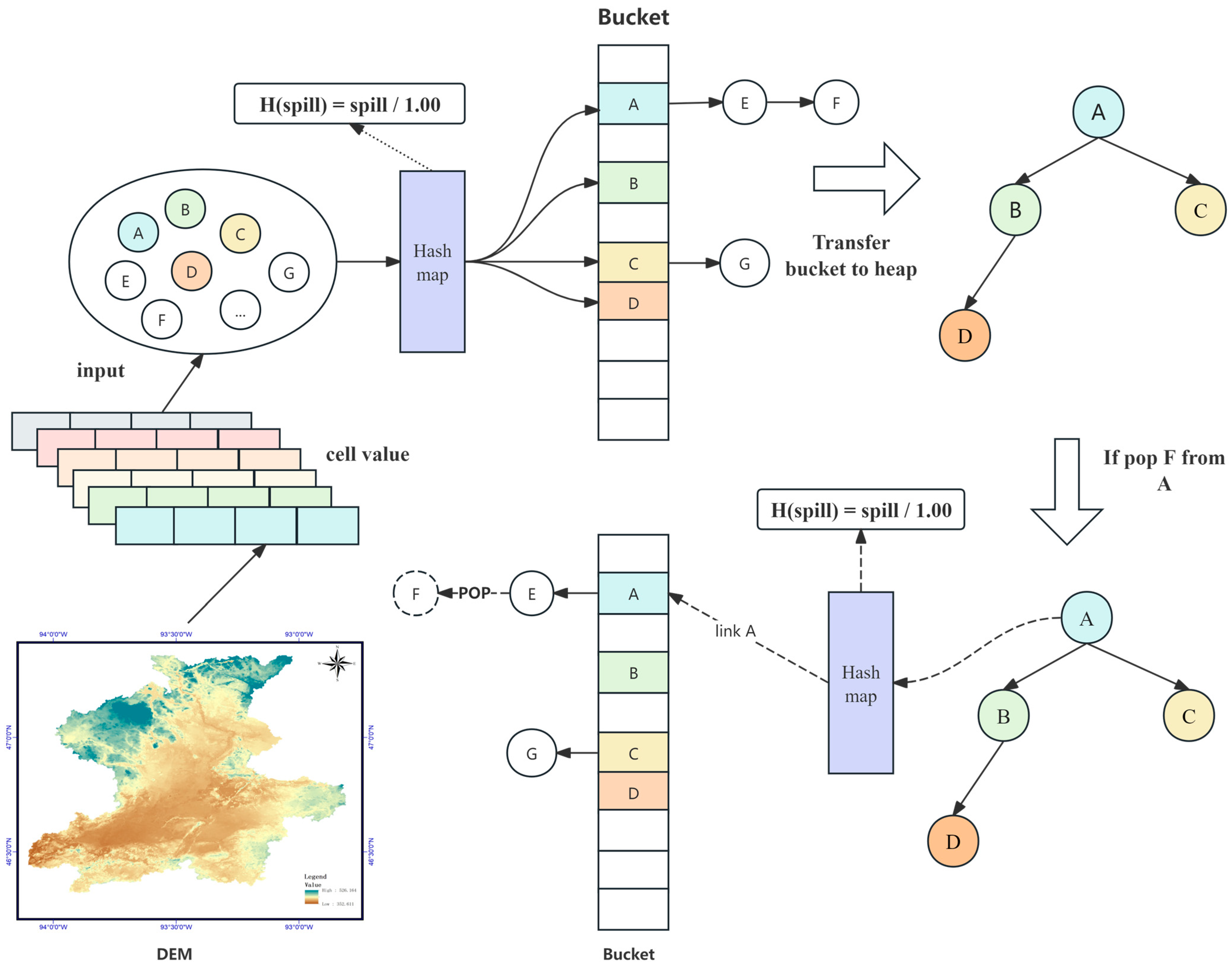
2.2.6. HHeap
2.3. Algorithm Processing
3. Results
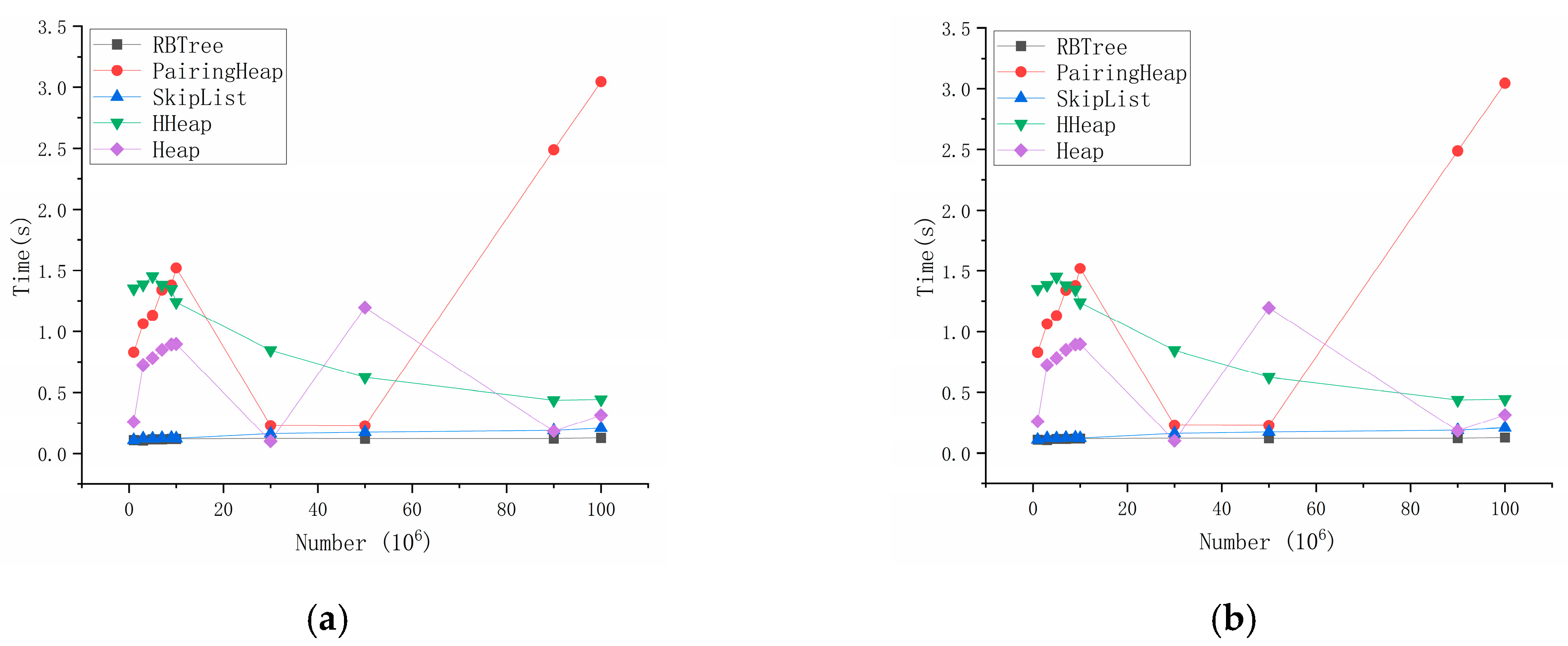
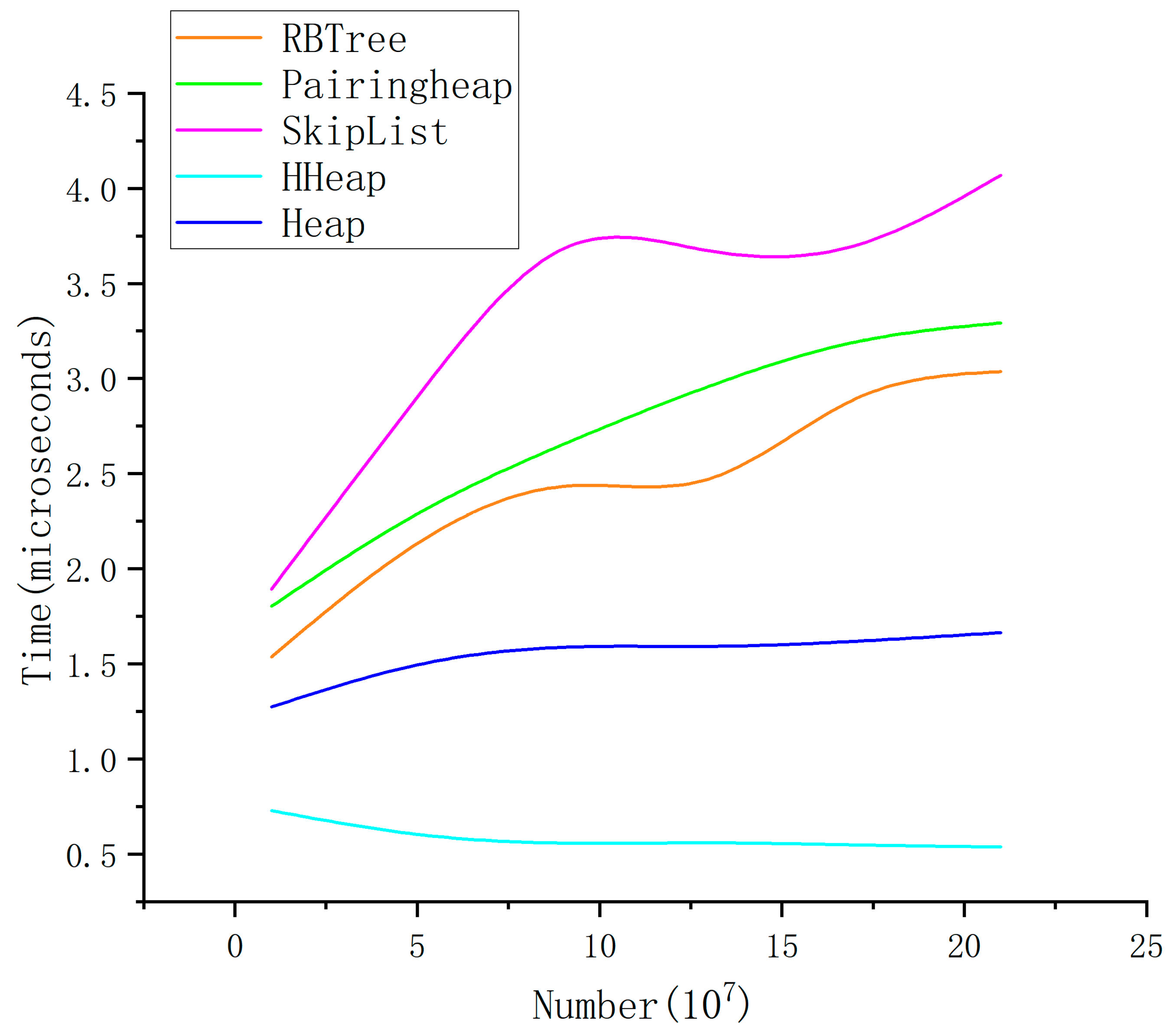
3.1. Enqueuing and Dequeuing Times
3.2. Hold Model
3.3. Practice
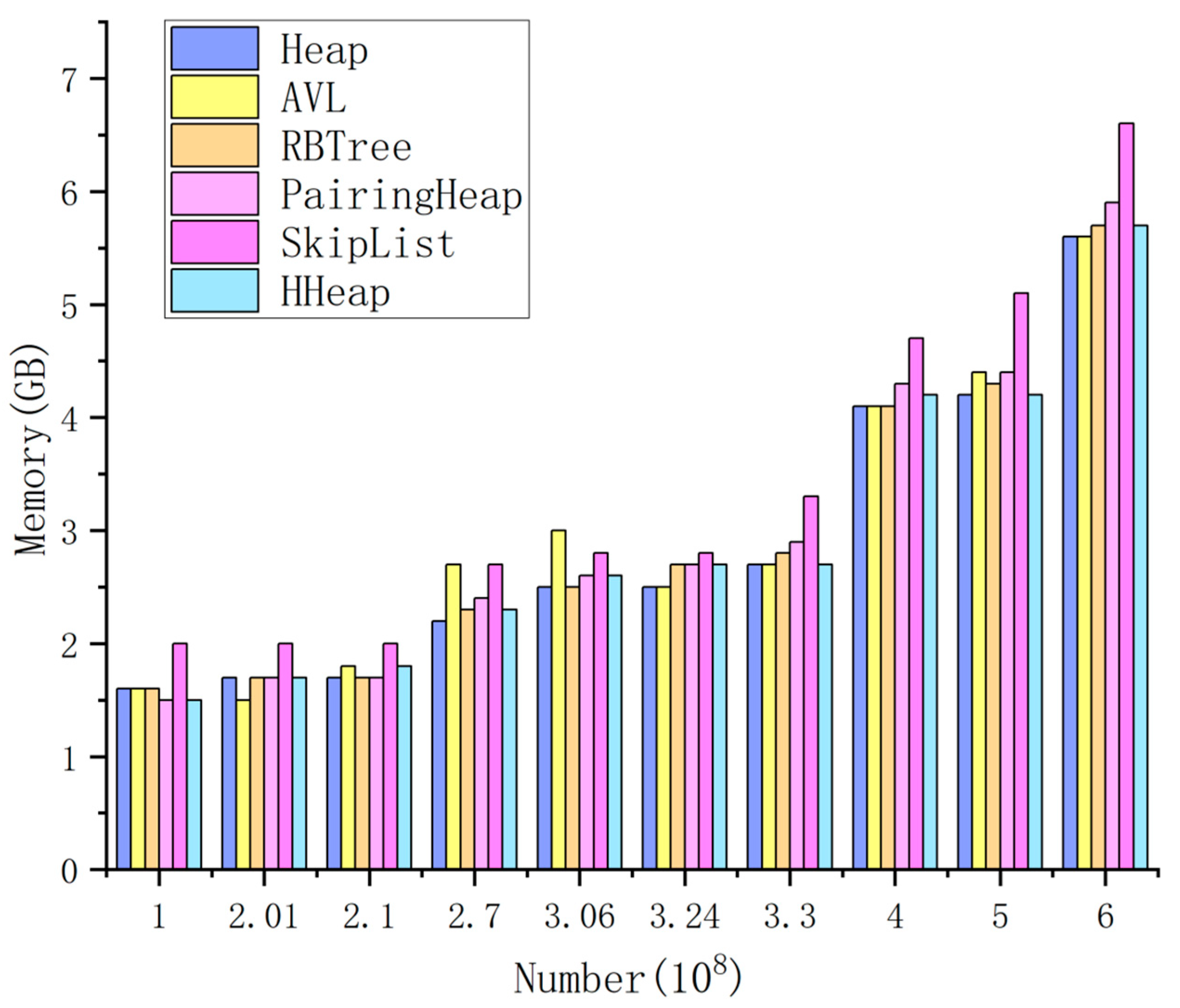
3.3.1. Memory Requirements
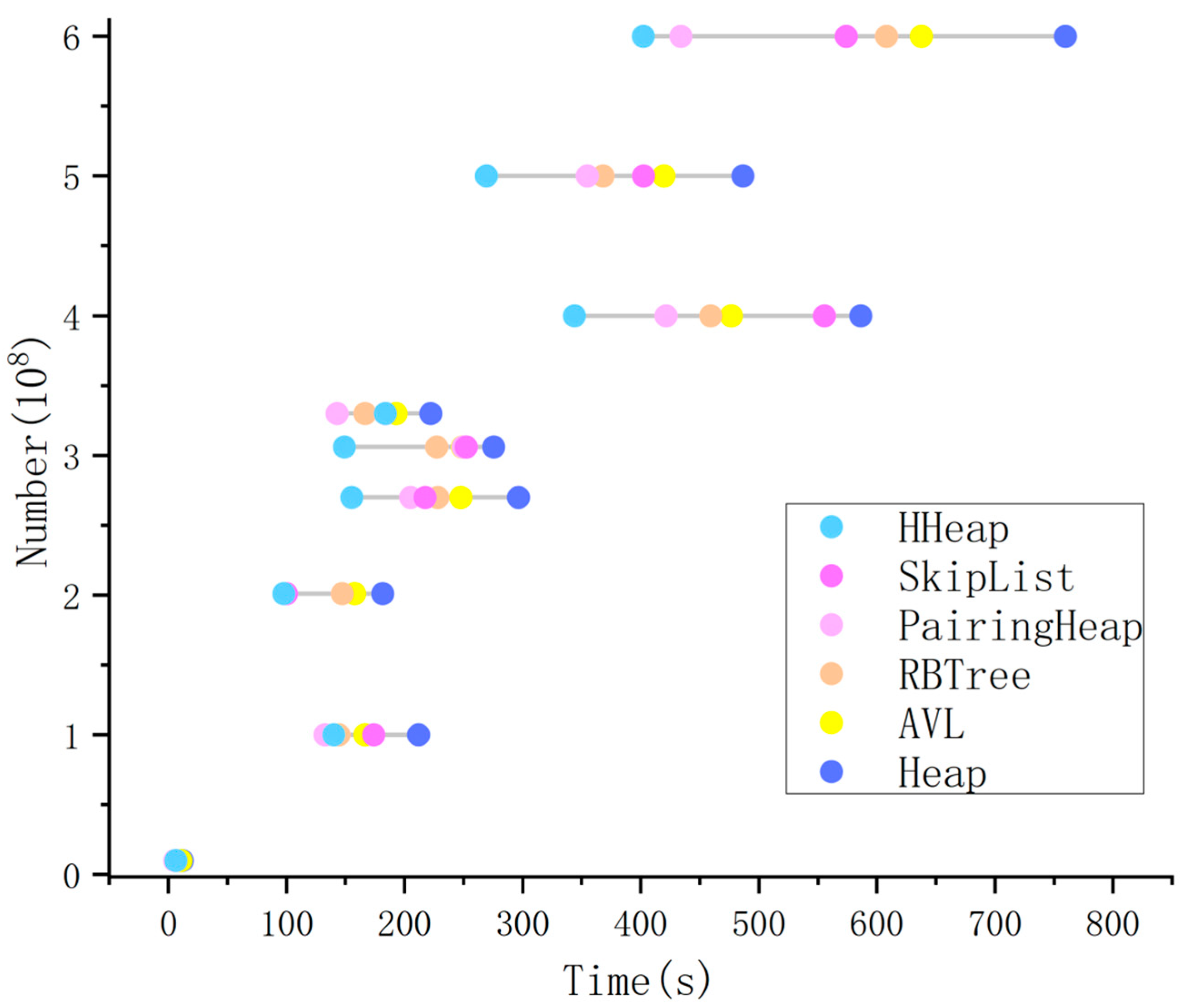
3.3.2. Computational Time
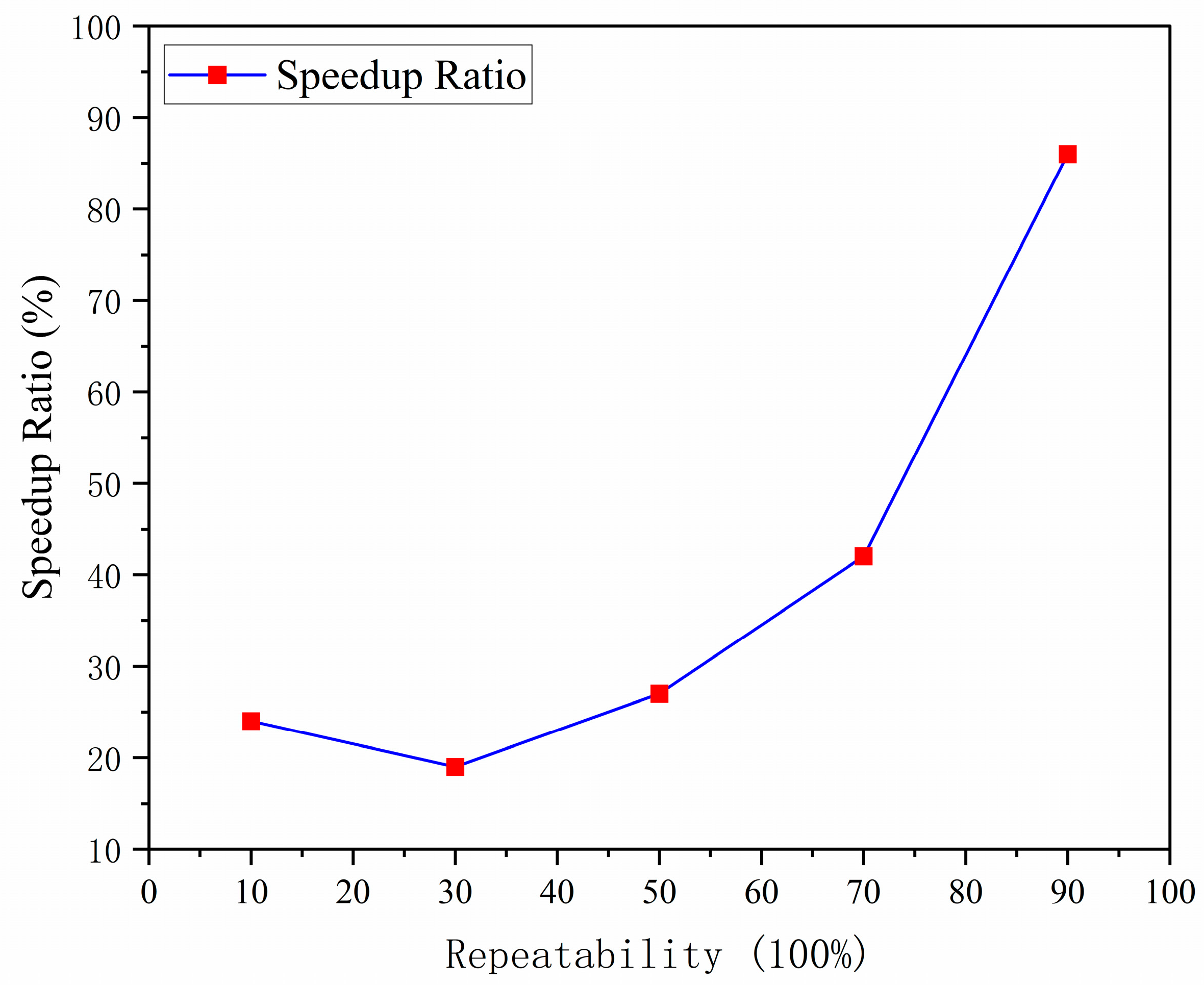
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mankowitz, D.J.; Michi, A.; Zhernov, A.; Gelmi, M.; Selvi, M.; Paduraru, C.; Leurent, E.; Iqbal, S.; Lespiau, J.-B.; Ahern, A.; et al. Faster Sorting Algorithms Discovered Using Deep Reinforcement Learning. Nature 2023, 618, 257–263. [Google Scholar] [CrossRef]
- Jiang, A.-L.; Hsu, K.; Sanders, B.F.; Sorooshian, S. Topographic Hydro-Conditioning to Resolve Surface Depression Storage and Ponding in a Fully Distributed Hydrologic Model. Adv. Water Resour. 2023, 176, 104449. [Google Scholar] [CrossRef]
- Khanaum, M.M.; Qi, T.; Chu, X. Dynamic Partial Contributing Area (DPCA) Approach: Improved Hydrologic Modeling for Depression-Dominated Watersheds. J. Hydrol. 2025, 658, 133077. [Google Scholar] [CrossRef]
- Annand, H.J.; Wheater, H.S.; Pomeroy, J.W. The Influence of Roads on Depressional Storage Capacity Estimates from High-Resolution LiDAR DEMs in a Canadian Prairie Agricultural Basin. Can. Water Resour. J./Rev. Can. Ressour. Hydr. 2024, 49, 117–136. [Google Scholar] [CrossRef]
- Chen, L.; Deng, J.; Yang, W.; Chen, H. Hydrological Modelling of Large-Scale Karst-Dominated Basin Using a Grid-Based Distributed Karst Hydrological Model. J. Hydrol. 2024, 628, 130459. [Google Scholar] [CrossRef]
- Chu, X.; Yang, J.; Chi, Y.; Zhang, J. Dynamic Puddle Delineation and Modeling of Puddle-to-Puddle Filling-Spilling-Merging-Splitting Overland Flow Processes. Water Resour. Res. 2013, 49, 3825–3829. [Google Scholar] [CrossRef]
- Moges, D.M.; Virro, H.; Kmoch, A.; Cibin, R.; Rohith, A.N.; Martínez-Salvador, A.; Conesa-García, C.; Uuemaa, E. How Does the Choice of DEMs Affect Catchment Hydrological Modeling? Sci. Total Environ. 2023, 892, 164627. [Google Scholar] [CrossRef]
- Wang, Y.-J.; Qin, C.-Z.; Zhu, A.-X. Review on Algorithms of Dealing with Depressions in Grid DEM. Ann. GIS 2019, 25, 83–97. [Google Scholar] [CrossRef]
- Barták, V. How to Extract River Networks and Catchment Boundaries from DEM: A Review of Digital Terrain Analysis Techniques. J. Landsc. Stud. 2009, 2, 2–13. [Google Scholar]
- Wang, L.; Liu, H. An Efficient Method for Identifying and Filling Surface Depressions in Digital Elevation Models for Hydrologic Analysis and Modelling. Int. J. Geogr. Inf. Sci. 2006, 20, 193–213. [Google Scholar] [CrossRef]
- Callaghan, K.L.; Wickert, A.D. Computing Water Flow through Complex Landscapes—Part 1: Incorporating Depressions in Flow Routing Using FlowFill. Earth Surf. Dyn. 2019, 7, 737–753. [Google Scholar] [CrossRef]
- Barnes, R.; Callaghan, K.L.; Wickert, A.D. Computing Water Flow through Complex Landscapes—Part 2: Finding Hierarchies in Depressions and Morphological Segmentations. Earth Surf. Dyn. 2020, 8, 431–445. [Google Scholar] [CrossRef]
- Barnes, R.; Callaghan, K.L.; Wickert, A.D. Computing Water Flow through Complex Landscapes—Part 3: Fill–Spill–Merge: Flow Routing in Depression Hierarchies. Earth Surf. Dyn. 2021, 9, 105–121. [Google Scholar] [CrossRef]
- Zhou, G.; Wei, H.; Fu, S. A Fast and Simple Algorithm for Calculating Flow Accumulation Matrices from Raster Digital Elevation. Front. Earth Sci. 2019, 13, 317–326. [Google Scholar] [CrossRef]
- Lindsay, J.B. Efficient Hybrid Breaching-Filling Sink Removal Methods for Flow Path Enforcement in Digital Elevation Models. Hydrol. Process. 2016, 30, 846–857. [Google Scholar] [CrossRef]
- Lindsay, J.B. Pit-Centric Depression Removal Methods. Environ. Sci. 2020, 13, 1–5. [Google Scholar] [CrossRef]
- Metz, M.; Mitasova, H.; Harmon, R.S. Efficient Extraction of Drainage Networks from Massive, Radar-Based Elevation Models with Least Cost Path Search. Hydrol. Earth Syst. Sci. 2011, 15, 667–678. [Google Scholar] [CrossRef]
- Zhou, G.; Song, L.; Liu, Y. Parallel Assignment of Flow Directions over Flat Surfaces in Massive Digital Elevation Models. Comput. Geosci. 2022, 159, 105015. [Google Scholar] [CrossRef]
- Qin, C.-Z.; Zhan, L. Parallelizing Flow-Accumulation Calculations on Graphics Processing Units—From Iterative DEM Preprocessing Algorithm to Recursive Multiple-Flow-Direction Algorithm. Comput. Geosci. 2012, 43, 7–16. [Google Scholar] [CrossRef]
- Barnes, R. Parallel Priority-Flood Depression Filling for Trillion Cell Digital Elevation Models on Desktops or Clusters. Comput. Geosci. 2016, 96, 56–68. [Google Scholar] [CrossRef]
- Zhou, G.; Liu, X.; Fu, S.; Sun, Z. Parallel Identification and Filling of Depressions in Raster Digital Elevation Models. Int. J. Geogr. Inf. Sci. 2017, 31, 1061–1078. [Google Scholar] [CrossRef]
- Ikonen, L. Priority Pixel Queue Algorithm for Geodesic Distance Transforms. Image Vis. Comput. 2007, 25, 1520–1529. [Google Scholar] [CrossRef]
- Barnes, R.; Lehman, C.; Mulla, D. Priority-Flood: An Optimal Depression-Filling and Watershed-Labeling Algorithm for Digital Elevation Models. Comput. Geosci. 2014, 62, 117–127. [Google Scholar] [CrossRef]
- Zhou, G.; Sun, Z.; Fu, S. An Efficient Variant of the Priority-Flood Algorithm for Filling Depressions in Raster Digital Elevation Models. Comput. Geosci. 2016, 90, 87–96. [Google Scholar] [CrossRef]
- Wei, H.; Zhou, G.; Fu, S. Efficient Priority-Flood Depression Filling in Raster Digital Elevation Models. Int. J. Digit. Earth 2019, 12, 415–427. [Google Scholar] [CrossRef]
- Cordonnier, G.; Bovy, B.; Braun, J. A Versatile, Linear Complexity Algorithm for Flow Routing in Topographies with Depressions. Earth Surf. Dyn. 2019, 7, 549–562. [Google Scholar] [CrossRef]
- McDonnell, J.J.; Spence, C.; Karran, D.J.; van Meerveld, H.J.; Harman, C.J. Fill-and-Spill: A Process Description of Runoff Generation at the Scale of the Beholder. Water Resour. Res. 2021, 57, e2020WR027514. [Google Scholar] [CrossRef]
- Jain, A.; Kerbl, B.; Gain, J.; Finley, B.; Cordonnier, G. FastFlow: GPU Acceleration of Flow and Depression Routing for Landscape Simulation. Comput. Graph. Forum 2024, 43, e15243. [Google Scholar] [CrossRef]
- Dragicevic, K.; Bauer, D. A survey of concurrent priority queue algorithms. In Proceedings of the 2008 IEEE International Symposium on Parallel and Distributed Processing, Miami, FL, USA, 14–18 April 2008; IEEE: New York, NY, USA, 2008. [Google Scholar]
- Grammatikakis, M.D.; Liesche, S. Priority queues and sorting methods for parallel simulation. IEEE Trans. Softw. Eng. 2000, 26, 401–422. [Google Scholar] [CrossRef]
- Thorup, M. Equivalence between Priority Queues and Sorting. J. ACM 2007, 54, 28. [Google Scholar] [CrossRef]
- Bai, R.; Li, T.; Huang, Y.; Li, J.; Wang, G. An Efficient and Comprehensive Method for Drainage Network Extraction from DEM with Billions of Pixels Using a Size-Balanced Binary Search Tree. Geomorphology 2015, 238, 56–67. [Google Scholar] [CrossRef]
- Hendriks, C.L.L. Revisiting Priority Queues for Image Analysis. Pattern Recognit. 2010, 43, 3003–3012. [Google Scholar] [CrossRef]
- Ruiz-Lendínez, J.J.; Ariza-López, F.J.; Reinoso-Gordo, J.F.; Ureña-Cámara, M.A.; Quesada-Real, F.J. Deep Learning Methods Applied to Digital Elevation Models: State of the Art. Geocarto Int. 2023, 38, 2252389. [Google Scholar] [CrossRef]
- Atkinson, M.D.; Sack, J.-R.; Santoro, N.; Strothotte, T. Min-Max Heaps and Generalized Priority Queues. Commun. ACM 1986, 29, 996–1000. [Google Scholar] [CrossRef]
- Brown, R.A. Comparative Performance of the AVL Tree and Three Variants of the Red-Black Tree. Softw. Pract. Exp. 2025, 55, 1607–1615. [Google Scholar] [CrossRef]
- Guibas, L.J.; Sedgewick, R. A dichromatic framework for balanced trees. In Proceedings of the 19th Annual Symposium on Foundations of Computer Science (SFCS 1978), Washington, DC, USA, 16–18 October 1978; IEEE: New York, NY, USA, 1978; pp. 8–21. [Google Scholar]
- Schmoldt, A.; Benthe, H.F.; Haberland, G.; Mills, G.C.; Alperin, J.B.; Trimmer, K.B.; Krishna, S.R. Digitoxin Metabolism by Rat Liver Microsomes. Biochem. Pharmacol. 1975, 24, 1639–1641. [Google Scholar] [CrossRef]
- Fredman, M.L.; Sedgewick, R.; Sleator, D.D.; Tarjan, R.E. The Pairing Heap: A New Form of Self-Adjusting Heap. Algorithmica 1986, 1, 111–129. [Google Scholar] [CrossRef]
- Xing, L.; Vadrevu, V.S.P.K.; Aref, W.G. The Ubiquitous Skiplist: A Survey of What Cannot Be Skipped About the Skiplist and Its Applications in Data Systems. ACM Comput. Surv. 2025, 57, 1–37. [Google Scholar] [CrossRef]
- Pugh, W. Skip Lists: A Probabilistic Alternative to Balanced Trees. Commun. ACM 1990, 33, 668–676. [Google Scholar] [CrossRef]
- Doberkat, E.-E. Inserting a New Element into a Heap. BIT 1981, 21, 255–269. [Google Scholar] [CrossRef]
- Jones, D.W. An Empirical Comparison of Priority-Queue and Event-Set Implementations. Commun. ACM 1986, 29, 300–311. [Google Scholar] [CrossRef]
- LaMarca, A.; Ladner, R. The Influence of Caches on the Performance of Heaps. ACM J. Exp. Algorithmics 1996, 1, 4. [Google Scholar] [CrossRef]
| NO. | Width | Height | Number |
|---|---|---|---|
| 1 | 8236 | 22,030 | 181,439,080 |
| 2 | 17,252 | 11,673 | 201,382,596 |
| 3 | 13,938 | 15,116 | 210,686,808 |
| 4 | 16,897 | 16,427 | 277,567,019 |
| 5 | 21,925 | 13,967 | 306,226,475 |
| 6 | 21,037 | 15,412 | 324,222,244 |
| 7 | 19,409 | 17,116 | 332,204,444 |
| 8 | 27,160 | 18,307 | 497,218,120 |
| 9 | 20,311 | 33,681 | 684,094,791 |
| NO. | Width Optimization Strategies | Content | Benefits |
|---|---|---|---|
| 1 | Memory pool | Memory pool techniques further balance computational performance and memory efficiency through preallocation and mark-and-sweep reclamation. | Memory allocation and deallocation overhead are minimized, and cache locality is enhanced. |
| 2 | Memory cache | Access to heap nodes is optimized through a contiguous memory layout, leveraging cache locality to reduce cache misses and improve performance. | Cache misses are significantly reduced, thereby accelerating access to nodes. |
| 3 | Iteration replacing recursion | A while loop and explicit stacks or pointers are used to maintain the traversal path, thereby avoiding recursive calls. | The risk of stack overflow is eliminated; function-call overhead is minimized, making it suitable for handling massive data volumes. |
| 4 | Pointer to the minimum node | A pointer to the current global minimum element is dynamically maintained. | Achieve O(1) time complexity for the pop() operation, down from O(log N). |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, L.; Yuan, Y.; Wang, H.; Liu, H.; Wu, Q. Evaluation of Priority Queues in the Priority Flood Algorithm for Hydrological Modelling. Water 2025, 17, 3202. https://doi.org/10.3390/w17223202
Ma L, Yuan Y, Wang H, Liu H, Wu Q. Evaluation of Priority Queues in the Priority Flood Algorithm for Hydrological Modelling. Water. 2025; 17(22):3202. https://doi.org/10.3390/w17223202
Chicago/Turabian StyleMa, Lejun, Yue Yuan, Huan Wang, Huihui Liu, and Qiuling Wu. 2025. "Evaluation of Priority Queues in the Priority Flood Algorithm for Hydrological Modelling" Water 17, no. 22: 3202. https://doi.org/10.3390/w17223202
APA StyleMa, L., Yuan, Y., Wang, H., Liu, H., & Wu, Q. (2025). Evaluation of Priority Queues in the Priority Flood Algorithm for Hydrological Modelling. Water, 17(22), 3202. https://doi.org/10.3390/w17223202






