Simulation and Analysis of Real-Time Coupling of Free-Surface Flow and Pressure Flow in Hydropower Station Tailrace Tunnels Based on the Finite Volume Method
Abstract
1. Introduction
2. Mathematical Model and Its Solution
2.1. Governing Equations for Pressure Flow
2.2. Governing Equations for Free-Surface Flow
2.3. Combined Calculation Strategy for Pressure and Free-Surface Flows
3. Model Validation
3.1. Validation of the Pressure Flow Model
3.2. Validation of the Free-Surface Flow Model
3.3. Validation with Actual Engineering
4. Analysis of the Impact of the Free-Surface Section of Tailwater on Hydraulic Calculation—A Case Study of an Actual Power Station
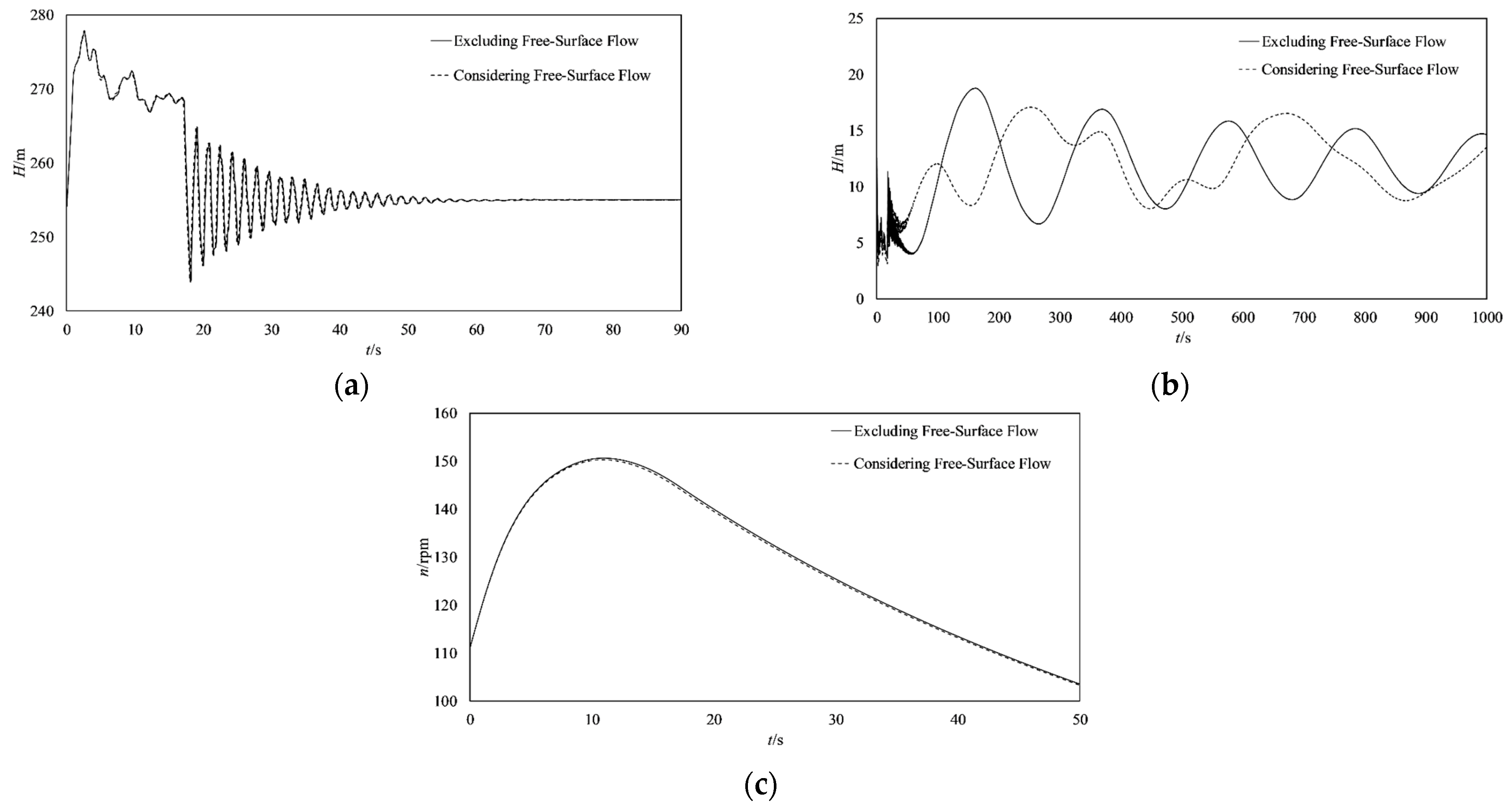
4.1. Calculation and Analysis of Load Rejection Conditions
4.2. Calculation and Analysis of Small Fluctuation Conditions
5. Conclusions
- (1)
- A coupled calculation model for pressure and free-surface flows, based on the second-order Godunov scheme of the finite volume method, was established. A generalized boundary condition for regulating pools and a variable time-step calculation method were proposed, which addressed the issue of real-time coupled calculation in the pressurized–free-surface transition zone.
- (2)
- For hydropower stations with free-surface tailrace tunnels, hydraulic fluctuations in free-surface flow exert a certain impact on the hydraulic characteristics of units and other flow-passing systems. During large-fluctuation hydraulic transient processes, when accounting for the influence of transient free-surface flow in the tailrace, the hydraulic characteristics of free-surface flow have minimal effect on the volute inlet pressure and unit speed, yet significantly affect the fluctuation period and extreme values of the draft tube inlet pressure. This is because the fully pressurized numerical solution method, relying on the simplified assumption of a closed system (which ignores the influence of the free water surface in the free-surface section), restricts pressure wave propagation within the pressurized pipeline, thereby preventing pressure fluctuation energy from being released through the free-surface section. Consequently, the calculation results are often more conservative. In contrast, the results obtained via the coupled pressure–free-surface solution method are more consistent with actual conditions and can reduce the construction volume of surge tanks and other surge-regulating structures to a certain extent, yielding better economic efficiency.
- (3)
- During small-fluctuation hydraulic transient processes, when the influence of the transient characteristics of free-surface flow in the tailrace tunnel is taken into account, the unit exhibits better regulation quality. This suggests that the free-surface flow in the tailrace tunnel is conducive to the stable operation of the unit, thereby providing new perspectives for operational optimization.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| D | pipe diameter; |
| U | flow variables H and V; |
| A | linearized coefficient matrix; |
| S | steady friction |
| Δx | spatial mesh size; |
| N | total number of segments; |
| F | flux vector; |
| H | piezometric head; |
| V | flow velocity; |
| a | wave speed; |
| g | gravitational acceleration; |
| x | distance along the pipe axis; |
| t | computing time; |
| ∆t | time interval of pressure flow; |
| f | Darcy–Weisbach pipe friction coefficient; |
| average value of variable U at the left side of the i + 1/2 interface at time n; | |
| average value of variable U at the right side of the i + 1/2 interface at time n; | |
| U | flow variables A and Q; |
| F | flux vector; |
| S | vector containing source terms; |
| ΔT | time interval of free-surface flow; |
| i | node number; |
| A | cross-sectional area of the free-surface section through which water flows; |
| Q | flow rate in the free-surface section; |
| p | hydrostatic pressure; |
| ρ | density of the water body; |
| S0 | bottom slope of the free-surface; |
| Sf | frictional resistance of the free-surface; |
| Fw | momentum term generated by the longitudinal variation in the free-surface width; |
| H0 | the water level of regulating pool; |
| As | regulating poo area; |
| Hu | Upstream reservoir water level; |
| V0 | Water flow velocity |
References
- Wylie, E.B.; Streeter, V.L.; Suo, L. Fluid Transients in Systems; Prentice Hall: Englewood Cliffs, NJ, USA, 1993. [Google Scholar]
- Yang, K.L. Research Progress and Frontier Scientific Issues in Hydraulic Control of Long-Distance Water Conveyance. J. Hydraul. Eng. 2016, 47, 424–435. [Google Scholar]
- Zhao, M.; Ghidaoui, M.S. Godunov-type solutions for water hammer flows. J. Hydraul. Eng.-Asce 2004, 130, 341–348. [Google Scholar] [CrossRef]
- Zhou, L.; Li, Y.; Karney, B.; Cheng, Y.; Liu, D. Godunov-type solutions for transient pipe flow implicitly incorporating Brunone unsteady friction. J. Hydraul. Eng. 2021, 147, 04021021. [Google Scholar] [CrossRef]
- Fox, J.A. Hydraulic Analysis of Unsteady Flow in Pipe; Macmillan International Higher Education: London, UK, 1977. [Google Scholar]
- Akimoto, T. Water Hammer and Pressure Pulsations; Zhi, P.F.; Xu, G.Q.; Yan, Y.F., Translators; Electric Power Industry Press: Beijing, China, 1981; Volume 2, pp. 36–40. [Google Scholar]
- Krivchenko, G.I. Transient Processes in Hydropower Stations; Chang, Z.T.; Zhou, W.T.; Wu, P.H., Translators; Water Resources and Electric Power Press: Beijing, China, 1981; Volume 5, pp. 38–40. [Google Scholar]
- Binnie, A.M. Fluid Transients in Hydro-Electric Engineering Practice. By C. JAEQER. Blackie, 1977. 413 pp. 218.50. J. Fluid Mech. 1978, 86, 793–794. [Google Scholar] [CrossRef]
- Chaudhry, M.H. Applied Hydraulic Transients; Chen, J.; Sun, S.J.; Zhang, Z.B., Translators; Sichuan Provincial Society of Hydropower Engineering: Chengdu, China, 1985. [Google Scholar] [CrossRef]
- Yang, L.H.; Li, S.H.; Hou, Y.M.; Fan, R.Q. Improvement of basic water hammer equations. J. Hydraul. Eng. 2007, 948–952. [Google Scholar]
- Wan, W.-Y.; Zhu, S.; Hu, Y.-J. Attenuation analysis of hydraulic transients with laminar-turbulent flow alternations. Appl. Math. Mech. 2010, 31, 1209–1216. [Google Scholar] [CrossRef]
- Li, H.; Chen, N.X.; Fan, H.G.; Liu, L.X.; Lin, X.H. Critical flow in city gate and horseshoe conduit. J. Tsinghua Univ. 1999, 29–31+34. [Google Scholar] [CrossRef]
- Zhang, M.Y. Response of Isotopic Composition of Various Water Sources to Typhoon Rainfall Events in a Small Humid Watershed in Lower Reaches of Yangtze River. Water Resour. Power 2020, 38, 80–83+20. [Google Scholar] [CrossRef]
- Cui, W.J.; Zhang, J.; Chen, S. Transient flow and scheduling strategy of long diversion open channel in a hydropower station. South–North Water Transf. Water Sci. Technol. 2017, 15, 138–142. [Google Scholar]
- Zhao, Y.; Zhou, L.; Liu, D.Y.; Zhang, Y.H.; Wang, J.Z.; Cao, Y.; Pan, T.W. Water hammer model based on finite volume method and Godunov-type scheme. Adv. Sci. Technol. Water Resour. 2019, 39, 76–81. [Google Scholar]
- Zheng, J.H.; Jiang, M.; Guo, R.; Li, G.D. Finite Volume Method for Hydraulic Transient Simulation in Pipelining for Sequential Transport. Chin. J. Comput. Mech. 2015, 3, 418–422+428. [Google Scholar]
- Roe, P.L. Approximate Riemann solvers, parameter vectors, and difference schemes. J. Comput. Phys. 1981, 43, 357–372. [Google Scholar] [CrossRef]
- Sanders, B.F.; Bradford, S.F. Network implementation of the two-component pressure approach for transient flow in storm sewers. J. Hydraul. Eng. 2011, 137, 158–172. [Google Scholar] [CrossRef]
- Zhang, D.W.; Cheng, X.T.; Huang, J.C.; He, X.Y. A Mathematical Model with High Applicability for Flow in Complex Open Channels. J. Hydraul. Eng. 2010, 41, 531–536. [Google Scholar]
- Guinot, V. Riemann solvers for water hammer simulations by Godunov method. Int. J. Numer. Methods Eng. 2000, 49, 851–870. [Google Scholar] [CrossRef]
- Hwang, Y.; Chung, N. A fast Godunov method for the water-hammer problem. Int. J. Numer. Methods Fluids 2002, 40, 799–819. [Google Scholar] [CrossRef]
- Leon, A.S.; Ghidaoui, M.S.; Schmidt, A.R.; García, M.H. An Efficient Finite-Volume Scheme for Modeling Water Hammer Flows. J. Water Manag. Model. 2007, 15, R227-21. [Google Scholar] [CrossRef]
- Sabbagh-Yazdi, S.R.; Mastorakis, N.E. Water Hammer Modeling by Godunov type Finite Volume Method. Int. J. Math. Comput. Simul. 2007, 1, 350–355. [Google Scholar]
- Sánchez-Barra, A.J.; Nicolás-López, R.; Valdiviezo-Mijangos, O.C.; Camacho-Galván, A. Dynamic modeling of managed pressure drilling applying transient Godunov scheme. J. Pet. Explor. Prod. Technol. 2016, 6, 169–176. [Google Scholar] [CrossRef][Green Version]
- Alcrudo, F.; Garcia-Navarro, P.; Saviron, J. Flux difference splitting for 1D open channel flow equations. Int. J. Numer. Methods Fluids 1992, 14, 1009–1018. [Google Scholar] [CrossRef]
- Glaister, P. Prediction of supercritical flow in open channels. Comput. Math. Appl. 1992, 24, 69–75. [Google Scholar] [CrossRef][Green Version]
- Toro, E.F. The weighted average flux method applied to the Euler equations. Philos. Trans. R. Soc. London. Ser. A Phys. Eng. Sci. 1992, 341, 499–530. [Google Scholar] [CrossRef]
- Fujihara, M.; Borthwick, A.G.L. Godunov-type solution of curvilinear shallow-water equations. J. Hydraul. Eng. 2000, 126, 827–836. [Google Scholar] [CrossRef]
- León, A.S.; Ghidaoui, M.S.; Schmidt, A.R.; Garcia, M.H. Application of Godunov-type schemes to transient free-surface-pressure flows. J. Hydraul. Res. 2009, 47, 147–156. [Google Scholar] [CrossRef]
- Zhou, L.; Li, Y.; Zhao, Y.; Ou, C.; Zhao, Y. An accurate and efficient scheme involving unsteady friction for transient pipe flow. J. Hydroinform. 2021, 23, 879–896. [Google Scholar] [CrossRef]
- Zhou, L.; Wang, X.L.; Zhang, H.L.; Hu, Y.; Wu, J.; Che, T.C. Finite volume method for simulating water hammer in pumping stations with free-surface flow and optimization of surge chamber. Trans. Chin. Soc. Agric. Eng. 2023, 39, 66–75. [Google Scholar]
- Sun, H.L.; Yang, F.; Li, G.H.; Chen, Y.M.; Ni, S.H. Influence of free-pressure transition flow in tailrace tunnel on operation stability of Baihetan Hydropower Station. Yangtze River 2019, 50, 165–168. [Google Scholar]



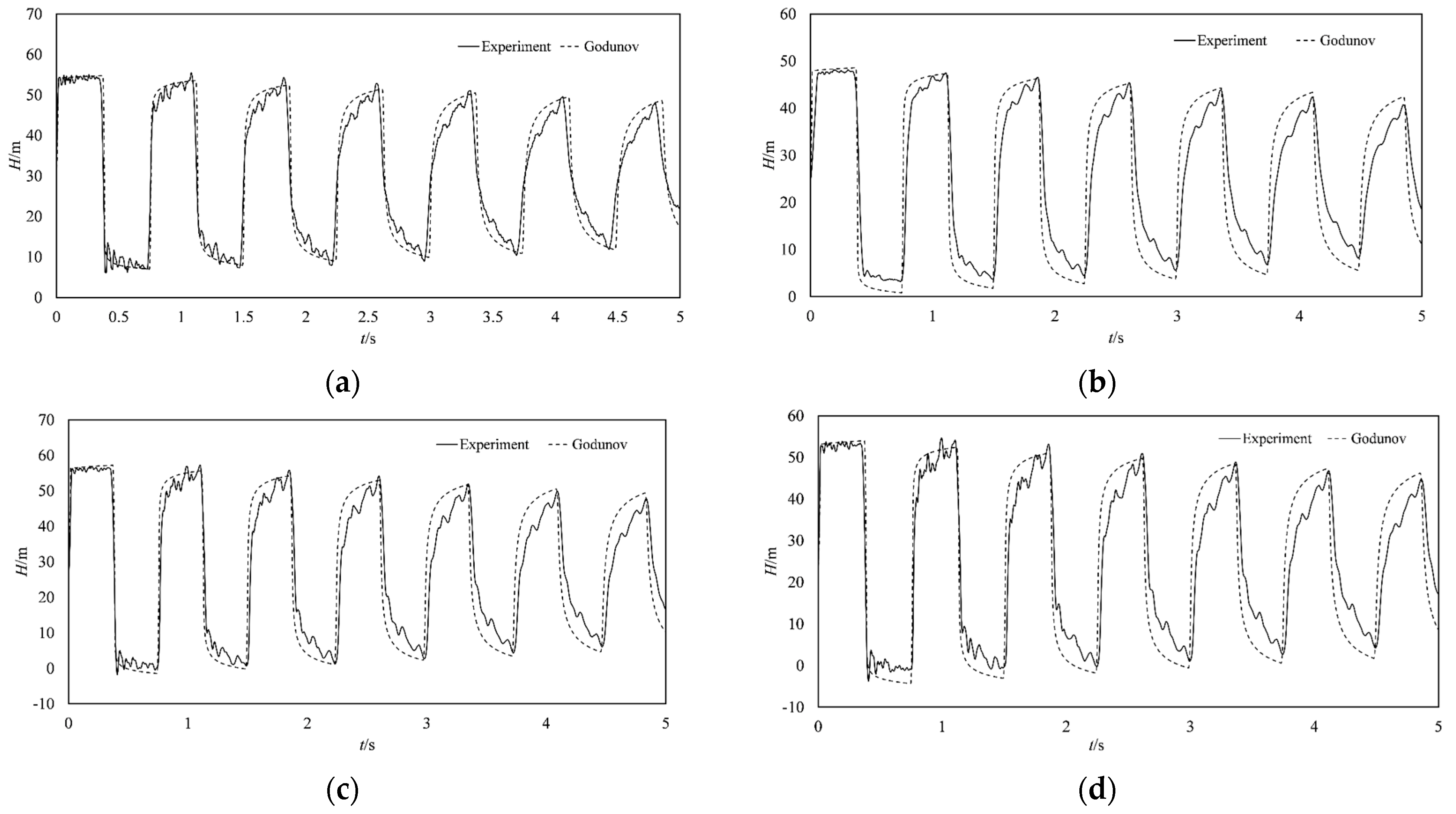








| Case | Upstream Reservoir Water Level Hu (m) | Water Flow Velocity V0 (m/s) |
|---|---|---|
| 1 | 30.36 | 0.18 |
| 2 | 24.18 | |
| 3 | 27.21 | 0.22 |
| 4 | 24.17 |
| Parameter | Measured Data | Calculated Data (Joint) |
|---|---|---|
| Unit status | 1#, 2#, 3# unit load rejection | |
| Upper reservoir water level (m) | 1761.62 | |
| Downstream tailwater level (m) | 1376.75 | |
| Output before unit load rejection (MW) | 61.1/61/61 | 60.62/61.53/59.4 |
| Opening degree before unit load rejection (%) | 76.5/75.8/73.5 | 76.5/75.8/73.5 |
| Initial pressure at the inlet of the volute (m) | 363.12/368.22/365.16 | 364.41/368.88/367.10 |
| Maximum pressure at the inlet of the volute (m) | 517.14/522.24/518.16 | 518.14/520.35/518.71 |
| Maximum speed rise rate of the unit (%) | 35.4/35.2/35.6 | 36.4/35.2/34.66 |
| Initial water level of the upstream surge chamber (m) | 1752.3 | 1752.3 |
| Maximum water level in the upstream surge chamber during the load rejection process (m) | 1765 | 1765 |
| Case | Upper Reservoir Water Level | Downstream Tailwater Level | Load Change |
|---|---|---|---|
| D1 | 825 | 582.14 | One unit full load rejection |
| D2 | 825 | 581.5 | One unit full load rejection |
| D3 | 825 | 579.44 | One unit full load rejection |
| D4 | 784.14 | 582.14 | One unit full load rejection |
| Small Fluctuation Calculation Cases | Upstream Water Level | Downstream Tailwater Level | |
|---|---|---|---|
| X1 | One unit is operating normally and shedding 5% of its load. | 825 | 581.5 |
| X2 | One unit is operating normally and shedding 10% of its load. | 825 | 581.5 |
| X3 | One unit is operating normally and shedding 5% of its load. | 784.14 | 582.14 |
| X4 | One unit is operating normally and shedding 10% of its load. | 784.14 | 582.14 |
| Case | Maximum Deviation xmax/% | Overshoot σ/% | Adjustment Time Tp/s | Number of Oscillations X |
|---|---|---|---|---|
| X1 (Excluding free-surface flow) | 0.8 | 11.8 | 16.8 | 0.5 |
| X1 (Considering free-surface flow) | 0.8 | 11.2 | 16.4 | 0.5 |
| X2 (Excluding free-surface flow) | 1.6 | 10.8 | 29.9 | 0.5 |
| X2 (Considering free-surface flow) | 1.5 | 9.6 | 28.5 | 0.5 |
| X3 (Excluding free-surface flow) | 1.3 | 11.9 | 24.1 | 0.5 |
| X3 (Considering free-surface flow) | 1.3 | 12.3 | 23.1 | 0.5 |
| X4 (Excluding free-surface flow) | 2.5 | 11.3 | 103.4 | 1.0 |
| X4 (Considering free-surface flow) | 2.4 | 8.0 | 62.4 | 0.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, X.; Fan, J.; Tian, Y.; Zhou, Y.; Chen, Q.; Li, X.; Zhou, L. Simulation and Analysis of Real-Time Coupling of Free-Surface Flow and Pressure Flow in Hydropower Station Tailrace Tunnels Based on the Finite Volume Method. Water 2025, 17, 3075. https://doi.org/10.3390/w17213075
He X, Fan J, Tian Y, Zhou Y, Chen Q, Li X, Zhou L. Simulation and Analysis of Real-Time Coupling of Free-Surface Flow and Pressure Flow in Hydropower Station Tailrace Tunnels Based on the Finite Volume Method. Water. 2025; 17(21):3075. https://doi.org/10.3390/w17213075
Chicago/Turabian StyleHe, Xin, Jinyong Fan, Yongxin Tian, Yuguo Zhou, Qianxun Chen, Xiaoliang Li, and Ling Zhou. 2025. "Simulation and Analysis of Real-Time Coupling of Free-Surface Flow and Pressure Flow in Hydropower Station Tailrace Tunnels Based on the Finite Volume Method" Water 17, no. 21: 3075. https://doi.org/10.3390/w17213075
APA StyleHe, X., Fan, J., Tian, Y., Zhou, Y., Chen, Q., Li, X., & Zhou, L. (2025). Simulation and Analysis of Real-Time Coupling of Free-Surface Flow and Pressure Flow in Hydropower Station Tailrace Tunnels Based on the Finite Volume Method. Water, 17(21), 3075. https://doi.org/10.3390/w17213075







