Beyond Deterministic Forecasts: A Scoping Review of Probabilistic Uncertainty Quantification in Short-to-Seasonal Hydrological Prediction

Abstract

This Scoping Review methodically synthesizes methodological trends in predictive uncertainty (PU) quantification for short-to-seasonal hydrological modeling-based forecasting. The analysis encompasses 572 studies from 2017 to 2024, with the objective of addressing the central question: What are the emerging trends, best practices, and gaps in this field? In accordance with the six-stage protocol that is aligned with PRISMA-ScR standards, 92 studies were selected for in-depth evaluation. The results of the study indicate the presence of three predominant patterns: (1) exponential growth in the applications of machine learning and artificial intelligence; (2) geographic concentration in Chinese, North American, and European watersheds; and (3) persistent operational barriers, particularly in data-scarce tropical regions with limited flood and streamflow forecasting validation. Hybrid statistical-AI modeling frameworks have been shown to enhance forecast accuracy and PU quantification; however, these frameworks are encumbered by constraints in computational demands and interpretability, with inadequate validation for extreme events highlighting critical gaps. The review emphasizes standardized metrics, broader validation, and adaptive postprocessing to enhance applicability, advocating robust frameworks integrating meteorological input to hydrological output postprocessing for minimizing uncertainty chains and supporting water management. This study provides an updated field mapping, identifies knowledge gaps, and prioritizes research for the operational integration of advanced PU quantification.

1. Introduction

Hydrological forecasting is fundamental to sustainable water resource management because it enables stakeholders to anticipate hydroclimatic variability and make informed decisions. Short-to-seasonal hydrological prediction encompasses forecast horizons from daily (1-day) to seasonal (up to 8 months) time scales, bridging operational flood forecasting and climate-informed water management planning. This temporal range specifically targets the critical gap between numerical weather prediction limits (~15 days) and long-term climate projections (>1 year), where hydrological memory and initial conditions provide predictability beyond meteorological skill. Predictive uncertainty (PU) quantification has emerged as a cornerstone for enhancing forecast reliability within this critical forecasting window.

Nevertheless, three primary bottlenecks persistently constrain probabilistic uncertainty quantification: (1) Methodological challenges—incomplete propagation of meteorological uncertainty through hydrological systems, lack of standardized validation protocols, and inadequate representation of extreme events; (2) Geographic inequities—concentrated validation in temperate, data-rich regions (72% of studies in Chinese, North American, and European watersheds) while 43% of global hydrological disasters occur in underrepresented tropical and arid regions; (3) Operational implementation gaps—persistent disconnect between academic innovation and real-world adoption due to computational demands, interpretability constraints, and limited operational framework standardization (35% adoption rate for Bayesian frameworks). These limitations systematically undermine early warning systems in data-scarce regions where reliable forecasting is most critically needed [1,2].

Recent advancements in Bayesian frameworks, machine learning, and hybrid methodologies have expanded PU quantification capabilities. However, extant syntheses remain fragmented: specialized reviews have addressed individual components including ML postprocessing [3,4], Bayesian frameworks [5], and ensemble streamflow forecasts [6], yet a comprehensive evaluation of emerging trends, cross-methodological comparisons, and operational integration pathways remains absent. This fragmentation impedes identification of scalable, adaptable operational frameworks suitable for diverse hydroclimatic regions. However, there are significant challenges that need to be addressed. These include the need for improved identification of the primary sources of uncertainty and development of scalable, adaptable operational frameworks for diverse regions [7].

The De León Pérez et al. [8] protocol applied in this Scoping Review (ScR) was designed to ensure reproducibility, given its substantial alignment with PRISMA-ScR standards [9,10]. However, it exhibits enhanced flexibility and is particularly well-suited for hydrological sciences. In this context, this Scoping Review addresses the central question: What are the emerging trends, best practices, and existing gaps in predictive uncertainty quantification for short-to-seasonal hydrological forecasting? The inquiry objectives are threefold: first, evaluate contemporary methodologies; second, identify patterns in statistical and machine learning-based approaches; third, detect limitations in existing frameworks. A complementary question guides operational relevance: How can these methodologies bridge the gap between theoretical advancements and operational implementation in diverse hydroclimatic regions?

This ScR analyzed 572 studies from 2017 to 2024, with 92 selected for comprehensive evaluation. The contribution includes updated field mapping, systematic gaps identification, and prioritized research directions for operational integration of advanced PU quantification. The manuscript organization follows: methodology (Section 2), results including foundational pre-2017 methodologies (Section 3), discussion (Section 4), and conclusions (Section 5). Following, a comprehensive description of the content of each Supplementary Material is presented. The present ScR is noteworthy for its transparent presentation of information, a quality that facilitates reader comprehension and paves the way for future research (or actualization) in the field. Consequently, the supplemental documentation provided here encompasses all extant support documentation to reproduce or enhance this ScR in the future.

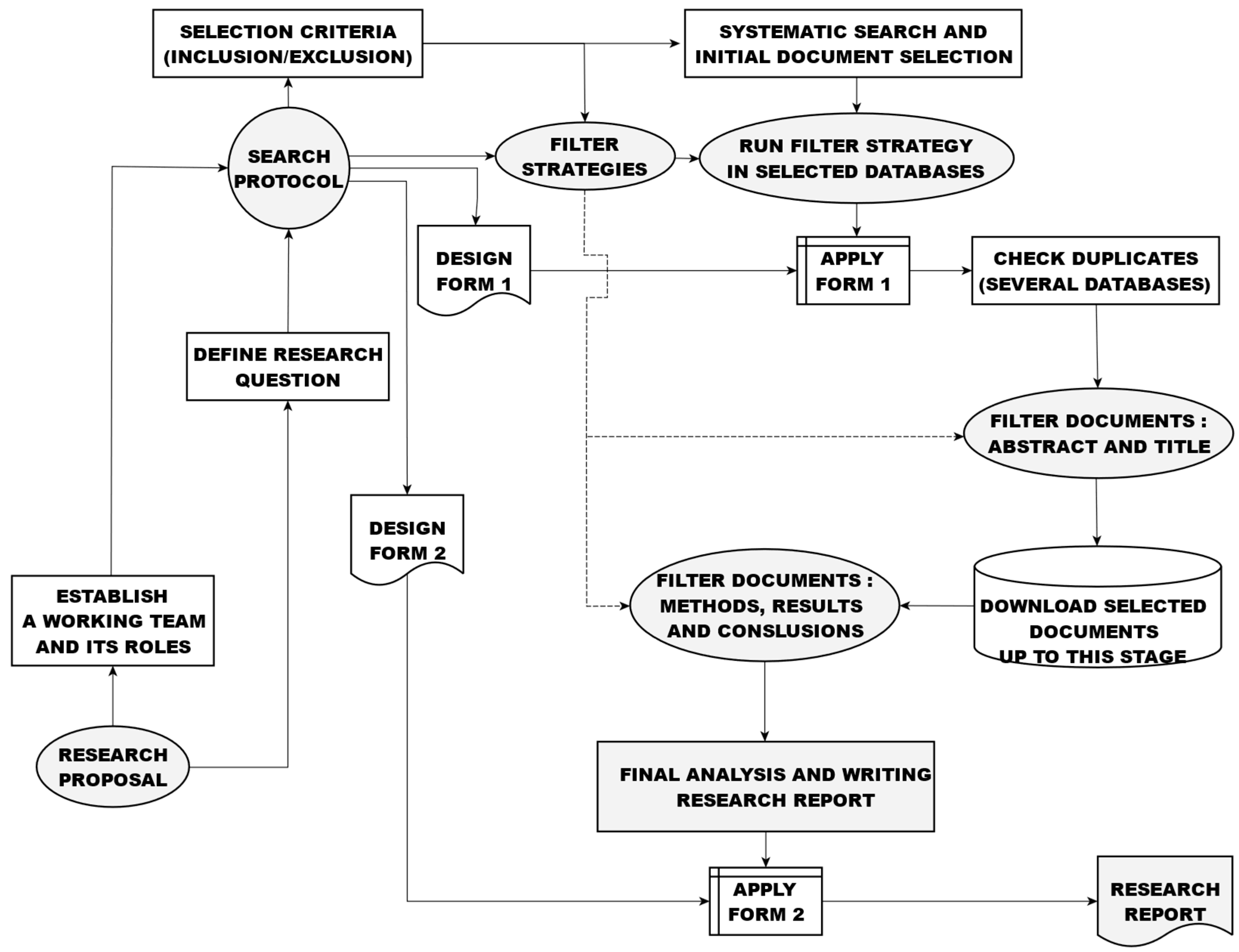
2. Methodology

This study utilized the structured framework proposed by De León Pérez et al. [8] which was meticulously designed for systematic syntheses in the domain of hydrological sciences (see Figure 1 for a flowchart of this framework). The protocol aligns with 88% of the PRISMA-ScR guidelines and prioritizes transparency, reproducibility, and minimization of selection bias through sequential filtering. The methodology under consideration integrates semiautomated database queries and rigorous document screening. It was predicated on a series of clearly delineated and predefined steps. This approach is intended to circumvent, or at least minimize, the omission of relevant papers and reduce selection bias.

2.1. Literature Search Strategy

A semi-automated search was conducted in Scopus [11] and Web of Science [12], which were selected for the comprehensive coverage of peer-reviewed literature [13,14,15,16]. The search prioritized Scopus and Web of Science due to their curated, peer-reviewed coverage in hydrology and water resources, standardized metadata, and reproducible export tools. A comprehensive search of complementary sources (e.g., Crossref, DOAJ, PubMed, Google Scholar) was conducted for reference chasing and verification purposes. However, these sources were not integrated into the primary corpus to mitigate potential issues such as non-peer-reviewed leakage, large-scale duplication, and indexing heterogeneity. This approach is consistent with the PRISMA-ScR (Preferred Reporting Items for Systematic Reviews and Meta-Analyses) guidelines, which emphasize transparent reporting of sources, criteria, and reproducibility (refer to the PRISMA-ScR flowchart in Figure 2). The Boolean search strategy combines the following three conceptual layers:

• Uncertainty components: uncertainty analysis, forecast uncertainty, error analysis
• Hydrological focus: hydrological forecasting, streamflow prediction, ensemble forecasts
• Methodological scope: probabilistic forecasts, machine learning, Bayesian frameworks

The full search equations optimized for each database’s syntax are detailed in Supplementary Material 1. These keywords were applied to refine the semi-automated search of each database, thereby ensuring the inclusion of relevant documents. The search period, which was concluded on 31 December 2024, was designed to provide the most up-to-date information, given that the objective of this ScR was to identify emerging trends in PU (results archived in Supplementary Material S3), because the aim was to identify current trends in the central topic of this ScR, without excluding pre-2017 seminal methodologies (see Section 3.1). Language filters prioritized English/Spanish publications that cover about 91% of the published papers in both databases used [17,18], while domain filters excluded non-hydrological fields (e.g., medicine, economics, social sciences).

2.2. Inclusion/Exclusion Criteria

The implementation of the inclusion and exclusion criteria necessitates a systematic analysis and invariably entails a certain degree of subjective interpretation. Consequently, the research team engaged in a deliberative process to formulate and meticulously implement a set of general criteria for the inclusion and exclusion of studies.

2.2.1. Inclusion Criteria

• Forecasting from days to seasonal;
• Research focused on predictive uncertainty in hydrological or meteorological forecasting;
• Research that identifies Uncertainty sources;
• Quantitative methods;
• Models with multiple realizations from different inputs, such as ensemble members;
• Application of Statistical, Probabilistic, Stochastic, or ML/AI methodologies that include analyzing or evaluating, or reducing the predictive uncertainty;
• Postprocessing methodologies;
• Hydrological variables (e.g., streamflow, precipitation, temperature…);
• Research with performance probabilistic metrics;
• Error models;
• Research with clear data sources or access to validating.

2.2.2. Exclusion Criteria

• Long-term climate projections (>1 year horizon);
• Real-time forecast (sub-daily);
• Parametric Uncertainty;
• Research that does not identify uncertainty sources;
• Qualitative or descriptive methods;
• Deterministic simulation models;
• Non-hydrological variables or domains (water quality, sediment without nexus with forecast, hydropower engineering…);
• Research without (or not standardized) quantitative validation (performance metrics);
• Research without data sources or access to validating.

The fundamental search equations are listed in

Table 1. Generic search equations applied to each scientific database.

Database	Generic Search Equation
Scopus	(TITLE-ABS-KEY (uncertainty AND hydro* AND forecast) AND PUBYEAR >2016) + language filters + domain filters + Conceptual layers (search refine terms)
WoS	TS = (uncertainty AND hydro* AND forecast) AND PY = (2017–2024) + language filters + domain filters + Conceptual layers (search refine terms)

. The complete and final two search equations applied to each scientific database are presented in Supplementary Material S1 and were configured differently in accordance with the specifications and tools of each database. Readers interested in updating, continuing, or expanding this ScR are encouraged to use these equations on a basis and adapt the terms to their needs. On the other hand, an assessment of the keywords was conducted using VOSViewer 1.6.20 [19].

2.3. Documents Referenced by Colleagues or Other Researchers

In addition to the direct searches conducted in the databases, the methodology employed for this ScR involved evaluating the records referenced by De León Pérez et al. [8], obtained from colleagues’ suggestions or manual searches. These records are incorporated into Supplementary Material S3 in a spreadsheet named “REFERENCED” (Table S3.3: Summary Form 1 with documents that have been cited by colleagues or in other research papers). Furthermore, seminal methodologies developed before the search period were included, taking into account that they have significantly influenced the field (see Section 3.1 Referent Methodologies Prior to 2017).

2.4. Document Selection

To evaluate the application of the inclusion and exclusion criteria (and refine them if necessary), four research team meetings were convened. The preliminary inclusion and exclusion criteria were presented during the preliminary meeting. Subsequently, a random sample of the retrieved documents was subjected to a review by one member of the research team and an external colleague. This sample comprises 56 documents, constituting approximately 10% of the total. The objective of this review was to evaluate Cohen’s kappa statistic [20,21]. A cut-off value of 0.6 was established according to

Table 2. Strength of agreement. Source: Adapted from Landis et al. [20].

Kappa Statistic1	Strength of Agreement
<0.00	Poor
0.00–0.20	Slight
0.21–0.40	Fair
0.41–0.60	Moderate
0.61–0.80	Substantial
0.81–1.00	Almost Perfect

. This value was selected based on the (aforementioned) degree of subjective interpretation that is inherent to every person, which is inevitable. Table 2 presents the range of the categorical strength of agreement according to the Kappa Statistic.

At this stage, the reviewers were members of the research team and an external peer reviewer. The result of the Cohen’s Kappa Statistic was 0.68 (see Supplementary Material S2 in sheet name: 1st_Evaluation, Table S2.1: Kappa Statistic for first evaluation (Title and Abstract)), which indicates that the strength of agreement (Table 2) is in the “Substantial” range for Cohen’s Kappa Statistic and exceeds the established cut-off.

In the subsequent meeting, the results of the cross-selection were presented, and the criteria were refined. Using these modified criteria, a random sample of the selected documents was subjected to a subsequent review by one member of the research team and an external colleague. The sample comprised 31 documents, constituting approximately 11% of the initial set of documents selected for review. The objective of this second review was to evaluate Cohen’s Kappa Statistic for the complete reading (and final selection) of the documents. The result of the Cohen’s Kappa Statistic was 0.68 (see Supplementary Material S2 in a spreadsheet named: 2nd_Evaluation, Table S2.2: Kappa Statistic for second evaluation (Methodology, Results and Conclusions)), which indicates that the strength of agreement (Table 2) is in the “Substantial” range for Cohen’s Kappa Statistic and exceeds the established cut-off.

The results demonstrate that the criteria inclusion/exclusion were clearly defined (with a strength agreement different from 1). Following the establishment of a set of clearly delineated criteria and their subsequent validation, a comprehensive review of the documents retrieved by one of the researchers was performed. It should be noted that this review was conducted by a single reviewer due to constraints on resource availability. A shorter final evaluation of 10 (11%) selected documents was conducted by the research director. The objective of this third review was to evaluate Cohen’s Kappa Statistic for the final selection of documents. The result of the Cohen’s Kappa Statistic was 0.77 (see Supplementary Material S2 in a spreadsheet named: 3rd_Evaluation, Table S2.3: Kappa Statistic for third evaluation (final selection)), which indicates that the strength of agreement (Table 2) is in the “Substantial” range for Cohen’s Kappa Statistic and exceeds the established cut-off.

3. Results

The application of equation search produced the filtered documents incorporated into Form 1: Supplementary Material S3 in sheet name “SCOPUS” (Table S3.1: Summary Form 1 with Scopus Database search) and sheet name “WoS” (Table S3.2: Summary Form 1 with Web of Science Database search); in the same file, the reader may find the identification by document if was duplicated, eighter was selected in the first read (Title and Abstract), either if was selected in the second read (Methodology, Results, and Conclusions). The documents selected in the present ScR were retrieved using the aforementioned methodology and deposited in Form 2 (See Supplementary Material S4). However, the initial results analysis is devoted to the presentation of referent methodologies prior to 2017, which are foundational to comprehending or assessing contemporary trends in PU.

These foundational methodologies have been incorporated to mitigate some temporal bias of the search period and contextualize developments from 2017 to 2024, since the integration of these foundational methodologies with AI/ML, as well as other statistical approaches, is a driving force behind contemporary hybrid frameworks.

3.1. Referent Methodologies Prior to 2017

This ScR focuses on trends in PU evaluation from 2017 to 2024. However, it is essential to acknowledge the foundational methods developed by important researchers prior to this period, which have significantly influenced the field. The first section provides a concise overview of some established methods for assessing PU. It should be noted that these methods are not exclusive because there are numerous alternative approaches.

3.1.1. Bayesian Forecasting System

In the late 1990s, the Bayesian Forecasting System (BFS) was presented by Roman Krzysztofowicz [22], which is based on the theory of Bayesian Forecast Processors (BFP). It combines an “a priori” distribution representing the uncertainty inherent in a process with a likelihood function related to the uncertainty in the process forecasts. Consequently, a posterior distribution conditional on the estimates is obtained [23]. The mathematical and theoretical foundations of BPF are rooted in Bayesian approaches to inference for stationary time series [24].

BFS represents a probabilistic theoretical framework for separating the uncertainty inherent in a deterministic hydrological model into two distinct components. One is generated by the input forecast, namely the Precipitation Uncertainty Processor—PUP [25], which evaluates the output uncertainty under the assumption of no hydrologic uncertainty. The other is the result of the hydrologic models. The Hydrologic Uncertainty Processor—HUP [26] assesses the output uncertainty under the assumption of no uncertainty in precipitation. This assessment is incorporated into an Uncertainty Integrator (INT), which generates the final probabilistic forecasts [27]. An alternative focus is the Precipitation-Dependent Hydrologic Uncertainty Processor (PD-HUP), which postulates that precipitation is the primary source of hydrological uncertainty. Consequently, uncertainty is not incorporated into the hydrological model [28]. For a comprehensive examination of this methodology, refer to [5].

3.1.2. Bayesian Model Averaging

Bayesian Model Averaging—BMA [29,30,31,32,33] is a robust technique that, like HUP, identifies the primary source of uncertainty as residing within the model itself, rather than in the forcings. BMA is distinguished by its superior reliability and accuracy as a statistical method for multiple model ensembles. This results in more competent and reliable predictive ability, which exceeds those obtained through the individual independent use of the models. Consequently, confidence in the effectiveness of the models is reinforced.

Hoeting Jennifer A. et al. [33] indicate that the researchers select a statistical model and presume that this model generates the data, thereby overlooking the potential for the uncertainty inherent in the model. In contrast, BMA addresses the uncertainty in model selection by employing a set of models and then averaging their inferences or predictions by assigning weights to each model using Bayes’ theorem. In this way, posterior probabilities were calculated, and the predictions were averaged, assigning a higher weight to those models that were more congruent with the observed data [34]. This allowed the uncertainty of the models to be averaged in proportion to the certainty of their prediction probability. However, despite the good results, the computational cost of BMA is high because its evaluation requires the use or operation of several models; in other words, the computational time depends on the number of models to be used because the logic of the method implies that the more models used, the better the result, but also the more time and computing power [35,36].

3.1.3. Model Conditional Processor

In 2008, an Italian researcher from the University of Bologna, Ezio Todini, proposed a novel methodology, designated as the Model Conditional Processor (MCP), which contributes to the assessment of PU by providing a systematic approach to combining observations with model forecasts in a multivariate normal space [37]. MCP permits the estimation of a comprehensive PU through the marginalization of parameter uncertainty, as opposed to relying on a single set of parameter values. This approach recognizes the variability in model parameters and their influence on predictions, thereby facilitating a more comprehensive understanding of the uncertainty. The methodology employs the Normal Quantile Transform [38,39,40] to transform both observations and model forecasts into a multivariate normal space. This transformation allows the derivation of joint and conditional probability distributions, thereby facilitating a more accurate assessment of the PU.

Overall, MCP enhances the understanding and management of PU in flood forecasting, which is crucial for effective decision-making in flood risk management, and represents a robust alternative to existing approaches, including the HUP and BMA models; however, it is subject to key limitations. First, its assumption of homoscedastic error variance frequently fails under conditions of heteroscedasticity, which is a common occurrence in hydrological processes. Second, its meta-Gaussian framework may inadequately capture the nonlinear dependencies among hydrological variables, limiting its applicability to complex systems. Finally, MCP’s reliability diminishes in extrapolative scenarios, such as extreme events or climate change contexts, highlighting its reduced robustness outside calibration conditions [41,42,43].

3.1.4. Generalized Likelihood Uncertainty Estimation

Generalized Likelihood Uncertainty Estimation (GLUE) is a statistical method to quantify the PU popularized by Beven in his pioneering paper “The Future of Distributed Models: Model Calibration and Uncertainty Prediction” [44]. According to Beven [45], this methodology represents a technique for estimating uncertainty in distributed hydrological models by evaluating multiple parameter configurations. In contrast to traditional methodologies that aim to identify an optimal set of parameters, this approach is based on attributing likelihood measures to various groupings of model parameters and employing these measures as weighting factors in the model projections.

The GLUE method has been the subject of criticism in the hydrological literature [46,47] because of its inability to provide an accurate estimate of PU. One of its primary shortcomings is its incompatibility with the Bayesian paradigm, which constrains the “learning” capacity of the method and diminishes the precision of parameter estimation. The use of less formal likelihoods in GLUE allows flexibility in parameter selection; however, this results in the generation of flat and imprecise posterior probability distributions. Furthermore, the method overestimates the PU owing to its inability to fit the observational data well with the model. As Mantovan and Todini [47] observed, while GLUE endeavors to address the phenomenon of “equifinality” (where multiple parameter configurations can describe the same phenomenon), the method fails to calculate the correct predictive probability. This is because the GLUE likelihoods, which are not formal probabilities, do not comply with Bayes’ theorem. Consequently, inconsistencies in the predictive results were observed. Furthermore, this inconsistency affects the comparability of the results, which can ultimately lead to risky management decisions. In the papers “Hydrological forecasting uncertainty assessment: Incoherence of the GLUE methodology” [47] and “Comment on: ‘On undermining the science?’ by Keith Beven” [46], the authors conducted a comprehensive analysis and discussion of the GLUE methodology.

In addressing these critiques, Beven et al. [48] adopt a reflective and constructive stance, proposing that under certain strong assumptions, GLUE can attain coherence, contingent upon the utilization of consistent prior information. While acknowledging the challenges posed by multiple sources of uncertainty in practical applications, the authors underscored the flexibility of GLUE, which enables a more nuanced assessment of the uncertainty in hydrological systems. Nevertheless, they also caution against the utilization of elementary formal likelihood functions as they may generate misleading outcomes. Instead, they proposed GLUE adaptability as a more robust alternative to traditional Bayesian approaches. Finally, they emphasized the necessity of a profound comprehension of the informational content of data to enhance uncertainty estimation in hydrological modeling. Subsequent advancements have demonstrated that this methodology can be updated with new data using a Bayesian procedure, thereby refining the uncertainty distribution of the model [49,50].

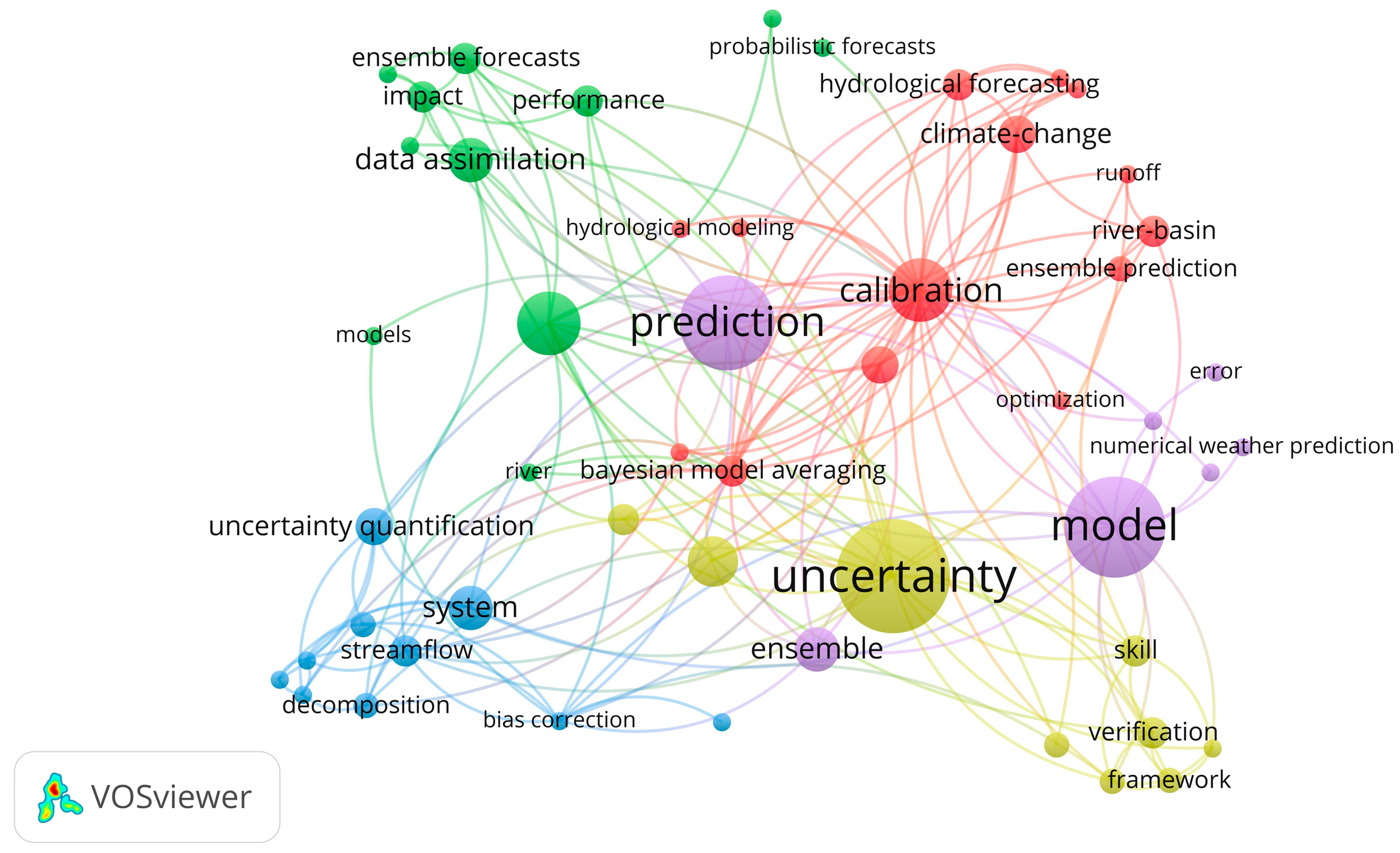
3.2. Selected Bibliography from Search Strategies

The flowchart (Figure 2) methodically delineates the trajectory of the document search and the results obtained at each stage up to the database obtained for the ScR. Bibliometric networks were produced in VOSViewer using keyword co-occurrence, revealing a notable correlation between the document’s keywords and the research question (see Figure 3 and Figure 4).

The final parameters were determined to be Resolution = 1.07, Attraction = 2.0, and Repulsion = 0. The Scopus map yielded six clusters, while the WoS map yielded five clusters. Co-occurrence maps (Figure 3 and Figure 4) provide substantiation of the thematic alignment with the research question, accentuating clusters with cores in “Prediction,” “Uncertainty,” “Uncertainty Analysis,” “Hydrological Modeling,” and “Forecasting” with elevated connectivity.

A total of 572 documents (see Figure 5 at panel «a») were retrieved from the semi-automatic search of the databases and included in Form 1 (Supplementary Material S2). Most of these documents were published in 2019, followed by a decline until 2021, followed by a recovery in 2022, reaching a level close to that of 2019. However, there was a sharp drop in 2023, and even more so in 2024. The oscillating pattern of production during the research period rises, falls, recovers, and then falls, suggesting a vulnerability of scientific productivity to external shocks. The significant decline in publications in 2020 (Figure 5 at panel «a») corresponds temporally with the onset of the COVID-19 pandemic, which imposed considerable restrictions, particularly on field projects and international collaborations in non-medical domains [51]. The subsequent recovery (2021–2022) can be attributed to the reactivation of funding for climate conservation and adaptation to virtual modalities. The further post-2022 decline points to factors that may be the subject of future bibliometric investigations into thematic saturation or the migration of researchers to more emerging areas, such as applied artificial intelligence and data science.

As illustrated in Figure 5 at panel «b», the selection process is delineated as such: A total of 51% of the records (282 out of 572) successfully advanced to the initial phase, which involved a title and summary review. However, a more stringent filtration process was evident, as only 16% (92 of 572) satisfied the methodological criteria in the comprehensive evaluation.

About the documentary classification (Figure 5 at panel «c»), it is evident that the most significant documentary sources found were articles, which constituted 95.6% of the 92 final documents retrieved. Of these, 90.2% were research articles, and 5.4% were reviews. Conference papers (2.2%) and book chapters (2.2%) constituted a minority of sources. Similarly, the publishers with the highest number of publications on this research topic are Elsevier, Springer Link, and MDPI, which together account for 60% of the articles retrieved Figure 5 at panel «d». As indicated by (Figure 5 at panel «e»), the Journal of Hydrology is responsible for 15% of the publications retrieved, followed by Water Resources Management (13%), Water (11%), and HESS (10%), which are specialized journals with a higher 5-year Impact Factor (2024) than 3.0 in the field of water resources and with significant prestige in the academic community.

A geographical analysis of the 92 documents retrieved reveals that 97 countries are mentioned as the locations of the cases studied (Figure 5 at panel «f»). China was the most frequently mentioned country, with 36 cases (37%), followed by several blocks of countries, including those in North America (Canada and the USA) with 16 cases (16.5%), and Europe with 12 cases (12.4%). These three regions account for more than 65% of the cases studied, which is consistent with the geographical distribution of the top 100 universities in global rankings.

The regional aggregation of observations, with a focus on China, North America, and Europe, aligns with global reviews identifying areas of elevated flood risk and research and data gaps in Africa and specific regions of Asia. This pattern reflects not only exposure and risk, but also data and infrastructure gaps that determine where research is conducted, validated, and transferred to operation [52]. Recent evidence from global flood risk mapping, adjusted for social vulnerability, has identified regions of high risk in countries with high population density and deprivation. This finding indicates that the accessibility and availability of hydrological and socioeconomic data play a critical role in the prioritization and generalization of methods [53].

3.3. Prevalent Methodologies Found

The extant literature from 2017 to 2024 demonstrates a clear evolution in predictive uncertainty (PU) quantification for hydrological forecasting, with two main methodological streams: statistical approaches and machine learning/artificial intelligence (ML/AI) methods (see Figure 6). Statistical methods, including Bayesian frameworks, ensemble techniques, and quantile-based approaches, offer robust probabilistic representations of the forecast uncertainty [31,33,44,54,55,56]. Concurrently, machine learning (ML) and artificial intelligence (AI) methods have rapidly gained traction because of their capacity to capture nonlinearities and leverage extensive datasets [3,4,57].

A prevalent contemporary technique involves the utilization of ensembles to obtain multiple forecast realizations, thereby considering various initial conditions of atmospheric variables. This approach is appealing because the unstable and chaotic dynamics of the global climate system preclude the determination of the initial state of meteorological forecasts with sufficient precision in advance. This finding indicates that the incorporation of multiple model outputs and observational data through advanced postprocessing methodologies has led to the provision of more comprehensive uncertainty bounds [6,58,59].

4. Discussion

The quantification of predictive uncertainty (PU) has emerged as a cornerstone for improving forecast reliability. This ScR analysis of 92 selected studies reveals a paradigmatic shift in uncertainty quantification methodologies over the 2017–2024 period (according to the current AI Revolution), demonstrating not only technological advancement but also a fundamental reconceptualization of how hydrological uncertainty would be approached. This transition coincides with the geographic concentration (about 74%, see Figure 5) observed in the Chinese, Australian, Indian, North American, and European watersheds, suggesting that methodological innovation is closely linked to computational infrastructure availability and institutional research priorities.

The temporal restriction to post-2017 literature captured this transformative period when AI technologies are rising, while preserving connections to foundational pre-2017 methodologies in Section 3.1 analysis. This approach revealed that while classical frameworks maintain theoretical relevance, their operational implementation is overshadowed by hybrid approaches that combine statistical rigor with ML flexibility. However, significant gaps persist in the operational adoption and methodological standardization of PU quantification. From 2017 to 2024, global operational systems have documented a series of forecast inaccuracies that have been exceeded during weather events. These inaccuracies can be primarily attributed to the presence of unquantified precipitation uncertainties [55,58].

In the subsequent sections, the methodologies found in this ScR for postprocessing and time series forecasting uncertainty enhancement of hydrological variables are discussed. In view of the extensive research on ensembles developed by Troin et al. [6] a specific section is not designated for discussion on this topic in this ScR.

4.1. Statistical Methods

Statistical methods provide transparent, interpretable frameworks for uncertainty quantification, with Bayesian and ensemble approaches offering rigorous probabilistic outputs [5,33]. Bayesian frameworks (e.g., HUP, BMA, MCP) demonstrate robust probabilistic rigor; the efficacy of these methods in integrating prior knowledge and generating probabilistic forecasts has been demonstrated [5,60,61]. However, their operational implementation is frequently constrained by computational demands and the necessity for well-defined priors, particularly in regions with limited data or high variability in data [36,54,62].

Darbandsari and Coulibaly [63] proposed an enhanced streamflow forecasting by integrating initial flow conditions: the HUP-BMA method reduced the forecast interval width by 28.42%, and CRPS by 17.86% compared to HUP; however, reliance on Normal Quantile Transformation (NQT) introduced biases in extreme flows, for this reason recently Cui et al. [64] proposed CHUP-BMA, replacing NQT with copulas (e.g., Student t), eliminating distributional assumptions and reducing interval width by 28.42% and CRPS by 17.86% versus HUP-BMA, achieving superior calibration (CR > 90%) with horizons up to 7 days. This approach resolves transformation-induced distortions and improves computational efficiency, thereby advancing probabilistic hydrology in operational settings and demonstrating iterative BMA refinement with CHUP-BMA, thereby addressing the key limitations of its predecessor [63,64].

MCP established another seminal Bayesian framework for PU quantification by estimating conditional probability densities, assuming joint normality in transformed spaces [37]. Barbetta et al. [65] introduced the multi-temporal/multi-model MCP (MCP-MT), which integrates Truncated Normal Distributions (TNDs) to differentiate hydrological phases (e.g., rising limbs and peak flows). This approach reduced the forecast interval widths by 28.42% and CRPS by 17.86% compared to single-temporal approaches. Additionally, Anele et al. [66], MCP has demonstrated adaptability beyond the domain of hydrology. Specifically, the application of MCP in urban water demand forecasting has demonstrated notable efficacy. Through the integration of autoregressive (ARMA), neural network (FFBP-NN), and hybrid models, MCP has been successful in reducing the validation RMSE from 1.677 to 1.329. Additionally, it enhances the NSE to 0.953, achieving 95% coverage within the 90% uncertainty bands.

Romero-Cuellar et al. [67] breakthrough innovation through Gaussian mixture clustering integration (GMCP) that systematically addresses heteroscedastic errors with quantifiable improvements (36.64% sharpness increase, 10.29% containing ratio improvement, 16.66% NSE enhancement in dry catchments). Barbetta et al. [55] built upon Todini’s foundational MCP, extending its application from single-model flood forecasting to multimodel reservoir inflow prediction. This advancement involved the concurrent utilization of up to five deterministic models, a significant enhancement of the original approach with quantifiable improvements: The 1-day forecast demonstrated a 72% reduction in error, and an NSE that increased from 0.86 to 0.98. For the 3-day forecasts, there was a 50% reduction in the error, resulting in an NSE that improved from 0.64 to 0.93.

The collective works [55,65,66,67] constitute a coherent methodological evolution of the MCP, demonstrating the progression from basic urban applications to complex hydrological systems and advanced theoretical extensions. This highlights MCP flexibility but revealed sensitivity to input data quality and the need for dynamic updating in systems with high seasonal variability; however, critical limitations persist, derived from temporally restricted datasets that compromise statistical robustness, the absence of integration with operational meteorological uncertainties, and dependence on normality assumptions that limit extreme event representation [68], and a lack of exhaustive validation against alternative uncertainty quantification methods.

4.2. AI-Driven Approaches

In the present manuscript, a distinction is established between Artificial Intelligence (AI) as the broader field encompassing techniques that enable machines to mimic human intelligence, and Machine Learning (ML) as a specific subset of AI focused on algorithms that learn patterns from data to make predictions. While these terms are frequently used interchangeably in hydrological literature, ML more precisely describes the data-driven methodologies analyzed in this review, including neural networks, support vector machines, and ensemble methods. The term AI is employed when referring to the broader technological revolution and its comprehensive implications for hydrology.

ML/AI approaches, including deep learning architectures (e.g., Long Short-Term Memory-LSTM, Gated Recurrent Unit-GRU, and bidirectional long short-term memory (BLSTM)) and tree-based algorithms (e.g., Random Forest and XGBoost), in addition to hybrid models, have been shown to offer notable advances in capturing complex nonlinear relationships and integrating diverse predictors.

AI-driven methods handle high-dimensional data, capture complex patterns, and improve forecasting skills, particularly when integrated with statistical postprocessing [4,57,69]. Nonetheless, these methodologies are frequently the subject of critique due to their “black box” nature and the risk of overfitting, particularly in the context of rare or extreme events [70,71].

They are also encumbered by significant technical challenges, including the need for model interpretability, trade-offs in hyperparameter optimization, and requirements for substantial computational resources. The incorporation of uncertainty quantification methods is undoubtedly beneficial; however, it introduces a degree of complexity that can impede operational implementation. In the future, research should focus on the development of computationally efficient algorithms that can be implemented in real time. In addition, there is a need to establish standardized protocols for cross-basin validation. These protocols should combine physics-based constraints with data-driven flexibility to create hybrid frameworks that can effectively address the challenges posed by these constraints. Furthermore, the development of explainable AI techniques and automated hyperparameter optimization would considerably augment the practical utility of these sophisticated methodologies in operational water resource management.

The analysis of AI-Driven Hydrological Forecasting Methods demonstrates evidence of remarkable advancements in probabilistic hydrological forecasting, encompassing Bayesian deep learning frameworks [69], hybrid ensemble approaches [57,72], multi-scale variable integration [72], and explainable machine learning with uncertainty quantification [71]. Nonetheless, it should be noted that these findings are subject to certain limitations.

The BLSTM framework proposed by [69] has achieved significant advancements in the multi-step domain. The framework successfully integrated variational inference, a technique that has been demonstrated to enhance the precision of predictions in intricate systems. This finding aligns with the framework’s ability to quantify epistemic and random uncertainties [4]. This framework achieved PICP values exceeding 0.950 for one-day forecasts. However, this performance comes at a computational cost that may be prohibitive for real-time operational systems in resource-constrained environments.

The XGB-GPR-BOA model proposed by Bai et al. [57] exemplifies the tension between methodological sophistication and practical applicability. While achieving superior deterministic accuracy (RMSE: 1.847 m³/s, R²: 0.965) in the Yangtze River Basin, its geographical specificity and limitation to one-step-ahead forecasts highlight a fundamental challenge: advanced AI methods often sacrifice generalizability for performance optimization. RF-GPR-MV [72] further illustrates this pattern, with 15–25% improvements in longer horizons (1- to 12-month forecasts) offset by computational complexity, which hinders real-time operational implementation. This recurring theme across the reviewed studies suggests that recent acceleration of AI/ML adoption in hydrology prioritizes accuracy over operational viability.

In contrast, Fan et al. [71] presented substantial methodological advancements in reservoir inflow forecasting with PI3NN. The PI3NN method addresses the critical gap between performance and explainability, achieving 90% coverage probability while maintaining interpretability through explicit uncertainty decomposition. However, only 23% of the AI-driven studies in the reviewed corpus provided comparable interpretability frameworks, indicating that the field has largely overlooked operational transparency requirements.

4.3. AI-Driven Plus Statistical Frameworks

The integration of ML/AI with Bayesian frameworks represents the most promising methodological evolution identified in this review; however, implementation challenges persist across the analyzed studies. Emerging hybrid approaches, such as ML/AI plus Bayesian frameworks, enhance performance compared to deterministic models and demonstrate robust performance in hydrological forecasting. Reference [73] employed BMA-ensemble approach achieved 80% NSE/R² improvements but introduces systematic biases through Box–Cox transformations that compromise extreme-flow representation—a critical limitation given the underrepresentation of extreme events across the reviewed corpus (<12% addressing 100-year floods).

In contrast, Cui et al. [74] proposed copula-HUP paired with DA-LSTM-RED, which achieved substantial performance gains (10–17% MAE reduction and 17.86% CRPS improvement compared to traditional HUP-BMA methods) but at elevated computational expenses for copula calibration.

While Li et al. [73] emphasized the capacity of Bayesian frameworks to integrate the strengths of multiple models, their deterministic forecasts are characterized by the absence of explicit uncertainty quantification and sensitivity to input transformations. Conversely, Cui et al. [74] advanced operational applicability by implementing attention mechanisms that prioritize critical variables (e.g., precipitation) and temporal dependencies. Nonetheless, this approach is associated with elevated computational expenses for copula calibration. This exemplifies the fundamental tension identified throughout the ScR. The reviewed studies consistently demonstrate that Bayesian-AI hybrids require specialized expertise for implementation, creating interoperability barriers, such as standardized APIs for basin agencies or operational users. This finding aligns with the geographic concentration observed in this ScR (Figure 5 at panel «f»), where advanced methodologies cluster in well-resourced research institutions rather than in operational water management agencies.

The collective evidence retrieved suggests that while hybrid frameworks successfully harmonize precision and uncertainty resolution, their computational and technical requirements may perpetuate the research-practice gap that limits real-world uncertainty quantification deployment.

4.4. Final Remarks

The ScR provides a comprehensive overview of recent advances in the assessment of predictive uncertainty and innovations in short-term and seasonal hydrological forecasting. The analysis in this ScR, based on 92 selected papers (see Supplementary Material 4), revealed trends, innovative approaches, and best practices that can guide future development in this field. The identified patterns demonstrate both remarkable progress and persistent limitations, which limit operational adoption.

The findings and knowledge gaps identified and derived from the state-of-the-art examination to answer the research question are presented below, according to the records from the consulted databases and documents collected from 2017 to December 2024. Significant progress has been made in developing robust methodologies, including Bayesian, AI-driven, and ensemble techniques. These methods have enhanced the quantification and reduction in the PU, particularly for short- to seasonal forecasting horizons. However, the operational application of these methods remains limited, particularly in regions characterized by complex hydroclimatic conditions or limited resources.

Bayesian approaches have evolved from theoretical frameworks to hybrid implementations that leverage AI-driven capabilities, while maintaining probabilistic rigor. However, the review revealed that computational demands and reliance on well-defined priors can curtail their applicability in data-scarce regions, creating an equity gap between resource-rich and resource-constrained operational environments. In addition, the integration of Bayesian frameworks with machine learning has emerged as a promising trend, offering enhanced predictive accuracy and uncertainty quantification. However, this synergy often suffers from overfitting and interpretability issues, particularly in high-dimensional datasets.

Based on the research developed by Troin et al. [6], it is evident that ensembles represent a highly effective strategy for capturing a broader range of potential outcomes and providing a more comprehensive characterization of PU. By leveraging diverse outputs from ensemble members, ensemble methods can enhance the robustness and reliability of forecasts by incorporating several initial conditions into hydrological applications.

The integration of remote sensing data and global climate predictors has yielded substantial advances in reducing forecasting uncertainties. This approach leverages the extensive spatial coverage and accessibility afforded by satellite-derived data. Nevertheless, the temporal resolution constraints and biases in satellite-derived datasets can impede the efficacy of this approach by amplifying uncertainties rather than mitigating them.

Although postprocessing techniques have demonstrated effectiveness across diverse hydroclimatic contexts, they remain underutilized in operational settings because of the lack of adaptive functions, factors, and parameters that enable regional customization without statistical rigidity. This finding underscores the persistent disconnection between academic innovation and operational implementation.

While AI-driven approaches offer flexibility and the ability to capture nonlinear patterns, they are not devoid of limitations. The dependence on large datasets and computational resources makes their implementation challenging in regions with a limited technical infrastructure. Additionally, the “black box” nature of these models can give rise to concerns regarding their interpretability and reliability, particularly in scenarios where decisions of significant importance are being made.

Finally, the regional concentration of studies may restrict the applicability of their findings to other areas with contrasting hydrological and climatic conditions; however, this limitation extends beyond simple geographic bias. The ScR revealed a systematic underrepresentation of data-scarce regions, where uncertainty quantification is most critical for disaster risk reduction and enhances water management and governance.

4.5. Limitations

The limitations identified in this ScR reflect both the methodological constraints and broader systemic challenges in hydrological uncertainty research. The heterogeneity of the methodological approaches employed in the reviewed studies may present challenges in directly comparing results.

Furthermore, it is important to acknowledge that a comprehensive ScR may be constrained by the lack of comprehensive coverage of all relevant studies owing to limitations in accessing databases and publications. Notwithstanding the implementation of rigorous methodologies and the establishment of inclusion criteria, there is invariably a risk of publication bias. Consequently, studies such as those found in the gray literature that present significant results may not have been published and, therefore, have not been incorporated into this review. Nevertheless, the value of this ScR should not be underestimated, as it provides an overview of the current state of research in this field following a rigorous protocol [8]. Indeed, it is highly relevant because of its timeliness at a time of rapid emergence of AI-driven methods and their combination with statistical methods, with the latter having a longer tradition in the field.

In terms of unifying the criteria for selecting articles, it should be noted that although an initial research question and a protocol of “clear” rules for selecting and including documents were established, there is an inevitable degree of subjectivity involved in the selection. At least four meetings were held to define the final inclusion and exclusion criteria. These were aimed at refining the precise focus of the research and thus the research questions.

4.6. On Future Research Directions

Despite advances in reducing the uncertainty in hydrological forecasting, several knowledge gaps persist and require further research. Some areas that require more attention are as follows:

• Choosing the primary source of uncertainty remains a challenge. Therefore, it is necessary to develop clear guidelines for selecting an ideal approach, depending on the situation.
• Postprocessing techniques have great potential for refining forecasts; however, their large-scale operational implementation remains limited. Further studies are required for the medium- and long-term horizons.
• Most advances have concentrated on forecasting streamflow and precipitation. However, there is a lack of research on reducing uncertainty in the forecasts of other key hydrological variables, such as water quality, soil moisture, and water tables.
• The reviewed studies revealed the development of predictors based on remotely sensed data. Integrating sources, such as radar, satellites, and global climate indices, is an underexploited opportunity to reduce uncertainty.

Future research endeavors must concentrate on several pivotal aspects to further understand and administer the uncertainty in seasonal hydrological forecasts. Primarily, it is imperative to formulate and appraise modeling methodologies that can more effectively encapsulate the variability and intricacy of hydrologic systems. This encompasses enhancing the depiction of physical processes, incorporating reliable observational data, and investigating novel modeling techniques such as artificial intelligence and machine learning approaches.

Future research opportunities include the development of hybrid frameworks integrating artificial intelligence and machine learning for capturing complex nonlinear relationships. Among the emerging methodological approaches, distributional regression techniques represent a particularly promising research direction. Recent studies have begun exploring methods that generate full probability distributions of target variables rather than single deterministic values, thereby providing richer representations of uncertainty that capture not only central tendencies but also variability and potential extremes [75,76]. Extension toward nonstationary multi-model approaches with adaptive clustering, integration with ensemble meteorological forecasts, implementation of robust spatio-temporal cross-validation, explicit treatment of meteorological forecast uncertainties, and evaluation of quantifiable socioeconomic benefits, which are fundamental elements for establishing practical operational utility in integrated water resource management under climate change conditions and increasing hydroclimatological variability.

Furthermore, it is necessary to cultivate enhanced interdisciplinary collaboration, thereby addressing uncertainty from multiple perspectives. Experts in hydrology, climatology, mathematical modeling, and water resource management must collaborate to develop integrated and holistic approaches. The establishment of research networks and implementation of collaborative projects can facilitate the exchange of knowledge and application of best practices on a global scale.

It is imperative that future research prioritize the practical applications of these advancements within specific contexts. Conducting case studies across various regions and watershed types can yield invaluable insights into the efficacy of disparate uncertainty reduction methodologies and their relevance to disparate scenarios. This encompasses an assessment of the economic and social ramifications of hydrological forecasts, in addition to the effective communication of uncertainty to stakeholders and decision-makers.

In addressing the central research question, which explores emerging trends, best practices, and gaps in predictive uncertainty quantification, this ScR unveils a landscape of significant advancements in hybrid frameworks. However, the study also reveals persistent limitations in operational adoption and geographic validation. Moreover, the secondary inquiry underscores the significance of hybrid methodologies that seamlessly integrate the rigor of statistical standards with AI adaptability. These methodologies are designed to promote equitable access to data in regions facing scarcity, while concurrently enabling a seamless transition from academic innovation to practical hydrological applications in the face of escalating climatic variability. The findings incorporated in

Table 3. Summary of findings/gaps and research directions with operational implications.

Finding/Gap	Research Dir.	Operational Imp.	References *
Incomplete propagation of forcing uncertainty (precipitation) to flow. Sub/Over-dispersed and biased raw ensembles in events.	* Explicitly coupling meteorological-hydrological ensembles with probabilistic postprocessing	Better calibrated prediction bands and better control of false alarms	[6,55,58,59]
	* Estimate predictive densities conditional on horizon and report CRPS, calibration, and coverage by time frame
Univariate post-processing by time frame ignores temporal correlations between sub-horizons and multivariate incoherences	* Extending hydrological postprocessing to multivariate/horizon-dependent approaches	Consistent exceedance probabilities over the entire forecast window and simultaneous improvement at operational thresholds	[6,37,55,65,78,79]
	* Compare multi and univariate approaches, maintaining time dependence in the predictive distribution
Heterogeneity of probabilistic metrics and protocols; limited comparability between studies.	* Establish a minimum battery of probabilistic metrics (CRPS, CRPSS, PICP, BS, BSS, R-Factor…) and reproducible spatio-temporal validation by basin and horizon.	Transparent comparison of methods and clear criteria for operational adoption.	[78,80]
Poor validation in tails/ends and composite events; skill degradation at high percentiles.	* Tailor-made evaluation designs (q95-q99), multiple thresholds, and Threat Score	More reliable flood/drought alerts, reduction in false alarms at peaks.	[6,52,53,55,65,79,81]
	* Use of truncated families and/or copulas for asymmetries and extreme dependencies
Research-operation disconnection and gap for computational cost and interpretability in AI + statistics hybrids.	* Parsimonious and explainable hybrids (e.g., multi-MCP with ML on residuals)	Robust implementation in real time with limited resources without losing calibration.	[80,82]
	* Explicit cost reporting and real-time deployment guidelines.

Note(s): * Some examples extracted from the Form 2 (Supplementary Material S4) to guide the reader.

and Figure 7 of this study are consistent with the principles of ScR, particularly the “mapping” and “charting” aspects of PRISMA-ScR (with an adapted protocol for the hydrological sciences). These principles advocate that a ScR should culminate in clear findings and identified gaps, thereby establishing a foundation for future research that builds upon the methodological patterns and gaps identified [77]. Below, Table 3 condenses the key gaps, priority research directions, and operational implications, while Figure 7 illustrates their dynamic interconnections through a Sankey diagram, highlighting how methodological gaps can inform future strategies for more robust quantification

5. Conclusions

This comprehensive Scoping Review of 92 studies from 2017 to 2024 elucidates a field undergoing methodological transformation, where traditional statistical frameworks are enhanced by machine learning innovations to address predictive uncertainty in short-to-seasonal hydrological forecasting. In addressing the fundamental question, which delves into emergent trends, optimal practices, and extant lacunae, three pivotal findings emerge: (1) The evolution toward Bayesian-ML hybrid methodologies has been shown to achieve substantial accuracy improvements. However, this evolution has also revealed a systematic disconnect between academic innovation and operational adoption. This disconnect is exacerbated by computational demands that create equity barriers. (2) Geographic and validation biases have been shown to limit generalizability. This limitation is particularly pronounced in data-scarce tropical and semi-arid regions. This limitation underscores the need for inclusive strategies in global disaster risk reduction. (3) Integration challenges have been shown to demand frameworks balanced between methodological rigor and practical viability. These frameworks must prioritize extreme event representation and operational transparency.

The secondary inquiry, which centers on the potential of these methodologies to span the divide between theoretical advancements and operational implementation in diverse hydroclimatic regions, underscores the significance of a robust framework that integrates hydrological postprocessing as a pivotal instrument to augment forecast accuracy and reliability. This framework must span from meteorological input postprocessing to hydrological postprocessing, minimizing the uncertainty chain for optimal water resource management, planning, and handling amid growing hydroclimatic variability.

In summary, while uncertainty quantification has achieved technical sophistication, future progress must emphasize geographic equity, standardized validations, and integrated postprocessing. This will allow for the translation of advancements into equitable and operational tools for global water sustainability.