1. Introduction
Climate change exerts multifaceted influences on physical, chemical, and biological processes across all scales of the Earth system, with particularly profound consequences for aquatic environments. These impacts include alterations in heat budgets, mixing regimes, circulation patterns, nutrient redistribution, and ecosystem functioning. The Sixth Assessment Report of the Intergovernmental Panel on Climate Change [
1] has documented clear evidence of rising temperatures, an increasing frequency of extreme weather events, shifts in wind regimes, and asymmetric changes in precipitation patterns from the latter half of the 20th century to the early 21st century. Recent global syntheses further show large, coherent shifts in lake thermal structure and stratification phenology under warming [
2], including the emergence of non-analog thermal conditions in many lakes [
3]. Understanding how these changes affect enclosed and semi-enclosed water bodies has emerged as an urgent scientific priority worldwide.
Enclosed systems such as lakes, bays, and lagoons are especially vulnerable, as their limited geomorphological connectivity to the open ocean and short external forcing–response timescales make the manifestation of climate change effects more immediate and pronounced [
4,
5]. In such systems, even subtle changes in air temperature or wind speed can substantially alter stratification structure, vertical mixing, oxygen distribution, and biological activity. These shifts can, in turn, drive hypoxia in bottom waters, eutrophication, increases in internal nutrient loading, and changes in the frequency and intensity of algal blooms, ultimately degrading water quality and ecosystem services [
6,
7]. Compounding this sensitivity, multi-decadal variability in near-surface winds (“atmospheric stilling” and its recovery) can strongly modulate lake mixing and internal dynamics [
8,
9].
Among the physical processes central to these changes are internal waves—gravity waves that propagate within density-stratified water masses under the restoring force of buoyancy. They are typically generated by wind stress, atmospheric pressure disturbances, or topographic perturbations at boundaries. In lakes and semi-enclosed seas, internal waves with timescales of days to weeks often dominate, driving mixing and transport processes throughout the water column via changes in wavelength and period [
10,
11,
12]. Internal waves can exhibit nonlinearity and dispersion, sometimes forming solitons or wave packets that propagate along the bottom boundary, enhancing turbulence and contributing to sediment resuspension and nutrient replenishment [
13]. Recent observations in large, deep lakes highlight the role of higher-mode internal/Poincaré waves in deep-water hydrodynamics [
14], and seiche-driven motions have been shown to influence nearshore nutrient fluxes [
15]. Unlike oceanic settings where barotropic tides interacting with topography generate internal tides, Lake Biwa is an inland, non-tidal basin; astronomical tides are negligible and do not produce internal tides. Accordingly, throughout this study “internal waves” refer to wind- and pressure-forced internal seiches and related motions rather than internal tides.
Recent studies have suggested that the period, amplitude, and spectral structure of internal waves may vary in response to fluctuations in climatic drivers [
16], raising the possibility that climate change could fundamentally alter sub-inertial (>30 h) internal wave regimes. For example, surface warming associated with rising air temperatures can stabilize stratification, modifying the vertical structure of internal waves; increases or decreases in wind speed can alter the efficiency of forced oscillations and the magnitude of energy input [
17]. Variations in precipitation can create freshwater surface layers, modifying density gradients and thereby influencing the phase speed and modal structure of internal waves [
18]. Converging advances—lake model ensembles coupled to climate scenarios [
19,
20] and diagnostic toolkits that quantify internal wave properties [
21]—now enable systematic, climate-aware assessments.
Despite these insights, research on the dynamic responses of internal waves to meteorological forcing remains largely confined to localized, short-term case studies, with few quantitative assessments based on long-term meteorological datasets, and numerical approaches have often lacked the spatiotemporal resolution and diagnostics needed for enclosed systems. This study provides the first comprehensive, model-based quantification—grounded in multi-decadal observations—of how interannual variability in air temperature, wind speed, and precipitation modulates internal wave characteristics (period, amplitude, and energy spectra) in enclosed and semi-enclosed waters. Specifically, this study (i) quantifies sensitivities of internal wave metrics to ±2σ perturbations in each meteorological driver; (ii) evaluates frequency-band energy redistribution relevant to vertical transport and benthic–pelagic coupling; and (iii) delivers transferable diagnostics that can be embedded in ecosystem and water quality models. These contributions explicitly bridge time series analysis with wave-dynamics theory and operational spectral tools, offering an actionable framework for climate-aware management.
To address these gaps, this study systematically evaluates the influence of observed climate variability over the past three decades (1980–2010) on internal wave characteristics using meteorological datasets for air temperature, wind speed, and precipitation, coupled with a high-resolution numerical fluid model and spectral analysis. ±2σ perturbations are imposed on each meteorological variable, based on deviations from the climatological mean, to examine how changes in vertical thermal structure and density stratification affect internal wave periods, amplitudes, and energy spectra. The analysis reveals that warming tends to weaken the amplitude of super-inertial (6–16 h) internal waves while enhancing sub-inertial (>30 h) internal waves, whereas wind speed increases amplify internal wave energy across all frequency bands. By integrating time series analysis with the theoretical framework of wave dynamics, this study delivers a consolidated, climate-aware quantification of internal wave responses in enclosed and semi-enclosed waters, providing foundations for future coupling to water quality and ecosystem models and for assessing how climate-driven vertical transport may influence bottom-water oxygen supply and sediment phosphorus release.
2. Methodology
2.1. Study Area and Model Configuration
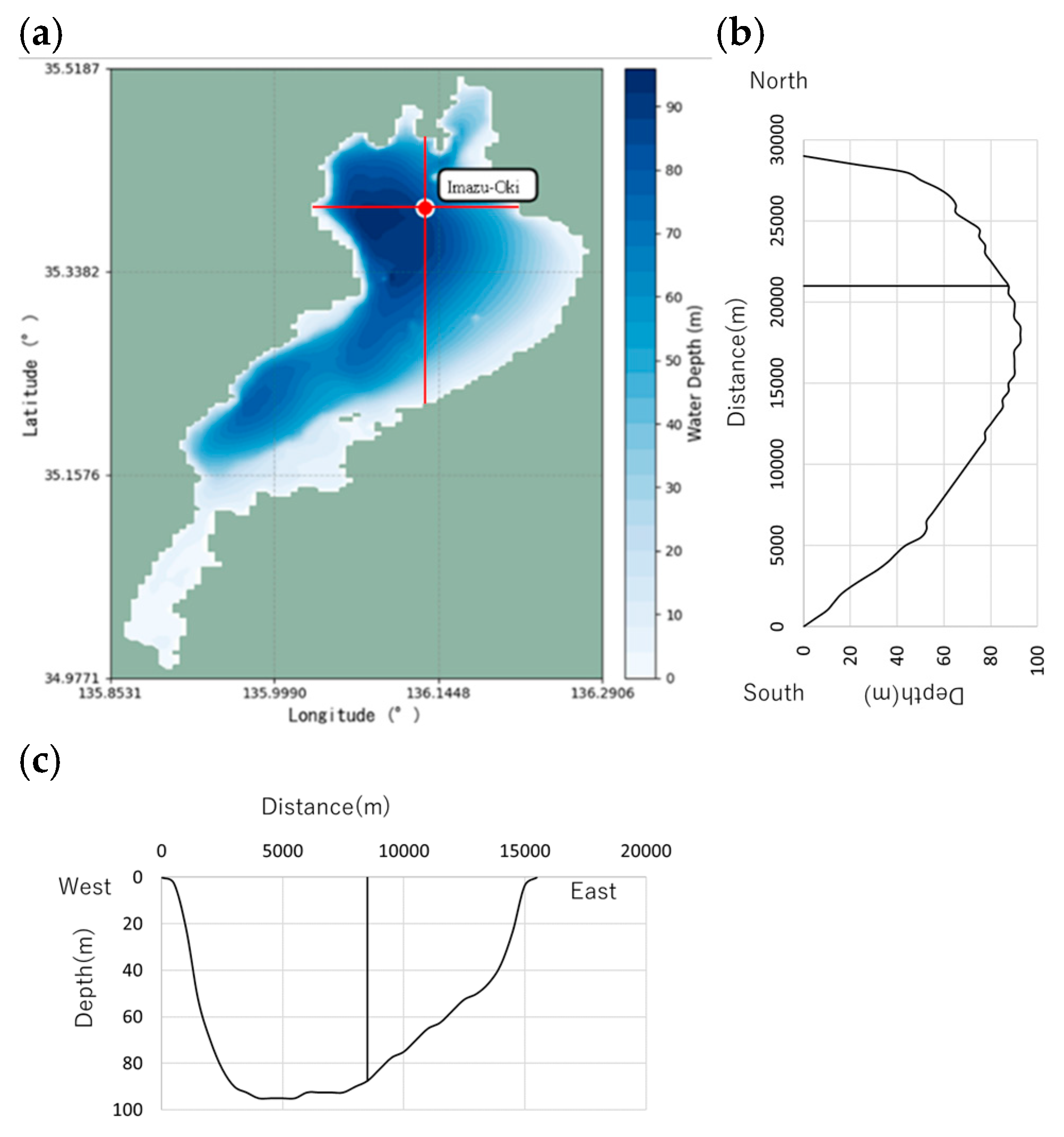
This study focuses on Lake Biwa, the largest freshwater lake in Japan.
Figure 1 presents the computational domain and bathymetry used in the hydrodynamic model. The horizontal domain spans 36 km × 65.5 km with a uniform horizontal resolution of 500 m. The vertical domain comprises 86 layers, extending from the lake surface to a maximum depth of 107.5 m. The vertical grid spacing is set to 0.5 m from the surface down to a depth of 20 m, gradually increasing to a maximum of 2.5 m with depth.
The governing equations include the momentum equations under the Boussinesq approximation, the hydrostatic approximation, the continuity equation, and the temperature conservation equation. These equations are formulated in a Cartesian coordinate system, with the origin located at the southwestern corner of the horizontal computational domain.
2.2. Hydrodynamic Model
In this study, the three-dimensional hydrodynamic model developed by Koue et al. [
22] was employed to conduct spectral analysis of internal waves within a lake. The model solves the incompressible Navier–Stokes and scalar-transport equations under the Boussinesq and hydrostatic approximations, with temperature as the active tracer governing density via a standard equation of state. Designed for realistic lake bathymetry and meteorological forcing, the model has been reported to reproduce thermal stratification and flow structures with high fidelity. In this study, the model’s validity was verified by comparing simulation results with observed temperature distributions and velocity data in Lake Biwa. The results demonstrated that the model successfully reproduced the seasonal development and breakdown of stratification, as well as large-scale circulation and localized vortical motion within the lake. These results indicate that the configuration provides a reliable basis for quantitative analysis of internal wave variability.
2.3. Sensitivity Analysis Using Perturbed Meteorological Forcings Reflecting Long-Term Climate Variability
To quantitatively evaluate the impact of atmospheric forcing on stratification dynamics under climate variability, we conducted numerical sensitivity experiments using pseudo-meteorological datasets derived from historical climate records. Based on observational data from the Hikone Local Meteorological Observatory spanning 30 years (1981–2010), coefficients of variation (standard deviation σ divided by the mean μ) were calculated for annual averages of air temperature, wind speed, and precipitation. These coefficients—0.21% for air temperature, 4% for wind speed, and 12% for precipitation—served as statistical proxies for moderate climatic perturbations potentially driven by long-term climate change.
For the sensitivity experiments, we selected a three-year period (2006–2008) and utilized reanalysis data from the GPV-MSM (Meso-Scale Model) as the baseline meteorological input. Each atmospheric variable was modified by multiplying the original time series by a factor of (1 ± 2σ/μ), thereby preserving the temporal variability of seasonal cycles, diurnal patterns, and high-frequency fluctuations, while systematically embedding perturbations equivalent to long-term climate anomalies. Air temperature perturbations were applied in absolute temperature units to maintain consistency in radiative and sensible heat flux calculations, while wind speed and precipitation were similarly scaled.
Simulation cases were categorized as follows: AT + 2σ and AT − 2σ for increased and decreased air temperature, WS + 2σ and WS − 2σ for enhanced and reduced wind speed, and PR + 2σ and PR − 2σ for augmented and diminished precipitation, respectively. The model outputs under these scenarios enabled the assessment of how individual climate elements influence stratification strength, internal wave spectra, and vertical mixing processes.
3. Spectral Analysis of Internal Waves (FFT Analysis)
This study quantitatively evaluates the periodic structure, amplitude variability, and energy distribution of internal waves occurring in a stratified water column, using time-frequency analysis derived from a numerical hydrodynamic model. A primary objective was to assess the impact of climate variability on vertical mixing and material transport by comparing spectral responses of internal waves under different meteorological scenarios.
3.1. Data Extraction and Preprocessing
Time series data of water temperature were extracted at four representative depths (0.5 m, 20 m, 60 m, and 80 m) at the central point of the simulation domain (offshore Imazu). The data were sampled at 3 h intervals, allowing for the resolution of a wide spectrum of internal wave scales, including diurnal and inertial frequencies. For each meteorological scenario, the analysis covered a continuous 60-day period within the model year spanning from April 2007 to March 2008. In addition, four characteristic stratification periods in Lake Biwa were identified and analyzed: spring (April–May), summer (August–September), autumn (October–November), and winter (December–January).
3.2. Spectral Computation via FFT
The frequency characteristics of internal waves were examined by applying a Fast Fourier Transform (FFT) to the detrended and windowed temperature time series at each depth. This transformation enabled the evaluation of energy distributions across the frequency spectrum.
3.3. Implementation of Fourier Transform
FFT was performed on the time series data to convert the temporal signal into its frequency components. The resulting complex Fourier coefficients were used to calculate the power associated with each frequency component. Specifically, the power spectral density (PSD) was computed to represent the distribution of energy across the frequency domain.
The squared magnitudes of the Fourier coefficients were calculated to obtain the PSD, thus revealing the frequency-dependent energy structure of internal waves. This approach enabled the identification of dominant periodicities and a quantitative assessment of internal wave energetics.
3.4. Power Spectral Density (PSD) Calculation
For each frequency bin, the absolute value of the corresponding Fourier coefficient was squared to obtain the PSD. This provided a visual and quantitative representation of the energy distribution across different frequency bands, facilitating interpretation of internal wave dynamics.
The discrete Fourier transform (DFT) was obtained by the discrete series x[
n] = x(
nΔ
t) (
n = 0, …,
N − 1; sampling interval Δ
t = 1/
fs), the forward DFT was defined as:
The (two-sided) periodogram PSD was then given by:
For real-valued records, a one-sided PSD was reported by doubling all bins except DC (and the Nyquist bin when
N is even):
This definition provides a quantitative distribution of variance across frequency, enabling direct interpretation of internal wave energetics.
3.5. Determination of Dominant Periods
Wave periods were obtained from spectral frequency via the following:
For interpretation, periods were grouped as super-inertial (6–16 h), near-inertial (~16–30 h), and sub-inertial (>30 h).
3.6. Spectral Response to Meteorological Forcing
The effects of varying meteorological parameters—air temperature (AT±), wind speed (WS±), and precipitation (PR±)—on internal wave dynamics were analyzed by comparing the PSDs across scenarios.
4. Seiche Periods from Merian’s Formula
Natural periods of longitudinal basin seiches are estimated using Merian’s formula under the shallow-water, one-dimensional, inviscid, and non-rotating assumptions. For an effective basin length
L and mean depth
, the barotropic long-wave speed is given by
. The period of the n-th longitudinal mode is obtained as
An equivalent expression is
For an open–closed geometry (one open end), node locations shift and the periods are given by
4.1. Baroclinic Extension (Internal Seiches)
In a stratified lake, the barotropic speed c is replaced by the first baroclinic long-wave speed
. Under a two-layer approximation with upper and lower layer thicknesses
,
and reduced gravity
, the phase speed and periods are computed as
Transverse modes are obtained by substituting basin width B for L.
4.2. Assumptions and Scope
The application of Merian’s formula presumes (i) shallow-water kinematics and weak transverse structure (), (ii) negligible rotation (), and (iii) an absence of dissipation. In natural basins, bottom friction and lateral irregularities typically lengthen slightly and dampen amplitudes; coupled-basin effects require dedicated treatment.
4.3. Application to Lake Biwa
Closed–closed boundaries were assumed for both sub-basins. Parameters were chosen to enable reproducibility, and calculations were performed separately for the North basin. Layer thicknesses were obtained from the median thermocline depth via and (effective depth H ≈ 44 m). Density differences Δρ were computed from representative surface/bottom temperatures using a freshwater equation of state.
Spring (weak stratification): .
Summer (strong stratification): .
Autumn (decaying stratification): ((period of mode n); L (effective length); B (width); (mean depth); g (gravity); , (layer thicknesses); Δρ (density difference); (reference density); g’ (reduced gravity); c, (barotropic/baroclinic speeds); f (Coriolis frequency)).
These eigen periods should be interpreted separately from near-inertial (~21 h at ≈ 35.2°) and diurnal forcing (24 h), which commonly produce spectral peaks lasting nearly one day through rotating internal gravity waves and forced responses.
5. Results
5.1. Thermocline Dynamics and Buoyancy Frequency Variability
Background stratification was evaluated for each scenario. Vertical profiles of buoyancy frequency (
N2) and temperature gradients were examined to characterize the depth and thickness of the thermocline. The buoyancy (Brunt–Väisälä) frequency quantifies the intrinsic stability of a stratified water column and the natural oscillation rate of displaced fluid parcels. It is defined as
where
g is gravitational acceleration,
is a reference density, and
is the vertical density gradient (positive
indicates statically stable stratification).
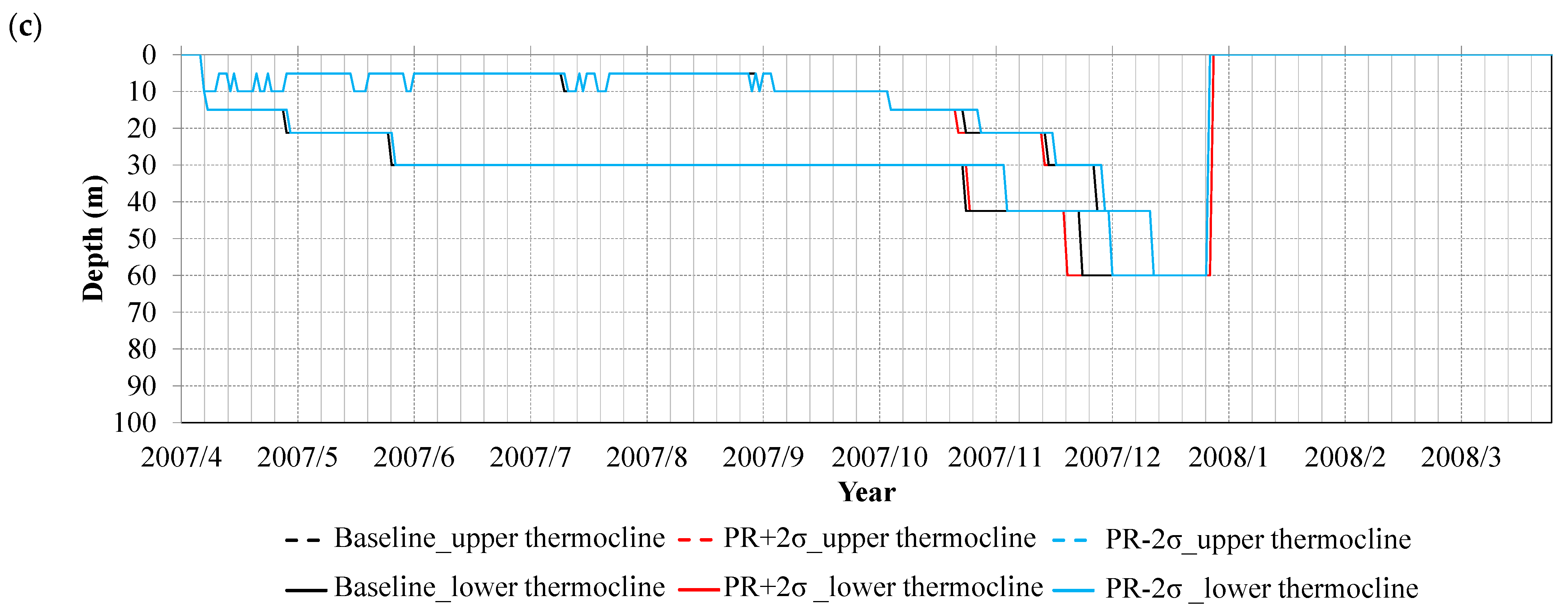
Figure 2 illustrates the diurnal variations in the upper and lower thermocline layers under each scenario.
Figure 3 displays the seasonal mean differences in buoyancy frequency between each scenario and the Baseline. Variations in thermocline structure were identified, which influence the propagation of internal waves.
Scenarios with increased air temperature (AT + 2σ) or reduced wind speed (WS − 2σ) produced stronger stratification, with the thermocline confined to a narrower depth range, whereas cooling (AT − 2σ) or enhanced wind forcing (WS + 2σ) resulted in weaker stratification and a deeper, more diffuse thermocline; precipitation changes (PR ± 2σ) had comparatively minor, surface-limited effects. Consistent with these patterns, the descent of the lower thermocline boundary is delayed under AT + 2σ and WS − 2σ (about half a month in WS − 2σ) and advances under WS + 2σ, while showing little deviation under AT − 2σ (
Figure 2a,b). These stratification responses are summarized in
Figure 3i,ii: outside winter, AT + 2σ and WS − 2σ exhibit positive
differences relative to the Baseline at ~10–20 m (enhanced static stability), whereas AT − 2σ and WS + 2σ show negative
differences around ~20 m (reduced static stability). These differences form the basis for interpreting subsequent variations in the internal wave energy spectrum.
5.2. Wave Spectra in the Surface Layer
Figure 4 shows wave energy spectra in the surface layer (0.5 m depth) under baseline and (i) AT ± 2σ, (ii) WS ± 2σ, and (iii) PR ± 2σ, in (a) Spring, (b) Summer, (c) Autumn, and (d) Winter. In the surface layer (upper ~5 m), the internal wave energy spectrum responds strongly to perturbations in air temperature and wind, with comparatively minor changes associated with precipitation. Under AT + 2σ (high-temperature scenario), energy in the super-inertial (6–16 h) band is reduced relative to the baseline, whereas sub-inertial components (tens of hours) tend to increase. As shown in
Figure 4i, spectral density in the 20–40 h range generally decreases under warming, suggesting a decrease in super-inertial (6–16 h) internal waves, while in the 90–130 h range the spectral density increases, indicating a relative enhancement of sub-inertial internal wave motions. This pattern implies that a warmer surface, associated with stronger stratification, suppresses high-frequency internal wave activity in the surface layer and permits relatively greater energy at low frequencies. Conversely, under AT − 2σ (low-temperature (cooling) scenario), super-inertial (6–16 h) spectral components are slightly strengthened relative to baseline, suggesting that weaker stratification invigorates higher-frequency internal waves in the surface layer. These results are consistent with theoretical expectations: stronger stratification can trap internal wave energy below the surface and reduce vertical mixing, thereby damping super-inertial (6–16 h) waves dependent on near-surface oscillatory motion, while amplifying standing oscillations at longer periods (sub-inertial) that engage the entire water column. The shift in energy from shorter to longer periods under warming reflects a non-linear adjustment of the internal wave spectrum to changes in upper-layer buoyancy frequency.
Changes in wind speed exert an even broader influence on the surface-layer internal wave spectrum. Under WS + 2σ (high-wind scenario), spectral energy across nearly the entire frequency range is amplified relative to baseline (
Figure 4ii). Energy peaks around 30–50 h and 90–130 h also increase, indicating that both the fundamental seiche (often ~100 h in Lake Biwa) and higher-frequency internal waves (down to ~1 day or shorter) become more energetic when wind forcing is stronger. Stronger winds impart greater momentum and energy to the lake, exciting more vigorous internal seiches and generating additional high-frequency activity through non-linear interactions and higher-mode excitation. In WS − 2σ (low-wind scenario), spectral energy diminishes across all periods (
Figure 4ii, blue curve), with reductions especially pronounced at the primary peaks. This uniform reduction in spectral intensity confirms that wind stress is a principal driver of internal wave field energy. The surface-layer internal wave system behaves as a resonant oscillator forced by wind: stronger winds deliver more energy to all modes, whereas weaker winds produce a quiescent internal wave field with reduced amplitudes across the spectrum.
Precipitation changes within the ±2σ range exert comparatively limited effects on the surface-layer internal wave spectrum. In both high- and low-precipitation scenarios, major spectral peaks (e.g., near 30 h and 100 h, corresponding to seiche modes) remain essentially unchanged from baseline in both position and magnitude (
Figure 4iii). The spectral curves for PR ± 2σ almost overlap the baseline, with only negligible differences in energy at any frequency. On multi-day time scales, direct effects of precipitation—such as freshwater lens formation or enhanced surface cooling—do not appreciably alter internal wave dynamics. Precipitation influences stratification mainly through surface buoyancy fluxes and volume inputs which, unless extreme, produce only minor changes compared to seasonal heating or wind-driven mixing. Short-term, intense rainfall events could create transient stratification anomalies (e.g., a thin buoyant surface layer) capable of altering internal wave phase speeds or mode shapes locally; however, such episodic effects are not captured in the quasi-steady spectral analysis presented here. Within the bounds of PR ± 2σ long-term precipitation variability, temperature and wind emerge as the dominant drivers of surface internal wave energy, with precipitation playing a minor role.
In summary, surface-layer results indicate that warmer conditions and weaker winds tend to diminish super-inertial (6–16 h) internal waves and overall internal wave energy, whereas cooler conditions and stronger winds enhance energy across the spectrum. The non-monotonic response to temperature—characterized by an energy shift from high to low frequencies under warming—highlights the sensitivity of the internal wave spectrum to stratification strength. Strong stratification can trap internal wave energy below the surface, preventing efficient coupling of super-inertial (6–16 h) waves to the surface [
23], while weaker stratification permits greater energy transmission to the surface and enhances higher-frequency oscillations. Wind forcing primarily acts as an energy source scaling with wind speed, influencing all frequencies. Consequently, climate-driven changes in wind patterns could produce nearly proportional changes in the overall vigor of the internal wave field, whereas warming alters the partitioning of that energy among wave scales.
5.3. Internal Wave Response in the Thermocline
Figure 5 shows internal wave energy spectra in the thermocline (~20 m depth) under baseline and (i) AT ± 2σ, (ii) WS ± 2σ, and (iii) PR ± 2σ, in (a) Spring, (b) Summer, (c) Autumn, and (d) Winter. In the thermocline region (approximately 10–20 m depth, coinciding with the thermocline or main density gradient), the internal wave spectral response differs from that at the surface. The thermocline is the depth at which the first internal seiche mode typically attains its maximum vertical displacement, making it a zone of concentrated internal wave activity. Simulations indicate that air temperature changes have a relatively strong influence on the internal wave spectrum in this mid-depth layer.
Under AT + 2σ (the high-temperature scenario), stratification strengthens relative to the baseline (
Figure 3i), forming a more diffuse yet stronger stratified layer. Correspondingly, changes appear in the distribution of internal wave spectral energy, with amplification observed particularly in the period bands associated with the first and second vertical modes (
Figure 5i). This result suggests that wave energy becomes concentrated within the thermocline, consistent with a “wave ducting” effect in which stronger stratification above and below acts as reflecting boundaries, trapping energy in the thermocline. This interpretation is consistent with theoretical descriptions [
24] of ducted internal wave energy in stratified layers.
At the same time, the high-temperature scenario produces a reduction in higher-frequency components at the thermocline. Super-inertial (6–16 h), higher-frequency waves—often associated with higher vertical modes or non-linear interactions—become less energetic when stratification is very strong. In contrast, under AT − 2σ, the low-temperature scenario allows some higher-mode energy to “leak” upward out of the thermocline, with the vertical structure of internal waves extending shallower as the thermocline weakens and mixes upward. Energy associated with higher modes is less confined to the thermocline, and weaker stratification permits these modes to propagate more freely in the vertical, effectively shallowing the oscillatory structure.
For wind speed perturbations, effects are more pronounced in the thermocline than at the surface (
Figure 5ii). A stronger wind anomaly (+2σ) increases total energy input to the lake, initially expressed in the surface layer, but a substantial portion of this energy subsequently propagates into the thermocline as internal waves form. High-wind scenarios exhibit a marked increase in spectral energy within the thermocline, which exceeds the response observed at the surface and is distributed more broadly rather than forming sharply peaked structures. Internal seiches, with their nodal point at the thermocline, become particularly energetic under stronger winds, resulting in elevated spectral density around the fundamental seiche period (~100 h) and its harmonics (~50 h). Low-wind scenarios display reduced energy across the spectrum. As the thermocline serves as the principal exchange layer between surface and deep waters, stronger winds primarily enhance energy transfer into waves spanning the thermocline. Once generated, part of this energy cascades to higher modes and frequencies within the thermocline, but the most consistent change is the overall energy level rather than a fundamental reshaping of the spectrum.
Changes in precipitation exert a more limited impact on the thermocline compared to variations in wind speed or air temperature (
Figure 5iii). Nevertheless, their effects are more evident in the thermocline than at the surface. While stratification in this depth range is primarily controlled by heat fluxes and wind-driven mixing, precipitation can still influence the thermocline indirectly, for example through surface cooling or buoyancy addition. In the ±2σ scenarios, these processes produce only modest, yet more discernible, signals in the thermocline relative to the surface.
In summary, air temperature changes, via modifications to stratification, induce adjustments in the internal wave spectral distribution at mid-depths. Warming promotes concentration of energy into discrete modal oscillations (yielding a double-peaked spectrum) and suppresses the short-period tail, consistent with ducting and selective frequency filtering. Cooling permits higher-mode energy to spread vertically and slightly increases higher-frequency waves. Wind speed predominantly modulates the amplitude of thermocline oscillations rather than introducing qualitative spectral changes, while precipitation effects remain minimal. These patterns underscore that the internal wave energy budget in the thermocline is highly sensitive to changes in the buoyancy frequency (N2) profile: strong stratification can trap and channel energy within the thermocline, whereas weaker stratification permits energy leakage to other depths and supports a broader vertical mode spectrum.
5.4. Wave Spectra Response in the Deep and Bottom Layer
Figure 6 and
Figure 7 shows wave energy spectra in the deep layer (60 m depth) and the bottom layer under baseline and (i) AT ± 2σ, (ii) WS ± 2σ, and (iii) PR ± 2σ, in (a) Spring, (b) Summer, (c) Autumn, and (d) Winter, respectively. In the deep bottom layer (60 m and 80 m depth), absolute internal wave energy is lower than in the surface or thermocline, reflecting the general decrease in wave amplitude with depth in a stratified lake. Nevertheless, the simulations reveal distinct changes in the way internal wave energy propagates to and reflects from the bottom under different meteorological conditions.
Under AT + 2σ, the high–air-temperature scenario, stronger upper-layer stratification and a slightly weakened near-bottom density gradient modify wave propagation and bottom-interaction characteristics (
Figure 6i and
Figure 7i). Consistent with internal wave theory, the downward energy flux tends to be reduced and a larger fraction of the energy reaching the deep layer is redirected upward rather than dissipated within the bottom boundary layer. However, spectral energy associated with sub-inertial components (including the fundamental seiche) does not show a clear increase at depth under warming conditions. These results indicate that stronger stratification alters the partitioning of internal wave energy but does not lead to an accumulation of sub-inertial energy in the deep layer.
In contrast, under AT − 2σ, the low–air-temperature scenario produces steeper deep stratification, with colder and denser water overlying slightly lighter water at the lakebed. This configuration promotes more effective transmission of internal wave energy into the bottom boundary layer, reducing reflection but enhancing dissipation and local interactions at the bed. In this case, spectral energy density for sub-inertial components at depth exhibits a measurable increase relative to the baseline, consistent with enhanced energy input into the deep boundary layer under cooler conditions.
Changes in wind speed exert a secondary but measurable influence on the deep layer. Strong winds increase the overall energy of the internal wave field, resulting in a moderate increase in bottom motions. High-wind scenarios exhibit somewhat greater deep current variance and more energetic bottom oscillations, although the spectral shape at depth remains largely unchanged. In low-wind scenarios, internal waves carry minimal energy to depth, producing near-quiescent bottom conditions and underscoring the dependence of deep-water motions on wind-driven energy input.
Precipitation changes exert virtually no direct influence on deep internal wave activity in these simulations, as precipitation effects remain confined to the surface layer (e.g., slight freshening or cooling) and do not significantly penetrate to depth over the time scales considered.
In summary, bottom-layer dynamics are modulated by stratification changes driven by air temperature. Under warming, stronger stratification modifies internal wave propagation and enhances the reflection of energy at depth, whereas cooling produces steeper deep stratification that favors transmission of energy into the bottom boundary layer. Wind speed primarily regulates the magnitude of energy reaching the bottom but does not alter the fundamental interaction mechanism with the bed. These results demonstrate that climate-driven changes in stratification influence the distribution and partitioning of internal wave energy in the deep layer, with contrasting outcomes under warming and cooling scenarios.
5.5. Mechanisms of Spectral Redistribution
Analyses reveal that internal waves in Lake Biwa respond to meteorological forcing in complex yet interpretable ways. In the case of temperature forcing, which produced the most nuanced changes, three principal mechanisms emerge through which stratification changes—and, by extension, climate changes—lead to spectral redistribution of internal wave energy:
Selective Frequency Damping and Amplification—Strengthened stratification (higher buoyancy frequency, N2) narrows the range of frequencies that can propagate efficiently, acting as a filter that suppresses high-frequency (super-inertial (6–16 h)) waves while favoring low-frequency (sub-inertial) motions. This spectral selectivity is reflected in the reduced super-inertial (6–16 h) energy and enhanced sub-inertial energy under the high-temperature scenario. Energy shifts toward the lake’s resonant seiche frequencies and away from broadband higher-frequency internal waves.
Vertical Ducting and Trapping of Wave Energy—Under strong stratification, internal wave energy tends to become trapped within the thermocline, a phenomenon associated with wave ducting. Energy that would normally propagate to the surface or bottom is retained at mid-depth, producing localized spectral peaks (e.g., twin peaks at specific frequencies under warming) and reducing energy leakage. Under strong stratification, energy that would otherwise be transferred to the surface or bottom tends to remain within the water column, leading to greater vertical redistribution of energy and reduced loss to boundary dissipation.
Changes in Energy Leakage to Boundaries—Stratification intensity alters the pathways through which internal wave energy is lost from the system. Under stronger stratification, leakage to the surface (as radiated surface waves or mixing into the atmosphere) and to the bottom (as turbulent dissipation in the boundary layer) is reduced because waves are more effectively trapped within the water column. Weaker stratification, by contrast, allows more efficient energy transfer to the surface mixed layer or bottom boundary layer, where dissipation occurs.
These mechanisms are dynamically interrelated and constitute direct pathways through which climate forcing can reshape the structure and energy budget of the internal wave field. The capacity to quantify such effects—for example, percentage changes in spectral energy at key frequencies or changes in reflection coefficients—enables incorporation of this feedback into future predictions of climate impacts on lakes. The implications extend beyond physical limnology: shifts in internal wave energy toward longer periods and confinement in deeper layers, as projected under warming scenarios, could reduce the frequency of vertical mixing events driven by higher-frequency waves. Such changes would likely influence nutrient resupply to surface waters and oxygenation of deep waters. The mechanistic framework described here provides a quantitative basis for evaluating these potential ecological and biogeochemical feedback.
6. Discussions
The sensitivity experiments identify coherent pathways by which interannual anomalies in air temperature and wind reorganize stratification and redistribute internal wave energy across depths and frequency bands. Stronger stratification under warming or reduced winds—evidenced by delayed deepening of the lower thermocline and positive
anomalies at ~10–20 m—shifts energy toward longer periods, whereas cooling or stronger winds weaken stratification and enhance higher-frequency energy. These patterns are consistent with multi-lake evidence that the stratification season is lengthening and intensifying under climate change, based on lake–climate model ensembles and long-term observations across the Northern Hemisphere [
2].
Wind magnitude emerges as a first-order control on the overall vigor of the internal wave field: +2σ wind forcing amplifies energy broadly across periods, while −2σ produces a quasi-uniform reduction. This scaling aligns with climate-scale analyses showing that “atmospheric stilling” and its partial recovery are largely manifestations of internal climate variability on ~20-year timescales—implying that multi-decadal wind anomalies can modulate lake energetics independent of long-term means [
8].
Three linked processes explain the spectral responses: (i) Selective frequency filtering: as
increases, the propagation window narrows, damping super-inertial (6–16 h), surface-coupled motions and favoring low-frequency seiche-scale energy. (ii) Vertical ducting and trapping within the thermocline: strengthened stratification above and below confines energy and accentuates discrete modal peaks. (iii) Altered boundary leakage: stronger stratification reduces transmission to the surface mixed layer and bottom boundary layer, changing how energy is dissipated. Recent observations and 3D modeling in a large, deep lake show that higher vertical-mode Poincaré/standing waves can intensify near-bottom currents, highlighting how modal structure governs deep-water dynamics—consistent with this mechanism-based interpretation [
14].
Redistribution toward longer periods and deeper trapping can reduce high-frequency shear near the surface and lower the frequency of short-timescale vertical exchange, while increasing energy residence at depth. Internal seiches and associated motions influence nearshore and benthic fluxes, including nutrient transport and internal phosphorus loading, processes increasingly represented in water quality models [
15].
Within ±2σ, precipitation changes have minor, surface-limited effects on spectra relative to temperature and wind. This matches recent syntheses emphasizing that heat fluxes and wind-driven mixing dominate seasonal stratification dynamics, whereas typical precipitation variability exerts weaker control except during transient extremes.
Climate-aware sensitivity experiments plus operational internal wave diagnostics—reflects two methodological advances: (a) lake-model and lake–climate coupling frameworks summarized in recent reviews, and (b) standardized diagnostics for extracting thermocline displacements, modal periods, and band-limited energies from observations or model output. Together they enable harmonized inter-site comparisons and reproducible climate-impact assessments [
19,
21].
First, global/hemispheric assessments emphasize stratification and surface temperature, while basin-resolved internal wave spectra and modal structures are under-reported for many lake types and regions. Second, joint perturbations (temperature × wind × precipitation) and non-linear interactions are rarely analyzed within a unified spectral framework. Third, boundary-layer processes (e.g., bottom-boundary dissipation, reflection coefficients) lag behind thermocline-motion observations, limiting closure from spectra to mixing rates. The present framework helps address the first two gaps by tying changes to depth-resolved spectral moments under controlled meteorological perturbations and can be extended with explicit boundary-layer diagnostics.
The ±2σ design isolates first-order sensitivities but not compound extremes (e.g., storm sequences) that inject high-frequency energy; quasi-steady spectral statistics may under-represent short-lived rainfall lenses or plume-refraction events. Parameterizations (turbulence closure, surface-flux formulas) can modulate shear production and tail energies; configuration metadata should accompany spectra for reproducibility in cross-study comparisons.
The results provide a transferable recipe for mapping climate anomalies to internal wave metrics pertinent to ecosystem models: (i) quantify how changes redistribute spectral energy with depth; (ii) track modal peaks relative to basin geometry; and (iii) estimate bottom/surface boundary-layer energy partitioning as a proxy for mixing.
7. Conclusions
This study explored how long-term variability in air temperature, wind speed, and precipitation may influence internal wave spectra and vertical energy distributions in Lake Biwa. Numerical experiments suggest that warming is associated with a redistribution of spectral energy in the surface and thermocline layers, with a tendency toward reduced high-frequency activity and relatively enhanced lower-frequency oscillations. These changes appear to reflect modifications of stratification that alter the buoyancy frequency profile and confine energy within the thermocline. In the deep layer, stronger stratification under warming may reduce the downward flux of energy without producing a clear increase in long-period motions. Cooling, in contrast, tends to allow greater penetration of energy into the bottom boundary layer, possibly increasing dissipation near the bed.
Wind forcing emerges as a key factor influencing internal wave energy across the water column. Stronger winds appear to enhance spectral energy in both fundamental and higher modes, while weaker winds reduce internal wave amplitudes more uniformly. Precipitation, within the tested variability range, exerts comparatively limited effects, with only minor signatures visible in the thermocline.
Taken together, these results indicate that air temperature and wind speed are likely to be the dominant climatic drivers of internal wave dynamics in Lake Biwa, while precipitation plays a secondary role. The findings suggest that projected climatic changes could alter the spectral balance of internal waves and the pathways of energy distribution across depths, potentially influencing mixing, transport, and ecosystem processes. However, these outcomes are model-based and subject to uncertainty, highlighting the need for continued observational and theoretical investigation.