Machine Learning Optimization of SWRO Membrane Performance in Wave-Powered Desalination for Sustainable Water Treatment
Abstract
1. Introduction
2. Proposed Methodology
2.1. Data Acquisition and Processing
2.2. Feature Selection and Model Configurations
3. Machine Learning Models
3.1. Support Vector Machine (SVM)
3.2. Gaussian Process Regression (GPR)
3.3. Multi-Layer Perceptron (MLP)
3.4. Decision Tree (DT)
3.5. Linear Regression (LR)
3.6. Evaluation Criteria
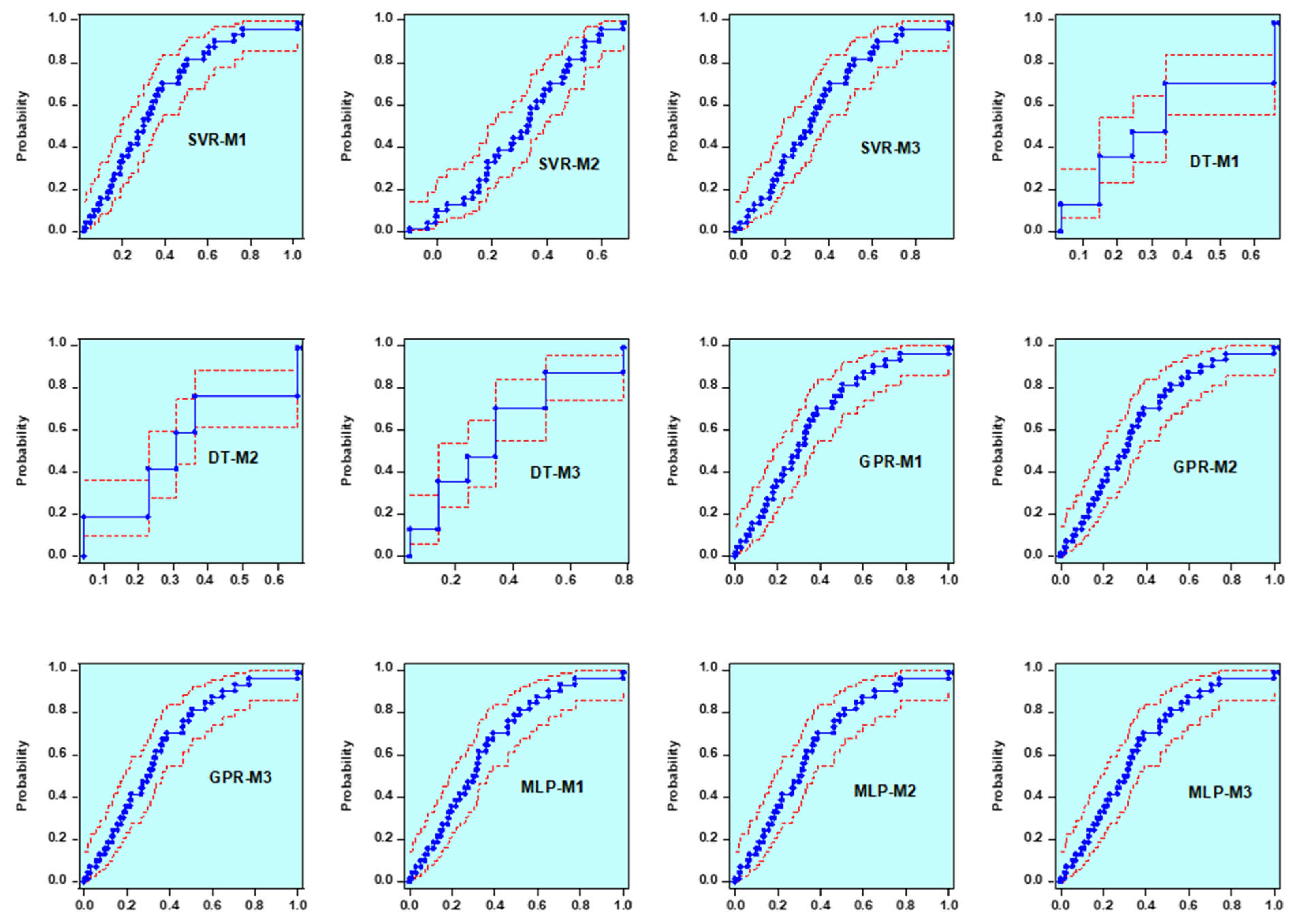
4. Results and Discussion
4.1. ML Models on the Prediction of Permeate Recovery
4.2. ML Models on the Prediction of Salt Rejection
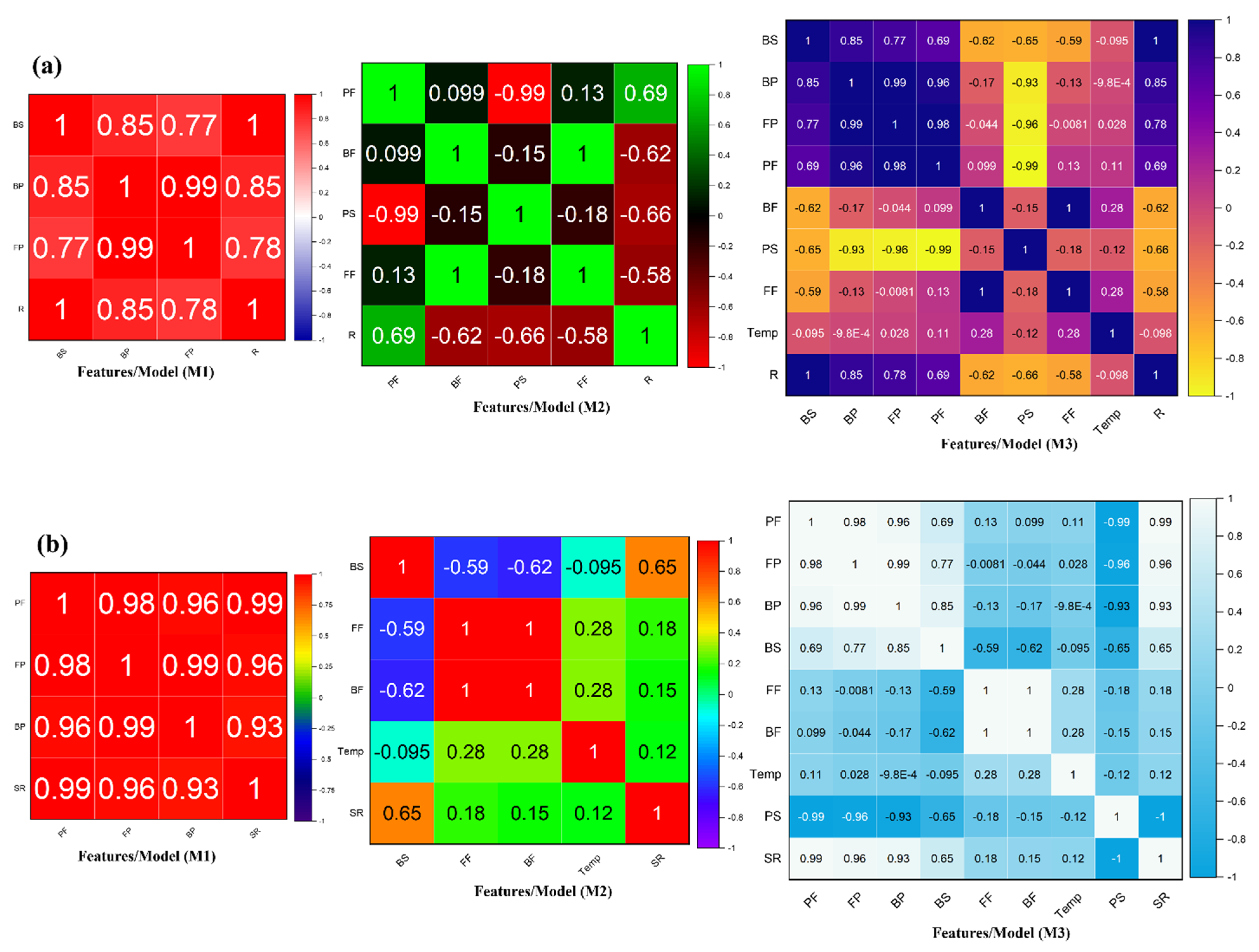
4.3. Sensitivity Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rosa, L.; Sangiorgio, M. Global Water Gaps Under Future Warming Levels. Nat. Commun. 2025, 16, 1192. [Google Scholar] [CrossRef] [PubMed]
- He, C.; Liu, Z.; Wu, J.; Pan, X.; Fang, Z.; Li, J.; Bryan, B.A. Future Global Urban Water Scarcity and Potential Solutions. Nat. Commun. 2021, 12, 4667. [Google Scholar] [CrossRef]
- Alenezi, A.; Alabaiadly, Y. Emerging Technologies in Water Desalination: A Review and Future Outlook. Energy Nexus 2025, 17, 100373. [Google Scholar] [CrossRef]
- Park, K.; Kim, J.; Yang, D.R.; Hong, S. Towards a Low-Energy Seawater Reverse Osmosis Desalination Plant: A Review and Theoretical Analysis for Future Directions. J. Memb. Sci. 2020, 595, 117607. [Google Scholar] [CrossRef]
- Tal, A. Addressing Desalination’s Carbon Footprint: The Israeli Experience. Water 2018, 10, 197. [Google Scholar] [CrossRef]
- Saavedra, A.; Valdés, H.; Mahn, A.; Acosta, O. Comparative Analysis of Conventional and Emerging Technologies for Seawater Desalination: Northern Chile as a Case Study. Membranes 2021, 11, 180. [Google Scholar] [CrossRef]
- Ahmad, T.; Zhang, D. A Critical Review of Comparative Global Historical Energy Consumption and Future Demand: The Story Told so Far. Energy Rep. 2020, 6, 1973–1991. [Google Scholar] [CrossRef]
- Nurjanah, I.; Chang, T.T.; You, S.J.; Huang, C.Y.; Sean, W.Y. Reverse Osmosis Integrated with Renewable Energy as Sustainable Technology: A Review. Desalination 2024, 581, 117590. [Google Scholar] [CrossRef]
- Okampo, E.J.; Nwulu, N. Optimisation of Renewable Energy Powered Reverse Osmosis Desalination Systems: A State-of-the-Art Review. Renew. Sustain. Energy Rev. 2021, 140, 110712. [Google Scholar] [CrossRef]
- Leijon, J.; Salar, D.; Engström, J.; Leijon, M.; Boström, C. Variable Renewable Energy Sources for Powering Reverse Osmosis Desalination, with a Case Study of Wave Powered Desalination for Kilifi, Kenya. Desalination 2020, 494, 114669. [Google Scholar] [CrossRef]
- Sitterley, K.A.; Cath, T.J.; Jenne, D.S.; Yu, Y.H.; Cath, T.Y. Performance of Reverse Osmosis Membrane with Large Feed Pressure Fluctuations from a Wave-Driven Desalination System. Desalination 2022, 527, 115546. [Google Scholar] [CrossRef]
- Mi, J.; Wu, X.; Capper, J.; Li, X.; Shalaby, A.; Wang, R.; Lin, S.; Hajj, M.; Zuo, L. Experimental Investigation of a Reverse Osmosis Desalination System Directly Powered by Wave Energy. Appl. Energy 2023, 343, 121194. [Google Scholar] [CrossRef]
- Dimitriou, E.; Camacho-Espino, J.; Anastasiou, A.; Papadakis, G. Experimental Investigation of the Performance of a Seawater Reverse Osmosis Desalination System Operating under Variable Feed Flowrate Pressure and Temperature Conditions. J. Environ. Chem. Eng. 2025, 13, 115778. [Google Scholar] [CrossRef]
- Wang, C.; Wang, L.; Dong, L.; Shon, H.K.; Kim, J. Specific Energy Consumption of Seawater Reverse Osmosis Desalination Plants Using Machine Learning. Desalination 2025, 602, 118654. [Google Scholar] [CrossRef]
- Ma, X.; Lan, C.; Lin, H.; Peng, Y.; Li, T.; Wang, J.; Azamat, J.; Liang, L. Designing Desalination MXene Membranes by Machine Learning and Global Optimization Algorithm. J. Memb. Sci. 2024, 702, 122803. [Google Scholar] [CrossRef]
- Priya, P.; Nguyen, T.C.; Saxena, A.; Aluru, N.R. Machine Learning Assisted Screening of Two-Dimensional Materials for Water Desalination. ACS Nano 2022, 16, 1929–1939. [Google Scholar] [CrossRef]
- Abba, S.I.; Usman, J.; Bafaqeer, A.; Salami, B.A.; Lawal, Z.K.; Lawal, A.; Usman, A.G.; Aljundi, I.H. Optimizing Sustainable Desalination Plants with Advanced ML-Based Uncertainty Analysis. Appl. Soft Comput. 2025, 169, 112624. [Google Scholar] [CrossRef]
- Ruiz-García, A.; Nuez, I.; Khayet, M. Performance Assessment and Modeling of an SWRO Pilot Plant with an Energy Recovery Device under Variable Operating Conditions. Desalination 2023, 555, 116523. [Google Scholar] [CrossRef]
- Yin, X.; Lei, M. Deep Reinforcement Learning Based Coastal Seawater Desalination via a Pitching Paddle Wave Energy Converter. Desalination 2022, 543, 115986. [Google Scholar] [CrossRef]
- Das, T.K.; Folley, M.; Lamont-Kane, P.; Frost, C. Performance of a SWRO Membrane under Variable Flow Conditions Arising from Wave Powered Desalination. Desalination 2024, 571, 117069. [Google Scholar] [CrossRef]
- Zhang, X.; Li, H.; Fan, Y.; Zhang, L.; Peng, S.; Huang, J.; Zhang, J.; Meng, Z. Predicting the Dynamic of Debris Flow Based on Viscoplastic Theory and Support Vector Regression. Water 2025, 17, 120. [Google Scholar] [CrossRef]
- Wang, S.; Gong, J.; Gao, H.; Liu, W.; Feng, Z. Gaussian Process Regression and Cooperation Search Algorithm for Forecasting Nonstationary Runoff Time Series. Water 2023, 15, 2111. [Google Scholar] [CrossRef]
- Kim, C.H.; Kim, M.; Sholahudin; Giannetti, N.; Saito, K. Systematic Development of Multilayer-Perceptron-Based Void Fraction Model. Int. Commun. Heat. Mass. Transf. 2025, 162, 108563. [Google Scholar] [CrossRef]
- Zhao, R.; Hong, L.; Ji, H.; Zhang, Q.; Zhang, S.; Li, Q.; Gong, H. Decision Tree Based Parameter Identification and State Estimation: Application to Reactor Operation Digital Twin. Nucl. Eng. Technol. 2025, 57, 103527. [Google Scholar] [CrossRef]
- Chen, B.; Ouyang, H.; Li, S.; Gao, L.; Ding, W. Photovoltaic Parameter Extraction through an Adaptive Differential Evolution Algorithm with Multiple Linear Regression. Appl. Soft Comput. 2025, 176, 113117. [Google Scholar] [CrossRef]
- Pan, Y.; Zeng, X.; Xu, H.; Sun, Y.; Wang, D.; Wu, J. Evaluation of Gaussian Process Regression Kernel Functions for Improving Groundwater Prediction. J. Hydrol. 2021, 603, 126960. [Google Scholar] [CrossRef]
- Prakash, A.K.; Xu, S.; Rajagopal, R.; Noh, H.Y. Robust Building Energy Load Forecasting Using Physically-Based Kernel Models. Energies 2018, 11, 862. [Google Scholar] [CrossRef]
- Talhami, M.; Wakjira, T.; Alomar, T.; Fouladi, S.; Fezouni, F.; Ebead, U.; Altaee, A.; AL-Ejji, M.; Das, P.; Hawari, A.H. Single and Ensemble Explainable Machine Learning-Based Prediction of Membrane Flux in the Reverse Osmosis Process. J. Water Process Eng. 2024, 57, 104633. [Google Scholar] [CrossRef]
- Ajali-Hernández, N.I.; Ruiz-Garćıa, A.; Travieso-González, C.M. ANN Based-Model for Estimating the Boron Permeability Coefficient as Boric Acid in SWRO Desalination Plants Using Ensemble-Based Machine Learning. Desalination 2024, 573, 117180. [Google Scholar] [CrossRef]
- Sharshir, S.W.; Joseph, A.; Abdalzaher, M.S.; Kandeal, A.W.; Abdullah, A.S.; Yuan, Z.; Zhao, H.; Salim, M.M. Using Multiple Machine Learning Techniques to Enhance the Performance Prediction of Heat Pump-Driven Solar Desalination Unit. Desalin. Water Treat. 2025, 321, 100916. [Google Scholar] [CrossRef]


| Training Phase | Testing Phase | |||||||
|---|---|---|---|---|---|---|---|---|
| RMSE | R2 | MSE | MAE | RMSE | R2 | MSE | MAE | |
| SVM-M1 | 0.015 | 1.000 | 0.000 | 0.012 | 0.014 | 1.000 | 0.000 | 0.012 |
| SVM-M2 | 0.066 | 0.900 | 0.004 | 0.048 | 0.077 | 0.890 | 0.006 | 0.047 |
| SVM-M3 | 0.031 | 0.980 | 0.001 | 0.024 | 0.021 | 0.990 | 0.000 | 0.019 |
| GPR-M1 | 0.009 | 1.000 | 0.000 | 0.007 | 0.007 | 1.000 | 0.000 | 0.005 |
| GPR-M2 | 0.005 | 1.000 | 0.000 | 0.003 | 0.001 | 1.000 | 0.000 | 0.001 |
| GPR-M3 | 0.009 | 1.000 | 0.000 | 0.006 | 0.002 | 1.000 | 0.000 | 0.001 |
| MLP-M1 | 0.021 | 0.990 | 0.000 | 0.015 | 0.006 | 1.000 | 0.000 | 0.003 |
| MLP-M2 | 0.038 | 0.970 | 0.001 | 0.023 | 0.008 | 1.000 | 0.000 | 0.002 |
| MLP-M3 | 0.058 | 0.940 | 0.003 | 0.035 | 0.006 | 1.000 | 0.000 | 0.002 |
| DT-M1 | 0.113 | 0.770 | 0.013 | 0.072 | 0.091 | 0.840 | 0.008 | 0.058 |
| DT-M2 | 0.156 | 0.590 | 0.024 | 0.112 | 0.107 | 0.790 | 0.011 | 0.079 |
| DT-M3 | 0.096 | 0.850 | 0.009 | 0.067 | 0.055 | 0.940 | 0.003 | 0.039 |
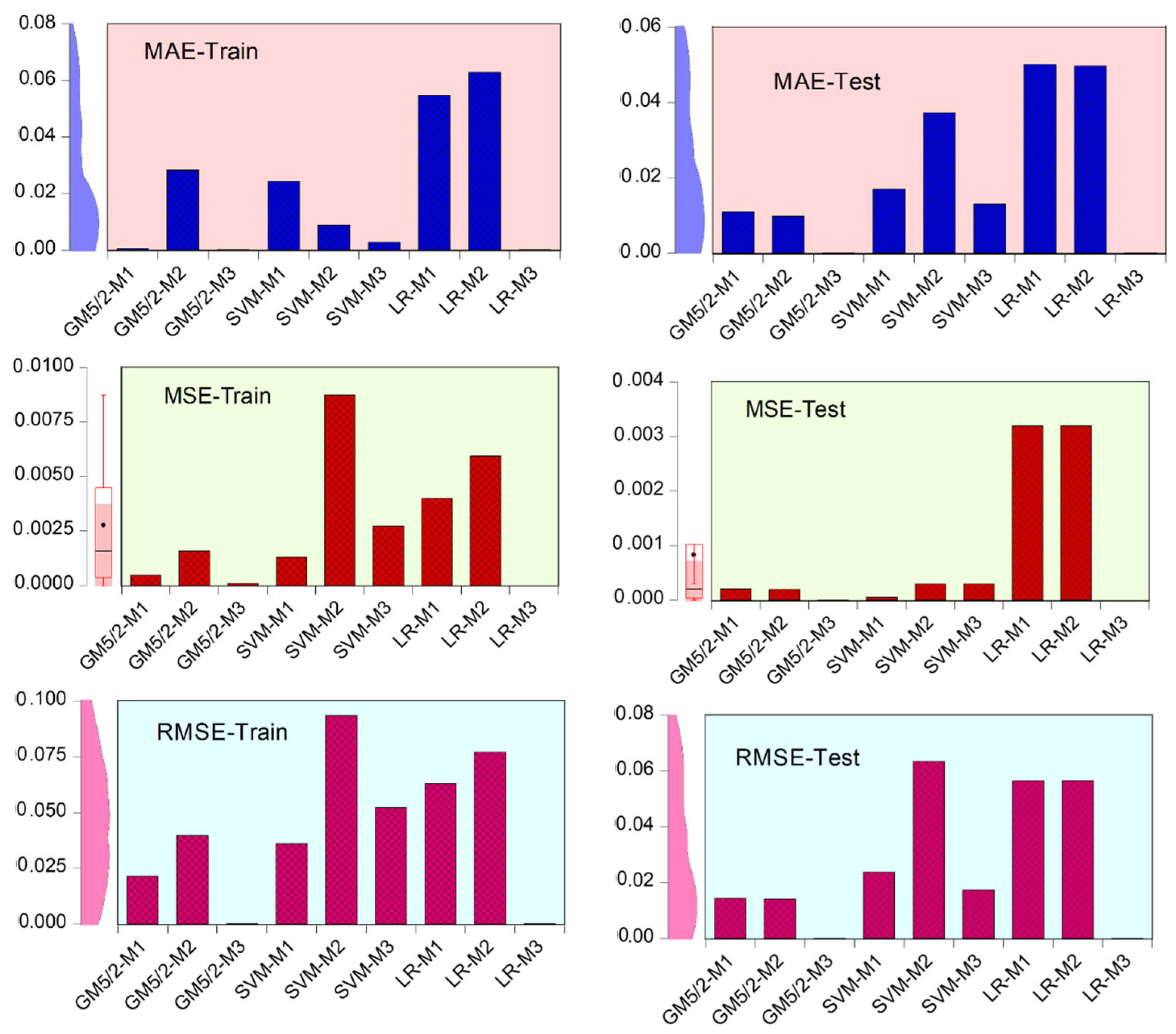
| Training Phase | Testing Phase | |||||||
|---|---|---|---|---|---|---|---|---|
| RMSE | R2 | MSE | MAE | RMSE | R2 | MSE | MAE | |
| GM5/2-M1 | 0.0214 | 0.9800 | 0.0005 | 0.0005 | 0.0143 | 0.9900 | 0.0002 | 0.0110 |
| GM5/2-M2 | 0.0397 | 0.9400 | 0.0016 | 0.0282 | 0.0140 | 0.9900 | 0.0002 | 0.0098 |
| GM5/2-M3 | 0.0000 | 1.0000 | 0.0001 | 0.0000 | 0.0000 | 1.0000 | 0.0000 | 0.0000 |
| SVM-M1 | 0.0359 | 0.9500 | 0.0013 | 0.0242 | 0.0237 | 0.9800 | 0.0001 | 0.0170 |
| SVM-M2 | 0.0935 | 0.6900 | 0.0087 | 0.0087 | 0.0634 | 0.8400 | 0.0003 | 0.0373 |
| SVM-M3 | 0.0521 | 0.9100 | 0.0027 | 0.0027 | 0.0173 | 0.9900 | 0.0003 | 0.0130 |
| LR-M1 | 0.0631 | 0.8600 | 0.0040 | 0.0546 | 0.0565 | 0.8700 | 0.0032 | 0.0501 |
| LR-M2 | 0.0770 | 0.7900 | 0.0059 | 0.0629 | 0.0566 | 0.8700 | 0.0032 | 0.0497 |
| LR-M3 | 0.0000 | 1.0000 | 0.0000 | 0.0000 | 0.0000 | 1.0000 | 0.0000 | 0.0000 |
| ML Model | Application | Data | Prediction Efficacy | References |
|---|---|---|---|---|
| LSTM-GA, LSTM-CSA | Hybrid (NF/RO) systems | Hybrid of simulation and real operational data | LSTM-GA (MAE-0.13) | [17] |
| ANN | SWRO with ERD | Pilot SWRO with ERD under variable conditions | MAE-0.0082 | [18] |
| Deep Reinforcement Learning | Wave-powered RO (simulated) | Simulated wave-powered RO using real wave data | Stable flow at 1200 m3/day | [19] |
| Ensemble ANN | SWRO for boron rejection | Full-scale plant; long-term data | MAE-7.93 × 10−8 | [29] |
| GPR, SVM, MLP, DT, LR | Wave-powered SWRO | Dynamic wave-driven flow | R2 -1.00, MAE-0.001 | The present study |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yogarathinam, L.T.; Abba, S.I.; Usman, J.; Jibrin, A.M.; Aljundi, I.H. Machine Learning Optimization of SWRO Membrane Performance in Wave-Powered Desalination for Sustainable Water Treatment. Water 2025, 17, 2896. https://doi.org/10.3390/w17192896
Yogarathinam LT, Abba SI, Usman J, Jibrin AM, Aljundi IH. Machine Learning Optimization of SWRO Membrane Performance in Wave-Powered Desalination for Sustainable Water Treatment. Water. 2025; 17(19):2896. https://doi.org/10.3390/w17192896
Chicago/Turabian StyleYogarathinam, Lukka Thuyavan, Sani I. Abba, Jamilu Usman, Abdulhayat M. Jibrin, and Isam H. Aljundi. 2025. "Machine Learning Optimization of SWRO Membrane Performance in Wave-Powered Desalination for Sustainable Water Treatment" Water 17, no. 19: 2896. https://doi.org/10.3390/w17192896
APA StyleYogarathinam, L. T., Abba, S. I., Usman, J., Jibrin, A. M., & Aljundi, I. H. (2025). Machine Learning Optimization of SWRO Membrane Performance in Wave-Powered Desalination for Sustainable Water Treatment. Water, 17(19), 2896. https://doi.org/10.3390/w17192896







