Abstract
Wastewater treatment plants (WWTPs) face increasing pressure to handle higher volumes of water due to climate change causing storm surges, which current infrastructure cannot handle. Aerobic granular sludge (AGS) is a promising alternative to activated sludge systems due to their improved settleability property, lowering the land footprint and improving efficiency. This research investigates the optimisation of a lab-scale sequencing batch reactor (SBR) into a continuous flow reactor through mathematical modelling, sensitivity analysis, and a computational fluid dynamic model. This is all applied for the future goal of scaling up the model designed to a full-scale continuous flow reactor. The mathematical model developed analyses microbial kinetics, COD degradation, and mixing flows using Reynolds and Froude numbers. To perform a sensitivity analysis, a Python code was developed to investigate the stability when influent concentrations and flow rates vary. Finally, CFD simulations on ANSYS Fluent evaluated the mixing within the reactor. An 82% COD removal efficiency was derived from the model and validated against the SBR data and other configurations. The sensitivity analysis highlighted the reactor’s inefficiency in handling high-concentration influents and fast flow rates. CFD simulations revealed good mixing within the reactor; however, they did show issues where biomass washout would be highly likely if applied in continuous flow operation. All of these results were taken under deep consideration to provide a new reactor configuration to be studied that may resolve all these downfalls.
1. Introduction
Being used for drinking, washing, and various industrial operations, water is an essential resource which supports life, ecosystems, and economic development. Access to clean and safe water is a fundamental human right recognised by the United Nations and is established as Sustainability Development Goal 6; therefore, national bodies set strict regulations for water treatment in the UK. In 2023, the UK consumed 301.83 litres per person per day, a 1.65% decrease from 2022 (306.86 litres per person per day) [1]. However, considering population increases in recent years fixed around 0.34%, if water consumption does not keep decreasing, by 2028 WWTPs (wastewater treatment plants) will need to increase their treatment capacities (U.K. Population 1950–2025, [2]).
In the past few decades, extreme weather events such as rainfall amount and number of storms in the UK have been on a steady increase [3]. This is in no doubt directly correlated to global warming and climate change due to their effects on rising sea levels and increasing temperatures, causing more evaporation. Due to these extreme weather events, large influxes of wastewater need to be treated instantaneously, which is not feasible, leading to spills. When sewage water overspills into water sources, it introduces high quantities of nitrogen and phosphorus pollutants, therefore stimulating algae growth. This is also known as eutrophication, which leads to reduced levels of oxygen in water sources, which has detrimental effects on ecosystems, such as the death of fish, insects, and other organisms.
Although water companies are meant to abide by strict regulations, in 2022 alone there were 3.6 million hours of spills due to storm overflows (“How much raw sewage is released into lakes, rivers and the sea?”, 2022). This outlines a fundamental treatment capacity issue with wastewater treatment plants (WWTPs) across the UK. Currently, the most common secondary wastewater treatment method is activated sludge with separate sedimentation tanks due to small flocs not settling within the reactor. Due to the batch configuration of sedimentation tanks, this limits the daily influent capacity of WWTPs, hence the inability to treat large influxes of wastewater. Available space for expansion of WWTPs in the UK is limited; therefore, most WWTPs are exploring ways to reduce their land footprint. Hence why the hunt for a better replacement for activated sludge is on the rise, with the need for continuous flow secondary biological water treatment without the need for sedimentation tanks.
Aerobic granular sludge (AGS) is a promising biological treatment process being researched since 1990. Unlike activated sludge, AGS forms self-aggregating granular biopolymers, which are larger dense particles with faster settling properties. This property makes AGS a highly efficient alterative eliminating the need for separate settling tanks. Currently, it has been applied in batch configurations by companies such as Nerada®, to replace existing activated sludge and settling tank processes. Despite being successful in its full-scale, batch implementation, resulting in a lower WWTP footprint, lower energy consumption, and successful pollutant removals, there are still limitations for treatment capacity per day. To maximise the potential of AGS technology, the application of continuous flow reactors is crucial. By successfully implementing AGS continuous flow reactors, it could enable WWTPs to handle larger quantities of wastewater per day, enhancing resilience to climate change and population growth.
In this study, results were shared from a researcher of a new existing laboratory-scale (AGS) reactor using samples from a wastewater treatment plant. From these results, a mathematical model was developed and validated by comparing the model removal efficiency to the laboratory results. Once completed, a Python code was written to generate graphs for concentrations of chemical oxygen demand (COD) and biomass. Also, the Python code was used to perform a sensitivity analysis on different parameters of the lab set-up and how they affect COD removal and biomass growth. Finally, a computational fluid dynamics (CFD) model was developed to simulate the mixing within the lab-scale reactor. An analysis of the efficiency of mixing based on the CFD results allows problem areas such as dead zones to be detected. The work conducted comes alongside personal recommendations of optimisation areas to improve the mixing efficiency, allowing the project to be handed down to the next person to carry these out. The long-term goal of this project is to scale up the reactor to a full-scale model and perform the same analysis.
In order to contribute to this area of research, this dissertation is organised as follows: First, a comprehensive literature review on the current processes in UK wastewater treatment, the properties and mechanisms of AGS, along with its current applications worldwide. Then recent breakthrough studies of AGS continuous flow reactors are discussed to present the future directions within the field. Section 3 outlines the methods used for this research, addressing the main methods used (e.g., assumptions, equations, CFD settings) and limitations that arose throughout the project. Next, Section 4 presents the results of the research, such as the calculation results for the mathematical model, the Python code graphs for the sensitivity analysis, and finally the CFD results. Finally, Section 5 will give suggested recommendations to pass on for the continuation of optimisation on this reactor set-up in order to prepare for future scale-up.
2. Literature Review
2.1. Conventional Wastewater Treatment Technologies
2.1.1. Key Stages of Wastewater Treatment
Conventional wastewater treatment processes can be sorted into four key stages: pretreatment, primary treatment, secondary treatment, and tertiary treatment.
The pretreatment stages consist of screening, grit chamber, and skimming tanks to remove large particles and debris. Screening removes large debris, such as pieces of wood, cloth, plastic, etc., from the wastewater to prevent the damage and blockages of equipment further along the treatment line [4]. Grit chambers are long narrow tanks which work as sedimentation tanks to remove sand, metal fragments, and broken glass, whilst allowing lighter organic materials to pass onto the primary treatment phase [4].
The main process in the primary treatment phase is primary sedimentation tanks, also known as primary settling tanks or clarifiers [5]. Sedimentation tanks allow organic matter and particles to settle to the bottom of the tank, forming a layer of sludge separate from the effluent water [5]. Also, skimming tanks are used in the primary stage to remove oil, fat, wax, and grease floating in the water [4].
Secondary treatment uses biological techniques to remove dissolved organic matter, nitrogen, and phosphorus by microbes absorbing them as food and converting them to CO2, water, and energy for growth [6]. Roughly 85% of organic pollutants and suspended solids are removed in secondary treatment [6]. Biological treatments are typically categorised into aerobic and anaerobic processes. Common aerobic treatments consist of activated sludge, aerated lagoons, the sequential batch reactor, trickling filter, membrane bioreactors, rotating biological contactors, and aerobic moving bed biofilm reactors [5]. The common anaerobic treatment methods are up-flow anaerobic sludge blankets and expanded granular sludge beds [5]. This research project focuses on secondary biological treatment methods, specifically with the comparison between activated granular sludge and aerobic granular sludge; therefore, Section 2.2 provides a more in-depth overview of these methods. After biological treatment, the wastewater is sent to a secondary sedimentation tank to settle sludge containing microorganisms (known as a thickening sludge) [5].
Finally, wastewater goes through tertiary treatment, a polishing stage used to further improve the quality of the effluent before discharge to the environment. It utilises biological, physical, and chemical methods to completely remove remaining organic ions, nutrients, suspended solids, microorganisms, and pollutants [7]. Tertiary treatment is typically used if companies have to meet stringent quality requirements. First, wastewater is sent through sand filtration to remove remaining suspended solids, and then it is disinfected. Chlorination is a common disinfection method because chlorine is a strong oxidiser which reacts with organic compounds [8]. Another disinfection method is ultraviolet technology used alone or combined with ultrasonication and ozone exposure. When combined, free radicals are produced which attach to the cell membranes of biological contaminants, allowing chemical oxidants to enter and attack internal cell structures [6].
2.1.2. Comparison of Secondary Treatments
Activated sludge is the most popular aerobic biological treatment method across multiple different industries’ wastewater [9]. It is a mixed culture of microorganisms (bacteria, fungal, and algal biomass) which are grown in aeration tanks where the oxygen-rich environment encourages these flocs of microorganisms to form [10]. Dissolved organic pollutants in the wastewater are decomposed and oxidised into carbon dioxide and water by the sludge [11]. Conventional activated sludge systems are now run continuously as either plug-flow reactors or completely mixed systems, where the feed enters a primary clarifier, followed by an aeration tank to mix the feed, sludge, and air, then a second clarifier to remove solids [12]. This is shown in Figure 1.

Figure 1.
A schematic diagram of a conventional activated sludge system [12].
Assistance by physiochemical methods is essential in activated sludge processes to enhance efficiency. Typical additives include coagulants, flocculants, and defoamers. Coagulants and flocculants are commonly used to remove suspended solids and phosphorus, thereby improving the biochemistry of the wastewater. Examples of these include ferric chloride and polyaluminium chloride as the most popular options [13]. Defoamers are essential to diminish the impact of greasy substances on the activated sludge, with linear alkylbenzene sulfonate being the most used in industry [13]. Consequently, the additives flow into and accumulate in the sludge, and overuse can harm the microbial community, hence reducing sludge activity and the efficiency of activated sludge treatment [13]. Table 1 provides a summary of the processes used in secondary biological treatment methods for wastewater, with their key characteristics, advantages, and limitations.

Table 1.
A summary table of the processes used in secondary biological treatment methods for wastewater, with their key characteristics, advantages, and limitations.
The advantages of activated sludge treatment are as follows:
- Applicable to multiple types of wastewaters.
- Achieves high average conversions of 90.85%, 95.74%, and 71.6% for COD, ammonia, nitrogen, and total nitrogen [13].
- Low installation cost [14].
The limitations of activated sludge treatment are as follows:
- Energy consumption is high due to aeration, with averages for WWTPs being 0.30 kWh/m3–0.65 kWh/m3 [15].
- High emissions of N2O, typically 90% of WWTPs N2O emissions [16].
- Excessive sludge generation.
Aerated lagoons are mechanically aerated ponds which oxidise organic matter using the suspended aerobic microorganisms [4]. There are two types of aerated lagoons: complete mixed lagoons and partial-mix lagoons. Complete mix lagoons aerate the wastewater continuously to stop solid sludge from settling. Partial-mix lagoons have aerators placed to provide oxygen rather than sufficient turbulence [4].
The advantages of aerated lagoons are as follows [4]:
- Low operation and management cost compared to activated sludge.
- Lower sludge generation.
The limitations of aerated lagoons are as follows [4]:
- Large land usage compared to the activated sludge process.
- Lower quality effluent.
- High energy input for aeration.
Trickling filters are another common biological method where wastewater is dispersed over a bed of rock, gravel, or plastic where microorganisms can grow and form a biofilm [4]. This allows a large area for aerobic bacteria to grow and treat wastewater circulated from the bottom of the filter and sprayed into the bed by a rotating arm [12].
The advantages of trickling filters are as follows [14]:
- Simplicity and reliability.
- Low power requirements.
The disadvantages of trickling filters are as follows [14]:
- The effluent needs additional treatment.
- Odour emission.
- The need for regular operator monitoring.
Membrane bioreactors use a combination of biological treatment, which removes pollutants from the wastewater, and membrane filtration, which separates the sludge generated from the effluent [4]. In submerged membrane bioreactors, aeration provides air and turbulence to reduce fouling, which is a common problem within them [4].
The advantages of membrane bioreactors are as follows [14]:
- Very high-quality effluent.
- Small reactor size.
The limitations of membrane bioreactors are as follows [14]:
- Membrane fouling and membrane maintenance.
- Higher power consumption, sometimes double the consumption of activated sludge.
- Higher capital and operational costs.
- Foaming.
Rotating Biological Contactors (RBCs) or Rotating cylindrical discs are partially submerged in wastewater so microorganisms can consume organic matter and form a biofilm on the surface. As the discs rotate, this promotes oxygen transfer and maintains turbulence to remove excess solids [4].
The advantages of rotating biological contactors are as follows [14]:
- Short retention time.
- Low energy consumption compared to active sludge.
- Low operating cost.
The limitations of rotating biological contactors are as follows [4]:
- The need for sludge removal.
- Sensitivity to wastewater characteristics.
2.2. Aerobic Granular Sludge
Aerobic granular sludge (AGS) has been developed and researched to be a better replacement for activated sludge in the biological treatment of wastewater. AGS is a compact group of dense, spherical, self-immobilised microbial granules which allows effective simultaneous nitrification, denitrification, and phosphate removal from wastewater [7]. Since its development in 1990, it is hoped to be a solution for numerous bottlenecks of conventional activated sludge systems, such as a high land footprint, high energy requirements for recirculating biomass and wastewater, and biomass–water separation [7].
2.2.1. Composition and Properties of AGS
Aerobic granules comprise various species of microorganisms subject to parameters such as the seed sludge, feed composition, and SBR operating conditions. However, AGS in treatment plants across the world consists of the following typical functional groups: heterotrophic bacteria, ammonia-oxidising bacteria, nitrite-oxidising bacteria, polyphosphate-accumulating organisms, denitrifying bacteria, and glycogen-accumulating organisms [17]. Extracellular polymeric substance (EPS)-producing bacteria are an essential microorganism present in AGS and are key for granule stability. The complex EPS matrix mainly consists of proteins and polysaccharides along with lipids, glycoproteins, nucleic acids, and humic acids [7]. These components bridge bacteria cells tightly together into an aggregate to form dense granules.
A distinct characteristic of AGS granules is their stratified layers of aerobic, anoxic, and anaerobic zones, as seen in Figure 2. This structure allows nitrification, denitrification, and phosphorus removal simultaneously, enhancing the quality of wastewater treatment, and is advantageous for handling various types of wastewaters. Nitrifying bacteria and some PAOs are located in the aerobic zone due to high dissolved oxygen requirements [10]. Denitrifying and most PAOs are located in the anaerobic/anoxic zones, along with glycogenic accumulating organisms located at the inner anaerobic/anoxic zone [10].

Figure 2.
A schematic diagram of the layered structure in aerobic granular sludge granules and their interactions [18].
Compared to the fluffy, irregular flocs of activated sludge, AGS’s structure contains dense, spherical particles with diameters greater than 200 µm, allowing it to have many operational advantages [10]. These larger, dense granules settle faster via sedimentation, with settling velocities greater than 10 m/s; therefore, separate settling tanks are not necessary, hence reducing the overall footprint for WWTPs [10]. By reducing the footprint, overall capital costs to build new biological treatment plants are reduced by 75%, and the energy consumption is reduced by up to 30% [19]. Also, the dense structure and microbial matrix have a high resistance to hydraulic shear forces and abrasion; in fact, AGS reactors need high shear forces to promote and regulate granule growth. All of these properties help promote high biomass retention, which allows larger organic loads to be treated and effective pollutant removal compared to conventional activated sludge [19,20]. Another advantageous property of AGS is the specific gravity of granules (around 1.01–1.017), which allows faster solid–liquid separation, therefore better effluent quality [10].
2.2.2. Formation Mechanisms of AGS
Under certain operational conditions, AGS granulation involves the microbial aggregation of flocculent sludge into a dense, self-immobilised structure as described in Section 3.1 [21]. Currently, there is no consensus on the exact mechanism of AGS granulation; however, the few leading hypotheses include the EPS hypothesis, the microbial self-aggregation hypothesis, and finally the four-step hypothesis (currently most favoured) [3].
The Four-Step Hypothesis
The four-step hypothesis encompasses the main aspects of granulation to provide a holistic view of AGS formation, from initial aggregation to final stabilisation. It recognises fundamentals linked to other existing hypotheses such as microbial self-aggregation, hydrodynamic forces and EPS production. A diagram overview of each step is shown in Figure 3.

Figure 3.
A diagram of the key stages of aerobic granular sludge formation [15].
Step 1 is bacteria floc cell-to-cell contact through physical interactions, e.g., hydrodynamic, diffusion, gravity, and thermodynamic forces, to start contact forming small aggregates [22]. Effective collisions of small cells form larger particles, some of which form the central core of AGS granules [22].
In Step 2, microaggregate formation becomes more stable through physical, chemical, and biochemical interactions. The physical forces involved, such as van der Waals force, thermodynamic force, and opposite cell charge attraction, initiate contact between small aggregates [22]. Chemical bonding, like ionic/triplet ionic pairing and inter-particulate bridging, also plays a role in strengthening attachment [21]. Finally, biochemical interactions such as cell membrane fusion occur, further reinforcing the formation of strong microbial aggregates [21]. The combination of these forces is essential to grow strong, stable AGS granules.
Step 3 involves the biosynthesis of EPS, which acts as a biological binding glue for cells within each aggregate [21]. Proteins and polysaccharides facilitate the binding and bridging by filling gaps between cells and enhance the hydrophobicity of the aggregates [22]. The rigidity of sludge particles is increased because EPS forms a matrix around cells.
Finally, step 4 involves granule maturation and stabilisation of primary granular sludge by hydraulic shear forces. When subjected to hydraulic shear forces via aeration, the aerobic granule growth is promoted, hence developing a 3-dimensional structure [23]. It also moulds the sludge into a compact, dense structure with reduced bacterial spacing and increases the stability of the granules [23]. Overall, this preserves the structure of granules needed for effective wastewater treatment.
Factors Affecting AGS Formation
There are several factors and conditions that significantly affect the formation of AGS, impacting its structure, stability, quality, and efficiency in removing pollutants. Hydraulic shear force is the most integral factor for AGS formation. At smaller hydraulic shear forces, aerobic granules do not aggregate into their usual dense structure but remain as loose flocs [21]. This is also linked to aeration velocity and dissolved oxygen levels. If aeration velocity is too high, hydraulic shear forces cause damage to the sludge structure, therefore causing particle washout [23]. Also, high dissolved oxygen levels are favoured because the particles formed were larger, hence better sedimentation [23]. In SBRs, settling time is important as it can remove unwanted flocculent sludge and promotes the secretion of EPS [23]. Other factors that affect granulation are organic loading rates, seed sludge composition, HRT, SRT, and temperature [21].
2.2.3. AGS in Wastewater Treatment
Since its first discovery in the 1990s, AGS technology has rapidly grown, with 70 full-scale applications worldwide, followed by many pilot/lab-scale research projects currently being conducted [21]. Typically, sequencing batch reactors (SBRs) have been used to implement AGS technology. These operate under cycles such as filling, reacting, settling, and draining all in one reactor and are very successful in aerobic granule cultivation and nutrient removal. Additionally, other systems such as plug flow reactors, uses of biofilters, hydro cyclones, and continuous flow reactors are all being researched and implemented to improve AGS systems [21]. This is further discussed in Section 4. Nereda® is a successful AGS system, used by water companies across the globe, operating on a 3-step cycle: simultaneous fill and draw, aeration, and fast settling [21].
AGS technology has found particular interest in Europe, especially in the Netherlands, which is the home of the first AGS plant, built in 2005 by Nereda®. Still currently running, this WWTP was designed to treat 0.25 million litres of industrial dairy wastewater per day via three SBRs [21]. Due to the combined aerobic and anaerobic structure of AGS granules, biological removal of micropollutants (pharmaceutical products), xenobiotic compounds, azo dyes, and metal ions is possible [10]. Hence, it has been applied to many types of industrial wastewater at lab scales and some full-scale set-ups, as seen in Table 2.

Table 2.
A summary of full-scale and lab-scale AGS reactors, including capacity and removal efficiencies.
In 2008, Nereda® opened the first-ever full-scale AGS municipal wastewater treatment plant in Gansbaai, South Africa, and was successful in treating 5 MLD [21]. However, it did not come without a few faults, such as power outages, high solid loading in the influent, and not keeping up with maintenance [21]. In the United Kingdom, there are nine WWTPs using AGS biotechnology and one new plant in the design phase. The largest is the Kendal Wastewater Treatment Plant for municipal waste, which has a capacity of 18.5 MLD (United Kingdom—Kendal, n.d.). This project officially opened in 2018 and was a combination of greenfield, brownfield, and retrofit developments to support the growing population in the area. After launch, the plant performed exceptional simultaneous nitrification, denitrification, and phosphorus removal (United Kingdom—Kendal, n.d.). Other benefits of the project include a reduced footprint compared to the previous existing plant, lower power requirements, sustainable costs, and increased treatment capacity (United Kingdom—Kendal, n.d.).
2.3. Continuous Flow Reactors
2.3.1. Continuous Flow Reactors in Wastewater Treatment
Continuous flow (CF) technology plays a crucial role in modern-day wastewater treatment facilities, allowing consistent treatment without interruption by handling large volumes of water. In continuous flow reactors, the influent flows through the reactor continuously and is treated uniformly. Most methods used in WWTPs are in continuous flow modes from pre-treatment to tertiary treatment, except sedimentation tanks. As stated in Section 2.2.1, in biological wastewater treatment CF reactors are traditionally continuous stirred tank reactors (CSTRs) or plug-flow reactors (PFRs). The application of AGS in continuous flow reactors is necessary, as it will reduce cost in retrofitting existing plant processes and can treat wastewater at higher capacities.
CSTRs are one of the most popular instrumentations used in wastewater treatment because agitation causes uniform mixing of reactants, pH, and temperature [26]. Their purpose is to offer efficient mixing between microorganisms and the influent in a stable environment to maximise pollutant removal; therefore, CSTRs are commonly used in activated sludge processes and anaerobic digestion [26]. Other benefits of CSTRs include consistent operating limits, high process control, and flexibility to handle varying composition in the influent. Plug flow reactors are also used in biological wastewater treatment. In plug flow reactors, water flows through a cylindrical reactor, often with baffles to create turbulence for homogenous mixing [27]. This allows more control of the reactions taking place and has a relatively compact design [27].
2.3.2. Comparison Between Continuous Flow Reactors and SBRs
Currently, all aerobic granular sludge reactors are in sequential batch reactor modes; however, the majority of WWTPs which utilise activated sludge are in continuous flow mode. Table 3 shows a comparison of characteristics between SBRs and continuous flow reactors to highlight their strengths and weaknesses.

Table 3.
A table comparing the characteristics of continuous flow reactors and sequential batch reactors.
2.3.3. Aerobic Granular Sludge Continuous Flow Reactors
Most wastewater treatment plants operate in continuous flow mode; therefore, finding solutions to apply AGS in continuous flow reactors is necessary. Currently, many laboratory experiments are being performed worldwide to find solutions for large-scale continuous flow AGS. Many different reactor configurations are being explored, such as alternating anaerobic upflow selectors, hydro cyclones, bubble column reactors with three-phase separators, bubble columns with external settling tanks, and many more [28,29]. Using baffles in CFAGS reactor designs has been found to improve granulation in continuous flow reactors, with one study achieving stable granules of an average size of 1.9 mm for 390 days [28]. Studies have found that the important factors for continuous flow aerobic granular sludge granulation are selection pressures, feast/famine conditions, shear force, reaction configuration, and the role of EPS [28]. Average pollutant removal results from laboratory-scale configurations are 80% > COD removal, 90% > nitrogen removal, and TP removal ranged from 60 to 95% [28].
Although these advanced reactor designs have shown great success on lab-scale models, their large-scale applicability is limited due to the complexity of the structures and the low flexibility for adjusting settling velocity [28]. Future directions are focusing on simpler reactor models which are adaptable to varying influent characteristics and obtain favourable granulation conditions. Promising reactor features include utilising sieves or meshes with pore sizes above 0.5 mm due to them offering high retention of large granules [28].
Cheng Yu et al. [30] performed a promising study converting an activated sludge wastewater treatment system in China to a microaerobic-aerobic continuous flow AGS system (seen in Figure 4). The configuration consisted of two microaerobic tanks (effective volume of 4095 m3) and two aerobic reactors both with effective volumes of 4504.5 m3 and 18 separators constructed with baffles. Using hydraulic retention times of approximately 7.9, 5.8, and 2.9 h for the microaerobic tanks, aerobic zones, and internal separators allowed for an overall treatment capacity of 2.5 × 104 m3 d−1 [30]. Granule size increased from 31.9 to 138.5 μm in 251 days, with 29.6% of particles > 200 μm and less than 10% being < 50 μm. The pollutant removal efficiencies also met the same standards as the previous AGS batch reactors. These factors show the great success of the study performed by [31].
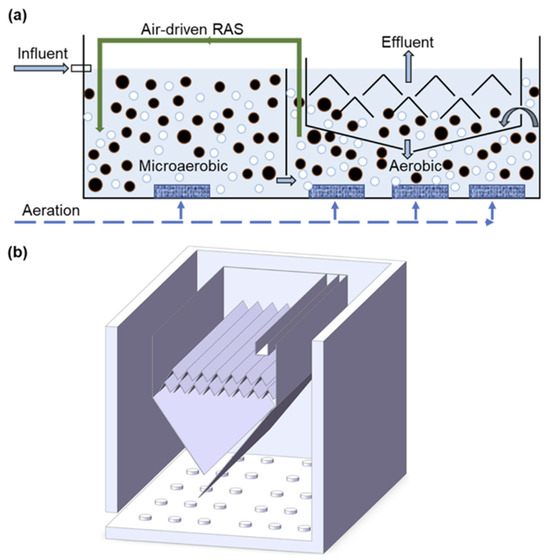
Figure 4.
Schematic diagram of the continuous-flow AGS system (a), and aerobic tank with internal separators (b) [32]. Black circles representing the AGS and the white circles the aeration input.
2.4. Knowledge Gaps in AGS Treatment and Future Directions
Continuous flow configurations show promising granulation of AGS; however, they come with instability issues with flexible inflows [1]. Due to storms, reactor sensitivity is an important issue to overcome because influent flow rates and pollutant concentrations are always varying. The use of computational fluid dynamics (CFD) is starting to increase when investigating lab-scale AGS reactors. It uses numerical analysis and algorithms to simulate fluid flow systems. For bubble column reactors, it is useful to show the mixing patterns of gas streams and bubble–liquid interactions; therefore, it can provide guidance on optimisation between lab and full-scale reactors.
While many laboratory-scale studies have demonstrated promising results of AGS sequencing batch reactors and continuous flow reactors, further research is required to optimise simple continuous flow configurations, especially for municipal wastewater treatment. Key gaps include understanding how to improve reactor stability and efficiency for varying influent concentrations and flow rates to simulate storm surge periods. This study aims to address how a continuous flow reactor can handle these influent variations by conducting a sensitivity analysis using a mathematically derived model and Python. Also, a CFD analysis was used to assess biomass suspension behaviour and mixing efficiency. Optimisation recommendations based on AGS behaviour in batch reactor configurations are included throughout to guide future research applications.
3. Methods
The purpose of this study is to utilise experimental data from a lab-scale AGS reactor to create and develop a CFD model which can inform reactor optimisation to ensure successful future scaling up to a pilot scale. Multiple methodical steps were undertaken, starting with developing a numerical model of the AGS reactor with the experimental data provided by Dr Rania Hamza with a corresponding Python code. Next, a SOLIDWORKS 2025 3D model reflecting the lab-scale set-up was curated to model the AGS turbulence via CFD using ANSYS Workbench 2024 R2 with the Fluid Flow (Fluent) analysis system.
3.1. Reactor Model
The reactor set-up consisted of a 10 cm internal diameter cylindrical reactor with a working volume of 4.8 L. Aeration was provided by a fine bubble diffuser at the bottom of the reactor with a superficial air velocity of 2.35 cm s−1 and air bubbles with diameters ranging from 0.5 mm to 2 mm. The reactor was operated under a cyclic schedule: filling (10 min), anaerobic/unaerated (35–50 min), aeration (150 min), settling (30–10 min), and decanting (10 min).
The mathematical model was made using 6 main topics: microbial kinetics, chemical oxygen demand, mass transfer, heat transfer, aeration and gas transfer, and hydrodynamics and mixing. Focusing on these areas allows an understanding of the behaviour of the sludge within the reactor.
The assumptions made for the model are as follows:
- Steady-state operation due to continuous flow configuration.
- AGS granule shapes are assumed to be perfectly spherical.
- Microbial growth follows a defined Monod kinetic model.
- Monod kinetics assumes reactions are irreversible and only one substrate is limiting [33].
- Due to aerating during the oxic phase, dissolved oxygen is non-limiting.
The parameters used in the model below are listed in Table 4 and at the beginning of the paper, listing correlated symbols, values, and units.

Table 4.
The parameters used in the mathematical model derived in Section 3.1, with their corresponding symbols, values, and units.
3.1.1. Microbial Kinetics
Monod kinetics is commonly applied to microbial mixed cultures such as activated sludge systems to understand the kinetics of the biological processes [34]. Due to its use on activated sludge systems, it was assumed Monod kinetics would be the best suitable fit for modelling the AGS kinetics. Equation (1) [11] is the Monod equation, an empirical mathematical model for microorganism growth.
The maximum specific growth rate of biomass, μmax, was computed by rearranging the general equation for exponential growth.
Then the half-saturation constant for the substrate, Ks, was computed using Monod kinetics. For the half-saturation constant, specific growth rate is 50% of the maximum specific growth rate.
Also, the estimated biomass yield coefficient, Yest, was determined using the change in the concentration of biomass and COD. This coefficient reflects how efficiently the microorganisms convert organic pollutants into biomass. Due to the instability of AGS reactors due to varying influent substrate concentrations, conditions, biomass decay, and time changes to the operating cycle, the biomass yield coefficient was averaged to calculate Yest. The biomass yield coefficient was computed for each cycle where biomass growth occurred, starting from operating day 548, where COD removal efficiency became consistently stable. These measurements are shown in Table 5. The yield coefficient is also an estimate because nitrification, denitrification, and phosphorus removal also occur within the reactor; therefore, some biomass growth will be a result to these processes.

Table 5.
A table of the change in COD concentration (mg L−1) and biomass concentration (mg L−1) for cycles from day 548 to 604.
The decay of biomass always occurs in biological processes; however, it is important that the rate of decay is slower than the rate of growth. If not, the efficiency of the system decreases due to a lack of biomass for reactions. Also, it is important that there is some form of decay; otherwise, excessive biomass growth will occur. From the data given, there are some periods of biomass decay, shown in Table 6, which was used to calculate the decay coefficient of the AGS.

Table 6.
The measured total solids concentration (mg L−1) at time t (hours) for a lab-scale aerobic granular sludge experiment.
Then, using the equation below [29], the decay coefficient was computed.
3.1.2. Chemical Oxygen Demand (COD)
The influent flow rate was first computed based on a 4 h retention time within a continuous flow reactor. Equation (6), the equation for hydraulic retention time, was rearranged to calculate the necessary flow rate. Decanting/filling the reactor operated using a 50% volume exchange rate; therefore, the volume is 2.4 L.
The COD degradation rate constant, rx, is essential for determining the effluent COD concentration. First, the specific substrate utilisation rate needs to be computed using the biomass yield coefficient Y and maximum specific growth rate as seen in Equations (7) and (8) [33].
Using the rate constant above, the effluent total COD concentration was estimated using Equation (9), and the Python code explained in Section 3.2 and displayed in Appendix A was applied to calculate effluent COD concentration.
3.1.3. Mass Transfer
Due to aerating during the oxic phase, dissolved oxygen is non-limiting. Dissolved oxygen concentration in the liquid phase (mg/L) = non-limiting >> 2 mg/L.
The oxygen concentration in the gas phase was computed using the ideal gas law to determine the number of moles of O2 in the air stream and then using molar mass to determine the concentration in mg L−1.
3.1.4. Aeration and Gas Transfer Variables
Due to aerating during the oxic phase, dissolved oxygen is non-limiting. Therefore, the dissolved oxygen concentration is effectively at saturation, making oxygen transfer rate (OTR) equal to oxygen uptake rate (OUR).
Because data for the oxygen concentration present in the reactor was not collected, a theoretical yield coefficient to relate COD oxidised by aerobic granules and oxygen uptake was determined. This will calculate a theoretical estimate for oxygen uptake within the reactor; hence, the results will not give an accurate measurement. The yield coefficient used was from a lab-scale AGS project performed by Liu et al., who computed Y as 0.68 mg O2/mg COD [35].
Aeration flow rate equation:
3.1.5. Heat Transfer
Even though the data provided for this study were obtained using a reactor kept at room temperature, 20.1 ± 2 °C, incorporating heat transfer into the mathematical model is essential for reactor scale-up. Due to the small volume of lab-scale reactors, uniform temperature is maintained because heat exchange to the environment is quicker. However, in full-scale reactors, internal temperature gradients occur because of a larger quantity of microbial metabolic heat generation and slower heat dissipation. Environmental temperature changes also impact heat transfer with the surroundings, disrupting the uniformity of reactor temperature. The microbial processes which occur in AGS are highly temperature sensitive; therefore, modelling heat transfer is important to maintain efficiency.
Mass flow rate is needed for calculating heat transfer rate; therefore, it was computed using influent flow rate and density.
Overall heat transfer coefficient [29]:
3.1.6. Hydrodynamics and Mixing
Good mixing in AGS reactors allows an even distribution of sludge particles throughout the reactor, thus improving substrate removal efficiency. Therefore, calculating Reynolds and Froude numbers will help analyse if optimisation is required to improve mixing.
Fluid velocity, necessary for calculating both Reynolds and Froude numbers, was computed using the influent flow rate and cross-sectional area.
The equation for the Reynolds number is shown in Equation (13). The Reynolds number is the ratio correlating inertial to viscous forces in a fluid and is used to determine the nature of a flow in terms of laminar or turbulent. It was used twice, first to determine the Reynolds number from liquid flowing into the reactor using the liquid superficial velocity and secondly to determine the Reynolds number from gas mixing using the superficial velocity of the gas [36].
The Froude number relates inertial forces in a process to the effects of gravity; therefore, it provides insight on what the dominant forces within a system are [36]. To assess the overall flow dynamics within the reactor, the hydraulic diameter was set to the reactor diameter, and to assess the bubble dynamics at the air inlet, 2 cm was used for the air inlet diameter. The equation for the Froude number is as follows:
3.2. Python Code
Python 3.11.9 was used on a Windows 11 laptop (13th Gen Intel (R) Core (TM) i5-1340P 8GB RAM) to develop a code to simulate the biological and physical processes within the reactor model developed in Section 2.1. The NumPy library was essential for numerical computations, especially importing solve_ivp from spicy.integrate to solve ODEs necessary for the biological and chemical processes in AGS. Matplotlib 3.10.3 was employed for graphical visualisation of the simulation outputs. See Appendix A for the Python code.
To simulate varying influents typically involved in wastewater treatment, a sensitivity analysis changing the parameters shown in Table 7 using the Python code. Testing influents with high COD concentrations and fast flow rates will simulate storm surge scenarios, whereas testing slow flow rates and influents with low COD concentrations will simulate drought scenarios.

Table 7.
The parameters that changed and their corresponding new values for the sensitivity analysis performed via Python.
3.3. CFD Model
Finally, computational fluid dynamics (CFD) models were performed on a Windows 11 PC (Intel(R) Core (TM) i7-10700T CPU 16GB RAM) using ANSYS Workbench R24 V2. ANSYS Workbench is an advanced, comprehensive platform for engineering simulations and workflows integrating geometry design, meshing, physical set-up, solving, and result post-processing. Additionally, for complicated models it allows integration of multiple analyses within one interface.
For this study, the specialised tool within the workbench employed was ANSYS Fluent, an industry-leading CFD software. It utilises advanced numerical methods to solve the Navier–Stokes equations, which govern fluid behaviour. These describe the motion of viscous fluids in terms of continuity, momentum, and energy.
3.3.1. Geometry
The geometry was designed in Ansys Design Modeller. A 2D 10 cm by 61.15 cm rectangle with a 2 cm air inlet along the bottom edge was sketched on the XY plane using the polyline function. To ensure all dimensions were accurate, they were specified using the default dimensions tool. To create a surface body, Surface from Sketches was used to generate the reactor surface. This is shown in Figure 5. Next, the surface type was changed from solid to liquid.
Figure 5.
The surface body of a 10 cm diameter by 61.15 cm tall reactor generated in ANSYS Design Modeller.
Due to the complexity of aerobic granular sludge reactor CFD and the lack of access to a powerful computer with a high CPU, the CFD was performed in 2D. To further improve results, the application of 3D CFD would be advisable for future research before scaling up.
3.3.2. Meshing
Meshing was generated using Ansys Mesher. Before forming the mesh, the air inlet and pressure outlet were named “Air Inlet” and “Pressure Outlet”, respectively, in order for Ansys to recognise these as boundary conditions in the set-up stage. A refined, high-quality mesh is integral for successful, accurate computational results; therefore, an analytical approach was adopted. The aerator produces 1 mm diameter air bubbles; hence, an element size of 0.5 mm was chosen to capture the small bubbles and AGS granules. Mesh defeaturing was activated to remove any small geometric features that complicate the mesh, such as holes or close vertices. The defeature size was kept at the default setting (0.0025 mm). Except for changing smoothing to high, all other settings were kept at default for the main mesh and are listed in Table 8.

Table 8.
The default settings under sizing in ANSYS Meshing.
Employing inflation layers along the reactor walls is essential for resolving near-wall velocity gradients. The smooth transition inflation option was chosen with the default transition ratio of 0.272, a maximum of 4 layers, and the inflation growth rate of 1.2. These settings ensure the mesh cell size is smaller close to the walls and gradually increases into the centre of the reactor.
Finally, a body of influence was applied at the air inlet surface to set a smaller local mesh size, allowing better simulation of the gas bubbles. The type used was Element Size, with a size of 0.25 mm and a default growth rate of 1.2.
Figure 6 shows the generated mesh. The number of nodes and cells are 253,471 and 251,962, respectively. After improving the mesh quality in ANSYS Fluent and evaluating mesh quality, the maximum orthogonality was 0.839 and the minimum aspect ratio was 6.43. Both these values fit within the recommended regions for a good-quality mesh.

Figure 6.
An image of the mesh generated shown in the ANSYS Fluent interface.
3.3.3. Set-Up and Governing Equations
Firstly, in ANSYS Fluent gravitational acceleration was applied in the Y direction with a magnitude of −9.81, and transient time was selected. The pressure-based solver was chosen because it can solve low-speed incompressible flow accurately and requires less memory. Next, the water and sludge granules needed to be added to the materials list (air is already a default material). Water was easily added via the ANSYS Fluent materials database; however, the available version of ANSYS could not create a new material for AGS. Therefore, to work around this limitation, water was copied as a material, but the density was changed to 1070 kg m−3 and the viscosity was set to 0.005 kg m−1s−1 to model the AGS granules.
In this study, the Eulerian–Eulerian multiphase model was adopted to simulate the 3-phase interaction present in AGS reactors and is commonly used in bubble column simulations. It is similar to the Lagrangian model except it utilises a fixed reference grid to track movement over time [7]. Each phase interacts with each other via inter-phase transfer terms and operates using the following governing equations:
- 1.
- Continuity Equation
- 2.
- Momentum Balance
- 3.
- Energy Balance
Water was then set as the primary phase, the new AGS material was set as the second phase with an average granular diameter of 1 mm, and air was the final phase with a bubble diameter of 1 mm. Table 9 shows the interphase force configuration selected for the 4 different phase interactions present between water, sludge, and air. The lift coefficient for water–air interaction was changed to Saffman–Mei to accurately model the lift force in a bubble column reactor for low- to moderate-Reynold-number flows.

Table 9.
Table of the interphase force settings chosen to perform a CFD model of the hydrodynamics in an aerobic granular sludge lab-scale reactor.
- 4.
- Wall shear stress
Assumption of non-Newtonian fluid due to the suspension of granula [37]
where y is the average shear rate in s−1, K is consistency index in Pa sn, g is gravitational acceleration, ρ is density of fluid in (kg m−3), Ug is superficial gas velocity in m s−1, and n is flow index.
Non-Equilibrium Wall Function
Non-equilibrium wall functions allow for pressure gradients and strain effects to be considered and can provide somewhat better results if viscosity variations near the wall are not extreme, making their application more suitable for AGS reactors than standard wall functions.
where u+ is dimensionless velocity, k is von Karman constant (0.41), E is wall roughness factor, y+ is dimensionless wall distance, and B is an empirical constant (5 assuming smooth walls).
The viscous model chosen was RNG k-ε with enhanced wall treatment. The RNG k-ε model handles complex multiphase models more accurately than the standard k-ε model, especially for bubble-induced flow. Enhanced wall functions ensure turbulence is modelled accurately near walls, which is important because wall shear will affect oxygen transfer. Next, the volume fraction at the air inlet was set to 1, and velocity was set to 0.0235 m s−1, as specified in the laboratory-scale model. The pressure outlet had a backflow air volume fraction of 1.
Table 10 presents the numerical solution methods chosen for the model. The Coupled scheme, Least Squares Cell-Based gradient, PRESTO! pressure method, and Second-Order Upwind momentum were all set for the stability, accuracy, and convergence of the complex system that needed to be simulated. However, the First-Order Upwind methods were trade-offs in order for faster results due to limitations explained at the end of this section. The settings used still produce good results, but the recommendations would be to use Second-Order Upwind for turbulence and volume fraction.

Table 10.
Table of the chosen solution methods to perform a CFD model of the hydrodynamics in an aerobic granular sludge lab-scale reactor.
Before running calculations, hybrid initialisation generated an initial field, and then the volume fraction of air was patched to 0, and the AGS volume fraction was patched to 0.2. Finally, the calculation time step was reduced to 0.001 s for increased stability because it calculates smaller, gradual updates to the solution.
A major limitation arose in this project when it came to running the calculations. The university computers have a “log-off” application installed that logs out computers if left idle for 2 h, which could not be uninstalled. Therefore, simulations could not be run for as long as originally planned (overnight simulations). This did have a detrimental effect on the results, which is further talked about in Section 4.3.
4. Results and Discussion
4.1. Mathematical Reactor Model
4.1.1. Microbial Kinetics
Comparison between the specific growth rate of AGS is difficult because many operating conditions, such as temperature, pH, oxygen levels, and substrate concentration, can have an effect Table 9, Table 10 and Table 11. However, for a laboratory-scale reactor, the computed value of 0.22 d−1 seems accurate when comparing to studies such as [21] (μmax = 0.266 d−1). Desireddy and Sabumon conducted an AGS experiment at ~30 °C and achieved an NH4+-N µmax of 1.92 d−1 and a COD µmax of 0.096 d−1, showing how conditions can drastically change the growth rates of biomass.

Table 11.
The computed results for the microbial kinetics of an AGS reactor at 20 C, 1 atm mathematical model, and referenced literature values.
Table 11.
The computed results for the microbial kinetics of an AGS reactor at 20 C, 1 atm mathematical model, and referenced literature values.
| Parameter | Symbol | Calculated Value | Referenced Values | Citation |
|---|---|---|---|---|
| Maximum specific growth rate | μmax | 0.22 d−1 = 0.0092 h−1 | 0.266 h−1 | |
| Half-saturation constant | Ks | 55 mg L−1 | ||
| Biomass Yield Coefficient | YB | 0.47 mg biomass/mg COD | 0.24–0.68 mg biomass/mg COD 0.33–0.37 mg biomass/mg COD | [38] [39] |
| Decay coefficient | b | 0.0059 h−1 |
The computed biomass yield coefficient from the data suggests 47% of the substrate is converted into biomass, with the remaining being used for energy or by-product formation. This suggests the substrate is being utilised efficiently without producing excessive biomass, ideal for maintaining granule stability. Yield coefficients are highly dependent on temperature, influent substrate concentration, and sludge retention time (SRT); hence, values vary from study to study. In one study, where the effect of SRT was researched, yield values increased from 0.24 to 0.48, 0.61, and 0.68 mg biomass/mg COD with a corresponding SRT of 30, 20, and 15 days [4]. Another study using an AGS-biofilm reactor achieved a biomass yield of 0.33–0.37 mg biomass/mg COD [38]. Given these reference values, the coefficient of 0.47 seems reasonable and accurate.
The computed decay coefficient (0.0059 h−1) was validated by plotting theoretical solid concentrations (computed using 0.0059 h−1) against measured solid concentrations, as seen in Figure 7. The very close alignment between both data sets supports the accuracy of the calculated value. Small decay coefficients suggest minimal biomass loss; therefore, reactor performance is more likely to be stable.
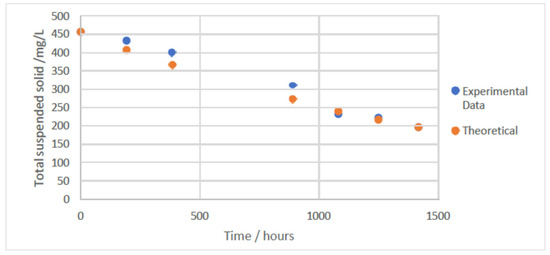
Figure 7.
A graph showing the experimental biomass total suspended solids (mg L−1) against the theoretical total suspended solids (mg L−1) computed using the estimated decay coefficient for an AGS reactor at 20 °C and 1 atm.
4.1.2. Chemical Oxygen Demand (COD)
The mathematical model gave excellent results for predicting COD removal efficiency (82.8%) Table 11 and Table 12. This fits closely within the data set provided, which reported a removal efficiency of 80% ± 9%, confirming the reliability of the model. Compared to other similar lab-scale AGS continuous flow reactors, the results are consistent. For example, Miyake et al. achieved a COD removal efficiency of ~80% in a 4 L reactor. Furthermore, Hamza et al. have previously performed other AGS-SBR systems, one of which they investigated for high-strength organic wastewater treatment, which reported an exceptional removal efficiency of ~96 ± 2.7% [20]. Another study used a 24.2 L double column cyclic aerobic granular reactor (DCCAGR) and achieved COD removal efficiencies of 97% [31]. These comparisons reinforce the predicted performance of the continuous flow model, but there is room for further improvement. Improvements could include experimenting with different configurations, for example, adding baffles or two continuous flow reactors in series. Also changing operational conditions such as aerator flow rate to improve mixing and increasing temperature for biomass growth rate. Performing future experiments with these adjustments may identify areas of optimisation for the model.
In terms of real-world application, an 82.8% removal efficiency and 32 mg L−1 comply with the UK wastewater treatment compliance limits set by the Environment Agency. These are a concentration maximum of 125 mg L−1 and a minimum percentage reduction of 75% [40,41].

Table 12.
The computed results for the COD removal in an AGS reactor at 20 C, 1 atm mathematical model, and referenced literature values.
Table 12.
The computed results for the COD removal in an AGS reactor at 20 C, 1 atm mathematical model, and referenced literature values.
| Parameter | Symbol | Calculated Value | Referenced Values | Citation |
|---|---|---|---|---|
| Flow rate | Qi | 0.6 L h−1 | ||
| Specific substrate utilisation rate | Umax | 0.022 mg COD mg biomass-1 h−1 | ||
| COD degradation rate constant | rx | 59.8 h−1 | ||
| Effluent total COD concentration | Se | 32 mg L−1 | ||
| COD removal efficiency (%) | 82.8% | ~80% | [42] | |
| ~96 ± 2.7% | [21] | |||
| 97% | [31] |
4.1.3. Mass Transfer
- Moles of O2, NO2 = 0.008725 mol L−1
- Oxygen concentration in the gas phase = 280 mg L−1
4.1.4. Aeration and Gas Transfer Variables
- Oxygen transfer rate = oxygen uptake rate = 211 mg O2/L/h
- Aeration flow rate = 0.000184 m3 s−1
4.1.5. Heat Transfer
- Mass flow rate = 14.4 kg h−1
- Heat transfer rate (W) = 0.0202 W
- Overall heat transfer coefficient = 0.084 W/m2 °C
The estimated heat transfer rate of 0.0202 W and overall heat coefficient of 0.084 W/m2°C in the reactor align with the expectations stated in Section 3.1.5 due to the small-scale system. Direct studies on specific heat transfer coefficients in aerobic granular sludge full-scale applications have not been accurately studied to the current date, making direct comparison difficult. This highlights a critical gap in the literature around AGS continuous flow reactors and the need for future research into the thermal dynamics of large-scale AGS systems.
However, parallels can be drawn from research regarding activated sludge systems. A yearlong study was conducted on a wastewater plant in Linköping, finding the activated sludge systems had a temperature change of 0.43 °C, 55% of the total temperature change in the plant [43]. This emphasises the role secondary biological processes have in driving heat transfer in wastewater treatment. AGS, with its distinctive properties and behaviour, may exhibit similar behaviour.
4.1.6. Hydrodynamics and Mixing
The airflow Reynolds number, 469, suggests a laminar flow regime in the reactor, as it is well below the critical value of 2000 Table 13. This indicates the movement of air bubbles up through the reactor does not cause chaotic mixing which would damage sludge granule structure. However, the low Reynolds number could suggest insufficient mixing between the three phases. Increasing superficial gas velocity to 0.03 m s−1 increases the Reynolds number to 599; by performing an experimental evaluation of the trade-off between power consumption for higher aeration and removal efficiency, it can be reviewed. Finally, the fluid flow Reynolds number, 1.7, suggests the movement of influent into the reactor has negligible effects on the hydrodynamics. This means disturbance to the sludge distribution will not be affected.

Table 13.
The computed results for the hydrodynamics of a continuous flow AGS reactor at 20 °C 1 atm mathematical model.
The overall Froude number and bubble formation Froude number (0.0237 and 0.0531, respectively) indicate that gravitational forces will dominate the flow dynamics Table 13. For AGS reactors, low Froude numbers would be ideal, as they will allow fast settling, minimise shear stress, and enable effective oxygen transfer from rising bubbles.
4.2. Python Code Sensitivity Analysis
4.2.1. Standard Mathematical Model Python Results
Figure 8 illustrates the relationship between COD removal and biomass growth in a continuous flow AGS reactor, predicted by the model derived in Section 3.1. Within the 4 h HRT, a significant decrease in COD concentration was observed, along with a steady increase in biomass. This demonstrates how the reactor effectively degrades organic matter while promoting biomass growth.
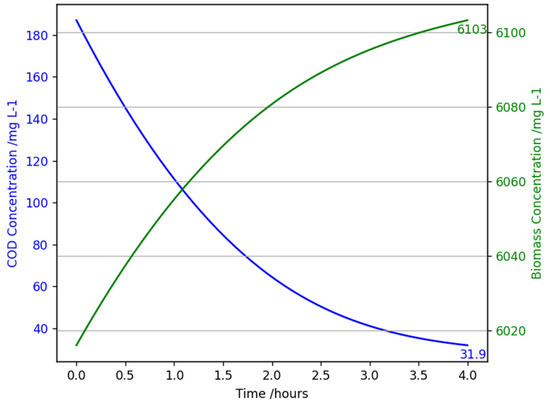
Figure 8.
A graph showing chemical oxygen demand concentration (mg L−1) and biomass concentration (mg L−1) against time (hours) for the mathematical model of an aerobic granular sludge continuous flow reactor with an influent chemical oxygen demand of 187 mg/L, at 20 °C, 1 atm, and an HRT of 4 h.
A total of 82% of influent COD was removed, which shows the high efficiency of the reactor; for a more in-depth analysis, refer to Section 4.1.2. As expected, rapid removal initially occurs due to high substrate availability and plateaus over time, most likely due to substrate diffusion limitations and biomass saturation. The green curve in Figure 8 shows the biomass growth starting at 6016 mg L−1 increasing to 6103 mg L−1 in the 4 h period. Notably, the biomass growth in the model is larger than the observed biomass growth from the data provided; however, comparison is hard due to measurements being taken every 7 days. From the data set, the average growth in a 7-day cycle was 1048 mg L−1. This discrepancy could stem from a few factors. There are many complexities of real-world systems, especially in bioreactors, which the mathematical model cannot fully reflect. These include inhibitory byproducts, complete COD conversion into biomass, substrate diffusion limitations in the granules, and the possible variation in reactor conditions. These will cause slower biomass growth.
The results validate the success of the mathematical model’s ability to predict the performance of an AGS reactor, demonstrating effective COD removal and successful biomass stability. These are both important for ensuring long-term reactor operation. However, assumptions of uniform mixing and ideal conditions for biomass growth will overestimate the computed values, which need to be taken into consideration.
4.2.2. High COD Concentration Sensitivity Analysis Results
Handling varying influents is integral in wastewater treatment; therefore, testing a high-strength influent is important to analyse the applicability of the model and its capability under challenging conditions. Figure 9 demonstrates that when handling a higher strength influent (400 mg L−1), the reactor model predicts an estimated COD concentration of 157 mg L−1 and removal efficiency of 60.75%. Compared to Figure 8, where the removal efficiency was 82%, this is a 21% decrease. In the data set, the highest influent concentration used was 340 mg L−1 and the sequential batch reactor achieved an effluent of 131 mg L−1 (61% removal efficiency). Again, this shows the rigour of the mathematical model.
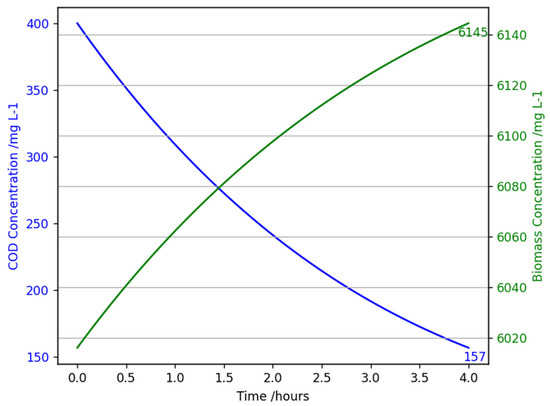
Figure 9.
A graph showing chemical oxygen demand concentration (mg L−1) and biomass concentration (mg L−1) against time (hours) for the mathematical model of an aerobic granular sludge continuous flow reactor with an influent chemical oxygen demand of 400 mg/L, at 20 °C, 1 atm, and an HRT of 4 h.
High organic loading rates (OLR) can overwhelm microbial communities due to substrate saturation, where the biomass can no longer degrade COD effectively. Also, dissolved oxygen demand increases significantly, respectively, to the increase in organic matter to be broken down. Consequently, not the increasing aeration rate led to reduced polysaccharide production, therefore inhibiting EPS production (biomass growth) [44]. Overall, contributing to the insufficient removal rate of substrates.
In terms of full-scale operation, a 60.75% removal efficiency and effluent concentration of 157 mg L−1 do not comply with effluent standards set for wastewater treatment facilities. In the UK these standards are a concentration maximum of 125 mg L−1 and a minimum percentage reduction of 75% [40,41]. Further model refinement and testing varying operational conditions, such as increasing HRT and increasing aeration flow rate is recommended to investigate if the requirements can be met. For real-world application, recycle streams or an extra AGS CF reactor could be retrofitted alongside the main reactor to further improve effluent quality. These different configurations will increase the retention time without the need of reducing influent flow rate.
Microbial growth in Figure 9 is larger than that predicted in Figure 8, 128 mg L−1 compared to 87 mg L−1 because the COD removed is greater, 240 mg COD L−1 compared to 150 mg COD L−1. However, the model does not consider the complex mechanism present when substrate overload occurs as discussed above.
4.2.3. Low COD Concentration Sensitivity Analysis
As expected, Figure 10 presents the improvement of removal efficiency when influent concentration is smaller, 87.9% compared to 82%. As seen by the green line, the biomass growth is slower than the results at standard conditions (47 mg L−1 compared to 87 mg L−1) as the overall amount of COD removal is less than at higher concentrations. To validate the accuracy of the model, provided data using a cycle with an influent flow rate of 98 resulted in an 85.7% removal of substrate. Subsequently, this shows the predicted efficiency is within a reasonable range of the lab results.
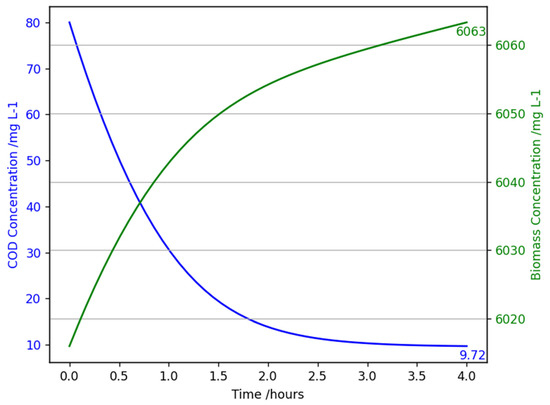
Figure 10.
A graph showing chemical oxygen demand concentration (mg L−1) and biomass concentration (mg L−1) against time (hours) for the mathematical model of an aerobic granular sludge continuous flow reactor with an influent chemical oxygen demand of 80 mg/L, at 20 °C, 1 atm, and an HRT of 4 h.
The results are well below the UK wastewater treatment compliance limits set by the Environment Agency; hence, in terms of handling low-concentration influents, optimisation is not necessary. This is because the ratios of substrate to biomass to oxygen concentrations are more ideal, reducing saturation and biomass inhibitory effects. Economically, the operational simplicity of the system design will be cost-effective for low COD concentration periods since the same aeration power achieves a better removal efficiency.
4.2.4. High Flow Rate Sensitivity Analysis
The capability of handling influxes of water is integral for full-scale wastewater treatment processes; to simulate this situation, the flow rate was doubled to 1.2 L h−1. Predicted effluent removal efficiency decreased to 54.1% with an effluent concentration of 85.8 mg COD L−1, as shown in Figure 11. High flow rates pose multiple operational challenges, such as reduced HRT, limiting the available time for substrate degradation and increasing the chances of potential biomass washout. These lead to a reduced reactor efficiency, as seen in a study performed by Wang et al. using high-strength wastewater, confirming the sludge volume index being significantly higher and substrate removal lower for low HRTs.

Figure 11.
A graph showing chemical oxygen demand concentration (mg L−1) and biomass concentration (mg L−1) against time (hours) for the mathematical model of an aerobic granular sludge continuous flow reactor with an influent chemical oxygen demand of 187 mg/L, at 20 °C, 1 atm, and an HRT of 2 h (flow rate = 1.2 L h−1).
Unfortunately, the predicted results fall well below the UK waterboard standards for wastewater treatment effluent and therefore would result in fines for noncompliance. Optimisation of reactor configuration/conditions is required to verify potential for scalability. A reactor configuration that may improve effluent concentration would be 2 continuous flow reactors in series because this will increase the HRT. This configuration would come with an economic trade-off due to the expenses of retrofitting an additional reactor and larger energy consumption from aeration; however, it will allow plants to handle storm surges and the risk of spills.
4.2.5. Low Flow Rate Sensitivity Analysis
Reducing flow rate (increasing HRT to 8 h) significantly improved reactor performance, as seen in Figure 12. Effluent COD concentration was computed to be 17 mg L−1, yielding a removal efficiency of 90.9%, exceeding UK wastewater treatment standards. Longer HRT provides an extended reaction time, allowing more COD degradation and biomass activity, reducing the possibility of substrate inhibition. Also, longer HRT improves biomass growth, hence better settleability, minimising biomass washout [2]. This contributes to enhanced reactor long-term stability.
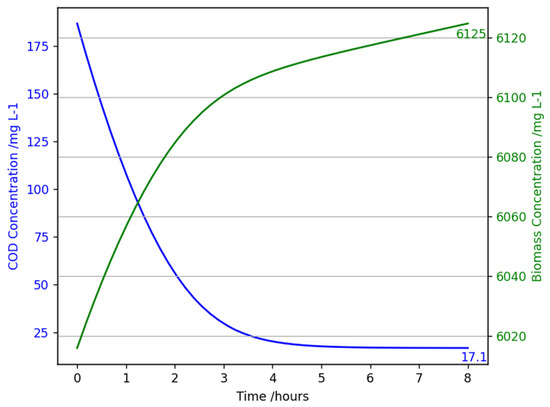
Figure 12.
A graph showing chemical oxygen demand concentration (mg L−1) and biomass concentration (mg L−1) against time (hours) for the mathematical model of an aerobic granular sludge continuous flow reactor with an influent chemical oxygen demand of 187 mg/L, at 20 °C, 1 atm, and an HRT of 8 h (flow rate = 0.3 L h−1).
The model’s predicted removal efficiency aligns with reported findings for investigations on varying HRT in AGS reactors. Studies on SBRs using high strength wastewater have reported removal efficiencies over 95% and an SVI30 of 44.5 mL/g at an 8 h HRT [2]. The study concluded that an 8 h HRT produced the most successful results out of a range of 4.6 h−1 to 16 h−1 [2].
The model’s accuracy in predicting a high removal efficiency for low flow rate conditions shows refinement regarding situations such as off-peak hours or droughts is not necessary. However, the results coupled with literature findings suggest optimising the standard model HRT to 8 h is recommended. This can be performed by either increasing the working volume of the reactor or, depending on real-world application, changing the influent flow rate from 0.6 to 0.3 L h−1. From an operational perspective, another advantage of maintaining a high HRT is it will optimise energy consumption again, allowing a very high removal efficiency without additional aeration power. Moreover, the results adhere to waterboard compliance limits, supporting sustainable wastewater management practices and contributing to achieving sustainability goals.
4.3. CFD Results
As seen in Figure 13 and Figure 14, the distribution of aerobic granular sludge within the reactor is well distributed, with most of the sludge at the bottom of the reactor and a small gradient effect to the top. Where the simulation shows the airstream in Figure 14, it can be seen that as air rises, some granules are being carried up with it. The figures show the velocity of the air stream is not too harsh, where structural damage could happen to the bed, and the mixing at the bottom of the reactor is good. Had the simulation been able to run for a longer period of time, we believe the results would have shown efficient mixing throughout the reactor, integral for oxygen diffusion between the biomass and substrate, therefore driving good or bad performance. In order to enhance substrate removal, the aeration flow rate could be increased by only a small amount to 2.5–2.8 cm s−1.
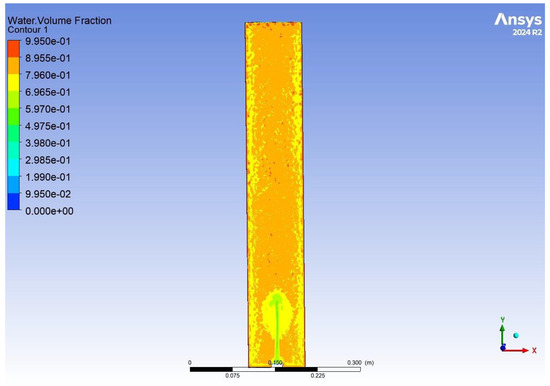
Figure 13.
The results of a CFD simulation showing the water volume fraction distributed throughout an aerobic granular sludge reactor.
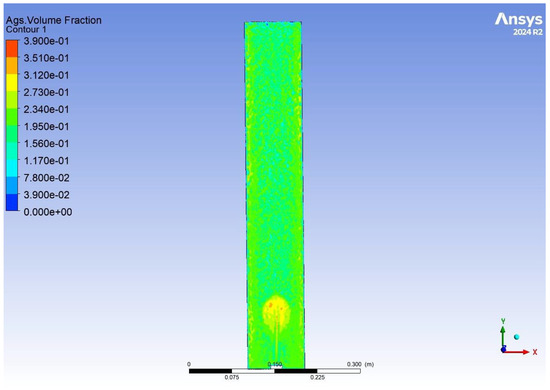
Figure 14.
The results of a CFD simulation showing the AGS volume fraction distributed throughout an aerobic granular sludge reactor.
Also, the CFD results show that biomass washout would occur during effluent withdrawal if a settling period was not integrated. A recommendation to solve this would be a configuration of 2 continuous flow reactors in series with alternating intermittent aerators.
5. Future Recommendations
- First due to the many limitations of the currently available computational resources, performing a 3D CFD simulation needs to be conducted on a computer unit equipped with ultra-fast processors and efficient cooling systems. This would enable the formation of a refined mesh small enough to pick up the interactions between small air bubbles, granular sludge and water. Improved computational capacity would run calculations quicker, leading to providing more accurate CFD results for the reactor model.
- To investigate reactor configurations which can effectively treat unstable influent conditions, my recommendation is to perform a lab-scale set-up of 2 continuous flow reactors in series with alternating, intermittent aeration. This set-up allows a higher retention time for when high concentration and high flow rate feeds are used, therefore improving reactor performance and stability in real-world scenarios. Also, the reactor design is simple, which is important for considering scale-up as many current continuous flow configurations are too complicated to be applied at large scales. Intermittent aeration will allow small settling periods in continuous operation, reducing the amount of biomass washout. With this set-up, performance evaluations should be conducted regarding varying HRTs and aeration flow rates.
- Finally, more research on pilot-scale reactors is necessary when scaling up from a laboratory to a successful full-scale application. This has not been widely applied in the AGS research field. Therefore, future work should use the same height-to-diameter ratio to develop the mathematical model in this study to guide scale-up efforts. Also using computational fluid dynamics simulations, predictions of reactor performance can be made. Modelling the two reactors in series as stated before should be prioritised, as it will determine if the configuration can achieve the desired performance for real-world influent variations.
6. Conclusions
This dissertation has provided significant insight into the modelling of continuous flow aerobic granular sludge reactors, addressing what their limitations and optimisation areas for handling varying influents are. Transitioning data from a sequencing batch reactor into continuous flow using Monod kinetic equations produced great results of effluent concentration and removal efficiency, 32 mg L−1 and 82.8%, respectively. This shows the reactor performance is stable, efficient, and cost-effective. These values were validated against the experimental data provided and other research papers. Although, being within the interval of the lab-scale reactor measured results and abiding by regulations set by the UK waterboard, there is room for improvement to achieve a removal efficiency above 90%, as this will reinforce reactor stability for varying influents.
To further develop the capability for continuous flow AGS reactors through periods of storm surges, drought and off-peak times, a sensitivity analysis was performed via a Python code. While fantastic results for the simulation of reduced flow rate and low-concentration influent were generated, the model could not withstand storm surge scenarios. The computed results gave removal efficiencies of 54.1% for fast flow rates and 60.75% for high influent COD concentrations, both of which do not meet the UK waterboard requirements. CFD results were generated, offering additional insight to the hydrodynamics of the system; however, there were many limitations. These include not being able to add AGS as a new material onto ANSYS (ways to work around this are explained in Section 3.3) and not being able to run long CFD calculations. Despite this, the results generated revealed a potential issue of microbial washout.
Considering all of these results, in my opinion the current reactor configuration with the most potential for a successful full-scale application would be a series of two continuous flow reactors with intermittent aeration. Many current potential configurations include external baffles, hydro cyclones, and three-phase separators which are too complex and unstable to scale up,; therefore, to increase retention time (a key parameter driving effluent removal), two simple cylindrical reactors is a reasonable solution. To address microbial washout, a period of settling will be required. A lab-scale experiment with this configuration will need to be conducted to investigate how intermittent aeration will affect microbial washout as well as effluent removal efficiency. Other future recommendations regarding the next potential steps of scaling up are detailed in Section 5.
The development of highly efficient, flexible, and cost-effective wastewater treatment is currently very important. With climate change and ever-growing populations, the need to handle high wastewater flow rates is a necessity to save freshwater sources from being polluted. By advancing our understanding of continuous flow reactors, this research provides a good foundation for designing efficient, sustainable solutions to protect our environment and ensure water companies can adhere to regulatory compliance in the future.
Author Contributions
Conceptualization, M.G.H.; Methodology, M.S. and M.G.H.; Software, M.S.; Validation, R.S. and R.H.; Formal analysis, M.G.H.; Data curation, R.S. and R.H.; Writing—original draft, M.S. and M.G.H.; Writing—review & editing, I.M.T.A.S.; Supervision, M.G.H.; Funding acquisition, I.M.T.A.S. All authors have read and agreed to the published version of the manuscript.
Funding
The authors extend their appreciation to the Deanship of Research and Graduate Studies at King Khalid University for funding this work through the Small Research Project under grant number RGP1/70/46.
Data Availability Statement
The data presented in this study are available on request from the corresponding author due to commercial sensitivity.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
References
- Yan, J.-L.; Cui, Y.-W.; Huang, J.-L. Continuous flow reactors for cultivating aerobic granular sludge: Configuration innovation, principle and research prospect. J. Chem. Technol. Biotechnol. 2021, 96, 2721–2734. [Google Scholar] [CrossRef]
- Waste Water Treatment Works: Treatment Monitoring and Compliance Limits. Available online: https://www.gov.uk/government/publications/waste-water-treatment-works-treatment-monitoring-and-compliance-limits/waste-water-treatment-works-treatment-monitoring-and-compliance-limits?utm_source=chatgpt.com#lut-for-bod-and-cod (accessed on 19 November 2024).
- Liu, S.; Zhou, M.; Daigger, G.T.; Huang, J.; Song, G. Granule formation mechanism, key influencing factors, and resource recycling in aerobic granular sludge (AGS) wastewater treatment: A review. J. Environ. Manag. 2023, 338, 117771. [Google Scholar] [CrossRef] [PubMed]
- Gandhi, V.; Shah, K. Advances in Wastewater Treatment I; Materials Research Forum LLC: Millersville, PA, USA, 2021. [Google Scholar]
- Kato, S.; Kansha, Y. Comprehensive review of industrial wastewater treatment techniques. Environ. Sci. Pollut. Res. 2024, 31, 51064–51097. [Google Scholar] [CrossRef] [PubMed]
- Kesari, K.K.; Soni, R.; Jamal, Q.M.S.; Tripathi, P.; Lal, J.A.; Jha, N.K.; Siddiqui, M.H.; Kumar, P.; Tripathi, V.; Ruokolainen, J. Wastewater Treatment and Reuse: A Review of its Applications and Health Implications. Water Air Soil Pollut. 2021, 232, 208. [Google Scholar] [CrossRef]
- Jain, R.K.; Cui, Z.C.; Domen, J.K. (Eds.) Chapter 4—Environmental Impacts of Mining. In Environmental Impact of Mining and Mineral Processing; Butterworth-Heinemann: Boston, MA, USA, 2016; pp. 53–157. [Google Scholar] [CrossRef]
- Zagklis, D.P.; Bampos, G. Tertiary Wastewater Treatment Technologies: A Review of Technical, Economic, and Life Cycle Aspects. Processes 2022, 10, 2304. [Google Scholar] [CrossRef]
- Tran, H.T.; Lesage, G.; Lin, C.; Nguyen, T.B.; Bui, X.-T.; Nguyen, M.K.; Nguyen, D.H.; Hoang, H.G.; Nguyen, D.D. Chapter 3—Activated sludge processes and recent advances. In Current Developments in Biotechnology and Bioengineering; Bui, X.-T., Nguyen, D.D., Nguyen, P.-D., Ngo, H.H., Pandey, A., Eds.; Elsevier: Amsterdam, The Netherlands, 2022; pp. 49–79. [Google Scholar] [CrossRef]
- Islam, M.D.; Mahdi, M.M. Chapter 1—Evaluation of micro-pollutants removal from industrial wastewater using conventional and advanced biological treatment processes. In Biodegradation and Detoxification of Micropollutants in Industrial Wastewater; Haq, I., Kalamdhad, A.S., Shah, M.P., Eds.; Elsevier: Amsterdam, The Netherlands, 2022; pp. 1–26. [Google Scholar] [CrossRef]
- Mahlangu, O.T.; Nthunya, L.N.; Motsa, M.M.; Richards, H.; Mamba, B.B. Chapter 12—Treatment of trace organics and emerging contaminants using traditional and advanced technologies. In Development in Wastewater Treatment Research and Processes; Shah, M.P., Ed.; Elsevier: Amsterdam, The Netherlands, 2023; pp. 243–264. [Google Scholar] [CrossRef]
- Yeasmin, F.; Rasheduzzaman, M.; Manik, M.; Hasan, M.M. Activated Sludge Process for Wastewater Treatment. In Advanced and Innovative Approaches of Environmental Biotechnology in Industrial Wastewater Treatment; Shah, M.P., Ed.; Springer Nature: Singapore, 2023; pp. 23–50. [Google Scholar] [CrossRef]
- Luo, B.; He, H.; Yan, Y.; Wang, Y.; Yang, X.; Liu, Y.; Xu, J.; Huang, W. Flocculants for the High-Concentration Activated Sludge Method and the Effectiveness of Urban Wastewater Treatment. Water 2024, 16, 2281. [Google Scholar] [CrossRef]
- Al-Asheh, S.; Bagheri, M.; Aidan, A. Membrane bioreactor for wastewater treatment: A review. Case Stud. Chem. Environ. Eng. 2021, 4, 100109. [Google Scholar] [CrossRef]
- Siatou, A.; Manali, A.; Gikas, P. Energy Consumption and Internal Distribution in Activated Sludge Wastewater Treatment Plants of Greece. Water 2020, 12, 1204. [Google Scholar] [CrossRef]
- Campos, J.L.; Valenzuela-Heredia, D.; Pedrouso, A.; Val del Río, A.; Belmonte, M.; Mosquera-Corral, A. Greenhouse Gases Emissions from Wastewater Treatment Plants: Minimization, Treatment, and Prevention. J. Chem. 2016, 2016, 3796352. [Google Scholar] [CrossRef]
- Ekholm, J.; Persson, F.; de Blois, M.; Modin, O.; Gustavsson, D.J.I.; Pronk, M.; van Loosdrecht, M.C.M.; Wilén, B.-M. Microbiome structure and function in parallel full-scale aerobic granular sludge and activated sludge processes. Appl. Microbiol. Biotechnol. 2024, 108, 334. [Google Scholar] [CrossRef] [PubMed]
- United Kingdom—Kendal, n.d. Nereda a product of Royal HaskoningDHV [Online]. Available online: https://nereda.royalhaskoningdhv.com/en/projects/united-kingdom-kendal (accessed on 19 November 2024).
- Purba, L.D.A.; Ibiyeye, H.T.; Yuzir, A.; Mohamad, S.E.; Iwamoto, K.; Zamyadi, A.; Abdullah, N. Various applications of aerobic granular sludge: A review. Environ. Technol. Innov. 2020, 20, 101045. [Google Scholar] [CrossRef]
- Rosa-Masegosa, A.; Muñoz-Palazon, B.; Gonzalez-Martinez, A.; Fenice, M.; Gorrasi, S.; Gonzalez-Lopez, J. New Advances in Aerobic Granular Sludge Technology Using Continuous Flow Reactors: Engineering and Microbiological Aspects. Water 2021, 13, 1792. [Google Scholar] [CrossRef]
- Hamza, R.A.; Iorhemen, O.T.; Zaghloul, M.S.; Tay, J.H. Rapid formation and characterization of aerobic granules in pilot-scale sequential batch reactor for high-strength organic wastewater treatment. J. Water Process Eng. 2018, 22, 27–33. [Google Scholar] [CrossRef]
- Dawen, G.; Nabi, M. Aerobic Granular Sludge. In Novel Approaches Towards Wastewater Treatment: Effective Strategies and Techniques; Dawen, G., Nabi, M., Eds.; Springer Nature: Cham, Switzerland, 2024; pp. 91–165. [Google Scholar] [CrossRef]
- Kan, X.; Ji, B.; Zhang, J.; Liu, Z.; Xu, Y.; Zhao, L.; Shi, B.; Pu, J.; Zhang, Z. Advances in aerobic granular sludge stabilization in wastewater. Desalination Water Treat. 2024, 319, 100513. [Google Scholar] [CrossRef]
- Hamza, R.; Rabii, A.; Ezzahraoui, F.; Morgan, G.; Iorhemen, O.T. A review of the state of development of aerobic granular sludge technology over the last 20 years: Full-scale applications and resource recovery. Case Stud. Chem. Environ. Eng. 2022, 5, 100173. [Google Scholar] [CrossRef]
- Nancharaiah, Y.V.; Sarvajith, M. Aerobic granular sludge process: A fast growing biological treatment for sustainable wastewater treatment. Curr. Opin. Environ. Sci. Health 2019, 12, 57–65. [Google Scholar] [CrossRef]
- Praveenkumar, T.R.; Alahmadi, T.A.; Salmen, S.H.; Verma, T.N.; Gupta, K.K.; Gavurová, B.; Sekar, M. Impact of sludge density and viscosity on continuous stirred tank reactor performance in wastewater treatment by numerical modelling. J. Taiwan Inst. Chem. Eng. 2024, 166, 105368. [Google Scholar] [CrossRef]
- Fadillah, G.; Alarifi, N.T.S.; Suryawan, I.W.K.; Saleh, T.A. Advances in designed reactors for water treatment process: A review highlighting the designs and performance. J. Water Process Eng. 2024, 63, 105417. [Google Scholar] [CrossRef]
- Samaei, S.H.-A.; Chen, J.; Xue, J. Current progress of continuous-flow aerobic granular sludge: A critical review. Sci. Total Environ. 2023, 875, 162633. [Google Scholar] [CrossRef] [PubMed]
- Haaksman, V.A.; van Dijk, E.J.H.; Al-Zuhairy, S.; Mulders, M.; Loosdrecht MCMvan Pronk, M. Utilizing anaerobic substrate distribution for growth of aerobic granular sludge in continuous-flow reactors. Water Res. 2024, 257, 121531. [Google Scholar] [CrossRef] [PubMed]
- Yu, C.; Wang, K.; Zhang, K.; Liu, R.; Zheng, P. Full-scale upgrade activated sludge to continuous-flow aerobic granular sludge: Implementing microaerobic-aerobic configuration with internal separators. Water Res. 2024, 248, 120870. [Google Scholar] [CrossRef] [PubMed]
- Long, B.; Yang, C.; Pu, W.; Yang, J.; Liu, F.; Zhang, L.; Cheng, K. Rapid cultivation of aerobic granular sludge in a continuous flow reactor. J. Environ. Chem. Eng. 2015, 3 Pt A, 2966–2973. [Google Scholar] [CrossRef]
- Hodaifa, G.; Paladino, O.; Malvis, A.; Seyedsalehi, M.; Neviani, M. Chapter 10 - Green techniques for wastewaters. In Advanced Low-Cost Separation Techniques in Interface Science; Kyzas, G.Z., Mitropoulos, A.C., Eds.; Interface Science and Technology; Elsevier: Amsterdam, The Netherlands, 2019; Volume 30, pp. 217–240. [Google Scholar] [CrossRef]
- Liu, Y. Overview of some theoretical approaches for derivation of the Monod equation. Appl. Microbiol. Biotechnol. 2007, 73, 1241–1250. [Google Scholar] [CrossRef] [PubMed]
- Galinha, C.F.; Sanches, S.; Crespo, J.G. Chapter 6—Membrane bioreactors. In Fundamental Modelling of Membrane Systems; Luis, P., Ed.; Elsevier: Amsterdam, The Netherlands, 2018; pp. 209–249. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, Y.-Q.; Wang, Z.-W.; Yang, S.-F.; Tay, J.-H. Influence of substrate surface loading on the kinetic behaviour of aerobic granules. Appl. Microbiol. Biotechnol. 2005, 67, 484–488. [Google Scholar] [CrossRef] [PubMed]
- Rapp, B.E. Chapter 9—Fluids. In Microfluidics: Modelling, Mechanics and Mathematics; Rapp, B.E., Ed.; Micro and Nano Technologies; Elsevier: Oxford, UK, 2017; pp. 243–263. [Google Scholar] [CrossRef]
- Castellanos, R.M.; Dias, J.M.R.; Dias Bassin, I.; Dezotti, M.; Bassin, J.P. Effect of sludge age on aerobic granular sludge: Addressing nutrient removal performance and biomass stability. Process Saf. Environ. Prot. 2021, 149, 212–222. [Google Scholar] [CrossRef]
- de Sousa Rollemberg, S.L.; Tavares Ferreira, T.J.; Bezerra dos Santos, A. Evaluation of an aerobic granular sludge reactor with biological filtration (AGS-BF reactor) in municipal wastewater treatment: A new configuration. Bioresour. Technol. Rep. 2022, 19, 101172. [Google Scholar] [CrossRef]
- Miyake, M.; Hasebe, Y.; Furusawa, K.; Shiomi, H.; Inoue, D.; Ike, M. Efficient aerobic granular sludge production in simultaneous feeding and drawing sequencing batch reactors fed with low-strength municipal wastewater under high organic loading rate conditions. Biochem. Eng. J. 2022, 184, 108469. [Google Scholar] [CrossRef]
- UK Population 1950–2025. Available online: https://www.macrotrends.net/global-metrics/countries/GBR/united-kingdom/population (accessed on 24 November 2024).
- UK Daily Water Consumption Per Person by Type 2023. Statista. Available online: https://www.statista.com/statistics/1323641/household-metered-unmetered-daily-water-consumption-england-and-wales/ (accessed on 18 November 2024).
- Arnell, M.; Ahlström, M.; Wärff, C.; Saagi, R.; Jeppsson, U. Plant-wide modelling and analysis of WWTP temperature dynamics for sustainable heat recovery from wastewater. Water Sci. Technol. 2021, 84, 1023–1036. [Google Scholar] [CrossRef]
- Zhao, Z.; Wang, S.; Shi, W.; Li, J. Recovery of Stored Aerobic Granular Sludge and Its Contaminants Removal Efficiency under Different Operation Conditions. BioMed Res. Int. 2013, 2013, 168581. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Li, J.; Zhang, X.; Chen, Z.; Shen, J.; Kang, J. Impact of hydraulic retention time on swine wastewater treatment by aerobic granular sludge sequencing batch reactor. Environ. Sci. Pollut. Res. Int. 2021, 28, 5927–5937. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).