Deep Signals: Enhancing Bottom Temperature Predictions in Norway’s Mjøsa Lake Through VMD- and EMD-Boosted Machine Learning Models
Abstract
1. Introduction
2. Material and Methods
2.1. Study Region and Data
2.2. Model Structure
2.3. Long Short-Term Memory Network (LSTM)
2.4. Support Vector Machine (SVM)
2.5. Gaussian Process Regression (GPR)
2.6. Multilayer Perceptron (MLP)
2.7. Random Forest
2.8. Variational Mode Decomposition (VMD)
2.9. Empirical Mode Decomposition (EMD)
- Identify all local maxima and minima of the original signal;
- Construct upper and lower envelopes by interpolating the maxima and minima using cubic splines, yielding respectively;
- Compute the local mean envelope a(n) as the average of these two as follows:
- Subtract the mean from the original data:
- Evaluate whether h(n) satisfies the two conditions for being classified as an IMF:
- The number of zero crossings and extrema must differ by at most one;
- The mean of the envelope should be zero (or sufficiently close).If the conditions are met, h(n) is designated as the first IMF ϕ(n);
- Otherwise, the process is repeated on .
2.10. Model Performance Assessment
3. Results
4. Discussion
5. Conclusions and Recommendations
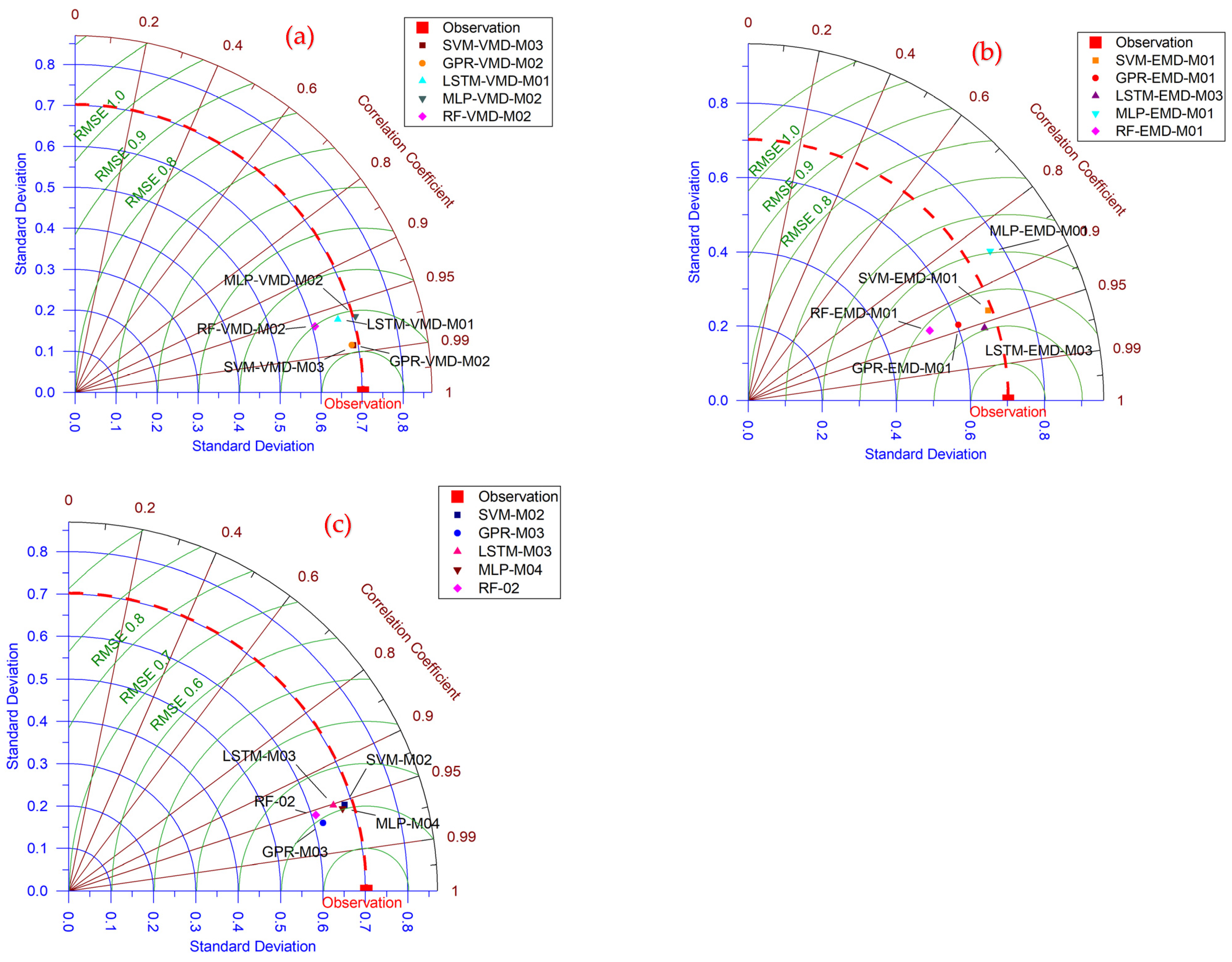
- In the baseline analysis (i.e., without decomposition), the most successful configuration was GPR using the M03 input structure. This structure was obtained by cross-correlation, suggesting that this method positively contributes to the model performance. The SVM-M02 model followed closely, ranking as the second-best performer in terms of accuracy;
- The findings also suggest that including all variables identified by cross-correlation can negatively impact model accuracy. Therefore, the number of input features should be optimized—ideally through iterative testing or validation methods;
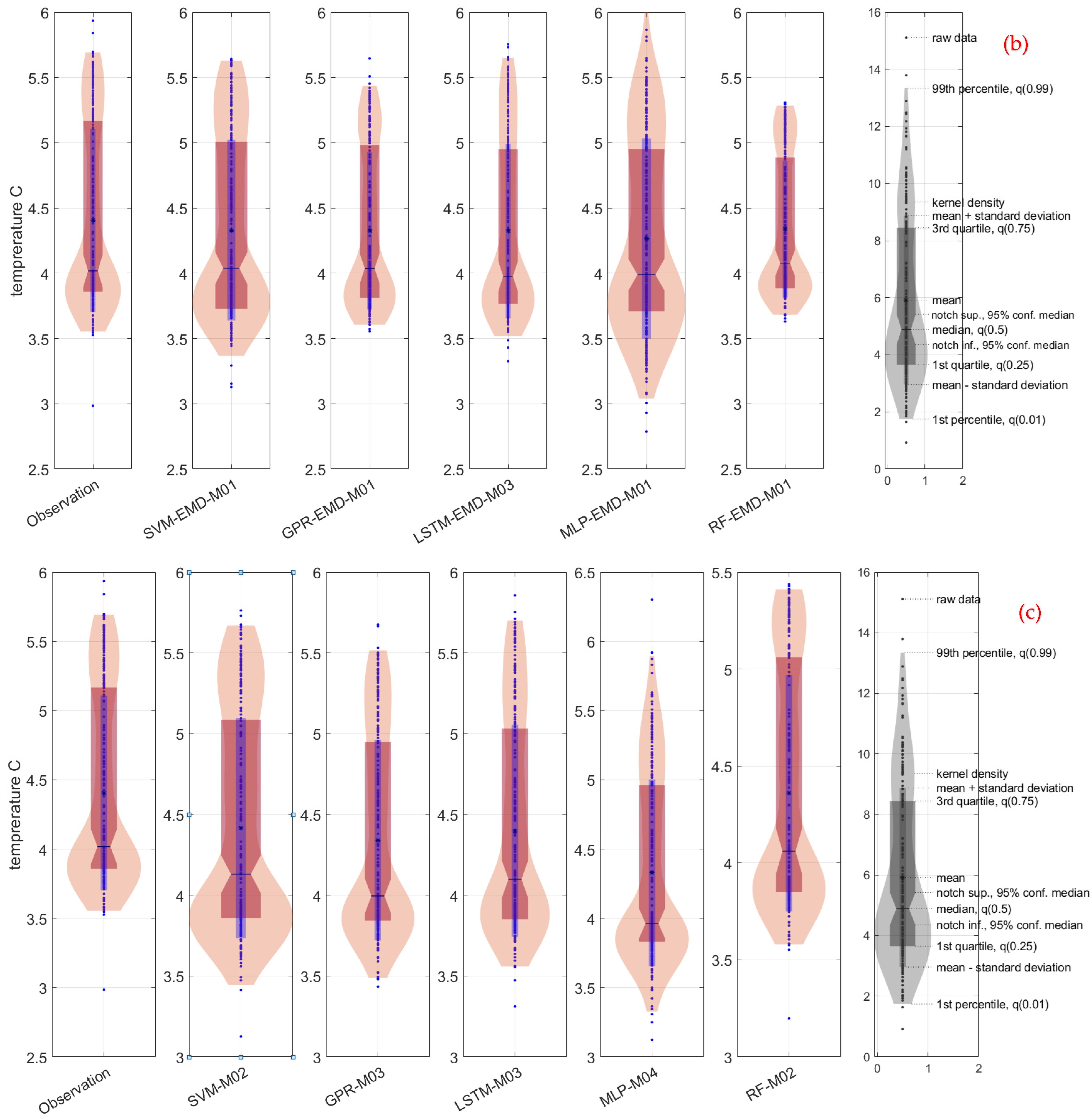
- Among EMD-enhanced models, the LSTM-EMD-M03 configuration produced the highest performance. This model utilized the M03 input structure, which incorporated all cross-correlated lagged variables. These results indicate that LSTM, when paired with the appropriately selected input configuration and EMD preprocessing, can be effective in lake temperature modeling;
- Despite its success in some configurations, the overall application of EMD did not yield consistent improvements. In most cases, EMD led to a reduction in performance metrics across all algorithms, indicating that its effectiveness is model-dependent and should be applied selectively;
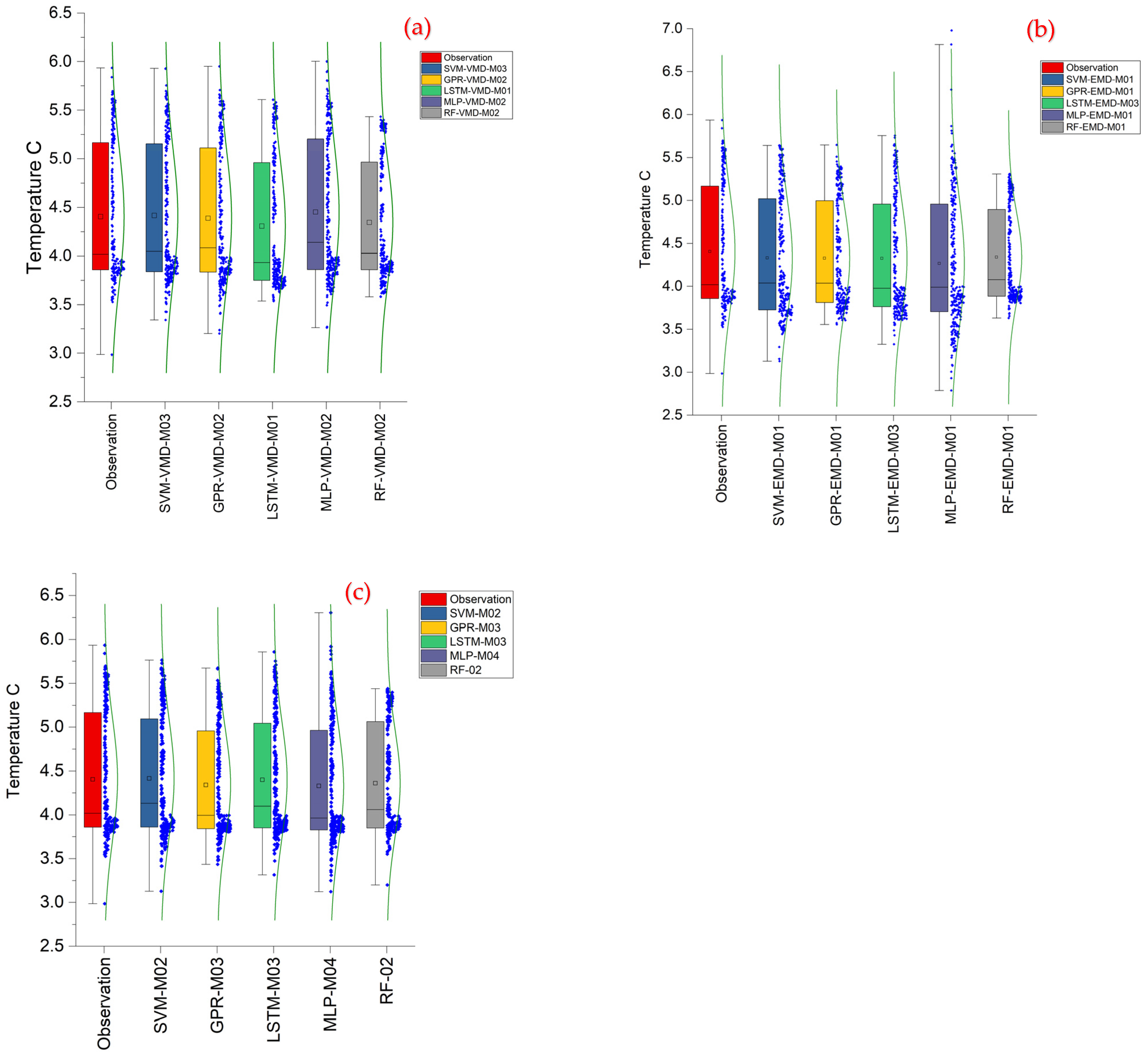
- In the analyses performed with VMD, the general model performance metrics have improved. However, there are some exceptions such as MLP-M04. Despite this, the top results in each algorithm class are VMD-based. In addition to these, SVM with M03 lags were determined to be the most successful models in VMD;
- VMD, on the other hand, generally improved model performance across all algorithms. While some exceptions were observed, such as the MLP-M04 configuration, VMD yielded the most accurate results overall. The SVM-VMD-M03 model was the most effective across all tests;
- In this study, the M04 input structure was sequentially lagged one after the other while determining the model input structure. It was found that this structure gave more effective results than the models created with cross-correlation in some algorithms and separations;
- The cross-correlation method was found to be beneficial for identifying informative input features. However, care must be taken to avoid including too many parameters, which can degrade model performance. Interestingly, in some models and decomposition settings, the simpler M04 configuration—built from consecutive lagged values without formal selection—outperformed more complex input structures derived from cross-correlation.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Butcher, J.B.; Nover, D.; Johnson, T.E.; Clark, C.M. Sensitivity of lake thermal and mixing dynamics to climate change. Clim. Chang. 2015, 129, 295–305. [Google Scholar] [CrossRef]
- Woolway, R.I.; Sharma, S.; Weyhenmeyer, G.A.; Debolskiy, A.; Golub, M.; Mercado-Bettín, D.; Perroud, M.; Stepanenko, V.; Tan, Z.; Grant, L. Phenological shifts in lake stratification under climate change. Nat. Commun. 2021, 12, 2318. [Google Scholar] [CrossRef]
- Feldbauer, J.; Mesman, J.P.; Andersen, T.K.; Ladwig, R. Learning from a large-scale calibration effort of multiple lake temperature models. Hydrol. Earth Syst. Sci. 2025, 29, 1183–1199. [Google Scholar] [CrossRef]
- Piccolroaz, S.; Zhu, S.; Ladwig, R.; Carrea, L.; Oliver, S.; Piotrowski, A.; Ptak, M.; Shinohara, R.; Sojka, M.; Woolway, R. Lake water temperature modeling in an era of climate change: Data sources, models, and future prospects. Rev. Geophys. 2024, 62, e2023RG000816. [Google Scholar] [CrossRef]
- O’Reilly, C.M.; Sharma, S.; Gray, D.K.; Hampton, S.E.; Read, J.S.; Rowley, R.J.; Schneider, P.; Lenters, J.D.; McIntyre, P.B.; Kraemer, B.M. Rapid and highly variable warming of lake surface waters around the globe. Geophys. Res. Lett. 2015, 42, 10773–10781. [Google Scholar] [CrossRef]
- Pilla, R.M.; Williamson, C.E.; Adamovich, B.V.; Adrian, R.; Anneville, O.; Chandra, S.; Colom-Montero, W.; Devlin, S.P.; Dix, M.A.; Dokulil, M.T. Deeper waters are changing less consistently than surface waters in a global analysis of 102 lakes. Sci. Rep. 2020, 10, 20514. [Google Scholar] [CrossRef]
- Noori, R.; Woolway, R.I.; Jun, C.; Bateni, S.M.; Naderian, D.; Partani, S.; Maghrebi, M.; Pulkkanen, M. Multi-decadal change in summer mean water temperature in Lake Konnevesi, Finland (1984–2021). Ecol. Inform. 2023, 78, 102331. [Google Scholar] [CrossRef]
- Noori, R.; Bateni, S.M.; Saari, M.; Almazroui, M.; Torabi Haghighi, A. Strong warming rates in the surface and bottom layers of a boreal lake: Results from approximately six decades of measurements (1964–2020). Earth Space Sci. 2022, 9, e2021EA001973. [Google Scholar] [CrossRef]
- Bégin, P.N.; Tanabe, Y.; Kumagai, M.; Culley, A.I.; Paquette, M.; Sarrazin, D.; Uchida, M.; Vincent, W.F. Extreme warming and regime shift toward amplified variability in a far northern lake. Limnol. Oceanogr. 2021, 66, S17–S29. [Google Scholar] [CrossRef]
- Kraemer, B.M.; Anneville, O.; Chandra, S.; Dix, M.; Kuusisto, E.; Livingstone, D.M.; Rimmer, A.; Schladow, S.G.; Silow, E.; Sitoki, L.M. Morphometry and average temperature affect lake stratification responses to climate change. Geophys. Res. Lett. 2015, 42, 4981–4988. [Google Scholar] [CrossRef]
- Noori, R.; Woolway, R.I.; Saari, M.; Pulkkanen, M.; Kløve, B. Six decades of thermal change in a pristine lake situated north of the Arctic Circle. Water Resour. Res. 2022, 58, e2021WR031543. [Google Scholar] [CrossRef]
- Schwefel, R.; MacIntyre, S.; Cortés, A. Summer temperatures, autumn winds, and thermal structure under the ice in arctic lakes of varying morphometry. Limnol. Oceanogr. 2025, 70, 1817–1834. [Google Scholar]
- Oleksy, I.A.; Richardson, D.C. Climate change and teleconnections amplify lake stratification with differential local controls of surface water warming and deep water cooling. Geophys. Res. Lett. 2021, 48, e2020GL090959. [Google Scholar] [CrossRef]
- Gai, B.; Kumar, R.; Hüesker, F.; Mi, C.; Kong, X.; Boehrer, B.; Rinke, K.; Shatwell, T. Catchments amplify reservoir thermal response to climate warming. Water Resour. Res. 2025, 61, e2023WR036808. [Google Scholar] [CrossRef]
- Råman Vinnå, L.; Medhaug, I.; Schmid, M.; Bouffard, D. The vulnerability of lakes to climate change along an altitudinal gradient. Commun. Earth Environ. 2021, 2, 35. [Google Scholar] [CrossRef]
- Adrian, R.; O’Reilly, C.M.; Zagarese, H.; Baines, S.B.; Hessen, D.O.; Keller, W.; Livingstone, D.M.; Sommaruga, R.; Straile, D.; Van Donk, E. Lakes as sentinels of climate change. Limnol. Oceanogr. 2009, 54, 2283–2297. [Google Scholar] [CrossRef]
- Woolway, R.I.; Kraemer, B.M.; Lenters, J.D.; Merchant, C.J.; O’Reilly, C.M.; Sharma, S. Global lake responses to climate change. Nat. Rev. Earth Environ. 2020, 1, 388–403. [Google Scholar] [CrossRef]
- Zhang, F.; Ono, N.; Kanaya, S. Interpret Gaussian process models by using integrated gradients. Mol. Inform. 2025, 44, e202400051. [Google Scholar]
- Mi, C.; Sadeghian, A.; Lindenschmidt, K.-E.; Rinke, K. Variable withdrawal elevations as a management tool to counter the effects of climate warming in Germany’s largest drinking water reservoir. Environ. Sci. Eur. 2019, 31, 19. [Google Scholar] [CrossRef]
- Ficke, A.D.; Myrick, C.A.; Hansen, L.J. Potential impacts of global climate change on freshwater fisheries. Rev. Fish Biol. Fish. 2007, 17, 581–613. [Google Scholar] [CrossRef]
- Jankowski, T.; Livingstone, D.M.; Bührer, H.; Forster, R.; Niederhauser, P. Consequences of the 2003 European heat wave for lake temperature profiles, thermal stability, and hypolimnetic oxygen depletion: Implications for a warmer world. Limnol. Oceanogr. 2006, 51, 815–819. [Google Scholar] [CrossRef]
- Jansen, J.; Woolway, R.I.; Kraemer, B.M.; Albergel, C.; Bastviken, D.; Weyhenmeyer, G.A.; Marcé, R.; Sharma, S.; Sobek, S.; Tranvik, L.J.; et al. Global increase in methane production under future warming of lake bottom waters. Glob. Change Biol. 2022, 28, 5427–5440. [Google Scholar] [CrossRef]
- Bonacina, L.; Fasano, F.; Mezzanotte, V.; Fornaroli, R. Effects of water temperature on freshwater macroinvertebrates: A systematic review. Biol. Rev. 2023, 98, 191–221. [Google Scholar]
- North, R.P.; North, R.L.; Livingstone, D.M.; Köster, O.; Kipfer, R. Long-term changes in hypoxia and soluble reactive phosphorus in the hypolimnion of a large temperate lake: Consequences of a climate regime shift. Glob. Change Biol. 2014, 20, 811–823. [Google Scholar] [CrossRef]
- Di Nunno, F.; Zhu, S.; Ptak, M.; Sojka, M.; Granata, F. A stacked machine learning model for multi-step ahead prediction of lake surface water temperature. Sci. Total Environ. 2023, 890, 164323. [Google Scholar] [CrossRef]
- Anderson, E.J.; Stow, C.A.; Gronewold, A.D.; Mason, L.A.; McCormick, M.J.; Qian, S.S.; Ruberg, S.A.; Beadle, K.; Constant, S.A.; Hawley, N. Seasonal overturn and stratification changes drive deep-water warming in one of Earth’s largest lakes. Nat. Commun. 2021, 12, 1688. [Google Scholar] [CrossRef]
- Ayala, A.I.; Moras, S.; Pierson, D.C. Simulations of future changes in thermal structure of Lake Erken: Proof of concept for ISIMIP2b lake sector local simulation strategy. Hydrol. Earth Syst. Sci. 2020, 24, 3311–3330. [Google Scholar] [CrossRef]
- Yousefi, A.; Toffolon, M. Critical factors for the use of machine learning to predict lake surface water temperature. J. Hydrol. 2022, 606, 127418. [Google Scholar] [CrossRef]
- Read, J.S.; Jia, X.; Willard, J.; Appling, A.P.; Zwart, J.A.; Oliver, S.K.; Karpatne, A.; Hansen, G.J.; Hanson, P.C.; Watkins, W. Process-guided deep learning predictions of lake water temperature. Water Resour. Res. 2019, 55, 9173–9190. [Google Scholar] [CrossRef]
- Mukonza, S.S.; Chiang, J.-L. Micro-climate computed machine and deep learning models for prediction of surface water temperature using satellite data in Mundan water reservoir. Water 2022, 14, 2935. [Google Scholar] [CrossRef]
- Rezaei, M.; Moghaddam, M.A.; Azizyan, G.; Shamsipour, A.A. Prediction of agricultural drought index in a hot and dry climate using advanced hybrid machine learning. Ain Shams Eng. J. 2024, 15, 102686. [Google Scholar] [CrossRef]
- Oruc, S.; Hinis, M.A.; Tugrul, T. Evaluating performances of LSTM, SVM, GPR, and RF for drought prediction in Norway: A wavelet decomposition approach on regional forecasting. Water 2024, 16, 3465. [Google Scholar] [CrossRef]
- Oruc, S.; Tugrul, T.; Hinis, M.A. Beyond Traditional Metrics: Exploring the potential of Hybrid algorithms for Drought characterization and prediction in the Tromso Region, Norway. Appl. Sci. 2024, 14, 7813. [Google Scholar] [CrossRef]
- Rahmati, O.; Panahi, M.; Kalantari, Z.; Soltani, E.; Falah, F.; Dayal, K.S.; Mohammadi, F.; Deo, R.C.; Tiefenbacher, J.; Bui, D.T. Capability and robustness of novel hybridized models used for drought hazard modeling in southeast Queensland, Australia. Sci. Total Environ. 2020, 718, 134656. [Google Scholar] [PubMed]
- Chen, Y.; Hu, X.; Zhang, L. A review of ultra-short-term forecasting of wind power based on data decomposition-forecasting technology combination model. Energy Rep. 2022, 8, 14200–14219. [Google Scholar]
- Abdelhady, H.U.; Troy, C.D. A deep learning approach for modeling and hindcasting Lake Michigan ice cover. J. Hydrol. 2025, 649, 132445. [Google Scholar]
- Chambers, D.P. Evaluation of empirical mode decomposition for quantifying multi-decadal variations and acceleration in sea level records. Nonlinear Process. Geophys. 2015, 22, 157–166. [Google Scholar] [CrossRef]
- Ma, X.; Zhang, Y.; Wang, Y. Performance evaluation of kernel functions based on grid search for support vector regression. In Proceedings of the 2015 IEEE 7th International Conference on Cybernetics and Intelligent Systems (CIS) and IEEE Conference on Robotics, Automation and Mechatronics (RAM), Siem Reap, Cambodia, 15–17 July 2015; pp. 283–288. [Google Scholar]
- Coughlin, K.; Tung, K.K. Empirical mode decomposition and climate variability. In Hilbert-Huang Transform and Its Applications; World Scientific: Singapore, 2005; pp. 149–165. [Google Scholar]
- Sun, X.; Lin, Z. The regional features of temperature variation trends over China by empirical mode decomposition method. ACTA Geogr. Sin.-Chin. Ed. 2007, 62, 1132. [Google Scholar]
- Molla, M.K.I.; Rahman, M.S.; Sumi, A.; Banik, P. Empirical mode decomposition analysis of climate changes with special reference to rainfall data. Discret. Dyn. Nat. Soc. 2006, 2006, 045348. [Google Scholar] [CrossRef]
- Merabet, K.; Heddam, S. Improving the accuracy of air relative humidity prediction using hybrid machine learning based on empirical mode decomposition: A comparative study. Environ. Sci. Pollut. Res. 2023, 30, 60868–60889. [Google Scholar] [CrossRef]
- Bisoi, R.; Dash, P.K.; Parida, A.K. Hybrid variational mode decomposition and evolutionary robust kernel extreme learning machine for stock price and movement prediction on daily basis. Appl. Soft Comput. 2019, 74, 652–678. [Google Scholar] [CrossRef]
- Lahmiri, S. Comparing variational and empirical mode decomposition in forecasting day-ahead energy prices. IEEE Syst. J. 2015, 11, 1907–1910. [Google Scholar] [CrossRef]
- İlkentapar, M.; Citakoglu, H.; Talebi, H.; Aktürk, G.; Spor, P.; Çağlar, Y.; Akşit, S. Advanced hybrid machine learning methods for predicting rainfall time series: The situation at the Kütahya station in Türkiye. Model. Earth Syst. Environ. 2025, 11, 362. [Google Scholar] [CrossRef]
- Coşkun, Ö.; Citakoglu, H. Prediction of the standardized precipitation index based on the long short-term memory and empirical mode decomposition-extreme learning machine models: The Case of Sakarya, Türkiye. Phys. Chem. Earth Parts A/B/C 2023, 131, 103418. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013; 1535p. [Google Scholar]
- Stefanidis, K.; Varlas, G.; Papaioannou, G.; Papadopoulos, A.; Dimitriou, E. Trends of lake temperature, mixing depth and ice cover thickness of European lakes during the last four decades. Sci. Total Environ. 2022, 830, 154709. [Google Scholar] [PubMed]
- Jansen, J.; Simpson, G.L.; Weyhenmeyer, G.A.; Härkönen, L.H.; Paterson, A.M.; del Giorgio, P.A.; Prairie, Y.T. Climate-driven deoxygenation of northern lakes. Nat. Clim. Chang. 2024, 14, 832–838. [Google Scholar] [CrossRef]
- Baalsrud, K. The rehabilitation of Norway’s largest lake. Water Sci. Technol. 1982, 14, 21–30. [Google Scholar]
- Orderud, G.I.; Vogt, R.D. Trans-disciplinarity required in understanding, predicting and dealing with water eutrophication. Int. J. Sustain. Dev. World Ecol. 2013, 20, 404–415. [Google Scholar] [CrossRef][Green Version]
- Muñoz-Sabater, J.; Dutra, E.; Agustí-Panareda, A.; Albergel, C.; Arduini, G.; Balsamo, G.; Boussetta, S.; Choulga, M.; Harrigan, S.; Hersbach, H. ERA5-Land: A state-of-the-art global reanalysis dataset for land applications. Earth Syst. Sci. Data 2021, 13, 4349–4383. [Google Scholar][Green Version]
- Gumus, B.; Oruc, S.; Yucel, I.; Yilmaz, M.T. Impacts of climate change on extreme climate indices in Türkiye driven by high-resolution downscaled CMIP6 climate models. Sustainability 2023, 15, 7202. [Google Scholar] [CrossRef]
- Betts, A.K.; Reid, D.; Crossett, C. Evaluation of the FLake Model in ERA5 for Lake Champlain. Front. Environ. Sci. 2020, 8, 609254. [Google Scholar] [CrossRef]
- Balsamo, G.; Salgado, R.; Dutra, E.; Boussetta, S.; Stockdale, T.; Potes, M. On the contribution of lakes in predicting near-surface temperature in a global weather forecasting model. Tellus A Dyn. Meteorol. Oceanogr. 2012, 64, 15829. [Google Scholar][Green Version]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Xiao, C.; Sun, J. Recurrent neural networks (RNN). In Introduction to Deep Learning for Healthcare; Springer: Berlin/Heidelberg, Germany, 2021; pp. 111–135. [Google Scholar]
- Jiang, Q.; Tang, C.; Chen, C.; Wang, X.; Huang, Q. Stock price forecast based on LSTM neural network. In Proceedings of the International Conference on Management Science and Engineering Management, Melbourne, Australian, 1–4 August 2018; Springer: Berlin/Heidelberg, Germany, 2018; pp. 393–408. [Google Scholar]
- Agarwal, H.; Mahajan, G.; Shrotriya, A.; Shekhawat, D. Predictive data analysis: Leveraging RNN and LSTM techniques for time series dataset. Procedia Comput. Sci. 2024, 235, 979–989. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, W.; Zang, H.; Xu, D. Is the LSTM model better than RNN for flood forecasting tasks? A case study of Huayuankou station and Loude station in the lower Yellow River Basin. Water 2023, 15, 3928. [Google Scholar]
- Sumathy, R.; Sohail, S.F.; Ashraf, S.; Reddy, S.Y.; Fayaz, S.; Kumar, M. Next word prediction while typing using LSTM. In Proceedings of the 2023 8th International Conference on Communication and Electronics Systems (ICCES), Coimbatore, India, 1–3 June 2023; pp. 167–172. [Google Scholar]
- Karevan, Z.; Suykens, J.A. Spatio-temporal stacked LSTM for temperature prediction in weather forecasting. arXiv 2018, arXiv:1811.06341. [Google Scholar] [CrossRef]
- Jia, H.; Zhou, X. Water quality prediction method based on LSTM-BP. In Proceedings of the 2020 12th International Conference on Intelligent Human-Machine Systems and Cybernetics (IHMSC), Hangzhou, China, 22–23 August 2020; pp. 27–30. [Google Scholar]
- Wen, X.; Li, W. Time series prediction based on LSTM-attention-LSTM model. IEEE Access 2023, 11, 48322–48331. [Google Scholar]
- Sherstinsky, A. Fundamentals of recurrent neural network (RNN) and long short-term memory (LSTM) network. Phys. D Nonlinear Phenom. 2020, 404, 132306. [Google Scholar] [CrossRef]
- Zhang, Z. Customizing Kernels in Support Vector Machines; University of Waterloo: Waterloo, ON, Canada, 2007. [Google Scholar]
- Fathi Hafshejani, S.; Moaberfard, Z. A new trigonometric kernel function for support vector machine. Iran J. Comput. Sci. 2023, 6, 137–145. [Google Scholar]
- Lu, D.-G.; Li, G.-B. Reproducing kernel-based support vector machine for structural reliability analysis. In Proceedings of the 12th International Conference on Applications of Statistics and Probability in Civil Engineering, Vancouver, BC, Canada, 12–15 July 2015. [Google Scholar]
- Wang, W.; Xu, Z.; Lu, W.; Zhang, X. Determination of the spread parameter in the Gaussian kernel for classification and regression. Neurocomputing 2003, 55, 643–663. [Google Scholar] [CrossRef]
- Kusuma, M.; Kudus, A. Penerapan Metode Support Vector Regression (SVR) pada Data Survival KPR PT. Bank ABC, Tbk. Bdg. Conf. Ser. Stat. 2022, 2, 167–172. [Google Scholar] [CrossRef]
- Wang, S.; Deng, Z.; Chung, F.; Hu, W. From Gaussian kernel density estimation to kernel methods. Int. J. Mach. Learn. Cyber. 2013, 4, 119–137. [Google Scholar] [CrossRef]
- Schulz, E.; Speekenbrink, M.; Krause, A. A tutorial on Gaussian process regression: Modelling, exploring, and exploiting functions. J. Math. Psychol. 2018, 85, 1–16. [Google Scholar] [CrossRef]
- Niu, T.; Xu, Z.; Luo, H.; Zhou, Z. Hybrid Gaussian process regression with temporal feature extraction for partially interpretable remaining useful life interval prediction in Aeroengine prognostics. Sci. Rep. 2025, 15, 11057. [Google Scholar] [CrossRef]
- Cutajar, K. Broadening the Scope of Gaussian Processes for Large-Scale Learning; Sorbonne Université: Jussieu, Paris, 2019. [Google Scholar]
- Sun, A.Y.; Wang, D.; Xu, X. Monthly streamflow forecasting using Gaussian process regression. J. Hydrol. 2014, 511, 72–81. [Google Scholar] [CrossRef]
- Chang, C.; Zeng, T. A hybrid data-driven-physics-constrained Gaussian process regression framework with deep kernel for uncertainty quantification. J. Comput. Phys. 2023, 486, 112129. [Google Scholar] [CrossRef]
- Zhao, S.; Lu, J.; Yang, J.; Chow, E.; Xi, Y. Efficient two-stage gaussian process regression via automatic kernel search and subsampling. arXiv 2024, arXiv:2405.13785. [Google Scholar] [CrossRef]
- Hong, S.; Zhou, Z. Remaining useful life prognosis of bearing based on Gauss process regression. In Proceedings of the 2012 5th International Conference on BioMedical Engineering and Informatics, Chongqing, China, 16–18 October 2012; pp. 1575–1579. [Google Scholar]
- Übeylı, E.D.; Güler, I. Multilayer perceptron neural networks to compute quasistatic parameters of asymmetric coplanar waveguides. Neurocomputing 2004, 62, 349–365. [Google Scholar] [CrossRef]
- Mishra, S.; Prusty, R.; Hota, P.K. Analysis of Levenberg-Marquardt and Scaled Conjugate gradient training algorithms for artificial neural network based LS and MMSE estimated channel equalizers. In Proceedings of the 2015 International Conference on Man and Machine Interfacing (MAMI), Bhubaneswar, India, 17–19 December 2015; pp. 1–7. [Google Scholar]
- Kim, S.; Singh, V. Spatial Disaggregation of Areal Rainfall Using Two Different Artificial Neural Networks Models. Water 2015, 7, 2707–2727. [Google Scholar] [CrossRef]
- El Chaal, R.; Aboutafail, M.O. A comparative study of back-propagation algorithms: Levenberg-Marquart and BFGS for the formation of multilayer neural networks for estimation of fluoride. Commun. Math. Biol. Neurosci. 2022, 2022, 37. [Google Scholar]
- Hashim, F.R.; Daud, N.N.; Mokhtar, A.S.; Rashidi, A.F.; Ahmad, K. Optimization of ECG Peaks (Amplitude and Duration) in Predicting ECG Abnormality using Artificial Neural Network. Indian J. Sci. Technol. 2017, 10, 1–5. [Google Scholar] [CrossRef][Green Version]
- Moness, M.; Diaa-Eldeen, T. Experimental nonlinear identification of a lab-scale helicopter system using MLP neural network. In Proceedings of the 2017 13th International Computer Engineering Conference (ICENCO), Cairo, Egypt, 27–28 December 2017; pp. 166–171. [Google Scholar]
- Nawi, N.M.; Khan, A.; Rehman, M.Z.; Aziz, M.A.; Herawan, T.; Abawajy, J.H. An Accelerated Particle Swarm Optimization Based Levenberg Marquardt Back Propagation Algorithm; Springer International Publishing: Cham, Switzerland, 2014; pp. 245–253. [Google Scholar]
- Kim, T.-W.; Valdés, J.B. Nonlinear model for drought forecasting based on a conjunction of wavelet transforms and neural networks. J. Hydrol. Eng. 2003, 8, 319–328. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. In Machine learning; Springer: Berlin/Heidelberg, Germany, 2001; Volume 45, pp. 5–32. [Google Scholar]
- En-Nagre, K.; Aqnouy, M.; Ouarka, A.; Naqvi, S.A.A.; Bouizrou, I.; El Messari, J.E.S.; Tariq, A.; Soufan, W.; Li, W.; El-Askary, H. Assessment and prediction of meteorological drought using machine learning algorithms and climate data. Clim. Risk Manag. 2024, 45, 100630. [Google Scholar] [CrossRef]
- Shang, K.; Xu, L.; Liu, X.; Yin, Z.; Liu, Z.; Li, X.; Yin, L.; Zheng, W. Study of urban heat island effect in Hangzhou metropolitan area based on SW-TES algorithm and image dichotomous model. Sage Open 2023, 13, 21582440231208851. [Google Scholar] [CrossRef]
- Choi, C.; Kim, J.; Han, H.; Han, D.; Kim, H.S. Development of water level prediction models using machine learning in wetlands: A case study of Upo wetland in South Korea. Water 2019, 12, 93. [Google Scholar] [CrossRef]
- Biau, G.; Scornet, E. A random forest guided tour. Test 2016, 25, 197–227. [Google Scholar] [CrossRef]
- Yu, P.-S.; Yang, T.-C.; Chen, S.-Y.; Kuo, C.-M.; Tseng, H.-W. Comparison of random forests and support vector machine for real-time radar-derived rainfall forecasting. J. Hydrol. 2017, 552, 92–104. [Google Scholar] [CrossRef]
- Tyralis, H.; Papacharalampous, G.; Langousis, A. A brief review of random forests for water scientists and practitioners and their recent history in water resources. Water 2019, 11, 910. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational mode decomposition. IEEE Trans. Signal Process. 2013, 62, 531–544. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, F.; Jiang, Z.; He, S.; Mo, Q. Complex variational mode decomposition for signal processing applications. Mech. Syst. Signal Process. 2017, 86, 75–85. [Google Scholar] [CrossRef]
- Danandeh Mehr, A.; Reihanifar, M.; Alee, M.M.; Vazifehkhah Ghaffari, M.A.; Safari, M.J.S.; Mohammadi, B. VMD-GP: A new evolutionary explicit model for meteorological drought prediction at ungauged catchments. Water 2023, 15, 2686. [Google Scholar] [CrossRef]
- Maji, U.; Pal, S. Empirical mode decomposition vs. variational mode decomposition on ECG signal processing: A comparative study. In Proceedings of the 2016 International Conference on Advances in Computing, Communications and Informatics (ICACCI), Jaipur, India, 21–24 September 2016; pp. 1129–1134. [Google Scholar]
- Wang, Y.; Markert, R. Filter bank property of variational mode decomposition and its applications. Signal Process. 2016, 120, 509–521. [Google Scholar] [CrossRef]
- Fortin, M.; Glowinski, R. Augmented Lagrangian Methods: Applications to the Numerical Solution of Boundary-Value Problems; Elsevier: Amsterdam, The Netherlands, 2000; Volume 15. [Google Scholar]
- Giesen, J.; Laue, S. Combining ADMM and the Augmented Lagrangian Method for Efficiently Handling Many Constraints. In Proceedings of the IJCAI, Macao, Chian, 10–16 August 2019; pp. 4525–4531. [Google Scholar]
- Mutinda, J.K.; Langat, A.K.; Mwalili, S.M. Forecasting Temperature Time Series Data Using Combined Statistical and Deep Learning Methods: A Case Study of Nairobi County Daily Temperature. Int. J. Math. Math. Sci. 2025, 2025, 4795841. [Google Scholar] [CrossRef]
- Liu, J.; Wang, K.; Zhao, M.; Chen, Y.; Li, X. Enhanced concrete crack detection using nonlinear ultrasonic signal denoising and feature enhancement with CEEMDAN, VMD and GRU. Meas. Sci. Technol. 2024, 36, 016164. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. London. Ser. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Flandrin, P.; Rilling, G.; Goncalves, P. Empirical mode decomposition as a filter bank. IEEE Signal Process. Lett. 2004, 11, 112–114. [Google Scholar] [CrossRef]
- ur Rehman, N.; Mandic, D.P. Empirical mode decomposition for trivariate signals. IEEE Trans. Signal Process. 2009, 58, 1059–1068. [Google Scholar] [CrossRef]
- Sarangi, S.; Biswal, C.; Sahu, B.K.; Samanta, I.S.; Rout, P.K. Fault detection technique using time-varying filter-EMD and differential-CUSUM for LVDC microgrid system. Electr. Power Syst. Res. 2023, 219, 109254. [Google Scholar]
- Calvo, M.S.; Lee, H.S. Enhanced complete ensemble EMD with superior noise handling capabilities: A robust signal decomposition method for power systems analysis. Eng. Rep. 2024, 6, e12862. [Google Scholar] [CrossRef]
- Rilling, G.; Flandrin, P.; Goncalves, P. On empirical mode decomposition and its algorithms. In Proceedings of the IEEE-EURASIP Workshop on Nonlinear Signal and Image Processing NSIP-03, Grado, Italy, 8–11 June 2003. [Google Scholar]
- Barnhart, B.; Eichinger, W. Empirical mode decomposition applied to solar irradiance, global temperature, sunspot number, and CO2 concentration data. J. Atmos. Sol.-Terr. Phys. 2011, 73, 1771–1779. [Google Scholar] [CrossRef]
- Wang, J.; Du, G.; Zhu, Z.; Shen, C.; He, Q. Fault diagnosis of rotating machines based on the EMD manifold. Mech. Syst. Signal Process. 2020, 135, 106443. [Google Scholar] [CrossRef]
- Zeiler, A.; Faltermeier, R.; Keck, I.R.; Tomé, A.M.; Puntonet, C.G.; Lang, E.W. Empirical mode decomposition-an introduction. In Proceedings of the 2010 International Joint Conference on Neural Networks (IJCNN), Barcelona, Spain, 18–23 July 2010; pp. 1–8. [Google Scholar]
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Randall, R.B.; Antoni, J. Why EMD and similar decompositions are of little benefit for bearing diagnostics. Mech. Syst. Signal Process. 2023, 192, 110207. [Google Scholar] [CrossRef]
- Looney, D.; Mandic, D.P. Emperical mode decompoaition for simultateous image enhancement and fusion. In Image Fusion Algorithms and Applications; Imperial College: London, UK, 2008; pp. 327–339. [Google Scholar]
- Zheng, D.; Zhang, W.; Alemu, S.; Wang, P.; Bitew, G.; Wei, D.; Yue, J. Short-term renewable generation and load forecasting in microgrids. In Microgrid Protection and Control; Elsevier: Amsterdam, The Netherlands, 2021; pp. 57–96. [Google Scholar] [CrossRef]
- Khan, M.M.H.; Muhammad, N.S.; El-Shafie, A. Wavelet based hybrid ANN-ARIMA models for meteorological drought forecasting. J. Hydrol. 2020, 590, 125380. [Google Scholar] [CrossRef]
- Zhang, D. A Coefficient of Determination for Generalized Linear Models. Am. Stat. 2017, 71, 310–316. [Google Scholar] [CrossRef]
- Ehteram, M.; Ahmed, A.N.; Ling, L.; Fai, C.M.; Latif, S.D.; Afan, H.A.; Banadkooki, F.B.; El-Shafie, A. Pipeline scour rates prediction-based model utilizing a multilayer perceptron-colliding body algorithm. Water 2020, 12, 902. [Google Scholar] [CrossRef]
- Zhu, S.; Ptak, M.; Yaseen, Z.M.; Dai, J.; Sivakumar, B. Forecasting surface water temperature in lakes: A comparison of approaches. J. Hydrol. 2020, 585, 124809. [Google Scholar] [CrossRef]
- Feigl, M.; Lebiedzinski, K.; Herrnegger, M.; Schulz, K. Machine-learning methods for stream water temperature prediction. Hydrol. Earth Syst. Sci. 2021, 25, 2951–2977. [Google Scholar] [CrossRef]
- Tuğrul, T.; Hinis, M.A. Performance enhancement of models through discrete wavelet transform for streamflow forecasting in Çarşamba River, Türkiye. J. Water Clim. Chang. 2025, 16, 736–756. [Google Scholar] [CrossRef]
- Tuğrul, T.; Hinis, M.A. Improvement of drought forecasting by means of various machine learning algorithms and wavelet transformation. Acta Geophys. 2025, 73, 855–874. [Google Scholar] [CrossRef]
- Tuğrul, T.; Hınıs, M.A.; Oruç, S. Comparison of LSTM and SVM methods through wavelet decomposition in drought forecasting. Earth Sci. Inform. 2025, 18, 139. [Google Scholar] [CrossRef]
- Chen, L.; Wang, L.; Ma, W.; Xu, X.; Wang, H. PID4LaTe: A physics-informed deep learning model for lake multi-depth temperature prediction. Earth Sci. Inform. 2024, 17, 3779–3795. [Google Scholar] [CrossRef]
- Citakoglu, H.; Aktürk, G.; Demir, V. Hybrid machine learning for drought prediction at multiple time scales: A case study of Ağrı station, Türkiye. Acta Geophys. 2025, 73, 1643–1677. [Google Scholar] [CrossRef]
- Citakoglu, H.; Coşkun, Ö. Comparison of hybrid machine learning methods for the prediction of short-term meteorological droughts of Sakarya Meteorological Station in Turkey. Environ. Sci. Pollut. Res. 2022, 29, 75487–75511. [Google Scholar] [CrossRef] [PubMed]
- Tong, Y.; Feng, L.; Wang, X.; Pi, X.; Xu, W.; Woolway, R.I. Global lakes are warming slower than surface air temperature due to accelerated evaporation. Nat. Water 2023, 1, 929–940. [Google Scholar] [CrossRef]
- Bachmann, R.W.; Canfield, D.E., Jr.; Sharma, S.; Lecours, V. Warming of near-surface summer water temperatures in lakes of the conterminous United States. Water 2020, 12, 3381. [Google Scholar] [CrossRef]





| 1950–2024 | Number of Data | Mean | Standard Deviation | Min. | Max. |
|---|---|---|---|---|---|
| Training data 70% | 630 | 4.29 | 0.60 | 2.63 | 5.75 |
| Test data 30% | 270 | 4.41 | 0.69 | 2.58 | 5.83 |
| Model | Inputs | Output | ||||||
|---|---|---|---|---|---|---|---|---|
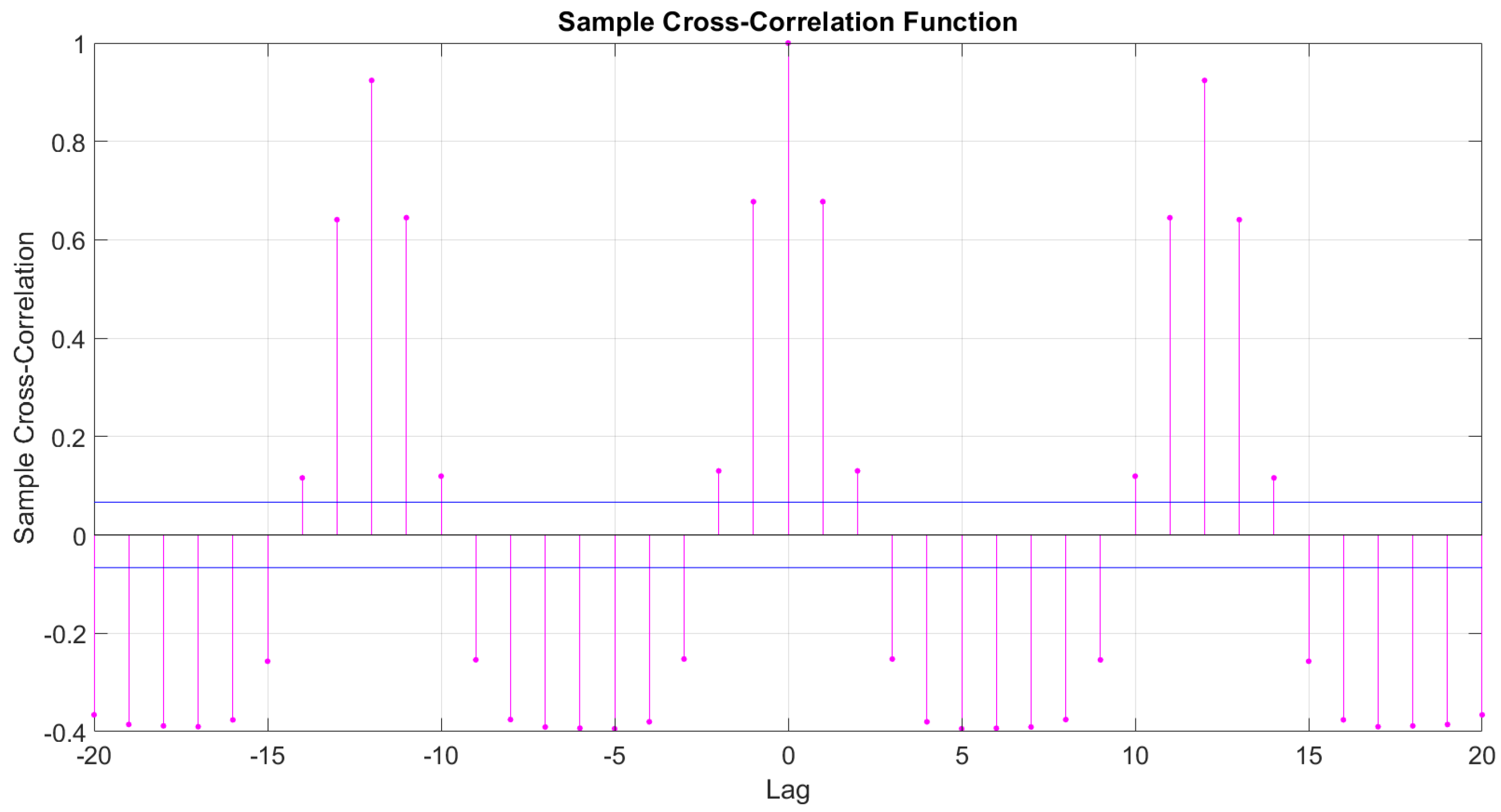
| M01 | t − 13 | t − 11 | t − 1 | t − 12 | t | |||
| M02 | t − 2 | t − 13 | t − 11 | t − 1 | t − 12 | t | ||
| M03 | t − 9 | t − 2 | t − 13 | t − 11 | t − 1 | t − 12 | t | |
| M04 | t − 7 | t − 6 | t − 5 | t − 4 | t − 3 | t − 2 | t − 1 | t |
| SVM | GPR | ||||||||||||
| r | NSE | KGE | PI | RSR | RMSE | r | NSE | KGE | PI | RSR | RMSE | ||
| M01 | 0.9532 | 0.9073 | 0.9507 | 0.0248 | 0.3038 | 0.2133 | M01 | 0.9439 | 0.8793 | 0.8621 | 0.0284 | 0.3468 | 0.2435 |
| M02 | 0.9547 | 0.9110 | 0.9462 | 0.0243 | 0.2978 | 0.2091 | M02 | 0.9617 | 0.9103 | 0.8769 | 0.0243 | 0.2990 | 0.2099 |
| M03 | 0.9546 | 0.9109 | 0.9470 | 0.0243 | 0.2980 | 0.2092 | M03 | 0.9662 | 0.9186 | 0.8786 | 0.0231 | 0.2848 | 0.2000 |
| M04 | 0.9143 | 0.8140 | 0.9120 | 0.0358 | 0.4304 | 0.3022 | M04 | 0.9617 | 0.9109 | 0.9158 | 0.0242 | 0.2980 | 0.2092 |
| SVM-EMD | GPR-EMD | ||||||||||||
| r | NSE | KGE | PI | RSR | RMSE | r | NSE | KGE | PI | RSR | RMSE | ||
| M01 | 0.9367 | 0.8637 | 0.9328 | 0.0303 | 0.3685 | 0.2587 | M01 | 0.9415 | 0.8669 | 0.8462 | 0.0299 | 0.3642 | 0.2557 |
| M02 | 0.9173 | 0.8243 | 0.9148 | 0.0348 | 0.4184 | 0.2938 | M02 | 0.9273 | 0.8438 | 0.8364 | 0.0326 | 0.3945 | 0.2770 |
| M03 | 0.9392 | 0.8602 | 0.9349 | 0.0307 | 0.3732 | 0.2620 | M03 | 0.9276 | 0.8443 | 0.8496 | 0.0326 | 0.3938 | 0.2765 |
| M04 | 0.9029 | 0.7909 | 0.8939 | 0.0382 | 0.4565 | 0.3205 | M04 | 0.9349 | 0.8571 | 0.9037 | 0.0311 | 0.3773 | 0.2649 |
| SVM-VMD | GPR-VMD | ||||||||||||
| r | NSE | KGE | PI | RSR | RMSE | r | NSE | KGE | PI | RSR | RMSE | ||
| M01 | 0.9733 | 0.9472 | 0.9574 | 0.0185 | 0.2293 | 0.1610 | M01 | 0.9608 | 0.9210 | 0.9448 | 0.0228 | 0.2806 | 0.1970 |
| M02 | 0.9856 | 0.9709 | 0.9757 | 0.0137 | 0.1703 | 0.1195 | M02 | 0.9857 | 0.9710 | 0.9710 | 0.0136 | 0.1700 | 0.1193 |
| M03 | 0.9859 | 0.9717 | 0.9755 | 0.0135 | 0.1679 | 0.1179 | M03 | 0.9858 | 0.9709 | 0.9624 | 0.0137 | 0.1702 | 0.1195 |
| M04 | 0.9855 | 0.9708 | 0.9723 | 0.0137 | 0.1707 | 0.1198 | M04 | 0.9814 | 0.9613 | 0.9751 | 0.0158 | 0.1962 | 0.1378 |
| LSTM | MLP | ||||||||||||
| r | NSE | KGE | PI | RSR | RMSE | r | NSE | KGE | PI | RSR | RMSE | ||
| M01 | 0.9231 | 0.8380 | 0.8622 | 0.0333 | 0.3958 | 0.4018 | M01 | 0.9105 | 0.8171 | 0.9083 | 0.0356 | 0.4268 | 0.2997 |
| M02 | 0.9530 | 0.8992 | 0.9256 | 0.0259 | 0.3111 | 0.3168 | M02 | 0.8937 | 0.7941 | 0.8834 | 0.0381 | 0.4529 | 0.3180 |
| M03 | 0.9515 | 0.9050 | 0.9187 | 0.0251 | 0.312 | 0.3079 | M03 | 0.9502 | 0.8900 | 0.9387 | 0.0271 | 0.3310 | 0.2324 |
| M04 | 0.9436 | 0.8522 | 0.8231 | 0.0315 | 0.3542 | 0.3837 | M04 | 0.9579 | 0.9058 | 0.9399 | 0.0249 | 0.3063 | 0.2151 |
| LSTM-EMD | MLP-EMD | ||||||||||||
| r | NSE | KGE | PI | RSR | RMSE | r | NSE | KGE | PI | RSR | RMSE | ||
| M01 | 0.9528 | 0.8914 | 0.9369 | 0.0269 | 0.3100 | 0.3289 | M01 | 0.8518 | 0.6279 | 0.8222 | 0.0524 | 0.6088 | 0.4275 |
| M02 | 0.9508 | 0.8804 | 0.9061 | 0.0282 | 0.3278 | 0.3452 | M02 | 0.5323 | -0.7901 | 0.2685 | 0.1389 | 1.3354 | 0.9377 |
| M03 | 0.9562 | 0.9008 | 0.9315 | 0.0256 | 0.2978 | 0.3143 | M03 | 0.8379 | 0.5976 | 0.7719 | 0.0549 | 0.6332 | 0.4446 |
| M04 | 0.7994 | 0.5884 | 0.7959 | 0.0567 | 0.8754 | 0.6403 | M04 | 0.7831 | -0.0041 | 0.4058 | 0.0894 | 1.0002 | 0.7023 |
| LSTM-VMD | MLP-VMD | ||||||||||||
| r | NSE | KGE | PI | RSR | RMSE | r | NSE | KGE | PI | RSR | RMSE | ||
| M01 | 0.9636 | 0.9091 | 0.9318 | 0.0244 | 0.313 | 0.3009 | M01 | 0.9223 | 0.8313 | 0.9190 | 0.0340 | 0.4099 | 0.2878 |
| M02 | 0.9489 | 0.8684 | 0.9291 | 0.0296 | 0.3854 | 0.3619 | M02 | 0.9653 | 0.9256 | 0.9628 | 0.0221 | 0.2723 | 0.1912 |
| M03 | 0.9593 | 0.8864 | 0.9201 | 0.0274 | 0.3342 | 0.3365 | M03 | 0.8676 | 0.7050 | 0.8443 | 0.0463 | 0.5421 | 0.3806 |
| M04 | 0.9681 | 0.9234 | 0.9412 | 0.0224 | 0.2772 | 0.2762 | M04 | 0.9469 | 0.8825 | 0.9270 | 0.0280 | 0.3422 | 0.2403 |
| RF | |||||||||||||
| r | NSE | KGE | PI | RSR | RMSE | ||||||||
| M01 | 0.9523 | 0.8982 | 0.8633 | 0.0260 | 0.3184 | 0.2236 | |||||||
| M02 | 0.9561 | 0.9023 | 0.8611 | 0.0254 | 0.312 | 0.2191 | |||||||
| M03 | 0.9549 | 0.8965 | 0.8452 | 0.0262 | 0.3211 | 0.2254 | |||||||
| M04 | 0.9572 | 0.8768 | 0.8421 | 0.0285 | 0.3504 | 0.2460 | |||||||
| RF-EMD | |||||||||||||
| r | NSE | KGE | PI | RSR | RMSE | ||||||||
| M01 | 0.9336 | 0.8282 | 0.7393 | 0.0341 | 0.414 | 0.2905 | |||||||
| M02 | 0.9365 | 0.8257 | 0.7232 | 0.0343 | 0.4167 | 0.2926 | |||||||
| M03 | 0.9328 | 0.8150 | 0.7164 | 0.0354 | 0.4293 | 0.3015 | |||||||
| M04 | 0.8926 | 0.7367 | 0.6623 | 0.0431 | 0.5122 | 0.3596 | |||||||
| RF-VMD | |||||||||||||
| r | NSE | KGE | PI | RSR | RMSE | ||||||||
| M01 | 0.9617 | 0.9060 | 0.8574 | 0.0249 | 0.3060 | 0.2148 | |||||||
| M02 | 0.9642 | 0.9125 | 0.8586 | 0.0240 | 0.2952 | 0.2073 | |||||||
| M03 | 0.9647 | 0.9114 | 0.8561 | 0.0241 | 0.2972 | 0.2087 | |||||||
| M04 | 0.9693 | 0.9257 | 0.8873 | 0.0220 | 0.2720 | 0.1910 | |||||||
| LSTM | MLP | RF | GPR | SVM | |
|---|---|---|---|---|---|
| Model nodes | 2 | - | - | - | - |
| Epoch | 25–35–45 | - | - | - | - |
| Interpolate method | linear | - | - | - | - |
| Optimizer | ADAM | - | - | Bayesian | - |
| Learning rate | 0.05 | - | - | - | - |
| Activation | - | Relu | - | - | - |
| Solver | - | Adam | - | - | - |
| Lambda | - | 0.0001 | - | - | - |
| Alpha | - | Constant | - | - | - |
| Hidden layer | - | 1 to 4 | - | - | - |
| Trees | - | - | 150 | - | - |
| Nodes | - | - | 6 | - | - |
| Features | - | - | sqrt | - | - |
| Depth | - | - | 6 | - | - |
| Criterion Func. | - | - | Gini | - | - |
| Decision Func. | - | - | - | - | 1-and-1 |
| Kernel Func. | - | - | - | - | rbf |
| Kernel coefficient | - | - | - | - | 0.001–1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oruc, S.; Hınıs, M.A.; Selek, Z.; Tuğrul, T. Deep Signals: Enhancing Bottom Temperature Predictions in Norway’s Mjøsa Lake Through VMD- and EMD-Boosted Machine Learning Models. Water 2025, 17, 2673. https://doi.org/10.3390/w17182673
Oruc S, Hınıs MA, Selek Z, Tuğrul T. Deep Signals: Enhancing Bottom Temperature Predictions in Norway’s Mjøsa Lake Through VMD- and EMD-Boosted Machine Learning Models. Water. 2025; 17(18):2673. https://doi.org/10.3390/w17182673
Chicago/Turabian StyleOruc, Sertac, Mehmet Ali Hınıs, Zeliha Selek, and Türker Tuğrul. 2025. "Deep Signals: Enhancing Bottom Temperature Predictions in Norway’s Mjøsa Lake Through VMD- and EMD-Boosted Machine Learning Models" Water 17, no. 18: 2673. https://doi.org/10.3390/w17182673
APA StyleOruc, S., Hınıs, M. A., Selek, Z., & Tuğrul, T. (2025). Deep Signals: Enhancing Bottom Temperature Predictions in Norway’s Mjøsa Lake Through VMD- and EMD-Boosted Machine Learning Models. Water, 17(18), 2673. https://doi.org/10.3390/w17182673










