Abstract
In this study, we benchmark various machine learning techniques against a synthetic but physically based reference time series (model-simulated (ERA5-Land/FLake) bottom-temperature series) and assess whether decomposition methods (VMD and EMD) improve forecast accuracy using Support Vector Machine (SVM), Multi-Layer Perceptron (MLP), Random Forest (RF), Gaussian Process Regression (GPR), and Long Short-Term Memory (LSTM) with the monthly average data of Mjøsa, the largest lake in Norway, between 1950 and 2024 from the ERA5-Land FLake model. A total of 70% of the dataset was used for training and 30% was reserved for testing. To assess the performance several metrics, correlation coefficient (r), Nash–Sutcliffe efficiency (NSE), Kling–Gupta efficiency (KGE), Performance Index (PI), RMSE-based RSR, and Root Mean Square Error (RMSE) were used. The results revealed that without decomposition, the GPR-M03 combination outperforms other models (with scores r = 0.9662, NSE = 0.9186, KGE = 0.8786, PI = 0.0231, RSR = 0.2848, and RMSE = 0.2000). Considering decomposition cases, when VMD is applied, the SVM-VMD-M03 combination achieved better results compared to other models (with scores r = 0.9859, NSE = 0.9717, KGE = 0.9755, PI = 0.0135, RSR = 0.1679, and RMSE = 0.1179). Conversely, with decomposition cases, when EMD applied, LSTM-EMD-M03 is explored as the more effective combination than others (with scores r = 0.9562, NSE = 0.9008, KGE = 0.9315, PI = 0.0256, RSR = 0.2978, and RMSE = 0.3143). The results demonstrate that GPR and SVM, coupled with VMD, yield high correlation (e.g., r ≈ 0.986) and low RMSE (~0.12), indicating the ability to reproduce FLake dynamics rather than as accurate predictions of measured bottom temperature.
1. Introduction
Research over the past decade confirms that rising air temperatures are reflected in higher water temperatures—not only at the surface but throughout the water column in lakes and in many terrestrial and marine environments [1,2,3]. Lakes, in particular, stand out because they are part of the global water cycle: they buffer streamflow, harbor biodiversity, influence drinking-water supply, and underpin a range of ecosystem services [3,4]. Broadly speaking, lake waters have been warming faster than the overlying atmosphere and even the oceans [5,6,7], a pattern already noted in our Norwegian data and projected to strengthen under most climate scenarios [8]. The ecological stakes are high because accelerated warming threatens both the quantity and the quality of what is arguably one of the planet’s most critical freshwater reserves [6,8,9,10], placing added pressure on lakes’ ability to support fisheries, recreation, and potable-water demands worldwide.
Despite this global warming trend, surface-water temperatures do not increase at the same rate and are not consistent with those of deep-water lake temperatures. For example, as Noori et al. [8] reported in their study, O’Reilly et al. [5] revealed a significant global mean surface warming rate of 0.34 °C per decade, while Pilla et al. [6] noted that globally, lake surface water temperatures are warming more rapidly than air temperatures. However, changes in deepwater temperatures and vertical thermal structure remain poorly understood [6,11,12]. This divergence between the surface and deepwater thermal regimes is intensifying both strength and duration of thermal stratification in lakes [8,13,14]. Supporting these, Råman Vinnå et al. [15] also indicate that although surface temperature increases are projected across all lakes, projected changes in other thermal properties, such as bottom water temperatures, stratification patterns as well as ice cover, more strongly depend on lake specific characteristics such as lake volume and altitude.
Lake bottom temperatures are particularly important since they have a direct relation with lake physics (stratification and mixing), oxygen dynamics (O2), nutrient cycling, aquatic habitat and biota, climate change indicator, greenhouse gas emissions (CH4). For instance, the thermal structure of a lake manages the water density variations which impacts the stratification levels. In a warming climate, this thermal structure can be intensified, and the mixing regimes of the lake can be altered [16,17,18]. Moreover, lake bottom water temperatures also affect the oxygen solubility, warmer bottom temperatures can lead to faster depletion of the dissolved oxygen [19,20,21,22] which is also a threat considering the future climate change scenarios as Butcher et al. [1] stated. Studies, such as those by Zhang et al. [18], Bonacina et al. [23], North et al. [24], have noticed that intensified or prolonged stratification, linked to warming, potentially contribute to eutrophication because of increased primary production. In addition, temperature is a fundamental variable governing the distribution, physiology, and life cycles of aquatic species. Bottom temperatures are crucial for aquatic organisms who live on or in the bottom substrate of a water body and serve as a thermal refuge for cold-water fish species [20,23,25] and increasing bottom temperatures can damage the habitat and leads to change in the community structure of the cold-water species. It is also mentioned that lakes integrate climatic changes, making them effective “sentinels” [26], although surface temperature increases are extensively documented, alterations in the complete thermal structure, encompassing bottom temperatures and stratification patterns, are critical physical indicators of climate change effects [16,17]. All these alterations in lake water temperature and thermal stratification influence lake ecosystem dynamics as mentioned above [27] which signals the need to incorporate climate impacts into vulnerability assessments and adaptation efforts for lakes and are essential for understanding lake ecosystem responses to climate change [5,11]. On the other hand, studies focused on lake bottom temperature predictions are limited to the best of our knowledge. The literature mainly focuses on surface temperature and other characteristics of lakes rather than bottom temperatures (Figure 1).
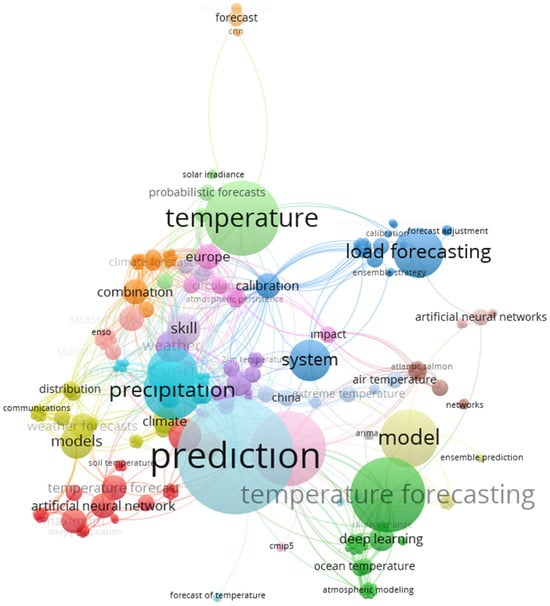
Figure 1.
Topics studied related to temperature.
Exploring the dynamics of water temperature is highly beneficial for understanding the past and current states of lakes and forecasting the possible trajectories lakes may take in the future. Machine learning (ML) and deep learning (DL) models are recognized as powerful techniques for obtaining more accurate, region-specific climate predictions by employing observed data and modifying the predictability of climate systems. These approaches have gained widespread application across different scientific fields which is triggered by the growing availability of big data. Considering lake water temperature prediction, access to large datasets has also enhanced the effectiveness of ML models, contributing to monitoring and management of ecosystems [25,28,29,30]. A wide range of ML techniques are now commonly used in predictive modeling frameworks. Adaptive neuro-fuzzy inference systems (ANFIS), artificial neural networks (ANN), random forests (RF), long short-term memory networks (LSTM), Gaussian process regression (GPR), and support vector machines (SVM) can be examples of those techniques [31,32,33]. These models are particularly well-suited for climate-related research, since large, high-dimensional datasets with nonlinear relationships and missing or noisy data arise in this field. As such, ML and DL based methods have proved their capabilities in addressing complex problems in environmental monitoring and natural hazard forecasting, such as ice cover prediction, lake temperature forecasting, estimating the lake depth values, or drought forecasting [29,34,35,36].
Furthermore, there are widely used techniques for analyzing non-stationary climate time series, isolating trends, and improving prediction models for extreme climate phenomena. For instance, Empirical Mode Decomposition (EMD) and Variational Mode Decomposition (VMD) have emerged as effective analytical methods for interpreting complex environmental and climatic data. EMD has been widely used to analyze nonlinear, non-stationary climate and environmental time series, expose patterns like multi-decadal trends, regional climate variability, and extreme events such as heatwaves, floods, and sea-level rise. However, when extracting long-term trends, studies present that EMD can also introduce some distortions which lead to use it with caution for precise prediction tasks. Variational Mode Decomposition (VMD), a newer method, has shown outperforming outcomes compared to EMD in forecasting tasks (like energy prices and stock trends). By offering more stable and accurate signal decomposition, VMD increasingly favored extreme event prediction and complex time series modeling application.
On the other hand, each method may have its own advantages and weaknesses. Chambers [37] noted the limitations of EMD, particularly its challenges in accurately identifying multi-decadal variability and the distortions in sea-level acceleration estimates in records. However, despite these limitations, EMD has also exhibited successful performance in discovering patterns, such as distinct high-temperature variability and oscillations in Shanghai over a 50-year period [38], and interannual climate variability from atmospheric data [39]. EMD was further utilized by Sun and Lin [40] to identify region-specific warming and cooling trends across China, underscoring the spatial complexities of climate change. Similarly, Molla et al. [41] demonstrated EMD’s utility in revealing intrinsic scales of rainfall variability, linking global warming with increased occurrences of extreme weather events such as droughts, floods, and heatwaves. Recent developments also show enhanced predictive capabilities when combining these decomposition methods with machine learning; Merabet and Heddam [42] illustrated significant accuracy improvements in forecasting relative humidity when using EMD or VMD alongside machine learning models. In comparative analyses, Bisoi et al. [43] found VMD superior to EMD for daily stock price prediction, while Lahmiri [44] confirmed VMD-based neural network ensembles outperformed EMD-based models in accurately forecasting energy prices, emphasizing VMD’s strength in managing complex nonlinear signals. In addition to studies in the literature, hybrid models, or data preprocessing methods, are frequently used to improve model results. These methods generally yield highly effective results in forecasting meteorological data. Many researchers have reported these results in their studies. For instance, İlkentapar et al. [45] developed forecasting models, including VMD and EMD, for the Kütahya region’s rainfall forecast. They used three different machine learning techniques in their own study. Their results indicated the positive impact of data preprocessing applications on the model results. Another study related to data preprocessing is Coşkun and Citakoglu [46]. Their study investigated model performance in predicting drought indices. Their study utilized machine learning techniques such as LSTM and ELM, which both VMD and EMD utilize. They chose the standardized drought index (SPI) as drought index. The results indicate that VMD yields better results. Generally, two or three machine learning methods are utilized in the literature. Data preprocessing methods have also been applied to these methods. However, it appears that the number of machine learning methods used is insufficient. Furthermore, new drought index methods have not attracted much attention from researchers. SPI is traditionally used. The key innovations in this study are the estimation of an unusual parameter and the large number of machine learning methods used. Furthermore, RF and MLP are rarely used with hybrid methods. This study investigates the performance of these algorithms with hybrid methods. Moreover, studies using such methods to determine lake temperatures have rarely been conducted before. In general studies on lake temperature focus on surface or mixed-layer and only a few studies have applied machine learning to forecast modeled bottom temperatures. There is also a need to explore whether signal decomposition techniques improve such forecasts, which constitutes one of the innovative methodological perspectives of this study.
The lakes in Northern Europe and high-latitude freshwater lakes experience the most rapid increase in surface air temperature [8,47,48,49] and significant changes in ice phenology, which influence lake thermal stratification and extend the duration of lake warming [2]. As Norwegian lakes also face shifting thermal regimes, continuous research and monitoring will be essential for effective lake management in a warming climate. The aim of this study is to evaluate and compare the performance of five machine learning models and signal processing techniques, LSTM, SVM, GPR, RF, and MLP, each integrated with Variational Mode Decomposition (VMD) and Empirical Mode Decomposition (EMD) for predicting lake bottom temperatures in one of the biggest lake, Mjøsa, of Norway. By assessing the strengths and limitations of each method, the objective is to improve the accuracy and reliability of lake bottom temperature predictions, thereby supporting water resource management, lake ecosystem monitoring, risk assessment, and ecological conservation efforts in the study region.
Despite extensive research on lake surface temperature dynamics, studies directly addressing bottom temperature predictions remain limited. This gap is significant, as bottom temperatures directly affect critical ecological processes, including thermal stratification, oxygen dynamics, and aquatic habitats. This study aims to fill this gap by evaluating the effectiveness of decomposition methods (VMD and EMD) paired with multiple machine learning algorithms (SVM, LSTM, MLP, GPR, RF). Specifically, we hypothesize that integrating these decomposition techniques substantially enhances the predictive accuracy of lake bottom temperature models. Our findings reveal that the SVM algorithm combined with VMD (SVM-VMD-M03) consistently provides superior predictive performance across most configurations, highlighting the potential of this approach for future lake temperature forecasting efforts.
2. Material and Methods
Predicting lake bottom temperature is a complex task. This study reviews five ML methods—SVM, LSTM, MLP, GPR, and RF—and two signal decomposition methods—VMD and EMD—which are applicable to such environmental predictions. Moreover, MATLAB R2023a program was used for all analyses.
2.1. Study Region and Data
Lake Mjøsa, located in southeastern Norway, is the country’s largest lake, covering approximately 365 km2 with average depth 150–153 m and maximum depth 453 m (Figure 2). Positioned in a densely populated and agriculturally productive region, Mjøsa functions as both a hydrological and geographic centerpiece—receiving inflow from several tributaries and discharging into the Vorma River, which later connects to the Glomma, Norway’s longest river [50]. The lake plays a crucial role in providing drinking water for over 200,000 residents in urban centers such as Hamar, Gjøvik, and Lillehammer. After experiencing severe eutrophication during the mid-20th century due to nutrient runoff and industrial waste, a national rehabilitation initiative in the late 1970s dramatically improved water quality and turned Mjøsa into a model case of successful freshwater restoration [50,51].
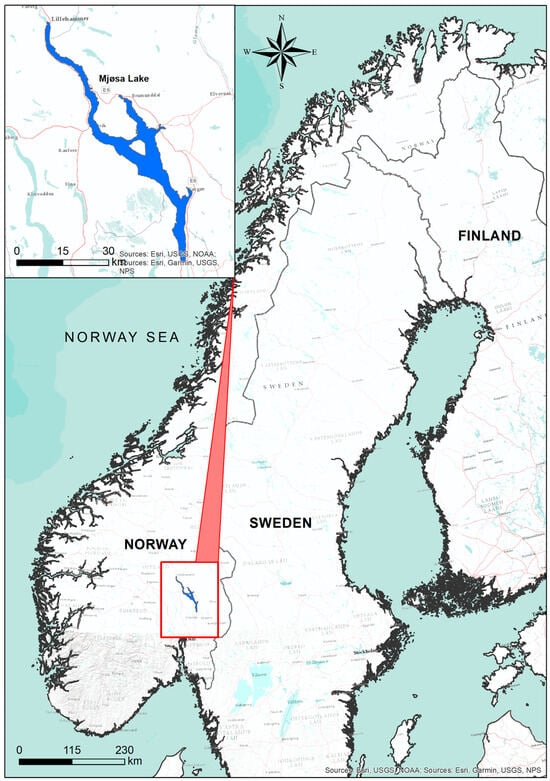
Figure 2.
Global location of the study area.
Lake bottom temperature data were obtained from the ERA5-Land monthly averaged dataset, from 1950 to the present, provided by the Copernicus Climate Change Service (C3S) (Table 1) (Figure 3). The ERA5-Land dataset is a reanalysis of global climate and historical weather data and provided by the European Centre for Medium-Range Weather Forecasts (ECMWF) [52]. Ranging from 1950 to the present, ERA5-Land provides access to hourly, high-resolution data of various surface variables. The ERA5-Land is a customized variant of ERA5 data on land. The biggest difference from the original is that the horizontal resolution is 0.10° × 0.10° instead of 0.25° × 0.25°, which makes it possible to operate on more precise scales [53]. ERA5-Land uses the FLake lake model. The variable “lake_bottom_temperature” is defined as the temperature of the water at the bottom of inland water bodies. This variable is model-simulated by ECMWF’s Freshwater Lake (FLake) model within the land surface scheme [52]. FLake is a 1D parametric lake model that represents the lake’s thermal vertical structure with two layers as follows: a well-mixed surface layer and a stratified deep layer extending to the lakebed [52]. The bottom temperature output is therefore not a direct measurement but the model’s prognostic estimate of the deepest water temperature. FLake is driven by the same meteorological inputs as the reanalysis (air temperature, wind, humidity, radiation, etc.) and it uses lake-specific parameters (location, surface area, and depth) from global datasets [54]. For Lake Mjøsa (maximum depth of ~453 m), the model keeps the lake depth constant and allows the deep layer to act as a large heat reservoir [55]. This means the simulated bottom water remains cold and relatively stable (often near 4 °C, consistent with the densest water in deep temperate lakes) unless strong mixing events occur. It is worth to acknowledge that FLake imposes a simplified temperature profile, characterized by a shape factor rather than a fully resolved gradient, and that it does not explicitly resolve heat flux into bottom sediments or any inflowing water exchanges [54,55]. Despite these simplifications, FLake has been shown to reproduce lake thermal behavior realistically for a wide range of lake depths [52]. In fact, previous validations of ERA5/ERA5-Land indicate that modeled lake temperatures (including deep-layer temperatures) have shown realistic behavior [54]. We thus consider the ERA5-Land lake bottom temperature a physically meaningful and validated data source for characterizing Lake Mjøsa’s deep-water thermal regime, providing a physically consistent, spatially and temporally continuous reference that is otherwise unavailable from in situ measurements.

Table 1.
Data statistics.
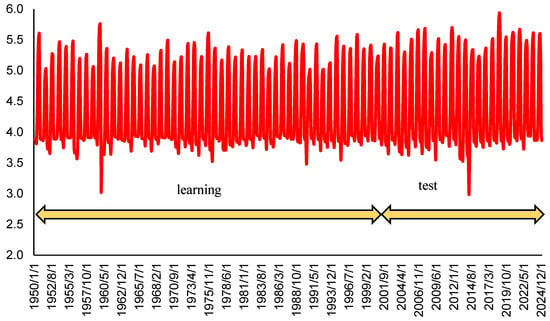
Figure 3.
Dataset (ERA5-Land bottom temperature) for Mjøsa (°C vs. Date).
2.2. Model Structure
This feature includes four different models designed to facilitate machine learning techniques. The cross-correlation method was used to create model structures. The results obtained from this method are described in Figure 4. The analysis performed according to the study models is outlined in Table 2.
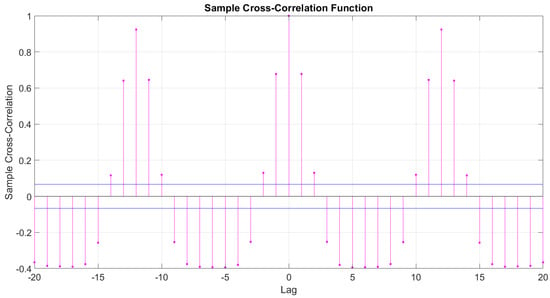
Figure 4.
The result of cross-correlation.

Table 2.
Structure of models.
The cross-correlation analysis was applied to the lake bottom temperature time series itself; the input variables t − n listed in Table 2 refer to lagged bottom temperature observations (e.g., t − 13 is the temperature 13 months before t). We did not use ERA5 air-temperature data as predictors, although such variables are available in ERA5-Land.
2.3. Long Short-Term Memory Network (LSTM)
LSTM networks are recurrent neural networks (RNNs) designed to describe sequential data, notably long-range relationships. LSTMs, introduced by Hochreiter and Schmidhuber [56], solve the vanishing gradient problem that is a significant challenge in the RNN backpropagation. The LSTM design uses internal memory cells and three gates, namely input, forget, and output gates to store, retain, and discard information. These gates dynamically control information flow, allowing the network to recall or forget inputs over long periods [57]. This feature allows LSTMs to store essential information throughout long sequences, making them ideal for time-series forecasting and sequence prediction [58,59]. Their capacity to learn temporal patterns without gradient instability makes them popular in various prediction processes [60].
LSTM networks are also commonly used for sequence modeling problems, particularly when temporal context is required. They demonstrated good performance in applications such as speech recognition, natural language processing and time-series forecasting [58,61]. Furthermore, LSTMs capture dependencies across historical sequences. This ability makes them a suitable tool for forecasting meteorological variables, lake temperatures, and water quality for environmental monitoring [62,63]. Their capability in describing and capturing sequential patterns allows them to effectively forecast multivariate time-series regression and sequence classification in both structured data, such as meteorological data, and unstructured data, such as text or sensor signals [64].
The main difference between an LSTM and a traditional recursive network is that an LSTM cell has a unique memory component at each time step. This cell state, along with the weighted input and the previous output is used to calculate the new hidden layer output and cell state. Details are as follows:
where and represent the previous and current cell memories, respectively. : input gates, : forget gate, and : output gates.
In long short-term memory (LSTM) architectures, the matrices , , and correspond to the weights linking the input vector to the input, forget, and output gates, respectively. The vectors , , and are the associated biases for each of these gates. These gates utilize the sigmoid activation function (), which is applied element-wise to produce gate values between 0 and 1, effectively controlling the information flow, specifying the permissible quantity of each component to be allowed passage. The number of zero signifies “allow no passage,” whereas a value of one signifies “permit unrestricted passage.” The graphic below clearly depicts the three utilized gates. This mechanism allows the model to selectively retain or forget information, enhancing its ability to learn complex patterns over time (Figure 5).
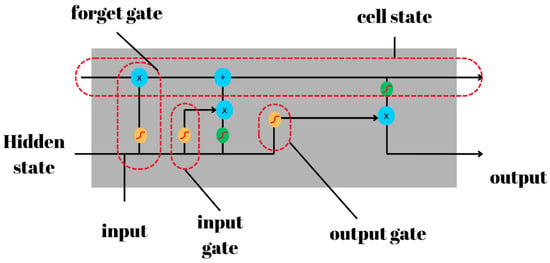
Figure 5.
The LSTM unit contains a forget gate, output gate, and input gate. The orange circle represents the sigmoid activation function while the green circle represents a activation function. Additionally, the “x” and “+” symbols are the element-wise multiplication and addition operator.
Consequently, this results in more accurate predictions and improved overall performance in various tasks. Its formula is as follows:
In addition, is hyperbolic tangent function. Both functions are the activation functions to map the nonlinearity. In this way, this mapping increases the accuracy of predictions.
At each time step , the vectors , , , and represent the input gate, forget gate, output gate, and cell state, respectively—all of which match the dimensionality of the output vector . The operator denotes the element-wise (Hadamard) multiplication. Hadamard multiplication, also known as the Hadamard product, is a binary operation that creates a new matrix (or vector), with each element being the product of the corresponding elements of the input matrices given two matrices (or vectors) of the same dimensions. If you have two matrices (or vectors) and , both of size , the Hadamard product is also of size , where
These gating mechanisms, introduced by Hochreiter and Schmidhuber [56], allow LSTM cells to selectively remember or forget information over long sequences, thereby solving the vanishing gradient problem that affects standard RNNs. Sherstinsky [65] provides a tutorial on RNN and LSTM fundamentals, highlighting LSTM’s effectiveness in a broad range of applications.
2.4. Support Vector Machine (SVM)
Support Vector Machines (SVMs) and their regression variant (SVR) are powerful supervised learning models that rely on kernel functions to capture complex data structures. A substantial body of research has focused on improving their predictive accuracy and generalization by applying various kernel design, parameter tuning, and application-specific adaptations [38,66,67,68]. Kernel parameters also play a crucial role in model effectiveness. Wang et al. [69] investigate the spread parameter () of the Gaussian kernel, showing that the generalization ability of SVMs depends on choosing within an optimal range. Kusuma and Kudus (2022) [70] highlight SVR’s robustness in handling real-world regression problems with small sample sizes and noisy features. Wang et al. [71] bridge Gaussian kernel density estimation (GKDE) with kernel-based learning methods such as SVM and SVR. They show that Gaussian kernel-based SVMs can be interpreted as probabilistic classifiers, offering a theoretical framework that justifies their performance from a Bayesian perspective.
Together, these studies demonstrate the advanced nature of kernel function design and optimization in SVM/SVR research. They collectively highlight the importance of kernel selection, parameter tuning, and structural enhancements to improve both accuracy and generalization across diverse applications.
The mathematical formulation of SVM is presented in Equation (9), defining the relationship between input and output variables as follows:
where denotes a high dimensional feature space, represents weight of the output variable, and referred as the bias term.
2.5. Gaussian Process Regression (GPR)
Gaussian Process Regression (GPR) is a non-parametric, Bayesian machine learning approach that provides a robust framework for modeling uncertainty in regression and classification tasks [72,73]. Unlike traditional parametric models, GPR defines a distribution over possible functions, allowing it to flexibly model complex, nonlinear relationships without a fixed functional form assumption [18]. A key strength of GPR is its use of adaptable covariance (kernel) functions, which controls the smoothness, periodicity, and non-stationarity of the model output while also allowing the incorporation of prior knowledge [74]. Furthermore, GPR provides probabilistic predictions with calibrated uncertainty intervals, which is a particularly useful technique in fields such as hydrology, climate science, and environmental forecasting which accommodate a high level of uncertainty [18,75]. Recent developments have improved the scalability and interpretability of GPR by combining it with deep kernel learning techniques and physics-informed constraints, which extends its applicability to large-scale and more specific types problems [76,77].
A Gaussian process (GP) is defined as a collection of random variables any finite number of which has a joint Gaussian distribution [78] and a GP is completely specified by its mean function and covariance function :
2.6. Multilayer Perceptron (MLP)
Artificial Neural Networks (ANNs) are computational models inspired by biological neurons and have proven effectiveness for both classification and regression across different scientific and engineering problems. Among various ANN architectures (Figure 6), the Multilayer Perceptron (MLP) remains a widely adopted structure due to its ability to approximate complex, nonlinear functions through multiple layers of interconnected neurons [79]. A key aspect affecting ANN performance is the training algorithm used to adjust network weights. The Levenberg–Marquardt (LM) algorithm is particularly notable for its fast convergence and high accuracy, particularly when compared to conventional methods such as backpropagation or gradient descent. Mishra et al. [80] demonstrated that LM outperforms scaled conjugate gradient methods in minimizing prediction errors when training MLPs for communication signal equalization. Moreover, in hydrology and environmental modeling studies, Kim and Singh [81] highlighted that LM-based training enhances ANN accuracy in rainfall disaggregation tasks, outperforming other algorithms in terms of sensitivity to network architecture. Similarly, El Chaal and Aboutafail [82] found that LM achieved superior mean squared error and correlation results in water quality estimation compared to Broyden-Fletcher-Goldfarb-Shanno (BFGS) optimization.
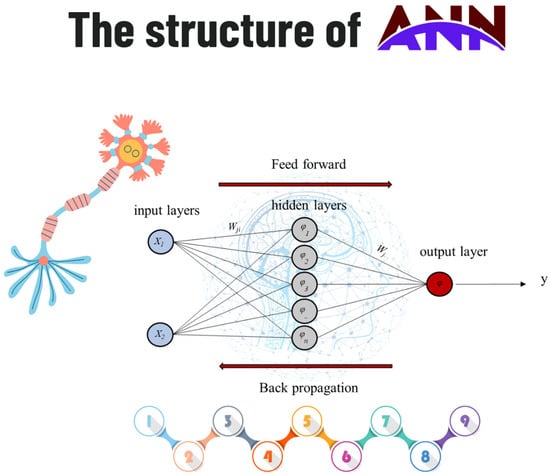
Figure 6.
The schematic of ANN architecture where φj or : activation function applied at the output neuron, y: the predicted value of the kth output at time step t, : weight connecting the jth neuron in the hidden layer to the kth neuron in the output layer, φj or : activation function applied at the jth hidden neuron, : the ith input variable at time step t.
Furthermore, the LM algorithm has also demonstrated successful outcomes and has been applied in biomedical and engineering domains. For instance, Hashim et al. [83] achieved over 92% accuracy in detecting ECG abnormalities using MLPs trained via LM. Similarly, Moness and Diaa-Eldeen [84] used LM in a real-time nonlinear helicopter control system and validated its reliability for system identification. Additionally, LM has been paired with metaheuristic optimizers such as Particle Swarm Optimization to escape local minima, further improving ANN convergence in complex modeling tasks [85]. Collectively, these studies highlight the robustness, precision, and cross-disciplinary applicability of LM-trained MLP models.
Let the following notations define the architecture of a Multilayer Perceptron (MLP) neural network at time step t:
where N is the number of samples, m is the number of hidden neurons,
= the ith input variable at time step t;
= weight that connects the ith neuron in the input layer and the jth neuron in the hidden layer;
= bias for the jth hidden neuron;
= activation function of the hidden neuron;
= weight that connects the jth neuron in the hidden layer and kth neuron in the output layer;
= bias for the kth output neuron;
= activation function for the output neuron; and is the forecasted kth output at time step t.
These notations follow the formulation described by Kim and Valdés [86].
2.7. Random Forest
Random forest (RF), introduced by Breiman [87], is a machine learning technique used for both the classification and the regression problems [88]. By utilizing a single dataset, multiple models are trained, which also increases the prediction accuracy. In practice, the method follows three stages as follows: data subdivision, obtaining decision trees for these subdivisions, and development of the final prediction by averaging the predictions obtained from trees [88,89]. Random forest has several key advantages, such as high accuracy-low errors and computational speed as Choi et al. [90] indicated. Moreover, ease of hyper-parameter tuning during runtime is also an advantage for RF compared to ANN and SVR [63,88]. For more details, readers can refer to Breiman [87], Biau and Scornet [91], Yu et al. [92], and Tyralis et al. [93].
2.8. Variational Mode Decomposition (VMD)
Variational Mode Decomposition (VMD), by Dragomiretskiy and Zosso [94], is a non-recursive, fully adaptive signal decomposition method designed to extract intrinsic modes of a time series based on their spectral characteristics and to overcome some limitations of the traditional decomposition methods. Unlike traditional empirical approaches such as EMD, VMD formulates the mode decomposition task as a constrained variational optimization problem [35], aiming to minimize the bandwidth of each mode around its central frequency [95], demonstrating higher efficiency in removing high frequency noises without diminishing much of the signal amplitude [96,97].
VMD initially transforms the real-valued mode into an analytic signal with a single-sided frequency spectrum:
The single-sided spectrum is subsequently shifted to a zero-frequency baseband, and the effective bandwidth of the signal is determined using the L2-norm of the time derivative. The suggested CVMD generalizes by decomposing the complex signal into two single-sided frequency spectra utilizing an optimal band-pass filter, as elaborated in the subsequent section. The VMD method is written as a constrained variational problem [94]:
The limitation in the aforementioned equation can be mitigated by using a quadratic penalty and Lagrangian multipliers . The augmented Lagrangian is defined as follows:
where α denotes the balancing parameter of the “data-fidelity” constraint. The associated unconstrained problem in Equation (16) is subsequently addressed via the Alternating Direction Method of Multipliers (ADMM). All modes with i < k, derived from solutions in the Fourier domain, are refined by Wiener filtering utilizing a filter adjusted to the current center frequency in the positive spectrum, that is as follows:
where the center frequency is accordingly updated as the center of gravity of the corresponding mode’s power spectrum . The incorporation of Wiener filtering within the algorithm enhances the robustness of VMD against sampling and noise. The is calculated as follows:
The center frequencies of the modes are initialized in two manners in this study, through a uniform distribution and at zero. Typically, varying results may be obtained when an alternative initialization is utilized. The parameter α is designated with a suitable value [95,98].
To solve the constrained optimization problem, the VMD algorithm employs an augmented Lagrangian method and alternate direction method of multipliers (ADMM), enabling efficient and stable convergence [99,100].
Compared to earlier decomposition techniques, VMD addresses several shortcomings, including pattern mixing, endpoint effects, and the challenge of defining precise stopping conditions therefore exhibits strong robustness against noise and mode mixing [101], making it useful for analyzing complex, non-stationary signals in fields such as hydrology, structural health monitoring, and fault diagnosis [101,102].
2.9. Empirical Mode Decomposition (EMD)
Empirical Mode Decomposition (EMD), proposed by Huang et al. [103], is a widely used signal decomposition technique. EMD can adaptively decompose a non-stationary and nonlinear time series into a finite set of intrinsic mode functions (IMFs) and a residual component, based entirely on the local characteristics of the data [104,105,106,107]). The method operates without any predefined basis that makes it particularly suitable for analyzing natural signals across various fields, such as climate, hydrology, geophysics, and fault detection [108,109,110].
The EMD algorithm comprises an iterative sifting process, which can be described in the following steps [106,111]:
- Identify all local maxima and minima of the original signal;
- Construct upper and lower envelopes by interpolating the maxima and minima using cubic splines, yielding respectively;
- Compute the local mean envelope a(n) as the average of these two as follows:
- Subtract the mean from the original data:
- Evaluate whether h(n) satisfies the two conditions for being classified as an IMF:
- The number of zero crossings and extrema must differ by at most one;
- The mean of the envelope should be zero (or sufficiently close).If the conditions are met, h(n) is designated as the first IMF ϕ(n);
- Otherwise, the process is repeated on .
This iterative process continues until all IMFs are extracted. The final remaining signal, which contains no more oscillatory components, is considered the residual [112,113]. Thus, EMD decomposes a signal into a series of IMFs representing distinct frequency components and a residual capturing the long-term trend [114,115].
2.10. Model Performance Assessment
Various statistical metrics were used for performance assessment. These metrics are the correlation coefficient (R), the root mean square error (RMSE), the Nash–Sutcliffe efficiency (NSE), RMSE-Standard Deviation Ratio (RSR), Kling–Gupta efficiency (KGE) and Performance Index (PI), defined in Equations (21), (22), (23), (24), (25), and (26), respectively.
In Equations (21)–(26), = the predicted value, = the observed value, N = the number of data, = average observed value, and = average predicted value.
Correlation coefficient (r) can be calculated as in Equation (21) [116]:
RMSE is calculated in Equation (22) [117]:
NSE is calculated in Equation (23) [33]:
RMSE-Standard Deviation Ratio (RSR), as defined in Equation (24) [118]:
Also, Kling–Gupta efficiency (KGE) and Performance Index (PI) performances criteria were used to determine model performances (Equations (25) and (26)).
3. Results
In this study, lake bottom temperature data from Lake Mjøsa in Norway were analyzed using several machine learning algorithms. Four different input configurations, generated based on cross-correlation analysis, were evaluated separately. To improve the predictive performance, both EMD and VMD methods were applied. The dataset was split into 70% for training and 30% for testing.
All statistical results related to the study area are presented in Table 3. In this table, models with the best performance metrics have been shown in bold. According to the findings, the highest performance among all models, without any decomposition, was obtained by the GPR algorithm with the M03 input configuration (r = 0.9662, NSE = 0.9186, KGE = 0.8786, PI = 0.0231, RSR = 0.2848, and RMSE = 0.2000). This was followed by the SVM model using the M02 input structure which also demonstrated strong performance (r = 0.9547, NSE = 0.9110, KGE = 0.9462, PI = 0.0243, RSR = 0.2978, and RMSE = 0.2091). Although the performance metrics of these two models are close, the GPR-M03 model outperformed the others in most of the evaluation criteria. The next best results were obtained from by the MLP, LSTM, and RF algorithms, respectively. Overall, the GPR algorithm emerged as the most effective machine learning method in this study, with the M03 input structure showing the best performance. The M03 configuration is composed of lagged temperature data at times t − 12, t − 1, t − 11, t − 13, t − 2 and t − 9. These findings suggest that the number of input data selected via cross-correlation should be optimized carefully. Implementing all the lagged variables to the models can negatively affect the performance. An additional remarkable finding was observed for the M04 input configuration. The GPR model using M04 input structure achieved the second-best performance within its algorithm category, GPR. The input structure of this model was based on consecutively lagged temperature values and did not rely on any feature selecting method. Under certain conditions, it is also important to note that input structures developed without any formal feature selection technique may still provide reliable performance.

Table 3.
Results of all models.
In this study, EMD and VMD methods were applied to improve the predictive performance of ML models. These decomposition methods were incorporated into each algorithm-input structure configuration and the performance results obtained are summarized in the table above. Among the models that used EMD, the best performance was achieved by the LSTM-EMD-M03 configuration (r = 0.9562, NSE = 0.9008, KGE = 0.9315, PI = 0.0256, RSR = 0.2978, and RMSE = 0.3143). Another notable result was obtained from the GPR-EMD-M01 model which also showed relatively strong performance with EMD (r = 0.9415, NSE = 0.8669 KGE = 0.8462, PI = 0.0299, RSR = 0.3642, and RMSE = 0.2557), although it lagged behind the LSTM-EMD-M03 model in all performance metrics except RMSE. These findings suggest that M03 model input structure revealed the highest performance when coupled with EMD, showing the effectiveness of cross-correlation as a method for constructing the model input structures. In this input structure, all lagged variables determined by cross-correlation were used. However, it is worth mentioning that configurations generated via cross-correlation yielded varying performances among the algorithms. For instance, while best performance of LSTM was obtained using M03 configuration, the GPR algorithm achieved its best EMD-enhanced performance with M01 configuration.
When the analysis results made with EMD are examined, it generally falls behind the performance of the analyses made without EMD. Despite these individual successes, the overall performance of the EMD-enhanced models tended to be lower than that of models trained without decomposition. For this reason, effective results could not be obtained with EMD, which was applied to improve the model performances, and decreases in performance metrics were detected. In fact, in some models, the performance metrics belonging to that model were determined to be negative as a result of the analysis. In general, the application of EMD did not result in significant performance improvements, and in several cases, a decline in key evaluation metrics was observed. In fact, for some algorithm–input combinations, the application of EMD led to negative performance scores, indicating substantial deterioration in model accuracy. This suggests that while EMD may benefit certain model types or input configurations, it does not universally enhance predictive performance and should be applied selectively.
VMD was another decomposition method applied in this study to enhance model performances similar to EMD. The results of the VMD based analyses are presented in Table 3. Upon examination of those results, it was observed that VMD improved the predictive capabilities of almost all models and algorithms. In fact, VMD yielded the most effective results overall, outperforming both the baseline and EMD-enhanced analyses.
Among all tested configurations, the most effective result was achieved by the SVM-VMD-M03 algorithm, using the M03 input structure in conjunction with VMD. This model SVM-VMD-M03 produced outstanding results across all evaluation metrics (r = 0.9859, NSE = 0.9717, KGE = 0.9755, PI = 0.0135, RSR = 0.1679, and RMSE = 0.1179). Besides providing best results among the VMD-coupled models, it also surpassed all models evaluated in the study. Therefore, this combination of model input structure and machine learning algorithm can be considered the most suitable for predicting lake bottom temperature in Lake Mjøsa.
This model is followed by GPR-VMD-M02 as the second-best performer. The performance values of this model are r = 0.9857, NSE = 0.9710, KGE = 0.9710, PI = 0.0136, RSR = 0.1700, and RMSE = 0.1193. With slightly lower—but still exceptional—metrics, GPR-VMD-M02 presented very close results with the performance metrics of the SVM-VMD-M03 model. However, although the difference is minimal, SVM-VMD-M03 maintained a better prediction performance over GPR-VMD-M02 in all metrics.
On the other hand, as in EMD, not all models benefited from the coupling of VMD. One of these is the MLP-M04 model. The performance metrics for this model in its original (non-VMD) form are r = 0.9579, NSE = 0.9058, KGE = 0.9399, PI = 0.0249, RSR = 0.3063, and RMSE = 0.2151. After applying VMD, they changed to r = 0.9469, NSE = 0.8825, KGE = 0.9270, PI = 0.0280, RSR = 0.3422, and RMSE = 0.2403 after VMD. These results indicate that VMD may not uniformly improve the performance and, in some cases, may introduce noise or disrupt the learning dynamics of certain algorithms and negatively affect the model performance.
The analyses indicate that the selection of model input parameters is critical since it plays a significant role in determining the performance of the model. In this study, a cross-correlation approach was applied to identify the relevant input structure. However, using all correlated lags does not universally improve performance, which is observed in GPR-VMD or MLP-VMD configurations. For this reason, it is necessary to use an optimal subset of input features rather than incorporating all available correlated data.
In this study, in addition to statistical evaluation methods, visual assessment tools were also used to identify the most successful model configuration for the study area. One such method is the Taylor diagram, which provides a concise graphical representation of model performance by simultaneously displaying correlation, standard deviation, and root mean square error. To compare the statistically best performing models, in this study, the Taylor diagrams were constructed, and the results are shown in Figure 7.
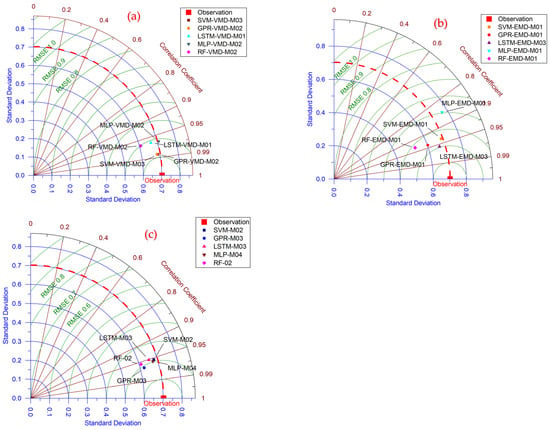
Figure 7.
Comparison of the results of the most successful models in the Taylor diagram: SVM-VMD-M03 (analysis of M03 with SVM including VMD), SVM-EMD-M01 (analysis of M01 with SVM including EMD), SVM-M02 (analysis of M02 with SVM), etc., and (a) analysis for VMD, (b) analysis for EMD, and (c) analysis for without decomposition.
According to this figure, the SVM-VMD-M03 and GPR-VMD-M02 models, both generated using VMD, were identified as being the closest to the observed value. The performance metrics of these models were found to be closely aligned to each other, which is also consistent with the statistical evaluation. Similarly, for model results obtained from EMD coupling, the LSTM-EMD-M03 configuration was found to be nearest to the observed values and presented the strongest agreement on the Taylor diagram. These results also align with the previous statistical performance results. The model closest to the observation values for the baseline (non-decomposed) analysis was GPR-M03. These findings confirm the consistency between the visual analysis provided by the Taylor diagram and the statistical evaluation metrics.
Figure 8 presents the results of a visual comparison using violin diagrams, allowing for an intuitive assessment of how closely the most successful models, based on statistical performance metrics, resemble the observed data distribution. This figure serves as a supplementary evaluation tool, complementing the numerical analyses presented earlier. In the comparison of VMD based models, the SVM-VMD-M03 configuration was determined to be the most closely approximated model to the observed values shape. In addition, as previously discussed, this model was followed by GPR-VMD-M02 in terms of statistical performance, with only small differences in their respective statistical performance metrics. The violin diagram further indicates that the SVM-VMD-M03 model not only resembles more closely the distributional shape of the observed values but also shows better agreement with the mean and median values. The SVM-VMD-M03 model outperforms the GPR-VMD-M02 model in terms of central tendency and distributional agreement, making it the top performer model overall in the VMD coupled category.
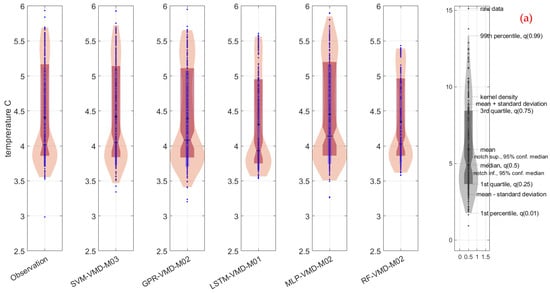
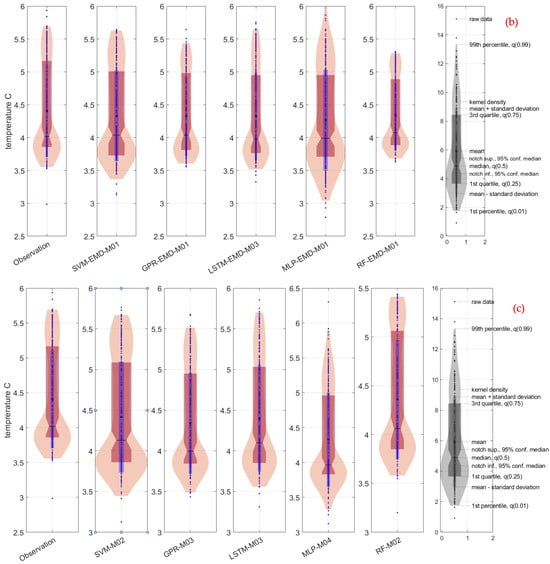
Figure 8.
Comparison of the results of the most successful models in the violin diagrams: SVM-VMD-M03 (analysis of M03 with SVM including VMD), SVM-EMD-M01 (analysis of M01 with SVM including EMD), SVM-M02 (analysis of M02 with SVM), etc., and (a) analysis for VMD, (b) analysis for EMD, and (c) analysis for without decomposition.
For the EMD coupled analysis, the model that is most consistent with the observed values is LSTM-EMD-M03. This model not only captured extreme values more accurately than other models but also showed high agreement with the mean of the observed data, indicating the ability to reflect distributional extremes and central trends. In the baseline (non-decomposed) analysis, GPR-M03 demonstrated the best performance. In particular, this model captured the shape of the distribution and detected the extreme values. Additionally, its kernel density closely mirrored that of the observed data, indicating a high level of statistical and visual agreement. The violin plot analysis supports the statistical findings and offers additional insights into how well each model captures the full distribution of lake bottom temperature values, including central trends and outliers.
Figure 9 presents the box normal plots used to compare the most successful algorithms within each modeling class. Based on the visual assessment, the GPR-M03 model produces results most closely aligned to the observed data in the baseline (non-decomposed) analysis. In particular, the mean and median values of this model closely interact with those of the observations. In the decomposition-based analyses, SVM-VMD-M03 configuration displays very similar properties with the observed data. The mean, median, and extreme values of this model are in close agreement with the observed distribution. Similarly, in the EMD-based analysis, the LSTM-EMD-M03 model shows better performance than the other EMD models. The patterns observed in the box normal plots are consistent with the statistical results presented earlier.
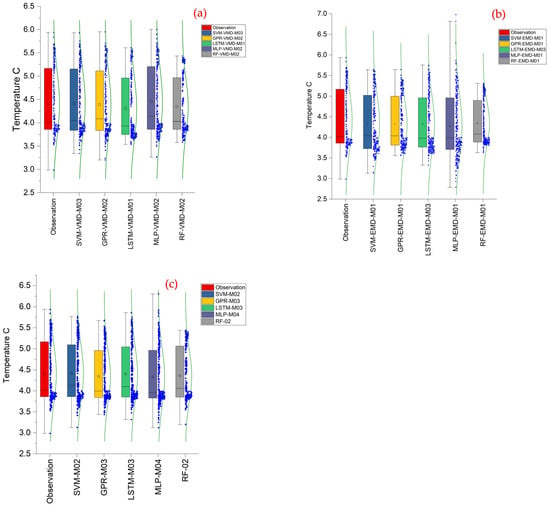
Figure 9.
Comparison of the results of the most successful models in the box normal diagram: SVM-VMD-M03 (analysis of M03 with SVM including VMD), SVM-EMD-M01 (analysis of M01 with SVM including EMD), SVM-M02 (analysis of M02 with SVM), etc., and (a) analysis for VMD, (b) analysis for EMD, and (c) analysis for without decomposition.
Figure 10 shows the box plots of the error distributions for each algorithm, model input configuration, and decomposition method. These box plots allow for a comparison of model performance considering the prediction errors. Upon detailed evaluation of the plots and comparison with the observed values, the most successful result in the VMD coupled analyses was performed by SVM-VMD-M03. In the EMD-based analyses, LSTM-EMD-M03 produced the lowest error rate, while in the baseline (non-decomposed) analysis, the GPR-M03 configuration demonstrated the best performance with lower error rates compared to the other models. Therefore, the visual error box plots represent consistent results with those of the statistical evaluation display earlier and confirm that the top performing configurations identified through statistical metrics also demonstrate successful behavior in terms of error distribution.

Figure 10.
Comparison of the results of the most successful models in the error box-plots diagram: SVM-VMD-M03 (analysis of M03 with SVM including VMD), SVM-EMD-M01 (analysis of M01 with SVM including EMD), SVM-M02 (analysis of M02 with SVM), etc., and (a) analysis for VMD, (b) analysis for EMD, and (c) analysis for without decomposition.
4. Discussion
In this study, the monthly average bottom temperature data of Lake Mjøsa—located in southeastern Norway (north of Oslo) and recognized as the largest lake in Norway—were analyzed using several machine learning algorithms, including LSTM, SVM, GPR, RF, and MLP. With these algorithms, four different model input structures were tested and two decomposition techniques, Variational Mode Decomposition (VMD) and Empirical Mode Decomposition (EMD), were used to improve the model performance. The dataset split into 70% for learning and 30% for testing purposes.
Some of the findings in this study are in agreement with results from previous studies in the literature. For instance, Zhu et al. [119] developed temperature prediction models using machine learning for eight lakes in Poland. In their studies, they incorporated wavelet transform along with LSTM and MLP machine learning algorithms. While they used daily surface temperatures, they reported that LSTM with wavelet transform yield highly effective results. Similarly, in this study, LSTM and its decompositions were proven to be one of the promising algorithms that produce effective results.
Although many machine learning algorithms focus on lakes, they often address different physical parameters of the lakes. For instance, Feigl et al. [120] used step-wise linear regression, RF, eXtreme Gradient Boosting (XGBoost), feed-forward neural networks (FNNs), and two types of recurrent neural networks (RNNs) algorithms to model the flow of streams feeding lakes in Austria. Contrary to this study, their models used multiple input variables such as precipitation, temperature, and streamflow. They stated that RNN produced the best results among the algorithms for regional analyses while RF also demonstrated strong performance. However, a key difference is that the current study used lagged values as input variables, an approach that has been shown to improve model accuracy in various studies [121,122,123]. Chen et al. [124] also developed a model to predict future temperatures in Mendota and Sparkling Lakes using four different methods, two of which were variants of LSTM. Physical models were integrated for comparison and concluded that the results of LSTM-based models and hybrid models were superior, and they outperformed other models. This conclusion is partially supported in this study, where the LSTM algorithm coupled with EMD demonstrated effective results. However, it is worth saying that LSTM, generally, is not directly compared with traditional methods. In this study, although LSTM, a relatively new method, produced strong results, it was slightly outperformed by SVM and MLP depending on the study area and data used. One novel contribution of this study is the comparison of LSTM to innovative algorithms and the determination of how model input structures influence performance.
Moreover, this study examined the influence of VMD and EMD on predictive accuracy. These decomposition techniques are frequently preferred in the literature to improve model outcomes. For instance, Citakoglu et al. [125] applied several machine learning models, LSBoosting, ANFIS, SVM, GPR, and M5 model tree (M5Tree), to drought forecasting in Ağrı, Türkiye. They created hybrid models using VMD and stated that VMD enhanced models demonstrated improved performance. Similarly, Citakoglu and Coşkun [126] conducted a drought analysis using precipitation data from 1960 to 2020 in the Sakarya region, and developed drought forecasting models using various algorithms including SVM, GPR, ANN, ANFIS, k-nearest neighbors (KNN) algorithms and created different input structures based on auto-correlation. Their findings emphasized that wavelet transform, VMD, and EMD can improve model performance, and they concluded that VMD-GPR was the most effective configuration. Studies in the literature may reveal varying results. These may be due to the region or method studied, as well as to measurement or individual errors. While, in this study, we acknowledged that lake bottom temperatures may increase faster than meteorological parameters, such as air temperature, some studies suggest otherwise [127,128].
The machine learning methods and input structures used in this study provide a basis for future research on lake bottom temperature forecasting in the study area. Consequently, both the machine learning algorithms with input structures and the decomposition techniques applied here may serve as reference points for future studies focused on lake thermal dynamics and related environmental processes.
5. Conclusions and Recommendations
Bottom temperature regulates stratification strength, hypolimnetic oxygen, nutrient release, and cold-water habitat variables with high ecological relevance and drinking-water implications in large, deep Norwegian lakes. Unlike surface-temperature, bottom temperature responses to climate change remain poorly documented worldwide that creating a clear knowledge gap that our study targets. Mjøsa is Norway’s largest drinking-water source; accurate forecasts of hypolimnetic temperatures therefore have immediate practical value whether it is observed or reanalysis data (in-situ observations or ERA5-Land/FLake reanalysis).
The modeling architecture we developed (lag selection + VMD/EMD + SVM/LSTM/GPR/MLP/RF) is data-agnostic; with appropriate inputs and calibration it can be transferred to other targets (water-level, inflow, or water-quality forecasting), as several of our earlier publications on streamflow and drought demonstrate.
In this study, the monthly average bottom temperatures of Lake Mjøsa, located in southeastern Norway (north of Oslo) and recognized as the largest lake in Norway, were analyzed using five machine learning algorithms as follows: LSTM, SVM, GPR, RF, and MLP. Four distinct input structures were employed, and two decomposition techniques, Variational Mode Decomposition (VMD) and Empirical Mode Decomposition (EMD), were applied to enhance model performance. The key findings from the study are summarized as follows:
- In the baseline analysis (i.e., without decomposition), the most successful configuration was GPR using the M03 input structure. This structure was obtained by cross-correlation, suggesting that this method positively contributes to the model performance. The SVM-M02 model followed closely, ranking as the second-best performer in terms of accuracy;
- The findings also suggest that including all variables identified by cross-correlation can negatively impact model accuracy. Therefore, the number of input features should be optimized—ideally through iterative testing or validation methods;
- Among EMD-enhanced models, the LSTM-EMD-M03 configuration produced the highest performance. This model utilized the M03 input structure, which incorporated all cross-correlated lagged variables. These results indicate that LSTM, when paired with the appropriately selected input configuration and EMD preprocessing, can be effective in lake temperature modeling;
- Despite its success in some configurations, the overall application of EMD did not yield consistent improvements. In most cases, EMD led to a reduction in performance metrics across all algorithms, indicating that its effectiveness is model-dependent and should be applied selectively;
- In the analyses performed with VMD, the general model performance metrics have improved. However, there are some exceptions such as MLP-M04. Despite this, the top results in each algorithm class are VMD-based. In addition to these, SVM with M03 lags were determined to be the most successful models in VMD;
- VMD, on the other hand, generally improved model performance across all algorithms. While some exceptions were observed, such as the MLP-M04 configuration, VMD yielded the most accurate results overall. The SVM-VMD-M03 model was the most effective across all tests;
- In this study, the M04 input structure was sequentially lagged one after the other while determining the model input structure. It was found that this structure gave more effective results than the models created with cross-correlation in some algorithms and separations;
- The cross-correlation method was found to be beneficial for identifying informative input features. However, care must be taken to avoid including too many parameters, which can degrade model performance. Interestingly, in some models and decomposition settings, the simpler M04 configuration—built from consecutive lagged values without formal selection—outperformed more complex input structures derived from cross-correlation.
Beyond the technical results, this study emphasizes the practical significance of lake temperature forecasting. Temperature changes in lake ecosystems can adversely affect aquatic life, surrounding biodiversity, and local socio-environmental systems. The ability to forecast lake temperature dynamics using machine learning and decomposition techniques provides an important tool for early warning and adaptive planning. These results can support decision-makers in environmental management, particularly in anticipating and mitigating adverse temperature-driven ecological impacts. This study will serve as a guide for future modeling studies regarding this topic.
This study is limited to four input structures and a single lake system. Expanding the number and diversity of input configurations, incorporating other influential environmental variables (e.g., wind, radiation), and applying the methodology to additional lake systems could enrich the analysis and generalizability of the findings. Future studies may also explore hybrid modeling frameworks and integrate physical and data-driven approaches for further performance enhancement. Finally, all hyper-parameters used in this study are shown in Table 4.

Table 4.
Hyperparameters for all algorithms.
Furthermore, the main limitation of this study is the absence of in situ water temperature measurements. Lake bottom temperature was taken from the ERA5-Land reanalysis, where it is a model-derived field produced by the FLake module; it therefore carries the structural approximations and parameter assumptions (e.g., mean (static) lake depth, lake-shape factor) of that scheme. Representing the entire deep-water column with a single “bottom” node may underestimate vertical thermal variability, especially in strongly stratified deep lakes. In addition, our machine learning models were driven only by lagged bottom temperature values of the target; key drivers (air temperature, wind, radiation, etc.) were not included, raising the risk that the models leverage statistical autocorrelation rather than physical causality. Finally, model skill is evaluated against the same ERA5-Land series that serves as training data, no independent validation with independent observed lake temperatures was possible. The assessment reflects relative performance among algorithms rather than absolute predictive accuracy for real-world conditions.
Future work should test the approach on lakes that possess long-term, depth-resolved temperature profiles so that both reanalysis output and machine learning forecasts can be validated against in-situ observations. ERA5-Land bottom temperature fields could be bias-corrected using such measurements, refining FLake parameters (particularly lake depth and shape factor) for local conditions. Incorporating meteorological predictors like surface air temperature, wind speed, net radiation, snow/ice cover into hybrid/physics informed models (e.g., physics-informed LSTM networks) should improve physical realism. Multi-dataset comparisons that include other reanalysis (GLDAS, NLDAS) and high-resolution satellite-derived lake surface temperatures can help quantify structural uncertainty. Coupling bottom temperature projections to ecological and water-quality features (hypolimnetic oxygen depletion, methane release) would support create an interdisciplinary framework for climate-adaptation planning of lake and reservoir systems. Lake Mjøsa is hydropower-regulated (outflow controlled at Svanfoss), so inter-annual water-level variability is dominated by operational rules rather than purely hydro-climatic drivers which complicating a direct comparison of ML skill. Bottom temperature, by contrast, responds primarily to atmospheric forcing and internal heat storage, making it a suitable testbed for the signal-decomposition techniques (EMD/VMD) we evaluate. Extending to multi-variable prediction (e.g., coupling our thermal model with a water-balance model for lake levels) would also be a valuable next step for water level forecasting for different operational periods.
Author Contributions
Conceptualization, S.O. and M.A.H.; Formal analysis, T.T.; Methodology, T.T., S.O. and M.A.H.; Supervision, S.O. and M.A.H.; Visualization, T.T., S.O. and M.A.H.; Writing—original draft, T.T. and S.O.; Writing—review and editing, T.T., S.O., Z.S. and M.A.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding. APC was supported/funded by UiT, the Arctic University of Norway.
Data Availability Statement
The original contributions presented in the study are included in the article. The raw data supporting the conclusions of this article will be made available by the authors upon reasonable request.
Acknowledgments
During the preparation of this work, the authors used ChatGPT and Quillbot in order to improve readability, edit grammar, and language of some parts of the manuscript. After using this tool/service, the authors reviewed and edited the content as needed and take full responsibility for the content of the publication.
Conflicts of Interest
The authors declare that there is no conflict of interest.
References
- Butcher, J.B.; Nover, D.; Johnson, T.E.; Clark, C.M. Sensitivity of lake thermal and mixing dynamics to climate change. Clim. Chang. 2015, 129, 295–305. [Google Scholar] [CrossRef]
- Woolway, R.I.; Sharma, S.; Weyhenmeyer, G.A.; Debolskiy, A.; Golub, M.; Mercado-Bettín, D.; Perroud, M.; Stepanenko, V.; Tan, Z.; Grant, L. Phenological shifts in lake stratification under climate change. Nat. Commun. 2021, 12, 2318. [Google Scholar] [CrossRef]
- Feldbauer, J.; Mesman, J.P.; Andersen, T.K.; Ladwig, R. Learning from a large-scale calibration effort of multiple lake temperature models. Hydrol. Earth Syst. Sci. 2025, 29, 1183–1199. [Google Scholar] [CrossRef]
- Piccolroaz, S.; Zhu, S.; Ladwig, R.; Carrea, L.; Oliver, S.; Piotrowski, A.; Ptak, M.; Shinohara, R.; Sojka, M.; Woolway, R. Lake water temperature modeling in an era of climate change: Data sources, models, and future prospects. Rev. Geophys. 2024, 62, e2023RG000816. [Google Scholar] [CrossRef]
- O’Reilly, C.M.; Sharma, S.; Gray, D.K.; Hampton, S.E.; Read, J.S.; Rowley, R.J.; Schneider, P.; Lenters, J.D.; McIntyre, P.B.; Kraemer, B.M. Rapid and highly variable warming of lake surface waters around the globe. Geophys. Res. Lett. 2015, 42, 10773–10781. [Google Scholar] [CrossRef]
- Pilla, R.M.; Williamson, C.E.; Adamovich, B.V.; Adrian, R.; Anneville, O.; Chandra, S.; Colom-Montero, W.; Devlin, S.P.; Dix, M.A.; Dokulil, M.T. Deeper waters are changing less consistently than surface waters in a global analysis of 102 lakes. Sci. Rep. 2020, 10, 20514. [Google Scholar] [CrossRef]
- Noori, R.; Woolway, R.I.; Jun, C.; Bateni, S.M.; Naderian, D.; Partani, S.; Maghrebi, M.; Pulkkanen, M. Multi-decadal change in summer mean water temperature in Lake Konnevesi, Finland (1984–2021). Ecol. Inform. 2023, 78, 102331. [Google Scholar] [CrossRef]
- Noori, R.; Bateni, S.M.; Saari, M.; Almazroui, M.; Torabi Haghighi, A. Strong warming rates in the surface and bottom layers of a boreal lake: Results from approximately six decades of measurements (1964–2020). Earth Space Sci. 2022, 9, e2021EA001973. [Google Scholar] [CrossRef]
- Bégin, P.N.; Tanabe, Y.; Kumagai, M.; Culley, A.I.; Paquette, M.; Sarrazin, D.; Uchida, M.; Vincent, W.F. Extreme warming and regime shift toward amplified variability in a far northern lake. Limnol. Oceanogr. 2021, 66, S17–S29. [Google Scholar] [CrossRef]
- Kraemer, B.M.; Anneville, O.; Chandra, S.; Dix, M.; Kuusisto, E.; Livingstone, D.M.; Rimmer, A.; Schladow, S.G.; Silow, E.; Sitoki, L.M. Morphometry and average temperature affect lake stratification responses to climate change. Geophys. Res. Lett. 2015, 42, 4981–4988. [Google Scholar] [CrossRef]
- Noori, R.; Woolway, R.I.; Saari, M.; Pulkkanen, M.; Kløve, B. Six decades of thermal change in a pristine lake situated north of the Arctic Circle. Water Resour. Res. 2022, 58, e2021WR031543. [Google Scholar] [CrossRef]
- Schwefel, R.; MacIntyre, S.; Cortés, A. Summer temperatures, autumn winds, and thermal structure under the ice in arctic lakes of varying morphometry. Limnol. Oceanogr. 2025, 70, 1817–1834. [Google Scholar]
- Oleksy, I.A.; Richardson, D.C. Climate change and teleconnections amplify lake stratification with differential local controls of surface water warming and deep water cooling. Geophys. Res. Lett. 2021, 48, e2020GL090959. [Google Scholar] [CrossRef]
- Gai, B.; Kumar, R.; Hüesker, F.; Mi, C.; Kong, X.; Boehrer, B.; Rinke, K.; Shatwell, T. Catchments amplify reservoir thermal response to climate warming. Water Resour. Res. 2025, 61, e2023WR036808. [Google Scholar] [CrossRef]
- Råman Vinnå, L.; Medhaug, I.; Schmid, M.; Bouffard, D. The vulnerability of lakes to climate change along an altitudinal gradient. Commun. Earth Environ. 2021, 2, 35. [Google Scholar] [CrossRef]
- Adrian, R.; O’Reilly, C.M.; Zagarese, H.; Baines, S.B.; Hessen, D.O.; Keller, W.; Livingstone, D.M.; Sommaruga, R.; Straile, D.; Van Donk, E. Lakes as sentinels of climate change. Limnol. Oceanogr. 2009, 54, 2283–2297. [Google Scholar] [CrossRef]
- Woolway, R.I.; Kraemer, B.M.; Lenters, J.D.; Merchant, C.J.; O’Reilly, C.M.; Sharma, S. Global lake responses to climate change. Nat. Rev. Earth Environ. 2020, 1, 388–403. [Google Scholar] [CrossRef]
- Zhang, F.; Ono, N.; Kanaya, S. Interpret Gaussian process models by using integrated gradients. Mol. Inform. 2025, 44, e202400051. [Google Scholar]
- Mi, C.; Sadeghian, A.; Lindenschmidt, K.-E.; Rinke, K. Variable withdrawal elevations as a management tool to counter the effects of climate warming in Germany’s largest drinking water reservoir. Environ. Sci. Eur. 2019, 31, 19. [Google Scholar] [CrossRef]
- Ficke, A.D.; Myrick, C.A.; Hansen, L.J. Potential impacts of global climate change on freshwater fisheries. Rev. Fish Biol. Fish. 2007, 17, 581–613. [Google Scholar] [CrossRef]
- Jankowski, T.; Livingstone, D.M.; Bührer, H.; Forster, R.; Niederhauser, P. Consequences of the 2003 European heat wave for lake temperature profiles, thermal stability, and hypolimnetic oxygen depletion: Implications for a warmer world. Limnol. Oceanogr. 2006, 51, 815–819. [Google Scholar] [CrossRef]
- Jansen, J.; Woolway, R.I.; Kraemer, B.M.; Albergel, C.; Bastviken, D.; Weyhenmeyer, G.A.; Marcé, R.; Sharma, S.; Sobek, S.; Tranvik, L.J.; et al. Global increase in methane production under future warming of lake bottom waters. Glob. Change Biol. 2022, 28, 5427–5440. [Google Scholar] [CrossRef]
- Bonacina, L.; Fasano, F.; Mezzanotte, V.; Fornaroli, R. Effects of water temperature on freshwater macroinvertebrates: A systematic review. Biol. Rev. 2023, 98, 191–221. [Google Scholar]
- North, R.P.; North, R.L.; Livingstone, D.M.; Köster, O.; Kipfer, R. Long-term changes in hypoxia and soluble reactive phosphorus in the hypolimnion of a large temperate lake: Consequences of a climate regime shift. Glob. Change Biol. 2014, 20, 811–823. [Google Scholar] [CrossRef]
- Di Nunno, F.; Zhu, S.; Ptak, M.; Sojka, M.; Granata, F. A stacked machine learning model for multi-step ahead prediction of lake surface water temperature. Sci. Total Environ. 2023, 890, 164323. [Google Scholar] [CrossRef]
- Anderson, E.J.; Stow, C.A.; Gronewold, A.D.; Mason, L.A.; McCormick, M.J.; Qian, S.S.; Ruberg, S.A.; Beadle, K.; Constant, S.A.; Hawley, N. Seasonal overturn and stratification changes drive deep-water warming in one of Earth’s largest lakes. Nat. Commun. 2021, 12, 1688. [Google Scholar] [CrossRef]
- Ayala, A.I.; Moras, S.; Pierson, D.C. Simulations of future changes in thermal structure of Lake Erken: Proof of concept for ISIMIP2b lake sector local simulation strategy. Hydrol. Earth Syst. Sci. 2020, 24, 3311–3330. [Google Scholar] [CrossRef]
- Yousefi, A.; Toffolon, M. Critical factors for the use of machine learning to predict lake surface water temperature. J. Hydrol. 2022, 606, 127418. [Google Scholar] [CrossRef]
- Read, J.S.; Jia, X.; Willard, J.; Appling, A.P.; Zwart, J.A.; Oliver, S.K.; Karpatne, A.; Hansen, G.J.; Hanson, P.C.; Watkins, W. Process-guided deep learning predictions of lake water temperature. Water Resour. Res. 2019, 55, 9173–9190. [Google Scholar] [CrossRef]
- Mukonza, S.S.; Chiang, J.-L. Micro-climate computed machine and deep learning models for prediction of surface water temperature using satellite data in Mundan water reservoir. Water 2022, 14, 2935. [Google Scholar] [CrossRef]
- Rezaei, M.; Moghaddam, M.A.; Azizyan, G.; Shamsipour, A.A. Prediction of agricultural drought index in a hot and dry climate using advanced hybrid machine learning. Ain Shams Eng. J. 2024, 15, 102686. [Google Scholar] [CrossRef]
- Oruc, S.; Hinis, M.A.; Tugrul, T. Evaluating performances of LSTM, SVM, GPR, and RF for drought prediction in Norway: A wavelet decomposition approach on regional forecasting. Water 2024, 16, 3465. [Google Scholar] [CrossRef]
- Oruc, S.; Tugrul, T.; Hinis, M.A. Beyond Traditional Metrics: Exploring the potential of Hybrid algorithms for Drought characterization and prediction in the Tromso Region, Norway. Appl. Sci. 2024, 14, 7813. [Google Scholar] [CrossRef]
- Rahmati, O.; Panahi, M.; Kalantari, Z.; Soltani, E.; Falah, F.; Dayal, K.S.; Mohammadi, F.; Deo, R.C.; Tiefenbacher, J.; Bui, D.T. Capability and robustness of novel hybridized models used for drought hazard modeling in southeast Queensland, Australia. Sci. Total Environ. 2020, 718, 134656. [Google Scholar] [PubMed]
- Chen, Y.; Hu, X.; Zhang, L. A review of ultra-short-term forecasting of wind power based on data decomposition-forecasting technology combination model. Energy Rep. 2022, 8, 14200–14219. [Google Scholar]
- Abdelhady, H.U.; Troy, C.D. A deep learning approach for modeling and hindcasting Lake Michigan ice cover. J. Hydrol. 2025, 649, 132445. [Google Scholar]
- Chambers, D.P. Evaluation of empirical mode decomposition for quantifying multi-decadal variations and acceleration in sea level records. Nonlinear Process. Geophys. 2015, 22, 157–166. [Google Scholar] [CrossRef]
- Ma, X.; Zhang, Y.; Wang, Y. Performance evaluation of kernel functions based on grid search for support vector regression. In Proceedings of the 2015 IEEE 7th International Conference on Cybernetics and Intelligent Systems (CIS) and IEEE Conference on Robotics, Automation and Mechatronics (RAM), Siem Reap, Cambodia, 15–17 July 2015; pp. 283–288. [Google Scholar]
- Coughlin, K.; Tung, K.K. Empirical mode decomposition and climate variability. In Hilbert-Huang Transform and Its Applications; World Scientific: Singapore, 2005; pp. 149–165. [Google Scholar]
- Sun, X.; Lin, Z. The regional features of temperature variation trends over China by empirical mode decomposition method. ACTA Geogr. Sin.-Chin. Ed. 2007, 62, 1132. [Google Scholar]
- Molla, M.K.I.; Rahman, M.S.; Sumi, A.; Banik, P. Empirical mode decomposition analysis of climate changes with special reference to rainfall data. Discret. Dyn. Nat. Soc. 2006, 2006, 045348. [Google Scholar] [CrossRef]
- Merabet, K.; Heddam, S. Improving the accuracy of air relative humidity prediction using hybrid machine learning based on empirical mode decomposition: A comparative study. Environ. Sci. Pollut. Res. 2023, 30, 60868–60889. [Google Scholar] [CrossRef]
- Bisoi, R.; Dash, P.K.; Parida, A.K. Hybrid variational mode decomposition and evolutionary robust kernel extreme learning machine for stock price and movement prediction on daily basis. Appl. Soft Comput. 2019, 74, 652–678. [Google Scholar] [CrossRef]
- Lahmiri, S. Comparing variational and empirical mode decomposition in forecasting day-ahead energy prices. IEEE Syst. J. 2015, 11, 1907–1910. [Google Scholar] [CrossRef]
- İlkentapar, M.; Citakoglu, H.; Talebi, H.; Aktürk, G.; Spor, P.; Çağlar, Y.; Akşit, S. Advanced hybrid machine learning methods for predicting rainfall time series: The situation at the Kütahya station in Türkiye. Model. Earth Syst. Environ. 2025, 11, 362. [Google Scholar] [CrossRef]
- Coşkun, Ö.; Citakoglu, H. Prediction of the standardized precipitation index based on the long short-term memory and empirical mode decomposition-extreme learning machine models: The Case of Sakarya, Türkiye. Phys. Chem. Earth Parts A/B/C 2023, 131, 103418. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013; 1535p. [Google Scholar]
- Stefanidis, K.; Varlas, G.; Papaioannou, G.; Papadopoulos, A.; Dimitriou, E. Trends of lake temperature, mixing depth and ice cover thickness of European lakes during the last four decades. Sci. Total Environ. 2022, 830, 154709. [Google Scholar] [PubMed]
- Jansen, J.; Simpson, G.L.; Weyhenmeyer, G.A.; Härkönen, L.H.; Paterson, A.M.; del Giorgio, P.A.; Prairie, Y.T. Climate-driven deoxygenation of northern lakes. Nat. Clim. Chang. 2024, 14, 832–838. [Google Scholar] [CrossRef]
- Baalsrud, K. The rehabilitation of Norway’s largest lake. Water Sci. Technol. 1982, 14, 21–30. [Google Scholar]
- Orderud, G.I.; Vogt, R.D. Trans-disciplinarity required in understanding, predicting and dealing with water eutrophication. Int. J. Sustain. Dev. World Ecol. 2013, 20, 404–415. [Google Scholar] [CrossRef][Green Version]
- Muñoz-Sabater, J.; Dutra, E.; Agustí-Panareda, A.; Albergel, C.; Arduini, G.; Balsamo, G.; Boussetta, S.; Choulga, M.; Harrigan, S.; Hersbach, H. ERA5-Land: A state-of-the-art global reanalysis dataset for land applications. Earth Syst. Sci. Data 2021, 13, 4349–4383. [Google Scholar][Green Version]
- Gumus, B.; Oruc, S.; Yucel, I.; Yilmaz, M.T. Impacts of climate change on extreme climate indices in Türkiye driven by high-resolution downscaled CMIP6 climate models. Sustainability 2023, 15, 7202. [Google Scholar] [CrossRef]
- Betts, A.K.; Reid, D.; Crossett, C. Evaluation of the FLake Model in ERA5 for Lake Champlain. Front. Environ. Sci. 2020, 8, 609254. [Google Scholar] [CrossRef]
- Balsamo, G.; Salgado, R.; Dutra, E.; Boussetta, S.; Stockdale, T.; Potes, M. On the contribution of lakes in predicting near-surface temperature in a global weather forecasting model. Tellus A Dyn. Meteorol. Oceanogr. 2012, 64, 15829. [Google Scholar][Green Version]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Xiao, C.; Sun, J. Recurrent neural networks (RNN). In Introduction to Deep Learning for Healthcare; Springer: Berlin/Heidelberg, Germany, 2021; pp. 111–135. [Google Scholar]
- Jiang, Q.; Tang, C.; Chen, C.; Wang, X.; Huang, Q. Stock price forecast based on LSTM neural network. In Proceedings of the International Conference on Management Science and Engineering Management, Melbourne, Australian, 1–4 August 2018; Springer: Berlin/Heidelberg, Germany, 2018; pp. 393–408. [Google Scholar]
- Agarwal, H.; Mahajan, G.; Shrotriya, A.; Shekhawat, D. Predictive data analysis: Leveraging RNN and LSTM techniques for time series dataset. Procedia Comput. Sci. 2024, 235, 979–989. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, W.; Zang, H.; Xu, D. Is the LSTM model better than RNN for flood forecasting tasks? A case study of Huayuankou station and Loude station in the lower Yellow River Basin. Water 2023, 15, 3928. [Google Scholar]
- Sumathy, R.; Sohail, S.F.; Ashraf, S.; Reddy, S.Y.; Fayaz, S.; Kumar, M. Next word prediction while typing using LSTM. In Proceedings of the 2023 8th International Conference on Communication and Electronics Systems (ICCES), Coimbatore, India, 1–3 June 2023; pp. 167–172. [Google Scholar]
- Karevan, Z.; Suykens, J.A. Spatio-temporal stacked LSTM for temperature prediction in weather forecasting. arXiv 2018, arXiv:1811.06341. [Google Scholar] [CrossRef]
- Jia, H.; Zhou, X. Water quality prediction method based on LSTM-BP. In Proceedings of the 2020 12th International Conference on Intelligent Human-Machine Systems and Cybernetics (IHMSC), Hangzhou, China, 22–23 August 2020; pp. 27–30. [Google Scholar]
- Wen, X.; Li, W. Time series prediction based on LSTM-attention-LSTM model. IEEE Access 2023, 11, 48322–48331. [Google Scholar]
- Sherstinsky, A. Fundamentals of recurrent neural network (RNN) and long short-term memory (LSTM) network. Phys. D Nonlinear Phenom. 2020, 404, 132306. [Google Scholar] [CrossRef]
- Zhang, Z. Customizing Kernels in Support Vector Machines; University of Waterloo: Waterloo, ON, Canada, 2007. [Google Scholar]
- Fathi Hafshejani, S.; Moaberfard, Z. A new trigonometric kernel function for support vector machine. Iran J. Comput. Sci. 2023, 6, 137–145. [Google Scholar]
- Lu, D.-G.; Li, G.-B. Reproducing kernel-based support vector machine for structural reliability analysis. In Proceedings of the 12th International Conference on Applications of Statistics and Probability in Civil Engineering, Vancouver, BC, Canada, 12–15 July 2015. [Google Scholar]
- Wang, W.; Xu, Z.; Lu, W.; Zhang, X. Determination of the spread parameter in the Gaussian kernel for classification and regression. Neurocomputing 2003, 55, 643–663. [Google Scholar] [CrossRef]
- Kusuma, M.; Kudus, A. Penerapan Metode Support Vector Regression (SVR) pada Data Survival KPR PT. Bank ABC, Tbk. Bdg. Conf. Ser. Stat. 2022, 2, 167–172. [Google Scholar] [CrossRef]
- Wang, S.; Deng, Z.; Chung, F.; Hu, W. From Gaussian kernel density estimation to kernel methods. Int. J. Mach. Learn. Cyber. 2013, 4, 119–137. [Google Scholar] [CrossRef]
- Schulz, E.; Speekenbrink, M.; Krause, A. A tutorial on Gaussian process regression: Modelling, exploring, and exploiting functions. J. Math. Psychol. 2018, 85, 1–16. [Google Scholar] [CrossRef]
- Niu, T.; Xu, Z.; Luo, H.; Zhou, Z. Hybrid Gaussian process regression with temporal feature extraction for partially interpretable remaining useful life interval prediction in Aeroengine prognostics. Sci. Rep. 2025, 15, 11057. [Google Scholar] [CrossRef]
- Cutajar, K. Broadening the Scope of Gaussian Processes for Large-Scale Learning; Sorbonne Université: Jussieu, Paris, 2019. [Google Scholar]
- Sun, A.Y.; Wang, D.; Xu, X. Monthly streamflow forecasting using Gaussian process regression. J. Hydrol. 2014, 511, 72–81. [Google Scholar] [CrossRef]
- Chang, C.; Zeng, T. A hybrid data-driven-physics-constrained Gaussian process regression framework with deep kernel for uncertainty quantification. J. Comput. Phys. 2023, 486, 112129. [Google Scholar] [CrossRef]
- Zhao, S.; Lu, J.; Yang, J.; Chow, E.; Xi, Y. Efficient two-stage gaussian process regression via automatic kernel search and subsampling. arXiv 2024, arXiv:2405.13785. [Google Scholar] [CrossRef]
- Hong, S.; Zhou, Z. Remaining useful life prognosis of bearing based on Gauss process regression. In Proceedings of the 2012 5th International Conference on BioMedical Engineering and Informatics, Chongqing, China, 16–18 October 2012; pp. 1575–1579. [Google Scholar]
- Übeylı, E.D.; Güler, I. Multilayer perceptron neural networks to compute quasistatic parameters of asymmetric coplanar waveguides. Neurocomputing 2004, 62, 349–365. [Google Scholar] [CrossRef]
- Mishra, S.; Prusty, R.; Hota, P.K. Analysis of Levenberg-Marquardt and Scaled Conjugate gradient training algorithms for artificial neural network based LS and MMSE estimated channel equalizers. In Proceedings of the 2015 International Conference on Man and Machine Interfacing (MAMI), Bhubaneswar, India, 17–19 December 2015; pp. 1–7. [Google Scholar]
- Kim, S.; Singh, V. Spatial Disaggregation of Areal Rainfall Using Two Different Artificial Neural Networks Models. Water 2015, 7, 2707–2727. [Google Scholar] [CrossRef]
- El Chaal, R.; Aboutafail, M.O. A comparative study of back-propagation algorithms: Levenberg-Marquart and BFGS for the formation of multilayer neural networks for estimation of fluoride. Commun. Math. Biol. Neurosci. 2022, 2022, 37. [Google Scholar]
- Hashim, F.R.; Daud, N.N.; Mokhtar, A.S.; Rashidi, A.F.; Ahmad, K. Optimization of ECG Peaks (Amplitude and Duration) in Predicting ECG Abnormality using Artificial Neural Network. Indian J. Sci. Technol. 2017, 10, 1–5. [Google Scholar] [CrossRef][Green Version]
- Moness, M.; Diaa-Eldeen, T. Experimental nonlinear identification of a lab-scale helicopter system using MLP neural network. In Proceedings of the 2017 13th International Computer Engineering Conference (ICENCO), Cairo, Egypt, 27–28 December 2017; pp. 166–171. [Google Scholar]
- Nawi, N.M.; Khan, A.; Rehman, M.Z.; Aziz, M.A.; Herawan, T.; Abawajy, J.H. An Accelerated Particle Swarm Optimization Based Levenberg Marquardt Back Propagation Algorithm; Springer International Publishing: Cham, Switzerland, 2014; pp. 245–253. [Google Scholar]
- Kim, T.-W.; Valdés, J.B. Nonlinear model for drought forecasting based on a conjunction of wavelet transforms and neural networks. J. Hydrol. Eng. 2003, 8, 319–328. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. In Machine learning; Springer: Berlin/Heidelberg, Germany, 2001; Volume 45, pp. 5–32. [Google Scholar]
- En-Nagre, K.; Aqnouy, M.; Ouarka, A.; Naqvi, S.A.A.; Bouizrou, I.; El Messari, J.E.S.; Tariq, A.; Soufan, W.; Li, W.; El-Askary, H. Assessment and prediction of meteorological drought using machine learning algorithms and climate data. Clim. Risk Manag. 2024, 45, 100630. [Google Scholar] [CrossRef]
- Shang, K.; Xu, L.; Liu, X.; Yin, Z.; Liu, Z.; Li, X.; Yin, L.; Zheng, W. Study of urban heat island effect in Hangzhou metropolitan area based on SW-TES algorithm and image dichotomous model. Sage Open 2023, 13, 21582440231208851. [Google Scholar] [CrossRef]
- Choi, C.; Kim, J.; Han, H.; Han, D.; Kim, H.S. Development of water level prediction models using machine learning in wetlands: A case study of Upo wetland in South Korea. Water 2019, 12, 93. [Google Scholar] [CrossRef]
- Biau, G.; Scornet, E. A random forest guided tour. Test 2016, 25, 197–227. [Google Scholar] [CrossRef]
- Yu, P.-S.; Yang, T.-C.; Chen, S.-Y.; Kuo, C.-M.; Tseng, H.-W. Comparison of random forests and support vector machine for real-time radar-derived rainfall forecasting. J. Hydrol. 2017, 552, 92–104. [Google Scholar] [CrossRef]
- Tyralis, H.; Papacharalampous, G.; Langousis, A. A brief review of random forests for water scientists and practitioners and their recent history in water resources. Water 2019, 11, 910. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational mode decomposition. IEEE Trans. Signal Process. 2013, 62, 531–544. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, F.; Jiang, Z.; He, S.; Mo, Q. Complex variational mode decomposition for signal processing applications. Mech. Syst. Signal Process. 2017, 86, 75–85. [Google Scholar] [CrossRef]
- Danandeh Mehr, A.; Reihanifar, M.; Alee, M.M.; Vazifehkhah Ghaffari, M.A.; Safari, M.J.S.; Mohammadi, B. VMD-GP: A new evolutionary explicit model for meteorological drought prediction at ungauged catchments. Water 2023, 15, 2686. [Google Scholar] [CrossRef]
- Maji, U.; Pal, S. Empirical mode decomposition vs. variational mode decomposition on ECG signal processing: A comparative study. In Proceedings of the 2016 International Conference on Advances in Computing, Communications and Informatics (ICACCI), Jaipur, India, 21–24 September 2016; pp. 1129–1134. [Google Scholar]
- Wang, Y.; Markert, R. Filter bank property of variational mode decomposition and its applications. Signal Process. 2016, 120, 509–521. [Google Scholar] [CrossRef]
- Fortin, M.; Glowinski, R. Augmented Lagrangian Methods: Applications to the Numerical Solution of Boundary-Value Problems; Elsevier: Amsterdam, The Netherlands, 2000; Volume 15. [Google Scholar]
- Giesen, J.; Laue, S. Combining ADMM and the Augmented Lagrangian Method for Efficiently Handling Many Constraints. In Proceedings of the IJCAI, Macao, Chian, 10–16 August 2019; pp. 4525–4531. [Google Scholar]
- Mutinda, J.K.; Langat, A.K.; Mwalili, S.M. Forecasting Temperature Time Series Data Using Combined Statistical and Deep Learning Methods: A Case Study of Nairobi County Daily Temperature. Int. J. Math. Math. Sci. 2025, 2025, 4795841. [Google Scholar] [CrossRef]
- Liu, J.; Wang, K.; Zhao, M.; Chen, Y.; Li, X. Enhanced concrete crack detection using nonlinear ultrasonic signal denoising and feature enhancement with CEEMDAN, VMD and GRU. Meas. Sci. Technol. 2024, 36, 016164. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. London. Ser. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Flandrin, P.; Rilling, G.; Goncalves, P. Empirical mode decomposition as a filter bank. IEEE Signal Process. Lett. 2004, 11, 112–114. [Google Scholar] [CrossRef]
- ur Rehman, N.; Mandic, D.P. Empirical mode decomposition for trivariate signals. IEEE Trans. Signal Process. 2009, 58, 1059–1068. [Google Scholar] [CrossRef]
- Sarangi, S.; Biswal, C.; Sahu, B.K.; Samanta, I.S.; Rout, P.K. Fault detection technique using time-varying filter-EMD and differential-CUSUM for LVDC microgrid system. Electr. Power Syst. Res. 2023, 219, 109254. [Google Scholar]
- Calvo, M.S.; Lee, H.S. Enhanced complete ensemble EMD with superior noise handling capabilities: A robust signal decomposition method for power systems analysis. Eng. Rep. 2024, 6, e12862. [Google Scholar] [CrossRef]
- Rilling, G.; Flandrin, P.; Goncalves, P. On empirical mode decomposition and its algorithms. In Proceedings of the IEEE-EURASIP Workshop on Nonlinear Signal and Image Processing NSIP-03, Grado, Italy, 8–11 June 2003. [Google Scholar]
- Barnhart, B.; Eichinger, W. Empirical mode decomposition applied to solar irradiance, global temperature, sunspot number, and CO2 concentration data. J. Atmos. Sol.-Terr. Phys. 2011, 73, 1771–1779. [Google Scholar] [CrossRef]
- Wang, J.; Du, G.; Zhu, Z.; Shen, C.; He, Q. Fault diagnosis of rotating machines based on the EMD manifold. Mech. Syst. Signal Process. 2020, 135, 106443. [Google Scholar] [CrossRef]
- Zeiler, A.; Faltermeier, R.; Keck, I.R.; Tomé, A.M.; Puntonet, C.G.; Lang, E.W. Empirical mode decomposition-an introduction. In Proceedings of the 2010 International Joint Conference on Neural Networks (IJCNN), Barcelona, Spain, 18–23 July 2010; pp. 1–8. [Google Scholar]
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Randall, R.B.; Antoni, J. Why EMD and similar decompositions are of little benefit for bearing diagnostics. Mech. Syst. Signal Process. 2023, 192, 110207. [Google Scholar] [CrossRef]
- Looney, D.; Mandic, D.P. Emperical mode decompoaition for simultateous image enhancement and fusion. In Image Fusion Algorithms and Applications; Imperial College: London, UK, 2008; pp. 327–339. [Google Scholar]
- Zheng, D.; Zhang, W.; Alemu, S.; Wang, P.; Bitew, G.; Wei, D.; Yue, J. Short-term renewable generation and load forecasting in microgrids. In Microgrid Protection and Control; Elsevier: Amsterdam, The Netherlands, 2021; pp. 57–96. [Google Scholar] [CrossRef]
- Khan, M.M.H.; Muhammad, N.S.; El-Shafie, A. Wavelet based hybrid ANN-ARIMA models for meteorological drought forecasting. J. Hydrol. 2020, 590, 125380. [Google Scholar] [CrossRef]
- Zhang, D. A Coefficient of Determination for Generalized Linear Models. Am. Stat. 2017, 71, 310–316. [Google Scholar] [CrossRef]
- Ehteram, M.; Ahmed, A.N.; Ling, L.; Fai, C.M.; Latif, S.D.; Afan, H.A.; Banadkooki, F.B.; El-Shafie, A. Pipeline scour rates prediction-based model utilizing a multilayer perceptron-colliding body algorithm. Water 2020, 12, 902. [Google Scholar] [CrossRef]
- Zhu, S.; Ptak, M.; Yaseen, Z.M.; Dai, J.; Sivakumar, B. Forecasting surface water temperature in lakes: A comparison of approaches. J. Hydrol. 2020, 585, 124809. [Google Scholar] [CrossRef]
- Feigl, M.; Lebiedzinski, K.; Herrnegger, M.; Schulz, K. Machine-learning methods for stream water temperature prediction. Hydrol. Earth Syst. Sci. 2021, 25, 2951–2977. [Google Scholar] [CrossRef]
- Tuğrul, T.; Hinis, M.A. Performance enhancement of models through discrete wavelet transform for streamflow forecasting in Çarşamba River, Türkiye. J. Water Clim. Chang. 2025, 16, 736–756. [Google Scholar] [CrossRef]
- Tuğrul, T.; Hinis, M.A. Improvement of drought forecasting by means of various machine learning algorithms and wavelet transformation. Acta Geophys. 2025, 73, 855–874. [Google Scholar] [CrossRef]
- Tuğrul, T.; Hınıs, M.A.; Oruç, S. Comparison of LSTM and SVM methods through wavelet decomposition in drought forecasting. Earth Sci. Inform. 2025, 18, 139. [Google Scholar] [CrossRef]
- Chen, L.; Wang, L.; Ma, W.; Xu, X.; Wang, H. PID4LaTe: A physics-informed deep learning model for lake multi-depth temperature prediction. Earth Sci. Inform. 2024, 17, 3779–3795. [Google Scholar] [CrossRef]
- Citakoglu, H.; Aktürk, G.; Demir, V. Hybrid machine learning for drought prediction at multiple time scales: A case study of Ağrı station, Türkiye. Acta Geophys. 2025, 73, 1643–1677. [Google Scholar] [CrossRef]
- Citakoglu, H.; Coşkun, Ö. Comparison of hybrid machine learning methods for the prediction of short-term meteorological droughts of Sakarya Meteorological Station in Turkey. Environ. Sci. Pollut. Res. 2022, 29, 75487–75511. [Google Scholar] [CrossRef] [PubMed]
- Tong, Y.; Feng, L.; Wang, X.; Pi, X.; Xu, W.; Woolway, R.I. Global lakes are warming slower than surface air temperature due to accelerated evaporation. Nat. Water 2023, 1, 929–940. [Google Scholar] [CrossRef]
- Bachmann, R.W.; Canfield, D.E., Jr.; Sharma, S.; Lecours, V. Warming of near-surface summer water temperatures in lakes of the conterminous United States. Water 2020, 12, 3381. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).