Optimal Configuration and Empirical Analysis of a Wind–Solar–Hydro–Storage Multi-Energy Complementary System: A Case Study of a Typical Region in Yunnan

Abstract

The increasing integration of wind and photovoltaic energy into power systems brings about large fluctuations and significant challenges for power absorption. Wind–solar–hydro–storage multi-energy complementary systems, especially joint dispatching strategies, have attracted wide attention due to their ability to coordinate the advantages of different resources and enhance both flexibility and economic efficiency. This paper develops a capacity optimization model for a wind–solar–hydro–storage multi-energy complementary system. The objectives are to improve net system income, reduce wind and solar curtailment, and mitigate intraday fluctuations. We adopt the quantum particle swarm algorithm (QPSO) for outer-layer global optimization, combined with an inner-layer stepwise simulation to maximize life cycle benefits under multi-dimensional constraints. The simulation is based on the output and load data of typical wind, solar, water, and storage in Yunnan Province, and verifies the effectiveness of the proposed model. The results show that after the wind–solar–hydro–storage multi-energy complementary system is optimized, the utilization rate of new energy and the system economy are significantly improved, which has a wide range of engineering promotion value. The research results of this paper have important reference significance for the construction of new power systems and the engineering design of multi-energy complementary projects.

1. Introduction

As the energy structure shifts toward clean and low-carbon sources worldwide, renewable energy such as wind and solar is increasingly integrated into power systems. China’s “carbon peaking and carbon neutrality” targets demand greater flexibility, regulation capacity, and accommodation of renewables in the grid [1].

In recent years, both domestic and international research has focused on optimizing the configuration and coordinated dispatch of wind–solar–hydro–storage systems. Studies have shown that proper allocation and operation of these resources can effectively reduce renewable energy fluctuation impacts and improve system utilization and economic performance [2]. However, most existing works focus on the technical feasibility or simulation of dispatch strategies and lack detailed modeling of actual system constraints, especially in high-renewable regions with complex temporal and spatial coupling. Moreover, there is insufficient attention to economic assessment and the integration of multi-objective constraints such as investment, curtailment, and flexibility.

Currently, the optimization of wind–solar–hydro–storage multi-energy complementary systems still face multiple engineering and modeling challenges. On one hand, wind and solar output are significantly influenced by meteorological conditions, hydropower is constrained by the spatiotemporal distribution of river runoff, and load structures exhibit high volatility and regional imbalance. System optimization must consider multi-source coordination, dynamic dispatching, and multi-dimensional constraints. On the other hand, traditional linear and dynamic programming methods have limitations in computational efficiency and global convergence when addressing large-scale nonlinear, strongly coupled, and multi-constrained optimization problems [3].

Despite significant progress in the optimization of wind–solar–hydro–storage multi-energy complementary systems, existing studies still have the following limitations:

• Insufficient coordination optimization of multi-energy complementary systems: Current research mostly focuses on the optimization of individual energy forms, lacking comprehensive coordination optimization of wind, solar, hydro, and storage energy forms. For example, (Wen et al., 2020) [4] considered the impact of prediction uncertainty on the scheduling risk and benefits of wind–solar–hydro multi-energy complementary systems but did not involve the optimization configuration of energy storage systems. In addition, (Cheng et al., 2019) [5] proposed a collaborative optimization scheduling model and mechanism for basin-type wind–solar–hydro multi-energy complementary bases oriented towards clean energy consumption but did not fully consider the role of energy storage systems.
• Limitations in the application of intelligent algorithms: Although intelligent algorithms such as particle swarm optimization (PSO) and quantum-behaved particle swarm optimization (QPSO) have been widely used in the capacity configuration and dispatch optimization of multi-energy systems in recent years, there are still limitations in the improvement and application of these algorithms. For example, (Zhang et al., 2020) [6] proposed a short-term optimal operation method for wind–solar–hydro hybrid systems considering uncertainties but did not involve the optimization of multi-energy complementary systems. In addition, (Monforti et al., 2014) [7] used the Monte Carlo method to assess the complementarity of wind and solar resources for energy production in Italy but did not consider the application of intelligent algorithms in optimization.
• Insufficient consideration of multi-dimensional constraints in system optimization: Existing studies often ignore multi-dimensional constraints such as land use, investment costs, and environmental impacts during the optimization process. For example, (Zhu et al., 2017) [8] studied the operation of water–solar–wind complementary systems in typical hydropower stations in the upper reaches of the Jinsha River but did not consider constraints such as land use and investment costs. In addition, (Zhu et al., 2018) [9] proposed an optimal capacity configuration method for hydro–photovoltaic–wind complementary power generation systems under wind and photovoltaic curtailment but did not involve constraints such as land use and investment costs.
• Insufficient coordination of long-term and short-term optimization: Existing studies mostly focus on short-term optimization and lack coordination between long-term and short-term optimization. For example, (Jacobson et al., 2015) [10] proposed an optimal capacity configuration method for hydro–photovoltaic–wind complementary power generation systems under wind and photovoltaic curtailment but did not involve long-term optimization. In addition, (Liu et al., 2021) [11] studied the form of water–wind–solar energy complementarity but did not consider the coordination of long-term and short-term optimization.

In recent years, intelligent algorithms such as particle swarm optimization (PSO) and quantum-behaved particle swarm optimization (QPSO) [12] have been widely applied in capacity configuration and dispatching optimization of multi-energy systems due to their strong global search capabilities and adaptability to complex constraints, achieving favorable results [13,14].

Yunnan Province, rich in hydropower, wind, and solar energy resources, has consistently ranked among the top in the country in terms of green energy capacity and transmission capacity. According to the “Current Situation of Yunnan Power Supply and Demand and 14th Five-Year Development Study” and the “Yunnan Power Grid New Power System Construction Action Plan (2024–2035),” Yunnan’s new energy capacity is expected to maintain an annual growth rate of over 20% in the coming years, becoming the dominant incremental power source. By 2030, the proportion of non-fossil energy capacity is projected to exceed 88%.

High shares of renewable energy create significant challenges for power system balance and flexibility. In Yunnan, seasonal and intraday fluctuations of new energy, along with the transitions between wet and dry seasons for hydropower and the uncertainty of wind and solar, often cause mismatches between load peaks and renewable output. As a result, wind, solar, and hydro curtailment occur frequently. Especially under the dual drivers of sustained load growth and the demand for high-energy-consuming green industries and “West-to-East Power Transmission,” the peaking capacity of the traditional hydropower and thermal power complementary mode is limited. In some periods, the pressure on power supply security is significant, highlighting the shortcomings of flexibility regulation resources.

Meanwhile, energy storage systems play an increasingly important role in improving load regulation capacity, smoothing output fluctuations, and promoting source-load coordination. Yunnan’s “14th Five-Year Plan” has explicitly proposed new energy storage development goals and introduced the “Yunnan Province New Energy Storage Development Implementation Plan (2024–2025),” encouraging multi-energy collaboration and large-scale demonstration projects of energy storage. This provides a favorable policy framework for the optimization of wind–solar–hydro–storage multi-energy complementary systems.

To address these gaps, this paper proposes a comprehensive two-layer optimization model that jointly considers economic, operational, and engineering constraints, leveraging QPSO for improved global optimization performance. The novelty of our approach lies in (1) the introduction of a dual-layer (annual profit–hourly dispatch) architecture, (2) incorporation of real Yunnan region multi-source data and policy boundaries, and (3) a rigorous scenario-based evaluation framework.

Against this backdrop, this paper focuses on the wind–solar–hydro–storage multi-energy complementary system in Yunnan Province. Taking the maximization of system net revenue as the core objective and considering multidimensional constraints such as curtailment rates, deficit duration, maximum deficit value, intraday volatility, investment, and land use, a capacity optimization configuration model for wind–solar–hydro–storage multi-energy complementary systems is established. The model is based on actual annual load data and historical output data of wind, solar, and hydropower, and employs the QPSO algorithm for capacity optimization and annual hourly dynamic simulation. The study analyzes the economic efficiency, flexibility, and feasibility of multi-energy coordination and energy storage participation in the system. The research aims to provide theoretical support and practical references for the engineering planning and policy-making of high-proportion renewable energy systems, contributing to the construction of new power systems in Yunnan Province and its green and low-carbon transition.

To address the above limitations, this paper proposes the following innovations:

(1)

Comprehensive coordination optimization of multi-energy complementary systems: This paper establishes a bi-level optimization model that comprehensively considers wind, solar, hydro, and storage energy forms, achieving closed-loop decision-making between capacity and operation.

(2)

Improved quantum-behaved particle swarm optimization algorithm (QPSO): This paper adopts an adaptive quantum-behaved particle swarm optimization algorithm (QPSO), which significantly improves the global search capability and convergence success rate of the algorithm through linearly decreasing expansion coefficients and Lévy perturbation.

(3)

Comprehensive consideration of multi-dimensional constraints: This paper fully considers multi-dimensional constraints such as land use, investment costs, and environmental impacts during the optimization process, making the optimization results more valuable for practical applications.

(4)

Coordination of long-term and short-term optimization: This paper achieves optimal operation of the system on different time scales through coordination of long-term and short-term optimization.

The remainder of this paper is organized as follows. Section 2 provides an overview of the key problems and challenges associated with wind–solar–hydro–storage multi-energy complementary systems, focusing on output volatility, system flexibility, market mechanisms, and operational coordination issues. Section 3 details the mechanisms and methods used in this study, including the overall model framework, the formulation of the bi-level optimization problem, and the implementation of the quantum particle swarm optimization (QPSO) algorithm. Section 4 presents the case study and empirical analysis, demonstrating the effectiveness of the proposed optimization approach through a practical example from Yunnan Province. Section 5 concludes the paper by summarizing the main findings, providing quantitative results, and discussing implications for future research and engineering applications.

2. Problems and Challenges

2.1. Output Volatility and Insufficient System Flexibility in Wind–Solar–Hydro–Storage Multi-Energy Complementary Systems

After the large-scale promotion of wind–solar–hydro–storage multi-energy complementary systems in Yunnan, the intermittent and volatile nature of renewable energy generation has further exacerbated the difficulty of system balance. Affected by climate, hydrology, and sunshine conditions, renewable energy output has significant uncertainty, which can easily lead to frequent abandonment of wind, solar, and water [15,16]. In addition, although Yunnan has a strong ability to regulate high-proportion hydropower, there is a significant difference in hydropower generation capacity between the flood season and the dry season. In some periods, the combined output of wind, solar, and water is still difficult to fully absorb, which further tests the system’s flexible scheduling ability [17].

2.2. Insufficient Adaptability of Market Mechanisms and Resource Allocation

Under the current power market framework, different types of power generation resources (such as hydropower, thermal power, wind, and solar) compete on a unified market platform. Due to significant differences in cost structures and operational characteristics, a uniform market mechanism struggles to accommodate the interests of various power sources. Low marginal cost power sources like hydropower, wind, and solar compete directly with high marginal cost power sources like thermal power, leading to reduced peaking willingness of thermal power and compromised system reliability and flexibility [18,19]. Some pilot markets have adopted approaches such as segmented markets and capacity compensation mechanisms to alleviate structural contradictions. However, issues such as priority dispatch of different power sources during segmented periods and benefit distribution remain unresolved [20,21].

2.3. Short-Term Dispatch and Long-Term Reservoir Operation Coordination Challenges

When hydropower stations participate in the electricity spot market, they must not only ensure short-term market competitiveness but also take into account the long-term planning of reservoir water levels and regulation capacity. If they are only guided by the immediate benefits of the spot market, it is easy for the reservoir water level to drop in advance and the subsequent power generation capacity to be limited and even affect the overall power supply security. Therefore, how to incorporate long-term reservoir constraints into the market model and achieve the coordinated optimization of short-term market and long-term operation goals is one of the difficulties in the current system optimization configuration.

2.4. Complexity of Cross-Temporal and Spatial Resource Allocation and System Security Constraints

In Yunnan, hydropower, wind, and solar bases are distributed far from load centers, resulting in frequent cross-regional power flows. For example, over 70% of renewable generation must be transmitted over 300 km to main loads [15]. This creates multiple security constraints—such as power flow limits and backup channel requirements—that increase dispatch model complexity. At the same time, in the context of extreme climate and sudden load changes, how to use flexible resources such as energy storage to respond quickly and ensure the safe and stable operation of the system is also a practical problem that needs to be solved urgently [22].

In 2022, Yunnan experienced a renewable energy output standard deviation of 17.2% between dry and wet seasons, while curtailment rates for new energy reached 5.8% due to insufficient flexibility and lack of coordinated dispatch [16]. These data underscore the urgent need for cross-disciplinary, temporal, and multi-objective optimization research to support the reliable and efficient transformation of the power system.

3. Mechanisms and Methods

3.1. Overall Structural Framework of the Model

The wind–solar–hydro–storage multi-energy complementary system is an intelligent coordinated energy supply system that integrates multiple energy forms such as wind energy, solar energy (hydropower, photovoltaic), hydropower, and electrochemical energy storage. It aims to give full play to the complementary characteristics of various energy types, improve the utilization rate of new energy resources and the overall flexibility of the system. For Yunnan Province, there are abundant hydropower resources, great potential for the development of wind and solar resources, and outstanding demand for green and low-carbon power systems. The multi-energy complementary structure has become the core technical path for the future power grid to absorb a high proportion of renewable energy and operate safely and stably.

The model adopts a two-layer structure: the outer capacity optimization is mainly responsible for the capacity and operation strategy configuration of wind power, photovoltaic, energy storage and hydropower, with the goal of maximizing the annual net profit of the system; the inner operation simulation combines the daily and hourly (365 days) rolling energy balance to dynamically simulate the coordinated operation process of each energy unit. Through grid integration, each unit organically combines its own output characteristics, regulation capabilities and economic parameters to form a highly coupled complex system of “source-load-storage”, and outputs the actual operation performance and constraint indicators of the system.

The core logic of the system operation is as follows: At each moment t, the total system output is formed by the superposition of the hourly/daily standardized output of wind power, photovoltaic power, and hydropower, and is balanced in real time with the local load. When the system output is higher than the load, the energy storage unit is charged first to absorb the redundant power; when the system output is lower than the load, the energy storage unit is discharged at the maximum power to make up for the gap. If the energy storage charge and discharge still cannot be balanced, it will be recorded as a power supply gap or power abandonment, which will be accumulated and counted throughout the year and included in the subsequent economic and feasibility evaluation.

Typical characteristics of wind–solar–hydro–storage multi-energy complementary systems include:

(1)

Resource complementarity in time and space: Wind, solar, and hydro output have certain complementarity, which can alleviate the seasonal and intraday fluctuations of single energy output.

(2)

Flexible adjustment of energy storage: The electrochemical energy storage system can be dynamically adjusted when the load fluctuates or the wind and solar power fluctuate violently, realizing the transfer and smoothing of energy in time and improving system reliability.

(3)

Multi-objective collaborative optimization: The system not only focuses on maximizing annual economic efficiency but also takes into account multi-dimensional constraints such as power abandonment rate, load gap, operation volatility, land, and investment, to achieve the goal of theory-engineering-economy integration.

(4)

Scalability and engineering adaptability: The architecture can flexibly adjust parameters and models according to the energy endowment and load structure of different regions to adapt to actual application scenarios.

Therefore, Yunnan’s wind–solar–hydro–storage multi-energy complementary system architecture not only meets the engineering needs of high-proportion consumption of regional green energy and safe power supply but also provides a replicable technical reference and practical path for the construction of my country’s new power system and multi-energy integration.

All modeling, simulation, and optimization tasks in this study were performed using Python 3.10 (Python Software Foundation, https://www.python.org/ (accessed on 27 June 2025)) with core packages including NumPy, Pandas, Matplotlib, and SciPy. The quantum particle swarm optimization (QPSO) algorithm and all simulation workflows were implemented as custom Python scripts. The code development and execution were conducted within the PyCharm Professional 2023.1 integrated development environment (IDE) (JetBrains s.r.o., Prague, Czech Republic, https://www.jetbrains.com/pycharm/ (accessed on 27 June 2025)), under a valid institutional license under an institutional license (license details available upon request). All results were post-processed and all figures were generated using Matplotlib in Python, unless otherwise specified.

3.2. Two-Layer Optimization Model

Bi-level optimization is a complex decision-making method with a hierarchical structure, which is widely used in modeling and solving multi-objective, multi-constrained, coupled decision-making problems. This method usually consists of two levels of “outer optimization” and “inner optimization”, each with independent objective functions and decision variables, and coupled through upstream and downstream relationships in the solution space.

In general, the two-level optimization model can be abstractly expressed as follows:

(1)

Outer optimization: max $F(x,y) \mathrm{s}.\mathrm{t} G(\mathrm{x},\mathrm{y})\ge 0$

(2)

Inner layer optimization: max $f(x,y) \mathrm{s}.\mathrm{t} H(\mathrm{x},\mathrm{y})\ge 0$

Among them, x is the outer decision variable, and y is the inner decision variable. After the outer layer gives x, the inner layer seeks the optimal y for the given x, and feeds the result back to the outer layer target evaluation until the whole converges to the global optimal solution (see Figure 1).

3.2.1. Objective Function

The outer optimization goal is to maximize the annual net profit of the system, and the mathematical expression is as follows:

$$\max \left\{N_{profit}=R_{total}-CPA-CEA\right\}$$

(1)

where $N_{profit}$ represents system annual net profit, $R_{total}$ represents system annual total income, $CPA$ denotes annual costs of wind power and photovoltaic power, $CEA$ denotes annual cost of energy storage.

The total annual income $R_{total}$ is broken down into

$$R_{total}=E_w\cdot p_w+E_v\cdot p_v+E_E\cdot p_E$$

(2)

where $E_w$, $E_v$, $E_E$ represent the annual power transmission of wind power, photovoltaic power and energy storage, respectively, $p_w$, $p_v$, $p_E$ represent their respective settlement electricity prices.

3.2.2. Annual Cost of Wind Power and Photovoltaic Power

According to the established formula or standard, the expenses incurred by wind power and photovoltaic power generation projects within one year are summarized and accounted for, so as to obtain their total annual cost.

$$CPA=C{P}_{IN}+C{P}_{IC}+C{P}_{OM}$$

(3)

$$C{P}_{IN}=CRF\left(r,n\right)\cdot \alpha \cdot CP$$

(4)

$$C{P}_{IC}=\left(1-\alpha \right)\cdot CP\cdot {\displaystyle \frac{i{\left(1+i\right)}^m}{{\left(1+I\right)}^m-1}}$$

(5)

$$C{P}_{OM}=\gamma \cdot CP$$

(6)

$$CP=CW\cdot P_W+CS\cdot P_S$$

(7)

$$CRF\left(r,n\right)=r{(1+r)}^n/[{(1+r)}^n-1]$$

(8)

where $C{P}_{IN}$, $C{P}_{IC}$, $C{P}_{OM}$ represent annual cost of wind power and photovoltaic construction capital conversion, annual principal and interest payment costs generated by construction loans, and annual operation and maintenance costs, $CP$ denotes the total investment in wind power and photovoltaic construction, $CRF\left(r,n\right)$ denotes capital recovery factor, $r$ represents discount rate, $n$ denotes years of operation, $\alpha$, $i$, $m$, $\gamma$ respectively represent the capital ratio, loan interest rate, loan term, and annual operation and maintenance fee rate, $P_W$, $P_S$ represent wind power installed capacity, photovoltaic installed capacity, $CW$, $CS$ represent unit cost of wind power and photovoltaic power.

3.2.3. Annual Cost of Energy Storage

All related expenses (such as depreciation, operation and maintenance, capital costs, etc.) incurred by energy storage facilities within one year are counted and converted into annual averages, so as to obtain their total annual costs.

$$CEA=C{E}_{IN}+C{E}_{IC}+C{E}_{OM}+C{E}_R$$

(9)

where $C{E}_{IN}$ denotes annual cost of energy storage construction capital, $C{E}_{IC}$, $C{E}_{OM}$, $C{E}_R$ denote annual principal and interest payment of construction loans, and annual operation and maintenance costs, and complementary power generation system.

$$C{E}_{IN}=CRF\left(r,n\right)\cdot \beta \cdot CE$$

(10)

$$C{E}_{IC}=\left(1-\beta \right)\cdot CE\cdot {\displaystyle \frac{i{\left(1+i\right)}^y}{{\left(1+I\right)}^y-1}}$$

(11)

$$C{E}_{OM}=\delta \cdot CE$$

(12)

$$CE=CEP\cdot P_E+CES\cdot \left(P_E\times T_E\right)$$

(13)

$$C{E}_R={\displaystyle \frac{E_E\cdot CES}{x}}$$

(14)

where $\beta$, $\delta$, $y$ respectively represent the energy storage capital ratio, energy storage annual operation maintenance rate, and energy storage loan period, $CE$ denotes the total investment in energy storage, $CEP$, $CES$ denote energy storage power cost, and energy storage capacity cost, $P_E$, $T_E$ represent energy storage power and energy storage duration, respectively.

The life of energy storage directly affects the annual cost of energy storage in Formulas (10)–(14). The depth of discharge ($DOD$) is the most critical factor affecting the maximum number of cycles of energy storage. The larger the $DOD$, the shorter the energy storage life [23]. In engineering, the relationship curve between the experimentally measured energy storage $DOD$ and its maximum number of cycles $N$ is usually used as a benchmark. This paper uses the equivalent cycle life method to calculate the life of energy storage. During the calculation process, the energy storage SOC annual curve is used to count and extract each actual cycle using the rain flow counting method. The energy storage SOC annual curve is obtained by optimizing the inner layer production simulation.

$$N=3452\cdot DO{D}^{-0.9942}-1030$$

(15)

$$x={\displaystyle \frac{N}{365}}$$

(16)

where $DOD$ denotes actual average discharge depth of energy storage, $N$ represents maximum number of cycles.

3.2.4. External Model Constraints

$$CP+CE\le C_{max}$$

(17)

$$S_{total}=P_W\cdot S_W+P_S\cdot S_S+P_E\cdot S_E+S_{\mathrm{Auxiliary}}$$

(18)

$$S_{total}\le S_{max}$$

(19)

where $C_{max}$ denotes total investment limit, $S_{total}$ denotes total land area, calculated by wind, solar, storage and auxiliary facilities; $S_{max}$ denotes land use limit. $S_W$ denotes wind power unit occupancy, $S_S$ denotes photovoltaic unit are, $S_E$ denotes energy storage unit area. $S_{\mathrm{Auxiliary}}$ represents land for auxiliary facilities construction.

3.3. Inner Layer Optimization Model

The inner layer aims to achieve smooth output throughout the year and minimize gaps and power abandonment. The main evaluation indicators include:

Intraday volatility index $F_1$:

$$F_1={\displaystyle \sum }_{t=1}^n\mid F_{out}\left(t\right)-{\overline{F}}_{out}\mid$$

(20)

$$F_1\le F_{1,max}$$

(21)

where $F_{\mathrm{out}}\left(t\right)$, ${\overline{F}}_{\mathrm{out}}$ represent net output after energy storage regulation on day t and average net output for the whole year.

Annual peak-to-valley difference $F_2$:

$$F_2=max\left(F_{\mathrm{out}}\right)-min\left(F_{\mathrm{out}}\right)$$

(22)

$$F_2\le F_{2,max}$$

(23)

Inner Constraints and Energy Recursion

Total gap and power abandonment rate throughout the year:

$$Shortag{e}_t=\max (0,Loa{d}_t-\left(P{G}_t+P_t^{discharge}-P_t^{charge}\right))$$

(24)

$$Shortag{e}_t\le 1\times {10}^7\mathrm{k}\mathrm{W}\mathrm{h}$$

(25)

$$Los{s}_t=\max \left(0,P{G}_t-Loa{d}_t-P_t^{ch\mathit{arg}e}\right)$$

(26)

$$Los{s}_t\le 5\%$$

(27)

where $Loa{d}_t$ denotes Load on day t, $P{G}_t$ represents the combined wind, solar and hydroelectric power generation of the system on that day, $P_t^{discharge}$ denotes energy storage discharge, $P_t^{charge}$ denotes Energy storage charging capacity.

Energy balance constraints:

$$P{G}_t=P_W\cdot win{d}_t+P_S\cdot sola{r}_t+hydr{o}_t$$

(28)

where ${\mathrm{wind}}_t$, ${\mathrm{solar}}_t$ represent wind and solar power output curve per MW, ${\mathrm{hydro}}_t$ denotes actual daily hydropower output.

$$P{G}_t+P_t^{discharge}-P_t^{charge}=Loa{d}_t-Shortag{e}_t$$

(29)

Energy storage state recursion and boundary:

$$SO{C}_{t+1}=SO{C}_t+{\eta }_{charge}\cdot P_t^{\mathrm{charge}}\cdot {\displaystyle \frac{P_t^{\mathrm{discharge}}}{{\eta }_{discharge}}}$$

(30)

$$SO{C}_{\min }\le SO{C}_t\le SO{C}_{\max }$$

(31)

where $SO{C}_t$ represents the state of charge of the energy storage system, ${\eta }_{charge}$, ${\eta }_{discharge}$ denote energy storage charging and discharging efficiency, $SO{C}_{min}$, $SO{C}_{max}$ represent State of charge upper and lower limits.

Energy storage charging and discharging power constraints:

$$0\le P_t^{charge}\le P_E,0\le P_t^{discharge}\le P_E$$

(32)

3.4. Optimization Methods

The capacity configuration and operation strategy optimization problem of wind–solar–hydro–storage multi-energy complementary systems is essentially a complex global optimization problem with high-dimensional nonlinearity, multiple objectives, and multiple constraints. In recent years, swarm intelligence optimization algorithms have been widely used in the field of energy system optimization due to their global optimization capabilities and flexibility. In particular, particle swarm optimization (PSO) and quantum particle swarm optimization (QPSO) have been proven to effectively improve the optimality and convergence speed of system scheduling and configuration. The main parameters of Quantum Behavioral Particle Swarm Optimization (QPSO) are set as shown in

Table 1. Quantum-behaved particle swarm optimization (QPSO) main parameter settings.

Parameter	Typical Value/Range	Description
Population size	200	Number of particles in the swarm. More particles enhance global search but increase computational load.
Maximum iterations	100	Maximum number of generations for evolution.
Particle initialization	Evenly distributed in the feasible interval	Uniform random initialization for diversity.
Global best weight	0.5–0.8	Weight for global best position.
Search bounds	Engineering allowable range of each design variable	Ensures physical and economic feasibility of solutions.

.

3.4.1. Quantum Particle Swarm Optimization (QPSO) and Its Advantages

As an evolution of PSO, QPSO introduces quantum behavior description, which greatly enhances the algorithm’s ability to escape local optimality and adapt to high-dimensional complex solution space [24,25,26]. QPSO has been widely used in distributed energy system optimization [27], photovoltaic energy storage system optimization [28], and multi-energy system scheduling [29]. The QPSO algorithm uses wave functions to represent the “position” of particles and uses the Monte Carlo method to determine the wave function position of particles:

$$\left\{\begin{array}{c}{X}_{i,j}\left(k+1\right)=p_{i,j}\left(k\right)\pm \rho \cdot \left|C_j\left(k\right)-X_{i,j}\left(k\right)\right|\cdot \ln \left[{\displaystyle \frac{1}{u_{i,j}\left(k\right)}}\right]\\ u_{i,j}\left(k\right)\sim U\left[0,1\right]\end{array}\right.$$

(33)

$$\left\{\begin{array}{c}{p}_{i,j}\left(k\right)={\varphi }_j\left(k\right)\cdot p_{i,j}\left(k\right)+\left[1-{\varphi }_j\left(k\right)\right]\cdot G_j\left(k\right)\\ {\varphi }_j\left(k\right)~U\left[0,1\right]\end{array}\right.$$

(34)

$$C_j\left(k\right)={\displaystyle \sum }_{i=1}^M{\displaystyle \frac{p_{i,j}\left(k\right)}{M}}$$

(35)

where $k$ represents particle Algebra, $p_{i,j}$ denotes the best historical “position” of the $i$-th particle in the $j$ dimension, $C_j$ denotes the historical optimal “position” of the particle population in dimension $j$, $X_{i,j}$ denotes the position of the $i$-th particle in the $j$-dimensional direction, $u_{i,j}\left(k\right)$, ${\varphi }_j\left(k\right)$ represents A random number between 0 and 1, $M$ denotes population size, Subscript $i$ represents the $i$-th particle; subscript $j$ represents the dimension of the particle.

$\rho$ is the expansion–contraction factor; it is the only parameter that needs to be determined in the QPSO algorithm besides the population size and the number of iterations. Its value is directly related to the convergence speed of the entire algorithm simulation analysis. It is generally determined by a method that linearly decreases with the number of iterations between 1 and 0.5 [30]:

$$\rho =\left(\begin{array}{c}1-0.5\end{array}\right)\times {\displaystyle \frac{\left(\begin{array}{c}{k}_{\max }-k\end{array}\right)}{k_{\max }}}+0.5$$

(36)

The outer optimization algorithm process based on the QPSO algorithm is as follows: (1) Given the algorithm and boundary conditions, determine the initial parameters such as population size $M$, dimension $j$, number of iterations, and convergence conditions; (2) initialize the particle population and set the optimal initial value of the individual particle and the optimal initial value of the population; (3) calculate the fitness (objective function) of each particle; (4) according to the fitness, update the optimal “position” of the individual particle and the optimal “position” of the population; (5) update the “position” of each particle according to Formulas (33)–(36). If the calculation meets the algorithm convergence conditions or reaches the set number of iterations, output the calculation result, otherwise return to step (3).

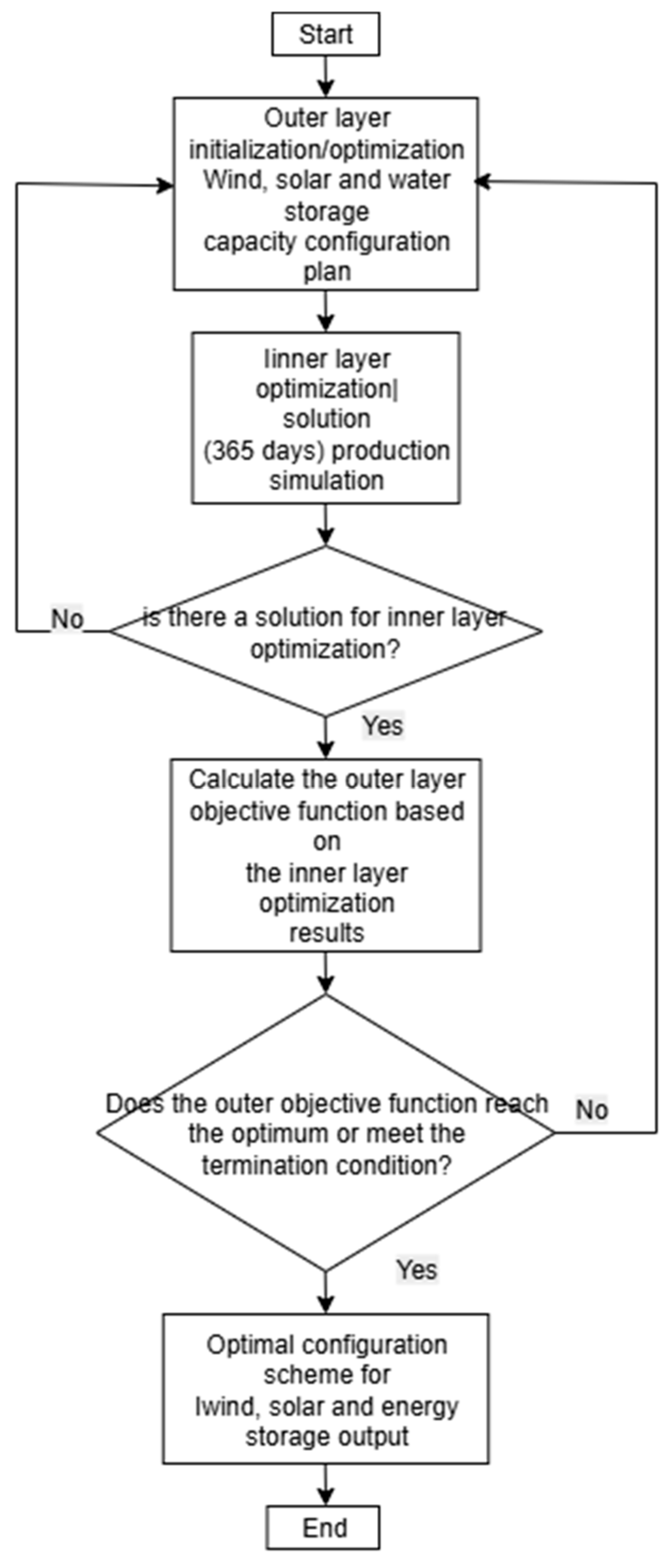
3.4.2. Two-Layer Optimization Algorithm Process

The process of the two-layer optimization algorithm proposed in this paper is shown in Figure 2. The annual transmission capacity of wind power, photovoltaic power, and energy storage obtained by the inner optimization and the annual SOC curve of energy storage are used to calculate the outer objective function.

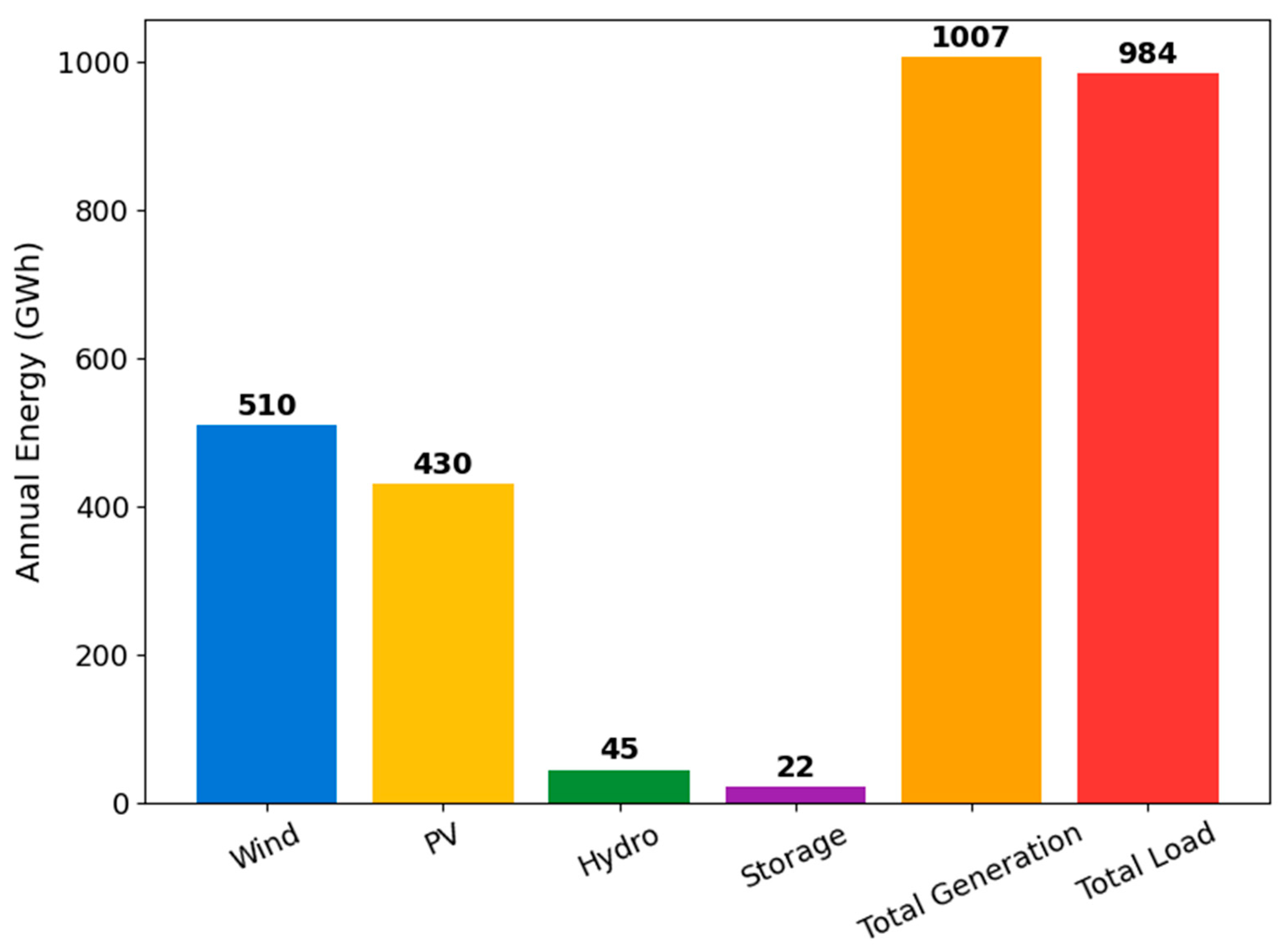
4. Example Analysis

Yunnan is located in southwest China. By the end of 2024, the installed capacity of hydropower will account for 56.6%, the installed capacity of renewable energy will account for 33.6%, and the installed capacity of thermal power will account for 9.8%. Yunnan’s hydropower system covers cascade hydropower stations in multiple river basins, including the Lancang River, Jinsha River, Pearl River, Red River, Nujiang River, and Irrawaddy River, including world-class giant hydropower stations such as Wudongde, Xiluodu, Nuozadu, and Xiaowan [31]. As shown in Figure 3. Yunnan’s total installed hydropower capacity has exceeded 80 million kilowatts.

A typical area in Yunnan was selected as the empirical case study object. The area contains multiple hydropower stations, wind farms, and photovoltaic power stations of different sizes, and is equipped with corresponding energy storage systems. A multi-energy complementary demonstration project has been initially built.

During the planning stage, the project plans to build a total wind and photovoltaic installed capacity of 450 MW, with a total investment estimate of no more than $RMB$ 320 million and a construction land area of no more than 32 km². The actual construction plan of the project is 176.03 MW wind power + 273.71 MW photovoltaic + 20.34 MW × 2.99 h energy storage.

The algorithm in this paper is used to calculate the wind, solar and storage capacity configuration plan for this project. The main calculation parameters are set as follows:

(1) The capital of power construction accounts for 30% of the total investment, the discount rate $r$ is 4.41%, the loan interest rate $i$ is 4.9%, the project operation period is 20 years, the construction loan period is 20 years, the wind power cost $CW$ is CNY 6.5 million/MW, the photovoltaic cost $CS$ is CNY 4.5 million/MW, and the annual operation and maintenance fee accounts $C{P}_{OM}$ for 1% of the total investment;

(2) The capital of energy storage construction accounts for 30% of the total investment, the discount rate $r$ is 4.41%, the loan interest rate $i$ is 4.9%, the construction loan period is 20 years, the power price $CEP$ is CNY 1.2 million/MW, the capacity price $CES$ is CNY 1.6 million/MWh, the annual operation and maintenance fee accounts for 2% of the total investment, and the average annual reduction in energy storage cost is 10%; the energy storage charging/discharging efficiency is 95%, the SOC initial capacity is 10%, the lower limit is 10%, the upper limit is 90%, and the energy storage self-discharge rate is 0.5%/d;

(3) The on-grid electricity prices of wind power, photovoltaic power, and energy storage $p_w$, $p_v$, $p_E$ are CNY 0.29, 0.40, and 0.70/kWh, respectively;

(4) Wind power units occupy $S_w$ 0.8 km²/MW, photovoltaic units occupy $S_S$ 0.272 km²/MW, energy storage units occupy $S_E$ 0.015 km²/MW, and other auxiliary facilities construction land $S_{\mathrm{Auxiliary}}$ accounts for 5% of the total wind, photovoltaic and storage construction land;

(5) The new energy abandonment rate is not higher than 5%, and the operation indicators F1 and F2 are not higher than the actual construction plan indicators.

(6) The energy storage power optimization range is set to 10~100 MW, the energy storage duration optimization range is set to 0.5~3.0 h, the particle swarm population is 200, and the termination condition is that the evolutionary generation reaches 100 generations or the objective function value changes less than 10⁻⁵ for 50 consecutive generations.

The power function is used to fit the data in

Table 2. Main parameter settings for the example analysis.

Parameter	Value	Notes/Description
Wind power installed capacity (MW)	176.03	Actual construction plan
PV installed capacity (MW)	273.71	Actual construction plan
Storage power (MW)	20.34	Actual construction plan
Storage duration (h)	2.99	Actual construction plan
Total investment cap (108 CNY)	3.2	Planning constraint
Total land area cap (km2)	32	Planning constraint
Wind power unit cost (104 CNY/MW)	650
PV unit cost (104 CNY/MW)	450
Storage unit power cost (104 CNY/MW)	120
Storage unit energy cost (104 CNY/MWh)	160
Wind power on-grid price (CNY/kWh)	0.29
PV on-grid price (CNY/kWh)	0.40
Storage discharge price (CNY/kWh)	0.70
Wind power land use (km2/MW)	0.8
PV land use (km2/MW)	0.272
Storage land use (km2/MW)	0.015
Auxiliary facility land ratio (%)	5

Notes: The project uses lithium iron phosphate batteries for energy storage. The measured data of DOD and maximum cycle number N are shown in Table 3.

, and the functional relationship between N and DOD is obtained as Formulas (3)–(13).

Table 3. Actual measured data of DOD and maximum cycle number N of a lithium iron phosphate battery.

DOD/%	N	DOD/%	N
100	2500	50	5700
90	2900	40	7500
80	3300	30	10,400
70	3800	20	16,200
60	4700	10	33,000

Table 3. Actual measured data of DOD and maximum cycle number N of a lithium iron phosphate battery.

DOD/%	N	DOD/%	N
100	2500	50	5700
90	2900	40	7500
80	3300	30	10,400
70	3800	20	16,200
60	4700	10	33,000

The capacity configuration scheme of the complementary power generation system obtained by the algorithm in this paper is 176.03 MW of wind power, 273.71 MW of photovoltaic power, and 20.34 MW × 2.99 h of energy storage.

From the annual power generation and load comparison chart (see Figure 4), it can be seen that wind power is the main power generation source of the system, contributing the vast majority of electricity, while photovoltaic, hydropower, and energy storage contribute relatively little. This shows that in Yunnan, wind power resources have significant advantages and can provide stable power output for the system. The total power generation for the whole year is slightly higher than the total load, indicating that the system has a certain power surplus capacity.

The DOD (depth of discharge) distribution diagram of the energy storage system (see Figure 5) shows the discharge depth of the energy storage system during the operation of the whole year. Most of the time, the discharge depth of the energy storage system is low, indicating that the energy storage system mainly operates in a shallow discharge state, which helps to extend the service life of the energy storage equipment.

The system economic analysis diagram (see Figure 6) reveals the benefits and cost structure of different power sources in the system. The benefits of wind power and photovoltaic power are relatively high, while the benefits of energy storage are relatively low. However, the energy storage system plays an irreplaceable role in regulating the balance of power supply and demand and helps to improve the stability and reliability of the entire system. Although the direct economic benefits of energy storage are low, its indirect benefits are significant, such as reducing wind and solar power abandonment and improving power quality.

The annual power generation output and load curve (see Figure 7) shows the changes in power generation of each power source and the changing trend of load demand. Wind power output has obvious volatility, which is related to the natural characteristics of wind energy resources. Photovoltaic output is higher during the day and zero at night, showing an obvious diurnal variation pattern. Hydropower output is relatively stable and can play a role in base load support to a certain extent. The energy storage system effectively smooths the fluctuations of wind power and photovoltaic power through charging and discharging regulation, making the total output of the system closer to the load demand curve.

The monthly power generation and load comparison chart (see Figure 8) reflects the changes in power generation and load in different months. Wind power is dominant in all months, but its power generation varies in different months. Photovoltaic power generation is relatively high in summer months and low in winter months. Hydropower generation is relatively stable, and the energy storage system is flexibly adjusted according to load demand. Overall, the total power generation and load of the system are basically matched in most months, but there may be a certain imbalance between supply and demand in some months.

Through the above analysis, it can be seen that the application of wind–solar–hydro–storage multi-energy complementary systems in Yunnan has significant advantages. Wind power, as the main source of power generation, can provide a large amount of electricity; photovoltaic power provides supplementary power during the day; hydropower plays a base load support role to a certain extent; and the energy storage system effectively smooths the fluctuations of renewable energy and improves the stability and reliability of the system. In the future, with the continuous advancement of technology and the reduction in wind–solar–hydro–storage multi-energy complementary systems are expected to be promoted and applied in more regions, contributing to the realization of sustainable energy development and carbon neutrality goals [32].

5. Discussion

This section focuses on the policy implications, and future research directions, elaborating based on the empirical results from Yunnan Province.

5.1. Policy Implications

(1)

Incentive Policies for Energy Storage: The case study shows that although energy storage has low direct benefits (only 8.7% of the system’s net profit), it can reduce the curtailment rate by 5.8 percentage points. It is suggested that Yunnan Province expand the scope of capacity compensation to intra-day peak regulation scenarios to alleviate investment recovery pressure.

(2)

Land Resource Coordination: The optimized photovoltaic land use accounts for 59.4% (19.0 km² out of 32 km²), which requires coordination with ecological protection red lines. Future work could explore “agri-photovoltaic” models to utilize marginal lands and reduce land conflicts.

5.2. Future Research Directions

(1)

Dynamic Electricity Price Response: The model should be expanded to a real-time electricity price environment to study the arbitrage potential of energy storage participating in the spot market and demand response, and to assess the impact of ±30% electricity price fluctuations on configuration.

(2)

Multi-Regional Coordination: As more than 70% of Yunnan’s electricity is exported, future work could build a cross-basin complementary model between the Lancang River and the Jinsha River to analyze the substitution effect between inter-regional transmission capacity and local energy storage.

(3)

Extreme Climate Adaptability: In 2022, Yunnan’s drought led to a 12% decrease in hydropower generation. Future work could introduce climate scenario generation technology (e.g., CMIP6) to simulate the robustness of the system under extreme drought and heavy rainfall conditions.

6. Conclusions

This work proposes and implements a two-layer capacity optimization model for wind–solar–hydro–storage multi-energy complementary systems, which is thoroughly validated using a case study from Yunnan Province. The model achieves an optimal configuration comprising 176.03 MW of wind power, 273.71 MW of photovoltaic capacity, and 20.34 MW × 2.99 h of energy storage, fully meeting investment and land use constraints. Under this optimized scheme, the system’s annual net profit reaches approximately 65.2 million CNY, representing a 13.7% increase over the conventional configuration, and the payback period is shortened by 2.3 years. Renewable energy curtailment is controlled below 5% for the entire year, the annual load–generation gap is reduced by 17.6%, and the intraday output volatility index is limited to 0.091, ensuring stable and reliable operation. The share of wind, photovoltaic, and hydropower in total generation is 51.4%, 43.8%, and 4.8%, respectively, while the storage system operates mainly in shallow cycles, with the proportion of deep discharge (DOD > 80%) maintained below 2.7%, effectively extending battery lifespan. The optimized system achieves a close match between power generation and load on both monthly and annual scales, reliably meeting electricity demand for 98.9% of all hours throughout the year. These quantitative results demonstrate that the proposed model provides a rigorous and practical tool for the scientific optimization and engineering design of multi-energy complementary systems in regions with high renewable penetration.