GIS-Based Spatial Autocorrelation and Multivariate Statistics for Understanding Groundwater Uranium Contamination and Associated Health Risk in Semiarid Region of Punjab, India
Abstract
1. Introduction
2. Materials and Methods
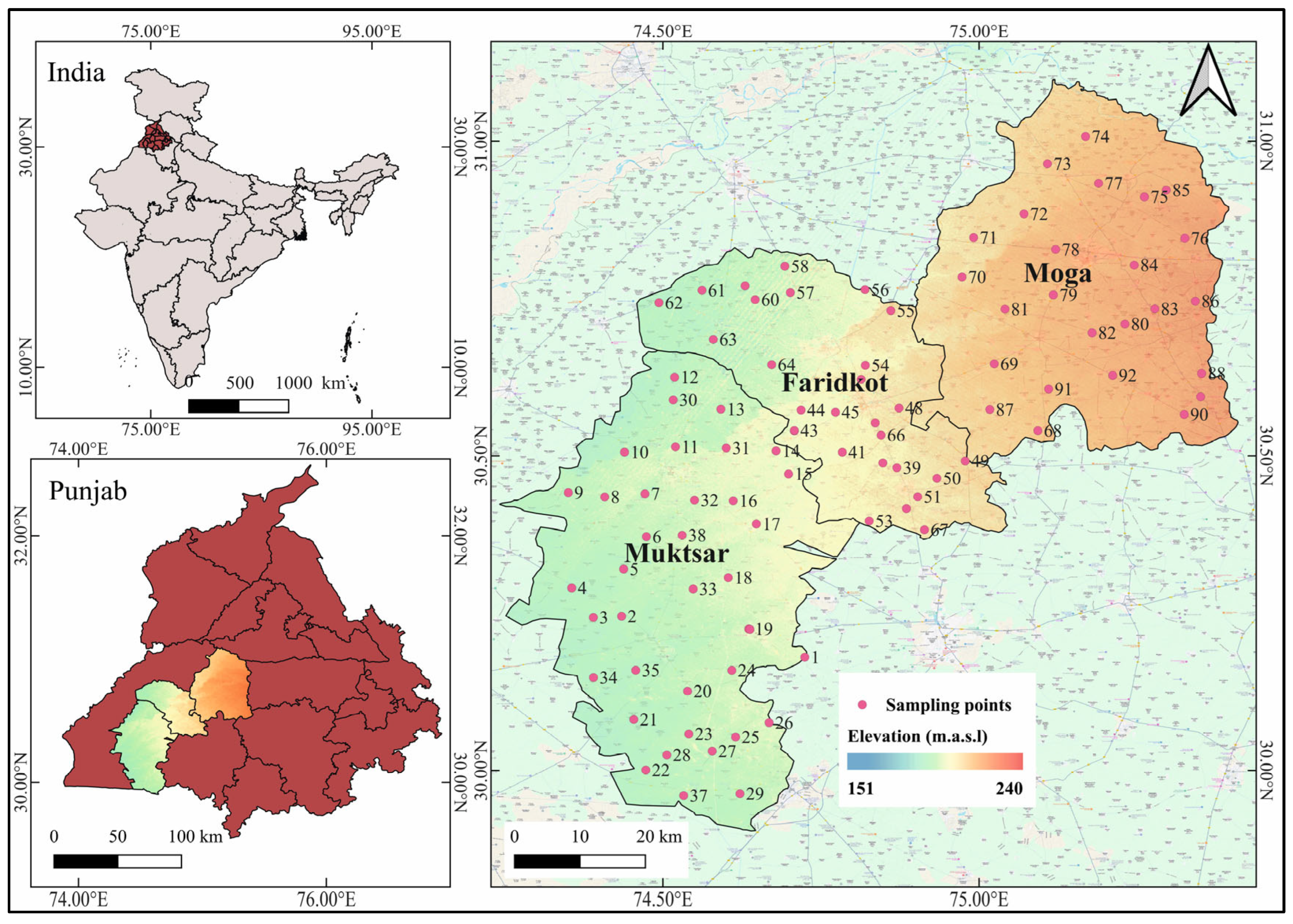
2.1. Study Area
2.2. Sampling and Analysis of Groundwater
2.3. Physicochemical Analysis of Groundwater
2.4. Analytical Quality Assurance and Control
2.5. Statistical Analysis
Random Forest Regression
2.6. Spatial Autocorrelation Using Moran’s Index
2.7. Analysis of Spatial Clusters and Spatial Outliers
2.7.1. Moran’s Scatterplot and GIS Analysis
- High–high (HH): Areas with high U levels that are surrounded by similarly high concentrations.
- Low–low (LL): Locations with low U concentrations surrounded by similarly low values.
- High–low (HL): The U levels that are close to low levels.
- Low–high (LH): The U levels that are low and encircled by high values.
2.7.2. Detection and GIS-Based Mapping of Key Spatial Patterns
2.8. Health Risk Assessment
Noncarcinogenic Health Risk
3. Results and Discussion
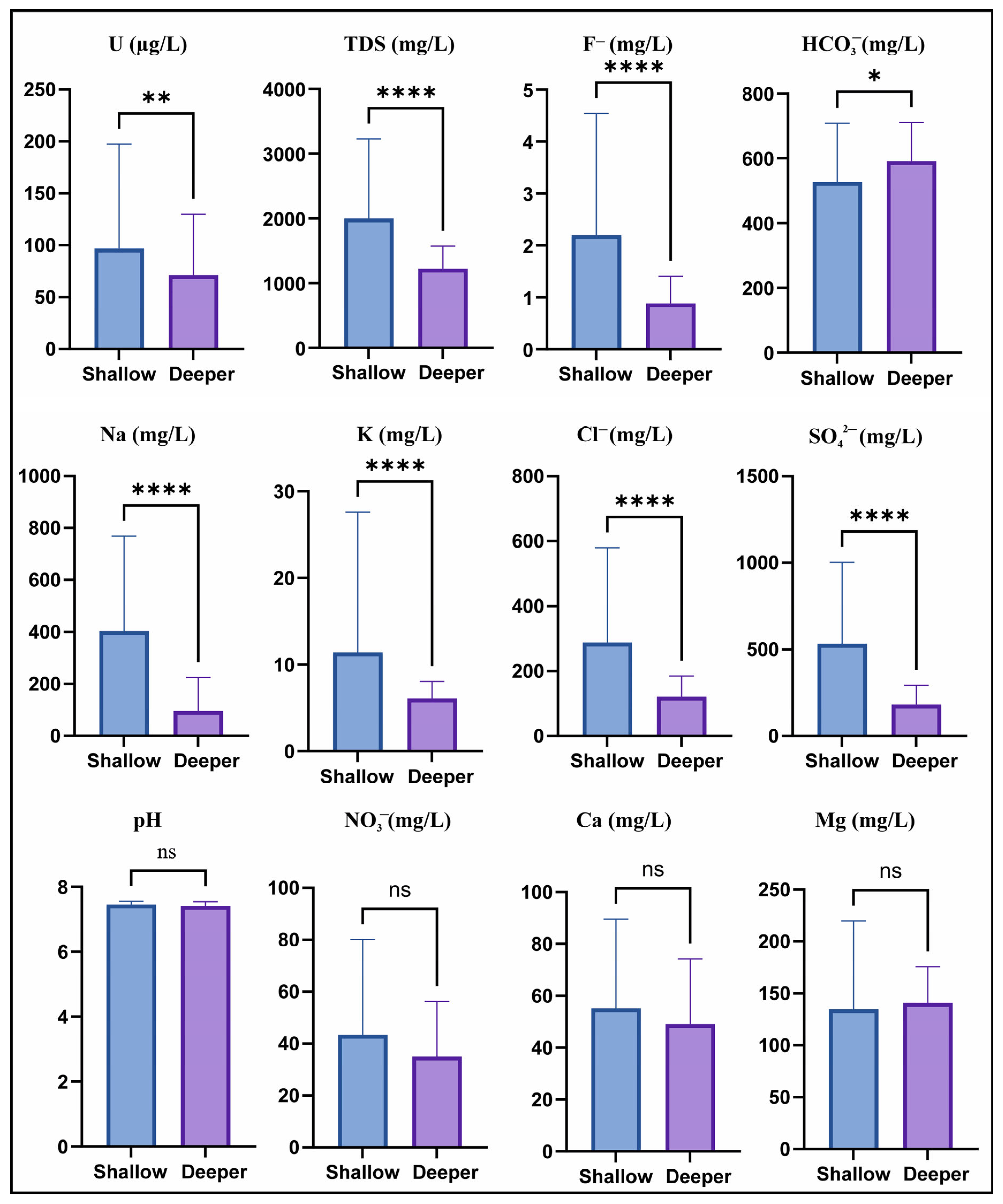
3.1. Distribution of Groundwater Quality Parameters in Shallow and Deeper Groundwater
3.2. Hydrogeochemistry of Groundwater of the Study Area
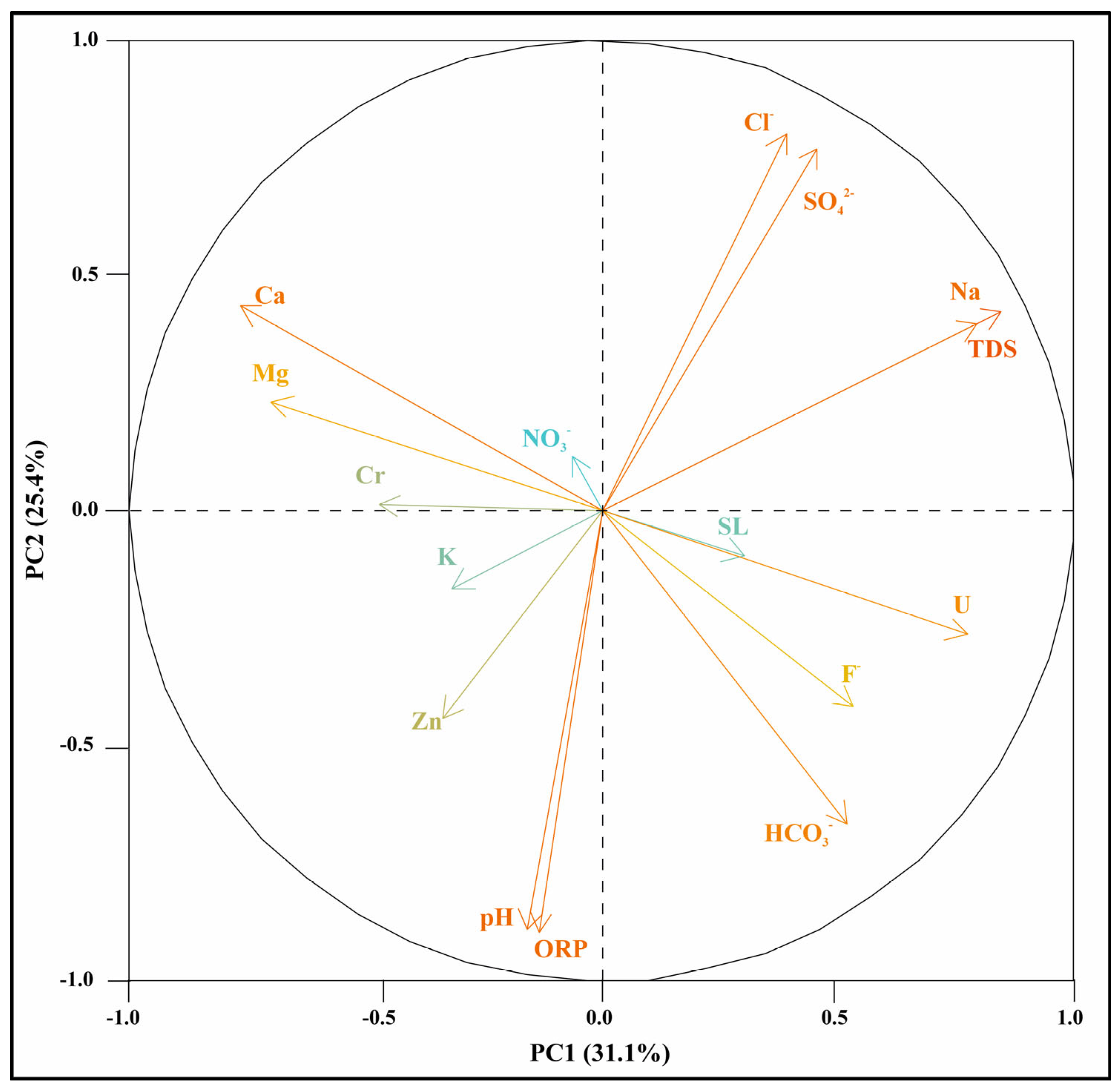
3.3. Multivariate Statistical Analysis
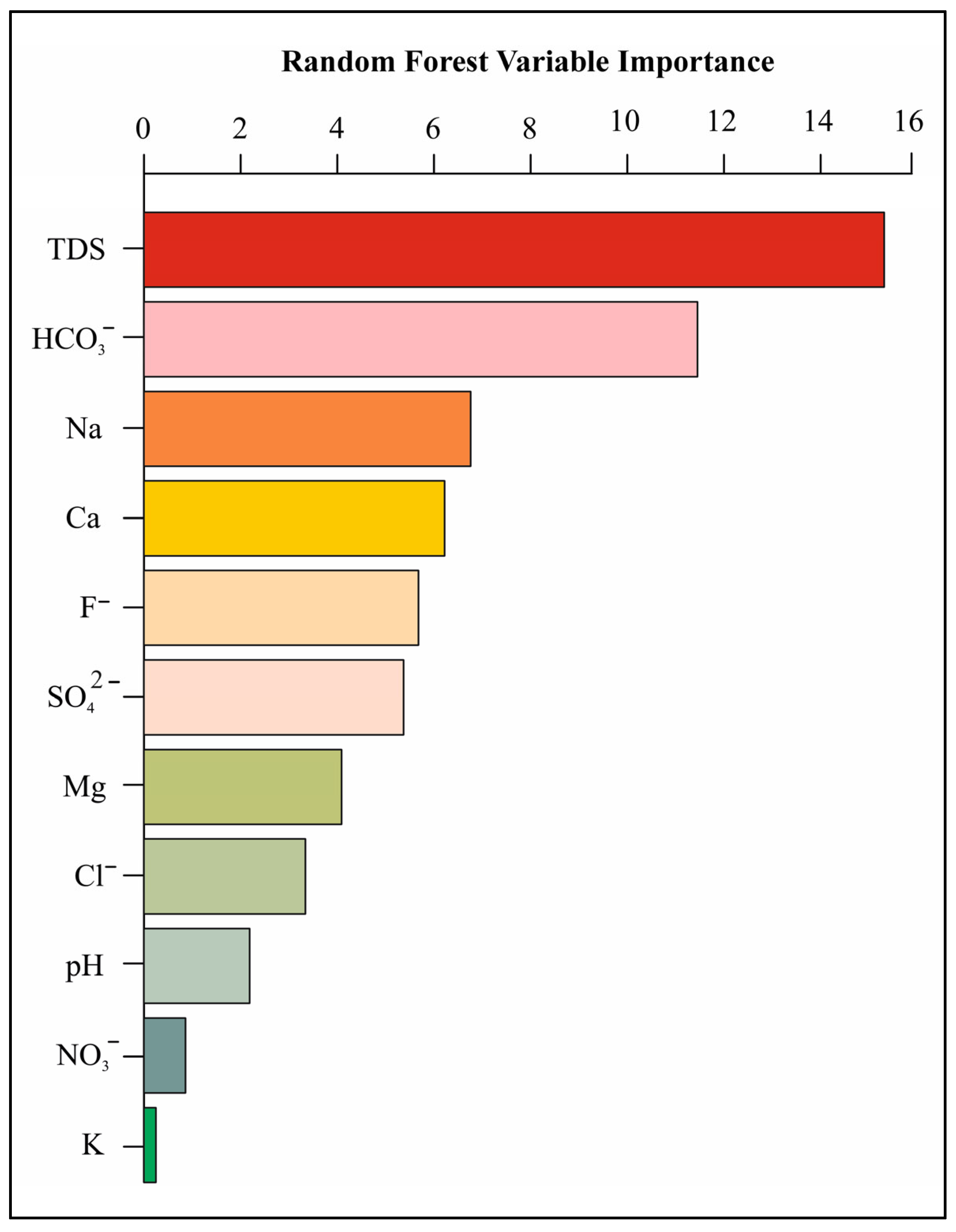
Prediction of Important Groundwater Quality Parameters Controlling Occurrence of U in the Groundwater Using Random Forest Model
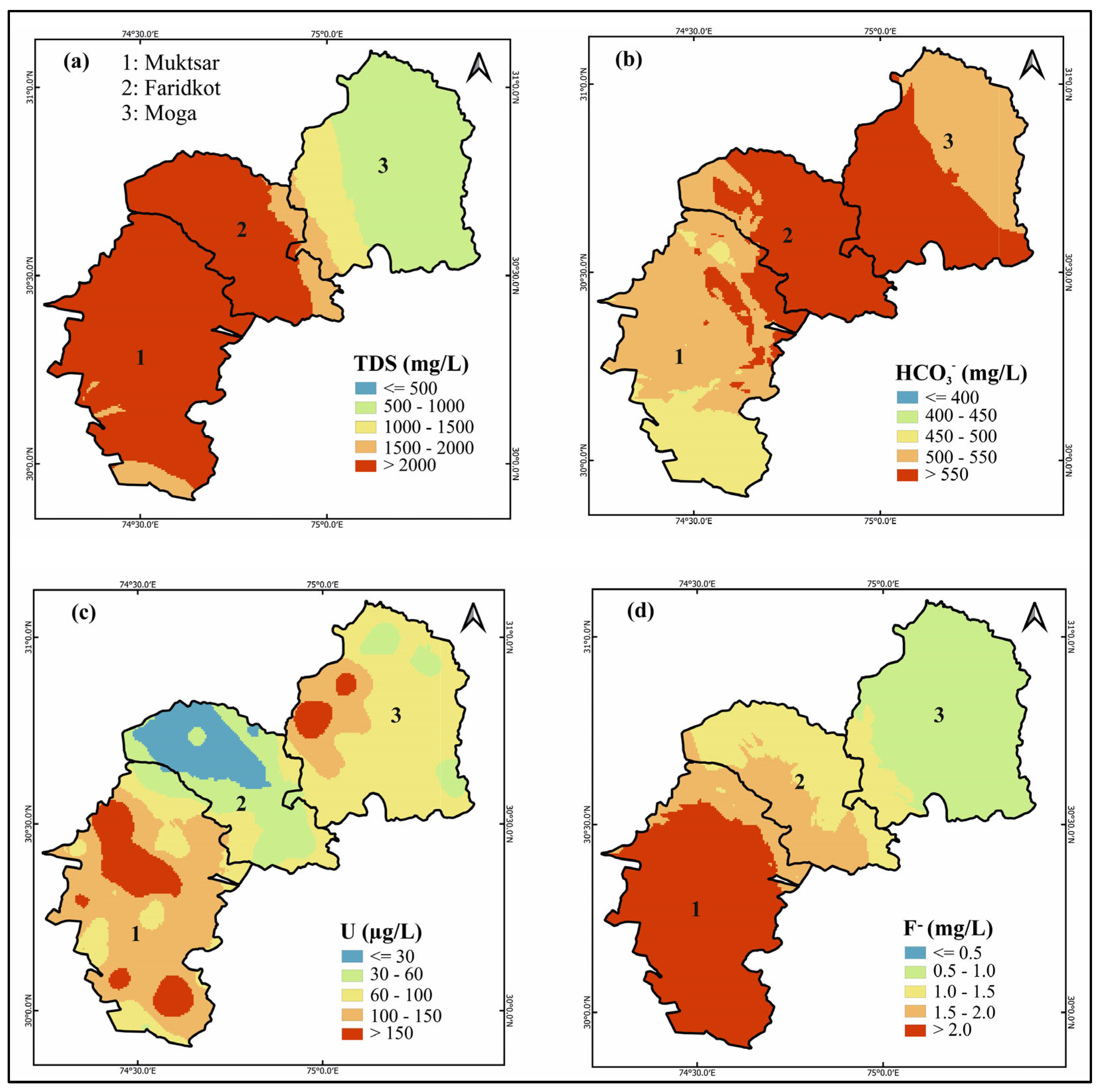
3.4. Geospatial Distribution of TDS, HCO3−, U, and F− in the Groundwater
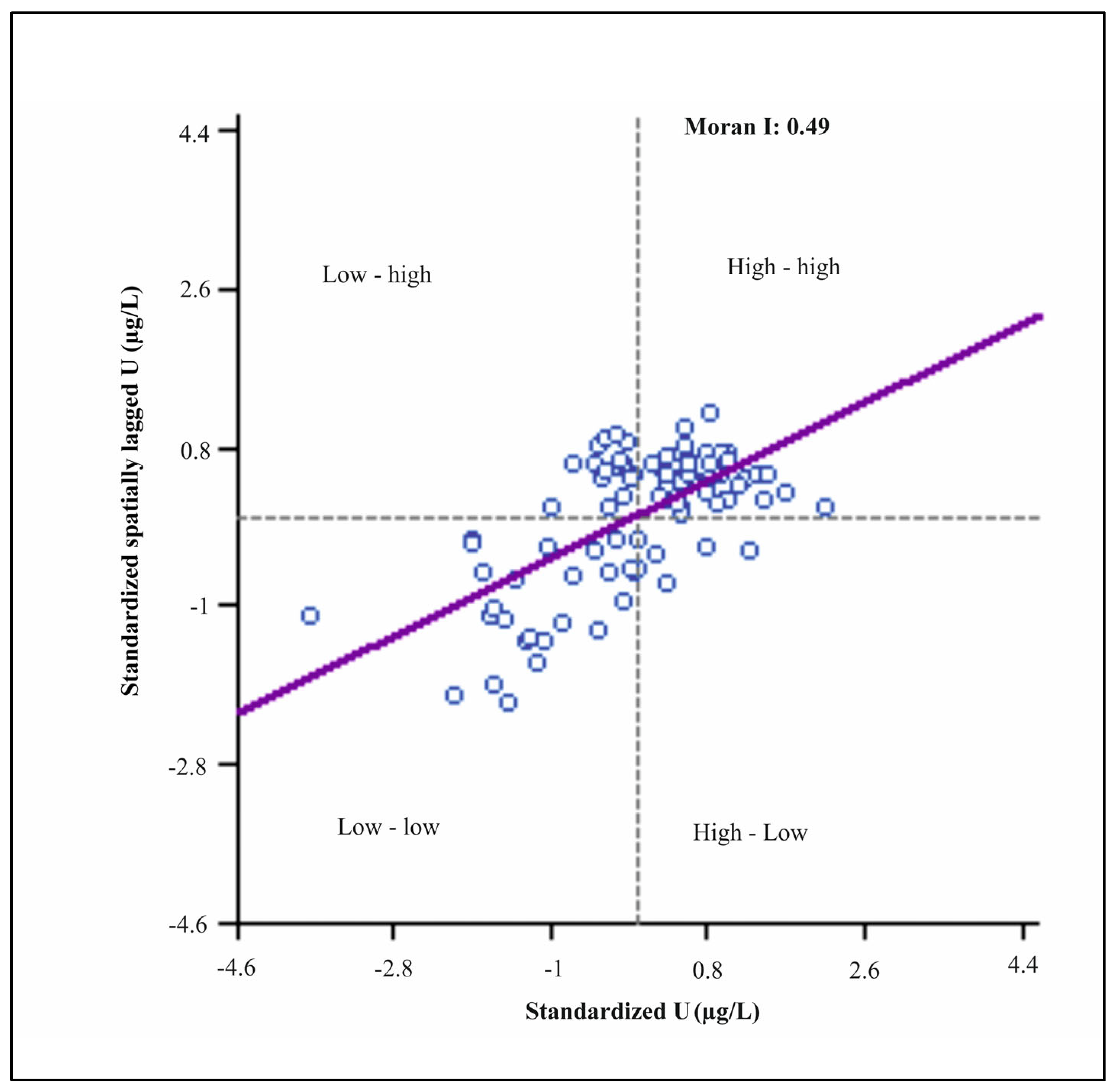
3.5. Moran’s I and Spatial Autocorrelation
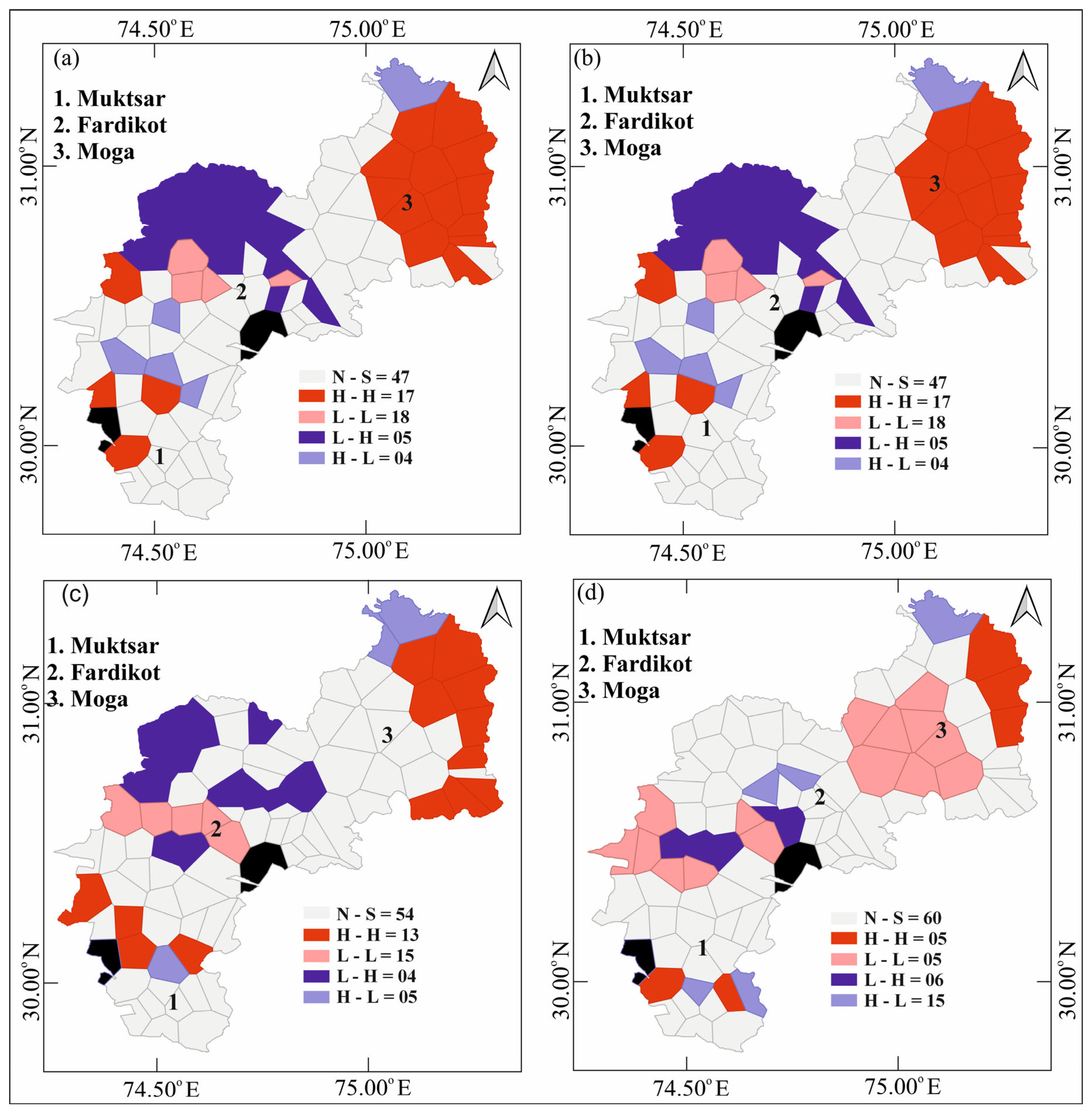
Spatial Clusters and Spatial Outliers’ Identification and Mapping
3.6. Human Health Risk
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sun, Y.; Xu, S.G.; Kang, P.P.; Fu, Y.Z.; Wang, T.X. Impacts of Artificial Underground Reservoir on Groundwater Environment in the Reservoir and Downstream Area. Int. J. Environ. Res. Public Health 2019, 16, 1921. [Google Scholar] [CrossRef]
- Fagoyinbo, C.V.O.; Dairo, V.A. Groundwater Contamination and Effective Ways of Rectification. Int. J. Inf. Res. Rev. 2016, 3, 1749–1756. [Google Scholar]
- Scanlon, B.R.; Fakhreddine, S.; Rateb, A.; de Graaf, I.; Famiglietti, J.; Gleeson, T.; Grafton, R.Q.; Jobbagy, E.; Kebede, S.; Kolusu, S.R.; et al. Global Water Resources and the Role of Groundwater in a Resilient Water Future. Nat. Rev. Earth Environ. 2023, 4, 87–101. [Google Scholar] [CrossRef]
- Mishra, R.K. Fresh Water Availability and Its Global Challenge. Br. J. Multidiscip. Adv. Stud. 2023, 4, 1–78. [Google Scholar] [CrossRef]
- Dhaloiya, A.; Singh, J.P. Spatio-Temporal Patterns of Groundwater Level Changes in Southwestern Indian Punjab. Water Sci. Technol. Water Supply 2024, 24, 497–516. [Google Scholar] [CrossRef]
- Priyan, K. Issues and Challenges of Groundwater and Surface Water Management in Semi-Arid Regions. In Groundwater Resources Development and Planning in the Semi-Arid Region; Springer: Cham, Switzerland, 2021; pp. 1–17. [Google Scholar] [CrossRef]
- Geris, J.; Comte, J.-C.; Franchi, F.; Petros, A.K.; Tirivarombo, S.; Selepeng, A.T.; Villholth, K.G. Surface Water-Groundwater Interactions and Local Land Use Control Water Quality Impacts of Extreme Rainfall and Flooding in a Vulnerable Semi-Arid Region of Sub-Saharan Africa. J. Hydrol. 2022, 609, 127834. [Google Scholar] [CrossRef]
- Zamani, M.G.; Moridi, A.; Yazdi, J. Groundwater Management in Arid and Semi-Arid Regions. Arab. J. Geosci. 2022, 15, 362. [Google Scholar] [CrossRef]
- Islam, F.; Tariq, A.; Guluzade, R.; Zhao, N.; Shah, S.U.; Ullah, M.; Hussain, M.L.; Ahmad, M.N.; Alasmari, A.; Alzuaibr, F.M.; et al. Comparative Analysis of GIS and RS Based Models for Delineation of Groundwater Potential Zone Mapping. Geomat. Nat. Hazards Risk 2023, 14, 2216852. [Google Scholar] [CrossRef]
- Singh, N.; Chaudhary, U.A.; Khan, M.A.; Fatima, N.; Hasan, M.; Hussain, A. Comprehensive Analysis of Groundwater Quality: Multidimensional Perspective. Nat. Volatiles Essent. Oils 2024, 11, 1–13. [Google Scholar]
- Tiouiouine, A.; Jabrane, M.; Kacimi, I.; Morarech, M.; Bouramtane, T.; Bahaj, T.; Yameogo, S.; Rezende-Filho, A.T.; Dassonville, F.; Moulin, M.; et al. Determining the Relevant Scale to Analyze the Quality of Regional Groundwater Resources While Combining Groundwater Bodies, Physicochemical and Biological Databases in Southeastern France. Water 2020, 12, 3476. [Google Scholar] [CrossRef]
- Machiwal, D.; Cloutier, V.; Güler, C.; Kazakis, N. A Review of GIS-Integrated Statistical Techniques for Groundwater Quality Evaluation and Protection. Environ. Earth Sci. 2018, 77, 681. [Google Scholar] [CrossRef]
- Conant, B.; Robinson, C.E.; Hinton, M.J.; Russell, H.A.J. A Framework for Conceptualizing Groundwater-Surface Water Interactions and Identifying Potential Impacts on Water Quality, Water Quantity, and Ecosystems. J. Hydrol. 2019, 574, 609–627. [Google Scholar] [CrossRef]
- Alcaine, A.A.; Schulz, C.; Bundschuh, J.; Jacks, G.; Thunvik, R.; Gustafsson, J.-P.; Mörth, C.-M.; Sracek, O.; Ahmad, A.; Bhattacharya, P. Hydrogeochemical Controls on the Mobility of Arsenic, Fluoride and Other Geogenic Co-Contaminants in the Shallow Aquifers of Northeastern La Pampa Province in Argentina. Sci. Total Environ. 2020, 715, 136671. [Google Scholar] [CrossRef] [PubMed]
- Mukherjee, A.; Saha, D.; Harvey, C.F.; Taylor, R.G.; Ahmed, K.M.; Bhanja, S.N. Groundwater Systems of the Indian Sub-Continent. J. Hydrol. Reg. Stud. 2015, 4, 1–14. [Google Scholar] [CrossRef]
- Alarcón-Herrera, M.T.; Bundschuh, J.; Nath, B.; Nicolli, H.B.; Gutierrez, M.; Reyes-Gomez, V.M.; Nuñez, D.; Martín-Dominguez, I.R.; Sracek, O. Co-Occurrence of Arsenic and Fluoride in Groundwater of Semi-Arid Regions in Latin America: Genesis, Mobility and Remediation. J. Hazard. Mater. 2013, 262, 960–969. [Google Scholar] [CrossRef]
- Bhattacharya, P.; Ahmed, K.M.; Hasan, M.A.; Broms, S.; Fogelström, J.; Jacks, G.; Sracek, O.; von Brömssen, M.; Routh, J. Mobility of Arsenic in Groundwater in a Part of Brahmanbaria District, NE Bangladesh. Manag. Arsen. Environ. Soil Hum. Health 2006, 95–115. [Google Scholar]
- Kumar, R.; Mittal, S.; Peechat, S.; Sahoo, P.K.; Sahoo, S.K. Quantification of Groundwater–Agricultural Soil Quality and Associated Health Risks in the Agri-Intensive Sutlej River Basin of Punjab, India. Environ. Geochem. Health 2020, 42, 4245–4268. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Nicot, J.P.; Reedy, R.C.; Kurtzman, D.; Mukherjee, A.; Nordstrom, D.K. Elevated Naturally Occurring Arsenic in a Semiarid Oxidizing System, Southern High Plains Aquifer, Texas, USA. Appl. Geochem. 2009, 24, 2061–2071. [Google Scholar] [CrossRef]
- Das, N.G.; Das, A.; Sarma, K.; Kumar, M. Provenance, Prevalence and Health Perspective of Co-Occurrences of Arsenic, Fluoride and Uranium in the Aquifers of the Brahmaputra River Floodplain. Chemosphere 2018, 194, 755–772. [Google Scholar] [CrossRef]
- Das, N.; Sarma, K.P.; Patel, A.K.; Deka, J.P.; Das, A.; Kumar, A.; Shea, P.J.; Kumar, M. Seasonal Disparity in the Co-Occurrence of Arsenic and Fluoride in the Aquifers of the Brahmaputra Flood Plains, Northeast India. Environ. Earth Sci. 2017, 76, 1–15. [Google Scholar] [CrossRef]
- Kumar, A.; Karpe, R.K.; Rout, S.; Gautam, Y.P.; Mishra, M.K.; Ravi, P.M.; Tripathi, R.M. Activity Ratios of 234 U/238 U and 226 Ra/228 Ra for Transport Mechanisms of Elevated Uranium in Alluvial Aquifers of Groundwater in South-Western (SW) Punjab, India. J. Environ. Radioact. 2015, 151, 311–320. [Google Scholar] [CrossRef]
- Mukherjee, A.; Scanlon, B.R.; Fryar, A.E.; Saha, D.; Ghosh, A.; Chowdhuri, S.; Mishra, R. Solute Chemistry and Arsenic Fate in Aquifers between the Himalayan Foothills and Indian Craton (Including Central Gangetic Plain): Influence of Geology and Geomorphology. Geochim. Cosmochim. Acta 2012, 90, 283–302. [Google Scholar] [CrossRef]
- IS 10500: 2012; BIS Indian Standard Drinking Water—Specification. BIS: New Delhi, India, 2012.
- Coyte, R.M.; Jain, R.C.; Srivastava, S.K.; Sharma, K.C.; Khalil, A.; Ma, L.; Vengosh, A. Large-Scale Uranium Contamination of Groundwater Resources in India. Environ. Sci. Technol. Lett. 2018, 5, 341–347. [Google Scholar] [CrossRef]
- CGWB. Uranium Occurrence in Shallow Aquifer in India; Central Ground Water Board, Government of India: CHQ Faridabad, India, 2020; pp. 1–48. Available online: https://www.cgwb.gov.in/old_website/WQ/URANIUM_REPORT_2019-20.pdf (accessed on 26 June 2025).
- Bangotra, P.; Sharma, M.; Mehra, R.; Jakhu, R.; Singh, A.; Gautam, A.S.; Gautam, S. A Systematic Study of Uranium Retention in Human Organs and Quantification of Radiological and Chemical Doses from Uranium Ingestion. Environ. Technol. Innov. 2021, 21, 101360. [Google Scholar] [CrossRef]
- Zamora, M.L.; Tracy, B.L.; Zielinski, J.M.; Meyerhof, D.P.; Moss, M.A. Chronic Ingestion of Uranium in Drinking Water: A Study of Kidney Bioeffects in Humans. Toxicol. Sci. 1998, 43, 68–77. [Google Scholar] [CrossRef]
- Ransom, K.M.; Nolan, B.T.; Traum, J.A.; Faunt, C.C.; Bell, A.M.; Gronberg, J.A.M.; Wheeler, D.C.; Rosecrans, C.Z.; Jurgens, B.; Schwarz, G.E.; et al. A Hybrid Machine Learning Model to Predict and Visualize Nitrate Concentration throughout the Central Valley Aquifer, California, USA. Sci. Total Environ. 2017, 601–602, 1160–1172. [Google Scholar] [CrossRef]
- Feng, F.; Jia, Y.; Yang, Y.; Huan, H.; Lian, X.; Xu, X.; Xia, F.; Han, X.; Jiang, Y. Hydrogeochemical and Statistical Analysis of High Fluoride Groundwater in Northern China. Environ. Sci. Pollut. Res. 2020, 27, 34840–34861. [Google Scholar] [CrossRef]
- Gupta, P.K.; Maiti, S. Enhancing Data-Driven Modeling of Fluoride Concentration Using New Data Mining Algorithms. Environ. Earth Sci. 2022, 81, 89. [Google Scholar] [CrossRef]
- Vesselinov, V.V.; Alexandrov, B.S.; O’Malley, D. Contaminant Source Identification Using Semi-Supervised Machine Learning. J. Contam. Hydrol. 2018, 212, 134–142. [Google Scholar] [CrossRef]
- Wang, B.; Tan, Z.; Sheng, W.; Liu, Z.; Wu, X.; Ma, L.; Li, Z. Identification of Groundwater Contamination Sources Based on a Deep Belief Neural Network. Water 2024, 16, 2449. [Google Scholar] [CrossRef]
- Cai, J.; Wang, P.; Shen, H.; Su, Y.; Huang, Y. Water Level Prediction of Emergency Groundwater Source and Its Impact on the Surrounding Environment in Nantong City, China. Water 2020, 12, 3529. [Google Scholar] [CrossRef]
- Shirmohammadi, B.; Vafakhah, M.; Moosavi, V.; Moghaddamnia, A. Application of Several Data-Driven Techniques for Predicting Groundwater Level. Water Resour. Manag. 2012, 27, 419–432. [Google Scholar] [CrossRef]
- Adamowski, J.; Chan, H.F. A Wavelet Neural Network Conjunction Model for Groundwater Level Forecasting. J. Hydrol. 2011, 407, 28–40. [Google Scholar] [CrossRef]
- Barzegar, R.; Moghaddam, A.A.; Tziritis, E.; Fakhri, M.S.; Soltani, S. Identification of Hydrogeochemical Processes and Pollution Sources of Groundwater Resources in the Marand Plain, Northwest of Iran. Environ. Earth Sci. 2017, 76, 1–16. [Google Scholar] [CrossRef]
- Gupta, D.; Natarajan, N. Prediction of Uniaxial Compressive Strength of Rock Samples Using Density Weighted Least Squares Twin Support Vector Regression. Neural Comput. Appl. 2021, 33, 15843–15850. [Google Scholar] [CrossRef]
- Rahmati, O.; Choubin, B.; Fathabadi, A.; Coulon, F.; Soltani, E.; Shahabi, H.; Mollaefar, E.; Tiefenbacher, J.; Cipullo, S.; Ahmad, B.B.; et al. Predicting Uncertainty of Machine Learning Models for Modelling Nitrate Pollution of Groundwater Using Quantile Regression and UNEEC Methods. Sci. Total Environ. 2019, 688, 855–866. [Google Scholar] [CrossRef]
- Singh, C.K.; Rina, K.; Singh, R.P.; Mukherjee, S. Geochemical Characterization and Heavy Metal Contamination of Groundwater in Satluj River Basin. Environ. Earth Sci. 2013, 71, 201–216. [Google Scholar] [CrossRef]
- Taherdangkoo, R.; Yang, H.; Akbariforouz, M.; Sun, Y.; Liu, Q.; Butscher, C. Gaussian Process Regression to Determine Water Content of Methane: Application to Methane Transport Modeling. J. Contam. Hydrol. 2021, 243, 103910. [Google Scholar] [CrossRef]
- Norouzi, H.; Moghaddam, A.A. Groundwater Quality Assessment Using Random Forest Method Based on Groundwater Quality Indices (Case Study: Miandoab Plain Aquifer, NW of Iran). Arab. J. Geosci. 2020, 13, 912. [Google Scholar] [CrossRef]
- Ouedraogo, I.; Defourny, P.; Vanclooster, M. Validating a Continental-Scale Groundwater Diffuse Pollution Model Using Regional Datasets. Environ. Sci. Pollut. Res. 2017, 26, 2105–2119. [Google Scholar] [CrossRef] [PubMed]
- Uddin, M.G.; Imran, M.H.; Sajib, A.M.; Hasan, M.A.; Diganta, M.T.M.; Dabrowski, T.; Olbert, A.I.; Moniruzzaman, M. Assessment of Human Health Risk from Potentially Toxic Elements and Predicting Groundwater Contamination Using Machine Learning Approaches. J. Contam. Hydrol. 2024, 261, 104307. [Google Scholar] [CrossRef]
- Khosravi, K.; Sartaj, M.; Tsai, F.T.-C.; Singh, V.P.; Kazakis, N.; Melesse, A.M.; Prakash, I.; Tien Bui, D.; Pham, B.T. A Comparison Study of DRASTIC Methods with Various Objective Methods for Groundwater Vulnerability Assessment. Sci. Total Environ. 2018, 642, 1032–1049. [Google Scholar] [CrossRef]
- Kombo, O.H.; Kumaran, S.; Sheikh, Y.H.; Bovim, A.; Jayavel, K. Long-Term Groundwater Level Prediction Model Based on Hybrid KNN-RF Technique. Hydrology 2020, 7, 59. [Google Scholar] [CrossRef]
- Ransom, K.M.; Nolan, B.T.; Stackelberg, P.E.; Belitz, K.; Fram, M.S. Machine Learning Predictions of Nitrate in Groundwater Used for Drinking Supply in the Conterminous United States. Sci. Total Environ. 2021, 807, 151065. [Google Scholar] [CrossRef]
- Talukdar, S.; Mallick, J.; Sarkar, S.K.; Roy, S.K.; Islam, A.R.M.T.; Praveen, B.; Naikoo, M.W.; Rahman, A.; Sobnam, M. Novel Hybrid Models to Enhance the Efficiency of Groundwater Potentiality Model. Appl. Water Sci. 2022, 12, 62. [Google Scholar] [CrossRef]
- Chen, Y. An Analytical Process of Spatial Autocorrelation Functions Based on Moran’s Index. PLoS ONE 2021, 16, e0249589. [Google Scholar] [CrossRef]
- Chen, Y. Spatial Autocorrelation Equation Based on Moran’s Index. Sci. Rep. 2023, 13, 19296. [Google Scholar] [CrossRef]
- Jaber, A.S.; Hussein, A.K.; Kadhim, N.A.; Bojassim, A.A. A Moran’s I Autocorrelation and Spatial Cluster Analysis for Identifying Coronavirus Disease COVID-19 in Iraq Using GIS Approach. Casp. J. Environ. Sci. 2021, 20, 55–60. [Google Scholar]
- Zhalehdoost, A.; Taleai, M. A Review of the Application of Machine Learning and Geospatial Analysis Methods in Air Pollution Prediction. Pollution 2022, 8, 904–933. [Google Scholar] [CrossRef]
- Singh, S.; Park, J. Drivers of Change in Groundwater Resources: A Case Study of the Indian Punjab. Food Secur. 2018, 10, 965–979. [Google Scholar] [CrossRef]
- Bajwa, B.S.; Kumar, S.; Singh, S.; Sahoo, S.K.; Tripathi, R.M. Uranium and Other Heavy Toxic Elements Distribution in the Drinking Water Samples of SW-Punjab, India. J. Radiat. Res. Appl. Sci. 2017, 10, 13–19. [Google Scholar] [CrossRef]
- CGWB. Ground Water Quality in Shallow Aquifer Of Punjab; Department of Water Resources; River Development and Ganga Rejuvenation, Ministry of Jal Shakti: Chandigarh, India, 2023; pp. 1–96. Available online: https://www.cgwb.gov.in/cgwbpnm/public/uploads/documents/1708597073344550179file.pdf (accessed on 26 June 2025).
- Bala, R.; Karanveer; Das, D. Occurrence and Behaviour of Uranium in the Groundwater and Potential Health Risk Associated in Semi-Arid Region of Punjab, India. Groundw. Sustain. Dev. 2022, 17, 100731. [Google Scholar] [CrossRef]
- Sahoo, P.K.; Virk, H.S.; Powell, M.; Kumar, R.; Pattanaik, J.K.; Salomão, G.N.; Mittal, S.; Chouhan, L.; Nandabalan, Y.K.; Tiwari, R.P. Meta-Analysis of Uranium Contamination in Groundwater of the Alluvial Plains of Punjab, Northwest India: Status, Health Risk, and Hydrogeochemical Processes. Sci. Total Environ. 2022, 807, 151753. [Google Scholar] [CrossRef] [PubMed]
- Krishan, G.; Kumar, B.; Sudarsan, N.; Rao, M.S.; Ghosh, N.C.; Taloor, A.K.; Bhattacharya, P.; Singh, S.; Kumar, C.P.; Sharma, A.; et al. Isotopes (Δ18O, ΔD and 3H) Variations in Groundwater with Emphasis on Salinization in the State of Punjab, India. Sci. Total Environ. 2021, 789, 148051. [Google Scholar] [CrossRef]
- Mittal, S.; Sahoo, P.K.; Sahoo, S.K.; Kumar, R.; Tiwari, R.P. Hydrochemical Characteristics and Human Health Risk Assessment of Groundwater in the Shivalik Region of Sutlej Basin, Punjab, India. Arab. J. Geosci. 2021, 14, 847. [Google Scholar] [CrossRef]
- Chaudhari, U.; Kumari, D.; Tyagi, T.; Mittal, S.; Sahoo, P.K. Geochemical Signature and Risk Assessment of Potential Toxic Elements in Intensively Cultivated Soils of South-West Punjab, India. Minerals 2024, 14, 576. [Google Scholar] [CrossRef]
- CGWB. Groundwater Information Booklet, Muktsar District Punjab; Central Ground Water Board: Chandigarh, India, 2013; pp. 1–22. Available online: https://www.cgwb.gov.in/old_website/District_Profile/Punjab/Muktsar.pdf (accessed on 26 June 2025).
- CGWB. Ground Water Information Booklet Faridkot District, Punjab; Central Ground Water Board: Chandigarh, India, 2013; pp. 1–22. Available online: https://www.cgwb.gov.in/old_website/District_Profile/Punjab/Faridkot.pdf (accessed on 26 June 2025).
- CGWB. Ground Water Information Booklet Moga District, Punjab; Central Ground Water Board: Chandigarh, India, 2013; pp. 1–17. Available online: https://www.cgwb.gov.in/old_website/District_Profile/Punjab/Moga.pdf (accessed on 26 June 2025).
- APHA. Standard Methods for the Examination of Water and Wastewater, 23rd ed.; American Public Health Association: Washington, DC, USA, 2017; Available online: https://www.pdfdrive.com/apha-23rd-edition-chapters-6000-10000-e60360404.html (accessed on 26 June 2025).
- Rathore, D.P.S.; Tarafder, P.K.; Balaram, V. Challenges for Reliable Analysis of Uranium in Natural Waters Using Laser-Induced Fluorimetry/LED-Fluorimetry in the Presence of Fluoride and Diverse Humic Substances in Hot Arid Regions and Future Advances—Review. Environ. Sci. Adv. 2024, 3, 511–521. [Google Scholar] [CrossRef]
- Sahoo, P.K.; Dall’Agnol, R.; Salomão, G.N.; Ferreira, S.; Silva, M.S.; Walfir, P.; Lima, M.; Angélica, R.S.; Augusto, C.; Furtado, M.; et al. Regional-Scale Mapping for Determining Geochemical Background Values in Soils of the Itacaiúnas River Basin, Brazil: The Use of Compositional Data Analysis (CoDA). Geoderma 2020, 376, 114504. [Google Scholar] [CrossRef]
- Sunkari, E.D.; Adams, S.J.; Okyere, M.B.; Bhattacharya, P. Groundwater Fluoride Contamination in Ghana and the Associated Human Health Risks: Any Sustainable Mitigation Measures to Curtail the Long Term Hazards. Groundw. Sustain. Dev. 2022, 16, 100715. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Ayotte, J.D.; Flanagan, S.E.; Morrow, W.R. Occurrence of Uranium and 222Radon in Glacial and Bedrock Aquifers in the Northern United States; US Department of the Interior, US Geological Survey: Reston, VA, USA, 2007. [CrossRef]
- Nolan, B.T.; Gronberg, J.M.; Faunt, C.C.; Eberts, S.M.; Belitz, K. Modeling Nitrate at Domestic and Public-Supply Well Depths in the Central Valley, California. Environ. Sci. Technol. 2014, 48, 5643–5651. [Google Scholar] [CrossRef]
- Tan, Z.; Yang, Q.; Zheng, Y. Machine Learning Models of Groundwater Arsenic Spatial Distribution in Bangladesh: Influence of Holocene Sediment Depositional History. Environ. Sci. Technol. 2020, 54, 9454–9463. [Google Scholar] [CrossRef] [PubMed]
- Wheeler, D.C.; Nolan, B.T.; Flory, A.R.; DellaValle, C.T.; Ward, M.H. Modeling Groundwater Nitrate Concentrations in Private Wells in Iowa. Sci. Total Environ. 2015, 536, 481–488. [Google Scholar] [CrossRef] [PubMed]
- Rosecrans, C.Z.; Belitz, K.; Ransom, K.M.; Stackelberg, P.E.; McMahon, P.B. Predicting Regional Fluoride Concentrations at Public and Domestic Supply Depths in Basin-Fill Aquifers of the Western United States Using a Random Forest Model. Sci. Total Environ. 2022, 806, 150960. [Google Scholar] [CrossRef]
- Breiman, L. Out-of-Bag Estimation; Department of Statistics, University of California: Oakland, CA, USA, 1996; pp. 1–13. [Google Scholar]
- Danesh, T.; Ouaret, R.; Floquet, P.; Negny, S. Hybridization of Model-Specific and Model-Agnostic Methods for Interpretability of Neural Network Predictions: Application to a Power Plant. Comput. Chem. Eng. 2023, 176, 108306. [Google Scholar] [CrossRef]
- Kuhn, M. Building Predictive Models in R Using the Caret Package. J. Stat. Softw. 2008, 28, 1–26. [Google Scholar] [CrossRef]
- Molnar, C. Iml: An R Package for Interpretable Machine Learning. J. Open Source Softw. 2018, 3, 786. [Google Scholar] [CrossRef]
- Zhang, Y.; Rashid, A.; Guo, S.; Jing, Y.; Zeng, Q.; Li, Y.; Adyari, B.; Yang, J.; Tang, L.; Yu, C.; et al. Spatial Autocorrelation and Temporal Variation of Contaminants of Emerging Concern in a Typical Urbanizing River. Water Res. 2022, 212, 118120. [Google Scholar] [CrossRef]
- Isnan, S.; Bin Abdullah, A.F.; Shariff, A.R.; Ishak, I.; Syed Ismail, S.N.; Appanan, M.R. Moran’s I and Geary’s C: Investigation of the Effects of Spatial Weight Matrices for Assessing the Distribution of Infectious Diseases. Geospat. Health 2025, 20. [Google Scholar] [CrossRef]
- Anselin, L. Local Indicators of Spatial Association-LISA. Geogr. Anal. 1995, 27, 93–115. [Google Scholar] [CrossRef]
- Getis, A.; Ord, J.K. The Analysis of Spatial Association by Use of Distance Statistics. Geogr. Anal. 1992, 24, 189–206. [Google Scholar] [CrossRef]
- Arum, P.R.; Anggraini, L.; Nur, I.M.; Purnomo, E.A. Panel Data Spatial Regression Modeling with a Rook Contiguity Weighting Function on the Human Development Index in West Sumatera Province. JTAM (J. Teor. Dan Apl. Mat.) 2024, 8, 1–14. [Google Scholar] [CrossRef]
- Ijumulana, J.; Ligate, F.; Irunde, R.; Bhattacharya, P.; Maity, J.P.; Ahmad, A.; Mtalo, F. Spatial Uncertainties in Fluoride Levels and Health Risks in Endemic Fluorotic Regions of Northern Tanzania. Groundw. Sustain. Dev. 2021, 14, 100618. [Google Scholar] [CrossRef]
- Noel, D.D. Normality Assessment of Several Quantitative Data Transformation Procedures. Biostat. Biom. Open Access J. 2021, 10, 51–65. [Google Scholar] [CrossRef]
- Yu, H.; Sang, P.; Huan, T. Adaptive Box–Cox Transformation: A Highly Flexible Feature-Specific Data Transformation to Improve Metabolomic Data Normality for Better Statistical Analysis. Anal. Chem. 2022, 94, 8267–8276. [Google Scholar] [CrossRef]
- Yan, J.; Liu, Z.; Yang, H.; Li, W.; Wang, T.; Xie, Q.; Liu, C.; Wang, X.; Wang, H. Identifying Hotspots and Classifying the Spatial Distribution Pattern of KarstCollapse Pillars with Moran’s Index in Coal Mine. Preprints 2025. [Google Scholar] [CrossRef]
- Xie, W.-F.; Li, J.-K.; Peng, K.; Zhang, K.; Ullah, Z. The Application of Local Moran’s I and Getis–Ord Gi* to Identify Spatial Patterns and Critical Source Areas of Agricultural Nonpoint Source Pollution. J. Environ. Eng. 2024, 150, 04024011. [Google Scholar] [CrossRef]
- Risk Assessment Guidance for Superfund; USEPA: Washington, DC, USA, 1989.
- Exposure Factors Handbook; USEPA, Office of Remedial Response: Washington, DC, USA, 2002.
- Chen, H.; Teng, Y.; Lu, S.; Wang, Y.; Wang, J. Contamination Features and Health Risk of Soil Heavy Metals in China. Sci. Total Environ. 2015, 512–513, 143–153. [Google Scholar] [CrossRef]
- Freeze, R.A.; Cherry, J.A. Groundwater; Prentice Hall: Hoboken, NJ, USA, 1979. [Google Scholar]
- Pant, D.; Keesari, T.; Sharma, D.; Rishi, M.; Singh, G.; Jaryal, A.; Sinha, U.K.; Dash, A.; Tripathi, R.M. Study on Uranium Contamination in Groundwater of Faridkot and Muktsar Districts of Punjab Using Stable Isotopes of Water. J. Radioanal. Nucl. Chem. 2017, 313, 635–639. [Google Scholar] [CrossRef]
- Chandrasekar, T.; Chidambaram, S.; Prasanna, M.V.; Rajendiran, T.; Mathivanan, M.; Natesan, D.; Samayamanthula, D.R. Potential Interplay of Uranium with Geochemical Variables and Mineral Saturation States in Groundwater. Appl. Water Sci. 2021, 11, 1–18. [Google Scholar] [CrossRef]
- Kumar, M.; Kumari, K.; Singh, U.K.; Ramanathan, A.L. Hydrogeochemical Processes in the Groundwater Environment of Muktsar, Punjab: Conventional Graphical and Multivariate Statistical Approach. Environ. Geol. 2008, 57, 873–884. [Google Scholar] [CrossRef]
- Chaudhari, U.; Mehta, M.; Sahoo, P.K.; Mittal, S.; Tiwari, R.P. Co-Occurrence of Geogenic Uranium and Fluoride in a Semiarid Belt of the Punjab Plains, India. Groundw. Sustain. Dev. 2023, 23, 101019. [Google Scholar] [CrossRef]
- Rao, N.S.; Marghade, D.; Dinakar, A.; Chandana, I.; Sunitha, B.; Ravindra, B.; Balaji, T. Geochemical Characteristics and Controlling Factors of Chemical Composition of Groundwater in a Part of Guntur District, Andhra Pradesh, India. Environ. Earth Sci. 2017, 76, 1–22. [Google Scholar] [CrossRef]
- Sharma, D.A.; Rishi, M.S.; Keesari, T.; Pant, D.; Singh, R.; Thakur, N.; Sinha, U.K. Distribution of Uranium in Groundwaters of Bathinda and Mansa Districts of Punjab, India: Inferences from an Isotope Hydrochemical Study. J. Radioanal. Nucl. Chem. 2017, 313, 625–633. [Google Scholar] [CrossRef]
- Singh, C.K.; Rina, K.; Singh, R.P.; Shashtri, S.; Kamal, V.; Mukherjee, S. Geochemical Modeling of High Fluoride Concentration in Groundwater of Pokhran Area of Rajasthan, India. Bull. Environ. Contam. Toxicol. 2011, 86, 152–158. [Google Scholar] [CrossRef]
- Rasool, A.; Farooqi, A.; Xiao, T.; Ali, W.; Noor, S.; Abiola, O.; Ali, S.; Nasim, W. A Review of Global Outlook on Fluoride Contamination in Groundwater with Prominence on the Pakistan Current Situation. Environ. Geochem. Health 2018, 40, 1265–1281. [Google Scholar] [CrossRef]
- Sharma, C.; Mahajan, A.; Garg, U.K. Fluoride and Nitrate in Groundwater of South-Western Punjab, India—Occurrence, Distribution and Statistical Analysis. Desalination Water Treat. 2014, 57, 3928–3939. [Google Scholar] [CrossRef]
- Hundal, H.S.; Singh, K.; Singh, D.; Kumar, R. Arsenic Mobilization in Alluvial Soils of Punjab, North–West India under Flood Irrigation Practices. Environ. Earth Sci. 2012, 69, 1637–1648. [Google Scholar] [CrossRef]
- Ahada, C.P.S.; Suthar, S. Assessing Groundwater Hydrochemistry of Malwa Punjab, India. Arab. J. Geosci. 2018, 11, 17. [Google Scholar] [CrossRef]
- Alam, N.; Kumar, A.; Singh, D.K.; Kumar, S.; Husain, M.A.; Neidhardt, H.; Eiche, E.; Marks, M.; Biswas, A. Testing the Hypothesis of Fluoride and Uranium Co-Mobilization into Groundwater by Competitive Ion Exchange in Alluvial Aquifers of Southern Punjab, India. J. Hazard. Mater. 2025, 492, 138267. [Google Scholar] [CrossRef]
- Patnaik, R.; Lahiri, S.; Chahar, V.; Naskar, N.; Sharma, P.K.; Avhad, D.K.; Srivastava, A. Study of uranium mobilization from Himalayan Siwaliks to the Malwa region of Punjab state in India. J. Radioanal. Nucl. Chem. 2016, 308, 913–918. [Google Scholar] [CrossRef]
- Khan, M.N.; Mobin, M.; Abbas, Z.K.; Alamri, S.A. Fertilizers and Their Contaminants in Soils, Surface and Groundwater. Encycl. Anthr. 2018, 5, 225–240. [Google Scholar] [CrossRef]
- Kaur, G.; Kumar, R.; Mittal, S.; Sahoo, P.K.; Vaid, U. Ground/Drinking Water Contaminants and Cancer Incidence: A Case Study of Rural Areas of South West Punjab, India. Hum. Ecol. Risk Assess. Int. J. 2019, 27, 205–226. [Google Scholar] [CrossRef]
- Zhou, P.; Gu, B. Extraction of Oxidized and Reduced Forms of Uranium from Contaminated Soils: Effects of Carbonate Concentration and PH. Environ. Sci. Technol. 2005, 39, 4435–4440. [Google Scholar] [CrossRef]
- Kerketta, A.; Kapoor, H.S.; Sahoo, P.K. Meteorological and Hydrogeochemical Control on the Co-Occurrence of Geogenic Contaminants in the Alluvial Aquifers of Northwest India. Groundw. Sustain. Dev. 2024, 26, 101283. [Google Scholar] [CrossRef]
- Rout, S.; Ravi, P.M.; Kumar, A.; Tripathi, R.M. Study on Speciation and Salinity-Induced Mobility of Uranium from Soil. Environ. Earth Sci. 2015, 74, 2273–2281. [Google Scholar] [CrossRef]
- Burow, K.R.; Belitz, K.; Dubrovsky, N.M.; Jurgens, B.C. Large Decadal-Scale Changes in Uranium and Bicarbonate in Groundwater of the Irrigated Western U.S. Sci. Total Environ. 2017, 586, 87–95. [Google Scholar] [CrossRef] [PubMed]
- Kelly, S.D.; Kemner, K.M.; Brooks, S.C. X-Ray Absorption Spectroscopy Identifies Calcium-Uranyl-Carbonate Complexes at Environmental Concentrations. Geochim. Cosmochim. Acta 2007, 71, 821–834. [Google Scholar] [CrossRef]
- Liesch, T.; Hinrichsen, S.; Goldscheider, N. Uranium in Groundwater—Fertilizers versus Geogenic Sources. Sci. Total Environ. 2015, 536, 981–995. [Google Scholar] [CrossRef]
- Lopez, A.M.; Wells, A.; Fendorf, S. Soil and Aquifer Properties Combine as Predictors of Groundwater Uranium Concentrations within the Central Valley, California. Environ. Sci. Technol. 2020, 55, 352–361. [Google Scholar] [CrossRef]
- Sharma, T.; Bajwa, B.S.; Kaur, I. Contamination of Groundwater by Potentially Toxic Elements in Groundwater and Potential Risk to Groundwater Users in the Bathinda and Faridkot Districts of Punjab, India. Environ. Earth Sci. 2021, 80, 1–15. [Google Scholar] [CrossRef]
- Riedel, T.; Kübeck, C. Uranium in Groundwater—A Synopsis Based on a Large Hydrogeochemical Data Set. Water Res. 2018, 129, 29–38. [Google Scholar] [CrossRef]
- Nolan, J.; Weber, K.A. Natural Uranium Contamination in Major U.S. Aquifers Linked to Nitrate. Environ. Sci. Technol. Lett. 2015, 2, 215–220. [Google Scholar] [CrossRef]
- Rosen, M.R.; Burow, K.R.; Fram, M.S. Anthropogenic and Geologic Causes of Anomalously High Uranium Concentrations in Groundwater Used for Drinking Water Supply in the Southeastern San Joaquin Valley, CA. J. Hydrol. 2019, 577, 124009. [Google Scholar] [CrossRef]
- Ijumulanaa, J.; Ligatea, F.; Bhattacharyaa, P.; Mtalob, F.; Zhang, C. Spatial Analysis and GIS Mapping of Regional Hotspots and Potential Health Risk of Fluoride Concentrations in Groundwater of Northern Tanzania. Sci. Total Environ. 2020, 735, 139584. [Google Scholar] [CrossRef] [PubMed]
- Moran, P.A.P. Notes on Continuous Stochastic Phenomena. Biometrika 1950, 37, 17. [Google Scholar] [CrossRef]
- Zhang, C.; Luo, L.; Xu, W.; Ledwith, V. Use of Local Moran’s I and GIS to Identify Pollution Hotspots of Pb in Urban Soils of Galway, Ireland. Sci. Total Environ. 2008, 398, 212–221. [Google Scholar] [CrossRef]
- Zhai, Y.; Zhao, X.; Teng, Y.; Li, X.; Zhang, J.; Wu, J.; Zuo, R. Groundwater Nitrate Pollution and Human Health Risk Assessment by Using HHRA Model in an Agricultural Area, NE China. Ecotoxicol. Environ. Saf. 2017, 137, 130–142. [Google Scholar] [CrossRef]
- Kumar, D.; Singh, A.; Jha, R.K.; Sahoo, B.B.; Sahoo, S.K.; Jha, V. Source Characterization and Human Health Risk Assessment of Nitrate in Groundwater of Middle Gangetic Plain, India. Arab. J. Geosci. 2019, 12, 339. [Google Scholar] [CrossRef]
- Mridha, D.; Priyadarshni, P.; Bhaskar, K.; Gaurav, A.; De, A.; Das, A.; Joardar, M.; Chowdhury, N.R.; Roychowdhury, T. Fluoride Exposure and Its Potential Health Risk Assessment in Drinking Water and Staple Food in the Population from Fluoride Endemic Regions of Bihar, India. Groundw. Sustain. Dev. 2021, 13, 100558. [Google Scholar] [CrossRef]
- Onipe, T.; Edokpayi, J.N.; Odiyo, J.O. A Review on the Potential Sources and Health Implications of Fluoride in Groundwater of Sub-Saharan Africa. J. Environ. Sci. Health Part A 2020, 55, 1078–1093. [Google Scholar] [CrossRef] [PubMed]
| Parameters | Units | Min | Max | Med | Avg | SD | Min | Max | Med | Avg | SD | Permissible Limit [92] | % Samples > Permissible Limit | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Shallow (<180 ft) | Deeper (>180 ft) | Shallow | Deeper | |||||||||||
| pH | 6.7 | 8.2 | 7.4 | 7.4 | 0.33 | 6.9 | 8.3 | 7.4 | 7.4 | 0.35 | 6.5–8.5 | 0 | 0 | |
| EC | μS/cm | 312 | 9147 | 2967 | 3371 | 1889 | 275 | 4236 | 1250 | 1632 | 988.6 | − | − | |
| TDS | mg/L | 208 | 6397 | 2016 | 2339 | 1324.8 | 184.2 | 2843 | 837.5 | 1094.5 | 663.8 | 500 | 97 | 81 |
| ORP | mV | 12.8 | 215 | 151 | 118.3 | 72.5 | 23.7 | 218 | 151 | 124.3 | 70.5 | − | − | |
| Salinity | mg/L | 30.7 | 2780 | 635 | 730.1 | 683.2 | 117 | 1230 | 530 | 572 | 241.4 | − | − | |
| HCO3− | mg/L | 100 | 1200 | 500 | 491 | 166.7 | 200 | 1000 | 500 | 507.6 | 154.6 | 200 | 91 | 93 |
| F− | mg/L | 0.3 | 14.4 | 1.7 | 2.2 | 2.3 | 0.3 | 1.98 | 0.8 | 0.9297 | 0.41 | 1.5 | 54 | 15 |
| Cl− | mg/L | 10.37 | 1507.81 | 180.48 | 276.93 | 292.3 | 12 | 240 | 31 | 59.54 | 65.9 | 250 | 35 | 0 |
| NO3− | mg/L | 1.143 | 166.86 | 28.61 | 38.94 | 31.7 | 4.34 | 35 | 18 | 18.22 | 8.4 | 50 | 25 | 0 |
| SO42− | mg/L | 16.54 | 1936.14 | 404 | 525.64 | 466.7 | 31 | 529 | 164 | 179.8 | 114.8 | 200 | 74 | 36 |
| Na | mg/L | 6.98 | 1540.14 | 320.7 | 409.83 | 363.2 | 2.9 | 440.9 | 25.2 | 99.03 | 131.7 | 200 | 66 | 18 |
| K | mg/L | 2.04 | 105.66 | 8.02 | 12.45 | 2.56 | 11.5 | 6 | 6.181 | 1.9 | − | − | ||
| Ca | mg/L | 6.4 | 600 | 65.6 | 109.4 | 118 | 0 | 405 | 135 | 135.5 | 92.8 | 75 | 45 | 72 |
| Mg | mg/L | 20.32 | 1255.5 | 228 | 316.3 | 277.9 | 279 | 961 | 558 | 551.4 | 160.4 | 30 | 91 | 100 |
| Zn | μg/L | BDL | 50.1 | 13.9 | 17.4 | 17.6 | BDl | 31.8 | 5.1 | 7.8 | 9.4 | 5000 | 0 | 0 |
| Pb | μg/L | BDL | 7 | 0 | 0.9 | 2.3 | BDL | 7 | 0 | 0.9 | 2.3 | 10 | 0 | 0 |
| As | μg/L | BDL | 6.9 | 0 | 3.4 | 2.7 | BDL | 8.2 | 0 | 3.1 | 4.1 | 10 | 0 | 0 |
| U | μg/L | 0.6 | 456.65 | 62.87 | 95.81 | 98.02 | 8.14 | 349 | 60.9 | 75.5 | 65.7 | 30 | 76 | 84 |
| Data Treatment | High–High | High–Low | Low–High | Low–Low | Not Significant |
|---|---|---|---|---|---|
| U | |||||
| CLR transformed, q1 | 17 | 18 | 4 | 5 | 47 |
| CLR transformed, q2 | 17 | 18 | 4 | 5 | 47 |
| CLR transformed, q3 | 13 | 15 | 5 | 4 | 54 |
| CLR transformed, q4 | 5 | 5 | 15 | 6 | 60 |
| Data Treatment | Moran’s I | SD | E | z-Score | p-Value |
|---|---|---|---|---|---|
| U | |||||
| CLR transformed, q1 | 0.49 | 0.06 | −0.01 | 7.8 | 0.001 |
| CLR transformed, q2 | 0.35 | 0.04 | −0.01 | 7.4 | 0.001 |
| CLR transformed, q3 | 0.18 | 0.04 | −0.01 | 4.6 | 0.001 |
| CLR transformed, q4 | −0.12 | 0.03 | −0.01 | −2.3 | 0.009 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chaudhari, U.; Kumari, D.; Mittal, S.; Sahoo, P.K. GIS-Based Spatial Autocorrelation and Multivariate Statistics for Understanding Groundwater Uranium Contamination and Associated Health Risk in Semiarid Region of Punjab, India. Water 2025, 17, 2064. https://doi.org/10.3390/w17142064
Chaudhari U, Kumari D, Mittal S, Sahoo PK. GIS-Based Spatial Autocorrelation and Multivariate Statistics for Understanding Groundwater Uranium Contamination and Associated Health Risk in Semiarid Region of Punjab, India. Water. 2025; 17(14):2064. https://doi.org/10.3390/w17142064
Chicago/Turabian StyleChaudhari, Umakant, Disha Kumari, Sunil Mittal, and Prafulla Kumar Sahoo. 2025. "GIS-Based Spatial Autocorrelation and Multivariate Statistics for Understanding Groundwater Uranium Contamination and Associated Health Risk in Semiarid Region of Punjab, India" Water 17, no. 14: 2064. https://doi.org/10.3390/w17142064
APA StyleChaudhari, U., Kumari, D., Mittal, S., & Sahoo, P. K. (2025). GIS-Based Spatial Autocorrelation and Multivariate Statistics for Understanding Groundwater Uranium Contamination and Associated Health Risk in Semiarid Region of Punjab, India. Water, 17(14), 2064. https://doi.org/10.3390/w17142064







