Linear vs. Non-Linear Regional Flood Estimation Models in New South Wales, Australia
Abstract
1. Introduction
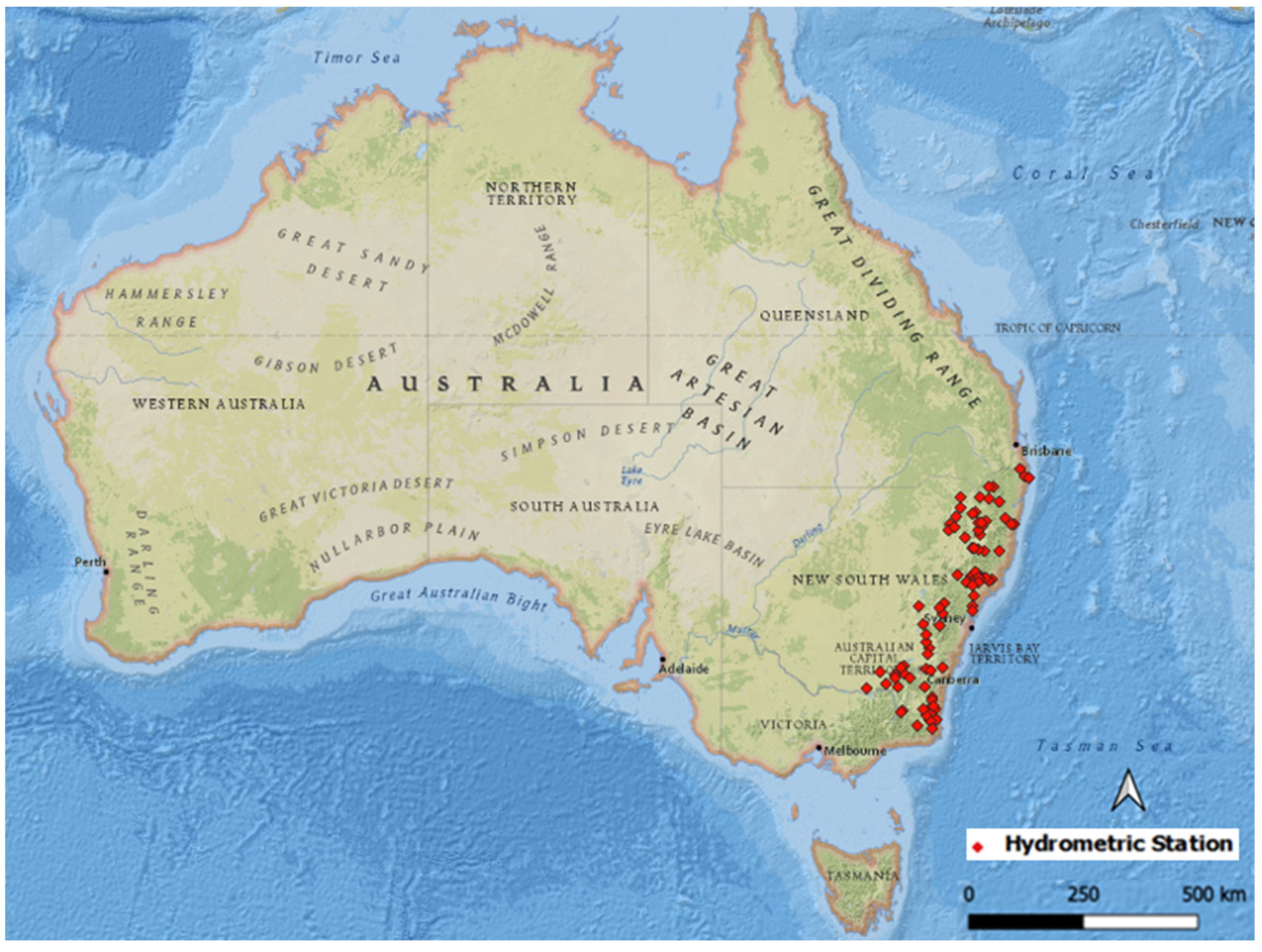
2. Study Area and Data Selection
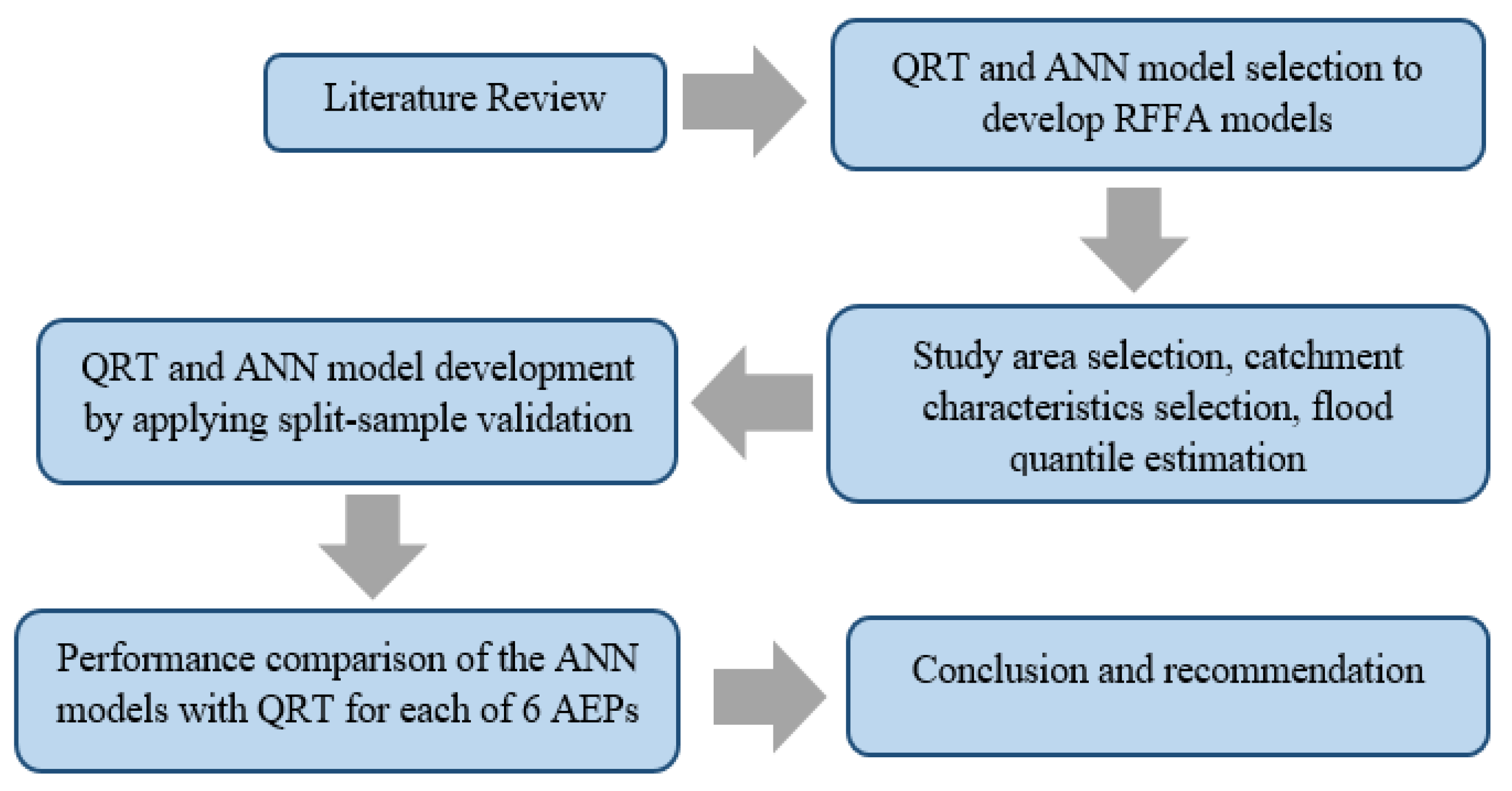
3. Methodology
3.1. QRT
3.2. ANN
3.3. Statistical Indices
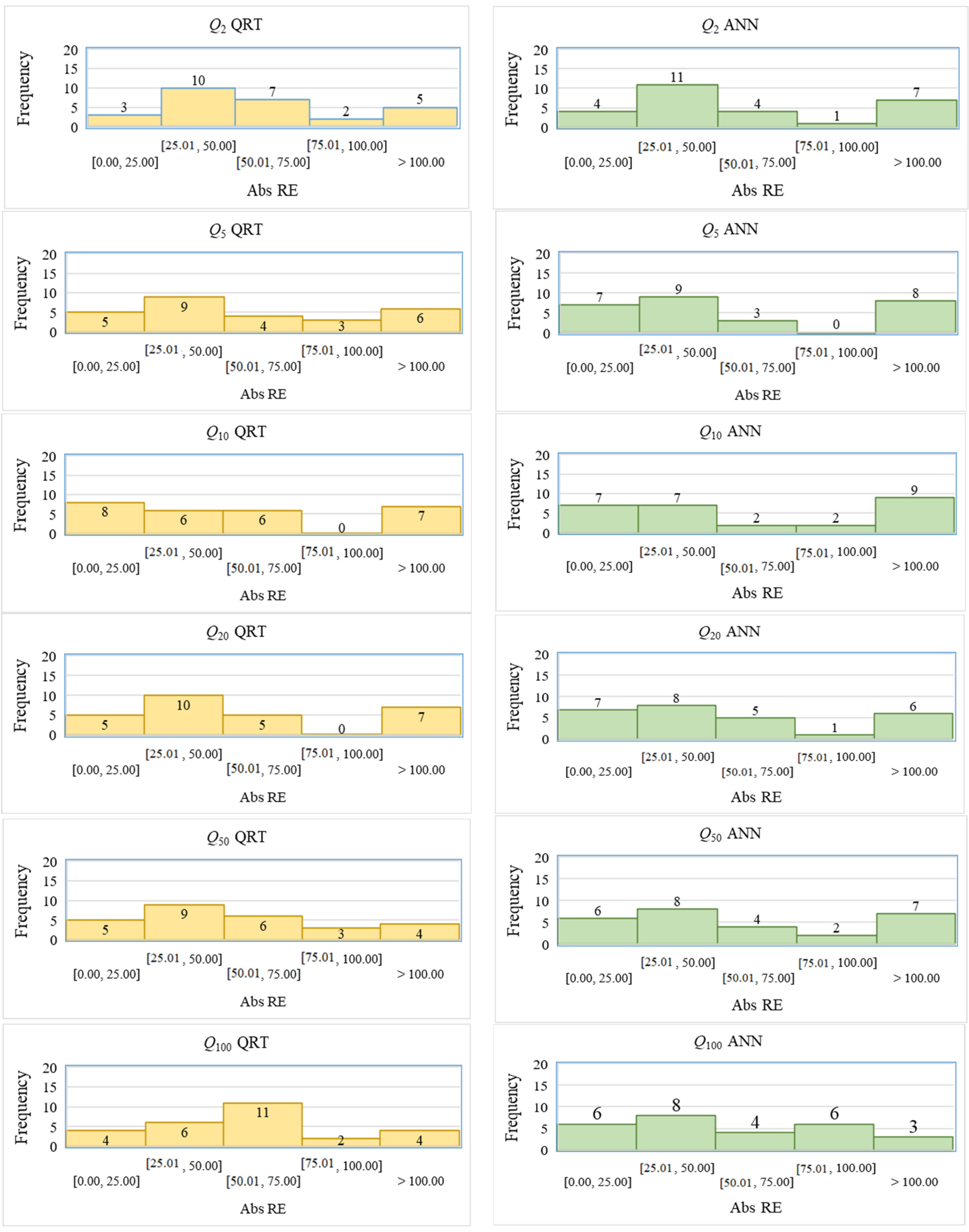
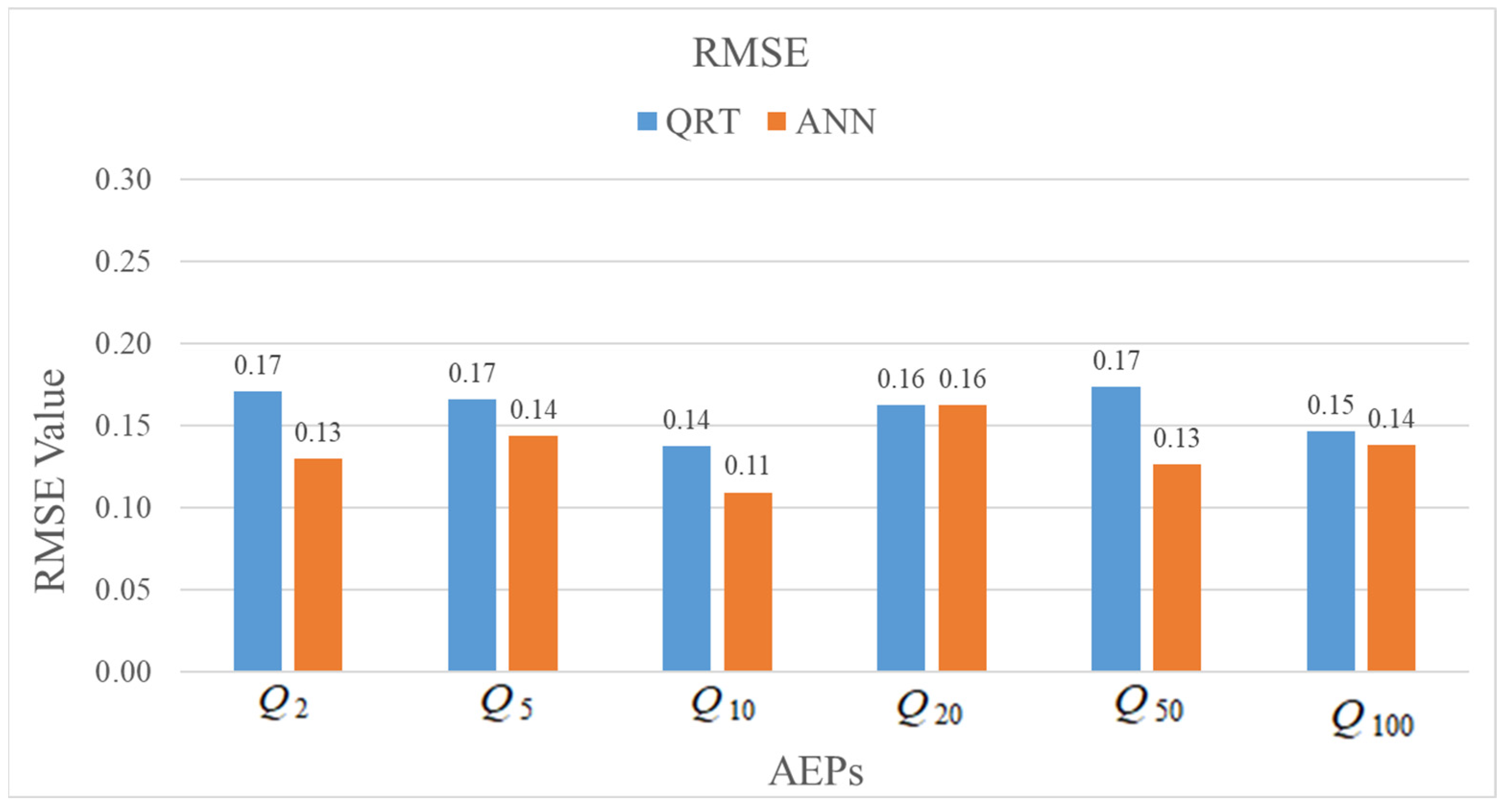
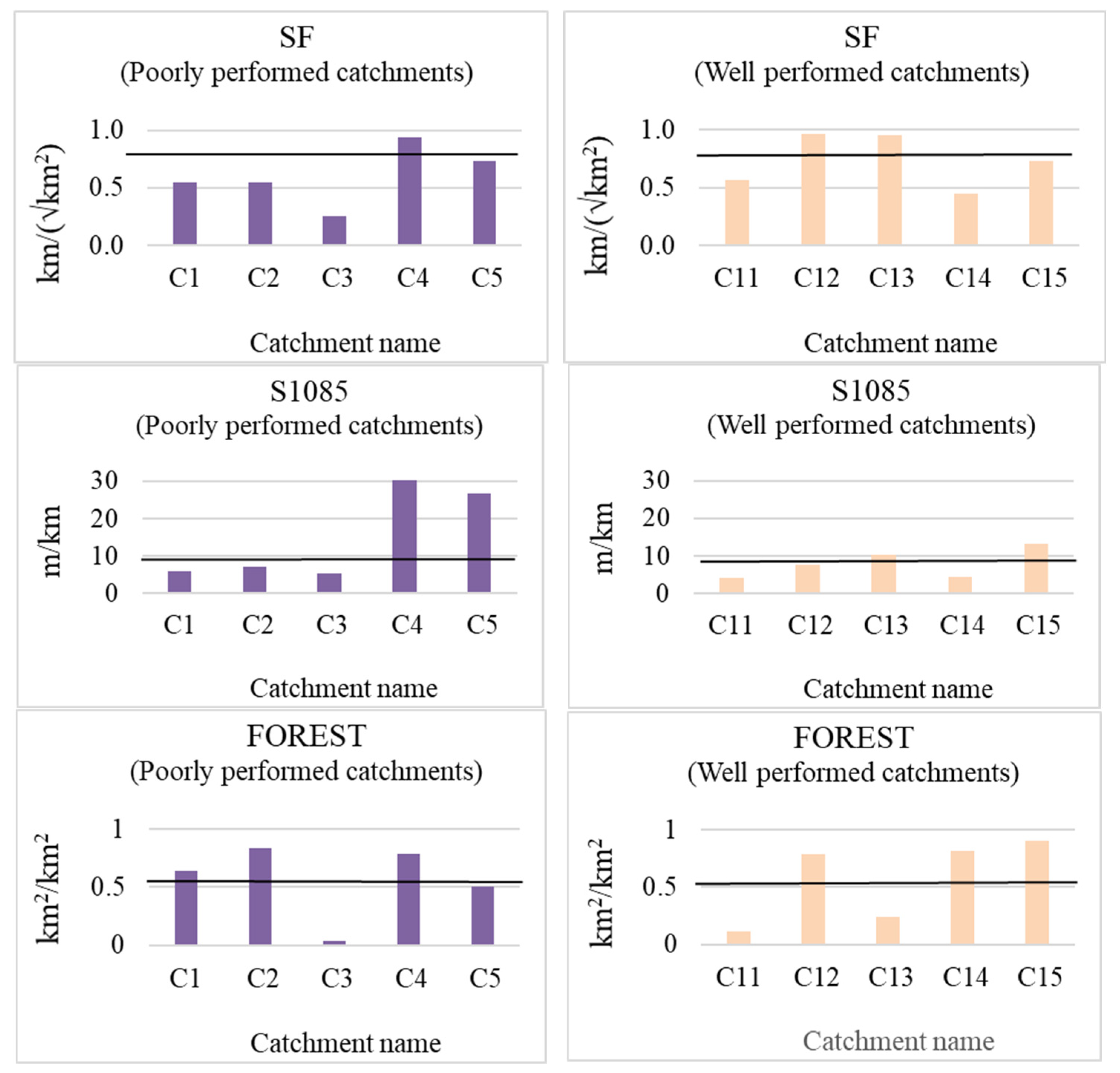
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jongman, B.; Ward, P.J.; Aerts, J.C.J.H. Global exposure to river and coastal flooding: Long term trends and changes. Glob. Environ. Change 2012, 22, 823–835. [Google Scholar] [CrossRef]
- Pinos, J.; Quesada-Román, A. Flood Risk-Related Research Trends in Latin America and the Caribbean. Water 2021, 14, 10. [Google Scholar] [CrossRef]
- Nofal, O.M.; Van De Lindt, J.W. Understanding flood risk in the context of community resilience modeling for the built environment: Research needs and trends. Sustain. Resilient Infrastruct. 2022, 7, 171–187. [Google Scholar] [CrossRef]
- Kuczera, G.; Franks, S. At-site flood frequency analysis. In Australian Rainfall & Runoff, Chapter 2, Book 3; Ball, J., Babister, M., Nathan, R., Weeks, W., Weinmann, E., Retallick, M., Testoni, I., Eds.; Commonwealth of Australia: Sydney, Australia, 2019. [Google Scholar]
- Cunnane, C. Review of statistical models for flood frequency estimation. In Hydrologic Frequency Modelling; Springer: Dordrecht, The Netherlands, 1987; pp. 49–95. [Google Scholar]
- Shu, C.; Ouarda, T.B.M.J. Flood frequency analysis at ungauged sites using artificial neural networks in canonical correlation analysis physiographic space. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Sen, Z. Regional drought and flood frequency analysis: Theoretical consideration. J. Hydrol. 1980, 46, 265–279. [Google Scholar] [CrossRef]
- Pilgrim, D.H.; Cordery, I. Chapter 9: Flood Runoff. Handbook of Hydrology; McGraw-Hill: New York, NY, USA, 1993. [Google Scholar]
- Rahman, A.; Haddad, K.; Zaman, M.; Kuczera, G.; E Weinmann, P. Design Flood Estimation in Ungauged Catchments: A Comparison Between the Probabilistic Rational Method and Quantile Regression Technique for NSW. Australas. J. Water Resour. 2011, 14, 127–139. [Google Scholar] [CrossRef]
- Dalrymple, T. Flood-Frequency Analyses (No. 1543); US Government Printing Office: Washington, DC, USA, 1960. [Google Scholar]
- Smith, A.; Sampson, C.; Bates, P. Regional flood frequency analysis at the global scale. Water Resour. Res. 2015, 51, 539–553. [Google Scholar] [CrossRef]
- Stedinger, J.R.; Tasker, G.D. Regional Hydrologic Analysis: 1. Ordinary, Weighted, and Generalized Least Squares Compared. Water Resour. Res. 1985, 21, 1421–1432. [Google Scholar] [CrossRef]
- Ouarda, T.B.M.J.; Ba, K.M.; Diaz-Delgado, C.; Carsteanu, A.; Chokmani, K.; Gingras, H.; Quentin, E.; Trujillo, E.; Bobée, B. Intercomparison of regional flood frequency estimation methods at ungauged sites for a Mexican case study. J. Hydrol. 2008, 348, 40–58. [Google Scholar] [CrossRef]
- Archfield, S.A.; Pugliese, A.; Castellarin, A.; Skøien, J.O.; Kiang, J.E. Topological and canonical kriging for design flood prediction in ungauged catchments: An improvement over a traditional regional regression approach? Hydrol. Earth Syst. Sci. 2013, 17, 1575–1588. [Google Scholar] [CrossRef]
- Faulkner, D.; Warren, S.; Burn, D. Design floods for all of Canada. Canad. Water Resour. J. Rev. Canad. Ressour. Hydr. 2016, 41, 398–411. [Google Scholar] [CrossRef]
- Chebana, F.; Charron, C.; Ouarda, T.B.M.J.; Martel, B. Regional Frequency Analysis at Ungauged Sites with the Generalized Additive Model. J. Hydrometeorol. 2014, 15, 2418–2428. [Google Scholar] [CrossRef]
- Msilini, A.; Charron, C.; Ouarda, T.B.M.J.; Masselot, P. Flood frequency analysis at ungauged catchments with the GAM and MARS approaches in the Montreal region, Canada. Can. Water Resour. J Rev. Can. Ressour. Hydr. 2022, 47, 111–121. [Google Scholar] [CrossRef]
- Kuichling, E. The Relation Between the Rainfall and the Discharge of Sewers in Populous Districts. Trans. Am. Soc. Civ. Eng. 1889, 20, 1–56. [Google Scholar] [CrossRef]
- Pilgrim, E.; Institution of Engineers Australia Pilgrim, D.H.; Canterford, R.P. Australian Rainfall and Runoff; Institution of Engineers: Sydney, Australia, 1987. [Google Scholar]
- Hosking, J.R.M.; Wallis, J.R. Some statistics useful in regional frequency analysis. Water Resour. Res. 1993, 29, 271–281. [Google Scholar] [CrossRef]
- Bates, B.C.; Rahman, A.; Mein, R.G.; Weinmann, P.E. Climatic and physical factors that influence the homogeneity of regional floods in southeastern Australia. Water Resour. Res. 1998, 34, 3369–3381. [Google Scholar] [CrossRef]
- Haddad, K.; Rahman, A. Regional flood frequency analysis in eastern Australia: Bayesian GLS regression-based methods within fixed region and ROI framework–Quantile Regression vs. Parameter Regression Technique. J. Hydrol. 2012, 430, 142–161. [Google Scholar] [CrossRef]
- Gupta, V.K.; Mesa, O.J.; Dawdy, D.R. Multiscaling theory of flood peaks: Regional quantile analysis. Water Resour. Res. 1994, 30, 3405–3421. [Google Scholar] [CrossRef]
- Rahman, A.S.; Khan, Z.; Rahman, A. Application of independent component analysis in regional flood frequency analysis: Comparison between quantile regression and parameter regression techniques. J. Hydrol. 2020, 581, 124372. [Google Scholar] [CrossRef]
- Sivakumar, B.; Singh, V.P. Hydrologic system complexity and nonlinear dynamic concepts for a catchment classification framework. Hydrol. Earth Syst. Sci. 2012, 16, 4119–4131. [Google Scholar] [CrossRef]
- Sharafati, A.; Haghbin, M.; Motta, D.; Yaseen, Z.M. The application of soft computing models and empirical formulations for hydraulic structure scouring depth simulation: A comprehensive review, assessment and possible future research direction. Arch. Comput. Methods Eng. 2021, 28, 423–447. [Google Scholar] [CrossRef]
- Jingyi, Z.; Hall, M. Regional flood frequency analysis for the Gan-Ming River basin in China. J. Hydrol. 2004, 296, 98–117. [Google Scholar] [CrossRef]
- Dawson, C.; Abrahart, R.; Shamseldin, A.; Wilby, R. Flood estimation at ungauged sites using artificial neural networks. J. Hydrol. 2006, 319, 391–409. [Google Scholar] [CrossRef]
- Allahbakhshian-Farsani, P.; Vafakhah, M.; Khosravi-Farsani, H.; Hertig, E. Regional flood frequency analysis through some machine learning models in semi-arid regions. Water Resour. Manag. 2020, 34, 2887–2909. [Google Scholar] [CrossRef]
- Vafakhah, M.; Bozchaloei, S.K. Regional analysis of flow duration curves through support vector regression. Water Resour. Manag. 2020, 34, 283–294. [Google Scholar] [CrossRef]
- Seckin, N.; Guven, A. Estimation of peak flood discharges at ungauged sites across Turkey. Water Resour. Manag. 2012, 26, 2569–2581. [Google Scholar] [CrossRef]
- Zorn, C.R.; Shamseldin, A.Y. Peak flood estimation using gene expression programming. J. Hydrol. 2015, 531, 1122–1128. [Google Scholar] [CrossRef]
- Garmdareh, E.S.; Vafakhah, M.; Eslamian, S.S. Regional flood frequency analysis using support vector regression in arid and semi-arid regions of Iran. Hydrol. Sci. J. 2018, 63, 426–440. [Google Scholar] [CrossRef]
- Bozchaloei, S.K.; Vafakhah, M. Regional analysis of flow duration curves using adaptive neuro-fuzzy inference system. J. Hydrol. Eng. 2015, 20, 06015008. [Google Scholar] [CrossRef]
- Desai, S.; Ouarda, T.B. Regional hydrological frequency analysis at ungauged sites with random forest regression. J. Hydrol. 2021, 594, 125861. [Google Scholar] [CrossRef]
- Esmaeili-Gisavandani, H.; Zarei, H.; Tehrani, M.R.F. Regional flood frequency analysis using data-driven models (M5, random forest, and ANFIS) and a multivariate regression method in ungauged catchments. Appl. Water Sci. 2023, 13, 139. [Google Scholar] [CrossRef]
- Tramblay, Y.; El Khalki, E.M.; Khedimallah, A.; Sadaoui, M.; Benaabidate, L.; Boulmaiz, T.; Boutaghane, H.; Dakhlaoui, H.; Hanich, L.; Ludwig, W.; et al. Regional flood frequency analysis in North Africa. J. Hydrol. 2024, 630, 130678. [Google Scholar] [CrossRef]
- Jarajapu, D.C.; Rathinasamy, M.; Agarwal, A.; Bronstert, A. Design flood estimation using extreme Gradient Boosting-based on Bayesian optimization. J. Hydrol. 2022, 613, 128341. [Google Scholar] [CrossRef]
- Mangukiya, N.K.; Sharma, A. Alternate pathway for regional flood frequency analysis in data-sparse region. J. Hydrol. 2024, 629, 130635. [Google Scholar] [CrossRef]
- Filipova, V.; Hammond, A.; Leedal, D.; Lamb, R. Prediction of flood quantiles at ungauged catchments for the contiguous USA using Artificial Neural Networks. Hydrol. Res. 2022, 53, 107–123. [Google Scholar] [CrossRef]
- Aziz, K.; Haque, M.M.; Rahman, A.; Shamseldin, A.Y.; Shoaib, M. Flood estimation in ungauged catchments: Application of artificial intelligence based methods for Eastern Australia. Stoch. Environ. Res. Risk Assess. 2017, 31, 1499–1514. [Google Scholar] [CrossRef]
- Rahman, A.; Haddad, K.; Kuczera, G.; Weinmann, E. Regional Flood Methods. In Australian Rainfall and Runoff: A Guide to Flood Estimation. Book 3, Peak Flow Estimation; Commonwealth of Australia: Sydney, Australia, 2019; pp. 105–146. [Google Scholar]
- Zalnezhad, A.; Rahman, A.; Nasiri, N.; Vafakhah, M.; Samali, B.; Ahamed, F. Comparing Performance of ANN and SVM Methods for Regional Flood Frequency Analysis in South-East Australia. Water 2022, 14, 3323. [Google Scholar] [CrossRef]
- Haddad, K.; Rahman, A.; Zaman, M.; Shrestha, S. Applicability of Monte Carlo cross validation technique for model development and validation using generalised least squares regression. J. Hydrol. 2013, 482, 119–128. [Google Scholar] [CrossRef]
- Mcculloch, W.S.; Pitts, W.H. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Rathore, P.S.; Dadich, N.; Jha, A.; Pradhan, D. Effect of learning rate on neural network and convolutional neural network. Int. J. Eng. Res. Technol. 2018, 6, 1–8. [Google Scholar]
- Ying, X. An overview of overfitting and its solutions. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2019; Volume 1168, p. 022022. [Google Scholar]
- Deng, T. Effect of the number of hidden layer neurons on the accuracy of the back propagation neural network. Highlights Sci. Eng. Technol. 2023, 74, 462–468. [Google Scholar] [CrossRef]
- Jackson, E.K.; Roberts, W.; Nelsen, B.; Williams, G.P.; Nelson, E.J.; Ames, D.P. Introductory overview: Error metrics for hydrologic modelling—A review of common practices and an open source library to facilitate use and adoption. Environ. Model. Softw. 2019, 119, 32–48. [Google Scholar] [CrossRef]
- Rima, L.; Haddad, K.; Rahman, A. Generalised Additive Model-Based Regional Flood Frequency Analysis: Parameter Regression Technique Using Generalised Extreme Value Distribution. Water 2025, 17, 206. [Google Scholar] [CrossRef]
- Ali, S.; Rahman, A. Development of a kriging-based regional flood frequency analysis technique for South-East Australia. Nat. Hazards 2022, 114, 2739–2765. [Google Scholar] [CrossRef]
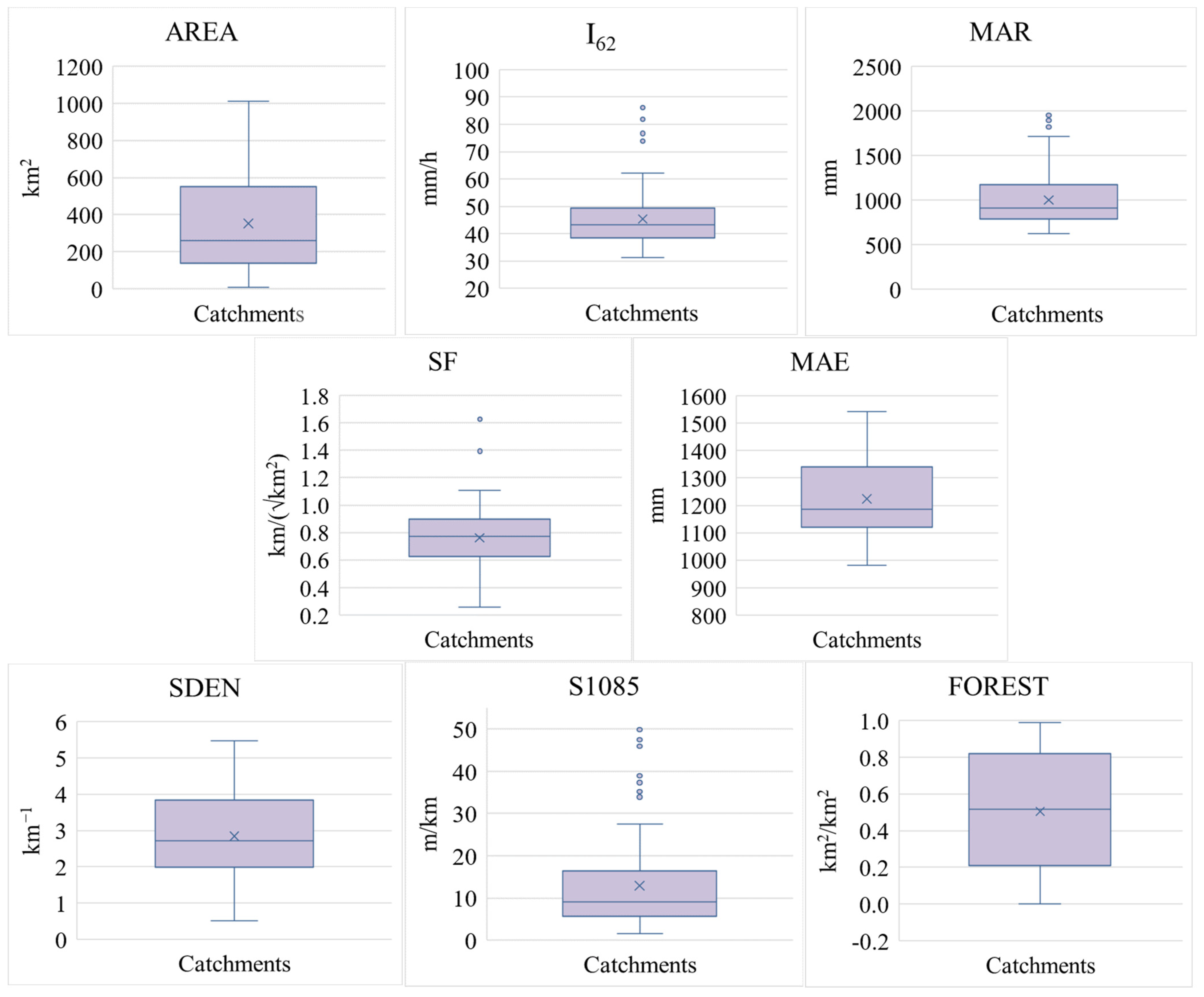


| Acronym and Unit | Description | Influence Status | Min | Max | Mean | Median |
|---|---|---|---|---|---|---|
| AREA, km2 | Catchment area | Direct | 8 | 1010 | 353.60 | 260.00 |
| I62, mm/h | Precipitation having duration of 6 h and 2-year return period | Direct | 31.30 | 87.30 | 45.10 | 43.10 |
| MAR, mm | Mean annual rainfall | Indirect | 626.17 | 1953.23 | 990.40 | 909.90 |
| SF | Shortest distance between the catchment’s centroid and outlet divided by the square root of AREA | Direct | 0.26 | 1.63 | 0.76 | 0.77 |
| MAE, mm | Mean annual potential evapotranspiration | Indirect | 980.40 | 1543.30 | 1222.80 | 1185.60 |
| SDEN, km−1 | Ratio of total stream length and AREA | Direct | 0.52 | 5.47 | 2.84 | 2.70 |
| S1085, m/km | Slope of mainstream considering 75% length | Direct | 1.54 | 49.86 | 13.02 | 9.08 |
| FOREST | Fraction of the forested area of the catchment | Indirect | 0.0001 | 0.99 | 0.50 | 0.52 |
| Variables | AREA | I62 | MAR | SF | MAE | SDEN | S1085 | FOREST |
|---|---|---|---|---|---|---|---|---|
| AREA | 1.00 | |||||||
| I62 | −0.21 | 1.00 | ||||||
| MAR | −0.31 | 0.83 | 1.00 | |||||
| SF | −0.05 | 0.03 | −0.06 | 1.00 | ||||
| MAE | −0.09 | 0.67 | 0.53 | 0.14 | 1.00 | |||
| SDEN | −0.18 | 0.37 | 0.36 | 0.04 | 0.39 | 1.00 | ||
| S1085 | −0.33 | −0.12 | −0.02 | 0.05 | −0.29 | −0.08 | 1.00 | |
| FOREST | −0.12 | 0.33 | 0.40 | −0.01 | −0.03 | 0.05 | 0.39 | 1.00 |
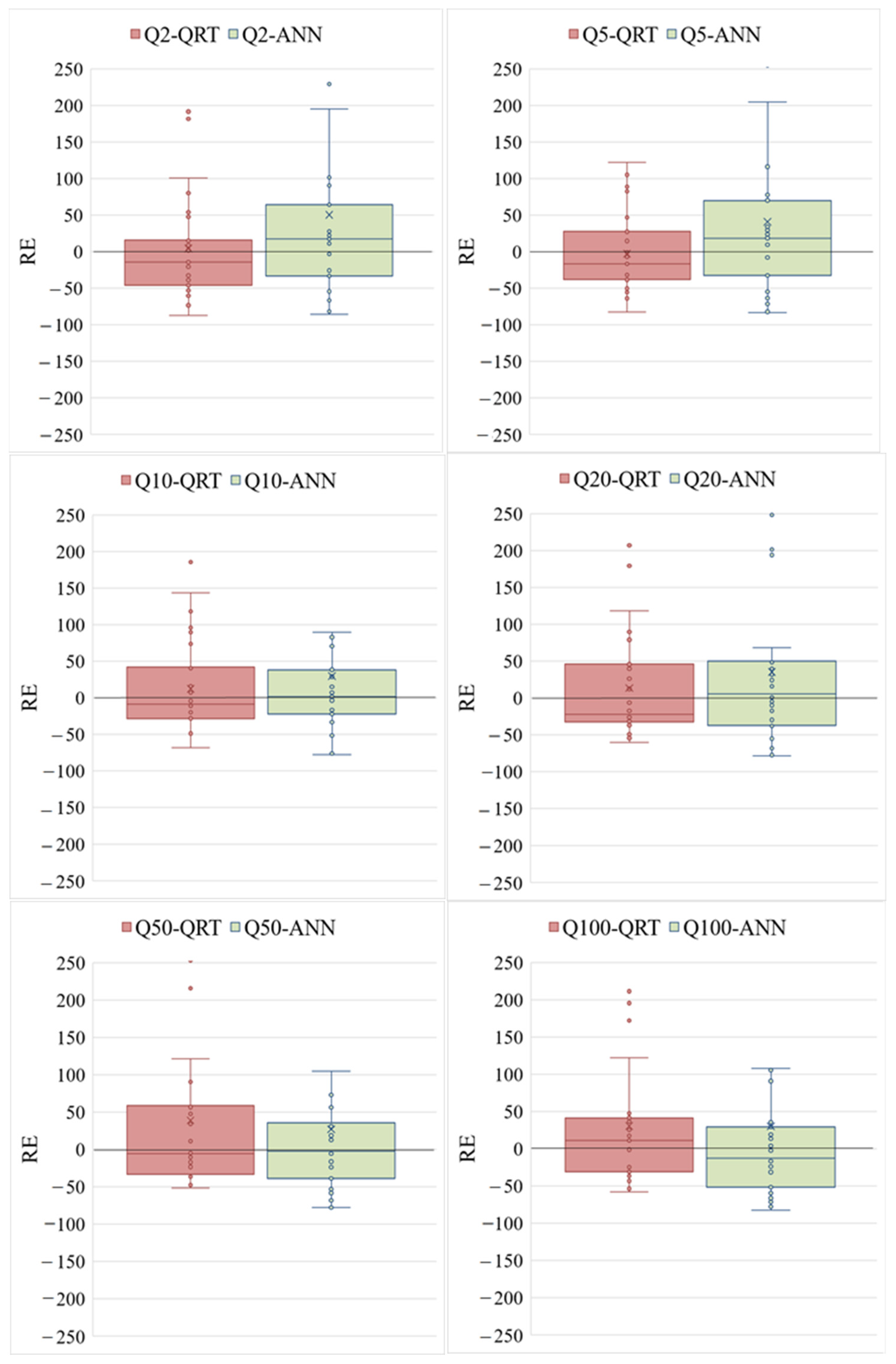
| AEP | REr QRT | REr ANN | Bias QRT | Bias ANN | Median Qr QRT | Median Qr ANN |
|---|---|---|---|---|---|---|
| Q2 | 39.12 | 33.79 | −0.072 | −0.001 | 0.86 | 1.17 |
| Q5 | 38.40 | 32.82 | −0.087 | 0.007 | 0.83 | 1.18 |
| Q10 | 40.40 | 31.89 | −0.014 | −0.015 | 0.91 | 1.01 |
| Q20 | 37.14 | 39.56 | −0.017 | 0.007 | 0.77 | 1.05 |
| Q50 | 36.95 | 36.95 | 0.053 | −0.032 | 0.94 | 0.98 |
| Q100 | 36.30 | 35.49 | 0.033 | −0.064 | 1.11 | 0.87 |
| Overall Median | 37.44 | 35.45 | −0.050 | 0.026 | 0.89 | 1.06 |
| Study | Method | Adopted Data | Validation Technique | Comment |
|---|---|---|---|---|
| Rima et al. [51] | GAM and PRT | 88 gauged catchments of NSW, Australia | LOO validation | GAM REr in the range of 34–40%, log-log REr in the range of 36–45% |
| Ali and Rahman [52] | Kriging-based RFFA | 558 catchments from eastern Australia | LOO validation | For NSW, Australia, REr in the range of 28.2–35.9% |
| Zalnezhad et al. [43] | ANN compared with SVM for RFFA | 188 catchments from southeast Australia | Split-sample validation | ANN REr in the range of 33–54%, SVM REr in the range of 36–48% |
| Aziz et al. [41] | ANN and GEP compared with QRT for RFFA | 452 stations from eastern Australia | Split-sample validation | ANN REr in the range of 36–45%, GEP REr in the range of 38–46%, QRT REr in the range of 43–65% |
| ARR19 RFFA model [42] | PRT-based RFFA | 558 catchments of eastern Australia | LOO validation | For NSW, Australia, REr in the range of 57.3–64.1% |
| This study | ANN compared with QRT for RFFA | 88 gauged catchments of NSW, Australia | Split-sample validation | ANN REr in the range 31.9–39.6%, QRT REr in the range of 36.3–40.4% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Afrin, N.; Rafi, R.S.M.H.; Haddad, K.; Rahman, A. Linear vs. Non-Linear Regional Flood Estimation Models in New South Wales, Australia. Water 2025, 17, 1845. https://doi.org/10.3390/w17131845
Afrin N, Rafi RSMH, Haddad K, Rahman A. Linear vs. Non-Linear Regional Flood Estimation Models in New South Wales, Australia. Water. 2025; 17(13):1845. https://doi.org/10.3390/w17131845
Chicago/Turabian StyleAfrin, Nilufa, Ridwan S. M. H. Rafi, Khaled Haddad, and Ataur Rahman. 2025. "Linear vs. Non-Linear Regional Flood Estimation Models in New South Wales, Australia" Water 17, no. 13: 1845. https://doi.org/10.3390/w17131845
APA StyleAfrin, N., Rafi, R. S. M. H., Haddad, K., & Rahman, A. (2025). Linear vs. Non-Linear Regional Flood Estimation Models in New South Wales, Australia. Water, 17(13), 1845. https://doi.org/10.3390/w17131845






