Advancements in Hydrological Modeling: The Role of bRNN-CNN-GRU in Predicting Dam Reservoir Inflow Patterns
Abstract
1. Introduction
2. Materials and Methods
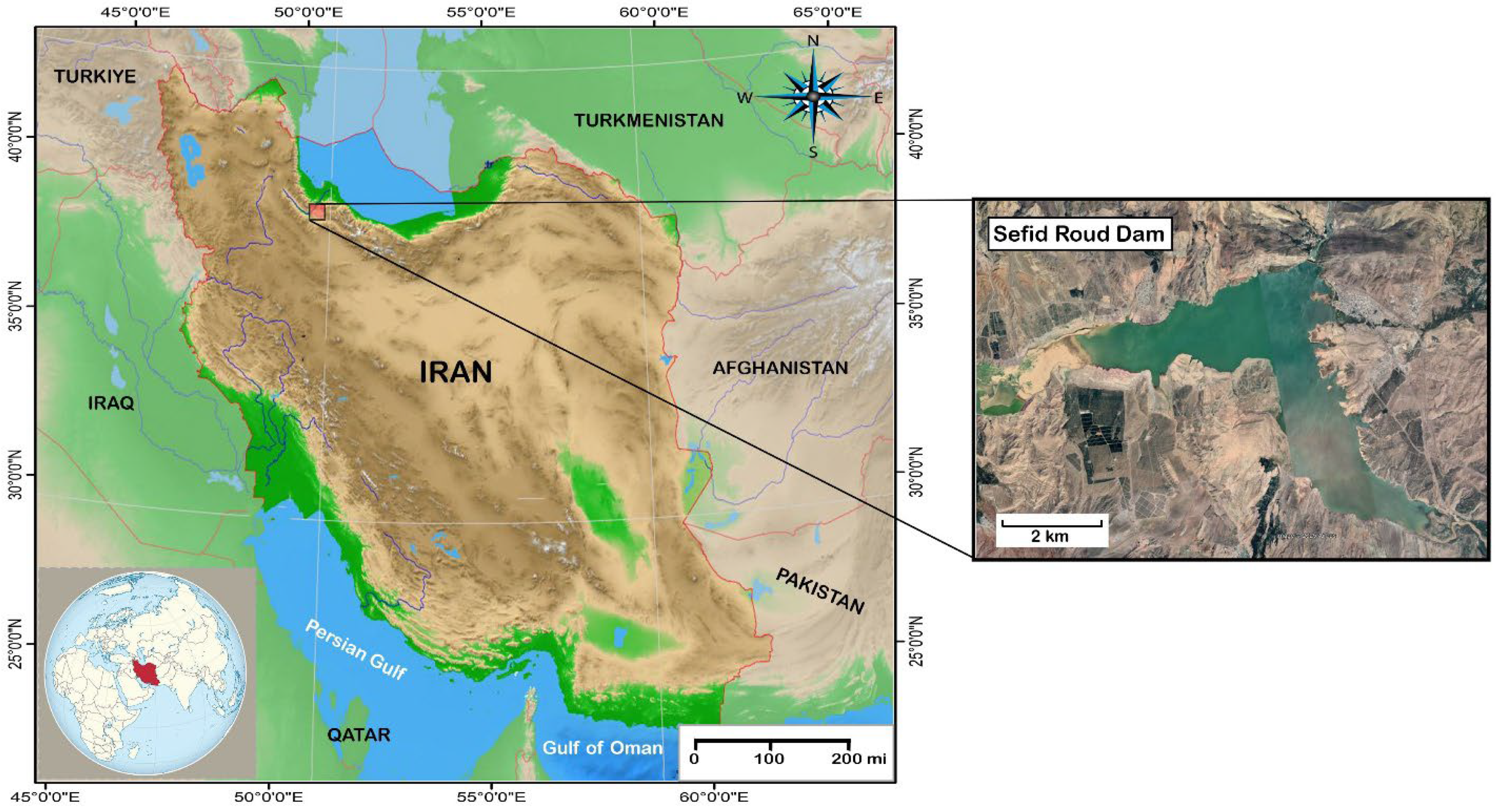
2.1. Overview of the Study Area
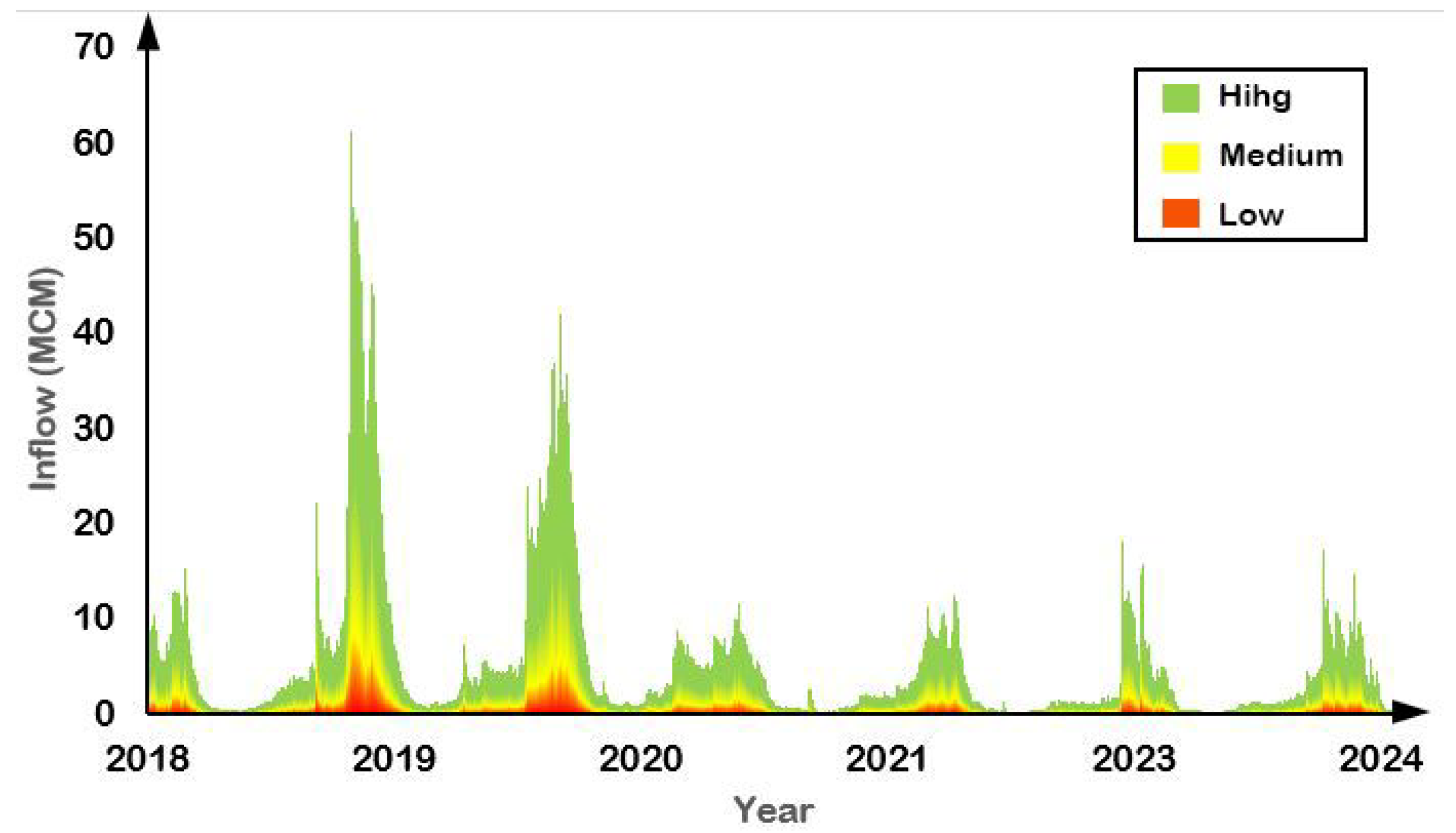
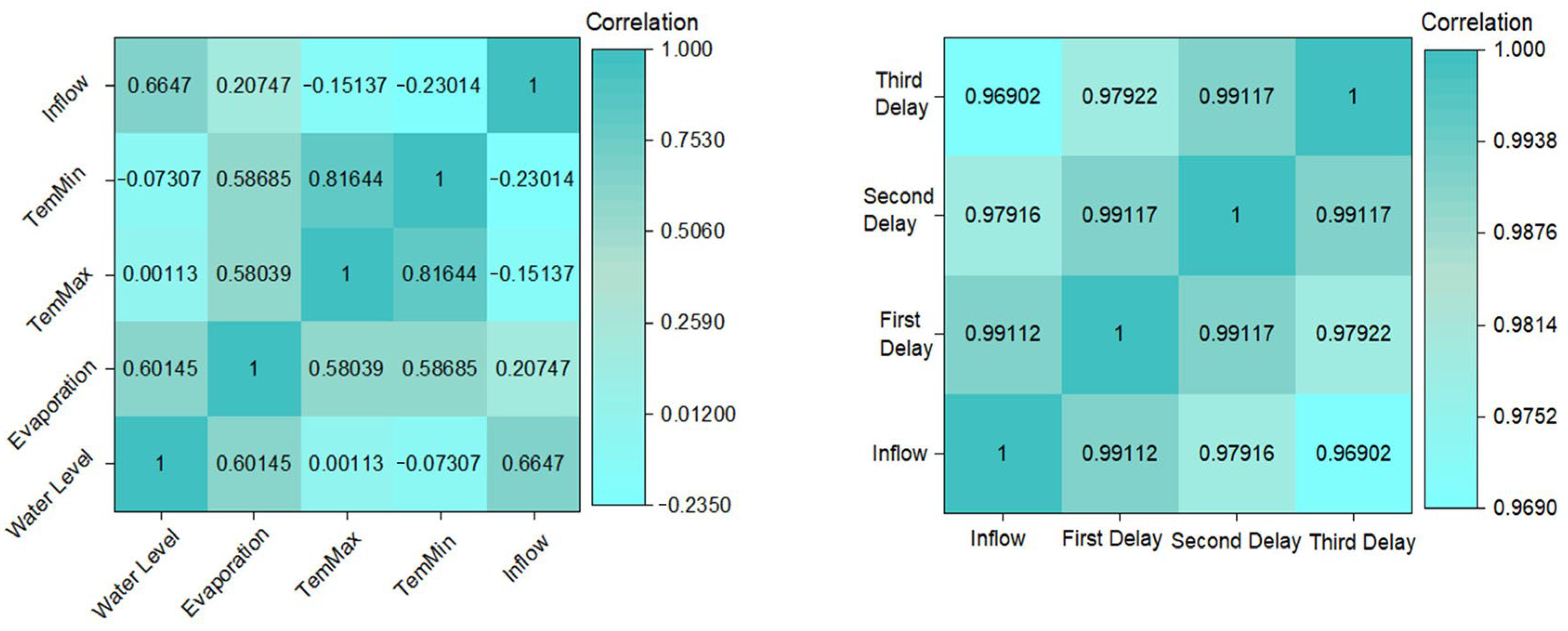
2.2. Overview of the Data Collection and Data Preprocessing
2.3. An Overview of DNN, GRU, and LSTM
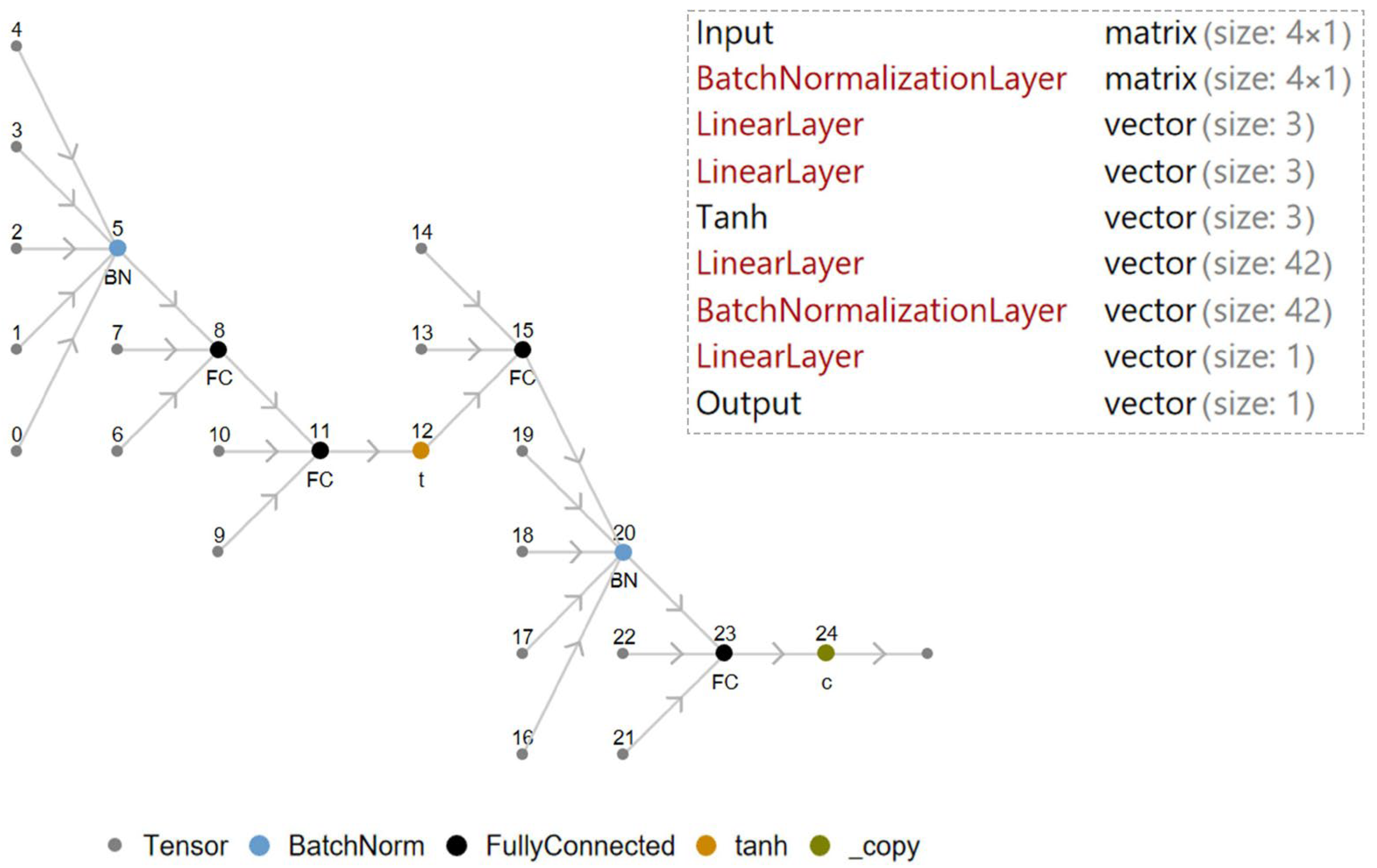
2.4. GRU-LSTM and bRNN-CNN-GRU Hybrid Model
2.5. Model Training Scenarios
2.6. Model Evaluation Metrics
3. Experimental Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Khedre, A.M.; Ramadan, S.A.; Ashry, A.; Alaraby, M. Abundance and Risk Assessment of Microplastics in Water, Sediment, and Aquatic Insects of the Nile River. Chemosphere 2024, 353, 141557. [Google Scholar] [CrossRef] [PubMed]
- Połomski, M.; Wiatkowski, M. Impounding Reservoirs, Benefits and Risks: A Review of Environmental and Technical Aspects of Construction and Operation. Sustainability 2023, 15, 16020. [Google Scholar] [CrossRef]
- García-Feal, O.; González-Cao, J.; Fernández-Nóvoa, D.; Astray Dopazo, G.; Gómez-Gesteira, M. Comparison of machine learning techniques for reservoir outflow forecasting. Nat. Hazards Earth Syst. Sci. Discuss. 2022, 2022, 1–27. [Google Scholar] [CrossRef]
- Babaei, M.; Moeini, R.; Ehsanzadeh, E. Artificial Neural Network and Support Vector Machine Models for Inflow Prediction of Dam Reservoir (case study: Zayandehroud Dam Reservoir). Water Resour. Manag. 2019, 33, 2203–2218. [Google Scholar] [CrossRef]
- Emadi, A.; Zamanzad-Ghavidel, S.; Boroomandnia, A.; Fazeli, S.; Sobhani, R. Modeling the Total Outflow of Reservoirs Using Wavelet-Developed Approaches: A Case Study of the Mahabad Dam Reservoir, Iran. Water Supply 2023, 23, 4645–4671. [Google Scholar] [CrossRef]
- Chang, Z.; Jiang, Z.; Wang, P. Inflow combination forecast of reservoir based on SWAT, XAJ model and Bayes model averaging method. Water Supply 2022, 22, 8440–8464. [Google Scholar] [CrossRef]
- Rahman, K.U.; Balkhair, K.S.; Almazroui, M.; Masood, A. Sub-Catchments Flow Losses Computation Using Muskingum–Cunge Routing Method and HEC-HMS GIS Based Techniques, Case Study of Wadi Al-Lith, Saudi Arabia. Model. Earth Syst. Environ. 2017, 3, 4. [Google Scholar] [CrossRef]
- Salvati, A.; Moghaddam Nia, A.; Salajegheh, A.; Shirzadi, A.; Shahabi, H.; Ahmadisharaf, E.; Clague, J.J. A Systematic Review of Muskingum Flood Routing Techniques. Hydrol. Sci. J. 2024, 69, 810–831. [Google Scholar] [CrossRef]
- Myronidis, D.; Ioannou, K.; Fotakis, D.; Dörflinger, G. Streamflow and Hydrological Drought Trend Analysis and Forecasting in Cyprus. Water Resour. Manag. 2018, 32, 1759–1776. [Google Scholar] [CrossRef]
- Nguyen, X.H. Combining Statistical Machine Learning Models with ARIMA for Water Level Forecasting: The Case of the Red River. Adv. Water Resour. 2020, 142, 103656. [Google Scholar]
- Wegayehu, E.B.; Muluneh, F.B. Multivariate streamflow simulation using hybrid deep learning models. Comput. Intell. Neurosci. 2021, 2021, 5172658. [Google Scholar] [CrossRef] [PubMed]
- Zhou, F.; Chen, Y.; Liu, J. Application of a new hybrid deep learning model that considers temporal and feature dependencies in rainfall–runoff simulation. Remote Sens. 2023, 15, 1395. [Google Scholar] [CrossRef]
- Guo, W.D.; Chen, W.B.; Chang, C.H. Prediction of hourly inflow for reservoirs at mountain catchments using residual error data and multiple-ahead correction technique. Hydrol. Res. 2023, 54, 1072–1093. [Google Scholar] [CrossRef]
- Moeini, R.; Nasiri, K.; Hosseini, S.H. Predicting the Water Inflow into the Dam Reservoir Using the Hybrid Intelligent GP-ANN-NSGA-II Method. Water Resour. Manag. 2024, 38, 4137–4159. [Google Scholar] [CrossRef]
- Neshaei, S.A.; Mehrdad, M.A.; Molatefat, S.H. Investigation of discharge and sedimentation rates of the sefid-roud river after de-siltation of the sefid-roud dam, Iran. WIT Trans. Ecol. Environ. 2017, 221, 1–12. [Google Scholar]
- García, S.; Luengo, J.; Herrera, F. Data Preprocessing in Data Mining; Springer International Publishing: Cham, Switzerland, 2015; Volume 72, pp. 59–139. [Google Scholar]
- Wang, S.; Celebi, M.E.; Zhang, Y.D.; Yu, X.; Lu, S.; Yao, X.; Tyukin, I. Advances in data preprocessing for biomedical data fusion: An overview of the methods, challenges, and prospects. Inf. Fusion 2021, 76, 376–421. [Google Scholar] [CrossRef]
- Peng, S.; Sun, S.; Yao, Y.D. A survey of modulation classification using deep learning: Signal representation and data preprocessing. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 7020–7038. [Google Scholar] [CrossRef]
- Lee, S.; Kim, J.; Bae, J.H.; Lee, G.; Yang, D.; Hong, J.; Lim, K.J. Development of multi-inflow prediction ensemble model based on auto-sklearn using combined approach: Case study of soyang river dam. Hydrology 2023, 10, 90. [Google Scholar] [CrossRef]
- Petropoulos, F.; Svetunkov, I. A simple combination of univariate models. Int. J. Forecast. 2020, 36, 110–115. [Google Scholar] [CrossRef]
- Abdel-Aal, R.E. Univariate modeling and forecasting of monthly energy demand time series using abductive and neural networks. Comput. Ind. Eng. 2008, 54, 903–917. [Google Scholar] [CrossRef]
- Yang, L.; Shami, A. On hyperparameter optimization of machine learning algorithms: Theory and practice. Neurocomputing 2020, 415, 295–316. [Google Scholar] [CrossRef]
- Agatonovic-Kustrin, S.; Beresford, R. Basic concepts of artificial neural network (ANN) modeling and its application in pharmaceutical research. J. Pharm. Biomed. Anal. 2000, 22, 717–727. [Google Scholar] [CrossRef] [PubMed]
- Mai, H.V.T.; Nguyen, T.A.; Ly, H.B.; Tran, V.Q. Investigation of ANN Model Containing One Hidden Layer for Predicting Compressive Strength of Concrete with Blast-Furnace Slag and Fly Ash. Adv. Mater. Sci. Eng. 2021, 2021, 5540853. [Google Scholar] [CrossRef]
- Mittal, S. A Survey on Modeling and Improving Reliability of DNN Algorithms and Accelerators. J. Syst. Archit. 2020, 104, 101689. [Google Scholar] [CrossRef]
- Zhen, L.; Bărbulescu, A. Comparative Analysis of Convolutional Neural Network-Long Short-Term Memory, Sparrow Search Algorithm-Backpropagation Neural Network, and Particle Swarm Optimization-Extreme Learning Machine Models for the Water Discharge of the Buzău River, Romania. Water 2024, 16, 289. [Google Scholar] [CrossRef]
- Xu, S.; Li, J.; Liu, K.; Wu, L. A parallel GRU recurrent network model and its application to multi-channel time-varying signal classification. IEEE Access 2019, 7, 118739–118748. [Google Scholar] [CrossRef]
- Choe, D.E.; Kim, H.C.; Kim, M.H. Sequence-Based Modeling of Deep Learning with LSTM and GRU Networks for Structural Damage Detection of Floating Offshore Wind Turbine Blades. Renew. Energy 2021, 174, 218–235. [Google Scholar] [CrossRef]
- Ge, K.; Zhao, J.Q.; Zhao, Y.Y. Gr-gnn: Gated recursion-based graph neural network algorithm. Mathematics 2022, 10, 1171. [Google Scholar] [CrossRef]
- Madaeni, F.; Chokmani, K.; Lhissou, R.; Gauthier, Y.; Tolszczuk-Leclerc, S. Convolutional neural network and long short-term memory models for ice-jam predictions. Cryosphere 2022, 16, 1447–1468. [Google Scholar] [CrossRef]
- Sunny, M.A.I.; Maswood, M.M.S.; Alharbi, A.G. Deep learning-based stock price prediction using LSTM and bi-directional LSTM model. In Proceedings of the 2020 2nd Novel Intelligent and Leading Emerging Sciences Conference (NILES), Giza, Egypt, 24–26 October 2020; pp. 87–92. [Google Scholar]
- Le, X.H.; Ho, H.V.; Lee, G.; Jung, S. Application of long short-term memory (LSTM) neural network for flood forecasting. Water 2019, 11, 1387. [Google Scholar] [CrossRef]
- Nifa, K.; Boudhar, A.; Ouatiki, H.; Elyoussfi, H.; Bargam, B.; Chehbouni, A. Deep Learning Approach with LSTM for Daily Streamflow Prediction in a Semi-Arid Area: A Case Study of Oum Er-Rbia River Basin, Morocco. Water 2023, 15, 262. [Google Scholar] [CrossRef]
- Yu, Y.; Si, X.; Hu, C.; Zhang, J. A review of recurrent neural networks: LSTM cells and network architectures. Neural Comput. 2019, 31, 1235–1270. [Google Scholar] [CrossRef] [PubMed]
- Cao, B.; Li, C.; Song, Y.; Qin, Y.; Chen, C. Network Intrusion Detection Model Based on CNN and GRU. Appl. Sci. 2022, 12, 4184. [Google Scholar] [CrossRef]
- Jafari, S.; Byun, Y.C. A CNN-GRU Approach to the Accurate Prediction of Batteries’ Remaining Useful Life from Charging Profiles. Computers 2023, 12, 219. [Google Scholar] [CrossRef]
- Chai, T.; Draxler, R.R. Root Mean Square Error (RMSE) or Mean Absolute Error (MAE). Geosci. Model Dev. Discuss. 2014, 7, 1525–1534. [Google Scholar]
- Ćalasan, M.; Aleem, S.H.A.; Zobaa, A.F. On the Root Mean Square Error (RMSE) Calculation for Parameter Estimation of Photovoltaic Models: A Novel Exact Analytical Solution Based on Lambert W Function. Energy Convers. Manag. 2020, 210, 112716. [Google Scholar] [CrossRef]
- Asuero, A.G.; Sayago, A.; González, A.G. The correlation coefficient: An overview. Crit. Rev. Anal. Chem. 2006, 36, 41–59. [Google Scholar] [CrossRef]
- Duc, L.; Sawada, Y. A Signal-Processing-Based Interpretation of the Nash–Sutcliffe Efficiency. Hydrol. Earth Syst. Sci. 2023, 27, 1827–1839. [Google Scholar] [CrossRef]
- Santos, A.A.; Nogales, F.J.; Ruiz, E. Comparing univariate and multivariate models to forecast portfolio value-at-risk. J. Financ. Econom. 2013, 11, 400–441. [Google Scholar] [CrossRef]
- Moodi, F.; Jahangard Rafsanjani, A.; Zarifzadeh, S.; Zare Chahooki, M.A. Advanced Stock Price Forecasting Using a 1D-CNN-GRU-LSTM Model. J. AI Data Min. 2024, 12, 393–408. [Google Scholar]
- Hadiyan, P.P.; Moeini, R.; Ehsanzadeh, E. Application of Static and Dynamic Artificial Neural Networks for Forecasting Inflow Discharges, Case Study: Sefidroud Dam Reservoir. Sustain. Comput. Inform. Syst. 2020, 27, 100401. [Google Scholar] [CrossRef]
- Li, H.; Zhang, L.; Zhang, Y.; Yao, Y.; Wang, R.; Dai, Y. Water-Level Prediction Analysis for the Three Gorges Reservoir Area Based on a Hybrid Model of LSTM and Its Variants. Water 2024, 16, 1227. [Google Scholar] [CrossRef]
- Yao, Z.; Wang, Z.; Wang, D.; Wu, J.; Chen, L. An Ensemble CNN-LSTM and GRU Adaptive Weighting Model Based Improved Sparrow Search Algorithm for Predicting Runoff Using Historical Meteorological and Runoff Data as Input. J. Hydrol. 2023, 625, 129977. [Google Scholar] [CrossRef]
- Zamani, M.G.; Nikoo, M.R.; Al-Rawas, G.; Nazari, R.; Rastad, D.; Gandomi, A.H. Hybrid WT–CNN–GRU-Based Model for the Estimation of Reservoir Water Quality Variables Considering Spatio-Temporal Features. J. Environ. Manag. 2024, 358, 120756. [Google Scholar] [CrossRef]
- Khorram, S.; Jehbez, N. Enhancing Accuracy of Forecasting Monthly Reservoir Inflow by Using Comparison of Three New Hybrid Models: A Case Study of the Droodzan Dam in Iran. Iran. J. Sci. Technol. Trans. Civil. Eng. 2024, 48, 3735–3759. [Google Scholar] [CrossRef]
- Shabbir, M.; Chand, S.; Iqbal, F.; Kisi, O. Novel Hybrid Approach for River Inflow Modeling: Case Study of the Indus River Basin, Pakistan. J. Hydrol. Eng. 2025, 30, 04025006. [Google Scholar] [CrossRef]






| Statistical Criteria | Maximum | Average | Minimum | Standard Deviation | Number of Zero |
|---|---|---|---|---|---|
| Water Level (m) | 272.79 | 252.01 | 236.81 | 10.83 | 0 |
| Evaporation (MCM) | 0.541 | 0.116 | 0 | 0.098 | 5 |
| Min Temperature (°C) | 40.6 | 12.28 | −3 | 7.86 | 8 |
| Max Temperature (°C) | 45.0 | 23.91 | 0 | 8.22 | 3 |
| River Inflow (MCM) | 41.99 | 4.026 | 0.009 | 5.94 | 0 |
| Type of Parameters | Values/Layer |
|---|---|
| Network Type | Feed-forward propagation |
| Data Division | Train (80%) Test (20%) |
| Number of Hidden Layers (Neurons) | 10–55 |
| Batch Size | 34–210 |
| learning Function | 0.01–0.046 |
| Activation Function | Ramp, Tanh, Cosh |
| Normalization Function | Batch Normalization |
| Training Function | Adam |
| Scenario | Input | Model | Output |
|---|---|---|---|
| Scenario (1) | Water Level, Evaporation, Tmin, Tmax | DNN, GRU-LSTM, bRNN-CNN-GRU | Reservoir Inflow |
| Scenario (2) | First Delay, Second Delay, Third Delay | DNN, CNN-LSTM, bRNN-CNN-GRU | Reservoir Inflow |
| Scenario | Model | r | RMSE (MCM) | NSE |
|---|---|---|---|---|
| Scenario (1) | DNN | 0.7803 | 2.0176 | 0.5785 |
| GRU-LSTM | 0.8276 | 1.9853 | 0.5984 | |
| bRNN-CNN-GRU | 0.8706 | 1.7217 | 0.7323 | |
| Scenario (2) | DNN | 0.9485 | 1.3354 | 0.8132 |
| GRU-LSTM | 0.9677 | 0.8584 | 0.9233 | |
| bRNN-CNN-GRU | 0.9734 | 0.7099 | 0.9474 |
| Scenario | Model | Maximum | Average | Minimum | Standard Deviation |
|---|---|---|---|---|---|
| Actual | 17.194 | 2.762 | 0.043 | 3.095 | |
| Scenario (1) | DNN | 8.343 | 3.203 | 0.183 | 2.302 |
| GRU-LSTM | 13.376 | 2.497 | 0.026 | 2.766 | |
| bRNN-CNN-GRU | 16.391 | 2.631 | 0.450 | 2.512 | |
| Scenario (2) | DNN | 15.508 | 3.629 | 1.772 | 2.758 |
| GRU-LSTM | 14.517 | 2.757 | 0.770 | 2.620 | |
| bRNN-CNN-GRU | 16.186 | 2.795 | 0.195 | 2.971 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdi, E.; Taghi Sattari, M.; Milewski, A.; Ibrahim, O.R. Advancements in Hydrological Modeling: The Role of bRNN-CNN-GRU in Predicting Dam Reservoir Inflow Patterns. Water 2025, 17, 1660. https://doi.org/10.3390/w17111660
Abdi E, Taghi Sattari M, Milewski A, Ibrahim OR. Advancements in Hydrological Modeling: The Role of bRNN-CNN-GRU in Predicting Dam Reservoir Inflow Patterns. Water. 2025; 17(11):1660. https://doi.org/10.3390/w17111660
Chicago/Turabian StyleAbdi, Erfan, Mohammad Taghi Sattari, Adam Milewski, and Osama Ragab Ibrahim. 2025. "Advancements in Hydrological Modeling: The Role of bRNN-CNN-GRU in Predicting Dam Reservoir Inflow Patterns" Water 17, no. 11: 1660. https://doi.org/10.3390/w17111660
APA StyleAbdi, E., Taghi Sattari, M., Milewski, A., & Ibrahim, O. R. (2025). Advancements in Hydrological Modeling: The Role of bRNN-CNN-GRU in Predicting Dam Reservoir Inflow Patterns. Water, 17(11), 1660. https://doi.org/10.3390/w17111660











