An Interpretable Deep Learning Approach Integrating PatchTST, Quantile Regression, and SHAP for Dam Displacement Interval Prediction
Abstract
1. Introduction
2. Methodology
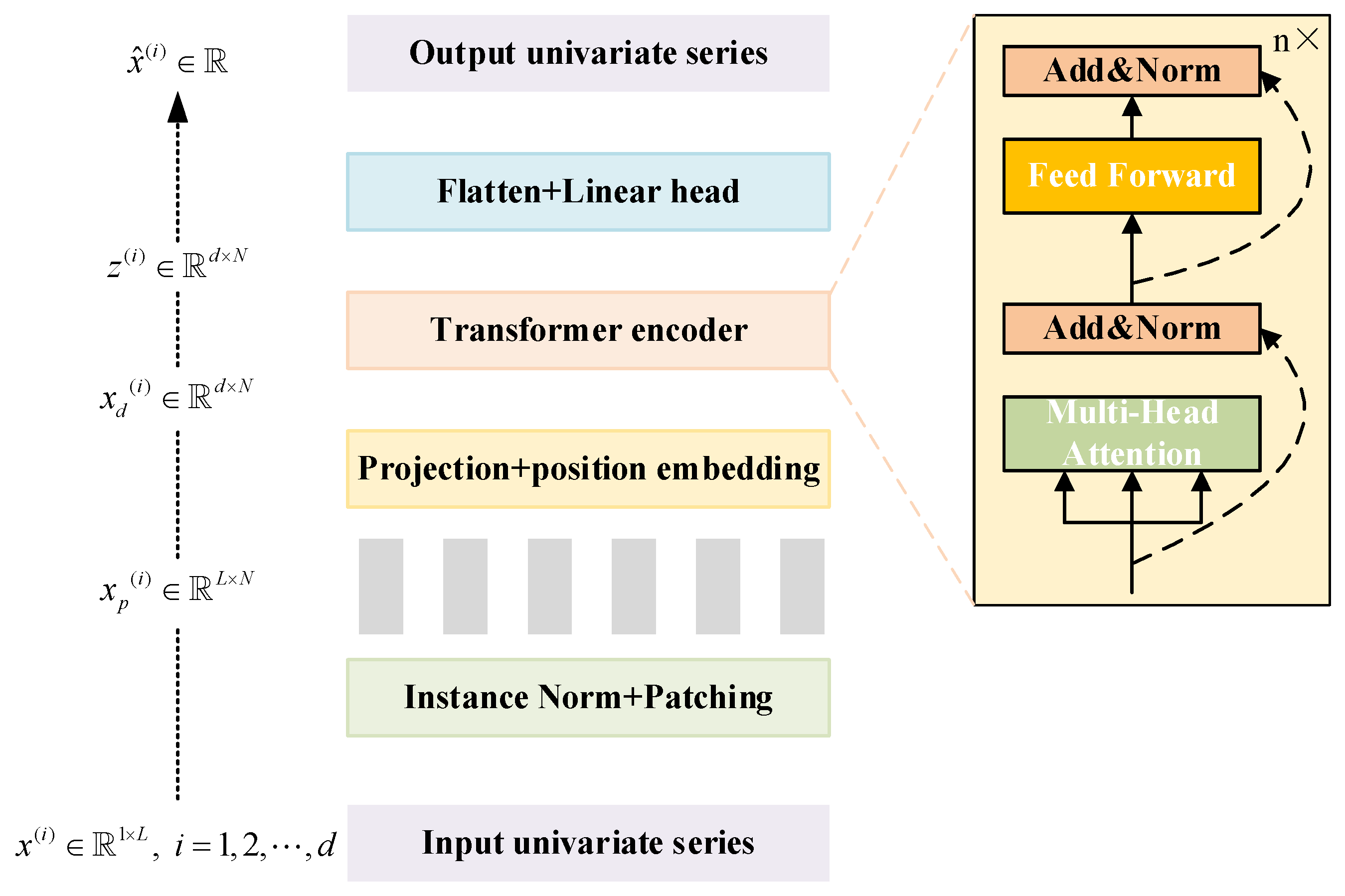
2.1. Patch Time Series Transformer
- (1)
- Patch Embedding
- (2)
- Multi-head Self-Attention
- (3)
- Feed-forward Neural Network (FFN)
- (4)
- Residual Connection and Normalisation
- (5)
- Predictive Output Layer
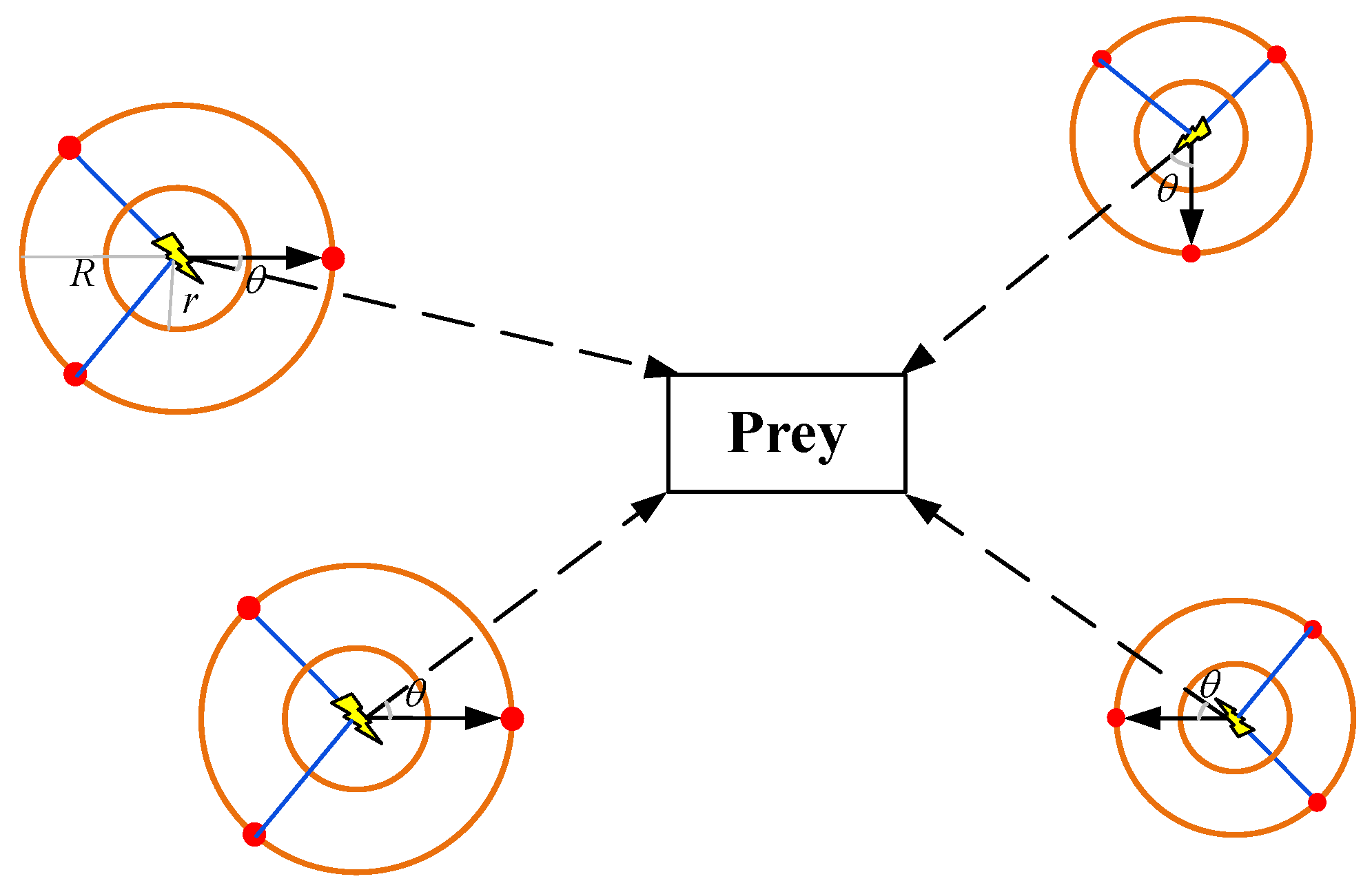
2.2. Sand Cat Swarm Optimization Algorithm
2.3. Prediction Interval Construction Method Based on Quantile Regression
2.4. Shapley Additive Explanations
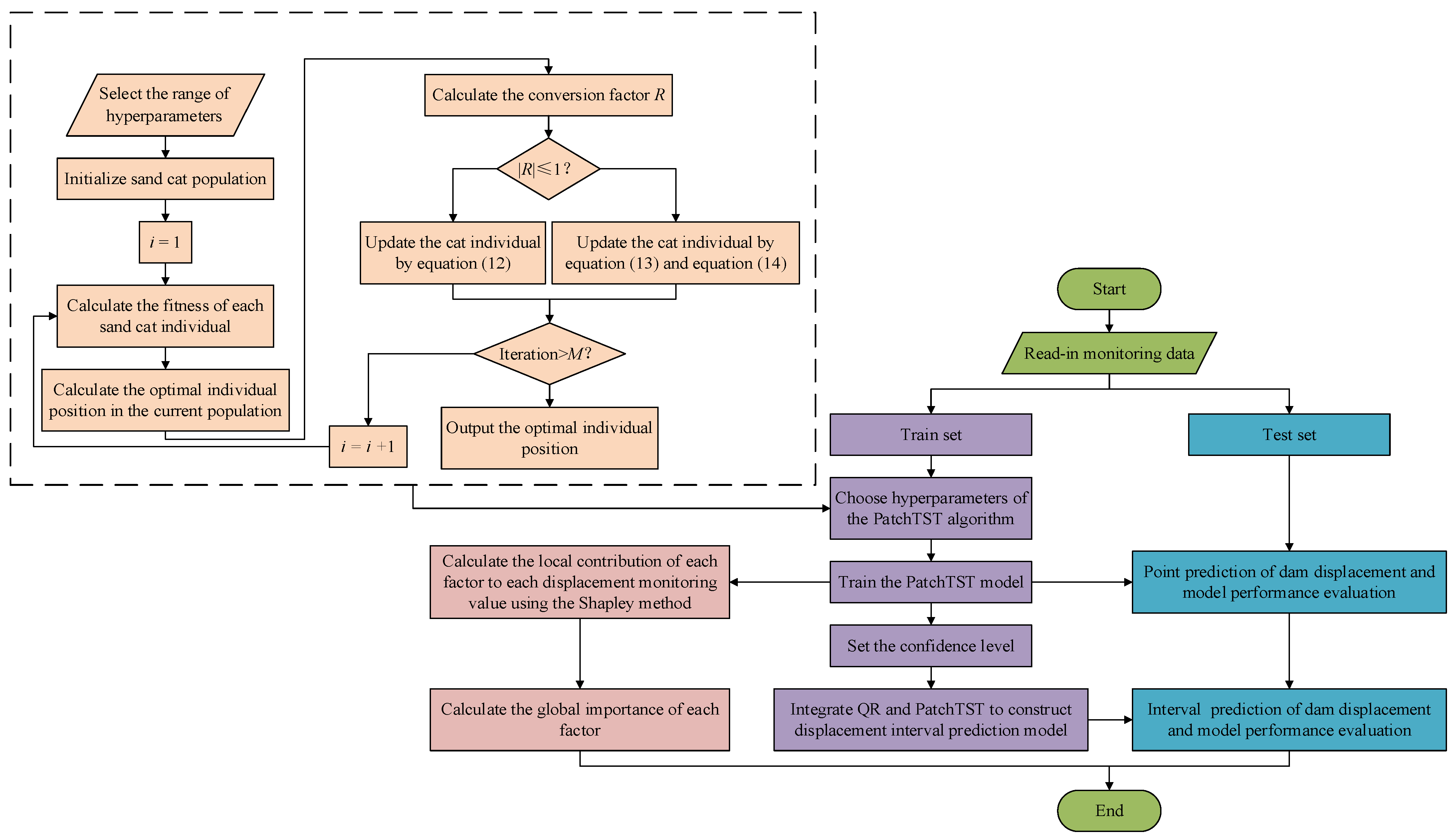
2.5. The Implementation Framework of the Proposed Method
3. Case Study
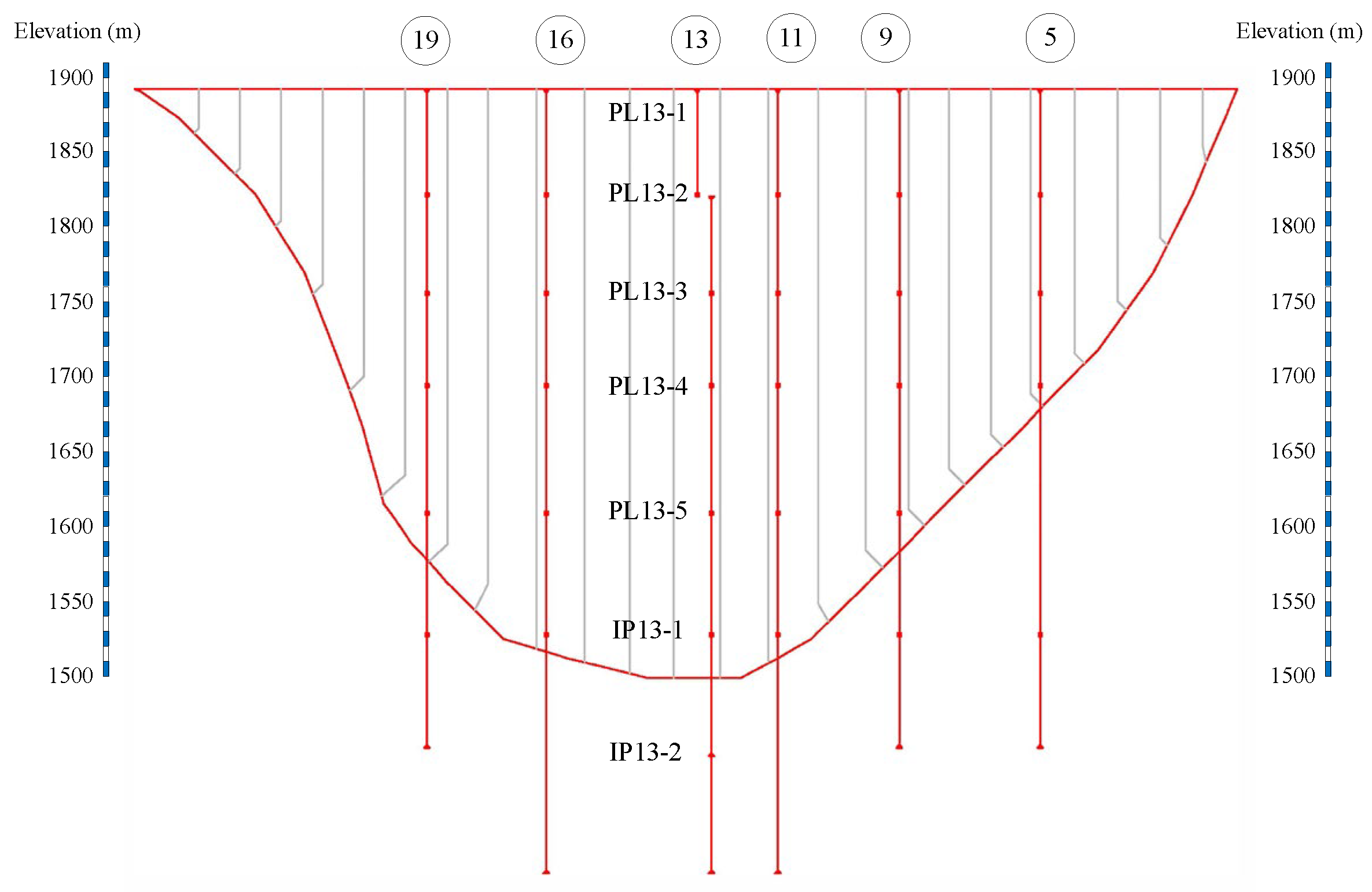
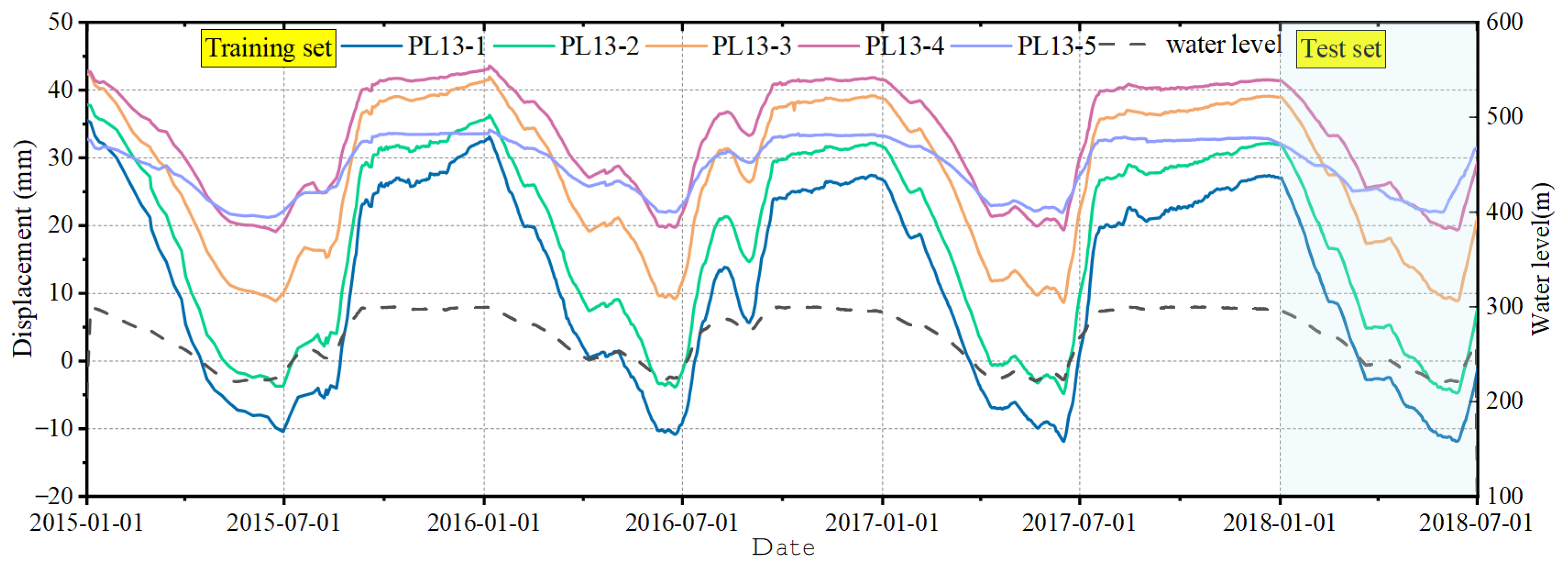
3.1. Engineering Introduction
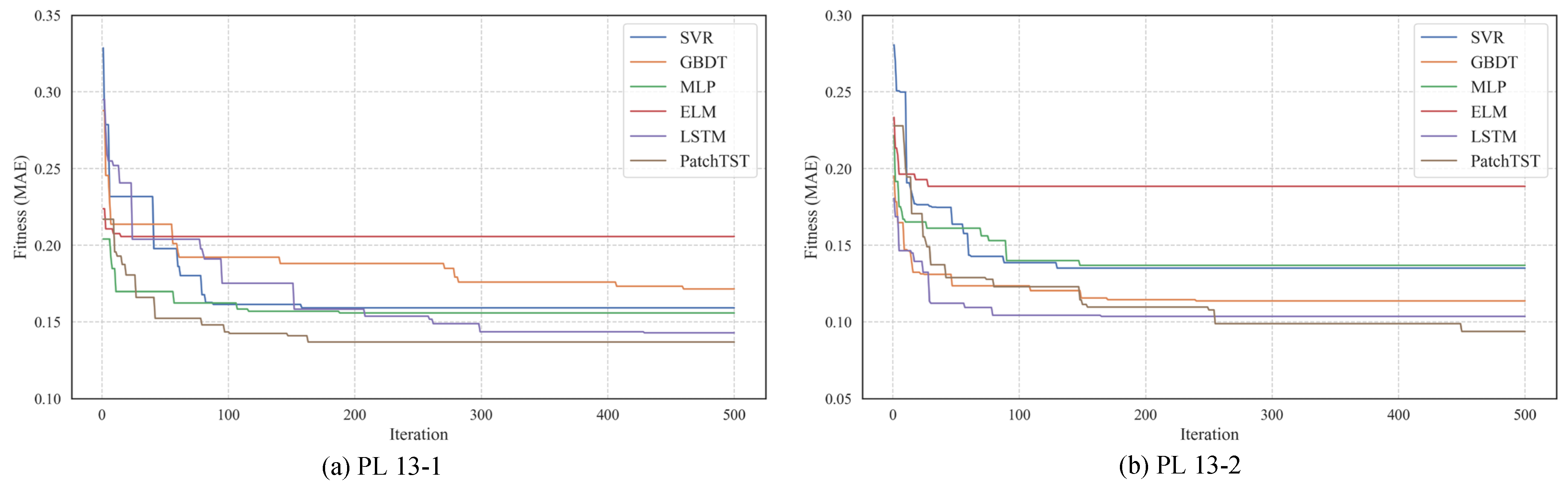
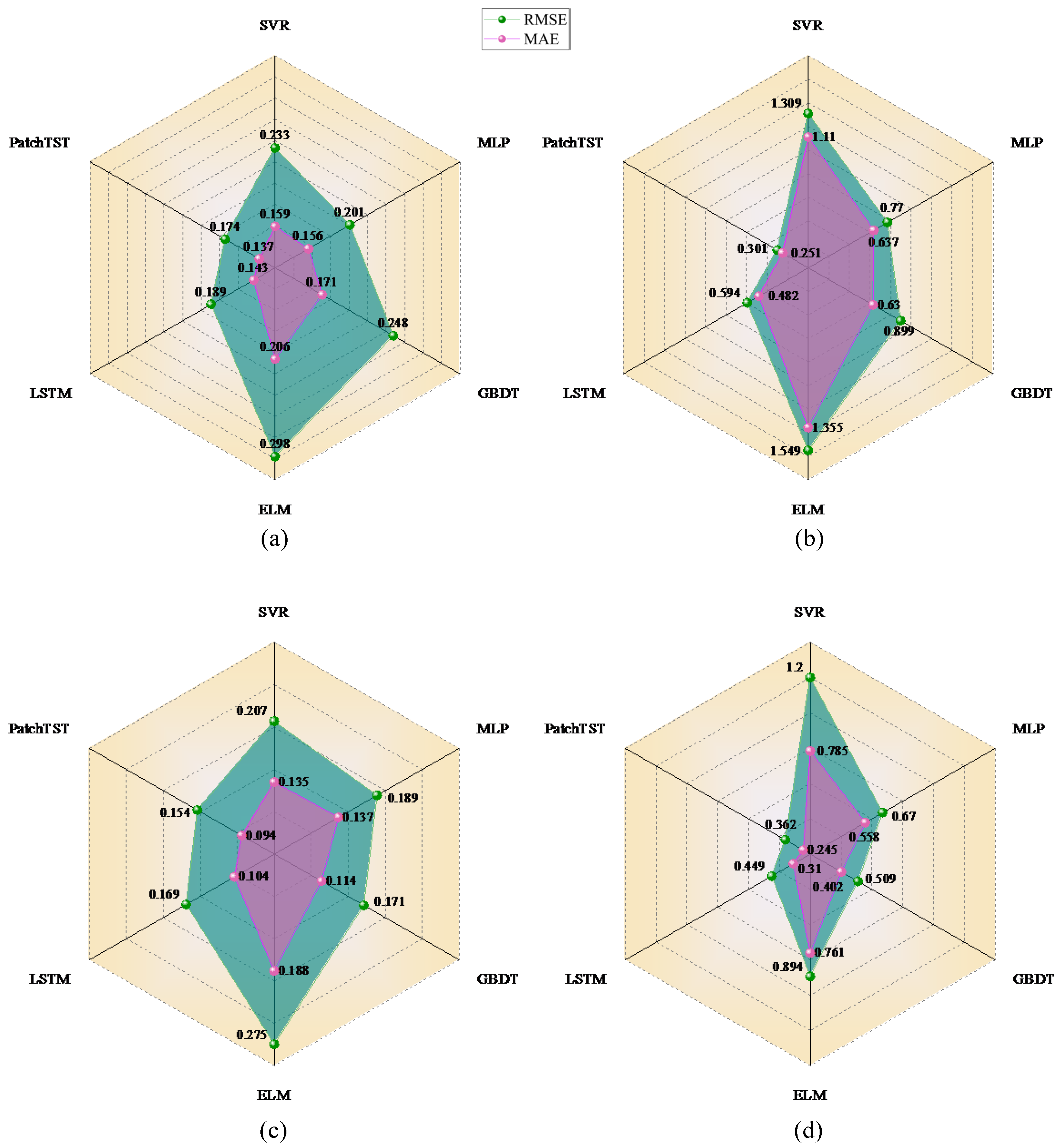
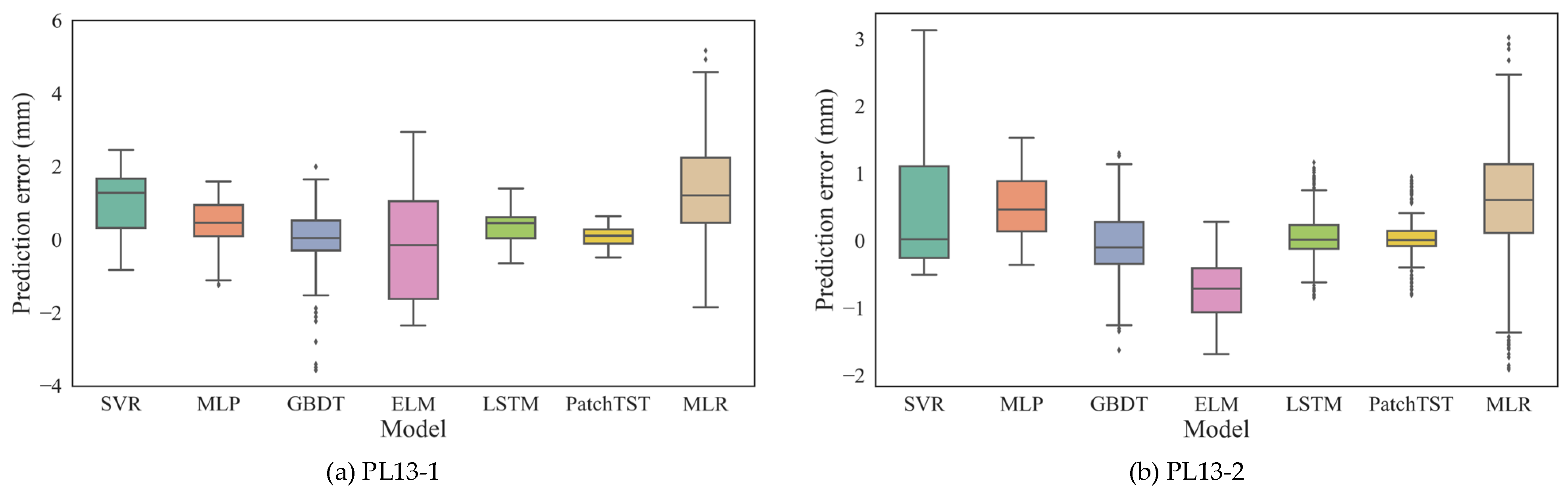
3.2. Point Prediction of Dam Displacement
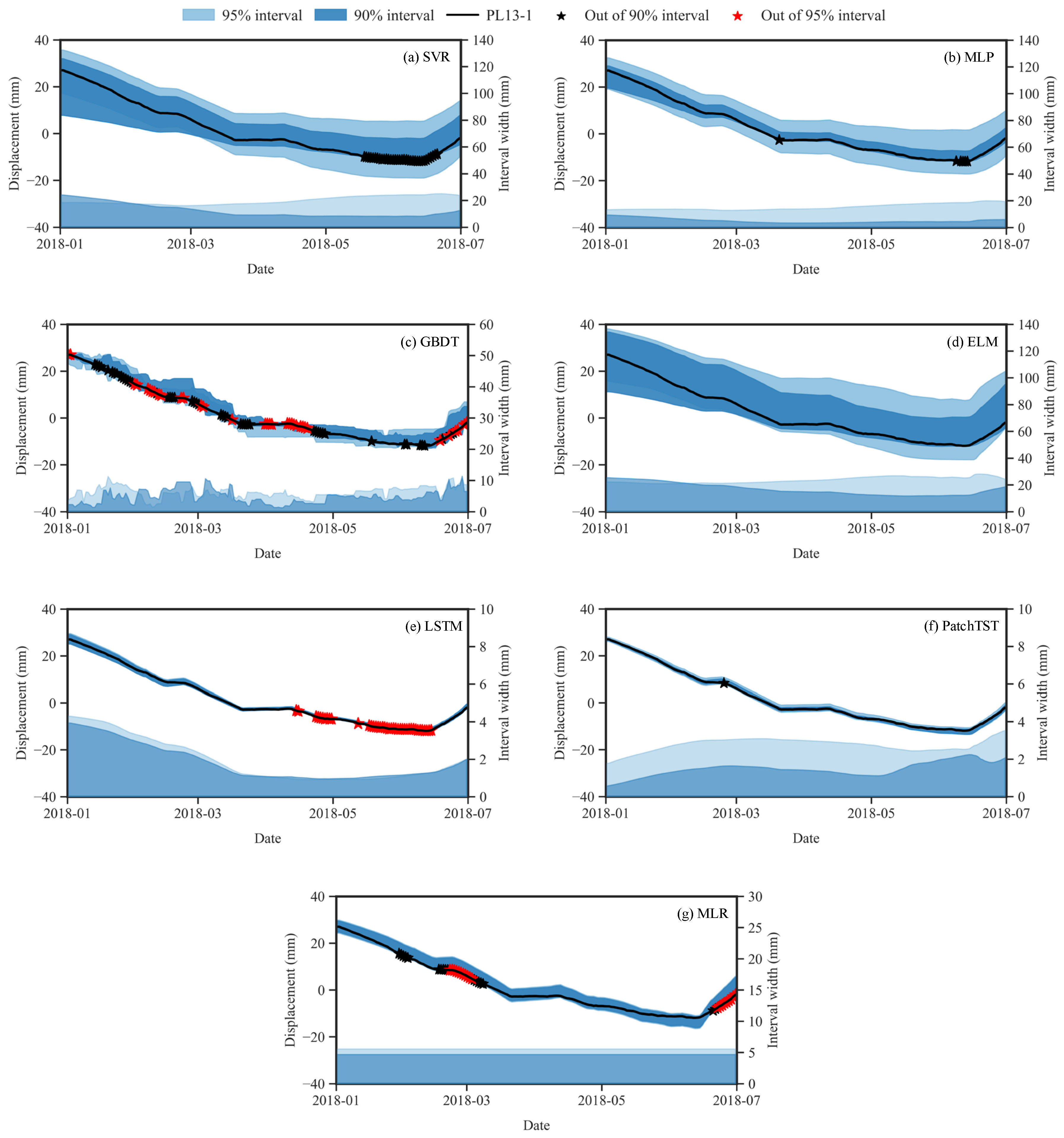
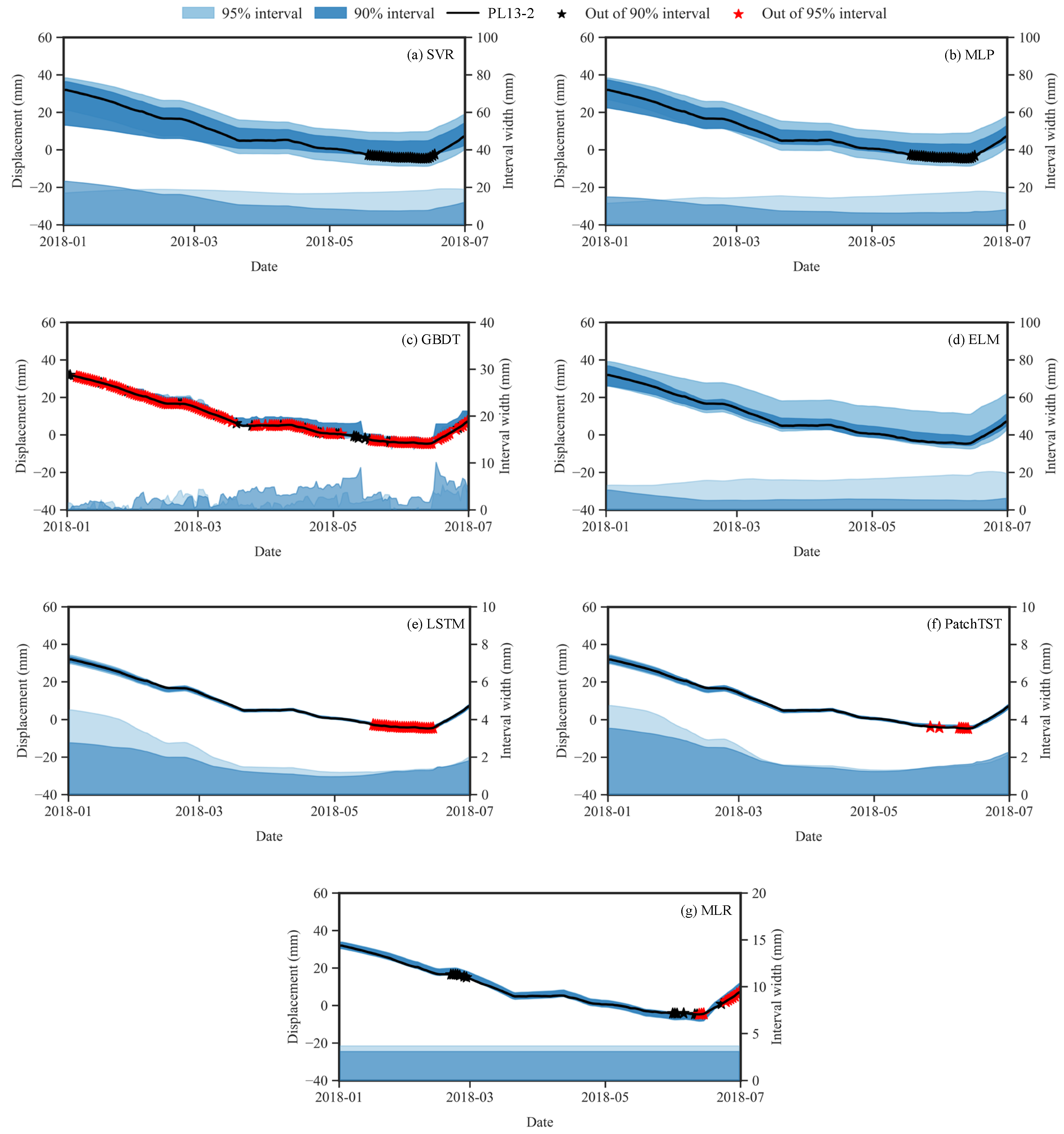
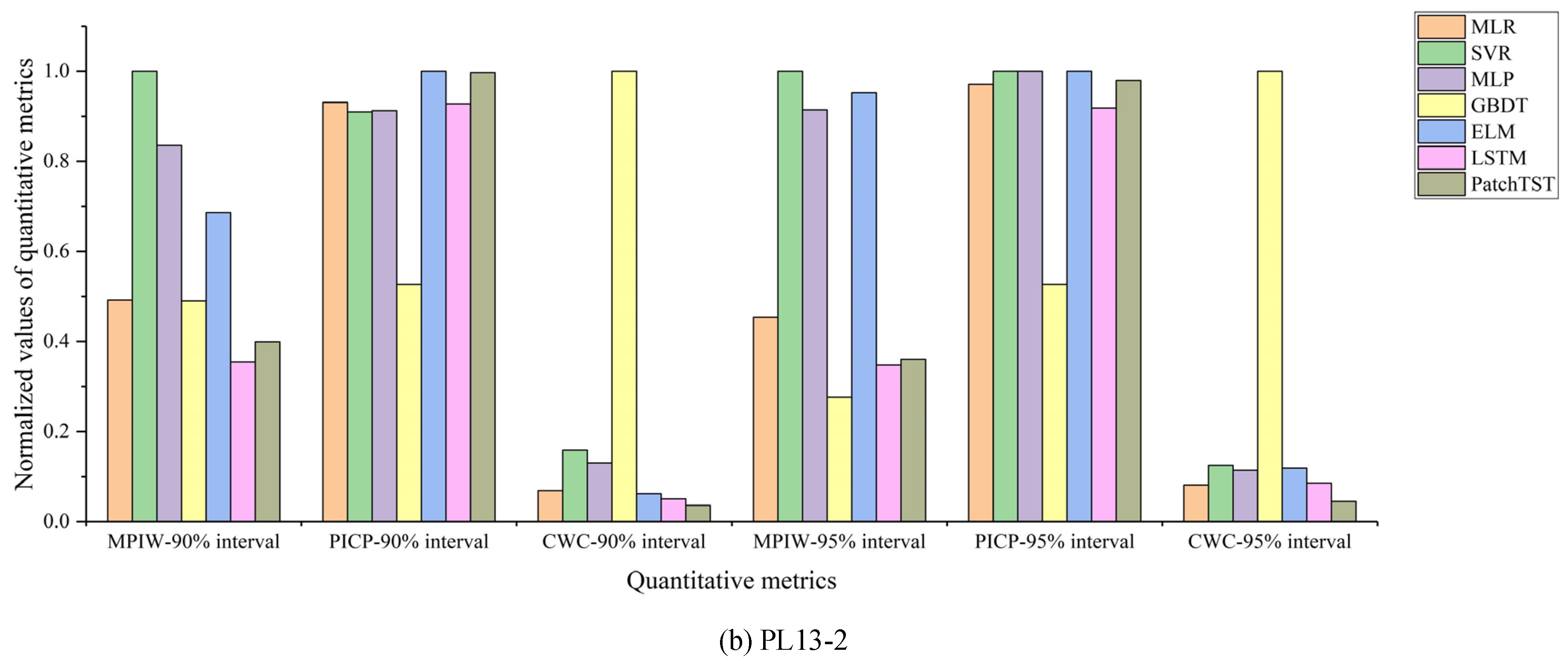
3.3. Interval Prediction of Dam Displacement
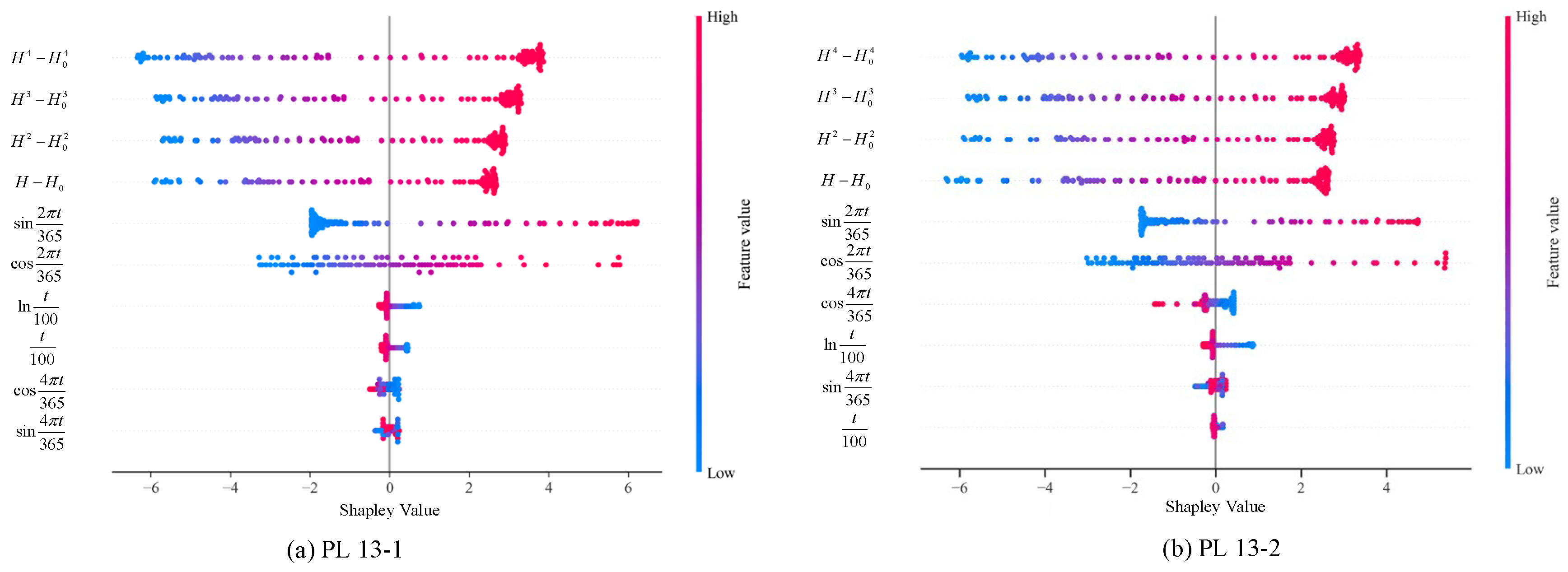
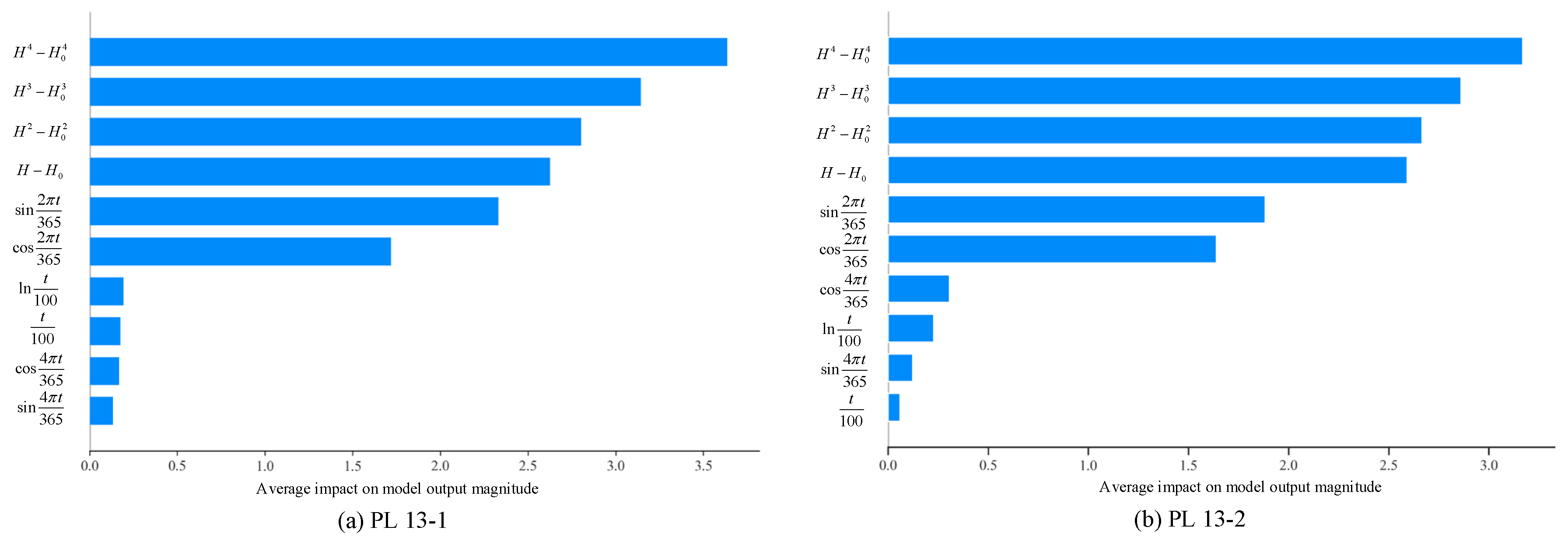
3.4. Analysis of Dam Displacement Driving Mechanism
4. Conclusions and Future Discussions
- Leveraging the PatchTST network optimized by the SCSO algorithm, the proposed model achieved superior predictive accuracy, consistently outperforming conventional MLR models, machine learning models (e.g., SVR, MLP, GBDT, ELM), and even deep models like LSTM across multiple metrics and monitoring points. In addition, the SCSO algorithm exhibited rapid convergence and strong stability during optimization, effectively enhancing model generalization.
- By incorporating quantile regression, the SCSO-PatchTST model produced reliable PIs that consistently achieved higher coverage probabilities under narrow interval widths, outperforming other benchmark models at the same CLs. Such results underscore both the model’s robustness in uncertainty modeling and its reliability in delivering stable interval predictions under varying conditions.
- The SHAP analysis enhances the interpretability of the model by quantifying the contributions of input factors and identifying water pressure and seasonal temperature as the dominant factors. Furthermore, it elucidates their driving mechanism as the primary external loads influencing the dam’s displacement response. The evaluation results are consistent with established mechanisms of dam deformation, thereby reinforcing the physical credibility of the model.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bian, K.; Wu, Z. Data-Based Model with EMD and a New Model Selection Criterion for Dam Health Monitoring. Eng. Struct. 2022, 260, 114171. [Google Scholar] [CrossRef]
- Zhu, M.; Chen, B.; Gu, C.; Wu, Y.; Chen, W. Optimized Multi-Output LSSVR Displacement Monitoring Model for Super High Arch Dams Based on Dimensionality Reduction of Measured Dam Temperature Field. Eng. Struct. 2022, 268, 114686. [Google Scholar] [CrossRef]
- Yuan, D.; Wei, B.; Xie, B.; Zhong, Z. Modified Dam Deformation Monitoring Model Considering Periodic Component Contained in Residual Sequence. Struct. Control. Health Monit. 2020, 27, e2633. [Google Scholar] [CrossRef]
- Ren, Q.; Li, M.; Kong, T.; Ma, J. Multi-Sensor Real-Time Monitoring of Dam Behavior Using Self-Adaptive Online Sequential Learning. Autom. Constr. 2022, 140, 104365. [Google Scholar] [CrossRef]
- Cao, W.; Wen, Z.; Feng, Y.; Zhang, S.; Su, H. A Multi-Point Joint Prediction Model for High-Arch Dam Deformation Considering Spatial and Temporal Correlation. Water 2024, 16, 1388. [Google Scholar] [CrossRef]
- Salazar, F.; Morán, R.; Toledo, M.Á.; Oñate, E. Data-Based Models for the Prediction of Dam Behaviour: A Review and Some Methodological Considerations. Arch. Comput. Methods Eng. 2017, 24, 1–21. [Google Scholar] [CrossRef]
- Wu, Z. Theory and Application of Safety Monitoring in Hydraulic Structures; Higher Education Press: Beijing, China, 2003. [Google Scholar]
- Mata, J.; Tavares de Castro, A.; Sá da Costa, J. Constructing Statistical Models for Arch Dam Deformation. Struct. Control. Health Monit. 2014, 21, 423–437. [Google Scholar] [CrossRef]
- Santillán, D.; Salete, E.; Vicente, D.J.; Toledo, M.Á. Treatment of Solar Radiation by Spatial and Temporal Discretization for Modeling the Thermal Response of Arch Dams. J. Eng. Mech. 2014, 140, 05014001. [Google Scholar] [CrossRef]
- Lu, T.; Gu, H.; Gu, C.; Shao, C.; Yuan, D. A Multi-Point Dam Deformation Prediction Model Based on Spatiotemporal Graph Convolutional Network. Eng. Appl. Artif. Intell. 2025, 149, 110483. [Google Scholar] [CrossRef]
- Lin, C.; Li, T.; Chen, S.; Liu, X.; Lin, C.; Liang, S. Gaussian Process Regression-Based Forecasting Model of Dam Deformation. Neural Comput. Appl. 2019, 31, 8503–8518. [Google Scholar] [CrossRef]
- Yuan, D.; Gu, C.; Qin, X.; Shao, C.; He, J. Performance-Improved TSVR-Based DHM Model of Super High Arch Dams Using Measured Air Temperature. Eng. Struct. 2022, 250, 113400. [Google Scholar] [CrossRef]
- Kao, C.-Y.; Loh, C.-H. Monitoring of Long-Term Static Deformation Data of Fei-Tsui Arch Dam Using Artificial Neural Network-Based Approaches. Struct. Control. Health Monit. 2013, 20, 282–303. [Google Scholar] [CrossRef]
- Salazar, F.; Toledo, M.A.; Oñate, E.; Morán, R. An Empirical Comparison of Machine Learning Techniques for Dam Behaviour Modelling. Struct. Saf. 2015, 56, 9–17. [Google Scholar] [CrossRef]
- Li, M.; Li, M.; Ren, Q.; Li, H.; Song, L. DRLSTM: A Dual-Stage Deep Learning Approach Driven by Raw Monitoring Data for Dam Displacement Prediction. Adv. Eng. Inform. 2022, 51, 101510. [Google Scholar] [CrossRef]
- Lu, T.; Gu, C.; Yuan, D.; Zhang, K.; Shao, C. Deep Learning Model for Displacement Monitoring of Super High Arch Dams Based on Measured Temperature Data. Measurement 2023, 222, 113579. [Google Scholar] [CrossRef]
- Fang, C.; Jiao, Y.; Wang, X.; Lu, T.; Gu, H. A Dam Displacement Prediction Method Based on a Model Combining Random Forest, a Convolutional Neural Network, and a Residual Attention Informer. Water 2024, 16, 3687. [Google Scholar] [CrossRef]
- Li, M.; Ren, Q.; Li, M.; Fang, X.; Xiao, L.; Li, H. A Separate Modeling Approach to Noisy Displacement Prediction of Concrete Dams via Improved Deep Learning with Frequency Division. Adv. Eng. Inform. 2024, 60, 102367. [Google Scholar] [CrossRef]
- Lee, E.; Kam, J. Deciphering the Black Box of Deep Learning for Multi-Purpose Dam Operation Modeling via Explainable Scenarios. J. Hydrol. 2023, 626, 130177. [Google Scholar] [CrossRef]
- Zhao, E.; Li, Y.; Zhang, J.; Li, Z. Interval Prediction Model of Deformation Behavior for Dam Safety during Long-Term Operation Using Bootstrap-GBDT. Struct. Control. Health Monit. 2023, 2023, 6929861. [Google Scholar] [CrossRef]
- Wang, S.; Xu, Y.; Gu, C.; Bao, T.; Xia, Q.; Hu, K. Hysteretic Effect Considered Monitoring Model for Interpreting Abnormal Deformation Behavior of Arch Dams: A Case Study. Struct. Control. Health Monit. 2019, 26, e2417. [Google Scholar] [CrossRef]
- Zhang, K.; Gu, C.; Zhu, Y.; Li, Y.; Shu, X. A Mathematical-Mechanical Hybrid Driven Approach for Determining the Deformation Monitoring Indexes of Concrete Dam. Eng. Struct. 2023, 277, 115353. [Google Scholar] [CrossRef]
- Shu, X.; Bao, T.; Li, Y.; Zhang, K.; Wu, B. Dam Safety Evaluation Based on Interval-Valued Intuitionistic Fuzzy Sets and Evidence Theory. Sensors 2020, 20, 2648. [Google Scholar] [CrossRef]
- Wu, D.; Tang, Y. An Improved Failure Mode and Effects Analysis Method Based on Uncertainty Measure in the Evidence Theory. Qual. Reliab. Eng. Int. 2020, 36, 1786–1807. [Google Scholar] [CrossRef]
- Lin, P.; Zhang, X.; Gong, L.; Lin, J.; Zhang, J.; Cheng, S. Multi-Timescale Short-Term Urban Water Demand Forecasting Based on an Improved PatchTST Model. J. Hydrol. 2025, 651, 132599. [Google Scholar] [CrossRef]
- Zhang, W.; Zhan, H.; Sun, H.; Yang, M. Probabilistic Load Forecasting for Integrated Energy Systems Based on Quantile Regression Patch Time Series Transformer. Energy Rep. 2025, 13, 303–317. [Google Scholar] [CrossRef]
- Nie, Y.; Nguyen, N.H.; Sinthong, P.; Kalagnanam, J. A Time Series Is Worth 64 Words: Long-Term Forecasting with Transformers. arXiv 2023, arXiv:2211.14730. [Google Scholar]
- Seyyedabbasi, A.; Kiani, F. Sand Cat Swarm Optimization: A Nature-Inspired Algorithm to Solve Global Optimization Problems. Eng. Comput. 2022, 39, 2627–2651. [Google Scholar] [CrossRef]
- Wu, D.; Rao, H.; Wen, C.; Jia, H.; Liu, Q.; Abualigah, L. Modified Sand Cat Swarm Optimization Algorithm for Solving Constrained Engineering Optimization Problems. Mathematics 2022, 10, 4350. [Google Scholar] [CrossRef]
- Nohara, Y.; Matsumoto, K.; Soejima, H.; Nakashima, N. Explanation of Machine Learning Models Using Shapley Additive Explanation and Application for Real Data in Hospital. Comput. Methods Programs Biomed. 2022, 214, 106584. [Google Scholar] [CrossRef]
- Kim, Y.; Kim, Y. Explainable Heat-Related Mortality with Random Forest and SHapley Additive exPlanations (SHAP) Models. Sustain. Cities Soc. 2022, 79, 103677. [Google Scholar] [CrossRef]
- Espandar, R.; Lotfi, V. Comparison of Non-Orthogonal Smeared Crack and Plasticity Models for Dynamic Analysis of Concrete Arch Dams. Comput. Struct. 2003, 81, 1461–1474. [Google Scholar] [CrossRef]
- Kang, F.; Liu, X.; Li, J. Temperature Effect Modeling in Structural Health Monitoring of Concrete Dams Using Kernel Extreme Learning Machines. Struct. Health Monit. 2020, 19, 987–1002. [Google Scholar] [CrossRef]
- Wen, Z.; Zhou, R.; Su, H. MR and Stacked GRUs Neural Network Combined Model and Its Application for Deformation Prediction of Concrete Dam. Expert Syst. Appl. 2022, 201, 117272. [Google Scholar] [CrossRef]
- Zhang, S. A Reservoir Dam Monitoring Technology Integrating Improved ABC Algorithm and SVM Algorithm. Water 2025, 17, 302. [Google Scholar] [CrossRef]
- Yang, D.; Gu, C.; Zhu, Y.; Dai, B.; Zhang, K.; Zhang, Z.; Li, B. A Concrete Dam Deformation Prediction Method Based on LSTM With Attention Mechanism. IEEE Access 2020, 8, 185177–185186. [Google Scholar] [CrossRef]
- Salazar, F.; Toledo, M.Á.; Oñate, E.; Suárez, B. Interpretation of Dam Deformation and Leakage with Boosted Regression Trees. Eng. Struct. 2016, 119, 230–251. [Google Scholar] [CrossRef]
- Zhu, Y.; Gu, C.; Zhao, E.; Song, J.; Guo, Z. Structural Safety Monitoring of High Arch Dam Using Improved ABC-BP Model. Math. Probl. Eng. 2016, 2016, 6858697.1–6858697.9. [Google Scholar] [CrossRef]
- Dai, B.; Gu, C.; Zhao, E.; Zhu, K.; Cao, W.; Qin, X. Improved Online Sequential Extreme Learning Machine for Identifying Crack Behavior in Concrete Dam. Adv. Struct. Eng. 2019, 22, 402–412. [Google Scholar] [CrossRef]
- Ren, Q.; Li, M.; Kong, R.; Shen, Y.; Du, S. A Hybrid Approach for Interval Prediction of Concrete Dam Displacements Under Uncertain Conditions. Eng. Comput. 2021, 39, 1285–1303. [Google Scholar] [CrossRef]


| Model | Hyperparameters | Initial Range | Optimal Parameter | ||
|---|---|---|---|---|---|
| PL13-1 | PL13-2 | ||||
| PatchTST | n_heads | [2, 8] | 5 | 4 | |
| d_model | [32, 256] | 128 | 128 | ||
| learning_rate | [0.0001, 0.01] | 1.12 × 10−3 | 6.45 × 10−4 | ||
| batch size | [16, 128] | 32 | 64 | ||
| SVR | C | [10−3, 103] | 128.48 | 156.39 | |
| γ | [10−3, 1] | 4.75 × 10−3 | 1.36 × 10−3 | ||
| LSTM | units | [32, 256] | 128 | 256 | |
| num_layers | [1, 3] | 2 | 2 | ||
| learning_rate | [0.0001, 0.01] | 1.23 × 10−3 | 7.12 × 10−4 | ||
| GBDT | n_estimators | [100, 1000] | 299 | 813 | |
| learning_rate | [0.01, 0.5] | 8.82 × 10−2 | 2.13 × 10−1 | ||
| max_depth | [3, 10] | 4 | 5 | ||
| subsample | [0.5, 1] | 9.73 × 10−1 | 9.38 × 10−1 | ||
| MLP | num_layers | [10, 500] | 89 | 105 | |
| learning_rate | [0.0001, 0.01] | 5.40 × 10−3 | 1.91 × 10−2 | ||
| ELM | L | [10, 500] | 351 | 216 | |
| Monitoring Points | Model | Train Set | Test Set | ||||
|---|---|---|---|---|---|---|---|
| RMSE | MAE | R2 | RMSE | MAE | R2 | ||
| PL 13-1 | MLR | 1.413 | 1.134 | 0.989 | 1.865 | 1.584 | 0.973 |
| SVR | 0.233 | 0.159 | 1.000 | 1.309 | 1.110 | 0.987 | |
| MLP | 0.201 | 0.156 | 1.000 | 0.770 | 0.637 | 0.995 | |
| GBDT | 0.248 | 0.171 | 1.000 | 0.899 | 0.630 | 0.994 | |
| ELM | 0.298 | 0.206 | 1.000 | 1.549 | 1.355 | 0.982 | |
| LSTM | 0.189 | 0.143 | 1.000 | 0.594 | 0.482 | 0.997 | |
| PatchTST | 0.174 | 0.137 | 1.000 | 0.301 | 0.251 | 0.999 | |
| PL 13-2 | MLR | 0.936 | 0.712 | 0.995 | 1.124 | 0.963 | 0.99 |
| SVR | 0.207 | 0.135 | 1.000 | 1.200 | 0.785 | 0.988 | |
| MLP | 0.189 | 0.137 | 1.000 | 0.670 | 0.558 | 0.996 | |
| GBDT | 0.171 | 0.114 | 1.000 | 0.509 | 0.402 | 0.998 | |
| ELM | 0.275 | 0.188 | 1.000 | 0.894 | 0.761 | 0.994 | |
| LSTM | 0.169 | 0.104 | 1.000 | 0.449 | 0.310 | 0.998 | |
| PatchTST | 0.154 | 0.094 | 1.000 | 0.362 | 0.245 | 0.999 | |
| Monitoring Points | Model | 90% Interval | 95% Interval | ||||
|---|---|---|---|---|---|---|---|
| MPIW | PICP | CWC | MPIW | PICP | CWC | ||
| PL 13-1 | MLR | 4.669 | 0.794 | 18.145 | 5.562 | 0.889 | 15.798 |
| SVR | 12.435 | 0.811 | 42.714 | 19.948 | 1.000 | 19.948 | |
| MLP | 5.142 | 0.967 | 5.142 | 15.365 | 1.000 | 15.365 | |
| GBDT | 4.802 | 0.689 | 44.410 | 6.157 | 0.811 | 30.848 | |
| ELM | 16.854 | 1.000 | 16.854 | 23.783 | 1.000 | 23.783 | |
| LSTM | 1.833 | 0.806 | 6.525 | 1.955 | 0.778 | 12.873 | |
| PatchTST | 1.469 | 0.994 | 1.469 | 2.758 | 1.000 | 2.758 | |
| PL 13-2 | MLR | 3.093 | 0.867 | 7.395 | 3.685 | 0.944 | 7.598 |
| SVR | 12.779 | 0.828 | 39.033 | 17.895 | 1.000 | 17.895 | |
| MLP | 8.922 | 0.833 | 26.358 | 14.971 | 1.000 | 14.971 | |
| GBDT | 3.068 | 0.278 | 1545.362 | 1.372 | 0.278 | 1141.050 | |
| ELM | 6.011 | 1.000 | 6.011 | 16.232 | 1.000 | 16.232 | |
| LSTM | 1.606 | 0.861 | 3.978 | 2.165 | 0.844 | 8.385 | |
| PatchTST | 2.035 | 0.994 | 2.035 | 2.328 | 0.961 | 2.328 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, K.; Zheng, S. An Interpretable Deep Learning Approach Integrating PatchTST, Quantile Regression, and SHAP for Dam Displacement Interval Prediction. Water 2025, 17, 1661. https://doi.org/10.3390/w17111661
Zhang K, Zheng S. An Interpretable Deep Learning Approach Integrating PatchTST, Quantile Regression, and SHAP for Dam Displacement Interval Prediction. Water. 2025; 17(11):1661. https://doi.org/10.3390/w17111661
Chicago/Turabian StyleZhang, Kang, and Sen Zheng. 2025. "An Interpretable Deep Learning Approach Integrating PatchTST, Quantile Regression, and SHAP for Dam Displacement Interval Prediction" Water 17, no. 11: 1661. https://doi.org/10.3390/w17111661
APA StyleZhang, K., & Zheng, S. (2025). An Interpretable Deep Learning Approach Integrating PatchTST, Quantile Regression, and SHAP for Dam Displacement Interval Prediction. Water, 17(11), 1661. https://doi.org/10.3390/w17111661






