Seasonal Variations of Hydraulic Exchange Between Surface Water and Groundwater in an Alluvial Plain Setting Using 222Rn
Abstract
1. Introduction
2. Data
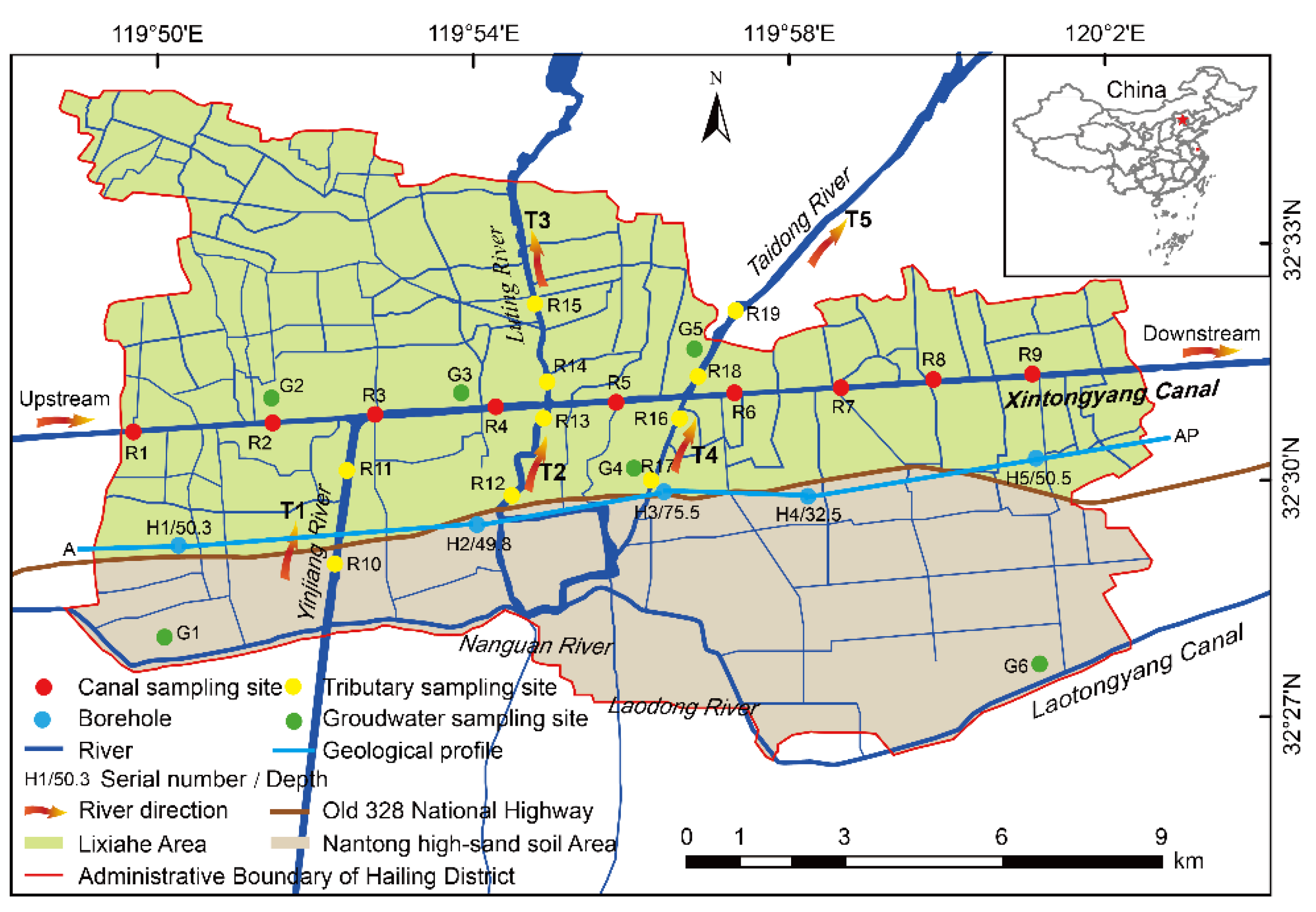
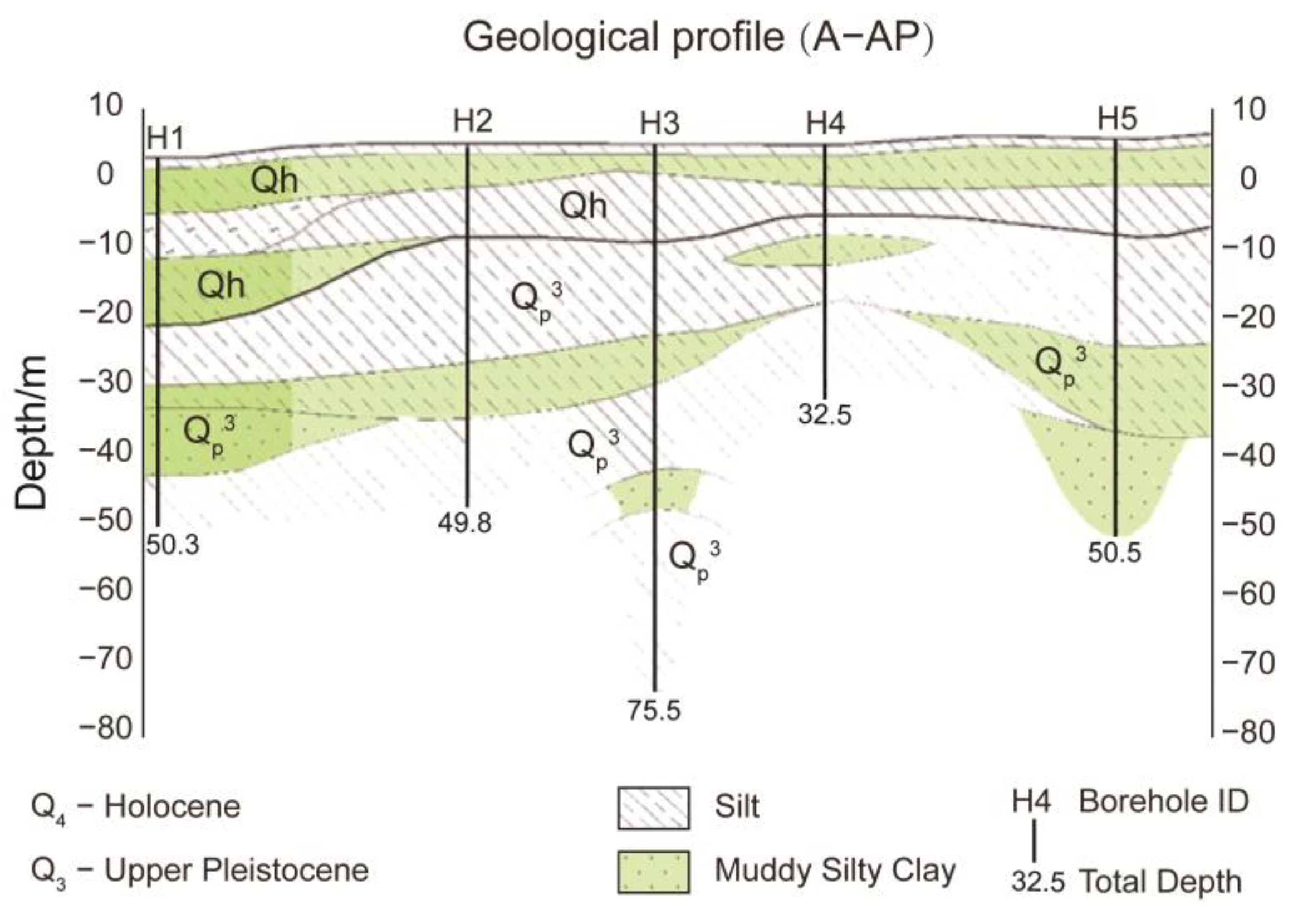
2.1. Site Description
2.2. Sampling Methodology
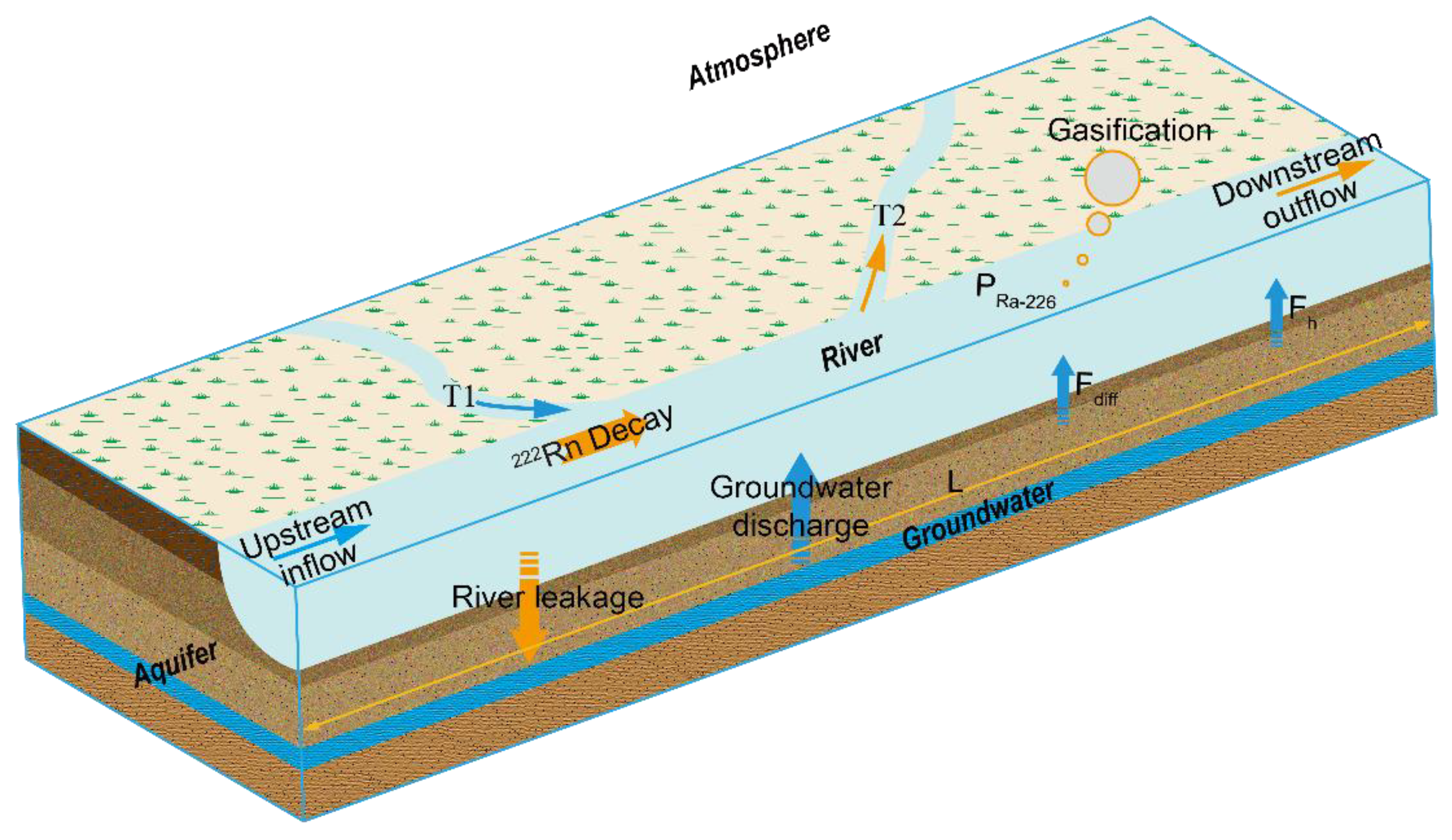
3. Modelling Methods
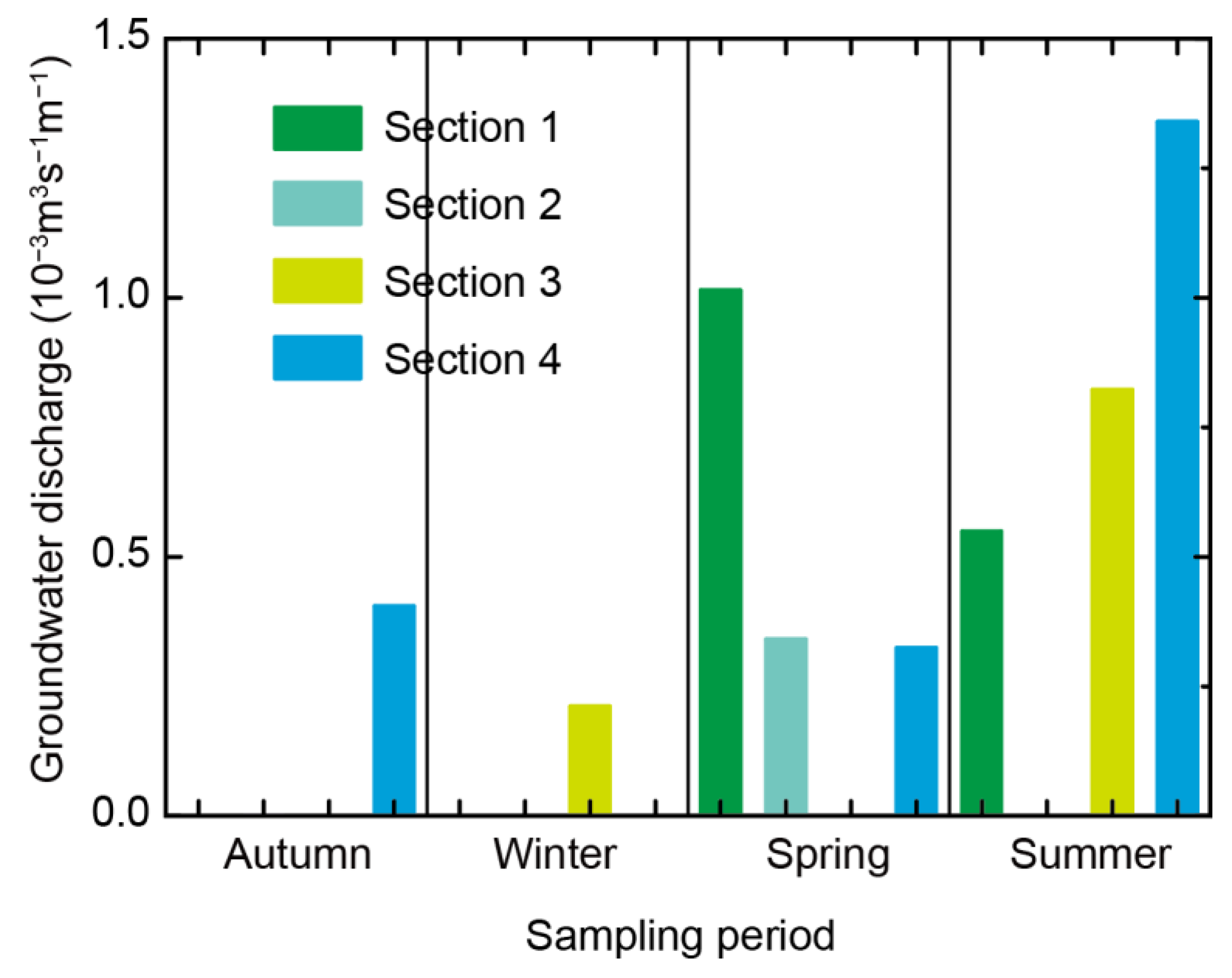
4. Results and Discussion
4.1. 222Rn Activity in the Canal and Groundwater
4.2. The Effect of Hyporheic Exchange
4.3. Estimation of Surface Water–Groundwater Interaction
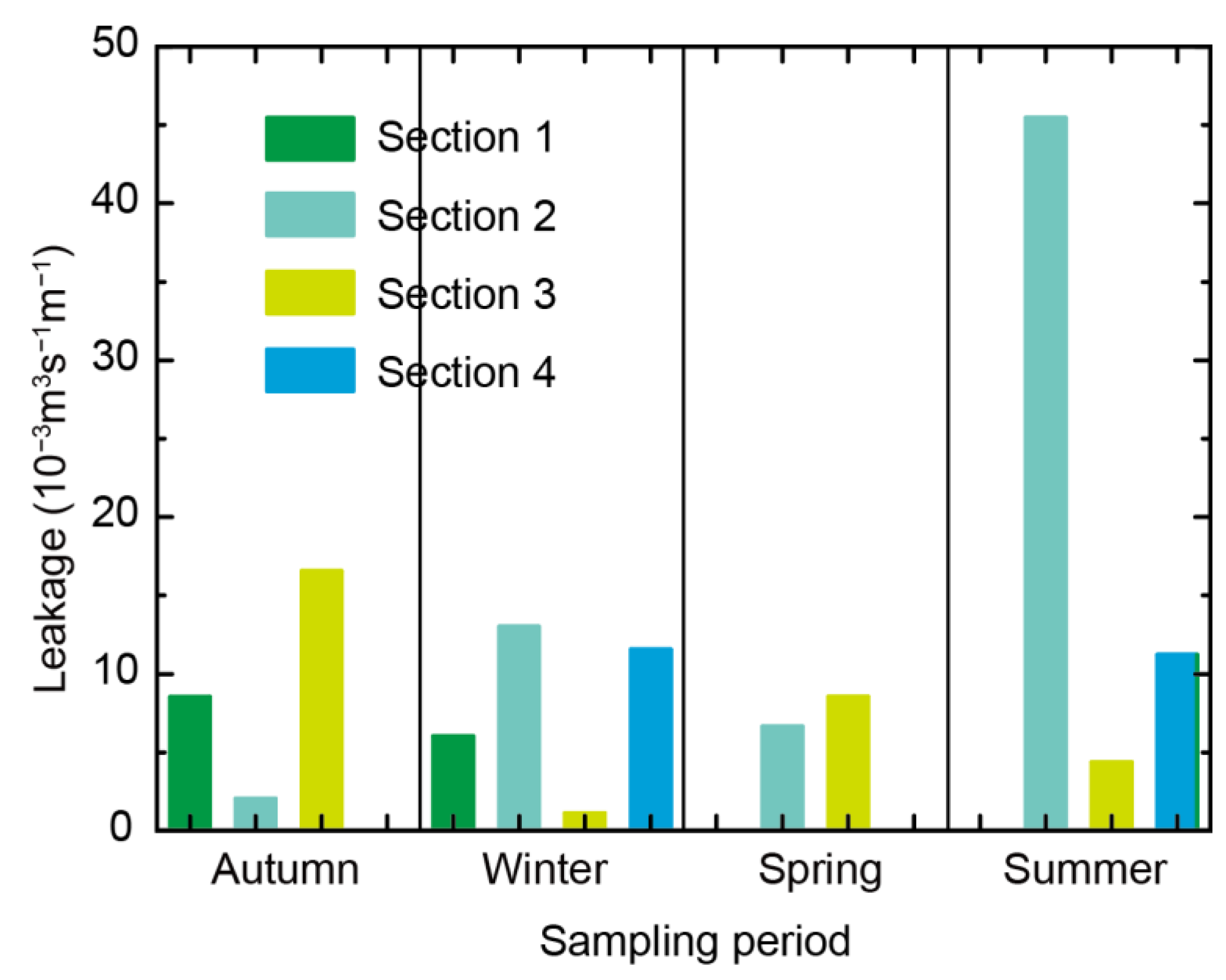
4.4. Seasonal Hydraulic Exchange Between the Canal and Groundwater
4.5. Uncertainty Evaluation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lewandowski, J.; Meinikmann, K.; Krause, S. Groundwater–Surface Water Interactions: Recent Advances and Interdisciplinary Challenges. Water 2020, 12, 296. [Google Scholar] [CrossRef]
- Shen, C.; Riley, W.J.; Smithgall, K.R.; Melack, J.M.; Fang, K. The fan of influence of streams and channel feedbacks to simulated land surface water and carbon dynamics. Water Resour. Res. 2016, 52, 880–902. [Google Scholar] [CrossRef]
- Jasechko, S.; Seybold, H.; Perrone, D.; Fan, Y.; Kirchner, J.W. Widespread potential loss of streamflow into underlying aquifers across the USA. Nature 2021, 591, 391–395. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Xu, X.; Xiang, Z.; Yang, D.; Zhang, X.; Xu, B. Distribution characteristics and influence factors of radium and radon isotopes in the lower reaches of the Yellow River. Mar. Environ. Sci. 2018, 37, 1–7. [Google Scholar]
- Luo, X.; Jiao, J.J.; Wang, X.-S.; Liu, K. Temporal 222Rn distributions to reveal groundwater discharge into desert lakes: Implication of water balance in the Badain Jaran Desert, China. J. Hydrol. 2016, 534, 87–103. [Google Scholar] [CrossRef]
- Sadat-Noori, M.; Santos, I.R.; Sanders, C.J.; Sanders, L.M.; Maher, D.T. Groundwater discharge into an estuary using spatially distributed 222Rn time series and radium isotopes. J. Hydrol. 2015, 528, 703–719. [Google Scholar] [CrossRef]
- Fleckenstein, J.H.; Krause, S.; Hannah, D.M.; Boano, F. Groundwater-surface water interactions: New methods and models to improve understanding of processes and dynamics. Adv. Water Resour. 2010, 33, 1291–1295. [Google Scholar] [CrossRef]
- Atkins, M.L.; Santos, I.R.; Ruiz-Halpern, S.; Maher, D.T. Carbon dioxide dynamics driven by groundwater discharge in a coastal floodplain creek. J. Hydrol. 2013, 493, 30–42. [Google Scholar] [CrossRef]
- Makings, U.; Santos, I.R.; Maher, D.T.; Golsby-Smith, L.; Eyre, B.D. Importance of budgets for estimating the input of groundwater-derived nutrients to an eutrophic tidal river and estuary. Estuar. Coast. Shelf Sci. 2014, 143, 65–76. [Google Scholar] [CrossRef]
- Stellato, L.; Di Rienzo, B.; Di Fusco, E.; Rubino, M.; Marzaioli, F.; Allocca, V.; Salluzzo, A.; Rimauro, J.; Romano, N. Surface water–groundwater connectivity implications on nitrate cycling assessed by means of hydrogeologic and isotopic techniques in the Alento river basin (Salerno, Italy): Preliminary data. J. Rend. Online Soc. Geol. 2016, 41, 80–83. [Google Scholar] [CrossRef]
- Harvey, J.W.; Newlin, J.T.; Krupa, S.L. Modeling decadal timescale interactions between surface water and ground water in the central Everglades, Florida, USA. J. Hydrol. 2006, 320, 400–420. [Google Scholar] [CrossRef]
- Wilcox, D.A.; Sweat, M.J.; Carlson, M.L.; Kowalski, K.P. A water-budget approach to restoring a sedge fen affected by diking and ditching. J. Hydrol. 2006, 320, 501–517. [Google Scholar] [CrossRef]
- Wolski, P.; Savenije, H.H.G. Dynamics of floodplain-island groundwater flow in the Okavango Delta, Botswana. J. Hydrol. 2006, 320, 283–301. [Google Scholar] [CrossRef]
- McBride, M.S.; Pfannkuch, H.O. Distribution of seepage within lakebeds. J. Res. U.S. Geol. Surv. 1975, 3, 505–512. [Google Scholar]
- Schiavo, M.; Riva, M.; Guadagnini, L.; Zehe, E.; Guadagnini, A. Probabilistic identification of Preferential Groundwater Networks. J. Hydrol. 2022, 610, 127906. [Google Scholar] [CrossRef]
- Kalbus, E.; Reinstorf, F.; Schirmer, M. Measuring methods for groundwater-surface water interactions: A review. Hydrol. Earth Syst. Sci. 2006, 10, 873–887. [Google Scholar] [CrossRef]
- Johnston, S.G.; Hirst, P.; Slavich, P.G.; Bush, R.T.; Aaso, T. Saturated hydraulic conductivity of sulfuric horizons in coastal floodplain acid sulfate soils: Variability and implications. Geoderma 2009, 151, 387–394. [Google Scholar] [CrossRef]
- Cey, E.E.; Rudolph, D.L.; Parkin, G.W.; Aravena, R. Quantifying groundwater discharge to a small perennial stream in southern Ontario, Canada. J. Hydrol. 1998, 210, 21–37. [Google Scholar] [CrossRef]
- Sophocleous, M. Interactions between groundwater and surface water: The state of the science. Hydrogeol. J. 2002, 10, 52–67. [Google Scholar] [CrossRef]
- Schmidt, A.; Schubert, M. Using 222Rn-222 for tracing groundwater discharge into an open-pit lignite mining lake—A case study. Isot. Environ. Health Stud. 2007, 43, 387–400. [Google Scholar] [CrossRef]
- Atkinson, A.P.; Cartwright, I.; Gilfedder, B.S.; Hofmann, H.; Unland, N.P.; Cendon, D.I.; Chisari, R. A multi-tracer approach to quantifying groundwater inflows to an upland tributory; assessing the influence of variable groundwater chemistry. Hydrol. Process. 2015, 29, 1–12. [Google Scholar] [CrossRef]
- Ortega, L.; Manzano, M.; Custodio, E.; Hornero, J.; Rodríguez-Arévalo, J. Using 222Rn to identify and quantify groundwater inflows to the Mundo River (SE Spain). Chem. Geol. 2015, 395, 67–79. [Google Scholar] [CrossRef]
- Irvine, D.J.; Singha, K.; Kurylyk, B.L.; Briggs, M.A.; Sebastian, Y.; Tait, D.R.; Helton, A.M. Groundwater-Surface water interactions research: Past trends and future directions. J. Hydrol. 2024, 644, 23. [Google Scholar] [CrossRef]
- Jing, Y.; Zhongbo, Y.; Peng, Y.; Ala, A. Assessment of groundwater quality and 222Rn distribution in the Xuzhou region, China. Environ. Monit. Assess. 2018, 190, 549. [Google Scholar]
- Dulaiova, H.; Burnett, W.C. Are groundwater inputs into river-dominated areas important? The Chao Phraya River–Gulf of Thailand. Limnol. Oceanogr. 2006, 51, 2232–2247. [Google Scholar] [CrossRef]
- Burnett, W.C.; Peterson, R.N.; Santos, I.R.; Hicks, R.W. Use of automated 222Rn measurements for rapid assessment of groundwater flow into Florida streams. J. Hydrol. 2010, 380, 298–304. [Google Scholar] [CrossRef]
- Peterson, R.N.; Santos, I.R.; Burnett, W.C. Evaluating groundwater discharge to tidal rivers based on a Rn-222 time-series approach. Estuar. Coast. Shelf Sci. 2010, 86, 165–178. [Google Scholar] [CrossRef]
- Cartwright, I.; Hofmann, H.; Sirianos, M.A.; Weaver, T.R.; Simmons, C.T. Geochemical and 222Rn constraints on baseflow to the Murray River, Australia, and timescales for the decay of low-salinity groundwater lenses. J. Hydrol. 2011, 405, 333–343. [Google Scholar] [CrossRef]
- Smerdon, B.D.; Gardner, W.P.; Harrington, G.A.; Tickell, S.J. Identifying the contribution of regional groundwater to the baseflow of a tropical river (Daly River, Australia). J. Hydrol. 2012, 464–465, 107–115. [Google Scholar] [CrossRef]
- Unland, N.P.; Cartwright, I.; Andersen, M.S.; Rau, G.C.; Reed, J.; Gilfedder, B.S.; Atkinson, A.P.; Hofmann, H. Investigating the spatio-temporal variability in groundwater and surface water interactions: A multi-technical approach. Hydrol. Earth Syst. Sci. Discuss. 2013, 10, 3795–3842. [Google Scholar]
- Frei, S.; Gilfedder, B.S. FINIFLUX: An implicit finite element model for quantification of groundwater fluxes and hyporheic. Water Resour. Res. 2015, 51, 6776–6786. [Google Scholar] [CrossRef]
- Webb, J.R.; Santos, I.R.; Robson, B.; Macdonald, B.; Jeffrey, L.; Maher, D.T. Constraining the annual groundwater contribution to the water balance of an agricultural floodplain using 222Rn: The importance of floods. Water Resour. Res. 2017, 53, 544–562. [Google Scholar] [CrossRef]
- Xie, Y.; Cook, P.G.; Shanafield, M.; Simmons, C.T.; Zheng, C. Uncertainty of natural tracer methods for quantifying river–aquifer interaction in a large river. J. Hydrol. 2016, 535, 135–147. [Google Scholar] [CrossRef]
- Yang, J.; Yu, Z.; Yi, P.; Frape, S.K.; Gong, M.; Zhang, Y. Evaluation of surface water and groundwater interactions in the upstream of Kui river and Yunlong lake, Xuzhou. J. Hydrol. 2020, 583, 124549. [Google Scholar] [CrossRef]
- Santos, I.R.; De Weys, J.; Eyre, B.D. Groundwater or floodwater? Assessing the pathways of metal exports from a coastal acid sulfate soil catchment. Environ. Sci. Technol. 2011, 45, 9641–9648. [Google Scholar] [CrossRef]
- Cook, P.G. Estimating groundwater discharge to rivers from river chemistry surveys. Hydrol. Process. 2013, 27, 3694–3707. [Google Scholar] [CrossRef]
- Zheng, M.J.; Wan, C.W.; Du, M.D.; Zhou, X.D.; Yi, P.; Aldahan, A.; Jin, H.J.; Luo, D.L.; Yu, Z.B.; Gong, M. Application of Rn-222 isotope for the interaction between surface water and groundwater in the Source Area of the Yellow River. Nord. Hydrol. 2016, 47, 1253–1262. [Google Scholar] [CrossRef]
- Anderson, A.M.; Allen, D.M.; Venditti, J.G. Sensitivity of Subsurface Permeability in Coastal Deltas to Their Morphodynamic and Geomorphic Characteristics. Water Resour. Res. 2023, 59, e2022WR034136. [Google Scholar] [CrossRef]
- Xu, Y. Experimental Investigation of Flow Characteristics in Porous Media at Low Reynolds Numbers (Re→0) under Different Constant Hydraulic Heads. Water 2019, 11, 2317. [Google Scholar] [CrossRef]
- Dimova, N.T.; Burnett, W.C.; Chanton, J.P.; Corbett, J. Application of 222Rn-222 to investigate groundwater fluxes into small shallow lakes. J. Hydrol. 2013, 486, 112–122. [Google Scholar] [CrossRef]
- Cook, P.G.; Favreau, G.; Dighton, J.C.; Tickell, S. Determining natural groundwater influx to a tropical river using radon, chlorofluorocarbons and ionic environmental tracers. J. Hydrol. 2003, 277, 74–88. [Google Scholar] [CrossRef]
- Su, X.; Xu, W.; Yang, F.; Zhu, P. Using new mass balance methods to estimate gross surface water and groundwater exchange with naturally occurring tracer 222Rn in data poor regions: A case study in northwest China. Hydrol. Process. 2015, 29, 979–990. [Google Scholar] [CrossRef]
- Yi, P.; Yang, J.; Wang, Y.; de Paul Mugwanezal, V.; Chen, L.; Aldahan, A. Detecting the leakage source of a reservoir using isotopes. J. Environ. Radioact. 2018, 187. [Google Scholar] [CrossRef] [PubMed]
- Peterson, R.N.; Burnett, W.C.; Taniguchi, M.; Chen, J.; Santos, I.R.; Ishitobi, T. 222Rn and radium isotope assessment of submarine groundwater discharge in the Yellow River delta, China. J. Geophys. Res. 2008, 113, C09021. [Google Scholar] [CrossRef]
- Schmidt, A.; Gibson, J.; Santos, I.R.; Schubert, M.; Tattrie, K.; Weiss, H. The contribution of groundwater discharge to the overall water budget of two typical Boreal lakes in Alberta/Canada estimated from a 222Rn mass balance. Hydrol. Earth Syst. Sci. 2010, 14, 79–89. [Google Scholar] [CrossRef]
- Ellins, K.E.; Roman-Mas, A.; Lee, R. Using 222 Rn to examine groundwater/surface discharge interaction in the Rio Grande de Manati, Puerto Rico. J. Hydrol. 1990, 115, 319–341. [Google Scholar] [CrossRef]
- Peng, T.H.; Takahashi, T.; Broecker, W.S. Surface 222Rn measurements in the North Pacific Ocean station Papa. J. Geophys. Res. 1974, 79, 1772–1780. [Google Scholar] [CrossRef]
- MacIntyre, S.; Wanninkhof, R.; Chanton, J.P. Trace gas exchange across the air–water interface in freshwater and coastal marine environments. In Biogenic Trace Gases: Measuring Emissions from Soil and Water; Matson, P.A., Hariss, R.C., Eds.; Blackwell Science: Hoboken, NJ, USA, 1995; pp. 52–57. [Google Scholar]
- Stellato, L.; Petrella, E.; Terrasi, F.; Belloni, P.; Belli, M.; Sansone, U.; Celico, F. Some limitations in using 222Rn to assess river–groundwater interactions: The case of Castel di Sangro alluvial plain (central Italy). Hydrogeol. J. 2008, 16, 701–712. [Google Scholar] [CrossRef]
- Corbett, D.R.; Burnett, W.C.; Cable, P.H.; Clark, S. A multiple approach to the determination of radon fluxes from sediments. J. Radioanal. Nucl. Chem. 1998, 236, 247–253. [Google Scholar] [CrossRef]
- Oh, Y.H.; Kim, G. Large seasonal changes in the recharge of seawater in a subterranean estuary revealed by a 222Rn tracer. Hydrol. Process. 2016, 30, 2525–2532. [Google Scholar] [CrossRef]
- Perrier, F.; Richon, P.; Gautam, U.; Tiwari, D.R.; Shrestha, P.; Sapkota, S.N. Seasonal variations of natural ventilation and 222Rn-222 exhalation in a slightly rising dead-end tunnel. J. Environ. Radioact. 2007, 97, 220–235. [Google Scholar] [CrossRef] [PubMed]
- Hejduk, S.; Kasprzak, K. Specific features of water infiltration into soil with different management in winter and early spring period. J. Hydrol. Hydromech. 2010, 58, 175–180. [Google Scholar] [CrossRef]
- Wang, S. Freezing Temperature Controls Winter Water Discharge for Cold Region Watershed. Water Resour. Res. 2019, 55, 10479–10493. [Google Scholar] [CrossRef]




| 222Rn (Bq/m3) | ±σ | 222Rn (Bq/m3) | ±σ | 222Rn (Bq/m3) | ±σ | 222Rn (Bq/m3) | ±σ | ||
|---|---|---|---|---|---|---|---|---|---|
| Seasons | Autumn | Winter | Spring | Summer | |||||
| Location | |||||||||
| R1 | 2039 | 271 | 2157 | 352 | 2255 | 340 | 745 | 216 | |
| R2 | 430 | 75 | 2521 | 740 | 2118 | 240 | 2366 | 270 | |
| R3 | 1287 | 213 | 2049 | 226 | 3435 | 416 | 1381 | 315 | |
| R4 | 1755 | 376 | 1833 | 440 | 2250 | 540 | 681 | 240 | |
| R5 | 1696 | 256 | 1386 | 237 | 3384 | 492 | 265.1 | 48 | |
| R6 | 415 | 75 | 1484 | 410 | 2574 | 360 | 1731 | 410 | |
| R7 | 429 | 114 | 1741 | 537 | 1714 | 430 | 1837 | 282 | |
| R8 | 1246 | 166 | 291 | 102 | 1660 | 402 | 2166 | 402 | |
| R9 | 2140 | 393 | 898 | 313 | 3265 | 413 | 2626 | 413 | |
| R10 | 2425 | 693 | 2013 | 440 | 919 | 240 | 1536 | 440 | |
| R11 | 1399 | 372 | 1725 | 196 | 847 | 120 | 511 | 144 | |
| R12 | 2399 | 792 | 1725 | 340 | 847 | 310 | 511 | 190 | |
| R13 | 1740 | 536 | 2356 | 438 | 2029 | 556 | 1385 | 198 | |
| R14 | 429 | 147 | 1890 | 295 | 2162 | 512 | 307 | 86 | |
| R15 | 862 | 278 | 875 | 169 | 2593 | 769 | 586 | 169 | |
| R16 | 1282 | 221 | 1700 | 455 | 3350 | 676 | 2789 | 327 | |
| R17 | 418 | 102 | 2912 | 540 | 2211 | 540 | 286 | 90 | |
| R18 | 874 | 246 | 1430 | 238 | 2368 | 403 | 1898 | 210 | |
| R19 | 847 | 263 | 2335 | 610 | 2982 | 610 | 260 | 90 | |
| G1 | 36,155 | 2005 | 14,530 | 1241 | 34,825 | 2480 | 12,789 | 2239 | |
| G2 | 31,684 | 3398 | 21,207 | 2275 | 45,985 | 2341 | 16,827 | 1766 | |
| G3 | 27,755 | 1969 | 15,202 | 1240 | 37,620 | 2430 | 12,983 | 949 | |
| G4 | 30,447 | 2456 | 20,683 | 1422 | 45,339 | 2426 | 11,366 | 966 | |
| G5 | 29,122 | 2609 | 19,892 | 1576 | 45,794 | 2554 | 15,632 | 1711 | |
| G6 | 29,651 | 1592 | 17,512 | 669 | 38,912 | 2701 | 19,092 | 1488 | |
| No. | Date | Distance | Width | Depth | T | Velocity | Flux | 222Rn | ±σ |
|---|---|---|---|---|---|---|---|---|---|
| (m) | (m) | (m) | (°C) | (m/s) | (m3/s) | (Bq/m3) | |||
| R1 | t1 | 0 | 100 | 4.06 | 28.6 | 0.05 | 20.30 | 2039 | 271 |
| R3 | t1 | 4650 | 120 | 6.24 | 28.8 | 0.08 | 59.90 | 1287 | 213 |
| R5 | t1 | 9160 | 115 | 5.51 | 28.8 | 0.08 | 50.69 | 1696 | 256 |
| R7 | t1 | 14,050 | 84 | 5 | 27.8 | 0.05 | 21.00 | 429 | 114 |
| R9 | t1 | 17,570 | 87 | 4.35 | 28.3 | 0.06 | 22.71 | 2140 | 393 |
| R11 | t1 | 4262 | 120 | 4.85 | 28.1 | 0.12 | 69.77 | 1399 | 372 |
| R13 | t1 | 7980 | 76 | 4.63 | 30 | 0.09 | 31.68 | 1740 | 536 |
| R14 | t1 | 7980 | 92 | 4.75 | 27.2 | 0.08 | 34.94 | 429 | 147 |
| R16 | t1 | 10,611 | 66 | 4.5 | 27.1 | 0.15 | 44.55 | 1282 | 221 |
| R18 | t1 | 10,611 | 60 | 4.21 | 27 | 0.08 | 20.20 | 874 | 246 |
| R1 | t2 | 0 | 100 | 4.06 | 6.1 | 0.07 | 28.42 | 2157 | 352 |
| R3 | t2 | 4650 | 120 | 6.24 | 6.7 | 0.12 | 89.86 | 2049 | 226 |
| R5 | t2 | 9160 | 115 | 5.51 | 7.1 | 0.08 | 50.69 | 1386 | 237 |
| R7 | t2 | 14,050 | 84 | 5 | 7 | 0.11 | 46.20 | 1741 | 537 |
| R9 | t2 | 17,570 | 87 | 4.35 | 7 | 0.02 | 7.57 | 898 | 313 |
| R11 | t2 | 4262 | 120 | 4.85 | 8.4 | 0.17 | 96.90 | 1725 | 196 |
| R13 | t2 | 7980 | 76 | 4.63 | 7.2 | 0.08 | 28.16 | 2356 | 438 |
| R14 | t2 | 7980 | 92 | 4.75 | 7 | 0.09 | 39.31 | 1890 | 295 |
| R16 | t2 | 10,611 | 66 | 4.5 | 7 | 0.12 | 35.64 | 1700 | 455 |
| R18 | t2 | 10,611 | 60 | 4.21 | 7.4 | 0.14 | 36.07 | 1430 | 238 |
| R1 | t3 | 0 | 100 | 4.06 | 15.7 | 0.07 | 28.42 | 2255 | 340 |
| R3 | t3 | 4650 | 120 | 6.24 | 13.3 | 0.11 | 82.37 | 3435 | 416 |
| R5 | t3 | 9160 | 115 | 5.51 | 14.7 | 0.085 | 53.86 | 3384 | 492 |
| R7 | t3 | 14,050 | 84 | 5 | 16.1 | 0.05 | 21.00 | 1714 | 430 |
| R9 | t3 | 17,570 | 87 | 4.35 | 15.8 | 0.06 | 22.71 | 3265 | 413 |
| R11 | t3 | 4262 | 120 | 4.85 | 15 | 0.08 | 46.51 | 847 | 120 |
| R13 | t3 | 7980 | 76 | 4.63 | 14.9 | 0.13 | 45.76 | 2029 | 556 |
| R14 | t3 | 7980 | 92 | 4.75 | 15.2 | 0.1 | 43.68 | 2162 | 512 |
| R16 | t3 | 10,611 | 66 | 4.5 | 16.4 | 0.04 | 11.88 | 3350 | 676 |
| R18 | t3 | 10,611 | 60 | 4.21 | 15.6 | 0.05 | 12.62 | 2368 | 403 |
| R1 | t4 | 0 | 100 | 4.06 | 27.4 | 0.16 | 64.96 | 745 | 216 |
| R3 | t4 | 4650 | 120 | 6.24 | 27 | 0.12 | 89.86 | 1381 | 315 |
| R5 | t4 | 9160 | 115 | 5.51 | 27.6 | 0.16 | 101.38 | 265.1 | 48 |
| R7 | t4 | 14,050 | 84 | 5 | 28.4 | 0.2 | 84.00 | 1837 | 282 |
| R9 | t4 | 17,570 | 87 | 4.35 | 28.2 | 0.13 | 49.20 | 2626 | 413 |
| R11 | t4 | 4262 | 120 | 4.85 | 27.5 | 0.125 | 72.68 | 511 | 144 |
| R13 | t4 | 7980 | 76 | 4.63 | 27 | 0.32 | 112.63 | 1385 | 198 |
| R14 | t4 | 7980 | 92 | 4.75 | 27 | 0.11 | 48.05 | 307 | 86 |
| R16 | t4 | 10,611 | 66 | 4.5 | 28 | 0.16 | 47.52 | 2789 | 327 |
| R18 | t4 | 10,611 | 60 | 4.21 | 27.6 | 0.17 | 42.08 | 1898 | 210 |
| Sampling Period | Section | Canal Tract | Calculation by Radon Mass Balance | Calculation by Flow Balance | ||||
|---|---|---|---|---|---|---|---|---|
| qr (10−3·m3/ (s·m)) | qg (10−3·m3/(s·m)) | Interaction Processes | qr (10−3·m3/ (s·m)) | qg (10−3·m3/(s·m)) | Interaction Processes | |||
| autumn | 1 | R1–R3 | 8.5 | 0.0 | (a) | 6.5 | 0.0 | (a) |
| 2 | R3–R5 | 2.0 | 0.0 | (a) | 1.3 | 0.0 | (a) | |
| 3 | R5–R7 | 16.5 | 0.0 | (a) | 11.1 | 0.0 | (a) | |
| 4 | R7–R9 | 0.0 | 0.4 | (b) | 0.0 | 0.5 | (b) | |
| winter | 1 | R1–R3 | 6.0 | 0.0 | (a) | 7.6 | 0.0 | (a) |
| 2 | R3–R5 | 13.0 | 0.0 | (a) | 6.2 | 0.0 | (a) | |
| 3 | R5–R7 | 1.1 | 0.2 | (a)/(b) | 0.8 | 0.0 | (a) | |
| 4 | R7–R9 | 11.6 | 0.0 | (a) | 11.0 | 0.0 | (a) | |
| spring | 1 | R1–R3 | 0.0 | 1.0 | (b) | 0.0 | 1.6 | (b) |
| 2 | R3–R5 | 6.7 | 0.3 | (a)/(b) | 6.8 | 0.0 | (a) | |
| 3 | R5–R7 | 8.6 | 0.0 | (a) | 6.6 | 0.0 | (a) | |
| 4 | R7–R9 | 0.0 | 0.3 | (b) | 0.0 | 0.5 | (b) | |
| summer | 1 | R1–R3 | 0.0 | 0.5 | (b) | 10.3 | 0.0 | (a) |
| 2 | R3–R5 | 45.5 | 0.0 | (a) | 11.8 | 0.0 | (a) | |
| 3 | R5–R7 | 4.4 | 0.8 | (a)/(b) | 4.7 | 0.0 | (a) | |
| 4 | R7–R9 | 11.2 | 1.3 | (a)/(b) | 9.9 | 0.0 | (a) | |
| 222Rn Samples for Surface Water | 222Rn Samples for Groundwater | “Background” 222Rn | Hydraulic Exchange Flux |
|---|---|---|---|
| 11–34.8% | 3.8–17.5% | 20% | 4–39% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, J.; Li, M.; Wang, R.; Shen, T.; Liu, M.; Yang, L. Seasonal Variations of Hydraulic Exchange Between Surface Water and Groundwater in an Alluvial Plain Setting Using 222Rn. Water 2025, 17, 1639. https://doi.org/10.3390/w17111639
Yang J, Li M, Wang R, Shen T, Liu M, Yang L. Seasonal Variations of Hydraulic Exchange Between Surface Water and Groundwater in an Alluvial Plain Setting Using 222Rn. Water. 2025; 17(11):1639. https://doi.org/10.3390/w17111639
Chicago/Turabian StyleYang, Jing, Minjuan Li, Rui Wang, Tongqing Shen, Mingjun Liu, and Libin Yang. 2025. "Seasonal Variations of Hydraulic Exchange Between Surface Water and Groundwater in an Alluvial Plain Setting Using 222Rn" Water 17, no. 11: 1639. https://doi.org/10.3390/w17111639
APA StyleYang, J., Li, M., Wang, R., Shen, T., Liu, M., & Yang, L. (2025). Seasonal Variations of Hydraulic Exchange Between Surface Water and Groundwater in an Alluvial Plain Setting Using 222Rn. Water, 17(11), 1639. https://doi.org/10.3390/w17111639






